In silico design of additively manufacturable composite synthetic vascular conduits and grafts with tuneable compliance
Oisín
Byrne
 ab,
Fergal
Coulter
ab,
Fergal
Coulter
 ac,
Ellen T.
Roche
ac,
Ellen T.
Roche
 de and
Eoin D.
O'Cearbhaill
de and
Eoin D.
O'Cearbhaill
 *ab
*ab
aSchool of Mechanical and Materials Engineering, UCD Centre for Biomedical Engineering, University College Dublin, Belfield, Ireland
bCÚRAM, the SFI Research Centre for Medical Devices, Ireland
cComplex Materials, Department of Materials, ETH Zurich, Zurich, Switzerland
dDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA
eInstitute for Medical Engineering and Science, Massachusetts Institute of Technology, Cambridge, MA, USA
First published on 9th March 2021
Abstract
Benchtop testing of endovascular medical devices under accurately simulated physiological conditions is a critical part of device evaluation prior to clinical assessment. Currently, glass, acrylic and silicone vascular models are predominantly used as anatomical simulator test beds for in vitro testing. However, most current models lack the ability to mimic the non-linear radial compliance of native vessels and are typically limited to being compliance-matched at a single mean pressure comparison point or not at all. Hence, a degree of caution needs to be shown when analysing results from such models under simulated physiological or pathophysiological conditions. Similarly, the clinical translation of proposed biomimetic compliance-matched vascular grafts has undoubtedly been curtailed due to performance and material limitations. Here, we propose a new design for synthetic vessels where compliance can be precisely modulated across a wide physiological pressure range by customising design parameters. Building on previously demonstrated methods of 3D printing composite compliant cylindrical structures, we demonstrate proof of principle in creating composite vascular constructs designed via a finite element model. Our constructs are 3D printable and consist of a soft silicone matrix with embedded polyurethane fibres. The fibre layer consists of circumferential sinusoidal waves with an amplitude that can be altered to result in tuneable internal radial compliances of 5.2–15.9%/mmHg × 10−2 at a mean pressure of 100 mmHg. Importantly, the design presented here allows preservation of the non-linear exponentially decaying compliance curve of native arteries and veins with an increasing mean pressure. This model offers a design toolbox for 3D printable vascular models that offer biomimetic compliance. The robust nature of this model will lead to rapidly accelerating the design process for biomimetic vascular anatomical simulators, lumped parameter model flow loops, endovascular device benchtop testbeds, and compliance-matched synthetic grafts.
Introduction
There is a need for more biomimetic synthetic vascular conduits that facilitate more accurate benchtop assessment of endoluminal devices, but also for the design of the next generation of vascular grafts. Whilst modulating design parameters such as wall thickness and Young's modulus offers a means of controlling compliance at a single mean pressure point, e.g. 100 mmHg, biological tissue behaves in a non-linear fashion over a wide strain range. There remains a need for methods to produce synthetic models with tissue-like compliance for a range of benchtop testing and clinical applications. The necessity for compliance-matching of synthetic grafts to the host artery has been well documented with respect to vascular prostheses and remains a significant challenge to the field.1–4 Currently used synthetic prostheses (Dacron, ePTFE) offer a constant low compliance response resulting from designs that meet competing requirements (burst strength, fatigue resistance, kink radius, suture retention) which compromise on compliance characteristics. The same challenge exists for synthetic benchtop models and compliance and burst strength properties are often inversely related.Synthetic vascular models are a valuable resource for in vitro testing of medical devices. They can be manufactured to specific uniform5 or non-uniform6 shapes and sizes, are low-cost,7,8 offer repeatable results and are non-perishable. Traditionally, synthetic models have been rigid.9 Glass models have been used for optical flow visualisation and particle image velocimetry measurements (PIV).10,11 With advances in rapid prototyping technology, rigid anatomical models can be fabricated using Polyjet 3D printing in combination with transparent resins such as VeroClear (Stratasys, Eden Prairie, MN).12
Compliant models made from silicone and latex materials are often used in the mechanical characterisation and durability testing of endovascular devices such as stents.13 Multi-step dip-spin coating, lost-core casting, and moulding are the predominant fabrication methods of compliant models.7,14,15 Use of the theoretical compliance formula, eqn (1) where D0 is the inner diameter, E is the Young's modulus and h is the wall thickness, allows compliance to be estimated.5,16
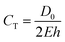 | (1) |
However, the use of a homogeneous hyperelastic material in the composition of these synthetic vessels means that they do not stiffen in a biomimetic fashion in response to increases in pressure, thus limiting the accuracy of these experimental models over a range of physiological pressures. Using constant compliance conduits could result in inaccurate conduit deformations during endoluminal device deployment and subsequently during testing. Composite synthetic vessels, such as those provided by SynDaver (Florida, USA), can more accurately simulate the physiological behaviour of blood vessels, however they are limited in customisability and to the range that is commercially available.
Silicone (with a wall thickness of 0.4–0.85 mm) is most commonly used to create compliant vessels.5 Anatomically realistic compliant arterial phantoms have been manufactured from a commercially available rubber (TangoPlus FullCure 930®, Objet Ltd, Rehovot, Israel) using PolyJet 3D printing. By varying the printed wall thickness (0.6–1.5 mm), distensibility within the physiological pressure range can be customised on a patient-specific basis.6 Ahmadzadeh et al.17 blended silicone oil by various volume fractions (0–0.73) with silicone elastomer to result in Young's moduli, E in the range (0.02–0.57 MPa) which encompasses Young's moduli of many biological tissues. Similarly, in Morris et al.,18 a patient-specific stiffness-matched (1.2 MPa) thin-walled flexible abdominal aortic aneurysm (AAA) perfusion model was created by mixing silicone oil (Dow Corning, UK) by weight (5%) with silicone elastomer. In ref. 16 and 19, the dependence of Young's modulus on the curing temperature (20–150 °C) of a common silicone, Sylgard-184 (Dow Corning, UK) was evaluated which resulted in silicones with Young's moduli in the range (1.25–2.6 MPa).
High fidelity ex vivo models, sourced from harvested tissue, have also been investigated for the purpose of evaluating endoluminal devices, such as drug-eluting stents.20 Despite the apparent benefits of ex vivo models, experimental reproducibility can be hindered by inherent biological variability,21,22 and its mechanical properties vary according to age and state – healthy or diseased.23 Young animal tissue, for example, may not match the biomechanics or calibre of the intended human target vessel.24 Tissue requires delicate dissection and closure of side branches before use, is susceptible to leaks, and has a limited lifespan unless fixed.
With the end goal of creating a tuneable compliance biomimetic synthetic model of medium-large diameter vessels, we turn to native vessels for inspiration and examine their fundamental compliance behaviour. In Fig. 1A(i), mean compliance values of native vessels within physiological pressure ranges (mean pressure 100 mmHg ± 20 mmHg) are outlined (adapted from ref. 25) to serve as targets for synthetic conduit development. In Fig. 1A(ii), characteristic compliance curves are plotted for a wide mean pressure range from 30–100 mmHg for a typical artery and vein, in contrast to stiff non-compliant synthetic grafts (adapted from ref. 1). Here, the non-linear exponentially decaying arterial compliance is evident owing to its multi-laminar heterogeneous collagen–elastin structure.2,26 At low pressures, elastin fibres (elastic modulus: 0.6–1 MPa), which account for 50% of the dry weight of major arteries, stretch giving rise to high compliance. This increase in compliance as pressure decreases is important as it will preserve pulsatile energy in cases of shock, hence flow will be preserved and optimised.27 At high pressures – greater than 120 mmHg – a portion of the collagen fibres (elastic modulus: 1 GPa) stretch to bear the load.3,28 At intermediate pressures (80–120 mmHg) corresponding to the normal in vivo operating range, i.e. the transition region, the load is successively shifted from elastin to collagen which results in a progressive and gradual decrease in compliance.3,26,28–30 The heterogeneous structure of arteries is critical to their function and therefore should be recapitulated in synthetic models. It ensures stability in vivo which protects against pathological conditions such as aneurysms and ‘blowout’ at high pressures.21 Additionally, it gives rise to features including the Windkessel effect which supports energy efficient transmission of continuous flow with minimal energy loss and dampening of pressure fluctuations.21,31
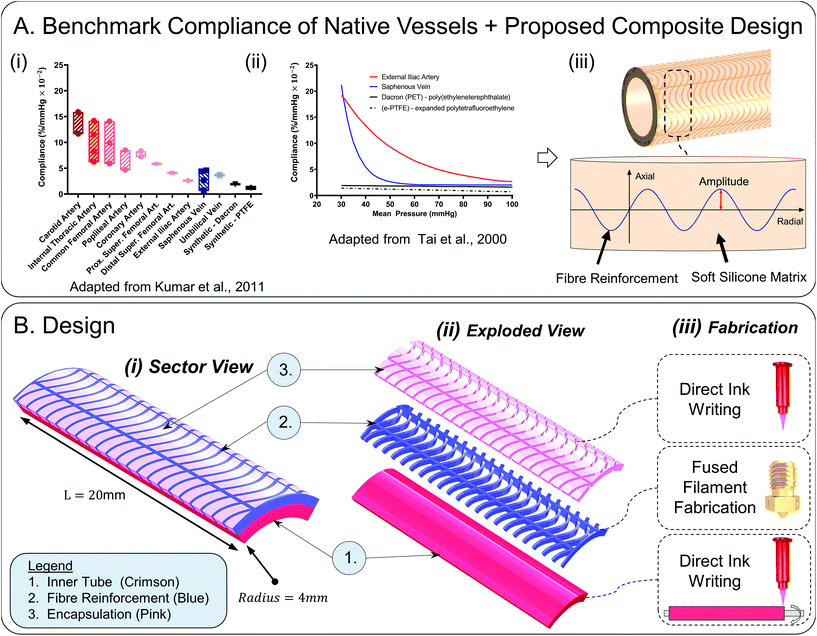 | ||
| Fig. 1 (A) Benchmark compliance of native vessels and our proposed design (i) bar chart of mean radial compliance values of common blood vessels and synthetic grafts within the physiological pressure range (approximate range: 80–120 mmHg) (adapted from Kumar et al.1,3,4,23–25,33–37). The hatched areas highlight the range of mean compliances. The mean physiological pressure about which compliance was calculated varies according to the study and is 100 mmHg ± 20 mmHg. (ii) Benchmark compliance curves of artery, vein, and current synthetic grafts on the market across a wider mean pressure range (30–100 mmHg) (adapted from Tai et al.1) the reader is referred to ref. 21 for a comparison of the compliance of diseased versus healthy young adult and healthy age, blood-pressure and sex matched adult arteries. (iii) Proposed design: 3D printable sinusoidal fibres of varying amplitude embedded in a soft silicone matrix allows compliance to be tuned. 1(B) Design (i) computer aided design of 20 mm sector of interest showing constituent layers; inner tube, reinforcing fibres, gel encapsulation layer, (ii) exploded view of constituent layers (iii) fabrication methodology: direct ink writing in combination with fused filament fabrication on a rotating mandrel substrate ref. 32. | ||
In previous work,32 we developed advanced manufacturing methods to deposit composite material elastomeric structures onto a rotating cylindrical mandrel using rotational-axis additive manufacturing (AM) techniques. The benefits of our AM methods for this application compared to other fabrication regimes include capacity to fabricate cylindrically shaped structures, precise deposition of thermoplastic and thermoset elastomeric materials of varying mechanical properties, significant design freedom where designs can be digitally customised using a parametric visual design software Grasshopper3D, and compatibility with mass-customisation and manufacturing scale-up.
We have previously shown capacity to numerically model the performance of similar composite cylindrical structures using finite element analysis (FEA),32 which was subsequently experimentally validated. In this paper, we utilise our experience in advanced material processing and numerical analysis techniques of cylindrical constructs to propose a holistic design for synthetic vascular conduits with tuneable biomimetic compliance. We use FEA as a robust engineering method to probe the design space as it is a fast method to decipher design concepts whilst allowing subsequent individual design parameter optimisation. We identify a sinusoidal fibre reinforcement of varying amplitude embedded in a soft elastomeric matrix as a design that will support the desired compliance behaviour, Fig. 1A(iii).
Materials and methods
Synthetic vessel composition and functional design
The materials used in this publication include Ecoflex™ 00-10 (shore hardness 00-10), Ecoflex™ gel (shore hardness 000-35), SmoothSil™-940 (shore hardness 40A), Sil-Poxy® glue and Platcat© cure accelerator (Smooth-On Inc., PA, USA), Filaflex® (shore hardness 82A and 95A, Recreus Industries S.L.™, Alicante, Spain).Synthetic vessels are composed of three layers, each with an important mechanical function, Fig. 1B. The inner tube (thickness: 0.8 mm) serves as an impermeable low stiffness matrix (100% modulus: 55.2 kPa) that can mimic the role of elastin in natural blood vessels. It is desirable to have a larger change in radius relative to the lower pressure radius (ΔR/R, eqn (3)) in the low mean pressure range for an initially high compliance. The stiffness of the inner tube was minimised for this purpose. A soft room temperature vulcanisation (RTV) silicone – Ecoflex 00-10 was selected for the inner layer which can be formed by direct ink writing (DIW) as described in ref. 32. The entire proposed design can be readily fabricated using the previously described additive manufacturing (AM) techniques.32
The fibre reinforcement layer (Filaflex-82A) consists of a series of repeating sine waves, Fig. 1B(ii). The governing equation of the sinewave fibres is given below (eqn (2)). The radial fibres are designed to be slack at low pressure and become taut as mean pressure is increased. In the axial direction, fibres are straight, so the design is anisotropic. The mechanical properties of the fibre material, including its elastic and bending properties, have a critical influence on compliance. A semi-flexible filament allows the fibres to gradually straighten primarily by the mode of bending when transmural pressure is increased.
| y = A·sin(F)(x − C) + S | (2) |
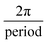 , C = circumferential shift, S = axial shift.
, C = circumferential shift, S = axial shift.
The fibre layer can be manufactured using fused filament fabrication (FFF) with a 0.15 mm bore nozzle. By optimising radial fibre width (0.2 mm) and centre spacing (0.97 mm), the inner tube will expand uniformly, and inter-fibre matrix bulging will be avoided. Other customisable parameters of the fibre layer include amplitude (0–2 mm), fibre layer thickness (0.6 mm), number of axial fibres (10), number of radial fibres (21) for a 20 mm sector, and fibre stiffness, Fig. 2(D).
The final conduit layer is the encapsulation layer which serves to ensure that the underlying layers expand and contract in unison under cyclic loading. Without encapsulation, a clearance gap could potentially arise between the inner tube and reinforcing fibres which will result in a delayed stiffening as mean pressure is increased. To minimise the stiffening effect of the encapsulation on the underlying fibres, Ecoflex Gel 000-35 was selected which bonds to the inner Ecoflex 00-10 layer.
Tensile testing
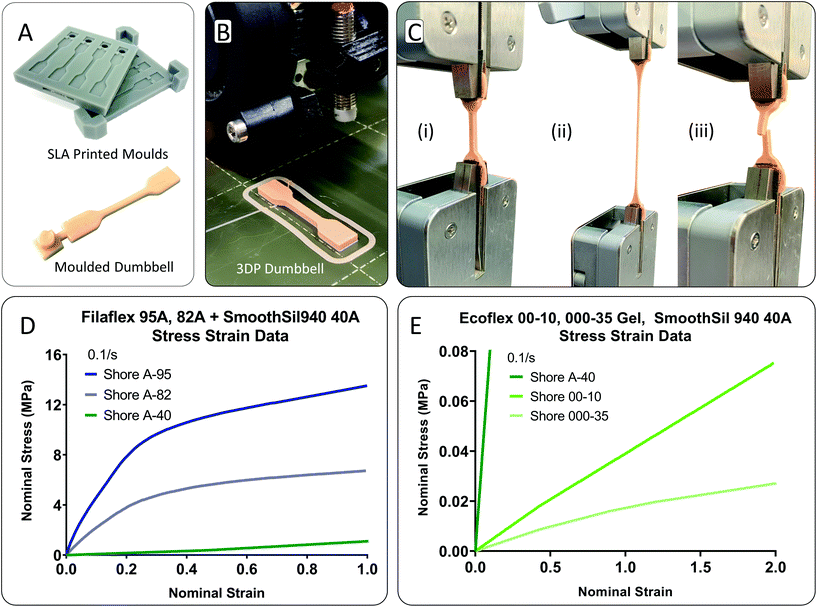
Dumbbell samples from a range of elastomeric materials were tested following test standard ISO-37 ‘rubber, vulcanized or thermoplastic—determination of tensile stress–strain properties’.33 Type 4 samples were chosen for compatibility with the width of the testing grips. Moulding was used to cast the silicone samples. Two-part moulds were 3D printed on a Form-2 SLA printer using grey resin and a Z layer height resolution of 25 μm. This resolution minimised printed part striations. To minimise seamlines along the joining of the mould, no clearance distance was incorporated between the top and bottom mould parts in CAD, Fig. 2A. Platcat© was added 4 wt% to part A of the RTV silicone to accelerate cure time. Additionally, the moulds were placed intermittently in a fan oven at 50 °C to accelerate curve. The thermoplastic dumbbell samples were directly 3D printed from filament feedstock using a PRUSA-i3 original 3D printer, Fig. 2B. Samples were printed individually to maximise interlayer adhesion. The fibre print direction was parallel to the long axis of the sample.34 Knurled nuts were used to ensure the system was tight and correctly aligned before testing. A calibrated Ametek Lloyd LS1 (loadcell: 100 N × 0.001 N resolution, 0.5% accuracy) universal tester was used for testing. To minimise sample slippage, Sil-Poxy glue in combination with sandpaper (P220 grit) was used for testing of silicone samples, Fig. 2C. Cyanoacrylate glue and sandpaper was used for testing of the thermoplastic samples. Engineering strain values were derived from the displacement of the moving crosshead, recorded from the internal encoder. Samples were preconditioned before testing to negate stress softening effects and achieve a constant representative result.35,36 Firstly, a prestress load was applied at a slow speed of 20 mm min−1. A prestress value of 0.0138 MPa was used for Ecoflex gel, 0.0150 MPa for Ecoflex 00-10, and 0.0175 MPa for SmoothSil-940. The pre-stress value for each material was determined on a trial-and-error basis by noting the smallest value needed to straighten the sample. Then, the sample was held for a short period (arbitrarily 60 s) to allow the sample to normalise and straighten fully in the grips. No hold time was used for Ecoflex gel as the material will stress relax and the feedback in the machine will correct for the stress reduction leading to a premature test of the sample due to its extremely soft nature, Fig. 2E. Then, the samples were cycled from 0 to 0.5 strain at a strain rate of 0.1 s−1 for 12 cycles, and pulled to failure at a constant strain rate of 0.1 s−1. For the Filaflex materials, samples were preconditioned to 0.15 strain. Test data in Fig. 2D and E was recorded from the final pull to failure test. Regarding failure zone, the dominant region was within the narrow portion of the sample due to the dumbbell sample shape, Fig. 2C(iii). Fig. 2D and E highlights the engineering stress–strain test results. Note the extremely low stress levels exerted by the RTV silicones in the 0–0.5 strain range and the absence of any J-shaped stiffening as strain increases.Finite element analysis
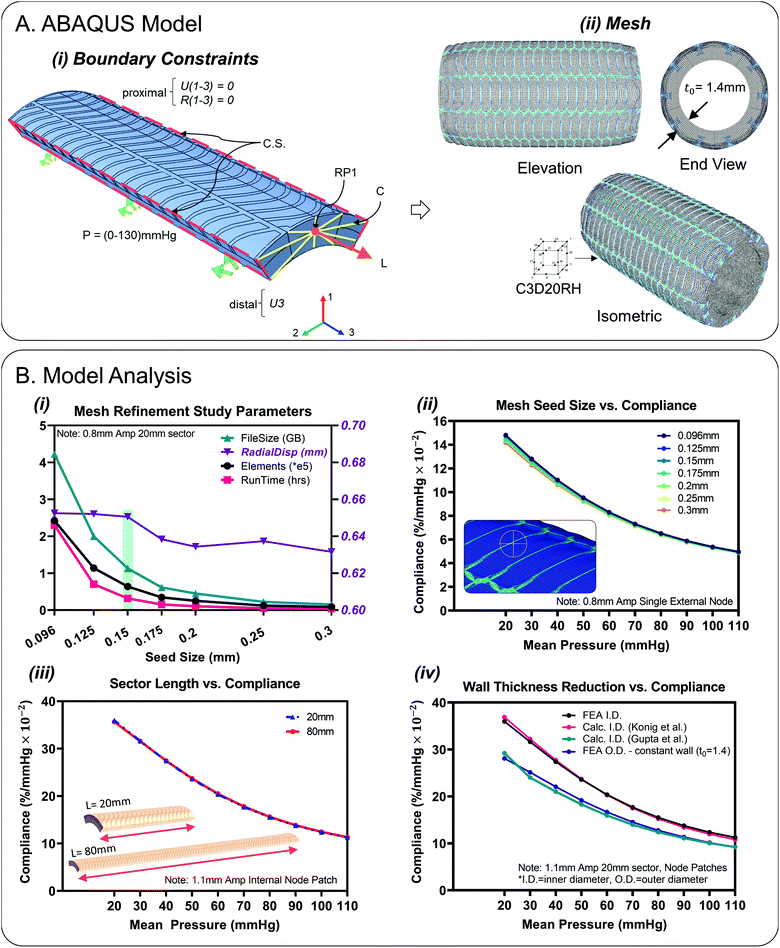
Quasi-static finite element simulations of conduit (8 mm I.D., 20 mm sector length) pressurisation up to and exceeding normal physiological ranges were performed using Abaqus CAE (V6.14-1, Dassault Systèmes®, RI, USA) in tandem with the ICHEC computational cluster.37 Cyclic symmetry was utilised and sectors of 1/5 the circumference were modelled, Fig. 3A. The single sector results could then be patterned for a 360° visualisation, Fig. 3A(ii). Each sector consisted of separate material sections that were constrained by a tie constraint. The inner tube was composed of Ecoflex 00-10 (density (ρ): 1040 kg m−3). The fibre reinforcement layer was composed of Filaflex 82A (ρ: 1120 kg m−3) and the encapsulation layer was Ecoflex gel 000-35 (ρ: 980 kg m−3). An estimated Poisson's ratio value of υ = 0.495 was applied to all materials to simulate nearly fully incompressible behaviour. Uniaxial stress strain data was inputted from tensile testing, Fig. 2(D and E). Hyperelastic strain energy density functions (SEDF) were fitted to the test data in the low strain range (0–2.0). For the mathematical formulation of these SEDF, the reader is referred to the ABAQUS handbook.38 The SEDF used for each material was selected based on stability and closeness of fit (Ecoflex 00-10: Ogden N = 1), (Filaflex 82A: Ogden N = 2), (Ecoflex gel 000-35, Filaflex 95A, SmoothSil-940: polynomial N = 2).Simulations contained of an initial, pretension and pressurisation step respectively that were solved implicitly by the general/static solver. The initial step consisted of implementation of a cyclic symmetry interaction applied to symmetry planes, Fig. 3A(i). Boundary conditions were applied to only the sector ends which would mimic experimental constraints, Fig. 3A(i). A thin (0.15 mm) end-face fibre ring was added at the ends to help apply BC's, Fig. 1B(i). The proximal sector end was encastered (U1–3 = 0, R1–3 = 0) which represented fixation to a stationary luer connector. On the distal end, only axial displacement was permitted (U3). A kinematic coupling constraint was applied between a central reference point (RP1) and coupling nodes on the distal face to simulate the application of pretension. A pretension load (of 30–60 g) is needed to keep the test conduit straight experimentally in accordance with ISO-7198 ‘cardiovascular implants and extracorporeal systems – vascular prostheses – tubular vascular grafts and vascular patches’.24,39,40 As this model is cyclic symmetric, a force of 0.0588399 N (6 g) (i.e., 1/5th of 30 g) was applied to the reference point (RP1) to simulate pretension. The third step consisted of a linearly ramped pressure load of 0–0.0173319 MPa (0–130 mmHg) uniformly applied to the lumen of the sector. Result outputs were requested at evenly spaced time intervals of 0.0769231 s i.e., 10 mmHg. Radial displacements (U1) results were transformed in terms of a locally defined cylindrical co-ordinate system for ease of post-processing.
Hybrid quadratic hexahedral elements of type reduced integration (C3D20RH) were selected for the mesh to achieve accuracy and numerical efficiency, Fig. 3A(ii). Mesh sensitivity studies were carried out which resulted in an optimum average seed size of 0.15 mm for designs including fibres with widths of 0.2 mm (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 finite elements for the 1.1 mm amplitude design), Fig. 3B(i). Beyond this refinement level, diminishing returns were observed in terms of total radial displacement discrepancy (1.9 μm) between the 0.15 mm seed size and the finer 0.096 mm seed size, Fig. 3B(i). The corresponding compliance curves as a function of seed size are illustrated in Fig. 3B(ii), based on a single reference node located on the external surface of the conduit, the position of which is fixed for successive mesh refinements. Using a 0.15 mm mesh seeding, 9 elements were observed across the wall thickness. For the composite design model, the sector length chosen was 20 mm. This length was deemed sufficient to negate boundary effects at the sector ends. No difference was observed between results for the 20 mm strip versus the full length 80 mm strip, Fig. 3B(iii). Full length (80 mm) plain silicone only models (SmoothSil-940) were also investigated for comparison purposes Fig. 5(ii).
080 finite elements for the 1.1 mm amplitude design), Fig. 3B(i). Beyond this refinement level, diminishing returns were observed in terms of total radial displacement discrepancy (1.9 μm) between the 0.15 mm seed size and the finer 0.096 mm seed size, Fig. 3B(i). The corresponding compliance curves as a function of seed size are illustrated in Fig. 3B(ii), based on a single reference node located on the external surface of the conduit, the position of which is fixed for successive mesh refinements. Using a 0.15 mm mesh seeding, 9 elements were observed across the wall thickness. For the composite design model, the sector length chosen was 20 mm. This length was deemed sufficient to negate boundary effects at the sector ends. No difference was observed between results for the 20 mm strip versus the full length 80 mm strip, Fig. 3B(iii). Full length (80 mm) plain silicone only models (SmoothSil-940) were also investigated for comparison purposes Fig. 5(ii).
In this paper, % radial compliance is quantified using eqn (3) below as outlined in ISO-7198. A number of metrics27,41–43 exist within the field to characterise the stiffness properties of synthetic and native vessels but % radial compliance, a structural property for a localised length of conduit was selected because the cross section of the conduits remain circular when luminal pressure is increased. Radial compliance (with units: %/100 mmHg) referred to in this paper is normalised by the conduit radius at the lower pressure (RP1) and is distinct from the standard physiological definition of total vascular compliance (ΔV/ΔP) with units (ml per mmHg).43 In eqn (3), RP2 is the inner radius at the higher pressure P2 in mmHg, and RP1 is the inner radius at the lower pressure P1.
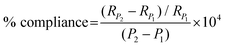 | (3) |
As the presented design is a composite, the effect of wall thickness reduction as pressure is increased is of interest for compliance calculations. Additionally, in cases where only external diameter can be measured accurately experimentally due to the limitations of experimental equipment (for example ref. 18 and 44), the following section serves to investigate various methods of approximating luminal compliances for the composite conduits in the hypothetical scenario where only external diameter can be measured. These calculated values of luminal compliance are then compared with direct internal compliance values. According to ISO-7198, inner radius may be calculated from outside diameter measurements by subtracting a constant wall thickness. Alternatively, if wall thickness changes under pressurisation, a volume-based calculation method is recommended.
Actual luminal compliance vs. calculated luminal compliance
Fig. 3B(iv) highlights inner diameter compliance results based on different wall thickness formulations for the composite design. ‘FEA I.D.’ represents compliance determined directly from internal diameter FEA displacements and is most accurate. For, ‘Calc. I.D. Konig et al.’, inner compliance was calculated indirectly by taking FEA outer diameter displacements and subtracting a calculated value for wall thickness.45 This method correlates closely with direct internal measurement. For ‘Calc. I.D. Gupta et al.’, wall thickness and subsequently inner diameter compliance was calculated assuming wall incompressibility.3,24 Wall thickness was determined from the three principal stretches and then subtracted from FEA outer diameter displacements. Note, axial stretch values were determined from FEA and were found to be constant throughout the pressurisation step (λ1 = 0.99). This formulation resulted in lower compliance than the previous two methods. Finally, for ‘FEA O.D. – constant wall (t0 = 1.4)’, i.e., the ISO-7198 standard method, compliance is calculated by subtracting a constant wall thickness across all pressures which results in a slightly lower compliances compared to direct internal measurements.Results
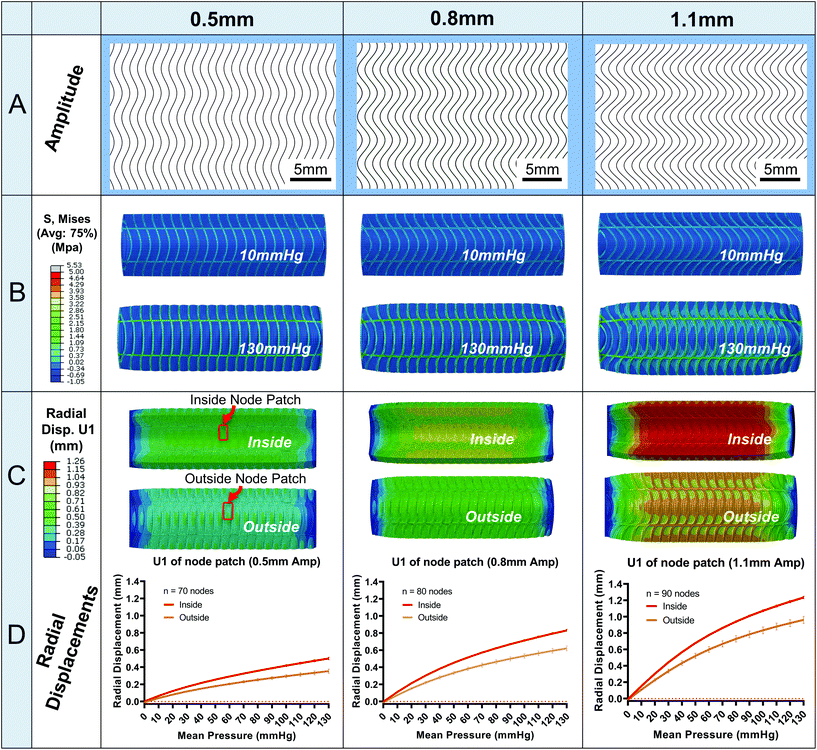
Fig. 4 illustrates the results for three sample amplitude designs (0.5, 0.8, 1.1 mm, Fig. 4A). In Fig. 4B, the Von Mises (MPa) stress contour plots are shown. The fibre layer experiences higher stress magnitudes compared to the silicone matrix at 10 mmHg up to 130 mmHg. Importantly, maximum Von Mises stress does not exceed 4 MPa for any of the designs including the 80 mm model. An exception to this can occur on the sector end faces where artificial stress concentrations may arise. Upon investigation of these few areas, they can be dismissed due to artefacts arising from localised areas of poor mesh quality.In Fig. 4C, radial displacement contours are plotted. As expected, radial displacement is higher on the luminal side (0.845 mm for the 0.8 Amp) of the conduit compared to abluminal surface (0.673 mm for the 0.8 Amp) which will give rise to higher internal compliances compared to external, Fig. 5D. The larger internal radial displacements can be attributed to slightly larger Von Mises stresses on the inside surface. Also, radial displacement is supressed on sector ends. This is due to the boundary constraints applied which are designed to mimic a full-length experimental model, i.e., attachment to luer connectors.
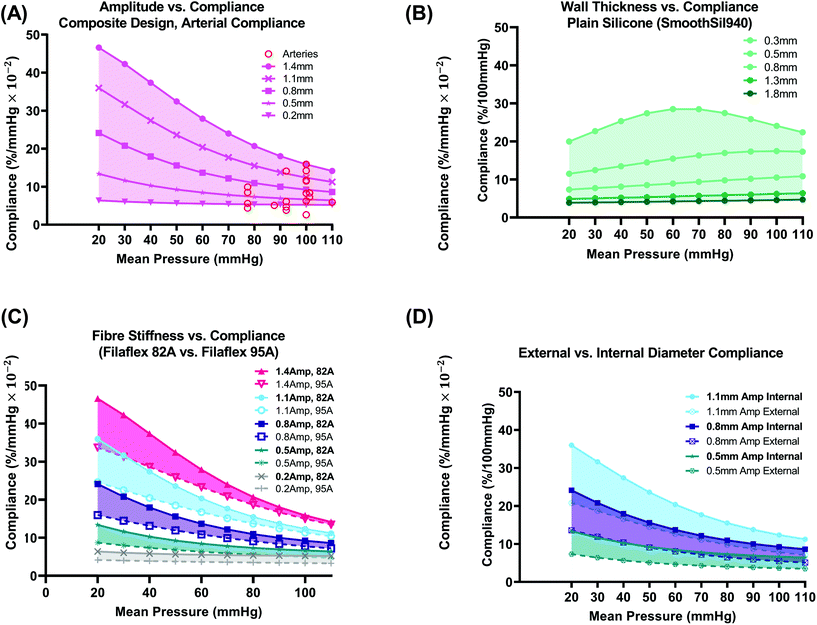 | ||
| Fig. 5 Composite design vs. plain silicone (a): varying amplitude vs. internal compliance plots for the same conduits shown in Fig. 4C (fibre material – Filaflex-82A). Arterial compliance values from the literature (red circles) that are also outlined in Fig 1A(i) are plotted for comparison. (B) Plain silicone (SmoothSil-940) varying wall thickness vs. internal compliance. (C) Fibre stiffness (82A or 95A) vs. internal compliance. (D) External vs. internal diameter compliance for three sample amplitudes (0.5, 0.8, 1.1 mm) from C. | ||
In Fig. 4D, radial displacement values are plotted (mean ± SD) for the designs illustrated in the contour plots in Fig. 4C. Displacements are from the central cell node patch located in the middle third of the conduit, Fig. 4C. The patch encompasses nodes from silicone and fibre areas for a representative result. Note, the variation in radial displacements are very small and difficult to differentiate using only contour plots. Hence, the variations are better understood by the standard deviations plotted in Fig. 4D. There is more radial displacement variation on the abluminal surface compared to the luminal surface for all amplitude designs, e.g., 0.579–0.673 mm radial displacement for the abluminal surface of 0.8 Amp versus 0.805 mm–0.845 mm for the luminal surface. Radial displacements are also initially negative at 0 mmHg because of the pretension load. For context, the preload resulted in an average axial strain of 0.79% for the 1.1 Amp design. Finally, the displacement plots are non-linear and exhibit a similar shape to human vessels in ref. 24 and 28.
Conduits (8 mm I.D.) with internal radial compliances in the range 5.24–15.87%/mmHg × 10−2 at a mean pressure of 100 mmHg can be produced simply by varying fibre amplitude (fibre material modelled as Filaflex 82A), Fig. 5(A). This range encompasses compliance values of many human arteries 2.6–15.89%/mmHg × 10−2, recorded in the literature, as outlined in Fig. 1A(i) and plotted here in Fig. 5(A)-red circles. Arterial compliance varies according to factors such as artery source and species, type, anatomical location, size, age, degree of healthiness, biological variation, and variation arising from the experimental methods used to characterise compliance.
The largest amplitude (1.4 mm) design results in the highest compliance across all mean pressures. At 20 mmHg, the 1.4 mm amplitude has a high compliance of 46.59%/mmHg × 10−2 and at 110 mmHg, it has a compliance of 14.14%/mmHg × 10−2. The 1.4 mm design also results in the greatest reduction in compliance (20.24%) compared to other amplitudes. The smallest 0.2 mm amplitude results in the lowest compliance of all designs and demonstrates an almost constant compliance response. The mean compliance across all pressures for the 0.2 mm amplitude design was 5.59%/mmHg × 10−2. This can be attributed almost solely to the stretching of the circumferential fibres due to their low amplitude. The 0.2 mm amplitude result reinforces the requirement to utilise a larger amplitude wave to ensure preservation of the non-linear exponentially decaying compliance response.
In Fig. 5(B), radial compliance is plotted for a plain silicone conduit as a function of varying the physical wall thickness (0.3, 0.5, 0.8, 1.3, 1.8 mm). The inner diameter (∅ = 8 mm) is constant for all thicknesses. This serves as a benchmark for which to compare against. The type of silicone used was SmoothSil-940. This silicone has a hardness of 40A. Silicones of similar hardness have been used as benchtop synthetic vessels.18 The sector length was 80 mm to minimise boundary effects that may arise for an unreinforced elastomer. Sector length was not investigated for the plain silicone design. Again, seed size was 0.15 mm and compliance was determined directly from luminal displacements. We see that a range of compliances 4.59–24.11%/mmHg × 10−2 can be produced at a mean pressure of 100 mmHg using wall thicknesses in the range (0.3–1.8 mm). However, the shape of the compliance curve varies and a slight rise in compliance as mean pressure is increased is visible. Additionally, a constant increase in wall thickness will not equate to a constant shift in compliance. Hence, a numerical model such as the one presented here would be beneficial in determination of the wall thickness-radial compliance relationship for plain silicone models prior to fabrication. In human arteries, compliance will vary according to pretension.24 Here, the pretension load (∼0.059 N) was constant throughout for comparison of composite and plain silicone designs respectively.
In Fig. 5(C), the effect of fibre stiffness on the compliance of the composite design was investigated. Two thermoplastic filaments were modelled, Filaflex 82A (stress: 2.23 MPa at 10% strain) and Filaflex 95A (stress: 4.67 MPa at 10% strain). By using Filaflex 95A filament, compliance can be reduced in the low to mean pressure range (20–60 mmHg) without a significant change in compliance in the high-pressure range.
In Fig. 5(D), the difference between internal and external diameter compliance is plotted. In the low-pressure range, the difference is more pronounced. At 100 mmHg, the difference for the 0.8 mm amplitude design is 3.75%/mmHg × 10−2. This difference results from differences in stress distribution between internal and external surfaces and from different material properties on internal and external surfaces.
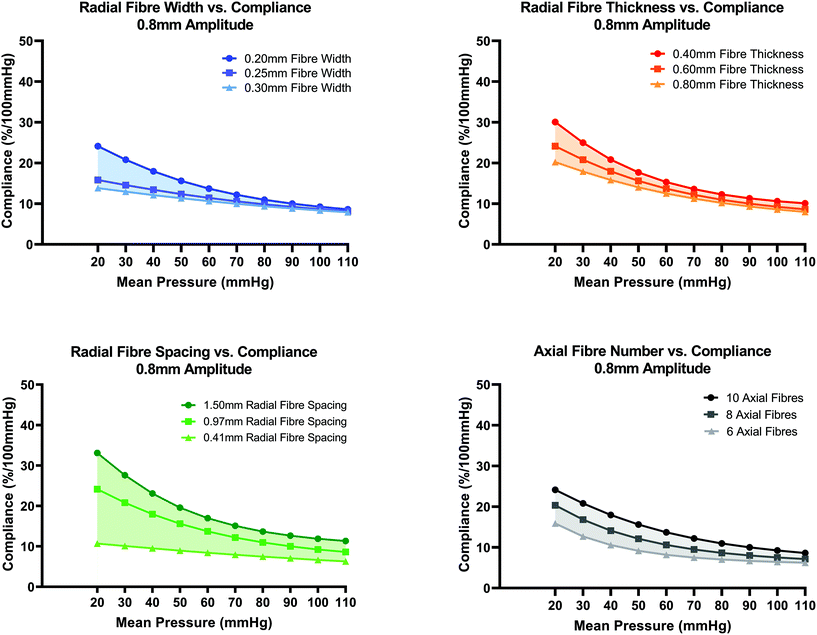
In Fig. 6(A–D), the effect of additional fibre layer design parameters namely width, thickness, radial fibre spacing distance and number of axial fibres on compliance was investigated. By increasing the fibre width from 0.2 mm to 0.25 mm or 0.3 mm, a loss of the non-linearity of the compliance curve is evident, Fig. 6(A). When fibre width is increased to 0.25 mm and 0.3 mm, compliance remains a decreasing function of increasing mean pressure but the high compliance (30.06%) of the 0.2 mm fibre width design at 20 mmHg is reduced to 24.13% and 20.22% for the 0.25 mm and 0.30 mm fibre width designs respectively. No major change to the compliance curve is evident for mean pressures in the range 80–110 mmHg. Fibre widths less than 0.2 mm were not investigated in this study due to the perceived challenge of FDM fibres below that scale.
In Fig. 6(B), increasing the fibre layer thickness results in a downward shift in the compliance curve with more noticeable influence for mean pressures in the range (20–50 mmHg) compared to pressures in the range (60–110 mmHg). This reduction in compliance with increasing thickness agrees with the theoretical compliance formulation, eqn (1). In Fig. 6(C), the effect of changing radial fibre spacing from the standard value of 0.97 mm to 0.41 mm and 1.50 mm is shown. Compliance can be tuned to a greater extent for mean pressures in the range 80–110 mmHg by varying radial fibre spacing distance compared to the previous two fibre parameters (width and thickness). Increasing radial fibre spacing to 1.5 mm results in an average increase in compliance of 4.17% for pressures in the range 20–110 mmHg. When spacing is reduced to 0.41 mm, a loss in non-linearity of the compliance curve is evident owing to the increased number of fibres present that resist the radial pressure load.
In Fig. 6(D), conduits with 6, 8 and 10 axial fibres were investigated. The cyclic symmetry constraint was updated accordingly to account for varied number of axial fibres. For the model with 8 axial fibres, a 90° quadrant sector was created, and for 6 axial fibres, a 120° sector model. Axial pretension load (N) magnitudes were increased accordingly to account for the larger area sector ends. The total axial pretension load (30 g) remained constant however. By reducing the number of axial fibres from 10 to 8 and 6, the number of radial wave peaks per 360° reduces from 10 to 8 and 6 respectively. The length of a single 360° fibre for the 8 and 6 axial fibre designs were therefore shorter in length compared to the original design with 10 axial fibres which gives rise to lower compliance for all pressures as the radial fibre wave will behave stiffer due to its shorter initial length. The general trend in Fig. 6(D) is that decreasing the number of axial fibres from 10 to 8 and 6 results in a downward shift in compliance.
Discussion and conclusion
Benchmark silicone vessels, e.g., SmoothSil-940 thick-walled cylindrical tubes, lack the ability to match the non-linear compliance of native vessels and in cases of hyper or hypotension, silicone vessels will offer a largely constant compliance response, Fig. 5(B). For a thin walled (0.3 mm) SmoothSil-940 conduit, an irregularly shaped curve is seen. An exponentially decaying compliance curve is more representative of native arteries and we have demonstrated capacity to mimic this exponentially decaying slope using an additively manufacturable composite design. Compliances in the range of 5.2–15.9%/mmHg × 10−2 at 100 mmHg can be theoretically achieved in our model for an 8 mm diameter conduit simply by varying amplitude of the stiffer, thermoplastic component.It can be observed that radial displacements are reasonably uniform on the inner surface despite the composite structure. This highlights the functional effect of the inner Ecoflex 00-10 layer in combination with adequate fibre spacing which serves to uniformly distribute the radial pressure. This is important from an applications perspective where uniformity of the endogenous surface would result in a better test bed for evaluation of endovascular devices such as stents.8 Moreover, for graft applications, a uniform I.D. radial displacement profile would be important from a hemodynamic and a remodelling perspective.
A numerical approach allows the designer to efficiently determine how individual parameters affect compliance. Here, we investigated the effect of changing fibre layer design parameters in isolation and future work could seek to investigate different combinations of fibre layer design parameters. Using our multi-directionally loaded model, one can probe internal or external compliances or quantify wall thickness. Additionally, programmable anisotropy could be introduced through incorporation of a secondary wave in the axial direction. In this work, we focussed on transverse radial compliance. By leveraging of the design freedom of rotational axis additive manufacturing, compliance could be gradated at the anastomosis zones by incorporation of different amplitude radial fibres.46 Additionally, multi-scale models can be investigated by scaling the assembly. Here, a 20 mm sector length was investigated. This length was found to be adequate to mitigate boundary effects for reinforced designs with the following configuration, 8 mm I.D., 10 axial fibres, wall thickness of 1.4 mm. Shorter sectors (length of 6 mm) were also investigated but boundary effects encroached on the central region of interest as confirmed by radial displacement contour plots. Model run time was 19 minutes for a 20 mm sector and four times more efficient than the full-length 80 mm sector.
The most immediate application of this work would be to produce synthetic vessels that match target compliance values of healthy medium-large sized human arteries. For example, the radial compliance of healthy common femoral arteries with mean diastolic diameter of 8.7 (±1.6) mm is 14.1 (±11.1)%/mmHg × 10−2, (MABP: 92.3 (±10.9)).21 Selecting a 1.1 mm amplitude design proposed here will result in a compliance of 13.77%/mmHg × 10−2 at a mean pressure of 90 mmHg which closely matches the target common femoral artery compliance. Moreover, sheep carotid artery, a commonly used pre-clinical study vessel has a compliance of 12–14%/mmHg × 10−2 which is in close approximation to that of the 1.1 mm amplitude design.47
Limitations of this FEA model include the following: the intraluminal pressure load is applied statically; however physiological pressure waveforms oscillate on average at 1.3 Hz (ref. 48) with approximately 1/3 of the cardiac cycle spent in systole and 2/3 in diastole. This may have implications from a materials perspective for elastomers that exhibit viscoelastic behaviour.17 To characterise the materials in this paper, a strain rate of 0.1 s−1 was used which has been reported previously when testing Ecoflex silicones in combination with thorough thermo-viscoelastic characterisation.35 In ref. 35, Ecoflex 00-30, a similar silicone was found to exhibit minimal strain rate dependence that occurs only above a strain of 2.0. The strain range of interest for the composite designs was approximately 0–0.5. In ref. 13 and 17, the compliance of plain silicone models was found to be minimally affected by loading frequency in the low frequency range. The use of engineering stress strain data as inputs to the model could also limit the model's accuracy.
Future work will aim to experimentally validate the proposed designs in accordance with ISO-7198. Subsequently, areas where this work could have future impact include firstly in benchtop tissue analogues for mechanical testing of medical devices. Furthermore, the proposed composite sinusoidal wave design could potentially be employed to fabricate compliance-matched synthetic grafts, e.g., coronary, peripheral, or arteriovenous fistulae. In such areas, there is currently no consensus on the optimum compliance needed before implantation and compliance may change post implantation due to tissue remodelling.27 The methods presented here would allow the fabrication of biomimetic high and low compliance grafts according to what is deemed most advantageous for specific clinical indications.
Author contributions
Oisín Byrne: conceptualization, formal analysis, investigation, methodology, software, writing – original draft; Fergal Coulter: supervision, writing – review & editing, methodology; Ellen T. Roche: supervision, resources, writing – review & editing, methodology, investigation; Eoin D. O'Cearbhaill: supervision, writing – original draft, writing – review & editing, methodology, resources, funding acquisition, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication has emanated from research supported in part by a research grant from Science Foundation Ireland (SFI) and is co-funded under the European Regional Development Fund under grant number 13/RC/2073_2. This work was also funded by a Fulbright Ireland Student Award, (https://www.fulbright.ie/).References
- N. R. Tai, H. J. Salacinski and A. Edwards, et al., Compliance properties of conduits used in vascular reconstruction, Br. J. Surg., 2000, 87, 1516–1524 CrossRef CAS PubMed.
- S. Sarkar, T. Schmitz-Rixen and G. Hamilton, et al., Achieving the ideal properties for vascular bypass grafts using a tissue engineered approach: A review, Med. Biol. Eng. Comput., 2007, 45, 327–336 CrossRef PubMed.
- B. S. Gupta and V. A. Kasyanov, Biomechanics of human common carotid artery and design of novel hybrid textile compliant vascular grafts, J. Biomed. Mater. Res., 1997, 34, 341–349 CrossRef CAS.
- R. Walden, G. J. L′italien and J. Megerman, et al., Matched Elastic Properties and Successful Arterial Grafting, Arch. Surg., 1980, 115, 1166–1169 CrossRef CAS PubMed.
- M. A. Cortez, R. Quintana and R. B. Wicker, Multi-step dip-spin coating manufacturing system for silicone cardiovascular membrane fabrication with prescribed compliance, Int. J. Adv. Manuf. Technol., 2007, 34, 667–679 CrossRef.
- G. Biglino, P. Verschueren and R. Zegels, et al., Rapid prototyping compliant arterial phantoms for in-vitro studies and device testing, J. Cardiovasc. Magn. Reson., 2013, 15, 1–7 CrossRef PubMed.
- K. L. Ruedinger, R. Medero and A. Roldán-Alzate, Fabrication of Low-Cost Patient-Specific Vascular Models for Particle Image Velocimetry, Cardiovasc. Eng. Technol., 2019, 10, 500–507 CrossRef PubMed.
- N. Kaneko, T. Mashiko and T. Ohnishi, et al., Manufacture of patient-specific vascular replicas for endovascular simulation using fast, low-cost method, Sci. Rep., 2016, 6, 1–7 CrossRef PubMed.
- K. Sugiu, J. B. Martin and B. Jean, et al., Artificial cerebral aneurysm model for medical testing, training, and research, Neurol. Med. Chir., 2003, 43, 69–72 CrossRef PubMed.
- D. A. De Zélicourt, K. Pekkan and L. Wills, et al., In vitro flow analysis of a patient-specific intraatrial total cavopulmonary connection, Ann. Thorac. Surg., 2005, 79, 2094–2102 CrossRef PubMed.
- W. E. Stehbens, G. R. Stehbens and C. J. Fee, Flow Through S–Shaped Glass Models Simulating Arterial Tortuosities, Q. J. Exp. Physiol., 1987, 72, 201–213 CrossRef CAS PubMed.
- K. I. Aycock, P. Hariharan and B. A. Craven, Particle image velocimetry measurements in an anatomical vascular model fabricated using inkjet 3D printing, Exp. Fluids, 2017, 58, 1–8 CrossRef CAS.
- R. Rajesh, E. R. Strope and K. S. Price, et al., Frequency dependent hysteresis of silicone and latex mock arteries used in stent testing, Biomed. Sci. Instrum., 2005, 41, 163–168 Search PubMed.
- K. Arcaute and R. B. Wicker, Patient-specific compliant vessel manufacturing using dip-spin coating of rapid prototyped molds, J. Manuf. Sci. Eng. Trans. ASME, 2008, 130, 0510081–05100813 Search PubMed.
- A. Sulaiman, L. Boussel and F. Taconnet, et al., In vitro non-rigid life-size model of aortic arch aneurysm for endovascular prosthesis assessment, Eur. J. Cardiothoracic Surg., 2008, 33, 53–57 CrossRef PubMed.
- P. H. Geoghegan, N. A. Buchmann and C. J. T. Spence, et al., Fabrication of rigid and flexible refractive-index-matched flow phantoms for flow visualisation and optical flow measurements, Exp. Fluids, 2012, 52, 1331–1347 CrossRef CAS.
- S. M. H. Ahmadzadeh and D. W. L. Hukins, Feasibility of using mixtures of silicone elastomers and silicone oils to model the mechanical behaviour of biological tissues, Proc. Inst. Mech. Eng., Part H, 2014, 228, 730–734 CrossRef PubMed.
- L. Morris, F. Stefanov and N. Hynes, et al., An Experimental Evaluation of Device/Arterial Wall Compliance Mismatch for Four Stent-Graft Devices and a Multi-layer Flow Modulator Device for the Treatment of Abdominal Aortic Aneurysms, Eur. J. Vasc. Endovasc. Surg., 2016, 51, 44–55, DOI:10.1016/j.ejvs.2015.07.041.
- I. D. Johnston, D. K. McCluskey and C. K. L. Tan, et al., Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering, J. Micromech. Microeng., 2014, 24, 035017 CrossRef CAS.
- B. Maurel, C. Sarraf and F. Bakir, et al., A New Hemodynamic Ex Vivo Model for Medical Devices Assessment, Ann. Vasc. Surg., 2015, 29, 1648–1655, DOI:10.1016/j.avsg.2015.06.066.
- N. R. M. Tai, A. Giudiceandrea and H. J. Salacinski, et al., In vivo femoropopliteal arterial wall compliance in subjects with and without lower limb vascular disease, J. Vasc. Surg., 1999, 30, 936–945 CrossRef CAS.
- J. O. Arndt and J. Klauske, The Diameter of the Intact Carotid Artery in Man and its Change with Pulse Pressure, Department of Physiology of the Free University of Berlin, 1968, vol. 240 Search PubMed.
- J. A. Shaw, B. A. Kingwell and A. S. Walton, et al., Determinants of coronary artery compliance in subjects with and without angiographic coronary artery disease, J. Am. Coll. Cardiol., 2002, 39, 1637–1643, DOI:10.1016/S0735-1097(02)01842-9.
- C. J. van Andel, Mechanical properties of porcine and human arteries: Implications for coronary anastomotic connectors: Invited commentary, Ann. Thorac. Surg., 2003, 76, 64–65 CrossRef.
- V. A. Kumar, L. P. Brewster and J. M. Caves, et al., Tissue Engineering of Blood Vessels: Functional Requirements, Progress, and Future Challenges, Cardiovasc. Eng. Technol., 2011, 2, 137–148 CrossRef PubMed.
- C. Singh, C. Wong and X. Wang, Medical Textiles as Vascular Implants and Their Success to Mimic Natural Arteries, J. Funct. Biomater., 2015, 6, 500–525 CrossRef CAS PubMed.
- H. J. Salacinski, S. Goldner and A. Giudiceandrea, et al., The mechanical behavior of vascular grafts: A review, J. Biomater. Appl., 2001, 15, 241–278 CrossRef CAS PubMed.
- P. B. Dobrin, Mechanical behavior of vascular smooth muscle in cylindrical segments of arteries in vitro, Ann. Biomed. Eng., 1984, 12, 497–510 CrossRef CAS PubMed.
- C. H. Lin, Y. C. Kao and Y. H. Lin, et al., A fiber-progressive-engagement model to evaluate the composition, microstructure, and nonlinear pseudoelastic behavior of porcine arteries and decellularized derivatives, Acta Biomater., 2016, 46, 101–111 CrossRef PubMed.
- R. E. Shadwick, Mechanical Design in Arteries, 1999, vol. 3313, pp. 3305–3313 Search PubMed.
- G. G. Belz, Elastic properties and Windkessel function of the human aorta, Cardiovasc. Drugs Ther., 1995, 9, 73–83 CrossRef CAS PubMed.
- O. Byrne, F. Coulter and M. Glynn, et al., Additive Manufacture of Composite Soft Pneumatic Actuators, Soft Robot., 2018, 5(6), 726–736 CrossRef PubMed.
- 2011 I 37. ISO 37 2011 Plastics—Thermomechanical, 2015, 44.
- H. K. Yap, H. Y. Ng and C. H. Yeow, High-Force Soft Printable Pneumatics for Soft Robotic Applications, Soft Robot., 2016, 3, 144–158 CrossRef.
- Z. Liao, M. Hossain and X. Yao, Ecoflex polymer of different Shore hardnesses: Experimental investigations and constitutive modelling, Mech. Mater., 2020, 144, 103366 CrossRef.
- M. A. Johnson and M. F. Beattyt, Balloon, 1995, 33, 223–245 CAS.
- Irish Centre for High-end computing (ICHEC) [Internet]. Available from: https://www.ichec.ie/.
- Corp DSS, Abaqus/CAE 6.14 User's Guide/Hyperelastic behavior of rubberlike materials, 2014 Search PubMed.
- ISO, ISO 7198 - Cardiovascular implants and extracorporeal systems—Vascular prostheses—Tubular vascular grafts and vascular patches. 2016, 2016 Search PubMed.
- G. Konig, T. N. McAllister and N. Dusserre, et al., Mechanical properties of completely autologous human tissue engineered blood vessels compared to human saphenous vein and mammary artery, Biomaterials, 2009, 30, 1542–1550 CrossRef CAS PubMed.
- R. G. Gosling and M. M. Budge, Terminology for Describing the Elastic Behavior of Arteries, Hypertension, 2003, 41, 1180–1182 CrossRef CAS PubMed.
- G. Gamble, J. Zorn and G. Sanders, et al., Estimation of arterial stiffness, compliance, and distensibility from M-mode ultrasound measurements of the common carotid artery, Stroke, 1994, 25, 11–16 CrossRef CAS PubMed . Available from: http://www.ncbi.nlm.nih.gov/pubmed/8266356.
- B. A. Haluska, L. Jeffriess and J. Brown, et al., A comparison of methods for assessing total arterial compliance, J. Hum. Hypertens., 2010, 24, 254–262 CAS.
- A. Fernández-Colino, F. Wolf and S. Rütten, et al., Small Caliber Compliant Vascular Grafts Based on Elastin-Like Recombinamers for in situ Tissue Engineering, Front. Bioeng. Biotechnol., 2019, 7, 1–13 CrossRef PubMed.
- G. Konig, T. N. McAllister and N. Dusserre, et al., Mechanical properties of completely autologous human tissue engineered blood vessels compared to human saphenous vein and mammary artery, Biomaterials, 2009, 30, 1542–1550 CrossRef CAS PubMed.
- W. Trubel, H. Schima and M. Czerny, et al., Experimental comparison of four methods of end-to-side anastomosis with expanded polytetrafluoroethylene, Br. J. Surg., 2004, 91, 159–167 CrossRef CAS PubMed.
- T. Fukunishi, C. A. Best and T. Sugiura, et al., Tissue-engineered small diameter arterial vascular grafts from cell-free nanofiber PCL/chitosan scaffolds in a sheep model, PLoS One, 2016, 11, 1–15 CrossRef PubMed.
- R. Avram, G. H. Tison and K. Aschbacher, et al., Real-world heart rate norms in the Health eHeart study, npj Digit Med., 2019, 2, 58 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2021 |