Unravelling the structural complexity and photophysical properties of adamantyl-based layered hybrid perovskites

Abstract

Layered hybrid perovskites comprising adamantyl spacer (A) cations based on the A₂FA_n−1Pb_nI_3n+1 (n = 1–3, FA = formamidinium) compositions have recently been shown to act as promising materials for photovoltaic applications. While the corresponding perovskite solar cells show performances and stabilities that are superior in comparison to other layered two-dimensional formamidinium-based perovskite solar cells, the underlying reasons for their behaviour are not well understood. We provide a comprehensive investigation of the structural and photophysical properties of this unique class of materials, which is complemented by theoretical analysis via molecular dynamics simulations and density functional theory calculations. We demonstrate the formation of well-defined structures of lower compositional representatives based on n = 1–2 formulations with (1-adamantyl)methanammonium spacer moieties, whereas higher compositional representatives (n > 2) are shown to consist of mixtures of low-dimensional phases evidenced by grazing incidence X-ray scattering. Furthermore, we reveal high photoconductivities of the corresponding hybrid perovskite materials, which is accompanied by long charge carrier lifetimes. This study thereby unravels features that are relevant for the performance of FA-based low-dimensional hybrid perovskites.

---

Introduction

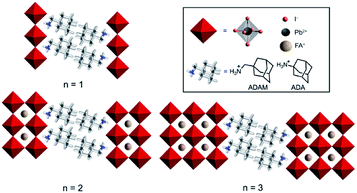
Hybrid organic–inorganic perovskite materials remain attractive for various optoelectronic applications.^1–3 Their layered two-dimensional (2D) analogues have demonstrated superior environmental stabilities.^4,5 They are predominantly based on S₂Y_n−1M_nX_3n+1 compositions, where S represents a monofunctional organic spacer cation, Y stands for the central cation (commonly methylammonium (MA), formamidinium (FA) or Cs⁺), M for a divalent metal (mainly Pb²⁺ and Sn²⁺) and X for a halide anion (I⁻, Br⁻, Cl⁻). This development has been particularly important for FA-based hybrid perovskite systems, since their perovskite phase stabilization remains challenging.^6–9 In this regard, there have been very few examples to date that involve low-dimensional perovskite systems incorporating FA as a central cation.^10–13 We have recently shown that this can be achieved by using (1-adamantyl)methanammonium (ADAM or A) as an organic spacer cation.¹³ As a result, performances of the corresponding solar cells that surpass those of the state-of-the-art FA-based two-dimensional (2D) perovskites under ambient preparation conditions were demonstrated, which could not be achieved in absence of the methylene-linker, as in the case of the 1-adamantylammonium (ADA or A′) analog.¹³ However, the underlying reasons for this behaviour have not been entirely understood, despite their importance for the structure–property relationships that are critical for guiding advanced molecular design.

Herein, we investigate the structural and photophysical properties of layered hybrid perovskites based on the A₂FA_n−1Pb_nI_3n+1 (A = ADAM) and A′₂FA_n−1Pb_nI_3n+1 (A′ = ADA) compositions (Fig. 1) by a combined methodological approach including grazing incidence wide angle X-ray scattering (GIWAXS) and time-resolved microwave photoconductivity measurements, which are complemented by molecular dynamics (MD) simulations and density functional theory (DFT) calculations. As a result, we scrutinize the phase purity of different compositional representatives and their preferred orientation, as well as the corresponding photoconductivity and charge carrier dynamics, which provide important insights for the advanced design of layered hybrid perovskite materials and their applications.

Fig. 1 Schematic representation of adamantyl-based layered hybrid perovskites based on the S₂FA_n−1Pb_nI_3n+1 (n = 1–3; S = ADAM or A, ADA or A′) composition. ADAM = (1-adamantyl)methanammonium; ADA = 1-adamantylammonium.

Results and discussion

We investigated thin films of A₂FA_n−1Pb_nI_3n+1 and A′₂FA_n−1Pb_nI_3n+1 (n = 1–3) compositions. The materials were prepared by solution deposition methods of stoichiometric amounts of the corresponding precursors (AI, A′I, FAI, and PbI₂) in accordance with the previously reported procedures.¹³ The precursors were dissolved in a (4 : 1 v/v) solvent mixture of N,N-dimethylformamide (DMF) and dimethyl sulfoxide (DMSO). The precursor solution was spin-coated on the substrates at ambient temperature, which was followed by subsequent annealing at 150 °C for 15 min. The reported compositions (n) are based on the stoichiometry of the precursors, without making assumptions about the resulting structure, and are thus referred to as nominal. We employed two different substrates in the study, either microscopic glass or fluorine doped tin oxide (FTO) coated with mp-TiO₂, which has been previously employed in photovoltaic devices.¹³ In addition, we used quartz substrates to assess the photoconductivities of materials in thin films and powders.^14,15 The powders of the perovskite materials were accessed mechanochemically by grinding the precursors in a ball mill based on previously reported procedures.^13,16–18 The methods are detailed in the Experimental section, as well as the ESI.†

Structural properties

Thin films based on A₂FA_n−1Pb_nI_3n+1 and A′₂FA_n−1Pb_nI_3n+1 (n = 1–3) compositions were investigated by using X-ray diffraction (XRD; Fig. 2) and GIWAXS (Fig. 3 and S1–S3, ESI†) for the purpose of understanding their structural properties. Their structure was previously assessed at the atomic-level by solid-state nuclear magnetic resonance (NMR) spectroscopy, suggesting the formation of new iodoplumbate phases that are likely to be associated with layered perovskites.¹³ As reported earlier, XRD patterns of A₂FA_n−1Pb_nI_3n+1 on FTO/mp-TiO₂ substrates reveal the appearance of signals in the 2θ range below 10°, which is indicative of the formation of low-dimensional hybrid perovskite structures (Fig. 2a).^19–22 This is particularly the case for films based on n = 1 compositions, showing periodic patterns that are typical for layered 2D structures (Fig. 2a).^19–22 However, A′₂FA_n−1Pb_nI_3n+1 analogues feature a number of signals in the 2θ < 10° range irrespective of their composition (n = 1–3) as a result of the formation of complex mixtures of various phases (Fig. 2b), which could correspond to intermediate phases or other low-dimensional polymorphs.¹³ Additional high resolution X-ray reflectivity (XRR) for the layered structures of A₂FA_n−1Pb_nI_3n+1 systems are shown in the ESI (Fig. S1†). XRR was used to complement the GIWAXS analysis in order to investigate the out-of-plane structure of the samples at q_xy = 0 since GIWAXS cannot access the true specular (out-of-plane) scattering due to a non-negligible q_x-component. All compositions show out-of-plane peaks that correspond to low-dimensional perovskite structures. The n = 1 nominal composition features a signal at q_z = 0.35 Å⁻¹ that corresponds to the two-dimensional n = 1 layered perovskite structure (Fig. S1, ESI†), whereas the n = 2 nominal composition reveals the formation of distinct structures characteristic for this composition. However, the XRR patterns for n > 2 nominal compositions show no clear indications of the formation of distinct phases with n = 3 or n = 4 layered perovskites. Instead, the n = 2 layered structure is still present, in addition to 3D perovskite phase and the hexagonal FAPbI₃ polytype. Intensities of the peaks corresponding to the 2D layered phase gradually decrease with the increase of the nominal concentration of the inorganic component (n) (Fig. S1, ESI†). For the n = 4 nominal composition, the n = 1 phase and the non-perovskite hexagonal phase of FAPbI₃ could be identified (Fig. S1 and Table S2, ESI†). Based on the q-value of the first strong maximum, we estimate that the n = 1 layered structure can be characterized by an interlayer spacing of d = 18.0 Å that corresponds to the long unit cell axis of the 2D structure and is in line with the layered phase stacked with perovskite slabs oriented mostly parallel to the substrate (‘face-on’; Fig. 3d, blue circle). In the sample with n = 1 nominal composition a second co-existing n = 1 polymorph phase was observed, featuring a weak, but resolvable signal at q_z = 0.38 Å⁻¹ as well as higher order reflections (Fig. S1 and Table S2, ESI†), that correspond to an interlayer spacing of 16.5 Å. This might be ascribed to another n = 1 layered polymorph featuring a slightly different orientation of the organic spacer molecule. By analysis of the dependence on the angle of incidence (i.e. penetration depth) of our GIWAXS data (Fig. S3, ESI†), we find that the second n = 1 polymorph is located predominantly close to the substrate. For n = 2 composition, GIWAXS measurements reveal that the long unit cell axis is extended, whereas the short unit cell dimensions remain similar for both n = 1 and n = 2 phases (Table S1, ESI†). This is consistent with insertion of another perovskite sheet into the unit cell of the layered structure.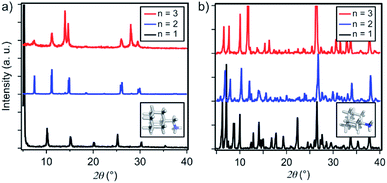

Fig. 2 Structural properties of thin films. XRD patterns of (a) A₂FA_n−1Pb_nI_3n+1 and (b) A′₂FA_n−1Pb_nI_3n+1 on FTO/mp-TiO₂ substrates for n = 1 (black), n = 2 (blue) and n = 3 (red) compositions in accordance with the previous report.¹³ Inset shows DFT-optimised (B3LYP/6-31G(d)) structures of the spacers (a) A and (b) A′.

Fig. 3 Orientation of thin films with respect to the substrate. GIWAXS reciprocal space maps for perovskite thin films at angle of incidence 0.12°, based on A₂FA_n−1Pb_nI_3n+1 formulations with nominal (a) n = 1, (b) n = 2 and (c) n = 3 compositions on FTO/mp-TiO₂ substrates. Markers denote calculated peak positions based on the structures obtained via optimizing unit cell parameters, using DFT calculations as starting values. Ring-shaped features at q-values of 1.88, 2.36 and 2.65 Å⁻¹ in the reciprocal space maps originate from the substrate (TiO₂). (d) Schematic representation of face-on/parallel (blue circle), side-on/perpendicular (red) and tilted (∼49°) (black) orientations. Markers in (c) correspond to the respective n = 2 structures depicted in (d), which were found for the sample with nominal n = 3 composition. Specific n = 3 structures could not be observed under these conditions.

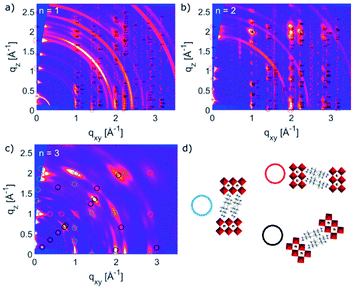
The structural complexity was further analysed by considering the presence of various orientations for different compositions with respect to the substrate, which were evaluated by GIWAXS (Fig. 3a–c and S2, ESI†).^4,5,26 The GIWAXS data for n = 1 composition show the presence of Bragg reflections that indicate a well oriented layered structure mostly parallel to the substrate (‘face-on’), as well as weak rings that correspond to randomly oriented layered structures (Fig. 3a). The system based on n = 2 composition is also well oriented ‘face-on’, as suggested by the defined spot pattern (Fig. 3b), which shows no rings that would indicate randomly oriented domains. The nominal n = 3 composition, however, shows presence of the n = 2 structure with three different preferred orientations (Fig. 3c and d).^{13,20,22–25} This complexity has been previously indicated by solid-state nuclear magnetic resonance (NMR) spectroscopy, without the capacity to clearly distinguish between the n = 2 and n > 2 structures at the atomic level by means of ¹³C, ¹⁴N or ¹⁵N NMR spectra.¹³ Moreover, n > 2 compositions also feature additional signals associated with the 3D perovskite α-FAPbI₃ and δ-FAPbI₃ phases.

To further analyse the orientation complexity of the layered structures quantitatively, we have calculated Herman's orientation parameter based on the GIWAXS angular maps, which agrees well with the qualitative description (Fig. S4, ESI†). Complex phase mixtures were also obtained for A′₂FA_n−1Pb_nI_3n+1 (n = 1–3) compositions (Fig. S2c, ESI†), which supports the previous reports.¹³ However, the additional phases cannot be directly associated with new (e.g. n = 3) structural forms. This apparent absence of the n > 2 structures under experimental conditions, which was observed for both A and A′ spacers, was evaluated by the theoretical analysis of their structural and optoelectronic properties.

Theoretical insights

Towards better understanding of the properties of A₂FA_n−1Pb_nI_3n+1 and A′₂FA_n−1Pb_nI_3n+1 (n = 1–3) perovskites, classical molecular dynamics (MD) simulations were performed in conjunction with density functional theory (DFT) calculations for different compositions (n = 1–3; for computational details refer to the Sections S3 and S4 of the ESI†). The initial structures for DFT calculations were extracted from the classical MD simulations (Fig. S5–S8, ESI†), which suggest that perovskite materials based on A and A′ spacers adopt a Ruddlesden–Popper structure at ambient temperature (298 K). Classical MD simulations at higher temperatures (>400 K) also provided some information about the thermal stability of the systems. In case of spacer A′, we find that the corner-sharing network of Pb–I octahedra slowly transforms into edge-sharing configurations upon increasing the temperature, which does not occur in the case of spacer A. This suggests that the experimentally observed structures for hybrid perovskites based on spacer A′ might be a mixture of corner and edge-sharing octahedra, which could lead to phase mixtures and unfavourable optoelectronic properties in comparison to those based on spacer A. This behaviour could be the result of the steric effects of the bulky carbocyclic backbones in the spacer layer and their interaction with the inorganic framework. Specifically, presence of the flexible methylene linker results in higher structural adaptability of the spacer A, as well as higher penetration depth into the inorganic framework, which was assumed to potentially result in templating effects.^13,16,17,27

To probe the templating role of the spacer, the structures obtained by MD simulations were subsequently optimized by performing DFT calculations, which show that a layered Ruddlesden–Popper structure is maintained, with ordered stacking of the spacers along the out-of-plane a-axis in optimized structures, whereas two different alignments with respect to c-axis occur (denoted as α; Fig. 4 and S9, ESI†). Furthermore, we compared the penetration depths of the spacers into the inorganic slabs, which were estimated by the N⋯Pb distance between the nitrogen atom of the amino group of the spacer (N) and the nearest inorganic slab (PbI₄ plane). The penetration depth into the inorganic slabs was shown to be strongly correlated with the average tilting angle between Pb–I octahedra, which in turn determines the overall structural and optoelectronic properties.^16,28,29 For A₂FA_n−1Pb_nI_3n+1 (n = 1–3) the structure gradually becomes more cubic for higher n values. This is accompanied by larger penetration depths as reflected by the N⋯Pb distances (Table S3, ESI†). On the contrary, the A′₂FA_n−1Pb_nI_3n+1 system (Table S4, ESI†) shows pronounced out-of-plane octahedral distortions (Fig. S9, ESI†), as higher penetration of the ammonium termini is counteracted by the steric requirements of the bulky adamantyl core, preventing the formation of a cubic structure. To evaluate the structural stability of the resulting layered perovskites, we also analysed the hydrogen bond lenghts between amino group nitrogens of each spacer (N) and iodide ions (I) of the same inorganic slab (N⋯I distance), which were shown to be important indicators of structural stability.^16,29,30 In principle, a more cubic inorganic slab with intra-octahedral tilting angles approaching 90° provides a larger inter-octahedral space, and consequently larger NH⋯I distances. The DFT calculations suggest that A and A′ spacers show a subtle interplay between the interactions in the organic and inorganic layers with a less pronounced templating effect of the inorganic framework towards a cubic phase as compared to spacers featuring longer alkyl-chain-anchoring groups.^16,29 This is in accordance with their bulky shape interfering with the penetration into the perovskite slabs. In this regard, the absence of the methylene group in A′ could be attributed to considerably more distorted structures of A′₂(FA)_n−1Pb_nI_3n+1 systems, even for n = 1 composition. To assess the effect of these structural features on the spacer layer, we compared the thickness of the organic spacer layer defined by the Pb⋯Pb distances between the consecutive inorganic layers (d₁) as well as the distance between the adjacent spacers (d₂) (Fig. 4b, Tables S3 and S4, ESI†). The parameters (d₁, d₂) were not found to exhibit a clear trend upon incorporating the organic spacer cation into the inorganic layer. This indicates a less pronounced templating effect of the inorganic slabs as compared to other long-alkyl-chain-containing spacers, such as 5-ammonium valeric acid (5-AVA) and n-butylammonium (BA) cations.^16,27,29

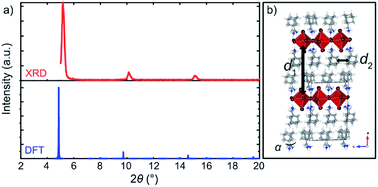Fig. 4 Structural properties of A₂PbI₄. (a) Comparison of the XRD patterns of the DFT-predicted structure (blue) of A₂PbI₄ (n = 1) with the corresponding experimental data on microscopic glass (red). (b) DFT-calculated structure indicating two characteristic distances, d₁ (interlayer distance measured by the average Pb⋯Pb distance between the adjacent inorganic slabs) and d₂ (distance between the organic spacers in the layer). For more details, refer to the ESI Section S3.†

The dynamics of the spacer molecules is further affected by the interactions with the inorganic slabs as evidenced by the 5 ps long DFT-based Born–Oppenheimer molecular dynamics simulations of A₂PbI₄ and A′₂PbI₄ as model systems, where we monitored the changes of N⋯Pb distances and out-of-plane tilting angles (Fig. S10 and S11, ESI†). Both A and A′ spacers were found to rotate freely around their central axes, with a preferred molecular orientation for the spacer A. The penetration depth is preserved throughout the finite temperature trajectory of A₂PbI₄ (Fig. S10, ESI†), which is in agreement with the higher thermal stability of this system. In contrast, for the A′-based system, a broader distribution of N⋯Pb distances is observed, in accordance with the pronounced structural distortion (Fig. S10, ESI†). Similarly, the out-of-plane octahedral angles (Fig. 4b) for A₂PbI₄ and A′₂PbI₄ compositions reveal a much broader distribution for the latter (Fig. S11, ESI†).

To validate the DFT-predicted structures, the XRD pattern was simulated for A₂PbI₄ (Fig. 4a; details are provided in the Section S4 of the ESI†). The patterns of the theoretically predicted structure for the n = 1 composition are in good agreement with the experimentally observed data, with a minor shift that can be ascribed to the different conditions under which the experiment and the simulation are performed, e.g. finite temperature effects and dispersion effects.³¹ In particular, the lowest angle peaks were found to correspond to 18.0 Å and 18.4 Å (Table S1, ESI†) inter-spacer distances in the experimental samples and the DFT-optimized fully periodic structures, respectively. This evidences that the models are in a very good agreement with experimentally obtained structures.

The absence of higher compositional representatives (n > 2) under the applied experimental conditions can be rationalized by calculating the enthalpies of formation (ΔH) for the obtained structures,²¹ which slightly increase with the increasing number of inorganic layers (n) in A₂FA_n−1Pb_nI_3n+1 systems (for details see Section S4, ESI†). Similarly, positive values of formation enthalpies for A′₂FA_n−1Pb_nI_3n+1 systems suggest low stability of their RP phases, in accordance with the experimental evidence. This could potentially be circumvented for A₂FA_n−1Pb_nI_3n+1 phases by employing smaller ions in the composition, such as Cs and Br,^10,11,32 which can stabilize the perovskite (α) phase over the non-perovskite (δ) FAPbI₃ phase, and consequently, might facilitate the observation of higher compositional representatives.^6,13

Optoelectronic properties

The effect of the structure on the electronic properties of the system was analysed by UV-vis absorption spectroscopy (Fig. 5a).¹³ UV-vis absorption spectra of A₂FA_n−1Pb_nI_3n+1 systems suggest a gradual decrease in the optical band gap (E_g) with increasing number of inorganic slabs (n),^22,26,33 along with the presence of typical excitonic features (Fig. 5a).^33–35 Moreover, the n = 1–2 compositions show well-defined spectral signals (Fig. 5a, black and blue), whereas n > 2 compositions feature multiple signals that appear to be in line with the previously reported structural complexity (Fig. 5a, red).^13,20,33 Similarly, the A′-based A′₂FA_n−1Pb_nI_3n+1 systems show higher spectral complexity for n > 1 compositions (Fig. 5b).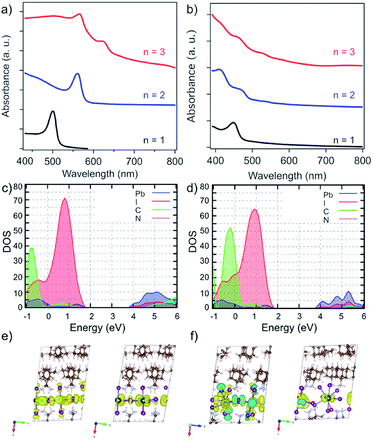

Fig. 5 Optoelectronic properties of perovskite thin films. UV-vis absorption spectra of perovskite thin films based on (a) A₂FA_n−1Pb_nI_3n+1 and (b) A′₂FA_n−1Pb_nI_3n+1 (n = 1–3) compositions on FTO/mp-TiO₂ substrates in accordance with the previous report.¹³ Calculated partial density of states for (c) A₂PbI₄ and (d) A′₂PbI₄ with (e and f) the corresponding frontier molecular orbitals (top of the valence band (left) and bottom of the conduction band (right)).

The electronic properties were calculated at PBE0 level³⁶ including spin–orbit coupling (SOC) effects for the n = 1–3 compositions of A₂FA_n−1Pb_nI_3n+1 and A′₂FA_n−1Pb_nI_3n+1 (Tables S5 and S6, ESI†). Following the expected trend, increasing the inorganic layer thickness (n) results in decreased band gaps (Table S5, ESI†). The calculated band gap of 2.83 eV for A₂PbI₄ system, in the absence of excitonic effects, exceeds the measured optical band gap by 0.43 eV, which is in accordance with the reported exciton binding energies of around 400 meV for Ruddlesden–Popper phases (Fig. 5c and Table S5, ESI†).³³ The calculated A′-based structures, however, exhibit larger band gaps as compared to their A-based counterparts, presumably as a result of the disruption of the corner-sharing Pb–I network inducing a notable gap opening (Fig. 5b and Table S6, ESI†).

To characterize the transport properties, we calculated the effective masses in the in-plane and out-of-plane directions for both A and A′-based systems (Tables S5 and S6, ESI†). Similar to the previously studied layered hybrid perovskites,^16,28,29 effective masses in the in-plane direction decrease with the increasing thickness of the inorganic perovskite layer, indicating better charge transfer consistent with lower band gaps for higher compositional representatives (n). However, large effective masses in the out-of-plane direction imply a breakdown of the band transport model, similar to other layered perovskite systems that were previously investigated, such as those based on BA and 5-AVA.²⁹ The partial density of states, as well as the frontier molecular orbitals, show no contribution from the organic part to the band edges for either A- and A′-based systems (Fig. 5c–f). In general, however, the effective masses for A′-based systems are larger than those of A-based systems in all directions, which can also be rationalized by the severely distorted structure that has been evidenced experimentally. These electronic properties directly affect the charge-carrier dynamics that is thereby hereafter investigated exclusively for the A₂FA_n−1Pb_nI_3n+1 systems.

Charge carrier dynamics

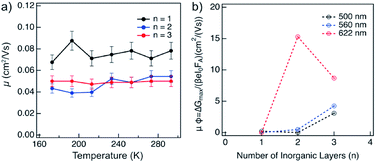
The charge carrier dynamics were studied by time-resolved microwave conductivity (TRMC) measurements using high frequency microwaves upon excitation.^14,15 Under these conditions, the change in conductivity due to generated free charge carriers is probed with high frequency microwaves. If the charge carriers are mobile, they absorb part of the incoming microwave power (ΔG_max) which is proportional to the change in conductivity of the material (Δσ).

The charge carriers in the material can be generated with either a high energy electron pulse (pulse-radiolysis TRMC) or by laser excitation (photoconductivity-TRMC). Generation by irradiation with high energy electrons allows to determine the mobility of charge carriers (μ) directly in the material prepared mechanosynthetically without considering the effect of orientation or being influenced by the exciton binding energy of the material (as is the case of photoexcited experiments).^14,15 The mobility of charge carriers was probed in layered hybrid perovskites of different A₂FA_n−1Pb_nI_3n+1 (n = 1–3) compositions, which is expected to increase with the number of inorganic layers (n).¹⁴ The mobility appears to be higher for n = 1 as compared to n = 2–3 compositions of the corresponding perovskite powders, and it is not substantially affected by temperature in the range between 180–300 K (Fig. 6a), which suggests presence of a large concentration of trap states across compositions under these conditions. The dynamics of charge carrier decays supports this hypothesis as featuring a rather fast recombination at the ns timescale (Fig. S13, ESI†). The recombination of charge carriers is not influenced by the initial charge carrier concentration (10¹⁴ to 10¹⁶ cm⁻³) at room temperature (Fig. S13, ESI†). At lower temperatures, this behaviour is consistent for n = 1 composition (Fig. 6a and S14, ESI†). However, for n = 2 and n = 3 compositions, the conductivity slightly increases after the pulse (Fig. S14 and S15, ESI†), which suggests the existence of phases with higher conductivity within the material. This agrees with the formation of different phases in n > 1 compositions. The lifetime of charge carriers increases with the number of inorganic layers from the order of hundreds of ns for n = 1 to hundreds of μs for n = 2 and n = 3 compositions (Fig. S14, ESI†), with further increase at lower temperatures (Fig. S16, ESI†).

Fig. 6 Conductivities in layered hybrid perovskite powders and thin films based on A₂FA_n−1Pb_nI_3n+1 perovskite with different compositions (n = 1–3). (a) Evolution of mobilities in powders at various temperatures and (b) conductivities in thin films deposited on quartz substrates at ambient temperature (298 K). The initial charge carrier concentration was estimated to be 10¹⁴ to 10¹⁶ cm⁻³ at 298 K.

The photoconductivity determined on thin films after laser excitation is by definition the product of charge mobility (μ) and quantum yield of free charge carrier formation (φ), based on the following eqn (1)

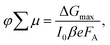where I₀ is the number of photons per unit area, β is based on the dimensions of the microwave cavity, e is the elementary charge, and F_A is the fraction of the absorbed light. As discussed, these measurements are influenced by the exciton binding energy in the material which is usually large (∼350 meV) in layered hybrid perovskites.^14,15,33

Thin films of A₂FA_n−1Pb_nI_3n+1 (n = 1–3) were photoexcited at three different wavelengths corresponding to the excitonic peaks of the different number of inorganic layers (Fig. 5a), namely 500 nm for n = 1, 560 nm for n = 2 and 622 nm for n = 3 compositions (Fig. 6b). The photoconductivity was found to increase with the number of inorganic layers, which is in agreement with reports on layered 2D perovskites in which the exciton binding energy decreases with the number of inorganic layers, increasing the yield of dissociation of charge carriers (φ).¹⁴ However, upon excitation at 622 nm, we can observe that the photoconductivity is higher for the n = 2 than for n = 3 compositions, which is likely the result of higher phase purity and better orientation of the n = 2 representatives.

Notwithstanding, the photoconductivity values for n = 3 are in the order of magnitude of FAPbI₃ films measured with the same technique (8–60 cm² V⁻¹ s⁻¹; Fig. S17, ESI†), which is likely the result of the presence of the 3D perovskite phase in the composition. For n = 1 composition, the conductivities are comparable to other layered perovskite films measured with the same technique (0.1–0.3 cm² V⁻¹ s⁻¹),¹⁴ whereas the values for n = 2 composition are in the 0.5–5 cm² V⁻¹ s⁻¹ range that is relevant for optoelectronics. The charge carrier dynamics in the films suggests that the recombination kinetics follows a second order behaviour (Fig. S18, ESI†). However, the lifetime gets longer as the number of inorganic layers increases.

The lifetime of the decay for n = 1 compositions is around 400 ns, which is longer than for n-butylammonium or phenylethylammonium systems that decay at ∼100–200 ns.¹⁴ The longer components of the decay for n = 2 and n = 3 compositions are in the order of 40 μs and 400 μs, respectively (Fig. 7), which is longer than the lifetime for FAPbI₃ of about 2 μs (Fig. S17, ESI†). At these longer time scales, the decay traces show a first order behaviour, suggesting that there are two decay regimes. This behaviour may potentially also be the result of the transport of carriers in the perpendicular direction that results in improved spatial charge separation, which is relevant for future optoelectronic device applications.

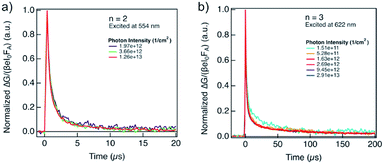Fig. 7 Evolution of photoconductivities in hybrid perovskite thin films based on A₂FA_n−1Pb_nI_3n+1 formulation with (a) n = 2 and (b) n = 3 nominal compositions as a function of photon intensity, highlighting long charge carrier lifetimes in the order of μs. Photoconductivity is defined by the eqn (1) as a product of charge mobility (μ) and quantum yield of free charge carrier formation (φ).

Conclusions

We have investigated the structural properties of adamantyl-based layered hybrid perovskites of A₂FA_n−1Pb_nI_3n+1 compositions, which were complemented by molecular dynamics simulations and density functional theory calculations. Our study reveals the formation of well-defined layered hybrid perovskite structures for the representatives based on the (1-adamantyl)methanammonium spacer in n = 1–2 compositions. On the contrary, higher compositional representatives (n > 2) are proven to be based on mixtures of lower-dimensional and 3D perovskite phases, which was evidenced by GIWAXS measurements. This was further in accordance with the decrease in the formation enthalpies for the increasing number of inorganic layers (n). Finally, we analysed the photophysical properties to observe high photoconductivities for layered hybrid perovskite structures with (1-adamantyl)methanammonium-based systems despite their structural complexity, while featuring longer charge carrier lifetimes in the order of tens to hundreds of μs that can be accounted for their photovoltaic performance. This provides an important incentive for the use of formamidinium-based layered hybrid perovskites in optoelectronics.

Experimental

Materials and methods

Perovskite powders were synthesized by grinding the reactants in an electric ball mill (Retsch Ball Mill MM-200) using a grinding jar (10 ml) and a ball (ø10 mm) for 30 min at 25 Hz. The resulting powders were annealed at 150 °C for 15 min to reproduce the thin film synthetic procedure based on the reported conditions.³⁷ Thin films were fabricated through a stepwise preparation process in accordance with the reported procedure.¹³ The quartz substrates were cleaned with oxygen plasma for 15 min. The perovskite film was deposited by spin-coating onto the substrate. The precursor solutions of A₂FA_n−1Pb_nI_3n+1 and A′₂FA_n−1Pb_nI_3n+1 perovskite films (n = 1, 2, 3) of the concentration of 0.4 M were prepared in a nitrogen-filled glovebox by dissolving the stoichiometric quantities of PbI₂, FAI, and either ADAMI (AI) or ADAI (A′I) in the solvent mixture comprised of N,N-dimethylformamide (DMF) and dimethyl sulfoxide (DMSO) with the volume ratio of DMF/DMSO = 4 : 1. The perovskite film spin-coating procedure was performed in a glovebox under inert nitrogen atmosphere by a consecutive two-step spin-coating process at first 1000 rpm for 10 s with a ramp of 200 rpm s⁻¹ and second 4000 rpm for 20 s with a ramp of 2000 rpm s⁻¹. Subsequently, the sample was annealed at 150 °C for 15 min. Further experimental details are provided in the ESI.†

X-ray scattering experiments

X-ray scattering experiments were done at beamline ID10 of the ESRF with a photon energy of 22 keV under nitrogen atmosphere. As a calibrant for the scattering experiments, LaB₆ was used. The sample–detector distance was 295 mm, while the beam size was 20 μm in vertical direction and 120 μm in horizontal direction. GIXD data was measured under an angle of incidence of 0.12° with a Cyberstar point detector. GIWAXS data was measured with a PILATUS 300k area detector under angles of incidence between 0.02°–0.20°. Powder diffraction data was calculated with Mercury software. Scattering data analysis was performed with self-written Python and Matlab-based software.

Time-resolved microwave conductivity measurements

Time-resolved microwave conductivity measurements were used to probe changes in conductivity of layered hybrid perovskites by using high frequency microwaves after the excitation by either high energy electron pulse or a laser. The relative mobility of charge carriers was estimated by pulse-radiolysis TRMC. The samples prepared by mechanosynthesis were irradiated with short pulses of 3 MeV electrons from a Van de Graaff accelerator. TRMC upon laser photoexcitation under conditions specified in the corresponding figure captions was used to analyse thin films.

Molecular dynamics simulations

Molecular dynamics simulations were performed by relying on the methods described in detail in the ESI.† A fixed-point charge interatomic potential was chosen for Pb and I from the literature.³⁸ The Generalized Amber Force Field (GAFF) was used to parameterize the ligand and formamidinium ions. We have chosen a 1.0 nm cutoff for nonbonded interactions and three-dimensional periodic boundary conditions were applied for each simulation. Long range electrostatic interactions are treated with the particle–particle–particle–mesh Ewald method. We employ the SHAKE algorithm³⁹ to constrain the bond length of hydrogen atoms. The time step used in all of the simulations is 2 fs. All simulations are performed with the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code (31 Mar 2017).⁴⁰ The systems were first minimized with a conjugate gradient algorithm with a tolerance of maximum residual force of 10⁻³ kcal mol⁻¹ Å⁻¹. After minimization, the systems were relaxed with an equilibrium run which was carried out in the isothermal–isobaric ensemble. We used a velocity rescaling thermostat⁴¹ with a relaxation time of 0.1 ps. The Parrinello–Rahman barostat was used to keep the pressure equal to the standard atmospheric pressure.⁴² The relaxation time of the barostat was set to 10 ps. We used a triclinic variable cell barostat in all of our simulations. With this setup, the temperature was slowly increased from 0 K to T (temperature) in 10 ns. Then we perform 30 ns simulations at the constant temperature. To calculate the autocorrelation function (ACF), we perform MD simulations for five different temperatures (at 200 K, 250 K, 300 K, 350 K and 400 K). The simulations were run to verify the stability and calculations of the dynamics of the spacers at different temperatures, and for the final structure, they are quenched to 0 K.

Density functional theory calculations

Density functional theory calculations were performed by relying on the method described in detail in the ESI.†Ab initio calculations based on the Generalized Gradient Approximation (GGA) of Density Functional Theory (DFT) for A₂FA_n−1Pb_nI_3n+1 and A′₂FA_n−1Pb_nI_3n+1 (n = 1, 2 and 3) were performed using the Quantum Espresso package.⁴³ The Perdew–Burke–Ernzerhof functional revised for solids (PBEsol)⁴⁴ was selected, which has shown to well reproduce measured electronic and structural properties of Ruddlesden–Popper (RP) phases, such as the recently reported AVA₂MA_n−1Pb_nI_3n+1 systems.^16,29 Dispersion interactions were considered by applying the empirical D2 dispersion correction.³¹ To calculate the band gaps, we employed a higher level of theory by applying the PBE0 functional³⁶ together with incorporating spin–orbit coupling (SOC) effects.⁴⁵ Valence-core electron interactions were modelled via ultrasoft pseudopotentials with a plane wave basis set of 40 Ry kinetic energy cutoff for the wavefunction and 280 Ry for the density. For band gap calculations, norm-conserving pseudopotentials with 80 Ry wavefunction cutoff and 320 Ry density cutoff were employed. The Brillouin zone was sampled by a 2 × 2 × 1 k-point grid for all cases. A finite temperature (FT) analysis was carried out by performing 5 ps of constant volume (NVT) Born–Oppenheimer MD for A₂PbI₄ and A′₂PbI₄, excluding the first 1 ps of equilibration. The initial temperature was set to 300 K and was controlled by the velocity rescaling thermostat implemented in Quantum Espresso.⁴² The same Brillouin zone sampling as in the static calculations was adopted for MD simulations. Charge carrier effective masses were calculated using our in-house code.²⁸

Author contribution

The manuscript was written by J. V. M., F. J., M. M., E. K., L. M., and M. C. G.-R. with the support of all authors. The project was conceptualized by J. V. M., who coordinated the investigation. M. C. G.-R. and F. C. G. performed the photoconductivity measurements and analysis of charge carrier dynamics with the support of W. T. in the interpretation. Y. L. and A. D. prepared the samples for the analysis and performed basic structural characterization. F. J., M. M., P. A., and U. R. performed, analyzed and interpreted the molecular dynamics simulations and DFT calculations. A. H., E. K. and L. M. performed the X-ray scattering measurements and the analysis with the support of M. I. D. and F. S., while A. U. conducted the XRD measurements. S. M. Z., B. C., and A. H. were involved in the discussion and provided support in project coordination, while M. G. directed the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. V. M., S. M. Z., and M. G. are grateful to the European Union's Horizon 2020 research and innovation program under grant agreement No. 826013 (IMPRESSIVE) as well as the King Abdulaziz City for Science and Technology (KACST) for financial support. U. R. acknowledges SNSF Grant No. 200020-165863, NCCR-MUST, NRP70, and the SINERGIA interdisciplinary research program EPISODE for funding. The work at Delft University of Technology (M. C. G.-R. and F. C. G) is funded by the European Research Council Horizon 2020 ERC Grant Agreement No. 648433. We are grateful to the DFG for funding and the European Synchrotron Radiation Facility (ESRF) for the provision of synchrotron radiation and Oleg Konovalov for assistance in using beamline ID10.

References

1. M. Grätzel, Nat. Mater., 2014, 13, 838–842.
2. Y. Rong, Y. Hu, A. Mei, H. Tan, M. I. Saidaminov, S. I. Seok, M. D. McGehee, E. H. Sargent and H. Han, Science, 2018, 361, eaat8235.
3. A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103.
4. G. Grancini and M. K. Nazeeruddin, Nat. Rev. Mater., 2018, 4, 4–22.
5. L. Mao, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 1171–1190.
6. G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988.
7. N. Pellet, P. Gao, G. Gregori, T.-Y. Yang, M. K. Nazeeruddin, J. Maier and M. Grätzel, Angew. Chem., Int. Ed., 2014, 53, 3151–3157.
8. Z. Yang, C.-C. Chueh, P.-W. Liang, M. Crump, F. Lin, Z. Zhu and A. K. Y. Jen, Nano Energy, 2016, 22, 328–337.
9. W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Science, 2017, 356, 1376–1379.
10. G. Li, T. Zhang, N. Guo, F. Xu, X. Qian and Y. Zhao, Angew. Chem., Int. Ed., 2016, 55, 13460–13464.
11. R. Hamaguchi, M. Yoshizawa-Fujita, T. Miyasaka, H. Kunugita, K. Ema, Y. Takeoka and M. Rikukawa, Chem. Commun., 2017, 53, 4366–4369.
12. J. Yan, W. Fu, X. Zhang, J. Chen, W. Yang, W. Qiu, G. Wu, F. Liu, P. Heremans and H. Chen, Mater. Chem. Front., 2017, 2, 121–128.
13. J. V. Milić, J.-H. Im, D. J. Kubicki, A. Ummadisingu, J.-Y. Seo, Y. Li, M. A. Ruiz Preciado, M. I. Dar, S. M. Zakeeruddin, L. Emsley and M. Grätzel, Adv. Energy Mater., 2019, 131, 1900284.
14. M. C. Gélvez-Rueda, E. M. Hutter, D. H. Cao, N. Renaud, C. C. Stoumpos, J. T. Hupp, T. J. Savenije, M. G. Kanatzidis and F. C. Grozema, J. Phys. Chem. C, 2017, 121, 26566–26574.
15. R. Herckens, W. T. M. Van Gompel, W. Song, M. C. Gélvez-Rueda, A. Maufort, B. Ruttens, J. D'Haen, F. C. Grozema, T. Aernouts, L. Lutsen and D. Vanderzande, J. Mater. Chem. A, 2018, 6, 22899–22908.
16. A. Q. Alanazi, D. J. Kubicki, D. Prochowicz, E. A. Alharbi, M. E. F. Bouduban, F. Jahanbakhshi, M. Mladenović, J. V. Milić, F. Giordano, D. Ren, A. Y. Alyamani, H. Albrithen, A. Albadri, M. H. Alotaibi, J.-E. Moser, S. M. Zakeeruddin, U. Rothlisberger, L. Emsley and M. Grätzel, J. Am. Chem. Soc., 2019, 141, 17659–17669.
17. J. V. Milić, D. J. Kubicki, L. Emsley and M. Grätzel, Chimia, 2019, 73, 317–323.
18. D. Prochowicz, M. Saski, P. Yadav, M. Grätzel and J. Lewiński, Acc. Chem. Res., 2019, 52, 3233–3243.
19. L. Mao, W. Ke, L. Pedesseau, Y. Wu, C. Katan, J. Even, M. R. Wasielewski, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 3775–3783.
20. Y. Li, J. V. Milić, A. Ummadisingu, J.-Y. Seo, J.-H. Im, H.-S. Kim, Y. Liu, M. I. Dar, S. M. Zakeeruddin, P. Wang, A. Hagfeldt and M. Grätzel, Nano Lett., 2019, 19, 150–157.
21. C. M. M. Soe, G. P. Nagabhushana, R. Shivaramaiah, H. Tsai, W. Nie, J.-C. Blancon, F. Melkonyan, D. H. Cao, B. Traoré, L. Pedesseau, M. Kepenekian, C. Katan, J. Even, T. J. Marks, A. Navrotsky, A. D. Mohite, C. C. Stoumpos and M. G. Kanatzidis, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 58–66.
22. D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 7843–7850.
23. L. N. Quan, M. Yuan, R. Comin, O. Voznyy, E. M. Beauregard, S. Hoogland, A. Buin, A. R. Kirmani, K. Zhao, A. Amassian, D. H. Kim and E. H. Sargent, J. Am. Chem. Soc., 2016, 138, 2649–2655.
24. J. Liu, J. Leng, K. Wu, J. Zhang and S. Jin, J. Am. Chem. Soc., 2017, 139, 1432–1435.
25. A. H. Proppe, R. Quintero-Bermudez, H. Tan, O. Voznyy, S. O. Kelley and E. H. Sargent, J. Am. Chem. Soc., 2018, 140, 2890–2896.
26. C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Chem. Mater., 2016, 28, 2852–2867.
27. D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12.
28. N. Ashari-Astani, S. Meloni, A. H. Salavati, G. Palermo, M. Grätzel and U. Rothlisberger, J. Phys. Chem. C, 2017, 121, 23886–23895.
29. N. Ashari-Astani, F. Jahanbakhshi, M. Mladenović, A. Q. M. Alanazi, I. Ahmadabadi, M. R. Ejtehadi, M. I. Dar, M. Grätzel and U. Rothlisberger, J. Phys. Chem. Lett., 2019, 10, 3543–3549.
30. S. Ahmad, P. Fu, S. Yu, Q. Yang, X. Liu, X. Wang, X. Wang, X. Guo and C. Li, Joule, 2019, 3, 794–806.
31. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
32. Z. Wang, Q. Lin, F. P. Chmiel, N. Sakai, L. M. Herz and H. J. Snaith, Nat. Energy, 2017, 2, 17135.
33. J. C. Blancon, H. Tsai, W. Nie, C. C. Stoumpos, L. Pedesseau, C. Katan, M. Kepenekian, C. M. M. Soe, K. Appavoo, M. Y. Sfeir, S. Tretiak, P. M. Ajayan, M. G. Kanatzidis, J. Even, J. J. Crochet and A. D. Mohite, Science, 2017, 355, 1288–1292.
34. Y. Chen, Y. Sun, J. Peng, J. Tang, K. Zheng and Z. Liang, Adv. Mater., 2017, 131, 1703487.
35. L. Gan, J. Li, Z. Fang, H. He and Z. Ye, J. Phys. Chem. Lett., 2017, 8, 5177–5183.
36. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
37. D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Péchy, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10055–10061.
38. C. Caddeo, M. I. Saba, S. Meloni, A. Filippetti and A. Mattoni, ACS Nano, 2017, 11, 9183–9190.
39. J.-P. Ryckaert, G. Cicciotti and H. J. C. Berndsen, J. Comput. Phys., 1977, 23, 327–341.
40. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
41. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
42. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
43. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
44. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
45. P. Umari, E. Mosconi and F. De Angelis, Sci. Rep., 2014, 4, 4467.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta05022a

‡ These authors contributed equally.

§ M. I. D. are currently affiliated with the Cavendish Laboratory at the University of Cambridge, United Kingdom. M. M. is also affiliated with the Scientific Computing Laboratory, Center for the Study of Complex Systems, Institute of Physics Belgrade, University of Belgrade, Pregrevica 118, 11080 Belgrade, Serbia. A. U. is currently a Swiss National Science Foundation Fellow at the Cavendish Laboratory, University of Cambridge, 19 J J Thomson Avenue, Cambridge CB3 0HE, United Kingdom.

---