Apparent phototaxis enabled by Brownian motion

Abstract

Biomimetic behaviour in artificially created active matter that allows deterministic and controlled motility has become of growing interest in recent years. It is well known that phototrophic bacteria optimize their position with respect to light by phototaxis. Here, we describe how our fully artificial, magnetic and photocatalytic microswimmers undergo a specific type of behaviour that strongly resembles phototaxis: when crossing an illuminated stripe the particles repeatedly turn back towards the light once they reach the dark region, without any obvious reason for the particles to do so. In order to understand the origin of this behaviour we analyze different influences and elucidate through experiments and theoretical considerations that this behavior arises from a combination of orientational stabilization through activity and destabilizing Brownian motion. This interplay shows beautifully how simple physical effects can combine into complex behaviours.

---

Introduction

Tactic behaviour is emerging as one of the most important features in active matter.¹ Its most frequent biological analogue is phototaxis which refers to a light-oriented change of location of a motile organism. Especially phototrophic microorganisms, i.e. bacteria or algae converting water and carbon dioxide to carbohydrates and oxygen, require light to perform photosynthesis and therefore benefit strongly from optimizing the light conditions in their surroundings. Cyanobacteria are capable of distinguishing between different wave lengths and directions of light.² This is especially remarkable since bacteria are considered too small to sense gradients across their bodies and rely on detecting variations over time.³ Schuergers et al. discovered that the unicellular cyanobacterium Synechocystis can directly sense light by using their bodies as tiny microlenses,⁴ a mechanism that is known to be also employed by the larger volvox algae.⁵

Biological variability makes understanding the mechanism of phototaxis complicated. This includes different taxes as well as the molecular base of photosensors and other strategies employed to detect and subsequently respond to light.^6–9 Even though a complete understanding of the different mechanisms and their implementations is still to be achieved, first agent based models describe phototactic behaviour, e.g. in colonies of cyanobacteria^10,11 or use mesoscale dynamics simulations to study the phototactic behavior of self-thermophoretic Janus particles.¹² First artificial creation of tactic behaviours mostly mimic phototaxis, i.e. the response to a gradient of light, as was shown for droplets.^13,14 Liquid crystal droplets driven helically by molecular motors were shown to respond to irradiation with re-orientation.¹⁵ Microsized approaches include photo-activated microparticles exposed to an inhomogeneous laser field,¹⁶ carbo-nitride particles following the light source,¹⁷ self-electrophoretic silicon nanotrees with TiO₂ nanowire heads that enable steering through their self-shading effect¹⁸ and spiropyran terminated polymer particles whose phototactic propulsion is driven by UV-induced interfacial tension gradient.¹⁹

Inspired by this natural behavior, herein we investigate a phenomenon that strongly resembles a subcategory of phototactic motility: scotophobicity. Using biological definitions, we can describe scotophobic behaviour as ‘fear of darkness’ or motion away from unilluminated areas. Our photocatalytic titania based micromotors swim upon irradiation and when exposed to a restricted light stripe, they cross the illuminated area and once reaching the dark area they repeatedly turn back towards the light. Here, we elucidate the origins of this behaviour and shed light on the underlying position-stabilizing mechanisms and destabilizing influence of Brownian motion that enable this behaviour. Additionally, we provide reasons for these mechanisms in phase portraits obtained via boundary element method.

Results and discussion

We study this intriguing behaviour using light-driven, self-propelled colloids made of anatase TiO₂ obtained by calcination under nitrogen atmosphere which let all probes turn their colour from white to black. This color is caused by free oxygen vacancies^20,21 and the powder X-ray diffraction data show that all samples have anatase as their predominant crystal phase (ESI,† Fig. S1 XRD-patterns).

A Janus geometry is conferred to the spheres using a thin ferromagnetic nickel gold bilayer.

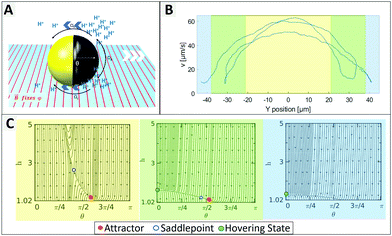
An ultraviolet (UV) light-emitting diode (385 nm) focused through the objective was used as the light source to power the motion. Upon UV irradiation an asymmetric gradient arises by catalytic decomposition of hydrogen peroxide (see Fig. 1A) and sets the particle in motion.²² The in-plane ferromagnetic nickel layer enables control over the swimming direction by an external magnetic field (see setup ESI,† Fig. S2 and S3).²³ How the application of UV light and a magnetic field affects the motion behaviour of the Au@Ni@TiO₂ particles can be seen in Fig. 1B–E.

Fig. 1 (A) Schematic of photocatalytically induced motion, (B–E) track lines of selected particles in 0.5% H₂O₂. (B) No UV light, no magnet; (C) 100% UV, no magnet; (D) 100% UV, B⃑ = 5 mT; (E) 100% UV with restricted UV area (bright), B⃑ = 5 mT. Scale bar 25 μm.

As shown in Fig. 1B, in absence of UV light the particles are catalytically inactive and only passive molecular motion is observed (Brownian motion, BM). When exposed to light, the photocatalytic reaction produces a product gradient which induces active motion of the microswimmers. Due to the unguided way of movement, the particle tracks display a random walk (Fig. 1C), which is best described as enhanced Brownian motion. By installing a constant magnetic field (MF) in the experimental setup, the particles orient preferentially according to the magnetic field lines^24,25 and move in straight paths in defined directions (Fig. 1D). If the illuminated area is additionally restricted to a narrow stripe, an unexpected swimming behaviour is observed, which is shown in Fig. 1E. Herein, the microswimmers, still moving in straight lines comparable to Fig. 1D, turn after leaving the irradiated zone and migrate back towards the higher light intensity. At a first glance, this phenomenon could be understood as a kind of phototaxis, or more precisely, scotophobicity, or fear of darkness. However, differently from biological phototroph microorganisms there is no obvious reason why particles would show such behaviour. In quest of the distinct cause for the particles’ behaviour, we tested our particles systematically under different conditions. So the influence of the orientation of MF towards the light stripe, different hydrogen peroxide concentrations and intensity of UV light were tested.

The MF was set to a level of B⃑ = 5 mT, which ensured homogeneity of field (see ESI,† Fig. S3 field lines) as well as sufficient momentum for stable particle alignment.^21,23,26 There were no indications that variations in magnetic field strength could further improve particle guidance. Although major dependency of particle velocity on the magnetic field strength is reported for some microswimmers,^27,28 we found no significant effect in the probed Au@Ni@TiO₂ system. When the MF was reoriented in a way that the particle tracks went diagonally with respect to the light stripe, the apparent phototaxis was also observable (see ESI,† Fig. S4 different angles and corresponding particle responses) and even without any magnetic field a less pronounced effect could be noted. The nickel thickness had little influence on the response, see ESI,† Fig. S5. Thus besides excluding the orientation of MF as a critical factor with respect to the phenomenon, we also confirm the apparent phototaxis, or constant swimming orientation in irradiated zones combined with a tendency to flip and invert the swimming direction, as a rather robust behavior that shows over a variety of experimental conditions. The next question to answer is where this constant swimming orientation originates from. Looking in detail at the different processes influencing the behavior (see overview ESI,† Fig. S8) we notice that the particle orientation is fixed in the horizontal plane by the magnetic field. Fig. S9 in the ESI† shows the resulting sinusoidal potential created by the magnetic field that becomes 0 only if the particles cap is aligned with B. This is the case for ϕ = n × π meaning any rotation around the y axis that maintains the cap orientation parallel to B is allowed. Therefore, the magnetic field fixes ϕ, while it has no effect on θ.

To identify individual processes leading to such tendencies we consider swimming positions for different illumination states and compare the findings to observed behaviours. Plotting the measured velocity of a microswimmer depending on its position within the field of view the light stripe is located approximately between −20 and 20 μm (more details in ESI,† Fig. S10), where Fig. 2 shows an increased speed up to 65 μm s⁻¹. In the green area the speed reduces due to a lower light intensity, followed by an activity and velocity decrease. This green area corresponds to the edge of the light stripe which gets most of its irradiation from scattered light, which is visualized in ESI,† Fig. S10. The measured velocity of an exemplary 1.6 μm particle depending on the y-position and the corresponding phase portraits are shown in Fig. 2 (detailed information on phase portraits is given in the Fig. ST1, ESI†).

Fig. 2 (A) Schematic of a Au@Ni@TiO₂ particle near a boundary that translates and rotates under the presence of wall interactive hydrodynamic (Ω_h) and chemical (Ω_c) as well as gravitational (Ω_g) forces and torques. (B) Velocity depending on swimming position of a 1.6 μm particle with respect to the stripe. (C) Phase portraits displaying the particle trajectory in the h–θ plane, where θ and h are particle's orientation and the height of its center of mass from the wall. The phase portraits can be assigned to the active zone (yellow) with a stable attractor (or stable sliding state), the transition zone (green) with a hovering state and a dominant saddle point strongly destabilizing the attractor, as well as the dark zone (blue) showing only a hovering state.

The UV light acts as a trigger that initiates the generation of protons from the uncapped TiO₂ surface. The resulting concentration gradient along the vicinity of the particle surface manifests as a slip velocity that causes the particle to propel in a direction opposite to the cap. Near a boundary different forces and torques play an important role in governing the dynamics of the bottom-heavy particle (see Fig. 2A). The phase portraits signify the dynamic evolution of the particle height (distance of its center of mass from the wall, h) and orientation (θ) and therefore indicate the swimming position.

In Fig. 2C the yellow graph assumes a high light intensity resulting in high activity and therefore in a high self propulsive velocity. The dominating effect of chemical wall interactions can be observed from the large basin of attraction in the phase portrait.²⁹ For all configurations within the basin of attractions, the lines converge towards the red attractor. The counteracting wall hydrodynamic interactions and gravity balance the chemical wall interactions, resulting in a steady sliding of the particle at an angle slightly larger than θ = π/2 which inhibits changes of direction, so that the particle moves in a straight line.

When the UV light intensity is reduced (see green area of Fig. 2C), the self-propulsive force and the chemically induced torque decrease and the attractor becomes less dominant and less stable with a meta-stable saddle point in its vicinity (see green area of Fig. 2C). This indicates that even small random fluctuations can shift the system away from the attractor leading to reduced orientational stability. When the light intensity is minimal (blue domain in Fig. 2B and C), the particle behaves effectively as inert resulting in its sedimentation without exhibiting any sliding. We thus conclude that the intensity of the UV light plays a crucial role in stabilizing the particles propulsion, while in the dark region the orientation of the particle can be easily flipped.

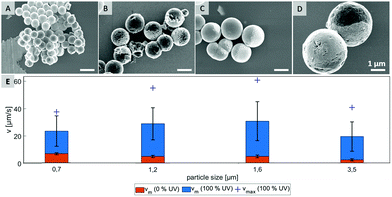
In order to test what is causing the flipping in the not irradiated area, we hypothesize that Brownian motion might be the culprit and focus of investigation on testing several particle types that differ in size. Four different samples, which are characterized by scanning electron microscopy in Fig. 3 were probed. By varying preparation methods we obtained particles with average diameters in range from 0.7 μm to 3.5 μm (see ESI,† Fig. S6).

Fig. 3 SEM pictures of Janus particles with average sizes of 0.7 μm (A), 1.2 μm (B), 1.6 μm (C), 3.5 μm (D) and their velocities (E) in 0.5% H₂O₂ solution (v_m – mean velocity at given UV intensity, v_max – velocity of fastest particle), scale bar 1 μm.

As shown in Fig. 3E, the mean velocity of the particle motion in absence of UV light (orange bars) is decreasing with larger diameter, as expected for passive Brownian motion.³⁰ Note that the average Brownian speeds for these particles at given imaging and step frequencies are in approximate agreement with the theoretically obtained diffusion coefficients. In contrast, the velocity of active motion does not display any size dependency, as expected for catalytic swimmers due to the size-dependant viscous drag force.^30,31 The different photo-catalytic properties are predominant against the size related effects of colloidal movement. Each sample originated from a different synthesis, thus they are characterized by different surface properties like grain size, porosity and crystal structures, which are crucial factors for catalysis. Besides the differing mean velocities, observations reveal important variations in the particles’ general swimming behaviour. Fig. 4 illustrates some representative track lines for each batch of particles.

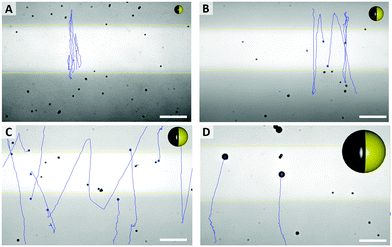Fig. 4 Typical pathways of particles, with different average sizes ((A) 0.7 μm, (B) 1.2 μm, (C) 1.6 μm, (D) 3.5 μm) and particle sketches in relative sizes (see Videos in ESI,† S1–S4). Scale bar 25 μm.

Most distinctly, particles show different tendencies to change their direction. The smallest species of 0.7 μm switches its main direction several times within its path, even within the fully irradiated area. Furthermore, this sample type penetrates the dark stripe only for few micrometers, which is in good agreement of the strong influence of Brownian motion on such small particles. In contrast, there are almost no turns occurring in the tracks of the biggest, 3.5 μm sized particles. The two intermediate sizes, 1.2 μm and 1.6 μm particles moved in between these extremes and inverted the direction readily after having moved to the dark area.

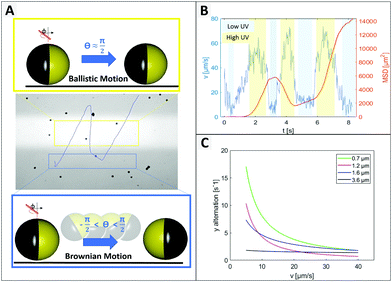
As expected from the theoretical predictions given above, reverting the motion direction is enabled specifically in the region of lower activity (green in Fig. 2C), while fixed during active propulsion. To investigate the origin of the flipping that reverses the swimming direction, we observed in Fig. 4 that small particles change direction more frequently, pointing towards a size dependent effect. Additionally, the bottom heaviness tendency increases with increasing size due to a direct influence on the gravitational torque. Thus, the smaller the particle is, the easier is to flip into any orientation. A closer look at one of these generic particle tracks is taken in Fig. 5 (exemplary for 1.6 μm particle). In Fig. 5B the particle's velocity and mean square displacement (MSD) are plotted against the time. In connection with Fig. 5A, it gets evident that the velocity drops when the swimmer crosses to the dark zone and the point of turning coincides with lowest speed. These findings were confirmed in another type of experiment where the particles’ tendency to turn back was tested for different velocities and particle sizes (see Fig. 5C). To this end the particle tracks were analyzed regarding the switching position in y direction, upwards to downwards or reverse. This number was averaged over time and plotted against the mean velocity of the observed swimmer. Variation of speed was realized by changing the intensity of UV light from 20% to 100% in steps of 20. Minimum 15 particle paths were analyzed for each light condition and batch of samples.

Fig. 5 Instantaneous particle velocity depending on vertical position. (A) Trajectory of an individual micromotor (with imperfection in coverage for better path visualization) and scheme of fixed (see yellow box) or enabled (see blue box) rotation around θ. (B) Analysis of velocity and MSD from particle in (A). (C) Shows the tendency of a particle to turn back, depending on its velocity and size. The y alternation indicates the average number of directional changes in y direction per second. This was counted for movement in UV area only.

Fig. 5C displays the trend that larger or faster moving samples undergo less directional changing. Additionally, higher peroxide concentration also leading to higher speeds, causes less events of turning (see ESI,† Fig. S7). In general, it is well-understood that the reorientation rate of colloidal particles is determined by the rotational diffusion time t_rot = 8πηR³/k_BT_inert which only depends on the particle radius R, the solvent viscosity η and the thermal energy k_BT.¹⁶ However, Lozano et al. also discuss, that the reorientation rate must respond to the activity (in their case the local light intensity), otherwise no directed motion were possible.¹⁶

As we have previously described, the particle orientation is stabilized within the illuminated area due to activity (see Fig. 2). This stabilization is reduced in less illuminated areas, for which, we observe an increased opportunity for Brownian motion to kick in and re-orient the particles so that they can escape the dark areas and perform what seems to be a ‘phototactic behaviour’. Finally, this behaviour is an intricate combination of simple physical effects. Since Brownian motion originates from the random collisions with solvent molecules, it is intrinsic, such that smaller colloids are more influenced by it than larger colloids. Brownian motion is constantly present in all areas of the experiment, independent of the illumination, i.e. also in the irradiated area. However, for larger particles in the illuminated area the stabilization through activity is stronger than the Brownian motion. For the smallest particle size, both effects seem to have a similar magnitude as can be seen in Fig. 5A, so that the mostly straight path is occasionally also destabilized within the active region. This strong size dependence of the direction reversal confirms that it is indeed caused by Brownian motion destabilizing the fixed position of the particle.

Conclusion

We report an unprecedented behaviour for magnetically guided photocatalytic microswimmers. This behavior consists in crossing a light stripe, followed by a subsequent direction change (without receiving any additional stimulus). This leads to ‘swimming back to the light’ that resembles the biological phenomenon of scotophobicity, a subclass of phototaxis. Studying the different influences that contribute to this behavior, we find that neither the magnetic field nor the peroxide content have important effects on the behaviour. Instead, we identify the particle size as critical factor with its direct influence on the rotational diffusion time, related via the particles’ Brownian motion. Theoretical analysis of the strength of the attractor that leads to a stable swimming angle show that a loss of activity results in a smaller basin of attraction and to a more ready turning when Brownian motion deviates the particle position slightly from the attractor. Due to the constant magnetic field and the magnetization of the particles, this turn can only occur in vertical direction and is fixed to multiples of π and therefore leads to such behaviour. Here, we would like to point out how a combination of simple physical effects can lead to a complex, but robust behaviour that nature achieves using multi-step mechanisms. This independent shuttling behaviour can pave the way towards cargo transport mechanisms that work independently of permanent control.

Experimental section

Chemicals

Titanium(IV) isopropoxide (Alfa Aesar Co. Ltd); dodecylamine (Fluka); formic acid (Sigma Aldrich); titanium(IV) tetrabutoxide (Sigma Aldrich); sodium hydroxide (Gruessing GmbH); sodium chloride (VWR); hydroxypropyl cellulose (Sigma Aldrich) As solvents methanol, acetonitrile and ethanol were used in analytical grade without any additional treatment.

Synthesis of TiO₂ microparticles 0.7 μm³²

180 μL distilled water were added to a mixture of 45 mL acetonitrile and 110 mL methanol. After adding 280 mg DDA, the solution was stirred for 10 min using a 500 mL two-necked flask. Subsequently, 1 mL TTIP was added within 5 min using a syringe pump. It was stirred continuously at 600 rpm room temperature for a further 72 h. The resulting suspension was centrifuged at 2000 rpm for 2.5 min, the supernatant was discarded and the precipitate dispersed in 15 mL methanol. The particles were washed 3 times with 15 mL methanol each and then dried for 3 h at 80 °C.

Synthesis of TiO₂ microparticles 1.2 μm³²

70 μL distilled water was added to a mixture of 30 mL acetonitrile and 61 mL methanol. After adding 538 mg DDA, the solution was stirred for 10 min at 35 °C in a 500 mL two-necked flask. Subsequently, 1 mL TTIP was added within 5 min using a syringe pump followed by 25 min stirring at 40 °C. Stirring was continued with 600 rpm at room temperature for a further 72 h. The resulting suspension was centrifuged at 2000 rpm for 2.5 min, the supernatant was discarded and the precipitate redispersed in 15 mL methanol. The particles were thus washed 3 times with 15 mL methanol each and then dried for 3 h at 80 °C.

Synthesis TiO₂ microparticles 1.6 μm³³

100 μL of a 0.1 M NaCl solution and 425 μL titanium(IV) tetrabutoxide were added to 25 mL of ethanol. After 18 minutes of stirring, the solution was aged at room temperature for 24 h to promote gel formation. The resulting solid was washed three times with 15 mL ethanol and 15 mL deionized water, and dried for 3 h at 80 °C.

Synthesis TiO₂ microparticles 3.5 μm^33,34

1.3 mL titanium(IV) isopropoxide was mixed with 30 mL ethanol and 0.35 mL formic acid. The resulting solution was transferred to a Teflon autoclave, sealed and heated up to 150 °C for 12 h. After chilling to room temperature, the resulting particles were washed three times with 15 mL ethanol and twice with 15 mL deionized water.

Calcination

Finally, all particles were calcined at 600 °C for 2 h under a nitrogen atmosphere in a tubular oven. The heating rate was 5 K per minute.

Creating Au@Ni@TiO₂ Janus structures

Using Langmuir–Blodgett trough,³⁵ monolayers of calcined TiO₂ particles were coated with a nickel layer (between 10 nm and 50 nm) and 30 nm gold subsequently using physical vapour deposition.

Observation of particle behaviour

To observe the particles behavior in diluted H₂O₂ the Janus particles were treated as following. The Janus particles were detached from the cover glass using an ultrasonic bath. Some microliters of this suspension were mixed with H₂O₂ and spread onto a cleaned and plasma-treated cover glass. An inverted optical microscope (Carl Zeiss Microscope GmbH) and a “N-Achroplan” 63×/0.95 M27 objective were used for observation. The microscope used was equipped with a Zeiss Colibri LED lamp, which provided additional illumination of the glass plates from the bottom side. So, this bottom side was additionally exposed by UV light (385 nm). To visualize the UV exposed area, it was overlaid with green light (555 nm). With the help of an aperture UV and green light, could be restricted to a rectangle shaped section of the observed area. During the experiment, the radiant power of the UV lamp was varied in the range from 20% to 100% (63 mW/315 mW). The particle behavior was recorded with a Zeiss camera (Axiocam 702 Mono) and a frame rate of 40 fps. A precise analysis of the trajectories was done using the software “fiesta”.³⁶

Phase portraits

To obtain phase portraits, first we need a knowledge of the particle velocity U and Ω. This particle velocity comprises of both the effects of self-propulsion and gravity induced sedimentation. The self-propulsion velocity counterpart is obtained by the utilizing the classical theory of diffusiophoresis along with the help of a numerical approach that has been previously used by Uspal et al.^29,37 The contribution due to gravity is obtained directly from the gravitational force and torque acting on the particle. The particle velocity is calculated corresponding to a grid of values of (h,θ) that refer to different particle configurations. Next, to obtain the particle trajectories for different initial configurations, numerical integration is done by interpolating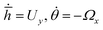 , where h̄ = hR, R being the particle radius. The calculations are carried out for h ≥ 1.02 to prevent any loss of any numerical accuracy. These trajectories gives us a better visualization of the particle dynamics and are represented in the form of the phase portraits, the particle configuration is shown in ESI,† Fig. ST2.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank MN Popescu for constructive discussions and help with the phase portraits. LN, LLW and JS acknowledge the Volkswagen foundation for the Freigeist fellowship (grant number 91619), as well as the Kaercher foundation for financial support. LLW thanks china scholarship council.

Notes and references

1. J. Armitage, Advances in microbial physiology, 1999, 41, pp. 229–289.
2. M. Kim, mBio, 2017, 8, e00498-17.
3. G. H. Wadhams and J. P. Armitage, Nat. Rev. Mol. Cell Biol., 2004, 5, 1024–1037.
4. N. Schuergers, T. Lenn, R. Kampmann, M. V. Meissner, T. Esteves, M. Temerinac-Ott, J. G. Korvink, A. R. Lowe, C. W. Mullineaux and A. Wilde, eLife, 2016, 5, e12620.
5. J. O. Kessler, A. M. Nedelcu, C. A. Solari and D. E. Shelton, in Cells Acting as Lenses: A Possible Role for Light in the Evolution of Morphological Asymmetry in Multicellular Volvocine Algae, ed. I. Ruiz-Trillo and A. M. Nedelcu, Springer Netherlands, Dordrecht, 2015, pp. 225–243.
6. W. D. Hoff, M. A. van der Horst, C. B. Nudel and K. J. Hellingwerf, in Prokaryotic Phototaxis, ed. T. Jin and D. Hereld, Humana Press, Totowa, NJ, 2009, pp. 25–49.
7. A. Wilde and C. W. Mullineaux, FEMS Microbiol. Rev., 2017, 41, 900–922.
8. J. P. Armitage and K. J. Hellingwerf, Photosynth. Res., 2003, 76, 145–155.
9. G. Jékely, Philos. Trans. R. Soc., B, 2009, 364, 2795–2808.
10. P. Varuni, S. N. Menon and G. I. Menon, Sci. Rep., 2017, 7, 1–10.
11. Y. Yang, V. Lam, M. Adomako, R. Simkovsky, A. Jakob, N. C. Rockwell, S. E. Cohen, A. Taton, J. Wang, J. C. Lagarias, A. Wilde, D. R. Nobles, J. J. Brand and S. S. Golden, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E12378.
12. N. Yu, X. Lou, K. Chen and M. Yang, Soft Matter, 2019, 15, 408–414.
13. D. Zhang, Y. Sun, M. Li, H. Zhang, B. Song and B. Dong, J. Mater. Chem. C, 2018, 6, 12234–12239.
14. S. Kaneko, K. Asakura and T. Banno, Chem. Commun., 2017, 53, 2237–2240.
15. F. Lancia, T. Yamamoto, A. Ryabchun, T. Yamaguchi, M. Sano and N. Katsonis, Nat. Commun., 2019, 10, 1–8.
16. C. Lozano, B. Ten Hagen, H. Löwen and C. Bechinger, Nat. Commun., 2016, 7, 1–10.
17. Z. Ye, Y. Sun, H. Zhang, B. Song and B. Dong, Nanoscale, 2017, 9, 18516–18522.
18. B. Dai, J. Wang, Z. Xiong, X. Zhan, W. Dai, C.-C. Li, S.-P. Feng and J. Tang, Nat. Nanotechnol., 2016, 11, 1087.
19. W. Li, X. Wu, H. Qin, Z. Zhao and H. Liu, Adv. Funct. Mater., 2016, 26, 3164–3171.
20. B. Jang, A. Hong, H. E. Kang, C. Alcantara, S. Charreyron, F. Mushtaq, E. Pellicer, R. Büchel, J. Sort, S. S. Lee, B. J. Nelson and S. Pané, ACS Nano, 2017, 11, 6146–6154.
21. Q. Long Wang, C. Wang, R. Feng Dong, Q. Qi Pang and Y. Peng Cai, Inorg. Chem. Commun., 2018, 91, 1–4.
22. B. Jang, A. Hong, H. E. Kang, C. Alcantara, S. Charreyron, F. Mushtaq, E. Pellicer, R. Büchel, J. Sort, S. S. Lee, B. J. Nelson and S. Pané, ACS Nano, 2017, 11, 6146–6154.
23. R. Dong, Q. Zhang, W. Gao, A. Pei and B. Ren, ACS Nano, 2016, 10, 839–844.
24. J. Yan, S. C. Bae and S. Granick, Adv. Mater., 2015, 27, 874–879.
25. P. Fischer and A. Ghosh, Nanoscale, 2011, 3, 557–563.
26. I. S. Khalil, V. Magdanz, S. Sanchez, O. G. Schmidt and S. Misra, Int. J. Adv. Robot. Syst., 2015, 12, 1–7.
27. L. Baraban, D. Makarov, O. G. Schmidt, G. Cuniberti, P. Leiderer and A. Erbe, Nanoscale, 2013, 5, 1332–1336.
28. B. Landry, V. Girgis and J. G. Gibbs, Small, 2020, 16, 2003375.
29. W. E. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 434–438.
30. S. Ebbens, M.-H. Tu, J. R. Howse and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 020401.
31. F. Mou, L. Kong, C. Chen, Z. Chen, L. Xu and J. Guan, Nanoscale, 2016, 8, 4976–4983.
32. S. Tanaka, D. Nogami, N. Tsuda and Y. Miyake, J. Colloid Interface Sci., 2009, 334, 188–194.
33. C. Chen, F. Mou, L. Xu, S. Wang, J. Guan, Z. Feng, Q. Wang, L. Kong, W. Li, J. Wang and Q. Zhang, Adv. Mater., 2017, 29, 1603374.
34. J. Widoniak and G. Maret, Chem. Mater., 2004, 6–11.
35. G. Roberts, Langmuir-Blodgett Films, Springer Science & Business Media, 2013.
36. F. Ruhnow, D. Zwicker and S. Diez, Biophys. J., 2011, 100, 2820–2828.
37. J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99.

---

Footnote

† Electronic supplementary information (ESI) available: Videos, experimental setup and theoretical approach. See DOI: 10.1039/d0sm01603a

---