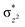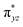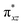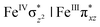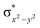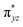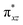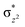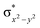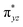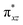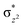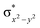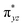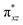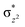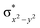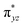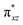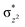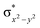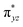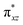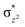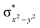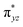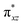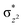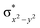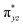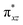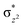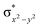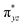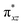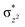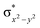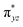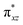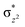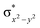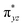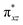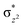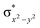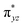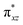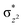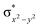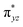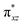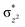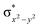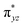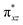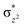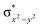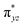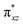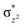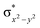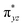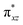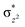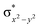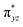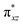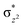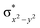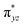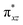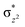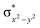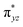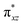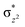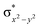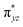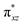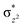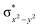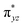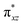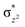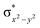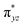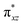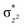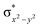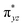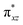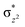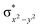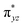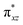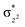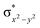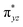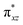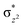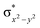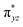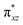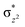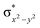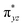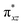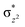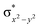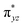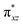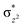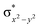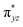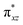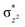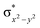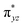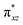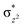Open Access Article
Open Access ArticleDeciphering the origin of million-fold reactivity observed for the open core diiron [HO–FeIII–O–FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) O]2+ species towards C–H bond activation: role of spin-states, spin-coupling, and spin-cooperation†
O]2+ species towards C–H bond activation: role of spin-states, spin-coupling, and spin-cooperation†
Mursaleem
Ansari
a,
Dhurairajan
Senthilnathan
*b and
Gopalan
Rajaraman
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Bombay, Mumbai 400076, India. E-mail: rajaraman@chem.iitb.ac.in
bCenter for Computational Chemistry, CRD, PRIST University, Vallam, Thanjavur, Tamilnadu 613403, India
First published on 18th June 2020
Abstract
High-valent metal–oxo species have been characterised as key intermediates in both heme and non-heme enzymes that are found to perform efficient aliphatic hydroxylation, epoxidation, halogenation, and dehydrogenation reactions. Several biomimetic model complexes have been synthesised over the years to mimic both the structure and function of metalloenzymes. The diamond-core [Fe2(μ-O)2] is one of the celebrated models in this context as this has been proposed as the catalytically active species in soluble methane monooxygenase enzymes (sMMO), which perform the challenging chemical conversion of methane to methanol at ease. In this context, a report of open core [HO(L)FeIII–O–FeIV(O)(L)]2+ (1) gains attention as this activates C–H bonds a million-fold faster compared to the diamond-core structure and has the dual catalytic ability to perform hydroxylation as well as desaturation with organic substrates. In this study, we have employed density functional methods to probe the origin of the very high reactivity observed for this complex and also to shed light on how this complex performs efficient hydroxylation and desaturation of alkanes. By modelling fifteen possible spin-states for 1 that could potentially participate in the reaction mechanism, our calculations reveal a doublet ground state for 1 arising from antiferromagnetic coupling between the quartet FeIV centre and the sextet FeIII centre, which regulates the reactivity of this species. The unusual stabilisation of the high-spin ground state for FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is due to the strong overlap of
O is due to the strong overlap of 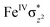 with the
with the 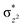 orbital, reducing the antibonding interactions via spin-cooperation. The electronic structure features computed for 1 are consistent with experiments offering confidence in the methodology chosen. Further, we have probed various mechanistic pathways for the C–H bond activation as well as –OH rebound/desaturation of alkanes. An extremely small barrier height computed for the first hydrogen atom abstraction by the terminal FeIV
orbital, reducing the antibonding interactions via spin-cooperation. The electronic structure features computed for 1 are consistent with experiments offering confidence in the methodology chosen. Further, we have probed various mechanistic pathways for the C–H bond activation as well as –OH rebound/desaturation of alkanes. An extremely small barrier height computed for the first hydrogen atom abstraction by the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit was found to be responsible for the million-fold activation observed in the experiments. The barrier height computed for –OH rebound by the FeIII–OH unit is also smaller suggesting a facile hydroxylation of organic substrates by 1. A strong spin-cooperation between the two iron centres also reduces the barrier for second hydrogen atom abstraction, thus making the desaturation pathway competitive. Both the spin-state as well as spin-coupling between the two metal centres play a crucial role in dictating the reactivity for species 1. By exploring various mechanistic pathways, our study unveils the fact that the bridged μ-oxo group is a poor electrophile for both C–H activation as well for –OH rebound. As more and more evidence is gathered in recent years for the open core geometry of sMMO enzymes, the idea of enhancing the reactivity via an open-core motif has far-reaching consequences.
O unit was found to be responsible for the million-fold activation observed in the experiments. The barrier height computed for –OH rebound by the FeIII–OH unit is also smaller suggesting a facile hydroxylation of organic substrates by 1. A strong spin-cooperation between the two iron centres also reduces the barrier for second hydrogen atom abstraction, thus making the desaturation pathway competitive. Both the spin-state as well as spin-coupling between the two metal centres play a crucial role in dictating the reactivity for species 1. By exploring various mechanistic pathways, our study unveils the fact that the bridged μ-oxo group is a poor electrophile for both C–H activation as well for –OH rebound. As more and more evidence is gathered in recent years for the open core geometry of sMMO enzymes, the idea of enhancing the reactivity via an open-core motif has far-reaching consequences.
Introduction
High-valent metal–oxo complexes are of great interest due to their potent catalytic abilities.1–25 Dinuclear metal–oxo complexes have different types of metal centres, but iron is the most common metal centre to oxidise C–H bonds through the dioxygen activation mechanism, in which high-valent oxo–iron species are often postulated and demonstrated to act as the actual oxidising species.26–33 Membrane-bound methane monooxygenases (MMOs) containing copper are known,34–37 but the longest known MMOs are soluble proteins containing a dinuclear iron active site.27,38–40 The high-valent intermediate Q of soluble methane monooxygenase (sMMO) is a two-electron oxidant that effects the hydroxylation of methane.41–47 For these reasons, complexes based on high-valent iron have been proved to be a compelling tool in the activation of inert C–H bonds, both in biochemical and synthetic oxidation processes.48–50The active site structure of the sMMO possesses an [FeIV2(μ-O2)] diamond core motif,45,51–56 and this unit is known to be responsible for the activation of inert C–H bonds such as those of methane.57 This has inspired several groups to utilise both heme50,58–60 and non-heme61 ligand frameworks to synthesise biomimetic models, which are both structural and functional mimics of the enzyme.62 Among various reported diiron enzymes that possess diiron(IV) at the active centre, two classes of enzymes clearly emerge with enzymes such as sMMO or ToMO performing hydroxylation of aliphatic and aromatic substrates while enzymes such as Δ9 desaturase (Δ9D)63–65 perform desaturation of alkanes. The first step for both reactions is common. i.e. C–H bond activation while the second step involves competitive rebound of the –OH group (recombination) vs. activation of the second C–H bond (elimination) leading to an alkene as shown in Scheme 1.66 There is also another class of diiron enzymes which catalyse the conversion of nucleotides to deoxynucleotides and among several classes, class Ia ribonucleotide reductases (RNR) are relevant to mention here as they employ μ-oxo–FeIII/III2 to activate the C–H bond with very high selectivity.26
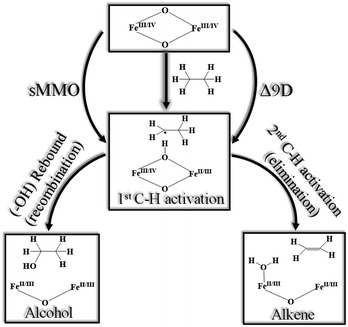 | ||
| Scheme 1 Generic mechanism for hydroxylation vs. desaturation by using sMMO (soluble methane monooxygenase)43 and Δ9D (stearoyl-ACP Δ9-desaturase).63 | ||
Various biomimetic dinuclear iron(IV) models were synthesised, and their reactivity were tested to understand their mechanistic features. Depending on the nature of ligands/bridging groups, there are two classes of dinuclear iron–oxo catalysts with some catalysts performing efficient hydroxylation and others desaturation. Examples of these catalysts include (i) [FeIV2(μ-O)(TAML)]2+ species reported by Collins and co-workers, which perform efficient hydroxylation of the benzylic substrate.12 (ii) [FeIV2(μ-O)2(TPA)2]4+ reported by Xue et al., which is a dinuclear iron complex that efficiently performs desaturation with 9,10-dihydroanthracene (DHA) to produce naphthalene.10,67,68 (iii) [FeIV2(μ-O)2L]4+ (where L = N,N-bis-(3′,5′-dimethyl-4′-methoxypyridyl-2′-methyl)-N′-acetyl-1,2-diaminoethane) reported by Que and co-workers, which also performs desaturation to yield cyclohexene from cyclohexane.69 (iv) N-bridged high-valent heme diiron–oxo species reported by Sorokin and co-workers, which can activate alkanes such as methane and perform efficient hydroxylation.70–72 In light of these results, a report by Xue et al. on [X–FeIII–O–FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ dinuclear unit gains attention as this complex is found to perform C–H activation nearly million-fold faster than other known complexes, and can perform both hydroxylation and desaturation depending on the nature of the substrate.67 The nature of the active complex species in this reaction was unambiguously established earlier by Münck and co-workers using a bunch of spectroscopic tools (Mössbauer, EPR, and UV-visible).73,74
O]2+ dinuclear unit gains attention as this complex is found to perform C–H activation nearly million-fold faster than other known complexes, and can perform both hydroxylation and desaturation depending on the nature of the substrate.67 The nature of the active complex species in this reaction was unambiguously established earlier by Münck and co-workers using a bunch of spectroscopic tools (Mössbauer, EPR, and UV-visible).73,74
Theoretical studies play an important role in this area to obtain insight into the electronic structure of catalytically active species, and also to probe the mechanism of catalytic transformations.59,75 There are numerous reports in the literature on the electronic structure and mechanistic studies of mononuclear high-valent iron–oxo species, but there are only limited studies on dinuclear iron–oxo species.71,72,76,77 This is essentially due to the presence of numerous spin states arising from the exchange coupling between the two metal centres, and these states are often challenging to compute.57 In this work, we aim to discuss the electronic structure of dinuclear iron oxidants to rationalise the extremely high reactivity that is observed for the [HO(L)FeIII–O–FeIV(O)(L)]2+ (where L is tris(pyridine-2-yl)methyl amine)) open core complex with the cyclopentane (CP) substrate using density functional theory (DFT). By studying the mechanistic features, we aim to answer the following intriguing questions which remain open in this area for a long time (i) what is the origin of million-fold reactivity towards C–H bond cleavage observed for this open core diiron–oxo species? (ii) Is a terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O more reactive than a bridged one? if so why? (iii) While most of the mono and dinuclear iron–oxo species perform selective hydroxylation or desaturation, this complex was found to perform both at ease, why? (iv) How important is the spin-state in controlling the reactivity in dinuclear systems? (v) The two iron centres are coupled via strong exchange interaction, is this strong-coupling offers an electronic/spin-cooperativity enabling higher/diverse reactivity?
O more reactive than a bridged one? if so why? (iii) While most of the mono and dinuclear iron–oxo species perform selective hydroxylation or desaturation, this complex was found to perform both at ease, why? (iv) How important is the spin-state in controlling the reactivity in dinuclear systems? (v) The two iron centres are coupled via strong exchange interaction, is this strong-coupling offers an electronic/spin-cooperativity enabling higher/diverse reactivity?
Computational details
All calculations reported were performed using the Gaussian 09 suite of programs.78 By analysing these results along with all the previous observations, here we have chosen the B3LYP-D3 (ref. 79) functional for our study. The LACVP basis set comprising the LanL2DZ – Los Alamos effective core potential for Fe (ref. 80–82) and a 6-31G*83 basis set for the other atoms (carbon, nitrogen, oxygen, hydrogen, and chlorine) (B-I) were employed for geometry optimisation and frequency calculations. Single point calculations were performed using a def2-TZVP84,85 basis set (B-II) on the optimised geometries. The solvation energies were computed using the PCM solvation model,86 where acetonitrile was used as a solvent. The fragment approach available in the Gaussian 09 program has been employed to obtain open-shell singlet states87 and also to converge difficult multiplets. All the reported energies are B3LYP-D3 solvation energy (at the BS-II level) incorporating zero-point energy corrections (at the BS-I level) at 298.15 K. Additionally, for comparison, we have also given free-energy corrected energy values in the ESI (see Table S4a–c for C–H activation in the ESI).† To account for the effect of polarisation, the whole computations have been repeated (see Scheme 2) by adding two per-chlorite counter ions i.e. [HO(L)FeIII–O–FeIV(O)(L)]2+2[OClO3]−. The transition states were characterised by a single imaginary frequency which pertains to the desired motion as visualised in Chemcraft88 and Molden.89 The choice of functional for this study is based on our as well as other groups' reports on diiron(IV)–oxo complexes.67,77,90–94 Also, de Visser et al.72 tested a series of functionals (B3LYP, B3LYP*, BP86, M06-L, and PBE0) on μ-nitrido–diiron(IV)–oxo species and supported the use of the B3LYP functional for the reproduction of structure, spin state patterns, and spectral parameters.72,95–100 Furthermore, Chen et al. employed a similar methodology for their study on C–H/O–H/O–O bond activation using diiron(IV)–oxo species to gain insights into various mechanistic aspects and showed that this methodology can reproduce various experimental spectral parameters, offering confidence in the methodology chosen here.101–103 In our calculations, we have chosen cyclopentane as the substrate to test the hydroxylation vs. desaturation mechanism for simplicity, while experimentally tetrahydrofuran (THF), and other alkanes are used as the substrates. As both the substrates have similar C–H bond dissociation energy,104,105 and earlier experimental and theoretical studies have been undertaken using cyclopentane, here we chose to study the mechanism with this substrate.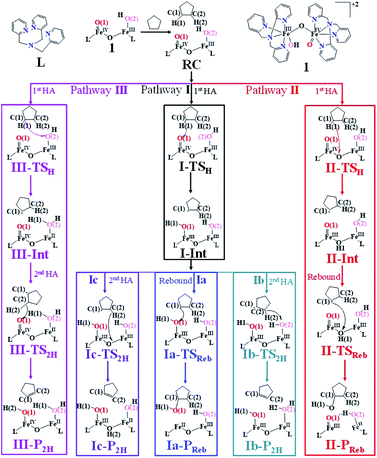 | ||
| Scheme 2 The schematic mechanism of oxidation of cyclopentane by complex 1 [HO(L)FeIII–O–FeIV(O)(L)]2+. | ||
In diiron complexes, the magnetic exchange (J) between both iron centres is computed by employing the following spin Hamiltonian,
| Ĥ = −JS1·S2 |
| ΔE‡ = ΔEdef + ΔEint | (1a) |
| ΔEint = ΔEorb + ΔEel + ΔEPauli(steric) | (1b) |
The total deformation energy (ΔEdef) is defined as the energy required for distorting the substrate and the oxidant to their geometries in the transition state (TS). The ΔEint is the interaction energy, which is the energy between the deformed reactants as they are brought to their distances in the TS. The interaction energy (eqn (1b)) can be stabilising (ΔEint < 0) due to the fact that the orbital mixing term (ΔEorb) is dominant and there is a favourable electrostatic interaction (ΔEel). Alternatively, ΔEint can be destabilising (ΔEint > 0) because of steric repulsions (labelled in eqn (1b) as ΔEPauli(steric)).115
Results and discussion
Que and co-workers reported a dinuclear [HO(L)FeIII–O–FeIV(O)(L)]2+ (1) complex (where L is tris((4-methoxy-3,5-dimethylpyridin-2-yl)methyl)amine) and thoroughly characterized the same using several spectroscopic techniques. Anisotropic EPR signals at g = 2.00, which broaden when 57Fe containing nuclear spins are introduced, reveal that the ground state spin for this molecule is S = 1/2 and the signals originate from iron centres and are not radical based. Mössbauer spectra reveal strong antiferromagnetic coupling between two Fe centres with the FeIII site (Sa) being in the high-spin state (Sa = 5/2) and the FeIV site being in the high-spin quintet state (Sb = 2) leading to a ground spin state ST = 1/2.8 Species 1 is found to be an aggressive oxidant towards a variety of substrates and the measured kinetics reveal that its reactivity is as good as that of taurine: α-ketoglutarase dioxygenase (TauD) as well as a shape-selective catalyst [Fe(TpPh2)OBz] (where TpPh2 = hydrotris(3,5-diphenylpyrazol-1-yl)borate and OBz = benzoate) – a rare feat to achieve in biomimetic chemistry.66 Particularly, species 1 is found to perform the oxygen atom transfer reaction with diphenyl(pentafluorophenyl)phosphine and activate the C–H bonds of DHA to anthracene and convert even inert substrates such as tetrahydrofuran (THF) to γ-butyrolactone very efficiently. Particularly 1 is found to cleave the C–H bond nearly 100 to million-fold faster compared to several dinuclear Fe systems containing the diamond-core motif.8 Further, the catalytic abilities of 1 are at least six times better compared to some of the strongest diiron(IV)–oxo species known.69 Above all, its efficacy to perform C–H bond activation followed by elimination to yield anthracene and with THF its ability to perform C–H bond activation followed by –OH rebound to yield tetrahydrofuran-2-ol (that eventually undergoes further oxidation to yield the observed γ-butyrolactone product) have puzzled us to look into its electronic structure and its catalytic abilities. This is rather a unique feat compared to other oxidants such as 1 due to both elimination and –OH rebound at ease, unlike other biomimetic models or enzymes which are generally selective towards desaturation or hydroxylation. In the forthcoming section, we first establish the electronic structure of 1, and in the subsequent sections, its catalytic potential is explored.Electronic structure of [HO(L)FeIII–O–FeIV(O)(L)]2+ (1)
The presence of two iron centres leads to the existence of various spin states, and strong coupling between the two centres results in a very complex spin state structure for 1. For example, the FeIII centre can have spin Sa = 5/2, 3/2, and 1/2 while the FeIV centre can have spin Sb = 2, 1, and 0 as their individual spin states. Further, the nature of the coupling between the two centres could be ferromagnetic or antiferromagnetic leading to different total spin multiplicity. Due to the difference in the oxidation state and the ligand environment, it is possible that two Fe centres could exhibit different spin states from each other. These three scenarios lead to fifteen different spin states that are possible for 1, and all these states are listed in Table 1. To understand the origin of the high-spin state observed for both the FeIII and FeIV centres, we performed calculations on fictitious models of complex 1 where the individual Fe centres are replaced by diamagnetic analogs to get a grasp on the spin ladder of Sa and Sb (models are [HO(L)FeIII–O–TiIV(O)(L)]2+, [HO(L)CoIII–O–FeIV(O)(L)]2+ and [HO(L)GaIII–O–FeIV(O)(L)]2+; note here that all the substituted metal ions have the S = 0 ground state).116 These model studies reveal that the FeIII centre has the Sa = 5/2 ground state with the Sa = 1/2 first excited state lying at 43.6 kJ mol−1 and the 3/2 state at 58.8 kJ mol−1 from the ground state. For the FeIV centre, Sb = 2 is found to be the ground state for both CoIII and GaIII ion substitutions with the Sb = 1 first excited state being 55.2 and 41.3 kJ mol−1 higher, respectively.This reveals that independent of the spin-coupling, the FeIV centre has a high-spin ground state. As S = 1 is the ground state for the popular [N4PyFeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ species,117–127 it is clear that replacing one of the nitrogen donors with an oxygen donor weakens the ligand field leading to the stabilisation of the unusual S = 2 state (a reduction of 0.56 eV in the ΔE(dxz − dx2−y2) orbital gap, see Fig. S1 and S2 in the ESI†). Additionally, calculations performed on the mononuclear [O(L)FeIV–OH2]2+ fictitious model derived from the dinuclear motif yield S = 1 as the ground state with S = 2 marginally higher in energy (5.6 kJ mol−1). This suggests that the second metal centre is important in stabilising the S = 2 state at the FeIV
O]2+ species,117–127 it is clear that replacing one of the nitrogen donors with an oxygen donor weakens the ligand field leading to the stabilisation of the unusual S = 2 state (a reduction of 0.56 eV in the ΔE(dxz − dx2−y2) orbital gap, see Fig. S1 and S2 in the ESI†). Additionally, calculations performed on the mononuclear [O(L)FeIV–OH2]2+ fictitious model derived from the dinuclear motif yield S = 1 as the ground state with S = 2 marginally higher in energy (5.6 kJ mol−1). This suggests that the second metal centre is important in stabilising the S = 2 state at the FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O site.
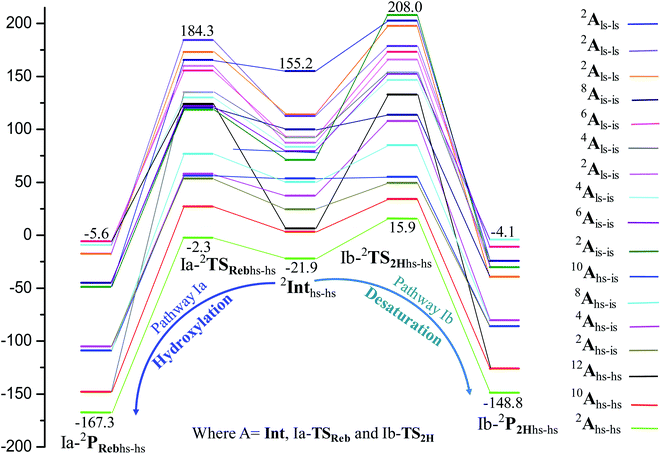
O site.
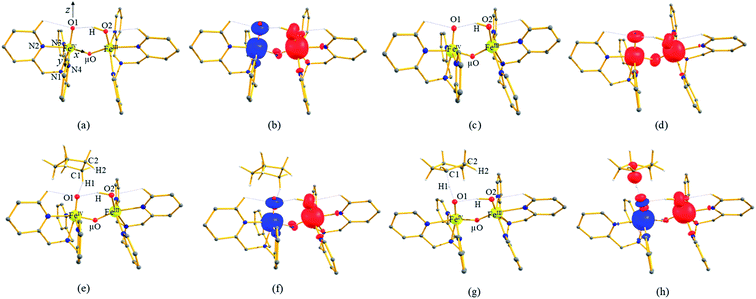
To further probe the origin of the high-spin ground state, we have also carried out calculations on [HO(L)FeIV–O–FeIV(O)(L)]3+ models wherein both the FeIV centres were found to have the S = 1 ground state coupled ferromagnetically to each other leading to an overall S = 2 state. Here the individual high-spin state of FeIV is 35.8 kJ mol−1 higher in energy compared to their corresponding triplet state revealing a fact that it is the +3 oxidation state of the neighbouring metal ion that weakens the ligand field leading to the stabilisation of the S = 2 state (see Fig. S3 and Table S2 in the ESI†).128 Among all the states computed, the 21hs–hs doublet state is found to be the ground state and this is followed by 101hs–hs, 81hs–is, 41hs–is, 61hs–ls, 81is–hs, 21is–hs, 61is–is, 21is–is, 41is–ls, 61ls–hs, 41ls–hs, 41ls–is, 21ls–is, and 21ls–ls states in the order of increasing energy with an energy margin of 15.6, 46.3, 48.4, 67.6, 37.8, 32.6, 74.7, 73.0, 112.4, 46.3, 80.8, 99.3, 98.9 and 136.6 kJ mol−1 respectively (see Table 1). Our energy calculations reveal that the FeIII (Sa) and FeIV (Sb) centres possess a high spin state as their ground state, and these states are antiferromagnetically coupled leading to the ST = 1/2 ground state, and this is also consistent with the experiments.9,129 This result is also consistent with other dinuclear {FeIII–μ(O)–FeIV} reports where ST = 1/2 is found to be the ground state.8 While traditionally DFT methods have been used to compute the energetics, recently several ab initio methods such as CASSCF/NEVPT2 and DLPNO-CCSD(T) are gaining attention in obtaining numerically superior results, although they have their limitations in terms of active space/size of the models.118,127,130–138 The optimised structure, and the spin density plot of the 21hs–hs state are shown in Fig. 1a and b, where both the Fe centres are in a distorted octahedral geometry (see also Table S3 in the ESI†).139 The 3d atomic orbitals of the iron atom of FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species form bonding and antibonding combinations with the oxygen atomic orbitals. Here the δ-type dxy orbital is found to be the lowest in energy followed by a degenerate pair of singly occupied π* orbitals made from the antibonding combinations of the oxygen 2px (2py) with the iron 3dxz (3dyz) atomic orbitals. The singly occupied orbital of the dx2−y2 is antibonding in the in-plane Fe–N/μO linkage while one virtual dz2 orbital has an antibonding character along the N1–FeIV–O1 axis (see Fig. 1a and S2 in the ESI†). The FeIII and FeIV high-spin states were found to have the electronic configurations of (δxy)1 (
O species form bonding and antibonding combinations with the oxygen atomic orbitals. Here the δ-type dxy orbital is found to be the lowest in energy followed by a degenerate pair of singly occupied π* orbitals made from the antibonding combinations of the oxygen 2px (2py) with the iron 3dxz (3dyz) atomic orbitals. The singly occupied orbital of the dx2−y2 is antibonding in the in-plane Fe–N/μO linkage while one virtual dz2 orbital has an antibonding character along the N1–FeIV–O1 axis (see Fig. 1a and S2 in the ESI†). The FeIII and FeIV high-spin states were found to have the electronic configurations of (δxy)1 ( )1 (
)1 ( )1 (
)1 ( )1 (
)1 (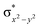 )1 and (δxy)1 (
)1 and (δxy)1 (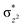 )1 (
)1 (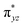 )1 (
)1 (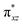 )1 (
)1 (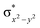 )0, respectively, for the 21hs–hs state (see also Fig. S2† for 21hs–hs and Fig. S4 in the ESI† for other spin states).
)0, respectively, for the 21hs–hs state (see also Fig. S2† for 21hs–hs and Fig. S4 in the ESI† for other spin states).
In 21hs–hs, the hydroxo group in the FeIII centre and oxo group in the FeIV centre have strong H-bonding interaction (O(1)–H = 1.856 Å), and this significantly reduces the ∠FeIV–μO–FeIII angle to 123° compared to 154° known for other unsupported diiron species.12 Additionally, the trans-N–FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond angle is found to be 169°, and this bent significantly compared to most of the mononuclear FeIV
O bond angle is found to be 169°, and this bent significantly compared to most of the mononuclear FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species and has been attributed to higher reactivity in [N2Py2QFeIV
O species and has been attributed to higher reactivity in [N2Py2QFeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ species. This ferryl-bent that has also been witnessed in the reported X-ray structure140 suggests that the bending can also lower the energy of the
O]2+ species. This ferryl-bent that has also been witnessed in the reported X-ray structure140 suggests that the bending can also lower the energy of the 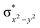 orbital. Here the ferryl-bent observed is more severe than the reported complex due to the presence of the additional metal centre, strong H-bonding interaction between the FeIV
orbital. Here the ferryl-bent observed is more severe than the reported complex due to the presence of the additional metal centre, strong H-bonding interaction between the FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit and the –OH group of the FeIII centre and the C–H⋯O interactions between the ferryl-oxygen and the hydrogen atom of the pyridine rings.140,141 The earlier spectroscopic and theoretical study also confirms that the angle is very acute for this species, and the estimated angle is consistent with the value obtained from EXAFS measurements.8,73 The Fe–μO bond distances are found to be 1.865 Å and 1.757 Å for the FeIII and FeIV site, respectively. This clearly reveals a strong valence localisation enforced due to strong structural distortions around the FeIV
O unit and the –OH group of the FeIII centre and the C–H⋯O interactions between the ferryl-oxygen and the hydrogen atom of the pyridine rings.140,141 The earlier spectroscopic and theoretical study also confirms that the angle is very acute for this species, and the estimated angle is consistent with the value obtained from EXAFS measurements.8,73 The Fe–μO bond distances are found to be 1.865 Å and 1.757 Å for the FeIII and FeIV site, respectively. This clearly reveals a strong valence localisation enforced due to strong structural distortions around the FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit. The terminal Fe–O(2)H(O1) distance is found to be 1.828 Å (1.641 Å) (see Fig. 1a). Our computed data are in agreement with earlier theoretical results and experiments.46,67,73
O unit. The terminal Fe–O(2)H(O1) distance is found to be 1.828 Å (1.641 Å) (see Fig. 1a). Our computed data are in agreement with earlier theoretical results and experiments.46,67,73
The Wiberg bond index142 computed for FeIII–μO and FeIV–μO is 0.62 and 0.80, respectively, revealing a single bond character between Fe and μO centres. The Wiberg bond index for the terminal FeIII–O(2) and FeIV–O(1) is estimated to be 0.62 and 1.30, revealing single and double bond characters for FeIII and FeIV centres, respectively. Natural bond orbital (NBO) analysis (see also Fig. S5 in the ESI†) reveals that the ionicity of the FeIV–μO bond is smaller compared to the FeIII–μO bond. The spin natural orbitals (SNOs) with atomic spin density values estimated for 21hs–hs (see Fig. S6 in the ESI†) reveal four β-spin (five α-spin) electrons for the FeIV (FeIII) centre. The high-spin FeIV centre undergoes pseudo-Jahn–Teller distortion (axial compression) possessing a longer Fe–N(L) distance and shorter FeIV–O(1) distance (see Table S4a in the ESI†). These distortions in the coordination environment of FeIV lead to a pure valence localisation picture, as stated earlier,8 and is supported by the computed spin density plots (see Fig. 1b). The bridging μO atom has net positive spin density reflecting stronger delocalisation of spins from the dominant α carrier FeIII while the terminal hydroxo/oxo (0.38/−0.48) group is found to have strong delocalisation of spins from the metal centre143 (see Table S5a in the ESI†). Of particular relevance is the spin density of the terminal oxygen connected to the FeIV unit, where significant negative spin density is detected, revealing an oxyl radical character that is responsible for the high reactivity of such species earlier.67,72,144
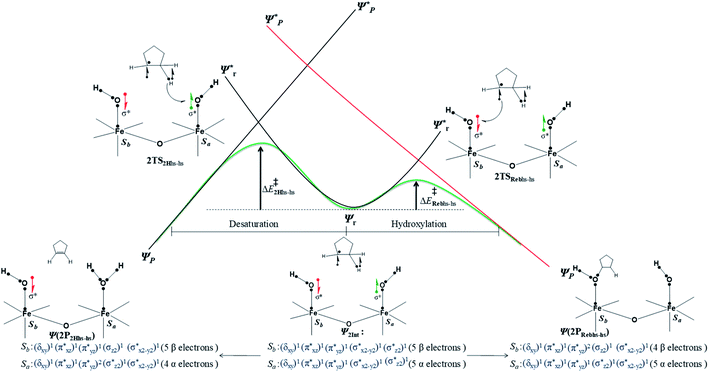
The second most important state is 101hs–hs that lies very close to the ground state and corresponds to a ferromagnetic coupling between high-spin FeIII and FeIV centres. Here the geometry is very similar to 21hs–hs, with a notable difference being slightly longer FeIV–O(1) distances (1.642 Å) (see Fig. 1c and Table S4a in the ESI†). Computed spin density values for the first excited spin state (101hs–hs) with respect to 21hs–hs on the FeIV and FeIII were found to be 3.04 and 4.04, respectively (see Fig. 1d) also suggesting a valence localisation of the spins. The magnetic coupling of the complex 1 for a high spin (S = 2 and S = 5/2) is computed using the ground state structure employing the standard protocol,145 and this gives a J value of −137.3 cm−1, and this matches well with the experimental estimate of −90 ± 20 cm−1 reported using EPR studies73 offering confidence in the estimated structures and properties. Here, we have computed the overlap integral between two SOMOs of the Fe centres108 and a significant overlap is noted between the SOMOs of dyz and dxz orbitals of FeIII and FeIV centres, respectively, and this strong overlap is found to be responsible for the strong antiferromagnetic coupling observed (see Tables S6 and S7 in the ESI†). In the subsequent section, the reactivity of species 1 is discussed towards cyclopentane as a substrate for the hydroxylation and desaturation reaction. We discuss first the 1st hydrogen abstraction from cyclopentane as a substrate and later expand the mechanism to hydroxylation vs. desaturation pathways as discussed earlier.
First hydrogen atom abstraction
Based on reported experimental evidence on 1 and related studies, we have adapted various mechanistic pathways for the hydroxylation and dehydrogenation reaction,120,146,147 as shown in Scheme 2. The first hydrogen atom abstraction can be due to (i) the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) centre (pathway I) (ii) or by the μ-oxo bridge that lies between the FeIV and FeIII centres (pathway II) (iii) or by the terminal FeIII–O(2)H species (pathway III). The individual pathways assumed are further diverged into either hydroxylation that can happen via rebound or second hydrogen atom abstraction leading to desaturation. In pathway I, the first hydrogen atom abstraction from cyclopentane via the transition state (I-TSH) leads to the formation of the radical intermediate (I-Int).
O(1) centre (pathway I) (ii) or by the μ-oxo bridge that lies between the FeIV and FeIII centres (pathway II) (iii) or by the terminal FeIII–O(2)H species (pathway III). The individual pathways assumed are further diverged into either hydroxylation that can happen via rebound or second hydrogen atom abstraction leading to desaturation. In pathway I, the first hydrogen atom abstraction from cyclopentane via the transition state (I-TSH) leads to the formation of the radical intermediate (I-Int).
This radical intermediate can either undergo the –OH rebound step viaIa-TSreb and yield the hydroxylated product (Ia-Preb; pathway Ia) or undergo second hydrogen abstraction viaIb-TS2H leading to cyclopentene (Ib-P2H; pathway Ib). Additionally, the second hydrogen atom could also be abstracted by the μ-oxo bridge present at the I-IntviaIc-TS2H (pathway Ic), leading to desaturation. In pathway II, the hydrogen abstraction by the μ-oxo bridge led to II-Int, and this in the subsequent step undergoes –μOH rebound hydroxylation leading to the hydroxylated product. In pathway III, the first hydrogen atom abstraction leads to III-Int, which subsequently undergoes second hydrogen atom abstraction (viaIII-TS2H) by the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) leading to the desaturated product.
O(1) leading to the desaturated product.
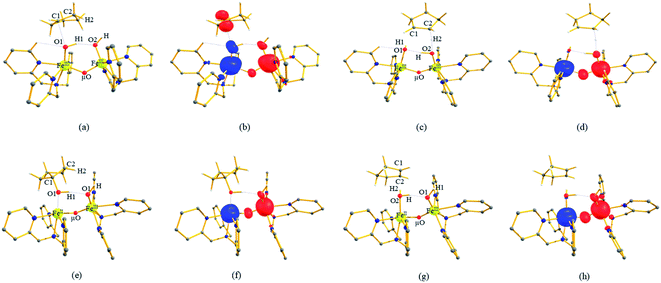
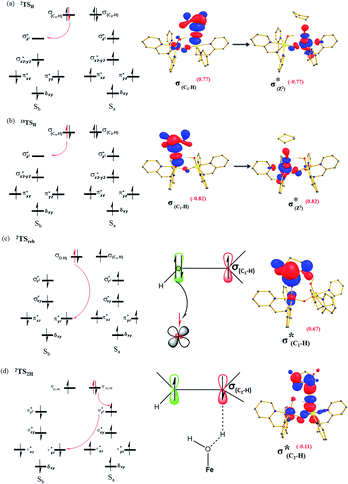
The computed potential energy surface (PES) for the oxidation of cyclopentane is shown in Fig. 2 (pathway I). In the first step, a weak reactant complex formation is assumed with the substrate, and the O⋯H interaction between O(1) and a hydrogen atom of the substrate. We have computed nine possible spin states with 2RChs–hs as the ground state, with the 10RChs–hs, 8RChs–is, 4RChs–is, 6RCis–is, 2RCis–is, 4RCls–is, 2RCls–is, and 2RCls–ls states lying at 0.9, 23.2, 18.9, 60.2, 58.7, 85.1, 85.3 and 164.6 kJ mol−1, respectively. Formation of species RC from the reactant is found to be slightly exothermic by −18.1 kJ mol−1 justifying the need to invoke such complex formation. The optimised structures are similar to the ground state structure estimated with some minor alterations (see Fig. 1e and f and Table S4a† for structural parameters, and spin density Table S5a in the ESI†). The O(1)–H(1) and C(1)–H(1) bond distances of the 2RChs–hs state are computed to be 2.575 Å and 1.097 Å, respectively.
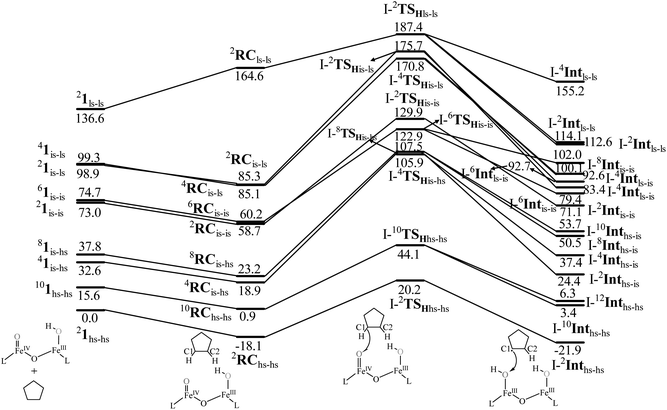 | ||
| Fig. 2 B3LYP-D3 computed energy for the C–H bond hydroxylation of cyclopentane (CP) by species 1 (energies are in kJ mol−1). | ||
In pathway I, our computed results show that the I-2TSHhs–hs is the lowest-lying with an extremely small barrier height of 38.3 kJ mol−1 while the I-10TSHhs–hs, I-8TSHhs–is, I-4TSHhs–is, I-6TSHis–is, I-2TSHis–is, I-4TSHls–is, I-2TSHls–is and I-2TSHls–ls transition states lie higher at 62.2, 125.6, 124.0, 141.0, 148.0, 188.9, 193.8, and 205.5 kJ mol−1 respectively with respect to RC. Clearly, all the spin states are higher in energy and the reactivity at this step is dictated by the antiferromagnetically coupled states of high-spin FeIII and FeIV centres with a small but a finite possibility of the ferromagnetically coupled state also participating in the mechanism. From the reactant, the barrier is merely 20.2 kJ mol−1, revealing an extremely low barrier height to activate relatively inert substrates such as cyclopentane, and this is consistent with the million-fold reactivity order observed in the experiments. The lower barrier height observed for the I-2,10TSHhs–hs species suggests a possible two-state reactivity scenario as noted for mononuclear FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes.52,53 However, the stark difference here is that these states arise due to the difference in exchange coupling and therefore are expected to be very close-lying in energy. The optimised structure of the I-2TSHhs–hs for the C–H bond activation is shown in Fig. 1g. For the I-2TSHhs–hs species, the FeIV–O(1) bond length is found to be elongated to 1.752 Å from 1.639 Å and the C(1)–H(1) bond to 1.230 Å from 1.097 Å (see Fig. 1e and g and S9†). The O(1)–H(1)–C(1) (cyclopentane) bond angle is determined to be 170° while the FeIV–O(1)–H(1) angle is found to be 157°. The lengthening of the bond in the C–H⋯O1 interaction (2.425 Å from 2.312 Å) in I-TSH reflects the fact that the oxyl group has lower electron-donating capability relative to the more negatively charged oxo ligand. This step is found to be the rate-determining step for both alkene and hydroxylation reactions (see below). As expected for the FeIV
O complexes.52,53 However, the stark difference here is that these states arise due to the difference in exchange coupling and therefore are expected to be very close-lying in energy. The optimised structure of the I-2TSHhs–hs for the C–H bond activation is shown in Fig. 1g. For the I-2TSHhs–hs species, the FeIV–O(1) bond length is found to be elongated to 1.752 Å from 1.639 Å and the C(1)–H(1) bond to 1.230 Å from 1.097 Å (see Fig. 1e and g and S9†). The O(1)–H(1)–C(1) (cyclopentane) bond angle is determined to be 170° while the FeIV–O(1)–H(1) angle is found to be 157°. The lengthening of the bond in the C–H⋯O1 interaction (2.425 Å from 2.312 Å) in I-TSH reflects the fact that the oxyl group has lower electron-donating capability relative to the more negatively charged oxo ligand. This step is found to be the rate-determining step for both alkene and hydroxylation reactions (see below). As expected for the FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, the reaction takes place at the FeIV
O group, the reaction takes place at the FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) unit and proceeds via the σ channel, and this mechanism has been well-established for mononuclear FeIV
O(1) unit and proceeds via the σ channel, and this mechanism has been well-established for mononuclear FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes.148–150 In the σ channel, one electron from the substrate that has the same spin as the remaining electrons in the FeIV centre is transferred into the σ*(Fe
O complexes.148–150 In the σ channel, one electron from the substrate that has the same spin as the remaining electrons in the FeIV centre is transferred into the σ*(Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) antibonding orbital during C–H bond activation by a high-spin FeIV
O) antibonding orbital during C–H bond activation by a high-spin FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) centre. One of the most important characteristic features that occur upon approaching the transition state is the FeIV–O(1)–H(1) angle in I-TSH, and these angles for the σ-pathway are close to 180°.151–153 An analysis of the group spin densities and charges (based on Mülliken analysis) indicates that cyclopentane at I-2TSHhs–hs has a radical character with the group spin density estimated to be ρC(1) = 0.39 (where ρ = spin density) with small overall charge (group charge QC(1) = −0.12). The spin values on the H(1) (transferred hydrogen) increase from 0.00 to 0.02 at the transition state but at the same time, the electron shifts to the
O(1) centre. One of the most important characteristic features that occur upon approaching the transition state is the FeIV–O(1)–H(1) angle in I-TSH, and these angles for the σ-pathway are close to 180°.151–153 An analysis of the group spin densities and charges (based on Mülliken analysis) indicates that cyclopentane at I-2TSHhs–hs has a radical character with the group spin density estimated to be ρC(1) = 0.39 (where ρ = spin density) with small overall charge (group charge QC(1) = −0.12). The spin values on the H(1) (transferred hydrogen) increase from 0.00 to 0.02 at the transition state but at the same time, the electron shifts to the 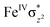 orbital of FeIV
orbital of FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) leading to attenuation of spin density from −0.48 to 0.02 in I-2TSHhs–hs at the oxo centre. The spin density on the iron ion in I-2TSHhs–hs increases from −3.03 to −3.78. The change in the spin density value suggests a β-electron transfer from the substrate to the
O(1) leading to attenuation of spin density from −0.48 to 0.02 in I-2TSHhs–hs at the oxo centre. The spin density on the iron ion in I-2TSHhs–hs increases from −3.03 to −3.78. The change in the spin density value suggests a β-electron transfer from the substrate to the 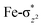 orbital of the FeIV centre accompanied by FeIV attaining the +3 oxidation state (see Fig. 3).153,154 Thus, the proposed mechanism consists of a Proton-Coupled Electron Transfer (PCET) process from the substrate115,155 to the FeIV centre. Fig. 3 shows the electron-shift diagram for the PCET step for both doublet and dectet spin states with interacting orbitals and SNO occupation. In the RC, the FeIII iron centres of the doublet and dectet have five unpaired α electrons in the d-orbital.
orbital of the FeIV centre accompanied by FeIV attaining the +3 oxidation state (see Fig. 3).153,154 Thus, the proposed mechanism consists of a Proton-Coupled Electron Transfer (PCET) process from the substrate115,155 to the FeIV centre. Fig. 3 shows the electron-shift diagram for the PCET step for both doublet and dectet spin states with interacting orbitals and SNO occupation. In the RC, the FeIII iron centres of the doublet and dectet have five unpaired α electrons in the d-orbital.
 | ||
| Fig. 3 Electron shift diagrams of I-TSH for both (a) I-2TSHhs–hs, (b) I-10TSHhs–hs, (c) Ia-2TSrebhs–hs and (d) Ib-2TS2Hhs–hs with SNOs and their occupation (noted in parentheses). | ||
The FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) (Sb) centre has four unpaired electrons which have spin-up α orientation in 10RChs–hs and β orientation in the 2RChs–hs. At the I-2TSHhs–hs and I-10TSHhs–hs transition states, one electron is transferred to the FeIV σ*(dz2) orbital and the spin orientation of the transferred electron is β and α, respectively for the I-2TSHhs–hs and I-10TSHhs–hs transition states. Even though the PCET step of both the spin-states offers exchange-enhanced reactivity (EER) stabilisation,137,152,156,157 this is likely to be larger for the doublet state than for the dectet state. Also, at the transition state, the ϕC and dx2−y2 orbitals are found to have significant overlap revealing retention of the estimated antiferromagnetic coupling at the reactant level (see Tables S8 and S9 in the ESI†).
O(1) (Sb) centre has four unpaired electrons which have spin-up α orientation in 10RChs–hs and β orientation in the 2RChs–hs. At the I-2TSHhs–hs and I-10TSHhs–hs transition states, one electron is transferred to the FeIV σ*(dz2) orbital and the spin orientation of the transferred electron is β and α, respectively for the I-2TSHhs–hs and I-10TSHhs–hs transition states. Even though the PCET step of both the spin-states offers exchange-enhanced reactivity (EER) stabilisation,137,152,156,157 this is likely to be larger for the doublet state than for the dectet state. Also, at the transition state, the ϕC and dx2−y2 orbitals are found to have significant overlap revealing retention of the estimated antiferromagnetic coupling at the reactant level (see Tables S8 and S9 in the ESI†).
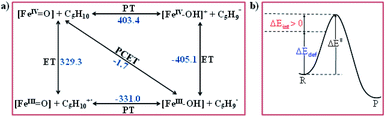
To further understand the nature of the hydrogen transfer mechanism, we have constructed a thermodynamic cycle considering PCET (proton-coupled electron transfer), PT–ET (proton transfer followed by electron transfer), and ET–PT (electron transfer followed by proton transfer) pathways (see Fig. 4).93,95,97,98 Our calculations reveal a significant energy penalty for the PT–ET and ET–PT steps. Further spin density values (see Fig. 1h and 5) indicate that the transition state resembles FeIII–OH species suggesting the PCET type mechanism as revealed by the computed energetics. Additionally, the mechanism can also be differentiated by computing deformation energies (ΔEdef) at the transition state and comparing it against the gas-phase barrier (ΔE‡) and interaction energies (ΔEint) as stated earlier by Shaik and co-workers.115 Our calculated ΔE‡, ΔEdef, and ΔEint values are 59.9, 22.7, and 36.0 kJ mol−1, respectively revealing ΔEdef < ΔE‡ and ΔEint > 0 scenarios and thus strongly favouring PCET processes of the C–H bond of cyclopentane and not HAT (also see ESI† for additional text on PCET vs. HAT).115
To further understand the electronic co-operation between the two metal centres, we have replaced the neighbouring FeIII ion by CoIII and GaIII ions and computed the corresponding transition state at the S = 2 surface. The barrier height estimated for this fictitious model is found to be 44.4 and 31.3 kJ mol−1 with respect to the reactant (see Fig. S10 and S11 in the ESI†) for CoIII and GaIII substitutions, respectively. This barrier height computed is higher compared to the FeIII centre revealing the importance of spin-cooperation in dictating the reactivity of species 1. This barrier height computed for the fictitious [HO(L)CoIII–O–FeIV(O)(L)]2+ models is similar to the estimate found for mononuclear enzyme TauD as well as the model catalysts [TpOBzFeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O], for the first hydrogen atom abstraction from cyclopentane where spin-cooperation is absent.66
O], for the first hydrogen atom abstraction from cyclopentane where spin-cooperation is absent.66
A hydrogen atom abstraction leads to an intermediate {(OH)FeIII–μ(O)–FeIII(OH)} (I-Int). Considering the exchange interaction between Sa and Sb iron centres and spin on the cyclopentyl radical coupled to the unpaired electrons on both iron centres, there are seventeen possible spin states, and we have computed all spin states for this species. Compared to the reactant energies, the I-2Inths–hs state is found to be the lowest-lying at −21.9 kJ mol−1 (see Fig. 5a and b) followed by I-12Inths–hs, I-10Inths–hs, I-10Inths–is, I-8Inths–is, I-4Inths–is, I-2Inths–is, I-8Intis–is, I-6Intis–is, I-2Intis–is, I-4Intls–ls, I-2Intls–ls, I-2Intls–ls, I-6Intls–is, I-4Intls–is, I-4Intls–is and I-2Intls–is states at 6.3, 3.4, 53.7, 50.5, 37.4, 24.4, 100.0, 79.4, 71.1, 155.2, 114.0, 112.6, 92.7, 92.6, 83.4 and 87.3 kJ mol−1 energies, respectively. As spin-down electron shifts from σ(C(1)–H(1)) to the metal centre, a spin-up radical character develops at the surface as revealed by significant spin density at the carbon centre in all the intermediates computed (ρC(1) = 0.93 for I-2Inths–hs with QC(1) = 0.04 and see Fig. S12 in the ESI† for the orbital interaction diagram). The calculated energies reveal that I-2Inths–hs is thermodynamically stable (28.2 kJ mol−1) relative to I-12Inths–hs, and this is the manifestation of antiferromagnetic interaction between the metal centres. As we move from left to right in Fig. 2, the strength of antiferromagnetic coupling is enhanced and this is due to the addition of a β electron to the σ*(dz2) at the Sb iron centre in the doublet state which maximises the d- orbital overlap between the two Fe centres (see Fig. S13 in the ESI†).
In pathway II, the barrier for the first hydrogen atom abstraction by the μ-oxo bridge is found to be 160.1 kJ mol−1 with respect to the RC, and this is nearly eight times larger than the transition state computed using pathway I at the doublet surface (see Fig. 8). The optimised structure and spin density plot of the II-2RChs–hs, II-2TSHhs–hs, and II-2Inths–hs are shown in Fig. S14a–f in the ESI.† Here at the II-TSH, the FeIV–O(1)–H(1) angle is found to be 106° revealing π type reactivity as the substrate is hindered and cannot approach in a linear fashion as required for a lower barrier σ channel observed in pathway I (see Fig. S15a in the ESI†). The first hydrogen atom abstraction leads to the formation of the II-Int [HO(L)FeIII–O–FeIII(O)(L)]2+ intermediate. The formation of this species is found to be endothermic by 60.1 kJ mol−1. As the two Fe centres are antiferromagnetically coupled, the spin density at the μ-oxo bridge is found to be only 0.05, suggesting a significantly reduced radical character (compared to ferryl-oxygen in the FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) unit) and hence a larger barrier height. This suggests that when both terminal and bridge μ-oxo are present in the complex, the reactivity is expected to occur via the terminal FeIV
O(1) unit) and hence a larger barrier height. This suggests that when both terminal and bridge μ-oxo are present in the complex, the reactivity is expected to occur via the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit. Also, in enzymes such as sMMO where bis μ-oxo bridged dimers are proposed, the reactivity may be triggered by the open-ended structure where the μ-oxo bridge first undergoes cleavage to generate a terminal FeIV
O unit. Also, in enzymes such as sMMO where bis μ-oxo bridged dimers are proposed, the reactivity may be triggered by the open-ended structure where the μ-oxo bridge first undergoes cleavage to generate a terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) unit followed by hydrogen atom abstraction as has been suggested very recently.13
O(1) unit followed by hydrogen atom abstraction as has been suggested very recently.13
In pathway III, the first hydrogen abstraction by the terminal FeIII–O(2)H is estimated to have a barrier of 126.2 kJ mol−1, which is nearly six times larger compared to the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) group considered in pathway I at the doublet surface (see Fig. 6). The optimised structure and spin density plot of the III-2TSHhs–hs and III-2Inths–hs are shown in Fig. S16a–d in the ESI.† The FeIII–O(2)–H(1) angle here is found to be 130° revealing a π-type pathway as the linear approach is restricted by the additional hydrogen atom present (see Fig. S15b†). Besides as FeIII is an exchange saturated state and poorer electrophile compared to FeIV
O(1) group considered in pathway I at the doublet surface (see Fig. 6). The optimised structure and spin density plot of the III-2TSHhs–hs and III-2Inths–hs are shown in Fig. S16a–d in the ESI.† The FeIII–O(2)–H(1) angle here is found to be 130° revealing a π-type pathway as the linear approach is restricted by the additional hydrogen atom present (see Fig. S15b†). Besides as FeIII is an exchange saturated state and poorer electrophile compared to FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species as revealed by a significantly less radical character (spin density of 0.38 at the oxygen atom of the –OH group) the barrier height estimated is in line with the expectation. The abstraction of the hydrogen atom leads to the formation of III-Int, which in the subsequent step is expected to undergo second hydrogen atom abstraction by the terminal FeIV
O species as revealed by a significantly less radical character (spin density of 0.38 at the oxygen atom of the –OH group) the barrier height estimated is in line with the expectation. The abstraction of the hydrogen atom leads to the formation of III-Int, which in the subsequent step is expected to undergo second hydrogen atom abstraction by the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) unit leading to the desaturated product. The formation of III-Int is endothermic by 78.6 kJ mol−1.
O(1) unit leading to the desaturated product. The formation of III-Int is endothermic by 78.6 kJ mol−1.
 | ||
| Fig. 6 Potential energy surface computed (energies are in kJ mol−1) for C–H activation of cyclopentane by species 21hs–hs comparing the lowest estimate of barrier heights obtained from various pathways computed in Scheme 2. | ||
It is important to note here that the substitution of the –OH group by –F in the Fe(III) centre was found to enhance the reactivity significantly.67,158 We also performed additional calculations on the [F(L)FeIII–O–FeIV(O)(L)]2+ species to see if the spin-cooperation discussed is visible upon substitution by –F and our orbital analysis reveals that there is significant overlap between the d-orbitals of the two Fe centres suggesting strong spin-cooperation (see Fig. S17a–c in the ESI†). Due to strong hydrogen bonding interactions, compound 1 was found to have a syn conformation as its ground state, while the [F(L)FeIII–O–FeIV(O)(L)]2+ complex was found to have an anti conformation as its ground state. This significantly reduces the steric strain of the substrate approaching the complex, lowering the barrier height. This has been explored thoroughly earlier by Neese et al.67
Hydroxylation vs. desaturation
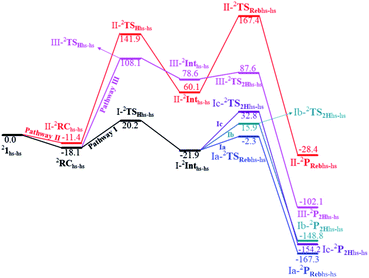
In the next step of pathway I, there are three possible pathways (i) rebound of the O–H group to the cyclopentyl radical (pathway Ia) or (ii) second hydrogen abstraction from the cyclopentyl radical (pathway Ib) by the terminal FeIII–O(1)H(1) group (see Scheme 2) or (iii) second hydrogen abstraction by the μ-oxo bridge from the cyclopentyl radical (pathway Ic).66,159 Here, all three steps have a common intermediate species, which is generated by the hydrogen abstraction from the C(1)–H(1) bond of cyclopentane. The FeIII–OH intermediate species has the capability to perform –OH rebound to yield hydroxylation or can abstract the second hydrogen atom leading to the desaturation product. Various factors dictate how the reaction diverges from the intermediate. Here in this example studied, it is capable of performing both the reactions suggesting that the barrier height for –OH rebound and desaturation are likely to be affordable unlike in other dinuclear Fe(IV)–oxo dimers where –OH rebound has not been witnessed.13 The divergence is dictated by many factors such as the nature of the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, the organic substrate, the steric hindrance, the coordinated ligands, the spin state during the reaction pathways, and the nature of magnetic coupling that exists between the two metal centres. The conversion of the cyclopentyl radical to the corresponding cyclopentanol through the rebound pathway (pathway Ia) is shown in Scheme 2. We have calculated Ia-12TSrebhs–hs, Ia-10TSrebhs–hs, Ia-2TSrebhs–hs, Ia-10TSrebhs–is, Ia-8TSrebhs–is, Ia-4TSrebhs–is, Ia-2TSrebhs–is, Ia-8TSrebis–is, Ia-6TSrebis–is, Ia-2TSrebis–is, Ia-4TSrebls–ls, Ia-2TSrebls–ls, Ia-2TSrebls–ls, Ia-6TSrebls–is, Ia-4TSrebls–is, Ia-4TSrebls–is and Ia-2TSrebls–is transitions states and Ia-2TSrebhs–hs is found to be the lowest in energy which is found to be 19.6 kJ mol−1 followed by 146.1, 49.1, 78.3, 98.7, 79.8, 74.4, 142.7, 143.8, 140.5, 187.5, 198.4, 206.2, 177.5, 157.1, 152.1, and 180.7 kJ mol−1 respectively with respect to the I-Int (see Fig. 7).
O bond, the organic substrate, the steric hindrance, the coordinated ligands, the spin state during the reaction pathways, and the nature of magnetic coupling that exists between the two metal centres. The conversion of the cyclopentyl radical to the corresponding cyclopentanol through the rebound pathway (pathway Ia) is shown in Scheme 2. We have calculated Ia-12TSrebhs–hs, Ia-10TSrebhs–hs, Ia-2TSrebhs–hs, Ia-10TSrebhs–is, Ia-8TSrebhs–is, Ia-4TSrebhs–is, Ia-2TSrebhs–is, Ia-8TSrebis–is, Ia-6TSrebis–is, Ia-2TSrebis–is, Ia-4TSrebls–ls, Ia-2TSrebls–ls, Ia-2TSrebls–ls, Ia-6TSrebls–is, Ia-4TSrebls–is, Ia-4TSrebls–is and Ia-2TSrebls–is transitions states and Ia-2TSrebhs–hs is found to be the lowest in energy which is found to be 19.6 kJ mol−1 followed by 146.1, 49.1, 78.3, 98.7, 79.8, 74.4, 142.7, 143.8, 140.5, 187.5, 198.4, 206.2, 177.5, 157.1, 152.1, and 180.7 kJ mol−1 respectively with respect to the I-Int (see Fig. 7).
 | ||
| Fig. 7 B3LYP-D3 computed PES for the formation of C5H11OH/C5H10 through intermediates leading to desaturation and hydroxylation (energies are in kJ mol−1). | ||
In Ia-2TSrebhs–hs, the α electron of ϕ(C1) has to transfer to the 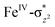 of the FeIII (Sb) iron centre to form coordinated cyclopentanol with the FeII (Sb) iron centre (see Fig. 8a and b, 3c and S18 in the ESI†). As the Ia-10TSrebhs–hs state already has all the α d-orbitals occupied, it can only accept a β electron from the ϕ(C1) to the
of the FeIII (Sb) iron centre to form coordinated cyclopentanol with the FeII (Sb) iron centre (see Fig. 8a and b, 3c and S18 in the ESI†). As the Ia-10TSrebhs–hs state already has all the α d-orbitals occupied, it can only accept a β electron from the ϕ(C1) to the 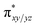 of the FeIII (Sb) centre. This leads to a reduction in the overall spin multiplicity and hence relatively a larger barrier. For the 21hs–hs state, the hydrogen atom abstraction is found to occur in the σ channel while the rebound step is found to occur in the π channel. It is observed that the FeIII–O(1)–C(1) angles of the Ia-2TSrebhs–hs (139°) are different from the I-2TSHhs–hs (155°).160 During the formation of the I-Int, both the FeIII centres are exchange saturated, and hence higher spin states require additional pairing energy leading to relatively larger barrier heights. At the doublet spin surface, however, both the spin-up and spin-down electrons are separated in a spin-polarised state offering flexibility in accepting either spin-down or spin-up electrons without compromising the overall spin multiplicity as shown in the electron-shift diagram in Fig. S19 in the ESI.† Thus, the antiferromagnetic coupling between the two Fe centres was found to be crucial in dictating the diverse reactivity observed. Furthermore, we have also computed all seventeen transition states corresponding to the second hydrogen atom abstraction of the cyclopentyl radical (pathway Ib) with Ib-2TS2Hhs–hs being found to have the lowest barrier height (37.8 kJ mol−1) followed by Ib-12TS2Hhs–hs, Ib-10TS2Hhs–hs, Ib-2TS2Hhs–hs, Ib-10TS2Hhs–is, Ib-8TS2Hhs–is, Ib-4TS2Hhs–is, Ib-2TS2Hhs–is, Ib-8TS2His–is, Ib-6TS2His–is, Ib-2TS2His–is, Ib-4TS2Hls–ls, Ib-2TS2Hls–ls, Ib-2TS2Hls–ls, Ib-6TS2Hls–is, Ib-4TS2Hls–is, Ib-4TS2Hls–is and Ib-2TS2Hls–is transitions states with a barrier height of 154.7, 56.1, 77.1, 107.1, 130.1, 71.3, 135.8, 174.6, 229.9, 224.7, 219.8, 200.7, 195.2, 175.6168.7 and 188.1 kJ mol−1, respectively. For the Ib-2TS2Hhs–hs transition state (see Fig. 8c and d), the FeIII–O(2)H bond is further elongated (1.940 Å) compared to the intermediate and the newly formed O(2)–H(2) and H(2)–C(2) bonds are 1.336 Å and 1.291 Å long respectively.
of the FeIII (Sb) centre. This leads to a reduction in the overall spin multiplicity and hence relatively a larger barrier. For the 21hs–hs state, the hydrogen atom abstraction is found to occur in the σ channel while the rebound step is found to occur in the π channel. It is observed that the FeIII–O(1)–C(1) angles of the Ia-2TSrebhs–hs (139°) are different from the I-2TSHhs–hs (155°).160 During the formation of the I-Int, both the FeIII centres are exchange saturated, and hence higher spin states require additional pairing energy leading to relatively larger barrier heights. At the doublet spin surface, however, both the spin-up and spin-down electrons are separated in a spin-polarised state offering flexibility in accepting either spin-down or spin-up electrons without compromising the overall spin multiplicity as shown in the electron-shift diagram in Fig. S19 in the ESI.† Thus, the antiferromagnetic coupling between the two Fe centres was found to be crucial in dictating the diverse reactivity observed. Furthermore, we have also computed all seventeen transition states corresponding to the second hydrogen atom abstraction of the cyclopentyl radical (pathway Ib) with Ib-2TS2Hhs–hs being found to have the lowest barrier height (37.8 kJ mol−1) followed by Ib-12TS2Hhs–hs, Ib-10TS2Hhs–hs, Ib-2TS2Hhs–hs, Ib-10TS2Hhs–is, Ib-8TS2Hhs–is, Ib-4TS2Hhs–is, Ib-2TS2Hhs–is, Ib-8TS2His–is, Ib-6TS2His–is, Ib-2TS2His–is, Ib-4TS2Hls–ls, Ib-2TS2Hls–ls, Ib-2TS2Hls–ls, Ib-6TS2Hls–is, Ib-4TS2Hls–is, Ib-4TS2Hls–is and Ib-2TS2Hls–is transitions states with a barrier height of 154.7, 56.1, 77.1, 107.1, 130.1, 71.3, 135.8, 174.6, 229.9, 224.7, 219.8, 200.7, 195.2, 175.6168.7 and 188.1 kJ mol−1, respectively. For the Ib-2TS2Hhs–hs transition state (see Fig. 8c and d), the FeIII–O(2)H bond is further elongated (1.940 Å) compared to the intermediate and the newly formed O(2)–H(2) and H(2)–C(2) bonds are 1.336 Å and 1.291 Å long respectively.
At the Ib-2TS2Hhs–hs state the O(2)–H(2)–C(2) (cyclopentyl radical) bond angle is determined to be 166° while the FeIII–O1–H1 angle is also determined to be 157°. The σ channel reactivity observed here is unusual compared to other systems and the presence of two Fe centres and significant electronic cooperativity that operates between them facilitate such behaviour.
A closer look at the orbital diagram and orbital occupation reveals an interesting picture wherein at the Ib-2TS2Hhs–hs transition state, an α electron from C2–H gets transferred to the σ*(dz2) of the FeIII (Sa) iron centre, and at the same time, it has lost another α electron to the second FeIII (Sb) centre, i.e. an electron transfer from the substrate triggers a simultaneous internal electron transfer from one FeIII centre to the second Fe centre revealing the presence of electronic cooperativity between the two FeIII centres. We have witnessed such electronic cooperativity earlier in dinuclear iron(IV)–oxo90 and iron(IV)–oxo–nitrido species71 and detecting a similar scenario here in the mixed-valence iron(III/IV) dimer reveals a similar pattern among dinuclear complexes. After transferring an electron from the cyclopentyl radical, the Sa remains as the FeIII–O(2)H group while Sb becomes an FeII–O(1)H(1) centre (see Fig. 3d and S20 in the ESI†).
In pathway Ia, the –OH group is expected to rebound to the cyclopentyl radical to give cyclopentanol (Ia-Preb). Here, we have computed eight possible spin states with Ia-10Prebhs–hs lying at −147.8 kJ mol−1 (from the 21hs–hs state, see ESI† for other energies). The thermodynamic formation of this product is estimated to be −167.3 kJ mol−1, indicating the facile formation of this product. In the 2Prebhs–hs state, both the iron centres are antiferromagnetically coupled with the coupling constant (J) being −150.5 cm−1 (see Fig. 8e and f for the optimised structure, and for the spin density plot of SNOs see Fig. S21 in the ESI†). In pathway Ib, the terminal –O(2)H group is expected to abstract a second hydrogen atom from the cyclopentyl radical to give cyclopentene (Ib-2P2Hhs–hs lying at −148.8 kJ mol−1 with a J value of −141.4 cm−1, see Fig. 8g and h and S22 for SNOs in the ESI†). Additional calculations performed incorporating counterions reveal that relative energies of the doublet and dectet pathways are not altered significantly (see Fig. S23 in the ESI†).
In pathway Ic, the μ-oxo atom abstracts a second hydrogen atom from the cyclopentyl radical (I-Int1) to produce cyclopentene (Ic-P2H) viaIc-TS2H (see Scheme 2 and Fig. S24 in the ESI†). The calculated barrier height is found to be 54.7 kJ mol−1 at the doublet surface. This clearly suggests that pathway Ic is less favourable compared to Ib and this is likely due to the accessibility of the bridged oxygen atom and the constraint that it imposed on the substrate compared to the terminal metal–oxo species. In pathway II, the {(O)FeIII–μ(OH)–FeIII(OH)} intermediate species is expected to rebound with the cyclopentyl radical to produce cyclopentanol, and this is found to have a prohibitively high barrier (189.6 kJ mol−1 at the doublet surface for II-2TSreb) suggesting that the hydroxylation is unlikely to proceed via the μ-O/μ-OH bridges. The formation of cyclopentanol is also found to be energetically less favoured compared to pathway Ia (see Fig. 6). In pathway III, the second hydrogen atom abstraction from the cyclopentyl radical via the transition state (III-2TS2H) is expected to yield a desaturated product. Here the estimated barrier is 9.0 kJ mol−1 from the preceding intermediate III-2Int, which is strongly destabilised (endothermic compared to the reactant) leading to a desaturated product. Our computed energetics reveal that both pathways II and III are energetically demanding (compared to pathway I), and hence the reaction is unlikely to proceed through these pathways (see Fig. 6).
Discussion
While orbital selection rules for the choice of hydroxylation vs. desaturation are clear for mononuclear FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups,66,159 for dinuclear species these are not established. Several experimental reports claim robust reactivity for dinuclear metal–oxo species compared to the monomeric one, and this has high-relevance to the very high reactivity reported for sMMO enzymes possessing dinuclear Fe centres. Generally, for mononuclear iron(IV)–oxo species, hydroxylation has been observed for many catalysts (with the substrate which are not specifically biased towards desaturation) while this is a rare feat in diiron(IV)–oxo chemistry. A terminal FeIII–OH formed with mononuclear complexes tends to rebound with the radical as they are poor electrophiles to abstract another hydrogen atom from the mono-radical species produced. In the case of dinuclear iron(IV)–oxo species, the intermediate generated is {FeIII–μ(OH)–FeIV} or {FeIII–μ(OH)μ(O)–FeIV} species where the –OH groups are bridged between two Fe centres. This raises the rebound barriers significantly as the μ-OH bridge is not in a favorable orientation to have a greater overlap with the radical SOMOs to generate the desired hydroxylated product. To form hydroxylation products, significant distortion at the coordination sphere is required, and this adds a significant energy penalty to the rebound barriers. Additionally, once the first hydrogen atom is abstracted by the diiron(IV)–oxo group, this results in {FeIII–μ(OH)–FeIV} type species, and here the –OH groups are still bonded to one of the FeIV centres and are thus not necessarily poor electrophiles to abstract the second hydrogen atom from the substrate. Therefore, these species tend to form desaturation rather than hydroxylation. However, the scenario is very different for the [HO(L)FeIII–O–FeIV(O)(L)]2+ active complex that has been reported to perform both hydroxylation as well as desaturation.8 Here we intend to understand the mechanistic pathway by which this complex performs both activities at ease. The first hydrogen atom abstraction has been assumed to take place by terminal FeIV
O groups,66,159 for dinuclear species these are not established. Several experimental reports claim robust reactivity for dinuclear metal–oxo species compared to the monomeric one, and this has high-relevance to the very high reactivity reported for sMMO enzymes possessing dinuclear Fe centres. Generally, for mononuclear iron(IV)–oxo species, hydroxylation has been observed for many catalysts (with the substrate which are not specifically biased towards desaturation) while this is a rare feat in diiron(IV)–oxo chemistry. A terminal FeIII–OH formed with mononuclear complexes tends to rebound with the radical as they are poor electrophiles to abstract another hydrogen atom from the mono-radical species produced. In the case of dinuclear iron(IV)–oxo species, the intermediate generated is {FeIII–μ(OH)–FeIV} or {FeIII–μ(OH)μ(O)–FeIV} species where the –OH groups are bridged between two Fe centres. This raises the rebound barriers significantly as the μ-OH bridge is not in a favorable orientation to have a greater overlap with the radical SOMOs to generate the desired hydroxylated product. To form hydroxylation products, significant distortion at the coordination sphere is required, and this adds a significant energy penalty to the rebound barriers. Additionally, once the first hydrogen atom is abstracted by the diiron(IV)–oxo group, this results in {FeIII–μ(OH)–FeIV} type species, and here the –OH groups are still bonded to one of the FeIV centres and are thus not necessarily poor electrophiles to abstract the second hydrogen atom from the substrate. Therefore, these species tend to form desaturation rather than hydroxylation. However, the scenario is very different for the [HO(L)FeIII–O–FeIV(O)(L)]2+ active complex that has been reported to perform both hydroxylation as well as desaturation.8 Here we intend to understand the mechanistic pathway by which this complex performs both activities at ease. The first hydrogen atom abstraction has been assumed to take place by terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) species which has the lowest barrier among all (38.3 kJ mol−1 at the antiferromagnetically coupled doublet surface but merely 20.2 kJ mol−1 from the reactant) followed by the terminal FeIII–O(2)H species (126.2 kJ mol−1 at the doublet surface) and μ-oxo bridged oxygen (160.1 kJ mol−1 at the doublet surface). Clearly, calculations reveal that the first hydrogen atom abstraction is triggered here by the terminal FeIV
O(1) species which has the lowest barrier among all (38.3 kJ mol−1 at the antiferromagnetically coupled doublet surface but merely 20.2 kJ mol−1 from the reactant) followed by the terminal FeIII–O(2)H species (126.2 kJ mol−1 at the doublet surface) and μ-oxo bridged oxygen (160.1 kJ mol−1 at the doublet surface). Clearly, calculations reveal that the first hydrogen atom abstraction is triggered here by the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) as the other two possible centres are much poorer electrophiles. The million-fold reactivity that is observed essentially stems from the fact that the first hydrogen atom abstraction, which is the rate-determining step here, is found to be extremely small with this complex. To analyse and understand this particular feature, we have compared the barrier height for C–H bond activation by this complex for DHA (where DHA = 9,10-dihydroanthracene and this substrate is more common in the literature) with available di and mononuclear FeIV
O(1) as the other two possible centres are much poorer electrophiles. The million-fold reactivity that is observed essentially stems from the fact that the first hydrogen atom abstraction, which is the rate-determining step here, is found to be extremely small with this complex. To analyse and understand this particular feature, we have compared the barrier height for C–H bond activation by this complex for DHA (where DHA = 9,10-dihydroanthracene and this substrate is more common in the literature) with available di and mononuclear FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species and found that the barriers are extremely small and in fact, they are three times smaller than Cpd I models estimated (see Table S10 in the ESI†).161
O species and found that the barriers are extremely small and in fact, they are three times smaller than Cpd I models estimated (see Table S10 in the ESI†).161
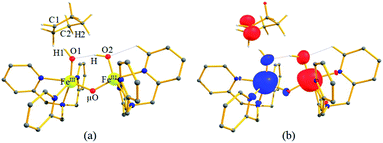
We have further probed the electronic origin of this lower barrier wherein the empty 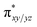 of the FeIV centre is important as it accepts electrons during the course of reactivity. This orbital is found to strongly mix with the
of the FeIV centre is important as it accepts electrons during the course of reactivity. This orbital is found to strongly mix with the 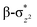 orbital of the FeIII centre (see Fig. 9a). Such orbital mixing sometimes called as cross-interaction has been known in dinuclear complexes for some time.162 Further at the transition state as well, the
orbital of the FeIII centre (see Fig. 9a). Such orbital mixing sometimes called as cross-interaction has been known in dinuclear complexes for some time.162 Further at the transition state as well, the 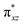 overlap is visible, reducing the antibonding interactions between the metal d-orbital and the ligand at the HOMO (see Fig. 9b) offering a spin-cooperation between the two centres. Additionally, the ferryl-bent which has been mentioned earlier, also a reason for the lowering of the
overlap is visible, reducing the antibonding interactions between the metal d-orbital and the ligand at the HOMO (see Fig. 9b) offering a spin-cooperation between the two centres. Additionally, the ferryl-bent which has been mentioned earlier, also a reason for the lowering of the 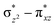 orbital as the bent seen in 1 is much larger than the largest ferryl-bent reported in mononuclear complexes.140,141 Additional analysis performed in the CoIII/GaIII fictitious model reveals stabilisation of
orbital as the bent seen in 1 is much larger than the largest ferryl-bent reported in mononuclear complexes.140,141 Additional analysis performed in the CoIII/GaIII fictitious model reveals stabilisation of 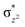 in the presence of FeIII ions (see Fig. S25 in the ESI†).
in the presence of FeIII ions (see Fig. S25 in the ESI†).
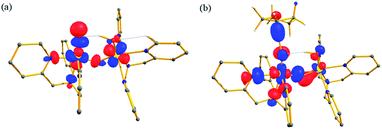 | ||
| Fig. 9 Computed orbital diagram corresponding to the (a) LUMO of the 21hs–hs and (b) HOMO of the I-2TSHhs–hs. | ||
To further understand the origin of the differences among different pathways studied, we carefully looked into the frontier orbitals. The orientation of frontier orbitals offers clues on the flexibility available for the substrate for its reactivity. In the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, the σ* dz2 orbital is found to be high lying in energy compared with the other four orbitals of the iron centre. This triggers the lower energy σ-pathway for the hydrogen atom abstraction. Further, the energy gap between the acceptor and donor orbitals gives some clues on the reactivity pattern as has been demonstrated for other FeIV
O bond, the σ* dz2 orbital is found to be high lying in energy compared with the other four orbitals of the iron centre. This triggers the lower energy σ-pathway for the hydrogen atom abstraction. Further, the energy gap between the acceptor and donor orbitals gives some clues on the reactivity pattern as has been demonstrated for other FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species.163 We have calculated the energy difference between the LUMO of the Fe
O species.163 We have calculated the energy difference between the LUMO of the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O σ* and σCH orbitals of the adjacent C–H bond of cyclopentane to be 1.09 eV for the 21hs–hs spin state, while for the 101hs–hs spin state it is found to be 1.35 eV in the gas phase. These HOMO–LUMO gaps suggest that the 21hs–hs spin state is more reactive towards C–H activation of cyclopentane than the 101hs–hs spin state. These two values are comparable with the earlier reported model complexes for methane and cyclohexane as a substrate.90,163 If a similar analysis is carried out assuming terminal FeIII–O(2)H or the bridged μ-oxo as the electrophile, it can be found that the energy gap between those frontier molecular orbitals (FMO) is 3.72 and 4.64 eV, respectively. These are much higher than that of the terminal FeIV
O σ* and σCH orbitals of the adjacent C–H bond of cyclopentane to be 1.09 eV for the 21hs–hs spin state, while for the 101hs–hs spin state it is found to be 1.35 eV in the gas phase. These HOMO–LUMO gaps suggest that the 21hs–hs spin state is more reactive towards C–H activation of cyclopentane than the 101hs–hs spin state. These two values are comparable with the earlier reported model complexes for methane and cyclohexane as a substrate.90,163 If a similar analysis is carried out assuming terminal FeIII–O(2)H or the bridged μ-oxo as the electrophile, it can be found that the energy gap between those frontier molecular orbitals (FMO) is 3.72 and 4.64 eV, respectively. These are much higher than that of the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species, revealing the origin of sluggish reactivity for these electrophilic groups present in 1. Additionally, the position of the substrate also adds a significant energy penalty as the linear σ pathway is not found for both pathways II and III. Likewise, we have calculated the energy gap between the LUMO of the CoIII/GaIII fictitious model and FMO of the targeted σCH of the cyclopentane. The gap is found to be 1.69/1.62 eV, suggesting a higher reactivity for species 1 towards cyclopentane than both the CoIII/GaIII fictitious models.
O species, revealing the origin of sluggish reactivity for these electrophilic groups present in 1. Additionally, the position of the substrate also adds a significant energy penalty as the linear σ pathway is not found for both pathways II and III. Likewise, we have calculated the energy gap between the LUMO of the CoIII/GaIII fictitious model and FMO of the targeted σCH of the cyclopentane. The gap is found to be 1.69/1.62 eV, suggesting a higher reactivity for species 1 towards cyclopentane than both the CoIII/GaIII fictitious models.
To assess further, deformation energies for the corresponding transition states are computed, and these are estimated to be 29.9, 118.1, and 71.9 kJ mol−1 for I-2TSHhs–hs, II-2TSHhs–hs, and III-2TSHhs–hs, respectively. The deformation energy at the transition state contributes 78% to the barrier height in pathway I, while in pathways II and III, these were estimated to be 74 and 57%, respectively. Interestingly, while deformation is the major contributor for pathways I and II, in pathway III, other contributions dominate the barrier height. A closer look at the interaction energy reveals that in pathway III the interaction energy is very significant compared to pathways I and II. This may be attributed to the fact that the FeIII–OH centre is already exchange saturated (see Table S11 in the ESI†).
To further understand the structural origin of the effects that are observed, we have also plotted the structure overlay of I-2RChs–hs, I-2TSHhs–hs, II-2TSHhs–hs, and III-2TSHhs–hs (see Fig. 10). This overlay structure reveals that the I-2TSHhs–hs deviated the least from the I-2RChs–hs compared to other two transition states (RMSD for the complex (cyclopentane) 0.38 (0.21) compared to 3.13 (0.58) and 1.28 (0.18) Å for II-2TSHhs–hs and III-2TSHhs–hs, respectively) and hence required very low reorganisation energy. This could be due to the preference for the σ pathway, which attempts to keep the substrate slightly further from the ligand moiety compared to the π pathway that is observed for the other two transition states.
Further, we have also estimated the BDEOH/DCH values5,72,164–171 for the three different pathways we described and our calculated BDEO1H1/DC1H1 values for the I-2Inths–hs, II-2Inths–hs, and III-2Inths–hs are 382.0/388.6, 311.0/390.7 and 284.6/389.0 kJ mol−1 (see the Thermochemistry section for equations eqn (1)–(3) in the ESI† for details). These values suggest that the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species is a much better oxidant than either terminal FeIII–OH or bridged μ-oxo for hydroxylation as well as desaturation reactions. Therefore, the terminal FeIV
O species is a much better oxidant than either terminal FeIII–OH or bridged μ-oxo for hydroxylation as well as desaturation reactions. Therefore, the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species is found to be a more powerful oxidant of hydrogen atom transfer from cyclopentane than FeIII–OH or bridged μ-oxo due to the increased basicity of the iron–hydroxo species that is formed. This is mainly due to the presence of orbital reorganisation that affects the electron affinity of the oxidant. Besides, we have carefully analysed bond parameters of the bond breaking of the C–H bond to the transition state structure from the reactant complex as well as the O–H bond formation of the intermediate species from the corresponding transition state structure.164 These two parameters (% BBCH and % BFOH) are generally correlated with an activation energy of the C–H bond during hydrogen atom abstraction (see Table S12 in the ESI†). Depending on whether a transition state is reactant-like or product-like, one can relate this to the estimated barrier height. By comparing the bond parameters, the I-2TSHhs–hs transition state is found to be an early transition state compared to II-2TSHhs–hs and III-2TSHhs–hs (see Fig. S26 and S27 in the ESI†). This also supports the energetics computed.164
O species is found to be a more powerful oxidant of hydrogen atom transfer from cyclopentane than FeIII–OH or bridged μ-oxo due to the increased basicity of the iron–hydroxo species that is formed. This is mainly due to the presence of orbital reorganisation that affects the electron affinity of the oxidant. Besides, we have carefully analysed bond parameters of the bond breaking of the C–H bond to the transition state structure from the reactant complex as well as the O–H bond formation of the intermediate species from the corresponding transition state structure.164 These two parameters (% BBCH and % BFOH) are generally correlated with an activation energy of the C–H bond during hydrogen atom abstraction (see Table S12 in the ESI†). Depending on whether a transition state is reactant-like or product-like, one can relate this to the estimated barrier height. By comparing the bond parameters, the I-2TSHhs–hs transition state is found to be an early transition state compared to II-2TSHhs–hs and III-2TSHhs–hs (see Fig. S26 and S27 in the ESI†). This also supports the energetics computed.164
Further, we have analysed the corresponding transition state for the hydroxylation (Ia-2TSrebhs–hs) and second hydrogen atom abstraction (Ib-2TS2Hhs–hs) reaction, to assess why rebound is slightly preferred over second hydrogen atom abstraction for species 1. The computed lower bound barrier for –OH rebound from FeIII–O(1)H(1) species is 19.6 kJ mol−1 while for second hydrogen abstraction from the FeIII–O(2)H is estimated to be 37.9 kJ mol−1 with respect to the I-Inths–hs species. In the case of the second hydrogen abstraction, the barrier is higher, which is correlated with the approach of the cyclopentyl radical towards the hydroxyl group, and the total deformation energy is computed to be 50.5 kJ mol−1 for the Ib-2TS2Hhs–hs species. As the barrier computed is 37.9 kJ mol−1, the difference of 12.6 kJ mol−1 is due to the electronic contribution to the transition state. The deformation energy computed for the –OH rebound transition state is much lower (23.9 kJ mol−1 see Fig. S28 in the ESI†). Here, electronic contribution dominates over the steric effect, i.e., the observed barrier heights are lower than the deformation energy of the transition state. Additionally, a very large dipole moment of 13.0 D for Ia-2TSrebhs–hs species was estimated, while rather a smaller dipole moment was detected (4.6 D) for the Ib-2TS2Hhs–hs species. We have also estimated the percentages of interaction/bond formation between O(1)/O(2) and C(1)/H(2) atoms for the formation of the product and it was found that the rebound transition state is a relatively early transition state compared to second hydrogen atom abstraction reflecting the estimated barrier heights (see Table S13 in the ESI†).
Further, we have attempted to understand the selectivity of the reaction mechanism with the help of the valence bond (VB) curve-grossing diagram (see Fig. 11). These types of VB diagrams were used previously to explain the electronic level selectivity of rebound and second hydrogen abstraction pathway.164,165,172–174 In the entire discussion of this section, we have considered only those used previously to explain the electronic level selectivity of the thermodynamically low-lying doublet state intermediate (I-2Int). In reactant 1, the iron–oxo centre (Sb) has four spin-down electrons with the FeIV state and the iron–hydroxo centre (Sa) has five up-spin electrons with the FeIII state. The combined effect of EET and antiferromagnetically coupled stabilisation leads to the C–H activation of cyclopentane through Ib-2TSHhs–hs, and this has been discussed elaborately in previous sections. The transition state leads to the hydroxylated intermediate (I-2Int), and in this intermediate, both iron centres (Sa and Sb) have a similar electronic occupation in the core orbital and difference in spin orientation. In the VBT diagram, we have demonstrated the pathway electronic level selectivity of the hydroxylation product viaIa-2TSrebhs–hs and the second hydrogen abstraction product via the Ib-2TS2Hhs–hs transition state (see Fig. S13 in the ESI†).
The mechanistic features and electronic cooperativity that is observed during the course of reactions are captured well by the valence bond curve crossing diagram. In valence bond theory, the ground state wave function has been represented as ψ, and its corresponding excited state wave function has been represented as ψ*. Here, the intermediate wave function (ψI) has been considered as a hypothetical reactant part (ψr), and the product wave function is denoted as ψP. The electronic configuration changes of both Sb and Sa centres in Ib-2TS2Hhs–hs and Ia-2TSrebhs–hs have been discussed for getting clarity on the higher selectivity of hydroxylation over second hydrogen abstraction. The energy barrier height from the intermediate to the product is directly proportional to the excitation energy from ψr to 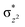 .175 The comparison of the VB structure of both products from intermediate configurations gives qualitative insights into the chemical and physical components of the transition state. In the case of Ia-2TSrebhs–hs, the association of the spin-up electron ϕ(C1) of the substrate with the 2pz(O) orbital of the hydroxyl bond and the (
.175 The comparison of the VB structure of both products from intermediate configurations gives qualitative insights into the chemical and physical components of the transition state. In the case of Ia-2TSrebhs–hs, the association of the spin-up electron ϕ(C1) of the substrate with the 2pz(O) orbital of the hydroxyl bond and the (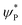 )1orbital of the Sb centre in the intermediate (ψr) alters the overall MO picture. The core orbital occupation configuration changes from (δxy)1, (
)1orbital of the Sb centre in the intermediate (ψr) alters the overall MO picture. The core orbital occupation configuration changes from (δxy)1, (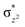 )1, (
)1, (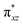 )1, (
)1, (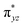 )1, and (
)1, and (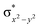 )1 to (δxy)1, (
)1 to (δxy)1, (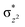 )1, (
)1, (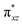 )1, (
)1, (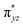 )1, and (
)1, and (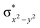 )1 and the activation energy simply depends on the electron association steps. The promotion gap (Greb) of Ia-2TSrebhs–hs depends on the ionisation potential of the substrate (IEAlk), the electron affinity of the acceptor part on the intermediate (EAFe(III)–OH) and the energy of the intermediate with changes in their molecular orbital energies,
)1 and the activation energy simply depends on the electron association steps. The promotion gap (Greb) of Ia-2TSrebhs–hs depends on the ionisation potential of the substrate (IEAlk), the electron affinity of the acceptor part on the intermediate (EAFe(III)–OH) and the energy of the intermediate with changes in their molecular orbital energies,
| Greb = IEAlk − EAFe(III)–OH + EFe(III)–OH + EMO |
In the case of Ib-2TS2Hhs–hs, the second hydrogen abstraction barrier is determined by the energy of the σCH bond of the intermediate that is broken into atomic orbitals (Eσ(C–H)). In addition, it is based on the energy of the acceptor intermediate (EFe(III)–OH). Apart from that, the energy barrier height also depends on molecular orbital changes with electronic reorganisation energy within the orbital because of the need of internal electron flipping for effective product formation. The dissociated hydrogen radical with the 1s(H) orbital is combined with the 2pz(O) orbital of hydroxyl oxygen, and the core orbital electronic configuration changes from (δxy)1, (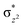 )1, (
)1, (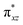 )1, (
)1, (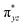 )1, and (
)1, and (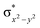 )1 to (δxy)1, (
)1 to (δxy)1, (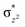 )1, (
)1, (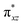 )2, (
)2, (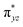 )1, and (
)1, and (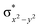 )1 at the Sa iron centre. Hence the promotion gap (G2H) will be the sum of (Eσ(C–H)) dissociation, the energy of the substrate (EFe(III)–OH), and molecular orbital changes for electronic reorganisation with electron flipping.
)1 at the Sa iron centre. Hence the promotion gap (G2H) will be the sum of (Eσ(C–H)) dissociation, the energy of the substrate (EFe(III)–OH), and molecular orbital changes for electronic reorganisation with electron flipping.
| G2H = Eσ(C–H) − EAFe(III)–OH + EMO (both molecular orbital changes and electron flipping from spin-up to spin-down) |
Thus, for these reasons, Ia-2TSrebhs–hs will have a smaller EMO and promotion gap for excitation than the Ib-2TS2Hhs–hs. The small excitation energy, as well as higher reactivity of the Ia-2TSrebhs–hs transition state was clearly demonstrated by the VBT curve crossing diagram.
Conclusions
The conclusion derived from this work is summarized below(i) Calculations support the experimental observation of the doublet ground state for [HO(L)FeIII–O–FeIV(O)(L)]2+ and various factors such as ferryl-bent and the weaker ligand field offered by the μ-oxo group contribute to the unusual stabilisation of the high-spin terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. In [HO(L)FeIII–O–FeIV(O)(L)]2+ species there are three different electrophilic oxygen atoms that can abstract a hydrogen atom from the substrate. Our calculations suggest that the terminal FeIV
O group. In [HO(L)FeIII–O–FeIV(O)(L)]2+ species there are three different electrophilic oxygen atoms that can abstract a hydrogen atom from the substrate. Our calculations suggest that the terminal FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (pathway I) is very aggressive as the barrier height computed is very small (20.2 kJ mol−1 from the reactant) compared to μ-oxo/terminal FeIII–OH (pathway II/III) species which have 6–8 times higher barrier heights. This is essentially due to steric effects in the case of the μ-oxo bridge and electronic effects in the case of FeIII–OH species.
O (pathway I) is very aggressive as the barrier height computed is very small (20.2 kJ mol−1 from the reactant) compared to μ-oxo/terminal FeIII–OH (pathway II/III) species which have 6–8 times higher barrier heights. This is essentially due to steric effects in the case of the μ-oxo bridge and electronic effects in the case of FeIII–OH species.
(ii) A million-fold reactivity observed for this species essentially stems from the extremely low first hydrogen atom abstraction barrier compared to several other mono/dinuclear iron–oxo species. The lower barrier observed here is attributed to various factors such as spin-cooperation, significant ferryl bending, and favourable 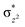 overlap.
overlap.
(iii) After the abstraction of the first hydrogen atom, the reaction is expected to proceed via either –OH rebound or abstraction of the second hydrogen atom leading to desaturation. Our calculations rule out –OH rebound/desaturation from the μ-OH group (pathway II/Ic) or desaturation by the terminal FeIII–OH species (pathway III) and suggest that either –OH rebound from the terminal FeIII–OH (pathway Ia with a barrier height of 19.6 kJ mol−1) or desaturation by the terminal FeIII–OH is favourable (barrier height 37.8 kJ mol−1 pathway Ib). A closer look at the electronic structure reveals an internal electron transfer from one Fe centre to the other during the second hydrogen atom abstraction that lowers the barrier height significantly. As such spin-cooperation is not possible in mononuclear complexes, they prefer to perform hydroxylation over desaturation for unbiased substrates and this substantiates the origin of the dual catalytic abilities that are observed for the [HO(L)FeIII–O–FeIV(O)(L)]2+ species.
To this end, here we have described in detail the electronic structure of the [HO(L)FeIII–O–FeIV(O)(L)]2+ species and probed its origin of very high-reactivity observed compared to other mono/dinuclear oxo species. Our results unequivocally reveal the importance of spin-states, spin-coupling, and cooperation of spin moments between the two centres that control the reactivity and product selectivity. The conception of the open core being more reactive compared to a diamond-core motif in diiron–oxo chemistry has far-reaching consequences as the nature of the active catalyst at the sMMO enzyme is elusive. Substitution of the –OH group with other groups was found to influence the reactivity significantly, and our group is currently working on this aspect, which will be reported in future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. R. would like to acknowledge the financial support from DST and SERB (DST/SJF/CAS-03/2018–19; CRG/2018/000430) India, and IIT Bombay for the high-performance computing facility. D. S. thanks SERB, India for the award of Core Research Grant (EMR/2017/000745) and Prof. S. Shaik (Hebrew University of Jerusalem) for his help and comments. M. A. would like to thank IIT Bombay for financial support.Notes and references
- M. A. Ehudin, D. A. Quist and K. D. Karlin, J. Am. Chem. Soc., 2019, 141, 12558–12569 CrossRef CAS PubMed.
- S. Kal, A. Draksharapu and L. Que Jr, J. Am. Chem. Soc., 2018, 140, 5798–5804 CrossRef CAS PubMed.
- M. A. Ehudin, L. B. Gee, S. Sabuncu, A. Braun, P. Moënne-Loccoz, B. Hedman, K. O. Hodgson, E. I. Solomon and K. D. Karlin, J. Am. Chem. Soc., 2019, 141, 5942–5960 CrossRef CAS PubMed.
- S. Ghafoor, A. Mansha and S. P. de Visser, J. Am. Chem. Soc., 2019, 141, 20278–20292 CrossRef CAS.
- K. Mittra and M. T. Green, J. Am. Chem. Soc., 2019, 141, 5504–5510 CrossRef CAS.
- T. H. Yosca, M. C. Langston, C. M. Krest, E. L. Onderko, T. L. Grove, J. Livada and M. T. Green, J. Am. Chem. Soc., 2016, 138, 16016–16023 CrossRef CAS PubMed.
- G. Xue, A. T. Fiedler, M. Martinho, E. Münck and L. Que, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20615–20620 CrossRef CAS.
- G. Xue, R. De Hont, E. Münck and L. Que Jr, Nat. Chem., 2010, 2, 400–405 CrossRef CAS PubMed.
- G. Xue, D. Wang, R. De Hont, A. T. Fiedler, X. Shan, E. Münck and L. Que, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20713–20718 CrossRef CAS PubMed.
- G. Xue, A. Pokutsa and L. Que Jr, J. Am. Chem. Soc., 2011, 133, 16657–16667 CrossRef CAS.
- C. Kim, Y. Dong and L. Que, J. Am. Chem. Soc., 1997, 119, 3635–3636 CrossRef CAS.
- A. Ghosh, F. Tiago de Oliveira, T. Yano, T. Nishioka, E. S. Beach, I. Kinoshita, E. Münck, A. D. Ryabov, C. P. Horwitz and T. J. Collins, J. Am. Chem. Soc., 2005, 127, 2505–2513 CrossRef CAS.
- G. E. Cutsail III, R. Banerjee, A. Zhou, L. Que Jr, J. D. Lipscomb and S. DeBeer, J. Am. Chem. Soc., 2018, 140, 16807–16820 CrossRef PubMed.
- G. Capocasa, F. Sessa, F. Tavani, M. Monte, G. Olivo, S. Pascarelli, O. Lanzalunga, S. Di Stefano and P. D'Angelo, J. Am. Chem. Soc., 2019, 141, 2299–2304 CrossRef CAS.
- P. Verma, K. D. Vogiatzis, N. Planas, J. Borycz, D. J. Xiao, J. R. Long, L. Gagliardi and D. G. Truhlar, J. Am. Chem. Soc., 2015, 137, 5770–5781 CrossRef CAS PubMed.
- S. Sahu and D. P. Goldberg, J. Am. Chem. Soc., 2016, 138, 11410–11428 CrossRef CAS.
- R. Fan, J. Serrano-Plana, W. N. Oloo, A. Draksharapu, E. Delgado-Pinar, A. Company, V. Martin-Diaconescu, M. Borrell, J. Lloret-Fillol and E. Garcia-Espana, J. Am. Chem. Soc., 2018, 140, 3916–3928 CrossRef CAS PubMed.
- I. Monte Pérez, X. Engelmann, Y. M. Lee, M. Yoo, E. Kumaran, E. R. Farquhar, E. Bill, J. England, W. Nam and M. Swart, Angew. Chem., Int. Ed., 2017, 56, 14384–14388 CrossRef.
- K. Ray, F. F. Pfaff, B. Wang and W. Nam, J. Am. Chem. Soc., 2014, 136, 13942–13958 CrossRef CAS PubMed.
- M. Guo, T. Corona, K. Ray and W. Nam, ACS Cent. Sci., 2018, 5, 13–28 CrossRef.
- M. Maldonado-Domínguez and M. Srnec, J. Am. Chem. Soc., 2020, 142, 3947–3958 CrossRef.
- X. Lu, X.-X. Li, Y.-M. Lee, Y. Jang, M. S. Seo, S. Hong, K.-B. Cho, S. Fukuzumi and W. Nam, J. Am. Chem. Soc., 2020, 142, 3891–3904 CrossRef CAS.
- S. Banerjee, A. Draksharapu, P. M. Crossland, R. Fan, Y. Guo, M. Swart and L. Que Jr, J. Am. Chem. Soc., 2020, 142, 4285–4297 CrossRef CAS.
- C. Colomban, E. V. Kudrik, P. Afanasiev and A. B. Sorokin, J. Am. Chem. Soc., 2014, 136, 11321–11330 CrossRef CAS.
- X. Engelmann, D. D. Malik, T. Corona, K. Warm, E. R. Farquhar, M. Swart, W. Nam and K. Ray, Angew. Chem., Int. Ed., 2019, 58, 4012–4016 CrossRef CAS PubMed.
- L. M. Dassama, A. Silakov, C. M. Krest, J. C. Calixto, C. Krebs, J. M. Bollinger Jr and M. T. Green, J. Am. Chem. Soc., 2013, 135, 16758–16761 CrossRef CAS PubMed.
- B. J. Wallar and J. D. Lipscomb, Chem. Rev., 1996, 96, 2625–2658 CrossRef CAS PubMed.
- M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841–2888 CrossRef CAS PubMed.
- E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S.-K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y.-S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235–350 CrossRef CAS PubMed.
- M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986 CrossRef CAS PubMed.
- V. J. DeRose, K. E. Liu, S. J. Lippard and B. M. Hoffman, J. Am. Chem. Soc., 1996, 118, 121–134 CrossRef CAS.
- B. Singh, J. R. Long, F. Fabrizi De Biani, D. Gatteschi and P. Stavropoulos, J. Am. Chem. Soc., 1997, 119, 7030–7047 CrossRef CAS.
- V. V. Vu, T. M. Makris, J. D. Lipscomb and L. Que Jr, J. Am. Chem. Soc., 2011, 133, 6938–6941 CrossRef CAS PubMed.
- H. Nguyen, A. K. Shiemke, S. J. Jacobs, B. J. Hales, M. E. Lidstrom and S. I. Chan, J. Biol. Chem., 1994, 269, 14995–15005 CAS.
- A. C. Rosenzweig, C. A. Frederick and S. J. Lippard, Nature, 1993, 366, 537–543 CrossRef CAS PubMed.
- L. Que and W. B. Tolman, Nature, 2008, 455, 333–340 CrossRef CAS PubMed.
- C. Krebs, D. Galonić Fujimori, C. T. Walsh and J. M. Bollinger, Acc. Chem. Res., 2007, 40, 484–492 CrossRef CAS PubMed.
- A. L. Feig and S. J. Lippard, Chem. Rev., 1994, 94, 759–805 CrossRef CAS.
- M. Merkx and S. J. Lippard, J. Biol. Chem., 2002, 277, 5858–5865 CrossRef CAS PubMed.
- K. Yoshizawa and Y. Shiota, J. Am. Chem. Soc., 2006, 128, 9873–9881 CrossRef CAS PubMed.
- A. C. Rosenzweig, H. Brandstetter, D. A. Whittington, P. Nordlund, S. J. Lippard and C. A. Frederick, Proteins: Struct., Funct., Genet., 1997, 29, 141–152 CrossRef CAS.
- K. Kim and S. J. Lippard, J. Am. Chem. Soc., 1996, 118, 4914–4915 CrossRef CAS.
- A. M. Valentine, S. S. Stahl and S. J. Lippard, J. Am. Chem. Soc., 1999, 121, 3876–3887 CrossRef CAS.
- S.-K. Lee and J. D. Lipscomb, Biochemistry, 1999, 38, 4423–4432 CrossRef CAS PubMed.
- T. C. Brunold, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20641–20642 CrossRef PubMed.
- P. E. Siegbahn and R. H. Crabtree, J. Am. Chem. Soc., 1997, 119, 3103–3113 CrossRef CAS.
- B. F. Gherman, B. D. Dunietz, D. A. Whittington, S. J. Lippard and R. A. Friesner, J. Am. Chem. Soc., 2001, 123, 3836–3837 CrossRef CAS PubMed.
- M. Costas, Coord. Chem. Rev., 2011, 255, 2912–2932 CrossRef CAS.
- W. Nam, Acc. Chem. Res., 2007, 40, 522–531 CrossRef CAS PubMed.
- S. P. de Visser, J. Am. Chem. Soc., 2006, 128, 9813–9824 CrossRef CAS PubMed.
- L. J. Murray and S. J. Lippard, Acc. Chem. Res., 2007, 40, 466–474 CrossRef CAS PubMed.
- C. E. Tinberg and S. J. Lippard, Acc. Chem. Res., 2011, 44, 280–288 CrossRef CAS PubMed.
- L. Shu, J. C. Nesheim, K. Kauffmann, E. Münck, J. D. Lipscomb and L. Que, Science, 1997, 275, 515–518 CrossRef CAS PubMed.
- V. C.-C. Wang, S. Maji, P. P.-Y. Chen, H. K. Lee, S. S.-F. Yu and S. I. Chan, Chem. Rev., 2017, 117, 8574–8621 CrossRef CAS PubMed.
- E. C. Wilkinson, Y. Dong, Y. Zang, H. Fujii, R. Fraczkiewicz, G. Fraczkiewicz, R. S. Czernuszewicz and L. Que, J. Am. Chem. Soc., 1998, 120, 955–962 CrossRef CAS.
- M. H. Sazinsky and S. J. Lippard, J. Am. Chem. Soc., 2005, 127, 5814–5825 CrossRef CAS PubMed.
- S.-P. Huang, Y. Shiota and K. Yoshizawa, Dalton Trans., 2013, 42, 1011–1023 RSC.
- B. Meunier, S. P. De Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980 CrossRef CAS PubMed.
- S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS PubMed.
- S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110, 949–1017 CrossRef CAS PubMed.
- A. B. Sorokin, E. V. Kudrik and D. Bouchu, Chem. Commun., 2008, 2562–2564 RSC.
- L. H. Do and S. J. Lippard, J. Am. Chem. Soc., 2011, 133, 10568–10581 CrossRef CAS PubMed.
- J. A. Broadwater, J. Ai, T. M. Loehr, J. Sanders-Loehr and B. G. Fox, Biochemistry, 1998, 37, 14664–14671 CrossRef CAS PubMed.
- L. J. Murray, S. G. Naik, D. O. Ortillo, R. García-Serres, J. K. Lee, B. H. Huynh and S. J. Lippard, J. Am. Chem. Soc., 2007, 129, 14500–14510 CrossRef CAS PubMed.
- V. V. Vu, J. P. Emerson, M. Martinho, Y. S. Kim, E. Münck, M. H. Park and L. Que, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14814–14819 CrossRef CAS PubMed.
- D. Usharani, D. Janardanan and S. Shaik, J. Am. Chem. Soc., 2010, 133, 176–179 CrossRef PubMed.
- G. Xue, C. Geng, S. Ye, A. T. Fiedler, F. Neese and L. Que Jr, Inorg. Chem., 2013, 52, 3976–3984 CrossRef CAS PubMed.
- Y. Dong, H. Fujii, M. P. Hendrich, R. A. Leising, G. Pan, C. R. Randall, E. C. Wilkinson, Y. Zang and L. Que Jr, J. Am. Chem. Soc., 1995, 117, 2778–2792 CrossRef CAS.
- D. Wang, E. R. Farquhar, A. Stubna, E. Münck and L. Que, Nat. Chem., 2009, 1, 145–150 CrossRef CAS.
- E. V. Kudrik, P. Afanasiev, L. X. Alvarez, P. Dubourdeaux, M. Clémancey, J.-M. Latour, G. Blondin, D. Bouchu, F. Albrieux and S. E. Nefedov, Nat. Chem., 2012, 4, 1024–1029 CrossRef CAS.
- M. Ansari, N. Vyas, A. Ansari and G. Rajaraman, Dalton Trans., 2015, 44, 15232–15243 RSC.
- M. G. Quesne, D. Senthilnathan, D. Singh, D. Kumar, P. Maldivi, A. B. Sorokin and S. P. de Visser, ACS Catal., 2016, 6, 2230–2243 CrossRef CAS.
- R. F. De Hont, G. Xue, M. P. Hendrich, L. Que Jr, E. L. Bominaar and E. Münck, Inorg. Chem., 2010, 49, 8310–8322 CrossRef CAS PubMed.
- H. Zheng, S. J. Yoo, E. Münck and L. Que, J. Am. Chem. Soc., 2000, 122, 3789–3790 CrossRef CAS.
- M.-H. Baik, M. Newcomb, R. A. Friesner and S. J. Lippard, Chem. Rev., 2003, 103, 2385–2420 CrossRef CAS PubMed.
- P. E. Siegbahn, Inorg. Chem., 1999, 38, 2880–2889 CrossRef CAS PubMed.
- P. Jayapal, A. Ansari and G. Rajaraman, Inorg. Chem., 2015, 54, 11077–11082 CrossRef CAS PubMed.
- M. J. Frisch, et al., GAUSSIAN 09 (Revision 02), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. H. Dunning Jr and P. J. Hay, Modern Theoretical Chemistry, Plenum, New York, 1976, pp. 1–28 Search PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef CAS.
- C. Schaefer, C. Huber and R. Ahlrichs, Chem. Phys., 1994, 100, 5829–5835 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- D. H. Ess and T. C. Cook, J. Phys. Chem. A, 2012, 116, 4922–4929 CrossRef CAS PubMed.
- G. A. Zhurko, ChemCraft software, version 1.6, 2014 Search PubMed.
- S. Portmann and H. P. Luthi, Chimia, 2000, 54, 766–770 CAS.
- A. Ansari, M. Ansari, A. Singha and G. Rajaraman, Chem.–Eur. J., 2017, 23, 10110–10125 CrossRef CAS PubMed.
- C. Wang and H. Chen, J. Am. Chem. Soc., 2017, 139, 13038–13046 CrossRef CAS PubMed.
- K. Yoshizawa, Acc. Chem. Res., 2006, 39, 375–382 CrossRef CAS PubMed.
- P. Jayapal and G. Rajaraman, Phys. Chem. Chem. Phys., 2012, 14, 9050–9053 RSC.
- D. E. Ferreira, W. B. De Almeida, A. Neves and W. R. Rocha, Phys. Chem. Chem. Phys., 2008, 10, 7039–7046 RSC.
- R. Kumar, A. Ansari and G. Rajaraman, Chem.–Eur. J., 2018, 24, 6818–6827 CrossRef CAS PubMed.
- R. Kumar, B. Pandey and G. Rajaraman, J. Indian Chem. Soc., 2019, 96, 825–836 CAS.
- B. Pandey, M. Jaccobab and G. Rajaraman, Chem. Commun., 2017, 53, 3193–3196 RSC.
- B. Pinter, A. Chankisjijev, P. Geerlings, J. N. Harvey and F. De Proft, Chem.–Eur. J., 2018, 24, 5281–5292 CrossRef CAS PubMed.
- S. Essafi, D. P. Tew and J. N. Harvey, Angew. Chem., Int. Ed., 2017, 56, 5790–5794 CrossRef CAS.
- P. Rydberg, R. Lonsdale, J. N. Harvey, A. J. Mulholland and L. Olsen, J. Mol. Graphics Modell., 2014, 52, 30–35 CrossRef CAS PubMed.
- C. Wang, C. Zhao, L. Hu and H. Chen, J. Phys. Chem. Lett., 2016, 7, 4427–4432 CrossRef CAS PubMed.
- C. Zhao and H. Chen, ACS Catal., 2017, 7, 3521–3531 CrossRef CAS.
- J. Lu, B. Bi, W. Lai and H. Chen, Angew. Chem., Int. Ed., 2019, 58, 3795–3799 CrossRef CAS.
- Z. Tian, A. Fattahi, L. Lis and S. R. Kass, J. Am. Chem. Soc., 2006, 128, 17087–17092 CrossRef CAS PubMed.
- Y.-R. Luo, Comprehensive handbook of chemical bond energies, CRC Press, 2007 Search PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- T. Lovell, W.-G. Han, T. Liu and L. Noodleman, J. Am. Chem. Soc., 2002, 124, 5890–5894 CrossRef CAS.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127 RSC.
- A. Diefenbach and F. M. Bickelhaupt, J. Phys. Chem. A, 2004, 108, 8460–8466 CrossRef CAS.
- R. Strozier, P. Caramella and K. Houk, J. Am. Chem. Soc., 1979, 101, 1340–1343 CrossRef CAS.
- D. H. Ess and K. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647 CrossRef CAS PubMed.
- C. Y. Legault, Y. Garcia, C. A. Merlic and K. Houk, J. Am. Chem. Soc., 2007, 129, 12664–12665 CrossRef CAS PubMed.
- D. Usharani, D. C. Lacy, A. Borovik and S. Shaik, J. Am. Chem. Soc., 2013, 135, 17090–17104 CrossRef CAS PubMed.
- Note here that GaIII is a general dopant for FeIII and there are several experimental reports in the literature where FeIII is replaced by GaIII. (a) A. Cornia, M. Mannini, R. Sessoli and D. Gatteschi, Eur. J. Inorg. Chem., 2019, 552–568 CrossRef CAS; (b) P. King, T. C. Stamatatos, K. A. Abboud and G. Christou, Angew. Chem., Int. Ed., 2006, 45, 7379–7383 CrossRef CAS PubMed.
- E. J. Klinker, J. Kaizer, W. W. Brennessel, N. L. Woodrum, C. J. Cramer and L. Que Jr, Angew. Chem., Int. Ed., 2005, 44, 3690–3694 CrossRef CAS PubMed.
- Q. M. Phung, C. Martín-Fernández, J. N. Harvey and M. Feldt, J. Chem. Theory Comput., 2019, 15, 4297–4304 CrossRef CAS PubMed.
- M. J. Collins, K. Ray and L. Que, Inorg. Chem., 2006, 45, 8009–8011 CrossRef CAS PubMed.
- J. Kaizer, E. J. Klinker, N. Y. Oh, J.-U. Rohde, W. J. Song, A. Stubna, J. Kim, E. Münck, W. Nam and L. Que, J. Am. Chem. Soc., 2004, 126, 472–473 CrossRef CAS.
- J. Bautz, P. Comba, C. Lopez de Laorden, M. Menzel and G. Rajaraman, Angew. Chem., Int. Ed., 2007, 46, 8067–8070 CrossRef CAS PubMed.
- K. Benzing, P. Comba, B. Martin, B. Pokrandt and F. Keppler, Chem.–Eur. J., 2017, 23, 10465–10472 CrossRef CAS PubMed.
- P. Comba, S. Fukuzumi, C. Koke, B. Martin, A. M. Löhr and J. Straub, Angew. Chem., Int. Ed., 2016, 55, 11129–11133 CrossRef CAS PubMed.
- K. Anandababu, R. Ramasubramanian, H. Wadepohl, P. Comba, N. Johnee Britto, M. Jaccob and R. Mayilmurugan, Chem.–Eur. J., 2019, 25, 9540–9547 CrossRef CAS PubMed.
- P. Comba, H. Rudolf and H. Wadepohl, Dalton Trans., 2015, 44, 2724–2736 RSC.
- C. V. Sastri, J. Lee, K. Oh, Y. J. Lee, J. Lee, T. A. Jackson, K. Ray, H. Hirao, W. Shin and J. A. Halfen, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19181–19186 CrossRef CAS PubMed.
- P. Comba, D. Faltermeier, S. Krieg, B. Martin and G. Rajaraman, Dalton Trans., 2020, 49, 2888–2894 RSC.
- S. A. Stoian, G. Xue, E. L. Bominaar, L. Que Jr and E. Münck, J. Am. Chem. Soc., 2014, 136, 1545–1558 CrossRef CAS PubMed.
- B. E. Sturgeon, D. Burdi, S. Chen, B.-H. Huynh, D. E. Edmondson, J. Stubbe and B. M. Hoffman, J. Am. Chem. Soc., 1996, 118, 7551–7557 CrossRef CAS.
- M. Feldt, Q. M. Phung, K. Pierloot, R. A. Mata and J. N. Harvey, J. Chem. Theory Comput., 2019, 15, 922–937 CrossRef PubMed.
- Q. M. Phung and K. Pierloot, Chem.–Eur. J., 2019, 25, 12491–12496 CrossRef CAS PubMed.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS PubMed.
- A. Altun, M. Saitow, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 1616–1632 CrossRef CAS PubMed.
- B. Mondal, F. Neese, E. Bill and S. Ye, J. Am. Chem. Soc., 2018, 140, 9531–9544 CrossRef CAS.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef.
- H. Chen, J. Song, W. Lai, W. Wu and S. Shaik, J. Chem. Theory Comput., 2010, 6, 940–953 CrossRef CAS PubMed.
- H. Chen, W. Lai and S. Shaik, J. Phys. Chem. Lett., 2010, 1, 1533–1540 CrossRef CAS.
- H. Chen, W. Lai, J. Yao and S. Shaik, J. Chem. Theory Comput., 2011, 7, 3049–3053 CrossRef CAS PubMed.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- W. Rasheed, A. Draksharapu, S. Banerjee, V. G. Young Jr, R. Fan, Y. Guo, M. Ozerov, J. Nehrkorn, J. Krzystek, J. Telser and L. Que Jr, Angew. Chem., Int. Ed., 2018, 57, 9387–9391 CrossRef CAS.
- S. Rana, J. P. Biswas, A. Sen, M. Clémancey, G. Blondin, J.-M. Latour, G. Rajaraman and D. Maiti, Chem. Sci., 2018, 9, 7843–7858 RSC.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- J. Cano, E. Ruiz, S. Alvarez and M. Verdaguer, Comments Inorg. Chem., 1998, 20, 27–56 CrossRef CAS.
- M. Swart and M. Costas, Spin states in biochemistry and inorganic chemistry: influence on structure and reactivity, John Wiley & Sons, 2015 Search PubMed.
- E. Ruiz, S. Alvarez, A. Rodriguez-Fortea, P. Alemany, Y. Pouillon and C. Massobiro, Magnetism: Molecules to Materials, ed. J. S. Miller and M. Drillon, Wiley-VCH, Weinheim, 2001 Search PubMed.
- H. Basch, K. Mogi, D. G. Musaev and K. Morokuma, J. Am. Chem. Soc., 1999, 121, 7249–7256 CrossRef CAS.
- D. Usharani, D. Janardanan, C. Li and S. Shaik, Acc. Chem. Res., 2012, 46, 471–482 CrossRef PubMed.
- L. Bernasconi, M. J. Louwerse and E. J. Baerends, Eur. J. Inorg. Chem., 2007, 3023–3033 CrossRef CAS.
- M. L. Neidig, A. Decker, O. W. Choroba, F. Huang, M. Kavana, G. R. Moran, J. B. Spencer and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12966–12973 CrossRef CAS PubMed.
- C. Geng, S. Ye and F. Neese, Angew. Chem., Int. Ed., 2010, 49, 5717–5720 CrossRef CAS PubMed.
- P. Barman, A. K. Vardhaman, B. Martin, S. J. Wörner, C. V. Sastri and P. Comba, Angew. Chem., Int. Ed., 2015, 54, 2095–2099 CrossRef CAS PubMed.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS PubMed.
- H. Tang, J. Guan, H. Liu and X. Huang, Dalton Trans., 2013, 42, 10260–10270 RSC.
- X. Sun, C. Geng, R. Huo, U. Ryde, Y. Bu and J. Li, J. Phys. Chem. B, 2014, 118, 1493–1500 CrossRef CAS PubMed.
- M. Jaccob, A. Ansari, B. Pandey and G. Rajaraman, Dalton Trans., 2013, 42, 16518–16526 RSC.
- D. Usharani, D. Janardanan, C. Li and S. Shaik, Acc. Chem. Res., 2013, 46, 471–482 CrossRef CAS.
- D. Janardanan, Y. Wang, P. Schyman, L. Que Jr and S. Shaik, Angew. Chem., Int. Ed., 2010, 49, 3342–3345 CrossRef CAS.
- M. Puri and L. Que Jr, Acc. Chem. Res., 2015, 48, 2443–2452 CrossRef CAS PubMed.
- J. F. Hull, D. Balcells, E. L. Sauer, C. Raynaud, G. W. Brudvig, R. H. Crabtree and O. Eisenstein, J. Am. Chem. Soc., 2010, 132, 7605–7616 CrossRef CAS PubMed.
- H. Tang, J. Guan, L. Zhang, H. Liu and X. Huang, Phys. Chem. Chem. Phys., 2012, 14, 12863–12874 RSC.
- L. Ji, A. S. Faponle, M. G. Quesne, M. A. Sainna, J. Zhang, A. Franke, D. Kumar, R. van Eldik, W. Liu and S. P. de Visser, Chem.–Eur. J., 2015, 21, 9083–9092 CrossRef CAS PubMed.
- R. Hotzelmann, K. Wieghardt, U. Floerke, H. J. Haupt, D. C. Weatherburn, J. Bonvoisin, G. Blondin and J. J. Girerd, J. Am. Chem. Soc., 1992, 114, 1681–1696 CrossRef CAS.
- L. Bernasconi and E. J. Baerends, J. Am. Chem. Soc., 2013, 135, 8857–8867 CrossRef CAS PubMed.
- S. Shaik, D. Kumar and S. P. de Visser, J. Am. Chem. Soc., 2008, 130, 10128–10140 CrossRef CAS PubMed.
- D. Kumar, B. Karamzadeh, G. N. Sastry and S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 7656–7667 CrossRef CAS PubMed.
- S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 1087–1097 CrossRef CAS PubMed.
- D. Kumar, G. N. Sastry and S. P. De Visser, Chem.–Eur. J., 2011, 17, 6196–6205 CrossRef CAS PubMed.
- S. P. de Visser, D. Kumar, S. Cohen, R. Shacham and S. Shaik, J. Am. Chem. Soc., 2004, 126, 8362–8363 CrossRef CAS PubMed.
- T. H. Yosca, J. Rittle, C. M. Krest, E. L. Onderko, A. Silakov, J. C. Calixto, R. K. Behan and M. T. Green, Science, 2013, 342, 825–829 CrossRef CAS PubMed.
- T. H. Yosca, A. P. Ledray, J. Ngo and M. T. Green, J. Biol. Inorg Chem., 2017, 22, 209–220 CrossRef CAS PubMed.
- M. T. Green, Curr. Opin. Chem. Biol., 2009, 13, 84–88 CrossRef CAS PubMed.
- S. P. de Visser, J. Am. Chem. Soc., 2009, 132, 1087–1097 CrossRef PubMed.
- S. Kumar, A. S. Faponle, P. Barman, A. K. Vardhaman, C. V. Sastri, D. Kumar and S. P. de Visser, J. Am. Chem. Soc., 2014, 136, 17102–17115 CrossRef CAS PubMed.
- D. Kumar, G. N. Sastry and S. P. De Visser, Chem.–Eur. J., 2011, 17, 6196–6205 CrossRef CAS PubMed.
- S. S. Shaik, J. Am. Chem. Soc., 1981, 103, 3692–3701 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02624g |
| This journal is © The Royal Society of Chemistry 2020 |