Open Access Article
Open Access ArticleAnisotropy-induced directional self-transportation of low surface tension liquids: a review
Mohammad Soltani
 and
Kevin Golovin
and
Kevin Golovin
 *
*
Okanagan Polymer Engineering Research & Applications Laboratory, Faculty of Applied Science, University of British Columbia, Canada. E-mail: kevin.golovin@ubc.ca
First published on 7th November 2020
Abstract
Inspired by natural surfaces such as butterfly wings, cactus leaves, or the Nepenthes alata plant, synthetic materials may be engineered to directionally transport liquids on their surface without external energy input. This advantageous feature has been adopted for various mechanical and chemical processes, e.g. fog harvesting, lubrication, lossless chemical reactions, etc. Many studies have focused on the manipulation and transport of water or aqueous droplets, but significantly fewer have extended their work to low surface tension (LST) liquids, although these fluids are involved in numerous industrial and everyday processes. LST liquids completely wet most surfaces which makes spontaneous transportation an active challenge. This review focuses on recently developed strategies for passively and directionally transporting LST liquids.
1 Introduction
The ability to directionally transport liquid droplets has naturally developed in several instances. For example, desert beetles, spider silk, and cactus stems are all capable of collecting water from humid air.1–7 Due to recent advances in micro/nanofabrication methods, scientists have developed bio-inspired surface structures that also achieve directional liquid transportation. These surfaces have shown promise in various fields, such as micro-fluidics, oil–water separation, thin-film lubrication, and heat management.8–15 The transportation of water droplets on these engineered surfaces is well studied, both experimentally and theoretically.16–22 Considerably fewer studies have demonstrated directional transportation of Low Surface Tension (LST) liquids. Here we review surfaces that utilize physical texture gradients to uniquely enable the directional transportation of LST liquids.A droplet deposited on a solid surface creates a solid/liquid/vapor contact line as a result of an equilibrium between interfacial tensions. In the absence of any anisotropy, the droplet will move/expand equally in all directions in response to external pressure. Wetting is caused by a capillary force, which scales with the product of surface tension and a characteristic length. Accordingly, wetting may be manipulated by a gradient in either the surface tension or the characteristic physical length. A surface tension gradient may be induced by intrinsic surface chemistry variation23–27 or by external stimuli such as an electric field, light, temperature, vibration, or a magnetic field.28–35 In comparison, engineered surfaces exhibiting anisotropic surface texture are beneficial for power-free, spontaneous liquid transportation.
As LST liquids generally spread on most surface chemistries, rather than forming droplets, achieving a chemical wettability gradient for the wetting driving force is difficult. However, droplet formation (non-zero contact angles) can occur in the case of underwater deposition, on very low surface energy materials, and on specially engineered rough surfaces. Therefore, this review mainly discusses surfaces with textural anisotropy, although the limited studies utilizing a chemical gradient are also discussed.
2 Theoretical analysis
2.1 Smooth surfaces
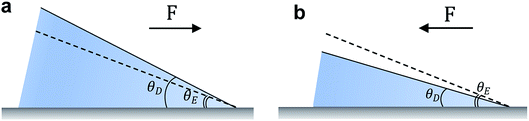
When a liquid droplet is deposited on a chemically homogenous and smooth surface, the equilibrium balance in the interfacial plane at a point along the contact line is,
γSV − γSL − γLV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θE = 0 θE = 0
| (1) |
F(θD) = γSV − γSL − γLV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θD θD
| (2) |
2.2 Imperfect surfaces
Fabricating surfaces that solely exhibit θE is extremely challenging. For real engineering surfaces, a range of droplet contact angles may be observed. The equilibrium contact angle will fall in-between the receding, θR, and advancing, θA, contact angles. The difference between these angles is termed contact angle hysteresis, which arises from surface roughness, chemical heterogeneities, surface deformation, liquid adsorption and retention, molecular rearrangement on wetting, and/or vapor undersaturation (such as in the typical case of droplets in air).36 Associated with the work necessary to wet the surface, the barrier of contact angle hysteresis against droplet motion is expressed as, FH = γLVw(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR − cos
θR − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA), where w is the droplet base width in the direction perpendicular to motion.37 Depending on the surface chemistry and roughness, droplets may move by sliding, rolling, or a combination of these mechanisms.38 In every case, the driving force must overcome the contact angle hysteresis for droplet motion to occur.
θA), where w is the droplet base width in the direction perpendicular to motion.37 Depending on the surface chemistry and roughness, droplets may move by sliding, rolling, or a combination of these mechanisms.38 In every case, the driving force must overcome the contact angle hysteresis for droplet motion to occur.
For a moving droplet, energy may be dissipated either in the immediate vicinity of the triple contact line (microscale) or within the bulk liquid volume as viscous flow (macroscale). In general, both contribute to resisting droplet motion but depending on the characteristics of the solid/liquid interface, one term may be dominant.
The relation between droplet velocity and the force experienced may be obtained by integrating the viscous stresses along the droplet interface.39 Assuming the small angle case where the lubrication approximation remains valid, i.e. tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ θ, Fig. 2 shows the velocity distribution, v(z), at the wedge border of a spreading liquid which is set to 0 near the solid surface and 1.5V at z = θx. Here, V is the velocity averaged over the thickness of the wedge, x is distance from three-phase contact line, and θx is the local thickness of the liquid. Note that the upper surface has higher velocity than the moving contact line. As demonstrated in experimental studies,40 a marked point at the upper surface moves faster than the contact line, quite similar to the motion of treads on a tank. The velocity gradient is given by,
θ ≈ θ, Fig. 2 shows the velocity distribution, v(z), at the wedge border of a spreading liquid which is set to 0 near the solid surface and 1.5V at z = θx. Here, V is the velocity averaged over the thickness of the wedge, x is distance from three-phase contact line, and θx is the local thickness of the liquid. Note that the upper surface has higher velocity than the moving contact line. As demonstrated in experimental studies,40 a marked point at the upper surface moves faster than the contact line, quite similar to the motion of treads on a tank. The velocity gradient is given by,
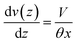 | (3) |
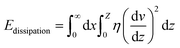 | (4) |
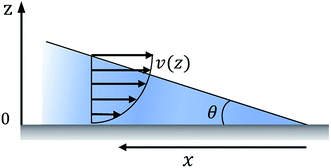 | ||
Fig. 2 The velocity distribution of a spreading droplet in the immediate vicinity of the triple contact line. Here the lubrication approximation is assumed, i.e. tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ θ. θ ≈ θ. | ||
Substituting (3) into (4) and truncating the upper and lower limits of the integral as x = L (the droplet size) and x = a (the molecular size), respectively, yields,39
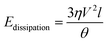 | (5) |
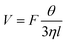 | (6) |
The first experimental data produced by Hoffman41 showed that the dimensionless coefficient l is of the order ∼15 on a dry surface, but is reduced to ∼5 if the surface is prewetted by the liquid.
According to eqn (6), if the viscous dissipation is dominant, the droplet velocity follows V ∼ Fθ/ηl. In contrast, when dissipation mostly occurs along the contact line, θ is given by Tanner's Law θ ∼ (lηV/γ)1/3 (ref. 42) and subsequently,
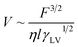 | (7) |
The total resistance to droplet motion is the sum of contact line and viscous dissipation, but the extent to which each contributes may be found using the above velocity–force relations, eqn (6) and (7). Note that the resistance due to viscous forces is negligible at the onset of the motion (V ≈ 0).
Considering the above mechanics, two strategies have been developed for transporting LST liquid droplets which we designate as spread and slip. The difference between these strategies can be explained by the dynamics of the contact line during transportation. During spreading the contact line advances along the surface while the wetted surface underneath the droplet remains wet. In contrast, slip is characterized by receding of the contact line at the trailing end of the droplet.
3 Spread
In this section, we review the different approaches that enable the guided transportation of LST liquids through spreading in a preferential direction. As LST liquids usually recede at low contact angles on smooth surfaces, increased roughness leads to even lower receding contact angles according to the Wenzel model,43 making slip difficult. For example, if a LST liquid droplet exhibits an equilibrium contact angle of θE = 30° on a smooth surface, the droplet will not recede if the surface area is increased by only 15.5%. Hence, the majority of studies investigating LST liquids transport rely on the spread-mode of transportation.3.1 Planar, curvature-driven spreading
A curved liquid interface experiences a pressure difference known as the Laplace pressure, which is defined as Δp = γLV(1/r1 + 1/r2), where r1 and r2 are the principal radii of curvature of the interface. This pressure decreases with the radius of curvature which can cause droplets to deform or wet additional surface area to alleviate the pressure. Numerous studies have exploited a Laplace pressure difference as the driving force for directional LST liquid transportation. The general strategy has been to create surfaces with a pattern exhibiting extreme wettability contrast, such that the liquid is confined in the more wettable channels surrounded by a repellent background. The challenge with LST liquids is to obtain this background, as LST liquids are naturally wetting to all surface chemistries. An underwater wettability contrast is one way to achieve such a contrast.Wettability underwater can be significantly different than in air. When a superhydrophobic surface (contact angle with water greater than 150° and low hysteresis) with superhydrophilic (complete spread of water) pattern is immersed in water, water spreads and fills only the superhydrophilic pattern. After underwater deposition of a LST liquid droplet, the air trapped within the superhydrophobic pores is replaced by the LST liquid, i.e. underwater oleophilicity (having a strong affinity for oils). On the other hand, the trapped water in the hydrophilic regions prevents the penetration of the LST liquid, i.e. extreme underwater oleophobicity (repellent to oils). The modified contact angle for this new composition of solid/water/oil interface can be described as,44
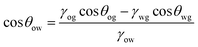 | (8) |
Using a wedge-shaped wettability pattern, Huang et al.45 studied the underwater transportation of LST liquids. Aluminum substrates were chemically etched, followed by stearic acid modification. Masked cold plasma treatment was used to create the wettable patterns. As shown in Fig. 3a, after the deposition of a dichloromethane droplet, its motion was characterized by either a fast-moving front edge or a slow-moving bulge. On the presuffued oleophilic channel, the front edge was driven by surface tension and hemiwicking, whereas the trailing bulge was driven by the Laplace pressure difference generated by the track geometry. As the liquid advanced along the channel, the bulge merged with the film ahead until the Laplace pressure difference was insufficient to induce motion. The net Laplace pressure difference in the liquid bulge can be estimated by,46
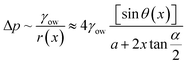 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(x) is the local curvature of the liquid along the channel direction x, w(x) is the local channel width where w(0) = a, and α is the wedge angle. Due to the complex variation of θ(x) along the channel, the authors used an experimental method to obtain the theoretical relation for liquid travel distance, velocity, and acceleration. Analogous to the Washburn equation,47 the following was proposed as the relation between time t, wedge angle, and travel distance,
θ(x) is the local curvature of the liquid along the channel direction x, w(x) is the local channel width where w(0) = a, and α is the wedge angle. Due to the complex variation of θ(x) along the channel, the authors used an experimental method to obtain the theoretical relation for liquid travel distance, velocity, and acceleration. Analogous to the Washburn equation,47 the following was proposed as the relation between time t, wedge angle, and travel distance,
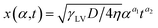 | (10) |
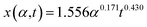 | (11) |
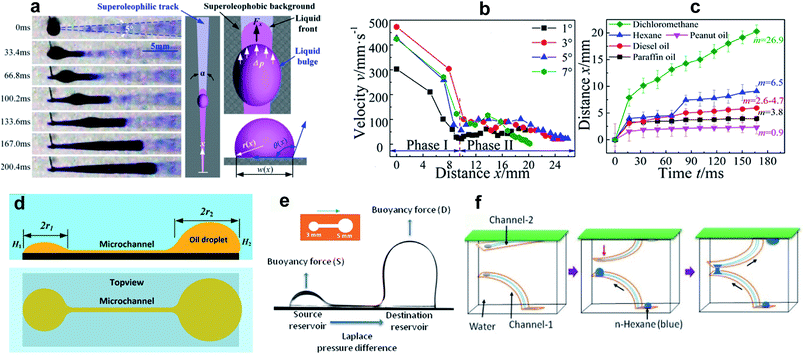 | ||
| Fig. 3 (a) Snapshots of dichloromethane transportation on a horizontal wedge-shaped pattern underwater. (b) The velocity vs. distance along the channel. Phase I and Phase II represent the channel width narrower and wider than the capillary length, respectively. (c) The travel distance with time at a wedge angle of 4° for liquids with different surface tension/viscosity. Reprinted with permission from ref. 45. Copyright (2016) American Chemical Society. (d) Schematic of oil transportation subjected to a Laplace pressure difference between two wetted dots connected through a channel. Reprinted with permission from ref. 48. Copyright (2018) American Chemical Society. (e) The dynamics of n-hexane underwater transportation between two reservoirs considering buoyancy and, (f) schematic of the 3D designed pathway for oil transportation between two flexible channels. Reprinted with permission from ref. 49. Copyright (2020) American Chemical Society. | ||
For wedge angles of α = 1°, 3°, 5°, and 7°, the above equation was consistent with the Washburn relation.
It was observed that the moving liquid experienced two phases of transportation velocity, which were related to the capillary length, k−1 = (γ/ρg)1/2, where ρ and g are the liquid density and gravitational acceleration, respectively. For a channel width smaller than the capillary length, the velocity was larger in comparison to channels wider than k−1 (phases I and II of Fig. 3b). To investigate the effect of surface tension γ and viscosity η on droplet transportation, the experiment was repeated using a variety of LST liquids including paraffin oil, hexane, peanut oil, dichloromethane, and diesel oil (surface tensions in the range of 18–35.5 mN m−1). According to the results (Fig. 3c), higher values of m = (γ/η)1/2 corresponded to a larger liquid travel distance.
Yang et al.48 used an alternate fabrication method to perform a more quantitative study on the subject. They used the ink-masked oxidization of copper foils to pattern two smooth dot reservoirs connected by a smooth channel. When dichloromethane droplets were deposited underwater on the smooth reservoir, the triple contact line was confined to the boundary of the reservoir until it reached the advancing contact angle of the outer oleophobic (contact angle ∼125° with oil) substrate. As the diameter of the reservoirs were different, the Laplace pressure gradient drove the droplet with a higher radius of curvature along the channel until the two reservoirs were in dynamic equilibrium (Fig. 3d). This pressure-induced driving force can be described as,48
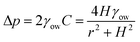 | (12) |
A broad range of LST liquids are less dense than water, so underwater transportation of these liquids can be challenging due to buoyancy. In a recent study, Upadhyay et al.49 used a vapor-based etching method to create a similar dots-channel pattern on a copper surface. Underwater, certain volumes of n-hexane were repeatedly injected into the source reservoir, and the droplet transport to the destination reservoir was governed by the Laplace pressure difference between the two reservoirs (Fig. 3e). After reaching a critical volume, the droplet split from the destination reservoir due to buoyancy. The changes in volume and contact angle at the reservoirs were measured to quantify the effect of buoyancy on the transportation dynamics. The increase in the volume of the destination droplet led to an increase in the buoyancy force, which in turn enhanced the flow from the source to the reservoir.
The use of copper tape rather than a rigid substrate made it possible to fabricate flexible patterned surfaces, which potentially enables new applications for 3D liquid transportation. As an example, the authors used two arc-shaped channels (see Fig. 3f) where the source and destination reservoir of channel-1 faced the destination and source reservoir of channel-2. Driven by buoyancy and the pressure difference, a droplet injected on the channel-1 source reservoir moved to the destination reservoir. The droplet then touched the source reservoir of channel-2, which similarly directed the liquid to the destination reservoir. More complex designs can be envisaged to transport LST liquid droplets along a predetermined path underwater.
3.2 Conical structures
Conical structures have also shown the capability to directionally transport liquids.51–56 As shown in Fig. 4a, the increasing radius along the axis serves as the gradient in the characteristic length of these structures. The difference in the radii of curvature generates a Laplace pressure difference. Hence, a droplet deposited on a conical structure tends to move away from the tip to the regions of lower curvature. The pressure gradient along the axis is given by,57
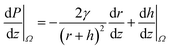 | (13) |
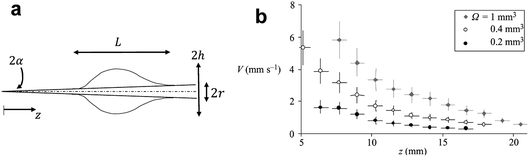 | ||
| Fig. 4 (a) The shape of a droplet on a conical fiber. (b) The velocity of different volumes of silicone oil droplets (η = 5 mPa s) along the conical fiber. Reprinted with permission from ref. 57. Copyright (2004) Cambridge University Press. | ||
Spontaneous droplet motion on a conical fiber was studied by Quere et al.57 They deposited various droplet volumes (0.2–1 mm3) of silicone oil with a viscosity range of 5–100 mPa s on a conical copper fiber. The fibers were prewetted to prevent a change in droplet volume. The measured velocity was shown to decrease at larger radii and increase with droplet volume (Fig. 4b). The authors derived the following scaling law to predict the velocity of a moving droplet on a horizontal conical fiber,
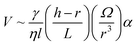 | (14) |
In a recent study, Hu et al.58 comparatively investigated underwater directional transportation of 1,2-dichloroethane droplets on tapered structures exhibiting different surface curvatures. For dry and wet superhydrophobic conical fibers, the transport velocities of 0.6 mm s−1 and 5 mm s−1 were reported, respectively. In comparison to conical fibers, the developed trigonal pyramid with concave curved surfaces exhibited an alternate transport strategy and higher velocity, up to 32.9 mm s−1. The faster transportation was attributed to the increased length covered by the liquid and the convex shape of the advancing meniscus on the curved surfaces, which is typically concave when spreading on conical fibers.
3.3 Bio-mimetic wedge corner structures
The Nepenthes alata plant can spread water from the inner side to the outer side of its peristome. The underlying mechanism was first revealed by Chen et al. in 2016.59 Their multiscale structure can be described as two-order hierarchical microgrooves with distributed microcavities along the second-order grooves. The arc-shape structure of the microcavities enhances capillary rise in the direction of liquid transportation, while contact line pinning at the microcavity's sharp edge prevents spreading in the reverse direction (Fig. 5a).60–63 This enhanced capillary effect can be explained by a capillary rise at the corner formed by two vertical plates making a small angle (Fig. 5b). For an infinitesimal difference between bottom opening angle, α1, and top opening angle, α2, the capillary height rise H(x) may be expressed as,64,65
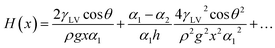 | (15) |
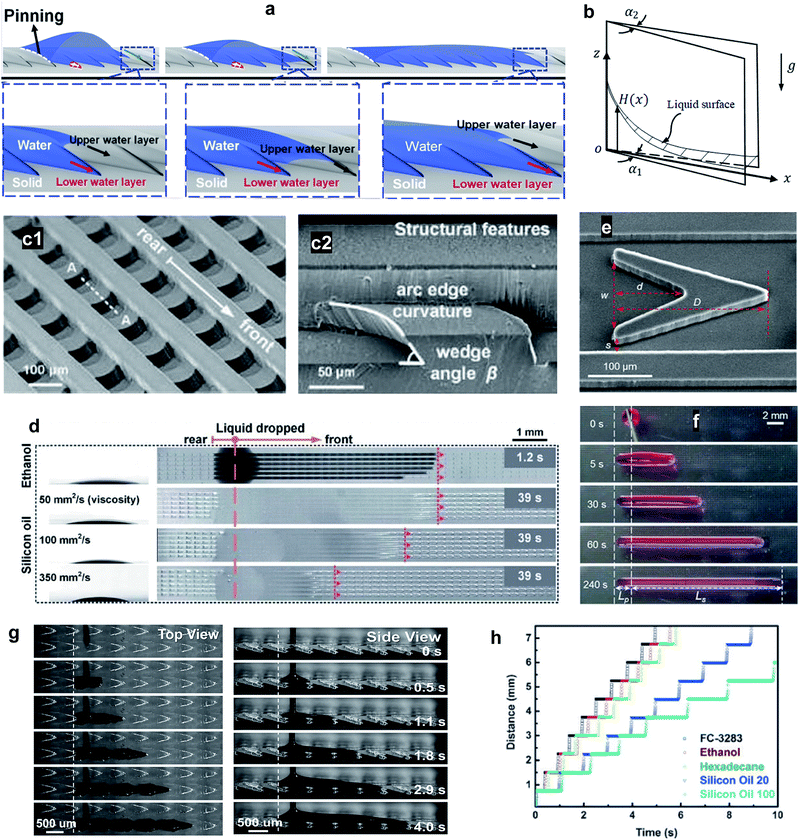 | ||
| Fig. 5 (a) 3D illustration of the directional liquid transportation on the peristome of a pitcher plant. Reprinted with permission from ref. 71. Copyright (2018) American Chemical Society. (b) Capillary rise at the corner formed by two vertical plates with wedge angles of α1 at the bottom and α2 at the top. (c1) Structure of a bio-inspired, unidirectional liquid spreading surface and, (c2) cross section view (indicated by line A–A). (d) Unidirectional spreading of LST liquids including ethanol and silicon oil with viscosities of 50, 100, and 350 mm2 s−1. Reprinted with permission from ref. 6. Copyright (2017) Royal Society of Chemistry. (e) SEM image of a single V-shaped post where s, w, d, and D indicate the inlet width of the side channel, the inlet width of the cavity, the length of the cavity, and the length of the V-shaped post, respectively. The transportation performance of the designed structure is demonstrated by (f) optical images of time-dependent unidirectional transport of a ∼5 μL paraffin oil droplet. Reprinted with permission from ref. 72. Copyright (2020) American Chemical Society. (g) Unidirectional transportation of both viscous and non-viscous liquids was achieved, as shown by (h) time sequences of the directional transportation distance. The slope of the curve indicates the flow velocity which increases with increasing surface energy, decreasing liquid surface tension, and decreasing liquid viscosity. Reprinted with permission from ref. 73. Copyright (2016) WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
Engineered surfaces that resemble the structure of the peristome of pitcher plants involve a complex fabrication process. Instead, Li et al.72 designed simple V-shaped posts aligned in parallel microchannels. The sharp edges of the V-shapes prevented backflow in the pinning direction, so the asymmetry of the V-shapes was crucial to achieving unidirectional liquid transport (Fig. 5e). The designed surface was capable of directionally spreading different lubricating oils along the surfaces such as paraffin oil, mineral oil, PAO-4, and silicone oil (Fig. 5f).
Li et al.73 developed an artificial peristome-mimetic surface using high-resolution stereo-lithography. The surface featured arrayed microcavities along the axial direction with a typical length, width, and depth of 700 μm, 250 μm, and 150 μm, respectively (Fig. 5g). A variety of liquids with different viscosity and surface tension were tested (Fig. 5h), and unidirectional transportation for liquids with surface tension as low as 9.5 mN m−1 (FC-72) was achieved.
4 Slip
4.1 Re-entrant micropatterns
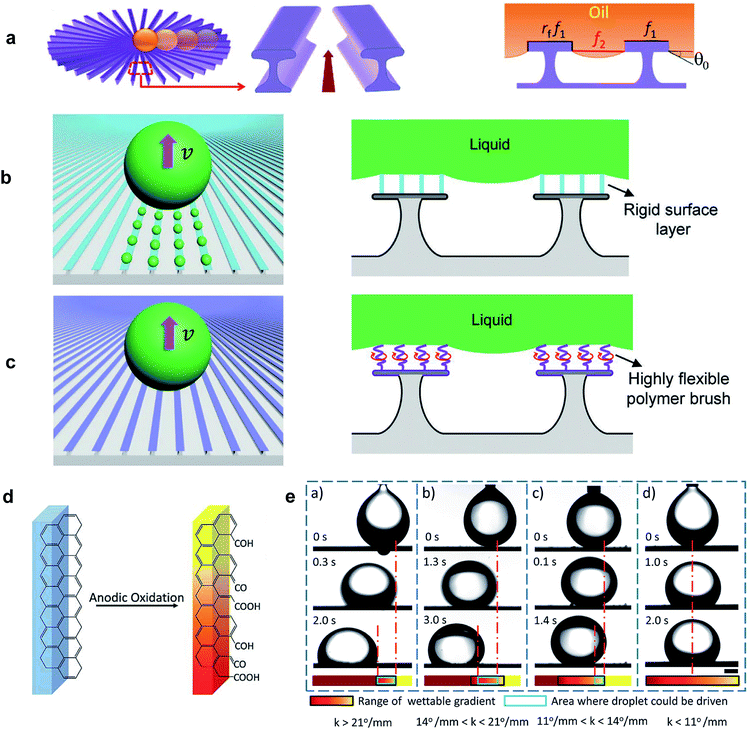
Dissimilar to spreading, during slip the trailing end of a LST droplet recedes from the solid surface while the front wetting line advances. As LST liquids make equilibrium contact angles less than 90° on all smooth surfaces, increasing roughness will not enhance the repellency of the surface according to the Wenzel model.43 However, it has been shown that re-entrant topography is capable of pinning the liquid/air interface, which leads to a metastable Cassie–Baxter state.74,75 A higher intrinsic contact angle leads to greater capillary resistance of this composite interface.Li et al.76 used a radial array of re-entrant structures to generate directional oil transportation. The undercut enabled the Cassie–Baxter state, and the surface was coated with a fluoropolymer to maximize the intrinsic contact angle. The radial structure caused an increase in the solid fraction in contact with the liquid towards the center, which induced an inward wettability gradient (Fig. 6a). The driving force arose from this wettability gradient and excess free energy was released as the droplet wet the additional solid surface. Hexadecane was used as the model LST liquid to evaluate spontaneous droplet transportation. Depending on the structural parameters, three modes of droplet motion were observed: toward the center, pinned, and outward.
 | ||
| Fig. 6 (a) Schematic of the radial array of micropatterns for directional oil transportation.76 (b) Microscopic liquid residue left during liquid transportation on a coating with low-flexibility chains and, (c) residue-free transportation of liquids using a liquid-like coating. Liquid-like refers to the highly flexible polymer brushes where their chain segments are mobile and free to rotate at room temperature. Reprinted with permission from ref. 77. Copyright (2019) WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. (d) Schematic of the chemical composition gradient on graphite plates under gradiented current and oxidation time treatment. (e) Travel distance of an underwater 10 μL oil droplet (chloroform) on the horizontal graphite surfaces with different wettable gradient, k. The scale bar is 1 mm. Reprinted with permission from ref. 78. Copyright (2017) Royal Society of Chemistry. | ||
During pinning, the driving force was insufficient to overcome contact angle hysteresis. Backward flow was observed when the space between the stripes was higher than the critical spacing necessary to support the Cassie–Baxter state, and a wetting transition occurred, beginning from the outer areas which then pulled the droplet outward. Based on this observation and theoretical analysis, it was inferred that directional transportation could be optimized by reducing the angle between the stripes or increasing the stripe width. Through a high magnification optical microscope, it was also shown that when the droplet approached the center area, the receding contact line left liquid residue on the stripes—though invisible to the naked eye. The authors reported LST liquid velocities between 24.0–29.8 mm s−1 for their fabricated surfaces exhibiting different wettability gradients, and a slight increase was reported by decreasing the liquid surface tension.
In 2019, Huang et al.77 carried out an extended investigation on the formation mechanism of microscopic liquid residues on similar re-entrant profiles. They revealed that the liquid residue is governed by a dynamic wetting process rather than simply the contact angle hysteresis of the surface. Two different PFOS (perfluoro-octyltrichlorosilane) and PFPE (perfluorinated polyether) polymer chains were grafted on the micropatterned silicon wafer substrates. In contrast to the rigid functional groups of perfluoro-alkylsilane coatings like PFOS, PFPE polymer chains are highly flexible (Fig. 6b and c). The directional liquid transportation on uncoated, PFOS-coated, and PFPE-coated surfaces was studied using various LST liquids including oleic acid, non-volatile 1-ethyl-3-methylimidazolium ethyl sulfate (IL1), bis(hydroxyethyl)dimethylammonium-methanesulfonate (IL2), low-volatility polydimethylsiloxane (PDMS), and n-hexadecane. All the liquids left microscopic residues on the uncoated surface. There was also considerable mass loss of oleic acid and PDMS during transportation on the PFOS-coated surface. In contrast, the PFPE-coated surface effectively suppressed the formation of liquid residue for most of the liquids (except PDMS). The PFPE-coated surface also provided the highest transportation velocity (up to 122 mm s−1) which was attributed to its lower contact angle hysteresis and robust Cassie–Baxter state.
4.2 Surface tension gradient
Liquid transportation induced by anisotropy in surface tension forces is a classical wetting phenomenon, known as the Marangoni effect.79 This surface tension gradient has primarily been achieved by variation in temperature or composition of the liquid at the interface,29 but a chemical wettability gradient on a solid surface has also been demonstrated to induce liquid motion. Several studies have developed special coating processes to obtain this wettability gradient and have successfully reported directional transportation of water droplets.13,52 The dynamics of wetting on such surfaces is highly dependent on both the wetted area and contact angle hysteresis.53 Moreover, in contrast to water droplets, LST liquids are highly wetting to most surfaces, which limits the possible range that the wettability gradient may achieve. Additionally, the higher contact area leads to higher contact line resistance due to hysteresis. Hence, very few studies have demonstrated LST liquid transportation induced by a surface energy gradient.In a recent study, Shang et al.78 used gradients in current and oxidation time to introduce a chemical gradient onto a graphite plate (Fig. 6d). The surface exhibited a modest wettable gradient for water in air (k = 2.86° mm−1), but higher values were measured when an oil droplet was deposited on the hydrophilic surface underwater. The authors observed a decrease in travel distance, from 1.57 mm for k = 26° mm−1, to zero-motion at k = 11° mm−1 (Fig. 6e). Here, the force that drives the oil droplet towards the more wettable region can be expressed as F ∼ πγR(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θB −cos
θB −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA), where R is the base radius of the droplet, γ is the surface tension of the oil, and θA and θB are the contact angles at the less wettable and more wettable sides of the droplet, respectively.80 In addition to the surface hysteresis force, the surface's large resistance to underwater motion significantly limited the travel distance. Regardless, a gradient in surface energy has been utilized to perform a variety of tasks for LST liquid droplets, including lossless capturing, collecting, transferring, and sorting.81–84
θA), where R is the base radius of the droplet, γ is the surface tension of the oil, and θA and θB are the contact angles at the less wettable and more wettable sides of the droplet, respectively.80 In addition to the surface hysteresis force, the surface's large resistance to underwater motion significantly limited the travel distance. Regardless, a gradient in surface energy has been utilized to perform a variety of tasks for LST liquid droplets, including lossless capturing, collecting, transferring, and sorting.81–84
Further, Movafaghi et al.85 precisely tailored surface energy domains by UV irradiation of fluorinated superomniphobic surfaces (highly repellent to both water and LST liquids). This allowed them to sort droplets by controlling the mobility of droplets based on their surface tension (γLV = 28.7 mN m−1 to γLV = 72.1 mN m−1). After droplet deposition on top of the tilted surface, each discrete perpendicular domain allowed certain high surface tension droplets to freely roll past the domain while trapping other lower surface tension droplets.
5 Evaluation
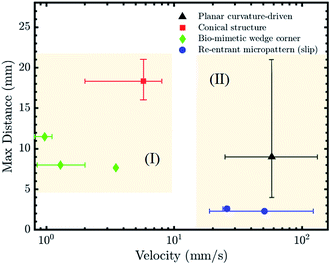
Different parameters may be used to evaluate the effectiveness of the above strategies for LST liquid transportation. The travel distance as a function of liquid velocity for the previously discussed strategies is plotted in Fig. 7. To the best of our knowledge, velocity and travel speed have not been investigated for surface energy gradients and LST liquids.As discussed in the ‘Theoretical Analysis’ section, a pre-existing liquid film on the channel reduces the viscous effects by three times and brings the contact angle near zero as the droplet moves on the pre-wetted substrate. Hence, the curvature-driven motion of the droplet inside a wet channel exhibits relatively higher velocity. The re-entrant structures also provide a driving force for fast droplet transportation. This can be achieved by the specifically arranged micro-stripes that induce a considerable wettability gradient over a short length, in addition to the minimized solid–liquid contact area (Fig. 7, Zone (II)).
The main challenge facing the directional transportation of LST liquids using channels exhibiting a wettability contrast is creating the oleophobic background for the patterns. While hydrophilic surfaces in air may become oleophobic underwater, this limits the potential of this strategy to submerged applications. Although more challenging to fabricate, re-entrant structures have the benefit of LST liquid transport in air and exhibit relatively lossless and fast liquid transportation, at least with certain surface chemistries.
Bio-mimetic wedge-corner structures involve a complex fabrication process in comparison to the planar patterns but have shown the ability to transport LST liquids with a broad range of surface tension and viscosity, although at lower speeds (Fig. 7, Zone (I)). The designed structure allowed the liquids to move in one direction while remaining pinned in the reverse direction, and this persisted for every distributed microgroove.
The LST liquid transportation performance of the conical structures is highly dependent on the fiber radius. In terms of application, its simple 3D design can be beneficial to develop multi arrays of conical structures for a large area condenser or to improve the heat transfer efficiency of a system.
6 Applications
LST liquids are involved in a broad range of industrial processes, from macroscale lubrication to microscale fluidic devices.10,86–89 The surfaces developed with structural asymmetry have demonstrated practical applications in high-resolution printing, bio detectors, and heat transfer.90–95 In the case of an underwater composite solid/oil/water interface, using an oleophobic/philic pattern can serve as an oil–water separation device.49 As shown in Fig. 8a, when an emulsion was deposited in the reservoir, the dyed water was released into the surrounding water, and the oil droplet remained pinned to the oleophilic pattern. The underwater, curvature-driven surfaces have also been used to develop a one-way valve for microfluidic devices (Fig. 8b).45 Driven by the Laplace pressure gradient, a deposited oil droplet on the wettable channel can spread from the narrow end to the wider part, and the pattern resists motion in the reverse direction.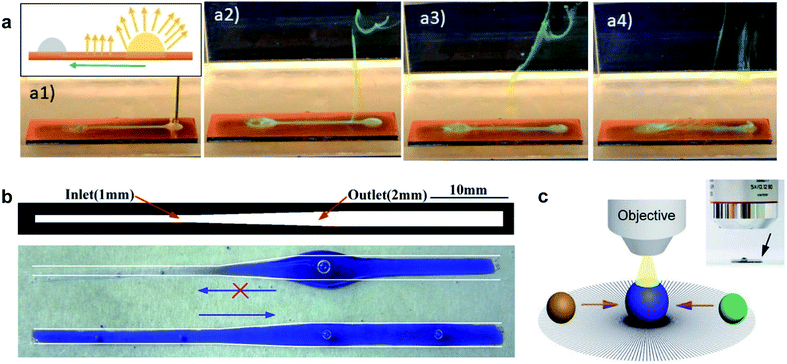 | ||
| Fig. 8 (a) Snapshots of dyed water removal from a water-in-oil emulsion on the wettability contrast channel. Reprinted with permission from ref. 49. Copyright (2020) American Chemical Society. (b) One-way valve developed on a channel for microfluidic devices. Reprinted with permission from ref. 45. Copyright (2016) American Chemical Society. (c) The potential application of the developed radial re-entrant microstructures in a reaction analysis. Reprinted with permission from ref. 77. Copyright (2019) WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
Re-entrant microstructures enable slip for the transportation for LST liquids. This lossless transportation of liquids would be of high value for microfluidic systems, bioassays, or chemical analysis. For example, high-accuracy analysis was demonstrated using a radial array of micropatterns (Fig. 8c).77 The analyte droplets spontaneously moved toward the center where the two droplets merged, and a microscope above the setup was used to monitor the reaction.
7 Conclusion and perspectives
Bio-mimetic surfaces have been developed to enable the directional transportation of liquid droplets. However, LST liquids either partially or completely wet all surface chemistries which limits the functionality of these surfaces. In this review, the developed strategies to passively transport LST liquids are categorized in either the spread or slip mode of transportation. In the spread mode of transportation, a droplet spreads preferentially in one direction and is pinned in the reverse direction, with potential applications in self-lubrication, microfluidic devices, etc. The slip mode can potentially enable lossless transportation of LST liquids as the contact line recedes from the trailing end of the droplet. Droplet transportation velocity and maximum travel distance were used to compare the performance of these strategies. The wettability behavior of LST liquids brings up challenges that limit the functionality of each method; the oleophobic background for patterned channels on smooth surfaces, the complex fabrication of wedge corner structures along with their low transportation velocities, and the limited travel distance for conical structure and re-entrant patterns. The development of a versatile method that satisfies all the requirements for LST liquids transportation remains an active challenge. However, current strategies have shown promise towards the guided transportation of LST liquids.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Syilx Okanagan Nation for use of their unceded territory, the land on which the research was conducted. We acknowledge the support of the Department of National Defence, through contract CFPMN1-026.References
- A. R. Parker and C. R. Lawrence, Water capture by a desert beetle, Nature, 2001, 414(6859), 33–34, DOI:10.1038/35102108.
- Y. Zheng, et al., Directional water collection on wetted spider silk, Nature, 2010, 463(7281), 640–643, DOI:10.1038/nature08729.
- J. Ju, H. Bai, Y. Zheng, T. Zhao, R. Fang and L. Jiang, A multi-structural and multi-functional integrated fog collection system in cactus, Nat. Commun., 2012, 3(1), 1–6, DOI:10.1038/ncomms2253.
- H. Chen, et al., Ultrafast water harvesting and transport in hierarchical microchannels, Nat. Mater., 2018, 17(10), 935–942, DOI:10.1038/s41563-018-0171-9.
- M. Prakash, D. Quéré and J. W. M. Bush, Surface tension transport of prey by feeding shorebirds: The capillary ratchet, Science, 2008, 320(5878), 931–934, DOI:10.1126/science.1156023.
- H. Chen, L. Zhang, Y. Zhang, P. Zhang, D. Zhang and L. Jiang, Uni-directional liquid spreading control on a bio-inspired surface from the peristome of Nepenthes alata, J. Mater. Chem. A, 2017, 5(15), 6914–6920, 10.1039/c7ta01609c.
- T. Wang, et al., Apex structures enhance water drainage on leaves, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(4), 1890–1894, DOI:10.1073/pnas.1909924117.
- K. H. Chu, R. Xiao and E. N. Wang, Uni-directional liquid spreading on asymmetric nanostructured surfaces, Nat. Mater., 2010, 9(5), 413–417, DOI:10.1038/nmat2726.
- K. Li, et al., Structured cone arrays for continuous and effective collection of micron-sized oil droplets from water, Nat. Commun., 2013, 4(1), 1–7, DOI:10.1038/ncomms3276.
- S. V. Kirner, et al., Mimicking bug-like surface structures and their fluid transport produced by ultrashort laser pulse irradiation of steel, Appl. Phys. A Mater. Sci. Process., 2017, 123(12), 1–13, DOI:10.1007/s00339-017-1317-3.
- S. Daniel, M. K. Chaudhury and J. C. Chen, Fast drop movements resulting from the phase change on a gradient surface, Science, 2001, 291(5504), 633–636, DOI:10.1126/science.291.5504.633.
- P. S. Brown and B. Bhushan, Bioinspired materials for water supply and management: Water collection, water purification and separation of water from oil, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 2016, 374, 2073, DOI:10.1098/rsta.2016.0135.
- X. Hou, et al., Interplay between materials and microfluidics, Nat. Rev. Mater., 2017, 2(5), 17016, DOI:10.1038/natrevmats.2017.16.
- H. Dai, Z. Dong and L. Jiang, Directional liquid dynamics of interfaces with superwettability, Sci. Adv., 2020, 6(37), eabb5528, DOI:10.1126/sciadv.abb5528.
- S. Zhou, L. Jiang and Z. Dong, Bioinspired Surface with Superwettability for Controllable Liquid Dynamics, Adv. Mater. Interfaces, 2020, 2000824, DOI:10.1002/admi.202000824.
- H. Wu, et al., Smart design of wettability-patterned gradients on substrate-independent coated surfaces to control unidirectional spreading of droplets, Soft Matter, 2017, 13(16), 2995–3002, 10.1039/c6sm02864k.
- J. Li and Z. Guo, Spontaneous directional transportations of water droplets on surfaces driven by gradient structures, Nanoscale, 2018, 10(29), 13814–13831, 10.1039/c8nr04354j.
- J. Li, Y. Song, H. Zheng, S. Feng, W. Xu and Z. Wang, Designing biomimetic liquid diodes, Soft Matter, 2019, 15(9), 1902–1915, 10.1039/c9sm00072k.
- J. Song, et al., High-efficiency bubble transportation in an aqueous environment on a serial wedge-shaped wettability pattern, J. Mater. Chem. A, 2019, 7(22), 13567–13576, 10.1039/c9ta02095k.
- M. Reyssat, F. Pardo and D. Quéré, Drops onto gradients of texture, EPL, 2009, 87(3), 1–6, DOI:10.1209/0295-5075/87/36003.
- X. Wang, Z. Wang, L. Heng and L. Jiang, Stable Omniphobic Anisotropic Covalently Grafted Slippery Surfaces for Directional Transportation of Drops and Bubbles, Adv. Funct. Mater., 2020, 30(1), 1–10, DOI:10.1002/adfm.201902686.
- J. Li, J. Li, J. Sun, S. Feng and Z. Wang, Biological and Engineered Topological Droplet Rectifiers, Adv. Mater., 2019, 31(14), 1–21, DOI:10.1002/adma.201806501.
- M. K. Chaudhury and G. M. Whitesides, How to Make Water Run Uphill, vol. 256, June, 1992 Search PubMed.
- S. Daniel, S. Sircar, J. Gliem and M. K. Chaudhury, Ratcheting motion of liquid drops on gradient surfaces, Langmuir, 2004, 20(10), 4085–4092, DOI:10.1021/la036221a.
- N. Moumen, R. Shankar Subramanian and J. B. McLaughlin, Experiments on the motion of drops on a horizontal solid surface due to a wettability gradient, Langmuir, 2006, 22(6), 2682–2690, DOI:10.1021/la053060x.
- Y. Ito, et al., The movement of a water droplet on a gradient surface prepared by photodegradation, Langmuir, 2007, 23(4), 1845–1850, DOI:10.1021/la0624992.
- S. Morgenthaler, C. Zink and N. D. Spencer, Surface-chemical and -morphological gradients, Soft Matter, 2008, 4(3), 419–434, 10.1039/b715466f.
- K. Ichimura, S. K. Oh and M. Nakagawa, Light-driven motion of liquids on a photoresponsive surface, Science, 2000, 288(5471), 1624–1626, DOI:10.1126/science.288.5471.1624.
- F. Brochard, Motions of Droplets on Solid Surfaces Induced by Chemical or Thermal Gradients, Langmuir, 1989, 5(2), 432–438, DOI:10.1021/la00086a025.
- W. C. Nelson and C.-J. ‘CJ’ Kim, Droplet Actuation by Electrowetting-on-Dielectric (EWOD): A Review, J. Adhes. Sci. Technol., 2012, 26(12–17), 1747–1771, DOI:10.1163/156856111X599562.
- A. Li, et al., Programmable droplet manipulation by a magnetic-actuated robot, Sci. Adv., 2020, 6(7), eaay5808, DOI:10.1126/sciadv.aay5808.
- J. A. Lv, Y. Liu, J. Wei, E. Chen, L. Qin and Y. Yu, Photocontrol of fluid slugs in liquid crystal polymer microactuators, Nature, 2016, 537(7619), 179–184, DOI:10.1038/nature19344.
- X. Noblin, R. Kofman and F. Celestini, Ratchetlike motion of a shaken drop, Phys. Rev. Lett., 2009, 102(19), 1–4, DOI:10.1103/PhysRevLett.102.194504.
- G. Kwon, D. Panchanathan, S. R. Mahmoudi, M. A. Gondal, G. H. McKinley and K. K. Varanasi, Visible light guided manipulation of liquid wettability on photoresponsive surfaces, Nat. Commun., 2017, 8 DOI:10.1038/ncomms14968.
- F. Mugele and J. C. Baret, Electrowetting: From basics to applications, J. Phys. Condens. Matter, 2005, 17 DOI:10.1088/0953-8984/17/28/R01.
- P. G. De Gennes, Wetting: Statics and dynamics, Rev. Mod. Phys., 1985, 57(3), 827–863, DOI:10.1103/RevModPhys.57.827.
- S. Daniel and M. K. Chaudhury, Rectified motion of liquid drops on gradient surfaces induced by vibration, Langmuir, 2002, 18(9), 3404–3407, DOI:10.1021/la025505c.
- L. Gao and T. J. McCarthy, Contact angle hysteresis explained, Langmuir, 2006, 22(14), 6234–6237, DOI:10.1021/la060254j.
- P.-G. de Gennes, F. Brochard-Wyart, D. Quéré, P.-G. de Gennes, F. Brochard-Wyart, and D. Quéré, Special Interfaces, 2004 Search PubMed.
- C. G. Ngan and B. D. V. Elizabeth, On the nature of the dynamic contact angle: An experimental study, J. Fluid Mech., 1982, 118, 27–40, DOI:10.1017/S0022112082000949.
- R. L. Hoffman, A study of the advancing interface. I. Interface shape in liquid-gas systems, J. Colloid Interface Sci., 1975, 50(2), 228–241, DOI:10.1016/0021-9797(75)90225-8.
- L. H. Tanner, The spreading of silicone oil drops on horizontal surfaces, J. Phys. D Appl. Phys., 1979, 12(9), 1473–1484 CrossRef CAS.
- R. N. Wenzel, Resistance of solid surfaces to wetting by water, Ind. Eng. Chem., 1936, 28(8), 988–994, DOI:10.1021/ie50320a024.
- M. Liu, S. Wang, Z. Wei, Y. Song and L. Jiang, Bioinspired design of a superoleophobic and low adhesive water/solid interface, Adv. Mater., 2009, 21(6), 665–669, DOI:10.1002/adma.200801782.
- S. Huang, et al., Underwater Spontaneous Pumpless Transportation of Nonpolar Organic Liquids on Extreme Wettability Patterns, ACS Appl. Mater. Interfaces, 2016, 8(5), 2942–2949, DOI:10.1021/acsami.5b08596.
- A. Ghosh, R. Ganguly, T. M. Schutzius and C. M. Megaridis, Wettability patterning for high-rate, pumpless fluid transport on open, non-planar microfluidic platforms, Lab Chip, 2014, 14(9), 1538–1550, 10.1039/c3lc51406d.
- E. W. Washburn, The Dynamics of Capillary Flow, Phys. Rev., 1921, 17(3), 273–283, DOI:10.1103/PhysRev.17.273.
- X. Yang, V. Breedveld, W. T. Choi, X. Liu, J. Song and D. W. Hess, Underwater Curvature-Driven Transport between Oil Droplets on Patterned Substrates, ACS Appl. Mater. Interfaces, 2018, 10(17), 15258–15269, DOI:10.1021/acsami.8b02413.
- R. K. Upadhyay and P. R. Waghmare, Underwater Oil Drop Storage, Guided Transport, and Oil/Water Separation Using Surfaces with Wettability Contrast Prepared through a Vapor-Based Etching Method, ACS Appl. Mater. Interfaces, 2020, 12(9), 11144–11154, DOI:10.1021/acsami.9b18508.
- J. Melin, W. Van Der Wijngaart and G. Stemme, Behaviour and design considerations for continuous flow closed-open-closed liquid microchannels, Lab Chip, 2005, 5(6), 682–686, 10.1039/b501781e.
- G. McHale, M. I. Newton and B. J. Carroll, The shape and stability of small liquid drops on fibers, Oil Gas Sci. Technol., 2001, 56(1), 47–54, DOI:10.2516/ogst:2001006.
- H. B. Eral, et al., Drops on functional fibers: From barrels to clamshells and back, Soft Matter, 2011, 7(11), 5138–5143, 10.1039/c0sm01403f.
- T. Xu, Y. Lin, M. Zhang, W. Shi and Y. Zheng, High-Efficiency Fog Collector: Water Unidirectional Transport on Heterogeneous Rough Conical Wires, ACS Nano, 2016, 10(12), 10681–10688, DOI:10.1021/acsnano.6b05595.
- P. Renvoisé, J. W. M. Bush, M. Prakash and D. Quéré, Drop propulsion in tapered tubes, EPL, 2009, 86(6), 3–8, DOI:10.1209/0295-5075/86/64003.
- J. Ju, et al., Cactus stem inspired cone-arrayed surfaces for efficient fog collection, Adv. Funct. Mater., 2014, 24(44), 6933–6938, DOI:10.1002/adfm.201402229.
- J. Ju, K. Xiao, X. Yao, H. Bai and L. Jiang, Bioinspired conical copper wire with gradient wettability for continuous and efficient fog collection, Adv. Mater., 2013, 25(41), 5937–5942, DOI:10.1002/adma.201301876.
- É. Lorenceau and D. Quéré, Drops on a conical wire, J. Fluid Mech., 2004, 510(510), 29–45, DOI:10.1017/S0022112004009152.
- B. Hu, et al., Ultrafast Self-Propelled Directional Liquid Transport on the Pyramid-Structured Fibers with Concave Curved Surfaces, J. Am. Chem. Soc., 2020, 142(13), 6111–6116, DOI:10.1021/jacs.9b13286.
- H. Chen, et al., Continuous directional water transport on the peristome surface of Nepenthes alata, Nature, 2016, 532(7597), 85–89, DOI:10.1038/nature17189.
- J. Li and L. Wang, Coalescence-induced transition between unidirectional and bidirectional propagation of droplets, Mater. Horizons, 2020, 7(8), 2078–2084, 10.1039/d0mh00459f.
- C. Li, H. Dai, C. Gao, T. Wang, Z. Dong and L. Jiang, Bioinspired inner microstructured tube controlled capillary rise, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(26), 12704–12709, DOI:10.1073/pnas.1821493116.
- P. Concus and R. Finn, On The Behavior Of A Capillary Surface In A Wedge, Proc. Natl. Acad. Sci., 1969, 63(2), 292–299, DOI:10.1073/pnas.63.2.292.
- C. Li, C. Yu, S. Zhou, Z. Dong and L. Jiang, Liquid harvesting and transport on multiscaled curvatures, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(38), 23436–23442, DOI:10.1073/pnas.2011935117.
- F. J. Higuera, A. Medina and A. Liñán, Capillary rise of a liquid between two vertical plates making a small angle, Physics of Fluids, 2008, 20(10), 102102, DOI:10.1063/1.3000425.
- A. Ponomarenko, D. Quéré and C. Clanet, A universal law for capillary rise in corners, J. Fluid Mech., 2011, 666, 146–154, DOI:10.1017/S0022112010005276.
- F. Box, C. Thorogood and J. H. Guan, Guided droplet transport on synthetic slippery surfaces inspired by a pitcher plant, J. R. Soc. Interface, 2019, 16(158), 1–7, DOI:10.1098/rsif.2019.0323.
- S. Zhou, C. Yu, C. Li, Z. Dong and L. Jiang, Programmable unidirectional liquid transport on peristome-mimetic surfaces under liquid environments, J. Mater. Chem. A, 2019, 7(31), 18244–18248, 10.1039/c9ta04770k.
- H. Chen, L. Zhang, P. Zhang, D. Zhang, Z. Han and L. Jiang, A Novel Bioinspired Continuous Unidirectional Liquid Spreading Surface Structure from the Peristome Surface of Nepenthes alata, Small, 2017, 13(4), 1–6, DOI:10.1002/smll.201601676.
- W. Sun, L. Tang, W. Hong, Y. Zhan, B. Yang and J. Liu, A novel microstructure inspired from Nepenthes alata and lizard skin and its enhanced uni-directional liquid spreading property, RSC Adv., 2019, 9(14), 7842–7848, 10.1039/C8RA08768G.
- S. Zhou, C. Yu, C. Li, L. Jiang and Z. Dong, Droplets Crawling on Peristome-Mimetic Surfaces, Adv. Funct. Mater., 2020, 30(12), 1908066, DOI:10.1002/adfm.201908066.
- C. Yu, C. Li, C. Gao, Z. Dong, L. Wu and L. Jiang, Time-Dependent Liquid Transport on a Biomimetic Topological Surface, ACS Nano, 2018, 12(6), 5149–5157, DOI:10.1021/acsnano.8b01800.
- X. Li, J. Li and G. Dong, Bioinspired Topological Surface for Directional Oil Lubrication, ACS Appl. Mater. Interfaces, 2020, 12(4), 5113–5119, DOI:10.1021/acsami.9b20345.
- C. Li, N. Li, X. Zhang, Z. Dong, H. Chen and L. Jiang, Uni-Directional Transportation on Peristome-Mimetic Surfaces for Completely Wetting Liquids, Angew. Chem. Int. Ed., 2016, 55(48), 14988–14992, DOI:10.1002/anie.201607514.
- A. B. D. Cassie and S. Baxter, Wettability of porous surfaces, Trans. Faraday Soc., 1944, 40(5), 546, 10.1039/tf9444000546.
- A. Tuteja, et al., Designing superoleophobic surfaces, Science, 2007, 318(5856), 1618–1622, DOI:10.1126/science.1148326.
- J. Li, Q. H. Qin, A. Shah, R. H. A. Ras, X. Tian and V. Jokinen, Oil droplet self-transportation on oleophobic surfaces, Sci. Adv., 2016, 2(6), 1–7, DOI:10.1126/sciadv.1600148.
- S. Huang, J. Li, L. Liu, L. Zhou and X. Tian, Lossless Fast Drop Self-Transport on Anisotropic Omniphobic Surfaces: Origin and Elimination of Microscopic Liquid Residue, Adv. Mater., 2019, 31(27), 1–8, DOI:10.1002/adma.201901417.
- W. Shang, S. Deng, S. Feng, Y. Xing, Y. Hou and Y. Zheng, One-step fabricated wettable gradient surface for controlled directional underwater oil-droplet transport, RSC Adv., 2017, 7(13), 7885–7889, 10.1039/c6ra28710g.
- C. Marangoni, Sul principio della viscosita superficiale dei liquidi stabilito dalsig, J. Plateau. Il Nuovo Cimento (1869-1876), 1871, 5(1), 239–273, DOI:10.1007/BF02718643.
- O. Bliznyuk, H. P. Jansen, E. S. Kooij, H. J. W. Zandvliet and B. Poelsema, Smart design of stripe-patterned gradient surfaces to control droplet motion, Langmuir, 2011, 27(17), 11238–11245, DOI:10.1021/la201671w.
- E. Zhang, Z. Cheng, T. Lv, L. Li and Y. Liu, The design of underwater superoleophobic Ni/NiO microstructures with tunable oil adhesion, Nanoscale, 2015, 7(45), 19293–19299, 10.1039/c5nr05375g.
- J. Yong, et al., Femtosecond laser controlling underwater oil-adhesion of glass surface, Appl. Phys. A Mater. Sci. Process., 2015, 119(3), 837–844, DOI:10.1007/s00339-015-9044-0.
- J. Jiang, et al., Directional pumping of water and oil microdroplets on slippery surface, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(7), 2482–2487, DOI:10.1073/pnas.1817172116.
- S. Movafaghi, et al., Superomniphobic Papers for On-Paper pH Sensors, Adv. Mater. Interfaces, 2019, 6(13), 1–6, DOI:10.1002/admi.201900232.
- S. Movafaghi, W. Wang, A. Metzger, D. D. Williams, J. D. Williams and A. K. Kota, Tunable superomniphobic surfaces for sorting droplets by surface tension, Lab Chip, 2016, 16(17), 3204–3209, 10.1039/c6lc00673f.
- K. Choi, A. H. C. Ng, R. Fobel and A. R. Wheeler, Digital microfluidics, Annu. Rev. Anal. Chem., 2012, 5, 413–440, DOI:10.1146/annurev-anchem-062011-143028.
- L. Shang, Y. Cheng and Y. Zhao, Emerging Droplet Microfluidics, Chem. Rev., 2017, 117(12), 7964–8040, DOI:10.1021/acs.chemrev.6b00848.
- S. P. R. Kobaku, et al., Wettability engendered templated self-assembly (WETS) for fabricating multiphasic particles, ACS Appl. Mater. Interfaces, 2015, 7(7), 4075–4080, DOI:10.1021/am507964k.
- C. Li, H. Dai, C. Gao, T. Wang, Z. Dong and L. Jiang, Bioinspired inner microstructured tube controlled capillary rise, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(26), 12704–12709, DOI:10.1073/pnas.1821493116.
- J. Z. Wang, Z. H. Zheng, H. W. Li, W. T. S. Huck and H. Sirringhaus, Dewetting of conducting polymer inkjet droplets on patterned surfaces, Nat. Mater., 2004, 3(3), 171–176, DOI:10.1038/nmat1073.
- K. K. Liu, R. G. Wu, Y. J. Chuang, H. S. Khoo, S. H. Huang and F. G. Tseng, Microfluidic systems for biosensing, Sensors, 2010, 10(7), 6623–6661, DOI:10.3390/s100706623.
- H. J. Cho, D. J. Preston, Y. Zhu and E. N. Wang, Nanoengineered materials for liquid-vapour phase-change heat transfer, Nat. Rev. Mater., 2016, 2(2), 1–17, DOI:10.1038/natrevmats.2016.92.
- C. Li, L. Wu, C. Yu, Z. Dong and L. Jiang, Peristome-Mimetic Curved Surface for Spontaneous and Directional Separation of Micro Water-in-Oil Drops, Angew. Chemie - Int. Ed., 2017, 56(44), 13623–13628, DOI:10.1002/anie.201706665.
- Y. Si and Z. Dong, Bioinspired Smart Liquid Directional Transport Control, Langmuir, 2020, 36(3), 667–681, DOI:10.1021/acs.langmuir.9b03385.
- J. Song, et al., Fabrication of long-term underwater superoleophobic al surfaces and application on underwater lossless manipulation of non-polar organic liquids, Sci. Rep., 2016, 6(1), 1–8, DOI:10.1038/srep31818.
| This journal is © The Royal Society of Chemistry 2020 |