Exploring the difference of bonding strength between silver(I) and chalcogenides in block copolymer systems

Abstract

Silver(I)–chalcogenide interactions have been widely found in the mineral paragenesis and are of great significance in medicinal systems. An accurate understanding of the intrinsic nature of these interactions would provide the basis for comprehending the involved natural and biological behaviors. However, few systematic works exploring the relative strength of silver(I)–chalcogenide bonds had been reported before. Thus, by combining single-molecule force spectroscopy (SMFS) from a kinetic point of view with quantum chemical studies from a thermodynamic point of view, we successfully quantified the relative strength of Ag(I)–X (X = S, Se, and Te from a chalcogenide-containing A–B–A block copolymer) interactions. Both results suggested that the order of Ag(I)–X bond strength is Ag(I)–S < Ag(I)–Se < Ag(I)–Te. These findings revealed the relative strength and nature of silver(I)–chalcogenide interactions and laid the foundation for various potential applications in supramolecular chemistry, electronics and many other fields.

---

Introduction

Among silver-containing minerals, argentite (Ag₂S),¹ naumannite (Ag₂Se)² and hessite (Ag₂Te)³ are three major inputs for the smelting of silver.^4–6 The mineral paragenesis between silver(I) and chalcogenides inspired us to explore the intrinsic essence of the relationship from macroscopic coexistence to the microscopic interactions. Furthermore, investigating the relative strength of silver(I)–chalcogenide interactions is also of great importance for systems such as chalcogenide-protected silver surfaces and nanoparticles. So an accurate understanding of the intrinsic nature of silver(I)–chalcogenide interactions could provide means for regulating the structures and functionalities of these systems and developing their applications.

In recent years, researchers have investigated the interactions between silver(I) and chalcogenide-containing molecules.^7–9 Pedersen synthesized macrocyclic polyether sulfides, which are good complexing agents for silver and gold.¹⁰ Kudelski and co-workers demonstrated that cysteine layers adsorbed on the silver surface by the sulfur moiety and the terminal amino or the carboxyl group.¹¹ Besides, Shao et al. found that the bonding between silver(I) cations and S atoms on P=S brought distinct changes in the optical properties of heterasumanenes.¹² Although both selenium (Se) and tellurium (Te) are located in the same main group (VIA column) as sulfur, the research on Ag(I)–Se and Ag(I)–Te has been relatively limited over the past several decades.^11,12 Li and Xu compared the liquid membrane transport rates of silver(I) cations by heteromacrocyclic polyether and an order of selenabenzo-crown > thiabenzo-crown > tellurabenzo-crown was obtained.¹³ Later, Liu and Inoue found that partially covalent interaction between the silver(I) cation and Se donor in selenacrown ether may contribute to the high stability of the complexation.¹⁴ But further explorations of the property and relationship of interaction between silver(I) cations and chalcogenides are still scarce and controversial. Meanwhile, coordination between selenium-containing amino acids, such as selenocystine (SeCys) or selenomethionine (SeMet), and metal ions played an important role in verifying the biological behaviour and specific chemical derivative transformation of natural processes.¹⁵ Therefore, the Ag(I)–X (X = S, Se, and Te) coordination chemistry and the relative strength comparison of the above three kinds of chemical bonds are in need of further development.

Single-molecule force spectroscopy has been widely applied as a powerful tool to investigate intra- and intermolecular interactions,^16,17 including the elasticity of macromolecules,¹⁸ the unfolding force of proteins¹⁹ and so on.^20,21 As an advanced technology, atomic force microscopy (AFM)-based single-molecule force spectroscopy (SMFS) has been utilized to explore molecular interactions in complicated systems due to its extensive environmental adaptability and a broad range of detectable forces from pN to nN.

Selenium and tellurium containing polymers have been widely used in cancer therapy,²² self-healing materials²³ and tunable structural color materials²⁴ due to their unique and sensitive responsiveness to oxidation–reduction environments^25,26 and visible light.²⁷ Besides the coordination behaviour between chalcogenides and metals such as platinum²⁸ and gold²⁹ has also been demonstrated by the usage of chalcogenide containing polymers. Therefore, the selenium/tellurium containing polymer offered a proper vehicle to investigate the interaction between silver(I) and chalcogenides.

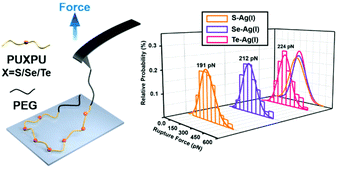
Herein, we explored the relative strength of silver(I)–chalcogenide interactions from both a kinetic point of view and a thermodynamic point of view. Specifically, the chalcogenide-containing block copolymer PEG-PUX-PEG was chosen as a model for the SMFS experiment and quantum chemical calculations were performed. The relative strength sequence was found to be Ag(I)–S < Ag(I)–Se < Ag(I)–Te (Scheme 1).

Scheme 1 Quantification of the bond strength between silver(I) and chalcogenides in sulfur/selenium/tellurium containing block copolymer systems by single-molecule force spectroscopy (SMFS).

Results and discussion

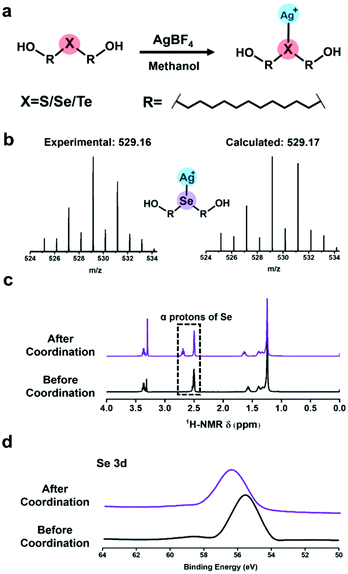
For clarity, di-(1-hydroxylundecyl) sulfide, selenide and telluride were denoted by HOC11S, HOC11Se, and HOC11Te respectively.

Preparation and characterization of (Ag/XC11OH)⁺ compounds

Before the SMFS experiments, the coordination behaviours of chalcogenides with silver(I) were firstly elucidated from the point of the solution phase. HOC11X (X = S, Se, and Te) was synthesized as described in our previous work.³⁰ To prepare (Ag/XC11OH)⁺ coordination compounds (Fig. 1a), the AgBF₄ was added into a methanol solution of HOC11X. And the solution was kept overnight in a shaking bed at 37 °C, yielding a black precipitate of (Ag/XC11OH)⁺. Taking the (Ag/SeC11OH)⁺ compound as an example, the powder was analysed by ESI-MS (Fig. 1b). The results of the observed molecular ion peak of (Ag/SeC11OH)⁺ remain highly consistent with the calculated results. Besides, the chemical shift of the α protons of selenium in dimethyl sulfoxide (DMSO) moved to the downfield due to the deshielding effect caused by the coordination between silver(I) cations and HOC11Se (Fig. 1c). To further confirm the coordination behaviour mentioned above, the obtained black precipitates were also studied by X-ray photoelectron spectroscopy (XPS). The bonding energy of the Se 3d peaks increased from 55.7 eV to 56.5 eV (Fig. 1d), revealing the electron transfer of selenium caused by the coordination with silver(I) cations. Similar to the characterization of (Ag/SeC11OH)⁺, the corresponding molecular ion peak of (Ag/SC11OH)⁺ and (Ag/TeC11OH)⁺ was found by ESI-MS (Fig. S1a†). And α protons of sulfur and tellurium also shifted to the downfield accordingly (Fig. S1b†). For the XPS result, both the bonding energies of S 2p and Te 3d increased (Fig. S1c†). All of the above results demonstrated that the chalcogenide-containing small organic molecule (HOC11X) could coordinate with the silver(I) of silver tetra fluoroborate (AgBF₄).

Fig. 1 The characterization of coordination behaviour between chalcogenide containing small molecules and silver tetra fluoroborate. (a) Chemical structure of the coordination compound for (Ag/XC11OH)⁺. (b) ESI-mass spectrum of (Ag/SeC11OH)⁺. (c) ¹H-NMR (400 MHz, DMSO, 25 °C). (d) XPS results of HOC11Se before and after coordination with silver(I) cations.

Characterization of self-assembled monolayers (SAM) on silver substrates

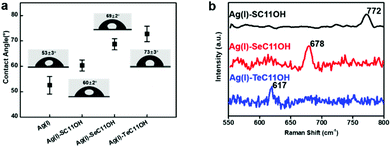
Similar to the coordination behaviour in the solution phase, the small molecule HOC11X could also form a self-assembled monolayer on the surface of silver substrates by a coordination bond (The surface of silver was oxidized to the form of silver(I) oxide by pre-treatment in advance, which was confirmed by X-ray photoelectron spectroscopy and X-ray diffraction in Fig. S2.†) After immersing the pre-treated silver substrates into an ethanol solution of HOC11X overnight under a N₂ atmosphere, a SAM on the silver surface could be obtained to compare and analyse various properties of different chalcogenides. Later, XPS was utilized to demonstrate the existence of SAMs on the silver substrates. Compared with the peaks observed for the powder of (Ag/XC11OH)⁺, the bonding energies of SAMs were 162.3 eV of S 2p (Fig. S3a†), 56.0 eV of Se 3d (Fig. S3b†), and 574.0 eV and 584.5 eV of Te 3d_5/2 and 3d_3/2 (Fig. S3c†), respectively, which were all smaller than the corresponding values obtained for the coordination compound in the solution phase. The reason for this was the formation of SAMs on the silver surfaces composed of silver(I) oxide instead of the free silver(I) cation, leading to the restriction of electron transfer during the coordination processes. In order to characterize the SAM on silver substrates more visually and accurately, we used time-of-flight secondary ion mass spectrometry (ToF-SIMS) to scan the SAM modified silver substrates. Taking the HOC11S modified silver surface as an example, S anions were uniformly distributed on a surface area of 200 × 200 μm from the mapping picture (Fig. 2a). For both the HOC11Se and HOC11Te modified surfaces, the Se anion and Te anion were well-distributed as well (Fig. 2b and c). From the perspective of quantification, the total counts of chalcogenide anions also increased significantly compared to the unmodified silver substrate. For the Se anion case, the value increased from 6.9 × 10³ to 5.3 × 10⁵. And the S anion and Te anion can also be observed to grow accordingly (Table S1†).

Fig. 2 TOF-SIMS results of silver substrates modified with HOC11X (X = S, Se, and Te) in the negative mode. (a) Left: TOF-SIMS mapping pictures of S⁻ ions on the silver substrate before (bottom) and after (top) being modified with HOC11S, in which the yellower the color, the higher the content of S⁻; Right: The peak at 32.0 represented one of the isotopes of sulfur. (b) The results of the silver substrate modified with HOC11Se and the peak at 80.0 represented one of the isotopes of selenium. (c) The results of the silver substrate modified with HOC11Te and the peak at 129.9 represented one of the isotopes of tellurium. All the above mapping pictures showed a little bit non-uniform distribution of chalcogenide anions, which was caused by the error of the instrument itself.

Having confirmed the existence of SAMs on silver substrates, the interfacial properties of HOC11X modified silver substrates were investigated by conducting water contact angle (WCA) experiments. For an unmodified silver surface, the WAC was 53 ± 3°. After modification with HOC11X, the WCA increased as a result of the hydrophobic alkane structure on the surface. The increments were in the order of HOC11S/Ag(I) (60 ± 2°), HOC11Se/Ag(I) (69 ± 2°) and HOC11Te/Ag(I) (73 ± 3°), which implied the growing compactness of HOC11X SAMs on the silver surface (Fig. 3a). Subsequently, atomic force microscopy (AFM) was employed to compare the surface morphologies before and after surface modification with HOC11X. It is worth noting that although the thickness of SAMs on the silver surface was less than 1 nm, there were tiny but noticeable differences between unmodified silver and modified silver surfaces, confirmed by two dimensional, three dimensional and phase images. The roughness also increased with the increasing compactness (Fig. S4†). Another powerful tool to distinguish whether the interactions between chalcogenides and silver(I) are coordination or not is Raman spectroscopy, which demonstrates that the interaction is coordination if the vibrational frequencies for C–X stretching modes do not shift towards the lower wavenumber after the SAMs form.³¹ The C–S vibrational signal appears at 767 cm⁻¹ for HOC11S powder, and nearly the same vibration (772 cm⁻¹) was observed after SAMs formed. Similar results were obtained for HOC11Se (before: 670 cm⁻¹, after: 678 cm⁻¹) and HOC11Te (before: 609 cm⁻¹, after: 617 cm⁻¹) (Fig. 3b and S5†). The above results revealed that the bonds formed between HOC11X and silver(I) were all coordination bonds.

Fig. 3 (a) Static water contact angle of silver only pre-treated and HOC11X modified silver substrates. (b) Raman spectra of SAMs composed of HOC11X formed on silver substrates in the range of 550–800 cm⁻¹.

The strength quantification of Ag(I)–X bonds by SMFS

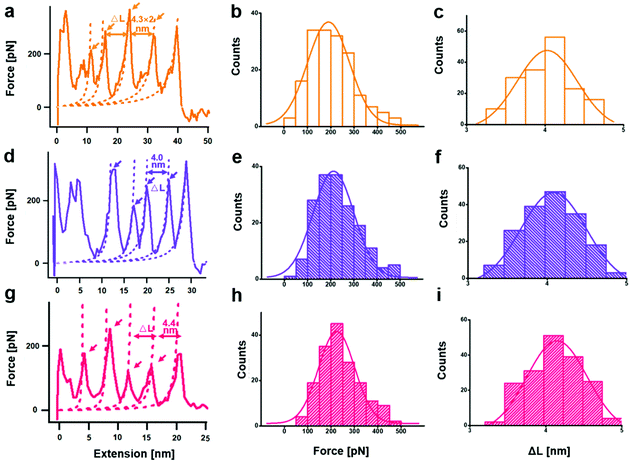
From a kinetic point of view, the established SMFS method was utilized to quantify the bond strength, which could contribute to the bottom-up rational design of coordination-based systems.^32,33 To measure the strength of Ag(I)–X bonds by AFM-based SMFS, the A–B–A-type chalcogenide-containing block copolymer (denoted by PEG-PUX-PEG) was designed and synthesized (the chemical structures are shown in Fig. S6†). The three kinds of polymers were composed of similar repeating units in the middle of the PU chain and PEG as a capping agent in both ends. In a typical SMFS experiment, the AFM tip could attach to the PEG segment of a single polymer via physical adsorption. Upon pulling, the interactions between the middle segment PUXPU and the substrate would be ruptured in sequence. The block copolymer PEG-PUX-PEG functioned as a probe to produce identifiable repeating force signals because of the equal spacing between two adjacent X atoms (approximately 4 nm). Specifically, the individual PEG-PUX-PEG polymer chain was captured from the silver surface at a constant pulling speed of 1000 nm s⁻¹ in the solvent of DMSO under the force spectroscopy mode of AFM. In more cases, the retracting F–E curves were analysed and fitted further though both approaching and retracting F–E curves could provide useful information. As shown in Fig. 4a, d and g, typical retracting F–E curves with a saw-tooth pattern were observed, which could be well fitted by the worm-like chain model with the persistence length (I_p = 0.35 nm) corresponding to the elasticity of PEG.³⁴ Besides, the length increment of the saw-tooth patterns obtained in all PEG-PUX-PEG experiments was systematically analysed. The most probable values of the length increments derived from the Gaussian fits were 4.01 ± 0.38 nm for PEG-PUS-PEG (Fig. 4c), 4.08 ± 0.41 nm for PEG-PUSe-PEG (Fig. 4f), and 4.15 ± 0.40 nm for PEG-PUTe-PEG (Fig. 4i), which were comparable to the theoretical distance between two adjacent X atoms (the calculated values were 3.94, 3.96, and 3.97 nm for S, Se, and Te, respectively).²⁹ All those results mentioned above indicated that the elastic behaviour of single PEG-PUX-PEG had been obtained (more F–E curves can be found in Fig. S7†).

Fig. 4 Single chain stretching of PEG-PUX-PEG from the silver substrate (X = S, Se, and Te from top to bottom). Typical force-extension curves for detaching individual (a) X = S, (d) X = Se, and (g) X = Te polymers from the silver surface. The dashed lines are worm-like chain fits (persistence length = 0.35 nm). Force distributions of the saw-tooth peaks for (b) Ag(I)–S, (e) Ag(I)–Se, and (h) Ag(I)–Te. The solid curves plotted over the histograms are the Gaussian fits for the distribution of force increments. Estimations of distance between adjacent saw-tooth peaks in the stretching curves of (c) Ag(I)–S, (f) Ag(I)–Se, and (i) Ag(I)–Te. The solid curves plotted over the histograms are the Gaussian fits for the distribution of length increments.

After confirming the single-molecule event, the selected rupture forces shown in Fig. 4a, d and g corresponded to the cleavage of Ag(I)–S, Ag(I)–Se, and Ag(I)–Te coordination bonds, respectively. The strength of Ag(I)–X bonds was rarely measured due to the limitation of molecule manipulation techniques and model constructions. The A–B–A-type block copolymer was an ideal model which offered multiple possible interaction sites (X–Ag(I)) and proper distance between adjacent sites (approximately 4 nm). Combined with the SMFS technology, the rupture force of hundreds of typical saw tooth-peak-containing force-extension curves was measured. But only saw-tooth peaks with a length increment of approximately 4 nm, which was the single-molecule unbinding force behaviour, were chosen for statistical analysis. (Note that the last peak of each curve was not counted to exclude the case of the detaching nonspecific interactions on both terminal ends of the linkage.) These selected data were plotted as histograms and then fitted by Gaussian functions to yield the most probable rupture forces. The PEG-PUS-PEG/Ag(I), PEG-PUSe-PEG/Ag(I), and PEG-PUTe-PEG/Ag(I) ruptures produced the most probable rupture forces of 190.6 ± 90.1, 212.2 ± 88.5, and 224.0 ± 77.2 pN, respectively (Fig. 4b, e and h). The strength order of Ag(I)–X bonds could be described by simply comparing those data, which revealed the bonding strength trend as Ag(I)–S < Ag(I)–Se < Ag(I)–Te. For deep understanding of these force unbinding processes, the rupture kinetics of these Ag(I)–X bonds has been investigated. Based on the Dudko–Hummer–Szabo method,³⁵ the rupture force histograms were transformed into force-dependent lifetimes (Fig. S8†). The detailed calculation method and results were shown in the part of following rupture kinetics. Briefly, Δx values of Ag(I)–S, Ag(I)–Se and Ag(I)–Te were not much different, while τ(F) was significantly different. The trend of τ(F) implied that the height of the activation barrier followed the order Ag(I)–S < Ag(I)–Se < Ag(I)–Te, which was the same sequence as the rupture forces we measured. Based on the above analysis, we could speculate that τ(F), which is the height of the activation barrier, was the main factor determining the difference in rupture forces.

Theoretical studies about the silver–chalcogenide interactions

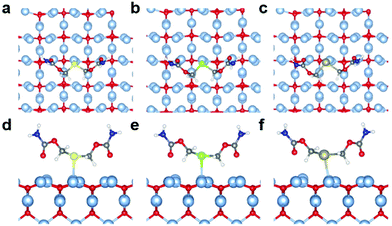
Quantum chemical calculations were performed using Density Functional Theory (DFT) to gain better insight into the Ag(I)–X bonding strength on selected X(ROCONH₂)₂/Ag₂O (X = S, Se, and Te; R = CH₂ and (CH₂)₃) models (the theoretical details could be found in the ESI†). The optimized configurations of X(CH₂OCONH₂)₂/Ag₂O (200) are shown in Fig. 5 and Table S2,† with apparent silver(I)–chalcogenide bonding interactions. The Ag(I)–X bonds are weaker than the single bonds as the bond distances are larger than the Pyykkö covalent single-bond lengths.³⁶ Compared with the reported experimental values of Ag(I)–X bond length (L_(X=S) = 2.54–2.63 Å;³⁷L_(X=Se) = 2.64–2.70 Å;³⁸L_(X=Te) = 2.79–2.84 Å (ref. 39)), the calculated result is 2.58 Å, 2.64 Å and 2.72 Å for Ag(I)–S, Ag(I)–Se and Ag(I)–Te, respectively, which is quite close to the reported value. Although the Ag(I)–X bond length increases with heavier chalcogenide elements due to the enlarging atomic radius of X, it becomes closer to the Pyykkö covalent single-bond length, indicating that the Ag(I)–Te bond is the strongest. Besides, it reveals that there is charge transfer from X(CH₂OCONH₂)₂ to the Ag₂O (200) surface as the Hirshfeld⁴⁰ net charges of [X(CH₂OCONH₂)₂] in X(CH₂OCONH₂)₂/Ag₂O (200) are positive. The projected density of states (PDOS) for the Ag atom that binds with X (Ag_a), the X atom and the X(CH₂OCONH₂)₂ molecule was also utilized to evaluate the Ag(I)–X interactions, as shown in Fig. S9.† We can see that there are strong orbital interactions between Ag_a and X(CH₂OCONH₂)₂ for the energy range from −6.0 to −2.0 eV relative to the Fermi level. As X becomes heavier, the Ag(I)–X bond strength will increase with enhanced orbital interactions in the lower energy range below the Fermi level.

Fig. 5 Top and side views of the optimized geometric structures for X(CH₂OCONH₂)₂/Ag₂O (200) (a, d) X = S; (b, e) X = Se and (c, f) X = Te. Colors: light blue, Ag; red, O; yellow, S; green, Se; dark yellow, Te; grey, C; blue, N; white, H.

Energy decomposition analyses (EDA) are further performed to explore the Ag(I)–X bonding interactions, as shown in Table 1. The bonding energy between X(CH₂OCONH₂)₂ and Ag₂O (200) is decomposed into the classical attractive electrostatic interaction energy ΔE_elstat, the Pauli repulsive energy ΔE_Pauli and the attractive orbital energy ΔE_orb. The bonding energies ΔE_bond are all negative, ranging from −12.91 kcal mol⁻¹ to −17.77 kcal mol⁻¹. As observed for the Ag(I)–X bond length, ΔE_bond also demonstrates that the bonding strength increases from Ag(I)–S to Ag(I)–Se to Ag(I)–Te, resulting from the increasing attractive electrostatic and orbital interactions. It can be found that the electrostatic interaction energy term ΔE_elstat plays the most dominant role in the total attraction with the contribution ranges from 66.6% to 68.7%, whereas the orbital energy ΔE_orb justifies that the covalent character of Ag(I)–X bonds is responsible for 31.3%–33.4% of the total attraction. Thus, based on the theoretical calculations, we can confirm the bonding strength trend of Ag(I)–S < Ag(I)–Se < Ag(I)–Te and conclude that the trend mainly derives from the attractive electrostatic interactions.

Table 1 Energy decomposition analysis (EDA) of the Ag₂O (200) + X(CH₂OCONH₂)₂ → X(CH₂OCONH₂)₂/Ag₂O (200) (X = S, Se, and Te) process at the BAND/PBE/TZP level. All energy terms are in the unit of kcal mol⁻¹

X	ΔEPauli	ΔEelstat^a	ΔEorb^a	ΔEtot
a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb.
S	97.98	−73.83(66.6%)	−37.06(33.4%)	−12.91
Se	102.85	−80.12(67.5%)	−38.50(32.5%)	−15.76
Te	127.41	−99.76(68.7%)	−45.42(31.3%)	−17.77

---

Conclusions

In summary, we explored the difference of bonding strength between silver(I) and chalcogenides in block copolymer systems at the single-molecule level from the perspective of kinetics and thermodynamics. Both results indicated that the strength of Ag(I)–X bonds increases in the sequence of Ag(I)–S < Ag(I)–Se < Ag(I)–Te. Furthermore, the mechanism and nature of Ag(I)–X interactions were unveiled from the aspect of relative strength of Ag(I)–X bonds. And the difference between Ag(I)–S and Ag(I)–Se is a little bit larger than the latter Ag(I)–Se and Ag(I)–Te, which implied that the Ag(I)–Se/Te interactions were more stable than Ag(I)–S. The results offered an important foundation for designing more efficient silver protection systems to replace the existing relatively weaker Ag(I)–S interaction and comprehending the relationship between natural mineral paragenesis and biological behaviour. We envision that our results will inspire new ideas about the application of systems involving silver(I)–chalcogenide interactions in catalysis, electronics and many other fields.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Basic Research Plan of China (2018YFA0208900), the National Natural Science Foundation of China (21734006), and the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (21821001). J. Li acknowledges support from the National Natural Science Foundation of China (No. 21433005, 21590792, 91645203, and 21521091). This work was partially sponsored by the Guangdong Provincial Key Laboratory of Catalysis (No. 2020B121201002). The computational work was partially supported by the Center for Computational Science and Engineering (SUSTech).

Notes and references

1. J. D. Dana, Danás new mineralogy: the system of mineralogy of James Dwight Dana and Edward Salisbury Dana–8th edentirely rewritten and greatly enlarged, 1997.
2. E. V. Shannon, Am. J. Sci., 1920, 50, 390.
3. A. J. Criddle, J. E. Chisholm and C. J. Stanley, Eur. J. Mineral., 1989, 1, 371.
4. M. Scaini, G. Bancroft, J. Lorimer and L. Maddox, Geochim. Cosmochim. Acta, 1995, 59, 2733.
5. R. C. Rouse, J. Solid State Chem., 1973, 6, 86.
6. A. Jasiński, Mineral. Mag., 1986, 50, 101.
7. A. N. Khlobystov, A. J. Blake, N. R. Champness, D. A. Lemenovskii, A. G. Majouga, N. V. Zyk and M. Schröder, Coord. Chem. Rev., 2001, 222, 155.
8. M. L. Tong, X. M. Chen, B. H. Ye and L. N. Ji, Angew. Chem., Int. Ed., 1999, 38, 2237.
9. K. S. Min and M. P. Suh, J. Am. Chem. Soc., 2000, 122, 6834.
10. C. J. Pedersen, J. Org. Chem., 1971, 36, 254.
11. A. Kudelski, A. Michota and J. Bukowska, J. Raman Spectrosc., 2005, 36, 709.
12. S. Wang, C. Yan, J. Shang, W. Wang, C. Yuan, H. L. Zhang and X. Shao, Angew. Chem., Int. Ed., 2019, 58, 3819.
13. W. Li, S. Gong, X. Liu, X. Lu and H. Xu, Chem. Res. Chin. Univ., 1996, 17, 501.
14. Y. Liu, S. P. Dong, Y. Inoue and T. Wada, J. Chem. Res., 1999, 284.
15. Y. Bai, Y. D. Wang, W. J. Zheng and Y. S. Chen, Colloids Surf., B, 2008, 63, 110.
16. F. R. Kersey, W. C. Yount and S. L. Craig, J. Am. Chem. Soc., 2006, 128, 3886.
17. R. W. Friddle, A. Noy and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13573.
18. K. Wang, X. Pang and S. Cui, Langmuir, 2013, 29, 4315.
19. C. He, C. Hu, X. Hu, X. Hu, A. Xiao, T. T. Perkins and H. Li, Angew. Chem., Int. Ed., 2015, 54, 9921.
20. K. Liu, Y. Song, W. Feng, N. Liu, W. Zhang and X. Zhang, J. Am. Chem. Soc., 2011, 133, 3226.
21. W. Huang, X. Wu, X. Gao, Y. Yu, H. Lei, Z. Zhu, Y. Shi, Y. Chen, M. Qin and W. Wang, Nat. Chem., 2019, 11, 310.
22. F. Li, T. Li, W. Cao, L. Wang and H. Xu, Biomaterials, 2017, 133, 208.
23. S. Ji, W. Cao, Y. Yu and H. Xu, Adv. Mater., 2015, 27, 7740.
24. C. Liu, Z. Fan, Y. Tan, F. Fan and H. Xu, Adv. Mater., 2020, 32, 1907569.
25. L. Wang, W. Wang, W. Cao and H. Xu, Polym. Chem., 2017, 8, 4520.
26. R. Fang, H. Xu, W. Cao, L. Yang and X. Zhang, Polym. Chem., 2015, 6, 2817.
27. S. Ji, W. Cao, Y. Yu and H. Xu, Angew. Chem., Int. Ed., 2014, 53, 6781.
28. W. Cao and H. Xu, Mater. Chem. Front., 2019, 3, 2010.
29. W. Xiang, Z. Li, C. Q. Xu, J. Li, W. Zhang and H. Xu, Chem. – Asian J., 2019, 14, 1481.
30. N. Ma, Y. Li, H. Ren, H. Xu, Z. Li and X. Zhang, Polym. Chem., 2010, 1, 1609.
31. Y. Xue, X. Li, H. Li and W. Zhang, Nat. Commun., 2014, 5, 1.
32. W. Cao, Y. Gu, M. Meineck, T. Li and H. Xu, J. Am. Chem. Soc., 2014, 136, 5132.
33. T. Li, F. Li, W. Xiang, Y. Yi, Y. Chen, L. Cheng, Z. Liu and H. Xu, ACS Appl. Mater. Interfaces, 2016, 8, 22106.
34. N. Liu, B. Peng, Y. Lin, Z. Su, Z. Niu, Q. Wang, W. Zhang, H. Li and J. Shen, J. Am. Chem. Soc., 2010, 132, 11036.
35. O. K. Dudko, G. Hummer and A. Szabo, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15755.
36. P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186.
37. A. J. Blake; and M. Schröder, Chem. Commun., 1997, 1943.
38. D. G. Booth;, W. Levason;, J. J. Quirk;, G. Reid; and S. M. Smith, J. Chem. Soc., Dalton Trans., 1997, 3493.
39. W. F. Liaw;, C. H. Lai;, S. J. Chiou;, Y. C. Horng;, C. C. Chou;, M. C. Liaw;, G. H. Lee; and S. M. Peng, Inorg. Chem., 1995, 34, 3755.
40. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0py01201g

---