Vibrational signature of the graphene nanoribbon edge structure from high-resolution electron energy-loss spectroscopy

Abstract

Bottom-up approaches exploiting on-surface synthesis reactions allow atomic-scale precision in the fabrication of graphene nanoribbons (GNRs); this is essential for their technological applications since their unique electronic and optical properties are largely controlled by the specific edge structure. By means of a combined experimental-theoretical investigation of some prototype GNRs, we show here that high-resolution electron energy-loss spectroscopy (HREELS) can be successfully employed to fingerprint the details of the GNR edge structure. In particular, we demonstrate how the features of HREEL vibrational spectra – mainly dictated by edge CH out-of-plane modes – are unambiguously related to the GNR edge structure. Moreover, we single out those modes which are localized at the GNR termini and show how their relative intensity can be related to the average GNR length.

---

Introduction

In the last decade, on-surface synthesis has established itself as a flexible and powerful strategy to realise novel nanomaterials, with tailored properties and functionalities.^1–3 The successful fabrication of atomically precise graphene nanoribbons (GNRs) was first demonstrated in 2010, by means of bottom-up surface-assisted techniques under ultra-high-vacuum (UHV) conditions.⁴ More recently, GNR production beyond the realm of UHV surface science has become also feasible thanks to fabrication techniques based on chemical vapour deposition (CVD),^5–9 thus opening the way to scaling-up and industrial production of high quality samples. Both UHV- and CVD-based approaches were exploited to create a rich toolbox of different GNR-based materials with a defined width, shape and composition which reflect on their optoelectronic properties; such systems are also suited to be combined to form hetero-junctions displaying specific electronic transport behavior.^10–12 In addition, the design and fabrication of novel GNRs, exhibiting localized edge states and non-trivial topological electronic phases, have been demonstrated, breaking new ground also in the fields of spintronics and quantum phase manipulation.^13–15

A ubiquitous feature common to all GNR-based materials is the high sensitivity of their properties and performance to the details of the atomic structure and topology. This calls for an appropriate set of diagnostic techniques to be established, which could ensure a precise assessment of GNR quality, in terms of their detailed molecular structure and morphology, on both UHV- and CVD-grown samples. Scanning microscopy was demonstrated to provide unbeatable atomically detailed images of the synthesized nanostructures, as well as spatially resolved maps of their electronic density-of-states. Spatial resolution represents nevertheless also a limitation, when assessment of the macroscopically averaged quality of the fabricated sample is needed. Moreover, atomic resolution of CVD-grown samples, with higher coverage and often some air-derived contaminants, is hardly obtainable. In this scenario, vibrational spectroscopy may provide valuable information. Raman spectroscopy has been extensively used to characterise graphene-based nanostructures and in particular GNRs. Notably, Raman-active width-^4,16–19 and length-dependent²⁰ low-energy vibrational modes allow one to identify the GNR dimensions, while the graphene-related G and D bands as well as the corresponding dispersions provide information on defect density.^16,17 The details of GNR edge topology could be instead assessed by IR spectroscopy and high-resolution electron energy-loss (HREEL) spectroscopy, which provide information on complementary features with respect to Raman ones.^6,7,21–23 In fact, HREEL vibrational spectra of GNRs are dominated by IR-active CH out-of-plane (opla) bending modes which are weakly coupled with the vibrations of the molecular skeleton,²⁴ and strongly related to the topology of CH bonds localized at the edges.²⁵ This relationship has been extensively addressed in the case of IR spectra of polycyclic aromatic hydrocarbons (PAHs) in the gas phase,²⁶ showing that the opla manifold lineshape can be univocally linked to the molecular shape and topology, allowing for a precise fingerprinting of different species.

In this paper, we investigate the potentialities of this approach in the notable case of GNRs, demonstrating that HREELS – aided by ad-hoc DFT-based calculations – can provide a precise characterization of GNR edge and termination, disclosing essential pieces of information, complementary to those obtained by local probes (STM/AFM) and Raman spectroscopy. We synthesized different types of nanoribbons – i.e. N = 7 armchair (7-aGNRs), N-doped and pristine chevron-type (N-chGNR and chGNR) – on Au single-crystals according to the well-established procedure described in ref. 4 and detailed in the Experimental section, and we compared their HREEL spectra to the outcomes of DFT simulations. We show that each GNR displays a peculiar lineshape, built up by the sum of distinct peaks, that can be attributed to specific edge-localized modes. In the case of 7-aGNRs, DFT calculations on the corresponding molecular dimer allow us to single out those specific HREELS modes which are localized at the GNR termini. The presence of these terminal modes and their relative intensity are related to the GNR average length. These findings can be extended to different kinds of GNRs and graphene-based heterostructures, bringing HREELS into the foregrounds as an accurate diagnostic tool for the assessment of the overall sample quality, in terms of molecular structure and morphology.

Results and discussion

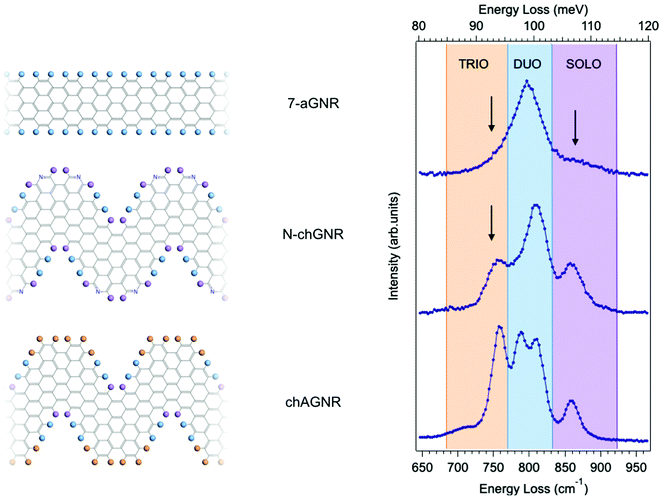
Classification of IR active modes in GNRs

Fig. 1 shows typical HREEL spectra of the investigated armchair and chevron-type GNRs grown on an Au(111) substrate. All spectra are dominated by a manifold – located in the [700–900] cm⁻¹ region – that is attributed to the C–H opla modes localized at the GNR edges. These spectral features can find a first rough explanation in the IR classification commonly used in the description of the PAH vibrational modes.²⁷ This classification identifies different frequency regions, as highlighted with shaded colors in Fig. 1 (right panel). Each of these regions corresponds to different CH opla modes and is named according to the number of CH neighbouring bonds involved in the vibration – i.e. the so-called TRIO, DUO and SOLO modes – as displayed by the colored circles in the molecular schemes of Fig. 1 (left panel), depicting ideal (i.e. infinite) species.

Fig. 1 Molecular schemes (left panel) and HREEL spectra (right panel) of the investigated GNRs. Specifically, from top to bottom: 7-aGNR, N-chGNR, and pristine chGNR. All spectra correspond to GNRs grown on the Au(111) surface, upon RT deposition. In the right panel, areas of different shaded colours identify the frequency range corresponding to different opla CH bending modes – i.e. TRIO (orange), DUO (light blue) and SOLO (purple). For each ideal GNR, the corresponding topological structures are indicated in the left panel with circles of the corresponding color.

The three GNRs studied here, i.e. 7-aGNRs, N-chGNR, and chGNR, represent perfect examples of edge structures of increasing complexity. In fact, according to the above general classification scheme, the single peak dominating the spectrum of armchair GNRs lies in the DUO region, the N-doped ch-GNR presents features in both DUO and SOLO regions, while the features of pristine ch-GNRs span all three regions. Despite this overall agreement, there are also features that fall outside the expected ranges, as highlighted by arrows in Fig. 1 (right panel). This is particularly evident for the peak observed at 752 cm⁻¹ (TRIO region) in the N-chGNR spectrum, but also apparent in the case of 7-aGNRs, where an asymmetric broadening of the main peak is observed in the TRIO region around 750 cm⁻¹, and a small shoulder appears around 860 cm⁻¹, in the SOLO region. Actually, the exact frequencies of CH opla normal modes depend on both the details of the edge configuration and the overall molecular structure, as demonstrated in the comprehensive work by Tommasini et al.²⁵ on PAHs. Hence, the above-highlighted discrepancies with respect to the edge structure classification can provide additional precious pieces of information regarding the structural details of actual GNRs; this calls for further theoretical and experimental investigation, which we will present in the following.

Lineshape analysis for armchair GNRs

In order to fully understand to which extent different GNR structures can impact the lineshape details of the opla manifold, we start by considering the simplest case of 7-aGNRs and compare the HREEL spectra of samples grown under different conditions. In fact, according to the literature,^2,4,28–31 different parameters can influence the sample quality and characteristics, the most relevant of which is the substrate deposition temperature (T_D). In particular, the longest GNRs can be obtained by deposition at around 200 °C,^4,28 where cyclodehydrogenation is sporadic and surface diffusion is enhanced, so that the polymer can grow with minor passivation by hydrogen released upon cyclodehydrogenation. In contrast, for RT deposition diffusion is limited and shorter GNRs are expected, as confirmed in our case by STM measurements (see Fig. S3†), which clearly show that GNRs obtained for T_D = RT are on the average shorter and more branched than those obtained for T_D = 200 °C. Finally, for deposition temperature above T_D = 200 °C^2,29 cyclodehydrogenation starts to take place, and hydrogen passivation strongly limits the polymer chain growth resulting in the formation of extremely short GNRs, as discussed in the following.

The HREEL spectra of GNRs grown at T_D = 200 °C (panel a), RT (panel b) and 310 °C (panel c) are shown in Fig. 2. For deposition at T_D = 200 °C (panel a), the lineshape is dominated by a single feature at 800 cm⁻¹, i.e., in the DUO region, in excellent agreement with ab initio calculations performed for the ideal, infinite 7-aGNR, here displayed as black bars (the corresponding atomic displacements are in Fig. S1†). For RT deposition (panel b), small but appreciable side components appear in the TRIO and SOLO regions, respectively. These peaks become more prominent for T_D = 310 °C, where they finally overcome the DUO mode.

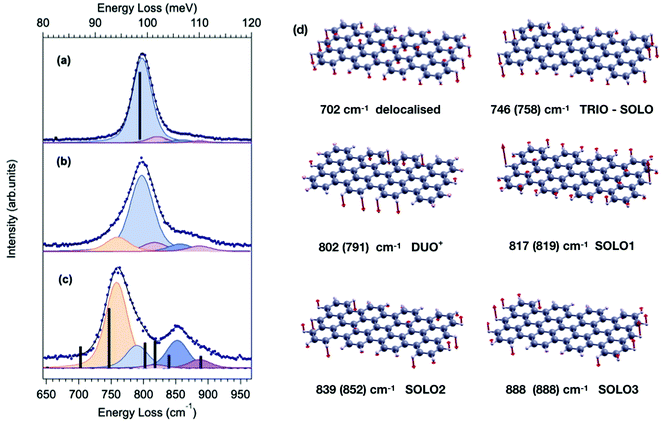Fig. 2 Comparison between HREEL spectrum of 7-aGNR grown in different conditions, i.e. different substrate deposition temperature T_D and coverage θ_ML: (a) T_D = 200 °C θ_ML = 0.26; (b) T_D = RT θ_ML = 0.33 (also depicted in the right panel of Fig. 1); (c) T_D = 310 °C θ_ML = 0.42. Blue dots represent experimental data, solid black lines are the respective fitting curves, whereas the fitting components are reported (with a small downward shift for the sake of clarity) as shaded curves. The intensity and frequency of the calculated Z-polarized IR-active modes of the 7-aGNR dimer and of the infinite 7-aGNR are reported as black bars in panel (a) and (c), respectively. The corresponding atomic displacements for the dimer are reported in panel (d), where the direction and magnitude of the displacement for each atom involved in the vibration are represented by red vectors. Experimental frequencies, as determined by the fitting procedure, are reported in parenthesis, for comparison.

In order to fully rationalize these novel features, we compute the ab initio IR spectrum for the shortest oligomer of the 7-aGNR, i.e. the dimer obtained from two DBBA monomers. The simulated Z-polarized IR modes are superimposed to the spectrum obtained at T_D = 310 °C in panel (c) of Fig. 2, and the corresponding atomic displacements are shown in panel (d) of Fig. 2. They show – in addition to the DUO mode at 802 cm⁻¹ typical of the corresponding infinite GNR – several new modes mainly localized at the GNR termini. In particular, the mode at 746 cm⁻¹ is attributed to the in-phase wagging of the three adjacent CH groups at the terminus corners (mainly TRIO character, with an out-of phase contribution of the terminus SOLO, hereafter named TRIO-SOLO), whereas the modes in the SOLO region (817, 839 and 888 cm⁻¹) are due to different out-of-phase and in-phase wagging of the CH bonds at the dimer zig-zag termini (hereafter: SOLO1, SOLO2, SOLO3). Finally, there is a mode at 702 cm⁻¹ that is essentially delocalized, as it involves all peripheral CH bonds and has also a backbone contribution.

The agreement between the simulated frequencies of the dimer modes and the experimental spectrum in Fig. 2(c) is indeed fairly good,‡ confirming that deposition at 310 °C results in the formation of extremely short GNR oligomers, and that under these conditions the CH opla manifold is dominated by modes localized at the termini. In contrast, these dimer-like terminal-mode components are nearly negligible for T_D = 200 °C (panel a), where long GNRs dominate. For RT deposition – for which the average GNR length is shorter than for T_D = 200 °C – an intermediate lineshape is observed, characterized by a sizeable contribution of terminal-modes. These observations thus strongly suggest that the intensity ratio between terminal-modes and lateral-edge-modes reflects the fraction of termini vs. edge CH atoms, which could be in turn related to the GNR average length, at least qualitatively. A more quantitative correlation would require instead a full STM-HREEL comparison, which is beyond the scope of this work.

Lineshape analysis for chevron-type GNRs

The lineshape analysis performed for 7-aGNRs can be extended to GNRs with different topologies, still considering the specific opla modes localized at both the GNR edges and termini. Fig. 3 shows the spectra for pristine and N-doped chevron-type GNRs, obtained by precursor deposition at T_D = 200 °C and T_D = RT. The IR active Z-polarized modes calculated for ideal, infinite chGNRs, both doped and pristine, are superimposed as black bars to the spectra measured for T_D = 200 °C samples, where longer GNRs are expected to be produced. Indeed, the agreement between simulated and experimental spectra is fairly good for both species,§ as also evidenced in Table 1, where experimental and theoretical frequencies of the opla manifold are reported, together with the character of the modes as resulting from inspection of the calculated atomic displacements (see Fig. S1†). At T_D = 200 °C, the spectrum of the N-chGNR (panel (a) of Fig. 3) is mainly dominated by a mode at 811 cm⁻¹ (light blue component), where all the CH groups at the edges are vibrating in-phase (DUO + SOLO), and a SOLO feature at 860 cm⁻¹ (light purple), localized at the bay region of the edge. Weaker features at 690 cm⁻¹ (grey, delocalized) and 894 cm⁻¹ (purple, SOLO outer edge) are also understood by comparison with theory. Conversely, the weak feature at 754 cm⁻¹ (TRIO region, light orange) lacks a theoretical counterpart. Its origin can be unravelled by comparison with the spectrum of the T_D = RT sample, where this feature is much stronger: even without a detailed calculation for chGNR oligomers, we can reasonably attribute it to the vibration of TERMINAL TRIO structures that characterize both pristine and N-doped finite chGNRs (see the molecular schemes reported in Fig. 3). Along the same line, the weak feature at 783 cm⁻¹ (dark orange), the intensity of which is found to increase for T_D = RT samples, is thus expected to have a TRIO contribution. By comparison with theory, it is tentatively assigned to a DUO − SOLO + TRIO mode, the in-phase TRIO contribution being the reason for the non-negligible intensity observed also for the T_D = 200 °C samples as compared to the nearly-zero intensity in the simulated spectrum.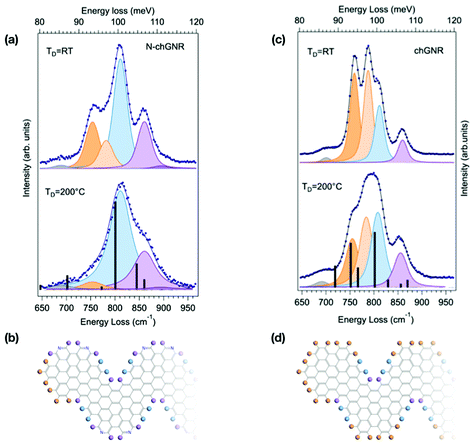

Fig. 3 Comparison between the HREEL spectra of N-doped (a) and pristine (c) chevron-type GNRs, obtained by deposition at T_D = 200 °C and at RT. The corresponding fitting components are shown as shaded curves, while calculated modes are displayed as black bars. The corresponding molecular schemes, showing the structure of the termini, are reported in (b) and (d), respectively. The top spectrum in (a) is also reported in the right panel of Fig. 1.

Table 1 Theoretical and experimental frequencies of the IR-active Z-polarized modes for different GNR species, together with their character, as individuated by inspection of the calculated atomic displacements (see Fig. S1†). Tentative assignments based on the shape of the terminals are in italics. Theoretical IR intensities are indicated in parentheses. The experimental frequencies are determined by the fitting procedure described in the Method section, with an uncertainty of ±4 cm⁻¹, and correspond to the positions of the fitting components displayed in Fig. 2 and 3

	Experiment (cm^−1)	Theory (intensity) (cm^−1)	Character
N-chGNR	690	722 (0.41)	Delocalized
	754	—	Terminal TRIO
	783	766 (0.01)	DUO − SOLO (+TRIO)
	811	824 (2.46)	DUO + SOLO
	860	870 (0.73)	SOLO (BAY)
	894	886 (0.29)	SOLO (EDGE)
chGNR	700	718 (0.94)	Delocalized
	756	751 (1.91)	TRIO
	782	766 (0.86)	TRIO + DUO − SOLO
	812	801 (2.38)	TRIO + DUO + SOLO
		829 (0.35)	DUO + SOLO
	856	869 (0.33)	SOLO (BAY)

---

We then consider the spectrum of pristine chGNRs, which shows a more complex lineshape (Fig. 3(a)), given the fact that this GNR species contains all three edge structure types, i.e. TRIO (edge and termini), DUO and SOLO. As for the N-doped case, a bay SOLO (856 cm⁻¹, purple) mode can be found in the higher-energy part of the opla manifold. The peak experimentally observed at 812 cm⁻¹ (light blue) takes contribution from two distinct modes, i.e. the DUO + SOLO predicted at 829 cm⁻¹, and the in-phase combination of TRIO, DUO and SOLO modes (TRIO + DUO + SOLO) at 801 cm⁻¹. The corresponding out-of-phase combination (TRIO + DUO − SOLO) is located at 782 cm⁻¹ (light orange). Interestingly, the corresponding mode for N-chGNR (experimentally observed at 783 cm⁻¹) has DUO − SOLO character and suppressed intensity, since the TRIO structure is disrupted by the presence of nitrogen. Finally, in the lower energy-part of the manifold, the pure TRIO mode, specific to this edge topology, is single-out at 756 cm⁻¹ (dark orange). By inspecting the T_D = RT spectrum, we can clearly observe an increase of the relative intensity of the two modes having a dominant TRIO character (i.e., 756 cm⁻¹ and 782 cm⁻¹ modes), in view of the further contribution of terminal TRIO structures. In agreement with the analysis for N-doped chGNRs and with the attribution based on DFT simulations, these findings indicate that modes localized at the termini can be clearly singled out by comparing HREEL spectra for samples produced under different growth conditions.

Conclusions

In conclusion, we have here presented the results of a combined experimental and theoretical investigation of the vibrational signatures of atomically precise graphene nanoribbons produced by on-surface synthesis. We have demonstrated the potentiality of HREELS in disclosing the details of the GNR edge structure, through the analysis of three prototypical GNRs, i.e. straight armchair, as well as pristine and N-doped chevron-type GNRs. The most prominent feature of GNR HREEL vibrational spectra is related to the CH opla manifold, which exhibits distinct lineshapes, characteristic of each GNR. The number of modes, their frequency and relative intensity are peculiar to each species and have been related – by means of DFT-based calculations – to the exact shape and topology of GNR edges and termini. Moreover, by distinguishing edge-localized vs. termini-localized modes, we show that their relative intensities can be qualitatively related to the average GNR length, thus providing us with a straightforward method to compare (and possibly optimise) the different growing conditions for each species and substrate. This approach has been successfully applied to different GNR species. HREELS should therefore be considered as an extremely valuable tool – complementary to Raman spectroscopy and scanning microscopy – for assessing the quality of GNRs and for gaining precious information on their actual morphology. Moreover, we envisage that this kind of characterization can be fruitfully extended to a whole range of graphene-based hydrogen-terminated nanostructures.

Materials and methods

Experimental

GNRs were synthesized by on-surface synthesis, following the procedure reported in ref. 4 on monocrystalline Au surfaces under ultra-high-vacuum (base pressure 5 × 10⁻¹⁰ mbar). Precursors were evaporated from a resistively heated glass crucible (T_evap = 186 °C) on the Au surfaces and kept at RT, 200 °C and 310 °C, respectively. Subsequent steps of polymerization at 200 °C (in the case of RT deposition) and cyclodehydrogenation at 400 °C were performed. 7-aGNRs were obtained from the 10,10′-dibromo-9,9′-bianthryl (DBBA) precursors, while chGNR and N-doped chGNR were derived from 6,11-dibromo-1,2,3,4-tetraphenyltriphenylene and 5,5′-(6,11-dibromo-1,4-diphenyltriphenylene-2,3-diyl)dipyridinemonomers, respectively. In particular, the spectra reported in Fig. 1, 2 and in upper panels of Fig. 3(a) and (c) correspond to samples grown on the Au(111) surface, while spectra reported in the lower panels of Fig. 3(a) and (c) were taken on the vicinal Au(788) surface.

All stages of growth were investigated by combining X-ray photoelectron Spectroscopy (XPS) with high resolution electron energy loss spectroscopy (HREELS). The sample coverage was estimated by quantitative analysis of the C 1s, N 1s and Au 4f core-level intensities and is reported in terms of fraction of monolayers (θ_ML), where one ML is defined as 4.5 × 10¹⁵ at cm⁻² for 7-aGNR and 2.7 × 10¹⁵ at cm⁻² for chGNRs, respectively. XPS measurements were performed using a non-monochromatic X-ray source (Mg K_α 1253.6 eV) and acquired with an Omicron EA-125 hemispherical analyser. HREELS measurements were performed with a LK 5000 spectrometer (3.5–5 meV resolution) in specular condition, with primary beam energy E_p = 7 eV. In this geometry, inelastic dipole scattering is the dominant electron energy loss mechanism and HREELS detects only those modes for which dynamic dipole moment is perpendicular to the surface. As shown in Fig. S2,† the subsequent steps of GNR formation, i.e. polymerization and cyclodehydrogenation, have been monitored by following the HREEL spectra evolution. In particular, the vanishing of the in-plane CH bending and stretching modes and the concomitant huge intensity increase of the adsorbate opla CH bonding modes represent a clear fingerprint of cyclodehydrogenation and GNR formation.^21,23

In Fig. 2 and 3, the spectral lineshapes have been interpolated by the sum of Voigt components, displayed as shaded curves. In particular, for all 7-aGNR spectra, curves were fitted considering five components, keeping their frequency (within ±4 cm⁻¹) and width, while varying their intensity. Analogous fitting procedures were performed also in the case of N-chGNR and pristine chGNR spectra. For samples grown on the Au(788) vicinal surface, the fit results in slightly broader components, reflecting a lower experimental resolution. In the case of 7-aGNRs, scanning tunneling microscopy (STM) measurements were also performed on selected samples in order to gain information on their morphology and length distribution. STM images were taken with an Omicron VT-SPM microscope working in constant-current mode at RT, with V = −0.25 V and I = 0.18 nA.

Computational details

Density-functional theory (DFT) simulations were performed within the local density approximation (LDA) for the exchange–correlation potential to investigate the ground-state structural properties of infinite (i.e. periodically repeated) GNRs and dimers from first principles. Norm-conserving pseudopotentials were employed, with a plane-wave cutoff energy of 70 Ry defining the basis set. A vacuum region of 15 Å in the nonperiodic directions was introduced to prevent interaction between periodic images. The atomic positions were fully optimized until forces within the cell were less than 5 × 10⁻⁴ au, using a 32 × 1 × 1 (4 × 1 × 1) k-point grid for the sampling of the Brillouin zone of armchair (chevron-type) GNRs. Phonon frequencies and IR intensities were calculated for the optimized structures by using an ab initio implementation of density functional perturbation theory (DFPT).³² This overall approach is known to provide results in very good agreement with experimental vibrational spectroscopy for C-based materials, see e.g.ref. 17, 16 and 33. All calculations here presented were carried out by employing the software available in the Quantum ESPRESSO package.^34,35

Author contributions

A. N., N. C., A. L. R. and V. D. R. planned the HREELS experiments. X.-Y. W. synthesized the monomers under the supervision of A. N. and X. F. and K. M. A. L. R., R. B., N. C., A. Rosi and V. D. R. designed, carried out and analyzed the HREELS experiments; R. B., V. C., N. C., A. Rosi and V. D. R. designed, carried out and analyzed the STM experiments; A. Ruini, D. P., and E. M. conceived the theoretical study. M. D. C. carried out the simulations. N. C., D. P., A. R., A. N. and V. D. R. wrote the manuscript. All the authors discussed the results and commented on the manuscript at all stages.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

This research was partly funded by SUPER “Supercomputing Unified Platform – Emilia-Romagna” (CUP E81F18000330007), a POR-FESR 2014–2020 Emilia Romagna Azione 1.5.1 project, and by the MaX (‘MAterials design at the eXascale’, www.max-centre.eu) European Centre of Excellence (European Union H2020-INFRAEDI-2018-1 programme, grant number 824143). Computational resources were provided by the user program of the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704.

References

1. L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters and S. Hecht, Nano-architectures by covalent assembly of molecular building blocks, Nat. Nanotechnol., 2007, 2, 687–691.
2. M. Bieri, M.-T. Nguyen, O. Gröning, J. Cai, M. Treier, K. Aït-Mansour, P. Ruffieux, C. A. Pignedoli, D. Passerone, M. Kastler, K. Müllen and R. Fasel, Two-dimensional polymer formation on surfaces: insight into the roles of precursor mobility and reactivity, J. Am. Chem. Soc., 2010, 132, 16669–16676.
3. J. Björk, Reaction mechanisms for on-surface synthesis of covalent nanostructures, J. Phys.: Condens. Matter, 2016, 28, 083002.
4. J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Atomically precise bottom-up fabrication of graphene nanoribbons, Nature, 2010, 466, 470–473.
5. H. Sakaguchi, Y. Kawagoe, Y. Hirano, T. Iruka, M. Yano and T. Nakae, Width-controlled sub-nanometer graphene nanoribbon films synthesized by radical-polymerized chemical vapor deposition, Adv. Mater., 2014, 4134–4138.
6. Z. Chen, et al., Synthesis of Graphene Nanoribbons by Ambient-Pressure Chemical Vapor Deposition and Device Integration, J. Am. Chem. Soc., 2016, 138, 15488–15496.
7. Z. Chen, H. I. Wang, N. Bilbao, J. Teyssandier, T. Prechtl, N. Cavani, A. Tries, R. Biagi, V. De Renzi, X. Feng, M. Kläui, S. De Feyter, M. Bonn, A. Narita and K. Müllen, Lateral Fusion of Chemical Vapor Deposited N = 5 Armchair Graphene Nanoribbons, J. Am. Chem. Soc., 2017, 139, 9483–9486.
8. Z. Chen, et al., Chemical Vapor Deposition Synthesis and Terahertz Photoconductivity of Low-Band-Gap N = 9 Armchair Graphene Nanoribbons, J. Am. Chem. Soc., 2017, 139, 3635–3638.
9. H. Sakaguchi, S. Song, T. Kojima and T. Nakae, Homochiral polymerization-driven selective growth of graphene nanoribbons, Nat. Chem., 2017, 9, 57–63.
10. J. Cai, C. A. Pignedoli, L. Talirz, P. Ruffieux, H. Söde, L. Liang, V. Meunier, R. Berger, R. Li, X. Feng, K. Müllen and R. Fasel, Graphene nanoribbon heterojunctions, Nat. Nanotechnol., 2014, 9, 896–900.
11. Y. C. Chen, T. Cao, C. Chen, Z. Pedramrazi, D. Haberer, D. G. De Oteyza, F. R. Fischer, S. G. Louie and M. F. Crommie, Molecular bandgap engineering of bottom-up synthesized graphene nanoribbon heterojunctions, Nat. Nanotechnol., 2015, 10, 156–160.
12. S. Blankenburg, J. Cai, P. Ruffieux, R. Jaafar, D. Passerone, X. Feng, K. Müllen, R. Fasel and C. A. Pignedoli, Intraribbon heterojunction formation in ultranarrow graphene nanoribbons, ACS Nano, 2012, 6, 2020–2025.
13. P. Ruffieux, S. Wang, B. Yang, C. Sánchez-Sánchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Müllen and R. Fasel, On-surface synthesis of graphene nanoribbons with zigzag edge topology, Nature, 2016, 531, 489–492.
14. O. Gröning, S. Wang, X. Yao, C. A. Pignedoli, G. Borin Barin, C. Daniels, A. Cupo, V. Meunier, X. Feng, A. Narita, K. Müllen, P. Ruffieux and R. Fasel, Engineering of robust topological quantum phases in graphene nanoribbons, Nature, 2018, 560, 209–213.
15. D. J. Rizzo, G. Veber, T. Cao, C. Bronner, T. Chen, F. Zhao, H. Rodriguez, S. G. Louie, M. F. Crommie and F. R. Fischer, Topological band engineering of graphene nanoribbons, Nature, 2018, 560, 204–209.
16. D. Rizzo, D. Prezzi, A. Ruini, V. Nagyte, A. Keerthi, A. Narita, U. Beser, F. Xu, Y. Mai, X. Feng, K. Müllen, E. Molinari and C. Casiraghi, Multiwavelength Raman spectroscopy of ultranarrow nanoribbons made by solution-mediated bottom-up approach, Phys. Rev. B, 2019, 100, 045406.
17. I. A. Verzhbitskiy, M. D. Corato, A. Ruini, E. Molinari, A. Narita, Y. Hu, M. G. Schwab, M. Bruna, D. Yoon, S. Milana, X. Feng, K. Müllen, A. C. Ferrari, C. Casiraghi and D. Prezzi, Raman fingerprints of atomically precise graphene nanoribbons, Nano Lett., 2016, 16, 3442–3447.
18. G. Borin Barin, et al., Surface-Synthesized Graphene Nanoribbons for Room Temperature Switching Devices: Substrate Transfer and ex Situ Characterization, ACS Appl. Nano Mater., 2019, 2, 2184–2192.
19. B. V. Senkovskiy, et al., Boron-Doped Graphene Nanoribbons: Electronic Structure and Raman Fingerprint, ACS Nano, 2018, 12, 7571–7582 , PMID: 30004663.
20. J. Overbeck, et al., A Universal Length-Dependent Vibrational Mode in Graphene Nanoribbons, ACS Nano, 2019, 13, 13083.
21. C. Bronner, S. Stremlau, M. Gille, F. Braüsse, A. Haase, S. Hecht and P. Tegeder, Aligning the band gap of graphene nanoribbons by monomer doping, Angew. Chem., Int. Ed. Engl., 2013, 52, 4422–4425.
22. N. Kalashnyk, K. Mouhat, J. Oh, J. Jung, Y. Xie, E. Salomon, T. Angot, F. Dumur, D. Gigmes and S. Clair, On-surface synthesis of aligned functional nanoribbons monitored by scanning tunnelling microscopy and vibrational spectroscopy, Nat. Commun., 2017, 8, 14735.
23. R. Denk, et al., Probing optical excitations in chevron-like armchair graphene nanoribbons, Nanoscale, 2017, 9, 18326–18333.
24. A. Centrone, L. Brambilla, T. Renouard, L. Gherghel, C. Mathis, K. Müllen and G. Zerbi, Structure of new carbonaceous materials: the role of vibrational spectroscopy, Carbon, 2005, 43, 1593–1609.
25. M. Tommasini, A. Lucotti, M. Alfè, A. Ciajolo and G. Zerbi, Fingerprints of polycyclic aromatic hydrocarbons (PAHs) in infrared absorption spectroscopy, Spectrochim. Acta, Part A, 2016, 152, 134–148.
26. S. R. Langhoff, Theoretical Infrared Spectra for Polycyclic Aromatic Hydrocarbon Neutrals, Cations, and Anions, J. Phys. Chem., 1996, 100, 2819–2841.
27. D. Lin-Vien, N. B. Colthup, W. G. Fateley and J. G. Grasselli, The handbook of infrared and Raman characteristic frequencies of organic molecules, Elsevier, 1991.
28. L. Talirz, P. Ruffieux and R. Fasel, On-Surface Synthesis of Atomically Precise Graphene Nanoribbons, Adv. Mater., 2016, 28, 6222–6231.
29. H. Söde, Electronic Properties of Atomically Precise Graphene Nanoribbons, Ph.D. thesis, 2015.
30. L. Massimi, O. Ourdjini, L. Lafferentz, M. Koch, L. Grill, E. Cavaliere, L. Gavioli, C. Cardoso, D. Prezzi, E. Molinari, A. Ferretti, C. Mariani and M. G. Betti, Surface-Assisted Reactions toward Formation of Graphene Nanoribbons on Au(110) Surface, J. Phys. Chem. C, 2015, 119, 2427–2437.
31. A. Batra, D. Cvetko, G. Kladnik, O. Adak, C. Cardoso, A. Ferretti, D. Prezzi, E. Molinari, A. Morgante and L. Venkataraman, Probing the mechanism for graphene nanoribbon formation on gold surfaces through X-ray spectroscopy, Chem. Sci., 2014, 5, 4419–4423.
32. S. Baroni, S. de Gironcoli and A. D. Corso, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515–562.
33. N. Mounet and N. Marzari, First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205214.
34. P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
35. P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901.

---

Footnotes

† Electronic supplementary information (ESI) available: A selection of DFT-calculated atomic displacements for infinite 7-AGNR, chGNR and N-chAGNR vibrational modes; HREEL extended vibrational spectra corresponding to monomer, polymer and GNR phases; STM images and corresponding statistical analysis relative to the 7-aGNR samples of Fig. 2panel (a) and (b). See DOI: 10.1039/d0nr05763k

‡ Minor discrepancies between theory and experiment can be easily justified considering that the experimental sample presents not only dimers, but rather a distribution of short oligomers with different lengths.

§ Small discrepancies between experimental and theoretical frequency values can be rationalized by recalling that theoretical frequencies are calculated for free-standing molecules, i.e. disregarding the possible effect of molecule–substrate interactions. In particular, these may be more relevant in the case of N-chGNR, thus possibly justifying the stronger differences between theory and experiments observed in this case.

---