Anomalous polarization switching and permanent retention in a ferroelectric ionic conductor†
Shuang
Zhou‡
a,
Lu
You‡
 *bc,
Apoorva
Chaturvedi
c,
Samuel A.
Morris
*bc,
Apoorva
Chaturvedi
c,
Samuel A.
Morris
 c,
Jason S.
Herrin
c,
Jason S.
Herrin
 c,
Na
Zhang
d,
Amr
Abdelsamie
c,
Yuzhong
Hu
c,
Jieqiong
Chen
c,
Yang
Zhou
e,
Shuai
Dong
f and
Junling
Wang
c,
Na
Zhang
d,
Amr
Abdelsamie
c,
Yuzhong
Hu
c,
Jieqiong
Chen
c,
Yang
Zhou
e,
Shuai
Dong
f and
Junling
Wang
 *c
*c
aSchool of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
bSchool of Physical Science and Technology, Soochow University, Suzhou 215006, China. E-mail: lyou@suda.edu.cn
cSchool of Materials Science and Engineering, Nanyang Technological University, Singapore 639798, Singapore. E-mail: jlwang@ntu.edu.sg
dHenan Key Laboratory of Photovoltaic Materials, School of Physics, Henan Normal University, Xinxiang, 453007, China
eSiyuan Laboratory, Guangzhou Key Laboratory of Vacuum Coating Technologies and New Energy Materials, Department of Physics, Jinan University, Guangzhou 510632, China
fSchool of Physics, Southeast University, Nanjing 211189, China
First published on 11th September 2019
Abstract
Ferroelectricity features the electrical switching of off-centered ions between the potential double well of the non-centrosymmetric lattice, while ionic conduction requires long-range hopping of ions across the lattice periodic potentials. The two seemingly mutually exclusive phenomena become strongly intertwined at the nanoscale in electrochemically active materials. However, the intrinsic coupling between ferroelectric switching and ionic activities in bulk crystalline materials remains largely unexplored. Here, we report anomalous polarization switching characteristics of a van der Waals (vdW) layered ferroelectric ionic conductor, CuInP2S6. By synergistic polarization switching and dielectric spectroscopy studies in both temperature and frequency domains, we reveal that the polarization switching kinetics of this compound is ionic-conduction-limited, due to the strong electrostatic interaction between ferroelectric and ionic defect dipoles. The crucial role of thermally-activated displacive instability of Cu ions is confirmed by the single-crystal X-ray crystallography results. The findings provide fundamental insight into the ionic kinetics under an electric field in crystals with coexisting dipole order (ferroelectricity) and disorder (ionic defect and conductivity). Last but not least, we demonstrate that the spontaneous ionic defect-polarization interlock can lead to permanent ferroelectric retention, which is essential for information storage.
New conceptsFerroelectric switching and solid state ionic conduction, are both characterized by the ionic displacement under an electric field, however, at different length and time scales. To what extent these two physical phenomena are connected to each other has been hitherto unknown. Here, by studying a prototypical ferroelectric ionic conductor, we spectroscopically resolved the polarization switching and ionic defect motion in temperature and time domains. The anomalous polarization switching kinetics in this material can be fully accounted for from the perspective of the intimate electrostatic coupling between ionic conduction and polarization switching, which sheds light on other related systems, such as “ferroionic” ultrathin films, ionic-mediated memristors for neuromorphic computing and organic–inorganic hybrid systems with both polar instability and ionic conductivity. Technologically more importantly, we propose that such ionic defect mediated polarization switching can serve as a symmetry-protected interlock for permanent information retention with no polarization loss up to 1 year. |
Introduction
Ferroelectrics possess long range ordering of electric dipoles, which can be reversibly switched by external fields. The origin of the finite electric polarization is the inversion symmetry breaking of the crystal lattice when cooling through Curie temperature. In most cases, this process involves off-center displacement/ordering of charged ions, which are statically confined by a double-well potential. With the development of modern ferroelectrics at the nanoscale, it is becoming increasingly well-known that charged ions or point defects may become mobile under high electric field in nanoelectronic devices. Due to the nature of strong electrostatic interaction, such electrochemical activity could closely couple or convolute with the existing polar order in ferroelectrics, leading to emergent phenomena such as ionic screening of polarization,1–8 chemical switching of polarization,9,10 ionically-mediated ferroelectric resistive switching,11–13 and ferroelectric-like behaviors in otherwise non-ferroelectric materials.14–18 Recently, the concept of a “ferroionic” state was brought about, highlighting the inextricable entanglement of ferroelectricity and ionic activities in nanoscale systems.19 Understanding the coupling between polarization and electrochemical switching processes is thus essential for the better manipulation and tuning of ferroic functionalities in the broad context of ionotronics.20 For example, the technologically promising ultrathin hafnium oxides have exhibited a “wake-up” effect and electrochemical activity in recent research.21–23 The memristors for neuromorphic computing involve non-volatile resistive states due to complex ionic switching kinetics.24–26 The hybrid perovskite family hosts a complex interplay between dipole order/disorder and ionic conduction, which deserves more exploration.27–29However, most of the previous studies focus mainly on the surface electrochemical states in ferroelectric thin films, which are usually investigated by scanning probe based techniques. Little is known about how the collective ionic activities interact with ferroelectric polarization in the bulk, particularly during the polarization switching process. This is because the most studied oxide ferroelectrics usually show very low ionic conductivity at room temperature.30 Though enhanced ionic conduction can be achieved at high temperature, it is difficult to study the polarization switching process due to the deteriorated ferroelectricity and high leakage.31 Ferroelectricity and superionic conduction can coexist in some alkaline or Ag ion conducting compounds.32–36 However, none of their ferroelectric switching properties have been reported. Another well-known ferroelectric ionic conductor is the KTiOPO4 (KTP) family, whose ferroelectric properties have been intensively studied and widely applied in nonlinear optics. Finite ionic conduction in these compounds is usually regarded as a detrimental factor to the polarization switching.37–41 The interplay between ionic kinetics and ferroelectric switching remained unexplored until very recently.42,43
In this study, we report anomalous polarization switching behaviors of a vdW layered ferroelectric, CuInP2S6 (CIPS). Through comprehensive polarization switching and dielectric spectroscopy studies in both temperature and frequency domains, we reveal that its unusual ferroelectric switching characteristics are closely linked with the onset of ionic conduction, which is driven by the displacive instability and thermally activated hopping of Cu ions in the lattice. Unlike conventional ferroelectrics, the spontaneous polarization of CIPS is strongly coupled to the Cu-based defect dipoles, whose switching speed limits the global polarization switching rate at room temperature and electrostatically pins the polarization at low temperature. The intimate coupling between the ferroelectric and defect polarizations results in a self-locking mechanism, which protects the written information from retention failure in this ferroelectric ionic conductor.
Results and discussion
Anomalous polarization switching kinetics of CuInP2S6
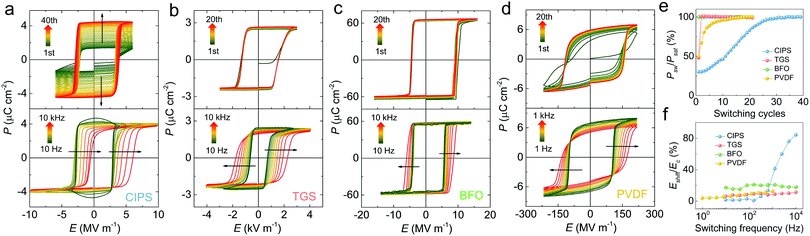
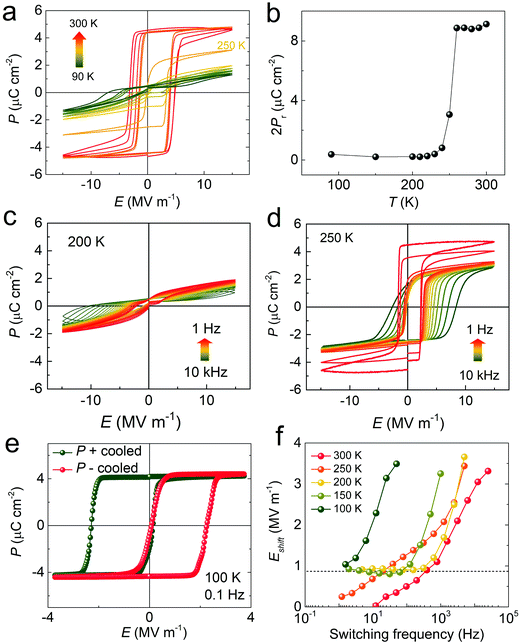
As a vdW layered ferroelectric, CIPS has received great attention recently in the exploration of ferroic 2D materials with exotic functionalities.44–48 Thanks to the weak interlayer vdW interaction, thin quasi-2D flakes can be mechanically isolated with their ferroelectric properties studied.49–52 However, a comprehensive understanding of the bulk polarization switching remains elusive despite some pioneering work.53 One reason could be that the leakage induced by finite ionic conduction of the material poses a significant challenge for the measurement of the macroscopic polarization–electric (P–E) field hysteresis loop.54–56 Furthermore, the spinodal phase separation of the Cu-deficient phase may also complicate the global polarization switching.57,58 Single crystals studied in this work were synthesized by chemical vapor transport (CVT) growth (Methods). Electron probe X-ray microanalyzer (EPMA) and single-crystal X-ray diffraction (SCXRD) were employed to confirm the stoichiometry and high crystallinity of the samples (Tables S1 and S2, ESI†), which ensures the intrinsic ferroelectric properties to be characterized. Typical ferroelectric hysteresis loops obtained from an as-grown CIPS crystal at room temperature are shown in Fig. 1, in comparison with some conventional ferroelectric materials. The upper panels of Fig. 1a–d show the cyclic P–E loops starting from their as-grown polarization states for different materials under constant electric field (about two times of the equilibrium EC) and frequency. For single-crystalline samples, the hysteresis loops usually reach saturation within 1–2 switching cycles, as observed for triglycine sulfate (TGS, single crystal) and BiFeO3 (BFO, epitaxial film) samples. In contrast, it takes tens of cycles for the P–E loop of CIPS single crystal to saturate, which is even much slower than the highly-disordered semicrystalline polyvinylidene fluoride (PVDF, film) sample (Fig. 1e). This behavior is a reminiscence of the de-aging effect in polycrystalline hard-doped ferroelectric ceramics,59–61 whose dipoles gradually align under repeated voltage cycling. However, once saturated, the hysteresis loop of CIPS is highly squared and repeatable, consistent with its single-crystalline nature. The lower panels of Fig. 1a–d are the P–E hysteresis loops measured at different switching frequencies. Again, CIPS behaves anomalously compared to other ferroelectric materials: with increasing frequency, its hysteresis loops gradually shift horizontally along the electric field axis, while others show symmetrical expansion of the loops, a common characteristic of ferroelectrics. The large shifts of the loops (Fig. 1f) suggest that the polarization of CIPS cannot be switched to the opposite state at high switching frequency, which agrees with the switching kinetics studies discussed later.Additionally, low temperature polarization switching studies reveal more abnormal behaviors (Fig. 2). If an unpoled CIPS crystal is directly cooled down to low temperature without any pre-poling process, we cannot obtain any well-defined P–E hysteresis loops, regardless of how large or how long the voltage we apply is (Fig. 2a and c). A proper square loop with saturated polarization can only be obtained at temperatures above 250 K. The double-hysteresis-like low temperature loops suggest strong pinning of the polarization by random fields in the pristine sample, which echoes with the disorder state observed in the initial P–E loops at room temperature (Fig. 1a). The difference is that at room temperature the polarization can be gradually depinned, but it cannot at low temperatures. At the intermediate temperature around 250 K, the depinning process is also pulse width dependent (Fig. 2d). However, if the CIPS crystal is pre-poled at room temperature and subsequently cooled to low temperatures, the square P–E loop can be preserved. Intriguingly, depending on the prepoled polarization direction, the obtained low-temperature loop would shift completely towards the positive or negative segment of the electric field axis (Fig. 2e). It is also possible to obtain separate double-hysteresis loops if the crystal is cooled down with a half of the polarization upward and the other half downward (Fig. S1, ESI†). The scenario is in analogue to the field-cooling induced exchange bias in magnetic systems. However, in our case no external field was applied during the cooling. A similar effect also exists in ferroelectrics due to the cooperative alignment of defect-dipoles by thermal annealing/aging.60,62,63 By measuring the P–E loops at various temperatures and frequencies, we found that the horizontal offset (Eshift) basically increases at high switching frequency, consistent with that observed in Fig. 1a. However, at low temperature it will converge to a fixed value at low switching frequency, while at temperatures above 250 K, the imprint field can be completely removed at low frequencies (Fig. 2f), resulting in a symmetrical P–E loop.
The unusual polarization switching characteristics observed in the CIPS single crystal drove us to perform a more comprehensive study on its switching kinetics. The conventional positive-up-negative-down (PUND) method was employed, in which remnant polarization (dPr) is obtained by subtracting the non-remnant component (Pr^) from the total switched polarization (Pr*) (Fig. 3f). The polarization switching spectra of different materials are shown in Fig. 3a–e. In contrast to the switching spectra of other ferroelectrics which span a wide range of pulse widths at different electric fields, that of CIPS is confined in a narrow range, regardless of the increase of the electric field. The data were then fitted to the classical Kolmogorov–Avrami–Ishibashi (KAI) model by assuming homogeneous nucleation and unrestricted domain growth, using the equation
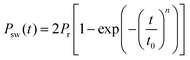 | (1) |
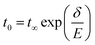 | (2) |
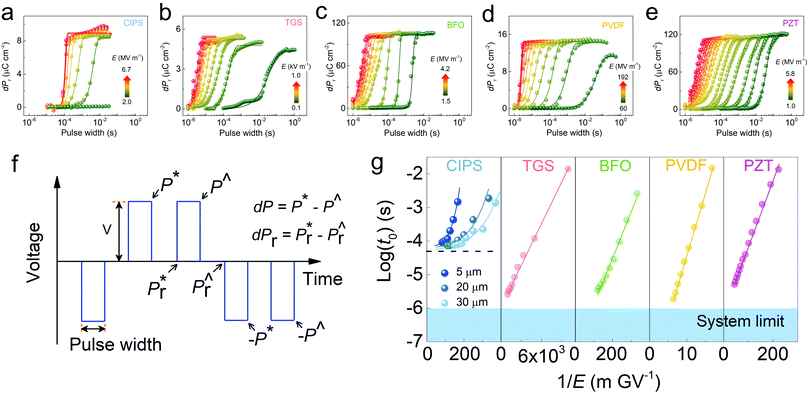
Does the Merz's law fail in CIPS? To understand it, we should note that the above switching kinetics is analyzed based on the remnant polarization (dPr), also known as the stable switched polarization. By examining additional information from the PUND measurements such as the polarization at the first (P*) and second (P^) voltage pulse top (Fig. 3f), more complicated switching kinetics can be unveiled. As shown in Fig. 4a, at low temperatures (150 K), no remnant polarization can be measured because only the pre-poled polarization is stable according to the low temperature P–E loops (Fig. 2e). However, we can still observe the temporary switching of the polarization as evidenced by the P* curve. The problem is, after the first upward voltage pulse, the polarization quickly relaxes back to its original state and we obtain an identical P^ curve during the second upward pulse, which leads to zero dP after the subtraction (P* − P^). Consistent with Fig. 2, the switched polarization only becomes stable above 250 K. Consequently, dP becomes non-zero (lower panel of Fig. 4a and Fig. S2 (ESI†) for complete temperature dependence). Apparently, there is a large disparity between the characteristic times of P* (polarization is switched but not stable) and dP (polarization is switched and maintained). By plotting the full spectra of P* and dPr (Fig. 3b), a stark difference can be discerned. While the dPr curve shows a lower limit around 10−4 s, the switching rate of P* can be much faster under large electric field. By plotting the log(t0) for P* and 1/E, a linear relationship is obtained, obeying the Merz's law (Fig. 4c and Fig. S3, ESI†). The mysterious polarization switching behaviors of CIPS can now be explained: while there is no thermodynamic limit for the polarization to switch, the switched polarization is only stable at a much slower characteristic time.
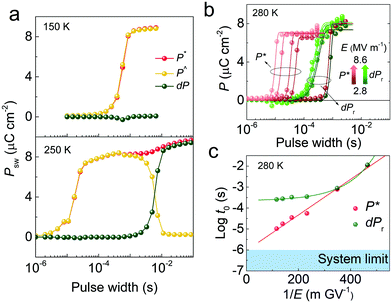 | ||
| Fig. 4 Bifurcated switching characteristics of CuInP2S6. (a) A comparison of switching kinetics of different polarization components (denoted in Fig. 3f) at 150 K and 250 K. (b) Switching kinetics of total polarization P* (red) and remnant polarization dPr (green) measured at 280 K. The solid lines are corresponding fits using the KAI model. (c) Log plot of KAI characteristic switching time t0versus 1/E for P* and dPr derived from (b). Linear fit using the Mertz’ law is obtained for P*. | ||
Temperature dependent dielectric spectroscopic and dc conduction of CuInP2S6
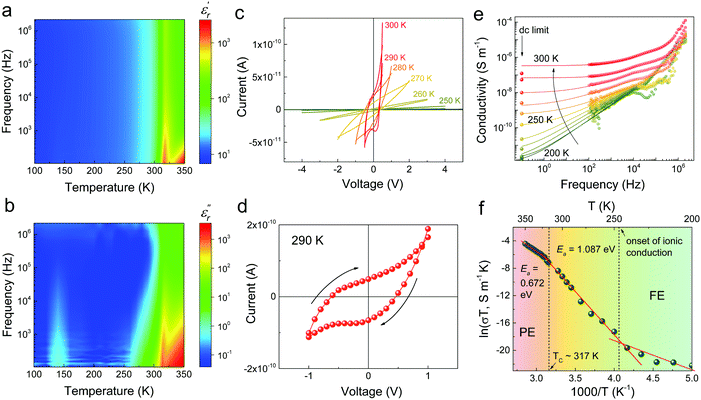
But what is causing the switching-rate-dependency in the stability of switched polarization? To answer this question, we carried out a detailed dielectric spectroscopy study in both temperature and frequency domains. The real and imaginary parts of the relative permittivity are plotted in Fig. 5a and b (see Fig. S4 (ESI†) for the line plots). The real permittivity map is characterized by a single anomaly at about 317 K, which corresponds to the first-order ferroelectric–paraelectric transition.64 The imaginary ε′′ reflects the energy loss due to the current conduction. Except for the small peak found at around 140 K due to the formation of dipole glass phase,65 the most prominent feature of Fig. 5b is the onset of low-frequency conductivity above 250 K. To extend the measurement frequency to the dc limit, current–voltage (I–V) curves were also recorded at different temperatures, as shown in Fig. 5c. The sample shows negligible dc current up to 250 K, above which the current increases sharply. Moreover, hysteresis between forward and reverse sweeping of the I–V curves becomes increasingly obvious (Fig. 5d). Such behavior shouldn’t appear in electronic conductors, considering the slow rate of the voltage sweep (∼0.1 Hz), but is a typical signature of ionic conduction, such as those widely observed in hybrid perovskites.27 From the imaginary part of permittivity, ac conductivity can be calculated based on the equation| σ = 2πfε0εr′′ |
| σ = σdc + A(2πf)s |
Temperature dependent crystal structural aspects of CuInP2S6
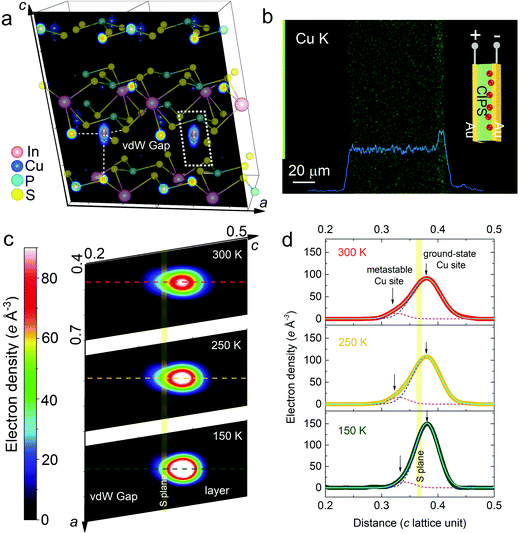
To gain further insight into the atomistic origin, temperature-dependent SCXRD was carried out and the atomic structures were then refined. The single crystal was measured before and after the electrical poling at room temperature. However, little difference is found in terms of the structural aspects. The main change is the inversion twin (polarization domain) ratio (from ∼0.5 to ∼0.2) and a slight increase in the copper electron density possibly due to the improvement of structural order after poling. Following our previous work,67 multiple sites with isotropic thermal parameters are assumed to better account for the super diffuse and elongated distribution of the electron density around the Cu site. The refined structure for the room-temperature poled sample is shown in Fig. 6a, superimposed with the electron density map of the ac plane (Fig. S5, ESI†). With decreasing temperature, the Cu electron density becomes less diffuse, consistent with the previous report53 (Fig. 6c). However, in addition to the strong anisotropy, the electron density distribution also shows clear asymmetry in the shape, which protrudes more towards the vdW gap than to the layer. By plotting the intensity line profile perpendicular to the layer (sulphur) plane as shown in Fig. 6d, it is possible to fit the asymmetric peaks using two Gaussian peak functions, which correspond to the ground-state (intralayer) and metastable (interlayer) Cu sites, respectively. At low temperature, the majority of the Cu atoms occupy the ground-state site. With elevating temperature, the width of the ground-state peak increases, suggesting large amplitude of the thermal hopping motion of Cu ions. Furthermore, the intensity weight of the metastable site also increases, which indicates higher probability for the interlayer hopping. This observation explains the onset of the ionic conduction due to the enhancement of thermally assisted site hopping above 250 K. The displacive instability of Cu ions stems from the second-order Jahn–Teller effect of the tetrahedrally coordinated Cu(I)–S complex, which favors both outside-tetrahedron (intralayer) and inside-tetrahedron (interlayer) configurations.68 At high temperature, the enhanced coupling between the Cu 4s and S sp orbitals across the vdW gap stabilizes the interlayer sites (Fig. 5a), which also potentially increases the ionic conductivity through inter-site hoppings. In order to verify that the charge carrier is indeed Cu ions, we carried out a dc stressing test on a CIPS single crystal sandwiched by two plate Au electrodes. The energy-dispersive X-ray spectroscopy (EDS) map of the cross-section of the device clearly demonstrates the accumulation of Cu atoms at the cathode (Fig. 6b). We didn’t find a noticeable change in the distribution of other elements (Fig. S6, ESI†), thus suggesting that the main charge carrier in CIPS is a Cu ion.Discussion
Based on all the experimental observations shown above, the origin of the anomalous polarization switching behavior and its connection to the ionic conduction in CIPS can be understood as follows. For the as-grown/unpoled CIPS crystals cooled from the high-temperature paraelectric phase through TC, there is no preference in the polarization directions. The populations of upward and downward domains are almost equal (50 to 50%), as evidenced by the twin parameter of the SCXRD results. In the meantime, due to the displacive instability of the Cu ions, some of them are thermally excited to the metastable sites within the vdW gap as shown in Fig. 6c. The majority of these in-gap states are electrically switchable, otherwise their population and position should remain the same at 150 K. However, due to inevitable crystal imperfections, such as vacancy/interstitial/antisite defects,58,69,70 a small amount of Cu ions (see Text S1 (ESI†) for the discussion of the defect concentration) are deeply trapped at the non-equilibrium sites, whose switching requires higher energy and longer time. Take note that since these defect structures are disordered (non-periodic) and of a small amount, they are invisible in the SCXRD. Considering the insensitivity of the switching behavior to the chemical stoichiometry (Table S1, ESI†), we propose that the most probable defective structure is similar to Frenkel pairs of Cu ions, which carry additional dipole moments. The defect-dipoles then coupled to the matrix polarization via the symmetry-conforming property mediated by the electrostatic interaction,71,72 when cooling through the TC (Fig. 7a). In turn, these defect-dipoles provide pinning fields that restrain the polarization reversal. As a result, we observe the slow saturation of the P–E loop in an as-grown crystal under repetitive voltage cycling (Fig. 1a). Note that although these defect complexes are domain pinning centers, they are still electrically switchable at room temperature, thanks to the Cu ionic conductivity of CIPS. Unfortunately, they become immobile at low temperature. Therefore, for an unpoled crystal directly cooled down to low temperatures, it is not possible to obtain a well-defined hysteresis loop till above 250 K (Fig. 2a), because all the ferroelectric domains are randomly pinned to their initial directions by the as-grown highly disordered defect-dipoles. In contrast, if the polarization of the crystal is pre-poled at room temperature, it is then possible to get saturated square loops at low temperature thanks to the electrical poling induced ordering of the defect complexes. However, the electrically poled defect-dipoles will produce a cooperative imprint field that stabilizes the pre-poled polarization state (Fig. 2e). In this case, the switched polarization will quickly relax back to its original state under the imprint field. Only at sufficiently high temperatures when the defect ions (Cu) become mobile, can the switched polarization be stable, because the defect-dipoles can now be switched as well. However, the different switching speeds for the ferroelectric polarization and defect-dipoles give rise to bifurcated characteristic times in the switching spectroscopic curves (Fig. 4). The seemingly “slow” switching speed of the CIPS crystal is due to the slow switching of the defect-dipoles, which is required to stabilize the switched polarization state. This also explains the horizontal shift of the hysteresis loops at high switching frequencies (Fig. 1a): the defect-dipoles have insufficient time to switch, causing the final switched state to be unstable. The reason that the onset temperature of switchable defect-dipoles and ionic conduction coincide with each other is because both of them originate from the thermally-driven displacive instability of the Cu ions. However, they exist for different time scales. At the dc limit, ionic conduction will lead to long-range migration of the Cu ions and thus the melting of the Cu sublattice, which destroys the ferroelectric order. In contrast, under short electrical pulse (<1 s), the Cu ions can only hop between short-range defective and thermal equilibrium sites (e.g. the creations and annihilations of Frenkel pairs), realizing the reversal of defect-dipoles. The interplays between ferroelectric polarization, defect-dipoles and ionic conductivity explain the anomalous polarization switching characteristics in CIPS.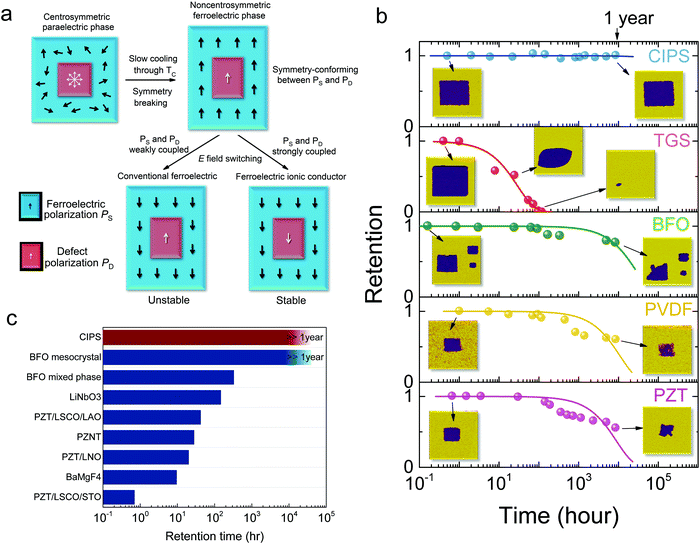 | ||
| Fig. 7 Permanent polarization retention of CuInP2S6 due to defect dipole-polarization interlock. (a) A schematic illustration of the interplay between ferroelectric and defect polarizations in both conventional ferroelectrics and ferroelectric ionic conductors. (b) A comparison of domain relaxation rates for different ferroelectric materials. The solid lines are fits using an exponential decay function. The insets show the corresponding PFM phase images for the data points. (c) A comparison of the retention time reported for different materials in the literature, including BFO mesocrystal,76 BFO mixed phase,75 LiNbO3,84 PZT/LSCO/LAO,83 PZNT,81 PZT/LNO,82 BaMgF4,85 and PZT/LSCO/STO.73 | ||
Although the dc ionic conduction is detrimental for ferroelectricity, the switchable defect-dipoles are beneficial for the polarization stability. After electrical switching, the defect-dipoles will be aligned to the direction that stabilizes the matrix polarization due to its symmetry-conforming nature. When the voltage is removed, the internal field generated by the defect-dipoles will serve as a guard to prevent the polarization from backswitching, which should lead to permanent retention in ferroelectric ionic conductors (Fig. 7a). To test this prediction, we compare the ferroelectric retention performance for various ferroelectric materials. In our experiment, one surface of the samples is coated with metal electrode while the other is left as an open surface for electrical switching using a scanning probe. The incomplete screening of the polarization should expedite the polarization backswitching process, which is widely used in ferroelectric retention studies.73–77 A square pattern with polarity opposite to the original polarization was written for each ferroelectric sample, and the domain relaxation with time (up to a year) was intermittently recorded by piezoelectric force microscopy (PFM) as shown in Fig. 7b (see Fig. S7–S11, ESI† for more details). Usually for ferroelectrics with self-poled monodomains, there exists an imprint field originating from either charged defects62,63 or heterointerfaces78–80 that stabilizes the original polarization direction. As a consequence, the switched polarization will gradually revert to its initial state, causing ferroelectric retention failure. The speed of polarization backswitching depends on a few factors, such as the magnitude of the imprint field, the energy barrier for the domain reversal, the relaxation rate of the screening charges, etc. As shown in Fig. 6b, TGS shows the fastest backswitching speed, which can be well described by the exponential decay model. The other three samples, BFO, PVDF, and PZT, do not follow a simple exponential decay, showing stepwise patterns that are commonly observed in ferroelectrics due to the random pinning of the domain wall movement by defects. Surprisingly, CIPS displays basically no change in the switched pattern after a year, suggesting an infinite time constant of decay. To the best of our knowledge, this result is among the longest retention times reported for ferroelectric domains written by AFM tip (Fig. 7c).73,75,76,81–85
To prove that the permanent polarization retention of CIPS is not affected by the domain size, a much smaller domain pattern (500 nm width and 50 μm depth) is created and remains stable up to a few months (Fig. S12, ESI†). Furthermore, the surface potential changes during the retention experiment (Fig. S7–S11, ESI†) also reveal that the switched domain stability of common ferroelectrics is strongly affected by the relaxation of surface charges, while CIPS shows robust domain stability irrespective of the surface charges. This indicates that a ferroelectric ionic conductor can screen the polarization by its own ionic charged species.
Conclusions
In summary, we report a comprehensive study on the polarization switching in a ferroelectric ionic conductor, CIPS, whose anomalous behaviors are found to correlate with its ionic conductivity. In particular, the strong coupling between the spontaneous polarization and the ionic conductivity lies in their common atomic origin, namely, the second-order Jahn–Teller instability that results in both off-centering and large thermal hopping parameters of the Cu ions. Such displacive instability of Cu ions also produces ionic defect dipoles that couple to the ferroelectric polarization and pin the polarization at low temperatures. At temperatures above 250 K, on one hand, the thermal hopping of Cu ions leads to the electrical switchability of the defect-dipoles, but their low speed poses a limit on the ferroelectric polarization switching due to the electrostatic coupling between them. On the other hand, the coupled switching between defect dipoles and ferroelectric polarization endows CIPS with an interlock to guard the switched polarization, leading to superior polarization retention. The interplay between polarization switching and ionic movement can be extended to other systems with similar ionic displacive instabilities and activities, such as ionic-mediated memristor synapses, ultrathin ferroionic films, and even hybrid organic–inorganic compounds. Furthermore, the defect dipole-polarization interlock mechanism makes ferroelectric ionic conductors ideal candidates for information storage applications.Methods
Materials synthesis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at ambient temperature.86 Thin plates (∼50–100 μm) with the polar b-axis perpendicular to the surface were obtained by cleaving the large single crystals.
1 at ambient temperature.86 Thin plates (∼50–100 μm) with the polar b-axis perpendicular to the surface were obtained by cleaving the large single crystals.
Compositional analyses and single-crystal X-ray crystallography
EPMA was carried out in a JEOL JXA-8530F instrument equipped with five wavelength-dispersive spectrometers (WDS). The surface of the CIPS crystal was coated with carbon to minimize the charging effect. Standards (Astimex Standards Ltd) of copper metal (Cu), InP (In and P) and Pyrite FeS2 (S) were used in the analysis. The obtained average composition of CIPS in atomic percentage is Cu1.00±0.03In0.99±0.01P1.94±0.01S6.07±0.02. Chemical analysis of the dc-stressed CIPS capacitor was measured by energy dispersive X-ray spectroscopy (EDS) equipped on a JSM-6360 scanning electron microscope (SEM).Single crystal XRD was conducted on a Bruker SMART APEX-II system. An Mo source along with a graphite monochromator was used to produce X-rays with a wavelength of 0.71073 Å. The X-ray intensity data were collected and integrated using the Bruker SAINT software package with a narrow frame algorithm. SADABS and XPREP programs were employed for multi-scan absorption corrections and evaluating the data symmetry. Symmetry equivalent reflections were merged whilst Friedel opposites were not merged. The data were then solved by SHELXT and refined on F2 using SHELXL-97.90 Electron density maps (observed Fourier maps) were produced using the MAPVIEW module in WinGX.91
All atoms in CIPS were refined using anisotropic thermal parameters except for the copper atoms, which were treated isotropically in order to accurately gauge atomic density position along the line of disorder. All possible copper sites were identified from difference maps. The inversion twin components which represent the domain fractions of opposite polarization directions were refined using the Flack parameters,92 before and after the electrical poling by using amorphous carbon coating as the electrodes. The high quality of the CIPS single crystal was substantiated by the exceptionally low R factors of the refinement.
Ferroelectric switching and dielectric spectroscopies
All samples were measured in the form of parallel plate capacitors with symmetric Au electrodes for single crystals and Pt top electrodes for thin films. Temperature dependent electrical measurements were conducted in a cryogenic micromanipulator probe station equipped with a heating stage. Ferroelectric hysteresis loops and PUND measurements were carried out using a commercial ferroelectric tester (Precision Multiferroic, Radiant Technologies). Dielectric data were collected using a commercial impedance LCR meter (E4980A, Agilent) from 100 Hz to 2 MHz. Current–voltage measurements were characterized by a pA meter/direct current (DC) voltage source (4140B, Hewlett Packard). The ionic migration test was performed by applying a constant dc bias on a CIPS capacitor under an electric field of ∼5 kV cm−1 for 30 min. Afterwards, the capacitor was cut from the middle, and the cross-sectional surface was polished and carbon-coated for SEM and EDS analyses.Ferroelectric domain retention measurements
PFM writing and imaging were carried out on a commercial atomic force microscope (Asylum Research MFP-3D) using a stiff Pt-coated silicon tip with a spring constant of ∼40 N m−1 (Nanoworld, NCHPt). For domain switching, a dc voltage was applied to the bottom electrode while the AFM probe was grounded. For domain imaging, 1–2 V ac voltage with a frequency of 10 kHz was applied to the conductive probe which drives the film surface to oscillate due to converse piezoelectric effect. The amplitude and phase of the oscillation were then recorded using a lock-in amplifier. Surface potential was imaged using scanning Kelvin probe microscopy (SKPM) using a dual-pass technique. The domain relaxations of all the samples were monitored intermittently up to a few months. During the time, the samples were stored under ambient conditions (25 °C, 30% relative humidity).Author contributions
L. Y. and J. W. conceived the idea and designed the experiments. A. C., N. Z., A. A. and Y. Z. synthesized the materials. S. Z. and L. Y. fabricated the devices with the help of Y. H. and J. C. S. Z. and L. Y. collected and analyzed the data of ferroelectric, dielectric and PFM measurements. S. A. M. and L. Y. performed single-crystal XRD and refinements. J. S. H. conducted EPMA measurement and analysis. S. D. provided theoretical interpretations. L. Y., S. Z. and J. W. co-wrote the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Guoliang Yuan and Prof. Hiroshi Funakubo for providing TGS and PZT samples. L. Y. and J. W. acknowledge support from the Ministry of Education, Singapore under grant AcRF Tier 1 RG118/17. S. Z. acknowledges the support from the National Natural Science Foundation of China (grant no. 11904176).References
- S. V. Levchenko and A. M. Rappe, Influence of Ferroelectric Polarization on the Equilibrium Stoichiometry of Lithium Niobate (0001) Surfaces, Phys. Rev. Lett., 2008, 100, 256101 CrossRef.
- M. F. Chisholm, W. Luo, M. P. Oxley, S. T. Pantelides and H. N. Lee, Atomic-Scale Compensation Phenomena at Polar Interfaces, Phys. Rev. Lett., 2010, 105, 197602 CrossRef.
- M. J. Highland, et al., Equilibrium Polarization of Ultrathin PbTiO3 with Surface Compensation Controlled by Oxygen Partial Pressure, Phys. Rev. Lett., 2011, 107, 187602 CrossRef CAS PubMed.
- Y.-M. Kim, et al., Direct observation of ferroelectric field effect and vacancy-controlled screening at the BiFeO3/LaxSr1−xMnO3 interface, Nat. Mater., 2014, 13, 1019 CrossRef CAS.
- T. Rojac, et al., Domain-wall conduction in ferroelectric BiFeO3 controlled by accumulation of charged defects, Nat. Mater., 2016, 16, 322 CrossRef.
- L. Xie, et al., Giant Ferroelectric Polarization in Ultrathin Ferroelectrics via Boundary-Condition Engineering, Adv. Mater., 2017, 29, 1701475 CrossRef.
- L. Li, et al., Defect-Induced Hedgehog Polarization States in Multiferroics, Phys. Rev. Lett., 2018, 120, 137602 CrossRef CAS.
- V. K. Sergei, K. Yunseok, D. F. Dillon and N. M. Anna, Surface-screening mechanisms in ferroelectric thin films and their effect on polarization dynamics and domain structures, Rep. Prog. Phys., 2018, 81, 036502 CrossRef.
- R. V. Wang, et al., Reversible Chemical Switching of a Ferroelectric Film, Phys. Rev. Lett., 2009, 102, 047601 CrossRef CAS.
- N. C. Bristowe, M. Stengel, P. B. Littlewood, J. M. Pruneda and E. Artacho, Electrochemical ferroelectric switching: Origin of polarization reversal in ultrathin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024106 CrossRef.
- C. H. Yang, et al., Electric modulation of conduction in multiferroic Ca-doped BiFeO3 films, Nat. Mater., 2009, 8, 485 CrossRef CAS.
- Q. H. Qin, et al., Resistive Switching in All-Oxide Ferroelectric Tunnel Junctions with Ionic Interfaces, Adv. Mater., 2016, 28, 6852–6859 CrossRef CAS.
- W. M. Lu, et al., Multi-Nonvolatile State Resistive Switching Arising from Ferroelectricity and Oxygen Vacancy Migration, Adv. Mater., 2017, 29, 8 Search PubMed.
- C. W. Bark, et al., Switchable Induced Polarization in LaAlO3/SrTiO3 Heterostructures, Nano Lett., 2012, 12, 1765–1771 CrossRef CAS.
- Y. Kim, et al., Ionically-Mediated Electromechanical Hysteresis in Transition Metal Oxides, ACS Nano, 2012, 6, 7026–7033 CrossRef CAS.
- A. Kumar, et al., Probing Surface and Bulk Electrochemical Processes on the LaAlO3–SrTiO3 Interface, ACS Nano, 2012, 6, 3841–3852 CrossRef CAS.
- P. Sharma, et al., Electromechanics of Ferroelectric-Like Behavior of LaAlO3 Thin Films, Adv. Funct. Mater., 2015, 25, 6538–6544 CrossRef CAS.
- R. K. Vasudevan, N. Balke, P. Maksymovych, S. Jesse and S. V. Kalinin, Ferroelectric or non-ferroelectric: Why so many materials exhibit “ferroelectricity” on the nanoscale, Appl. Phys. Rev., 2017, 4, 021302 Search PubMed.
- S. M. Yang, et al., Mixed electrochemical–ferroelectric states in nanoscale ferroelectrics, Nat. Phys., 2017, 13, 812 Search PubMed.
- S. V. Kalinin and N. A. Spaldin, Functional Ion Defects in Transition Metal Oxides, Science, 2013, 341, 858–859 CrossRef CAS.
- D. Zhou, et al., Wake-up effects in Si-doped hafnium oxide ferroelectric thin films, Appl. Phys. Lett., 2013, 103, 192904 CrossRef.
- M. Pešić, et al., Physical Mechanisms behind the Field-Cycling Behavior of HfO2-Based Ferroelectric Capacitors, Adv. Funct. Mater., 2016, 26, 4601–4612 CrossRef.
- S. Starschich, S. Menzel and U. Böttger, Evidence for oxygen vacancies movement during wake-up in ferroelectric hafnium oxide, Appl. Phys. Lett., 2016, 108, 032903 CrossRef.
- J. J. Yang, D. B. Strukov and D. R. Stewart, Memristive devices for computing, Nat. Nanotechnol., 2012, 8, 13 CrossRef.
- Z. Wang, et al., Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing, Nat. Mater., 2016, 16, 101 CrossRef.
- S. Boyn, et al., Learning through ferroelectric domain dynamics in solid-state synapses, Nat. Commun., 2017, 8, 14736 CrossRef CAS.
- Z. Xiao, et al., Giant switchable photovoltaic effect in organometal trihalide perovskite devices, Nat. Mater., 2014, 14, 193 CrossRef PubMed.
- C. Eames, et al., Ionic transport in hybrid lead iodide perovskite solar cells, Nat. Commun., 2015, 6, 7497 CrossRef CAS.
- Y.-M. You, et al., An organic-inorganic perovskite ferroelectric with large piezoelectric response, Science, 2017, 357, 306–309 CrossRef CAS.
- J. B. Goodenough, Oxide-ion conductors by design, Nature, 2000, 404, 821 CrossRef CAS PubMed.
- M. Li, et al., A family of oxide ion conductors based on the ferroelectric perovskite Na0.5Bi0.5TiO3, Nat. Mater., 2013, 13, 31 CrossRef.
- J. F. Scott, F. Habbal and J. A. Zvirgzds, Ferroelectric phase transition in the superionic conductor Ag26I18W4O16, J. Chem. Phys., 1980, 72, 2760–2762 CrossRef CAS.
- S. Hoshino, H. Fujishita, M. Takashige and T. Sakuma, Phase transition of Ag3SX (X = I, Br), Solid State Ionics, 1981, 3–4, 35–39 CrossRef CAS.
- S. Y. Stefanovich, V. B. Kalinin and A. Nogai, Ferroelectric-superionic conductor phase transitions in Na3Sc2(PO4)3 and ITS isomorphes, Ferroelectrics, 1984, 55, 325–328 CrossRef.
- S. Y. Stefanovich, V. K. Yanovsky, A. V. Astafyev, V. I. Voronkova and N. V. Yu, Ferroelectric-Superionic Conductor Phase Transitions in Crystals MeNbWO6·nH2O (Me = Tl, Rb), Jpn. J. Appl. Phys., 1985, 24, 373 CrossRef CAS.
- J. F. Scott, A comparison of Ag- and proton-conducting ferroelectrics, Solid State Ionics, 1999, 125, 141–146 CrossRef CAS.
- G. Rosenman, A. Skliar, M. Oron and M. Katz, Polarization reversal in KTiOPO4 crystals, J. Phys. D: Appl. Phys., 1997, 30, 277 CrossRef CAS.
- R. A. Stolzenberger and M. P. Scripsick, Recent advancements in the periodic poling and characterization of RTA and its isomorphs, Optoelectronics 99 – Integrated Optoelectronic Devices, SPIE, 1999, vol. 3610, p. 13 Search PubMed.
- G. Rosenman, et al., Polarization reversal and domain grating in flux-grown KTiOPO4 crystals with variable potassium stoichiometry, Appl. Phys. Lett., 2000, 76, 3798–3800 CrossRef CAS.
- C. Canalias, J. Hirohashi, V. Pasiskevicius and F. Laurell, Polarization-switching characteristics of flux-grown KTiOPO4 and RbTiOPO4 at room temperature, J. Appl. Phys., 2005, 97, 124105 CrossRef.
- V. Y. Shur, E. V. Pelegova, A. R. Akhmatkhanov and I. S. Baturin, Periodically poled crystals of KTP family: a review, Ferroelectrics, 2016, 496, 49–69 CrossRef CAS.
- M. Maglione, et al., Intrinsic ionic screening of the ferroelectric polarization of KTP revealed by second-harmonic generation microscopy, Opt. Mater. Express, 2016, 6, 137–145 CrossRef CAS.
- G. Lindgren, et al., Elasticity Modulation due to Polarization Reversal and Ionic Motion in the Ferroelectric Superionic Conductor KTiOPO4, ACS Appl. Mater. Interfaces, 2018, 10, 32298–32303 CrossRef CAS.
- L. Seixas, A. S. Rodin, A. Carvalho and A. H. Castro Neto, Multiferroic Two-Dimensional Materials, Phys. Rev. Lett., 2016, 116, 206803 CrossRef CAS.
- C. Gong, et al., Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546, 265 CrossRef CAS.
- B. Huang, et al., Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270 CrossRef CAS.
- C. Cui, F. Xue, W.-J. Hu and L.-J. Li, Two-dimensional materials with piezoelectric and ferroelectric functionalities, npj 2D Mater. Appl., 2018, 2, 18 CrossRef.
- M. Wu and P. Jena, The rise of two-dimensional van der Waals ferroelectrics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1365 Search PubMed.
- A. Belianinov, et al., CuInP2S6 Room Temperature Layered Ferroelectric, Nano Lett., 2015, 15, 3808–3814 CrossRef CAS.
- M. Chyasnavichyus, et al., Size-effect in layered ferrielectric CuInP2S6, Appl. Phys. Lett., 2016, 109, 172901 CrossRef.
- F. Liu, et al., Room-temperature ferroelectricity in CuInP2S6 ultrathin flakes, Nat. Commun., 2016, 7, 12357 CrossRef CAS.
- M. Si, P.-Y. Liao, G. Qiu, Y. Duan and P. D. Ye, Ferroelectric Field-Effect Transistors Based on MoS2 and CuInP2S6 Two-Dimensional van der Waals Heterostructure, ACS Nano, 2018, 12, 6700–6705 CrossRef CAS.
- V. Maisonneuve, V. B. Cajipe, A. Simon, R. Von Der Muhll and J. Ravez, Ferrielectric ordering in lamellar CuInP2S6, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 10860–10868 CrossRef CAS.
- V. Maisonneuve, et al., Ionic conductivity in ferroic CuInP2S6 and CuCrP2S6, Ferroelectrics, 1997, 196, 257–260 CrossRef CAS.
- J. Banys, J. Macutkevic, V. Samulionis, A. Brilingas and Y. Vysochanskii, Dielectric and ultrasonic investigation of phase transition in CuInP2S6 crystals, Phase Transitions, 2004, 77, 345–358 CrossRef CAS.
- N. Balke, et al., Locally Controlled Cu-Ion Transport in Layered Ferroelectric CuInP2S6, ACS Appl. Mater. Interfaces, 2018, 10, 27188–27194 CrossRef CAS.
- M. A. Susner, et al., High-Tc Layered Ferrielectric Crystals by Coherent Spinodal Decomposition, ACS Nano, 2015, 9, 12365–12373 CrossRef CAS PubMed.
- M. A. Susner, et al., Cation–Eutectic Transition via Sublattice Melting in CuInP2S6/In4/3P2S6 van der Waals Layered Crystals, ACS Nano, 2017, 11, 7060–7073 CrossRef CAS PubMed.
- M. I. Morozov and D. Damjanovic, Hardening-softening transition in Fe-doped Pb(Zr,Ti)O3 ceramics and evolution of the third harmonic of the polarization response, J. Appl. Phys., 2008, 104, 034107 CrossRef.
- J. Li, L. Fei and Z. Shujun, Decoding the Fingerprint of Ferroelectric Loops: Comprehension of the Material Properties and Structures, J. Am. Ceram. Soc., 2014, 97, 1–27 CrossRef CAS.
- Y. A. Genenko, J. Glaum, M. J. Hoffmann and K. Albe, Mechanisms of aging and fatigue in ferroelectrics, Mater. Sci. Eng., B, 2015, 192, 52–82 CrossRef CAS.
- D. Lee, et al., Active Control of Ferroelectric Switching Using Defect-Dipole Engineering, Adv. Mater., 2012, 24, 6490–6495 CrossRef CAS PubMed.
- A. R. Damodaran, E. Breckenfeld, Z. Chen, S. Lee and L. W. Martin, Enhancement of Ferroelectric Curie Temperature in BaTiO3 Films via Strain-Induced Defect Dipole Alignment, Adv. Mater., 2014, 26, 6341–6347 CrossRef CAS PubMed.
- A. Simon, J. Ravez, V. Maisonneuve, C. Payen and V. B. Cajipe, Paraelectric-Ferroelectric Transition in the Lamellar Thiophosphate CuInP2S6, Chem. Mater., 1994, 6, 1575–1580 CrossRef CAS.
- A. Dziaugys, J. Banys, J. Macutkevic, R. Sobiestianskas and Y. Vysochanskii, Dipolar glass phase in ferrielectrics: CuInP2S6 and Ag0.1Cu0.9InP2S6 crystals, Phys. Status Solidi A, 2010, 207, 1960–1967 CrossRef CAS.
- A. K. Jonscher, The ‘universal’ dielectric response, Nature, 1977, 267, 673 CrossRef CAS.
- L. You, et al., Origin of giant negative piezoelectricity in a layered van der Waals ferroelectric, Sci. Adv., 2019, 5, eaav3780 CrossRef.
- S.-H. Wei, S. B. Zhang and A. Zunger, Off-center atomic displacements in zinc blende semiconductor, Phys. Rev. Lett., 1993, 70, 1639–1642 CrossRef CAS PubMed.
- Q. He, et al., Antisite defects in layered multiferroic CuCr0.9In0.1P2S6, Nanoscale, 2015, 7, 18579–18583 RSC.
- M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Metal Thio- and Selenophosphates as Multifunctional van der Waals Layered Materials, Adv. Mater., 2017, 29, 1602852 CrossRef.
- X. Ren and K. Otsuka, Universal Symmetry Property of Point Defects in Crystals, Phys. Rev. Lett., 2000, 85, 1016–1019 CrossRef CAS PubMed.
- X. Ren, Large electric-field-induced strain in ferroelectric crystals by point-defect-mediated reversible domain switching, Nat. Mater., 2004, 3, 91 CrossRef CAS PubMed.
- C. S. Ganpule, et al., Polarization relaxation kinetics and 180° domain wall dynamics in ferroelectric thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 014101 CrossRef.
- S. H. Baek, et al., Ferroelastic switching for nanoscale non-volatile magnetoelectric devices, Nat. Mater., 2010, 9, 309–314 CrossRef CAS PubMed.
- H. Yen-Chin, et al., Giant Enhancement of Ferroelectric Retention in BiFeO3 Mixed-Phase Boundary, Adv. Mater., 2014, 26, 6335–6340 CrossRef PubMed.
- Y.-H. Hsieh, et al., Permanent ferroelectric retention of BiFeO3 mesocrystal, Nat. Commun., 2016, 7, 13199 CrossRef CAS PubMed.
- L. Li, et al., Atomic-Scale Mechanisms of Defect-Induced Retention Failure in Ferroelectrics, Nano Lett., 2017, 17, 3556–3562 CrossRef CAS PubMed.
- P. Yu, et al., Interface ferromagnetism and orbital reconstruction in BiFeO3-La0.7Sr0.3MnO3 heterostructures, Phys. Rev. Lett., 2010, 105, 027201 CrossRef CAS.
- P. Gao, et al., Direct Observations of Retention Failure in Ferroelectric Memories, Adv. Mater., 2012, 24, 1106–1110 CrossRef CAS.
- P. Gao, et al., Revealing the role of defects in ferroelectric switching with atomic resolution, Nat. Commun., 2011, 2, 591 CrossRef.
- A. Gruverman, et al., Nanoscale imaging of domain dynamics and retention in ferroelectric thin films, Appl. Phys. Lett., 1997, 71, 3492–3494 CrossRef CAS.
- J. W. Hong, et al., Nanoscale investigation of domain retention in preferentially oriented PbZr0.53Ti0.47O3 thin films on Pt and on LaNiO3, Appl. Phys. Lett., 1999, 75, 3183–3185 CrossRef CAS.
- T. K. Song, J.-G. Yoon and S.-I. Kwun, Microscopic Polarization Retention Properties of Ferroelectric Pb(Zr,Ti)O3 Thin Films, Ferroelectrics, 2006, 335, 61–68 CrossRef CAS.
- Y. Kan, et al., Critical radii of ferroelectric domains for different decay processes in LiNbO3 crystals, Appl. Phys. Lett., 2007, 91, 132902 CrossRef.
- H. Zeng, K. Shimamura, E. G. Villora, S. Takekawa and K. Kitamura, Domain growth kinetics and wall strain behavior in BaMgF4 ferroelectric crystal by piezoresponse force microscopy, J. Appl. Phys., 2007, 101, 074109 CrossRef.
- H. Ma, et al., Ferroelectric Polarization Switching Dynamics and Domain Growth of Triglycine Sulfate and Imidazolium Perchlorate, Adv. Electron. Mater., 2016, 2, 1600038 CrossRef.
- L. You, et al., Enhancing ferroelectric photovoltaic effect by polar order engineering, Sci. Adv., 2018, 4, eaat3438 CrossRef.
- F. Takashi, et al., Thick Epitaxial Pb(Zr0.35,Ti0.65)O3 Films Grown on (100)CaF2 Substrates with Polar-Axis-Orientation, Appl. Phys. Express, 2008, 1, 085001 CrossRef.
- W. J. Hu, et al., Universal Ferroelectric Switching Dynamics of Vinylidene Fluoride-trifluoroethylene Copolymer Films, Sci. Rep., 2014, 4, 4772 CrossRef.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- L. Farrugia, WinGX and ORTEP for Windows: an update, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- H. Flack, On enantiomorph-polarity estimation, Acta Crystallogr., Sect. A: Found. Crystallogr., 1983, 39, 876–881 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh01215j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |