Open Access Article
Open Access ArticleThermal activation of methane by MgO+: temperature dependent kinetics, reactive molecular dynamics simulations and statistical modeling†
Brendan C.
Sweeny
a,
Hanqing
Pan
b,
Asmaa
Kassem
b,
Jordan C.
Sawyer
a,
Shaun G.
Ard
*c,
Nicholas S.
Shuman
 c,
Albert A.
Viggiano
c,
Sebastian
Brickel‡
c,
Albert A.
Viggiano
c,
Sebastian
Brickel‡
 d,
Oliver T.
Unke§
d,
Oliver T.
Unke§
 d,
Meenu
Upadhyay
d,
Meenu
Upadhyay
 d and
Markus
Meuwly
d and
Markus
Meuwly
 *d
*d
aNRC Postdoc at Air Force Research Laboratory, Space Vehicles Directorate, Kirtland Air Force Base, New Mexico 87117, USA
bUSRA Space Scholar at Air Force Research Laboratory, Space Vehicles Directorate, Kirtland Air Force Base, New Mexico 87117, USA
cAir Force Research Laboratory, Space Vehicles Directorate, Kirtland Air Force Base, New Mexico 87117, USA. E-mail: rvborgmailbox@us.af.mil
dDepartment of Chemistry, University of Basel, Klingelbergstrasse 80, CH-4056 Basel, Switzerland. E-mail: m.meuwly@unibas.ch
First published on 23rd March 2020
Abstract
The kinetics of MgO+ + CH4 was studied experimentally using the variable ion source, temperature adjustable selected ion flow tube (VISTA-SIFT) apparatus from 300–600 K and computationally by running and analyzing reactive atomistic simulations. Rate coefficients and product branching fractions were determined as a function of temperature. The reaction proceeded with a rate of k = 5.9 ± 1.5 × 10−10(T/300 K)−0.5±0.2 cm3 s−1. MgOH+ was the dominant product at all temperatures, but Mg+, the co-product of oxygen-atom transfer to form methanol, was observed with a product branching fraction of 0.08 ± 0.03(T/300 K)−0.8±0.7. Reactive molecular dynamics simulations using a reactive force field, as well as a neural network trained on thousands of structures yield rate coefficients about one order of magnitude lower. This underestimation of the rates is traced back to the multireference character of the transition state [MgOCH4]+. Statistical modeling of the temperature-dependent kinetics provides further insight into the reactive potential surface. The rate limiting step was found to be consistent with a four-centered activation of the C–H bond, in agreement with previous calculations. The product branching was modeled as a competition between dissociation of an insertion intermediate directly after the rate-limiting transition state, and traversing a transition state corresponding to a methyl migration leading to a Mg–CH3OH+ complex, though only if this transition state is stabilized significantly relative to the dissociated MgOH+ + CH3 product channel. An alternative, non-statistical mechanism is discussed, whereby a post-transition state bifurcation in the potential surface could allow the reaction to proceed directly from the four-centered TS to the Mg–CH3OH+ complex thereby allowing a more robust competition between the product channels.
I. Introduction
The thermal activation of methane has long remained a “holy grail” in chemistry, offering the potential to transform the chemical economy by providing abundant feedstock for multitudes of value added chemicals.1–3 Gas phase ion reactivity combined with quantum chemical calculations provides the ability to study the mechanistic underpinnings of catalyzing this activation free from the complications inherent to bulk or solution phases.4–8 The observation of methane activation by MgO+ is of particular interest,9 as prior studies had focused on transition metals, such as the well performing but expensive palladium-based catalysts.10 Detailed understanding of methane activation by main group metal oxide species such as MgO+ presents the potential to develop cost effective catalysts for large scale utilization of this important chemical feedstock.Temperature-dependent kinetics offers insight into catalyst development in several ways. Comparing this data with statistical modeling of calculated reaction surfaces can confirm or refute a proposed mechanism as well as help identify energetic and entropic factors governing reactivity. We have employed this technique for several transition metal oxides reacting with methane,11,12 adding insight into the key rate limiting and product determining kinetic features of these systems. Additionally, the variation of rate coefficient and product branching for a given reaction as a function of temperature aids identifying the optimum conditions for a desired reaction product. Conversely, atomistic simulations based on accurate, reactive force fields provide molecular-level mechanistic insight into gas-phase reactions ranging from triatomics13–16 to systems such as the Diels–Alder reaction between 2,3-dibromo-1,3-butadiene and maleic anhydride.17
In the present work, we consider the hydrogen abstraction reaction
| 2MgO+ + 1CH4 → 1MgOH+ + 2CH3 | (1) |
| 2MgO+ + 1CH4 → 2Mg+ + 1CH3OH | (2) |
Reaction (1) has been previously investigated at room temperature using an ion trap apparatus and through electronic structure calculations at the density functional theory9 and at higher, correlated levels of theory.21 Although oxygen atom transfer from the oxide cation forming methanol is energetically preferred, it was only observed for <2% of reactions. The stationary points were calculated at the MP2/6-311(2d,2p) level, and were found to be in qualitative agreement with the observed efficiency of ∼40%. The rate limiting step was concluded to be a four-centered transition state leading to formation of a [CH3–MgOH]+ insertion complex, as opposed to a direct hydrogen abstraction pathway which was calculated to lie nearly isoenergetic with reactants and 0.1 eV above the four-centered TS. Previous work22 on the reaction of MnO+ + CH4 has highlighted the importance for entropic contributions, as in that case a direct hydrogen abstraction was found to be competitive with an energetically preferred four centered transition state similar to that for the system investigated here.
In the present work the temperature dependent kinetics is measured in an ion flow tube and compared with computations13 based on reactive molecular dynamics simulations and complementary computational studies. This provides a comprehensive characterization of the first step of the reaction and also highlights future possibilities to further investigate this important process.
II. Experimental methods
All measurements were performed on a recently described variable ion source, temperature adjustable selected ion flow tube (VISTA-SIFT).23 For these measurements a laser vaporization (LaVa) ion source was used. MgO+ ions were produced by ablating a translating, rotating magnesium rod (99.9%, ESPI metals) by ∼3 mJ per pulse of the second harmonic (532 nm) of an Nd:YAG (Litron) laser operating at 100 Hz. The ablated metal was entrained in a pulsed supersonic expansion (General Valve, Series 9) of a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 mixture of He/N2O/Ne at a backing pressure of 55 PSI with a pulse width of 200 μs, also operated at 100 Hz. Upon formation, ions are transported using a series of radio frequency (RF) ion guides and ion optics to a quadrupole mass filter. Mass-selected ions are injected into a 7.3 cm diameter, 1 m long flow tube via a Venturi inlet at ∼0.35 Torr of helium buffer allowing approximately 104–105 collisions for thermalization with the flow tube walls prior to introduction of the neutral reagent. The temperature of the flow tube is varied from 300 to 600 K by means of resistive heating. The reagent (CH4, 99.98% Sigma Aldrich) is added using a mass flow controller (MKS) 59 cm before the terminus of the flow tube providing 2–3 ms of reaction time prior to extraction through of 4 mm diameter aperture in a nose cone biased to ∼−5 V. The ions are transported using an RF ion guide to the entrance of an orthogonally-accelerated time-of-flight mass spectrometer. Relative abundances of reactant and product ions are monitored as a function of reagent concentration allowing determination of rate coefficients and product branching. The measured rate coefficients are ascribed an uncertainty of k ± 30%, while the product branching fraction uncertainty depends on temperature, see Table 1.
10 mixture of He/N2O/Ne at a backing pressure of 55 PSI with a pulse width of 200 μs, also operated at 100 Hz. Upon formation, ions are transported using a series of radio frequency (RF) ion guides and ion optics to a quadrupole mass filter. Mass-selected ions are injected into a 7.3 cm diameter, 1 m long flow tube via a Venturi inlet at ∼0.35 Torr of helium buffer allowing approximately 104–105 collisions for thermalization with the flow tube walls prior to introduction of the neutral reagent. The temperature of the flow tube is varied from 300 to 600 K by means of resistive heating. The reagent (CH4, 99.98% Sigma Aldrich) is added using a mass flow controller (MKS) 59 cm before the terminus of the flow tube providing 2–3 ms of reaction time prior to extraction through of 4 mm diameter aperture in a nose cone biased to ∼−5 V. The ions are transported using an RF ion guide to the entrance of an orthogonally-accelerated time-of-flight mass spectrometer. Relative abundances of reactant and product ions are monitored as a function of reagent concentration allowing determination of rate coefficients and product branching. The measured rate coefficients are ascribed an uncertainty of k ± 30%, while the product branching fraction uncertainty depends on temperature, see Table 1.
| T (K) | k tot | k NNtot | Efficiency | Product branching fractions | |
|---|---|---|---|---|---|
| Mg+ + CH3OH | MgOH+ + CH3 | ||||
| a Langevin–Gioumousis–Stevenson capture rate.24 | |||||
| 300 | 5.9 ± 1.5 | 2.46 | 53% | 0.08 ± 0.03 | 0.92 ± 0.03 |
| [3.9 ± 1.3] | [∼40%] | [<0.02] | [>0.98] | ||
| 400 | 6.2 ± 1.6 | 2.37 | 55% | 0.07 ± 0.02 | 0.93 ± 0.02 |
| 500 | 4.8 ± 1.2 | 2.34 | 43% | 0.05 ± 0.03 | 0.95 ± 0.03 |
| 600 | 4.4 ± 1.1 | 1.88 | 39% | 0.05 ± 0.04 | 0.95 ± 0.04 |
| 700 | 1.47 | ||||
III. Computational methods
For interpreting the experiments several computational approaches have been applied to provide a molecularly refined picture of the reactive step. One of them is based on statistical modeling within Rice–Ramsperger–Kassel–Marcus (RRKM) theory. A second one uses reactive MD simulations to determine thermal rates from explicit atomistic simulations.Reactive MD simulations were run either with CHARMM,25 using multisurface adiabatic reactive MD (MS-ARMD)26 or with the atomic simulation environment (ASE)27 when the neural network-learned potential energy surface (PES, see below) was used. It was found that certain parts of the reactive PES are sensitive to the level of the electronic structure calculations used. In order to provide a more comprehensive picture, the same quantities were determined from different methods and basis sets, ranging from density functional theory (DFT)-based approaches to CCSD(T) calculations. For a broader coverage of reaction products, DFT calculations were employed whereas the MgO+ + CH4 → MgOH+ + CH3 reaction itself was investigated with correlated methods. For a detailed study of the transition state region complete active space SCF (CASSCF) and CCSD(T) calculations were employed.
The choice of method depends primarily on which part of the PES was investigated. For the present system, DFT-based methods are effective for broadly sampling the PES and to assess the thermodynamics, while correlated methods (i.e. MP2) are still computationally effective for studying an individual reactive step based on a full-dimensional reactive PES. For a direct comparison with previous work,9 one PES was determined at the MP2/6-311G(2d,2p) level of theory whereas a second reactive PES was determined with a somewhat larger basis set (MP2/aug-cc-pVTZ) for direct comparison of the thermal rates k(T). Finally, higher-level methods (such as CCSD(T)) are best suited to investigate important details of the PES.
A. Statistical modeling
For the statistical modeling the stationary points along the reaction coordinate for MgO+ + CH4 were calculated at the TPSS0/TZVP level using Gaussian 0928 and the reported energies have been zero-point corrected employing harmonic frequencies. Stable intermediates and transition states were verified by the calculation of zero or a single imaginary harmonic frequency, respectively. Intrinsic reaction coordinate calculations verified the connections between stationary points.The calculated energies and vibrational and rotational frequencies along the reaction coordinate were inputs to statistical modeling of the reaction, described in detail elsewhere.29 Briefly, formation of an initial intermediate is determined using capture theory and the simplified statistical adiabatic channel model (SSACM),30,31 with reactant internal and collision energies varied over thermal distributions in a stochastic manner. Intermediates are assumed to be sufficiently long-lived that the fundamental statistical assumption of energy redistribution is met, and the fate of the intermediate determined by calculated unimolecular rate curves as a function of both energy and angular momentum, (E,J), for all exit channels.32,33 Importantly, ion–molecule reactions often involve barrierless formation of entrance complexes, leading to competition between a “loose” dissociation channel and a “tight” isomerization transition state; “loose” and “tight” states are affected differently by angular momentum, and proper consideration of J is necessary.34 The trajectories are followed until separated products are formed, reactants are re-formed, or an intermediate stabilized through collision with a buffer gas. The process is repeated until sufficient statistics have been accumulated, which typically requires 104 to 105 runs. The resulting calculated rate coefficients and product branching fractions are compared with the experimental data.
B. Reactive force fields
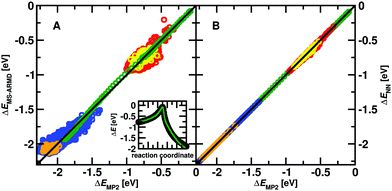
To parametrize the adiabatic barrier, the intrinsic reaction coordinate (IRC) of the reaction was also calculated at the MP2/6-311+G(2d,2p) level of theory. The structures along the IRC were extracted and their MS-ARMD energy evaluated. A genetic algorithm was used to parametrize the GAussian × POlynomial (GAPO) functions26 and to reproduce the energetics along the reaction path. While it is possible to correctly describe the transition between the van der Waals minimum (INT1) and the TS, see inset Fig. 1A, the energy between the reactant state (MgO+ + CH4) and INT1 is considerably underestimated. Compared with the value of −0.99 eV (−22.90 kcal mol−1) at the MP2/6-311+G(2d,2p) level of theory it is only −0.27 eV (−6.21 kcal mol−1) from the MS-ARMD parametrization. Hence, instead of a submerged barrier at the four-centered transition state (TS1) which can be reached from the reactant state, translational or internal energy is required for the reaction pathway: reactant → INT1 → TS1 → product.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures (validated on 5000 structures), randomly selected from a set of 154
000 structures (validated on 5000 structures), randomly selected from a set of 154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 structures calculated at the MP2/aug-cc-pVTZ level of theory. The correlation between the 4368 remaining structures (test set) and the predictions of the trained NN is R2 = 1–4.1 × 10−6, see Fig. S1 (ESI†). The dataset was constructed starting from 36
368 structures calculated at the MP2/aug-cc-pVTZ level of theory. The correlation between the 4368 remaining structures (test set) and the predictions of the trained NN is R2 = 1–4.1 × 10−6, see Fig. S1 (ESI†). The dataset was constructed starting from 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 structures for the CH4 + MgO+ and CH3+ + MgOH channels generated from simulations with the MS-ARMD force field, and then expanded using adaptive sampling38,39 similar to the procedure described in ref. 37. The NN constructs a descriptor vector for each atom which encodes information about its local chemical environment.40 The total energy of the system is obtained by combining ‘atomic energy contributions’ predicted from these descriptors. The NN is 10 layers deep with 64 neurons per layer.
063 structures for the CH4 + MgO+ and CH3+ + MgOH channels generated from simulations with the MS-ARMD force field, and then expanded using adaptive sampling38,39 similar to the procedure described in ref. 37. The NN constructs a descriptor vector for each atom which encodes information about its local chemical environment.40 The total energy of the system is obtained by combining ‘atomic energy contributions’ predicted from these descriptors. The NN is 10 layers deep with 64 neurons per layer.
C. Molecular dynamics simulations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), heated to the simulation temperature (12.5 ps), and equilibrated (12.5 ps). After a free dynamics (12.5 ps) for each system the centers of mass of the two molecules were positioned 13 Å apart (along the x-axis) and MgO+ was randomly rotated.
000 steps), heated to the simulation temperature (12.5 ps), and equilibrated (12.5 ps). After a free dynamics (12.5 ps) for each system the centers of mass of the two molecules were positioned 13 Å apart (along the x-axis) and MgO+ was randomly rotated.
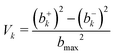 | (3) |
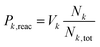 | (4) |
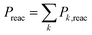 | (5) |
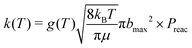 | (6) |
Simulations were performed for b = 0 to bmax (Δb = 0.5 Å) by accelerating the two molecules towards their common center of mass. As the MS-ARMD parametrization was unable to correctly describe the prereactive complex (see above), the energy difference between the MgO+ + CH4 asymptote and the prereactive complex (0.81 eV, 18.6 kcal mol−1) was included by scaling the velocities of all atoms accordingly, which amounts to an additional kinetic energy of ∼0.11 eV per atom, 2.5 (kcal mol−1) per atom of internal energy. This is akin to recent explorations of the Diels–Alder reaction between maleic acid and 2,3-dibromo-1,3-butadiene.17 A total of 3500 simulations per temperature were run with MS-ARMD, see Table S1 (ESI†).
For the simulations using the NN, two sets of simulations were run. In one of them, 3500 trajectories per temperature for tfin = 500 ps each, with drawing impact parameters b from a uniform distribution, see Table S2 (ESI†). For the second set, 1000 trajectories for each value of b, in intervals of 0.5 Å, at a given temperature was run for tfin = 50 ps using stratified sampling, see Tables S3 and S4 (ESI†). All these simulations were carried out with the ASE simulation environment,27 in the NVE ensemble and with Δt = 0.1 fs. The simulations were terminated after tfin or when the distance between the oxygen and carbon atom was larger than 15 Å. The upper limit (bmax) was determined from considering the opacity function, see Fig. 2 left inset.
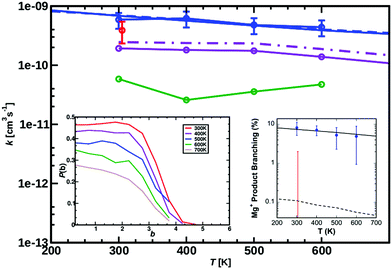 | ||
| Fig. 2 Measured rate coefficients (blue circles), and previously reported value (red circle)9 for reaction (1), MgO+ + CH4, from 300 to 600 K. Best-fit statistical modeling assuming TS1 as rate-limiting TS1 at −0.38 eV below the entrance channel (solid line) or capture limited (dashed line, barrier-independent). The Langevin limit is at 1.1 × 10−9 cm3 s−1 molecule−1. Calculated rate coefficients for temperatures from 300 to 700 K (ΔT = 100 K) MS-ARMD (green) and from the NN (solid violet line for Boltzmann rate and dashed dotted violet line for the capture rate). The TS from the NN lies −0.09 eV (−2.1 kcal mol−1) below the entrance channel, see black line in Fig. 8. The left inset reports the opacity function calculated from PhysNet at different temperatures. Right inset shows the measured product branching (blue circles), and modeled values (black solid and dashed lines). The previously reported upper limit (red error bar), is also shown. | ||
IV. Results and discussion
The measured rate coefficients and product branching fractions for reaction (1) are listed in Table 1 and shown in Fig. 2. The reaction proceeds at approximately half of the collision rate at 300 K and decreases ∝T−0.5±0.2. The current measurement is somewhat higher than, but not inconsistent with, the previously reported value.9 The reaction was found to primarily result in hydrogen atom transfer, although 8% of reactions proceeded by oxygen transfer resulting in the Mg+ + CH3OH product channel at 300 K. This is in mild disagreement with previous reports, which placed an upper limit of 2% branching to this channel at 300 K. The previous work also reports trace amounts of MgCH2+ + H2O which was not observed in the present experiments.9A. Statistical modeling
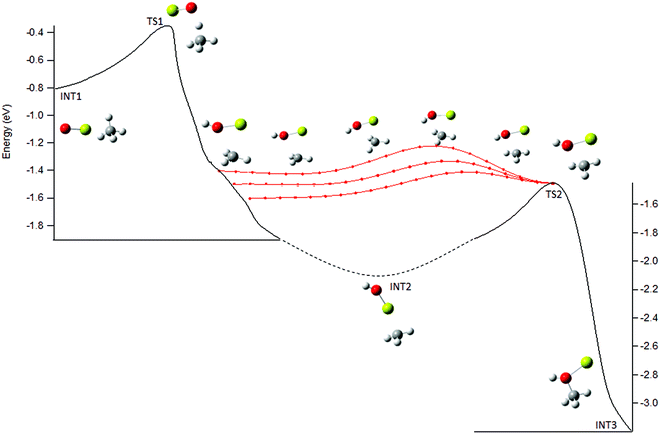
For the statistical modeling of the main reaction channels the relevant stationary points were calculated at the TPSS0/TZVP level, see Fig. 3. This profile is qualitatively consistent with that previously reported calculated at the MP2/6-311+G(2d,2p) level.9 The initial encounter complex formed is with the methane complexed to the metal, bound by 0.83 eV which is 0.43 eV (9.2 kcal mol−1) above the van der Waals complex, consistent with the results from the higher-level calculations. No other bound entrance complexes were identified. The reaction proceeds through a four-centered transition state (TS1) to an insertion complex (INT2) that is equivalent to a methyl bound to MgOH+. No TS corresponding to a direct activation of the C–H bond by end-on attack by the oxygen as mentioned in previous work,9 was identified; although the possibility of such a mechanism is discussed below. From INT2, competition occurs between direct dissociation into the MgOH+ + CH3 product, or traversing a transition state corresponding to a long range methyl migration (TS2) resulting in a deeply bound Mg–CH3OH+ (INT3) complex. INT3 can directly dissociate into either the Mg+ + CH3OH or the MgOH+ + CH3 product channels, with the former calculated to be preferred by 0.79 eV, just outside of agreement with experimentally derived reaction energetics of 0.57 ± 0.18 eV.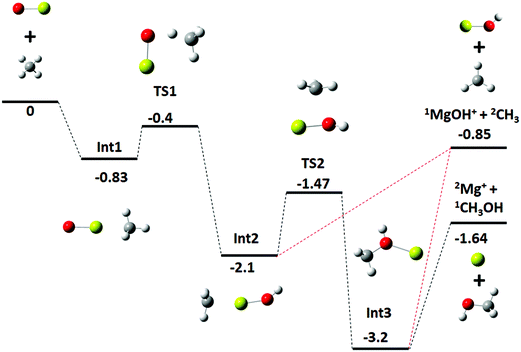 | ||
| Fig. 3 Energy profile for reaction (1), MgO+ + CH4, calculated at the TPSS0/TZVP level; calculated zero-point corrected energies (eV) are indicated for each stationary point. | ||
The experimental kinetics were compared to statistical modeling of the calculated reaction coordinate. Treating the MgO+ + CH4 association/dissociation into INT1 using phase-space theory (PST) and TS1 using RRKM theory models the total rate coefficients well (Fig. 2, solid blue line) by minimally adjusting the energy of TS1 to −0.38 ± 0.10 eV relative to reactants. The calculated lifetime of INT1 is ≫10−10 s at thermal energies, long enough that intra-molecular vibrational energy redistribution should likely be complete and the fundamental assumption of statistical theory valid. An alternative direct hydrogen abstraction channel was previously calculated to involve a TS 0.1 eV above TS1. That statistical behavior is expected based on the calculated INT1 lifetime along with the agreement between the experiment and the model suggests that the reaction does proceed statistically, primarily through TS1 at these energies. Still, it is possible that a smaller fraction proceeds by direct hydrogen abstraction although this channel is not included in the present model and the agreement between model and experiment without this channel supports its negligible impact on the results.
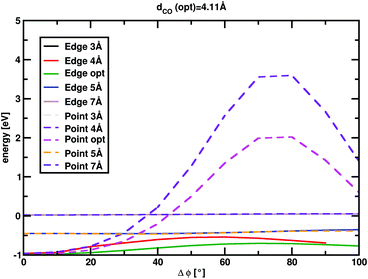
MgO+ + CH4 association/dissociation may proceed with rate coefficients below PST due to “rigidity” which is related to angular anisotropy of the potential along the dissociation coordinate.31 This is treated as an adjustable parameter in the following. The SSACM formalism is used to calculate unimolecular rate curves for loose dissociations from the PST-limit, where transitional modes are treated as product rotations, down to the RRKM-limit, where transitional modes are treated as fully conserved vibrations, as a function of a single “rigidity factor”. Increasing rigidity in the entrance channel necessarily lowers the modeled efficiency of the reaction as well as imparting a small negative temperature dependence due to the magnitude of the effect of rigidity increasing with energy. While lowering the energy of TS1 below −0.38 eV increases the reaction efficiency above the experiment, this increase may be compensated for by applying a rigidity factor (lowering the capture rate below the PST value) while maintaining a temperature dependence consistent with experiment. As a result, in the present case the modeling provides only an upper limit (−0.38 ± 0.1 eV) for the TS1 energy. In light of this, scans of the angular and dissociation coordinate were undertaken (Fig. 4). These results are not consistent with the large amount of anisotropy required to render this reaction capture controlled. Furthermore, previous work on very similar associations (FeO+, NiO+, and MnO+ with CH4) were all well modelled at the PST limit suggesting minimal, if any, impact of rigidity.11,12,22
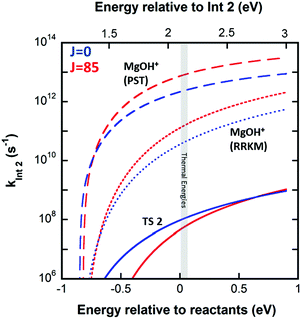
The product branching between reactions eqn (1) (leading to MgOH+) and eqn (2) (leading to Mg+) is determined by competition after the rate-limiting transition state (TS1). Fig. 5 displays several calculated rate curves for exiting INT2 at both J = 0 and J = 85. The latter is near the peak of the angular momentum distribution for this reaction at 300 K. For simplicity the rate curves shown are at the same energetic threshold, −0.85 eV relative to reactants. Three sets of curves are shown, (a) assuming a loose dissociation (bond fissure) by phase space theory, (b) dissociation at the RRKM limit (extremely tight), and (c) traversing the TS2 barrier. The PST curves (dashed) are orders of magnitude faster (∼104) than those for traversing TS2 (solid). This is independent of any adjustment to the various energetics. Such adjustments can be visualized by translating the curves left or right relative to each other. This modeling predicts essentially unit branching to MgOH+, inconsistent with the several percent of Mg+ observed. Increasing the “rigidity” of the dissociation bends the dissociation rate curve between the PST and RRKM limits shown in Fig. 5. Employing “rigidity” reduces the entropic preference of this channel over traversing TS2, see Fig. 5. However even at the RRKM-limit, less than 1% of products are predicted to form Mg+ without a significant energetic adjustment. In fact energy adjustments only are not sufficient to model the product branching observed. For this one must treat not only dissociation to the MgOH+ + CH3 product from INT2 at the RRKM limit, but from INT3 as well. Then the majority of complexes that make it to INT3 result in Mg+ + CH3OH formation.
Fig. 2 (right inset) reports the observed product branching as well as modeled predictions employing the RRKM limit for the dissociation to MgOH+ from both INT2 and INT3 while keeping the two channels isoenergetic at −0.85 eV relative to reactants (black dashed line). The product branching was only modeled well (right inset Fig. 2, black solid line) when further lowering the energy of TS2 to −1.55 eV, while the energies of both product channels are left as calculated. While this produces a suitable fit to the data, it remains unsatisfactory. Even treating dissociations to MgOH+ + CH3 from both INT2 and INT3 at the extreme of the RRKM limit, a good fit to the data requires that the energy of TS2 be no higher than −1.55 eV relative to reactants, which would suggest that TS2 is heavily stabilized (by at least 0.7 eV) relative to the MgOH+ + CH3 channel. This seems unlikely given that TS2 corresponds to a long range migration of the methyl group from the metal to the hydroxyl site, with minimal deformation to either the methyl or metal hydroxide unit, and would therefore be expected to be much closer to the energy of the MgOH+ + CH3 channel. While current DFT calculations have this TS lying 0.62 eV below this product channel, previous calculations using MP2 show them much closer to isoenergetic, with a difference of only 0.01 eV. Additionally, increasing the size of the basis set from TZVP to def2-TZVP or better accounting for long range interaction by using the CAM-B3LYP method raises the calculated energy of TS2 significantly. The parameters required to model the product branching under statistical assumptions appear possibly unphysical. This suggests that after passing TS1 the reaction may in fact proceed non-statistically.
Therefore, the potential surface in the post-transition state region was explored further. A shoulder along the IRC from TS1 to INT2 was observed with a structure very similar to that of TS2, see Fig. 6. The PES between this shoulder and TS2 was explored by incrementally adjusting a set of internal coordinates from several geometries along the IRC to those for TS2 (Fig. 6, red points). The PES in this region is rather flat providing an energetically feasible route directly to TS2 and thus INT3, effectively bypassing INT2, see Fig. 6. This feature could be a reaction path bifurcation (RPB), an example of post-transition state non-statistical dynamics. An RPB can be visualized as a ridge in the potential running from one TS to another, separating two valleys containing the intermediates.
The key kinetic step in determining the branching becomes the competition between following the minimum energy pathway to INT2, which would produce entirely the MgOH+ product, or traversing directly to TS2 and then INT3, where the competition between the two product channels is more robust. The presence of an RPB provides an explanation for why statistical assumptions are valid for reaction (1) prior to the rate-limiting TS1, but fail after that point. Calculation of the full potential surface in the region of TS1, INT2, TS2 coupled with quasiclassical trajectory calculations or exploration by direct dynamics calculations can verify the presence of an RPB for this system and provide a fuller exploration of the interesting non-statistical dynamics occurring.
B. Reactive MD simulations
The quality of the two reactive PESs is reported in Fig. 1 with a typical RMSD ∼ 0.04 eV (1 kcal mol−1) for the MS-ARMD PES and a much lower RMSD ∼ 10−4 eV (10−2 kcal mol−1) for the NN-trained PES. The IRC between Int1 and TS1 (inset in Fig. 1A) is well reproduced by the MS-ARMD PES. Note that the structures shown in Fig. 1B were not used for training the NN and act as an additional test set. The quality of the NN-fitted PES is evidently superior to that from the MS-ARMD fit in particular because globally, it correctly describes the relative energetics of the entrance channel, the van der Waals minimum (INT1) and TS. On the other hand, the MS-ARMD PES is computationally considerably more efficient.For the direct process MgO+ + CH4→ MgOH+ + CH3, reactive MD simulations have been carried out using the parametrized MS-ARMD PES. The rate coefficients for the investigated reaction for 300 to 600 K are shown in Fig. 2. Compared to experimental rates determined from electrospray ionization the results from MS-ARMD (5.9 × 10−11 cm−3 s−1 at 300 K) are about one order of magnitude smaller than previously experimentally determined k values (3.9 ± 1.3 × 10−10 cm−3 s−1 at 300 K),9 as well as the measured rates in the present work (5.9 × 10−10 cm−3 s−1 at 300 K; see Fig. 2). MS-ARMD simulations yield a mild T-dependence, in qualitative agreement with experiment.
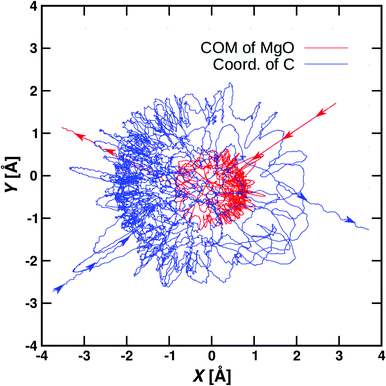
Using the NN-trained PES the temperature-weighted rate is about a factor of 5 smaller than that from experiment and the T-dependence follows the experimental rate. A typical reactive trajectory from such simulations is shown in Fig. 7. The NN also includes the possibility for dissociation to Mg+ + CH3OH which was indeed found for ∼10 out of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories. This is consistent, but not in quantitative agreement, with a low-probability channel found in the experiments, see Table 1. Considerably more statistics would be required for a direct comparison between experiment and simulations.
000 trajectories. This is consistent, but not in quantitative agreement, with a low-probability channel found in the experiments, see Table 1. Considerably more statistics would be required for a direct comparison between experiment and simulations.
Despite the different quality and shortcomings of the two PESs, simulations with both approaches (MS-ARMD and NN) underestimate the experiments and requires an explanation. Two possibilities are explored in the following: first the accuracy of the electronic structure calculations is considered and secondly the fact that a large fraction of the NN simulations is trapped in INT1 (3545, 700, 375, and 507 for T = 300, 400, 500, and 600 K, respectively) but could potentially react on longer time scales and thus contribute to the rate.
A difference of one order of magnitude in the rate corresponds to a change of ∼0.07 eV (∼1.5 kcal mol−1) in the relevant barrier assuming a single pathway and the validity of transition state theory. In other words, as all computed rates are smaller by that amount, the relevant barrier between INT1 and TS1 (see Fig. 1 and 3) for the reaction is probably overestimated from the electronic structure calculations. In order to better understand this, the energies for the stationary points were also determined at the CCSD(T)/aug-cc-pVTZ level of theory, see green trace in Fig. 8 which yields a barrier between INT1 and TS1 of 0.86 eV (19.8 kcal mol−1 reference energy to reactants) which is smaller than that at the MP2 level, but still overestimates the barrier height from analyzing the experimental rates (black dashed line in Fig. 8).
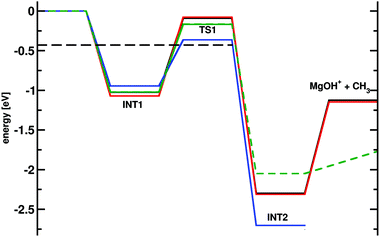 | ||
| Fig. 8 Potential energy surface (in eV) for the reaction of MgO+ with CH4 calculated at the MP2/6-311+G(2d,2p) (red) and MP2/aug-cc-pVTZ (black) levels of theory (see also Fig. 3 for comparison). Furthermore the results from CCSD(T)/aug-cc-pVTZ (green; solid from Gaussian0928 and dashed from Molpro43) and CASSCF/VDZ calculations (violet). The barrier height from statistical modeling of the experimental rates is the black dashed line. From INT2 the reaction can progress via a second TS and a stable intermediate, see Fig. 6. | ||
Typically, calculations at the CCSD(T) level of theory as employed here should provide accuracies better than 0.05 eV (1 kcal mol−1).44,45 Hence a difference of up to 0.22 eV (5 kcal mol−1) between the barrier height from analyzing experiment (−0.38 eV) and the computed one (ranging from MP2 = −0.07 eV to CCSD(T) = −0.17 eV) points towards another source of error. Hence, the T1 diagnostic as an indication for single- versus multi-reference character was considered.46 At the CCSD/aug-cc-pVTZ level of theory T1 of TS1 is 0.03 which exceeds the recommended value of 0.02 for single-reference character.46 For the reactant and product states the T1 diagnostic is considerably smaller than 0.02 and thus, a single-reference calculation should provide good results. At the CASSCF level of theory the TS structure is about 0.35 eV (8 kcal mol−1) below the entrance channel. This is consistent with the statistical modeling from the present work. Therefore, it is expected that including the multi-reference character of the wavefunction will lower the barrier and increase the rate, in agreement with the findings in Fig. 2.
For the present system the “gold standard” of quantum chemistry, i.e. CCSD(T), is not the method of choice due to its single reference character, in particular around TS1. Hence, for a better description of the energetics, a full-dimensional, reactive PES at the MRCI level of theory would be required which, given the system size, will be very challenging and is outside the scope of the present work. Such PESs have been recently determined for smaller, triatomic systems, e.g. for C + NO, N + NO or O + NO, for which such an approach is feasible.14,47
Next, for the reactive trajectories using the NN PES, the influence of the trajectories still trapped after 50 ps and 500 ps, respectively, in the van der Waals well on the total rate was quantified. Because the NN-PES supports the van der Waals, prereactive complex, an appreciable fraction of simulations still remain trapped there. The trapped fraction ranges from 90% at 300 K to 40% at 700 K, see Table S2 (ESI†). As the forward barrier (towards TS1) is lower than the reverse barrier (back to separated reactants) it is conceivable that an appreciable fraction of these trajectories will still react towards products, but on considerably longer time scales, due to IVR. Following previous work,48 the (unconverged) rate determined from NN-MD simulations was corrected by multiplying them with a Boltzmann factor 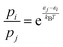 . Here, pi/pj is the ratio between the product and total probabilities, εj and εi are the energies of the entrance channel and the TS energy (1.02 eV and 0.93 eV), and kB and T the Boltzmann constant and the temperature, respectively. Correcting the rate determined from direct sampling yields rates on the order of ≈2.3 × 10−10, see Fig. 2 (solid violet for Boltzmann rate and solid dash-dotted for the capture rate), which agrees more favorably with the experimental rates, especially for low temperatures. The correction can also be considered as a way to extrapolate the rate from sampling a finite time interval to infinitely long simulations. Still, these rates are subject to the overestimation of the barrier between Int1 and TS1 due to the multireference character of TS1.
. Here, pi/pj is the ratio between the product and total probabilities, εj and εi are the energies of the entrance channel and the TS energy (1.02 eV and 0.93 eV), and kB and T the Boltzmann constant and the temperature, respectively. Correcting the rate determined from direct sampling yields rates on the order of ≈2.3 × 10−10, see Fig. 2 (solid violet for Boltzmann rate and solid dash-dotted for the capture rate), which agrees more favorably with the experimental rates, especially for low temperatures. The correction can also be considered as a way to extrapolate the rate from sampling a finite time interval to infinitely long simulations. Still, these rates are subject to the overestimation of the barrier between Int1 and TS1 due to the multireference character of TS1.
V. Conclusion
In this work, the temperature dependence of the rate coefficient and the product branching ratio for the reaction of MgO+ + CH4 have been determined from experiments and analyzed with reactive MD simulations (using MS-ARMD and a NN-trained PES) together with statistical modeling. The primary rate limiting step at thermal energies was confirmed to be a four-centered metal mediated C–H activation as had previously been postulated.9 With increasing temperature the thermal rate decreases slightly and formation of Mg+ reduces from 8% at 300 K to 5% at 700 K.The statistical modeling of the thermal rate yields a submerged barrier, −0.38 eV below the entrance channel. The product branching was only reproduced within the limits of the modeling with a significant stabilization of a TS corresponding to a long range methyl migration, as well as substantial “rigidity” imparted to dissociation into the MgOH+ + CH3 channel. Direct C–H activation by end on attack of the O atom9 was not found in the current calculations and the good agreement with experimental rates without this channel suggests minimal impact. Finally, calculations suggest the possibility of a post TS bifurcation in the potential surface which could be responsible for the observed product branching.
Thermal rates were also determined from atomistic simulations using two reactive force fields: one based on MS-ARMD and the other one using a NN trained on extensive reference data. The MS-ARMD simulations are run with excess collisional energy because the global PES can not describe the relative energetics of all states involved. The rates determined from MS-ARMD show a negative T-dependence, consistent with experiment, but are about one order of magnitude smaller. Rates from the simulations using the NN also show the correct, experimentally determined T-dependence and are smaller by about a factor of 5 compared with experiment. In terms of associated cost the more accurate NN is computationally more expensive (by a factor of ≈200 for a recently investigated reaction)17 to evaluate in MD simulations than MS-ARMD. Also, the number of reference structures required for the parametrization differs by about two orders of magnitude (5000 structures for MS-ARMD vs. 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for PhysNet). On the other hand, the NN clearly outperforms the parametrized FF in terms of quality. Nevertheless, MD simulations on both PESs come to similar conclusions which is reassuring. The MD simulations using the NN-trained PES also find formation of Mg+ but the fraction of these trajectories is much smaller than that observed experimentally.
000 for PhysNet). On the other hand, the NN clearly outperforms the parametrized FF in terms of quality. Nevertheless, MD simulations on both PESs come to similar conclusions which is reassuring. The MD simulations using the NN-trained PES also find formation of Mg+ but the fraction of these trajectories is much smaller than that observed experimentally.
Overall, by combining experiment and computational modeling a comprehensive understanding of the key step of thermal activation of methane by MgO+ was obtained. The rate limiting step involves a submerged barrier associated with a four-centered transition state as has been previously stipulated by calculations9 which leads to a negative temperature dependence of the rate. This is supported by the statistical modeling, the electronic structure calculations, and the reactive molecular dynamics simulations. The kinetics controlling the competition between energetically available product channels is poorly reproduced by statistical methods, possibly due to a bifurcation in the potential surface after the rate limiting step (TS1) leading to non-statistical behavior.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Swiss National Science Foundation through grants 200021-117810, 200020-188724, and the NCCR MUST (to M. M.) and by the Air Force Office of Scientific Research (AFOSR-19RVCOR042, to S. G. A.). B. C. S. and J. C. S. are supported by the National Research Council Research Associateship Program. S. G. A. received support in part through the Institute for Scientific Research of Boston College under Contract No. FA9453-10-C-0206.References
- G. A. Olah, Towards Oil Independence Through Renewable Methanol Chemistry, Angew. Chem., Int. Ed., 2013, 52(1), 104–107 CrossRef CAS PubMed
.
- W. S. Douglas, Catalysis: a step closer to a methanol economy, Nature, 2013, 495(7439), 54–55 CrossRef PubMed
.
- R. Palkovits, C. von Malotki, M. Baumgarten, K. Müllen, C. Baltes, M. Antonietti, P. Kuhn, J. Weber, A. Thomas and F. Schüth, Development of Molecular and Solid Catalysts for the Direct Low-Temperature Oxidation of Methane to Methanol, ChemSusChem, 2010, 3(2), 277–282 CrossRef CAS PubMed
.
- Y. Shiota and K. Yoshizawa, Methane-to-Methanol Conversion by First-Row Transition-Metal Oxide Ions: ScO+, TiO+, VO+, CrO+, MnO+, FeO+, CoO+, NiO+, and CuO+, J. Am. Chem. Soc., 2000, 122(49), 12317–12326 CrossRef CAS
.
- H. Schwarz, Chemistry with methane: Concepts rather than recipes, Angew. Chem., Int. Ed., 2011, 50(43), 10096–10115 CrossRef CAS PubMed
.
- J. Li, S. Zhou, J. Zhang, M. Schlangen, D. Usharani, S. Shaik and H. Schwarz, Mechanistic Variants in Gas-Phase Metal-Oxide Mediated Activation of Methane at Ambient Conditions, J. Am. Chem. Soc., 2016, 138(35), 11368–11377 CrossRef CAS PubMed
.
- H. Schwarz, Thermal hydrogen-atom transfer from methane: a mechanistic exercise Dedicated, in friendship and with admiration, to Yitzhak Apeloig and Sason Shaik, Chem. Phys. Lett., 2015, 629, 91–101 CrossRef CAS
.
- D. Schröder, Activation of Methane by Gaseous Metal Ions, Angew. Chem., Int. Ed., 2010, 49(5), 850–851 CrossRef PubMed
.
- D. Schröder and J. Roithová, Low-temperature activation of methane: it also works without a transition metal, Angew. Chem., Int. Ed., 2006, 45(34), 5705–5708 CrossRef PubMed
.
- T. Gensch, M. J. James, T. Dalton and F. Glorius, Increasing Catalyst Efficiency in C–H Activation Catalysis, Angew. Chem., Int. Ed., 2018, 57(9), 2296–2306 CrossRef CAS PubMed
.
- S. G. Ard, J. J. Melko, V. G. Ushakov, R. Johnson, J. A. Fournier, N. S. Shuman, H. Guo, J. Troe and A. A. Viggiano, Activation of Methane by FeO+: Determining Reaction Pathways through Temperature-Dependent Kinetics and Statistical Modeling, J. Phys. Chem. A, 2014, 118(11), 2029–2039 CrossRef CAS PubMed
.
- D. C. McDonald, B. C. Sweeny, S. G. Ard, J. J. Melko, J. E. Ruliffson, M. C. White, A. A. Viggiano and N. S. Shuman, Temperature and Isotope Dependent Kinetics of Nickel-Catalyzed Oxidation of Methane by Ozone, J. Phys. Chem. A, 2018, 122(33), 6655–6662 CrossRef CAS PubMed
.
- M. V. Ivanov, H. Zhu and R. Schinke, Theoretical investigation of exchange and recombination reactions in O(3P) + NO(2Π) collisions, J. Chem. Phys., 2007, 126(5), 054304 CrossRef CAS PubMed
.
- D. Koner, R. J. Bemish and M. Meuwly, The C(3P) + NO(X2Π) → O(3P) + CN(X2Σ+), N(2D)/N(4S) + CO(X1Σ+) reaction: rates, branching ratios, and final states from 15 K to 20000 K, J. Chem. Phys., 2018, 149(9), 094305 CrossRef PubMed
.
- P. J. S. B. Caridade, J. Li, V. C. Mota and A. J. C. Varandas, The O + NO(v) Vibrational Relaxation Processes Revisited, J. Phys. Chem. A, 2018, 122(24), 5299–5310 CrossRef CAS PubMed
.
- J. C. S. V. Veliz, D. Koner, M. Schwilk, R. J. Bemish and M. Meuwly, The N(4S) + O2(X3Σg−) ↔ O(3P) + NO(X2Π) Reaction: Thermal and Vibrational Relaxation Rates for the 2A2, 4A2 and 2A3 States, Phys. Chem. Chem. Phys., 2020, 22, 3927–3939 RSC
.
- U. Rivero, O. T. Unke, M. Meuwly and S. Willitsch, Reactive atomistic simulations of Diels-Alder reactions: The importance of molecular rotations, J. Chem. Phys., 2019, 151, 10 CrossRef PubMed
.
- N. Dalleska and P. Armentrout, Guided ion beam studies of reactions
of alkaline earth ions with O2, Int. J. Mass Spectrom., 1994, 134(2), 203–212 CrossRef CAS
.
- S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, Ion Energetics Data, In NIST Chemistry WebBook.
-
P. J. Linstrom and W. G. Mallar, NIST Chemistry Webbook, http://webbook.nist.gov Search PubMed
.
- T. Tian, X. Sun, T. Weiske, Y. Cai, C. Geng, J. Li and H. Schwarz, Reassessment of the Mechanisms of Thermal C-H Bond Activation of Methane by Cationic Magnesium Oxides: A Critical Evaluation of the Suitability of Different Density Functionals, ChemPhysChem, 2019, 20(14), 1812–1821 CrossRef CAS PubMed
.
- B. Sweeny, H. Pan, S. Ard, N. S. Shuman and A. A. Viggiano, On the Role of Hydrogen Atom Transfer (HAT) in Thermal Activation of Methane by MnO+: Entropy vs. Energy, Z. Phys. Chem., 2019, 233(6), 771–783 CAS
.
- B. C. Sweeny, S. G. Ard, A. A. Viggiano and N. S. Shuman, Reaction of Mass-Selected, Thermalized VnOm+ Clusters with CCl4, J. Phys. Chem. A, 2019, 123(23), 4817–4824 CrossRef CAS PubMed
.
- G. Gioumousis and D. P. Stevenson, Reactions of Gaseous Molecule Ions with Gaseous Molecules. V. Theory, J. Chem. Phys., 1958, 29, 294–299 CrossRef CAS
.
- B. R. Brooks, C. L. Brooks III, A. D. Mackerell Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, CHARMM: the biomolecular simulation program, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed
.
- T. Nagy, J. Y. Reyes and M. Meuwly, Multisurface Adiabatic Reactive Molecular Dynamics, J. Chem. Theory Comput., 2014, 10, 1366–1375 CrossRef CAS PubMed
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, K. James, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The Atomic Simulation Environment – A Python Library for Working with Atoms, J. Phys. Condens. Matter, 2017, 29(27), 273002 CrossRef PubMed
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, 2009 Search PubMed.
- B. C. Sweeny, S. G. Ard, D. C. McDonald II, O. Martinez Jr., A. A. Viggiano and N. S. Shuman, Discrepancy Between Experimental and Theoretical Predictions of the Adiabaticity of Ti+ + CH3OH, Chem. – Eur. J., 2017, 23(49), 11780–11783 CrossRef CAS PubMed
.
- W. Stevens, B. Sztáray, N. Shuman, T. Baer and J. Troe, Specific Rate Constants k(E) of the Dissociation of the Halobenzene Ions: Analysis by Statistical Unimolecular Rate Theories, J. Phys. Chem. A, 2009, 113(3), 573–582 CrossRef CAS PubMed
.
- J. Troe, Towards Simplified Thermal and Specific Rigidity Factors for Ion-Molecule Reactions and Ion Fragmentations, Z. Phys. Chem., 2009, 223, 347–357 CrossRef CAS
.
- M. Olzmann and J. Troe, Approximate determination of rovibrational densities of states ρ(E,J) and numbers of states W(E,J), Ber. Bunsenges. Phys. Chem., 1994, 98(12), 1563–1574 CrossRef CAS
.
-
M. Olzmann and J. Troe, Rapid Approximate Calculation of Numbers of Quantum States W(E,J) in the Phase Space Theory of Unimolecular Bond Fission Reactions, Ber. Bunsenges. Phys. Chem., 96, 10, 1327–1332, 1992 Search PubMed
.
- J. Troe, Rotational effects in complex-forming bimolecular reactions: Application to the reaction CH4 + O2+, Int. J. Mass Spectrom., 1987, 80, 17–30 CrossRef CAS
.
- V. Zoete, M. A. Cuendet, A. Grosdidier and O. Michielin, SwissParam: A Fast Force Field Generation Tool for Small Organic Molecules, J. Comput. Chem., 2011, 32(11), 2359–2368 CrossRef CAS PubMed
.
- J. Nelder and R. Mead, A simplex method for function minimization, Chem. Phys., 1965, 7, 308–313 Search PubMed
.
- O. T. Unke and M. Meuwly, PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges, J. Chem. Theory Comput., 2019, 15(6), 3678–3693 CrossRef CAS PubMed
.
- J. Behler, Representing potential energy surfaces by high-dimensional neural network potentials, J. Phys.: Condens. Matter, 2014, 26(18), 183001 CrossRef CAS PubMed
.
- Constructing high-dimensional neural network potentials: a tutorial review.
- O. T. Unke and M. Meuwly, A Reactive, Scalable, and Transferable Model for Molecular Energies from a Neural Network Approach Based on Local Information, J. Chem. Phys., 2018, 148(24), 241708 CrossRef PubMed
.
-
R. B. Bernstein, Atom-Molecule Collision Theory, Plenum Press, 1979 Search PubMed
.
- O. Denis-Alpizar, R. J. Bemish and M. Meuwly, Communication: vibrational relaxation of CO(1Σ) in collision with Ar(1S) at temperatures relevant to the hypersonic flight regime, J. Chem. Phys., 2017, 146(11), 1–5 CrossRef PubMed
.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS
.
- S. Parthiban, G. de Oliveira and J. M. L. Martin, Benchmark ab Initio Energy Profiles for the Gas-Phase SN2 Reactions Y− + CH3X → CH3Y + X− (X, Y = F, Cl, Br). Validation of Hybrid DFT Methods, J. Phys. Chem. A, 2001, 105(5), 895–904 CrossRef CAS
.
- F. Claeyssens, J. N. Harvey, F. R. Manby, R. A. Mata, A. J. Mulholland, K. E. Ranaghan, M. Schütz, S. Thiel, W. Thiel and H. J. Werner, High-accuracy computation of reaction barriers in enzymes, Angew. Chem., Int. Ed., 2006, 45(41), 6856–6859 CrossRef CAS PubMed
.
- T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36(S23), 199–207 CrossRef
.
- D. Koner, J. C. San Vicente Veliz, R. J. Bemish and M. Meuwly, Accurate reproducing kernel-based potential energy surfaces for the triplet ground states of N2O and dynamics for the N + NO ↔ O + N2 reaction, 2020, arXiv preprint arXiv:2002.02310.
- D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, Wave packet and statistical quantum calculations for the He + NeH + HeH+ + Ne reaction on the ground electronic state, J. Chem. Phys., 2014, 141(11), 114302 CrossRef PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00668h |
| ‡ Present address: Department of Chemistry – BMC, Uppsala University, BMC Box 576, 751 23 Uppsala, Sweden. |
| § Present address: Machine Learning Group, TU Berlin, Marchstr. 23, 10587 Berlin, Germany. |
| This journal is © the Owner Societies 2020 |