Benchmark ab initio and dynamical characterization of the stationary points of reactive atom + alkane and S_N2 potential energy surfaces

Abstract

We describe a composite ab initio approach to determine the best technically feasible relative energies of stationary points considering additive contributions of the CCSD(T)/complete-basis-set limit, core and post-CCSD(T) correlation, scalar relativistic and spin–orbit effects, and zero-point energy corrections. The importance and magnitude of the different energy terms are discussed using examples of atom/ion + molecule reactions, such as X + CH₄/C₂H₆ and X⁻ + CH₃Y/CH₃CH₂Cl [X, Y = F, Cl, Br, I, OH, etc.]. We test the performance of various ab initio levels and recommend the modern explicitly-correlated CCSD(T)-F12 methods for potential energy surface (PES) developments. We show that the choice of the level of electronic structure theory may significantly affect the reaction dynamics and the CCSD(T)-F12/double-zeta PESs provide nearly converged cross sections. Trajectory orthogonal projection and an Eckart-transformation-based stationary-point assignment technique are proposed to provide dynamical characterization of the stationary points, thereby revealing front-side complex formation in S_N2 reactions and transition probabilities between different stationary-point regions.

---

Gábor Czakó

Gábor Czakó received PhD at Eötvös University, Hungary (2007) and became a postdoctoral fellow at Emory University, USA (2008–2011), then a research associate at Eötvös University (2011–2015). He is currently an associate professor and the head of the MTA-SZTE Lendület Computational Reaction Dynamics Research Group at the University of Szeged. His current research involves PES developments, reaction dynamics, and ab initio thermochemistry. He received Polanyi Prize (2012), Junior Prima Prize (2012), DSc (2017), habilitation (2018), Bolyai Plaquette (2018), Science Prize of the Faculty (2018), and Momentum grant (2019) and published in Science, Science Advances, PNAS, Nature Chemistry, and Nature Communications.

Tibor Győri

Tibor Győri obtained his BSc and MSc degrees in chemistry at the University of Szeged, Szeged, Hungary, in 2016 and 2018, respectively. He took 1st place at the University Competition of Research Students and his MSc dissertation received the Excellence Prize of the Hungarian Chemical Society. He is currently a second-year PhD student at the University of Szeged in the group of Gábor Czakó. He is working on developing a program package for automatic construction of reactive potential energy surfaces.

Balázs Olasz

Balázs Olasz received his MSc degree in pharmaceutics at the University of Szeged, Szeged, Hungary, in 2014. In 2015 he joined the Computational Reaction Dynamics Research Group and started his PhD work under the supervision of Gábor Czakó. He studied the dynamics of the F^− + CH3I reaction using a new analytical potential energy surface. In 2018 he received a 6-month Richter Scholarship. In 2019 he defended his PhD dissertation based on 7 publications including high-profile papers in Chemical Science and Science Advances.

Dóra Papp

Dóra Papp received her PhD in theoretical chemistry at Eötvös University, Budapest, Hungary in 2017, then she joined Gábor Czakó's group as a postdoctoral researcher at the University of Szeged, Hungary. As an undergraduate student she did research in computational biochemistry to model protein aggregation and unfolding. She won the Scholarship of the Hungarian Republic, and completed a half-year-long research project at Chalmers University, Gothenburg, Sweden. During her PhD research she developed and applied a program which computes energies and lifetimes of ro-vibrational resonance states of polyatomic weakly-bound molecules. Her current research interest involves PES development and chemical reaction dynamics.

István Szabó

István Szabó obtained his PhD in theoretical chemistry at Eötvös University, Budapest, Hungary in 2016. As a member of the Czakó Group he focused on PES developments and reaction dynamics simulations of SN2 reactions. Subsequently, he joined Edina Rosta's group at King's College London, UK to gain expertise in QM/MM and Markov model-based analysis and enhanced sampling techniques. Supported by the Cavendish Laboratory at the University of Cambridge, UK he revealed key binding properties of cucurbit[n]uril “cages” for selective drug detection. Currently, István is working as senior cheminformatician at ChemPass Ltd on the development of an AI-driven drug discovery platform.

Viktor Tajti

Viktor Tajti received his BSc in molecular bionics engineering and MSc in info-bionics engineering at the University of Szeged, Szeged, Hungary, in 2017 and 2019, respectively. In 2018 he took 2nd place at the University Competition of Research Students. He is currently a first-year PhD student at the University of Szeged in the group of Gábor Czakó. He has implemented several computer codes used in the group and continues his undergraduate research on the dynamics of the F^− + CH3CH2Cl reaction.

Domonkos A. Tasi

Domonkos A. Tasi obtained his BSc and MSc degrees in chemistry at the University of Szeged, Szeged, Hungary, in 2015 and 2017, respectively. During his undergraduate studies he worked on an alternative interpretation of toxicity of metal oxide nanoparticles towards bacteria E. coli. Then he joined the Computational Reaction Dynamics Research Group and he is currently a third-year PhD student supervised by Gábor Czakó. In 2018 he received the National Young Talent Scholarship and in 2019 he obtained a Talent Scholarship in the PhD category. His current research focuses on benchmark ab initio and dynamics studies on SN2 reactions.

---

I. Introduction

Chemical thinking has been traditionally based on stationary structures of molecular systems. These stationary geometries (points) on a potential energy surface (PES) correspond to complexes (minima) and transition states (saddle points), which may play a key role in the dynamics and mechanisms of chemical reactions. Therefore, characterization of the structures and energies of these stationary points is essential to uncover reaction mechanisms, which is one of the main goals of chemistry.¹ The structure and energy of the transition state (TS) may determine the dynamics and outcome of a reaction, because reactant-like TSs (early barriers) are conveniently surmounted by faster collisions, whereas product-like late barriers prefer vibrational excitations to facilitate the reactivity.² Despite the key role of the stationary points of a reactive PES in chemistry, their experimental investigation is usually highly challenging or even impossible, because the complexes are often unstable and the transition states are not in equilibrium but sit at the top of an energy curve along the reaction coordinate. Some experimental insights can be obtained by advanced matrix isolation^3,4 or anion photo-electron spectroscopy (transition-state spectroscopy)^5–8 and crossed-beam scattering,^9,10 but the complete characterization of the stationary points requires theoretical work, which may guide, explain, and complement experiments.

Our group has investigated the dynamics and mechanisms and/or characterized the stationary points of several polyatomic reactive systems such as reactions of atoms (F, O, Cl, Br, and/or I) with methane¹¹ and ethane¹² as well as ions (F⁻, Cl⁻, Br⁻, I⁻, OH⁻, SH⁻, CN⁻, NH₂⁻, PH₂⁻) with methyl-,^13,14 ethyl-,¹⁵ and/or amino-halides.¹⁶ The story of our dynamics studies began with the atom + methane reactions, which have been investigated theoretically since the 90s by Espinosa-García and co-workers^17,18 based on semi-empirical PESs. In the 2000s a few ab initio-based analytical PESs were developed for the F and Cl + CH₄ reactions using different fitting strategies.^19–22 We reported our first analytical PES for the F + CH₄ reaction in 2009 (ref. 23) by fitting composite ab initio energies with the permutationally invariant polynomial approach.^24,25 Using the same strategy we also developed ab initio PESs for the Cl, O, and Br + CH₄ reactions in 2011, 2012, and 2013, respectively.^26–28 Reaction dynamics simulations on these PESs could be compared with experiments of prominent groups of Nesbitt,²⁹ Crim,³⁰ Zare,³¹ Yang,³² and Liu^33,34 and motivated PES developments by Manthe³⁵ and Zhang³⁶ and their co-workers. Our simulations²⁶ provided cold HCl rotational distributions in agreement with experiment³⁷ for the first time, new insights into the Polanyi rules for polyatomic processes,^26,38 rotational mode-specificity,^39,40 and angular dependence of a TS barrier height.¹⁰ In the case of S_N2 reactions one usually finds direct dynamics studies in the literature, where especially Hase and co-workers^41,42 have remarkable achievements. In 2013 we reported⁴³ the first high-level ab initio analytical PES for a S_N2 reaction (F⁻ + CH₃Cl) and investigated its dynamics with the quasiclassical trajectory (QCT) method. Later we also developed analytical PESs for the F⁻ + CH₃F and CH₃I reactions and several other PESs are currently under development in our group.^44,45 These analytical PESs played a key role in the discovery of the double-inversion mechanism,^46,47 characterization of front-side complex formation,⁴⁸ quantum dynamics computations,⁴⁹ and comparisons with experiments.^50,51 The new findings motivated other theoretical groups; thus, Hase and co-workers⁵² showed that double inversion is a non-intrinsic-reaction-coordinate pathway and Wang and co-workers^53,54 identified this mechanism in aqueous solutions.

The theoretical study of chemical reactions begins with the ab initio characterization of the stationary points, which guides the full-dimensional analytical PES developments and the QCT⁵⁵ and/or quantum dynamics^56–60 simulations. We aim to provide the best technically feasible structures and relative energies of the stationary points utilizing sophisticated composite ab initio approaches. The composite electronic structure techniques combine different methods and basis sets to compute the most accurate results with affordable computational time. Our work uses the ideas of the focal-point analysis (FPA) approach,^61,62 which, unlike the black-box type ab initio thermochemistry protocols such as CBS-n,⁶³ Gn,⁶⁴ Wn,⁶⁵ HEAT,⁶⁶etc., does not prescribe which specific methods and bases have to be used, but FPA suggests a 2-dimensional extrapolation scheme over methods (HF, MP2, CCSD, …) and basis sets (DZ, TZ, QZ, …) augmented with auxiliary corrections such as core correlation, relativistic effects, diagonal Born–Oppenheimer correction,⁶⁷ and zero-point vibrational energy. In our benchmark studies we combine the ideas of the FPA approach and the benefits of the novel explicitly-correlated F12 correlation methods^68,69 to obtain the most accurate structures and relative energies of the stationary points characterizing PESs of chemical reactions. In Section II we describe the details of this benchmark composite ab initio approach highlighting examples from our own work. In Section III we briefly provide insight into the mechanisms of several atom/ion + molecule reactions revealed by the stationary-point properties. In the following sections we address three questions which are rarely investigated. (1) The performance of ab initio methods and basis sets are usually tested at stationary points and/or along potential energy curves of diatomic molecules, whereas global PESs cover configurations far from the stationary geometries. Therefore, in Section IV we investigate the accuracy of different ab initio levels of theory at non-stationary geometries, thereby guiding PES developments.⁷⁰ (2) In Section V we show how the choice of the electronic structure theory affects the dynamics of a chemical reaction.⁷¹ (3) Finally, in Section VI we review our numerical methods to uncover the role of the stationary points in the dynamics.^48,72 Our perspectives end with summary and conclusions in Section VII.

II. Benchmark ab initio thermochemistry

A. Structures

We usually compute the benchmark stationary-point structures using the explicitly-correlated CCSD(T)-F12b method⁶⁹ with the aug-cc-pVTZ basis set.⁷³ For Br and I small-core relativistic effective core potentials with the corresponding pseudo-potential aug-cc-pVTZ-PP basis sets⁷⁴ are employed. Nowadays, CCSD(T)-F12b/aug-cc-pVTZ geometries can be obtained using the MOLPRO program package⁷⁵ for systems as large as F⁻ + CH₃CH₂Cl as we reported¹⁵ in 2017. The excellent basis-set convergence of the CCSD(T)-F12b method is demonstrated in Fig. 1 showing the structural parameters of the pre- (PREMIN) and post-reaction (POSTMIN) complexes and the Walden-inversion TS of the Cl⁻ + CH₃I reaction obtained by CCSD(T)-F12b as well as traditional CCSD(T) with the aug-cc-pVnZ (n = D, T, Q) basis sets.⁷⁶ As seen, in most cases, especially for the intramolecular distances, the CCSD(T)-F12b/aug-cc-pVTZ bond lengths agree with the QZ results within 0.001 Å, whereas the traditional CCSD(T) method gives much larger uncertainty. For example, the C–I distance at PREMIN is 2.182 (DZ), 2.185 (TZ), and 2.185 (QZ) Å with CCSD(T)-F12b, whereas the corresponding CCSD(T) values are 2.222, 2.193, and 2.189 Å, respectively. At the TS the C–I distances are 2.578(2.620), 2.577(2.584), and 2.576(2.579) Å with CCSD(T)-F12b(CCSD(T))/aug-cc-pVnZ, where n = D, T, and Q, respectively, showing again the excellent convergence of the CCSD(T)-F12b method. The advantage of the CCSD(T)-F12b method can be further supported by the fact that the CPU time of the CCSD(T) and CCSD(T)-F12b computations are similar, and both increase by about an order of magnitude as the basis size increases from n to n + 1.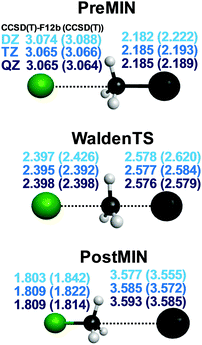

Fig. 1 Distance parameters (Å) of three representative stationary points of the Cl⁻ + CH₃I reaction obtained with the CCSD(T)-F12b and CCSD(T) (in parenthesis) methods using the aug-cc-pVnZ [n = D, T, Q] basis sets.⁷⁶

B. Approaching the CCSD(T)/CBS limit

In order to determine the best technically feasible relative energies of the stationary points, we perform single-point energy computations at the most accurate, usually CCSD(T)-F12b/aug-cc-pVTZ, geometries. Our first goal is to approach the CCSD(T)/complete-basis-set (CBS) limit. The traditional FPA route^61,62 is to perform HF,⁷⁷ MP2,⁷⁸ CCSD,⁷⁹ and CCSD(T)⁸⁰ computations with the aug-cc-pVnZ, where n = D, T, Q,… basis sets, and extrapolate the HF energy and the correlation energy increments to the CBS limits. For extrapolation usually 2-parameter asymptotic formulae^81,82 are employed which give the best CBS estimates if the largest basis-set results are used. Note that for HF extrapolation traditionally a 3-parameter expression⁸³ was used, but recent benchmark studies⁸⁴ showed that a 2-parameter formula⁸¹ provides slightly better CBS results. The energies obtained by different methods and basis sets are collected into a table, whose focal point is the “best method”/CBS result. The lower-level computations involved in the FPA tables help to estimate the uncertainty of the final result, which is an important and useful feature of the FPA analysis. The convergence of the HF, MP2, CCSD, and CCSD(T) relative energies of the stationary points of Fig. 1 with respect to the n = D, T, Q, and 5 basis sets, and their extrapolated CBS limits are shown in Fig. 2. In all cases the electron correlation effects are significant, as the HF method provides errors of about 3–5 kcal mol⁻¹ relative to the CCSD(T) energies. In most cases MP2 outperforms the CCSD method, but for the TS the MP2 results still have differences larger than 1 kcal mol⁻¹ relative to CCSD(T). The HF method usually approaches its CBS limit fast, because HF converges exponentially with respect to n.⁸⁵ For PREMIN and WaldenTS the basis set dependence of the correlation methods is also not significant, whereas the depth of the POSTMIN well, relative to the reactants, increases by about 2 kcal mol⁻¹ as n goes from 2 to 5. The CCSD(T)/5Z results approach the CCSD(T)/CBS limits within 0.5 kcal mol⁻¹ in all cases.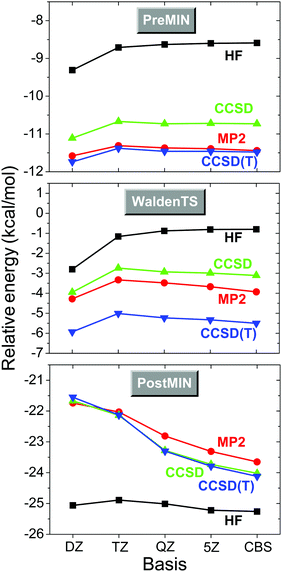

Fig. 2 Convergence of the energies, relative to those of the reactants, of three representative stationary points of the Cl⁻ + CH₃I reaction (see structures in Fig. 1) with respect to the methods (HF, MP2, CCSD, CCSD(T)) and basis sets (aug-cc-pVnZ, n = D, T, Q, 5, and CBS, complete basis set).⁷⁶

Fig. 3 compares the basis-set convergence of the standard CCSD(T) and the explicitly-correlated CCSD(T)-F12b methods for all the stationary points of the Cl⁻ + CH₃I system. As seen, the standard CCSD(T) method gives large errors of 2–3 kcal mol⁻¹ for POSTMIN and I⁻ + CH₃Cl products when DZ and TZ bases are used, whereas CCSD(T)-F12b is converged within 1 kcal mol⁻¹. Furthermore, the CCSD(T)-F12b/aug-cc-pVQZ level usually agrees with the CBS limit within about 0.2 kcal mol⁻¹ and the agreement is never worse than 0.5 kcal mol⁻¹, unlike in the CCSD(T) case. Thus, the explicitly-correlated CCSD(T)-F12b/aug-cc-pVQZ computations may replace the traditional CCSD(T) CBS extrapolations for chemically accurate (with uncertainty less than 1 kcal mol⁻¹) benchmark energy determinations. More detailed and critical comparisons of the convergence of the standard and F12 correlation methods can be found in ref. 86–88. We note that we usually use the F12b variant of the explicitly-correlated CCSD(T) method, because previous studies^89,90 showed that CCSD(T)-F12b has more monotonic basis set convergence behavior than the CCSD(T)-F12a method, though the two methods give very similar results.⁷⁰

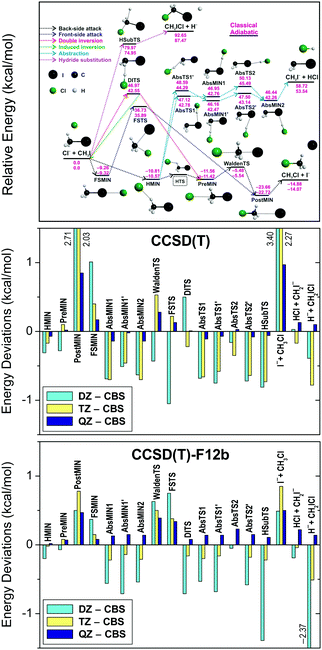Fig. 3 Deviations of the relative energies of the Cl⁻ + CH₃I stationary points (for notations see the upper panel showing the schematic potential energy surface) obtained with the CCSD(T) and CCSD(T)-F12b methods using the aug-cc-pVnZ [n = D, T, Q] basis sets with respect to the CCSD(T)/complete-basis-set (CBS) results.⁷⁶

C. Core and post-CCSD(T) correlations

The usual frozen-core electron correlation computations correlate the valence electrons only. The core–core and core–valence correlation effects can be taken into account by computing the difference between all-electron and frozen-core energies obtained by using the same basis set. We often determine the core-correlation effects using CCSD(T) or CCSD(T)-F12b with the aug-cc-pwCVTZ or cc-pCVTZ-F12 basis sets,^91,92 respectively.

Electron correlation contributions beyond the gold-standard CCSD(T) can be computed by the MRCC program⁹³via the CCSDT,⁹⁴ CCSDTQ,⁹⁵etc. and the CCSDT(Q),⁹⁶ CCSDTQ(P),⁹⁶etc. methods. In practice, we perform CCSD(T), CCSDT, and CCSDT(Q) computations with a double-zeta basis and calculate the post-CCSD(T) energy increments as δ[CCSDT] = CCSDT − CCSD(T) and δ[CCSDT(Q)] = CCSDT(Q) − CCSDT.

The core and post-CCSD(T) correlation effects for the stationary points of several systems, such as Cl⁻ + CH₃I (ref. 76), OH⁻ + CH₃Y (ref. 97), and X + C₂H₆ (ref. 12) [X, Y = F, Cl, Br, I], are shown in Fig. 4. Both effects have similar magnitudes of a few tenths of kcal mol⁻¹. The δ[CCSDT] and δ[CCSDT(Q)] contributions almost always have the same signs, whereas the core corrections usually have opposite signs, thereby partially canceling each other. However, for most of the S_N2 product channels and for the Br/I + C₂H₆ stationary points the core and post-CCSD(T) corrections have the same signs, resulting in additive energy effects of around 1–2 kcal mol⁻¹, which are clearly not negligible if sub-chemical accuracy is desired.

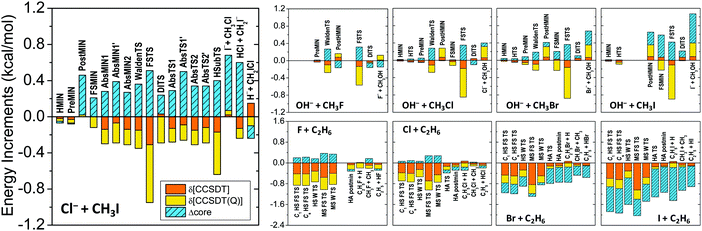Fig. 4 Post-CCSD(T), δ[CCSDT] = CCSDT − CCSD(T) and δ[CCSDT(Q)] = CCSDT(Q) − CCSDT, and core correlation (Δ_core) contributions to the relative energies of the stationary points of the Cl⁻ + CH₃I, OH⁻ + CH₃Y, and X + C₂H₆ [X, Y = F, Cl, Br, I] reactions. For computational details see ref. 76, 97, and 12, respectively. Stationary-point notations are shown in Fig. 3 (Cl⁻ + CH₃I) and Fig. 7 (X + C₂H₆). For OH⁻ + CH₃Y the notations mean H-bonded pre-reaction complex (HMIN), TS between HMIN and PreMIN (HTS), pre-reaction ion–dipole complex (PreMIN), Walden-inversion TS (WaldenTS), CH₃OH⋯Y⁻ complex (PostHMIN), front-side complex (FSMIN), front-side attack TS (FSTS), and double-inversion TS (DITS).

D. Scalar and spin–orbit relativistic effects

Scalar relativistic effects are usually smaller than the core correlation corrections as shown in Section IV. For Br and I the scalar relativistic effects are approximated by the effective core potentials (ECPs).⁷⁴ For lighter atoms we usually neglect this small effect or perform all-electron relativistic computations using the second-order Douglas–Kroll (DK)⁹⁸ Hamiltonian. For the Br + CH₄ system we showed that the ECP and the DK computations provide similar results.²⁸

Spin–orbit (SO) coupling may be substantial for some open-shell atoms and radicals, which can be computed using the Breit–Pauli operator in the interacting-states approach.⁹⁹ The different electronic states needed to set up the SO matrix can be obtained by multi-configurational self-consistent field (MCSCF)¹⁰⁰ or multi-reference configuration interaction (MRCI)¹⁰¹ methods. In our studies we investigated the reactions of water,¹⁰² methane,¹¹ and ethane¹² with halogen atoms, where SO effects can be significant in the entrance channel. We found that MRCI+Q/aug-cc-pVDZ computations, where +Q denotes the Davidson correction,¹⁰³ with a minimal active space provide reasonably accurate SO corrections.¹⁰² In a relativistic computation the ground electronic state of the halogen atom (²P) is split into a SO ground (²P_3/2) and a SO (²P_1/2) excited state. As the halogen atom approaches a molecule the ²P_3/2 state splits into a reactive ground state (SO₁) and a non-reactive excited state (SO₂), as shown for Cl + C₂H₆ in Fig. 5. Both SO₁ and SO₂ potentials feature van der Waals wells and then SO₁ merges into the reactive non-SO ground state and SO₂ approaches the non-SO excited state, which does not correlate with ground-state products. The other excited SO state (SO₃) correlating to ²P_1/2 also approaches the non-reactive non-SO excited state. The SO coupling significantly affects the depths of the van der Waals wells in the entrance channel, but the effects are quenching or partially quenching at the other stationary points, depending on the SO value and the proximity of the stationary point to the reactants. As also shown in Fig. 5, the largest effects are found for the TSs of the I + C₂H₆ reaction, usually 12–20%, because SO coupling is the strongest for I among halogens, and for the reactant-like hydrogen-abstraction TS of the F + C₂H₆ system, because here the electronic structure of the F atom is only slightly perturbed.¹² For the products and product-like minima the SO effects are negligible.

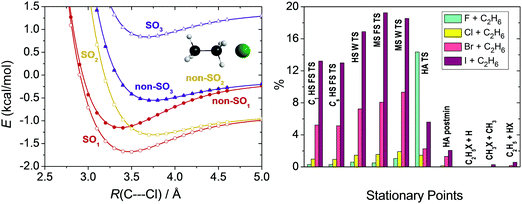Fig. 5 Potential energy curves obtained at the MRCI+Q(5,3)/aug-cc-pVDZ level as a function of the C₂H₆⋯Cl C_3v separation (left panel).¹² Deviation in percent between the computed energy difference of the spin–orbit (SO₁) and non-spin–orbit (non-SO₁) ground states regarding each stationary points (see Fig. 7 for notations) of the X + C₂H₆ [X = F, Cl, Br, I] reactions and the 1/3 of the experimental SO splitting of the halogen atoms (right panel).¹²

E. Zero-point energy corrections

In order to compute relative energies which are comparable with experiment the zero-point energy (ZPE) corrections have to be determined. We usually perform harmonic frequency computations with the CCSD(T)-F12b method using double- or triple-zeta basis sets depending on the size of the system. Harmonic ZPE corrections are shown for the stationary points of the X + C₂H₆ [X = F, Cl, Br, I] reactions in Fig. 6. As seen, the ZPE corrections are substantial, in the range of 2–6 kcal mol⁻¹ for most cases, especially for non-reactant-like structures. Therefore, it is clear that the ZPE effects have to be considered if chemical accuracy is desired. Anharmonicity may cause about 5% uncertainty, which is usually less than 0.1–0.3 kcal mol⁻¹. If the experiments are performed at non-zero temperature, e.g. 298 K, thermal corrections also have to be calculated considering temperature-dependent electronic, translational, vibrational, and rotational enthalpy changes, as, for example, we did for the F + CH₄ → HF + CH₃ reaction in ref. 23.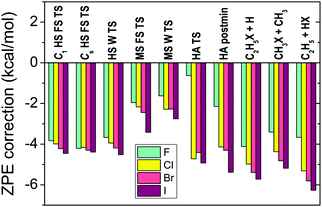

Fig. 6 Harmonic zero-point-energy corrections, obtained at CCSD(T)-F12b/aug-cc-pVDZ, to the relative energies corresponding to the different stationary points (see Fig. 7 for notations) of the X + C₂H₆ [X = F, Cl, Br, I] reactions.¹²

F. Composite energy

Once the above-described energies and their auxiliary corrections are computed at the benchmark structures (see II. A), we can determine the high-accuracy relative energies of the stationary points as

CCSD(T)/CBS + Δ_core + δ[CCSDT] + δ[CCSDT(Q)] + Δ_rel + Δ_SO + Δ_ZPE, (1)

where CCSD(T)/CBS (see II. B) is improved with additive corrections of core correlation (Δ_core, see II. C), post-CCSD(T) correlation contributions (δ[CCSDT] and δ[CCSDT(Q)], see II. C), scalar relativity (Δ_rel, see II. D), spin–orbit couplings (Δ_SO, see II. D), and zero-point energies (Δ_ZPE, see II. E).

G. Comparison with experiment

As mentioned in the Introduction, experimental determination of the relative energies of the stationary points is usually not feasible, except for the products (reaction enthalpies). Thus, the computed ZPE-corrected (adiabatic) relative energies can be compared with 0 K reaction enthalpies. In Table 1 we collected our computed benchmark adiabatic reaction energies and the available experimental results obtained from the 0 K heat of formation data of the Active Thermochemical Tables (ATcT).^104,105 As seen, for the 31 different atom/ion + molecule reactions, theory agrees with experiment with a root-mean-square deviation of only 0.34 kcal mol⁻¹, and the largest discrepancy (0.86 kcal mol⁻¹), where experiment has a substantial uncertainty of ±0.48 kcal mol⁻¹, is still below 1 kcal mol⁻¹. Thus, this comparison demonstrates that modern ab initio theory is capable to reproduce experiment within chemical accuracy, thereby confirming the accuracy of the theoretical predictions of the experimentally not available chemical properties. Note, that if static electron correlation is significant for a stationary point, which is not the case for the systems considered in the present study, multi-reference methods should be used to achieve high accuracy.

Table 1 Comparison between the best available experimental and our computed benchmark 0 K reaction enthalpies, given in kcal mol⁻¹, for several atom/ion + molecule reactions

Reaction	Ref.^a	Theory^a	Experiment^b	Δ
a Benchmark ab initio reaction enthalpies taken from the given references. b Data obtained from the latest version (1.122e)^104 of the Active Thermochemical Tables (ATcT).^105 Uncertainties are derived from the uncertainties of each 0 K enthalpy of formation given in ATcT using the Gaussian error-propagation law. c Absolute energy differences (in kcal mol^−1) between theory and experiment. d Obtained from the non-SO benchmark classical energy of 5.32 kcal mol^−1 (ref. 27), ΔZPE(CCSD(T)-F12b/aug-cc-pVTZ) of −4.08 kcal mol^−1, and ΔSO of +0.02 kcal mol^−1. e Obtained from the benchmark classical energy of −18.07 kcal mol^−1 (ref. 15) and a corrected ΔZPE of −4.06 kcal mol^−1.
F + CH4 → HF + CH3	23	−32.03	−31.91 ± 0.03	0.12
O + CH4 → OH + CH3	27	1.26^d	1.63 ± 0.02	0.37
Cl + CH4 → H + CH3Cl	106	20.86	21.11 ± 0.05	0.25
Cl + CH4 → HCl + CH3	106	1.03	1.15 ± 0.02	0.12
Br + CH4 → HBr + CH3	28	16.95	16.86 ± 0.04	0.09
F + C2H6 → H + C2H5F	12	−12.57	−11.98 ± 0.09	0.59
F + C2H6 → CH3 + CH3F	12	−21.10	−20.68 ± 0.07	0.42
F + C2H6 → HF + C2H5	12	−36.25	−35.98 ± 0.07	0.27
Cl + C2H6 → H + C2H5Cl	12	15.74	16.22 ± 0.07	0.48
Cl + C2H6 → CH3 + CH3Cl	12	5.57	5.72 ± 0.06	0.15
Cl + C2H6 → HCl + C2H5	12	−3.01	−2.92 ± 0.07	0.09
Br + C2H6 → H + C2H5Br	12	29.78	29.89 ± 0.07	0.11
Br + C2H6 → CH3 + CH3Br	12	19.29	18.96 ± 0.06	0.33
Br + C2H6 → HBr + C2H5	12	13.21	12.79 ± 0.08	0.42
I + C2H6 → H + C2H5I	12	44.14	44.44 ± 0.12	0.30
I + C2H6 → CH3 + CH3I	12	32.86	32.38 ± 0.06	0.48
I + C2H6 → HI + C2H5	12	29.50	28.89 ± 0.07	0.61
F^− + CH3Cl → HF + CH2Cl^−	46	25.24	26.10 ± 0.48	0.86
F^− + CH3Cl → Cl^− + CH3F	46	−30.92	−31.27 ± 0.08	0.35
F^− + CH3I → I^− + CH3F	45	−45.16	−45.16 ± 0.07	0.00
Cl^− + CH3I → I^− + CH3Cl	76	−14.07	−13.89 ± 0.06	0.18
F^− + CH3CH2Cl → Cl^− + HF + C2H4	15	−22.13^e	−22.22 ± 0.07	0.09
F^− + CH3CH2Cl → Cl^− + CH3CH2F	15	−33.18	−33.07 ± 0.11	0.11
OH^− + CH3F → F^− + CH3OH	97	−17.78	−17.79 ± 0.07	0.01
OH^− + CH3Cl → Cl^− + CH3OH	97	−49.08	−49.06 ± 0.06	0.02
OH^− + CH3Br → Br^− + CH3OH	97	−56.55	−56.56 ± 0.06	0.01
OH^− + CH3I → I^− + CH3OH	97	−62.67	−62.95 ± 0.06	0.28
NH2^− + CH3F → F^− + CH3NH2	14	−34.46	−34.72 ± 0.12	0.26
NH2^− + CH3Cl → Cl^− + CH3NH2	14	−66.18	−65.99 ± 0.11	0.19
NH2^− + CH3Br → Br^− + CH3NH2	14	−73.92	−73.49 ± 0.11	0.43
NH2^− + CH3I → I^− + CH3NH2	14	−80.43	−79.88 ± 0.11	0.55

---

III. Applications to atom/ion–molecule reactions

We applied the above-described benchmark ab initio composite techniques to characterize the stationary points of several atom + methane/ethane^11,12 and ion + methyl/ethyl-halide^13–15 reactions. As examples, Fig. 7 and 8 show schematic PESs of the X + C₂H₆ [X = Cl] (ref. 12) and F⁻ + CH₃CH₂Cl (ref. 15) reactions, respectively. The main reaction pathways are hydrogen abstraction and S_N2 leading to HX + C₂H₅ and Cl⁻ + CH₃CH₂F, respectively. The entrance channel of the X + CH₄/C₂H₆ [X = F, Cl, Br, I] reactions features shallow van der Waals wells with depths of 1 kcal mol⁻¹ (Fig. 5), whereas in the case of S_N2 reactions the ion–dipole complexes can be below the reactants by 18 kcal mol⁻¹, as shown in Fig. 8. For X + C₂H₆ substitution is a higher-energy channel via barriers between 20 and 80 kcal mol⁻¹ depending on X and the leaving group. Besides H substitution, found for X + CH₄ reactions as well,^106,107 for X + C₂H₆ CH₃ substitution can also occur.¹² Both product channels can be obtained via the usual Walden-inversion mechanism or through a front-side attack retention pathway as shown in Fig. 7. Front-side attack TS is also found for S_N2 reactions, with a classical barrier of 30.0 kcal mol⁻¹ for F⁻ + CH₃CH₂Cl, whereas the Walden-inversion TS is submerged by 11.3 kcal mol⁻¹. For S_N2 reactions our dynamics simulations revealed a new double-inversion retention pathway,⁴⁶ initiated by a proton-abstraction induced inversion followed by a second inversion via the Walden-inversion TS. For the first step of the double-inversion process we found a TS, which, in the case of F⁻, OH⁻, and NH₂⁻ nucleophiles, is below the front-side attack TS,^14,97 thereby opening the lowest energy retention pathway for several S_N2 reactions. (For F⁻ + CH₃CH₂Cl the double-inversion classical barrier height is 20.7 kcal mol⁻¹, as seen in Fig. 8.) Unlike for the S_N2 reactions of methyl-halides, for ethyl-halide systems, bimolecular elimination (E2) leading to, for example, Cl⁻ + HF + C₂H₄ (Fig. 8) can also occur via syn and anti pathways in competition with the S_N2 channel.^15,108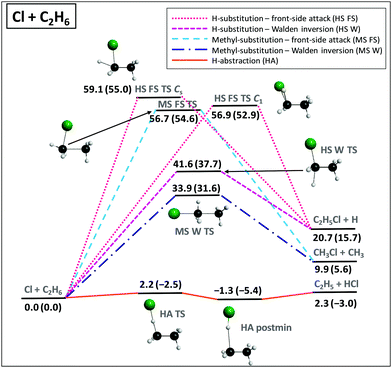

Fig. 7 Schematic potential energy surface showing the benchmark classical (adiabatic) relative energies, in kcal mol⁻¹, of the stationary points along the different pathways of the Cl + C₂H₆ reaction.¹² The classical energies are obtained as UCCSD(T)-F12b/aug-cc-pVQZ + Δ_core[UCCSD(T)/aug-cc-pwCVTZ] + UCCSDT(Q)/cc-pVDZ – UCCSD(T)/cc-pVDZ + Δ_SO and the adiabatic energies include Δ_ZPE[UCCSD(T)-F12b/aug-cc-pVDZ].

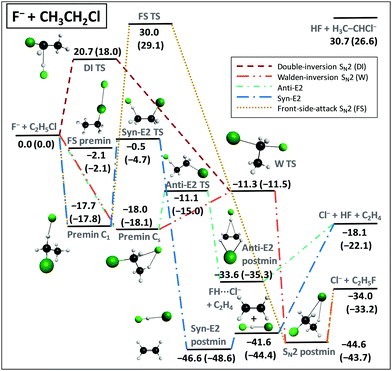Fig. 8 Schematic potential energy surface showing the benchmark classical (adiabatic) relative energies, in kcal mol⁻¹, of the stationary points along the different pathways of the F⁻ + CH₃CH₂Cl reaction.¹⁵ The data are taken from ref. 15 with a new Syn-E2 TS and corrected adiabatic energies for the Cl⁻ + HF + C₂H₄, HF + H₃C–CHCl⁻, and FH⋯Cl⁻ + C₂H₄ products. The classical energies are obtained as CCSD(T)-F12b/aug-cc-pVQZ + Δ_core[CCSD(T)-F12b/cc-pCVTZ-F12] and the adiabatic energies include Δ_ZPE[CCSD(T)-F12b/aug-cc-pVDZ].

As seen, the determination of the stationary points of reactive PESs provides a good picture about the possible reaction channels and pathways and their energetic requirements. However, to reveal the importance of the different mechanisms reaction dynamics simulations are necessary on full-dimensional PESs. We have developed such PESs and investigated the dynamics of several atom/ion + molecule reactions.^11,13 Detailed review of these dynamics studies can be found in ref. 11 and 13, here we just highlight the most important features of our work in context of the literature.

The key of our dynamics studies is that we represent the PESs by analytical functions obtained by fitting high-level ab initio energy points.^11,13,25 We can construct these PESs using a few tens of thousands of energies instead of billions of on-the-fly gradients needed for a direct dynamics study. Thus, the analytical PESs allow efficient and accurate dynamical investigations using either the QCT or quantum methods.^11,13 For atom + methane reactions such PESs were developed^17–22 before our benchmark work²³ published first for the F + CH₄ system in 2009. The unique feature of our atom + methane PESs was that we proposed^23,26–28 several composite ab initio methods to compute accurate energy points within affordable computational time based on the ideas described in Sec. II. Furthermore, we reported SO-corrected fully ab initio PESs for the first time for the F/Cl/Br + methane reactions.^26,28,109 Since then several groups have followed our ideas and developed SO-corrected PESs for reactions of halogen atoms with different molecules.^36,110–113 In the 2010s the use of the explicitly-correlated CCSD(T)-F12 methods has become widespread for PES developments,^{36,44,45,114–116} which may diminish the significance of the traditional (non-F12-based) composite methods.

For S_N2 reactions our group has played a pioneering role in developing analytical PESs.¹³ As mentioned in the Introduction we developed⁴³ the first full-dimensional high-level ab initio analytical PES for the F⁻ + CH₃Cl S_N2 reaction in 2013 and later we reported^44,45 analytical PESs for other S_N2 reactions as well. Unlike the traditional direct dynamics studies,^{9,41,42,52,108,122–126} the analytical PESs made the computations of millions of trajectories possible, allowing the discovery of low-probability reaction channels and determination of statistically accurate differential cross sections. Therefore, the analytical PESs played a key role in revealing a new reaction mechanism, called double inversion,⁴⁶ for S_N2 reactions and achieving unprecedented agreement between theory and detailed crossed-beam experiments.^50,51

As mentioned above more details about the dynamics can be found in ref. 11 and 13, here we discuss the effects of the choice of the electronic structure theory on the PES development⁷⁰ and dynamics⁷¹ in Sections IV and V, respectively. Furthermore, we show the role of the stationary points in the dynamics of a S_N2 reaction⁷² in Section VI.

IV. On the choice of the ab initio level for PES developments

In Section II we discussed the accuracy of the different ab initio levels of theory for stationary-point properties. However, global reactive PESs have to describe configurations far from the stationary points. In 2014 we reported⁷⁰ an ab initio investigation testing various methods and basis sets for 15 selected non-stationary configurations for each of the X + CH₄ [X = F, O, Cl] and X⁻ + CH₃Y [X/Y = F/F, OH/F, F/Cl] reactions. As an example, in Fig. 9 we show the performance of the standard MP2 and CCSD(T) as well as the explicitly-correlated MP2-F12, CCSD(T)-F12a, and CCSD(T)-F12b methods with various double-, triple-, and quadruple-zeta basis sets for the F⁻ + CH₃Cl system. MP2 and MP2-F12 methods give root-mean-square (RMS) errors of 2–3 kcal mol⁻¹, showing the limitations of MP2 theory. Interestingly standard CCSD(T) with the aug-cc-pVDZ basis provides an even larger RMS of about 3.5 kcal mol⁻¹. (Note that the same finding is found for the other systems as well.⁷⁰) Increasing the basis to aug-cc-pVTZ the RMS drops to 1 kcal mol⁻¹. If we use either CCSD(T)-F12a or CCSD(T)-F12b, which virtually give the same results, the RMS becomes less than 1 kcal mol⁻¹ even with the aug-cc-pVDZ basis. Therefore, the CCSD(T)-F12 methods are highly recommended for PES developments. Obviously, higher-level electronic structure calculations are directly related with higher computational cost. If tens of thousands of points are necessary to describe the PES in polyatomic systems, the computational effort could be very expensive, thus the careful choice of the ab initio method and basis is necessary.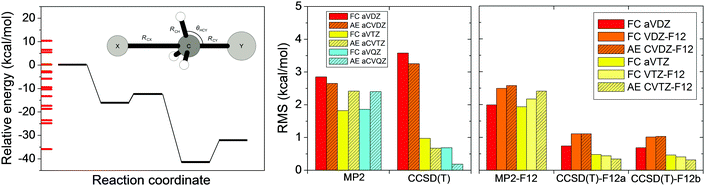

Fig. 9 Potential energy diagram and RMS errors of different standard and explicitly-correlated (F12) frozen-core (FC) and all-electron (AE) ab initio levels of theory for the F⁻ + CH₃Cl S_N2 reaction.⁷⁰ The RMS errors are based on 15 energy points, obtained by varying R_CX, R_CY, R_CH, and θ_HCY covering energies as indicated along the relative energy axis, and are relative to all-electron CCSD(T)-F12b/cc-pCVQZ-F12 reference data.

Fig. 10 shows the total correlation, the core correlation, and the scalar relativistic effects for the above-mentioned six reactions. As seen, electron correlation results in energy effects as large as 5 to 20 kcal mol⁻¹ in relative energies, showing that the Hartree–Fock method is an unreasonable choice for PES developments and direct dynamics studies. Core correlation and scalar relativity affect the PESs by 0.2–0.4 and ∼0.1 kcal mol⁻¹, respectively; therefore, these effects may be considered in spectroscopic studies, but may be negligible in PES developments for reaction dynamics computations.

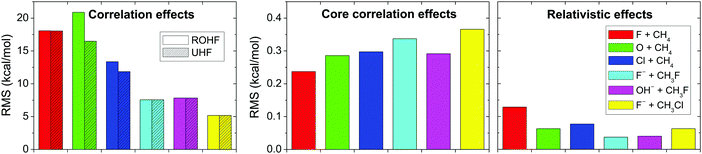Fig. 10 Electron correlation, core electron correlation, and scalar relativistic effects obtained as RMS deviations of 15 Hartree–Fock/aug-cc-pCVQZ, frozen-core CCSD(T)/aug-cc-pCVQZ, and Douglas–Kroll all-electron CCSD(T)/aug-cc-pCVQZ energies, respectively, relative to all-electron CCSD(T)/aug-cc-pCVQZ energy points for six different benchmark reactions.⁷⁰

V. Effects of the level of electronic structure theory on the reaction dynamics

Many studies investigated the accuracy of the various electronic structure methods for energy computations; however, little is known about their effects on the dynamics of chemical reactions. In 2018 we developed⁷¹ 20 different PESs for the F⁻ + CH₃I reaction using several ab initio (HF, MP2, MP2-F12, CCSD, CCSD-F12b, CCSD(T), CCSD(T)-F12b, OQVCCD(T)¹¹⁷) and density functional theory (DFT) (B97-1,¹¹⁸ PBE0,¹¹⁹ M06-2X,¹²⁰ B2PLYP¹²¹) methods with double- and/or triple-zeta basis sets. Then, quasiclassical trajectory computations were performed on these PESs and the effects of the level of electronic structure theory on the cross sections, reaction probabilities, angular and product internal energy distributions were revealed.

The cross sections of the S_N2 (I⁻ + CH₃F) and proton-abstraction (HF + CH₂I⁻) channels obtained at the different levels of theory are shown in Fig. 11. As seen, the reactivity of both channels significantly depends on the level of electronic structure theory. The MP2 S_N2 cross sections are about 50–80% of the HF value, depending on the basis set, whereas for the abstraction channel MP2 gives 2–3 times larger reactivity than HF without dispersion correction. In the case of HF and standard MP2 methods, increasing the basis size from DZ to TZ decreases the S_N2 reactivity by about 10–30% and increases the abstraction probability by about 100%. The MP2-F12 method gives TZ quality results with a DZ basis and in the case of the explicitly-correlated methods the DZ basis provides basis-set-converged cross sections as the MP2/TZ, MP2-F12/DZ, and MP2-F12/TZ results are virtually the same for both channels (Fig. 11). The CCSD(T) and CCSD(T)-F12b methods increase the corresponding MP2 cross sections by 20–40% and about 100% for the S_N2 and abstraction channels, respectively. In the case of the S_N2 channel the DFT functionals significantly overestimate the most accurate CCSD(T)-F12b cross sections. The B97-1 functional gives twice as large reactivity, whereas M06-2X overestimates CCSD(T)-F12b by about 30%. However, for the abstraction channel, B97-1 agrees well with the CCSD(T)-F12b result, but M06-2X gives twice larger reactivity.

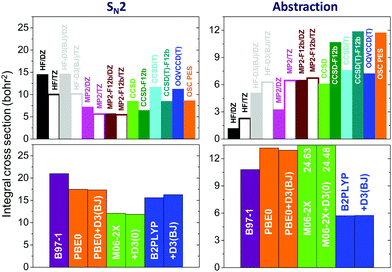Fig. 11 Cross sections for the F⁻ + CH₃I S_N2 and proton-abstraction reactions obtained by quasiclassical trajectory computations on various ab initio- and DFT-based analytical PESs at a collision energy of 35.3 kcal mol⁻¹.⁷¹ DZ and TZ denote aug-cc-pVDZ and aug-cc-pVTZ basis sets, respectively, the CCSD, CCSD-F12b, CCSD(T), CCSD(T)-F12b, and OQVCCD(T) methods are used with DZ and the DFT methods are used with TZ basis sets. D3(BJ) and D3(0) denote additive dispersion corrections^135,136 and the all-electron CCSD(T)-F12b/TZ-quality OSC PES is taken from ref. 45.

Product internal energy distributions for the S_N2 channel obtained on the different PESs are shown in Fig. 12, allowing comparison with the experimental results¹²² of the Wester group. At low collision energy (7.4 kcal mol⁻¹) the reaction produces internally hot CH₃F molecules and the distributions peak at the highest available energy (indicating complex-forming indirect dynamics), whereas at high collision energy (35.3 kcal mol⁻¹) the distributions become much broader. The HF method significantly overestimates the product internal energy by about 20 kcal mol⁻¹, in accord with the overestimated exothermicity. The correlation methods capture the main experimental features; the agreement is very good at low collision energy, but at high collision energy significant differences can be observed. MP2 produces too cold, whereas DFT gives too hot internal energy distributions at collision energy of 35.3 kcal mol⁻¹. The best agreement between theory and experiment is seen for the OQVCCD(T) method,¹¹⁷ which may perform better than CCSD(T) at multi-reference configurations. More work toward this direction would be desired in the near future.

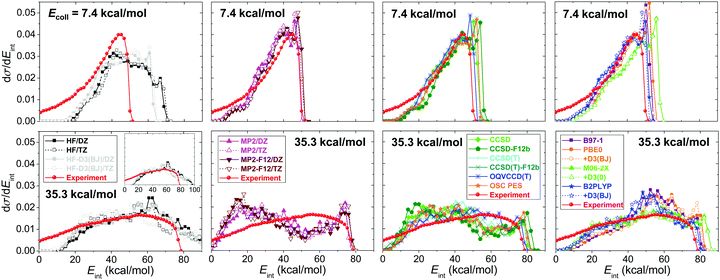Fig. 12 Normalized product internal energy distributions for the F⁻ + CH₃I S_N2 reaction obtained on various ab initio- and DFT-based analytical PESs (see Fig. 11 for notations) at collision energies of 7.4 and 35.3 kcal mol⁻¹.⁷¹ The experimental data are taken from ref. 122.

As the above findings show one should be aware of the fact that the different choices of the electronic structure theory can significantly affect the quantitative outcomes of the reaction dynamics simulations. This conclusion is in agreement with that of Hase and co-workers¹²³ who compared MP2 and B97-1 direct dynamics results for the F⁻ + CH₃I S_N2 reaction and found that B97-1 significantly overestimates the MP2 reactivity in accord with Fig. 11. If one is to develop the first PES for a system, we recommend using at least CCSD(T)-F12a/b with a DZ basis, otherwise some of the quantitative results may have large uncertainties.

VI. Role of the stationary points in the reaction dynamics

Reaction pathways are traditionally identified by visually inspecting several classical trajectory animations. One may observe that trajectories approach several stationary points before reaching the product region. One may also find interesting cases where reaction pathways avoid an energetically favorable minimum, as Hase and co-workers¹²⁴ found in the case of the OH⁻ + CH₃F S_N2 reaction. Thus, trajectory animations are usually very useful to provide a qualitative picture about the role of the stationary points in the dynamics and mechanisms of a chemical reaction. However, one cannot watch millions of trajectories; therefore, a quantitative analysis technique is needed. Recently we have developed such techniques as described briefly below.

Let us start the story with our joint experimental–theoretical study on the dynamics of the F⁻ + CH₃Cl S_N2 reaction.⁵⁰ Experiment revealed that the F⁻ + CH₃Cl reaction is more direct than F⁻ + CH₃I, in agreement with theory. We speculated, on one hand, that the deep F⁻⋯ICH₃ front-side minimum plays a key role in the dynamics of the F⁻ + CH₃I reaction, steering the reactants into a non-reactive orientation, thereby making the reaction indirect. On the other hand, the shallow F⁻⋯ClCH₃ complex does not divert the reactants away from the reactive F⁻⋯H₃CCl minimum. To quantify this prediction, we developed a trajectory orthogonal projection (TOP) method,⁴⁸ which projects the position of F⁻ onto one- or two-dimensional subspaces of the entrance channel. In the F⁻ + CH₃I case we orthogonally project the Cartesian coordinates of F⁻ along trajectories onto the C–I axis or one of the I–C–H planes and compute the distribution of the projected positions averaged over trajectories and time. TOP revealed that F⁻ spends significant time in the front-side complex region of the F⁻ + CH₃I reaction, whereas front-side complex formation is negligible in the F⁻ + CH₃Cl reaction. Following some pioneering work,¹²⁵ our study⁴⁸ provided the first quantitative dynamical characterization of front-side complex formation in S_N2 reactions.

For the F⁻ + CH₃I reaction about 15 stationary points have been found^45,126 by different electronic structure theories as shown in Fig. 13. In order to quantitatively characterize their role in the dynamics we developed a method which assigns every trajectory structure to a stationary point based on the best overlap of the geometries.⁷² In our implementation the best overlap is determined using an exact Eckart-transformation method,^127,128 which has been successfully used in our group for mode-specific quasiclassical polyatomic product analysis.^43,128,129 In short, we move both the stationary-point and the actual trajectory structures into the center of mass frame and construct a pseudo-rotational matrix,^127,128 which transforms the actual configuration into the Eckart frame^127,128 corresponding to the stationary-point geometry. If we take the permutational symmetry properly into account, we obtain the best overlap between the two structures. We perform this transformation for all the stationary points, and the assignment is made by minimizing the root-mean-square distances of the Cartesian coordinates of the actual trajectory geometry and the stationary points with respect to the different stationary-point structures. Note that similar automated reaction mechanism assignment technique was also reported by Taketsugu and co-workers,¹³⁰ where the trajectory geometries are assigned to structures along intrinsic reaction coordinates using a minimum-distance method via the Kabsch algorithm.¹³¹

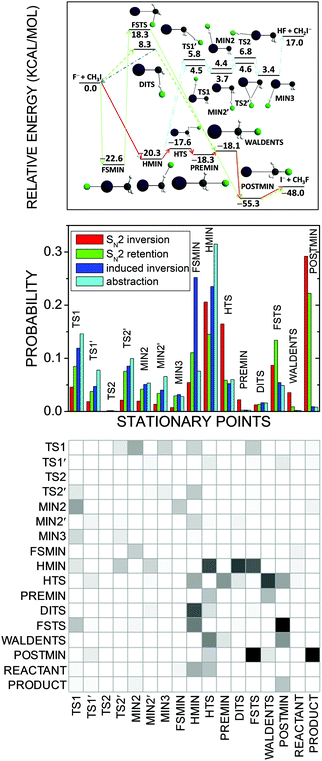Fig. 13 Schematic potential energy surface showing the stationary points and their classical relative energies (upper panel), normalized b-averaged stationary-point probability distributions (middle panel), and a b = 0 S_N2-inversion row → column transition probability matrix, where darker matrix elements mean higher probabilities (lower panel) for the F⁻ + CH₃I reaction at a collision energy of 35.3 kcal mol⁻¹.⁷² S_N2 inversion means Walden inversion, S_N2 retention denotes front-side attack and double inversion, induced inversion produces an inverted reactant via DITS, and abstraction means proton transfer from CH₃I to F⁻.

Fig. 13 shows the stationary-point probability distributions for the different mechanisms of the F⁻ + CH₃I reaction. In all cases the trajectories spend significant time in the front-side (FSMIN) and hydrogen-bonded (HMIN) minimum wells and near the hydrogen-bonded transition state (HTS). Interestingly, the formation of the traditional ion–dipole complex (PREMIN) is negligible for this reaction. This finding does not mean that the trajectory-point probability density is not high near PREMIN, but the configuration space of the PREMIN-like structures is much more localized than that of the HMIN-like geometries and this is the reason of the significantly higher probability of HMIN formation/assignment. The S_N2 trajectories are usually trapped in the post-reaction ion–dipole complex (POSTMIN) region, whereas for the induced-inversion (which provides an inverted reactant) and proton-abstraction channels POSTMIN formation is not significant (the small non-zero probabilities indicate recrossing dynamics). The indirect dynamics of the F⁻ + CH₃I reaction is underpinned by the fact that most of the proton-abstraction stationary points participate in the S_N2 channels as well. In order to provide more insights into the dynamics of the reaction, we computed stationary-point transition-probability matrices,⁷² as shown for the S_N2 inversion channel in Fig. 13. The matrix is nearly symmetric showing many forward–backward transitions between stationary points, confirming again the indirect nature of the F⁻ + CH₃I reaction. The trajectories usually enter into the HMIN and HTS regions, WALDENTS is most likely approached from HTS and PREMIN, and the S_N2 products are usually formed via POSTMIN. We also proposed to apply various distance and energy constraints into the analysis,⁷² which may provide additional insights into the mechanisms of chemical reactions.

VII. Summary and conclusions

Benchmark ab initio characterization of the stationary points of reactive PESs is the first step toward understanding the dynamics and mechanisms of chemical reactions. We determine the best technically feasible relative energies of the stationary points at CCSD(T)-F12b/triple-zeta geometries as given in eqn (1). The CCSD(T)/CBS limit may be obtained by extrapolation of traditional CCSD(T)/aug-cc-pVnZ [n = 4 and 5] energies or using the explicitly-correlated CCSD(T)-F12b method with a quadruple-zeta basis. The core (Δ_core) and post-CCSD(T) correlation effects are usually a few tenths of kcal mol⁻¹ and sometimes, but not always, cancel each other. Scalar relativistic effects (Δ_rel) are described by effective core potentials for heavy atoms, e.g., Br and I, and often neglected for first- and second-row elements as Δ_rel, which can be obtained by Douglas–Kroll computations, is usually less than Δ_core. Spin–orbit corrections (Δ_SO) can be determined by MRCI computations using the Breit–Pauli operator in the interacting-states approach⁹⁹ and can be significant for heavy open-shell species, such as Br and I atoms, and their weakly-bound complexes. Zero-point-energy corrections (Δ_ZPE) can be as large as a few kcal mol⁻¹, thus, cannot be neglected to achieve good agreement with experiment. The CCSD(T)-F12 methods with double- or triple-zeta basis sets are recommended for Δ_ZPE computations. Considering all the above energy terms, quantum chemistry can provide definitive relative energies with uncertainties well below 1 kcal mol⁻¹, as confirmed by comparisons to measured 0 K reaction enthalpies.

In the present paper we focus on single-reference coupled-cluster computations, which usually give accurate stationary-point properties as demonstrated here. However, it should be noted that CCSD(T) and CCSD(T)-F12 methods may fail to provide a good description of certain regions of the PES, especially where several coupled configurations come into play. In this case multi-reference methods such as MRCI¹⁰¹ or MRCC^132–134 should be used.

The above-described benchmark composite ab initio methods were applied to several atom + alkane and ion + molecule reactions.^11–15 The stationary-point structures and energies guide full-dimensional analytical PES developments, which allow efficient dynamical investigations. We developed and have been developing such PESs for several reactions,^11,13 which revealed a new double-inversion mechanism,⁴⁶ unexpected leaving-group effect,⁵⁰ and front-side complex formation for S_N2 reactions,⁴⁸ as well as in the case of atom + alkane reactions extended the validity of the Polanyi rules^26,38 and mapped the angle dependence of a transition-state barrier.¹⁰

We tested the performance of several ab initio methods and basis sets at non-stationary geometries and concluded that the explicitly-correlated CCSD(T)-F12 methods are strongly recommended for PES developments.⁷⁰ We also showed that the results of dynamics simulations such as cross sections, reaction probabilities, etc., may depend significantly, for example, by factors of 2, on the level of electronic structure theory.⁷¹ Converged cross sections may be obtained by using a CCSD(T)-F12 method with a double-zeta basis set.

We developed numerical analysis techniques to uncover the role of the stationary points in the dynamics of chemical reactions. Trajectory orthogonal projections,⁴⁸ Eckart-transformation-based stationary-point assignments,⁷² and stationary-point transition probability matrices⁷² reveal the probability distributions of the trajectory geometries in different stationary-point regions and transition probabilities between them, thereby uncovering front-side complex formation in S_N2 reactions and various reaction pathways. These numerical analysis methods complement traditional trajectory animations, and provide quantitative links between static stationary-point properties and reaction dynamics simulations. Therefore, we hope that our perspectives strengthen the connections between the fields of clamped-nuclei electronic structure theory and reaction dynamics.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the National Research, Development and Innovation Office-NKFIH, K-125317, the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT, and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for financial support. We acknowledge KIFÜ for awarding us access to computational resources based in Hungary at Szeged, Debrecen, and Budapest.

References

1. C. K. Ingold, Structure and Mechanisms in Organic Chemistry, Cornell Univ. Press, Ithaca, NY, 1953.
2. J. C. Polanyi, Science, 1987, 236, 680.
3. P. Ayotte, G. H. Weddle, J. Kim and M. A. Johnson, Chem. Phys., 1998, 239, 485.
4. J. M. Merritt, S. Rudić and R. E. Miller, J. Chem. Phys., 2006, 124, 084301.
5. D. M. Neumark, Annu. Rev. Phys. Chem., 1992, 43, 153.
6. R. Wester, A. E. Bragg, A. V. Davis and D. M. Neumark, J. Chem. Phys., 2003, 119, 10032.
7. M. Cheng, Y. Feng, Y. Du, Q. Zhu, W. Zheng, G. Czakó and J. M. Bowman, J. Chem. Phys., 2011, 134, 191102.
8. G. Mensa-Bonsu, D. J. Tozer and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2019, 21, 13977.
9. J. Zhang, J. Mikosch, S. Trippel, R. Otto, M. Weidemüller, R. Wester and W. L. Hase, J. Phys. Chem. Lett., 2010, 1, 2747.
10. H. Pan, F. Wang, G. Czakó and K. Liu, Nat. Chem., 2017, 9, 1175.
11. G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839.
12. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
13. I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 9005.
14. D. A. Tasi, Z. Fábián and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 7924.
15. V. Tajti and G. Czakó, J. Phys. Chem. A, 2017, 121, 2847.
16. B. Hajdu and G. Czakó, J. Phys. Chem. A, 2018, 122, 1886.
17. J. C. Corchado and J. Espinosa-García, J. Chem. Phys., 1996, 105, 3160.
18. J. Espinosa-García and J. C. Corchado, J. Chem. Phys., 1996, 105, 3517.
19. J. F. Castillo, F. J. Aoiz, L. Banares, E. Martinez-Nunez, A. Fernandez-Ramos and S. Vazquez, J. Phys. Chem. A, 2005, 109, 8459.
20. J. F. Castillo, F. J. Aoiz and L. Bañares, J. Chem. Phys., 2006, 125, 124316.
21. S. T. Banks and D. C. Clary, Phys. Chem. Chem. Phys., 2007, 9, 933.
22. C. Rangel, M. Navarrete, J. C. Corchado and J. Espinosa-García, J. Chem. Phys., 2006, 124, 124306.
23. G. Czakó, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 130, 084301.
24. B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577.
25. J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094.
26. G. Czakó and J. M. Bowman, Science, 2011, 334, 343.
27. G. Czakó and J. M. Bowman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7997.
28. G. Czakó, J. Chem. Phys., 2013, 138, 134301.
29. W. W. Harper, S. A. Nizkorodov and D. J. Nesbitt, J. Chem. Phys., 2000, 113, 3670.
30. R. J. Holiday, C. H. Kwon, C. J. Annesley and F. F. Crim, J. Chem. Phys., 2006, 125, 133101.
31. H. A. Bechtel, Z. H. Kim, J. P. Camden and R. N. Zare, J. Chem. Phys., 2004, 120, 791.
32. D. Zhang, J. Yang, Z. Chen, R. Chen, B. Jiang, D. Dai, G. Wu, D. H. Zhang and X. Yang, Phys. Chem. Chem. Phys., 2017, 19, 13070.
33. S. Yan, Y.-T. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723.
34. W. Zhang, H. Kawamata and K. Liu, Science, 2009, 325, 303.
35. T. Lenzen, W. Eisfeld and U. Manthe, J. Chem. Phys., 2019, 150, 244115.
36. J. Chen, X. Xu, S. Liu and D. H. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 9090.
37. C. Murray, B. Retail and A. J. Orr-Ewing, Chem. Phys., 2004, 301, 239.
38. Z. Zhang, Y. Zhou, D. H. Zhang, G. Czakó and J. M. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416.
39. R. Liu, F. Wang, B. Jiang, G. Czakó, M. Yang, K. Liu and H. Guo, J. Chem. Phys., 2014, 141, 074310.
40. G. Czakó, J. Phys. Chem. A, 2014, 118, 11683.
41. P. Manikandan, J. Zhang and W. L. Hase, J. Phys. Chem. A, 2012, 116, 3061.
42. J. Xie and W. L. Hase, Science, 2016, 352, 32.
43. I. Szabó, A. G. Császár and G. Czakó, Chem. Sci., 2013, 4, 4362.
44. I. Szabó, H. Telekes and G. Czakó, J. Chem. Phys., 2015, 142, 244301.
45. B. Olasz, I. Szabó and G. Czakó, Chem. Sci., 2017, 8, 3164.
46. I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972.
47. I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 3134.
48. I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917.
49. Y. Wang, H. Song, I. Szabó, G. Czakó, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322.
50. M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151.
51. M. Stei, E. Carrascosa, A. Dörfler, J. Meyer, B. Olasz, G. Czakó, A. Li, H. Guo and R. Wester, Sci. Adv., 2018, 4, eaas9544.
52. Y.-T. Ma, X. Ma, A. Li, H. Guo, L. Yang, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2017, 19, 20127.
53. P. Liu, D. Y. Wang and Y. Xu, Phys. Chem. Chem. Phys., 2016, 18, 31895.
54. P. Liu, J. Zhang and D. Y. Wang, Phys. Chem. Chem. Phys., 2017, 19, 14358.
55. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399–407.
56. J. Li, B. Jiang, H. Song, J. Ma, B. Zhao, R. Dawes and H. Guo, J. Phys. Chem. A, 2015, 119, 4667.
57. R. Welsch and U. Manthe, J. Chem. Phys., 2015, 142, 064309.
58. Y. Li, Y. Wang and D. Wang, J. Phys. Chem. A, 2017, 121, 2773.
59. H. Song and M. Yang, Phys. Chem. Chem. Phys., 2018, 20, 19647.
60. B. Fu and D. H. Zhang, J. Chem. Theory Comput., 2018, 14, 2289.
61. W. D. Allen, A. L. L. East and A. G. Császár, in Structures and Conformations of Non-Rigid Molecules, ed. J. Laane, M. Dakkouri, B. van der Veken and H. Oberhammer, Kluwer, Dordrecht, 1993, pp. 343–373.
62. A. G. Császár, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 1998, 108, 9751.
63. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193.
64. L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94, 7221.
65. J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843.
66. A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599.
67. N. C. Handy, Y. Yamaguchi and H. F. Schaefer, J. Chem. Phys., 1986, 84, 4481.
68. H.-J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126, 164102.
69. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
70. G. Czakó, I. Szabó and H. Telekes, J. Phys. Chem. A, 2014, 118, 646.
71. T. Győri, B. Olasz, G. Paragi and G. Czakó, J. Phys. Chem. A, 2018, 122, 3353.
72. B. Olasz and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 1578.
73. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007.
74. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
75. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
76. I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 5748.
77. W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Molecular Orbital Theory, Wiley, New York, 1986.
78. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
79. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910.
80. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
81. A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2006, 115, 330.
82. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639.
83. D. Feller, J. Chem. Phys., 1992, 96, 6104.
84. G. Tasi and A. G. Császár, Chem. Phys. Lett., 2007, 438, 139.
85. A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2006, 115, 330.
86. D. Feller and K. A. Peterson, J. Chem. Phys., 2013, 139, 084110.
87. N. Sylvetsky, K. A. Peterson, A. Karton and J. M. L. Martin, J. Chem. Phys., 2016, 144, 214101.
88. M. K. Kesharwani, N. Sylvetsky, A. Köhn, D. P. Tew and J. M. L. Martin, J. Chem. Phys., 2018, 149, 154109.
89. D. Feller, K. A. Peterson and J. G. Hill, J. Chem. Phys., 2010, 133, 184102.
90. D. Feller, J. Phys. Chem. A, 2015, 119, 7375.
91. K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 2002, 117, 10548.
92. J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108.
93. MRCC, a quantum chemical program suite written by M. Kállay, Z. Rolik, I. Ladjánszki, L. Szegedy, B. Ladóczki, J. Csontos and B. Kornis, see also Z. Rolik and M. Kállay, J. Chem. Phys., 2011, 135, 104111 , as well as: http://www.mrcc.hu.
94. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041.
95. M. Kállay and P. R. Surján, J. Chem. Phys., 2001, 115, 2945.
96. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
97. D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773.
98. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89.
99. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
100. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053.
101. K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101.
102. G. Czakó, A. G. Császár and H. F. Schaefer III, J. Phys. Chem. A, 2014, 118, 11956.
103. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
104. B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122e of the Thermochemical Network, Argonne NationalLaboratory, 2019, available at ATcT.anl.gov.
105. B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszewski, S. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979.
106. G. Czakó and J. M. Bowman, J. Chem. Phys., 2012, 136, 044307.
107. L. Krotos and G. Czakó, J. Phys. Chem. A, 2017, 121, 9415.
108. E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25.
109. G. Czakó and J. M. Bowman, Phys. Chem. Chem. Phys., 2011, 13, 8306.
110. J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 074309.
111. S. M. Remmert, S. T. Banks, J. N. Harvey, A. J. Orr-Ewing and D. C. Clary, J. Chem. Phys., 2011, 134, 204311.
112. T. Westermann, W. Eisfeld and U. Manthe, J. Chem. Phys., 2013, 139, 014309.
113. T. Lenzen, W. Eisfeld and U. Manthe, J. Chem. Phys., 2019, 150, 244115.
114. Q. Yu and J. M. Bowman, J. Chem. Theory Comput., 2016, 12, 5284.
115. J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302.
116. S. Sur, E. Quintas-Sánchez, S. A. Ndengué and R. Dawes, Phys. Chem. Chem. Phys., 2019, 21, 9168.
117. J. B. Robinson and P. J. Knowles, Phys. Chem. Chem. Phys., 2012, 14, 6729.
118. F. A. Hamprecht, A. J. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 6264.
119. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
120. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
121. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
122. J. Mikosch, J. Zhang, S. Trippel, C. Eichhorn, R. Otto, R. Sun, W. A. de Jong, M. Weidemüller, W. L. Hase and R. Wester, J. Am. Chem. Soc., 2013, 135, 4250.
123. R. Sun, C. J. Davda, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2015, 17, 2589.
124. L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875.
125. J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019.
126. J. Zhang, J. Xie and W. L. Hase, J. Phys. Chem. A, 2015, 119, 12517.
127. A. Y. Dymarsky and K. N. Kudin, J. Chem. Phys., 2005, 122, 124103.
128. G. Czakó, J. Phys. Chem. A, 2012, 116, 7467.
129. I. Szabó and G. Czakó, J. Chem. Phys., 2016, 145, 134303.
130. T. Tsutsumi, Y. Harabuchi, Y. Ono, S. Maeda and T. Taketsugu, Phys. Chem. Chem. Phys., 2018, 20, 1364.
131. W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 922.
132. X. Li and J. Paldus, J. Chem. Phys., 2003, 119, 5320.
133. F. A. Evangelista, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2006, 125, 154113.
134. F. A. Evangelista, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2007, 127, 024102.
135. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
136. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.

---

Footnote

† Present address: Department of Chemistry, King's College London, London SE1 1DB, UK.

---