Open Access Article
Open Access ArticleInfluence of structure–activity relationships on through-space intervalence charge transfer in metal–organic frameworks with cofacial redox-active units†
Bowen
Ding
,
Carol
Hua
 ,
Cameron J.
Kepert
* and
Deanna M.
D'Alessandro
,
Cameron J.
Kepert
* and
Deanna M.
D'Alessandro
 *
*
School of Chemistry, The University of Sydney, New South Wales, 2006 Australia. E-mail: cameron.kepert@sydney.edu.au; deanna.dalessandro@sydney.edu.au
First published on 29th October 2018
Abstract
Understanding charge transfer in redox-active metal–organic frameworks (MOFs) is of fundamental importance given the potential of these materials to be used in myriad applications including porous conductors, electrocatalysts and battery materials, amongst others. An important challenge is quantifying the spectroscopic features of these materials in order to elucidate their charge transfer properties. Herein, two topologically related Zn(II) and Cd(II) frameworks, [Zn2(DPPTzTz)2(SDC)2] (1-Zn) and [Cd2(DPPTzTz)2(SDC)2] (2-Cd) (where DPPTzTz = 2,5-bis(4-(4-pyridinyl)phenyl)thiazolo[5,4-d]thiazole and SDC = selenophene-2,5-dicarboxylate), incorporating cofacially stacked pairs of redox-active DPPTzTz ligands are presented. The differences in the through-space intervalence charge transfer properties of the mixed-valence forms of the two frameworks generated upon solid state spectroelectrochemical reduction are quantified using Marcus–Hush theory. Further, charge transfer theory is applied to calculate electron mobilities in both extended framework systems. A larger electronic coupling constant, Hab, of 118 cm−1 corresponding to an electron mobility, k, of 6.02 × 108 s−1 was observed for the Zn(II) analogue compared to the Cd(II) analogue (Hab = 61.2 cm−1 and k = 2.22 × 108 s−1) and was correlated primarily with the larger cofacial stacking distance and increasingly offset stacking geometry between DPPTzTz ligands in the latter. Establishing structure–activity relationships in electroactive MOFs, in addition to methods for quantifying their charge transfer properties, represents an important advance in fine tuning solid state materials for device applications.
Introduction
A key structural feature in a number of early photosynthetic unicellular organisms is a cofacially arranged photoreaction trap, often described as a ‘special pair’.1 This cofacial moiety plays a vital role in stabilising the photoexcited mixed-valence radical state using through-space intervalence charge transfer (IVCT) and facilitates the conversion of light to chemical energy. This intriguing phenomenon has been the focus of a number of qualitative biomimicry studies using discrete organic molecules mostly based on porphyrin derivatives.2 On the other hand, quantitative experimental and theoretical studies on inorganic systems featuring cofacial arrangements of ligands which display through-space IVCT have been relatively limited, and are exemplified by the work by Dinolfo and Hupp on discrete inorganic molecular rectangles.3Metal–organic frameworks (MOFs) offer an ideal platform for studying outer sphere electron transfer owing to their highly ordered nature and tunability which opens up opportunities to explore structure–activity relationships. MOFs also enable the effects of long-range order to be probed which are not possible in discrete systems.
Driven by a plethora of technological and industrial applications such as lightweight conductors, electrochromic devices and adaptive gas sorption materials, the study of electroactive MOFs has continued to gain momentum.4 By incorporating metal and/or ligand based redox-active components, interesting electronic and charge transfer behaviours can be introduced which can be harnessed for redox catalysis,5 energy storage6 and to induce conductivity7 in these materials. While the introduction of donors and acceptors into MOFs is one means of inducing charge transfer interactions,8 the inclusion of mixed-valence components is another key design strategy.9 Mixed-valence systems arise when either the metal or ligand based centres exist in different formal oxidation states; this results in a rapid oscillation of charge between the centres, manifesting in an IVCT absorption band.
To date, IVCT as a result of mixed valency in MOFs has only been observed to occur ‘through-bond’, but ‘through-space’ interactions can also be envisaged to occur.10 One of the most prominent examples is the framework [(NBu4)2FeIII2(dhbq)3]n (where NBu4 = tetrabutylammonium and dhbq = dihydroxybenzoquinone and represents dhbq2− and dhbq3− in the mixed-valence state),11 where charge transfer occurs between mixed-valence dhbq ligands via the FeIII centres. IVCT between mixed-valence FeII/FeIII centres is also observed in the cyanido framework Fe4III[FeII(CN)6]3·xH2O known as Prussian blue,12 which gives rise to its striking colour.
An important set of tools to study charge transfer in MOFs are in situ solid state spectroelectrochemical (SEC) techniques,13 where electrochemistry is coupled with spectroscopic methods. The two key SEC techniques for study of charge transfer in frameworks are electron paramagnetic resonance (EPR) SEC,8,14 which allows the formation and progression of radicals in a system to be monitored, and Vis-NIR SEC, which enables insights into the evolution of charge transfer bands. Although Vis-NIR SEC permits identification of new charge transfer bands, observations remain qualitative, as the development of reliable means for quantifying solid state reflectance spectroscopic data (i.e., obtaining extinction coefficients for charge transfer bands) is challenging. Quantifying spectroscopic data is crucial for application of Marcus–Hush theory which provides insight into the nature of charge transfer.15 The Robin and Day classification scheme can subsequently be applied,16 and materials can be considered in one of three classes: Class I represents redox-active materials where the centres do not interact electronically; Class II represents weakly coupled interacting centres with charge mainly localised on the sites; and Class III represents systems in which there is full delocalisation. From application of Marcus–Hush theory, increasingly detailed analyses can be obtained, including, for example, mobility calculations to connect with quantum analysis.17
Herein we describe two topologically related MOFs with Zn(II) and Cd(II) metal centres featuring cofacially stacked redox-active 2,5-bis(4-(4-pyridinyl)phenyl)thiazolo[5,4-d]thiazole (DPPTzTz) ligands and selenophene-2,5-dicarboxylate (SDC) co-ligands, namely [Zn2(DPPTzTz)2(SDC)2] (1-Zn) and [Cd2(DPPTzTz)2(SDC)2] (2-Cd). The through-space IVCT interaction originating from the cofacial arrangement of the ligand pairs is investigated using in situ SEC experiments and is quantified using Marcus–Hush theory, from which electron mobilities within cofacial units are calculated. This work represents one of the first studies to examine structure–activity relationships and their effect on IVCT in the solid state, thus providing important insights into through-space electronic communication in MOFs. Furthermore, the development of a protocol for quantifying solid state SEC spectra will be presented as a basis for applying Marcus–Hush theory to elucidate the nature of electron transfer within solid state materials.
Results and discussion
Synthesis and structural comparison
The solvothermal syntheses of 1-Zn and 2-Cd were achieved in DMF at 120 °C. The structure of 1-Zn was solved and refined in the monoclinic space group P21/c with unit cell parameters of a = 25.811(5), b = 18.453(4), c = 15.943(3) Å and β = 90.91(3)°, while 2-Cd was solved in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with unit cell parameters of a = 15.868(3), b = 19.123(4), c = 26.124(5) Å and α = 82.02(3), β = 87.25(3), γ = 89.73(3)°.
with unit cell parameters of a = 15.868(3), b = 19.123(4), c = 26.124(5) Å and α = 82.02(3), β = 87.25(3), γ = 89.73(3)°.
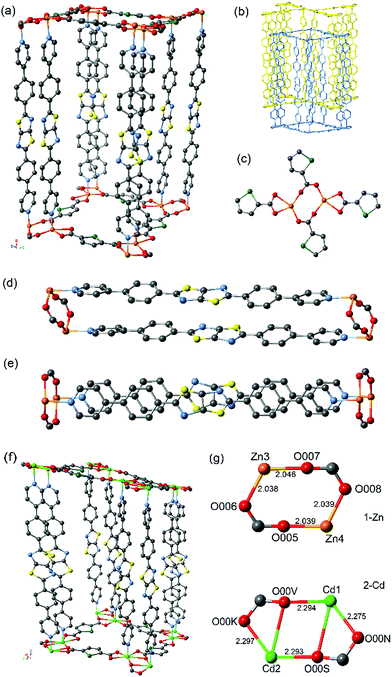
The frameworks are isotopological (Fig. 1) and consist of two interpenetrating 3D networks (Fig. 1b) with α-Po primitive cubic topology (pcu), where 2D layers of the SDC ligand and metal atoms are linked together by bridging DPPTzTz ligands. The metal centres for both 2-Cd and 1-Zn exhibit a distorted octahedral coordination sphere each consisting of four bound O-donors in the equatorial positions from the carboxylate groups of SDC ligands (see Fig. 1c) in addition to two N-donors on the axial positions from the pyridyl groups of the DPPTzTz ligand. 2-Cd contains significantly longer metal to nitrogen bond lengths (Cd–N = 2.161–2.267 Å) than 1-Zn, (Zn–N = 2.127–2.146 Å), suggesting a weaker M–N bond for 1-Cd when compared to 1-Zn. Additionally, 2-Cd exhibits a larger accessible void space of 29.6% when compared to 1-Zn with a value of 26.9%, as calculated by PLATON,18 which results from the longer coordination bond distances in 2-Cd leading to larger pore cavities.
The O-donors from two carboxylate groups in SDC are bound in a bridging manner to each of the metal centres to form a metal-based dimer (Fig. 1g). There is a noticeable difference in the geometry of the bridging carboxylate groups within each dimer, with those in 1-Zn adopting a bis-unidentate mode whereas those in 2-Cd adopt a partial bidentate-unidentate arrangement to give pseudo-heptacoordination, as is commonly observed for dimeric Cd units.19 The lower symmetry of the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group for 2-Cd results from the distortion of the bridging carboxylate groups of the Cd dimer, leading to two different Cd–O bond lengths (Cd1 – O00N = 2.275, Cd1 – O00V 2.294, Cd2 – O00S = 2.293 and Cd2 – O00K = 2.297 Å). There are two separate orientations of the dimers present, where the dimer pair of Cd3 and Cd4 is orientated 90° relative to Cd1 and Cd2, resulting in four unique Cd metal centres and thus a lowered crystal symmetry. In 1-Zn, however, the carboxylate groups are coordinated in a monodentate bridging orientation between the Zn dimer with approximately equal Zn–O bond lengths (Zn3 – O007 = 2.046, Zn3 – O006 = 2.038, Zn4 – O005 = 2.039 and Zn4 – O008 = 2.039 Å), resulting in only two unique Zn metal centre sites and thus, a higher symmetry monoclinic space group of P21/c.
space group for 2-Cd results from the distortion of the bridging carboxylate groups of the Cd dimer, leading to two different Cd–O bond lengths (Cd1 – O00N = 2.275, Cd1 – O00V 2.294, Cd2 – O00S = 2.293 and Cd2 – O00K = 2.297 Å). There are two separate orientations of the dimers present, where the dimer pair of Cd3 and Cd4 is orientated 90° relative to Cd1 and Cd2, resulting in four unique Cd metal centres and thus a lowered crystal symmetry. In 1-Zn, however, the carboxylate groups are coordinated in a monodentate bridging orientation between the Zn dimer with approximately equal Zn–O bond lengths (Zn3 – O007 = 2.046, Zn3 – O006 = 2.038, Zn4 – O005 = 2.039 and Zn4 – O008 = 2.039 Å), resulting in only two unique Zn metal centre sites and thus, a higher symmetry monoclinic space group of P21/c.
These significant differences in metal–oxygen bond lengths combined with the subtle change in the mode of coordination of the carboxylate to the metal centre at the metal–oxygen dimeric clusters in the two frameworks lead to differences in the properties of the cofacial π-stacking of the DPPTzTz ligands. This is due to the intimate role the carboxylate plays in controlling the interspacial distance between the two metal centres, which in turn directly influences the cofacial stacking geometry of DPPTzTz pairs (Fig. 1d). A slightly larger π-stacking distance between cofacial pairs of DPPTzTz ligands of 3.79 Å is observed for 2-Cd compared to 3.76 Å for 1-Zn. For both frameworks the cofacial stacking of one DPPTzTz ligand is offset with respect to the other DPPTzTz (Fig. 1e), and for 2-Cd this offset is more pronounced than observed in 1-Zn. This increase in offset of stacking for 2-Cd is also evidenced from the larger angle to the perpendicular at which the DPPTzTz ligands pillar adjacent SDC and metal 2D planes (ca. 8°), compared to ca. 1° in 1-Zn.
Positional disorder is present for the TzTz unit in 1-Zn representing the different orientations of the N and S atoms in the TzTz unit; however, for 2-Cd, favourable N–S interactions in the stacking of cofacial TzTz cores were observed as a result of the lower symmetry space group of P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The central TzTz unit is planar with respect to the adjacent phenyl rings, whilst the pyridyl group exhibits a small tilt of ca. 18°.
. The central TzTz unit is planar with respect to the adjacent phenyl rings, whilst the pyridyl group exhibits a small tilt of ca. 18°.
Electrochemical properties
For both 1-Zn and 2-Cd, the cyclic voltammetry (CV) in 0.1 M [n-Bu4N]PF6/MeCN electrolyte is characterised by DPPTzTz ligand based processes in the cathodic region (Fig. 2; refer to ESI Fig. S2† for electrochemical data on DPPTzTz). Upon application of a cathodic potential of −2.7 V vs. Fc+/Fc for 1-Zn, two distinct processes were observed at −1.9 and −2.5 V, corresponding to the quasi-reversible formation of the monoanion radical and dianion on each TzTz core respectively, as observed with previous MOFs incorporating the TzTz moiety.20 These processes were confirmed by square wave voltammetry (SQW) (ESI Fig. S3,† whilst the formation of the monoanion radical was also observed with greater clarity in 0.1 M KCl/H2O electrolyte (ESI Fig. S4†). Upon returning from −2.7 to 0 V, reverse processes to those observed in the forward scan were obtained. SQW suggests the occurrence of multiple hidden processes at −1.9 V, which may indicate the presence of electronic interactions within the material resulting in a mixing of radical states.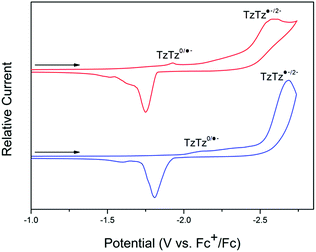 | ||
| Fig. 2 Solid state CV of 1-Zn (red) and 2-Cd (blue) in the cathodic region, performed at a scan rate of 100 mV s−1 in 0.1 M [n-Bu4N]PF6/MeCN. | ||
The 2-Cd framework displayed similar electrochemical behaviour to 1-Zn, with the redox processes generally shifted towards more reductive potentials. Upon application of a cathodic potential of −2.7 V vs. Fc+/Fc, two processes at −2.1 and −2.6 V corresponding to formation of the monoanion radical and dianion respectively on the TzTz moiety were observed in both the CV and SQW. A similar array of processes to those for 1-Zn was also observed upon returning the applied potential to 0 V.
Solid state spectroelectrochemistry
To elucidate the different redox states of both frameworks upon electrochemical reduction, solid state electron paramagnetic resonance (EPR) spectroelectrochemistry was performed, where similar behaviour was observed for both 1-Zn (Fig. 3, ESI Fig. S8†) and 2-Cd (ESI Fig. S10†).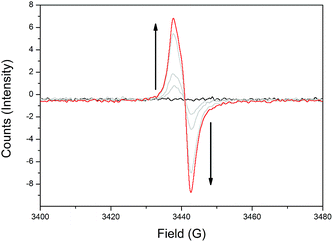 | ||
| Fig. 3 Solid state EPR SEC of 1-Zn in 0.1 M [n-Bu4N]PF6/MeCN, showing the appearance of the TzTz organic radical signal at g = 2.0043 upon initial reduction. | ||
Initially, as a reductive potential was applied to 1-Zn and 2-Cd, organic radical signals at g = 2.0043 and 2.0037, respectively, appeared and increased in intensity. This was attributed to formation of the monoanion radical state of the TzTz moieties. Further increasing the applied cathodic potential resulted in a reduction in the intensity of the radical bands for both materials. However, the intensity of this signal began to increase upon continued application of even higher cathodic potentials, which would not have been observed if there was straightforward reduction to the spin paired TzTz dianion state as seen in the solid state EPR SEC of DPPTzTz (ESI Fig. S6†). Thus the EPR SEC behaviour again suggests the occurrence of electronic communication in both 1-Zn and 2-Cd, resulting in a mixing of radical states. From structural data, this can be postulated to occur within the cofacial TzTz units. Upon returning the applied potential to 0 V, the EPR silent neutral states of both frameworks were reproduced, demonstrating redox reversibility.
Ex situ chemical reduction on both 1-Zn and 2-Cd was performed using lithium naphthalenide (LiNP) applied in stoichiometric ratios of 0.5, 1.0, 2.0 and 3.0 equivalents per TzTz core, to provide a comparison with trends observed in the in situ SEC data. As chemical reduction results in the intercalation of Li+ ions for charge balance with the reduced frameworks, the extent of reduction was determined by measuring the Li content against that of Zn or Cd respectively using ICP-AES (ESI Table S3†). An actual reduction extent of around 70% that of the theoretical value was observed for the 1-Zn samples, and of around 50% for the 2-Cd samples. These results, in conjunction with PXRD data demonstrating retention of crystallinity (ESI Fig. S12 and S14;† Pawley extraction of unit cell parameters provided in Tables S5 and S6†) upon reduction, show that the frameworks respond well to chemical reduction by LiNP and the resulting intercalation of Li+ ions.
EPR experiments were performed on chemically reduced samples to confirm the formation of the monoanion radical state. The radical signals for both 1-Zn and 2-Cd reduced samples occurred at comparable g-values (g = 2.0051 and 2.0024, respectively) to those generated electrochemically (ESI Fig. S15 and S16†).
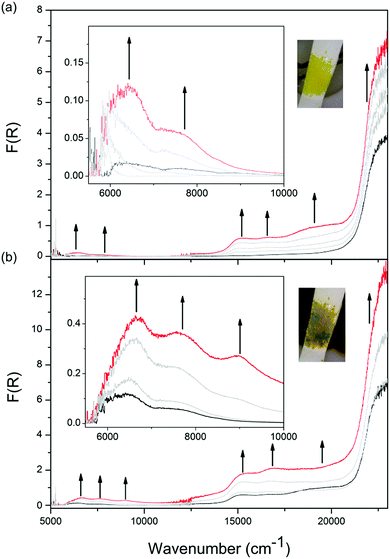
Solid state Vis-NIR SEC experiments were conducted on both 1-Zn (Fig. 4, ESI Fig. S7†) and 2-Cd (Fig. 5, ESI Fig. S9†), which revealed differing behaviour upon reduction which was correlated to subtle structural differences. The starting spectrum for the neutral state in the Vis-NIR SEC of 1-Zn was dominated by the edge of the UV-Vis π → π* transition for the DPPTzTz ligand at 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (peak position obtained from the UV-Vis-NIR spectrum of as-synthesised 1-Zn, ESI Fig. S17†). As an initial cathodic potential of −2.1 V vs. Ag/Ag+ was applied to 1-Zn, a set of bands in the visible region from 13
000 cm−1 (peak position obtained from the UV-Vis-NIR spectrum of as-synthesised 1-Zn, ESI Fig. S17†). As an initial cathodic potential of −2.1 V vs. Ag/Ag+ was applied to 1-Zn, a set of bands in the visible region from 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 25
000 to 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 appeared. These bands were assigned to intra-ligand radical processes for the monoanion radical of DPPTzTz, in accordance with the reductive Vis-NIR SEC behaviour of the DPPTzTz ligand itself (ESI Fig. S5a†). Two distinct bands also appeared in the NIR region (deconvoluted spectrum shown in ESI Fig. S23a†), which were not observed in the Vis-NIR SEC of the DPPTzTz ligand (ESI Fig. S5a†). The NIR bands were assigned to a through-space IVCT transition between cofacial DPPTzTz ligands, which exist in a mixed-valence state that involves the monoanion radical state of one DPPTzTz ligand in each cofacial pair. Increasing the applied reductive potential to −2.4 V in 1-Zn resulted in the equilibration of all visible region radical bands to their maximum intensities, suggesting that the radical mixed-valence state was being accessed fully throughout the 1-Zn sample. This corresponded to a colour change from yellow in the neutral state, to deep green in the mixed-valence state. In the NIR region, the IVCT band also intensified to its maximal value at −2.4 V. Further holding the potential at −2.4 V resulted in a moderate reduction in the intensities of the radical transitions in the visible region (ESI Fig. S7d†). This was correlated with the gradual reduction to the fully reduced double dianion state within a portion of DPPTzTz cofacial dimer units, in accord with trends observed in the Vis-NIR SEC of the DPPTzTz ligand itself (ESI Fig. S5b†). Reduction to the double dianion configuration also breaks the mixed-valence interaction within cofacial DPPTzTz dimers, consistent with the observed decrease in intensity of the mixed-valence IVCT transition in the NIR region.
000 cm−1 appeared. These bands were assigned to intra-ligand radical processes for the monoanion radical of DPPTzTz, in accordance with the reductive Vis-NIR SEC behaviour of the DPPTzTz ligand itself (ESI Fig. S5a†). Two distinct bands also appeared in the NIR region (deconvoluted spectrum shown in ESI Fig. S23a†), which were not observed in the Vis-NIR SEC of the DPPTzTz ligand (ESI Fig. S5a†). The NIR bands were assigned to a through-space IVCT transition between cofacial DPPTzTz ligands, which exist in a mixed-valence state that involves the monoanion radical state of one DPPTzTz ligand in each cofacial pair. Increasing the applied reductive potential to −2.4 V in 1-Zn resulted in the equilibration of all visible region radical bands to their maximum intensities, suggesting that the radical mixed-valence state was being accessed fully throughout the 1-Zn sample. This corresponded to a colour change from yellow in the neutral state, to deep green in the mixed-valence state. In the NIR region, the IVCT band also intensified to its maximal value at −2.4 V. Further holding the potential at −2.4 V resulted in a moderate reduction in the intensities of the radical transitions in the visible region (ESI Fig. S7d†). This was correlated with the gradual reduction to the fully reduced double dianion state within a portion of DPPTzTz cofacial dimer units, in accord with trends observed in the Vis-NIR SEC of the DPPTzTz ligand itself (ESI Fig. S5b†). Reduction to the double dianion configuration also breaks the mixed-valence interaction within cofacial DPPTzTz dimers, consistent with the observed decrease in intensity of the mixed-valence IVCT transition in the NIR region.
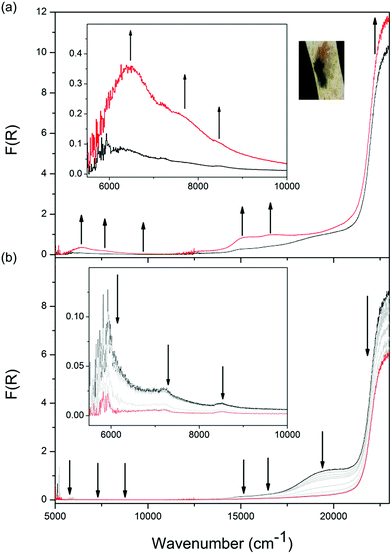
The Vis-NIR SEC behaviour of 2-Cd is similar to that of 1-Zn, aside from two key points of difference. Firstly, as the monoanion radical state was being accessed in 2-Cd, a further distinctive visible band at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 appeared at −2.1 V vs. Ag/Ag+ (ESI Fig. S9a†), which was not observed for 1-Zn. This was assigned to a ligand to metal charge transfer (LMCT) process in 2-Cd,21 facilitated by the more diffuse d-orbitals on Cd(II) compared to Zn(II). The LMCT transition at 19
000 cm−1 appeared at −2.1 V vs. Ag/Ag+ (ESI Fig. S9a†), which was not observed for 1-Zn. This was assigned to a ligand to metal charge transfer (LMCT) process in 2-Cd,21 facilitated by the more diffuse d-orbitals on Cd(II) compared to Zn(II). The LMCT transition at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 subsequently decreased as the applied potential was increased to −2.3 V (ESI Fig. S9b†).
000 cm−1 subsequently decreased as the applied potential was increased to −2.3 V (ESI Fig. S9b†).
The most significant difference between the Vis-NIR SEC behaviour of 2-Cd and 1-Zn was apparent when the applied potential was held at −2.4 V. For 1-Zn, this resulted in the accessing of the fully reduced double dianion configuration within only a portion of DPPTzTz dimer units. On the other hand, for 2-Cd a reduction in intensities for all bands except for the UV π → π* band was observed, resulting in the disappearance of all transitions associated with the radical in the visible and NIR regions (Fig. 5b). In the latter case, the behaviour suggests that the double dianion state for DPPTzTz cofacial dimers in 2-Cd is more readily accessed compared with 1-Zn.
The differences in the spectroelectrochemical behaviour at the potential at −2.4 V can be rationalised by considering the structural differences between 2-Cd and 1-Zn. From the crystallographic studies of both frameworks, it was observed that the DPPTzTz ligands in 2-Cd adopt a spatial configuration that is less favourable for cofacial interactions than in 1-Zn, with a larger cofacial distance and degree of slippage in the offset stacking. The variation in cofacial stacking results in weaker IVCT interactions in 2-Cd compared to 1-Zn, decreasing the favourability of the mixed-valence IVCT state (and increasing the favourability of the double dianion state) in 2-Cd. This observation is closely related to that made by Hupp et al. for through-space IVCT in discrete molecular rectangle systems,3b where an alignment of chromophores in the mixed-valence state increased the cofacial interactions, compared with the slipped conformation in the neutral state. Such structural influences on cofacial IVCT interactions are also alluded to by the unit cell parameters obtained from Pawley extractions of the PXRD patterns for 1-Zn and 2-Cd, where noticeably larger changes were observed for 2-Cd (particularly in the α-angle) compared to 1-Zn upon chemical reduction to the mixed-valence IVCT state.
Finally, to demonstrate redox reversibility for both frameworks, the applied potential was returned from −2.4 to 0 V, regenerating the starting spectrum in 1 h. The appearance of radical and NIR IVCT transitions were reproduced by UV-Vis-NIR experiments on chemically reduced samples of both 1-Zn and 2-Cd (ESI Fig. S17 and S18†).
Quantification of solid state SEC data and IVCT analysis
In order to apply Marcus–Hush theory to the IVCT bands, quantification of the molar extinction coefficient of the NIR band was performed. This was not achievable by direct solid state spectroscopic measurements of chemically reduced samples due to difficulties in ensuring that the samples would not auto-oxidise in air during the measurements. Thus, an alternate methodology was developed.Quantification of NIR bands was achieved by first determining the molar extinction coefficient of the π → π* band at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 cm−1 in the neutral frameworks using transmission measurements on KBr pellets containing the framework at various dilutions (see ESI†). From the extinction coefficient of the π → π* band in the neutral 1-Zn and 2-Cd systems, the molar extinction coefficient of the NIR bands in the mixed-valence frameworks were calculated using Vis-NIR SEC data (Fig. 4 and 5). This was performed by first converting the units of Kubelka–Munk F(R) to percent reflectance (% R), then to percent transmission (% T) by applying a modified form of the Kubelka–Munk theory22 (discussed in detail in the ESI†) and then finally to absorbance using A = 2 − log(% T) for both the UV-Vis π → π* band in the neutral frameworks, and the NIR IVCT band for the mixed-valence frameworks. Comparison of the absorbance value of the π → π* band of the neutral frameworks with that of the NIR IVCT band of the corresponding electrochemically reduced framework yielded the molar extinction coefficient of the NIR IVCT band as 64.8 cm−1 M−1 for 1-Zn and 19.6 cm−1 M−1 for 2-Cd. Note here that the lowest energy component of the NIR band manifold is used for the IVCT analysis as it corresponds to the thermal electron transfer pathway and can be used to assess the extent of delocalisation in the ground state.23,24
680 cm−1 in the neutral frameworks using transmission measurements on KBr pellets containing the framework at various dilutions (see ESI†). From the extinction coefficient of the π → π* band in the neutral 1-Zn and 2-Cd systems, the molar extinction coefficient of the NIR bands in the mixed-valence frameworks were calculated using Vis-NIR SEC data (Fig. 4 and 5). This was performed by first converting the units of Kubelka–Munk F(R) to percent reflectance (% R), then to percent transmission (% T) by applying a modified form of the Kubelka–Munk theory22 (discussed in detail in the ESI†) and then finally to absorbance using A = 2 − log(% T) for both the UV-Vis π → π* band in the neutral frameworks, and the NIR IVCT band for the mixed-valence frameworks. Comparison of the absorbance value of the π → π* band of the neutral frameworks with that of the NIR IVCT band of the corresponding electrochemically reduced framework yielded the molar extinction coefficient of the NIR IVCT band as 64.8 cm−1 M−1 for 1-Zn and 19.6 cm−1 M−1 for 2-Cd. Note here that the lowest energy component of the NIR band manifold is used for the IVCT analysis as it corresponds to the thermal electron transfer pathway and can be used to assess the extent of delocalisation in the ground state.23,24
By subsequently applying the relationships derived by Hush,15 it was deduced that both mixed-valence frameworks fall within the Class II designation of the Robin and Day classification scheme for electron transfer.16 For clarity, equations applied in this and the following mobility calculations are detailed in the ESI.† First, the bandwidths-at-half-height were experimentally determined to be 1090 cm−1 for 1-Zn and 1030 cm−1 for 2-Cd, which are narrower than those calculated theoretically (see ESI† eqn (1), values provided in Table 1). The electronic coupling constant Hab was then calculated (using ESI† eqn (2)), to be 118 cm−1 for 1-Zn and 61.2 cm−1 for 2-Cd. Since 2Hab ≪ νmax for both frameworks, this confirms that a localised through-space IVCT interaction occurs between the DPPTzTz ligand pairs in the mixed-valence form of both frameworks. The large difference in the electronic coupling values, denoted by Hab, for the frameworks is contrasted by the small difference of 0.03 Å in the TzTz cofacial stacking distance observed between 1-Zn and 2-Cd. This can be attributed to the difference in the relative slippage of TzTz units, where there is a larger offset in the cofacial stacking for 2-Cd which would diminish the extent of electronic coupling. The relative Hab values also reflect the exponential relationship derived by Hush for the distance dependence of electronic coupling in dimeric systems.15a
| Parameter | 1-Zn | 2-Cd |
|---|---|---|
| Energy of IVCT band (cm−1) | 6580 | 6340 |
| Absorbance | 0.314 | 0.128 |
| Molar extinction coefficient (cm−1 M−1) | 64.8 | 19.6 |
| Bandwidth-at-half-height (cm−1) | 1090 | 1030 |
| Theoretical bandwidth-at-half-height (cm−1) | 3900 | 3830 |
| H ab (cm−1) | 118 | 61.2 |
| Tunnelling matrix element Tda (eV) | 0.00371 | 0.00194 |
| Frequency factor νet (s−1) | 1.60 × 1012 | 4.47 × 1011 |
| Mobility k (s−1) | 6.02 × 108 | 2.22 × 108 |
Although charge mobility in discrete organometallic molecules exhibiting through-bond IVCT25 as well as for the special pair radical cation in bacterial photosynthesis26 has been quantified extensively, its calculation for solid state extended framework systems has not been performed thus far. This is primarily due to obstacles faced when quantifying molar extinction coefficients from solid state spectroscopic data. Herein, from the molar extinction coefficients quantified from solid state SEC data, the rates of charge transfer within cofacial DPPTzTz dimers were calculated for both 1-Zn and 2-Cd. As IVCT is localised within DPPTzTz dimers, which can be considered to be symmetrical systems with no significant electronic influence from outer sphere factors, the general equations and calculations applicable to symmetric discrete mixed-valence dimeric systems were used.17 Note that these relationships were developed from classical theory by Hush. First, the electron tunnelling matrix element Tda was calculated for both frameworks (ESI† eqn (3)), from which the frequency factor of electron transfer νet was calculated (ESI† eqn (4)) and applied to the Arrhenius-type equation (ESI† eqn (5)). The rates of electron transfer within cofacial dimer units of DPPTzTz were determined as k = 6.02 × 108 s−1 for 1-Zn and k = 2.22 × 108 s−1 for 2-Cd.
From the calculated values, it can be deduced that electron transfer occurs less favourably in 2-Cd when compared to 1-Zn. In comparison with discrete dimeric systems featuring through-bond IVCT however, these values for charge mobility are an order of magnitude smaller,22 potentially representing the higher energy penalty for charge transfer to occur through-space in comparison with through-bond. In the context of framework systems displaying IVCT, these calculations bridge the gap between theory and practice traditionally associated with solid state materials.
Conclusions
The difference in the charge transfer properties of two topologically related frameworks featuring Zn(II) and Cd(II) nodes and cofacially stacked pairs of the DPPTzTz redox-active ligand were investigated and attributed to the subtle changes in framework structures. Upon electrochemical reduction to the mixed-valence state, the Vis-NIR SEC of both frameworks revealed through-space IVCT within cofacial DPPTzTz pairs. The smaller intensity of the IVCT interaction in 2-Cd when compared to 1-Zn was correlated to the longer Cd–O bonds at the metal node, resulting in the DPPTzTz cofacial dimers adopting an increasingly slipped configuration with a lower degree of cofacial contact and increased stacking distance, therefore decreasing the IVCT interaction. Quantification of the NIR IVCT band was achieved for both frameworks from the solid state SEC spectra, facilitating the application of Marcus–Hush theory and allowing the electron mobility within cofacial DPPTzTz pairs in the mixed-valence state to be calculated.The development of a protocol for quantifying solid state SEC data has led to the application of an array of quantitative theoretical analyses. This greatly increases the level of application and correlation with charge transfer theory for extended framework materials. In the future, these materials can be exploited as structurally stable systems to model and study charge transfer in nature, whilst the greater theoretical understanding of IVCT will bring us closer to realising their use in applications including redox catalysis, artificial photosynthesis and electrochromic devices, amongst others.
Experimental
Materials
All reagents and solvents employed were obtained commercially, and used as received without further purification, unless otherwise stated. For electrochemical experiments, MeCN was dried over CaH2 and distilled under N2. Pd(PPh3)4 was synthesised according to literature procedure27 and dry THF was obtained from a Puresolv solvent purification system.General methods
Solution state 1H and 13C{1H} NMR spectra of all ligands were collected on either a Bruker AVANCEIII 300 MHz or 400 MHz spectrometer at 298 K. Deuterated solvents used for collection of spectra were obtained from Cambridge Isotope Laboratories, and their solvent residual signals were used as internal references for chemical shifts (δ). Electrospray Ionisation (ESI) mass spectrometry data were collected on a Bruker amaZon SL mass spectrometer, scanning along a mass range m/z 50–4000. The samples were dissolved in reagent grade MeOH or MeCN. Elemental analyses were performed at the Chemical Analysis Facility – Elemental Analysis Service at Macquarie University, NSW Australia. PXRD data were collected with a PANanalytical X'Pert PRO Multi-Purpose Diffractometer producing Cu-Kα (λ = 1.5406 Å) radiation, fitted with a solid state PIXcel detector. Air sensitive samples were measured in sealed glass capillary tubes. Thermogravimetric analysis (TGA) was performed on a TA Instruments Discovery TGA at a heating rate of 2 °C min−1, under a constant stream of N2 at a flow rate of ca. 0.02 mL min−1. All UV-Vis-NIR data were collected with a CARY5000 spectrometer interfaced to Varian Win UV software. Powder diffuse reflectance data were collected with a Harrick Praying Mantis attachment, with air sensitive samples being loaded into an ambient atmosphere Harrick air-tight dome in an Ar glove box. Transmission measurements for KBr pellets were performed with a simple pellet transmission bracket, whilst pellet diffuse reflectance data were obtained with a Harrick Omni-Diff probe attachment. EPR spectra were collected at RT on a benchtop Bruker EMXnano EPR spectrometer interfaced with Xenon software, with signals referenced to strong pitch. Measurements were made at a modulation amplitude of 1.00 G, with the microwave attenuation varied from 8 to 25 dB.Framework synthesis
Single crystals of [Zn2(DPPTzTz)2(SDC)2]n suitable for analysis were obtained using the same reaction conditions as described above, except with a 15-fold reduction in concentration of reagents.
Single crystals of [Cd2(DPPTzTz)2(SDC)2]n suitable for analysis were obtained from the sides of the bulk synthesis reaction vials.
Chemical reductions of all frameworks were performed under an inert atmosphere in an Ar glove box, with 0.1 M lithium naphthalenide (LiNP) in THF prepared according to a literature procedure.28 Varying amounts of the reductant solution, calculated to stoichiometric ratios relative to the TzTz core, were added to the framework powders and the resulting suspension allowed to sit for 1 h. The reduced powders were isolated by filtration, washed with dry THF (3 × 2 mL) and stored under an inert atmosphere within the glove box.
The ratio of Li+ against that of Zn2+ and Cd2+ in the reduced frameworks was used as a measure of the degree of chemical reduction and were determined using solution inductively coupled plasma atomic emission spectrometry (ICP-AES) at the Mark Wainwright Analytical Centre at the University of New South Wales, NSW Australia.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 (1-Zn) and SHELXT32 (2-Cd) and refined with SHELXL-2014/7.33 An absorption correction was applied for 2-Cd using XDS.34 A riding atom model with group displacement parameters was used for the hydrogen atoms.
31 (1-Zn) and SHELXT32 (2-Cd) and refined with SHELXL-2014/7.33 An absorption correction was applied for 2-Cd using XDS.34 A riding atom model with group displacement parameters was used for the hydrogen atoms.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509, Nind 21
509, Nind 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 (Rmerge 0.0995), Nobs 13
132 (Rmerge 0.0995), Nobs 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 593(I > 2θ(I)), Nvar 862, residuals ‡R1(F) 0.0580, wR2(F2) 0.1551, GoF(all) 0.955, Δρmin,max −1.787, 0.891 e− Å−3.
593(I > 2θ(I)), Nvar 862, residuals ‡R1(F) 0.0580, wR2(F2) 0.1551, GoF(all) 0.955, Δρmin,max −1.787, 0.891 e− Å−3.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group (#2), a 15.868(3), b 19.123(4), c 26.124(5) Å, α 82.02(3), β 87.25(3), γ 89.73(3)°, V 7841(3) Å3, Dc 1.318 g cm−3, Z 2, crystal size 0.08 × 0.06 × 0.04 mm, colour yellow, habit block, temperature 100(2) K, λ(synchrotron) 0.71073 Å, μ(synchrotron) 1.626 mm−1, T(XDS)min,max 0.3564, 0.4318, 2θmax 58.43°, hkl range −21 21, −25 25, −32 32, N 109
space group (#2), a 15.868(3), b 19.123(4), c 26.124(5) Å, α 82.02(3), β 87.25(3), γ 89.73(3)°, V 7841(3) Å3, Dc 1.318 g cm−3, Z 2, crystal size 0.08 × 0.06 × 0.04 mm, colour yellow, habit block, temperature 100(2) K, λ(synchrotron) 0.71073 Å, μ(synchrotron) 1.626 mm−1, T(XDS)min,max 0.3564, 0.4318, 2θmax 58.43°, hkl range −21 21, −25 25, −32 32, N 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850, Nind 28
850, Nind 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473 (Rmerge 0.0907), Nobs 18
473 (Rmerge 0.0907), Nobs 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 399(I > 2θ(I)), Nvar 1575, residuals ‡R1(F) 0.1193, wR2(F2) 0.3490, GoF(all) 1.286, Δρmin,max −2.335, 4.312 e− Å−3.
399(I > 2θ(I)), Nvar 1575, residuals ‡R1(F) 0.1193, wR2(F2) 0.3490, GoF(all) 1.286, Δρmin,max −2.335, 4.312 e− Å−3.
Solid state electrochemistry
Solid state cyclic voltammetry and square wave voltammetry experiments were performed with a BASi Epsilon Electrochemical Analyser with ferrocene/ferrocenium (Fc/Fc+) as an internal reference. Measurements were taken under an inert Ar atmosphere in 0.1 M [n-Bu4N]PF6/MeCN or KCl/H2O electrolyte in a single compartment cell, with a platinum counter electrode, an Ag/Ag+ quasi-reference electrode and a glassy carbon working electrode. For measurements in 0.1 M KCl/H2O an Ag/AgCl aqueous reference electrode was applied. Powder samples were immobilised onto the working electrode surface by dipping the electrode into a paste made with MeCN.Solid state Vis-NIR spectroelectrochemistry
Solid state Vis-NIR SEC data were collected using a CARY 5000 UV-Vis-NIR spectrometer, using a Harrick Omni-Diff probe and a custom SEC cell of Teflon construction featuring a platinum wire counter electrode, Ag/Ag+ quasi-reference electrode and 0.1 M [n-Bu4N]PF6/MeCN electrolyte.13a The sample was immobilised onto the conductive surface of an indium–tin–oxide (ITO) coated glass slide using Teflon tape to form the working electrode. The potential applied to the cell was controlled using an eDaq e-corder 410 potentiostat. Continuous diffuse reflectance scans of the sample were collected at various applied potentials.Solid state EPR spectroelectrochemistry
A Bruker EMXnano EPR spectrometer was used to collect solid state EPR SEC data. For organic radical data, the microwave attenuation was set to 8 dB and receiver gain was tuned to prevent signal saturation. The EPR SEC cell was constructed from a Pasteur pipette flame sealed at the thin end, filled to half way with 0.1 M [n-Bu4N]PF6/MeCN electrolyte. Three electrodes were connected to separate copper wire inserts, held in place and isolated from each other at points of connection with Teflon tape, were then dipped into the electrolyte in a staggered fashion, featuring a short bare platinum counter electrode, medium length Teflon coated Ag/Ag+ quasi-reference electrode and a long Teflon coated platinum working electrode, to prevent short circuiting. The tip of the working electrode was connected to a piece of platinum gauze encasing the sample onto which the cell was centred.35,36 EPR scans, referenced externally to strong pitch, were then run at various potentials and controlled using an eDaq e-corder 410 potentiostat.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the Australian Research Council, the Australian Synchrotron, the Vibrational Spectroscopy Core Facility and Sydney Nano at the University of Sydney for their support of this work. We also thank Associate Professor Brendan Abrahams for assistance in the collection of crystallographic data, Dr Ivan Kassal for discussion on the mobility calculations, and Emeritus Professor Noel Hush for his advice on aspects of the theoretical analysis.Notes and references
- (a) L. L. Shipman, T. M. Cotton, J. R. Norris and J. J Katz, Proc. Natl. Acad. Sci. U. S. A., 1976, 73, 1791 CrossRef CAS PubMed; (b) J. Deisenhofer, O. Epp, K. Miki, R. Huber and H. Michel, Nature, 1985, 318, 618 CrossRef CAS PubMed.
- (a) H. Ozeki, A. Nomoto, K. Ogawa, Y. Kobuke, M. Murakami, K. Hosoda, M. Ohtani, S. Nakashima, H. Miyasaka and T. Okada, Chem.–Eur. J., 2004, 10, 6393 CrossRef CAS PubMed; (b) Y. Kuramochi, A. Satake, M. Itou, K. Ogawa, Y. Araki, O. Ito and Y. Kobuke, Chem.–Eur. J., 2008, 14, 2827 CrossRef CAS PubMed; (c) A. C. Benniston, G. Copley, A. Harriman, D. Howegego, R. W. Garrington and W. Clegg, J. Org. Chem., 2010, 75, 2018 CrossRef CAS PubMed.
- (a) P. H. Dinolfo and J. T. Hupp, J. Am. Chem. Soc., 2004, 126, 16814 CrossRef CAS PubMed; (b) P. H. Dinolfo, M. E. Williams, C. L. Stern and J. T. Hupp, J. Am. Chem. Soc., 2004, 126, 12989 CrossRef CAS PubMed; (c) P. H. Dinolfo, S. J. Lee, V. Coropceanu, J. Bredas and J. T. Hupp, Inorg. Chem., 2005, 44, 5789 CrossRef CAS PubMed.
- D. M. D'Alessandro, Chem. Commun., 2016, 52, 8957 RSC.
- M. B. Solomon, T. L. Church and D. M. D'Alessandro, CrystEngComm, 2017, 19, 4049 RSC.
- L. Wang, Y. Han, J. Zhou, P. Qi and B. Wang, Coord. Chem. Rev., 2016, 307, 361 CrossRef CAS.
- (a) C. F. Leong, P. M. Usov and D. M. D'Alessandro, MRS Bull., 2016, 41, 858 CrossRef; (b) L. Sun, M. G. Campbell and M. Dinca, Angew. Chem., Int. Ed., 2016, 55, 3566 CrossRef CAS PubMed; (c) P. M. Usov, C. F. Leong and D. M. D'Alessandro, in Monographs in Supramolecular Chemistry, ed. R. Banerjee, Royal Society of Chemistry Publishing, Cambridge, 2017, p. 247 Search PubMed.
- C. F. Leong, B. Chan, T. B. Faust and D. M. D'Alessandro, Chem. Sci., 2014, 5, 4724 RSC.
- D. M. D'Alessandro, J. R. R. Kanga and J. S. Caddy, Aust. J. Chem., 2011, 64, 718 CrossRef.
- R. Murase, C. F. Leong and D. M. D'Alessandro, Inorg. Chem., 2017, 56, 14373 CrossRef CAS PubMed.
- L. E. Darago, M. L. Aubrey, C. J. Yu, M. I. Gonzalez and J. R. Long, J. Am. Chem. Soc., 2015, 137, 15703 CrossRef CAS PubMed.
- (a) D. Mapoch, D. Ruiz-Molina and J. Veciana, Chem. Soc. Rev., 2007, 36, 770 RSC; (b) B. Kong, C. Selomulya, G. Zheng and D. Zhao, Chem. Soc. Rev., 2015, 44, 7997 RSC.
- (a) P. M. Usov, C. Fabian and D. M. D'Alessandro, Chem. Commun., 2012, 48, 3945 RSC; (b) C. Hua, B. Chan, A. Rawal, F. Tuna, D. Collison, J. M. Hook and D. M. D'Alessandro, J. Mater. Chem. C, 2016, 4, 2535 RSC.
- P. R. Murray, D. Collison, S. Daff, N. Austin, R. Edge, B. W. Flynn, L. Jack, F. Leroux, E. J. L. McInnes, A. F. Murray, D. Sells, T. Stevenson, J. Wolowska and L. J. Yellowlees, J. Magn. Reson., 2011, 213, 206 CrossRef CAS PubMed.
- (a) N. S. Hush, Electrochim. Acta, 1968, 13, 1005 CrossRef CAS; (b) D. M. D'Alessandro and F. R. Keene, Chem. Rev., 2006, 106, 2270 CrossRef PubMed.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1967, 10, 247 CrossRef CAS.
- (a) T. J. Meyer, Chem. Phys. Lett., 1979, 64, 417 CrossRef CAS; (b) S. J. England, P. Kathirgamanathan and D. R. Rosseinsky, J. Chem. Soc., Chem. Commun., 1980, 840 RSC.
- A. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9 CrossRef CAS PubMed.
- M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782 CrossRef PubMed.
- (a) F. J. Rizzuto, T. B. Faust, B. Chan, C. Hua, D. M. D'Alessandro and C. J. Kepert, Chem.–Eur. J., 2014, 20, 17597 CrossRef CAS PubMed; (b) F. J. Rizzuto, C. Hua, B. Chan, T. B. Faust, A. Rawal, C. F. Leong, J. M. Hook, C. J. Kepert and D. M. D'Alessandro, Phys. Chem. Chem. Phys., 2015, 17, 11252 RSC.
- Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126 CrossRef CAS PubMed.
- P. Kubelka, J. Opt. Soc. Am., 1948, 38, 448 CrossRef CAS PubMed.
- K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655 CrossRef CAS PubMed.
- C. Hua, P. W. Doheny, B. Ding, B. Chan, C. J. Kepert and D. M. D'Alessandro, J. Am. Chem. Soc., 2018, 140, 6622 CrossRef CAS PubMed.
- D. M. D'Alessandro and F. R. Keene, Chem. Soc. Rev., 2006, 35, 424 Search PubMed.
- J. R. Reimers and N. S. Hush, J. Am. Chem. Soc., 2004, 126, 4132 CrossRef CAS PubMed.
- D. R. Coulson, L. C. Satek and S. O. Grim, in Inorganic Chemistry, John Wiley & Sons, Inc., Hoboken, 2007, p. 121 Search PubMed.
- N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877 CrossRef CAS PubMed.
- T. M. McPhillips, S. E. McPhillips, H. J. Chiu, A. E. Cohen, A. M. Deacon, P. J. Ellis, E. Garman, A. Gonzalez, N. K. Sauter, R. P. Phizackerley, S. M. Soltis and P. J. Kuhn, Synchrotron Radiat., 2002, 9, 401 CrossRef CAS.
- L. Farrugia, J. Appl. Crystallogr., 1999, 32, 837 CrossRef CAS.
- G. M. Sheldrick, SHELX97 programs for crystal structure analysis, University of Gottingen, Germany, 1997 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A, 2015, 71, 3 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A, 2015, 71, 3 CrossRef PubMed.
- W. Kabsch, Acta Crystallogr., 2010, D66, 125 CrossRef PubMed.
- C. Hua, A. Baldansuren, F. Tuna, D. Collison and D. M. D'Alessandro, Inorg. Chem., 2016, 55, 7270 CrossRef CAS PubMed.
- P. R. Murray, D. Collison, S. Daff, N. Austin, R. Edge, B. W. Flynn, L. Jack, F. Leroux, E. J. L. McInnes, A. F. Murray, D. Sells, T. Stevenson, J. Wolowska and L. J. Yellowlees, J. Magn. Reson., 2011, 213, 206 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1585897 and 1585898. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc01128a |
| ‡ R1 = Σ||Fo| − |Fc||/Σ|Fo| for Fo > 2σ(Fo); wR2 = (Σw(Fo2 − Fc2)2/Σ(wFc2)2)1/2 all reflections w = 1/[σ2(Fo2) + (0.2000P)2] where P = (Fo2 + 2Fc2)/3. |
| This journal is © The Royal Society of Chemistry 2019 |