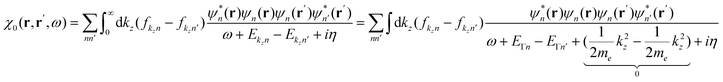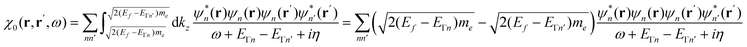Theory of hot electrons: general discussion

Sylwester Gawinkowski opened discussion of the paper by Javier Aizpurua: How many electrons are transferred by one ultrashort pulse? If you are thinking about applications in electronics, then it seems that this number may be too small. Is simply increasing the pulse energy and therefore significantly increasing the number of such emitted electrons possible?

Javier Aizpurua responded: From our calculations, we find that the average number of electrons transmitted by each pulse, for these particular conditions, is around 0.1 e for ∼100 nm long nanowires. This is small in terms of conduction, but it is measurable, and indeed our experimental colleagues at Konstanz and Luxembourg seem to obtain precisely this amount for such a situation. One should be careful when increasing the energy of the pulse. If you refer to the frequency of the pulse, then resonant effects can play a role and the current established is more complex. If you refer to an increase in power (amplitude increase), plasmonic gaps can handle a limited amount of power before melting, therefore there are limits to this too. We believe that the current rate is a good start for producing a more ambitious roadmap for ultrafast pulse-driven coherent optoelectronics.

Niclas Sven Mueller remarked: I am excited about the large gap sizes that you consider in your paper. These are much larger than 1 nm, where one would usually expect the onset of a tunnelling current for CW illumination. What is the scaling of the electron emission current with the gap size? What pump fluences are needed for a detectable net current?

Javier Aizpurua replied: You are right. Our range of distances is large enough so as to avoid the tunneling regime, and all of the current considered in our discussion is associated with ballistic transport of the electrons emitted by the strong optical field (note that this is the Fowler-Nordheim regime, which is completely different from photoemission by multiphoton absorption). The dependence of the current on the gap size can be derived from the quiver amplitude that we outline in our discussion: X_q = E₀/ω². This expression basically states that the quiver amplitude depends linearly on the amplitude of the field, which can be connected with the square root of the power applied in the pulse multiplied by an enhancement factor of the gap, G. As the gap distance, d_gap, is increased, the local field enhancement is reduced as 1/d_gap. Therefore, there will be a point at which the field induced in the gap will produce a very small quiver amplitude compared to the gap size (X_q≪d_gap), and thus the electrons will have very little chance to reach the electrode on the other side of the gap. The pump fluences needed to start detecting the current in the gap require a few picojoules per pulse, which generate fields of a few V nm⁻¹ in gaps of about 6 nm.

Mikael Kuisma asked: I have a question about your 2D equations of motion for a 3D system, where the kinetic energy in the z-direction is omitted and the k-point integration is replaced with varying occupation numbers. Is this an approximation of an exact formulation? I am asking this because we have observed that plasmons are sensitive to the electron-hole topology close to the Fermi level, i.e. long wavelength density fluctuations from holes just below the Fermi surface to electrons just above.

Looking at Equation 2 in your paper (DOI: 10.1039/c8fd00158h), I can see that one has omitted the kinetic energy towards the z-direction, which naively corresponds to infinite effective mass for electrons in the z-direction since 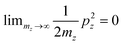. With the z-kinetic energy, the quadratic band dispersion due to the z translation symmetry of each band is given as 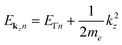. Now, in the irreducible response function, the poles are OK since the eigenvalue differences are conserved:

However, what about the occupation numbers when each band crosses the Fermi level at a different k_z? Upon such a crossing, the nature of excitations changes, as excitations from this band are no longer available, but this band can now accept excitations.

After taking a closer look at the equations of motion, I am now convinced that your approach is not only exact, but actually very intriguing. The exactness is actually easy to see; if we plug in the zero Kelvin Fermi distribution, 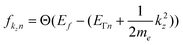, we find that the Heaviside function changes integration boundaries and then results in your occupation numbers:

My mistake is that I have been too used to thinking in terms of Grassman manifolds, i.e. the manifold of density matrices with eigenvalues of 1 and 0 only. Naturally, since your occupation values each have a distinct value, this correctly accounts for excitations from a partly occupied state to a less occupied state. In these 2D effective equations, instead of one Grassman manifold per k-point to represent the possible states of the system, one needs only one generalized flag manifold (i.e. the space of all density matrices with the given non integer occupations). Maybe this idea relating to the topology of electronic excitations could be used to analyze the collectivity of plasmons under continuous symmetries.

Javier Aizpurua answered: To the best of our knowledge, the equations of motion are correct. Although we numerically solve the 2D time-dependent problem, its formulation results from the reduction of the full 3D TDDFT equations in the Kohn–Sham form. Indeed, the invariance of the problem along the z-direction allows for a trivial factorization of the effect of the z-motion as 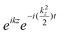. This leads to the corresponding weight factors, as given in the paper.

Johannes Lischner enquired: The method you present combines a potential from Maxwell’s equation with a solution of the Kohn–Sham equation. It appears as if this procedure double counts electron–electron interactions; they are first included through the dielectric function in the Maxwell equation solver and then again as the Hartree and exchange–correlation terms in the Kohn–Sham solver. Would it not be more accurate and simpler to solve the Kohn–Sham equations without electron–electron interactions? This would possibly allow for the modelling of larger systems and thus avoid the need to artificially localize the electron in an infinite wire (instead of modelling the full bow-tie structure).

Javier Aizpurua responded: In the current system discussed in our paper, the system is small enough to perform directly and exclusively the full quantum many-body calculation where an incident Gaussian pulse has been considered as the external perturbation that induces the response of the system. However, I mentioned in my presentation that, in practice, one often needs to treat larger systems (for example bow-tie antennas of several hundreds of nanometers), and in that case, one could implement an alternative strategy by decomposing the problem into two separate calculations: one involving the classical solution of the induced fields at the gap for the whole large system, and a second quantum calculation, more reduced to the area where current is produced (a few square nanometers), to properly account for all of the quantum aspects of the dynamics of the transport along the optical cycle.

We are pretty sure that in this procedure there is no double counting of the field enhancement. If one implemented TDDFT calculations with the aim of reproducing experimental data, the incident pulse could be set such that the self-consistent field in the junction would be equal to the field obtained by solving classical Maxwell’s equations for the actual experimental field profile. However, it should be noted that in our current discussion the incident pulse considered in the TDDFT calculations is a perfectly Gaussian one, and not an experimental one.

We have tested the use of this splitting of the problem into classical and quantum calculations, and made sure that we were not double counting the electron interactions and their corresponding fields. In particular, we compared the results of the full calculation and the split calculations for a small system, and found excellent agreement. I presume that the option you suggest (removing the electron–electron interactions) would rather jeopardize the results, and would not provide such an improvement in the size of the doable systems. Therefore, we prefer to adopt this split strategy which has thus far proven to be valid. We are implementing such an approach and expect to publish the results soon.

Naomi Halas questioned: In the experiments you are describing in your theoretical study of nanogaps, is a small bias voltage being applied, and is that not responsible for the currents being measured?

Javier Aizpurua replied: In this purely theoretical paper we consider a plasmonic gap illuminated with a Gaussian sub-cycle pulse. No constant fields were applied. Thus, the effects reported in this work result from the sensitivity of the optical field emission to the CEP of the incident pulse, and the photocurrents measured in the experiments are produced by the incoming photons. It would however be interesting to bias the cavity, and observe to what extent the current can be controlled by the application of such an external bias.

Jeremy Baumberg queried: I am looking to gain an intuitive understanding as to why, when the maximum field is in one direction, the current is in the other direction. A positive voltage should result in a positive current. Is there a sign convention issue, and are you perhaps looking at electron flux, not current?

Javier Aizpurua answered: Yes, the sign is an issue of sign convention. We are looking at the electron current density. Thus, the electric field oriented in the positive direction of the x-axis produces electron currents flowing in the negative direction of the x-axis. This positive electric field amplitude will extract electrons from the right-hand side electrode with negative velocity towards the left-hand side electrode, as the charge of the electrons is negative. This is what we show in Fig. 4 of our paper (DOI: 10.1039/c8fd00158h), where every polarization of the field moves electrons in the opposite direction within the gap.

Andrea Marini remarked: Your paper reports experimental evidence of optical rectification by a plasmonic gap supported by a nice and convincing theoretical explanation of the process, which arises from the highly nonlinear potential inside the gap. Can you please comment on the opportunities offered by plasmonic gaps concerning high-harmonic generation (HHG)? Did you observe HHG in your theoretical calculations or in the experiments carried out?

Javier Aizpurua responded: We would like to stress that no experimental results are reported in our theoretical work in the current paper. I only mentioned that this theoretical work can explain the results of experiments that are still to come. In the current work, we focused on the effect of the plasmonic gap on the generation of DC current as a response to an ultrafast single-cycle pulse. However, in the past we have also studied the non-linear response of plasmonic gaps as a response to continuous optical illumination, and yes, we have identified a strong non-linear response including HHG. Furthermore, we have identified that the non-linear response can be associated either with the intrinsic non-linearity of the metal for large gap separations, or with the non-linear tunneling current generated at very narrow gaps. You can find information on this in the papers by G. Aguirregabiria et al.¹ and Marinica et al.²

1 G. Aguirregabiria, D. C. Marinica, R. Esteban, A. K. Kazansky, J. Aizpurua and A. G. Borisov, Phys. Rev. B, 2018, 97, 115430.

2 D. C. Marinica, A. K. Kazansky, P. Nordlander, J. Aizpurua and A. G. Borisov, Nano Lett., 2012, 12, 1333–1339.

Jacob Khurgin said: Thank you for your great talk. I have a few short questions:

(1) Have you considered the effect of polarization of light?

(2) Is it possible to trace the electrons in the lateral (yz) plane after they exit the metal?

(3) What if you use two metals with different work functions (‘rectenna’)?

(4) Can you relate your work to that carried out early on by Baranova et al.¹ on directional photoemission for the fields where the average cube is not zero?

1 N. B. Baranova and B. Ya. Zel’dovich, J. Opt. Soc. Am. B, 1991, 8, 27–32.

Javier Aizpurua replied: (1) In our description we consider the polarization of light to be perpendicular to the interfaces forming the gap, as this is the component that maximizes the field emission. If one was to polarize the pulse along the walls of the gap, the ejected electrons would not end up at the opposite antenna arm. Moreover, field enhancement would be non-operative, meaning that a higher amplitude of the incident pulse would be required to reach the optical field ionization regime.

(2) Yes, in our calculations the axis of symmetry is the z-axis, where the dynamics are assumed to be translationally invariant. However, in the y direction the electrons follow a motion dictated by the boundary conditions across the gap and the local fields, thus this aspect of the motion is well considered in our calculations. In practice, a gap antenna is usually cut in the z direction (usually a few tens of nanometers), therefore the relevant motion when it comes to establishing the net current in the device can be assumed to be exclusively due to the transverse motion, with a relatively small contribution of lateral components.

(3) The use of metals with different work functions would be interesting. We have not modelled this explicitly, but one could anticipate that the effect will be either to enhance or mitigate the effect of the main peak of the incident pulse, depending on whether the polarization of the pulse peak extracts electrons from one or the other metal.

(4) The process that you refer to is particularly focused on the interference of two photons at frequency ω and one at frequency 2ω, which can produce directional emission originating from the non-linear response of the material. In our case, the source of directionality is clearly the polarization of the incident field, as pointed out above.

Anatoly Zayats enquired: There may be 2 different kinds of rectification in the illuminated tunnel junction. If the tunnelling junction consists of 2 different metals, the current–voltage curve will be asymmetric, which will automatically result in the rectification of the electric field of the incident light. On the other hand, in the considered geometry under ultrashort pulse illumination, nonlinear optical effects may be important, leading to nonlinear rectification, viz. second-order susceptibility. Which rectification did you consider?

Javier Aizpurua answered: The sources of optical rectification, i.e. a DC component of current arising from an AC excitation, that you mention are the standard ones, originating either from asymmetry in the material, which unbalances the flow of current at both sides of a heterogeneous metallic junction, or from an association with the second-order non-linear tensor response of the material. Additionally, for ultrasmall gaps there would be a source of nonlinearity associated with the tunneling current itself.¹ In our discussion, however, the source of the DC component of the current is the optical field emission (also quoted as strong AC field ionization) associated with the strong asymmetry of the single-cycle pulse itself. Different to multiphoton ionization, the optical field emission and thus the electron transport across the gap is sensitive to the carrier envelope phase (CEP). This CEP sensitivity is well known in atomic physics and in strong field emission from metallic tips. Thus, our ‘source’ of rectification is different and relies on the single-cycle temporal profile of the pulse.

1 G. Aguirregabiria, D. C. Marinica, R. Esteban, A. K. Kazansky, J. Aizpurua and A. G. Borisov, Phys. Rev. B, 2018, 97, 115430.

Francesca Baletto asked: Does the geometry (e.g. curvature) of the cylinders affect your results? How about in the case of a square nano-antenna in front of a cylindrical one? Do you think there is the opportunity to design plasmonic gaps?

Javier Aizpurua responded: As far as the junction is symmetric, the results reported here will not change qualitatively since the underlying physics of the strong optical field emission are very robust, provided that the field enhancement in the junction is sufficient to drive the system in this regime of strong field emission. For weak fields, one deals with photoemission by multiphoton absorption which is not sensitive to the CEP of the pulse. For asymmetric junctions like the one you have pointed out, i.e. a square nano-antenna in front of a cylindrical one, the net electron transfer will ultimately be influenced by the different geometries and, a priori, both regimes, i.e. optical field emission and multiphoton photoemission, will occur. Another aspect is the influence of the macroscopic shape (larger scale structures). The actual shape of the nanoantenna forming the gap sets the plasmonic resonance, and thus it will establish the spectral region in which the incident pulse might behave differently. The response of the gap near the plasmonic resonance introduces a phase shift in the induced field at those frequencies, and thus its spectral proximity to the energy of the incident pulse is a very relevant aspect. In this respect, the design of the shape and separation distance of the gap can be engineered to produce different spectral responses. In the current work we have focused on a small cylindrical system in order to focus on the physics of strong-field emission, rather than on the macroscopic plasmonic resonance.

Bart de Nijs opened discussion of Stephanie Reich’s paper: In your system, you rely on s-polarized light to excite dark modes in your self-assembled gold structures. However, if you send polarized light through a high (0.9) NA objective there will also be a nearly equal amount of p-polarized light after the objective. How does this affect your system, especially when multiple layers are probed where p-polarized light can potentially excite a vertical dipole in the stacked gold structures?

Stephanie Reich replied: We worried about this point as well and therefore performed experiments with 20× objectives (NA of 0.25). There is no difference between the spectra measured with 100× and 20× objectives despite the much larger spot size and smaller NA, as shown in Fig. 6 of our paper (DOI: 10.1039/c8fd00149a). We thereby ruled out a significant contribution of p-polarized radiation. We also note that the z-polarized plasmonic excitations are at much higher frequency in the bilayer system.

Preeti Deshpande remarked: In this work you have shown that the generation of dark plasmons is possible with a particle size of 40–50 nm. Will the system work if we increase the particle size to 140–150 nm in diameter? Does the field retardation in large size particles assist or inhibit dark plasmon generation?

What is the role of spacing between the particle layers? How will the system behave if we reduce the separation to sub-nm gaps?

Will the system work for other plasmonic materials, e.g. silver?

Stephanie Reich answered: The dark mode can also be excited in particle bilayers made up of nanoparticles with diameters of 100–200 nm. The activation mechanism has no upper limit. If the size of the nanoparticles themselves becomes comparable to the light wavelength, we expect the excitation of layer modes that combine the quadrupole excitation of the individual particles. We expect a very rich excitation spectrum in this situation. For the excitation and extraction of hot electrons however, smaller nanoparticles are preferred. Energetic electrons inside large nanoparticles will not reach the surface before losing their energy. It is thus of limited use for energy harvesting, catalysis and other applications that we have in mind for hot electrons.

The spacing between the particles creates plasmonic hotspots. We expect them to contribute to dephasing and thus increase the number of highly excited hot electrons. Reducing the nanoparticle separation below 0.5 nm will likely lift the localization of the electrons on the nanoparticles. The system will then behave like a piece of bulk metal.

The excitation of dark modes will occur for any plasmonic material (silver, aluminum, highly doped semiconductors etc.). There is nothing material specific in our reasoning. Of course, the frequency of the dark mode will strongly depend on the choice of material.

Yuri Diaz Fernandez said: I have two questions. (1) Have you tried different shapes of particles?

(2) What is the role of defects and how reproducible and scalable is your sample preparation method?

Stephanie Reich responded: (1) No, we have not. The plasmonic excitations that we consider are eigenmodes of the two-dimensional nanoparticle lattice. Other shapes will make it much harder to produce films with long range order.

2) Defects and stacking faults did not affect our experiments. We scanned large areas of the sample and reproducibly obtained identical spectra (see Fig. 6 of our paper). Most recent films extended over hundreds of microns. Increasing the size even further is the subject of ongoing work.

Bartlomiej Jankiewicz asked: Isn’t the stabilizing layer you used for the Au NPs influencing the efficiency of hot-electron generation? If you use, for example, Cu NPs instead of AuNPs, would there be a big drop in hot electron generation?

Stephanie Reich replied: Our key point is that the use of dark instead of bright modes for hot electron generation eliminates an undesired relaxation channel. Radiative relaxation, as occurs for bright modes, will carry away large quanta of energy (1–3 eV depending on the wavelength) without producing any hot electrons. Dark modes exhibit less radiative decay, i.e. more excited electrons remain available for hot electron generation. Any other parameter that affects hot electron generation, such as the choice of material, stabilizing layers, crystalline quality and so forth, will equally affect the dark and bright plasmon modes.

Jeremy Baumberg remarked: These are beautiful structures! I am trying to clarify your nomenclature, and am wondering about the use of the word ‘dark’. This system is far from a dimer, where the dark mode has the field transverse to each nanoparticle and not in the gaps. Can you show an additional plot of the field distribution at the low energy mode resonance in your bilayer system, in order to see where the light is concentrated? This would help in the understanding of whether it is concentrated in horizontal and vertical gaps (and thus rather similar to existing gap modes, e.g. in dimer-on-mirror work).

Essentially, since dark modes can arise from symmetry or poor coupling, is this quasistatically dark or some other sort of ‘dark’? How does the symmetry of light absorption to light emission work here? If you can excite the mode strongly then surely it must give about half absorption and half emission?

Stephanie Reich answered: The near-fields are concentrated in the vertical gaps. Electromagnetic hotspots form between the nanoparticles within the layer. For the plasmons considered in our paper, there is no sizable near-field between two layers.

Your second question points towards the fascinating aspects of ordered nanoparticle crystals. In our paper we defined ‘bright’ as plasmon modes with a finite dipole moment and ‘dark’ as plasmon modes with a vanishing dipole moment. This corresponds to the standard optical selection rules that you will find in textbooks on the symmetry analysis of crystals and which are widely applied to plasmonic systems as well. Standard symmetry analysis assumes that (i) the electromagnetic field has only a dipolar component and (ii) the light wavelength is infinite compared to the extension of the unit cell. While the second assumption is well justified for normal solids and molecules, it breaks down for the nanoparticle system we considered here, due to the large nanoparticle size. In our paper we performed a symmetry analysis for optical absorption by nanoparticle crystals under the assumption that the wavelength of light is identical to the translational periodicity along the crystal c-axis (hexagonal close-packed structure). Light at this wavelength excites gerade representations, among them the E_2g mode discussed in our paper. In the framework of your question, the mode is ‘quasistatically’ dark. In fact, we should expect rich phenomena in the optical spectra of ordered nanoparticle arrays due to field retardation, because plasmon excitation will depend on the propagation direction in addition to polarization direction.

A dipole-active bright mode (quasistatically bright mode) will radiate light in any direction, thus making radiative decay one of the prime relaxation channels for such a plasmon. The dark E_2g mode discussed in our paper can only radiate normal to the gold surface, as explained in the previous paragraph. The strongly limited solid angle of radiation suppresses radiative decay.

Naomi Halas commented: How does the dark mode you observe in your bilayer nanoparticle films relate to hot electrons, and what are you measuring that relates to hot electron generation in these materials?

Stephanie Reich responded: The dark plasmon is a source of excited electrons. Essentially, all processes for dark plasmons that lead from plasmon excitation to hot electron generation are identical to optically active bright modes, except for the missing radiative decay. This is an important advantage of dark modes, because radiative decay carries away large quanta of energy (1–3 eV depending on the wavelength) without producing any excited electrons. Tailoring hot electron extraction from dark modes follows the same principles as for bright modes, i.e. increasing surface scattering, producing hot spots as places for dephasing and so forth.

We measured the generation of hot electrons using transient absorption spectroscopy. This technique excites plasmon modes with a strong pump pulse and follows the decay of the temperature rise on a ps time scale using a probe pulse. The number of hot electrons created with an infrared pump pulse increased strongly in the bilayer compared to that in a monolayer, which is due to the excitation of the dark plasmon in the bilayer system. We have recent data that shows an increase of 50–60% of hot electron generation by the dark mode in comparison to that of the bright plasmon mode.

Romain Hernandez commented: How much more efficient is it to generate hot electrons by the dark mode rather than the bright mode?

In your experiment, a gold mirror is placed below the bilayer in order to enhance absorption. How can you extract hot carriers from the bilayer efficiently?

Stephanie Reich replied: We do not have a final answer to the first question. Our most recent (but still preliminary) transient absorption measurements showed an increase of 50–60% in hot electron population between spots with several layers (dark mode) and a monolayer (bright mode). This compares the generation rate at the same pump energy. On the other hand, we estimated that for 50 nm particles, the decay rate that contributes to hot electrons may be on the order of 130 meV. When we relate this value to the measured FWHM of the dark and bright modes, a factor of two appears to be an upper limit for the generation of hot electrons. This question is particularly difficult to answer for gold, because the bright mode overlaps too strongly with the interband transitions. Simulations and experiments on silver or aluminum layers would be highly beneficial.

With regards to the ‘bilayer above a gold mirror’ configuration, we introduced this configuration in order to further increase absorption by dark plasmons. It is not a required configuration for our experiments. Even in this configuration, the gold bilayer absorbs light through the generation of dark plasmons. The electrons may be extracted from the upper surface of the bilayer system.

Reinhard J. Maurer opened discussion of the paper by Priyank V. Kumar: You have observed direct hot-electron transfer from the metal to the adsorbate with probabilities of between 1–2%. One would imagine that the contribution of local density-of-states around the Fermi level that arises due to the CO molecular states would also be in the range of a few percentage points of the total DOS. From your current understanding, do you think that the electronic coupling magnitude or the local DOS will be more relevant in defining the effectiveness of particle-to-molecule electron transfer? If the local DOS dominates, one would assume that this ratio decreases with particle size. What dependence with respect to particle size have you observed or would you expect?

Priyank Vijaya Kumar responded: This is a good question. The probability values depend on two quantities: matrix elements and the joint density of states (DOS). From our current understanding, both these quantities play a role. However, we do not currently know what quantity dominates in which system. Having said that, in the few systems we have investigated, we have observed that the ratio decreases with particle size, as you mentioned. This suggests that the local DOS could have an upper hand in these systems. Therefore, one could simply compute the joint density of states as you mentioned and obtain a preliminary estimate for direct transfer.

Jeong Y. Park queried: In your theoretical model, you are focusing on direct hot electron transfer. However, from your results, 98% of the electrons are dissipated; perhaps some of them would go through indirect hot electron transfer. Can you comment on the possible probability of indirect hot electron transfer?

Priyank Vijaya Kumar answered: It is true that some of the 98% of the total electrons excited through plasmon decay could transfer to the molecule constituting indirect hot-electron transfer. It is difficult at this stage to estimate a probability since we have to account for electron–electron and electron–phonon scattering in our calculations, which has not yet been done.

Anatoly Zayats asked: Regarding plasmon lifetime, do you know how the lifetime depends on the size of nanoparticle and type of material? Will it be shorter for gold nanoparticles?

Priyank Vijaya Kumar replied: As the metal nanoparticle size increases, the plasmonic character of the excitation becomes stronger due to an increase in the number of electrons in the system. As such, we observe that the lifetime of the plasmon increases.

As for gold nanoparticles, the d-band is closer to the Fermi level than in the case of silver nanoparticles. This leads to stronger screening of the plasmon and a faster decay. Therefore, the lifetime is observed to be shorter.

Simon Freakley enquired: With one CO molecule you show that the distribution of transitions results in 1% direct injection to the CO. Will this scale linearly with increasing CO coverage on the particle and do you expect any cooperative effects with surface coverage that could influence the mechanism?

Do you see any difference in the behaviour of the CO depending on where it is sitting? Is one position more favourable for dissociation, activation or desorption upon illumination?

Priyank Vijaya Kumar responded: We certainly expect the probability of direct transfer to increase with increasing CO coverage. It is difficult to say whether this increase would be linear since there are many effects that influence the mechanism, such as the orientation of the molecule with respect to the applied electric field, hybridization of different CO molecules, interaction between CO molecules etc. As we have shown in the paper, we do observe different direct-transfer probabilities for different CO binding sites. From these probabilities alone, it would be far-fetched to state that a particular position would be more favorable for chemical transformation upon illumination since there are multiple other processes that occur which eventually result in a transformation.

Yuri Diaz Fernandez asked: Have you tried any polarization dependence calculations for this system? Can you also comment on the adsorption energy of CO on each site and how these energies relate to the experimental scenario?

Priyank Vijaya Kumar answered: Since our paper presents a preliminary investigation, we placed the CO molecule along the direction of the applied electric field (x-axis). The probability of the direct-transfer process certainly depends on the orientation of the CO molecule with respect to the applied electric field. If we change the direction of the applied electric field, i.e. along the y-axis, the probability is close to zero since the plasmon is perpendicular to the CO molecule and the relevant dipole transition cannot be excited.

Phillip Christopher queried: With the real time approach you used here is it possible to characterize which adsorbate states were involved in direct interactions with the plasmon oscillation and decay process?

Priyank Vijaya Kumar replied: Yes, the developed method is able to point out which adsorbate states are involved in the direct transfer transition.

Matteo Parente remarked: In your simulations you depict your system as a cluster of Ag on the surface of which one molecule of CO is adsorbed. In reality, however, Ag oxidizes. Therefore, from a more realistic point of view, your system would be a Ag cluster with a thin layer of Ag₂O and a molecule of CO adsorbed on top of the Ag₂O. Are you planning to take the silver oxide layer into account in your simulations, or do you have any evidence for explaining why the presence of this layer would not influence the mechanisms of charge transfer?

Priyank Vijaya Kumar responded: The oxide layer of Ag would certainly affect the mechanisms of charge transfer. Our simulations represented a proof-of-concept to show that we can now indeed capture direct-transfer transitions in plasmonic catalysis, and to shed some light on the physics of this mechanism. In order to start comparing with experimental investigations, thorough knowledge of the system under consideration is necessary, as you have mentioned. We hope that our computational tool can help in this regard in the future.

Laura Torrente-Murciano said: My question follows previous discussion about the effect of the degree of CO coverage and the effect of the contact area between the plasmonic and semiconductor particles. Based on that, would you maximise the direct transfer by covering the plasmonic particle with a semiconductor in a core–shell manner? As you mentioned that there is an optimum semiconductor size in the example presented in your paper, what do you think would be the optimum size of the shell?

Priyank Vijaya Kumar answered: Based on our current understanding, I would expect that we would maximize the direct transfer by forming a core–shell structure like you describe if the plasmonic properties of the core metallic nanoparticle remain unaffected. I’m not sure that we mentioned that there is an optimum semiconductor size in our paper. The optimum shell thickness depends on a few things. On the one hand, increasing shell thickness improves hybridization with the core and thus the direct transfer, but this effect should flatten out after a particular thickness is reached. On the other hand, increasing thickness could deteriorate the plasmonic properties of the core particle, which would result in a lower number of hot carriers and thus less charge transfer to the semiconductor. One has to weigh up these two factors and estimate an optimal shell thickness.

Johannes Lischner remarked: In your calculations, you describe the direct transfer of hot electrons into adsorbate states. This transfer is significant because of the strong chemical interactions between the nanoparticle and the adsorbate resulting in hybridized orbitals. Your calculations do not include indirect transitions resulting from the thermalization of excited electrons which are initially not resonant with the molecular orbitals. However, it appears likely that these indirect transitions are also significant because of the strong chemical interactions between adsorbate and nanoparticle.

Priyank Vijaya Kumar replied: I agree with your statement. It is likely that the indirect transfer rate increases due to strong chemical interactions between the adsorbate and nanoparticle. In order to verify this, one could further propagate our system and simulate the direct transfer by taking into account electron–electron and electron–phonon scattering.

Madasamy Thangamuthu communicated: (1) What happens to the HOMO–LUMO gap (7.9 eV) of CO after adsorption on Ag? Will it decrease to a smaller value?

(2) As you can see that silver can generate electrons with a maximum energy of 4 eV, if the HOMO–LUMO energy of CO does not change significantly then it is difficult to understand the energetics of the charge transfer. Please can you comment on this?

(3) Would this system work under a CW laser instead of a pulsed laser? Did you try any simulations using CW?

(4) What are the dimensions of the Ag nanoparticles? Does the number 147 represent the size?

Priyank Vijaya Kumar communicated in reply: (1) The HOMO and LUMO states of CO become hybridized with the states of the Ag nanoparticle. This is observed to slightly decrease the HOMO–LUMO gap of CO upon adsorption.

(2) What matters is the LUMO-Fermi level gap rather than the HOMO–LUMO gap when it comes to hot-electron-transfer based reactions. Here the LUMO-Fermi level gap is less than 4 eV, therefore there is potential for electrons to get transferred.

(3) We did not attempt any simulations using a CW laser, but we expect the physics to remain the same.

(4) The number 147 corresponds to the number of Ag atoms in the nanoparticle, and so is related to the size. The 147-atom Ag particle is about 1.5 nm in diameter.

Xiaofei Xiao returned to the discussion of the papers by Javier Aizpurua and Stephanie Reich: I found that in your projects, there exist small gaps. Indeed, more and more publications are focusing on very small gaps. For example, some of them are around 2 nm to 0.5 nm. However, the commonly used methods in simulations such as FDTD and FEM are those for classical electromagnetism. I have two questions. First, when should we consider quantum effects in our system? Second, when both quantum effects and classical electromagnetic phenomena exist, how do we carry out the simulation?

Javier Aizpurua answered: This question is very relevant for small gaps, as you say. We introduced in the past¹ a way to introduce quantum effects in ultrasmall gaps, making those quantum effects compatible with larger scale classical calculations. We referred to that effective method as a quantum-corrected model (QCM), which is nowadays extensively used to address quantum effects of tunneling and so on, in large plasmonic antennas. In the plasmonic gaps that we consider in this paper, the separation distance is maintained between 3 and 6 nm, therefore we certainly minimize quantum effects in this situation. One might still have non-local effects that can be properly addressed with effective model calculations, or by re-normalizing the local classical response with the Feibelman parameter. Nevertheless, for a gap of 3 nm, such as that considered here, classical calculations describe the optical response very well.

1 R. Esteban, A. G. Borisov, P. Nordlander and J. Aizpurua, Nat. Commun., 2012, 3, 825.

Stephanie Reich responded: Quantum effects become noticeable for gaps below 0.5 nm. With the 2 nm gaps used in our system, we remain in the regime of classical electromagnetism. There are hybrid approaches for ab initio calculations of plasmonic systems that consider quantum effects, but they remain restricted to smaller particles.

Jacob Khurgin opened discussion of the paper by Alexander O. Govorov: I have some inconvenient questions and remarks:

(1) Where does the energy of the absorbed plasmon go if not in hot carriers?

(2) I am very familiar with the Lindhard formula which describes the real part of epsilon adequately but uses phenomenological parameters to describe the absorption.

(3) Consider a simple picture of the standard photo-effect in a vacuum. The incident light is normal to the metal surface. Therefore no Landau damping can take place as it requires a longitudinal field. Nevertheless, hot carriers are clearly generated and the Fowler formula works well including the cut-off, without ever mentioning Landau damping. How does it work if the only carriers are generated near the Fermi surface?

Alexander Govorov replied: I think that your questions are very standard, and I do not see them as inconvenient. My answers are as follows:

(1) The total energy is conserved. Light energy turns into electronic energy. Electrons create phonons and, therefore, the electronic energy turns into heat. This is the standard picture. This mechanism gives the Drude formula, which is widely used and reported in almost all textbooks on solid state physics.

(2) The Lindhard formula is one of the key results in the physics of metals. It gives a good quantitative description without dissipation. With dissipation, it gives a correct physical picture.

(3) The first line of our paper (DOI: 10.1039/c8fd00145f) is “The generation of energetic electrons is an effect occurring in any plasmonic nanostructure.” My picture, and the picture given in textbooks (Drude model), is the following; the plasmon is made up mostly of many low-energy electrons (I call these carriers Drude electrons), since our system is weakly excited. A number of high-energy electrons are always present due to non-conservation of linear momentum near the surfaces (surface-scattering mechanism of plasmon decay) and due to defects/phonons via second-order processes. In large nanocrystals, the number of Drude electrons is much larger than the number of non-thermalized (photo-generated) high-energy electrons. In my later responses to Mikael Kuisma and Johannes Lischner, I provide a detailed description of the electronic structure of a plasmon, together with some textbook examples, and so I will not repeat it here. It is important to ask questions that are directly related to the discussed effects and not to mix different physical regimes. The Fowler law is for UV light, λ <250 nm, whilst I discuss the visible, red and IR regimes (>500 nm) where the Drude formula is well applied. For UV photons (>5 eV), it is known that the inter-band transition effects are very strong. The vertical transitions in the k-space with the excitation of hot electrons are possible for the UV photons because of the band structure effects. Other reasons for the generation of hot electrons in the case described in your question include the presence of a non-planar surface and defects/impurities and phonons via 2nd-order processes. As an additional note, for the effect of the generation of hot electrons near the surface, we use the term ‘surface-induced decay of plasmons’, as is also used in many related papers. This effect was calculated by Kreibig in 1975.¹

1 L. Genzel, T. P. Martin and U. Kreibig, Z. Phys. B: Condens. Matter, 1975, 21, 339–346.

Mikael Kuisma remarked: I think I know where the missing energy is (I am comparing Fig. 1e of ref. 1 with lots of low energy electrons to Fig. 3 of ref. 2, where the electron and hole distributions are equal, but are shifted exactly with the photon energy ℏω). It is in the energy of the electric field of the plasmon. We have carried out real-time TDDFT simulations of plasmons in nanoparticles using coherent light pulses.³ When the plasmon is formed we see these Drude electron–hole transitions near the Fermi level. They are in collective motion and all of them contribute to the induced surface density, hence causing a strong electric field. The energy stored in this field is the missing energy. To further scrutinize this, since the random phase approximation is a large part of the TDDFT response, after a quarter cycle there is a different number of these Drude excitations due to non-particle-conserving operators in RPA (aa and a^†a^†), and the energy is still conserved even when the electric field energy goes to zero since it is in the current.

On the other hand, we have found that the hot-carrier transitions are generated by this plasmon-induced electric field, and also that these transitions form such a strong background density of states that the hot-carrier generation may be treated using Fermi’s golden rule. As long as the collective motion of the Drude electrons is present, the plasmon will get absorbed into the hot-carrier transitions. Again, the energy is conserved, since these hot-carrier transitions have the energy of the photon. The fact that these Drude electrons appear in Professor Govorov’s hot-carrier distributions and in the non-energy conservation brought up by Professor Khurgin seems to reflect the presence of plasmons.

1 L. V. Besteiro, X.-T. Kong, Z. Wang, G. Hartland and A. O. Govorov, ACS Photonics, 2017, 4, 2759–2781.

2 R. Sundararaman, P. Narang, A. S. Jermyn, W. A. Goddard III and H. A. Atwater, Nat. Commun., 2014, 5, 5788.

3 D. B. Tanner, Optical Effects in Solids, Cambridge University Press, London, 2019.

Alexander Govorov responded: Thank you for your excellent comments. I think that I agree with some of your central comments, and those comments are fully consistent with the interpretation I gave after my talk.

I would like to make some remarks about plasmons, the Drude model and Drude electrons. The response of electron gas in real metals (like Au and Ag) is well described by the Drude dielectric function in the red and IR intervals. In the blue interval, we need to add the inter-band transitions. Overall, the Drude dielectric function describes very well the intra-band transitions. The Drude dielectric function comes from the response of mobile excited electrons and, in my papers, I call such excited electrons ‘Drude carriers’. Another suitable name for such electrons could be ‘intraband excitations’. As I will explain and illustrate below, such electrons and holes (or electron–hole pairs in the Fermi sea) have, of course, low-excitation energies and are generated near the Fermi level.

The above picture of excited electrons and holes with low-excitation energies (e–h pairs in the vicinity of the Fermi level) is the standard and well-established picture given in solid-state textbooks as well as in many research papers. Below, I will provide some examples from ‘classical’ textbooks.

Electrons in metals in the first approximation are free carriers, and it has been proven that a free electron cannot absorb a photon quantum ħω. The reason for this is that the linear momentum cannot be not conserved for such an absorption process and, therefore, the transition matrix element is equal to zero. Therefore, the application of Fermi’s golden rule for a free electron without dissipation or scattering gives zero. However, the electric field still acts strongly on the electron; an electron becomes accelerated in the classical electric field, and this acceleration effect is very strong. In the k-space (momentum space), the Fermi sea of electrons becomes shifted.¹ Therefore, the Drude model was proposed, which describes the acceleration and motion of free electrons in metals. The acceleration of the center of mass of a free electron in an electric field can be described using the classical Newton equation or with the quantum equations of motion, momentum and coordinate (the results will of course be similar). This is the spirit of the Drude conductivity that is the central equation in the transport theory of an electron gas in metals and doped semiconductors.^1,2

Fig. 8.4 in a recent book by David B. Tanner¹ illustrates the effect of acceleration of the Fermi sea in the presence of an external field. When the electrons get accelerated and then occupy excited states of momenta above the Fermi level, they of course scatter by phonons and defects. This scattering limits the effect of acceleration. Via scattering by phonons, the weakly-excited electrons (we assume weak fields and a linear regime) lose energy; this scattering process is described well by the transport rate given by Fermi’s golden rule, when an electron makes the following transition with the creation of one phonon: E1 → E2 + ħω_phonon. For this, one can refer to a famous textbook by Gerald. D. Mahan³ or many other textbooks. Fig. 8.4 in David Tanner's book¹ shows the scattering process in the excited (accelerated) Fermi sea.

The above physical picture produces excited electrons near the Fermi level, and I refer to such carriers as Drude electrons in our paper. In our paper, we used the quantum master equation for the density matrix to derive the related distributions of Drude electrons. However, the Boltzmann equation gives the same results for the Drude electrons and holes, since the process is quasi-classical in its nature. David Tanner's book¹ offers a nice description for the derivation within the Boltzmann formalism and show the solution. The excited electrons are located near the Fermi sea.

In the quantum approach used in our paper, we also obtained a number of non-thermalized high-energy electrons due to scattering by the surface and in hot spots. Near the surface and in the plasmonic hot spots, the linear momentum of the electron is not conserved, and we observe a number of high-energy electrons with energies of E_F + ħω. In this case, the electron can absorb the photon quantum directly. This effect is well known and is given by the theory presented by Kreibig et al;⁴ this theory describes the decay of plasmons due to surface scattering (generation of high-energy electrons near the surface).

In 3D boundless systems, a small number of high-energy electrons appear due to the weak second-order processes involving phonons and defects (non-conservation of momentum due to phonons and defects). However, in 3D, the majority of plasmonic electrons are Drude-like and have small excitation energies. Textbooks typically show only the low-energy (Drude) electrons that give the Drude model, because these electrons and currents govern the overall picture.^1,2,5

One important example of a solution of the Boltzmann equation for the plasmonic wave can be found in a book written by Charles Kittel.⁵ This example is based on the Boltzmann formalism and it again shows the distribution of excited electrons in the vicinity of the Fermi level. The reason why the excited electrons should be near the Fermi level is simple; the plasmonic system is weakly excited, i.e. in the linear regime.

With regards to your comment about the missing energy, the energy of the electromagnetic field turns into kinetic and potential energy of the electrons. In the first step, an electron gets accelerated and receives extra kinetic energy. The electron then scatters and gives energy to the lattice. The total energy is, of course, conserved. You also mentioned the “energy of the electric field of the plasmon” which looks like potential energy, and which is one form of energy in the system. Your observation is good and is fully consistent with the physics of the plasmon and with the 3D picture of a plasmon. In large nanocrystals, the majority of excited electrons will be Drude electrons with small energies near the Fermi level. I am looking forward to seeing your results as a published paper or as a posted pre-print. I also agree with your comment “They are in collective motion...”

With regards to your comment that “The energy stored in this field is the missing energy”, here we need here 2 energies: the kinetic energy (KE) and potential energy (PE). In a harmonic oscillation, these energies are equal. Regarding your comment beginning “To further scrutinize this...”, here one should be careful. Any many-body Hamiltonian has only the terms with the conservation of the number of particles, like a^†a and aa^†, or a^†a^†aa (see the textbooks written by Mahan³ or Platzman and Wolff⁶). Finally, with regards to your comment beginning “The fact that these Drude electrons...”, yes the Drude electrons form the plasmon. The total energy is conserved at all times perfectly, of course. The 3D case of the plasmon is well studied and documented in textbooks.

1 D. B. Tanner, Optical Effects in Solids, Cambridge University Press, London, 2019.

2 F. Wooten, Optical Properties of Solids, Academic Press, New York and London, 1972, ch. 4.

3 G. D. Mahan, Many-Particle Physics. Kluwer Academic/Plenum Publishers, New York, 3rd edn, 2000, sections 8.1–8.3, Scattering by impurities and phonons.

4 U. Kreibig and M. Vollmer, Optical Properties of Metal Clusters; Springer, Berlin, 1995, vol. 25.

5 C. Kittel, Quantum Theory of Solids, John Wiley and Sons, New York, 2nd edn, 1987, ch 16: Electrodynamics of metals, section: Mathematical Theory of the Anomalous Skin Effect, eqns. 28, 33 and 35. These equations tell us that the non-equilibrium energy-distribution function under illumination, which is obtained from the dynamic Boltzmann transport equation, is δ(E – E_F), which is a good approximation for low temperature plasma (E_F≫kT).

6 P. M. Platzman and P. A. Wolff, Waves and Interactions in Solid State Plasmas, Academic Press, New York, 1973.

Yonatan Sivan said: I would like to comment on energy conservation in the problem of the non-equilibrium electron distribution in a metal nanostructure under steady-state illumination, due to the various contradicting claims that have been made during this discussion.

Most theoretical studies of this problem consider only the electron system. Its energy increases due to photon absorption and decreases due to energy transfer to the phonons. However, the usual approach whereby the latter effect is described using a fixed e–ph collision rate discards a lot of the relevant physics. Indeed, the rate of energy transfer from the electrons to the phonons depends on the temperature difference between the systems (as we demonstrated in our earlier theory paper,¹ the non-equilibrium component does not affect this too much). This difference depends on the rate of energy transfer from the phonons to the environment, which itself depends on the particle size and shape. Thus, using a fixed e–ph collision rate for different particles and/or different illumination levels introduces severe quantitative errors, which invalidate the claims made regarding the dependence of hot electron numbers on these parameters. We believe that the only paper that has taken this issue into account is our own. Attempts to manually adjust the electron temperature can partially amend those quantitative errors, but are unlikely to yield self-consistent temperatures, unless they adopt the proper relations between the electron and phonon temperature. This can be done using the 2 temperature model that arises from our formulation (DOI: 10.1039/c8fd00147b).

Thus, overall, the energy goes to three different channels; part of it goes into raising the electron temperature, another part gets transferred to the phonons (and heats them up as well) and part establishes the non-equilibrium distribution of the electrons. As we demonstrated in our theory paper,¹ the amount of power going to the last channel (hot electrons) is incredibly small in comparison with the amount of power that results in the heating of the electrons and phonons. For pulsed illumination, which has been studied in many more theory papers, these considerations are not important; the energy of the electron system is not conserved, because the time scale for energy transfer to the environment is much slower than the pulse duration or energy transfer to the phonons.

1 Y. Dubi and Y. Sivan, 2018, arXiv:1810.00565 [physics.optics].

Alexander Govorov responded: During the meeting there were active discussions on the conservation of energy when light interacts with an electronic system. As I described after my presentation, the total energy should of course be conserved. Optical energy turns into electronic energy and the electronic energy turns into thermal heat via phonon emission. Our theoretical calculations conserve the total energy. The interesting question at the meeting was regarding the appearance of large numbers of low-energy electrons (Drude electrons) in the CW regime of excitation, which is the intrinsic/fundamental property of the plasmon wave. Textbooks and research papers on 3D plasmons describe this very well. These Drude electrons give the Drude dielectric constant that we use every day in our calculations of the photonic properties of metal nanostructures. In my responses to other questions, I have described the mechanism of the Drude response in detail; this is due to the acceleration of an electron in the field. The low-energy electron–hole pairs (Drude electrons) create the plasmonic currents and they are not connected by the energy ħω (Fermi’s golden rule with the delta function cannot be directly applied here), since the excited electrons (Drude electrons) are created via a different mechanism, i.e. via acceleration (the Drude model and picture). The acceleration can be calculated quasi-classically (using the Boltzmann equation or Newton equation) or via quantum mechanics (quantum density matrix); the results will be the same (please see my previous comments and discussion of some textbook examples). Regarding your comment “As we demonstrated in our theory paper, the amount of power going to the last channel (hot electrons) is incredibly small in comparison…”; my results are different. In our calculations, we do see essential numbers of nonthermal hot electrons and also essential power absorbed to create such electrons. Importantly, the above comment does not agree with the well-recognized theory reported by Uwe Kreibig.¹ Kreibig’s theory has been applied to many experiments, and there are hundreds of related theoretical papers that have used and developed further the concept of Kreibig’s decay term for the plasmon (the decay is due to surface scattering). One can refer to citations of the original Kreibig papers and his book.¹

The number of non-thermalized hot electrons with high energies (∼ħω above the Fermi level) can be essential for small nanoparticles and for nanocrystals with hot spots; the energy rate for the creation of non-thermalized hot electrons with high energies can be comparable to the Drude heat (creation of nearly-thermal electrons) for small nanoparticles and for nanocrystals with hot spots. For small nanoparticles, this was shown by Kreibig. For nanocrystals with hot spots, this has been shown in our papers. In our paper, we also gave (perhaps for the first time) the distributions of non-equilibrium electrons including the hot (non-thermalized) high-energy electrons and the Drude (nearly-thermalized) low-energy electrons near the Fermi level. The Drude (nearly-thermalized) low-energy electrons near the Fermi level give the plasmonic currents and charges. The hot (non-thermalized) high-energy electrons give the plasmon decay due to surface scattering, owing to non-conservation of linear momentum at the surface and in hot spots. Our paper (DOI: 10.1039/c8fd00145f) reports results for the linear regime when the temperature increase of the lattice is assumed to be small. Correspondingly, the electron gas is slightly out of equilibrium (the CW regime of continuous driving) and the electron system is being excited, having Drude electrons (plasmonic currents) with thermal excitation energies.

1 U. Kreibig and M. Vollmer, Optical Properties of Metal Clusters; Springer, Berlin, 1995, vol. 25.

Johannes Lischner queried: Textbook derivations of Fermi’s golden rule point out that energy is not conserved at short times. When light is absorbed by an interacting many-electron system, the relevant time scale is set by the quasiparticle lifetimes. If those are short, it appears as if energy is not conserved. Where does it go?

Alexander Govorov answered: Thank you for your question. This comment is in relation to time-dependent perturbation theory or Fermi’s golden rule applied to a quantum system. Indeed, Fermi’s golden rule assumes conservation of energy in the form of the delta function at long times. The probability of a transition has a multiplier of δ(E1 − E2 + ħω_photon) or similar. The total energy of the whole system (electrons + electromagnetic field) is conserved at all times, of course. We see this always in quasi-classical calculations (Boltzmann theory), classical calculations (Drude model) and quantum calculations (a master equation for the density matrix). The light energy is converted into the energy of electrons. Electrons then get accelerated and emit phonons, causing heating of the lattice. Therefore, we have 3 forms of energy (light energy, energy of electrons and heat) and the total energy is conserved. Physically, the plasmon oscillation comes from the free electrons moving in an oscillating external field, and this is a classical process. For example, we immediately observe that the plasmon frequency is a classical parameter. In other words, the acceleration of free electrons in an electric field is a classical process and, therefore, the quantum Fermi’s golden rule is not needed to describe such a process of acceleration of a free electron. However, Fermi’s golden rule is indeed involved in the kinetic coefficient for the e–phonon scattering rate; when we consider the emission of a single phonon by an accelerated electron in a Fermi sea, we indeed use conservation of energy during the collision event: δ(E1 − E2 − ħω_phonon). This picture can be seen for example in Fig. 8.4 in David Tanner's book on the physics of metals.¹

1 D. B. Tanner, Optical Effects in Solids, Cambridge University Press, London, 2019.

Jacob Khurgin enquired: According to your Lindhard-based theory the wavevector q is small. However, in order to conserve energy the phonons must be involved. Phonons have a large wavevector. Therefore, how is momentum conserved?

Alexander Govorov replied: I previously replied to related questions. Again, the total energy of the crystal + the field is conserved. This mechanism can be found in textbooks. It is called free electron absorption and is where the related Drude model is derived from. Regarding your query about the small wavevector q, unfortunately the Lindhard formula is not mine, and is instead a famous result reported by Lindhard. However, yes, the momentum of light q is small. With regards to your comment beginning “However, in order to conserve energy...", photons are indeed involved and have small momenta. In terms of how momentum is conserved, electrons give their momenta to phonons and to the crystal via defects.

Priyank Vijaya Kumar said: From your talk and ongoing discussion, I understand that there are two types of electrons: Drude electrons when plasmons are present, and hot electrons that are generated when a plasmon decays. We know that hot electrons are useful, however, can we use the Drude electrons to carry out any useful work e.g. chemical reactions? If so, is there any evidence for this?

Alexander Govorov responded: Thank you for this excellent question, which is a fundamental one. Plasmonics exhibits large losses when we try to apply it to devices. Yes, plasmons in nanocrystals are mostly made from low-energy electron–hole pairs in the Fermi sea. This is a picture reported in textbooks. However, we can generate a number of highly-excited electrons with energies ∼ E_F + ħω above the Fermi level when we strongly break the conservation of linear momentum of electrons near surfaces and hot spots. The use of thermalized electrons (with low energies after a pulse) and Drude electrons (under CW illumination) is not easy, but is possible. We need to extract these electrons somehow. One possibility is to construct a Schottky junction with a low barrier energy under applied voltage and try to extract such low-energy electrons. A previous paper has reported in this direction for a TiN–TiO₂junction (please see Figure 4d in this paper).¹ Alternatively, one could utilize these electrons in some kind of thermoelectric device.

1 A Naldoni, U. Guler, Z. Wang, M. Marelli, F. Malara, X. Meng, L. V. Besteiro, A. O. Govorov, A. V. Kildishev, A. Boltasseva and V. M. Shalaev, Adv. Opt. Mater., 2017, 5, 1601031.

Mikael Kuisma communicated in response to Priyank Vijaya Kumar: As long as the Drude electrons are collective, the answer is no with single electron–hole-pair generation, but perhaps with electron–electron scattering this could be possible. The situation is similar but opposite in BCS superconductors. Instead of collective repulsive Coulomb interactions, in superconductors there is a collective attractive interaction and one cannot break the coherence of the ground state with thermal excitations, because one needs to also supply the remaining energy cost in order to break the attractive coherence equal to the superconducting gap.

For coherent plasmon excitation, one cannot have a plasmon scattered into low-energy electron–hole transitions without gaining even more energy from breaking the coherence. In any case, the outcome of any process scattering the plasmon should conserve energy. Such processes exists with Drude electrons as one of their elements, i.e. multi electron–hole processes exist in electron–electron scattering.

Alexander Govorov further commented: These are some interesting comments, and we can discuss them further. However, regarding your comment “As long as the Drude electrons are collective, the answer is no...”, I think that we can use the energy of low-energy Drude electrons if we can extract them or if we can transfer the energy from them. Of course, it is much more challenging to use low-energy electrons then high-energy electrons. Please refer to my direct response to the question posed by Dr Kumar.

Jeremy Baumberg remarked: In the pulsed regime I am worried about the hot electron yield without damaging the samples. In realistic systems we find that even at 1–2 orders of magnitude less than 10⁸ W cm⁻², the atoms move around in the plasmonic gaps and this can be directly seen. There is evidence for this in other experiments also, and it is much worse for short pulses than long pulses or CW. Furthermore, would your model recommend always using many pulses or CW if you are doing photochemistry?

Alexander Govorov replied: Thank you for your comment/question. As far as I know from the comments of my experimental collaborators, these levels of optical flux (10⁸–10⁹; ∼80 fs pulse) do not noticeably change the crystal structure. The positions of the plasmonic peaks and the absorption spectra themselves do not change after these intense fs pulses. I believe that they mentioned this to me, but one is welcome to ask them personally. Overall, the systems under study^1,2 look robust. The systems have no real gaps, but they have spacers. One system¹ has spacers made of TiO₂ and sapphire. The other system² has a spacer of sapphire and a thin polymer layer on the surface of the Ag cube. The spacers are relatively thick (∼8 nm), but the length of the plasmonic gap is long (∼100 nm). It could be that the motion of single atoms does not occur in reference 1 since there is not an open metal surface in the gap. In reference 2, perhaps, the atomic motions cannot change the spectra.

1 H. Harutyunyan, A. B. F. Martinson, D. Rosenmann, L. K. Khorashad, L. V. Besteiro, A. O. Govorov and G. P. Wiederrecht, Nat. Nanotechnol., 2015, 10, 770–774.

2 M. E. Sykes, J. W. Stewart, G. M. Akselrod, X.-T. Kong, Z. Wang, D. J. Gosztola, A. B. F. Martinson, D. Rosenmann, M. H. Mikkelsen, A. O. Govorov and G. P. Wiederrecht, Nat. Commun.., 2017, 8, 986.

Jacob Khurgin opened discussion of Yonatan Sivan’s paper: When one considers the excitation of hot carriers under normal conditions, it is very simple to see that at any given time we have on average less than one plasmon per nanoparticle and, therefore, at any given time we have just one hot carrier pair generated which loses its energy via electron–electron scattering. My question is how can we then talk about ‘electron temperature’? In my view, the way to proceed is just to trace what happens with the energy after a few collisions, and the dependence will clearly be different from the Fermi- or Boltzmann-like exponential.

Yonatan Sivan responded: (1) Our formulation (nor any of the other theoretical descriptions of the problem we are familiar with) does not employ second quantization, so we do not talk about ‘plasmons’ and their decay, but rather about a direct excitation of e–h pairs by a photon.

(2) From the standpoint of statistical mechanics and within the semi-quantum approach we adopt (where we do not discretize the electron levels and numbers), the number of high energy non-thermal electrons is indeed extremely small.

Mikael Kuisma further commented: I think that Professor Khurgin raises a good point. Even though there is only one hot electron excitation on average and not a statistical distribution, one still needs to treat it as a quantum mechanical superposition. Say, after a coherent laser pulse, a nanoparticle system is in quantum superposition with the ground state and lots of many-body wavefunctions with one hot electron excitation, the ground state is still the most probable. Therefore, the hot electron distribution is not statistical, but rather quantum mechanical with typical interference of amplitude effects.

Now, at some point for the practical purposes of simulating photoreactions, one would like to collapse this superposition of hot electrons and perform, for example, surface hopping with single hot electron excitation of the system. However, the quantum superposition argument goes even further to a Schrödinger’s cat-like scenario. Consider a nanoparticle with N reactants, which after a coherent light pulse is either in state A or B. The final state of the full electron and nuclear wavefunction is a superposition of 2^N states (neglecting degrees of freedom other than the state of the reactants). In practice, this is of course computationally impossible, so the challenge for the surface science and quantum chemistry community is to find an answer to the question "when do you collapse the wavefunction so that you can simulate these systems in practice?"

Yonatan Sivan answered: This question is about aspects of the problem that we did not address. I will nevertheless try my best to answer it. The formulation we adopted is semi-quantum, in the sense that the photon absorption term in our Boltzmann equation is derived from Fermi’s golden rule and is incoherent, i.e. it is proportional to |E|² (this is different to the work of Andrea Marini (DOI: 10.1039/c8fd00153g), where this term is purely classical: coherent and linear in E). This ensures that integer quanta of electromagnetic energy, indeed ħω, are being absorbed, in-line with the photoelectric effect. This causes the creation of the non-thermal, high energy (so-called ‘hot’) electron shoulders that are seen in our distribution plots (See Fig. 2(c) in DOI: 10.1039/c8fd00147b). We also employed a similar formulation for the e–ph interactions. We believe that for particles bigger than a few nm this approach captures the essential aspects of the problem. Indeed, a more complete quantum mechanical formulation of this problem was adopted by the Govorov group, where they employ a density matrix formulation and discretize all electron energy states. They showed that the semi-quantum form we adopted reproduces nicely the ‘hot’ electron shoulders, obtained in the more complete quantum mechanical formulation for particle sizes as small as 2 nm (at least when looking at more than one particle at a time, as is done in almost all experiments).

Jacob Khurgin commented in response to Mikael Kuisma: I agree with this. However, where I see the problem is that after a couple of scatterings the hot carriers will be redistributed and this distribution will not be Fermi-like. I agree with the superposition description. What I find problematic is introducing some kind of effective electron temperature.

Naomi Halas said: There is no difference experimentally in most cases, photocatalysis being one of those cases, between a hot non-thermal electron distribution and a hot thermal electron distribution. However, it appears that theorists are making a distinction between the two and it seems as though you are only calling ‘hot electrons’ the electrons in a hot non-thermal electron distribution. Is this the case?

Yonatan Sivan replied: We find this question rather surprising. After all, the latest paper from the Halas group is titled "Quantifying hot carrier and thermal contributions in plasmonic photocatalysis".¹ As we understand it, the title (and contents of the paper) implies a very clear goal: to distinguish between reaction rates under external heating (responsible just for the ‘thermal contribution’, i.e. thermocatalysis) and under laser illumination (in which case, according to the authors, there is an additional contribution of the high energy, non-thermal ‘hot carriers/electrons’, i.e. photocatalysis). The nomenclature is explained in more detail in a later response to Jeremy Baumberg, and the difference in distributions is shown specifically in Figs. 1 and 2 of our paper (DOI: 10.1039/c8fd00147b). The methodology of these works was to try to reproduce the temperature distribution in a reaction created by laser illumination as accurately as possible, such that by subtracting the thermocatalytic contribution one can isolate the effects associated with the non-thermal (‘hot’) electrons, as the title of the 2018 Science paper¹ clearly implies. This goal and methodology is the same as that of some previous papers by the same group^2,3 as well as by other groups.

We strongly believe that it is important to distinguish between thermal and non-thermal effects, as there is also a mechanistic difference between them (as described in the papers by the Halas group).^1,2 If the effect is purely thermal, then the energy for the reaction comes from the thermal energy of the substrate (vibrations), although electrons can still play a role in the catalytic process (e.g. by reducing the reaction barrier). However, even if the reaction takes place through an electron-charging reaction path,² the electrons required for this path need to have high energy. In this case, one can ask: do these high-energy electrons that participate in the reaction come from the tails of the Fermi distribution, or do they come from a non-thermal distribution? Put differently, is the number of high-energy electrons available for the reaction higher because the distribution is at a sufficiently high temperature, or because the distribution is non-thermal (and hence there is the addition of high-energy electrons to the thermal distribution)?

This is not a semantic question, but a question of orders of magnitude, as there is a very small number of high-energy electrons in thermal distributions, but this number can increase by many orders of magnitude when there are non-thermal ‘hot electrons’. Therefore, if there were high-energy non-thermal (‘hot’) electrons participating in the reaction, one would expect a huge orders-of-magnitude increase in the reaction rate; unfortunately this has never been observed experimentally. If it were high-energy thermal electrons, then the reaction rate would be indistinguishable from the regular thermal reaction path (because it is determined by the same Arrhenius function). This last point, that the experimental data can be described by an Arrhenius plot, was exactly what we showed in the manuscript referred to by Professor Halas.⁴ This demonstrates that her claims of quantifying the different contributions of thermal effects and non-thermal electrons are not justified.

In any case, all of the above implies that the distinction Professor Halas mentions in her question has in fact been adopted by her team as well, and not just by theorists. We believe, unlike Professor Halas, that there are experimental ways to distinguish between them, e.g. by looking at photoemission from the metals, single particle spectroscopy and temperature measurements (such as those carried out by the Gross group, Maier group, Dionne group, etc.), or by carrying out clever control experiments (such as those carried out by Jie Liu’s group). It is now up to experimentalists to demonstrate unambiguously that a given experiment shows one and not the other. As we demonstrated in our poster and arXiv paper,^4,5 this seems to not be the case for many past experiments, including Professor Halas’ own attempts.

1 L. Zhou, D. F. Swearer, C. Zhang, H. Robatjazi, H. Zhao, L. Henderson, L. Dong, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Science, 2018, 362, 69–72.

2 S. Mukherjee, F. Libisch, N. Large, O. Neumann, L. V. Brown, J. Cheng, J. Britt Lassiter, E. A. Carter, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 240–247.

3 S. Mukherjee, L. Zhou, A. M. Goodman, N. Large, C. Ayala-Orozco, Y. Zhang, P. Nordlander and N. J. Halas, J. Am. Chem. Soc., 2014, 136, 64–67

4 Y. Sivan, I. W. Un and Y. Dubi, 2019, arXiv:1902.03169 [physics.chem-ph].

5 Y. Sivan, J. Baraban, I. W. Un and Y. Dubi, Comment on “Quantifying hot carrier and thermal contributions in plasmonic photocatalysis”, Science, 2019, 364, eaaw9367.

Alexander Govorov commented further: Thank you for these interesting comments, which should be useful for the current discussion. Regarding your comment beginning “There is no difference experimentally in most cases...”, this is a very good point to discuss. I think that this strongly depends on the situation and conditions. If the excitation is broad-band (solar-like spectrum or similar), the difference between the hot non-thermal electrons and the hot thermal electrons can indeed be small. However, I think that for monochromatic optical excitation, the difference can be very strong. Hot non-thermal electrons under weak excitation (such as in photodetectors or photochemistry) have a threshold energy above the Fermi level, E = E_Fermi + ħω. In contrast, hot thermal electrons have a smooth Boltzmann energy distribution. If we have an injection process into a barrier (TiO₂ for photochemistry) or to a surface molecule level with a well-defined energy, the above two distributions will give very different spectral responses. One example is the Fowler law that has the threshold photon energy, ħω > E_barriers. With regards to your comment “it appears that theorists are making a distinction...”, yes, our theoretical papers distinguish between non-thermalized and thermalized hot carriers. Indeed, we (in the papers where I am a co-author) often refer to non-thermalized hot carriers as simply ‘hot carriers’. This is indeed misleading, and I have commented on this at many conferences. In an attempt to somehow correct this situation, we have explained the term ‘hot carriers’ in our recent work.^1,2,3 I guess that the terms ‘hot non-thermalized carriers’ and ‘hot thermalized carriers’ could be considered, or simply ‘non-thermalized carriers’.

1 In ref. 2 is the following paragraph: “However, what are usually termed “hot” electrons fall into two disparate populations of excited carriers: “nonthermal” electrons with an initial stepwise distribution extending up to the photon energy from the Fermi level and possessing an indefinable temperature, and “thermal” electrons with a quasi-equilibrated Fermi–Dirac distribution and an electronic temperature elevated above that of the surrounding lattice.”

2 M. E. Sykes, J. W. Stewart, G. M. Akselrod, X.-T. Kong, Z. Wang, D. J. Gosztola, A. B. F. Martinson, D. Rosenmann, M. H. Mikkelsen, A. O. Govorov and G. P. Wiederrecht, Nat. Commun.., 2017, 8, 986.

3 DOI: 10.1039/c8fd00145f

Andrea Marini further responded to Naomi Halas: Regarding my paper (DOI: 10.1039/c8fd00153g), yes, in this case the electron distribution is out-of-equilibrium and non-thermal since, in addition to the increased electron temperature, the mean velocity of the electron plasma distribution is finite and oscillates following the external driving electromagnetic field. In our paper we show that the mean velocity can reach high values that are sufficient to generate collision quenching, which is the main reason for the predicted saturation of absorption.

Jeremy Baumberg remarked: I would first like to comment on Professor Halas’ question regarding the question of what to call ‘hot’; can we not get a hot Fermi thermalized distribution just by heating? The argument is that the material system falls apart for bulk heating. However, having hot-spots at this temperature keeps it viable, but allows spot catalysis. Is this scalable? Do you refer to this as hot electron effects?

I have a further question. I like your use of Occam’s razor, aiming to explain large numbers of phenomena just by heating if that is possible. Your work sets a challenge to experimental groups, in that it suggests that there are many highly localised hot spots in a complex nanoparticle/nanostructured sample, where high temperature thermal catalysis operates. Since catalysis exponentially depends on barrier heights, gross measurements pick out these hot spots only (rather like the original problem of single molecule SERS). Can you suggest any experimental approaches to quantify the number and characteristics of these hot spots?

Yonatan Sivan replied: Firstly, with regards to ‘hot’ vs. heat; as I understand things, ‘hot’ means non-thermal, namely, a distribution (rather than a single carrier) that differs from a Fermi–Dirac (FD) distribution (which by definition is thermal). The distribution in the latter case is defined by the temperature of the electron system. In that sense, we have inherited/adopted a highly confusing nomenclature; I suggest (and tend) to stick to thermal/non-thermal.

Now, for pulsed illumination, a non-thermal distribution is created upon absorption, but is then converted into a thermal distribution within 500fs to a few ps (depending on who you ask). There might then still be aspects of the problem that people confusingly refer to as ‘hot’—be it the difference between the electron and the lattice temperatures (bound to disappear within the first few/tens of ps; I like calling this situation quasi-equilibrium; electron and lattice systems are equilibrated within themselves but not with each other), the differences between the lattice and environmental temperatures (a situation I like to call internal equilibrium), or the differences in temperature between different parts of a (macroscopic, multi-particle) sample. All of these purely thermal situations are different from what I would call complete/external equilibrium, where all systems and all regions of space have the same temperature. I believe that the literature is coming into agreement on the differences between the first, non-thermal scenario (which requires a microscopic, even quantum mechanical, description) and the other thermal scenarios, which can all be modelled using ‘lumped’, averaged, and even classical heat equations. Certainly, the attempts reported in recent papers for distinguishing between photocatalysis and thermocatalysis (see recent work by Halas, Maier, Cortes and Schlücker, as well as perhaps that by Dionne and Giessen) are aimed exactly at distinguishing between what I call thermal and non-thermal effects. In that sense, I think that calling the latter ‘hot’ electron effects is anywhere between unintended to an intended way to keep things vague. I hope that the outcome of this meeting will be to try to clarify and standardize the nomenclature.

Finally, with regards to your question about suggestions of experimental approaches, I have already advocated several times for single particle experiments and wavelength dependent studies (searching for a potential drop of the non-thermal electron driven effect when going beyond the ħω wide non-thermal electron shoulders). Other suggestions were raised by Guillaume Baffou at NFO in August 2018. Among other things, he mentioned the different scaling of non-thermal and thermal effects with beam size and/or particle densities. His work is not yet published, however I believe it is being reviewed.

Naomi Halas addressed Yonatan Sivan and Jeremy Baumberg: Why do you think that a purely thermal model that predicts temperatures well above the melting temperature of the metal is a valid one?

Yonatan Sivan answered: This question refers to our temperature-shifted Arrhenius model which is, it should be noted, not a part of our Faraday Discussions paper, but rather was derived after the submission of that paper. It is described in a recent arXiv paper¹ that has been submitted for publication. The model is nothing but a typical Arrhenius model for the rate of chemical reactions, namely

where the reaction temperature T(I_inc) depends linearly on the incoming intensity I_incvia heating induced by photon absorption. Importantly, due to the exponential sensitivity of the reaction to the temperature, the temperature that results from the fitting of the data corresponds to the maximum temperature inside the reactor. Indeed, the calculations carried out in that paper (as well as the measurements reported in several other papers, e.g. a recent paper from Jie Liu’s group)² show a rather significant temperature inhomogeneity inside the reactor.

In our paper we initially applied this model to 2 papers by the Halas group^3,4 and one by the Linic group.⁵ First, we showed that the temperature measured in those experiments was lower than the actual temperature of the reaction. Second, we used the experimental data to deduce the maximal temperature rise of the reactor. In those three papers, the deduced temperature rise was limited to a few tens of degrees, well below the melting temperature of the metal nanoparticles. The model fits the experimental measurements perfectly with the bare minimum number of fit parameters.

In the last part of our arXiv paper¹ to which Professor Halas refers, we applied the temperature-shifted Arrhenius model to the 2018 Science paper by the Halas group.⁶ Here, we show again why the authors underestimated the reaction temperature, compute the reactor temperature using the sample description provided by the authors, and extract what we believe is the correct temperature from their own data for low intensities. As we have explained in a recently accepted ‘Technical Comment’ of ours in Science,⁹ this prediction of higher temperatures is in accordance with the underestimation of the temperature due to the incorrect high emissivity employed in this work (namely, the use of the default 0.95 value rather than the values of 0.02–0.2 associated with the materials in the pellet).

As for the previous papers, the agreement of our model with the experimental data is essentially perfect for average intensities up to about 4 W cm⁻² for which the temperature rise is moderate. However, unlike in the previous papers, higher illumination intensities were employed, such that the temperature rise was now much higher (at least several hundreds of degrees). For these higher temperatures, our prediction slightly overestimates the reaction rate (hence, the temperature). These two observations imply that the linear dependence of the temperature on the incoming intensity assumed so far should be replaced by a nonlinear model. Extensive experimental data and modelling obtained and carried out by us previously,^7,8 as well as various high temperature ellipsometry studies of metals,^10,11 show that for such high temperatures, the temperature rise is strongly nonlinear and, in particular, it is much slower than the linear prediction we have employed so far. A quadratic fit to the experimental data given in Fig. 1d of the 2018 Science paper by the Halas group⁶ shows that the maximal temperature reached is ∼1700 K for the highest intensity used (<I> = 9.6 W cm⁻²). This is significantly lower than what one would deduce from the linear model used for the low intensity data.

As for the question of melting, for small nanoparticles this is not a trivial issue. Indeed, it may not be precise to refer to the nanoparticles as being solid even at temperatures modestly above room temperature (e.g. for gold). Instead they are unstable, in the sense that the atoms continuously migrate and the nanoparticle internal morphology fluctuates with time between various nearly degenerate states; these effects might depend, among other aspects, on the environment and to the best of our knowledge have not been characterized for Cu–Ru nanoparticles.

Nevertheless, let us assume that the nanoparticles do undergo a well-defined phase transition, and furthermore that the melting temperature is significantly lower than the bulk melting temperature of Cu (but not of Ru). First and foremost, we must bear in mind that the temperature we extract from the experimental data is the maximum within the reactor. As mentioned earlier and shown in a paper of ours,¹ the temperatures of other parts of the reactor (most of its volume, in practice) are significantly lower, potentially by more than 50%. Thus, the question we should ask ourselves is how melting of the nanoparticles in a small part of the reactor affects the observed reaction rate. Overall, we tend to say that the effect will be, at most, rather small. This conjecture relies on several arguments:

1. The antenna–reactor nanoparticles in the pellet were unstructured and perhaps fluxional even at room temperature. Even if melting causes shape modifications to each particle, it will have a very small effect on average, and will not affect their properties in any deleterious way.

2. Due to the presence of the surrounding oxide support and an inert atmosphere well in excess of the Cu vapor pressure, any such melting is not expected to lead to any significant or irreversible effects on the nanoparticles. The particles then solidify once the light is turned off.

3. Despite the above, even if we do assume that the melted layer drips off/evaporates, moves, merges with other particles etc., this will only cause a slight change in the overall temperature distribution. Indeed, the absorption/heat source might become slightly distorted (its center shifted to a lower position within the layer). However, since clearly the final temperature distribution is determined primarily by the heat diffusion, the overall temperature distribution (and therefore the reaction rate) would change only slightly. This has been confirmed by extensive numerical simulations that we have been performing recently (to be published in the near future).

Either way, the possibility of morphological changes due to laser illumination should be accounted for in future experiments at high temperatures. In particular, one would want to measure the emission spectrum from the heated nanoparticle composite in a spectrally and even spatially resolved manner, in order to isolate the emission from the parts of the sample that supposedly melted. One could also characterize the nanoparticles before and after illumination to explore any such effects—in the absence of any such data, we are left only with speculation about what changes, if any, the nanoparticles undergo. This is in sharp contrast to the catalytic activity of the nanoparticles, where the experimental data and our model make it abundantly clear that the observations can be explained by purely thermal effects.

1 Y. Sivan, I. W. Un and Y. Dubi, 2019, arXiv:1902.03169 [physics.chem-ph].

2 X. Zhang, X. Li, M. E. Reish, D. Zhang, N. Q. Su, Y. Gutiérrez, F. Moreno, W. Yang, H. O. Everitt and J. Liu, Nano Lett., 2018, 18, 1714–1723.

3 S. Mukherjee, F. Libisch, N. Large, O. Neumann, L. V. Brown, J. Cheng, J. Britt Lassiter, E. A. Carter, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 240–247.

4 S. Mukherjee, L. Zhou, A. M. Goodman, N. Large, C. Ayala-Orozco, Y. Zhang, P. Nordlander and N. J. Halas, J. Am. Chem. Soc., 2014, 136, 64–67.

5 P. Christopher, H. Xin, A. Marimuthu and S. Linic, Nat. Mater., 2012, 11, 1044–1050.

6 L. Zhou, D. F. Swearer, C. Zhang, H. Robatjazi, H. Zhao, L. Henderson, L. Dong, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Science, 2018, 362, 69–72.

7 Y. Sivan and S.-W. Chu, Nanophotonics, 2017, 6, 317–328.

8 I. Gurwich and Y. Sivan, Phys. Rev. E, 2017, 96, 012212.

9 Y. Sivan, J. Baraban, I. W. Un and Y. Dubi, Comment on “Quantifying hot carrier and thermal contributions in plasmonic photocatalysis”, Science, 2019, 364, eaaw9367.

10 H. Reddy, U. Guler, A. V. Kildishev, A. Boltasseva and V. M. Shalaev, Opt. Mater. Express, 2016, 6, 2776–2802.

11 P.-T. Shen, Y. Sivan, C.-W. Lin, H.-L. Liu, C.-W. Chang and S.-W. Chu, Opt. Express, 2016, 24, 19254–19263.

Jeremy Baumberg further replied to Naomi Halas’ question: This is an extremely interesting question. One response is that we already have clear data from anti-Stokes to Stokes emission intensity ratios that molecular temperatures in a thermal model are 1000 K or larger, far above the melting point of the attached Au, but it is not trivially molten.^1,2 One explanation for this is that vibrational pumping produces such situations, but this is not a thermally equilibrated situation. Another important consideration is that the idea of a melting temperature for these nanoparticles is not what you are alluding to here, since even at room temperature it is well known that the surface mobility of the surface atoms is far higher than that of the bulk, and in the materials community these are considered to be a monolayer or so of molten atoms. As the temperature rises, these surface atoms increase even more dramatically in mobility, and bulk melting begins gradually from the surface. Hence the picture of a ‘melting temperature’ is not very robust in this system. Effectively the temperature varies through the nanoparticles.

It is thus clear that in these nanostructures, it is impossible to define a single uniform temperature, and efforts to calibrate chemistry to a single temperature are not going to capture the full complexity. Since catalysis is happening at specific sites on the irregular nanoparticle surfaces and junctions, it is perfectly possible for these to be hotter than the ‘melting temperature’, but also this is not needed in any model as far as I can see, since the inhomogeneity of temperature means that local thermal-enhanced chemistry is strongly possible. I believe that we have to improve our creation of structures and devices that allow us to probe this more carefully in order to make strong claims.

1 F. Benz, M. K. Schmidt, A. Dreismann, R. Chikkaraddy, Y. Zhang, A. Demetriadou, C. Carnegie, H. Ohadi, B. de Nijs, R. Esteban, J. Aizpurua and J. J. Baumberg, Science, 2016, 354, 726–729.

2 D. R. Ward, D. A. Corley, J. M. Tour and D. Natelson, Nat. Nanotechnol., 2011, 6, 33–38.

Giulia Tagliabue queried: In your equation you have no term accounting for the removal of carriers from the system. It is thus not surprising that all the energy is dissipated as heat and the final distribution has a very low fraction of hot-carriers. However, for plasmonic photocatalysis applications we expect to be continuously removing a number of hot-carriers through either indirect or direct transfer to an adsorbate or semiconductor, and this term is not present in your model. Do you have any insight as to how the steady-state distribution would change if you were to account for the energy removed through hot-carrier extraction?

Yonatan Sivan responded: This is an excellent question! The theoretical approach on which our Faraday Discussions paper relies aims to understand what happens inside the metal only. Accordingly, it accounts only for the main mechanism (e–h excitation by photons, e–e and e–h collisions); all other effects, including in particular electron tunnelling out, are far slower, as has been shown by many authors, including by Jacob Khurgin in his latest ACS Photonics paper.¹ The implications for photocatalysis were realized after completion of the paper. At the moment we can predict, based on the existing results, that the tunneling will be a small perturbation that will not change the electron distribution significantly. Thus, we predict that the spectrum of the electrons that tunnel will be the same as the distribution. We do plan to verify this prediction using numerical simulations in the very near future.

1 M. Grajower, U. Levy and J. B Khurgin, ACS Photonics, 2018, 5, 4030–4036.

Alexander Govorov provided a general comment: One advanced model, which describes the dynamics of excited electrons in nanocrystals, is called a 3-temperature model. It is a set of kinetic differential equations for three parameters: the number of non-thermalized high-energy (hot) electrons (these electrons come from direct absorption of one light quantum), electronic temperature and lattice temperature. During and after a pump pulse, the lattice temperature does not increase much, but the electronic temperature can be high. In the current literature, one can see numbers like dT ∼ 100 K–4000 K, depending on the intensity and the system.

Phillip Christopher responded: The work of E. Carpene¹ is relevant here.

1 E. Carpene, Phys. Rev. B, 2006, 74, 024301.

Anatoly Zayats commented further: If electron temperature is the same as lattice temperature, I would not consider such electrons as hot electrons, even if their temperature is higher than room temperature. My view is that hot electrons may be non-thermalized or thermalized, but should have a temperature higher than that of the lattice. For these reasons, in my view, the heating of metal on a hot-plate will have different effects to optical excitation.

Phillip Christopher addressed Yonatan Sivan: I have 2 comments on your paper and conclusions. My first comment is related to the use of a steady state distribution of hot charge carriers and phonons to understand the mechanisms of photocatalysis by continuous wave excitation of surface plasmons. It has been shown many times in quite detailed experiments that adsorbate-derived electronic states can interact with plasmons during their coherent oscillation and directly upon dephasing; these processes are often described as chemical interface damping. It has been shown that a significant fraction of absorbed photons derived from plasmon dephasing occur due to direct interactions with adsorbates when metal particles are in ‘chemical environments’, i.e. dephasing populates normally unpopulated adsorbate-derived electronic states. As a result, it is important to consider the temporal evolution of plasmon excitation and dephasing, and the potential for interactions between charge carriers and adsorbates through these processes in order to have a complete picture of how photoexcitation of plasmonic particles could facilitate catalytic processes. This is not captured in the steady state picture presented here.

My second comment is related to the broad-reaching conclusion of your paper that it is extremely unlikely that any reports of ‘faster’ chemistry are associated with non-thermal mechanisms. There have been many reports on the photodetection of hot carrier injection from plasmonic structures to surrounding materials with quite high quantum yields—much higher than would be possible based on the predictions made using the steady state model presented in your paper. Similarly, there have been reports of redox chemical conversions that require the transfer of charge. In non-redox catalytic processes, there have been reports of plasmon excitation leading to non-thermal reaction selectivity and anomalously large kinetic isotope effects (an increased temperature would decrease kinetic isotope effects within the formalism of transition state theory) in reactions where the rate was enhanced by plasmon excitation. While there certainly may be cases where enhanced catalytic reactivity is related to plasmon-induced heating, there is also overwhelming evidence that non-thermal mechanisms of energy exchange to species at the metal interface do occur under continuous wave illumination. The discrepancy between implications derived from the predictions of the model presented in your paper and the countless reports of plasmon-mediated non-thermal interactions with interfacial species is likely a result of the chemical interface damping interactions described above.

Yonatan Sivan replied: Thank you for your question. Let me start by re-iterating our main claims. What we find, using what we believe is the first ever complete quantitative theory for the (indeed, semi-quantum; see my previous response to Dr Kuisma) steady-state electron distribution, is that the generation of high energy non-thermal electrons is an incredibly inefficient process; only one out of every 1–100 billion absorbed photons generates a high energy electron and hole pair. Furthermore, a Fermi’s golden rule calculation shows that if a certain chemical reaction is enhanced by these high energy non-thermal electrons, then one should expect the reaction to become faster by the ratio of the population of high energy electrons with light to that without light. Since this ratio can be 10–15 orders of magnitude, and since no one has ever observed such a massive improvement of reaction rates in a photocatalysis experiment, an unavoidable conclusion is that in the latter experiments the faster reaction does not originate from the high energy electrons. Instead, the reaction was likely enhanced due to a purely thermal origin, i.e. due to the exponential sensitivity of the reaction to the number of electrons near the Fermi energy, those which obey Fermi–Dirac statistics. Indeed, as we showed in our previous work,¹ essentially all of the energy absorbed (save for the tiny amount of energy that establishes the non-equilibrium population) ends up just heating the metal. The thermal explanation is also found to be in line with our re-interpretation of the results of some of the more famous experimental papers, where we showed that the temperature measurements underestimated the actual temperature of the reaction. In particular, our thermal model can also capture the kinetic isotope effect as described previously.²

Nevertheless, what we show is not unequivocal proof that thermal effects are responsible for the catalytic reactions reported in those papers. Instead, we claimed that by virtue of Ockham’s razor, our far simpler, well-established and fully-quantitative classical thermal explanation is much more likely to explain the experimental findings compared with the sophisticated, qualitative-only quantum mechanical explanation provided in your own papers, as well as the purely empirical (thus, theory-free) reports by the Halas group. We believe this argument is particularly convincing in light of the incorrect temperature readings in those papers. In other words, this implies that the "evidence that non-thermal mechanisms of energy exchange to species at the metal interface do occur under continuous wave illumination" should undergo a re-examination rather than being considered "overwhelming", as you have said.

In that sense, our results do not mean that effects associated with these high energy non-thermal electrons were never observed. They are surely responsible for photo-detection experiments, as we heard during the opening lecture, for example (DOI: 10.1039/c9fd00001a), and might provide an explanation for some of the selectivity in reaction catalysis reported by Jie Liu’s group and surely others (although selectivity may also be, in some cases, explained by thermal effects). The effects you describe in your question are also potential signatures of hot electron action. However, our results prove that ‘hot’ electron effects are far more subtle (weaker) than previously thought.

As we obviously did not examine all of the papers that have been published on this topic, we believe this is now a challenge that the community has to confront—to re-examine all previous "countless reports of plasmon-mediated non-thermal interactions with interfacial species" (to quote from your question) with an awareness of previous mistakes in temperature evaluation, using our simple theory for non-thermal electron population, with the extensive temperature calculations we provide for complex particle clusters, and more importantly, adopting more careful temperature measurements (such as those carried out by Jie Liu’s group⁴ and by Cortes et al.⁵).

We do plan to contribute to this effort. As I previously stated in my response to Dr Tagliabue’s question, our first step would be to add electron tunneling to our equations, and see how much it affects the final temperature and what the overall efficiency of tunneling is. We could then also model the effects you describe in your question. It is already clear to us that we would need the assistance of people whose expertise is in those chemical effects, and of experimentalists, who can provide actual evidence and the necessary parameters for modelling. We would be delighted to collaborate with anyone who is interested, and to lend our modelling services. We would be delighted to be convinced that non-thermal effects are playing a role, whether via charge transfer, chemical interface damping, Schottky barrier crossing or any other mechanism, as these mechanisms might have a true impact on energy related challenges to humanity. However, it should be emphasized that in light of the above, the level of proof that shall be required will be higher than that provided in the many papers you refer to. In particular, obtaining unequivocal proof of hot electron action might be difficult using some of the approaches employed so far, namely, looking at macroscopic suspensions of metal nanoparticles and performing external heating control experiments. Indeed, since the reaction rate is exponentially sensitive to the local temperature, any tiny variation of the temperature (spatial or temporal) will be massively amplified and will dominate the overall reaction; thus, any small difference in the temperature distribution in the photocatalysis and thermocatalysis experiments will be incorrectly interpreted as due to ‘hot electrons’. This makes control experiments with macroscopic particles nearly useless in their ability to identify ‘hot’ electron effects. Alternative suggestions for control experiments are discussed in our recent arXiv paper.³

1 Y. Dubi and Y. Sivan, 2018, arXiv:1810.00565 [physics.optics].

2 P. Christopher, H. Xin, A. Marimuthu and S. Linic, Nat. Mater., 2012, 11, 1044–1050.

3 Y. Sivan, I. W. Un and Y. Dubi, 2019, arXiv:1902.03169 [physics.chem-ph].

4 X. Zhang, X. Li, M. E. Reish, D. Zhang, N. Q. Su, Y. Gutiérrez, F. Moreno, W. Yang, H. O. Everitt and J. Liu, Nano Lett., 2018, 18, 1714–1723.

5 E. Pensa, J. Gargiulo, A. Lauri, S. Schlücker, E. Cortés and S. A. Maier, Nano Lett., 2019, 19, 1867–1874.

Laura Fabris remarked: In your manuscript you seem to discount the role of shape, whilst many of us have shown experimentally that the shape does indeed make a difference in the efficiencies of photocatalytic systems. When in your manuscript you discuss the role of shape, you seem to comment on the results of several papers, but do not address them directly in the citations, therefore it is hard for one to determine which works you are referring to. I believe that removing the role of shape leads to a rather simplistic approach of the problem, and the way you suggest that spherical nanoparticles are less efficient than anisotropic ones just because of heat partition seems limiting. Can you comment in more detail regarding your view of the role of shape by also citing the literature that you use as a benchmark in your manuscript?

Yonatan Sivan responded: This is an excellent question, which addresses a rather complicated issue. First, I would like to note that we never (a priori) dismissed the role of particle shape altogether in (photo)catalysis experiments, but rather say something far more limited in scope—namely, that nanoparticle shape has no effect on determining the number of non-thermal high energy electrons. This is a result of our solution to the optical (i.e. Maxwell) and electronic (i.e. Boltzmann) equations, which in fact makes perfect sense. Indeed, e–e collisions are so fast that any gradients of charge created by an electric field (and their gradients) necessarily disappear almost completely in the steady-state. For the same reason, there are essentially no temperature gradients in metal nanoparticles, simply because the thermal conductivity in the metal is so high (see, for example, the discussion by Baffou, Quidant and G. de Abajo quoted in our manuscript (DOI: 10.1039/c8fd00147b). Admittedly, our formulation does not account for the possibility of field or temperature gradients, but rather we assume they are negligibly small by looking only at averaged quantities. The same assumption underlies all theory papers on this problem that we are familiar with (e.g. those by Govorov, Nordlander, Louie, Lischner etc.). We do plan to improve our formulation to prove this point, hopefully in the near future.

What the above implies is that the immense body of experimental evidence on the faster photocatalysis associated with ‘pointy’ particles has its origin in a chemical (rather than optical or electronic) consideration. For example, this can be associated with the different lattice facet exposed at a corner or weaker atom binding which makes that region of space more reactive. As Javier Aizpurua pointed out, we should at some point complement our optical+electronic models to account for such effects. Needless to say, this is a difficult task that currently lies beyond the capabilities of even the best theory groups.

Regarding the comparison of heat generation in a sphere and a rod, if you believe our claims that the photocatalysis ensues due to regular heating (at least in the papers we criticized from the opening lecture (DOI: 10.1039/c9fd00001a), our poster and the slides I showed during my own talk), then our results imply that metal spheres will be better (thermo)catalysts in comparison with rods. This conclusion again excludes any additional ‘chemical’ considerations. The efficiency we discussed in our paper is however associated with a different aspect—namely, the relative amount of power that ends up generating non-thermal high energy electrons in comparison with the absorbed power that ends up as regular heating. In that respect, the spheres are the least efficient, as they lose the smallest amount of heat to the environment. This is, however, a purely classical effect. In that respect, our conclusions differ from claims you can find in the literature (see, for example, work by the Govorov group¹).

1 L. V. Besteiro, X.-T. Kong, Z. Wang, G. Hartland and A. O. Govorov, ACS Photonics, 2017, 4, 2759–2781.

Reinhard J. Maurer commented: Your paper (DOI: 10.1039/c8fd00147b) finds that the data of a number of experimental works can be interpreted by assuming local surface heating (of both electrons and the lattice) rather than non-thermal electron-driven effects. Not considering many other works, where significant deviations of reaction paths from thermal conditions have been seen, this hypothesis could, in principle, be valid. However, it is important to stress that this does not mean that the corresponding adsorbate reaction dynamics will behave the same as they would in the case of a thermally equilibrated surface. Even if the experimentally observed effects would only arise from local surface heating and an elevated, yet thermal, distribution of hot electrons, the exchange of energy between the surface and the adsorbate that induces the corresponding enhancement of surface reactions is highly non-thermal. Our own work^1,2 and the works of many others in the field have clearly shown that the nonadiabatic energy transfer between adsorbate motion and hot electrons is highly directional and specific to particular vibrational modes. As such, just because the increased energy at the surface is distributed according to equilibrium statistics, this would not mean that the same is true for the adsorbate motion it induces. This is particularly true in realistic gas-flow experiments where reacting molecules do not have a sufficient surface residence time to fully equilibrate. Simple fits on reaction rates, either by varying adsorption energies or apparent temperatures, will not provide sufficient detail to capture the complex picture behind hot-electron-enhancement and, therefore, will not be able to inform how such effects can be controlled and optimised. Recent molecular beam scattering and ultrafast dynamics studies³ provide clear evidence of hot electron effects in reaction dynamics and provide the necessary data to develop more advanced theoretical models.

1 M. Askerka, R. J. Maurer, V. S. Batista and J. C. Tully, Phys. Rev. Lett., 2016, 116, 217601.

2 R. Maurer, B. Jiang, H. Guo and J. C. Tully, Phys. Rev. Lett., 2017, 118, 256001.

3 K.-I. Inoue, K. Watanabe, T. Sugimoto, Y. Matsumoto and T. Yasuike, Phys. Rev. Lett., 2016, 117, 186101.

Yonatan Sivan replied: We appreciate your comment, and would like to clarify some points raised in it:

(1) Our paper(s) and poster demonstrated unequivocally that one can use thermal Arrhenius theory to explain some of the results of main articles in the field of plasmonic photocatalysis, by reproducing the data with unprecedented accuracy. Notably, some of these papers did not offer any quantitative theory. This shows that the claims made in these papers for “hot electron-generated photo-catalysis” are not supported by the data. This has to be recognized as our main message.

(2) As we discussed in our paper and poster, some of these papers (but not all) also had serious flaws in their measurement procedures, which we now understand, leading them to the wrong conclusions, without even testing the standard theory at all.

(3) Our thermal interpretation of the data of those papers is in accordance with a simple Boltzmann equation theory for the steady-state non-equilibrium electron distribution in a metal. As was explained in our slides, our theory is, to date, the only one for which energy is conserved in the electron–phonon-environment system.

Having addressed these three points, I will now go on to address the rest of your remark. Never, in our papers nor our lecture, did we argue that all experiments in photocatalysis can be explained by thermal effects, nor do we think that. However, now that it is clear that thermal effects can lead to apparent photocatalysis, we argue that it should always be considered at least as an option. Take for example experiments which show catalytic selectivity. Selectivity can be explained as a thermal effect if the energy barriers of two reaction paths are close, but not too close. Is this the case, or are there really hot-electron dynamics in such experiments? One has to provide clear evidence one way or another.

We state that in order to have thermal effects, the molecules on the surface have to be in (quasi)thermal equilibrium with the surface, which happens at a time-scale defined by the thermal conductivities between molecules and surfaces (which is determined by a complicated combination of vibration–electron and vibration–vibration couplings, the two channels with which energy can go from the surface to the reactants). This requires that the gas flow in the devices is slow enough. This is implicitly assumed, as was clearly stated in our discussion on reaction rates in our paper (DOI: 10.1039/c8fd00147b), where the derivation of reaction rates from the Boltzmann equation assumes that the reaction times are much slower than the thermalization time-scale. Our own estimations clearly show (and will soon be published) that indeed, in the experiments we consider, the gas flow rate is more than slow enough to allow thermalization. Clearly, this is the reason why experiments that aim to explore hot-electron ‘dynamics’ use either molecular beams or ultrafast light pulses, since in these cases there is indeed no time for thermalization. In optics terms, this is the difference between pulsed illumination (or situations with rapidly moving molecules, like those you have studied) and continuous illumination (studied by us and in the papers we have criticized). Regarding your statement beginning “Even if the experimentally observed effects...”, this is only correct if the adsorbates do not thermalize with the surface. If that were true, it would have an experimental signature. Since we unambiguously proved that there is no apparent signature, one can conclude that in the experiments we discuss, there indeed seems to be thermalization of the adsorbents with the nanoparticle surface.

Jie Liu remarked: (1) I feel that there is a small disconnect between physicists and chemists at this meeting. We need to think about the processes in NPs together with their chemical environment. They form an integrated system rather than act separately.

(2) If plasmonic nanoparticles are heated to a super high temperature by light via a plasmonic effect, and they have an effect on the chemical reaction, is this plasmonic catalysis or is it just thermal catalysis?

Yonatan Sivan responded: (1) I agree, yet from the theory point of view even accounting correctly just for the nanoparticles is rather non-trivial and controversial. We should indeed also account for additional chemical aspects at a later stage, when there is an agreed formulation for treating the solid state and quantum mechanical aspects of the problem. We believe that our formulation provides the simplest comprehension of such a formulation.

(2) It is ‘plasmon-assisted’ catalysis, but the right question, in my opinion, is whether the mechanism responsible for faster reactions relies on thermal or non-thermal electrons, in other words, whether there is a difference between laser heating which pushes the system out of equilibrium (even though by an extremely small amount) and heating by a uniform external bath, in which case, the electron distribution is purely thermal. This also seems to be the exact motivation behind the recent thermocatalysis experiments conducted by many groups, including those of Halas, Maier, Martin, Baumberg and surely others. As we showed in our poster and slides, and in two papers^1,2 the results of some of the most famous papers in the field were incorrectly interpreted (in our opinion) as originating from non-thermal electrons, and can instead be shown to indicate the second scenario—that the reaction is accelerated by purely thermal electrons, such that the laser heating approach will suffer from all of the difficulties that make heating an unfavourable solution for catalysis.

1 Y. Sivan, I. W. Un and Y. Dubi, 2019, arXiv:1902.03169 [physics.chem-ph].

2 Y. Sivan, J. Baraban, I. W. Un and Y. Dubi, Comment on “Quantifying hot carrier and thermal contributions in plasmonic photocatalysis”, Science, 2019, 364, eaaw9367.

Alexander Govorov opened discussion of the paper by Andrea Marini: This is excellent work on plasmonic hydrodynamics. In your picture, the Fermi sea moves as a whole with an average time-dependent velocity. This average velocity of the Fermi sea is described by the Drude model in the linear regime. We then observe the excited electrons and holes with low energies near the Fermi sea, which I referred to in my talk as Drude electrons. Such electrons form the plasmon wave. I guess that your approach, being intrinsically non-linear, can be applied to many current time-resolved experiments where an electron gas in a nano-crystal becomes highly excited. Could you please comment more on how one can apply your theory to experimental situations?

Andrea Marini replied: Under experimental conditions, such as for a nanocrystal, the theory provided enables the calculation of the nonlinear and non-local infrared response of the electron plasma through a full numerical solution of Maxwell’s equations coupled with a hydrodynamical model. Our paper illustrates analytically that Ohmic losses can be reduced by exciting the nanocrystal with ultrashort pulses of peak intensities of the order of GW cm⁻² owing to collision quenching. Such analytical predictions, obtained for a homogeneous plasma, are expected to also hold for a nanocrystal. However, in such nanostructures Landau damping will play a relevant role, and the simultaneous dynamics resulting from Landau damping and electron collisions need to be clarified in future investigations (it is however expected that Landau damping will pose a lower limit to absorption).

Javier Aizpurua queried: You show in your paper a nice description of electron–electron and electron–phonon coupling in the description of the response of the electron gas. How could this be extended to include surfaces, where the Landau damping is substantial? In other words, how can you properly include dynamical screening in a semi-infinite metallic interface? For instance, I am thinking of the application of this to plasmonic waveguides. Furthermore, how can we treat the responses of metals that are not so free-electron, such as Al or Na? How can we extend your formalism to treat materials with d-electron bands, such as Au or Ag?

Andrea Marini answered: In the hydrodynamical model the Landau damping is accounted for by the evolution equation of the mean velocity v in the term (v⋅∇)v. In turn, the numerical solution of the hydrodynamical model in a semi-infinite interface, a plasmonic waveguide, or in an arbitrary nanostructure will incorporate such an effect. The extension of this model to metals with resonant d-bands would require non-perturbative recalculation of the collisional integral (which in our reported results was developed for a classical plasma through the Fokker-Planck-Landau theory of electron collisions) to the quantum regime and its embedding in semiclassical Maxwell-Bloch equations. Usually in the literature this is done perturbatively through an effective linear damping in the Lindblad formulation. Thus, such a formulation needs to be extended to the nonlinear regime in order to account for the nonlinear damping arising from electron collisions.

Conflicts of interest

There are no conflicts to declare.

---