Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Glass polymorphism and liquid–liquid phase transition in aqueous solutions: experiments and computer simulations
Johannes
Bachler
a,
Philip H.
Handle
 a,
Nicolas
Giovambattista
a,
Nicolas
Giovambattista
 *bc and
Thomas
Loerting
*bc and
Thomas
Loerting
 *a
*a
aInstitute of Physical Chemistry, University of Innsbruck, A-6020 Innsbruck, Austria. E-mail: thomas.loerting@uibk.ac.at
bBrooklyn College of the City University of New York, Brooklyn, NY 11210, USA. E-mail: NGiovambattista@brooklyn.cuny.edu
cPhD Programs in Physics and Chemistry, the Graduate Center of the City University of New York, New York, NY 10016, USA
First published on 26th September 2019
Abstract
One of the most intriguing anomalies of water is its ability to exist as distinct amorphous ice forms (glass polymorphism or polyamorphism). This resonates well with the possible first-order liquid–liquid phase transition (LLPT) in the supercooled state, where ice is the stable phase. In this Perspective, we review experiments and computer simulations that search for LLPT and polyamorphism in aqueous solutions containing salts and alcohols. Most studies on ionic solutes are devoted to NaCl and LiCl; studies on alcohols have mainly focused on glycerol. Less attention has been paid to protein solutions and hydrophobic solutes, even though they reveal promising avenues. While all solutions show polyamorphism and an LLPT only in dilute, sub-eutectic mixtures, there are differences regarding the nature of the transition. Isocompositional transitions for varying mole fractions are observed in alcohol but not in ionic solutions. This is because water can surround alcohol molecules either in a low- or high-density configuration whereas for ionic solutes, the water ion hydration shell is forced into high-density structures. Consequently, the polyamorphic transition and the LLPT are prevented near the ions, but take place in patches of water within the solutions. We highlight discrepancies and different interpretations within the experimental community as well as the key challenges that need consideration when comparing experiments and simulations. We point out where reinterpretation of past studies helps to draw a unified, consistent picture. In addition to the literature review, we provide original experimental results. A list of eleven open questions that need further consideration is identified.
1 Introduction
“Water, water, everywhere; Ne any drop to drink” recalls the “ancyent marinere”,† pointing towards the fact that, despite its abundance, water is almost always encountered as part of a solution, often concentrated enough to render it non-potable. Indeed, this reflects the fact that pure H2O is a formidable solvent, able to host an array of solutes spanning atoms, ions, inorganic and organic molecules, proteins, and polymers. One of the first scientists to systematically study aqueous solutions experimentally was Hofmeister who categorized solutes according to their ability to stabilize or destabilize protein solutions,3 establishing the so-called Hofmeister-series. Since his work, vast amounts of research have been devoted to the study of aqueous solutions, filling more than five volumes of Franks’ water treatise.4 With the advent of computers, numerical studies of aqueous solutions have become possible. Pioneering Monte-Carlo (MC) simulations were performed by Clementi et al. who studied aqueous LiF5 using Hartree–Fock interaction potentials.6–8 Nowadays, computational studies of aqueous solutions are not uncommon and involve sophisticated computational techniques, including ab initio Car–Parinello molecular dynamics (MD),9,10 hybrid quantum mechanical/molecular mechanical (QM/MM) methods,11,12 and the use of polarizable models.13–15Most experimental and computational studies of aqueous solutions have been performed at ambient conditions. Relevant topics addressed in the past include the dynamics and structure of water in the solvation shell of different solutes,5,10–12 the structure making and breaking abilities of solutes,16,17 hydrophobic solvation,18 and water-mediated interactions.18,19 Recently, more complex systems have been studied, including solutes at interfaces,20,21 and solutions at astrochemical conditions.22,23 Interestingly, computational and experimental studies of aqueous solutions at low temperatures, close to the crystallization (Tm) and/or glass transition temperature (Tg), are rather scarce with only a few studies focusing on the glass transition of some aqueous solutions at low pressures (see the review article of Angell24 and references therein). Not surprisingly, the behavior of aqueous solutions in the supercooled liquid (i.e., the liquid at T < Tm) or glass state (T < Tg), remains poorly understood. This lack of understanding is partially due to the fact that water exhibits glass polymorphism (polyamorphism) and may exist in more than one liquid state. Indeed, it is an open question under what conditions a given aqueous solution may exhibit polyamorphism and/or a liquid–liquid phase transition (LLPT) at low temperatures.
The aim of this perspective is to discuss recent experimental and computational studies of supercooled and glassy aqueous solutions with special emphasis on the possibility of an LLPT and polyamorphism. In order to achieve this goal, we briefly discuss the complex behavior of pure water in the liquid (Section 1.1) and glass state (Section 1.2) as well as general aspects of aqueous solutions (Section 1.3). These sections serve as a framework to understand the behavior of aqueous solutions containing salts (Section 2), simple alcohols (Section 3) and other solutes (Section 4).
1.1 Liquid water: anomalous properties and the liquid–liquid phase transition hypothesis
Water is a complex liquid with an extensive list of anomalous properties.25 For example, the density of liquid water increases upon isobaric cooling at 1 bar and reaches a maximum at 4 °C.26–28 At higher pressures, the temperature of maximal density (TMD) shifts to lower values. Interestingly, computer simulations also predict that water may exhibit a density minimum upon isobaric cooling.29 Several hypotheses were put forward in order to explain the complex behavior of water, including the presence of ρ, cp, and κT maxima/minima lines in the p–T plane. Among the most common scenarios are (i) Speedy's stability limit conjecture,30 (ii) the singularity free scenario31,32 and (iii) the liquid–liquid critical point (LLCP) scenario.33 These theoretical scenarios have been discussed extensively in the past and we refer the interested reader to ref. 28 and 34–39 for a detailed discussion. For the purpose of this perspective, we will focus on the LLCP scenario.The key features of this scenario are shown in the phase diagram of Fig. 1. The red line indicates, qualitatively, the temperatures at which water may exhibit a density maximum (solid line) and/or minimum (dashed line) at a given pressure. Besides density (ρ), there are other quantities, such as heat capacity (cp) and isothermal compressibility (κT) that show a non-monotonic behavior26,28 and may also exhibit a minimum and/or maximum upon isobaric cooling. The orange and green lines in Fig. 1 represent the temperatures at which cp(T) and κT(T) reach a maximum (solid lines) or minimum (dashed lines) at a given pressure.
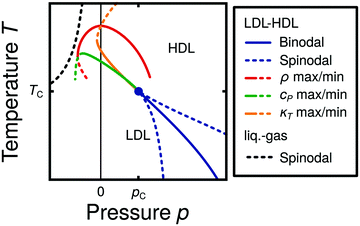 | ||
| Fig. 1 Schematic phase diagram for water in the LLCP scenario (based on ref. 29). The blue circle is the LLCP and the blue lines show the associated LLPT binodal and spinodal lines. The maxima (solid lines) and minima (dashed lines) in density (red) and thermodynamic response functions, i.e., isobaric heat capacity (green) and compressibility (orange), are also included. The dashed-black line represents the liquid–gas spinodal line. | ||
The LLCP scenario is based on classical computer simulations33 of the rigid ST2 model of water.40 In this scenario, water at low temperatures (T < 230 K) can exist in two different liquid states, a low-density (LDL) and a high-density liquid (HDL). As detailed in Fig. 1 LDL and HDL are separated by a first-order phase transition (binodal) line that ends at the LLCP. There, also the HDL → LDL and LDL → HDL spinodal lines are shown. Besides ST2 water which exhibits an unambiguous LLCP/LLPT,29,41–46 indications for an LLCP were also reported for other rigid water models.47–50 The estimated LLCP loci in different models are summarized in Table 1. Whether TIP4P/2005,51 one of the most accurate water models,52 exhibits an LLCP or not is currently under debate.53–61 Most computational studies (including the ones listed in Table 1) are consistent with the existence of an LLCP in TIP4P/2005. However, in the case of some water models such as SPC/E and mW, an LLCP/LLPT is not accessible. For example, in SPC/E water62 the LLCP is located below the Kauzmann temperature (TK),63–65 at which the system is stuck in one basin of the potential energy landscape, thwarting any structural changes required for the transformation between LDL and HDL.
| System | T c/K | p c/MPa | ρ c/(g cm−3) | Source |
|---|---|---|---|---|
| Unambiguous LLCP | ||||
| ST240 | 246 | 186 | 0.94 | Fig. 2 of ref. 29 |
| 237 ± 4 | 167 ± 24 | 0.99 ± 0.02 | Ref. 46 | |
| 247 ± 3 | 185 ± 15 | 0.96 ± 0.01 | Fig. 1 of ref. 42 | |
| LLCP located | ||||
| TIP4P66 | 190 | 150 | 1.06 | Ref. 47 |
| TIP4P-EW67 | 190 | 175 | 1.03 | Ref. 50 |
| TIP4P/200551 | 193 | 135 | 1.012 | Ref. 53 |
| 182 | 170 | 1.017 | Ref. 54 and 58 | |
| 182 | 158–162 | 1.02 | Ref. 59 | |
| 175 | 175 | 0.997 | Ref. 55 | |
| TIP5P68 | 217 ± 3 | 340 ± 20 | 1.13 ± 0.04 | Ref. 49 |
| TIP5P-E69 | 210 | 310 | 1.09 | Ref. 48 |
| LLCP likely inaccessible (Tc < TK) | ||||
| SPC/E62 | 130 ± 5 | 290 ± 30 | 1.10 ± 0.03 | Ref. 63 |
| 140–175 | 185–340 | ≈1.08 | Ref. 64 | |
| Experimental estimates | ||||
| H2O | ≈220 | ≈100 | — | Ref. 70 |
| H2O | ≈223 | ≈50 | — | Ref. 71 |
| D2O | ≈230 ± 5 | ≈50 ± 20 | — | Ref. 72 |
Interestingly, in this scenario the LLCP is directly connected with the presence of the ρ, cp, and κT maxima/minima lines in liquid water (see Fig. 1). Indeed, close to the critical point, thermodynamic response functions can be expressed in terms of the correlation length and hence, they must form a single line at T > Tc until they diverge at the LLCP.29,36,73–78 This line in the p–T plane is referred to as the Widom line. Computer simulations of water and simple model liquids that exhibit an LLCP also show that the Widom line indicates (T, p) values where the dynamical properties of the liquid change profoundly.78,79 Specifically, computer simulations show that water is a fragile liquid at temperatures above the Widom line. That is, the dynamic properties are non-Arrhenius and can be described, e.g., by the empirical Vogel–Fulcher–Tammann equation.80 At temperatures below the Widom line, however, it becomes a strong liquid (i.e., the dynamic properties follow the Arrhenius equation). The occurrence of this fragile to strong dynamical crossover (FSDC) in supercooled water is consistent with experiments.81–84
1.2 Glass polymorphism in water
Confirming the phase diagram of Fig. 1 has been challenging for experimentalists. Very recent experiments on supercooled nanodroplets85 and on supercooled stretched water86 indeed suggest the presence of a maximum in κT at −137 ≤ p < 0.1 MPa consistent with the possibility of an LLCP at positive p. We note however, that the significance of the results presented in ref. 85 is currently under debate.87,88 The direct experimental investigation of the LLCP hypothesis in the supercooled liquid close to the suspected LLCP, has so far been hampered by rapid crystallization. This has prompted many experimentalists to study water in the glass state, below the suspected Tc. If liquid water is subject to extremely fast isobaric cooling then crystallization can be avoided and water can be vitrified.89 In the LLCP scenario, cooling of LDL at low pressures leads to a low-density amorphous (LDA) ice while cooling of HDL at high pressures leads to a high-density amorphous (HDA) ice. The LDL ↔ HDL first-order phase transition, when extended into the glass state, becomes a first-order-like transition between LDA and HDA. Indeed, in the LLCP scenario, the experimentally observed LDA → HDA and HDA → LDA transformations correspond, respectively, to crossing the extensions of the LDL → HDL and HDL → LDL spinodal lines into the glass state.90–93Additional support for the LLCP scenario is provided by computational and experimental studies of the glass transition temperature of amorphous ice. These studies show that water has two distinct Tgs, one for LDA94–100 and one for HDA.83,101–104 This strongly suggests that LDA and HDA are the glassy proxies of LDL and HDL, respectively (see ref. 105 and 106 for recent reviews on this topic). Winkel et al.107 argue that the observed polyamorphic transition at 140 K takes place above both Tgs in the ultraviscous liquid domain of water. Further experimental support for the LLCP scenario stems from the behavior of isobars, showing slightly concave curvature at pressures exceeding 0.2 GPa.71 This is expected for the LLCP scenario but not for the singularity-free scenario.71 Furthermore, an apparent discontinuity in the melting lines of metastable high-pressure ices also speaks in favor of the LLCP hypothesis.70,72 These results even allow for an estimation of the LLCP locus (see Table 1).
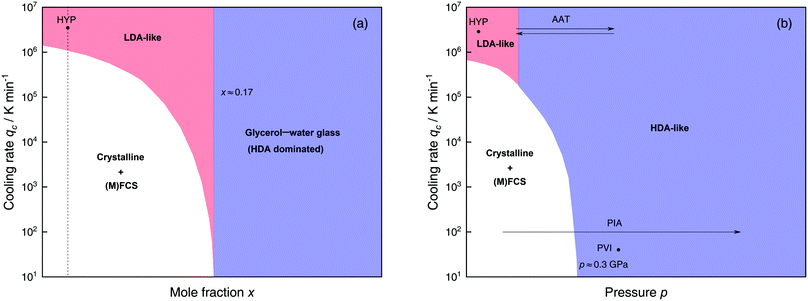
The most common routes to prepare LDA and HDA, followed in experiments and computer simulations are summarized in Fig. 2a. Specifically, the hyperquenching path HYP corresponds to ultrarapid cooling of liquid water at low pressure to produce LDA. Similarly, the pressure-vitrification path PVI involves cooling of liquid water at high pressure to produce HDA. HDA can also be prepared by pressure-induced amorphization (path PIA) of ice I.108,109 In addition, LDA and HDA can be interconverted by isothermal compression/decompression at T ≈ 125–140 K (amorphous–amorphous transition, path AAT).28,92,93,110
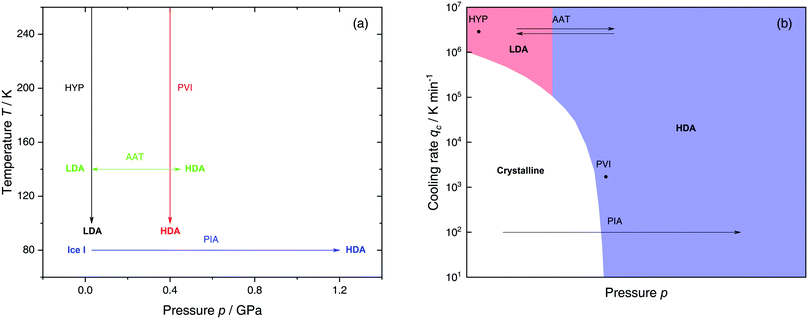 | ||
| Fig. 2 (a) Experimental routes commonly followed to prepare glassy water, namely hyperquenching of liquid droplets (HYP),89 pressure-vitrification of emulsified water (PVI),113 pressure-induced amorphization of ice I (PIA)109 and the first-order-like amorphous–amorphous transition (AAT).91,92 (b) Schematic diagram indicating the final state of samples obtained after cooling liquid water to 80 K using different pressures p and cooling rates qc. In addition, the constant temperature processes PIA and AAT from (a) are indicated by arrows. High-pressure crystalline states are ignored. | ||
We note that the minimum cooling rates qc necessary to prepare LDA/HDA from the liquid state (paths HYP and PVI in Fig. 2a) are strongly dependent on pressure. This is schematically shown in Fig. 2b. At ambient pressure, water is a bad glass former and crystallizes rapidly. Thus, the preparation of LDA requires hyperquenching, i.e., very high cooling rates (qc > 106–107 K min−1).89,111,112 By contrast, cooling the liquid at, e.g., qc = 102 K min−1 results in ice I. At p = 0.4 GPa, crystallization is easier to avoid and HDA can be prepared by cooling the liquid at qc ≈ 103 K min−1 (path PVI).113
Computational studies exploring the possibility of an LLPT and polyamorphism in aqueous solutions are almost exclusively performed using classical simulations with rigid molecular models. In this kind of computer simulations, crystallization events are very rare, an advantage relative to experiments. However, the limited time scales available in MD simulations, and computational power in the case of computer simulations in general, makes it challenging to directly access the LLPT in water, since the equilibration time increases dramatically at low temperature. That is, the system is glassy on the time scales probed in computer simulations at T ≈ Tc (an exception is the ST2 water model). For this reason, computational studies have also been used to study these non-equilibrium systems in simulations, as is done in experiments on amorphous ices. Here, computer simulations typically employ compression and/or cooling rates that are several orders of magnitude larger than the ones accessible in experiments.114–118 As shown in Fig. 2a, at these rates experiments show that indeed, isobaric cooling yields either LDA or HDA. Anyhow, a direct comparison of non-equilibrium simulations and non-equilibrium experiments is difficult, since the phenomenology of glassy systems depends on the rates studied and as discussed, they differ by orders of magnitude in the two cases. This is reflected through the standard units for qc being K ns−1 in MD simulations and K min−1 in experiments. Only recently the qc employed in simulations comes close to the highest cooling rates reached in hyperquenching experiments.119
1.3 Aqueous solutions
The properties of aqueous binary solutions are, as for the case of pure water, very sensitive to pressure and temperature. For glassy solutions, the preparation process also plays a fundamental role. For example, a solution may crystallize/vitrify partly or fully upon isobaric cooling, depending on qc and p. In addition, a systematic study of binary aqueous solutions needs to include the role of solute concentration. Specifically, the number of water molecules relative to the number of solute molecules determines the phase behavior and solution properties. Thus, it is reasonable to use the mole fraction x or, alternatively, the molar ratio R as concentration units. The mole fraction is defined as the number of moles of solute divided by the total amount of moles in mixture (pure water: x = 0) whereas R represents the ratio of water molecules to solute molecules (pure water: R = ∞). Note that for solutes which dissociate in aqueous solution, e.g., NaCl, the R value can be specified either per individual ion (Na+, Cl−) or whole species (NaClaq). In this work we choose R to be the number of water molecules per number of ion pairs (e.g., a NaCl–water solution with R = 5 consists of 1 NaCl per 5 H2O molecules).In aqueous solutions, the equilibrium liquid is stabilized with respect to ice I. That is, Tm is lowered, increasing the accessible T window. A remarkable natural example of this phenomenon is the Don Juan Pond located in Antarctica. This pond has such a large salt concentration that it refuses to freeze even at the harsh Antarctic conditions.120 In fact, the solution making up the pond freezes around −50 °C.120,121 This example illustrates that it is fairly easy to study cold aqueous solutions. Hence, one may conclude, erroneously, that it is possible to access the LLCP in water by adding some sort of solute, such as salt. However, extrapolating the properties of aqueous solutions to x → 0 (pure water) has proven to be quite difficult as water steadily loses its anomalous properties with increasing solute concentration.122–124 As a consequence, experimentalists have focused on the study of dilute solutions in the glass and/or highly-viscous liquid state, at concentrations where crystallization can be suppressed (although not entirely eliminated). The ultimate goal is to learn how solutions behave as a function of x and then, if possible, extrapolate the results to the case of x = 0 (pure water).
2 Solutions of salt in water
Experimental studies of liquid and glass polymorphism in salty aqueous solutions have mainly focused on LiCl, while computational studies concentrate on NaCl. This makes a direct comparison between experiments and computer simulations rather difficult. Hence, we discuss the experimental studies on LiCl–H2O solutions in Section 2.1 and results from computational studies based on NaCl–H2O solutions in Section 2.2. In Section 2.3 we briefly present research on aqueous systems containing other salts, e.g. bromides, nitrates, perchlorates and the ionic liquid hydrazinium trifluoroacetate.2.1 LiCl–H2O
Solutions of LiCl are the most studied binary aqueous systems in experiments. Many articles (e.g., ref. 125–129 and references therein) show the equilibrium phase diagram composed of four different LiCl hydrates with the eutectic between ice and LiCl·5H2O located at x ≈ 0.12 (R = 7.1).128 Strictly speaking this phase diagram is valid only for infinitely long (i.e., equilibrium) experiments. In reality, even for rather slow cooling experiments these hydrates do not form. The variables that determine the states formed are qc, p, x and T. Fig. 3 focuses on the states observed at liquid nitrogen temperature (T = 77 K), where the dependence on qc and x at ambient pressure is outlined in Fig. 3a and on qc and p for dilute solutions in Fig. 3b. Sections 2.1.1 and 2.1.2 describe experimental findings on the phase behavior of cooling at ambient and high pressure, respectively. Sections 2.1.3 and 2.1.4 focus on transitions encountered by these non-equilibrium systems, namely pressure-induced amorphization (PIA) and the polyamorphic transition (AAT), respectively.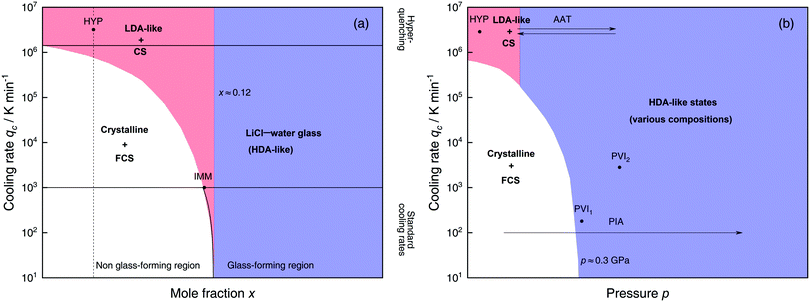 | ||
| Fig. 3 Schematic diagrams indicating the final state of samples obtained after cooling LiCl–water solutions to 77 K using different mole fractions x, pressures p and cooling rates qc. (a) Effect of qc on solutions with different mole fraction x cooled at 1 bar. (b) Effect of qc on dilute solutions (x ≈ 0.05, dashed line in (a)) cooled at different pressures p. In addition, the constant temperature processes PIA and AAT are indicated by arrows. For clarity high pressure crystalline states are neglected. The white regions correspond to mixtures of ice I and freeze-concentrated glassy solution (FCS, 0.12 < x < 0.14). Red (or blue) regions indicate non-crystalline solutions with water in an LDA-like (or HDA-like) state. FCS and CS are characterized as HDA-like containing significant amounts of salts. Points and arrows represent experiments: ref. 130 and 131 for HYP, ref. 126 for IMM, ref. 129 for PIA, original data from the present work for AAT, ref. 132 for PVI1 and ref. 133 and 134 for PVI2. | ||
At x < 0.12 ice crystallization speeds up appreciably. Thus, solutions below the eutectic composition experience competition between crystallization and vitrification. At x < 0.09 (R > 10, white area in Fig. 3a) ice formation is unavoidable using standard cooling rates (qc ≤ 103 K min−1) that can easily be reached in laboratories, e.g., by plunging the sample into liquid nitrogen.127 These cooling rates are employed to distinguish the glass-forming region (blue and parts of the red area in Fig. 3a) from the non-glass forming region (white area).24 Consequently, in the non-glass forming region ice crystals begin to segregate while the water content in the remaining supercooled solution decreases, lowering the melting point of ice. For instance, for x = 0.05 and qc = 100 K min−1 ice crystallization increases solute concentration in the remaining liquid, until the melting line of ice intersects with the glass transition line, typically at 0.12 < x < 0.14 (7.1 > R > 6)129 and T ≈ 137 K. Below this temperature freeze-concentration comes to a stop, the freeze-concentrated solution is reached and vitrifies upon further cooling. Ultimately, a solid mixture of pure hexagonal ice and glassy patches of freeze-concentrated LiCl–H2O solution (FCS) arises.
However, as nicely exposed in the early study by Angell and Sare126 the behavior of LiCl–H2O is even more complex. Rather than a crystalline substance also a second liquid may segregate from the parental liquid upon cooling (red area in Fig. 3a). In their work, aqueous LiCl solutions of x = 0.09 (R = 10) are quenched at qc ≈ 103 K min−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 to 77 K at ambient pressure (liquid–liquid immiscibility point IMM in Fig. 3a). Instead of forming a homogeneous glass the LiCl solution separates into two distinct parts, a water-rich and a salt-rich glass. Accordingly, the mixtures obtained in the red segment are composed of water-rich amorphous solids, reminiscent of LDA, and concentrated solution (CS, with x ≈ 0.12–0.14, just like the FCS).126 Angell and Sare further showed that upon heating, the water-rich LDA-like state crystallizes while the CS simply exhibits a glass transition. This purported immiscibility of two liquids with different concentrations in LiCl–water solutions sparked considerable interest in the field and its consequences are still a topic of debate.126,127,132,138–143
127 to 77 K at ambient pressure (liquid–liquid immiscibility point IMM in Fig. 3a). Instead of forming a homogeneous glass the LiCl solution separates into two distinct parts, a water-rich and a salt-rich glass. Accordingly, the mixtures obtained in the red segment are composed of water-rich amorphous solids, reminiscent of LDA, and concentrated solution (CS, with x ≈ 0.12–0.14, just like the FCS).126 Angell and Sare further showed that upon heating, the water-rich LDA-like state crystallizes while the CS simply exhibits a glass transition. This purported immiscibility of two liquids with different concentrations in LiCl–water solutions sparked considerable interest in the field and its consequences are still a topic of debate.126,127,132,138–143
The only way to avoid ice formation for dilute solutions x < 0.09 (R > 10) is the use of hyperquenching89,111,112 (qc > 106 K min−1). Yet, at these high rates, the LiCl–water solutions appear to still phase-separate into water-rich domains and CS. Phase separation is inferred from Raman spectra of vitrified solutions for x = 0.005–0.091 (R = 200–10), which can be expressed as linear combination of the scans of pure LDA and (vitrified) LiCl–H2O solution of x = 0.14 (R = 6).131 Because of the presence of LDA domains this region is depicted in red in Fig. 3a, including the small red segment (IMM) studied by Angell and Sare.126 The rapid phase segregation upon hyperquenching is striking as it implies that LiCl is barely soluble in LDA. This low solubility is consistent with the numerical simulations of Corradini et al. on the NaCl–H2O system (see Section 2.2).47,144–148
The phase separation into two non-crystalline parts described above has been observed in the glass state. Similar findings have also been obtained in the supercooled liquid state. Such a liquid–liquid separation in LiCl aqueous solutions was reported using neutron scattering methods. Specifically, using transient grating experiments, Bove et al.149 showed the onset of phase segregation at T = 190 K, in solutions of LiCl–water for x < 0.14 (R > 6). Below T = 190 K, the homogeneous solution separates into domains of concentrated solution and short-lived nanometer-sized water-rich domains. This represents the high-temperature analogue of observations in the hyperquenched states. However, it still remains unclear whether phase separation in salty solutions relates to the LDA–HDA separation in pure water or is simply a separation into two distinct solutions of different concentration.
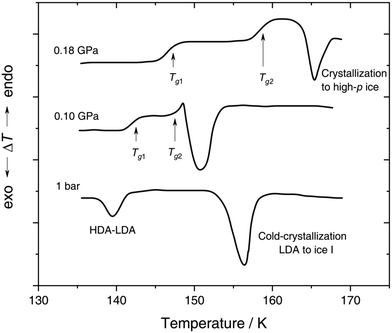 | ||
| Fig. 4 In situ DTA scans of x ≈ 0.05 (R = 20) LiCl–H2O solution vitrified at 0.25 GPa with qc ≈ 180 K min−1, then reheated at various pressures with a scanning rate of 8 K min−1. The figure is adapted from ref. 132. | ||
With increasing pressure, two distinct glass transitions gradually appear in the DTA scans (marked by arrows in Fig. 4). The double glass transition at p = 0.18 GPa is strong evidence that the solution is exhibiting liquid–liquid immiscibility during the isobaric cooling process and hence, is composed of two phase-separated glasses, one of which resembles pure HDA. By contrast solutions quenched at ambient pressure126,131 (cf. Section 2.1.1) contain pure LDA as one of the two separated glasses. The first glass transition Tg,1 marked by an arrow in Fig. 4 matches the glass transition temperature of pure HDA at 0.10 and 0.18 GPa (reported to be 140 ± 5 K and 145 ± 5 K, respectively106) very well. The second Tg observed by Kanno (see Fig. 4) at ≈155 K and 0.18 GPa pertains to the pressurized CS which does not crystallize. Please note that Kanno132 originally interpreted the double glass transition differently: the first Tg was assigned to the near-eutectic solution and the second Tg to a water-rich component, without taking HDA-like states into consideration.
Additional evidence that isobaric quenching of LiCl–water solutions at high pressures leads to phase-separation into a water-rich HDA state and a salt-rich HDA-like state is provided in ref. 133. Here, dilute LiCl–water solutions (x = 0.021–0.091, R ≈ 10–50) were cooled under pressure (p = 0.5 GPa) at qc ≈ 104 K min−1 (PVI2, Fig. 3b), and resulting vitrified aqueous solutions were characterized using Raman spectroscopy. Remarkably, for more concentrated solutions, the Raman scans can be expressed as linear combinations of the Raman spectra of pure HDA and the spectra of highly-concentrated LiCl–water solutions. The segregation into water-rich and concentrated solution naturally becomes more pronounced with increasing mole fraction of LiCl. Due to the spectral similarity of concentrated (HDA-like) solution and pure HDA it remains unclear if HDA is free from dissolved LiCl.133
For samples quench-recovered to 1 bar, X-ray analysis and low temperature DSC scans closely resemble the ones from pure water HDA samples. Signs for FCS are seen in the DSC scans in the form of a weak glass transition. Interestingly, the latent heat of the HDA → LDA transition per mole of water stays constant, even when the salt fraction is increased. This implies that not only the pure ice patches but also the water bound in FCS undergoes a transition upon heating at ambient pressure at the polyamorphic transition. The state attained after this transition cannot be pure LDA because it never cold-crystallizes upon further heating. Ruiz et al.129 suggest that this state is of low-density with significant amounts of salt embedded. By contrast, previous publications conclude that hydration water is forced into the HDA structure through the influence of ions even at ambient pressure.134–136,156 These apparently conflicting interpretations might be reconciled in different ways: (i) the polyamorphic transition occurs in the FCS part of the sample yet does not result in LDA but an LDA-like state of increased density; (ii) the transition in the FCS is not polyamorphic but continuous, slowly releasing enthalpy upon heating; and/or (iii) the transition is associated with water molecules being expelled from the salty solution, leaving behind a glassy solution of x = 0.14 (LiCl·6H2O) containing all the unfreezable water.
To distinguish between these scenarios currently not enough information is available and further experiments are required, e.g., annealing of PIA samples below the polyamorphic transition would allow to exclude either (i) or (ii).
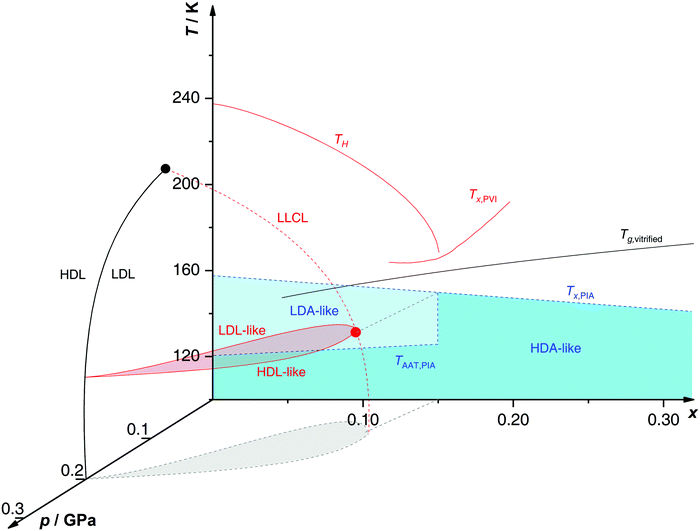
Proposed p–T–x state diagram. Fig. 5 shows a p–T–x diagram suggested by Suzuki and Mishima134 detailing the polyamorphism in LiCl–H2O (assuming ice formation can be avoided). The diagram is similar to a combination of Fig. 3a and b but leaving out the cooling rate dependence. Hence, it is valid for the comparatively long time scale given by qc ≈ 20–40 K min−1.134 Here, the p–T plane (at x = 0, cf.Fig. 1) is the well-known non-crystalline state diagram of water based on the LLPT hypothesis (assuming ice formation is avoided). Similarly, the T–x plane (at p = 0), corresponds to the (non-crystalline) state diagram of binary LiCl–H2O solutions at 1 bar. As described in the previous sections, cooling of LiCl–water solutions may lead to phase separation even without crystallization (indicated as the red immiscibility region). The most intriguing feature in Fig. 5 is the presence of an immiscibility dome connecting the ambient pressure immiscibility (colored in red) to the LLPT line in pure water (dashed lines). To explain the dome let us envision a solution at x = 0.05 pressure-vitrified at p = 0.3 GPa: Suzuki and Mishima134 regard such samples to be rather homogeneous, composed of LiCl dissolved in HDA (HDA–LiCl). Upon isothermal decompression at 130 K the dome is entered just below ≈0.2 GPa where almost salt-free LDA segregates from the HDA–LiCl.151,152 The involved separation resembles the polyamorphic HDA → LDA transition in pure water supplemented by changes in salt concentration. Parts of the solvent water transform from an HDL-like to an almost pure LDL-like state (path AAT in Fig. 3b). By contrast, decompression above 150 K leads to crystallization (not covered in the non-crystalline state diagram shown in Fig. 5). Thus, the proposed critical point at the apex of the dome (red point in Fig. 5) is not accessible in these experiments because it is preempted by crystallization. Note that crystallization to ice I only appears after the HDA → LDA AAT upon decompression.151,152 In other words LDA/LDL is found to be the mother of ice, as nicely phrased by Bullock and Molinero.157 This is also consistent with the findings of Bove et al.149 where nanophase segregation into water-rich clusters of low density and salt-rich solution occurs upon decreasing temperature after which ice I can grow.
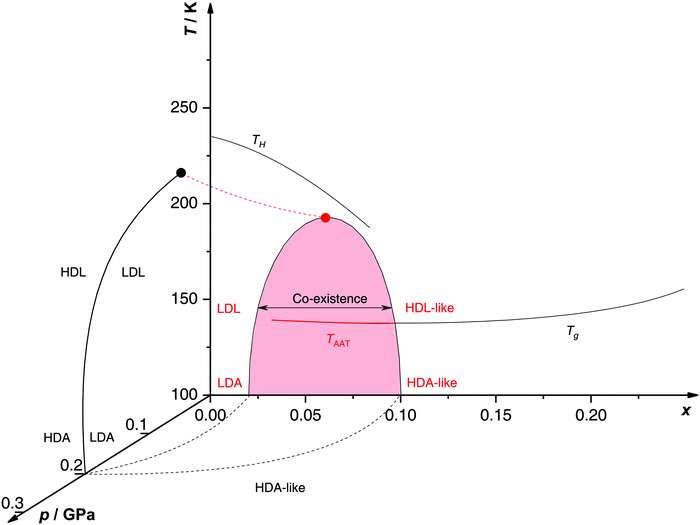 | ||
| Fig. 5 Non-crystalline state diagram of LiCl–H2O adapted from ref. 134. The dome (red: T–x plane at ambient pressure, black dashed lines: p–x plane at 100 K) separates regions in which solvent water appears as HDA- or LDA-like. This immiscibility dome appears as the LLPT line in the p–T plane where the red dashed line indicates a smooth connection. Additionally, the homogeneous nucleation temperature of emulsified solutions TH, the Tg line of homogeneously vitrified solutions and the amorphous–amorphous transition line TAAT from HDA-like to pure LDA are shown. Please note that this picture might be an oversimplification (see text). | ||
A different state diagram emerges when inspecting the work by Kanno,132 particularly as presented here in Fig. 4. According to Kanno132 liquid–liquid immiscibility is even found for PVI samples. That is, additional states would need to be present in the state diagram. This means that Fig. 5 might represent a simplification of a more complex scenario, where also HDA-like states show separation into almost pure HDA and CS (HDA-like structure). Upon decompression at 130 K (from 0.3 GPa), both domains need to be considered individually. In the water-rich segments of the sample HDA transforms to LDA just like in pure water whereas the salt-rich CS is hardly affected. It remains an open question which of the two scenarios is closest to reality, specifically, whether the transition to pure LDA upon decompression originates from pure HDA or HDA–LiCl.
Glass transition temperatures. One may now wonder whether the co-existing states are liquid or glassy at 140–150 K. This query requires knowledge of all three glass transition temperatures, namely for LDL, pure HDL (or HDL–LiCl) and near-eutectic CS. The glass transition temperature of CS (x = 0.12, R = 7.1) is ≈136 K at 1 bar,127 similar to Tg of pure water.83Tg(CS) barely depends on the initial concentration of solute127 (see also Tg line in Fig. 5). For x = 0.048 Tg(HDL) is estimated to be around 140 K at 0.1 GPa,101,152 compared with Tg(LDL) ≈ 130 K at 1 bar.130,158 All these Tgs are very close to the temperature range employed in Mishima's decompression experiments151,152 and vary by a few degrees depending on concentration, pressure and time scale of experiment. Consequently, it is not clear whether the transformations occur in the liquid, glass or mixed liquid–glass state. In the mixed case several scenarios are possible, namely (i) HDA expels pure LDL, (ii) HDL expels LDA which turns into LDL upon further decompression and (iii) HDL expels LDA which remains LDA. The latter is excluded based on the findings by Giovambattista et al.159 who show that Tg of LDA decreases with increasing pressure. Whether LDA or LDL is expelled depends most importantly on the time scale of the experiment, and whether HDA or HDL is present at the onset of the transition additionally depends on the choice of salt concentration.
Up to today it remains contested how the salt influences the Tg of the LDA-type states, where the type of preparation determines the outcome. For hyperquenched LDA samples Tg for dilute solutions (x < 0.09, R > 10) shows complex behavior involving a minimum and maximum as a function of x. This indicates an interplay of plasticization and anti-plasticization of the hydrogen bonding network caused by ions.127 In contrast such behavior is not observed for LDA samples prepared starting from hexagonal ice.158 This indicates that the distribution of ions is different in the different types of LDA samples. Possibly, there is not enough time for the ions to be expelled from LDA in the hyperquenching experiment (leading to a supersaturated amorphous state), whereas there is ample time for samples prepared based on slow procedures. Also for pressure-vitrified samples two distinct scenarios have been discussed: Kanno132 regards them as two immiscible solids whereas Mishima and Suzuki101,133,134,151,152 rather convey them to be homogeneous, namely LiCl dissolved in HDA (HDA–LiCl). HDA–LiCl shows the glass transition temperature as depicted by the black Tg line in Fig. 5.127 Once Tg intersects with the co-existence dome the homogeneous solution spontaneously decomposes according to HDA–LiCl → LDA + CS. That is, the glass transition line develops into phase segregation where the driving force is the insolubility of ions in the LDA matrix.131,151,152,160
This finding is corroborated by investigation of the melting line of ice IV under pressure.161 The solubility of salt in solution can be assessed based on the melting point depression. A sudden melting point depression is observed in case of melting ice IV to HDL–LiCl above 0.1 GPa, conforming that LiCl is soluble in HDL/HDA. By contrast no such depression is found when ice IV melts to LDL below 0.1 GPa. This immediately suggests that the salt dissolved in HDL is responsible for the depression whereas LDL is immiscible with LiCl. The change in melting behavior upon variation of pressure locates the LLPT line near 0.1 GPa in LiCl–H2O.
Reversibility of the LDA ↔ HDA transition. The work of Mishima151,152 is based on decompression experiments of glassy solutions vitrified under pressure. However, compression/decompression cycles probing the reversibility of the transformation between HDA ↔ LDA transformation in LiCl–water solutions have not been reported. Such experiments were performed for the case of water at T = 130–140 K.91 Since LiCl tends to suppress the formation of ice, a natural question is whether the reversible LDA ↔ HDA transformation in LiCl–water solutions can be observed at T > 140 K. Extending Mishima's work we here report new experiments on compression/decompression cycles probing for the reversible HDA ↔ LDA polyamorphism. Our pressure-cycling experiments might answer the question whether the phase separation is driven by water or the salt. In the former case the phase segregation indicates polyamorphism akin to pure water whereas in the latter case the dome is unrelated with an LLPT in a single component. Furthermore, the presence of the salt might raise the crystallization temperature of the amorphous samples allowing for measurements extended to higher temperatures in the non-crystalline state.
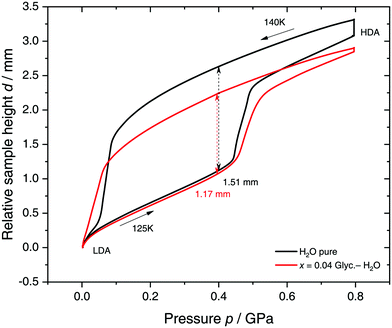
Specifically, we follow a similar protocol to the one used by Mishima91 to investigate polyamorphism (LDA ↔ HDA). Volume curves for both pure water and an x = 0.04 LiCl–water solution are shown in Fig. 6. The main point of Fig. 6 is the abrupt volume change at p ≈ 0.45 GPa during the compression of both pure water and the LiCl–water solution which signals the LDA → HDA first-order-like transition. During decompression, HDA transforms back to LDA at p ≈ 0.05 GPa, i.e., there is hysteresis between the up- and downstroke transition. The similarity between the pure water and LiCl–water curves in Fig. 6 immediately reinforces the notion that the dome in Fig. 5 is caused by polyamorphism in water. Just like in neat water (black curve) both the stepwise volume increase during compression (LDA → HDA) and stepwise decrease during decompression (HDA → LDA) are also observed for LiCl–H2O (red curve).
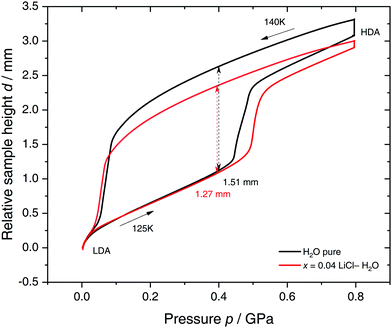 | ||
| Fig. 6 Reversible cycling between low- and high-density amorphous water states in pure water (black) and in x = 0.04 LiCl–H2O solution (red). Densification is indicated as double-headed arrow. 300 μL of solution were slow quenched (qc ≈ 10–100 K min−1) at 1 bar to 80 K, compressed isothermally at 80 K (PIA in Fig. 3b) and annealed following the protocol of Winkel et al.93 In the next step the HDA/LiCl sample was decompressed at 140 K and recompressed at 125 K (path AAT in Fig. 3b) following the protocol of Loerting et al.164 | ||
The double-arrows in Fig. 6 indicate the volume change during the transformation. Adding salt to water (x = 0.04) has the effect of reducing the volume change during the transformation, relative to the case of pure water, i.e., changes in the sample height (d) are 1.51 and 1.27 mm for pure water and the LiCl–water solution, respectively. This leads to a reduction in volume change of (1.51–1.27)/1.51 × 100% ≈ 16% indicating that there are less water molecules in the solution that participate in the LDA ↔ HDA transition. We note, however, that if one assumes that (i) the glassy solution is composed of water domains and domains of LiCl–H2O FCS (x = 0.12–0.14, R ≈ 7.1–6), and that (ii) the water molecules in the FCS domains do not participate in the polyamorphic transition, then the volume change in the glassy solution should be ≈28%, relative to the case of pure water. The fact that the volume change during the transition decreases by only ≈16% with addition of salt, leads us to believe that the FCS solution also densifies during compression, which is consistent with the work of Suzuki and Mishima.162 In other words, the reversible polyamorphic transition seems to take place between pure LDA and HDA while near-eutectic LiCl–H2O patches simply densify continuously. Perhaps, even slow mixing of FCS with HDA might be the case. This conclusion is supported by our additional experiments (not shown here) at higher decompression temperatures. Just like in pure water raising the temperature from 140 to 142 K results in crystallization of HDA to ice IX.163 That is, the salt does not help to extend the polyamorphic transition to higher temperatures, which reinforces that the polyamorphic transition takes place in pure water patches, with the salty patches acting as spectator only. The same conclusion was given as a conjecture by Mishima152 who observed that the transition pressure of HDA → LDA remains unaffected by the addition of salt (which is corroborated in Fig. 6).
Polyamorphism at higher pressures: HDA ↔ VHDA?. In pure water besides LDA and HDA polyamorphism also HDA and VHDA polyamorphism is debated vividly.28,137 VHDA can be interconverted reversibly with HDA via different thermodynamic paths.110,137 The HDA ↔ VHDA transition is not well understood and it has been speculated that this continuous transformation can be due to a (third) critical point in water buried deep in the glassy state.165
Relevant to this work, we note that HDA–VHDA polyamorphism was also probed in LiCl–water by Bove et al. at near-eutectic concentrations (x = 0.14, R = 6) utilizing neutron scattering as well as computer simulations.136 The experiments indicate a reversible transition from HDA–LiCl to VHDA–LiCl involving a very small density change. This finding was confirmed by both ab initio and classical MD simulations. According to the simulations the transition is associated with an increase of the coordination number of Li+ from 4.25 in HDA–LiCl to 5.25 in VHDA–LiCl. Interestingly, it was found that the underlying molecular-level mechanism involves one water molecule moving into the first hydration shell of the Li+ ions during the compression process and not a Cl− ion. However, this pressure-induced transformation is ten times broader than in pure water,164 covering a p-interval of ≈1.5 GPa. For comparison, MD simulations of pure water during the LDA → HDA transformation at similar conditions show that the glass–glass transformation expands over a p-range of only 0.1–0.3 GPa115,117 or even less.166,167 The smoothness and small density change in the HDA–LiCl → VHDA–LiCl transformation, relative to the LDA → HDA first-order like transition in pure water, supports the view where the reported glass–glass transformation in LiCl aqueous solutions with R = 6 is not related to the LLPT between LDL and HDL in pure water. For a solution of R = 6 one may expect only ≈1–2 water molecules between ions, assuming that the solution is homogeneous and no phase separation occurs. At such high concentrations, it is not possible to distinguish a hydration layer surrounding the ions separated by bulk-like water domains. That is, the movement of one water molecule from the second hydration shell to the first that characterizes HDA–VHDA polyamorphism is not possible. If the goal of studying water glass polymorphism with salts is to suppress ice formation while maintaining, somehow, the glass–glass transformations of bulk water, then much smaller concentrations (such as x = 0.04 used for the study of LDA ↔ HDA polyamorphism in Fig. 6) are required.
Paraphrasing, the experiments by Bove et al.136 are driven by changes in the distribution of ions but unrelated to water polyamorphism. Similar conclusions apply to the study of Suzuki and Mishima162 on vitrified solutions of x = 0.11. That glass polymorphism is not necessarily related to an LLPT at higher temperatures is also found in computer simulations of some water models, such as SPC/E, where a smooth LDA → HDA transformation is observed114,159 but an LLCP/LLPT, if it exists, may be located deep in the glassy state.63–65 In addition, we note that the relationship between glass and liquid polymorphism can depend on additional factors such as the preparation process of the starting glass (see, e.g., ref. 90, 116, 118, 168 and references therein).
2.2 NaCl–H2O
In a series of publications, Corradini and collaborators47,144–148,169 studied the phase behavior of NaCl–water solutions in the liquid state, over a wide range of T and p using MD simulations. Four (dilute) solutions are considered, x = 0, 0.0119 (R = 250/3), 0.0240 (244/6) and 0.0364 (R = 238/9), covering for instance the typical salt concentration in seawater (x ≈ 0.0098).47 In all cases, the MD simulations are performed using the TIP4P water model.66 The main focus of these studies is to search for the existence of an LLCP in NaCl solutions. Corradini et al.47 estimate that, for pure TIP4P water, an LLCP exists at pc = 150 MPa, Tc = 190 K and ρc = 1.06 g cm−3. In particular, as shown schematically in Fig. 7, they find that the LLCP shifts towards lower p and higher T as x increases. Interestingly, the LLCP is located at negative pressures in all solutions studied and, at the highest concentration, the LLCP is very close to the liquid → vapor spinodal line. In addition, increasing x has the effect of shrinking the LDL–HDL co-existence region (area between spinodal (dashed) lines in Fig. 7), expanding the HDL stability region towards low pressures while shrinking the LDL domain.47,144 It follows that adding NaCl to TIP4P water stabilizes HDL at low p and T, which is consistent with experiments on LiCl–water solutions.135,136,151,152,170 From a molecular point of view, the addition of NaCl to water was found to barely influence the water–water radial distribution functions. The small effects of adding salt to water that were detectable in the average structure of the solutions resemble the effect of increasing the external pressure on pure water.145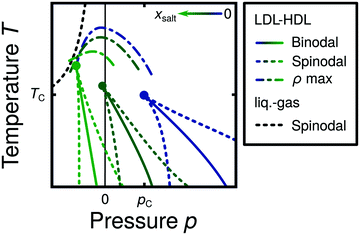 | ||
| Fig. 7 Schematic diagram based on MD simulations144 illustrating the effects of increasing the salt concentration on NaCl–water solutions (x increases from blue to green color). In the case of pure water, the LLCP is located at pc and Tc (blue lines). Adding NaCl shifts the LLPT and LLCP into the negative pressure domain and shrinks the LDL–HDL co-existence region between the two spinodals. At sufficiently large concentrations, the LLCP is expected to move below the liquid–gas spinodal lines, effectively vanishing. | ||
We note that the LLCP in (pure) TIP4P water reported in these studies occurs at very low temperatures, in the supercooled liquid regime,47 where equilibration times can become relatively large. In this regard, the computer simulations of ref. 47, 144, 146, 148 and 169 are rather short (<40–50 ns) and hence, longer MD simulations may be necessary in order to directly confirm the existence of an LLCP in TIP4P water as well as in the associated NaCl aqueous solutions. Nonetheless, there is strong evidence in ref. 47, 144, 146, 148 and 169 at higher temperatures, i.e., in the equilibrium liquid state, that supports the results summarized in Fig. 7. Specifically, as shown in Fig. 1, if the LLCP shifts towards lower p and higher T, one would expect a similar shift in the lines of κT, cV and cp maxima with increasing x. After all, at low temperatures, all these supercritical lines must meet at the Widom which connects to the LLCP. Although not necessary, one may also expect a similar shift in the TMD line as concentration increases. Corradini et al. show that, indeed, at all concentrations studied, the κT and cV maxima meet at low temperatures in the p–T plane close to the estimated LLCP.47,144,146,148,169 Similarly, the TMD line shifts towards lower p and T, as x increases (see Fig. 7).144,146
The MD simulations of NaCl aqueous solutions also show an FSDC when the system crosses the cV-maxima line upon isochoric cooling at low pressures.148 This is important because an FSDC has been found in water models such as ST2 and TIP5P78 that also exhibit an LLCP (see Table 1). The available data suggest that the FSDC in the studied NaCl aqueous solutions also shifts towards lower p and larger T with increasing x, as one would expect from Fig. 7.148
We note that the MD results for the NaCl solutions are in agreement with the experiments of Archer and Carter122 on NaCl–water solutions with x ≤ 0.0975 (R = 9.3), at ambient pressure and T ≥ 202 K. Specifically, it was found that the TMD line can be observed only up to x ≈ 0.0348 (R = 28). At x > 0.0348 crystallization interferes. The simulations show that both the TMD and cp maxima lines shift towards lower T as the salt concentration increases. Similar results were also found by Holzmann et al.171 who studied the effect of x and p on the behavior of NaCl–water solutions via MD simulations of TIP4P-Ew water. They also find that increasing x and/or p shift the TMD line towards lower T. We would like to note, however, that from the experimental perspective, the presence of an FSDC in salt–water solutions is still under extensive debate.172–180
An independent study of NaCl–water solutions related to the presence of liquid polymorphism in aqueous solutions was performed by Longinotti et al.181 In this work, replica exchange MD simulations of NaCl–water solutions are presented for p = 0.1 MPa, in a T-range corresponding to the equilibrium and supercooled liquid. Concentrations are limited to low values, x = 0.00343 (R = 872/3), 0.0115 (R = 858/10), 0.0233 (R = 838/20). These MD simulations employ the TIP5P-E water model182 for which the LLCP is accessible to equilibrium simulations and is well-characterized. The LLCP in this model is located at pc = 310 MPa, Tc = 210 K and ρc = 1.09 g cm−3.48 In addition, the ion force field employed in this work is specifically designed for TIP5P-E water.183 Longinotti et al. focus on the effects of x on the TMD line, cp-maxima line, and the FSDC at p = 0.1 MPa (cf.Fig. 1). They observe that, consistent with the work of Corradini et al.,144,146 all these supercritical lines shift towards lower T (at p = 0.1 MPa) with increasing amounts of NaCl. Interestingly, the results of Longinotti et al. are different from the picture provided in ref. 144 where the (TIP4P) LLCP moves to negative pressures with increasing x. If the LLCP in solutions of TIP5P-E water and NaCl was also located at negative pressures, cooling the solution at normal pressure should lead to a HDL → LDL phase transition upon cooling. Instead, Longinotti et al.181 only find a cp-maxima line which is inconsistent with the presence of an LLCP at p < 0.
The above named differences could very well be the result of the different force fields used. Indeed, one of the main challenges in classical computer simulations is the unknown sensitivity of the results to the force fields employed. It follows that results from classical computer simulations have to be taken with caution. Even in the case of pure water, different water models that show liquid polymorphism may exhibit the LLCP at different p and T (see Table 1). In the case of ion–water solutions, the force field chosen to represent the ion–ion and ion–water interactions provide additional complexity.184,185 For example, in the case of KCl–water solutions, different ion force fields can induce ion aggregates in biomolecular systems independently of the water model.186 In the case of LiCl–water solutions, Aragones et al.187 show that simple modification in the treatment of the ion–ion short-range interactions (i.e., Lennard-Jones) can lead to large improvement in the structure of the salt–water solution relative to experiments and even influence the tendency of ions to cluster (phase separate). For the case of TIP4P NaCl–water solutions, Corradini et al.146 compared results obtained in TIP4P water and NaCl employing two different force field for the ions and found that their MD simulation results are not sensitive to the ion force field.
A different approach to study the effect of salt on polyamorphism of water was used by Biddle et al.188 By performing theoretical calculations starting from the two-state thermodynamics model for pure water189 they found that increasing NaCl concentration significantly decreases the critical pressure while having barely an effect on the critical temperature.188 The LLPT model by Biddle et al.188 fits the experimental cp data of Archer and Carter122 on NaCl–H2O solutions well. This demonstrates that the measured behavior of cp is consistent with the occurrence of a LLPT.188
2.3 Other salt solutions
Glassy aqueous solutions of salts other than LiCl and NaCl have been studied intensely in experiments. Yet, these studies do not address the possibility that the corresponding solutions exhibit polyamorphism and/or an LLPT. Instead, homogeneous nucleation temperatures and glass transition temperatures are usually measured. As for the case of LiCl–water solutions, crystallization is common in dilute solutions at ambient pressure and standard cooling rates (qc ≤ 103 K min−1, see Fig. 3a). Only for high salt content these solutions can easily reach the glass state (glass-forming region).24 Angell and co-workers determined the glass-forming region for various chloride,127 nitrate127,190 and acetate solutions.191 For none of the salts, very dilute amorphous solutions were accessed. Additionally, they measured the homogeneous nucleation temperature TH in emulsified aqueous alkali halide solutions as a function of pressure.192,193 Compared to pure water, TH of ice is in general lower for salty solutions where the smaller ions have the largest effect.194 This is because smaller ions exert larger electro-restrictive forces and a higher pressure on the surrounding water molecules.Glass transition temperatures were determined for hyperquenched dilute aqueous solutions, namely LiCl (see Section 2.1.1), LiI, NaCl, CsCl, MgCl2, LiBr, KBr and tetra-n-butylammonium bromide.195 Remarkably, Tg decreases on the initial addition of the solute, reaches a minimum value, and then increases again. This is rather unusual in glass physics since the simple case is characterized by the Gordon–Taylor equation not allowing for any extrema in Tg.196 The location of the minimum is characteristic for each solute.195 This indicates two competing effects: a loosening of the H-bond network thereby lowering Tg (“plasticization”), and an “anti-plasticization” which is believed to relate to H-bonding with solutes, hydration of ions and stability of ion pairs, causing an increase in Tg.195 In this context, vitrified dilute nitrate197–201 and perchlorate197,202 solutions show more direct contact between ions (“contact-ion pairs”) whereas solvent-separated ion pairs are depleted compared to the liquid. The change of Tg(LDA) with changing x suggests that the ions are still contained in LDA for hyperquenched samples, possibly because the ions are kinetically trapped in an unstable state that would otherwise demix.
Non-ideal mixing suppresses water anomalies and hence, prevents a straightforward extrapolation of data obtained for solutions (x > 0) to the case of pure water (x = 0).122–124 In recent work, however, Zhao and Angell203 show that hydrazinium trifluoroacetate, a salt consisting of a weak-field cation and a simple anion, mixes almost ideally with water. In addition, they claim that crystallization is avoided in a rather concentrated solution (x = 0.156) during the cooling process with qc = 20 K min−1. The key finding is a sharp spike in heat capacity both on cooling and subsequent heating at ≈185 K and 1 bar which is interpreted as an LLPT. On the basis of the ion concentration employed, the authors estimate an effective pressure for water within the solution (at the observed LLPT) of 0.15–0.20 GPa.204,205 This is consistent with recent calculations, locating the LLPT of pure water between 186 K and 198 K at p = 0.15–0.20 GPa.39,189 Interestingly, with increasing solute concentration the heat capacity spike disappears, leaving behind a simple step in cp(T) as it is observed in common glass-forming aqueous solutions.203 This change from LLPT to glass transition may be related to the switch from water- to salt-dominated behavior upon increase of concentration. Finally, this observation is consistent with experiments on pure water by Winkel et al.,93,107 who suggest a decompression-induced LLPT at 0.076 GPa and 140 K.
The apparent first-order transition occurring in the hydrazinium trifluoroacetate aqueous solution was further probed using infrared studies and MD simulations.206 Most importantly, upon supercooling at 1 bar a discontinuous shift of the OH-stretch band position to higher frequencies is observed at ≈190 K, as expected for a first order LLPT. The spectra of the high-temperature and low-temperature liquid are similar to pure LDA and HDA, respectively. Crystallized samples, however, exhibit a different IR pattern. Evidence based on diffraction that this LLPT is indeed between two liquids is missing, though. In the future, it would be interesting to check for the absence of, e.g., crystalline hydrates based on diffraction experiments. Additionally, a systematic study of the purported LLPT as a function of pressure, e.g., compression/decompression cycles similar to the ones done by Mishima91 would improve our understanding for the relation of this transition to the LLPT in pure water. If the interpretation is correct one would expect cp to show a broader and flatter maximum upon dilution, associated with the crossing of the Widom line, rather than a spike, associated with the LLCP. Yet, this remains open to be demonstrated.
3 Solutions of alcohols in water
3.1 Glycerol–H2O
Glycerol (C3H8O3) has a widespread application in many industries207 including cosmetics, cryopreservation (e.g.ref. 208–211 and references therein), food212 and even manufacturing of adhesives, synthetic plastics and explosives.213 The ability to promote supercooling has also opened a vast field for fundamental science. Glycerol molecules compete with water for hydrogen bonds by effective integration into the H-bond network, ultimately leading to the suppression of water crystallization.214 The detailed underlying processes still remain elusive up to the present day. However, much effort has been made to fully characterize the complex phase behavior of aqueous glycerol solutions. The equilibrium phase diagram is of the eutectic type where the eutectic composition of x ≈ 0.28 (R ≈ 2.6) freezes around 225 K.215 By contrast to many salts glycerol (like glycerol-rich aqueous solutions) does neither form any hydrates nor crystallizes as a pure component. It is rather an excellent glass former with a Tg ≈ 190 K. As for the case of LiCl–water, the behavior of glycerol–water solutions in the glass and supercooled liquid state is poorly understood, where states not shown in the equilibrium phase diagram are involved. Our discussion on glycerol–water follows closely the discussion of Section 2 for LiCl–water. In Section 3.1, we describe the glassy states attained in experiments upon cooling the solutions at low- (Section 3.1.1) and high-pressure (Section 3.1.2). The pressure-induced transformations PIA and AAT are discussed in Section 3.1.3. MD simulation studies on glycerol–water are collected in Section 3.1.4, and Section 3.2 comprises low temperature studies in alcohol–water solutions other than glycerol.Glycerol-rich region: x = 0.38–1.00 (R = 1.6–0). In highly-concentrated glycerol–water solutions no signatures of polyamorphism and LLPT are found, in fact, the phase behavior and dynamics are relatively simple. Specifically, at all cooling rates the solutions can be vitrified without signs of ice formation (except when seeded). Broadband dielectric spectroscopy (BDS) studies on glycerol–water mixtures above x = 0.60 display only one main relaxation process.216,217 The T-dependence of the corresponding relaxation times follows the Vogel–Fulcher–Tammann equation80 (non-Arrhenius regime) indicating that the solutions are fragile (in the fragile/strong classification of liquids24). The maximally freeze-concentrated solution (MFCS), defined as the intersection of the Tg(x) line and the extrapolated Tm(x) line, has been found to be at x = 0.38 (R = 1.6).215–224 At and below this concentration, there are enough water molecules available to form hydrogen bonds with every OH group of the glycerol molecules.214
Intermediate region: x ≈ 0.17–0.38 (R ≈ 4.9–1.6). At 0.17 ≤ x ≤ 0.38 there are enough water molecules in the solution that allow for the formation of water domains at low temperatures.217,225 Accordingly, in the case of very slow cooling rates (qc < 1 K min−1, beyond the range in qc shown in Fig. 9a) these solutions phase-separate into ice and domains containing water and glycerol during the cooling process.221,224 As soon as ice crystals start to precipitate the supercooled glycerol–water domains become more and more concentrated until the corresponding concentration reaches the MFCS of x = 0.38. This phase separation upon crystallization is also observed in more dilute solutions (x < 0.17). However, already moderate cooling rates (≈10 K min−1) lead to full vitrification. Although phase separation can be prevented upon cooling, cold-crystallization becomes inevitable upon reheating. It was suggested that cold-crystallization of an x ≈ 0.20 solution yields a novel two-dimensionally ordered structure of ice.226–228 However, the existence of a new 2D ice phase is ambiguous because of the striking similarity to cubic ice.228–230
Since crystallization can still easily be avoided in glycerol–water solutions at x ≈ 0.17–0.38, it is natural to ask whether these solutions can exhibit liquid and/or glass polymorphism at low temperatures. This question was addressed by Murata and Tanaka in ref. 229. They presented experimental evidence of an isocompositional LLPT without macroscopic phase separation in glycerol–water solutions with x ≈ 0.17 which sparked particular interest in the field.231,232 However, the evidence for such an LLPT in glycerol mixtures near these concentrations has been challenged. Murata and Tanaka interpret microscopy images upon cooling the liquid solution (liquid I) to show transformation into another liquid (liquid II) of the same composition. They observe two types of mechanisms, nucleation and growth of liquid II at 180 K or spinodal decomposition of liquid I at 173 K. Upon reheating, the two liquids were reported to exhibit different glass transition temperatures. Murata and Tanaka concede that liquid II contains nanometre-sized ice crystals which grow to macroscopic size only at temperatures as high as 205 K, i.e., far above the observed LLPT. Based on Raman data of pure LDA and HDA at 30 K they suggest that liquid II is tetrahedrally ordered and thus relates to LDL of pure water whereas liquid I connects more to an HDL state. In both liquids glycerol molecules are mixed homogeneously with no sign of phase separation during the transition.
Soon after the experiments of Murata and Tanaka229 other groups investigated glycerol–water solutions at low temperatures, searching for the purported LLPT. In particular, Suzuki and Mishima230 focused on the “transformation of liquid I to II” using Raman spectroscopy. They pointed out that the conclusions by Murata and Tanaka mentioned above are questionable since it is “inappropriate that the 170 K-recorded Raman spectra are compared with the Raman spectra of two amorphous ices which are recorded at different temperature of ≈32 K”. According to Suzuki and Mishima230 the glycerol–H2O glass of x = 0.17 rather resembles a state fluctuating between LDL and HDL, instead of a pure HDL state as proposed by Murata and Tanaka.229 More specifically, Suzuki and Mishima230 regard this state to be supercritical, above the LLCP at 150 K (see Section 3.1.2). This supercritical fluid converts to what appears to be cubic ice at 170 K after 30 minutes. In other words, Murata and Tanaka might have observed crystallization of glycerol–water, rather than an LLPT.
The latter view is backed by independent findings of Popov et al.222 and Zhao et al.223 In both works the LLPT was reassigned to crystallization, where the second glass transition relates to the MFCS (x = 0.38) but not to a liquid of the same composition x = 0.17. At x = 0.17 immediate crystal growth is avoided upon cooling with moderate rates, but formation of ice nuclei is not. When reheated, the glassy matrix containing the nuclei first devitrifies at Tg ≈ 160 K, and subsequently the ice nuclei grow. This cold-crystallization causes the remaining glycerol–water solution to freeze-concentrate until the MFCS is reached. This MFCS shows a Tg ≈ 175 K, and thus, explains the second glass transition observed by Murata and Tanaka near 170 K. It is not valid however, to view this composition change induced by cold-crystallization as an LLPT.
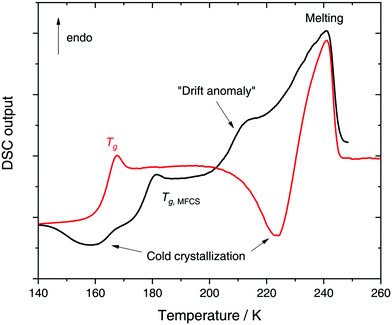
In a recent work we performed detailed experiments on amorphous glycerol–water and also conclude that solutions at x ≥ 0.20 do not exhibit polyamorphism.224 To show this, we include in Fig. 8 (red curve) the DSC scan of a glycerol–water glassy solution of x = 0.20 at 1 bar. This DSC scan shows a glass transition at Tg ≈ 160 K followed by cold-crystallization at ≈225 K. There are no signs of an HDA → LDA (AAT) exotherm before cold-crystallization intervenes. Tg ≈ 160 K in Fig. 8 (red curve) implies a glycerol content somewhere in between x = 0 (Tg = 136 K)105 and x = 0.38 (Tg,MFCS = 175 K, black curve). Furthermore, we find that samples with x = 0.20 quenched at ambient pressure to ≈80 K do not experience a sharp polyamorphic transformation upon isothermal compression (see also Section 3.1.3).224 This is because the samples contain water that is already in an HDA-like state at ambient pressure as opposed to the LDA-like state proposed by Murata and Tanaka.229 In the state diagram shown in Fig. 9a the solutions at x = 0.17 and 0.20 are, thus, located in the HDA-dominated domain (blue).
 | ||
| Fig. 9 Schematic diagrams indicating the final state of samples obtained after cooling glycerol–water solutions to 77 K using different mole fractions x, pressures p and cooling rates qc. (a) Effect of qc on solutions with different mole fraction x cooled at 1 bar. (b) Effects of qc on dilute solutions (x ≈ 0.05, dashed line in (a)) cooled at different pressures p. In addition, the constant temperature processes PIA and AAT are indicated by arrows. For clarity high pressure crystalline states are neglected. The white regions correspond to mixtures of ice I and (maximally) freeze-concentrated glassy solution ((M)FCS, x ≤ 0.38). Red (or blue) regions indicate non-crystalline solutions with water in an LDA-like (or HDA-like) state. Points and arrows represent experiments: ref. 195 for HYP, ref. 224 for PIA, ref. 230 for PVI/AAT and original data in the present work for AAT. | ||
Despite these arguments doubting the existence of an LLPT in glycerol–water solutions with x = 0.17–0.20,222–224,230 recent vibrational spectroscopy studies233 initiated reconsideration along the lines of Murata and Tanaka.229 Upon keeping liquid I for 100 min at 170 K the time-dependence of the transformation obeys the Avrami equation with an exponent n = 2.9. This is similar to the exponent reported for the purported LLPT in triphenyl phosphite (n = 3)234 but different from the exponent associated with crystallization of the liquid at 195 K (n = 1.7) and cold-crystallization of glassy water (n = 1.5 at <150 K‡). The exponents n < 2 were interpreted as nearly completed nucleation just before diffusion controlled growth of spherical particles.236–238 However, an exponent n = 3 is also expected for interface-controlled cold-crystallization.§ That is, similarity of exponents alone is not a sufficient criterion to conclude whether the solution is evolving via an LLPT or precipitation of ice. In addition, it is not clear whether triphenyl phosphite indeed exhibits an LLPT or not (e.g., formation of an interglacial phase239–241). In other words, the Avrami kinetics of a genuine LLPT is not known. In fact, the vibrational spectra above the alleged LLPT closely resemble the crystallized liquid, and so it still holds that the liquid–liquid transition was mistaken for crystallization of nanocrystals (small enough not to induce turbidity).
Water-rich region: x ≈ 0.00–0.17 (R = ∞–4.9). As the glycerol mole fraction decreases below x = 0.17, crystallization becomes more and more favorable over vitrification (see white area in Fig. 9a).216,217,222,225 Thus, most experiments in this concentration region focus on crystallized solutions.216,217,221,222,224,225 The only technique known to avoid crystallization in dilute solutions is hyperquenching. In fact, we are only aware of the hyperquenching experiments by Hofer et al.195 in which Tg was determined for glycerol–water (and other solutions) with x = 0–0.05. Interestingly, Tg(x) for glycerol–water solutions exhibits a minimum as observed in the case of salty water.195 This points to a homogeneous sample of LDA containing glycerol, just like in the case of hyperquenched LiCl solutions. By contrast to the case of LiCl the LDA–glycerol solution might be intrinsically stable, without the tendency to demix at higher temperature. In simulations vitrification can easily be achieved due to the accessible high cooling rates. This facilitates studies on glassy states of dilute glycerol–water as is elaborated in detail in Section 3.1.4.
Let us now move on from hyperquenched glassy solutions to partly crystallized glycerol–water solutions. Not surprisingly, they exhibit complex dynamics. Specifically, three main dielectric relaxation processes are observed as opposed to the single one in concentrated solutions (x ≥ 0.38).216,217,225 They are attributed to relaxation of (i) domains of pure hexagonal ice and (ii) MFCS, and to the (iii) so-called temperature-drift anomaly (see black line in Fig. 8).217,221,225 The origin of the drift anomaly is still under debate, but it has been observed for all partly crystallized solutions below x = 0.38.217,221,224,225 In DSC scans the drift anomaly appears above 200 K and overlaps with melting (see black curve in Fig. 8 for an example). Feldman and co-workers216,217,222,225 explained the temperature-drift anomaly by proposing the formation of a layer of non-crystalline, interfacial water between ice and MFCS that constantly exchanges water molecules with its surroundings. Consequently, the observed feature was regarded as a second glass transition.217,225 On the other hand, Inaba and Andersson221 dismissed a second glass transition by pointing out that the resulting Tg would be unfeasibly high. Not even inclusions of pure glycerol (Tg ≈ 185 K) could exhibit glass transitions at such high temperatures let alone pure water (Tg ≈ 136 K). Instead, they suggested that the temperature-drift anomaly is due to ice formation through cold-crystallization immediately followed by ice melting, similar to observations made for sucrose–water.242 In using optical microscopy Bogdan et al.243 even observed simultaneous melting and cold-crystallization of citric acid solutions and explained this finding by the presence of two different freeze-concentrated solutions: the first one produced by microscopic cryo-concentration in between small crystals, the second one produced by macroscopic cryo-concentration at the moving crystallization front. Thus, assuming similar behavior for glycerol–water the drift anomaly might be cold-crystallization of a more dilute freeze-concentrated solution, while a more concentrated one starts to melt.
By analyzing the hysteresis of the polyamorphic transition at different temperatures and concentrations, a co-existence region of high- and low-density glass states can be accessed (see red dome in Fig. 10). Suzuki and Mishima locate the LLCP in solution, at a given x, as the highest temperature of the co-existence region, i.e., they define the LLCP as the point where the polyamorphic transition in the glycerol–water system disappears. For example, at x ≈ 0.135, the LLCP is determined to be around p ≈ 0.045 GPa and T ≈ 150 K (red circle in Fig. 10).230,244
 | ||
| Fig. 10 Non-crystalline state diagram of glycerol–water. In black: the glass transition temperatures Tg of homogeneously vitrified solutions from ref. 218, and the LLCP of pure water (black circle) with the co-existence line between HDL and LDL from ref. 245. In red: polyamorphic behavior of emulsified PVI samples from ref. 230 and 244 with the homogeneous nucleation temperature TH, the cold crystallization temperature Tx, the LLCL spawning from the pure water critical point, and the LLCP of x = 0.135 solution at 150 K and 0.045 GPa (red circle). In blue: polyamorphic behavior of PIA bulk samples heated at 1 bar according to ref. 224 with the polyamorphic transition TAAT, the cold-crystallization temperature Tx and the end of polyamorphism at x > 0.15. The LLCP from ref. 230 is connected to the end of polyamorphism from ref. 224via the grey line nearly parallel to the pressure axis, highlighting the liaison of both studies. | ||
The existence of a two-phase region (red dome in Fig. 10) has already been proposed by Biddle et al.188 (see Section 2.2) based on thermodynamic arguments about the LLPT. The main difference in the p–T–x state diagrams proposed for glycerol–water (Fig. 10) and LiCl–H2O solutions (Fig. 5) is that, in the case of glycerol, there is no immiscibility dome at ambient pressure. Immiscibility occurs only at p ≈ 0.1–0.2 GPa. In other words, there is miscibility of glycerol, but immiscibility of LiCl with LDA-like solvent water states at low p.
Indeed, it has been proposed that the LLCP of pure water in the p–T plane (x = 0) originates a line of LLCPs in the p–T–x space (red dashed line in Fig. 10). This liquid–liquid critical line (LLCL) moves towards lower T and p as x increases and extrapolates to T = 0 K at x ≈ 0.15. It follows that, as x → 0.15, the LLCP of the glycerol–water solution moves into the glass domain and hence, the LLPT vanishes. Consequently, the observation of the AAT requires the vitrification of dilute solutions, but cannot be observed in the intermediate, i.e., glass-forming region (blue region in Fig. 9a). Procedures such as PVI, PIA or HYP are necessary to study polyamorphism in glycerol–water solutions.
Further support for the model of Biddle et al.188 is provided by Raman data of Suzuki and Mishima230 suggesting that glycerol is integrated homogeneously into water's H-bond network, both for the HDA and LDA matrix. Thus, the AAT may genuinely occur at constant x, i.e., is isocompositional. This contrasts the behavior in salty solutions as, e.g., described in Section 2.1.4 for the case of LiCl–H2O, where pure water domains and concentration changes are involved in the AAT.
In addition, Suzuki and Mishima conducted more detailed Raman studies on the polyamorphic transition in glassy glycerol–H2O solutions with x = 0.07 as a function of temperature.246 When heating pressure-vitrified samples at ambient pressure the backbone of glycerol displays significant changes depending on whether the solvent water is in an HDA-like or LDA-like state. In particular this change in glycerol conformation is observed concomitantly with the polyamorphic transition, suggesting that water polyamorphism may also affect the structure and dynamics of solutes (e.g., alcohols, polymers, proteins247–252).
When the HDA samples obtained by PIA are recovered and heated at 1 bar, the HDA → LDA transition takes place only at x ≤ 0.15 although PIA still occurs in more concentrated solutions. At 0.15 < x ≤ 0.32 one broad cold-crystallization exotherm is observed around 140–160 K, followed by the glass transition of restored MFCS (see black curve in Fig. 8 for the x = 0.20 solution). That is, glass polymorphism at 0.15 < x < 0.32 does not occur since LDA is suppressed at these concentrations. The absence of AAT/LLPT at x > 0.15–0.20 is reflected in Fig. 10 where above the critical concentration (x ≈ 0.15) the LLCL cannot be crossed, no matter the chosen pressure and temperature.
The dominance of HDA/HDL-like components at such concentrations (emphasized in Fig. 9b) goes hand in hand with glass forming properties.215 A preference for HDA/HDL states implies the suppression of crystallization because LDA/LDL is the precursor to ice I151,157 (see Section 2.1.4). In Fig. 10 it is evident that the HDA → LDA polyamorphic transition at 1 bar shifts to slightly higher temperatures upon adding glycerol whereas LDA crystallization shifts to lower temperatures.224 Consequently, the HDA state is stabilized over LDA with increasing x. The progress towards the high-density component is confirmed by very recent Raman experiments hinting that dissolved glycerol has a similar effect on the structure of water as pressure does.244 This is similar to the case of aqueous electrolyte solutions,153e.g., LiCl–H2O (see Section 2.1.4), albeit without electro-restrictive forces but H-bonding as the source of the internal pressure.
In Fig. 11 we present novel data on the volume change associated with compression/decompression cycles in solutions with x = 0.04 (see Section 2.1.4 for similar experiments on LiCl–H2O). The main goal is to test whether the LDA ↔ HDA (AAT) transformation found by Suzuki and Mishima230 using homogeneous glassy samples prepared by PVI can also be observed in the heterogeneous samples prepared by PIA. The sudden density change at p = 0.06 GPa for the downstroke and at p = 0.45 GPa for the upstroke (red curve in Fig. 11) signifies the AAT in both directions. The similarity with the volume change of pure water under the same process (black curve in Fig. 11) indicates that the transformations observed in the mixture are due to water switching between LDA-like and HDA-like states.
This comparison shows (i) the densification for the LDA → HDA transition in glycerol–water solutions is smaller than in pure water and (ii) the LDA → HDA transformation is smoother when glycerol is present. Identical volumes of x = 0.04 glycerol–water solutions and pure water contain roughly the same number of water molecules. Thus, one would expect almost identical densification at the polyamorphic transition. However, the sample height changes are 1.51 mm and 1.17 mm for pure water and the glycerol–water mixture, respectively (double-arrows in Fig. 11), i.e., the volume change during the LDA ↔ HDA transformation decreases roughly by 23% when glycerol is added (x = 0.04). This implies that not all water molecules experience the polyamorphic transition in the solution. The non-polyamorphic water molecules are in fact the ones that are trapped in the MFCS. These water molecules would account for ≈10% total step height decrease. However, Fig. 11 shows ≈23% difference in step height between black and red curves (see double headed arrows).
This can be explained by considering that (i) there are water molecules in the solution that do not exhibit polyamorphism (see Section 3.1.1), e.g., water molecules located in the interphase (between MFCS and water domains), or (ii) by a smaller density difference between the LDA and HDA water domains within the glycerol–water than in the case of pure water. Our MD simulations show that adding glycerol considerably increases the density of the LDA solution while barely changing the density of the HDA solution,253 supporting scenario (ii). Scenario (i) seems unlikely, since one would need more water molecules trapped in the interphase than in the MFCS. This would imply unreasonably large volumes of interphase in x = 0.04 glycerol–water. That is, we interpret these observations in the sense that the sample formed at high pressure by PIA consists of MFCS and HDA, which upon decompression converts to MFCS and LDA, where the LDA contains glycerol molecules, such that the LDA density significantly increases with increasing x. We note that our earlier experiments224 and MD simulations,253 as well as available experimental results230,244,254 confirm that glycerol is soluble both in LDA and HDA. These observations are in striking contrast to LiCl–H2O: whereas the difference in step height is slightly overestimated for LiCl–H2O (see double headed arrows in Fig. 6), it is underestimated for glycerol–water.
Next, we discuss briefly the crystallization temperature Tx of glycerol–water solutions prepared by different methods. Depending on the procedure followed for sample preparation glassy glycerol–water solutions exhibit noticeable differences in Tx (which is not surprising since glasses in general are history-dependent materials). The crystallization temperatures of glycerol–water samples during isobaric heating are shown in Fig. 10 at 1 bar (T–x plane) for samples formed via PIA (Tx,PIA, blue dashed line) and PVI (Tx,PVI, red line). The spread between Tx,PIA and Tx,PVI is remarkable. In particular, we note that the PVI samples always crystallize at much higher temperatures than PIA samples (≈30 K difference at x = 0.17). Crystallization commences well above the Tg of a homogeneously vitrified solution at 1 bar218 for the PVI samples but below Tg for the PIA samples. These differences in Tx can be due to three distinct causes: (i) PIA leads to heterogeneous amorphous samples consisting of water-rich and solute-rich domains, where crystallization of the water-rich domains takes place first, at temperatures similar to pure water; (ii) ice nucleation is triggered by the interphase224 or remnants of the process of PIA;255,256 or, (iii) an HDA-like sample does not experience the polyamorphic transition but instantly crystallizes to ice I. We regard (iii) to be unlikely since pure HDA samples are known to crystallize to high-pressure ice modifications (such as ice IV and ice XII).257 (ii) was shown to occur for pure water as an increase of Tx by up to 11 K was observed after removal of nanocrystalline domains through annealing.255,256 It is doubtful, however, whether the nanocrystalline/amorphous interphase in glycerol–water can also be removed with a similar procedure. (i) seems to be the most plausible explanation as complete homogenization after PIA is rather unlikely. This represents the main difference between samples prepared by PVI and PIA.
In order to study the LDA → HDA transformation in glycerol–water solutions, we first prepare glassy configurations at T = 80 K and p = 0.1 MPa, see Fig. 12a. These glassy mixtures are obtained by cooling an equilibrated (liquid) solution at constant pressure (p = 0.1 MPa) with a cooling rate qc = 1 K ns−1. At this cooling rate, crystallization is avoided and the aqueous solutions appear to be homogeneous. Instead, in the experiments of ref. 224, the cooling rates are slow, qc < 1 K min−1, and crystallization takes place at x ≤ 0.38. The glassy solutions obtained using the HYP process in the MD simulations are comparable to the ones prepared by Suzuki and Mishima230 using PVI, since in their experiments, the glasses are homogeneous and free of ice. The glasses prepared at p = 0.1 MPa and T = 80 K are then compressed at a compression rate of 100 MPa ns−1 (see Fig. 12b). During compression, at T = 80 K, the glassy solutions transform to the HDA state. However, the transformation becomes smoother with increasing glycerol content and the LDA → HDA transition in the mixtures is not observable for approximately x > 0.05. The underlying reasons for this are that (i) the density of the starting glassy mixture at p = 0.1 MPa increases rapidly during the preparation process (Fig. 12a), while (ii) the densities of the HDA solutions at p > 1000 MPa are practically independent of the glycerol content (x ≤ 0.10), see Fig. 12b. In other words, the starting glasses cannot reach an LDA state during cooling and they become more HDA-like with increasing x. The MD results are consistent with experiments that show that the LDA → HDA transformation in glycerol–water mixtures is undetectable for approximately x > 0.10–0.12.230
 | ||
| Fig. 12 (a) Density of glycerol–water solutions as function of temperature during cooling at p = 0.1 MPa from MD simulations (thin lines with error bars). The solutions are equilibrated at T = 300 K for x > 0 and T = 240 K for x = 0, and then cooled at rate qc = 1 K ns−1. Glycerol mole fractions are (bottom to top) x = 0 (black and red), 0.0014 (green), 0.0095 (dark green), 0.0202 (red), 0.0306 (blue), 0.0395 (maroon), 0.0495 (magenta), 0.0701 (violet), 0.10 (orange), and 0.1301 (indigo). For comparison, included are the densities of the solutions in equilibrium (symbols). The solutions are in the equilibrium liquid state at roughly T > 200 K and in the glassy state at approximately T < 150 K. Each data point during the cooling simulation is an average over a pressure window of 10 MPa and the error bars represent the standard deviation of the density over this p-interval. (b) Density as a function of pressure during isothermal compression at T = 80 K of the glassy solutions prepared in (a). At all temperatures, increasing glycerol concentration reduces the density change during the compression process. The LDA → HDA transformation can be identified at roughly x ≤ 0.05. At higher concentrations, the density of the starting glass is high, ρ ≥ 1.1 g cm−3. The compression/decompression rate is qp = 100 MPa ns−1. Reproduced from ref. 253. | ||
Regarding the decompression-induced HDA → LDA transitions, the simulations in ref. 253 show that this transformation is very smooth in glycerol–water mixtures, barely detectable at T > 120 K, and occurs at negative pressures. At comparable conditions, T ≈ 140–155 K and x < 0.10–0.12, the experiments of ref. 230 indicate that the density change during the HDA → LDA transformation is relatively sharp and it occurs at positive pressures.224,230,246,254 At the currently accessible compression/decompression rates in MD simulations, HDA does not seem to convert back to LDA at T ≤ 120 K even if negative pressures are considered. Instead, the density of HDA decreases continuously until the glass finally fractures at p ≈ –800 MPa. This is not inconsistent with the experiments of ref. 224 where it is shown that, upon decompression of the HDA-like mixtures, no transformation back to a less dense state occurs at T = 77 K and p > 0 MPa. We note that the MD simulations are able to reproduce the qualitative effects of varying T and x reported in experiments.224,230 Specifically, increasing T leads to a reduction of the hysteresis in ρ(p) during a compression–decompression cycle and increasing the glycerol content to smoother changes in ρ(p) during the LDA → HDA transformation. Interestingly, the results from the MD simulations were robust, not sensitive to the glycerol model used, even when the specific conformations adopted by the different glycerol models in the glass state differ.253,259
One of the main contributions of MD simulations is to provide a molecular-level description of the LDA → HDA transformation in the glass states, information that is not easily accessible in experiments. The structural changes accompanying the LDA → HDA transformation in pure water are well-known (see, e.g., ref. 260–262). Interestingly, similar structural changes are observed in the TIP4P/2005 glycerol–water mixtures. For example, Fig. 13 shows the water oxygen–water oxygen (Ow–Ow) radial distribution function in the LDA and HDA mixtures for x ≈ 0.03. During the LDA → HDA transformation (black curves) the HB network collapses with roughly one molecule displacing from the second hydration shell of LDA (r ≈ 4.5 Å) toward the first hydration shell (r ≈ 2.8 Å), filling the first interstitial shell (r ≈ 3.5 Å). One may wonder, if similar structural changes occur next to glycerol's OH groups. To show that this is indeed the case, we include in Fig. 13 (red lines) the RDFs of glycerol oxygens (Og) around water oxygens. Fig. 13 demonstrates that during the LDA → HDA transformation, glycerol Og atoms move closer to their nearest water neighbors, from the neighboring water molecule's second shell (r ≈ 4.5 Å) toward their first shell and filling the corresponding first interstitial shell (r ≈ 3–3.5 Å). However, and not surprisingly, the changes in the Ow–Og RDFs (red lines) are less pronounced than in the case of Ow–Ow RDFs (black lines) since a water molecule next to an OH group of glycerol is still surrounded mainly by other water molecules. We note that the role played by the glycerol model is relevant at the molecular level; specifically, the Og–Ow RDF is sensitive to the glycerol model considered.253 Yet, for both models studied in ref. 253, Og atoms tend to populate the interstitial space of the neighboring water molecules (r ≈ 3–3.5 Å) during the LDA → HDA transformation, as shown in Fig. 13.
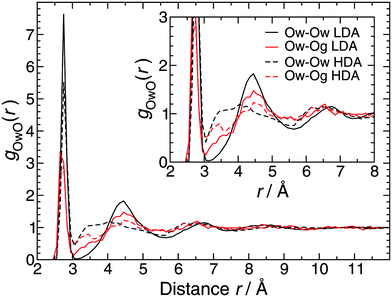 | ||
| Fig. 13 Radial distribution function of water (Ow) and glycerol (Og) oxygen atoms around water oxygens Ow from MD simulations at T = 80 K and p = 0.1 MPa, and x = 0.0306. During the LDA → HDA transformation, the main change in both Ow–Og and Ow–Ow RDFs (red and black lines, respectively) is the decrease of the peak located at r ≈ 4.5 Å (second hydration shell of water) and decrease in the depth of the minimum located at r ≈ 3.2–3.5 Å (first interstitial shell of water). The inset shows a magnification of the most relevant region. Reproduced from ref. 253. | ||
The similar collapse of the hydrogen bond (HB) network between water–water OH groups and water–glycerol OH groups is remarkable since it suggests that glycerol OH groups participate actively in the LDA → HDA transformation. In the case of non-hydrogen bonding solutes, such as ions, it is hard to imagine a shift of water molecules from a second hydration shell to a first interstitial shell, analogous to the HB collapse at water–water and water–glycerol OH groups. In this regard, the collapse of the HB network between water and alcohol OH groups makes alcohols rather special; alcohols allow for the suppression of ice (to a degree that depends on the type and the concentration of alcohol) while preserving the LDA → HDA transformation, at least in dilute solutions. It follows from the discussion above that molecules smaller than glycerol but with a high density of OH groups are good candidates to observe water glass polymorphism, provided they are also able to suppress crystallization. Candidates include, e.g., hydrogen peroxide.
The effects of adding glycerol on polyamorphism of glycerol–water solutions can also be estimated by looking at the supercritical lines (ρ maxima, κT maxima and cp maxima lines, see Fig. 1) in the supercooled solutions. For example, MD simulations of TIP4P/2005 water and the glycerol model based on ref. 263 show that the TMD line shifts towards lower temperatures with increasing glycerol concentrations.259 This suggests that adding glycerol to water tends to shift the LLCP to lower temperatures. Such findings are also supported by experiments since the densities obtained from these MD simulations in the liquid state are in remarkable agreement with experimental data for approximately x ≤ 0.20. Indeed, the computer simulations' results and experiments of glycerol–water solutions and brine–glycerol mixtures across the whole glycerol concentration range264,265 indicate that the mixtures' densities for approximately T < 350 K are well described by the following expression ρ(wg, T) = (1 − wg)ρ0w(T) + wρ0g(T), where, ρ0w(T) and ρ0g(T) are the densities of pure water and glycerol at temperature T, respectively. Consistent with the observed shift in the TMD line, ref. 259 also shows that adding glycerol shifts the compressibility maximum and the cp-maximum towards lower temperatures. In addition, we note that even for x ≤ 0.05, the diffusivity of TIP4P/2005 water in the solutions does not show an FSDC, at least for T ≥ 210 K (p = 0.1 MPa); at all concentrations the T-dependence of water diffusivity follows the Vogel–Fulcher–Tammann equation.80,266
3.2 Other alcohol–H2O solutions
The critical pressure of the LLPT does not depend on the type of solute but remains at 0.050 ± 0.005 GPa for all polyols. It is however evident that polyamorphism vanishes at lower concentrations for solutes with more OH-groups. This reflects more water molecules being directly bonded to a single polyol molecule, i.e., less water molecules remain to form a H2O-network. Consequently, near the critical concentration water forms mostly high-density states suppressing crystallization. Thus, it is not surprising that the homogeneous nucleation temperature TH is lower for solutes with more OH groups.254,273
The LLCP in TIP4P/2005 water has not been directly accessed at present as long simulation time scales are needed to equilibrate this water model. At present, the location of the LLCP in TIP4P/2005 water is estimated to be at 175–193 K (see Table 1). For example, a recent equation of state for TIP4P/2005 water has been obtained using a two-state water model.54,58 This equation of state indicates that the LLCP should be located at Tc = 182 K, pc = 170 MPa, and ρc = 1.017 g cm−3. Similarly, an equation of state for TIP4P/2005 water based on the potential energy landscape approach predicts that Tc = 175 K, pc = 175 MPa, and ρc = 0.997 g cm−3.55 In ref. 274, evidence of an LLCP at low temperatures was found for methanol–water solutions at x = 0.05 but not for x = 0.10. The LLCP location is estimated to be Tc = 193 K, pc = 96 MPa, and ρc = 1.003 g cm−3. This conclusion is based on (i) extrapolation of high-temperature isochores to low-temperatures, and (ii) the development of an inflection point in the isotherms upon cooling. The estimated LLCP location of the methanol–water solutions is almost identical to the location of the LLCP in bulk water in the early work of ref. 53. However, longer computer simulation times at low temperatures are needed in order to confirm the existence of an LLCP in methanol–water solutions of TIP4P/2005. We note that the MD simulation data of ref. 274, at the accessible equilibrium temperatures, are fully compatible with the predicted LLCP in methanol–water mixtures. Specifically, this study shows that the methanol–water solutions exhibit anomalous density maxima line in the p–T plane, as well as κT-maxima and αp maxima lines at T > Tc. In particular, the κT and αp maxima lines merge in the p–T plane upon cooling, as the hypothesized LLCP location is approached, in agreement with the scenario presented in Fig. 1.
The absence of an LLCP at x = 0.10 in ref. 274 is consistent with the location of the TMD lines in the p–T plane obtained for methanol–water solutions at different concentrations. Specifically, the TMD line of these solutions shifts towards lower temperatures as the methanol content increases, a result that is consistent with experiments.276 The results from MD simulations suggest that the features of the phase diagram of water, including the LLCP, shift towards lower temperatures with increasing amounts of methanol.
4 Other solutes in water
4.1 Polar solutes
For pressure-vitrified protein hydration water the diffraction profiles between 80 and 170 K can be expressed as a linear combination of a high-density state at 80 K and a low-density state at 170 K, suggesting an underlying first-order transition.277 The authors also argue that the unusually small changes in unit cell volume can only be rationalized assuming liquidity of water molecules during the transition, where the high mobility makes them capable of leaving the protein crystal. An additional effect that was not considered by the authors might be that the density difference between the HDA- and LDA-state is diminished in the presence of solute compared to pure water, as is the case in glycerol–water solutions (see Section 3).253 The dynamical transition between conformational states in pressure-vitrified proteins occurs already at very low temperatures (110 K) upon warming.248 This finding is striking, as such transitions have previously been observed only around 180–240 K.284,285 Interestingly, at 110 K also the polyamorphic transition of solvent water occurs.248,281 However, when avoiding the formation of HDA-type hydration water by cooling an identical protein crystal at ambient pressure, no increase in protein mobility is visible up to 180–240 K. Thus, it seems that the HDA → LDA transition in pressure-vitrified hydration water is accountable for the protein dynamical transition at cryogenic temperatures, whereas the mobility in LDA-type hydration water is not sufficient to trigger the transition at 110 K. One could speculate that this results from the water molecules being more mobile in the HDA than in the LDA state. Indeed, it has been shown that the dynamics in HDA near 110 K are two orders of magnitude faster than in LDA,286 reaching the relaxation times of an ultraviscous liquid. That is, the mobility of water is likely the driving factor for the conformational fluctuations of proteins as it has also been suggested in various MD simulation studies.287–289
The HDA → LDA transition kinetics also obeys the Avrami equation236–238 implying an underlying mechanism of nucleation and growth, i.e., a first order transition between two amorphous solids.277 That low-density amorphous domains nucleate within the HDA-matrix, which then grow on the expense of it, was shown by Tonauer et al.290 for the pure water case. This requires the development of sharp interfaces between two amorphous forms, a novel concept in glass physics observed first by Mishima et al.291 and Winkel et al.107
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 while the smallest experimental rate that avoids crystallization is qc ≈ 0.001–0.01 K ns−1.89,112 In the glass state, the LDA → HDA transformation is very smooth, relative to full-atomistic polyamorphic water models, such as the ST2 model. Ref. 297 presents a scenario for glassy states of mW in which there is only a single liquid and two amorphous states that meet at a triple point rather than the LLCP scenario in other (full-atomistic) water models.
296 while the smallest experimental rate that avoids crystallization is qc ≈ 0.001–0.01 K ns−1.89,112 In the glass state, the LDA → HDA transformation is very smooth, relative to full-atomistic polyamorphic water models, such as the ST2 model. Ref. 297 presents a scenario for glassy states of mW in which there is only a single liquid and two amorphous states that meet at a triple point rather than the LLCP scenario in other (full-atomistic) water models.
Le and Molinero160 studied a binary mixture consisting of mW and a generic hydrophilic solute S with mole fractions x = 0–0.50. During out-of-equilibrium MD simulations the liquid was vitrified at ambient pressure and qc = 10 K ns−1. Depending on the solute concentration, three scenarios are distinguished: (i) at x = 0.50, the solutions crystallize into a homogeneous mW–S crystal of intercalated planes of S and mW molecules, (ii) at x = 0.20–0.40, a homogeneous glass is obtained, and (iii) at x = 0.05–0.15, a nano-segregated glass is formed. These nano-segregated glasses consist of two domains with a characteristic dimension of ≈5 nm. One domain resembles LDA, the other consists of a concentrated glassy solution of S and mW. The results of ref. 160 suggest that LDL is a poor solvent for the hydrophilic solute S due to the tetrahedral order of LDL. This forces the solution to phase-separate during the (fast) cooling process (x = 0.05–0.15), leading to the formation of LDA and glassy solution domains. Interestingly, Le and Molinero further point out that the S–mW water solutions exhibit some similarity with real LiCl–, NaCl–, and KCl–water solutions.131 Specifically, in both cases there is phase separation into LDA and a salty glass even for hyperquenched samples, and the fraction of LDA in the glassy mixtures decreases linearly with x.
Although the S–mW water solution is not truly a salt–water mixture, these MD simulations present a picture of how phase separation may occur in real aqueous solutions. In particular, they show the important role that the presence of polyamorphism may have in salty solutions at low temperatures. We note that the effects of S–S and S–mW interactions should be taken into consideration when interpreting these results. Specifically, the generic hydrophilic solute S was not parameterized to reproduce any salt and the S–S interactions are very weak compared to S–mW interactions, which is not expected to be the case for, e.g., Li+ and Cl− ions in aqueous solution.
4.2 Apolar solutes
Experimental studies on polyamorphism in the presence of apolar solutes are scarce, or in fact non-existent. At least we are not aware of any publication detailing the influence of apolar solutes on the polyamorphic transition of water. This would certainly be a topic worthwhile of study. However, both MD simulations and thermodynamic approaches have been pursued.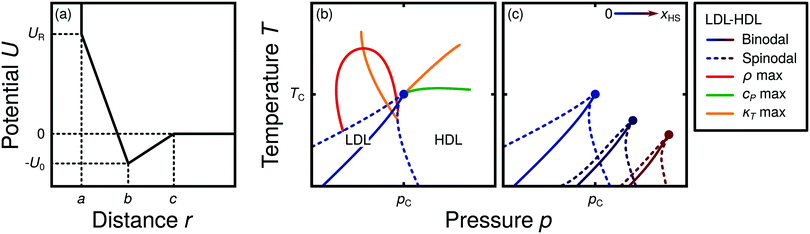 | ||
| Fig. 14 (a) The Jagla pair potential consists of two length scales defined by the hard-core distance, a, and the location of the potential minimum, b. The core-softened part extends between a and b. (b) State diagram of Jagla potential based on ref. 78 and 305. The blue features show the LLCP with associated binodal and spinodal lines. The extrema in density (red) and thermodynamic response functions, heat capacity (green) and compressibility (orange), are also shown. Note that the LLCP binodal line has a positive slope, in contrast to the negative slope for water models (see Fig. 1). (c) Effect of increasing concentration on the LLPT of solution composed of Jagla water-like particles and hard spheres (from ref. 312). Contraction increases from blue to maroon color, blue lines are taken from (b). | ||
Relevant to this work is that aqueous solutions of small hard spheres in a Jagla-particle solvent describe many properties of binary aqueous solutions containing small hydrophobic solutes. Specifically, they can show a minimum in the solubility of small hard spheres as function of temperature.310 This is consistent with experiments of small apolar solutes, such as alkanes and noble gases, in water where a solubility minimum occurs at T ≈ 310–350 K.310,311
MD simulation studies of hard-sphere solutes in a Jagla solvent are reported in ref. 312 and 313. The model mixture employed in these works is identical to the model system studied in ref. 310. At the mole fractions, x = 0.10–0.50 with a total of 1728 particles, the solutions do not phase-separate and hence, the low temperature domain of the mixtures can be investigated. In ref. 312, discrete MD simulations are used to characterize the effects of concentration on the location of the LLPT/LLCP. This study shows that (i) an increase in solute concentration shifts the LLCP to lower T and higher p (see Fig. 14c). In addition, (ii) all solutions studied exhibit an FSDC upon isobaric cooling at T > Tc, in the proximity of the LLCP. In particular, the Widom line shifts towards higher p and lower T upon increasing x, consistent with the shift in the location of the LLCP.313 (iii) In the case of x ≤ 0.40, a TMD line is found which, again, shifts towards higher p and lower T upon increasing x. Interestingly, (iv) the shift of the LLPT towards higher p leads to a stabilization of the LDL phase with increasing concentration and a reduction of the co-existence region (Fig. 14c). The increased stability of LDL in the presence of apolar solutes contrasts the increased stability of HDL in ionic solutions.47,144–148
Points (i)–(iv) could be due to the fact that in the Jagla model liquid, the LDL is a better solvent for the hard spheres considered.312 Interestingly, the MD simulations of ref. 48, based on TIP5P-Ew water and argon-like particles, also show that the solubility of the argon-like solute in TIP5P-Ew water is higher in LDL than in HDL.
We note that, when extrapolating the results of aqueous solutions based on the Jagla model to real aqueous solutions, one must take into consideration that the slope of the LLPT is positive, dp/dT|LLPT > 0, while dp/dT|LLPT < 0 in full-atomistic water models that show polyamorphism. The value of dp/dT|LLPT specifies the entropy difference between LDL and HDL. Indeed, the Clapeyron equation indicates that dp/dT|LLPT = ΔS/ΔV, where ΔS and ΔV are the changes in entropy and volume across the LDL → HDL first-order phase transition. It follows from this relationship that, in the Jagla solvent, the LDL has a larger entropy than HDL while in water, HDL is the liquid with the higher entropy. A change in the slope of the LLPT can affect the thermodynamic picture of the model considered.314 For example, as shown in ref. 303, 305 and 307, as the LLPT line in the p–T plane becomes parallel to the T-axis, the cp-maxima line at T > Tc vanishes.
5 Conclusions and outlook
The intriguing concepts of polyamorphism, dating back to experiments in 1984,109 and liquid–liquid phase transition (LLPT), dating back to simulations in 199233 are possibly related to the anomalous nature of liquid water. Although aqueous solutions have been a traditional topic in physics and chemistry for centuries, the study of polyamorphism in aqueous solutions has only emerged in the third millennium. Here, both computer simulations and experiments have advanced the frontiers of the field, where simulations mostly cover supercooled solutions and experiments mainly cover the amorphous solid. There are notable exceptions in which solid state polyamorphism is tackled in simulations253 and in which the LLPT is addressed in experiments.107,152,230Aspects such as phase separation, including ice formation, are common for experimentalists, limiting the accessible T and p region where solutions can be studied in the supercooled and glassy states. Crystallization is usually not an issue in computer simulations because of the small time scales currently accessible in MD simulations. In some sense, computer simulations and experiments complement each other by exploring different time scales. Computer simulations have explored time scales of ≤10 μs while experiments usually employ time scales of the order of minutes. However, the different time scales also imply that a direct comparison between simulations and experiments must be done carefully. Interestingly, for the case of pure water, the LDA → HDA transformation pressure at T = 80 K obtained in MD simulations at different compression rates extrapolates remarkably well to the experimental value.119 We note that the ever increasing computational power makes it possible to probe equilibrium systems at lower and lower temperature, and allows the application of smaller and smaller rates, thereby reducing the gap to experiments. As of now only one simulation study has reached the cooling rates used in hyperquenching experiments, while compression rates are still at least three orders of magnitude larger than the highest rate accessible to experiments.119 At the same time experimental techniques and procedures are constantly refined, making very high rates available and producing samples that could be in equilibrium at constantly lower temperatures, reducing the gap to simulations. Both approaches can also join the effort to study new systems, i.e., solutions, where the problems of equilibration and crystallization do not interfere, opening the possibility for direct evidence of a liquid–liquid critical point (LLCP).
The solutes discussed in this perspective encompass ionic, polar and hydrophobic substances where the latter have barely received any attention. Although NaCl could be considered the archetype of an ionic solute, all experiments on polyamorphism focus on LiCl–water. LiCl solutions on the other hand have only been investigated in a single study employing computer simulations,136 with almost all numerical studies on the LLPT devoted to NaCl–water. This testifies the separation between the two groups. As a model substance for polar solutes both communities study almost exclusively alcohols, where the benchmark case is glycerol. As of yet, literature on aldehydes, ketones, carboxylic acids etc. awaits publication.
In the present work we consolidate the computational and experimental work related to glass polymorphism and the LLPT of the last two decades. These studies are put into the context of the pioneering studies on vitrification of binary aqueous solutions. We augment this literature review with some original experiments aimed at resolving open questions. In this concluding section we attempt to elaborate on the difference between the solutes, especially alkali chlorides and glycerol. All solutions have in common that there is a concentration regime in which polyamorphism and LLPT are absent. This is always the case above the eutectic concentration (mole fraction x ≥ 0.28 for glycerol, x ≥ 0.12 for LiCl) but also even below (e.g., x ≈ 0.15 in glycerol–H2O).224,230 In dilute solutions (x < 0.05) the situation fundamentally changes and water may either occupy high-density or low-density states with a sharp first-order like transition between the two. These are the hallmarks of polyamorphism at low temperatures and the LLPT at high temperatures. A challenge in experiments is that dilute aqueous solutions, just like pure water, are bad glass-formers. That is, at standard cooling rates they crystallize (fully or partly), rather than vitrify. Hence, elaborate experimental techniques are required to study dilute amorphous solutions, such as hyperquenching (HYP), pressure-vitrification (PVI) and pressure-induced amorphization (PIA) of ice crystals. This has long been a disincentive for researchers to enter the field of polyamorphism in aqueous solution. Even if crystallization is avoided phase separation may interfere in salt solutions where water-rich and solute-rich liquids demix upon cooling.126 This demixing takes place not only for slowly cooled salt solutions but also for HYP131 and possibly PVI samples.132,133
By contrast, such behavior has not been reported in alcohol–water solutions. Instead, isocompositional vitrification takes place, both at ambient and high pressure. The variable pressure determines whether the dilute liquid solution turns into low-density amorphous (LDA) or high-density amorphous (HDA) ice upon cooling. Interestingly, increasing solute concentration and pressurizing seem to have similar effects on water's structure,153,244,253 forcing the solvent water into the HDA state. HDA-like patches form even around tiny amounts of salt whereas tiny amounts of alcohol are not sufficient to enforce HDA structures. In fact, alcohols can also be surrounded by LDA type solvent depending on the pressure used for vitrification. Simulations show a continuous development of the LDA type solvent towards higher densities with increasing x.253 In other words, only salts but not alcohols are insoluble in LDA. Nonetheless, the phase segregation to concentrated salty solution and LDA might be prevented on kinetic grounds for rapidly cooled solutions, as testified by a strong variation of Tg of hyperquenched solutions with x. Consequently, the polyamorphic transition between LDA and HDA in alcohol solutions appears to be of isocompositional nature. On the other hand, this might not be so in salt solutions where the LDA ↔ HDA transformation seems to take place in the salt free parts of the sample. That is, polyamorphism in salt solutions is only preserved due to phase separation.
The influence of solutes on the LLCP locus has been addressed in simulations and thermodynamic models. Currently, the best estimate for the LLCP of pure water in experiments is 0.05 GPa and 223 K.71 In general, the addition of solutes shifts the LLCP where direction and size of the shift depend on the type and concentration of the solute. While increasing x of NaCl moves the LLCP to lower (even negative) pressures and higher temperatures,144 hydrophobic solutes show the opposite effects.312
Despite the fact that the general picture presented here is largely coherent, there are still several details that need further investigation. A non-exhaustive list of these open questions comprises:
(i) Is it valid to connect the LLCP of water as a single component to the line of LLCPs in a binary (alcohol) solution?
Suzuki and Mishima230,244 locate the LLCPs in solutions by looking for the maximal concentration x(T) at which the polyamorphic transition can be observed and link these points with the LLCP in pure water. It is however unclear whether the end of polyamorphism in binary solutions is associated with the kind of critical phenomena known for critical points in a single component, such as opalescence or divergences in thermodynamic response functions.
(ii) Are all salts immiscible with LDA?
While the work by Hofer et al.130,195 and Ruiz et al.129 suggests the possibility of small amounts of salts retained in LDA, Suzuki and Mishima,134 Le and Molinero160 and Corti et al.156 support immiscibility.
(iii) Do LiCl–solutions phase-separate upon cooling under pressure?
Kanno132 and the early work of Suzuki and Mishima133 suggest phase segregation into concentrated solution and rather pure HDA whereas Suzuki and Mishima134,152 assume homogeneous vitrification in their later publications.
(iv) What is the origin of the drift anomaly present in DSC scans of crystallized glycerol–water solutions?
Inaba and Andersson221 explain it through cold-crystallization of dilute solution and melting of ice in concentrated solution taking place simultaneously while Feldman et al.217,225 propose an interfacial liquid layer, exchanging water molecules with its surroundings. We suggest that it can be explained by the melting of an interphase sandwiched between bulk ice and maximally freeze-concentrated domains.224
(v) How different are the high-density solutions prepared by PVI and by PIA of solutions containing ice?
Both routes seem to lead to an indistinguishable HDA state for pure water.113 For salt solutions the process of PIA undoubtedly starts from a phase segregated mixture whereas for PVI a homogeneous glass is inferred. Thus, the question is whether homogenization takes place upon PIA. This question has not been addressed directly so far since PVI was studied in Japan152,230 and PIA in Austria129,224 by different groups. Some indirect evidence suggests that PIA samples are heterogeneous, composed of (M)FCS and HDA, whereas PVI samples might either be homogeneous or heterogeneous (see (iv)).
(vi) Is it possible to design solutes with desired properties, e.g., increased resistance against crystallization in solution such that the “no man's land” can be entered?
Promising evidence for this case has been provided by ionic liquids that mix ideally with water.203 However, further work is needed for a conclusive answer. Extension of the work of ref. 203 and 206 to other ionic liquids would be very helpful. In particular, additional structural studies and compression/decompression experiments are desirable.
(vii) How do the kinetics of cold-crystallization differ from the kinetics of an LLPT?
This question has been touched in the work of Bruijn et al.,233 but has remained at an inconclusive stage. In the future, we expect strong effort to resolve the remarkably complex mechanism of nucleation and growth,317 which led to the controversy associated with the LLPT in glycerol–water solutions. Another important goal is to determine the rates of (cold-)crystallization and compare them with the kinetics of the LLPT at various temperatures and glycerol concentrations. Due to increasing viscosity upon adding glycerol crystallization rates are expected to slow down,229 thereby facilitating access to the LLPT. Such kinetics studies might also help finding the missing link between the rates of crystallization of liquid and of cold-crystallization of amorphous solid.318
(viii) Can the gap between experiments and simulations be closed?
This encompasses not only the considerable disparities between cooling/compression rates in experiments and simulations but also the type of solutions studied. Obviously, detailed MD simulation studies on LiCl–water would greatly improve our understanding of the LLPT/LLCP in these solutions. Similarly, more experimental work on the polyamorphism in NaCl–solutions is desired to complement the results from simulations.
(ix) What kind of water–solute interactions may contribute actively in the LDA–HDA transformation of water?
For example, in the case of glycerol, the OH groups of the solute seem to help the LDA → HDA transformation to evolve during compression, since a collapse of the HB network next to glycerol's OH groups occurs, just as it is found in bulk water. Instead, this is not the case for salts.
(x) Does the hydration water trigger dynamics in the solutes?
The studies on polyamorphism in pressure-vitrified protein solutions show a dynamical transition at surprisingly low temperature, when compared to the dynamical transition in ambient pressure cooled protein solutions. This low temperature transition has thus been associated with polyamorphism and the much higher mobility of water when in the HDA state. Very recently, a regular dynamical transition was observed for the first time in a non-biological macromolecule.319 This offers the possibility to study a wider array of pressure-vitrified macromolecule solutions. If a low temperature dynamical transition would be observed independently of the chemical nature of the macromolecule this transition is highly likely related to the unique behavior of water alone.
(xi) How do hydrophobic solutes influence polyamorphism in H2O?
So far hydrophobic solutes have only been studied in simple theoretical models. Hence, it would be promising to conduct experiments and full-atomistic simulations on polyamorphism in the presence of hydrophobic solutes. This is desirable since simulations in the Jagla model indicate a higher solubility of apolar solutes in LDA than HDA, which is the exact opposite from the observation in experiments on polar and ionic solutes.
We regard these eleven questions to be the most relevant questions in the field, which is still in its infancy given that it is less than two decades old, with only a handful of groups actively pursuing research in this direction. We hope that the present work highlighting the discrepancies and similarities between different systems and techniques as well as relevant open questions, will provide impetus to the field of liquid and glass polymorphism in aqueous solutions. Our ultimate goal is to inspire and motivate more researchers from experiment, simulation and theory to venture into the field and attempt “to boldly go where no man has gone before”.320
Glossary of abbreviations
| AAT | Amorphous–amorphous transition |
| BDS | Broadband dielectric spectroscopy |
| CS | Concentrated solution |
| DSC | Differential scanning calorimetry |
| DTA | Differential thermal analysis |
| FCS | Freeze-concentrated solution |
| FSDC | Fragile to strong dynamical crossover |
| HB | Hydrogen bond |
| HDA | High-density amorphous ice |
| HDL | High-density liquid |
| HYP | Hyperquenching |
| IMM | Immiscibility |
| IR | Infrared |
| LDA | Low-density amorphous ice |
| LDL | Low-density liquid |
| LLCL | Liquid–liquid critical line |
| LLCP | Liquid–liquid critical point |
| LLPT | Liquid–liquid phase transition |
| MC | Monte Carlo |
| MD | Molecular dynamics |
| MFCS | Maximally freeze-concentrated solution |
| PIA | Pressure-induced amorphization |
| PVI | Pressure-vitrification |
| QM/MM | Quantum mechanical/molecular mechanical |
| RDF | Radial distribution function |
| S | Solute |
| TMD | Temperature of maximum density |
| VHDA | Very high-density amorphous ice |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are indebted to all the colleagues whose work on aqueous solutions has inspired us over the years, including (in alphabetical order) C. Austen Angell, Roland Böhmer, Livia E. Bove, Sergey V. Buldyrev, Frédéric Caupin, Pablo G. Debenedetti, Paola Gallo, Chae Un Kim, Osamu Mishima, Maria-Antonietta Ricci, Francesco Sciortino, H. Eugene Stanley, Yoshiharu Suzuki, and Edward Whalley. Financial support by the Austrian Science Fund (FWF project I1392 to TL and Erwin Schrödinger Fellowship J3811 N34 to PHH) and the University of Innsbruck (NWF-Project 282396 to PHH) is gratefully acknowledged.References
- S. T. Coleridge, The Rime of the Ancyent Marinere, in Lyrical Ballads, ed. W. Wordsworth and S. T. Coleridge, Routledge, 2nd edn, reprint edn, 1996 Search PubMed.
- Iron Maiden, Rime Of The Ancient Mariner, Powerslave, 1984.
- F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 25, 1–30 Search PubMed.
- F. Franks, Water, a comprehensive treatise, Plenum, New York, 1972 Search PubMed.
- R. O. Watts, E. Clementi and J. Fromm, J. Chem. Phys., 1974, 61, 2550–2555 CrossRef CAS.
- E. Clementi and H. Popkie, J. Chem. Phys., 1972, 57, 1077–1094 CrossRef CAS.
- H. Kistenmacher, H. Popkie and E. Clementi, J. Chem. Phys., 1973, 58, 5627–5638 CrossRef CAS.
- H. Kistenmacher, G. C. Lie, H. Popkie and E. Clementi, J. Chem. Phys., 1974, 61, 546–561 CrossRef CAS.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471 CrossRef CAS PubMed.
- L. M. Ramaniah, M. Bernasconi and M. Parrinello, J. Chem. Phys., 1999, 111, 1587–1591 CrossRef CAS.
- B. M. Rode, C. F. Schwenk, T. S. Hofer and B. R. Randolf, Coord. Chem. Rev., 2005, 249, 2993–3006 CrossRef CAS.
- T. S. Hofer, A. K. H. Weiss, B. R. Randolf and B. M. Rode, Chem. Phys. Lett., 2011, 512, 139–145 CrossRef CAS PubMed.
- P. T. Kiss and A. Baranyai, J. Chem. Phys., 2013, 138, 204507 CrossRef PubMed.
- P. T. Kiss and A. Baranyai, J. Chem. Phys., 2014, 141, 114501 CrossRef PubMed.
- H. Jiang, Z. Mester, O. A. Moultos, I. G. Economou and A. Z. Panagiotopoulos, J. Chem. Theory Comput., 2015, 11, 3802–3810 CrossRef CAS PubMed.
- P. Ball and J. E. Hallsworth, Phys. Chem. Chem. Phys., 2015, 17, 8297–8305 RSC.
- Y. Marcus, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed.
- K. A. Dill, T. M. Truskett, V. Vlachy and B. Hribar-Lee, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 173–199 CrossRef CAS PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- P. Jungwirth, B. J. Finlayson-Pitts and D. J. Tobias, Chem. Rev., 2006, 1137–1139 CrossRef CAS.
- P. Jungwirth and B. Winter, Annu. Rev. Phys. Chem., 2008, 59, 343–366 CrossRef CAS PubMed.
- T. Encrenaz, Annu. Rev. Astron. Astrophys., 2008, 46, 57–87 CrossRef CAS.
- K. I. Öberg, Chem. Rev., 2016, 116, 9631–9663 CrossRef PubMed.
- C. A. Angell, Chem. Rev., 2002, 102, 2627–2650 CrossRef CAS PubMed.
- M. Chaplin, Water structure and science, http://www1.lsbu.ac.uk/water/.
- P. G. Debenedetti, J. Phys.: Condens. Matter, 2003, 15, R1669–R1726 CrossRef CAS.
- I. Brovchenko and A. Oleinikova, ChemPhysChem, 2008, 9, 2660–2675 CrossRef CAS PubMed.
- P. H. Handle, T. Loerting and F. Sciortino, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13336–13344 CrossRef CAS PubMed.
- P. H. Poole, I. Saika-Voivod and F. Sciortino, J. Phys.: Condens. Matter, 2005, 17, L431 CrossRef CAS.
- R. J. Speedy, J. Phys. Chem., 1982, 86, 982–991 CrossRef CAS.
- S. Sastry, P. G. Debenedetti, F. Sciortino and H. E. Stanley, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 6144–6154 CrossRef CAS PubMed.
- L. P. N. Rebelo, P. G. Debenedetti and S. Sastry, J. Chem. Phys., 1998, 109, 626–633 CrossRef CAS.
- P. H. Poole, F. Sciortino, U. Essmann and H. E. Stanley, Nature, 1992, 360, 324–328 CrossRef CAS.
- O. Mishima and H. E. Stanley, Nature, 1998, 396, 329 CrossRef CAS.
- C. A. Angell, Science, 2008, 319, 582–587 CrossRef CAS PubMed.
- P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. Pettersson, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- A. Nilsson and L. G. Pettersson, Nat. Commun., 2015, 6, 8998 CrossRef CAS PubMed.
- M. A. Anisimov, M. Duska, F. Caupin, L. E. Amrhein, A. Rosenbaum and R. J. Sadus, Phys. Rev. X, 2018, 8, 011004 Search PubMed.
- D. Paschek and R. Ludwig, Angew. Chem., Int. Ed., 2014, 53, 11699–11701 CrossRef CAS PubMed.
- F. H. Stillinger and A. Rahman, J. Chem. Phys., 1974, 60, 1545–1557 CrossRef CAS.
- F. Smallenburg, P. H. Poole and F. Sciortino, Mol. Phys., 2015, 113, 2791–2798 CrossRef CAS.
- M. J. Cuthbertson and P. H. Poole, Phys. Rev. Lett., 2011, 106, 115706 CrossRef PubMed.
- J. C. Palmer, F. Martelli, Y. Liu, R. Car, A. Z. Panagiotopoulos and P. G. Debenedetti, Nature, 2014, 510, 385–388 CrossRef CAS PubMed.
- J. C. Palmer, P. H. Poole, F. Sciortino and P. G. Debenedetti, Chem. Rev., 2018, 118, 9129–9151 CrossRef CAS PubMed.
- J. C. Palmer, A. Haji-Akbari, R. S. Singh, F. Martelli, R. Car, A. Z. Panagiotopoulos and P. G. Debenedetti, J. Chem. Phys., 2018, 148, 137101 CrossRef PubMed.
- Y. Liu, A. Z. Panagiotopoulos and P. G. Debenedetti, J. Chem. Phys., 2009, 131, 104508 CrossRef.
- D. Corradini, M. Rovere and P. Gallo, J. Chem. Phys., 2010, 132, 134508 CrossRef CAS PubMed.
- D. Paschek, Phys. Rev. Lett., 2005, 94, 217802 CrossRef PubMed.
- M. Yamada, S. Mossa, H. E. Stanley and F. Sciortino, Phys. Rev. Lett., 2002, 88, 195701 CrossRef PubMed.
- D. Paschek, A. Rüppert and A. Geiger, ChemPhysChem, 2008, 9, 2737–2741 CrossRef CAS PubMed.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- C. Vega and J. L. F. Abascal, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688 RSC.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2010, 133, 234502 CrossRef PubMed.
- J. W. Biddle, R. S. Singh, E. M. Sparano, F. Ricci, M. A. Gonzalez, C. Valeriani, J. L. Abascal, P. G. Debenedetti, M. A. Anisimov and F. Caupin, J. Chem. Phys., 2017, 146, 034502 CrossRef PubMed.
- P. H. Handle and F. Sciortino, J. Chem. Phys., 2018, 148, 134505 CrossRef PubMed.
- S. D. Overduin and G. N. Patey, J. Chem. Phys., 2013, 138, 184502 CrossRef CAS PubMed.
- S. D. Overduin and G. N. Patey, J. Chem. Phys., 2015, 143, 094504 CrossRef CAS PubMed.
- R. S. Singh, J. W. Biddle, P. G. Debenedetti and M. A. Anisimov, J. Chem. Phys., 2016, 144, 144504 CrossRef PubMed.
- T. Sumi and H. Sekino, RSC Adv., 2013, 3, 12743–12750 RSC.
- T. Yagasaki, M. Matsumoto and H. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 020301 CrossRef PubMed.
- K. T. Wikfeldt, A. Nilsson and L. G. M. Pettersson, Phys. Chem. Chem. Phys., 2011, 13, 19918–19924 RSC.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- A. Scala, F. W. Starr, E. La Nave, H. E. Stanley and F. Sciortino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 8016 CrossRef CAS PubMed.
- F. Sciortino, E. La Nave and P. Tartaglia, Phys. Rev. Lett., 2003, 91, 155701 CrossRef PubMed.
- A. Scala, F. W. Starr, E. La Nave, F. Sciortino and H. E. Stanley, Nature, 2000, 406, 166 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS PubMed.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- S. W. Rick, J. Chem. Phys., 2004, 120, 6085–6093 CrossRef CAS PubMed.
- O. Mishima and H. E. Stanley, Nature, 1998, 392, 164–168 CrossRef CAS.
- O. Mishima, J. Chem. Phys., 2010, 133, 144503 CrossRef PubMed.
- O. Mishima, Phys. Rev. Lett., 2000, 85, 334–336 CrossRef CAS PubMed.
- G. Franzese and H. E. Stanley, J. Phys.: Condens. Matter, 2007, 19, 205126 CrossRef.
- N. Giovambattista, in Liquid polymorphism, ed. H. E. Stanley, Wiley, Hoboken, NJ, 2013, vol. 103, pp. 113–138 Search PubMed.
- F. A. Gorelli, T. Bryk, M. Krisch, G. Ruocco, M. Santoro and T. Scopigno, Sci. Rep., 2013, 3, 1203 CrossRef CAS PubMed.
- P. F. McMillan and H. E. Stanley, Nat. Phys., 2010, 6, 479 Search PubMed.
- G. G. Simeoni, T. Bryk, F. A. Gorelli, M. Krisch, G. Ruocco, M. Santoro and T. Scopigno, Nat. Phys., 2010, 6, 503 Search PubMed.
- L. Xu, P. Kumar, S. V. Buldyrev, S.-H. Chen, P. H. Poole, F. Sciortino and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16558–16562 CrossRef CAS PubMed.
- F. W. Starr, F. Sciortino and H. E. Stanley, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 6757 CrossRef CAS PubMed.
- G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245–257 CrossRef CAS.
- K. Ito, C. T. Moynihan and C. A. Angell, Nature, 1999, 398, 492 CrossRef CAS.
- S. M. McClure, D. J. Safarik, T. M. Truskett and C. B. Mullins, J. Phys. Chem. B, 2006, 110, 11033–11036 CrossRef CAS PubMed.
- K. Amann-Winkel, C. Gainaru, P. H. Handle, M. Seidl, H. Nelson, R. Bohmer and T. Loerting, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17720–17725 CrossRef CAS PubMed.
- Y. Xu, N. G. Petrik, R. S. Smith, B. D. Kay and G. A. Kimmel, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14921–14925 CrossRef CAS PubMed.
- K. H. Kim, A. Spah, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, S. Kim, J. Park, K. H. Nam, T. Katayama and A. Nilsson, Science, 2017, 358, 1589–1593 CrossRef CAS PubMed.
- V. Holten, C. Qiu, E. Guillerm, M. Wilke, J. Rička, M. Frenz and F. Caupin, J. Phys. Chem. Lett., 2017, 8, 5519–5522 CrossRef CAS PubMed.
- F. Caupin, V. Holten, C. Qiu, E. Guillerm, M. Wilke, M. Frenz, J. Teixeira and A. K. Soper, Science, 2018, 360, eaat1634 CrossRef PubMed.
- K. H. Kim, A. Späh, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, S. Kim and J. Park, et al. , Science, 2018, 360, eaat1729 CrossRef PubMed.
- E. Mayer, J. Appl. Phys., 1985, 58, 663–667 CrossRef CAS.
- P. H. Handle and T. Loerting, J. Chem. Phys., 2018, 148, 124508 CrossRef PubMed.
- O. Mishima, J. Chem. Phys., 1994, 100, 5910–5912 CrossRef CAS.
- O. Mishima, L. D. Calvert and E. Whalley, Nature, 1985, 314, 76–78 CrossRef CAS.
- K. Winkel, M. S. Elsaesser, E. Mayer and T. Loerting, J. Chem. Phys., 2008, 128, 044510 CrossRef PubMed.
- J. A. McMillan and S. C. Los, Nature, 1965, 206, 806–807 CrossRef CAS.
- G. P. Johari, A. Hallbrucker and E. Mayer, Nature, 1987, 330, 552–553 CrossRef CAS.
- A. Hallbrucker, E. Mayer and G. P. Johari, J. Phys. Chem., 1989, 93, 4986–4990 CrossRef CAS.
- A. Hallbrucker, E. Mayer and G. P. Johari, Philos. Mag. B, 1989, 60, 179–187 CAS.
- G. P. Johari, A. Hallbrucker and E. Mayer, J. Chem. Phys., 1990, 92, 6742–6746 CrossRef CAS.
- R. S. Smith and B. D. Kay, Nature, 1999, 398, 788–791 CrossRef CAS.
- M. S. Elsaesser, K. Winkel, E. Mayer and T. Loerting, Phys. Chem. Chem. Phys., 2010, 12, 708–712 RSC.
- O. Mishima, J. Chem. Phys., 2004, 121, 3161–3164 CrossRef CAS PubMed.
- M. Seidl, M. S. Elsaesser, K. Winkel, G. Zifferer, E. Mayer and T. Loerting, Phys. Rev. B, 2011, 83, 100201 CrossRef.
- P. H. Handle, M. Seidl and T. Loerting, Phys. Rev. Lett., 2012, 108, 225901 CrossRef PubMed.
- J. N. Stern, M. Seidl-Nigsch and T. Loerting, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9191–9196 CAS.
- K. Amann-Winkel, R. Bohmer, F. Fujara, C. Gainaru, B. Geil and T. Loerting, Rev. Mod. Phys., 2016, 88, 20 CrossRef.
- T. Loerting, V. Fuentes-Landete, P. H. Handle, M. Seidl, K. Amann-Winkel, C. Gainaru and R. Bohmer, J. Non-Cryst. Solids, 2015, 407, 423–430 CrossRef CAS PubMed.
- K. Winkel, E. Mayer and T. Loerting, J. Phys. Chem. B, 2011, 115, 14141–14148 CrossRef CAS PubMed.
- O. Mishima, Nature, 1996, 384, 546–549 CrossRef CAS.
- O. Mishima, L. D. Calvert and E. Whalley, Nature, 1984, 310, 393–395 CrossRef CAS.
- T. Loerting, K. Winkel, M. Seidl, M. Bauer, C. Mitterdorfer, P. H. Handle, C. G. Salzmann, E. Mayer, J. L. Finney and D. T. Bowron, Phys. Chem. Chem. Phys., 2011, 13, 8783–8794 RSC.
- P. Brüggeller and E. Mayer, Nature, 1980, 288, 569–571 CrossRef.
- I. Kohl, L. Bachmann, A. Hallbrucker, E. Mayer and T. Loerting, Phys. Chem. Chem. Phys., 2005, 7, 3210–3220 RSC.
- O. Mishima and Y. Suzuki, J. Chem. Phys., 2001, 115, 4199–4202 CrossRef CAS.
- N. Giovambattista, H. E. Stanley and F. Sciortino, Phys. Rev. Lett., 2003, 91, 115504 CrossRef.
- J. Wong, D. A. Jahn and N. Giovambattista, J. Chem. Phys., 2015, 143, 074501 CrossRef PubMed.
- N. Giovambattista, F. Sciortino, F. W. Starr and P. H. Poole, J. Chem. Phys., 2016, 145, 224501 CrossRef PubMed.
- J. Engstler and N. Giovambattista, J. Chem. Phys., 2017, 147, 074505 CrossRef PubMed.
- N. Giovambattista, F. W. Starr and P. H. Poole, J. Chem. Phys., 2017, 147, 044501 CrossRef PubMed.
- P. H. Handle, F. Sciortino and N. Giovambattista, J. Chem. Phys., 2019, 150, 244506 CrossRef PubMed.
- G. H. Meyer, M. B. Morrow, O. Wyss, T. E. Berg and J. L. Littlepage, Science, 1962, 138, 1103–1104 CrossRef CAS PubMed.
- G. M. Marion, Antarct. Sci., 1997, 9, 92–99 CrossRef.
- D. G. Archer and R. W. Carter, J. Phys. Chem. B, 2000, 104, 8563–8584 CrossRef CAS.
- J. M. Borreguero and E. Mamontov, J. Phys. Chem. B, 2017, 121, 4168–4173 CrossRef CAS PubMed.
- M. Oguni and C. A. Angell, J. Chem. Phys., 1980, 73, 1948–1954 CrossRef CAS.
- A. Chrétien, R. Kohlmuller and A. P. Rollet, Nouveau traité de chimie minérale, Masson et Cie, 1966 Search PubMed.
- C. A. Angell and E. J. Sare, J. Chem. Phys., 1968, 49, 4713–4714 CrossRef CAS.
- C. A. Angell and E. J. Sare, J. Chem. Phys., 1970, 52, 1058–1068 CrossRef CAS.
- C. Monnin, M. Dubois, N. Papaiconomou and J.-P. Simonin, J. Chem. Eng. Data, 2002, 47, 1331–1336 CrossRef CAS.
- G. N. Ruiz, L. E. Bove, H. R. Corti and T. Loerting, Phys. Chem. Chem. Phys., 2014, 16, 18553–18562 RSC.
- K. Hofer, A. Hallbrucker, E. Mayer and G. P. Johari, J. Chem. Phys., 1989, 93, 4674–4677 CrossRef CAS.
- Y. Suzuki and O. Mishima, Phys. Rev. Lett., 2000, 85, 1322–1325 CrossRef CAS PubMed.
- H. Kanno, J. Phys. Chem., 1987, 91, 1967–1971 CrossRef CAS.
- Y. Suzuki and O. Mishima, J. Chem. Phys., 2002, 117, 1673–1676 CrossRef CAS.
- Y. Suzuki and O. Mishima, J. Chem. Phys., 2013, 138, 084507 CrossRef PubMed.
- Y. Suzuki and Y. Tominaga, J. Chem. Phys., 2011, 134, 244511 CrossRef PubMed.
- L. E. Bove, S. Klotz, J. Philippe and A. M. Saitta, Phys. Rev. Lett., 2011, 106, 125701 CrossRef CAS PubMed.
- T. Loerting, C. G. Salzmann, K. Winkel and E. Mayer, Phys. Chem. Chem. Phys., 2006, 8, 2810–2818 RSC.
- S. Y. Hsich, P. B. Macedo, C. J. Montrose and R. W. Gammon, J. Chem. Phys., 1972, 56, 1663–1669 CrossRef CAS.
- C. A. Angell, E. J. Sare, J. Donnella and D. R. MacFarlane, J. Phys. Chem., 1981, 85, 1461–1464 CrossRef CAS.
- H. Kanno, K. Shimada and K. Katoh, Chem. Phys. Lett., 1983, 103, 219–221 CrossRef CAS.
- D. R. MacFarlane, R. K. Kadiyala and C. A. Angell, J. Phys. Chem., 1983, 87, 235–238 CrossRef CAS.
- D. R. Macfarlane, R. K. Kadiyala and C. A. Angell, J. Chem. Phys., 1983, 79, 3921–3927 CrossRef CAS.
- D. R. Macfarlane, R. K. Kadlyala and C. A. Angell, J. Phys. Chem., 1983, 87, 1094–1095 CrossRef CAS.
- D. Corradini and P. Gallo, J. Phys. Chem. B, 2011, 115, 14161–14166 CrossRef CAS PubMed.
- D. Corradini, P. Gallo and M. Rovere, J. Chem. Phys., 2008, 128, 244508 CrossRef CAS PubMed.
- D. Corradini, P. Gallo and M. Rovere, J. Chem. Phys., 2009, 130, 154511 CrossRef CAS PubMed.
- D. Corradini, P. Gallo and M. Rovere, J. Phys.: Condens. Matter, 2010, 22, 284104 CrossRef CAS PubMed.
- P. Gallo, D. Corradini and M. Rovere, J. Chem. Phys., 2013, 139, 204503 CrossRef CAS PubMed.
- L. E. Bove, C. Dreyfus, R. Torre and R. M. Pick, J. Chem. Phys., 2013, 139, 044501 CrossRef CAS PubMed.
- D. R. MacFarlane, J. Scheirer and S. I. Smedley, J. Phys. Chem., 1986, 90, 2168–2173 CrossRef CAS.
- O. Mishima, J. Chem. Phys., 2005, 123, 154506 CrossRef PubMed.
- O. Mishima, J. Chem. Phys., 2007, 126, 244507 CrossRef PubMed.
- R. Leberman and A. K. Soper, Nature, 1995, 378, 364–366 CrossRef CAS PubMed.
- E. Williams and C. A. Angell, J. Phys. Chem., 1977, 81, 232–237 CrossRef CAS.
- B. Prével, J. F. Jal, J. Dupuy-Philon and A. K. Soper, J. Chem. Phys., 1995, 103, 1886–1896 CrossRef.
- H. R. Corti, F. J. Nores-Pondal and C. A. Angell, Phys. Chem. Chem. Phys., 2011, 13, 19741–19748 RSC.
- G. Bullock and V. Molinero, Faraday Discuss., 2014, 167, 371 RSC.
- G. N. Ruiz, K. Amann-Winkel, L. E. Bove, H. R. Corti and T. Loerting, Phys. Chem. Chem. Phys., 2018, 20, 6401–6408 RSC.
- N. Giovambattista, T. Loerting, B. R. Lukanov and F. W. Starr, Sci. Rep., 2012, 2, 390 CrossRef PubMed.
- L. Le and V. Molinero, J. Phys. Chem. A, 2011, 115, 5900–5907 CrossRef CAS PubMed.
- O. Mishima, J. Phys. Chem. B, 2011, 115, 14064–14067 CrossRef CAS PubMed.
- Y. Suzuki and O. Mishima, J. Phys.: Condens. Matter, 2009, 21, 155105 CrossRef PubMed.
- K. Winkel, M. Bauer, E. Mayer, M. Seidl, M. S. Elsaesser and T. Loerting, J. Phys.: Condens. Matter, 2008, 20, 494212 CrossRef.
- T. Loerting, W. Schustereder, K. Winkel, C. G. Salzmann, I. Kohl and E. Mayer, Phys. Rev. Lett., 2006, 96, 025702 CrossRef PubMed.
- P. H. Handle and T. Loerting, Phys. Rev. B, 2016, 93, 064204 CrossRef.
- J. Chiu, F. W. Starr and N. Giovambattista, J. Chem. Phys., 2013, 139, 184504 CrossRef PubMed.
- J. Chiu, F. W. Starr and N. Giovambattista, J. Chem. Phys., 2014, 140, 114504 CrossRef PubMed.
- P. H. Handle and T. Loerting, J. Chem. Phys., 2018, 148, 124509 CrossRef PubMed.
- D. Corradini, M. Rovere and P. Gallo, J. Phys. Chem. B, 2011, 115, 1461–1468 CrossRef CAS PubMed.
- R. Souda, J. Chem. Phys., 2006, 125, 181103 CrossRef PubMed.
- J. Holzmann, R. Ludwig, A. Geiger and D. Paschek, Angew. Chem., Int. Ed., 2007, 46, 8907–8911 CrossRef CAS PubMed.
- E. Mamontov, J. Phys. Chem. B, 2009, 113, 14073–14078 CrossRef CAS PubMed.
- M. E. Gallina, L. Bove, C. Dreyfus, A. Polian, B. Bonello, R. Cucini, A. Taschin, R. Torre and R. M. Pick, J. Chem. Phys., 2009, 131, 124504 CrossRef CAS PubMed.
- S. C. Santucci, L. Comez, F. Scarponi, G. Monaco, R. Verbeni, J.-F. Legrand, C. Masciovecchio, A. Gessini and D. Fioretto, J. Chem. Phys., 2009, 131, 154507 CrossRef CAS PubMed.
- E. Mamontov, A. Faraone, E. W. Hagaman, K. S. Han and E. Fratini, J. Phys. Chem. B, 2010, 114, 16737–16743 CrossRef CAS PubMed.
- D. A. Turton, C. Corsaro, D. F. Martin, F. Mallamace and K. Wynne, Phys. Chem. Chem. Phys., 2012, 14, 8067–8073 RSC.
- M. Nakanishi, P. Griffin, E. Mamontov and A. P. Sokolov, J. Chem. Phys., 2012, 136, 124512 CrossRef PubMed.
- E. Mamontov and M. Ohl, Phys. Chem. Chem. Phys., 2013, 15, 10732–10739 RSC.
- C. Corsaro, D. Mallamace, N. Cicero, S. Vasi, G. Dugo and F. Mallamace, Physica A, 2016, 442, 261–267 CrossRef CAS.
- S. Schneider and M. Vogel, J. Chem. Phys., 2018, 149, 104501 CrossRef CAS PubMed.
- M. P. Longinotti, M. A. Carignano, I. Szleifer and H. R. Corti, J. Chem. Phys., 2011, 134, 244510 CrossRef PubMed.
- S. W. Rick, J. Chem. Phys., 2004, 120, 6085–6093 CrossRef CAS PubMed.
- I. Gladich, P. Shepson, I. Szleifer and M. A. Carignano, Chem. Phys. Lett., 2010, 489, 113–117 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- M. Patra and M. Karttunen, J. Comput. Chem., 2004, 25, 678–689 CrossRef CAS PubMed.
- P. Auffinger, T. E. Cheatham and A. C. Vaiana, J. Chem. Theory Comput., 2007, 3, 1851–1859 CrossRef CAS PubMed.
- J. L. Aragones, M. Rovere, C. Vega and P. Gallo, J. Phys. Chem. B, 2014, 118, 7680–7691 CrossRef CAS PubMed.
- J. W. Biddle, V. Holten and M. A. Anisimov, J. Chem. Phys., 2014, 141, 074504 CrossRef PubMed.
- V. Holten and M. A. Anisimov, Sci. Rep., 2012, 2, 713 CrossRef CAS PubMed.
- C. A. Angell and R. D. Bressel, J. Phys. Chem., 1972, 76, 3244–3253 CrossRef CAS.
- C. A. Angell and J. C. Tucker, J. Phys. Chem., 1980, 84, 268–272 CrossRef CAS.
- H. Kanno, R. J. Speedy and C. A. Angell, Science, 1975, 189, 880–881 CrossRef CAS.
- H. Kanno and C. A. Angell, J. Phys. Chem., 1977, 81, 2639–2643 CrossRef CAS.
- K. Miyata, H. Kanno, T. Niino and K. Tomizawa, Chem. Phys. Lett., 2002, 354, 51–55 CrossRef CAS.
- K. Hofer, G. Astl, E. Mayer and G. P. Johari, J. Phys. Chem., 1991, 95, 10777–10781 CrossRef CAS.
- M. Gordon and J. S. Taylor, J. Appl. Chem., 1952, 2, 493–500 CrossRef CAS.
- E. Mayer, J. Phys. Chem., 1986, 90, 4455–4461 CrossRef CAS.
- G. Fleissner, A. Hallbrucker and E. Mayer, J. Phys. Chem., 1993, 97, 4806–4814 CrossRef CAS.
- G. Fleissner, A. Hallbrucker and E. Mayer, Chem. Phys. Lett., 1994, 218, 93–99 CrossRef CAS.
- G. Fleissner, A. Hallbrucker and E. Mayer, J. Phys. Chem., 1995, 99, 8401–8404 CrossRef CAS.
- G. Fleissner, A. Hallbrucker and E. Mayer, J. Phys. Chem. B, 1998, 102, 6239–6247 CrossRef CAS.
- M. Mitterböck, G. Fleissner, A. Hallbrucker and E. Mayer, J. Phys. Chem. B, 1999, 103, 8016–8025 CrossRef.
- Z. Zhao and C. A. Angell, Angew. Chem., Int. Ed., 2016, 55, 2474–2477 CrossRef CAS PubMed.
- T. Koop, B. Luo, A. Tsias and T. Peter, Nature, 2000, 406, 611–614 CrossRef CAS PubMed.
- B. Zobrist, U. Weers and T. Koop, J. Chem. Phys., 2003, 118, 10254–10261 CrossRef CAS.
- S. Woutersen, B. Ensing, M. Hilbers, Z. Zhao and C. A. Angell, Science, 2018, 359, 1127–1131 CrossRef CAS PubMed.
- Glycerine Producer's Association (New York), Nothing Takes the Place of Glycerine: 1583 Ways To Use It, Soap and Detergent Association, New York, 1949 Search PubMed.
- C. Polge, A. U. Smith and A. S. Parkes, Nature, 1949, 164, 666 CrossRef CAS PubMed.
- P. R. Davis-Searles, A. J. Saunders, D. A. Erie, D. J. Winzor and G. J. Pielak, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 271–306 CrossRef CAS PubMed.
- J. G. Baust, D. Gao and J. M. Baust, Organogenesis, 2009, 5, 90–96 CrossRef PubMed.
- G. D. Elliott, S. Wang and B. J. Fuller, Cryobiology, 2017, 76, 74–91 CrossRef CAS PubMed.
- M. P. Buera, Y. Roos, H. Levine, L. Slade, H. R. Corti, D. S. Reid, T. Auffret and C. A. Angell, Pure Appl. Chem., 2011, 83, 1567–1617 CAS.
- M. Paglario and M. Rossi, The Future of Glycerol, Royal Society of Chemistry, Cambridge, 2010 Search PubMed.
- J. A. Padró, L. Saiz and E. Guàrdia, J. Mol. Struct., 1997, 416, 243–248 CrossRef.
- L. B. Lane, Ind. Eng. Chem., 1925, 17, 924 CrossRef CAS.
- A. Puzenko, Y. Hayashi, Y. E. Ryabov, I. Balin, Y. Feldman, U. Kaatze and R. Behrends, J. Phys. Chem. B, 2005, 109, 6031–6035 CrossRef CAS PubMed.
- Y. Hayashi, A. Puzenko and Y. Feldman, J. Non-Cryst. Solids, 2006, 352, 4696–4703 CrossRef CAS.
- D. Harran, Bull. Soc. Chim. Fr., 1978, I40–I44 Search PubMed.
- S. Ablett, M. J. Izzard and P. J. Lillford, J. Chem. Soc., Faraday Trans., 1992, 88, 789–794 RSC.
- S. Sudo, M. Shimomura, N. Shinyashiki and S. Yagihara, J. Non-Cryst. Solids, 2002, 307–310, 356–363 CrossRef CAS.
- A. Inaba and O. Andersson, Thermochim. Acta, 2007, 461, 44–49 CrossRef CAS.
- I. Popov, A. Greenbaum Gutina, A. P. Sokolov and Y. Feldman, Phys. Chem. Chem. Phys., 2015, 17, 18063–18071 RSC.
- L. S. Zhao, Z. X. Cao and Q. Wang, Sci. Rep., 2015, 5, 15714 CrossRef CAS PubMed.
- J. Bachler, V. Fuentes-Landete, D. A. Jahn, J. Wong, N. Giovambattista and T. Loerting, Phys. Chem. Chem. Phys., 2016, 18, 11058–11068 RSC.
- Y. Hayashi, A. Puzenko, I. Balin, Y. E. Ryabov and Y. Feldman, J. Phys. Chem. B, 2005, 109, 9174–9177 CrossRef CAS PubMed.
- A. Inaba, N. Sakisato, A. K. Bickerstaffe and S. M. Clarke, J. Neutron Res., 2005, 13, 87–90 CrossRef CAS.
- A. Inaba, Pure Appl. Chem., 2006, 78, 1025–1037 CAS.
- O. D. C. Palacios, A. Inaba and O. Andersson, Thermochim. Acta, 2010, 500, 106–110 CrossRef CAS.
- K. Murata and H. Tanaka, Nat. Mater., 2012, 11, 436–443 CrossRef CAS PubMed.
- Y. Suzuki and O. Mishima, J. Chem. Phys., 2014, 141, 094505 CrossRef PubMed.
- A. Angell, Nat. Mater., 2012, 11, 362–364 CrossRef CAS PubMed.
- K. Murata and H. Tanaka, Nat. Commun., 2013, 4, 2844 CrossRef PubMed.
- J. R. Bruijn, T. H. van der Loop and S. Woutersen, J. Phys. Chem. Lett., 2016, 7, 795–799 CrossRef CAS PubMed.
- R. Kurita and H. Tanaka, Phys. Rev. B, 2006, 73, 104202 CrossRef.
- W. Hage, A. Hallbrucker, E. Mayer and G. P. Johari, J. Chem. Phys., 1994, 100, 2743–2747 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1941, 9, 177–184 CrossRef CAS.
- J. Mosses, C. D. Syme and K. Wynne, J. Phys. Chem. Lett., 2015, 6, 38–43 CrossRef CAS PubMed.
- C. D. Syme, J. Mosses, M. Gonzalez-Jimenez, O. Shebanova, F. Walton and K. Wynne, Sci. Rep., 2017, 7, 42439 CrossRef CAS PubMed.
- M. Tarnacka, O. Madejczyk, M. Dulski, P. Maksym, K. Kaminski and M. Paluch, J. Phys. Chem. C, 2017, 121, 19442–19450 CrossRef CAS.
- J. E. K. Schawe, Thermochim. Acta, 2006, 451, 115–125 CrossRef CAS.
- A. Bogdan, M. J. Molina, H. Tenhu and T. Loerting, J. Phys. Chem. A, 2015, 119, 4515–4523 CrossRef CAS PubMed.
- Y. Suzuki, J. Chem. Phys., 2018, 149, 204501 CrossRef PubMed.
- E. Whalley, D. D. Klug and Y. P. Handa, Nature, 1989, 342, 782–783 CrossRef CAS.
- Y. Suzuki and O. Mishima, J. Chem. Phys., 2016, 145, 024501 CrossRef PubMed.
- S. H. Chen, L. Liu, E. Fratini, P. Baglioni, A. Faraone and E. Mamontov, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9012–9016 CrossRef CAS PubMed.
- C. U. Kim, M. W. Tate and S. M. Gruner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20897–20901 CrossRef CAS PubMed.
- F. Mallamace, P. Baglioni, C. Corsaro, S. H. Chen, D. Mallamace, C. Vasi and H. E. Stanley, J. Chem. Phys., 2014, 141, 165104 CrossRef PubMed.
- F. Mallamace, C. Corsaro, P. Baglioni, E. Fratini and S. H. Chen, J. Phys.: Condens. Matter, 2012, 24, 064103 CrossRef PubMed.
- J. R. Authelin, A. P. MacKenzie, D. H. Rasmussen and E. Y. Shalaev, J. Pharm. Sci., 2014, 103, 2663–2672 CrossRef CAS PubMed.
- F. Mallamace, C. Corsaro, D. Mallamace, C. Vasi, S. Vasi and H. E. Stanley, J. Chem. Phys., 2016, 144, 064506 CrossRef PubMed.
- D. A. Jahn, J. Wong, J. Bachler, T. Loerting and N. Giovambattista, Phys. Chem. Chem. Phys., 2016, 18, 11042–11057 RSC.
- Y. Suzuki, J. Chem. Phys., 2017, 147, 064511 CrossRef PubMed.
- M. Seidl, K. Amann-Winkel, P. H. Handle, G. Zifferer and T. Loerting, Phys. Rev. B, 2013, 88, 289 CrossRef.
- M. Seidl, A. Fayter, J. N. Stern, G. Zifferer and T. Loerting, Phys. Rev. B, 2015, 91, 144201 CrossRef.
- C. G. Salzmann, T. Loerting, I. Kohl, E. Mayer and A. Hallbrucker, J. Phys. Chem. B, 2002, 106, 5587–5590 CrossRef CAS.
- J. Engstler and N. Giovambattista, J. Phys. Chem. B, 2018, 122, 8908–8920 CrossRef CAS PubMed.
- F. O. Akinkunmi, D. A. Jahn and N. Giovambattista, J. Phys. Chem. B, 2015, 119, 6250–6261 CrossRef CAS PubMed.
- J. L. Finney, A. Hallbrucker, I. Kohl, A. K. Soper and D. T. Bowron, Phys. Rev. Lett., 2002, 88, 225503 CrossRef CAS PubMed.
- D. T. Bowron, J. L. Finney, A. Hallbrucker, I. Kohl, T. Loerting, E. Mayer and A. K. Soper, J. Chem. Phys., 2006, 125, 194502 CrossRef CAS PubMed.
- T. Loerting and N. Giovambattista, J. Phys.: Condens. Matter, 2006, 18, R919–R977 CrossRef CAS.
- J. Blieck, F. Affouard, P. Bordat, A. Lerbret and M. Descamps, Chem. Phys., 2005, 317, 253–257 CrossRef CAS.
- Y. Marcus, Phys. Chem. Chem. Phys., 2000, 2, 4891–4896 RSC.
- K. Takamura, H. Fischer and N. R. Morrow, J. Pet. Sci. Eng., 2012, 98–99, 50–60 CrossRef CAS.
- B. Chen, E. E. Sigmund and W. P. Halperin, Phys. Rev. Lett., 2006, 96, 145502 CrossRef PubMed.
- G. Blond and D. Simatos, Thermochim. Acta, 1991, 175, 239–247 CrossRef CAS.
- K. Elamin, J. Sjostrom, H. Jansson and J. Swenson, J. Chem. Phys., 2012, 136, 104508 CrossRef PubMed.
- J. L. Green and C. A. Angell, J. Phys. Chem., 1989, 93, 2880–2882 CrossRef CAS.
- N. Karger and H. D. Ludemann, Z. Naturforsch., C: J. Biosci., 1991, 46, 313–317 CAS.
- S. S. N. Murthy and G. Singh, Thermochim. Acta, 2008, 469, 116–119 CrossRef CAS.
- A. Nagoe and M. Oguni, J. Phys.: Condens. Matter, 2010, 22, 325103 CrossRef PubMed.
- H. Kanno, K. Miyata, K. Tomizawa and H. Tanaka, J. Phys. Chem. A, 2004, 108, 6079–6082 CrossRef CAS.
- D. Corradini, Z. Su, H. E. Stanley and P. Gallo, J. Chem. Phys., 2012, 137, 184503 CrossRef PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. Wada and S. Umeda, Bull. Chem. Soc. Jpn., 1962, 35, 646–652 CrossRef CAS.
- C. U. Kim, B. Barstow, M. W. Tate and S. M. Gruner, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4596–4600 CrossRef CAS PubMed.
- C. U. Kim, Y. F. Chen, M. W. Tate and S. M. Gruner, J. Appl. Crystallogr., 2008, 41, 1–7 CrossRef CAS.
- C. U. Kim, Q. Hao and S. M. Gruner, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2006, 62, 687–694 CrossRef PubMed.
- C. U. Kim, R. Kapfer and S. M. Gruner, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2005, 61, 881–890 CrossRef PubMed.
- C. U. Kim, M. W. Tate and S. M. Gruner, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11765–11770 CrossRef CAS PubMed.
- S. Kriminski, C. L. Caylor, M. C. Nonato, K. D. Finkelstein and R. E. Thorne, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2002, 58, 459–471 CrossRef CAS PubMed.
- D. H. Juers and B. W. Matthews, Q. Rev. Biophys., 2004, 37, 105–119 CrossRef CAS PubMed.
- D. Ringe and G. A. Petsko, Biophys. Chem., 2003, 105, 667–680 CrossRef CAS PubMed.
- H. E. Stanley, P. Kumar, S. Han, M. G. Mazza, K. Stokely, S. V. Buldyrev, G. Franzese, F. Mallamace and L. Xu, J. Phys.: Condens. Matter, 2009, 21, 504105 CrossRef CAS PubMed.
- S. Lemke, P. H. Handle, L. J. Plaga, J. N. Stern, M. Seidl, V. Fuentes-Landete, K. Amann-Winkel, K. W. Köster, C. Gainaru, T. Loerting and R. Böhmer, J. Chem. Phys., 2017, 147, 034506 CrossRef PubMed.
- D. Vitkup, D. Ringe, G. A. Petsko and M. Karplus, Nat. Struct. Biol., 2000, 7, 34–38 CrossRef CAS PubMed.
- M. Tarek and D. J. Tobias, Phys. Rev. Lett., 2002, 88, 138101 CrossRef CAS PubMed.
- A. L. Tournier, J. Xu and J. C. Smith, Biophys. J., 2003, 85, 1871–1875 CrossRef CAS PubMed.
- C. M. Tonauer, M. Seidl-Nigsch and T. Loerting, J. Phys.: Condens. Matter, 2018, 30, 034002 CrossRef PubMed.
- O. Mishima, K. Takemura and K. Aoki, Science, 1991, 254, 406–408 CrossRef CAS PubMed.
- V. Molinero and E. B. Moore, J. Phys. Chem. B, 2009, 113, 4008–4016 CrossRef CAS PubMed.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B, 1985, 31, 5262–5271 CrossRef CAS PubMed.
- D. T. Limmer and D. Chandler, J. Chem. Phys., 2011, 135, 134503 CrossRef PubMed.
- E. B. Moore and V. Molinero, Nature, 2011, 479, 506–508 CrossRef CAS PubMed.
- E. B. Moore and V. Molinero, J. Chem. Phys., 2010, 132, 244504 CrossRef PubMed.
- D. T. Limmer and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9413–9418 CrossRef CAS PubMed.
- S. V. Buldyrev, G. Franzese, N. Giovambattista, G. Malescio, M. R. Sadr-Lahijany, A. Scala, A. Skibinsky and H. E. Stanley, Physica A, 2002, 304, 23–42 CrossRef CAS.
- S. V. Buldyrev, G. Malescio, C. A. Angell, N. Giovambattista, S. Prestipino, F. Saija, H. E. Stanley and L. Xu, J. Phys.: Condens. Matter, 2009, 21, 504106 CrossRef CAS PubMed.
- E. A. Jagla, J. Chem. Phys., 1999, 111, 8980–8986 CrossRef CAS.
- E. A. Jagla, Phys. Rev. E, 2001, 63, 061501 CrossRef CAS PubMed.
- G. Franzese, J. Mol. Liq., 2007, 136, 267–273 CrossRef CAS.
- J. Luo, L. Xu, E. Lascaris, H. E. Stanley and S. V. Buldyrev, Phys. Rev. Lett., 2014, 112, 135701 CrossRef PubMed.
- A. B. d. Oliveira, P. A. Netz, T. Colla and M. C. Barbosa, J. Chem. Phys., 2006, 124, 084505 CrossRef PubMed.
- J. Y. Luo, L. M. Xu, C. A. Angell, H. E. Stanley and S. V. Buldyrev, J. Chem. Phys., 2015, 142, 224501 CrossRef PubMed.
- L. Xu, S. V. Buldyrev, N. Giovambattista, C. Angell and H. E. Stanley, J. Chem. Phys., 2009, 130, 054505 CrossRef PubMed.
- J. Y. Abraham, S. V. Buldyrev and N. Giovambattista, J. Phys. Chem. B, 2011, 115, 14229–14239 CrossRef CAS PubMed.
- A. Gordon and N. Giovambattista, Phys. Rev. Lett., 2014, 112, 145701 CrossRef PubMed.
- S. Reisman and N. Giovambattista, J. Chem. Phys., 2013, 138, 064509 CrossRef PubMed.
- S. V. Buldyrev, P. Kumar, P. G. Debenedetti, P. J. Rossky and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20177–20182 CrossRef CAS PubMed.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- D. Corradini, S. V. Buldyrev, P. Gallo and H. E. Stanley, Phys. Rev. E, 2010, 81, 061504 CrossRef PubMed.
- D. Corradini, P. Gallo, S. V. Buldyrev and H. E. Stanley, Phys. Rev. E, 2012, 85, 051503 CrossRef CAS PubMed.
- H. M. Gibson and N. B. Wilding, Phys. Rev. E, 2006, 74, 019903 CrossRef.
- C. A. Cerdeiriña and P. G. Debenedetti, J. Chem. Phys., 2016, 144, 164501 CrossRef PubMed.
- S. Chatterjee and P. G. Debenedetti, J. Chem. Phys., 2006, 124, 154503 CrossRef PubMed.
- H. Laksmono, T. A. McQueen, J. A. Sellberg, N. D. Loh, C. Huang, D. Schlesinger, R. G. Sierra, C. Y. Hampton, D. Nordlund, M. Beye, A. V. Martin, A. Barty, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, K. Amann-Winkel, T. Loerting, L. G. Pettersson, M. J. Bogan and A. Nilsson, J. Phys. Chem. Lett., 2015, 6, 2826–2832 CrossRef CAS PubMed.
- M. D. Ediger and P. Harrowell, J. Chem. Phys., 2012, 137, 080901 CrossRef CAS PubMed.
- M. Zanatta, L. Tavagnacco, E. Buratti, M. Bertoldo, F. Natali, E. Chiessi, A. Orecchini and E. Zaccarelli, Sci. Adv., 2018, 4, eaat5895 CrossRef CAS PubMed.
- E. W. Roddenberry, in Star Trek, 1966.
Footnotes |
| † Depending on your cultural background you might know this line from ref. 1 or ref. 2. |
| ‡ We note that Bruijn et al.233 cite Avrami exponents from Hage et al.235 at 155 K while Hage et al. report the crystallization kinetics of HGW (LDA) below 150 K. |
| § Avrami exponents in general depend on the type of experiment, e.g., in surface sensitive techniques such as spectroscopy one dimension is lost, decreasing the exponent by one. |
| This journal is © the Owner Societies 2019 |