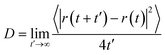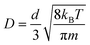Selective gas diffusion in two-dimensional MXene lamellar membranes: insights from molecular dynamics simulations

Abstract

Membrane gas separation has become increasingly important for modern industry, and the emerging two-dimensional (2D) lamellar membranes provide unprecedented possibilities to overcome the well-known permeability–selectivity trade-off of traditional membranes. However, the 2D materials currently available for lamellar membrane fabrication are very limited, and relevant experimental or simulation studies are scarce. Consequently, the understanding of gas diffusion in 2D nanochannels, though critical for developing more efficient lamellar membranes, is still quite poor. Very recently, we fabricated a 2D MXene lamellar membrane with exceptional gas separation performance (L. Ding, Y. Wei, L. Li, T. Zhang, H. Wang, J. Xue, L. X. Ding, S. Wang, J. Caro and Y. Gogotsi, Nat. Commun., 2018, 9, 155), and the gas transportation mechanism was studied thoroughly with Molecular Dynamics (MD) simulations in this work. The diffusion of different gases, such as H₂, He, CH₄, CO₂ and N₂, was simulated in 2D MXene nanogalleries with structural factors (e.g., interlayer distance and intercalating water) adjusted systematically. These gases were found to diffuse in the nanogalleries mainly via two mechanisms, activated diffusion and Knudsen diffusion. The main features of both diffusion mechanisms were discussed through studying the simulation trajectories carefully. The simulations also revealed that the MXene membrane structure significantly influenced the gas diffusion, such as the mechanism, diffusivity, and selectivity, and could thus be tuned to boost the gas separation performance as our recent experiment did. This simulation work provides a detailed microscopic understanding of gas diffusion in 2D nanochannels, and useful guidance for developing new 2D lamellar gas separation membranes with high performance.

---

Introduction

Membrane-based gas separation has shown advantages for a large variety of applications, e.g., low energy cost, high efficiency and simple operation,^1,2 but suffers from the well-known problem of permeability–selectivity (P–S) trade-off (e.g., the Robinson upper bound).³ The emerging 2D material-based membranes, which possess the merits of traditional membranes, and yet solve the P–S trade-off problem, have been attracting enormous attention.² There are two categories of 2D material-based membranes: nanosheet membranes and lamellar membranes (Fig. S1†).^4,5 Lamellar membranes are assembled from 2D material nanosheets with interlayer galleries providing molecular passages (Fig. S1†), which are quite desirable, due to advantages of tunable channel width, excellent mechanical strength, and easy fabrication and integration in comparison with nanosheet membranes.^5–7 However, the number of 2D materials available for lamellar membrane fabrication is quite limited: graphene (GA),^8,9 graphene oxide (GO),^10–14 Layered Double Hydroxides (LDH),¹⁵ molybdenum disulphide (MoS₂)^16,17 and tungsten disulfide (WS₂)¹⁸ (GA^5,6 membranes produced from reducing GO usually belong to lamellar membranes, while 2D MOFs^19,20 belong to nanosheet membranes), leading to only a few reports being available on gas separation experiments with lamellar membranes,^10–17 which usually show moderate separation performance (interestingly, experimental studies of liquid separation²¹ or ion sieving²² with lamellar membranes are a bit more frequently reported). Also, theoretical/simulation studies on gas transportation through 2D lamellar nanogalleries are scarce;^23,24 thus, the mechanism of transportation and separation of gas through 2D nanogalleries is far from being well understood. There have been abundant theoretical studies on gas transportation in 0D nanopores (e.g., nanopores in graphene,^25–27 C₃N₄,²⁸ C₂N,²⁹etc.; please note that these materials are 2D, but the nanopores in the nanosheets could be taken as 0D due to the monoatomic thickness), 1D nanochannels (CNT^30–32 or SiC³³ nanotubes), and 3D nanochannel networks (MOFs or zeolites).^34–36 Such studies on 2D lamellar nanochannels, however, are scarce, and yet they are urgently needed for studying or developing more efficient 2D lamellar membranes. For instance, the channel width and gas molecule–channel wall interactions have been proven to be essential for gas transportation in the aforementioned 0, 1, and 3D nanochannels.^{25,30,35–38} These factors should also be vital for gas transportation in lamellar nanochannels, and consequently, could be exploited to tune the gas transportation and enhance the gas separation performance. However, the understanding of these factors in the context of 2D nanogalleries is still very poor, as there have been very few relevant theoretical studies that mainly focus on two 2D materials, GA²⁴ and GO.^23,39

Very recently, we fabricated 2D lamellar membranes with an emerging 2D material, MXene.^40,41 MXenes are a large family of 2D carbides and nitrides with the general formula M_n+1X_nT_x, where M represents a transition metal, X carbon and/or nitrogen, and T the surface termination.^42–44 The MXene 2D membranes showed a range of merits, e.g., ultrafast water permeation,⁴⁵ precise ion sieving⁴⁶ and most importantly, unprecedented gas separation performance (H₂ permeability > 2200 barrer, H₂/CO₂ selectivity > 160), which exceeded the latest Robinson upper bound considerably.⁴¹ A thorough understanding of gas diffusion in 2D MXene nanogalleries should benefit developing even more efficient MXene or MXene-based membranes. It would even provide valuable insights for studying gas transportation or separation in lamellar membranes based on other 2D materials.^47–49 Such a transportation mechanism, however, usually involves a microscopic understanding, and is thus very challenging, especially for experiments. Alternatively, Molecular Dynamics (MD) simulations could be used to study the molecular transportation in nanochannels from a microscopic perspective, and have been employed in a range of lamellar membrane studies, aiming at molecular sieving^23,50–52 or fluid/gas transportation.^24,53,54

In this work, MD simulations were employed to study the diffusion of different gas molecules (He, H₂, CO₂, N₂, and CH₄) in 2D MXene nanogalleries whose structural factors were adjusted systematically. Two main mechanisms, activated diffusion and Knudsen diffusion,² were observed for gas diffusion in MXene nanogalleries, and their main features were discussed after studying the simulation data carefully. The structural factors of gas molecules (e.g., size and mass) and MXene nanogalleries (e.g., interlayer distance and intercalating water) were found to influence the gas diffusion significantly, while the gas–MXene interactions also counted to some extent. The simulation results agree well with our recent experiment⁴¹, and their significance in gas diffusion (e.g., diffusivity and selectivity) and 2D lamellar gas separation membrane design was discussed.

Models and methods

In the simulation, a certain number of gas molecules were placed in the nanogallery between two MXene (Ti₃C₂O₂) nanosheets, with the crystal structure taken from the literature⁵⁵ (Fig. 1). We mainly simulated 2 types of MXene nano-galleries in this work: one with 2.4 wt% water randomly distributed between MXene nanosheets to reproduce our recent experimental result (interlayer distance = 6.8 Å according to X-ray diffraction (XRD), water content ∼ 2.4 wt% as suggested by thermogravimetric analysis (TGA)),⁴¹ and the other one without water for comparison. The former type of MXene nano-gallery was referred to as MXene or hydrous MXene with d varying from 6 to 14 Å, while the latter was denoted as anhydrous MXene with d varying from 5 to 14 Å (when the intercalating species was absent, MXene nano-sheets could approach each other even more closely). In some cases, MXene nanogalleries with water content between 0 and 2.4 wt%, or with large d values ranging from 14 to 24 Å, were also simulated to further study the gas diffusion mechanism. The size of the MXene nanosheet was 5.5 nm × 5.3 nm (along the x–y direction) in the primary simulation box, and a periodic boundary condition (PBC) was applied. Although a typical MXene nanosheet usually possesses two other surface functional groups (–F and –OH), they account for less than 29% of the terminal groups in total. Our recent work also suggested that the influence of different surface functional groups on gas diffusion was similar,⁴¹ and thus we focused on Ti₃C₂O₂ herein.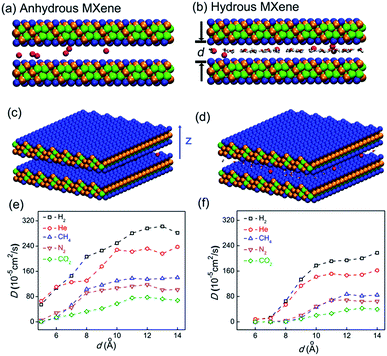

Fig. 1 Snapshot of simulation systems, where 6 He molecules diffuse in anhydrous MXene (a and c) or hydrous MXene ((b and d) also referred to as MXene). He, O, Ti, and C atoms are drawn as red, blue, orange, and green balls, respectively; water molecules are drawn as red and white lines. (e and f) Gas diffusion coefficient, D, in anhydrous MXene (e) and MXene (f) with different interlayer distances. The MXene (b) nanogallery contains 2.4 wt% water as the experimental thermogravimetric analysis (TGA) result suggested.⁴¹

The MXene nanosheets were modeled using the Universal Force Field (UFF) force field (FF)⁵⁶ with charge equilibration (QEq) charge,⁵⁷ which has been proven to accurately simulate the interactions of gas molecules with a range of nanoporous materials. Water was described using the SPC/E model.⁵⁸ The water contact angle (WCA), a key parameter for characterizing the molecule–MXene interfacial interaction, was calculated by simulating a water droplet on the MXene surface with the above FF parameters (see the ESI WCA section†). The simulated WCA was 55.0° (Fig. S2†), well consistent with the experimental value of 59.5°;⁵⁹ thus the above FF parameters were further validated. The N₂, CO₂ and CH₄ gas molecules were modeled using the transferable potentials for phase equilibria (TraPPE) FF,^60,61 and the united-atom parameters of H₂ and He were taken from other publications.^62,63 The FF parameters have been proven to accurately simulate the transport of these five gases in nanoporous materials (they also successfully simulated gas diffusion in MXene nanogalleries; see the ‘Results and discussion’ section).^34,64–66

In a typical simulation carried out using the Groningen Machine for Chemical Simulations (GROMACS) 4.6.7 package,⁶⁷ the system was firstly subjected to a 500-step steepest-descent energy minimization. Then, a 40 ns (nano-second) NVT simulation was performed (leap-frog algorithm with a time step of 2 fs), where a constant simulation temperature of 300 K was maintained using a Nose–Hoover thermostat.⁶⁸ The MXene atoms were frozen in the simulation since the nanosheets were rather rigid. Water molecules were also fixed, since the experimental TGA results indicated that they adsorbed onto MXene rather tightly at temperatures below 120 °C.⁴¹ The short-range interactions were evaluated using a neighbor list of 10 Å that was updated every ten steps, and the Lennard-Jones interactions were switched off smoothly between 8 and 9 Å. A long-range analytical dispersion correction was applied to the energy to account for the truncation of these interactions.⁶⁹ The electrostatic interactions were calculated using the reaction-field method.⁷⁰ The last 30 ns of the NVT simulation were used to calculate the gas diffusion coefficient with the Einstein relation

where 〈|r(t + t′) − r(t)|²〉 is the mean square displacement (MSD) for a given relative simulation time t′ (the coefficient in the denominator is 4 because the gas molecules diffused in the 2D x–y plane).

Different number of He molecules, varying from 1 to 12, were simulated. The gas molecules did not aggregate (see the xy-radial distribution function (xy-RDF), Fig. S3a†), and the interaction among them was negligible in comparison with their interaction with MXene nanosheets (Fig. S3b and Table S1†). Consequently, the number of gas molecules, ranging from 1 to 12, affected the diffusion coefficient in MXene nanogalleries insignificantly, though it did affect the diffusion coefficient when MXene nanosheets were absent as Gilliland's equation predicted (Fig. S4†). Thus we focused on simulations with 6 gas molecules in this work.

Results and discussion

Effect of interlayer distance on gas diffusion: activated diffusion vs. Knudsen diffusion

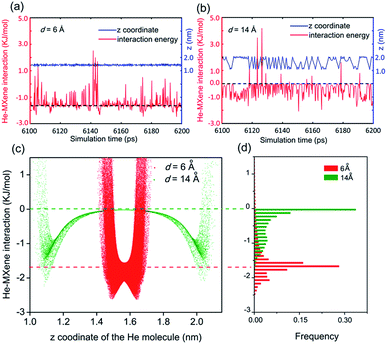
In experiments,^{12–14,17,53} gas transportation through nanochannels or nanogalleries is usually tuned via adjusting their width. Thus, the effect of the width, also referred to as the 'interlayer distance' in the context of nanogalleries, on gas diffusion was studied in detail herein. The diffusion coefficients, D, of 5 different gas molecules in MXene 2D nanogalleries with the interlayer distance (denoted as d) ranging from 5 to 14 Å (anhydrous MXene, Fig. 1a and c) or from 6 to 14 Å (hydrous MXene, Fig. 1b and d, also referred to as MXene in this work, containing 2.4 wt% intercalating water as our recent experiments showed;⁴¹ see the ‘Models and methods’ section for more details) are shown in Fig. 1. With d increasing, the gas diffusivity first increased quickly (d < 10 Å), and then varied rather slowly (d > 10 Å) (Fig. 1e and f).

As for MXene nanochannels with small d (d ≤ 6 Å for anhydrous MXene or d ≤ 8 Å for MXene), gas molecules with smaller kinetic diameters usually diffuse faster (although with slight deviations sometimes). D of He and H₂ could be 1 (anhydrous MXene, d ≤ 6 Å) or even 3 orders (MXene, d ≤ 7 Å) higher than those of the bigger molecules, CO₂, N₂ and CH₄ (D_CO2 is smaller than D_N2, though its kinetic diameter is smaller; the reason will be explained later in the ‘Gas–membrane interaction’ section). This led to an obvious cut-off among these gas molecules, even though the difference between their kinetic diameters is as small as 0.4 Å (H₂vs. CO₂; see Fig. S5†).

When the cut-off phenomenon became significant, the d of anhydrous MXene became ∼6 Å (that of MXene was larger; the reason will be explained later in the ‘Effect of intercalating water’ section), corresponding to a spacing of ∼3 Å (subtracting the van der Waals diameter of an oxygen atom, ∼3.0 Å), right between the kinetic diameter of H₂ and CO₂ (2.89 and 3.3 Å, respectively).² The average interaction energy (the magnitude) of gas molecules with small d MXene membranes (either anhydrous or hydrous MXene, d ≤ 7 Å) was quite large, e.g., a few times larger than that of large d MXene (e.g., d = 14 Å, see Fig. S6†). Furthermore, the interaction energy for small d MXene membranes (e.g., d = 6 Å, anhydrous MXene) showed a Gaussian distribution centered at the average value (Fig. 2d). A close analysis of the simulation trajectory revealed that when a gas molecule (e.g., He) diffused in MXene nanogalleries with d (e.g., 6 Å) as small as or comparable to its kinetic diameter (2.6 Å), it would always be close to the MXene wall and experience interactions with the wall continuously (Fig. 2a and c). This gas diffusion mechanism is referred to as activated or configurational diffusion,⁷¹ and some of its major features, e.g., the correlation between diffusivity and kinetic diameter and the cut-off phenomenon,^10,11 have been discussed in Fig. S5.† We further note that, as for activated diffusion, the interaction energy decreased sharply with d increasing (Fig. S6†), which may explain the quick increase of D in the small d range (d ≤ 10 Å).

Fig. 2 The time series of a helium molecule's z coordinate (blue), interaction energy with MXene sheets (red), which diffuses in anhydrous MXene nanogalleries with interlayer distance d = 6 Å (a) and 14 Å (b). (c) The He–MXene interaction energy–z coordinate scatter plot of a He molecule diffusing in d = 6 Å (red) or 14 Å (olive) anhydrous MXene nanogalleries. (d) The normalized distribution of He–MXene interaction energy for a He molecule diffusing in d = 6 Å (red) or 14 Å (olive) anhydrous MXene nanogalleries.

As for large d (>10 Å) MXene membranes, the D of gas molecules depended on their mass (m) instead of kinetic diameter, and the relationship roughly agreed with D ∼ m^−0.5 (Fig. S7,†D of CO₂ is lower than the D ∼ m^−0.5 prediction; the reason will be explained later in the ‘Gas–membrane interaction’ section). Consequently, the difference in D of different gases is much smaller than that of small d MXene nanogalleries: D_H2/D_CH4 is ∼2 for d > 10 Å (either anhydrous or hydrous MXene), while it is above 400 for d ≤ 5 Å (anhydrous MXene) or d ≤ 7 Å (MXene). There are 2 cross-overs in D of different gases: at d > 10 Å, D_He < D_H2 and D_N2 < D_CH4, which are the opposite of the cases of small d MXene membranes (d ≤ 6 Å for anhydrous MXene or ≤8 Å for MXene). These cross-overs indicate that the dominating factor for gas diffusion shifts from the kinetic diameter to molecular mass with the interlayer distance, d, increasing. In large d MXene membranes, the interaction energy (the magnitude) of gas molecules with MXene was considerably smaller than that of small d MXene membranes (Fig. S6†). Most of the time, the interaction energy is close to 0, since the gas–MXene wall distance is quite large (Fig. 2b–d, d = 14 Å). This phenomenon is in contrast to the trend observed for small d MXene membranes, where the interaction energy is usually well below 0 (Fig. 2a and d, d = 6 Å). The simulation trajectory (He, d = 14 Å) reveals that a gas molecule frequently collides with the MXene wall and returns to the bulk phase, where it is far from (gas–MXene distance ≥ 5 Å) and interacts weakly with (|gas–MXene interaction energy| < 0.2 kJ mol⁻¹, | | refers to the magnitude or absolute value) the MXene wall (Fig. 2b and its enlargement, Fig. S8†). These wall collisions change the gas molecule velocity dramatically in all three dimensions, x, y and z (Fig. S9†), and thus affect the gas diffusion to a large extent. The He atom's wall collision frequency was estimated to be ∼5 × 10¹¹ s⁻¹ per molecule from the trajectory, an order of magnitude higher than the collision frequency with other gas molecules (Fig. S10†). In addition, when a He molecule collides with other He molecules, the He–He interaction energy is usually much smaller than the He–MXene interaction energy (Table S1†). Thus, when d > 10 Å, the gas diffusion is dominated by its collisions with the MXene wall, rather than collisions with other gas molecules, leading to the well-known Knudsen diffusion with diffusivity scaling with m^−1/2 (Fig. S7†).^2,10,38 In contrast to small d nanogalleries, D varied quite slowly with d increasing, as the gas–MXene wall interaction changed slowly (Fig. 1 and S6†). Nevertheless, the diffusivity did increase with d increasing (Fig. S11†), agreeing with the equation for Knudsen diffusion:

where d is the interlayer distance, T is the temperature, m is the molecular mass and k_B is the Boltzmann constant.^72,73 It could be further expected that, with d further increasing, the collisions of gas molecules with the MXene wall would become less frequent as gas molecules would spend more time in travelling from the MXene wall to the opposite side. Thus, gas molecules would mainly locate in the bulk phase and their collisions with the MXene wall would become less important. In such circumstances, the other mechanism, the so-called ‘volume diffusion’, may begin to take place (however, this is beyond the scope of this study focusing on nanogalleries).

Influence of gas–membrane interaction on gas diffusion

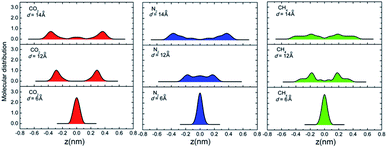
According to the above discussions, the dominating factor of gas diffusion for small d MXene membranes is basically the gas molecule size (kinetic diameter), while that for large d MXene membranes is the molecular mass. However, CO₂ is an exception, whose kinetic diameter (3.3 Å) is slightly smaller than that of N₂ (3.64 Å), and its mass is ∼1.5 times that of N₂. The diffusivity of CO₂ is usually considerably lower than that of N₂ (D_CO2/D_N2 < 0.6), in the d range of 5–14 Å. This phenomenon is observed for both anhydrous MXene and MXene (Fig. S5 and S7†), and we will focus on anhydrous MXene in this section for the sake of clarity. It is quite unexpected that when d ≤ 6 Å (anhydrous MXene) and the activated diffusion dominates gas molecule transport, D_CO2 is less than one half of D_N2, though its kinetic diameter is smaller. For comparison, CH₄, with the largest kinetic diameter, showed a much smaller D than D_N2 or D_CO2 for d ≤ 6 Å (anhydrous MXene). Even when d > 10 Å (anhydrous MXene) and Knudsen diffusion dominated the gas transportation, D_CO2 was much smaller than that predicted from the m^−1/2 equation (Fig. S7†). The smaller diffusivity or permeance of CO₂ than N₂ was also reported in recent molecular sieving membrane studies.^10–14,24 Thus, there should be other factors, other than size or mass, that also affect the diffusion of CO₂ significantly. In fact, the unexpected phenomenon of D_CO2 may be attributed to the fact that CO₂ possesses a much higher quadrupole and polarizability than other gases (e.g., the quadrupole values of CO₂, N₂, and CH₄ are −13.71 × 10⁴⁰, −4.91 × 10⁴⁰, and 0 C m², and the polarizability values are 29.1 × 10⁻²⁵, 17.4 × 10⁻²⁵, and 25.9 × 10⁻²⁵ cm³ respectively;⁷⁴ those of He and H₂ should be lower than those of N₂). This leads to the interaction energy (magnitude) of CO₂ with MXene being considerably higher than that of other gases (Fig. S6†), which hindered its diffusion. The stronger interactions of CO₂ with the MXene wall could also explain that CO₂ had a greater tendency to adsorb on the MXene wall than other gases (Fig. 3). Additional hypothetical simulations were performed, where the atomic charge of CO₂ was turned off. This decreased the magnitude of the CO₂^hyper–MXene interaction energy to 9.6 kJ mol⁻¹, and increased the diffusivity to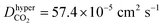 (a bit higher than D_N2, 45.3 × 10⁻⁵ cm² s⁻¹) in a d = 7 Å anhydrous MXene nanogallery. Such hypothetical simulations verified that gas–membrane interactions could affect the gas diffusion or permeance considerably, as discussed in recent experimental studies.^12,75

Fig. 3 Density distribution profiles of CO₂ (red), N₂ (blue) and CH₄ (green) molecules (along the interlayer distance, z direction) in anhydrous MXene nanogalleries with different d values. z = 0 refers to the middle of the nanogallery. At a small d of 6 Å, all gas molecules were located in the middle of the nanogalleries, while at large d, CO₂ molecules are more inclined to adsorb to the MXene wall than N₂ or CH₄.

Effect of intercalating water on gas diffusion

D of hydrous MXene membranes is usually smaller than that of anhydrous MXene (Fig. 1). This effect became more significant for small d or large gas molecules (Fig. S12†). For instance, for H₂, when d = 14 or 6 Å, D_anhydro/D_hydro is ∼1.5 and 15, respectively, while for CH₄, when d = 14 or 6 Å, D_anhydro/D_hydro is ∼1.7 and 650, respectively. This effect of water may be attributed to the fact that water scatters or blocks the gas diffusion. To be specific, when d was large, water molecules scatter the gas diffusion flow or roughen the potential surface for gas diffusion,^24,38 which decreased D of gas molecules. When d was small, water molecules blocked the gas diffusion so severely that a gas molecule could no longer push itself through the space between water and the MXene wall (Fig. S13†). Thus, in the hydrous MXene membrane, the 2D nanogalleries between MXene nanosheets were divided into narrow nanochannels to transport gas molecules. Compared with 2D nanogalleries, the diffusion width of gas molecules through nanochannels dropped greatly, while the tortuosity increased considerably. As a consequence, D of gas molecules dropped significantly for small d MXene membranes. Furthermore, these divided nanochannels would possess different widths, while most of the nanochannels may be too narrow to transport large gas molecules. In other words, the possible diffusion pathways of large gas molecules through the hydrous MXene membrane may be considerably fewer than those of smaller molecules. Consequently, the intercalating water affected D of large gas molecules more significantly than that of small molecules, and thus enhanced the molecular sieving effect of the MXene membrane. Such enhanced molecular sieving could be employed to increase the gas separation performance (see the ‘Selectivity’ and ‘Design’ sections below). Further simulations were carried out, with water content in the MXene membrane varying from 0 to 2.4 wt%. The effect of water on gas diffusion correlated with the water content well: when there was less water, the diffusivity of gas would be less affected; in other words, the behavior was closer to that observed for the anhydrous MXene membrane (Fig. S14†).

Selectivity of gas diffusion

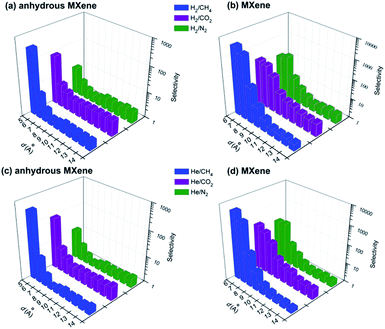
Based on the results in previous sections, the selectivity of the MXene membrane is discussed herein, which is a vital consideration for the industrial application of MXene membranes. The selectivity for gas molecule A with respect to another molecule B is defined as S_A/B = D_A/D_B, where D_A and D_B are the diffusion coefficients of species A and B. The selectivity of both anhydrous and hydrous MXene membranes is shown in Fig. 4, and we will focus on H₂ in this section, since D_H2 was usually similar to D_He.

Fig. 4 Selectivity of H₂ (a and b) and He (c and d) diffusion with respect to N₂ (olive), CO₂ (purple), and CH₄ (blue) for (a and c) anhydrous MXene and (b and d) MXene membranes. The selectivity is defined as S = D_He/D_gas (a and b) or D_H2/D_gas (c and d), where D_He, D_H2 and D_gas are the diffusion coefficients of He, H₂ and other gas molecules.

In the anhydrous MXene membrane with d as small as 5 Å, the selectivity for H₂ over big gas molecules (N₂, CO₂ and CH₄) is as high as 11, 82 and 346. The high S_H2/CH4 could be attributed to the large kinetic diameter of CH₄ (see the previous ‘Interlayer distance’ section), while the high S_H2/CO2 can be attributed to the strong interaction between MXene and CO₂ to a large extent. Nevertheless, S_H2/N2 of 11 is still higher than the values obtained in a range of other recent 2D material or MOF membrane gas separation studies with S_H2/N2 ranging from 3 to 10.^{10,13,14,16,17,76} The selectivity for H₂ drops quickly with d increasing, and fluctuates around some constants when d ≥ 8 Å. Such constants, S_H2/N2 ∼ 2.8, S_H2/CO2 ∼ 4.5 and S_H2/CH4 ∼ 2.4, are quite close to that predicted from the m^−1/2 equation (note that the dominant diffusion mechanism is Knudsen diffusion for large d nanogalleries; see the previous ‘Interlayer distance’ section), indicating a low separation performance of large d MXene membranes. Furthermore, the selectivity of large d (≥ 10 Å) MXene membranes for different gases over N₂ is quite close to those reported in recent studies on graphene²⁴ or MoS₂ (ref. 16) membranes (d ≥ 10 Å, Fig. S15†). This indicates that when gas diffuses in large d nanogalleries via the Knudsen mechanism, the membrane material may affect the selectivity less significantly than in small d nanogalleries.

As for hydrous MXene with d ≤ 8 Å, the selectivity for H₂ could be folds or even orders higher than that of anhydrous MXene. For instance, the selectivity for H₂ over N₂, CO₂ and CH₄ is 160, 173 and 1905 (d = 7 Å) or 110, 212 and 3340 (d = 6 Å, MXene) respectively, while for anhydrous MXene the corresponding values are 3, 7 and 3 (d = 7 Å) or 4, 8 and 8 (d = 6 Å). The selectivity of hydrous MXene drops with d increasing, but it drops much more slowly than for anhydrous MXene: at d of 8 Å, S_H2/N2, S_H2/CO2 and S_H2/CH4 are 17, 72 and 71, respectively; even when d = 10 Å, S_H2/CO2 is still as high as 9, which is higher than the recently reported values for MoS₂,^16,17 CMS⁷⁷ and PBI⁷⁸ membranes (at room temperature; note that the H₂ permeability of the MXene membrane is close to or considerably higher than that of these membranes). The high selectivity of hydrous MXene with d ≤ 10 Å could be attributed to the fact that when gas molecules move in the nanogallery via activated diffusion, water blocks the gas diffusion, especially for large gas molecules, and thus enhances the molecular sieving effect (see the ‘Effect of water’ section). Furthermore, the simulated selectivity of hydrous MXene (d = 6 or 7 Å, water content = 2.4 wt%) was quite close to that obtained in our recent experiment, where d = 6.8 Å, water content = 2.4 wt%, S_H2/He ∼1, S_H2/N2 ∼ 129, S_H2/CO2 ∼ 238 and S_H2/CH4 ∼ 780 (Fig. S16†).⁴¹ Such a close agreement further validated our simulation methodologies (e.g., simulation system setup and simulation parameters; also see the water contact angle (WCA) calculation in the ESI†) and discussions on the diffusion mechanism (see the ‘Effect of interlayer distance’ and ‘Effect of intercalating water’ sections). As for hydrous MXene with d ≥ 11 Å, however, the selectivity of hydrous MXene is quite close to that of anhydrous MXene, though D of hydrous MXene is smaller. The reason may be that when gas molecules move in wide nanogalleries (d ≥ 11 Å) via the Knudsen diffusion, the effect of water on the gas diffusion is similar among different gas species. Thus, the effect of water on different gases is cancelled when calculating the selectivity, S = D₁/D₂ (note that D of both anhydrous and hydrous MXene simply followed the m^−1/2 law when d ≥ 11 Å, Fig. S7†).

D _He was usually similar to D_H2, and D_He/D_H2 for all simulations, both for anhydrous and hydrous MXene, varied from 0.8 to 1.5 in this study. Thus, the selectivity for He over big gas molecules (N₂, CO₂ and CH₄) is quite similar to that for H₂, and the discussions on H₂ also apply to He. Particularly, the selectivity of MXene (d = 6 or 7 Å) for He over N₂, CO₂ and CH₄ is above 100 (N₂ and CO₂) or even 1000 (CH₄). The calculated selectivity is quite close to that obtained in our recent experiments (Fig. S16†).⁴¹ In addition, S_He/N2 and S_He/CH4 (d = 6 or 7 Å, MXene) are well above the required selectivity for industrial application.⁷⁹ The permeability (2402 barrer (ref. 41))–selectivity (over CH₄ or N₂) of the MXene membrane also exceeds the latest upper bound of Robeson's plot,^79,80 showing performance superior to most other organic and inorganic membranes.⁸⁰ All these results indicate the promising potential of the MXene lamellar membrane for H₂/He recycling, recovery or purification or other gas separation applications.^1,2,80

Design of lamellar membranes for gas separation

The above discussions provide valuable insights for designing efficient gas separation lamellar membranes with MXene⁴¹ or other 2D materials.^6,7 First, d could be a vital consideration in membrane design. To improve the selectivity for H₂ or He over big gas molecules (e.g., N₂, CO₂ or CH₄), d should be sufficiently small that gas molecules move mainly via the activated diffusion, which usually yields selectivity much higher than Knudsen diffusion (see the ‘Selectivity’ section, Fig. 4).² In this d range, the selectivity drops sharply, while D increases quickly with d increasing (Fig. 1). This quick change of S and D in opposite directions indicates that the ‘optimum’ d range for designing a lamellar membrane with high S and D should be rather narrow. In addition, the ‘optimum’ d value is not the sole consideration. A lamellar membrane may possess numerous nanogalleries with various widths, or d values, which leads to a width distribution. This d distribution should also be rather narrow, otherwise gas molecules would mainly be transported via large d nanogalleries with much higher diffusivity. Thus nanogalleries with large d would dominate the separation performance, and reduce the selectivity, which would drop sharply with d increasing (Fig. 4). Therefore, to fabricate a lamellar membrane (e.g., to purify or recover H₂ or He) with high selectivity (S) and permeability (P), we not only need to precisely control d to an ‘optimum’ value, but also further reduce the d distribution; in other words, we need to fabricate nanogalleries with nearly identical widths close to the ‘optimum’ value. As for anhydrous and hydrous MXene membranes, the ‘optimum’ d range is estimated to be ∼5 Å and 6–8 Å, respectively, with the criteria that S_H2/CO2 > 70 and D_H2 > 7 × 10⁻⁵ cm² s⁻¹ (Fig. 1 and 4). In other words, we need to tune the d values of all nanogalleries in the membrane to just one or two atom thickness (the typical diameter of an atom is ∼0.33 nm), while three atom thickness may even be too large. This task is far from trivial, which may explain why there have been very scarce gas separation studies with lamellar membranes. In our recent experimental study, highly ordered nanogalleries with nearly identical d values of ∼6.8 Å have been fabricated with MXene nanosheets, as deduced from the extremely sharp 002 peak of XRD patterns and TEM images.⁴¹ This MXene membrane yielded very high S_H2/CH4, S_H2/N2 and S_H2/CO2 of 780, 129, and 238, and a high H₂ permeability of 2402 barrer (membrane thickness = 2 μm, ideal selectivity), which exceeded the latest upper bound considerably. The significant influence of the nanogallery's orderness or interlayer distance (d) on the gas separation performance has also been reported in recent studies on GO lamellar membranes,^10,12,14e.g., even increasing d from 7.1 to 7.7 Å could decrease S_H2/CO2 sharply from 100 to 8.5.¹² We also note that gas molecule sieving may be much more difficult than ion sieving,^22,50–52 since the diameter of an ion with its hydration shell (e.g., ∼7 Å)² is much larger than gas molecules. Second, the intercalating species, e.g., water, regulated the gas transportation not only simply by changing the width, d, of the nanochannels, but also by blocking the gas diffusion and enhancing the molecular sieving effect (see the ‘Effect of intercalating water’ section). The active role of water in regulating the gas diffusion has also been reported in recent GO studies.^24,81 Consequently, the intercalating species could increase S considerably, and thus allow high S for lamellar membranes with a slightly wider d distribution. This could make fabricating high performance lamellar membranes more feasible. Interestingly, the density of intercalating species (e.g., water) may decrease D (Fig. S14†) but increase S considerably (Fig. 4), since denser intercalating species would block the diffusion of big gas molecules more severely. Thus the intercalating species density could be employed to further tune the performance of lamellar membranes. Last but not least, the interaction between the nanogallery wall and gas molecules could be employed to suppress the diffusion of some gas molecules (e.g., CO₂) specifically and thus enhance the gas separation (see the ‘Gas–membrane interaction’ section). This effect has been reported in our recent MXene experimental study,⁴¹ which yielded an S_H2/CO2 of 238, two times as high as S_H2/N2, with the mechanism discussed in the ‘Gas–membrane interaction’ section. This phenomenon has also been discussed in recent experimental studies on membrane gas separation.^12,75 We also note that a typical MXene nanosheet usually possesses two other surface terminations (–F and –OH) besides –O, while –O accounts for the majority of terminations.⁴¹ Our recent⁴¹ study suggested that the influence of different surface terminations on gas transportation in MXene membranes was insignificant, e.g. much weaker than that of the interlayer distance or intercalating species, which may change the selectivity or diffusivity by several hundred fold (Fig. 4 and S12†).

Conclusions

In this work, gas diffusion in the interlayer nanogalleries of MXene membranes was thoroughly studied via MD simulations, which yielded a molecular understanding of selective gas diffusion through the nanogalleries between MXene nanosheets. The structural factors of gas molecules (e.g., size, mass, dipole and quadrupole) and MXene membranes (e.g., interlayer distance and intercalating species) were found to affect the gas diffusion significantly, which led to different diffusion mechanisms and diffusivity and consequently, highly efficient gas separation overcoming the P–S trade-off of common membranes. The simulation results and findings were in good agreement with our recent experiment.⁴¹ This study provides valuable insights not only for understanding the gas transportation in 2D MXene nanogalleries, but also for designing efficient lamellar membranes with various 2D materials, which would benefit a wide range of scientific and industrial fields.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Financial support from the National Science Foundation of China (21506066, 21606086 and 51621001), Guangzhou Technology Project (201804010219 and 201707010317), Guangdong Natural Science Funds for Distinguished Young Scholar (2017A030306002), Natural Science Foundation of Guangdong Province (2014A030312007) and Fundamental Research Funds for the Central Universities is gratefully acknowledged. CPU hours allocated by the Guangzhou Supercomputer Center of China are gratefully acknowledged.

Notes and references

1. D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–438.
2. L. Wang, M. S. H. Boutilier, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Nat. Nanotechnol., 2017, 12, 509–522.
3. H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, 1138–1148.
4. B. Mi, Science, 2014, 343, 740–742.
5. T. S. Yang, H. Lin, X. R. Zheng, K. P. Loh and B. H. Jia, J. Mater. Chem. A, 2017, 5, 16537–16558.
6. G. Liu, W. Jin and N. Xu, Chem. Soc. Rev., 2015, 44, 5016–5030.
7. P. Sun, K. Wang and H. Zhu, Adv. Mater., 2016, 28, 2287–2310.
8. S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728–732.
9. K. Celebi, J. Buchheim, R. M. Wyss, A. Droudian, P. Gasser, I. Shorubalko, J. I. Kye, C. Lee and H. G. Park, Science, 2014, 344, 289–292.
10. H. W. Kim, H. W. Yoon, S. M. Yoon, B. M. Yoo, B. K. Ahn, Y. H. Cho, H. J. Shin, H. Yang, U. Paik and S. Kwon, Science, 2013, 342, 91–95.
11. H. Li, Z. Song, X. Zhang, Y. Huang, S. Li, Y. Mao, H. J. Ploehn, Y. Bao and M. Yu, Science, 2013, 342, 95–98.
12. J. Yang, D. Gong, G. Li, G. Zeng, Q. Wang, Y. Zhang, G. Liu, P. Wu, E. Vovk, Z. Peng, X. Zhou, Y. Yang, Z. Liu and Y. Sun, Adv. Mater., 2018, 1705775.
13. J. Shen, G. Liu, K. Huang, Z. Chu, W. Jin and N. Xu, ACS Nano, 2016, 10, 3398–3409.
14. B. Qi, X. He, G. Zeng, Y. Pan, G. Li, G. Liu, Y. Zhang, W. Chen and Y. Sun, Nat. Commun., 2017, 8, 825.
15. Y. Liu, N. Wang, Z. Cao and J. Caro, J. Mater. Chem. A, 2014, 2, 1235–1238.
16. D. Wang, Z. Wang, L. Wang, L. Hu and J. Jin, Nanoscale, 2015, 7, 17649–17652.
17. A. Achari, S. Sahana and M. Eswaramoorthy, Energy Environ. Sci., 2016, 9, 1224–1228.
18. L. Sun, Y. Ying, H. Huang, Z. Song, Y. Mao, Z. Xu and X. Peng, ACS Nano, 2014, 8, 6304–6311.
19. X. Wang, C. Chi, K. Zhang, Y. Qian, K. M. Gupta, Z. Kang, J. Jiang and D. Zhao, Nat. Commun., 2017, 8, 14460.
20. Y. Peng, Y. Li, Y. Ban, H. Jin, W. Jiao, X. Liu and W. Yang, Science, 2014, 346, 1356–1359.
21. Q. Yang, Y. Su, C. Chi, C. T. Cherian, K. Huang, V. G. Kravets, F. C. Wang, J. C. Zhang, A. Pratt and A. N. Grigorenko, Nat. Mater., 2017, 16, 1198–1203.
22. L. Chen, G. Shi, J. Shen, B. Peng, B. Zhang, Y. Wang, F. Bian, J. Wang, D. Li and Z. Qian, Nature, 2017, 550, 415–418.
23. W. Li, X. Zheng, Z. Dong, C. Li, W. Wang, Y. Yan and J. Zhang, J. Phys. Chem. C, 2016, 120, 26061–26066.
24. S. P. Jiao and Z. P. Xu, ACS Appl. Mater. Interfaces, 2015, 7, 9052–9059.
25. Z. Yuan, A. G. Rajan, R. P. Misra, L. W. Drahushuk, K. V. Agrawal, M. S. Strano and D. Blankschtein, ACS Nano, 2017, 11, 7974–7987.
26. C. Sun, M. S. H. Boutilier, H. Au, P. Poesio, B. Bai, R. Karnik and N. G. Hadjiconstantinou, Langmuir, 2014, 30, 675–682.
27. Z. Tian, S. M. Mahurin, S. Dai and D. E. Jiang, Nano Lett., 2017, 17, 1802–1807.
28. F. Li, Y. Qu and M. Zhao, Carbon, 2015, 95, 51–57.
29. Y. Qu, F. Li and M. Zhao, J. Phys. Chem. C, 2017, 121, 17925–17931.
30. K. Chae and L. Huang, J. Chem. Phys., 2016, 144, 044708.
31. S. Yeganegi and F. Gholampour, Chem. Eng. Sci., 2016, 140, 62–70.
32. L. Liu, D. Nicholson and S. K. Bhatia, J. Phys. Chem. C, 2016, 120, 26363–26373.
33. K. Malek and M. Sahimi, J. Chem. Phys., 2010, 132, 014310.
34. R. J. Verploegh, S. Nair and D. S. Sholl, J. Am. Chem. Soc., 2015, 137, 15760–15771.
35. Q. Yang, D. Liu, C. Zhong and J. R. Li, Chem. Rev., 2013, 113, 8261–8323.
36. Z. W. Qiao, C. W. Peng, J. Zhou and J. W. Jiang, J. Mater. Chem. A, 2016, 4, 15904–15912.
37. C. Sun and B. Bai, J. Phys. Chem. C, 2018, 122, 6178–6185.
38. M. Majumder, N. Chopra and B. J. Hinds, ACS Nano, 2011, 5, 3867–3877.
39. S. Jiao and Z. Xu, ACS Nano, 2017, 11, 11152–11161.
40. L. Ding, Y. Wei, Y. Wang, H. Chen, J. Caro and H. Wang, Angew. Chem., Int. Ed., 2017, 56, 1825–1829.
41. L. Ding, Y. Wei, L. Li, T. Zhang, H. Wang, J. Xue, L. X. Ding, S. Wang, J. Caro and Y. Gogotsi, Nat. Commun., 2018, 9, 155.
42. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
43. M. Ghidiu, M. R. Lukatskaya, M. Q. Zhao, Y. Gogotsi and M. W. Barsoum, Nature, 2014, 516, 78–82.
44. B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098.
45. J. T. Wang, P. P. Chen, B. B. Shi, W. W. Guo, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2018, 57, 6814–6818.
46. C. E. Ren, K. B. Hatzell, M. Alhabeb, Z. Ling, K. A. Mahmoud and Y. Gogotsi, J. Phys. Chem. Lett., 2015, 6, 4026–4031.
47. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti and G. Pizzi, Nat. Nanotechnol., 2018, 13, 246–254.
48. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang and A. F. Ismach, ACS Nano, 2013, 7, 2898–2926.
49. J. Liu, H. Cao, B. Jiang, Y. Xue and L. Fu, Sci. China Mater., 2016, 59, 459–474.
50. R. K. Joshi, P. Carbone, F. C. Wang, V. G. Kravets, Y. Su, I. V. Grigorieva, H. A. Wu, A. K. Geim and R. R. Nair, Science, 2014, 343, 752–754.
51. A. Morelos-Gomez, R. Cruz-Silva, H. Muramatsu, J. Ortiz-Medina, T. Araki, T. Fukuyo, S. Tejima, K. Takeuchi, T. Hayashi, M. Terrones and M. Endo, Nat. Nanotechnol., 2017, 12, 1083–1089.
52. J. Abraham, K. S. Vasu, C. D. Williams, K. Gopinadhan, Y. Su, C. T. Cherian, J. Dix, E. Prestat, S. J. Haigh and I. V. Grigorieva, Nat. Nanotechnol., 2017, 12, 546–551.
53. B. Radha, A. Esfandiar, F. C. Wang, A. P. Rooney, K. Gopinadhan, A. Keerthi, A. Mishchenko, A. Janardanan, P. Blake and L. Fumagalli, Nature, 2016, 538, 222–228.
54. Y. J. Wang, L. B. Li, Y. Y. Wei, J. Xue, H. Chen, L. Ding, J. Caro and H. Wang, Angew. Chem., Int. Ed., 2017, 56, 8974–8980.
55. M. Khazaei, M. Arai, T. Sasaki, C. Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192.
56. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. G. Iii and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
57. E. S. Kadantsev, P. G. Boyd, T. D. Daff and T. K. Woo, J. Phys. Chem. Lett., 2013, 4, 3056–3061.
58. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
59. J. Liu, H. B. Zhang, R. Sun, Y. Liu, Z. Liu, A. Zhou and Z. Z. Yu, Adv. Mater., 2017, 29, 1702367.
60. J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682.
61. M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577.
62. F. Darkrim and D. Levesque, J. Chem. Phys., 1998, 109, 4981–4984.
63. O. Talu and A. L. Myers, AIChE J., 2001, 47, 1160–1168.
64. R. B. Rankin, J. Liu, A. D. Kulkarni and J. K. Johnson, J. Phys. Chem. C, 2009, 113, 16906–16914.
65. J. Liu, S. Keskin, D. S. Sholl and J. K. Johnson, J. Phys. Chem. C, 2011, 115, 12560–12566.
66. H. Wang and D. Cao, J. Phys. Chem. C, 2015, 119, 6324–6330.
67. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
68. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
69. M. R. Shirts, J. W. Pitera, W. C. Swope and V. S. Pande, J. Chem. Phys., 2003, 119, 5740–5761.
70. I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459.
71. X. Zou and G. Zhu, Adv. Mater., 2018, 30, 1700750.
72. S. K. Bhatia, M. R. Bonilla and D. Nicholson, Phys. Chem. Chem. Phys., 2011, 13, 15350–15383.
73. A. Ibrahim and Y. S. Lin, J. Membr. Sci., 2018, 550, 238–245.
74. P. Rallapalli, K. P. Prasanth, D. Patil, R. S. Somani, R. V. Jasra and H. C. Bajaj, J. Porous Mater., 2011, 18, 205–210.
75. N. Wang, A. Mundstock, Y. Liu, A. Huang and J. Caro, Chem. Eng. Sci., 2015, 124, 27–36.
76. X. Zhang, Y. Liu, S. Li, L. Kong, H. Liu, Y. Li, W. Han, K. L. Yeung, W. Zhu and W. Yang, Chem. Mater., 2014, 26, 1975–1981.
77. D. Shekhawat, D. R. Luebke and H. W. Pennline, U. S. Dep. Energy, 2003, 9–13.
78. T. Yang, Y. Xiao and T.-S. Chung, Energy Environ. Sci., 2011, 4, 4171–4180.
79. C. A. Scholes and U. Ghosh, J. Membr. Sci., 2016, 520, 221–230.
80. C. A. Scholes and U. K. Ghosh, Membranes, 2017, 7, 9.
81. R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335, 442–444.

---

Footnote

† Electronic supplementary information (ESI) available: Illustration of a lamellar membrane (Fig. S1) and more details of simulation results and analysis (Fig. S2–S16 and Table S1). See DOI: 10.1039/c8ta03701a

---