Multiparameter cell-tracking intrinsic cytometry for single-cell characterization

Abstract

An abundance of label-free microfluidic techniques for measuring cell intrinsic markers exists, yet these techniques are seldom combined because of integration complexity such as restricted physical space and incompatible modes of operation. We introduce a multiparameter intrinsic cytometry approach for the characterization of single cells that combines ≥2 label-free measurement techniques onto the same platform and uses cell tracking to associate the measured properties to cells. Our proof-of-concept implementation can measure up to five intrinsic properties including size, deformability, and polarizability at three frequencies. Each measurement module along with the integrated platform were validated and evaluated in the context of chemically induced changes in the actin cytoskeleton of cells. viSNE and machine learning classification were used to determine the orthogonality between and the contribution of the measured intrinsic markers for cell classification.

---

Introduction

Cells and their states can be identified by extrinsic markers, biochemical labels that target specific molecules on or in the cells, coupled with detection tags, such as fluorochromes, quantum dots, magnetic beads, and stable isotopes. Flow cytometry and mass cytometry are powerful analysis tools that are readily extensible to investigate 10s of extrinsic markers simultaneously within single cells, making it possible to identify rare subtypes and complex states of cells within heterogeneous populations.^1–3 These single-cell multiparametric extrinsic measurements have enabled numerous applications in biology and medicine.^4–6

Cells also possess intrinsic markers, which are the properties of cells that do not need labels to become apparent, such as size, shape, density, optical, mechanical, and electrical properties.⁷ Intrinsic markers are useful for measuring cell properties that do not have biochemical markers, and can complement or substitute label-based analysis where cost or time are paramount.^8–17 Several label-free macroscale and microscale techniques have been developed for bulk and, within recent decades, single-cell characterization and separation based on intrinsic markers.¹⁶ Microfluidic techniques in particular are appealing due to the plethora of different properties that can be measured and a variety of techniques that have been engineered to perform measurements of these properties.^7,18–23 Nevertheless, intrinsic markers are generally not tied to specific molecular pathways, but tend to integrate diverse pathways (e.g. cell size); therefore, intrinsic markers tend to suffer from a lack of specificity. In addition, similar to the case of extrinsic markers, a single intrinsic marker is often not sufficient for cell characterization in real-world applications where different cell states and populations within a complex mixture need to be identified and characterized.

To increase specificity, several studies have measured multiple intrinsic markers simultaneously within single cells. For example, size and deformability measurements of single cells have been shown together to increase specificity in a variety of samples.^24–31 Combinations of cell electrical signatures, e.g. multi-frequency impedance data, have shown similar benefits.^32,33 These multiparametric intrinsic studies show that additional intrinsic markers can be creatively extracted from the same measurement recordings without changing the experiment designs of the dominating measurement techniques, e.g. extracting size or morphology from visual readout or electrical impedance change, and that combinations of intrinsic markers can improve characterization.^24–33 Here we introduce a more general approach to multiparameter intrinsic cytometry that is readily extensible to different types of intrinsic markers.

There are several ways to develop a multiparameter intrinsic cytometry. One approach is to serially connect the outlet of one device to inlet of the next; however, with this approach, the identity of cells will be lost as they transit across devices. Another straightforward and commonly used approach in both extrinsic cytometry and intrinsic cytometry is to combine different measurement techniques into the same integrated space such that different intrinsic properties can be measured simultaneously. An undeniable limitation of this approach is the difficulty of integrating increasing numbers of measurement modalities within the same space and structures. Instead, we propose to spread measurement modules across space and record cell trajectories as they transit between modules. In this fashion, each module can be individually optimized, and the data obtained in each module can be correlated to individual cells using optical cell tracking.

To show a specific implementation of this approach, we developed a cytometry that measures size, polarizability at multiple frequencies, and deformability of single cells. We validated performance of each module and then showed how cell tracking can be used to correlate measurements back to individual cells, thus aggregating the data. We used the multiparametric data in the context of cytoskeletal disruption of HL60 cells to investigate the orthogonality between parameters and the importance of the each intrinsic marker as a predictor for the classification of cell populations of interest.

Results and discussion

Cytometer architecture and choice of modality

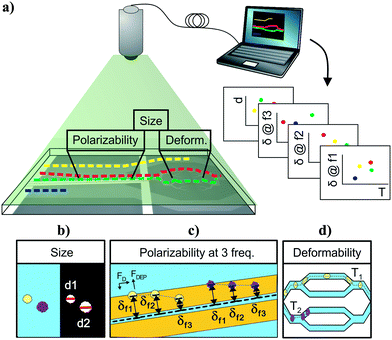
Cell-tracking cytometry comprises of three main subsystems: a microfluidic platform, microscope imaging, and image processing (Fig. 1a). The microfluidic platform consists of measurement modules for the intrinsic markers of interest. These modules are designed such that they encode the intrinsic markers of interest into the relative temporal and spatial positions of cells. Microscope imaging enables observation and recording of cell spatiotemporal positions in the microfluidic platform in the form of information-rich image stacks. The image processing subsystem then detects, tracks, and extracts the intrinsic markers of cells from the image stacks as well as associates intrinsic marker measurements from different modules corresponding to the same cells across the platform. This tracking-based intrinsic cytometry approach, which spreads the measurement modules out in space on the same microfluidic platform and links them via tracking, minimizes constraints on area and volume of microfluidic investigation chamber and on the measurement techniques (e.g. synchronization of readout signals or probing requirements).

Fig. 1 Multiparameter intrinsic cytometry. (a) Overview. Combining different microfluidic modules on one substrate along with cell tracking to correlate per-cell information across modules allows acquisition of multiparameter intrinsic properties. (b–d) Specific instantiation with five parameters. (b) Size module. Cell size (d₁, d₂) is obtained optically from images as cells flow through modules. (c) Multi-frequency nDEP spring module. Cells driven by hydrodynamic flow forces (F_D) experience an opposing nDEP forces (F_DEP) as they approach coplanar electrodes and reach different equilibrium positions (δ_f1, δ_f2, δ_f3) based on their polarizability at the applied frequency. By applying a sequence of three different frequencies, we obtain 3 measures of polarizability. (d) Deformability module. Cells deform as they transit through narrow channels. The transit time (T₁, T₂) is related to their deformability.

While different intrinsic markers can reflect different aspects of cells, we chose to study size, deformability, and polarizability of single cells on our platform. We chose size because cell size is determined by both intrinsic developmental programs and extracellular signals.³⁴ Cell size has been used as a marker to coarsely separate cell types and cell states, e.g. blood cell fractionation, platelet activation, separation of neuroblastoma cells and glioma cells.^35–37 Cell deformability signifies cytoskeletal or nuclear changes associated with disease progression and changes in cell states, and has been used to characterize changes of malaria-infected red blood cells, invasive cancer cells compared to benign cells of the same origin, activated and inactivated leukocytes, and pluripotency of stem cells.^14,17 Finally, cell polarizability consolidates information about cell morphology and composition, and has been shown to distinguish subtle changes in biological phenotypes, e.g. induced apoptosis in HL60 cells, stimulation of T and B lymphocytes, and induced differentiation in Friend murine erythroleukemia cell lines.³⁸ Overall, size, deformability, and polarizability of cells are promising label-free biomarkers that have been extensively investigated individually, but rarely studied all together.

Each intrinsic marker can be measured by a variety of techniques. Cell deformability measurement techniques include optical stretching, cell transit analysers, hydrodynamic forces, and others.¹⁶ Electrical properties of single cells can be measured by impedance cytometry, dielectrophoretic force balance techniques, and electrorotation techniques.^32,38 Size can be measured with image processing, Coulter resistive sizing, deterministic lateral displacement array, etc.^25,39,40 Here we chose techniques that translate the properties into spatiotemporal positions and are thus compatible with the cell-tracking cytometry approach.

Deformability module design and analysis

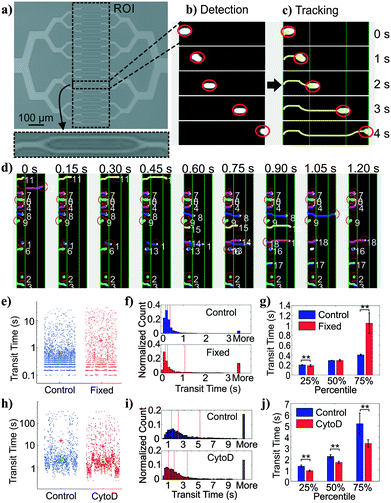
We adopted a constriction-based deformability measurement platform previously introduced by the Fletcher group.⁴¹ In the platform, suspended cells are squeezed through parallel constriction channels whose width is smaller than the cell diameter (Fig. 2a). More deformable cells are expected to transit through the constriction faster than less deformable cells (holding cell size and cell-surface interactions constant).

Fig. 2 Deformability measurement module and cell tracking. (a) Image of 32 parallel constriction channels and region of interest (ROI). The inset shows exploded view of two narrowest constriction channels. (b) Cell detection. Images of cells in videos are detected by adaptive thresholding and filtered by size. (c) Cell tracking. Detected cells in subsequent frames are assigned to tracks based on nearest-neighbor adjacency and direction of travel. Transit time is defined as the time for a cell to travel across the ROI. (d) Multiple object tracking. This approach allows many cell trajectories to be determined simultaneously. Shown are frames with identified cells denoted by numbers. (e) Measured transit times from control (n = 5270) and fixed (n = 1418) BA/F3s. (f) Histograms of cell transit time across 3 experiments over one device replicate. (g) Extracted quantiles of transit times (**, p < 0.01). (h) Measured transit times from control (n = 867) and cytochalasin D-treated (n =1371) HL60s. (i) Histograms of cell transit time across 6 experiments over three device replicates. (j) Extracted quantiles of transit times, or the 25, 50, and 75 percentiles of the transit time distribution (**, p < 0.01). (e and h) Red crosses and green squares depict mean and median of the distributions, respectively. (f and i) Red dash lines depict 25%, 50%, and 75% percentile of the distribution, respectively. (g and j) Error bars represent 95% confidence intervals.

On our platform, cells were detected from image stacks by thresholding the pixel intensity within the region of interest (ROI), followed by cell segmentation and tracking (Fig. 2b and c). The transit time of each cell was calculated as the difference between the time stamp when the cell first entered the ROI and the time stamp when the cell exited the ROI. Multiple cells could be detected at the same time with a customized tracking algorithm (Fig. 2d).

Deformability module validation

To validate the transit time measurements from the constriction-based deformability module, we performed two sets of experiments. First, we studied BA/F3 cells, a murine interleukin-3 dependent pro-B cell line, with and without 10 minute exposure to 4% paraformaldehyde crosslinking fixative, which has been previously used to provide additional rigidity to the cells. Cells that are fixed by cross-linking agents such as formaldehyde²⁷ or glutaraldehyde^42–47 are expected to have decreased deformability (negative change). Fig. 2e and f shows beeswarm plots and histograms of the extracted transit time for control and fixed BA/F3 cells. Qualitatively, in fixed cells we observed an increase in the cell population that has >3 seconds of transit time. Direct comparison of quartiles shows a ∼2.5-fold (1.05 s vs. 0.41 s) increase in the 75 percentile population in the fixed cells (Fig. 2g), supporting an increased transit time upon fixation.

To generalize beyond one cell type and one condition, we undertook experiments using HL60 cells, a human promyelocytic leukemia cell line, with and without exposure to cytochalasin D. Cytochalasin D is a potent actin polymerization inhibitor, which has been shown to increase cell deformability (positive change) by various deformability measurement techniques.^29,41,48Fig. 2h and i show beeswarm plots and histograms of control and 2 μM cytochalasin D treated cells. The transit time distributions of the two populations are not normally distributed, but rather are heavy-tailed. Qualitatively, the shape of the cytochalasin D treated transit time distribution is slightly more skewed toward lower transit times. In this case we find a significant decrease in the 75 percentile transit time (3.43 s vs. 5.12 s), consistent with an increase in deformability (Fig. 2j).

Together, these results demonstrate proper functioning of the deformability module coupled with image-based cell tracking.

Size and polarizability module design and analysis

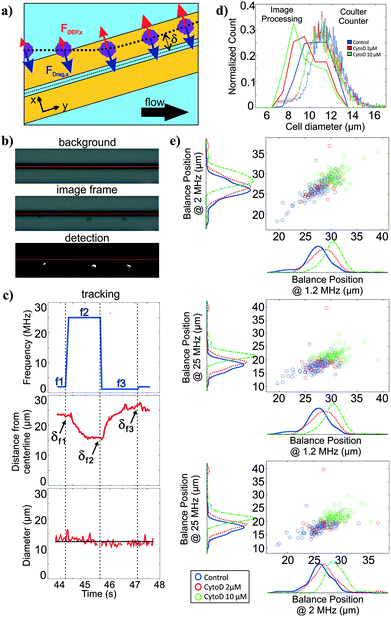
For polarizability measurement, we used a variant of the DEP spring previously introduced by our lab.⁴⁹ In this technique, a pair of parallel coplanar electrodes is positioned slightly slanted from the flow direction (Fig. 3a). Cells that are introduced into the channel are subjected to a hydrodynamic drag force and will migrate along the channel flow direction. Once cells encounter the electrodes, cells will be subjected to a negative DEP force that pushes the cells away from the electrode centerline. If the negative DEP force in the direction perpendicular to the electrode centerline is sufficient to counter balance the drag force, cells will continue to migrate along the direction of the electrode centerline. With this technique, the polarizability of cells can be inferred from a measurement of the balance position (δ) that arises as a competition between the fluid drag force and the negative DEP force. Cell polarizability can be reported as the real part of the Clausius–Mossotti factor (Re[CM]), which incorporates the geometry and electrical properties of cell compartments. The different compartments and their properties cause the Re[CM] to be frequency dependent. For example, subtle changes in the cytosolic compartment will be more prominent in the balance position measurements at a higher frequency range than changes in the cell membrane. Thus, probing cell polarizability at multiple frequencies provides richer electrical phenotypic information. The frequency sequence, which is a repeated set of three frequencies, was randomly chosen within the operative frequency range that will be most indicative of the Re[CM] spectra. We applied this frequency sequence to the electrodes for testing.

Fig. 3 Size and multi-frequency nDEP measurements through image processing. (a) Overview of DEP spring method (b) Images of cells on electrodes are thresholded after background subtraction. Red horizontal lines indicates the electrode centerline. (c) Extracted cell diameters and distance of the cell centroid from the electrode centerline relative to the applied frequency as a cell traversed the polarizability module. As there are many diameter measurements for each cell, the mean of the cell diameters measured across time is considered to be the extracted cell diameter. Balance positions (δ) are the equilibrium perpendicular distance between the cell centroid and the center of the electrodes. Three different frequencies are applied as the cells traverse the field of view, allowing determination of three balance positions, which are related to the polarizability. (d) Histogram of cell diameters as extracted from the image processing and from coulter counter measurements (e) Scatter plots with marginal histograms of balance points at three different frequencies for control (n = 194), 2μM (n = 51) and 10 μM (n = 144) CytoD treated HL60s. Blue, red, and green lines represent the linear regression models between balance positions at different frequencies for control, 2 μM, and 10 μM cytochalasin D treated HL60 cells

Similar to the deformability module, we use the image stacks to detect and track cells as they traverse the DEP spring (Fig. 3b). We extract the distance of the cell centroids from electrode centerline, and can obtain balance position measurements at multiple frequencies by correlating the cell position in time to the temporal frequency sequence (Fig. 3c). The imaging can also be used to extract cell diameter of each cell, using the frame stack to obtain multiple measures of the diameter as the cell traverses the field of view.

Size module validation

To validate the extracted cell diameters, we compared visually measured cell diameters to those measured using Coulter sizing for all three HL60 populations. Histograms of cell diameters extracted from image processing on our platform and cell diameters measured from coulter counter measurements for all three HL60 populations are shown in Fig. 3d. The average and standard deviation of cell diameters measured from Coulter counter for control, 2 μM and 10 μM cytochalasin D populations were 11.28 ± 1.41 μm, 11.04 ± 1.39 μm, 10.97 ± 1.34 μm, respectively, whereas they were 10.55 ± 1.21 μm, 9.81 ± 1.31 μm, 9.45 ± 1.38 μm, respectively, when measured via image processing. Thus, for each HL60 population, the average cell diameters obtained from image processing are <1.6 μm (17%) smaller than those measured via Coulter counter, which is not surprising given that image thresholding can lead to such systematic biases. While size accuracy can be achieved by calibrating the threshold value for a particular illumination, focusing, object material and background setting, such calibration can be burdensome as the imaging setting can fluctuate slightly during experiment and more so across experiments. For size measurement on our platform, accuracy is not as crucial as precision since we are only interested in relative size within and between cell populations.

Polarizability module validation

To validate the operation of the multi-frequency DEP spring module with cell tracking, we used HL60s exposed to cytochalasin D, which has been shown to impact cell actin structure in a dose-dependent manner.⁵⁰ Here we measured balance positions at three different frequencies of single cells in a single device. According to the CCD camera pixel size and the selected objective lens, the measured balance positions were determined with ±1.07 μm resolution. Extracted balance positions at three different frequencies of single cells are shown in scatter plots with marginal histograms in Fig. 3e. For each population, the balance positions generally decreased as the test frequency increased. For each test frequency, we observed positive shift in balance positions as the concentration of cytochalasin D increased even though cell diameters decreased, which implied an increase in Re[CM] magnitude. The imperfect linear relationships between all pairs of the three frequencies in the scatter plots suggest that additional information is obtained with each added frequency.

Multiparameter intrinsic characterization of single cells

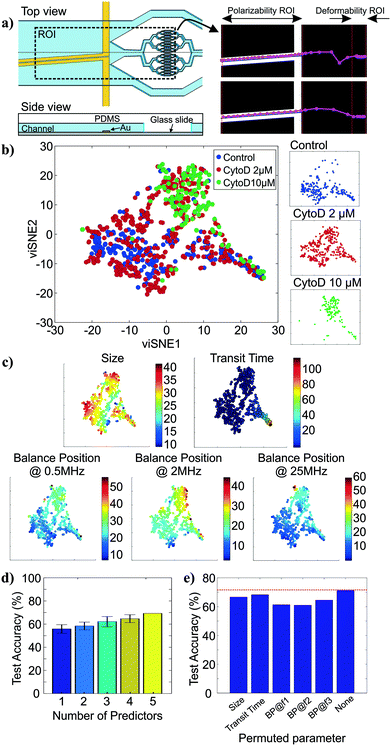
To show how cell tracking can be used to correlate multiple properties across different microfluidic elements, we created an intrinsic cytometer with size, deformability, and polarizability modules (Fig. 4a (left)). This device incorporated both electrode-based analysis (DEP spring) and PDMS microfluidics (deformability), two common microfluidic fabrication modalities. Broadly speaking, with our approach, the multiplicative nature of the yield of data within each module can cause substantial data loss as number of modules to be integrated increases. Therefore, it is important to ensure that the throughput of the modality corresponding to each marker in the pipeline is maximized and that the tracking algorithm is optimized to maintain the relations between markers of single cells. Particularly, on our first instantiation of this approach, we were able to extract all five markers of only 12% of cells that were detected on the platform (not shown). With further investigation and improvement on both the DEP spring module and the deformability module, we were able to increase the throughput from ∼100 cells per run (∼12% of all cell detections) to ∼400 cells per run (∼48% of all cell detections). The remaining ∼50% of cell detections did not have measurements of all 5 markers, partially because 1) we exclude transit time measurements of cells that came into contact with another, 2) some cells were not focused onto the investigation region of the DEP spring module and did not experience the negative DEP force which was required for the polarizability measurements, 3) some cells travelled faster than others through the DEP spring module and did not have enough time to experience all three frequencies in the frequency sequence. The yield can be further improved by enhancing the efficiency of cell focusing prior to DEP spring module measurements, and optimizing the frequency sequence, flow rate, and ROI of the DEP spring module.

Fig. 4 Multiparameter intrinsic measurements. a) Top view and side view of integrated platform schematic, drawn not to scale (left) and successful tracks of cells across different modules (right). b) viSNE maps of the multiparameter data for control (n = 240), 2 μM (n = 393) and 10 μM (n = 137) cytochalasin D treated HL60s. The two axes represent arbitrary units. c) viSNE maps colored by individual parameter measurements, namely size, transit time, and balance positions at 0.5 MHz, 2 MHz, and 25 MHz. d) Classification accuracy by the random forest classifiers on the test data set as the number of predictors used increases. e) Impact of each intrinsic marker on the classification accuracy of the random forest model, i.e. classification accuracy as the values of each marker are permuted.

We then performed assays examining the effect of cytochalasin D on the five intrinsic markers that we measured. Unlike the separate studies for deformability and polarizability modules in previous sections, here we can measure all five intrinsic markers and maintain the connections between these markers for single cells. Examples of tracks of cells as they traverse the different modules are shown in Fig. 4a (right). The extracted multiparameter data of single cells are shown in 5-by-5 scatter plots in Fig. S2.† viSNE is used to project the single-cell multiparameter data from the 5D space into 2D plots while preserving significant structures in the high-dimensional space. viSNE visualization of the multiparameter data as colored by population (exposure to cytochalasin D) is shown in Fig. 4b. The viSNE map reveals clear separation between the control population and the 10 μM cytochalasin D-treated population, while there is a high degree of overlap between most of the space occupied by the two populations and 2 μM cytochalasin D-treated population. To better understand the relations between the separation in viSNE visualization and the intrinsic marker measurements, the same viSNE map is relabelled according to each of the five intrinsic marker measurements and shown in Fig. 4c. In general, cells with larger size are distributed across the three natural clusters in the map while transit time gradually increases toward the tip of the cape-shaped region in the lower right quadrant of the map. Nevertheless, the trends in size and transit time did not seem to significantly contribute to the visual separation of cell populations in viSNE map. In contrast, the balance positions at three frequencies, which represent the polarizability marker, gradually increase toward the top right of the viSNE maps. Mentally overlaying the viSNE map with the population-based color scheme onto the viSNE map with the marker-based color scheme shows that the 10 μM cytochalasin D-treated population tends to have larger balance positions at all three tested frequencies than control populations. Meanwhile, the 2 μM cytochalasin D-treated population is not clearly separable from the other two populations with the five markers that we measured on our platform.

To quantitatively investigate the orthogonality between each intrinsic marker measured from our multiparameter platform, we computed Pearson's correlation coefficients between all pairs of markers (Fig. S3†). If two markers are highly correlated (i.e. less orthogonal), we might not need to measure both of them. Orthogonality between markers indicates how much additional information we are able to learn from measuring them and helps determine the optimal set of markers needed for cell classification. We observed stronger correlation (R > 0.36) in pairs of balance positions at two different frequencies than other pairs of markers (R < 0.10). With correlation coefficients (R) between −0.01 and 0.05, variation in cell size does not seem to have contributed to variation in transit time and balance positions. Similarly, transit time is not strongly correlated to balance position at each of the three frequencies (0.03 < R < 0.07). In general, none of the intrinsic marker pairs are strongly correlated to each other and we expect to gain additional information about the cells from each of the measured intrinsic markers.

To evaluate how the number of intrinsic markers measured for single cells affects the ability to distinguish between the treatment conditions, we trained random forest classifiers for all subsets of the 5 markers measured and computed averaged classification accuracies on the test set when only one intrinsic marker was used for classification compared to when 2, 3, 4, and all 5 markers were used for classification. The random forest algorithm was chosen because it is a non-parametric approach, which is intrinsically suited for multiclass classification. In other words, it does not make any assumptions about the shape of the decision boundaries between classes and therefore it is well suited for our classification problem where the decision boundaries between populations are expected to be highly nonlinear. We find that the classification accuracy generally increases as the number of intrinsic markers used increases (Fig. 4d), suggesting that all five intrinsic markers measured contribute to the characterization of the cell states of interest, particularly the exposure level of cytochalasin D drug. Nevertheless, even with all five markers, the average classification accuracy on the test set is ∼71.4%. The confusion matrix from the representative run of the random forest algorithm (Fig. S4†) shows that most classification errors originate from the reduced ability to distinguish the 2 μM cytochalasin D treated population from the control population and the 10 μM cytochalasin D treated population. This is consistent with observations from viSNE maps, which show partially overlapping regions between 2 μM cytochalasin D treated population and the other two populations (Fig. 4b). Furthermore, the importance of each marker on the accuracy of the model can be evaluated by permuting the values of the marker of interest and observing the changes in classification accuracy (Fig. 4e). Permutation of an unimportant marker should have little effect on model accuracy while permutation of an important marker should significantly decrease it. According to Fig. 4e, permutation of balance positions at all three frequencies decrease the model accuracy by ∼6.9–10.4%, which were more than those of size (∼4.8%) and transit time (∼3.0%), suggesting that the balance position markers contribute to classification accuracy more than the other two markers. Similar results were obtained by the same analysis with another nonparametric machine-learning algorithm, the support vector machine (SVM) with a Gaussian kernel (Fig. S5†). The only difference between the random forest model and the SVM model is the impact of size on the model accuracy.

Simultaneous electrical and mechanical characterizations of single cells have been demonstrated on various platforms and have been shown to improve classification accuracy when the two types of markers were combined compared to when they were individually tested.^51–56 Most of these platforms utilized electrical impedance measurements to measure cell impedance profiles as well as cell transit times through constriction.^53,54,56 While electrical-detection-based techniques are favorable for real-time applications due to simplicity in data extraction and processing, we opted for image-based techniques due to multiple reasons. First, more subtle features of cell properties can be harnessed from images without additional probes, e.g. surface roughness, aspect ratio, constriction entry time, elongation length, etc. Second, image-based techniques allow cell measurements to be parallelized within and across measurement modules, which compensates for tracking and data extraction time. Similarly for extrinsic markers, there have been efforts to change the analytical paradigm of conventional flow cytometry in order to improve cell throughput by acoustically focus cells in a parallelized fashion and use image-based detection to extract optical parameter data in order to remove the limitations from serially investigating one cell in a single focused stream at a time.^57,58 Last but not least, image-based techniques provide ease of potential integration of additional modules. Measurement techniques that translate their property directly into electrical signals are scarce, while the set of techniques that can be read out from images is large. By restraining ourselves to measurement techniques that enable visual readouts, the integration complexity with regard to output synchronization and processing is significantly reduced. In particular, our platform utilized a force-balanced technique called the DEP spring to characterize electrical properties of cells, which allows electrical properties of cells to be embedded in their spatiotemporal positions and eliminates the need for extra probes for electrical detection as well as the requirement for an impedance analysis system.

Our platform, which measures five intrinsic markers for single cells, is only a proof-of-concept demonstration. Additional markers which might be useful for cell characterization can be retrieved from the image stacks recorded with the current setup, e.g. constriction entry time, elongation length of deformed cells, and aspect ratio of undeformed cells. Elongation index, and separation of entry and transit behaviors have been shown to improve classification of benign and cancer cells based on deformability marker as well as have been used to estimate Young's modulus, hydrodynamic resistance, and cytoplasmic viscosity of cells.^24,59 While indirect markers are sufficient for cell classification purposes, extraction of fundamental intrinsic properties such as Young's modulus, viscosity, and polarizability should be considered in the device design and analysis for comparing the same properties across different measurement techniques and for robustness in the interpretability of the results. Furthermore, for applications where cell size is not known a priori or varies broadly, one can integrate the constriction-based module with varying constriction widths right after size separation module with corresponding lateral displacement of cell size, e.g., deterministic lateral displacement array, in order to maintain the ratio of cell size to constriction width, or choose to substitute the constriction-based module with other deformability measurement techniques which are less susceptible to cell size. Regardless, the main advantage of tracking-based intrinsic cytometry is versatility in the design and optimization of the microfluidic platform. The collection of intrinsic markers studied can be further expanded and optimized by adding or substituting the measurement modules on the platform, as currently we used only 24% of the entire field-of-view of the microscope with 5× objective. One can imagine extending the device footprint further by using 2.5× objective with trade-off on the image resolution and accuracy of the distance- or size-related measurements. With numerous label-free microfluidic techniques for measuring cell intrinsic properties, especially those equipped with visual readout capabilities, e.g. deterministic lateral displacement array, inertial microfluidics, acoustophoresis, optical techniques,⁷ there are many combinations of the microfluidic measurement modules that can be integrated with this approach to allow several intrinsic markers of single cells to be studied simultaneously. We envision our proposed approach as a general strategy to develop multiparameter intrinsic cytometry tools.

Conclusions

We proposed a new multiparameter intrinsic cytometry approach for characterizing single cells, by combining measurement of ≥2 intrinsic markers on the same platform and associating markers to single cells via tracking. In contrast to conventional approaches that integrate different measurement techniques in the same physical space and measure properties of single cells simultaneously, our approach distributes measurement across space and measures properties of cells in parallel fashion. This adaptation allows each measurement module to be optimized individually and makes the platform readily extensible to more measurement techniques as constraints on investigation space are mitigated. We demonstrated a proof-of-concept implementation that can measure five intrinsic markers of single cells, including size, deformability, and polarizability at three frequencies. By studying cell samples with drug-induced changes in cytoskeleton, individual modules were first validated separately and the fully integrated platform was demonstrated. Analyses of Pearson's linear correlation coefficients and supervised classification accuracy results both confirmed that additional information about the drug-induced structural changes of cells could be obtained with each additional intrinsic marker that we measured. Similar to the development of extrinsic markers and their countless biomedical applications, we anticipate intrinsic markers to become more useful in complex real-world applications once combinations of intrinsic markers can be investigated with ease.

Materials and methods

Cell culture

BA/F3 murine interleukin-3 dependent pro-B cell line was cultured according to ATCC protocols and were passaged ∼3–4 days at 1/10 dilution. The cell culture medium was prepared from RPMI-1640 with high glucose content, L-glutamine, and phenol red indicator, supplemented with 10% fetal bovine serum, 1% L-glutamine, 1% penicillin–streptomycin, 1% sodium pyruvate, and 1% MEM non-essential amino acids.

HL60 human acute promyelocytic leukemia cell line was cultured according to ATCC protocols and were passaged ∼2–3 days to maintain cell density between 1 × 10⁵ and 1 × 10⁶ cells per mL. The cell culture medium was prepared from RPMI-1640 with high glucose content, L-glutamine, and phenol red indicator, supplemented with 10% fetal bovine serum, and 1% penicillin–streptomycin.

Microfluidic device

For deformability experiment, the device consists of a PDMS layer which contains a 15 μm-high microfluidic channel with 32 parallel constriction channels, modified from Rosenbluth et al.,⁴¹ and shown in Fig. 2a. The widths of the narrowest constrictions are 10 μm for BA/F3 experiments and are 6 μm for HL60 experiments. The two constriction widths were chosen experimentally as the constriction channels had to be sufficiently narrow to be sensitive to the change in cell deformability and sufficiently wide to avoid channel clogging which decreased the number of available channels for testing. The microfluidic channels in PDMS is molded from an SU-8 silicon master or a plastic master mold replicated from the original mold, using standard microfabrication techniques. The PDMS layer is then bonded a glass slide after 2 minute exposure to oxygen plasma.

For polarizability and size experiment, the device is as described in Su et al.⁴⁹ The device consists of two main components: 1) a PDMS layer with 20 μm-by-2 mm-by-5 cm channel, which is molded from silicon or plastic master mold, and 2) a patterned electrode layer with 200 nm Au and 10 nm Ti on Pyrex wafer, which is fabricated using standard lift-off protocol. The two components are plasma bonded and sealed with two-part epoxy.

For multiparameter intrinsic cytometry experiment, the integrated platform design is shown in Fig. 4a and in Fig. S1.† The PDMS layer and the electrode layer of the cytometry are fabricated as previously described. The channel pattern in the PDMS layer is then aligned and plasma-bonded to the electrode patterns on Pyrex wafer. External electrical connections are soldered onto the predesignated electrode pads.

Cell assay

For deformability study, BA/F3 cells were incubated with 4% paraformaldehyde in Dulbecco's phosphate-buffered saline (DPBS) at room temperature for 10 minutes. For drug treatment studies, HL60 cells were exposed to 10% DMSO (for control), 2 μM or 10 μM cytochalasin D in addition to 1 μM calcein AM, and incubated at 37 °C for 1 hour. Calcein AM was added to cells to improve cell detection accuracy. Before each experiment, prepared cells are re-suspended in DPBS with 13% (w/v) Dextran at 1 × 10⁵–2 × 10⁵ cells per mL.

Cytometry experiment

Microfluidic channels are flushed with 0.5% (w/v) Pluronic-F108 in DI water until all bubbles are removed, and are passivated with 2% bovine serum albumin in DPBS for 1–2 hours to reduce non-specific binding between cell samples and channel walls. Cell samples are loaded into 1 mL Hamilton syringe, which is connected to the device via 0.01 ID PEEK™ tubing and sample-loop configuration. The device is connected to function generators via 50 Ω coaxial cable with BNC connectors. Constant flow is delivered by Chemyx Fusion 200 syringe pump. Due to difference in channel structures and cell diameters, flow rate is 1 μL min⁻¹ for BA/F3 experiments and 0.3 μL min⁻¹ for HL60 experiment. Customized MATLAB GUI described in Su et al.⁴⁹ is used to control Agilent 33220A function generator (for frequency <20 MHz), Aim TTi TGR1040 RF signal generator (for frequency ≥20 MHz) and PCO Sensicam QE camera. Imaging is performed with Zeiss Axio Imager m1m upright microscope. Once initiated, MATLAB GUI records time-lapsed videos along with the frame-by-frame frequency sequence generated by the function generator. The video recording settings including FOV, frame rate, and recording time, were optimized in terms of cell measurement throughput under the constraint of RAM capacity. Therefore, the recording conditions were different for the deformability module validation, polarizability module validation, and the integrated platform experiments. The field of view (FOV) for the deformability module validation, polarizability module validation, and the integrated platform experiments were ∼206 μm × 757 μm (H × V), 1373 μm × ∼103 μm (H × V), and ∼2065 μm × 757 μm (H × V), respectively. The recording frame rates for the deformability module validation, polarizability module validation, and integrated platform experiments were ∼20 frames per seconds, ∼32 frames per seconds, and ∼5.3 frames per seconds, respectively.

Cell detection and tracking

All image processing and analysis are performed in MATLAB®R2017a. For cell detection, intensity image in each frame of the time-lapsed videos is binarized via adaptive thresholding and connected components within specified area constraints are considered potential cell detections. The extracted cells centroid locations in each frame are then applied to the customized multi-object tracking algorithm.

For tracking, cell detections which correspond to the same cell across time are assigned to the same track by the Hungarian algorithm. The cost matrix supplied to the Hungarian algorithm can be depicted by,

cost(i, j) = distance between detection ‘i’ from previous frames and detection ‘j’ from the current frame × direction parameter × channel geometry parameter,

where i and j are indices for each detection of the previous frames and for each detection of the current frame, respectively. The distance between detections is used as one of the parameter in the cost matrix under the assumption that detections between frames of the same cells are closer together than detections between frames of different cells. Therefore, assignment of cells to tracks can be achieved by minimizing the distance or the cost matrix. Direction parameter and channel geometry parameter are included in the cost matrix to prevent assignment of any cell motions which are not possible, given a priori knowledge about the flow direction in the channel and the channel geometry. The distance cost will be replaced with an infinite cost if any impossible motion between detections are detected and the assignment between those detections will not be made as the Hungarian algorithm will try to minimize the cost function. For each frame of the time-lapsed video, the cost matrix is computed and the track assignments made by the Hungarian algorithm are updated. Any unassigned detections in the current frame will be assigned to new tracks and any tracks from the previous frames that are unassigned will be marked invisible and penalized. After a track has been penalized for more than predetermined number of frames, the cell corresponding to that track is considered to have left the field-of-view.

Data extraction

After tracking, locations of individual cells with respect to channel structure across time are specified. In addition to equivalent diameters, transit times, and balance positions at three frequencies of individual cells are extracted. Equivalent diameter is calculated from . Transit time is calculated from number of frames a cell stays in the deformability ROI divided by number of frames per seconds. Balance position at each frequency is calculated from the perpendicular distance from the electrode centerline to the cell centroid detected within the polarizability ROI when waveform of that specific frequency is applied. If there are more than one measurements of a specific parameter for a cell, the measurements are averaged to give the final extracted values.

Data analysis

The Wilcoxon rank sum tests (equivalently the Mann–Whitney U-test) were performed to compare transit time distributions with determination of statistical significance between populations.

Two-dimensional visualization of the multiparameter single-cell data was produced by visual interactive stochastic neighbor embedding (viSNE),⁶⁰ a nonlinear dimensionality reduction technique that maps data points from high-dimensional space to low-dimensional space while conserving the spatial relationship between nearest neighbors. The resulting two-dimensional projections, i.e. viSNE maps, allow visualization of the high-dimensional data, making it easier to analyze and interpret. To study relationship between the measured intrinsic markers and cell population, data points in viSNE maps representing single-cell data can be re-colored according to the cell population or according to measurement of each marker.

To evaluate the orthogonality between the measured intrinsic markers and the importance of each marker, we plot Pearson's linear correlation coefficients between all pairs of intrinsic markers and trained supervised machine learning algorithms, including random forest and SVM, to classify cell populations with 70% of the dataset and withhold the rest for testing. We trained with all 31 possible combinations of five markers used for classification ranging from one marker to five markers used. To elaborate, there are five cases each where number of markers used is one and four, and there are 10 cases each where number of markers used is two and three, and there are only 1 case where all five markers are used. In all cases, optimal training parameters were determined with Bayesian optimization, which searches for hyperparameters that minimize five-fold cross validation loss. We computed the average of the classification accuracy on the test set in different conditions and grouped them in terms of number of markers used. Impact of each marker on the model accuracy is evaluated by permuting values of that marker and observing decrease in model accuracy.

Conflicts of interest

The authors have no conflicts to declare.

Acknowledgements

We acknowledge financial support from the Bose Research Award and we thank Microsystems Technology Laboratories staff for microfabrication assistance.

References

1. P. K. Chattopadhyay, C.-M. Hogerkorp and M. Roederer, Immunology, 2008, 125, 441–449.
2. D. R. Bandura, V. I. Baranov, O. I. Ornatsky, A. Antonov, R. Kinach, X. Lou, S. Pavlov, S. Vorobiev, J. E. Dick and S. D. Tanner, Anal. Chem., 2009, 81, 6813–6822.
3. J. C. Love, M. Roederer, P. K. Chattopadhyay and T. M. Gierahn, Nat. Immunol., 2014, 15, 128.
4. A. Adan, G. Alizada, Y. Kiraz, Y. Baran and A. Nalbant, Crit. Rev. Biotechnol., 2017, 37, 163–176.
5. S. C. Bendall, E. F. Simonds, P. Qiu, E. D. Amir, P. O. Krutzik, R. Finck, R. V. Bruggner, R. Melamed, A. Trejo, O. I. Ornatsky, R. S. Balderas, S. K. Plevritis, K. Sachs, D. Pe'er, S. D. Tanner and G. P. Nolan, Science, 2011, 332, 687–696.
6. O. Ornatsky, D. Bandura, V. Baranov, M. Nitz, M. A. Winnik and S. Tanner, J. Immunol. Methods, 2010, 361, 1–20.
7. D. R. Gossett, W. M. Weaver, A. J. Mach, S. C. Hur, H. T. K. Tse, W. Lee, H. Amini and D. D. Carlo, Anal. Bioanal. Chem., 2010, 397, 3249–3267.
8. S. Suresh, J. Spatz, J. P. Mills, A. Micoulet, M. Dao, C. T. Lim, M. Beil and T. Seufferlein, Acta Biomater., 2005, 1, 15–30.
9. S. Suresh, J. Mater. Res., 2006, 21, 1871–1877.
10. G. Y. H. Lee and C. T. Lim, Trends Biotechnol., 2007, 25, 111–118.
11. D.-H. Kim, P. K. Wong, J. Park, A. Levchenko and Y. Sun, Annu. Rev. Biomed. Eng., 2009, 11, 203–233.
12. M. Diez-Silva, M. Dao, J. Han, C.-T. Lim and S. Suresh, MRS Bull., 2010, 35, 382–388.
13. Y. Zheng and Y. Sun, Micro Nano Lett., 2011, 6, 327–331.
14. D. Di Carlo, J. Lab. Autom., 2012, 17, 32–42.
15. X. Mao and T. Jun Huang, Lab Chip, 2012, 12, 4006–4009.
16. Y. Zheng, J. Nguyen, Y. Wei and Y. Sun, Lab Chip, 2013, 13, 2464–2483.
17. Y. Nematbakhsh and C. T. Lim, Acta Mech. Sin., 2015, 31, 268–273.
18. A. Lenshof and T. Laurell, Chem. Soc. Rev., 2010, 39, 1203–1217.
19. J. Voldman, Annu. Rev. Biomed. Eng., 2006, 8, 425–454.
20. J. Chen, J. Li and Y. Sun, Lab Chip, 2012, 12, 1753–1767.
21. C. W. S. Iv, C. D. Reyes and G. P. López, Lab Chip, 2015, 15, 1230–1249.
22. J. Autebert, B. Coudert, F.-C. Bidard, J.-Y. Pierga, S. Descroix, L. Malaquin and J.-L. Viovy, Methods, 2012, 57, 297–307.
23. A. A. S. Bhagat, H. Bow, H. W. Hou, S. J. Tan, J. Han and C. T. Lim, Med. Biol. Eng. Comput., 2010, 48, 999–1014.
24. H. W. Hou, Q. S. Li, G. Y. H. Lee, A. P. Kumar, C. N. Ong and C. T. Lim, Biomed. Microdevices, 2009, 11, 557–564.
25. G. Guan, P. C. Y. Chen, W. K. Peng, A. A. Bhagat, C. J. Ong and J. Han, J. Micromech. Microeng., 2012, 22, 105037.
26. E. S. Park, C. Jin, Q. Guo, R. R. Ang, S. P. Duffy, K. Matthews, A. Azad, H. Abdi, T. Todenhöfer, J. Bazov, K. N. Chi, P. C. Black and H. Ma, Small, 2016, 12, 1909–1919.
27. D. R. Gossett, H. T. K. Tse, S. A. Lee, Y. Ying, A. G. Lindgren, O. O. Yang, J. Rao, A. T. Clark and D. D. Carlo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7630–7635.
28. H. T. K. Tse, D. R. Gossett, Y. S. Moon, M. Masaeli, M. Sohsman, Y. Ying, K. Mislick, R. P. Adams, J. Rao and D. D. Carlo, Sci. Transl. Med., 2013, 5, 212ra163.
29. A. Mietke, A. Ekpenyong, A. Jacobi, C. Herold, D. Klaue, E. Fischer-Friedrich, J. Mansfeld, J. Guck, M. Wobus, N. Töpfner, O. Otto, P. Rosendahl, S. Girardo, S. Golfier, S. Pagliara and U. F. Keyser, Nat. Methods, 2015, 12, 199.
30. M. Xavier, P. Rosendahl, M. Herbig, M. Kräter, D. Spencer, M. Bornhäuser, R. O. C. Oreffo, H. Morgan, J. Guck and O. Otto, Integr. Biol., 2016, 8, 616–623.
31. D. Di Carlo, D. Kim, H. T. Tse, J. Lin, L. Peng, M. Dhar, P. Tseng and S. Karumbayaram, Microsyst. Nanoeng., 2017, 3, 17013.
32. T. Sun and H. Morgan, Microfluid. Nanofluid., 2010, 8, 423–443.
33. J. Chen, C. Xue, Y. Zhao, D. Chen, M.-H. Wu and J. Wang, Int. J. Mol. Sci., 2015, 16, 9804–9830.
34. A. C. Lloyd, Cell, 2013, 154, 1194–1205.
35. J. A. Davis, D. W. Inglis, K. J. Morton, D. A. Lawrence, L. R. Huang, S. Y. Chou, J. C. Sturm and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14779–14784.
36. D. W. Inglis, K. J. Morton, J. A. Davis, T. J. Zieziulewicz, D. A. Lawrence, R. H. Austin and J. C. Sturm, Lab Chip, 2008, 8, 925–931.
37. S. S. Kuntaegowdanahalli, A. A. S. Bhagat, G. Kumar and I. Papautsky, Lab Chip, 2009, 9, 2973–2980.
38. J. Voldman, Annu. Rev. Biomed. Eng., 2006, 8, 425–454.
39. W. H. Coulter, Proc. Natl. Electron. Conf., 1956, 12, 1034.
40. L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990.
41. M. J. Rosenbluth, W. A. Lam and D. A. Fletcher, Lab Chip, 2008, 8, 1062–1070.
42. M. Abkarian, M. Faivre and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 538–542.
43. H. Bow, I. V. Pivkin, M. Diez-Silva, S. J. Goldfless, M. Dao, J. C. Niles, S. Suresh and J. Han, Lab Chip, 2011, 11, 1065–1073.
44. J. P. Beech, S. H. Holm, K. Adolfsson and J. O. Tegenfeldt, Lab Chip, 2012, 12, 1048–1051.
45. P. Preira, V. Grandné, J.-M. Forel, S. Gabriele, M. Camara and O. Theodoly, Lab Chip, 2013, 13, 161–170.
46. Y. Zheng, J. Nguyen, C. Wang and Y. Sun, Lab Chip, 2013, 13, 3275–3283.
47. D. Holmes, G. Whyte, J. Bailey, N. Vergara-Irigaray, A. Ekpenyong, J. Guck and T. Duke, Interface Focus, 2014, 4, 20140011.
48. A. C. Hodgson, C. M. Verstreken, C. L. Fisher, U. F. Keyser, S. Pagliara and K. J. Chalut, Lab Chip, 2017, 17, 805–813.
49. H.-W. Su, J. L. Prieto and J. Voldman, Lab Chip, 2013, 13, 4109–4117.
50. T. Wakatsuki, B. Schwab, N. C. Thompson and E. L. Elson, J. Cell Sci., 2001, 114, 1025–1036.
51. Y. H. Cho, T. Yamamoto, Y. Sakai, T. Fujii and B. Kim, J. Microelectromech. Syst., 2006, 15, 287–295.
52. J. Chen, Y. Zheng, Q. Tan, Y. L. Zhang, J. Li, W. R. Geddie, M. A. S. Jewett and Y. Sun, Biomicrofluidics, 2011, 5, 014113.
53. J. Chen, Y. Zheng, Q. Tan, E. Shojaei-Baghini, Y. Liang Zhang, J. Li, P. Prasad, L. You, X. Yu Wu and Y. Sun, Lab Chip, 2011, 11, 3174–3181.
54. Y. Zheng, E. Shojaei-Baghini, A. Azad, C. Wang and Y. Sun, Lab Chip, 2012, 12, 2560–2567.
55. K. Wang, Y. Zhao, D. Chen, B. Fan, Y. Lu, L. Chen, R. Long, J. Wang and J. Chen, Sci. Data, 2017, 4, 170015.
56. Y. Zhou, D. Yang, Y. Zhou, B. L. Khoo, J. Han and Y. Ai, Anal. Chem., 2018, 90, 912–919.
57. R. Zmijan, U. S. Jonnalagadda, D. Carugo, Y. Kochi, E. Lemm, G. Packham, M. Hill and P. Glynne-Jones, RSC Adv., 2015, 5, 83206–83216.
58. D. M. Kalb, F. A. Fencl, T. A. Woods, A. Swanson, G. C. Maestas, J. J. Juárez, B. S. Edwards, A. P. Shreve and S. W. Graves, Anal. Chem., 2017, 89, 9967–9975.
59. A. Raj, M. Dixit, M. Doble and A. K. Sen, Lab Chip, 2017, 17, 3704–3716.
60. E. D. Amir, K. L. Davis, M. D. Tadmor, E. F. Simonds, J. H. Levine, S. C. Bendall, D. K. Shenfeld, S. Krishnaswamy, G. P. Nolan and D. Pe'er, Nat. Biotechnol., 2013, 31, 545–552.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc00240a

---