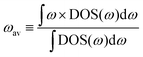Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning mobility and stability of lithium ion conductors based on lattice dynamics†
Sokseiha
Muy
a,
John C.
Bachman
b,
Livia
Giordano
 bc,
Hao-Hsun
Chang
d,
Douglas L.
Abernathy
bc,
Hao-Hsun
Chang
d,
Douglas L.
Abernathy
 e,
Dipanshu
Bansal
e,
Olivier
Delaire
ef,
Satoshi
Hori
g,
Ryoji
Kanno
g,
Filippo
Maglia
e,
Dipanshu
Bansal
e,
Olivier
Delaire
ef,
Satoshi
Hori
g,
Ryoji
Kanno
g,
Filippo
Maglia
 h,
Saskia
Lupart
h,
Peter
Lamp
h and
Yang
Shao-Horn
h,
Saskia
Lupart
h,
Peter
Lamp
h and
Yang
Shao-Horn
 *abd
*abd
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
cDipartimento di Scienza dei Materiali, Università di Milano-Bicocca, Milano 20125, Italy
dResearch Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
eMaterials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
fMechanical Engineering and Materials Science, Duke University, Durham, NC 27708, USA
gDepartment of Chemical Science and Engineering, School of Materials and Chemical Technology, Interdisciplinary Graduate School of Science and Engineering, Tokyo Institute of Technology, 4259 Nagatsuta, Midori, Yokohama 226-8502, Japan
hResearch Battery Technology, BMW Group, Munich 80788, Germany
First published on 20th February 2018
Abstract
Lithium ion conductivity in many structural families can be tuned by many orders of magnitude, with some rivaling that of liquid electrolytes at room temperature. Unfortunately, fast lithium conductors exhibit poor stability against lithium battery electrodes. In this article, we report a fundamentally new approach to alter ion mobility and stability against oxidation of lithium ion conductors using lattice dynamics. By combining inelastic neutron scattering measurements with density functional theory, fast lithium conductors were shown to have low lithium vibration frequency or low center of lithium phonon density of states. On the other hand, lowering anion phonon densities of states reduces the stability against electrochemical oxidation. Olivines with low lithium band centers but high anion band centers are promising lithium ion conductors with high ion conductivity and stability. Such findings highlight new strategies in controlling lattice dynamics to discover new lithium ion conductors with enhanced conductivity and stability.
Broader contextReplacing organic liquid electrolytes with solid lithium ion conductors in Li-ion batteries can boost the energy density and also increase battery safety. Current research and development of solid-state lithium ion batteries has been catalyzed by recent breakthroughs in solid lithium ion conductors that have ion conductivities rivaling those of conventional organic liquid electrolytes. However, known fast solid lithium ion conductors are not stable against lithium ion battery electrodes. Of significance, no fast lithium ion conductor known to date is stable against positive electrode materials in lithium ion batteries. Therefore, it is of great importance to design new lithium ion conductors having not only high Li conductivity but also being stable during battery operation. Increasing ion mobility and stability of lithium solid conductors is not straightforward and progress in the past decades has been achieved primarily by trial and error. Structural and chemical tuning via isovalent or aliovalent substitution of cation and/or anion in given structural families has led to steady increase in the lithium ion conductivity, and recent discovery of superionic lithium ion conductors. In this article, we report correlations between lattice dynamics and ion mobility or stability against electrochemical oxidation, and highlight opportunities to search for fast, stable lithium ion conductors based on low lithium band center but high anion band center. With rapid advances in the computational capability, we envision these descriptors to be used in high-throughput studies to screen not only lithium ion conductors but also other technologically relevant ion conductors such as oxygen or sodium ion conductors. |
Introduction
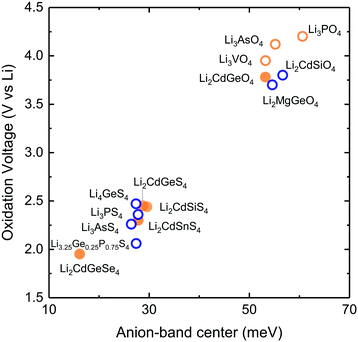
Replacing organic liquid electrolytes1,2 with solid lithium ion conductors in lithium ion batteries enables the use of the metallic lithium to markedly boost the energy density3,4 and also increases battery safety.5 Current research and development of solid-state lithium ion batteries has been catalyzed by recent breakthroughs in solid lithium ion conductors that have ion conductivities6–9 rivaling that of conventional organic liquid electrolytes.1 Although a number of structural families such as lithium superionic conductors (LISICON),10,11 garnets,12 NASICON-like (sodium superionic conductor),13 and perovskites14 have ion conductivities approaching that of liquid electrolytes, an increasing number of experimental15 and computational16,17 studies show that fast solid lithium ion conductors are not stable against lithium ion battery electrodes. Of significance, no known fast solid lithium conductors is stable against lithium ion positive electrode materials,16 highlighting critical needs to search for new lithium solid conductors with high lithium ion conductivity and stability.Increasing ion mobility and stability of lithium solid conductors is not straightforward and progress in the past decades has been achieved primarily by trial and error. Structural and chemical tuning via isovalent or aliovalent substitution of cation10,11 and/or anion18–20 in given structural families has led to steady increase in the lithium ion conductivity, and recent discovery of superionic lithium ion conductors.6–9 Recently a number of structure-based ion conductivity descriptors have been proposed to aid and accelerate the design of new superionic conductors including the volume of the unit cell10,13,21 the volume of lithium diffusion pathway,22 the anion in the structure,21 and the structure of the anion sublattices.23 For example, increasing lattice volume in the LISICON,10 NASICON-like,13 or perovskite14,21 structure can enhance ion conductivity and reduce activation energy.21 In addition, changing the anions by moving down in the periodic table (e.g. Li10GeP2X12, (X = O, S and Se)17 or Li3PX4 (X = O24 and S20)) and/or arranging anions in a body centered cubic lattice23 can increase lithium ion conductivity by reducing activation energy. Unfortunately, most of these descriptors have limited predictive power when applied across different structure families and chemistry of lithium ion conductors.21 Direct computation of Li-ion conductivity using ab initio molecular dynamics (AIMD) has also been pursued as a way to discover/design new materials with higher ionic conductivity.25,26 However, this method is computationally very demanding not to mention various practical limitations such as the need to extrapolate ionic conductivity from high temperature to room temperature. Moreover, no design principle is established for the stability of lithium solid conductors. Limited predictive power of reported conductivity descriptors and the lack of stability descriptor hampers the search for new lithium-ion conductors with enhanced conductivity and stability in order to meet all the requirements of solid-state lithium-ion batteries. In this article, we report a new approach to design lithium ion mobility and stability of lithium ion conductors using their lattice dynamical properties. We relate lithium ion mobility to lattice dynamics based on the following hypothesis: small energetic barrier for lithium ion migration (enthalpy of migration) is associated with large displacement amplitude from their equilibrium sites (Fig. 1a), rendering greater probability for lithium ions to explore multiple energy minima. Large excursions of mobile ions away from the equilibrium position are enabled in the soft atomic potential and also are associated with low phonon frequencies considering the Einstein model, where the amplitude of thermal displacement u of the ion is inversely proportional to the square of the frequency ωE using:27 〈|u|2〉 = 3kBT/mωE2, having kB, T and m denote the Boltzmann constant, temperature and the mass of the mobile species, respectively. In contrast, with a high migration barrier, the mobile species oscillate close to their equilibrium position with small thermal displacement amplitude and high frequency, and have low probability of hopping to adjacent sites. The hypothesis is supported by the following observations. The self-diffusion coefficient and the activation energy of metal atoms in body center cubic metal strongly correlate with the frequency of the longitudinal acoustic mode along the 〈111〉 direction (at reduced wavevector q = 2/3), being higher with lower frequency.28 Second, the computed migration enthalpy of oxygen diffusion via interstitialcy in rare-earth Ruddlesden–Popper phases shows strong positive correlation with reduced (more negative) force constant of the soft mode associated with the rotation of AO6 octahedra (A = rare-earth metal ions).29 Third, Wakamura has shown that the activation energy in Ag+, Na+ Cu+ and F− superionic conductors decreases with decreasing frequency of low-energy optical mode30 supporting the idea that low phonon frequency can be associated with high probability of ions hopping to the neighboring sites.21
 | ||
| Fig. 1 (a) Schematic of the energy landscape of lithium ions in lithium ion conductors. The potential energy as a function of the migration pathway distance, where the minima correspond to the equilibrium positions while the maxima correspond to the bottleneck or transition state, where lithium ions come to be the closest to anions (b) low-temperature (LT) structure of LISICON (space group Pmn21). (c) High-temperature (HT) structure of LISICON (space group Pnma), where lithium and phosphorus occupy the tetrahedral interstices, leaving all the octahedral sites empty, within the distorted hexagonal oxygen sublattice. All the LiO4 tetrahedra point in the same direction in LT-Li3PO424 while LiO4 tetrahedra of HT-Li3PO424 point in the two opposite directions. (d) Room-temperature ionic conductivity of some representative LISICON included in this study (Li3PO4-Pnma,24 Li3PS4-Pmn21,20 Li3.4Ge0.4P0.6O4-Pnma,10 Li3.25Ge0.25P0.75S4-Pnma18 and Li10SnP2S12-P63/nmc8). | ||
We elected to study a series of lithium ion conductors in the LISICON family derived from Li3PO4, to test the hypothesis that their lattice dynamics can greatly influence lithium ion mobility and stability. Lithium ion conductivity can be increased by up to 15 orders of magnitude10,11,18,20,21via cation and anion substitutions in this structural family relative to Li3PO4 (Fig. 1d). We also included Olivine structure which has the same (distorted) hexagonal close packed of anion sublattice as the LISICON compounds but differ in occupancy of Lithium ions which are located in octahedral sites as opposed to tetrahedral sites in LISICON structure. Although substitution (doping) and defects may alter migration pathway and mechanism and the activation energy, we have selected lithium ion conduction in LISICON and Olivine, having similar one-dimensional channels of Li ions within hexagonal anion sublattice. Previous work has shown that in Olivine, these one-dimensional channels serve as the dominant pathway for lithium migration and govern ion conduction in this structure.50 In Lisicon, although the diffusion pathway is three-dimensional,31 previous study has shown that the enthalpies of vacancies migration along each crystallographic direction are very similar and on the order of 0.7 eV in both γ-Li3PO4 and β-Li3PO4.32 It should be mentioned that depending on the concentration of mobile specie, the dominant diffusion mechanism might be interstitial instead of vacancy diffusion considered here. Nevertheless, we believe that the trends that we propose here remain valid as long as one considers the same mechanism with similar diffusion pathway regardless of the compound chemistries and structures. Isovalent substitution of oxygen by sulfur anion can enhance the ionic conductivity by six orders of magnitude, having reduced activation energy from 1.324 to 0.52 eV,20 and additional four orders of magnitude by aliovalent substitution of phosphorus by germanium, with decreasing activation energy from 0.52 to 0.21 eV.18 In this work, we systematically study the lattice dynamics of LISICONs derived from Li3PO4 by measuring the phonon density of states (DOS) of 17 compounds and one olivine compound as well as computing the phonon DOS of more than 20 compounds which are isostructural to LISICON and 6 olivines. The reader is referred to the Table S1 in (ESI†) for a complete list of compounds included in this study. From these data, combined with the measured activation energy, computed enthalpy of lithium ion migration of LISICONs and computed potential for electrochemical oxidation, the descriptors for lithium ion mobility and stability for oxidation were proposed.
Experimental and computation methods
All phonon DOS measurements were made at the Wide-angular range chopper spectrometer (ARCS) at the Spallation Neutron Source at Oak Ridge National Labs. Approximately 5 g of the samples were packed into aluminum canisters, which were sealed with a vanadium ring, unless spectra at elevated temperatures were measured where a qualitative (aluminum on aluminum) seal was used. All samples were sealed under argon. Temperatures were varied from 10 K to 600 K for select samples. Unless otherwise noted, the samples were measured at 100 K. The incident neutron energies were varied between 60, 100, and 200 meV. The resulting data were analyzed using the Mantid DGS Reduction package. For oxides, the background fraction was set as 1, the fraction of the total scattering to subtract as a constant background was 0.0–0.25 unless otherwise noted, the cutoff for the elastic peak removal was set as 10 meV, 3 bins after the cutoff were averaged to get the value of the density of states near the cutoff, the estimate of the Debye cutoff and the limit on the energy range were set depending on the calculated phonon density of states and where the last feature in the experimental density of states was noted (these parameters were used to remove any high energy background), and the range in wave vector that was used was from 7–12 Å−1. For sulfides, the parameters were the same except the range of wave vectors used was from 4–9 Å−1.For computations, we used density functional theory based on the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation33 as implemented in the VASP package.34 The core electrons were treated within the Projector Augmented Wave (PAW) method.35 Migration barriers for a lithium ion hopping were calculated using the climbing-image nudged elastic band method36 in a 2 × 2 × 1 supercell for LISICON (space group Pnma) while for the LISICON (space group Pnm21), a 2 × 2 × 2 supercell was employed. A 2 × 2 × 2 k-point grid was used and the cutoff of the kinetic energy was set to the default values as set in the pseudopotential files. For phonon calculations, the same supercells were used with finer k-point grid (3 × 3 × 3) and a higher energy cutoff (520 eV) in order to obtain more accurate values of the force. We have also used a higher cut-off energy of 700 eV for phonon DOS calculations but haven’t found any significant change (Fig. S1, ESI†) indicating that phonon DOS calculations are already well converged at 520 eV of cut-off energy. We have also tested LDA functional for phonon DOS calculations and found that the main effect of is to shift all the modes especially the high-energy feature in the DOS to higher frequencies resulting in an upward shift of band center (Fig. S1, ESI†) in agreement with previous study.37 However, the magnitude of the shift is small and fairly constant across different chemistries and crystal structures suggesting that LDA functional will result in a rigid shift to slightly higher energy but will not affect the trend. Finite displacement method was used for phonon calculations and the total as well as the atom-projected DOS were extracted using the phonopy package.38
To quantify the average vibrational frequency of a given material, we defined the ‘phonon band center’ which is the phonon frequency weighted by the DOS. Mathematically, it is written as:
If we replace DOS(ω) in this expression by the total phonon DOS, we obtain what we called ‘total phonon band center’. Similarly, if we replace DOS(ω) by one of the atom-projected DOS for instance Li-projected DOS, we obtain the ‘Lithium phonon band center’ which can also be viewed as the centroid of the Li-projected phonon DOS. The stability windows were computed following the method proposed by Richard et al.16 using the data from Materials project database39 and Pymatgen software package.40 The stability window was computed by constructing the grand potential phase diagram and varying the chemical potential of Li until the grand potential of the electrolytes were above the convex hull.41 Measured phonon DOS of 17 LISICON and LISICON-like compounds can be found in Fig. 2–4 and Fig. S2 (ESI†), computed phonon DOS of some of these compounds and additional LISICONs available in the ICSD can be found in Fig. 2 and Fig. S3 (ESI†). The measured phonon band centers (100 K) was in excellent agreement with computed values for 7 stoichiometric LISICONs, one substituted LISICON Li3.25Ge0.25P0.75S4 (chemically similar to Li10GeP2S12) and Li4GeO4 (Cmcm), as shown in Fig. 3. A systematic red shift of the computed total band center with respect to the measured total band center can be partially attributed to a well-known issue of overestimated lattice parameters associated with GGA functional (PBE)33 relative to measured values, giving rise to softening of high-energy modes and thus the total phonon band center.
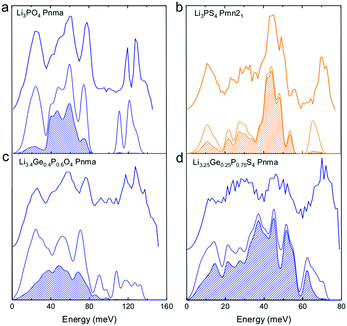 | ||
| Fig. 2 Measured phonon DOS and computed total and lithium-projected phonon DOS. Experimental phonon DOS collected at 100 K are shown on top while computed phonon DOS at 0 K on the bottom as well as the computed lithium-projected DOS (shaded). (a) Li3PO4 (Pnma) (b) Li3PS4 (Pmn21) (c) Li3.4Ge0.4P0.6O4 (Pnma) and (d) Li3.25Ge0.25P0.75S4 (Pnma). The measured phonon DOS data were obtained after background correction, optimizing lower and higher energy cut-off and details can be found in Fig. S4 (ESI†). The computed DOS were weighted by neutron scattering cross section of the different elements that make up the structures. The details of this procedure can be found in previous work.67 | ||
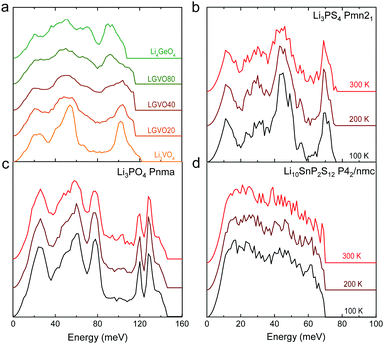 | ||
| Fig. 4 Measured phonon DOS as function of aliovalent substitution and temperature. (a) Measured phonon DOS of the series Li3+xGexV1−xO4 (x = 0, 0.2, 0.4, 0.8 and 1) (abbreviated as LGVO20, LGVO40 and LGVO80 for x = 0.2, 0.4 and 0.8 respectively) measured at 100 K. (b) The phonon DOS of Li3PS4 (Pnma) measured at 100, 200 and 300 K, which shows marked broadening at ∼50 meV. (c) The phonon DOS of Li3PO4 (Pnma) measured at 100, 200 and 300 K, which shows little variation with temperature. (d) The phonon DOS of Li10SnP2S12 that are featureless measured at 100, 200 and 300 K. The measured phonon DOS data were obtained after background correction, optimizing lower and higher energy cut-off and details can be found in Fig. S4 (ESI†). | ||
Results and discussions
Influence of chemical substitution and temperature on phonon DOS of lithium conductors
Cation and anion substitutions in the Li3PO4 structural family were shown to induce systematic changes by examining measured phonon DOS of 17 LISICON-like compounds and computed phonon DOS of 20 LISICONs. The measured and computed phonon DOS of Li3PO4 (Pnma), Li3PS4 (Pnm21), Li3.4Ge0.4P0.6O4 (Pnma) and Li3.25Ge0.25P0.75S4 (Pnma) are shown as example in Fig. 2a–d, and those of the other LISICON-like compounds can be found in Fig. 4 and Fig. S2, S3 of the (ESI†). The phonon DOS measured at 100 K (the upper spectrum of each panel in Fig. 2) is in quantitative agreement with the DOS computed from DFT at 0 K (the lower spectrum). Substitution of oxygen by sulfur led to significant softening of phonon modes. Li3PO4 (Pnma) in Fig. 2a and Li3.4Ge0.4P0.6O4 (Pnma) in Fig. 2c were found to have higher energy phonon DOS than Li3PS4 (Pnm21) in Fig. 2b and Li3.25Ge0.25P0.75S4 (Pnma) in Fig. 2d. Similar lattice softening were found for other sulfides relative to oxides in Fig. S2 and S3 (ESI†). Contribution from lithium ion vibrations (lithium-projected phonon DOS) in the measured total phonon DOS was identified by comparison with the computed atom-projected DOS, as shown in Fig. 2 and Fig. S3 (ESI†). Generally speaking, the computed phonon DOS of LISICONs show that low-energy, mid-energy and high-energy features originate mainly from the vibrations of anion sublattice, lithium sublattice and anion units involving non-mobile, structural cations (Fig. S3, ESI†) such as PO4, respectively. Of significance, Li3PO4 (Pnma) was found to have phonon DOS peaks in the range from 40–70 meV, which primarily came from lithium ion vibrations, as shown in Fig. 2a and Fig. S3 (ESI†). Substituting oxygen in Li3PO4 (Pnma) by sulfur to form Li3PS4 (Pnma and Pnm21) led to a downshifting (softening) of lithium ion vibrations from 40–70 meV to 40–50 meV (Fig. 2b and Fig. S2, S3, ESI†).Aliovalent cation substitution induces broadening of features in the phonon DOS, without significant softening. Phonon peaks, including the peak that primarily came from lithium ion vibrations in the range from 40–70 meV, was broadened systematically with increasing Ge substitution in Li3+xGexV1−xO4, where x = 0, 0.2, 0.4, 0.8 and 1 (Li3VO4, LGVO20, LGVO40, LGVO80 and Li4GeO4) in Fig. 4a. Similar broadening of lithium phonon DOS was observed for Li3.4Ge0.4P0.6O4 (Pnma) and Li3.25Ge0.25P0.75S4 (Pnma) upon substituting P with Ge in Li3PO4 (Pnma) and Li3PS4 (Pnm21), respectively, as shown in Fig. 2. On the other hand, isovalent cation substitution by heavier ions such as replacing P with V in Li3PO4 (Fig. S5a, ESI†) led to minimal downshifting of lithium band center but large downshifting of high-energy phonon modes involving non-mobile, structural cations, to the extent which shared similar energy to lithium phonon DOS in the case of sulfides (Fig. S5b, ESI†). Therefore, the broadening of lithium ion vibrations can be attributed to increasing disorder by introducing defects into the LISICON structure42 such as increasing partial occupancy in the lithium sublattice. This hypothesis is supported by marked broadening of lithium phonon modes observed for Li3PS4 upon increasing temperature from 100 K to 300 K while remaining phonon DOS features of less mobile PS4 units in Li3PS4 showed negligible changes, as shown in Fig. 4b. This broadening can be explained by greater lithium partial occupancy and large displacement amplitudes (anharmonicity)42 of lithium ions in Li3PS4 as expected from its low migration barrier (∼0.5 eV), in agreement with the concept discussed in Fig. 1a. Further support came from the observation that no broadening of lithium vibration modes at ∼50 meV was noted for Li3PO4 (Fig. 4c), since the partial lithium occupancy (or mobile lithium ion concentration) is low (∼2.05 × 108 cm−3 at 300 K using lithium vacancy formation energy of ∼1.7 eV),43 and small displacement amplitudes. Furthermore, Li10SnP2S12 (isostructural to Li10GeP2S12), with disordered lithium sublattice and liquid-like lithium ion conductivity at room temperature,8 was found to have phonon DOS so broadened that no peak feature was visible, which did not change upon heating from 100 to 300 K, as shown in Fig. 4d.
Correlation between Li-band center and enthalpy of migration
Softening of phonon DOS for LISICONs was found to correlate with decreasing measured activation energy for lithium ion conductivity. Increasing temperature has negligible influence on this phonon band center, which is supported by temperature-dependent phonon DOS in Fig. 4b and c, showing no softening of phonon frequencies with increasing temperature. Downshifting the total phonon band center was shown to markedly lower measured activation energy of stoichiometric LISICONs, as shown in Fig. 5a. Replacing oxygen with sulfur from Li3PO4 (Pnm21) to Li3PS4 (Pnm21) led to the largest downshift of the total phonon band center from ∼70 to ∼40 mV, which was correlated with reduction of activation energy from 1.4 eV24 to 0.5 eV20 in Fig. 5a. Measured activation energy of Li3PO4 (Pnma), Li3VO4 (Pmn21), Li3.4Ge0.4P0.6O4 (Pnma) and Li3+xGexV1−xO4 (x = 0.2, 0.4, 0.6 and 1) obtained in this study are in agreement with previous EIS measurements.10,24,44,45 As the measured activation energy of stoichiometric LISICONs consists of both enthalpy of defect formation and enthalpy of migration, such a correlation for stoichiometric LISICONs does not explicitly imply lowered lithium migration barrier with softening of the total phonon band center. We further show that the measured activation energy for 8 substituted LISICONs with partial lithium occupancy, which corresponds largely to lithium ion migration enthalpy, was decreased with softening of the total phonon band center. Li3.4Ge0.4P0.6S4 (P62/nmc) and Li3.25Ge0.25P0.75S4 (chemically similar to Li10GeP2S12), Li10SnP2S12 (P62/nmc)8 were found to have the lowest activation energy of ∼0.25 eV comparable to best superionic conductors6–9 with the lowest measured total band centers of ∼40 meV. Another interesting observation that we can draw from Fig. 5a is the clear separation between stoichiometric and non-stoichiometric compounds which follows two distinct trend lines whose difference is essentially related to the enthalpy of defect formation. It is well-known in perovskites that the enthalpy of migration of oxygen ions decreases with decreasing enthalpy of vacancy formation.46 Although, in this study, we do not consider the energetic of lithium defect formation energy, in light of the data shown in Fig. 5a, one might hypothesize that the enthalpy of Lithium defect formation might also correlate with phonon band center.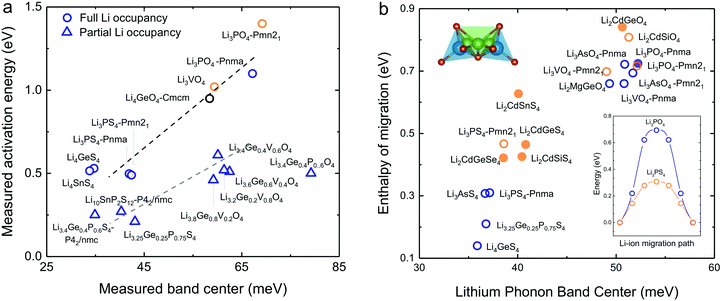 | ||
| Fig. 5 (a) Comparison between measured activation energy and measured (total) band center of 7 stoichiometric LISICONs and Li4GeO4 (Cmcm), where the activation energy contains contribution from the enthalpy of defect formation and migration enthalpy, and 8 substituted LISICONs with partial occupancy, where the activation energy is essentially the enthalpy of migration. The activation energy were measured using electrical impedance spectroscopy (EIS) (Fig. S6, ESI†), and are consistent with prior work Li3PO4 (Pnma),24 Li3VO4 (Pmn21),44 Li4GeO4 (Cmcm),45 and Li3+xGexV1−xO4 (x = 0.2, 0.4, and 0.6).10 Activation energy of Li3PS4 (Pnm21 and Pnma),20 Li4GeS4,19 Li4SnS4,68 and Li10SnP2S12 (P42/nmc)8 was taken from previous work. The blue and orange colours refer to the HT phase (space group Pmna) and the LT phase (space group Pmn21), respectively. (b) Correlation between computed enthalpy of migration and oxidation potential with computed phonon band center. The computed enthalpy of migration of 15 stoichiometric LISICONs known in the ICSD and 2 computed structures correlated well with the computed lithium band center at 0 K. | ||
As the total phonon band center can be weighted considerably for the vibrations of non-mobile species such as structural cations and anions, we further sought correlations between the band center of lithium-projected phonon DOS and activation energy. In addition, we computed the enthalpy of migration, which would allow us to systematically examine both stoichiometric LISICONs without partial occupancy and substituted LISICONs with partial occupancy. The downshifting of lithium phonon band center or average lithium ion vibration frequency was found to correlate with reduced migration barrier and thus greater lithium mobility, supporting the hypothesis described in Fig. 1a. Lithium ion migration enthalpy, which was defined as the difference between transition state energy and that of the initial/final configuration, was computed using nudge elastic band (NEB) calculations.36 Identical jump sequence along the diffusion pathway shown in Fig. 5b inset was used to compute the enthalpy of lithium ion migration even though this jump sequence might not be associated with the lowest migration enthalpy. In addition to 7 stoichiometric LISICON and one substituted LISICON in Fig. 3, we included 8 others stoichiometric LISICONs in the inorganic crystal structure database (ICSD) in Fig. 5b, which represent all stoichiometric LISICONs (excluding those containing transition metals) and two computed structures (Li2CdSiS4 and Li2CdGeSe4) to complete the series of Li2CdXS4 (X = Si, Ge and Sn) and Li2CdGeY4 (Y = O, S and Se). Decreasing computed lithium band center of 17 stoichiometric LISICONs and one substituted LISICON Li3.25Ge0.25P0.75S4 (chemically similar to Li10GeP2S12) was shown to markedly reduce the lithium ion enthalpy of migration of stoichiometric LISICON (computed) and Li3.25Ge0.25P0.75S4 (measured activation energy) from ∼0.85 to ∼0.15 eV, as shown in Fig. 5b. In contrast, the correlation with the computed ligand band center (Fig. S7a, ESI†) and total band center (Fig. S7b, ESI†) was poor. Similar to the trend of total band centers (Fig. 5a), replacing oxygen with sulfur had the largest influence in downshifting the lithium band center and decreasing enthalpy of lithium ion migration. The softening from ∼50 meV for Li3PO4 (Pnma) to ∼37 meV for Li3PS4 (Pnma) was correlated with a large drop in the migration barrier from ∼0.7 eV to ∼0.3 eV. Of significance, Li3.25Ge0.25P0.75S4 (chemically similar to Li10GeP2S12) were found to have the lowest measured (Fig. 5a) and computed enthalpy (Fig. 5b) of lithium ion migration of ∼0.2 eV, which is comparable to that of conventional liquid electrolytes used in lithium ion batteries1 and fast lithium ion conductors such as Li7P3S11,9 Li10GeP2S12,6 or Li9.54Si1.74P1.44S11.7Cl0.3.7 The softened or low average lithium vibration frequency and low migration barriers found for fast lithium conductors in this study, which would facilitate more frequent successful hopping of lithium ions also favor concerted hopping47 of lithium ions as opposed to isolated jumps in conventional ionic conductors. Therefore, computed lithium band center or the average lithium vibration frequency is proposed as one descriptor for lithium ion mobility for LISICONs and other lithium ion conductors.
Correlation between anion-band center and oxidation potential
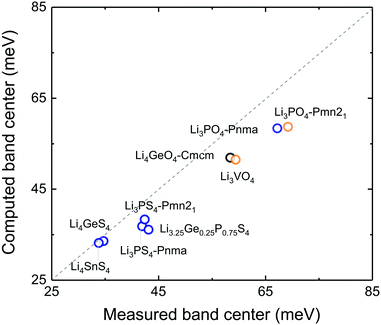
Lowering the anion phonon band center was found to greatly reduce the stability of these LISICONs against electrochemical oxidation, as shown in Fig. 6. The oxidation potential was defined as the potential above which LISICONs will be oxidized electrochemically by lithium ion removal from the lattice, which was computed using a thermodynamic approach as reported by Richards et al.16 Replacing oxygen with sulfur in the LISICON structure had the largest downshift of the anion phonon band center and largest reduction in the oxidation potential. While oxidative stability can be understood in term of electronic structures of the electrolytes which correlate with the thermodynamic driving force to oxidize the materials,41 the correlation between the oxidation potential and the anion band center shown in Fig. 6 might be kinetics in origin as lowering anion band center will make anion sublattice more mobile, thus lowering the kinetic barrier for the (decomposition) reactions. Moreover, the stability of a compound can be governed by kinetic properties (migration barriers) and thermodynamics properties. Well-known principles of understanding/controlling kinetics based on thermodynamics include the Evans–Polanyi principle or linear free energy relation, which relates the activation energy of chemical reactions (kinetics property) to the enthalpy of reactions (thermodynamics property). We believe that the correlation between the oxidation potential and anion band center is another instance of this type of ‘kinetic–thermodynamic’ relationships, which is thought in the following ways: as Li-band centers correlate with the enthalpy of lithium migration we argue that lowering the anion-band centers correlate with smaller enthalpy of anion migration (kinetic property), which promotes the kinetics of reactions. This kinetics property, by the Evans–Polanyi principle, correlates with oxidative stability (thermodynamic property) as measured by the oxidation potential. We recognize that more studies are needed to substantiate this idea. Nevertheless, we believe that this work will spur interests from the community to further explore this concept and its potential implications. Softening of the anion band center from Li3PO4 (Pnm21) to Li3PS4 (Pnma) by ∼30 meV is accompanied with reduction of the oxidation potential from ∼4 to ∼2.5 V vs. lithium. The computed oxidation potential of Li3PO4 (Pnm21) and Li3PS4 (Pnma) are in agreement with previous computation.16,17 The computed oxidation potential of Li3.25Ge0.25P0.75S4 is 0.21 V vs. lithium, which is close to the measured oxidation potential of chemically similar Li10GeP2S12.48 In addition, the oxidation potential of LISICONs was found to correlate strongly with computed anion band center (goodness of fits R2 = 0.97) and to a lesser extent with lithium band center (goodness of fits R2 = 0.92, Fig. S8a, ESI†) and total band center (goodness of fits R2 = 0.93, Fig. S8b, ESI†). There was no correlation between the reduction potential and the phonon band centers (Fig. S8c–e, ESI†), whose physical origin requires further studies. We also seek correlation between oxidation potential and oxygen/sulphur p-band center which have been used to understand the stability of perovskites under oxygen evolution reaction condition.49 However, as can be seen from Fig. S9a and b (ESI†), there is no clear correlation between p-band center and the oxidation potential or the anion band center although we can note that the oxidation potential is largely determined by the anion chemistry (oxides vs. sulfides) as reported previously in the literature41 and that oxides tend to have lower anion p-band center than sulfides as expected. It should be noted that the absence of correlation might also be due, at least partly, to the uncertainty in the computed p-band center arising from the underestimation of DFT band gap in these insulating compounds.33 Therefore, the anion band center is proposed as one descriptor for electrochemical oxidation stability of lithium ion conductors.Of significance, fast lithium ion conductors18 based on LISICONs such as Li3.25Ge0.25P0.75S4 have low enthalpy of lithium ion migration and softened lithium phonon DOS, which is accompanied with downshifted anion band center (Fig. S8f, ESI†). The correlation between lowered migration barrier with softened average lithium vibration frequency in Fig. 5b, and that between lowered oxidative stability with softened average anion vibration frequency in Fig. 6 highlight a trade-off between lithium ion mobility and oxidation stability for the design of lithium ion conductors. Moreover, extending the concept in Fig. 1a to anion mobility, lowered anion band centers can be accompanied by increased anion mobility, which can promote any solid-state reaction kinetics with electrode materials. Therefore, the interplay between lattice dynamics and ion mobility and stability highlights the need and opportunities to search for fast lithium ion conductors having low lithium band center but high anion band center which exhibit high ion conductivity and high oxidative stability in lithium ion batteries.
Overcoming the trade-off between mobility and stability
In search of lithium ion conductors with such lattice dynamics characteristics, we further examine Olivines that have the same hexagonal anion sublattice as the LISICON structure (Fig. 7c). The computed enthalpy of lithium ion migration and lithium band center for all the stoichiometric Olivines without transition metal ions listed in the ICSD (except LiCdPO4, LiScGeO4 and LiTmSiO4) are included in Fig. 7a, which demonstrates lithium band center as descriptor for lithium ion mobility in the two structural families (LISICONs and Olivines). Olivines, exhibit low lithium band centers and migration barriers comparable to that of LISICON thiophosphates (Fig. 7a) but high anion band centers comparable to those of LISICON phosphates (Fig. 7b). Computed migration barriers of Olivines studied here such as LiMgPO4 are comparable to those of other Olivine materials such as LiMPO4 (M = Mn, Fe, Co and Ni, 0.1–0.4 eV)50 and LiMXO4 (main group M2+–X5+, M2+–X5+; M = Mg, Ca, Sr, Ba, Sc, Y, Al, In, Ga and rare-earth elements; X = Si, Ge, Sn, P, As and Sb).51 In addition, the computed migration barrier (∼0.3 eV) of LiMgPO4 is in good agreement with NMR measurements for the site-to-site hopping (0.3–0.5 eV).52 Generally speaking, while compounds having high Li conductivity tend to have low stability, Olivine family was found to be an exception to this trend, which was rationalized in terms of the low Li-band center but high anion band center in these compounds (Fig. 7b). For example, new compositions such as LiMgAsO4 and LiInGeO4 could potentially have high ion conductivity (Fig. 7a) and stability (Fig. S10, ESI†). Unfortunately, the one-dimensional nature of diffusion pathway in the olivine structure makes it prone to anti-site defects which can result in an apparent activation energy much higher than the intrinsic migration barrier.53 For example, the long-range diffusion barrier measured by EIS for LiMgPO4 is 0.7–1.0 eV in previous work52 and also in this study, much higher than the intrinsic migration barrier (∼0.3 eV). Further studies are needed to increase the long-range ion conductivity of these Olivines by reducing anti-site defects using smaller particle sizes54 and/or having Li-excess in the lattice,55 which would potentially lead to the development of lithium superionic conductors with high stability against electrochemical oxidation.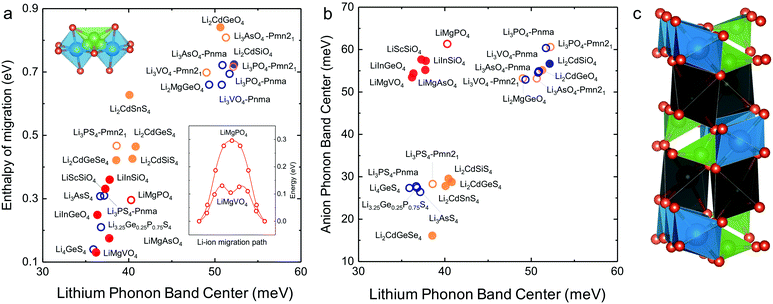 | ||
| Fig. 7 (a) Correlation between computed Li-band center and the computed enthalpy of migration including the Olivine structure. (b) Anion band centers and Li-band centers of Olivine compounds compared to LISICON compounds. (c) The Olivine is closely related to the LISICON structure by the fact that both have hexagonal anion sublattice but Li occupy octahedral interstice in Olivine unlike tetrahedral sites in LISICON. The jump sequence used to compute the migration barrier as well as the minimum energy pathway associated with this jump sequence in Olivine are shown in the inset. The enthalpy of migration in olivine was found to be lower than in LISICON. All the computed enthalpies of migration were calculated using the standard climbing image nudge elastic band method36 and the phonon band center is defined as the average phonon frequency weighted by phonon DOS. The blue and orange colours refer respectively to the HT phase (space group Pmna) and the LT phase (space group Pmn21), respectively while the red colour refers to the Olivine compounds. The filled circles are compounds that are known in the ICSD and/or computed in this work, where the lithium ion conductivity has not been measured experimentally. For more details, please refer to Table S1 (ESI†). | ||
Conclusion
In this study, we account for the first time, the trend in ionic mobility and electrochemical oxidation stability of lithium ion conductors from one common physical origin, lattice dynamics, or more precisely, atomic vibrational frequencies of ion conductor constituents, thus highlighting the critical role played by the lattice dynamics in governing the lithium ion conductivity and stability of lithium-ion conductors. Unlike previous studies on lattice dynamics in ion conductors (especially Ag+ conductors) which focus on the total phonon DOS (such low-energy peak in α-AgI phonon DOS) or zone-center phonons as measured from infrared and Raman spectroscopy,56,57 our study clarifies the influence of lattice dynamics on ionic conductivity by separating the effect of different sublattice and in particular the special role of the mobile species sublattice dynamics in the observed ionic mobility. The phonon DOS have been collected from a series of lithium conductors in the LISICON family using INS and computed by first-principles simulations to identify specific spectral features corresponding to the vibrations of sublattices involving lithium, anion and nonmobile structural cations. Replacing oxygen with sulfur greatly downshifts the lithium vibration frequencies while aliovalent cation substitution tends to broaden the lithium vibrational features in the phonon DOS. We show that low vibration frequencies of lithium ions correlate with enhanced lithium ion mobility in the LISICON and Olivine families, which can be used as one lithium ion mobility descriptor to predict new fast lithium conductors. Recent work on Argyrodite lithium conductors also showed the influence of lattice dynamics on the ionic conductivity.58 Future work is needed to define a more refined descriptor that would take into account not only the vibration frequency but also the vibrational pattern of each mode and weight in a way that reflects its importance to lithium diffusion as the measured and computed band centers or the average vibrational frequencies determined in this study do not explicitly take into account the specific vibration pattern of each mode. In addition, future experimental and computational studies should exploit the interplay between lattice dynamic and ion conductivity and stability for lithium ion conductors of different structural families21 beyond LISICON and Olivine. Moreover, further studies are needed to extend and examine the universality of such descriptors based on lattice dynamics to understand and potentially control ion mobility and stability of other ionic conductors such as Na+, Cu+ or O2− conductors. For example, copper sulfide (Cu2−xSe) with superionic Cu+ conductivity at room temperature is known to have low-energy phonon DOS and lattice thermal conductivity.59 Lattice dynamics was also found to play important role in the Na+ conductors Na3PS4−xSex60 as well as O2− conductors Nd2NiO4+δ61 and brownmillerites Sr(Fe,Co)O2.5.62 Lastly, although extensive database for material phonon DOS is not yet available due to high computational cost to compute phonon DOS, recent study has shown that it is possible to use a machine learning model to predict phonon-related properties such as vibrational free energy and entropy with high accuracy at a greatly reduced computational cost.63 Future advance in machine-learning computational material design represents an exciting opportunity to use this approach to explore more compositional space and to discover new ion conductors.64–66Author contributions
S. M., Y. S.-H. and J. C. B. proposed the concept. J. C. B. and H.-H. C. prepared the oxide materials. R. K. provided the sulphides samples. S. M., J. C. B., D. B. and O. D. performed the phonon DOS measurements and analysis. S. M. performed all the DFT calculations with L. G.'s help for the NEB calculations. S. M. and Y. S.-H. wrote the manuscript. All authors contributed to the discussion and revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research at MIT was supported by BMW. J. C. B. was supported in part from the National Science Foundation Graduate Research Fellowship (1122374) and H.-H. C. was in part supported from the Ministry of Science and Technology of Taiwan (102-2917-I-564-006-A1). D. B. acknowledges funding from the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under the Early Career Award No. DE-SC0016166 (P. I. Delaire). This work made use of the MRSEC Shared Experimental Facilities at MIT, supported by the National Science Foundation under award number DMR-0819762. The use of Oak Ridge National Laboratory's Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. DOE. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 and of the Extreme Science and Engineering Discovery Environment (XSEDE) which is supported by National Science Foundation grant number ACI-1548562.References
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef.
- W. Li, L. Chen, Y. Sun, C. Wang, Y. Wang and Y. Xia, Solid State Ionics, 2017, 300, 114–119 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 16030 CrossRef CAS.
- P. Bron, S. Johansson, K. Zick, J. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694–15697 CrossRef CAS PubMed.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631 CAS.
- A. Rodger, J. Kuwano and A. West, Solid State Ionics, 1985, 15, 185–198 CrossRef CAS.
- Y. Deng, C. Eames, B. Fleutot, R. David, J.-N. Chotard, E. Suard, C. Masquelier and M. S. Islam, ACS Appl. Mater. Interfaces, 2017, 9, 7050–7058 CAS.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- A. Martínez-Juárez, C. Pecharromán, J. E. Iglesias and J. M. Rojo, J. Phys. Chem. B, 1998, 102, 372–375 CrossRef.
- S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15, 3974–3990 CrossRef CAS.
- J. Auvergniot, A. Cassel, J.-B. Ledeuil, V. Viallet, V. Seznec and R. Dedryvère, Chem. Mater., 2017, 29, 3883–3890 CrossRef CAS.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2013, 6, 148 CAS.
- R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, A742–A746 CrossRef CAS.
- R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Solid State Ionics, 2000, 130, 97–104 CrossRef CAS.
- M. Tachez, J.-P. Malugani, R. Mercier and G. Robert, Solid State Ionics, 1984, 14, 181–185 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- M. Avdeev, M. Sale, S. Adams and R. P. Rao, Solid State Ionics, 2012, 225, 43–46 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- Y.-W. Hu, I. D. Raistrick and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1240–1242 CrossRef CAS.
- Z. Deng, B. Radhakrishnan and S. P. Ong, Chem. Mater., 2015, 27, 3749–3755 CrossRef CAS.
- Z. Deng, Z. Zhu, I.-H. Chu and S. P. Ong, Chem. Mater., 2017, 29, 281–288 CrossRef CAS.
- M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, Cambridge, New York, 1st edn, 2005 Search PubMed.
- U. Köhler and C. Herzig, Philos. Mag. A, 1988, 58, 769–786 CrossRef.
- X. Li and N. A. Benedek, Chem. Mater., 2015, 27, 2647–2652 CrossRef CAS.
- K. Wakamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 11593–11599 CrossRef CAS.
- Y. Deng, C. Eames, J.-N. Chotard, F. Lalère, V. Seznec, S. Emge, O. Pecher, C. P. Grey, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2015, 137, 9136–9145 CrossRef CAS PubMed.
- Y. A. Du and N. A. W. Holzwarth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 174302 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- R. Wahl, D. Vogtenhuber and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104116 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 CAS.
- H. Böttger, Principles of the Theory of Lattice Dynamics, Physik-Verlag, 1983 Search PubMed.
- Y. Du and N. Holzwarth, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174301 CrossRef.
- K. M. Mishra, A. K. Lal and F. Z. Haque, Solid State Ionics, 2004, 167, 137–146 CrossRef CAS.
- I. M. Hodge, M. D. Ingram and A. R. West, J. Am. Ceram. Soc., 1976, 59, 360–366 CrossRef CAS.
- T. T. Mayeshiba and D. D. Morgan, Solid State Ionics, 2016, 296, 71–77 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, ncomms15893 CrossRef PubMed.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590 CrossRef.
- A. Grimaud, K. J. May, C. E. Carlton, Y.-L. Lee, M. Risch, W. T. Hong, J. Zhou and Y. Shao-Horn, Nat. Commun., 2013, 4, 2439 Search PubMed.
- D. Morgan, A. V. der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30–A32 CrossRef CAS.
- R. Jalem, T. Aoyama, M. Nakayama and M. Nogami, Chem. Mater., 2012, 24, 1357–1364 CrossRef CAS.
- L. Enciso-Maldonado, M. S. Dyer, M. D. Jones, M. Li, J. L. Payne, M. J. Pitcher, M. K. Omir, J. B. Claridge, F. Blanc and M. J. Rosseinsky, Chem. Mater., 2015, 27, 2074–2091 CrossRef CAS.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10, 4123–4127 CrossRef CAS PubMed.
- C. Delacourt, P. Poizot, S. Levasseur and C. Masquelier, Electrochem. Solid-State Lett., 2006, 9, A352–A355 CrossRef CAS.
- K.-Y. Park, I. Park, H. Kim, G. Yoon, H. Gwon, Y. Cho, Y. S. Yun, J.-J. Kim, S. Lee, D. Ahn, Y. Kim, H. Kim, I. Hwang, W.-S. Yoon and K. Kang, Energy Environ. Sci., 2016, 9, 2902–2915 CAS.
- R. Alben and G. Burns, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 3746–3752 CrossRef CAS.
- P. Brüesch, W. Bührer and H. J. M. Smeets, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 970–981 CrossRef.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425 CrossRef CAS PubMed.
- T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869 CrossRef CAS.
- A. Perrichon, A. Piovano, M. Boehm, M. Zbiri, M. Johnson, H. Schober, M. Ceretti and W. Paulus, J. Phys. Chem. C, 2015, 119, 1557–1564 CAS.
- W. Paulus, H. Schober, S. Eibl, M. Johnson, T. Berthier, O. Hernandez, M. Ceretti, M. Plazanet, K. Conder and C. Lamberti, J. Am. Chem. Soc., 2008, 130, 16080–16085 CrossRef CAS PubMed.
- F. Legrain, J. Carrete, A. van Roekeghem, S. Curtarolo and N. Mingo, Chem. Mater., 2017, 29, 6220–6227 CrossRef CAS.
- N. Nosengo, Nat. News, 2016, 533, 22 CrossRef CAS PubMed.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- L. Ward and C. Wolverton, Curr. Opin. Solid State Mater. Sci., 2017, 21, 167–176 CrossRef CAS.
- D. Bansal, J. Hong, C. W. Li, A. F. May, W. Porter, M. Y. Hu, D. L. Abernathy and L. Delaire, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 054307 CrossRef.
- G. Sahu, Z. Lin, J. Li, Z. Liu, N. Dudney and C. Liang, Energy Environ. Sci., 2014, 7, 1053 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee03364h |
| This journal is © The Royal Society of Chemistry 2018 |