Tracking particles with large displacements using energy minimization†
Rostislav
Boltyanskiy
a,
Jason W.
Merrill
 b and
Eric R.
Dufresne
b and
Eric R.
Dufresne
 *c
*c
aDepartment of Physics, Yale University, New Haven, Connecticut 06520, USA
bDesmos, Inc., San Francisco, California 94103, USA
cDepartment of Materials, ETH Zürich, 8092 Zürich, CH, Switzerland. E-mail: eric.dufresne@mat.ethz.ch
First published on 22nd February 2017
Abstract
We describe a method to track particles undergoing large displacements. Starting with a list of particle positions sampled at different time points, we assign particle identities by minimizing the sum across all particles of the trace of the square of the strain tensor. This method of tracking corresponds to minimizing the stored energy in an elastic solid or the dissipated energy in a viscous fluid. Our energy-minimizing approach extends the advantages of particle tracking to situations where particle imaging velocimetry and digital imaging correlation are typically required. This approach is much more reliable than the standard squared-displacement minimizing approach for spatially-correlated displacements that are larger than the typical interparticle spacing. Thus, it is suitable for particles embedded in a material undergoing large deformations. On the other hand, squared-displacement minimization is more effective for particles undergoing uncorrelated random motion. In the ESI, we include a flexible MATLAB particle tracker that implements either approach with a robust optimal assignment algorithm. This implementation returns an estimation of the strain tensor for each particle, in addition to its identification.
Introduction
In a wide range of pure and applied sciences, the motion of objects needs to be tracked over time. The central difficulty is that while an object's trajectory is continuous through space and time, its position can only be sampled at discrete moments. When the objects of interest are far away from each other or otherwise distinguishable, tracking is simple. However, when many identical objects (which we refer to as particles) are near each other, tracking can be difficult.Particle tracking is employed across physics, biology, and many other fields. In soft matter physics, it has shed light on mechanical properties like rheology,1 and revealed microscopic processes underlying phase transitions,2 among many other applications. In biology, particle tracking is used across many length scales from the movement of single molecules, to the transport of organelles within cells, to movement of whole organisms such as flies, birds, fish, and humans.3–6
In the absence of Brownian motion, particles embedded in a material reveal its deformation field. In fluid mechanics, particle tracking reveals flow fields in the Lagrangian frame of reference.7 Traction force microscopy (TFM) quantifies the forces applied to a solid surface by tracking and analyzing motion of particles embedded within the solid. TFM was originally developed to quantify the forces exerted by adherent cells,8 but has recently been applied to a wide range of problems in biology and physics.9
The standard method of particle tracking first locates particles at each time point and then assigns identities by minimizing the sum of squared displacements across time points.10 While this method is rigorously correct for objects undergoing Brownian motion, it works very well across a wide range of applications, provided that the particles move a distance that is small compared to the typical interparticle separation. The improvement of this basic tracking approach has been an active area of research in recent years, driven by applications in the biomedical community. For a useful comparison of these particle tracking approaches, see ref. 11. When the displacements are large, it is helpful to employ a tracking algorithm that exploits knowledge of the system's kinematics. For example, particle tracking in dense turbulent fluid flows has been greatly improved by employing a “predictive tracker,” which exploits the inertial character of high Reynolds number fluid flow.12
Particle Imaging Velocimetry (PIV) and Digital Imaging Correlation (DIC) are widely used to assess the flow of fluids and deformation of solids.13–15 These methods assign velocities or displacements to locations in a material by cross-correlating patches of an image across time points. This is a robust and successful approach, even for systems with large displacements. However, it is inappropriate in cases where individual particle identities need to be followed over time or where the displacements need to be known at the resolution of individual particles. In these cases, image correlation and particle tracking can readily be combined in a two-step process. First, image correlation can be used to calculate coarse-grained displacements. Then, the standard particle tracking algorithms can readily identify particles based on the residual displacements.9
Here, we present an algorithm that extends particle tracking to the large-displacement regime, without an image correlation step. Our algorithm is optimized for tracking the motion of particles undergoing large spatially-correlated displacements, typical for tracers embedded in a deformed elastic solid or a flowing viscous fluid. As a useful by-product, it provides estimates of the local strain for each particle. We start by posing the tracking problem generally, and review the maximum likelihood method employed to track Brownian particles. Then, we describe our energy minimization approach and directly compare the results of the two methods for simulated and real data.
Optimal assignment
Suppose a set of particles, {p(k)(ti)}, where k is the particle index, are found at locations {![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (k)(ti)} at time ti and a set of particles {p(k)(tf)} are found at {
(k)(ti)} at time ti and a set of particles {p(k)(tf)} are found at {![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (k)(tf)} at time tf. We wish to connect particle positions across time to make trajectories. The particle identities are represented by a list, T, where T(l) = m if particle p(l)(ti) at time ti becomes particle p(m)(tf) at time tf.
(k)(tf)} at time tf. We wish to connect particle positions across time to make trajectories. The particle identities are represented by a list, T, where T(l) = m if particle p(l)(ti) at time ti becomes particle p(m)(tf) at time tf.
We find an optimal assignment of identities by minimizing a cost function. We associate a cost, cl,m, to each possible particle pairing. The total cost, C, is the sum of the costs of individual pairings across all of the particles, 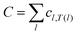 . We assign identities that minimize the cost using the robust and efficient Hungarian algorithm.16,17
. We assign identities that minimize the cost using the robust and efficient Hungarian algorithm.16,17
Since assigning particles is a combinatoric process, it rapidly becomes computationally overwhelming as the system size increases. While the Hungarian algorithm handles challenging combinatorics more effectively than previous implementations,10 it remains essential to limit the number of combinations by ruling out unphysical assignments, as described below.
Minimization of squared-displacements
The standard particle-tracking algorithm minimizes the sum of the squared displacements across all of the particles.10 This yields the most likely assignment of identities when particles undergo Brownian motion. In that case, the probability that the kth particle will be displaced by Δ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (k) in a time interval, Δt, is:
(k) in a time interval, Δt, is: | (1) |
Here, D is the diffusion coefficient and d is the number of spatial dimensions.18 Therefore, the probability of observing a specific set of displacements of N identical particles moving independently is:
 | (2) |
The most likely assignment of particle identities maximizes the total probability, P, which is equivalent to minimizing the total squared-displacement  . Therefore, one can optimally assign particle identities with a cost for each potential pairing, cl,m = |
. Therefore, one can optimally assign particle identities with a cost for each potential pairing, cl,m = |![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (l)(ti) −
(l)(ti) − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (m)(tf)|2.
(m)(tf)|2.
To accelerate the data analysis, one needs to rule out unphysical assignments. Typically, one specifies a maximum displacement a particle could have between time points, and assigns an infinite cost to all of the elements of c that correspond to displacements that would exceed this maximum. These elements are ignored in the combinatorial optimization.
In practice, minimizing the squared-distance works very well whenever particle displacements are small compared to the distance of a particle to its nearest neighbors.
Minimization of energy
In the case of large displacements, squared-distance minimizing trackers may not work effectively. Fortunately, however, these displacements often have strong spatial correlations. For example, particles embedded in a rigid material undergoing translation and rotation are fixed relative to their neighbors. Similarly, displacements of particles embedded in a liquid or solid undergoing large deformations are typically strongly correlated to their neighbors. In both of these cases, we do not wish to penalize displacements in the laboratory frame, but displacements relative to neighboring particles.In continuum mechanics, the variation of displacements over space is characterized by the strain. In the case of a linear, isotropic, elastic solid of Young's modulus, E, the stored energy is
 | (3) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) are the strain and displacement fields, respectively. In component form, these two are related as
are the strain and displacement fields, respectively. In component form, these two are related as  .19 Analogously, for a fluid of dynamic viscosity μ sheared with a strain rate
.19 Analogously, for a fluid of dynamic viscosity μ sheared with a strain rate  , the rate of energy dissipation is:20
, the rate of energy dissipation is:20 | (4) |
 only differ by a pre-factor.
only differ by a pre-factor.
Motivated by these two physical examples, we propose to assign particle identities by minimizing the stored/dissipated energy. The basic hypothesis is that tracking errors tend to exaggerate the strain/strain-rate, increasing the apparent stored/dissipated energy. Therefore, we implement a cost function cl,m = Tr(ε(l,m))2. The main challenge of the proposed algorithm is to identify the strain associated with a given particle pairing. Calculating the strain requires positions of particles and their nearest neighbors at two times.
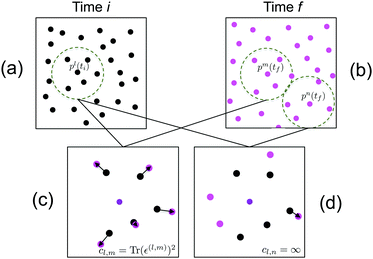
The neighbors of particle p(k), can be found in 2-D using the Delaunay triangulation. To ensure that the strain is uniform over the region where it is calculated, we only consider neighbors within a distance rmax of p(k). In Fig. 1(a and b), neighbors included in the strain calculation are within the dotted circles.
We use the method of Falk and Langer21 to calculate the strain associated with candidate particle pairs and their neighbors. The strain about a particle at position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) from the position of neighbors
from the position of neighbors ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (n) can be estimated as follows:
(n) can be estimated as follows:
 | (5) |
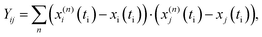 | (6) |
| Λij = XikYjk−1, | (7) |
 | (8) |
To properly calculate strain around a particle, one needs to accurately track its neighbors across time. Consider a particle at time ti, p(l)(ti) (in the center of the dotted circle in Fig. 1a) and a candidate corresponding particle at time tf, p(m)(tf) (in the center a dotted circle in Fig. 1b). To connect the neighbors of p(l)(ti) with those of p(m)(tf), we translate the candidate particles and their neighbors to the same location, as shown in Fig. 1(c and d). We then track the neighbors of the candidate pair by minimizing the square of the residual displacements. To accelerate the calculation, we rule out relative displacements that would exceed an expected maximum value of the strain. If the candidate pair produces at least d tracked neighbors, we calculate the strain for the candidate pairing according to eqn (8) and assign the pairing a cost cl,m = Tr(ε(l,m))2. Otherwise, the pairing is ruled out by setting the cost to infinity. Once all possible pairings have been assigned costs, the Hungarian algorithm is used to minimize the total cost across all of the particles.
Implementation of tracking algorithms
We implement the squared-distance-minimizing “diffusion tracker” and energy-minimizing “strain tracker” algorithms in MATLAB. In the ESI,† we include the main particle-tracking function, Tracker.m. We also include a script, Example.m, that allows the user to explore the examples described below. Details regarding use of the code are found in the comments as well as the text of ReadMe.pdf. A convenient by-product of our strain tracker is that it returns the symmetrized strain matrix for each tracked particle.Comparison of tracking strategies with simulated data
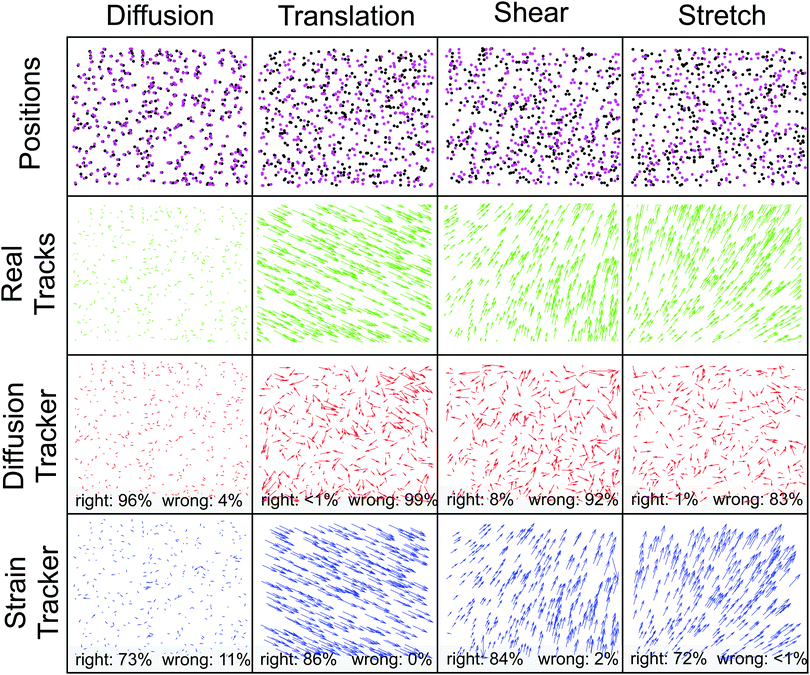
We compare the performance of the diffusion and strain trackers with simulated data. As shown in Fig. 2, we consider four types of particle motion: diffusion, translation, shear, and stretch. For each example, the first row of Fig. 2 shows the positions of particles at the first (black) and second (magenta) time points. The second row shows the correct displacement field in green. The third and fourth rows show the displacements determined by the diffusion tracker (red) and the strain tracker (blue).Not surprisingly, the diffusion tracker out-performs the strain tracker for the case of diffusion. For the example shown in the first column of Fig. 2, the diffusion tracker returns results for all of the particles. About 96% of these tracks are correct. On the other hand, the strain tracker provides correct identifications for only 73% of the particles, incorrect identifications for 11%, and no identification for 16%. These tracking errors impact quantitative measures of the particle motion. Even though the distributions of the particle displacements for the two trackers look similar, Fig. 3(a and b), tracking errors tend to introduce counts in the tails of the displacement distribution that have a significant impact on the mean-squared particle displacement (MSD). In this example, the MSD calculated from the diffusion tracker is within 2% of the correct value. However, the value calculated using the strain tracker is 30% greater than the correct value.
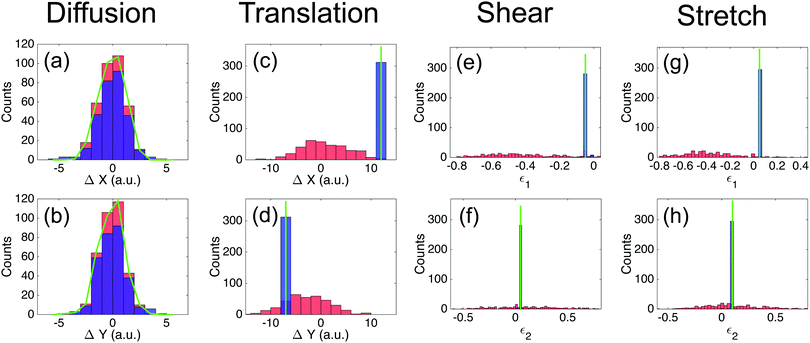 | ||
| Fig. 3 Histograms of individual particle displacements (a–d) and strain eigenvalues (e–h) from analysis of simulated data in Fig. 2. (a and b) are histograms of horizontal and vertical displacements, respectively, from simulated diffusion data. (c and d) are histograms of horizontal and vertical displacements, respectively, from simulated translation data. (e and f) are histograms of strain eignevalues from a simulated shear. (g and h) are histograms of strain eigenvalues from a simulated stretch. In all panels, results from the diffusion tracker are in red, those of the strain tracker are in blue, and the overlap is in purple. In green is an outline of the histogram of correct displacements in (a and b) and a vertical line corresponding to the correct values of displacements and strains in (c–h). | ||
On the other hand, for the cases of large displacements due to translation, shear, and stretch, the strain tracker is a much more reliable choice. For the remaining examples in Fig. 2, the diffusion tracker returns identifications for at least 84% of the particles, but returns correct identifications for no more than 8% of the total. On the other hand, the strain tracker returns indentifications for at least 74%, and nearly all of them are correct. Furthermore, the strain tracker's errors tend to be localized to the boundary of the field of view, which can be easily discarded when greater accuracy is required. The strain tracker not only accurately identifies particles, but it also correctly quantifies particle displacements and strains. The expected displacements and strains for the cases of translation, shear, and stretch are shown as vertical green lines in Fig. 3(c–h). The red histograms display the values for each particle returned by the diffusion tracker and the blue histograms report those from the strain tracker. The strain tracker consistently returns the correct values, while the incorrect tracks from the diffusion tracker return broadly distributed incorrect values.
In many applications, particles may exhibit a combination of large correlated displacements (e.g. due to flow) and uncorrelated random displacements (e.g. Brownian motion). We quantified the performance of both trackers for simulated Brownian particles in a fluid undergoing pure shear, varying the magnitude of the shear and the Brownian noise, as shown in Fig. 4. When the particle displacements due to either type of motion are small compared to the average interparticle spacing, 〈ri〉, they perform equally well. As the root-mean-squared magnitude of random displacements, η, is increased at a small value of the strain, both trackers start to make mistakes. While the strain-tracker maintains high fidelity up to η/〈ri〉 ≈ 0.1, the diffusion tracker maintains the same fidelity up to η/〈ri〉 ≈ 0.2.
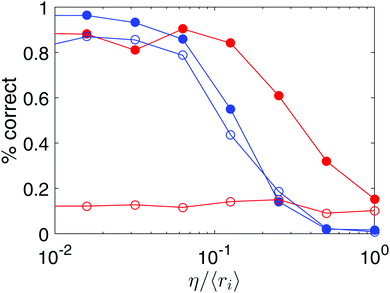 | ||
| Fig. 4 Mixture of random and correlated displacements. Percentage of particles correctly identified by the strain tracker (blue) and the diffusion tracker (red) in a pure shear deformation (as in Fig. 2, third column) as a function of superimposed random motion, quantified by the root-mean-squared magnitude of random displacements, η. Closed symbols are for a relatively small strain (ε ≈ 0.005), where the mean particle displacement is 0.13 〈ri〉. Open symbols are for a relatively large strain (ε ≈ 0.05), where the mean particle displacement is 1.13 〈ri〉. | ||
Comparison of tracking strategies with experimental data
In this section, we compare the diffusion and strain trackers with some experimental data.First, we assess both trackers' ability to identify particles during a relatively large and homogeneous strain. Here, we deform a silicone gel with embedded fluorescent tracers using a macroscopic deformation. We image the tracers over a small field of view, where we expect a reasonably uniform compression. We estimated the strain using a manually applied affine transformation to the particle locations, resulting in eigenvalues of −0.06 and −0.04. Then, we calculated particle displacements with the strain and diffusion trackers, as shown in Fig. 5(a and b). While both trackers return comparable results where the displacements are small (upper-left corner of the field of view), they disagree where the displacements are large. In this region, the diffusion tracker returns an uncorrelated displacement field, while the strain tracker returns the expected compression. Our strain tracker returns a strain tensor associated with the displacement of each tracked particle. Histograms of the strain eigenvalues of each particle are plotted in Fig. 5(c–f). For both trackers, the peaks of the histogram agree well with the expected values from the manual affine transformation. However, the diffusion tracker reports a much broader distribution, including some unphysical positive values.
Next, we consider an example from Traction Force Microscopy (TFM) where the strains have a much stronger spatial heterogeneity. In TFM, forces exerted by small objects, such as cells, are quantified by measuring the deformation of an elastic material they are adhered to. To quantify the deformation, fluorescent particles are embedded in the elastic material. Displacements caused by a fibroblast cell adherent to a silicone gel are presented in Fig. 5(g and h). The cell is fluorescently tagged and is displayed in inverted contrast. Overlaid on top of the cell image are displacements of the surface underneath the cell (scaled by a factor of 5), determined by the (g) the diffusion tracker and (h) strain tracker. While displacements measured by the strain tracker and diffusion tracker mostly agree, the diffusion tracker identifies some unexpected large strains near the center of the cell.
Conclusion
We have introduced a particle tracking algorithm based on the minimization of energy. This approach out-performs the conventional squared-displacement minimizing particle tracker when the displacements are larger than the interparticle spacing. On the other hand, our strain tracker may have difficulty when the strain changes significantly over the typical interparticle spacing. This can occur in the vicinity of strain singularities, such as cracks, and when particles are moving randomly, as in Brownian motion. Although, the code included in the ESI† is designed for two time points and two spatial dimensions, expanding to three dimensions and many time points is a straightforward modification. It may also be useful to combine the squared-displacement and energy minimizing approaches in order to handle systems with large correlated displacements and significant Brownian motion.Acknowledgements
We thank Madhusudhan Venkadesan, Katharine Jensen, and Robert Style for helpful discussions and support from the Army Research Office Multidisciplinary University Research Initiative (ARO MURI) W911NF-14-1-0403.References
- T. M. Squires and T. G. Mason, Fluid mechanics of microrheology, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- Y. Peng, Z. R. Wang, A. M. Alsayed, A. G. Yodh and Y. Han, Melting of multilayer colloidal crystals confined between two walls, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83(1), 011404 CrossRef CAS PubMed.
- R. Ardekani, A. Biyani, J. E. Dalton, J. B. Saltz, M. N. Arbeitman, J. Tower, S. Nuzhdin and S. Tavare, Three-dimensional tracking and behaviour monitoring of multiple fruit flies, J. R. Soc., Interface, 2013, 10(78), 20120547 CrossRef PubMed.
- A. D. Straw, K. Branson, T. R. Neumann and M. H. Dickinson, Multi-camera real-time three-dimensional tracking of multiple flying animals, J. R. Soc., Interface, 2011, 8(56), 395–409 CrossRef PubMed.
- Y. Katz, K. Tunstrom, C. C. Ioannou, C. Huepe and Iain D. Couzin, Inferring the structure and dynamics of interactions in schooling fish, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(46), 18720–18725 CrossRef CAS PubMed.
- M. Rodriguez, I. Laptev, J. Sivic, J.-Y. Audibert and IEEE, Density-aware person detection and tracking in crowds, 2011 IEEE International Conference on Computer Vision (ICCV), 2011, pp. 2423–2430 Search PubMed.
- H. T. Xu, N. T. Ouellette and E. Bodenschatz, Multifractal dimension of Lagrangian turbulence, Phys. Rev. Lett., 2006, 96(11), 114503 CrossRef PubMed.
- S. Munevar, Y. L. Wang and M. Dembo, Traction force microscopy of migrating normal and h-ras transformed 3t3 fibroblasts, Biophys. J., 2001, 80(4), 1744–1757 CrossRef CAS PubMed.
- R. W. Style, R. Boltyanskiy, G. K. German, C. Hyland, C. W. MacMinn, A. F. Mertz, L. A. Wilen, Y. Xu and E. R. Dufresne, Traction force microscopy in physics and biology, Soft Matter, 2014, 10(23), 4047–4055 RSC.
- J. C. Crocker and D. G. Grier, Methods of digital video microscopy for colloidal studies, J. Colloid Interface Sci., 1996, 179(1), 298–310 CrossRef CAS.
- N. Chenouard, I. Smal, F. De Chaumont, M. Maška, I. F. Sbalzarini, Y. Gong, J. Cardinale, C. Carthel, S. Coraluppi, M. Winter, A. R. Cohen, W. J. Godinez, K. Rohr, Y. Kalaidzidis, L. Liang, J. Duncan, H. Shen, Y. Xu, K. E. G. Magnusson, J. Jaldén, H. M. Blau, P. Paul-Gilloteaux, P. Roudot, C. Kervrann, F. Waharte, J.-Y. Tinevez, S. L. Shorte, J. Willemse, K. Celler, G. P. Van Wezel, H.-W. Dan, Y.-S. Tsai, C. O. De Solórzano, J.-C. Olivo-Marin and E. Meijering, Objective comparison of particle tracking methods, Nat. Methods, 2014, 11(3), 281–289 CrossRef CAS PubMed.
- N. T. Ouellette, H. T. Xu and E. Bodenschatz, A quantitative study of three-dimensional lagrangian particle tracking algorithms, Exp. Fluids, 2006, 40(2), 301–313 CrossRef.
- R. J. Adrian and J. Westerweel, Particle Imaging Velocimetry, Cambridge University Press, Cambridge, 2010 Search PubMed.
- B. Pan, K. Qian, H. Xie and A. Asundi, Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review, Meas. Sci. Technol., 2009, 20, 062001 CrossRef.
- E. Bar-Kochba, J. Toyjanova, E. Andrews, K.-S. Kim and C. Franck, A fast iterative digital volume correlation algorithm for large deformations, Exp. Mech., 2015, 55(1), 261–274 CrossRef.
- H. W. Kuhn, The Hungarian method for the assignment problem, Naval Research Logistics, 2005, 52(1), 7–21 CrossRef.
- Markus Buehren. Functions for the rectangular assignment problem. http://www.mathworks.com/matlabcentral/fileexchange/6543, 2004, accessed: 2016-09-01.
- H. C. Berg, Random Walks in Biology, Princeton University Press, Princeton, NJ, 1993 Search PubMed.
- L. D. Landau and E. M. Liftshitz, Theory of Elasticity, Butterworth-Heineman, Oxford, 1986 Search PubMed.
- P. K. Kundu and I. M. Cohen, Fluid Mechanics, Academic Press, Burlington, MA, 2008 Search PubMed.
- M. L. Falk and J. S. Langer, Dynamics of viscoplastic deformation in amorphous solids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57(6), 7192–7205 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm02011a |
| This journal is © The Royal Society of Chemistry 2017 |