Excitation of vibrational soft modes in disordered systems using active oscillation†‡
Elsen
Tjhung§
a and
Takeshi
Kawasaki
*b
aLaboratoire Charles Coulomb, UMR 5221, CNRS and Université Montpellier, Montpellier 34095, France
bDepartment of Physics, Nagoya University, Nagoya 464-8602, Japan. E-mail: kawasaki@r.phys.nagoya-u.ac.jp
First published on 12th May 2016
Abstract
We propose a new method to characterize the spatial distribution of particles' vibrations in solids with much lower computational costs compared to the usual normal mode analysis. We excite the specific vibrational mode in a two dimensional athermal jammed system by giving a small amplitude of active oscillation to each particle's size with an identical driving frequency. The response is then obtained as the real time displacements of the particles. We show remarkable correlations between the real time displacements and the eigen vectors obtained from conventional normal mode analysis. More importantly, from these real time displacements, we can measure the participation ratio and spatial polarization of particles' vibrations. From these measurements, we find three distinct frequency regimes which characterize the spatial distribution and correlation of particles' vibrations in jammed amorphous solids. Furthermore, we can possibly apply this method to a much larger system to examine the low frequency behaviour of amorphous solids with a much higher resolution of the frequency space.
I. Introduction
Vibrational properties in amorphous solids are ill-understood compared to those in crystalline solids. In crystalline solids, the Debye model explains that their vibrational density of states (VDOS) is expressed as D(ω) ∝ ωd−1 where ω is the vibrational frequency and d is the dimensionality.1 On the other hand, in amorphous solids, the low frequency VDOS shows excess mode spectra over that obtained from the Debye model. Although such low frequency vibrational modes are responsible for the anomalous dynamics and statics in amorphous materials, their physical origins remain elusive.Such low frequency excess vibrational modes are most often observed in athermal jammed solids.2–5 The jammed solids are categorized as one class of amorphous solids. Experimentally, such jammed solids are, in many cases, composed of soft materials such as emulsions,6 foams7 and large colloids.8,9 Interestingly, the VDOS in such systems shows a plateau of mode spectra in the low frequency region which extends to ω = 0 as the volume fraction approaches the jamming transition point from above.2,3,5 Furthermore the low frequency vibrational modes in athermal jammed solids (which are called soft modes) are also highly non-trivial. Here, some modes appear to be collective and extended throughout the space and others are quasi-localized,4,10 as in low temperature glasses.11–18 To characterize the spatial distribution and correlation of such vibrational modes is significant in jammed soft materials. Actually, it has numerous applications such as predicting where plastic deformations (leading to mechanical failure) might occur in space, which is called a soft spot.10
To obtain the spatial distribution and correlation of vibrational eigen modes in dense particle assemblies, normal mode analysis is frequently used.1 In such analysis, the vibrational modes are approximated as harmonic oscillators. Here, they are characterized by diagonalizing the Hessian matrix, which is composed of second derivatives of the potential energy with respect to the coordinates of the particles. Unfortunately, its computational and memory costs tend to be huge, because even when rotational motions are neglected, the matrix size is dN × dN, where N is the particle number. Thus in previous studies,2–5,12–17 small system sizes tend to be used. On the other hand, in order to study very low frequency modes, larger system sizes will be inevitable, and thus, another innovative method with low computational costs will be desired.
To characterize these spatial properties, the participation ratio is often measured.12–14,16–18 However, the participation ratio alone is not sufficient to characterize the degree of collectivity in the particles' vibrations – it only measures the degree of localization in the particles' vibrations. Thus, in this study, we shall introduce the average local polarization as a measure of collectivity in the vibrations of the particles.
In this paper, we outline a novel method to characterize the spatial distribution and correlation of vibrational modes without diagonalizing a huge Hessian matrix. Although our case study is a small system size of N = 1000, this method can be easily extended to much larger system sizes. It should also be noted that our method cannot directly obtain VDOS, it only tells us the spatial properties of the vibrational modes. A method to obtain VDOS without computing the Hessian matrix has already been described.19–22 Therefore, combined with our new method, we can obtain most of the basic vibrational quantities instead of the normal mode analysis. In our method, we excite a specific vibrational mode by giving active oscillation in each particle's diameter with an identical driving frequency. The response is then obtained as the real time displacements of the particles, which can be compared to the conventional normal modes obtained from the static Hessian matrix. We show a high degree of correlation between the real time displacements and the static normal modes. Furthermore, we also characterize the spatial structure of these vibrational normal modes by measuring the participation ratio12–14,16–18 and the polar order parameter. The results of these measurements are again found to be consistent for both the real time displacements and the static normal eigen mode. More importantly, from these measurements we can distinguish three distinct frequency regimes based on the spatial distribution of the particles' vibrations (whether they are extended and/or collective in space). Finally by directly measuring the real time displacements of the particles, we may obtain dynamical quantities such as the mean squared displacement (MSD). The MSD gives us the relative amplitude of particles' vibrations. In particular we find that particles vibrate over larger distances at lower frequency excitation. This is consistent with the experiments of colloidal particles23 where they find large vibrations of the particles at a lower frequency in the disordered structural regions.
This paper is organized as follows: in Section II, we will explain the numerical methods on the oscillatory driven particle dynamics and the normal mode analysis. In Section III, we will show the results especially on the comparisons between the normal mode analysis and our new method. In Section IV, we will give the summary and discussion of the present study.
II. Model and simulations
We consider a dense suspension of N soft spherical particles at zero temperature in a two-dimensional square box of linear size L with periodic boundary conditions on each side. The interaction between the particles is modelled by a short-ranged, purely repulsive, harmonic potential (similar to foams24):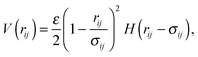 | (1) |
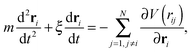 | (2) |
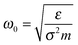 and the damping coefficient to be:
and the damping coefficient to be: 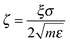 where σ is the typical diameter of the particles. Physically if ζ > 1, the vibration of the particles will be overdamped, and if ζ < 1, the vibration is underdamped. In this paper we shall fix ζ = 0.01 (underdamped regime) and ω0 = 1. Thus ω0 sets the timescale of our simulations. The dynamic eqn (2) is integrated numerically using the velocity Verlet scheme25 (see ESI,‡ for more detail).
where σ is the typical diameter of the particles. Physically if ζ > 1, the vibration of the particles will be overdamped, and if ζ < 1, the vibration is underdamped. In this paper we shall fix ζ = 0.01 (underdamped regime) and ω0 = 1. Thus ω0 sets the timescale of our simulations. The dynamic eqn (2) is integrated numerically using the velocity Verlet scheme25 (see ESI,‡ for more detail).
The system is then forced out of equilibrium by oscillating each particle's diameter σi(t) around its mean value σ0i:26
σi(t) = σ0i[1 + a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωdt + ψi)], cos(ωdt + ψi)], | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to avoid crystallization. We also introduce a fixed phase difference ψi = 2πi/N for each particle i so that the area fraction
2 to avoid crystallization. We also introduce a fixed phase difference ψi = 2πi/N for each particle i so that the area fraction 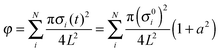 is constant in time. Throughout this paper, we consider an area fraction close to jamming transition with φ = 0.845 > φJ ∼ 0.8425 and a particle number N = 1000. Here, we use a small system size, because we calculate the Hessian matrix to compare the conventional normal mode analysis with our new method. In simulations, we also set the typical diameter of the particles as the unit of length such that σ = 1.
is constant in time. Throughout this paper, we consider an area fraction close to jamming transition with φ = 0.845 > φJ ∼ 0.8425 and a particle number N = 1000. Here, we use a small system size, because we calculate the Hessian matrix to compare the conventional normal mode analysis with our new method. In simulations, we also set the typical diameter of the particles as the unit of length such that σ = 1.
We start from a random initial configuration at time t = 0. We then introduce active oscillation in the particles' diameters according to eqn (3) with some fixed amplitude a and driving frequency ωd. If the amplitude of oscillation is large enough (above some critical value ac), the motion of the particles will be diffusive and the system will explore all the configurational space (ergodic) in the steady state.26,27 On the other hand if the amplitude of oscillation is less than ac (the regime in which we are interested in), the motion of all the particles will be periodic in the steady state. Thus in this vibrational state, the system is trapped in a local minimum of the total potential energy landscape. The total potential energy is defined to be:
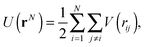 | (4) |
At the local energy minimum U(rN0), the Hessian matrix is defined as the second derivative of the potential energy with respect to the particles' positions (see the ESI‡ for more details):
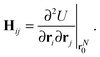 | (5) |
| H·eω = ω2eω. | (6) |
In summary, from a given static configuration rN0, we may calculate the Hessian matrix and subsequently a set of vibrational normal modes. However this information is not sufficient to predict how the particles will move in real time. Thus as one of the aims of this paper, we will make some comparisons between the vibrational normal modes and the real time particles' displacements.
III. Results
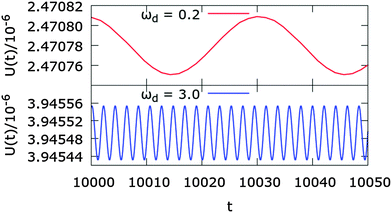
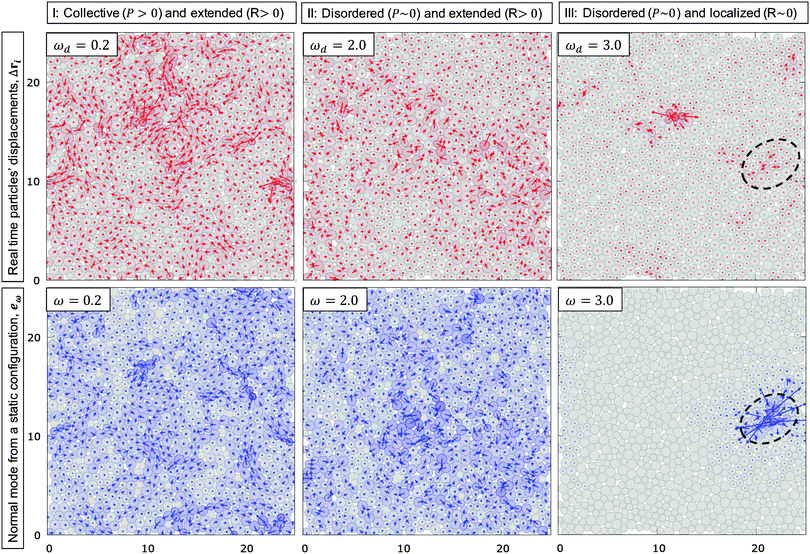
Since we are only interested in the vibrational steady state, we fix the oscillation amplitude to be much smaller than the critical amplitude ac (a = 10−6 in all our simulations). We then vary the driving frequency ωd from 0.1 to 3.0. In this regime, the system will evolve into a vibrational steady state where all the particles move or vibrate periodically with a frequency close to the driving frequency ωd. Therefore, the total potential energy U(t) = U(rN(t)) oscillates with frequency ωd (see Fig. 1). Note that in few cases, the system can also evolve into a vibrational steady state with a frequency double the driving frequency (period doubling).28 We do not consider these cases in this paper since they occur much less frequently in the limit a → 0. Here, we also note that the configurations obtained from the vibrational steady states are not fully distorted with the active vibrations in any frequencies ωd as the vibrational amplitude a is extremely small.In the steady state, we may look at the displacements of the particles between time t and t + Δt: Δri = ri(t + Δt) − ri(t), where the initial time t is larger than the time it takes for the system to reach a steady state and the delay time Δt is less than the period of oscillation 2π/ωd (note that the displacements of the particles are zero when Δt = 2π/ωd since the motion of the particles is periodic). Throughout this paper, we fix t = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and Δt = π/ωd in simulation units (unless mentioned otherwise). This delay time of equal to half the period of oscillation corresponds to the maximum displacements of the particles during one full oscillation cycle. In Fig. 2 top row, we plot the real time displacement fields of the particles for increasing driving frequencies from left to right. From these plots, we can distinguish three distinct frequency regimes based on two properties: collectivity and extensivity. Here, we categorize the representative modes as performed in ref. 4, but with an additional new definition of the collective measure. For small driving frequency or regime I (ωd = 0.2 in Fig. 2), the displacements of the particles appear to be collective and extended throughout the space. However for intermediate driving frequency or regime II (ωd = 2.0 in Fig. 2), the displacements of the particles become disordered but still extended throughout the space. Finally at high driving frequency or regime III (ωd = 3.0 in Fig. 2), the displacements of the particles become localized in space and disordered. See below for the quantitative definitions of these regimes by using the degrees of participation R and polarization P in the present study. Here, we note that P is a newly introduced degree of criterion, which has never been used in the previous studies.
000 and Δt = π/ωd in simulation units (unless mentioned otherwise). This delay time of equal to half the period of oscillation corresponds to the maximum displacements of the particles during one full oscillation cycle. In Fig. 2 top row, we plot the real time displacement fields of the particles for increasing driving frequencies from left to right. From these plots, we can distinguish three distinct frequency regimes based on two properties: collectivity and extensivity. Here, we categorize the representative modes as performed in ref. 4, but with an additional new definition of the collective measure. For small driving frequency or regime I (ωd = 0.2 in Fig. 2), the displacements of the particles appear to be collective and extended throughout the space. However for intermediate driving frequency or regime II (ωd = 2.0 in Fig. 2), the displacements of the particles become disordered but still extended throughout the space. Finally at high driving frequency or regime III (ωd = 3.0 in Fig. 2), the displacements of the particles become localized in space and disordered. See below for the quantitative definitions of these regimes by using the degrees of participation R and polarization P in the present study. Here, we note that P is a newly introduced degree of criterion, which has never been used in the previous studies.
To make a comparison with the vibrational normal modes, we compute the Hessian matrix from a single static configuration in the steady state. More specifically, we drive the system with a fixed oscillation amplitude a = 10−6 and fixed driving frequency ωd as before. The value of the driving frequency ωd is not important since they will all give the same distribution of normal modes as we shall see later. We wait until the system reaches a vibrational steady state and then we take a snapshot of the system. From this snapshot, we compute the Hessian matrix according to eqn (5), and after diagonalizing the Hessian matrix, we obtain a set of eigen modes (or normal modes) {eω} and a set of corresponding eigen frequencies {ω}. Note that since the system is still evolving periodically, the configuration of the system at this instantaneous time is not strictly at the local energy minimum, and thus, we found a small fraction (around 1%) of imaginary eigen frequencies (ω2 < 0) which does not affect the results that will be discussed below. The distribution of the eigen frequencies or vibrational density of states (VDOS) D(ω) is plotted in Fig. 3(A) for different driving frequencies ωd (the data are averaged over 16 independent simulations for a given ωd and binned with bin size = 0.05 on the ω-axis). D(ω) is normalized such that the area under the curve is equal to 1. As expected, VDOS does not depend on the driving frequency ωd. It only depends on the natural frequency ω0 and packing fraction φ of the system, as long as we are sufficiently close to the local energy minimum (i.e. a is small enough compared to ac). Moreover from the plot, we can identify a region of soft modes which is typical of the disordered system close to jamming density.
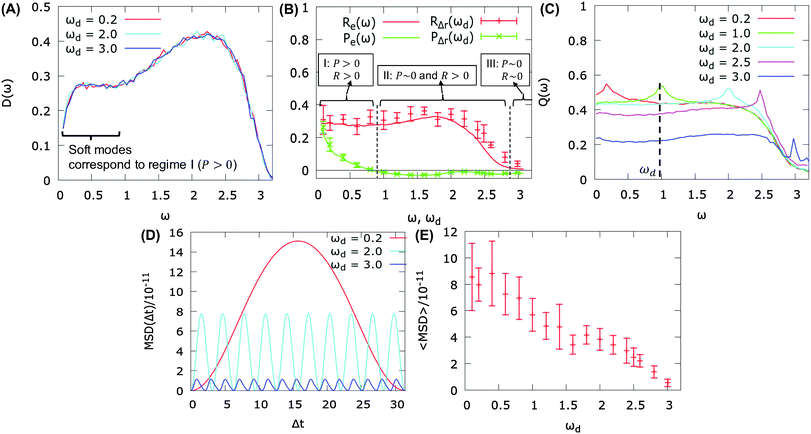 | ||
| Fig. 3 (A) Shows the vibrational density of states D(ω) or probability distribution of the eigen frequencies ω for different driving frequencies ωd, which is typical of a system close to jamming transition. (B) The three frequency regimes from the displacement fields (Δri) or eigen vectors (eω) can be distinguished by plotting the participation ratio R and polarization P as a function of driving frequency (ωd) or eigen frequency (ω) as introduced in eqn (9)–(11). (C) Shows the overlap function Q(ω), which is defined to be the dot product between the displacement field Δri and the eigenmode eω as introduced in eqn (12). (D) Shows the mean squared displacement (MSD) as a function of delay time Δt for different driving frequencies ωd as introduced in eqn (13) at the same amplitude of oscillation (a = 10−6). The MSD is periodic as expected, furthermore, the MSD for lower driving frequency is larger indicating that the particles vibrate over larger distances compared to high frequency excitation. (E) Shows the average MSD over one period as introduced in eqn (14), which increases as the driving frequency ωd is decreased. | ||
From the Hessian matrix above, we also plot the static vibrational normal modes eω in the bottom row of Fig. 2 for increasing eigen frequencies ω from left to right. Note that the vibrational normal modes plotted in the bottom row of Fig. 2 are obtained from the static configurations directly above them. For instance, the vibrational normal modes of ω = 3.0 (Fig. 2 bottom right) is obtained by diagonalising the Hessian matrix of the instantaneous particles' configuration in Fig. 2 top right. Incidentally, we may also identify three distinct eigen frequency regimes depending on the collectivity and extensivity of the normal modes, analogous to the real time displacement fields which we have observed in the top row of Fig. 2. Moreover, when we compare Fig. 2 bottom right to Fig. 2 top right, we may recognize a region of large overlap (dotted oval), signifying some degrees of correlation between real time displacements and vibrational normal modes obtained from a static configuration. Also note that when diagonalising the Hessian matrix, there exist several values of ω's which are very close to ωd = 3.0. Each of these eigen modes contributes to multiple localized regions of large displacements that we see in Fig. 2 top right (one of them is the region bounded by the dotted oval).
To quantify the collectivity of the displacement field Δri or the normal modes eω, we introduce a local polar order parameter Pi in the neighbourhood of particle i. More precisely, for the displacement field Δri, the local polar order parameter PiΔr is defined to be:
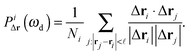 | (7) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) indicates summation over all particles j whose distance from particle i is less than
indicates summation over all particles j whose distance from particle i is less than ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and Ni is the total number of such neighbours around i. Here, we fix
and Ni is the total number of such neighbours around i. Here, we fix ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3.0 (in simulation units), although the result does not depend strongly on the value of
= 3.0 (in simulation units), although the result does not depend strongly on the value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Physically P ∼ 1 if all the particles in the neighbourhood of particle i move in the same direction and P ∼ 0 if they all move in a random direction (disordered or isotropic). Finally P ∼ −1 corresponds to anti-ferromagnetic order which is not considered here. Similarly we define the local polar order parameter for the normal modes Pie to be:
. Physically P ∼ 1 if all the particles in the neighbourhood of particle i move in the same direction and P ∼ 0 if they all move in a random direction (disordered or isotropic). Finally P ∼ −1 corresponds to anti-ferromagnetic order which is not considered here. Similarly we define the local polar order parameter for the normal modes Pie to be: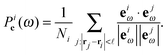 | (8) |
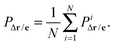 | (9) |
To quantify the degree of extensivity (or inversely, localization), we calculate the participation ratio R as defined in ref. 16 and 18. The participation ratio of the particles' displacements RΔr is defined to be:
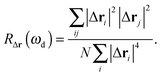 | (10) |
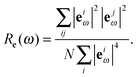 | (11) |
We also compute the correlation between the real time particles' displacements (which are dynamical quantities) and the normal modes of the Hessian matrix (which are static quantities). When comparing Fig. 2 top right with Fig. 2 bottom right, we have already seen a region of large overlap between the real time displacements and the eigen vectors (dotted oval in the figure). Thus, we define the overlap function Q(ω) to be the dot product between the displacement field Δri = ri(t + Δt) − ri(t) and the eigen vector eω:
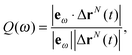 | (12) |
To quantify the relative magnitude of the particles' vibrations, we also compute the mean squared displacement (MSD) as a function of delay time Δt:
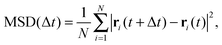 | (13) |
To analyze the dependence on the driving frequency more fully, we measure the average MSD over one period of oscillation:
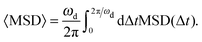 | (14) |
IV. Discussion and perspectives
In this study, we have constructed a new method to extract the specific vibrational modes as demonstrated in the normal mode analysis, by using oscillatory driven particles in a two dimensional dense disordered system. For the activation of the particle motions, we give a small amplitude of active oscillation in particle sizes with an identical driving frequency ωd. First we have checked that the particles demonstrate reversible motion by means of the total potential energy for any input frequency ωd, as shown in Fig. 1. Next we have shown the displacements of the driven particles for a half cycle (Δt = π/ωd) at several ωd values in the top row of Fig. 2. Then we have revealed that the distributions of displacement vectors remarkably depend on the values of ωd. For comparison, we have measured the eigen modes by means of the conventional normal mode analysis in the bottom row of Fig. 2. In particular, we observe overlapping regions between the real time displacements and the eigen vectors for the same frequency value, even though different techniques are applied. From the VDOS shown in Fig. 3(A), we have also checked that the normal mode analysis is not influenced by the external oscillations, because the oscillation amplitude is extremely small (a = 10−6). In Fig. 3(B) we have presented the degrees of spatial polarization and participation ratio for both methods, presented respectively as PΔr/e(ωd/ω) and RΔr/e(ωd/ω). It has been found that they behave, respectively, very similar, comparing the results obtained from both methods. Furthermore we have measured the direct correlations between the real time displacement vectors of the particles driven with ωd and the eigen vectors of the arbitrary modes ω obtained from the normal mode analysis by means of the overlap function Q(ω). As shown in Fig. 3(C), we have indeed found a clear correlation where ω = ωd. This means that our new method works well as performed in the normal mode analysis.From these analysis, we have revealed that both of the real time displacements for the oscillatory driven particles and the eigen vectors of normal mode analysis are composed of at least three different regimes such as regime I: the correlated extended regime (ω ∼ 0.2) due to PΔr/e > 0 with RΔr/e > 0, regime II: the disordered extended regime (ω ∼ 2.0) due to PΔr/e ∼ 0 with RΔr/e > 0, and regime III: the disordered localized regime (ω ∼ 3.0) due to PΔr/e ∼ 0 with RΔr/e ∼ 0 in the athermal amorphous solid close to φJ. Finally we have found that the typical amplitude of real time vibrations driven with low frequency oscillation is much larger than those with high frequency by measuring the one cycle mean squared displacement 〈MSD〉 as shown in Fig. 3(D) and (E). These results are consistent with the features of the eigen modes measured by the normal mode analysis.22,23
In this method, we are able to fully characterize the vibrational properties of amorphous materials (such as participation ratio R(ω) and polarization P(ω)) without the need for diagonalizing a large Hessian matrix. Nevertheless, this method appears to be unable to directly measure the VDOS (or D(ω)). But, the VDOS has been obtained from the Fourier transform of the velocity autocorrelation with respect to time without computing the Hessian matrix.19–22 Here, we note that the computational and memory costs for this velocity autocorrelation together with the Fourier transform are of the order of dN. Thus combining with our new method, we can obtain most of the basic vibrational quantities.
It should also be noted that when we oscillate the particles' diameters, the amplitude of oscillation should be kept small enough such that the response of the particles remains linear. In our case, we always check that the total potential energy U(t) is approximately sinusoidal with frequency equal to the driving frequency for each simulation run. Previously we also defined ac to be the critical amplitude above which the motion of the particles becomes irreversible. Below ac, the motion of the particles is reversible, but not necessarily linear. Nonlinearity in our system comes in the form of period-doubling, in which the particles vibrate with a frequency 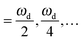 ,28 but the motion of the particles remains reversible. In ref. 26, finite size scaling shows that ac approaches to a finite value as N → ∞. Thus we can always find a reversible phase irrespective of the system size used. However in ref. 29 and 30, it has also been shown that the window of the linear regime with respect to a in the reversible phase scales as
,28 but the motion of the particles remains reversible. In ref. 26, finite size scaling shows that ac approaches to a finite value as N → ∞. Thus we can always find a reversible phase irrespective of the system size used. However in ref. 29 and 30, it has also been shown that the window of the linear regime with respect to a in the reversible phase scales as 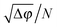 , where Δφ = φ − φJ. This means that the linear regime vanishes at the jamming transition point. And above jamming, the linear regime becomes narrower as N → ∞. Nevertheless, above jamming, we can always find a small enough value of a in which the response is still linear for large but finite N. In this paper we fix a = 10−6, but, we also perform several test simulations with a = 10−9 and we still find reliable results. This means we can easily extend our simulation to a large system size N ∼ 106 and still find a linear response with a = 10−9. Additionally, our method may also provide a useful tool to investigate the non-linear behaviour at large system sizes, close to jamming transition.
, where Δφ = φ − φJ. This means that the linear regime vanishes at the jamming transition point. And above jamming, the linear regime becomes narrower as N → ∞. Nevertheless, above jamming, we can always find a small enough value of a in which the response is still linear for large but finite N. In this paper we fix a = 10−6, but, we also perform several test simulations with a = 10−9 and we still find reliable results. This means we can easily extend our simulation to a large system size N ∼ 106 and still find a linear response with a = 10−9. Additionally, our method may also provide a useful tool to investigate the non-linear behaviour at large system sizes, close to jamming transition.
In future studies, by using our model, we will examine a much larger system size, not only for athermal jammed systems but also for thermal glasses. For instance in low temperature glasses, the scaled VDOS D(ω)/ωd−1 shows a peak in the low frequency regime, which is called the Boson peak. This has been observed in experimental systems such as oxide,31 metallic,32 and organic materials33 as well as numerical simulations of model glasses.22,34 As a related matter, the low frequency vibrational modes in thermal glasses appear to be quasi-localized and collective based on theoretical arguments,11 as well as numerical simulations12–16 and experiments.18 According to the experiments of colloidal particles,23 such characteristic behaviours of low frequency modes may originate from large vibrations due to structural defects, analogous to crystals. It is indicated that such low frequency modes could play a significant role in the appearance of a Boson peak.22 At even lower frequency, Debye modes also appear to be restored.17 To study such crossover behaviour, a much higher resolution of the frequency space will be needed, which requires much larger system sizes. However, conventional normal mode analysis requires a huge computational cost and thus a more efficient computational method will be desired. To perform such studies, we propose a model where thermal noise is applied in addition to the active oscillations in the particles' diameters. In particular, by using our analysis of both participation ratio R(ω) and average polarization P(ω), we may identify multiple frequency regimes in low temperature glasses, which may coincide with the appearance of the Boson peak at a low frequency16,18 as well as Debye modes at an extremely low frequency.17,35
Our model can also be easily extended to other forms of two-body potentials such as Lennard-Jones, Gaussian core, etc. In such a case, we oscillate the interaction range and then we expect the same results. It might also be interesting to consider other models of deformations which can excite a particular vibrational mode with a specific frequency. For instance, we might apply an oscillatory shear on the system. It is expected that the response of the system will correspond to the frequency of the oscillatory shear. However in the case of oscillatory shear, the response of the system might not be as isotropic as compared to our mode of deformation.
Finally our model also represents a unique example of active matter where the system is driven with a characteristic driving frequency ωd. Comparison of our actively oscillating particle system to the more mainstream self-propelled active particle system36,37 might also be illuminating, since self-propelled particles do not possess such a characteristic vibrational frequency.
In conclusion, by means of our new method to excite the specific modes, we have acquired results consistent with those of the normal mode analysis. Here the numerical costs for our new method is much lower than the normal mode analysis because we do not need to diagonalize a huge Hessian matrix. This makes it possible to perform vibrational analysis for much larger systems in the near future, which will significantly contribute to the studies of the vibrational properties in any solids including soft materials.
Acknowledgements
We are grateful to Maxime Clusel who provided us with the initial ideas and for the illuminating discussions. We thank Ludovic Berthier, Kunimasa Miyazaki, Akira Onuki, Atsushi Ikeda, Misaki Ozawa, and Kyohei Takae for variable discussions and comments. TK gratefully acknowledges funding from JSPS Kakenhi (No. 15H06263 and 16H06018). ET gratefully acknowledges funding from the European Research Council (ERC) under the European Union's (EU) Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement No. 306845.References
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Thomson Learning, 1976 Search PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Jamming at zero temperature and zero applied stress: The epitome of disorder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef PubMed.
- M. Wyart, L. E. Silbert, S. R. Nagel and T. A. Witten, Effects of compression on the vibrational modes of marginally jammed solids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051306 CrossRef PubMed.
- M. van Hecke, Jamming of soft particles: geometry, mechanics, scaling and isostaticity, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef CAS PubMed.
- E. Lerner, G. During and M. Wyart, A unified framework for non-Brownian suspension flows and soft amorphous solids, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4798–4803 CrossRef CAS PubMed.
- T. G. Mason, J. Bibette and D. A. Weitz, Yielding and Flow of Monodisperse Emulsions, J. Colloid Interface Sci., 1996, 179, 439 CrossRef CAS.
- B. Hertzhft, S. Kakadjian and M. Moan, Measurement and modeling of the flow behavior of aqueous foams using a recirculating pipe rheometer, Colloids Surf., A, 2005, 263, 153 CrossRef.
- J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, Cambridge, UK, 2012 Search PubMed.
- F. Boyer, E. Guazzelli and O. Pouliquen, Unifying Suspension and Granular Rheology, Phys. Rev. Lett., 2011, 107, 188301 CrossRef PubMed.
- M. L. Manning and A. J. Liu, Vibrational Modes Identify Soft Spots in a Sheared Disordered Packing, Phys. Rev. Lett., 2011, 107, 108302 CrossRef CAS PubMed.
- S. R. Elliott, A Unified Model for the Low-Energy Vibrational Behaviour of Amorphous Solids, EPL, 1992, 19, 201 CrossRef CAS.
- H. R. Schober and B. B. Laird, Localized low-frequency vibrational modes in glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 6746 CrossRef.
- H. R. Schober, C. Oligschleger and B. B. Laird, J. Non-Cryst. Solids, 1993, 156, 965 CrossRef.
- H. R. Schober and C. Oligschleger, Low-frequency vibrations in a model glass, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 11469 CrossRef CAS.
- A. Widmer-Cooper, H. Perry, P. Harrowell and D. R. Reichman, Irreversible reorganization in a supercooled liquid originates from localized soft modes, Nat. Phys., 2008, 4, 711 CrossRef CAS.
- A. Widmer-Cooper, H. Perry, P. Harrowell and D. R. Reichman, Localized soft modes and the supercooled liquid's irreversible passage through its configuration space, J. Chem. Phys., 2009, 131, 194508 CrossRef PubMed.
- S. N. Taraskin and S. R. Elliott, Anharmonicity and localization of atomic vibrations in vitreous silica, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8572 CrossRef CAS.
- K. Chen, W. G. Ellenbroek, Z. Zhang, D. T. N. Chen, P. J. Yunker, S. Henkes, C. Brito, O. Dauchot, W. van Saarloos, A. J. Liu and A. G. Yodh, Low-Frequency Vibrations of Soft Colloidal Glasses, Phys. Rev. Lett., 2010, 105, 025501 CrossRef PubMed.
- A. Rahman, M. J. Mandell and J. P. McTague, Molecular dynamics study of an amorphous Lennard-Jones system at low temperature, J. Chem. Phys., 1976, 64, 1564 CrossRef CAS.
- G. S. Grest, S. R. Nagel, A. Rahman and T. A. Witten Jr, Density of states and the velocity autocorrelation function derived from quench studies, J. Chem. Phys., 1981, 74, 3532 CrossRef CAS.
- A. Ikeda, L. Berthier and G. Biroli, Dynamic criticality at the jamming transition, J. Chem. Phys., 2013, 138, 12A507 Search PubMed.
- H. Shintani and H. Tanaka, Universal link between the boson peak and transverse phonons in glass, Nat. Mater., 2008, 7, 870 CrossRef CAS PubMed.
- P. Tan, N. Xu, A. B. Schofield and L. Xu, Understanding the Low-Frequency Quasilocalized Modes in Disordered Colloidal Systems, Phys. Rev. Lett., 2012, 108, 095501 CrossRef PubMed.
- D. J. Durian, Foam mechanics at the bubble scale, Phys. Rev. Lett., 1995, 75, 26 CrossRef PubMed.
- L. Verlet, Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard Jones Molecules, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- E. Tjhung and L. Berthier, Discontinuous fluidisation transition in actively-deforming particles: A new paradigm for collective motion in dense active systems, in preparation.
- T. Kawasaki and L. Berthier, Macroscopic yielding in jammed solids is accompanied by a non-equilibrium first-order transition in particle trajectories, 2015, arXiv:1507.04120.
- I. Regev, J. Weber, C. Reichhardt, K. A. Dahmen and T. Lookman, Reversibility and criticality in amorphous solids, Nat. Commun., 2015, 6, 8805 CrossRef CAS PubMed.
- C. F. Schreck, T. Bertrand, C. S. O'Hern and M. D. Shattuck, Repulsive contact interactions make jammed particulate systems inherently nonharmonic, Phys. Rev. Lett., 2011, 107, 078301 CrossRef PubMed.
- M. S. van Deen, J. Simon, Z. Zeravcic, S. Dagois-Bohy, B. P. Tighe and M. van Hecke, Contact changes near jamming, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 020202 CrossRef PubMed.
- B. Rufflé, G. Guimbretiére, E. Courtens, R. Vacher and G. Monaco, Glass-Specific Behavior in the Damping of Acousticlike Vibrations, Phys. Rev. Lett., 2006, 96, 045502 CrossRef PubMed.
- T. Scopigno, J.-B. Suck, R. Angelini, F. Albergamo and G. Ruocco, High-Frequency Dynamics in Metallic Glasses, Phys. Rev. Lett., 2006, 96, 135501 CrossRef CAS PubMed.
- B. Rufflé, D. A. Parshin, E. Courtens and R. Vacher, Boson Peak and its Relation to Acoustic Attenuation in Glasses, Phys. Rev. Lett., 2008, 100, 015501 CrossRef PubMed.
- J. Horbach, W. Kob and K. Binder, High frequency sound and the boson peak in amorphous silica, Eur. Phys. J. B, 2001, 19, 531 CrossRef CAS.
- N. Xu, V. Vitelli, A. J. Liu and S. R. Nagel, Anharmonic and quasi-localized vibrations in jammed solids – Modes for mechanical failure, EPL, 2010, 90, 56001 CrossRef.
- L. Berthier, Nonequilibrium glassy dynamics of self-propelled hard disks, Phys. Rev. Lett., 2014, 112, 220602 CrossRef PubMed.
- S. Henkes, Y. Fily and M. C. Marchetti, Active jamming: Self-propelled soft particles at high density, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 040301 CrossRef PubMed.
Footnotes |
| † PACS numbers: 05.10.−a,61.43.−j. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00788k |
| § Present address: Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK. |
| This journal is © The Royal Society of Chemistry 2017 |