Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Limiting the valence: advancements and new perspectives on patchy colloids, soft functionalized nanoparticles and biomolecules
Emanuela
Bianchi
 *ab,
Barbara
Capone
*ab,
Barbara
Capone
 ac,
Ivan
Coluzza
ac,
Ivan
Coluzza
 a,
Lorenzo
Rovigatti
a,
Lorenzo
Rovigatti
 ad and
Peter D. J.
van Oostrum
ad and
Peter D. J.
van Oostrum
 e
e
aFaculty of Physics, University of Vienna, Boltzmanngasse 5, A-1090 Vienna, Austria. E-mail: emanuela.bianchi@univie.ac.at
bInstitute for Theoretical Physics, Technische Universität Wien, Wiedner Hauptstraße 8-10, A-1040, Vienna, Austria
cDipartimento di Scienze, Università degli studi Roma Tre, Via della Vasca Navale 84, I-00146 Rome, Italy
dRudolf Peierls Centre for Theoretical Physics, 1 Keble Road, Oxford, OX1 3NP, UK
eDepartment of Nanobiotechnology, Institute for Biologically Inspired Materials, University of Natural Resources and Life Sciences, Muthgasse 11/II, A-1190 Vienna, Austria
First published on 28th June 2017
Abstract
Limited bonding valence, usually accompanied by well-defined directional interactions and selective bonding mechanisms, is nowadays considered among the key ingredients to create complex structures with tailored properties: even though isotropically interacting units already guarantee access to a vast range of functional materials, anisotropic interactions can provide extra instructions to steer the assembly of specific architectures. The anisotropy of effective interactions gives rise to a wealth of self-assembled structures both in the realm of suitably synthesized nano- and micro-sized building blocks and in nature, where the isotropy of interactions is often a zero-th order description of the complicated reality. In this review, we span a vast range of systems characterized by limited bonding valence, from patchy colloids of new generation to polymer-based functionalized nanoparticles, DNA-based systems and proteins, and describe how the interaction patterns of the single building blocks can be designed to tailor the properties of the target final structures.
1 Introduction
In the realm of rational materials design, specific structures at the nano- and micro-scale can be conceived for a vast range of technological applications: particular attention is for instance devoted to non-close-packed architectures, that can act as catalysts, filters, sensors, biomimetic scaffolds or drug delivery devices.1–3 Responsive open structures can indeed be used in biotechnological applications for tissue engineering, sensing and purification where self-repairing, switchable porosities and the ability to capture drugs are required.4,5 Additionally, materials containing ordered arrays of holes are also very interesting for functional devices in fields such as photonics, optoelectronics, thermophotovoltaics and energy storage technologies.6Rather than relying on externally controlled tools, many fabrication methods are nowadays based on self-assembly processes. Self-assembly is essentially the formation of some kind of order, perceived by humans and possibly quantified by some order parameter, as a result of the competition between various enthalpic and entropic factors.7 This holds for atomic or (bio)molecular systems as well as for much larger length scales, as for instance in colloidal systems, where the self-assembling units are typically orders of magnitude larger than atoms and molecules. Self-assembly in colloidal model systems shares a lot of similarities with self-assembly in atomic or molecular systems, with the added benefit that the large characteristic sizes allow for the easy inspection of the resulting structures and their dynamics.
In order to gain a greater control over the self-assembly, it is beneficial to impose additional constraints.8 Extra instructions can be for instance imparted upon the particles if their interactions are no longer merely isotropic but rather depend on their relative positions and orientations.9,10 Present-day approaches to rational materials design try to address the characteristics of the building blocks that are both experimentally feasible and able to stabilize mesoscopic structures of interest, looking meanwhile for the conditions that guarantee the assembly of these units into desired architectures. In the realm of artificial nano- and micro-sized units, patchy colloids,11,12i.e., particles with directional and selective interactions often induced by chemically or physically patterned surfaces, are regarded as promising building blocks for smart materials with designed symmetries and properties. The two main properties of these building blocks, i.e., the limited bonding valence and the directionality induced by the bonding sites, favor those architectures that are compatible with the features of the single unit.11,12
Beyond materials science, many naturally occurring systems are known to give rise to a wealth of self-assembled structures by virtue of some anisotropy.14 The effective interactions between the constituent entities of these systems are often complex and it remains challenging to identify the key elements for guiding and controlling their self-assembling processes. Assembly of biomolecules into supramolecular complexes is at the heart of many biological processes and the dynamic interplay of the different components leads to biological functionality.15 Complex interactions between biomolecules, such as lysozymes and other proteins, or supramolecular complexes, such as viruses, have been recently described as patchy, meaning that the effective interactions in these systems are characterized by limited valence and directionality.13,16–22
In this review, we present a selection of recent advancements in the field of anisotropically interacting units, focusing on patchy colloidal systems, recently developed soft functionalized nanoparticles and biomolecules. A selection of the limited valence systems discussed here is represented in Fig. 1. In order to span such a broad range of systems in a concise and clear fashion, we propose a classification of limited valence units according to the path leading to the production or formation of these different anisotropically interacting entities: we refer to patchy particles resulting from either the top-down or the bottom-up route. Of course, it is difficult to draw a hard line between the two paths since the emergence of anisotropic interactions is arguably based on self-assembly mechanisms in most of the cases. Here, we make the distinction according to whether or not the resulting units are characterized by internal degrees of freedom: the top-down route essentially results in hard particles with a pre-defined and fixed patchiness, while the bottom-up path leads to soft units with flexible bonding patterns. Within the top-down route, many synthesis techniques have been developed to produce functionalized units, mostly allowing the fabrication of patchy colloids where the patch size, number and distribution are determined at the synthesis level and maintained unaltered during the consecutive assembly.11,23–25 In contrast, within the bottom-up path, anisotropically interacting units arise through self-assembly of smaller, possibly flexibly linked, subunits.26,27 The particular features of such self-assembled patchy aggregates are extremely soft interactions and possible fluctuations in the number, position and/or size of the patches. Not all routes towards functionalized units can be classified in a neat way: for instance, patchy particles obtained by grafting polymer brushes to the surface of colloidal particles28 are the result of a self-organization process, but those patchy units do not have the degrees of freedom associated to a flexible patchiness. Another example where the proposed classification becomes ambiguous is represented by a new type of polymeric networks named vitrimers: vitrimers are malleable materials that can rearrange their topology without changing their average connectivity;29 the phase behavior of these systems has been recently described with a patchy model that combines a non-flexible particle geometry with a bond switching dynamics that mimics the bond exchange mechanism that is at the basis of the extraordinary properties of vitrimers.30 In addition, the proposed classification is inherently fluid as some systems might be categorized differently depending on the specific point of view: proteins can, for instance, be described as (charged) “top-down” patchy colloids or as “bottom-up” complex units (emerging from the folding process) with directional interaction sites. Nonetheless, with all its limitations, the proposed classification provides insight into the interplay between the design of anisotropic interaction patterns and the balance between entropy and enthalpy during assembly.
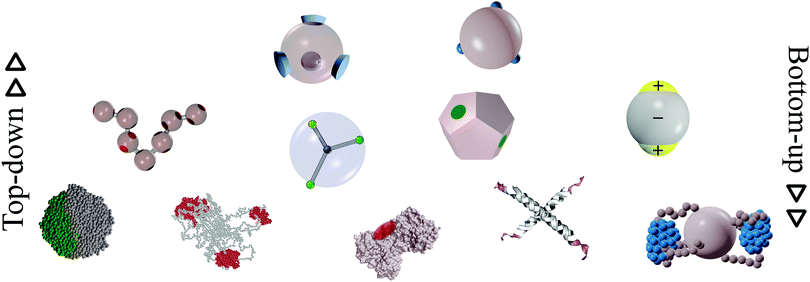 | ||
| Fig. 1 A selection of the limited-valence building blocks discussed in the text. From the top to the bottom of the figure, the single building blocks are loosely arranged in rows, according to their complexity. From left to right, top row: toy models of hard particles decorated with conical and point-like patches. Middle row: a polymer composed of patchy monomers, a soft particle with mobile patches, a patchy dodecahedron (exemplification of non-spherical patchy particles) and an inverse patchy colloid. Bottom row: a collapsed copolymer chain, a telechelic star polymer, a bovine lactoferricin with a superimposed orange patch,13 a tetravalent DNA nanostar and a polymer-grafted nanoparticle. | ||
This review is organized as follows: in Section 2 we present an overview of the experimental advancements in the field of top-down patchy colloids together with the related theoretical/numerical progress in the understanding of their self-assembly, while in Section 3 we focus on bottom-up patchy units, again presenting both experimental and theoretical/numerical states of the art. In both sections, we propose a selection of systems that we consider particularly promising to obtain a greater control over self-assembly processes. In particular, the discussion on top-down patchy systems focuses on the following topics: in Section 2.1 we consider the results accumulated so far on charged particles with oppositely charged patches, in Section 2.2 we propose a brief discussion on globular proteins in solutions that have been recently described as patchy entities, in Section 2.3 we present the interesting interplay between non-spherical shapes and anisotropic bonding patterns, while in Section 2.4 we touch upon the tantalizing perspective offered by encoding instruction for self-assembly in flexibly linked sequences of different types of patchy particles. Within the discussion on bottom-up patchy systems we focus on the following topics in more detail: the spontaneous formation of patchiness in polymer-based systems, reported in Section 3.1; the effect of anisotropic interactions on the hierarchical self-assembly of DNA-based systems, discussed in Section 3.2; and the relevance of patchiness in biological systems, analyzed in Section 3.3. Finally, in Section 4, we draw our concluding remarks.
2 Patchy particles from the top-down route
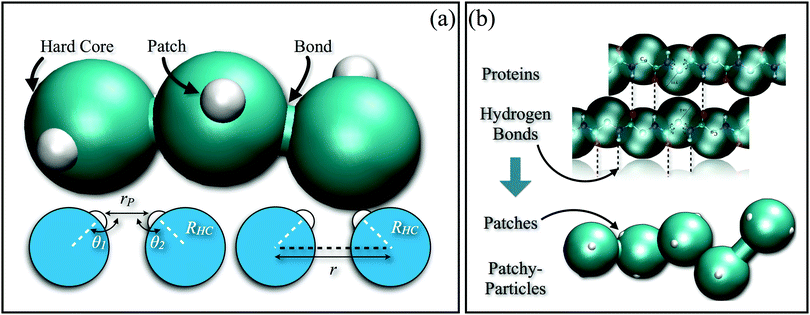
The common characteristic of anisotropically interacting units resulting from top-down synthesis approaches is the negligibility of fluctuations in the particles’ surface pattern and/or shape. In other words, most of the instructions for the self-assembly of these units is imparted at the synthesis level either by selectively modifying the surface of the particles or by following experimental protocols leading to non-spherical shapes, while any fluctuations are frozen in as permanent polydispersity. Consequently, after the synthesis, control over the self-assembly can be further attained only through a change in the chemical properties of the dispersing medium or by the presence or absence of external fields.The simplest type of patchy colloidal system is represented by the special case of Janus particles,31,32i.e., particles with two distinguishable hemispheres characterized by different surface properties. Fabrication methods yielding large volumes of Janus particles and guaranteeing a precise control over the properties of the two hemispheres have undergone impressive steps forward. Unfortunately, only a few of the developed techniques can be extended to produce more complex surface decorations. A very helpful classification of synthesis methods of patchy particles is presented in ref. 11, but we also encourage the interested reader to consult other, more recent, experimental overviews on patchy colloids.24,33 In the following, we briefly summarize the most used synthesis methods with the aim of providing an idea about present-day experimental challenges, such as the fine control over the surface patterns (size, shape, position and orientation of the patches), the richness of the pattern morphologies (number of patches per particle), and the scalability of the methods (amount of synthesized particles). For a schematic overview of the most common top-down synthesis methods we refer the reader to Fig. 5 of ref. 11.
A class of surface modification techniques that has been successfully applied to make several types of patchy particles for self-assembly studies is glancing angle deposition;34 here a layer of material, usually a metal or an oxide, is deposited from a glancing angle on particles in an ordered two-dimensional array34 or in the grooves of templates,35 to influence the size and shape of the patches through the casting of shadows. The subsequent etching of deposited patches to make these smaller36 can be combined with the possibility to lift off and flip the entire particle array to proceed with the modification of patches on the other side of the particles.37 The interactions between the patches can then be determined by a specific surface coating of the deposited material; for instance a gold layer can be functionalized with a thiol to make attractive, hydrophobic patches38 or charged regions.39 Another important category of synthesis methods is templating, in which some sacrificial material is used to temporarily shield part of the particle surface during its fractional modification. Most templating techniques yield Janus-like particles, but there are exceptions that yield two patches on spherical particles40,41 or even non-spherical particles with two polymeric caps resulting from partial etching of electrospun polymeric wires.42 Finally, a conceptually simple manner to make particles with one or two polar patches is based on contact printing, usually with a soft polydimethylsiloxane stamp on two-dimensional particle arrays.43 The size of the produced patches can be varied via the stiffness of the stamp,25 which can be easily modified through the mixing ratio between monomers and cross-linkers, the applied pressure and the amount of “ink” used. Both physical interactions, such as charge attractions and hydrophobicity,43 and chemical bonds can be used to fix the ink to the particles.25,44,45
To date, the aforementioned techniques allow for a fine control over the patch size and position, while the number of patches per particle is typically limited to one or two and the amount of particles produced in a single batch is little. Great efforts have been devoted to the creation of colloids with rich surface patterns, consisting of many patches arranged in geometrical patterns. In this direction, liquid interfaces and surface tension have been used to provide anisotropy in surprising ways. For instance, particles on the surface of an emulsion droplet form regular aggregates upon evaporation of the droplet.46 Controlled patch sizes result upon swelling these regular aggregates with a liquid monomer to be later polymerized.23 Interactions between the patches can be modified and made specific by functionalizing the patch surface with DNA23 or metal-coordination-based recognition units.47 The larger patches made in this way are protrusions on the particle surface. Alternative methods to make particles with protruding patches are based on swelling polymeric particles with an additional monomer48 or on condensing monomer droplets on oxide particles.49 A subsequent polymerisation step is then used to render these monomeric patches permanent. A multitude of relatively small protrusions of monomers can be polymerized to form areas with an effective surface roughness. In combination with depletion attractions induced by depletants on the scale of the roughness, neutral patches can be realized on otherwise attractive particles.50 Similarly, dimples left after a two-stage polymerization reaction51 or flat faces left after temporary melting at a flat substrate can be used to render inherently isotropic interactions such as depletion50,52 and van der Waals attractions53,54 directional.
Beyond the challenges in the particle synthesis, experimental methods to produce self-assembling building blocks with specific surface patterns also deal with challenges related to the achievement, and possibly the observation, of the desired assembly behavior. First of all, to facilitate the microscopic study of any self-assembled structure, it is advantageous that the particles are dispersed in a refractive index matching solvent, i.e., a solvent with the same refractive index as that of the particles.55 Moreover, for self-assembly to take place in the bulk, a relatively large amount of particles is needed that should also be density matched to suppress sedimentation or creaming towards a hard wall. This can be achieved by working with small particles: the gravitational length has to be large enough to make sedimentation irrelevant on the timescale of the experiment. However, the resolution of the used microscopy technique sets the lower bound to the particle size. One can afford to work with larger particles by density matching them in a properly chosen solvent mixture.56,57 Finally, it is important to note that the speed of diffusion and therefore the rate at which any self-assembly takes place depends strongly on the size of the particles. The choice of the composition of a colloidal system for self-assembly experiments is a compromise between requirements on the time scale, the length scale, the density, the refractive index and all those properties determining the colloidal interactions that should ideally lead to the desired assembly behavior, and all these factors complicate the fabrication of anisotropic particles for studies in three-dimensions more than in two-dimensions.
The spontaneous assembly of patchy colloids has been experimentally observed for instance in the formation of strings43 and micelles39 of Janus particles, in the site-specific aggregation of finite colloidal clusters58 or in the formation of an extended, two-dimensional crystal, known as kagome lattice.38 It is worth noting that assembly of patchy particles can be further influenced with external fields, especially in the case of conducting patches on dielectric particles.59–63 Under the influence of electric or magnetic fields, the formation of chains, staggered chains or close and loosely packed two-dimensional crystals can be induced.64 An overview of experiments in which external fields under different orientations are used is given in ref. 65. It is also worth noting that particles with an anisotropic surface chemistry can move in, possibly self-induced, gradients, a motion that bears similarities to the active swimming of some bacteria. These so-called active patchy colloids are beyond the scope of this review and we refer the interested reader to a number of excellent review articles.66–68
From the numerical and theoretical point of view, many model systems have been developed during the past few years to include patchy directional interactions in the pair potential between colloidal particles. Most of the patchy models proposed in the literature are designed to mimic the behaviour of top-down patchy colloids, as they usually consist of isotropically repulsive spherical units carrying a fixed and small number of attractive regions: patches are typically arranged on the particle surface and their positions are fixed in a pre-defined geometry. The most popular models are the Kern–Frenkel model,69 the sticky spots model70 and the orientational Lennard-Jones model.71 Despite their simplicity, these models have been successfully employed to investigate a huge range of phenomena, from the formation of quasicrystalline structures in the absence of an external field72,73 to reentrant gels74 and reentrant spinodals,75 while the self-assembly of such systems has been deeply investigated also under gravity,76 on substrates,77 or under shear.78,79 In parallel, theoretical tools developed to investigate the structure and thermodynamics of top-down patchy colloids have reached a mature stage. In this context, the theoretical cornerstone is provided by the Wertheim theory,80 which has been extended to support multi-component mixtures,81 patches of different types,82,83 multiple bonds per patch,84 ring-forming systems,85 systems in confined porous media86 and much more.87–89
The incredible variety of behaviors exhibited by the systems presented above is a testament to the versatility of building blocks with patterned surfaces. In the next sections we present some selected examples of systems composed of top-down patchy particles which we consider particularly promising both to assemble materials with desired properties and to gain a deeper understanding of complex systems that show a well-defined self-assembly behavior: in Sections 2.1 and 2.2 we highlight how heterogeneously charged colloids and proteins, respectively, are intrinsically patchy systems, in Section 2.3 we investigate the interplay between non-spherical particle shapes and specific interaction sites on the particle surface, while in Section 2.4 we describe in detail systems of self-folding colloidal strings composed of patchy units.
2.1 Charged patchy colloids
Non-homogeneously charged colloids have recently emerged as promising building blocks for target structures with specific properties at the nano- and micro-scale. Colloids characterized by well-defined surface regions carrying different surface charges can be generally described as charged patchy particles; in order to emphasize that these units are a different class of patchy colloids with respect to conventional patchy particles, they are often referred to as inverse patchy colloids (IPCs):90 the term inverse refers to the fact that, while conventional patchy systems are typically characterized by the presence of attractive regions on the surface of otherwise repulsive particles, IPCs carry extended patches that repel each other and attract those parts of the colloid that are free of patches. This class of systems was originally introduced to describe complex units emerging from the adsorption of charged polyelectrolyte stars onto the surface of oppositely charged colloids,91 but it now includes micro-scale particles manufactured with a binary92 or ternary41 distribution of the surface charge. Clearly, also Janus particles with differently charged hemispheres39,43,93 can be considered as (the simplest case of) IPC units. It is also worth noting that complex interactions between biomolecules, such as proteins and viruses, have been described as patchy (also see Section 2.2), making it possible to employ the models and techniques developed for IPC systems to achieve a deeper understanding of the assembly phenomena in these natural systems.Within the framework of materials design, the first elaborate model for heterogeneously charged particles was developed for colloids characterized by two charged polar patches and an oppositely charged equatorial belt.96 Subsequently, the idea to study simple models of particles with heterogeneously charged surfaces proliferated within the community. A charged patchy model was for instance developed to study the bulk aggregation behavior of charged Janus-like particles as a function of the patch size.97 A different modeling of charged Janus colloids was proposed to investigate the relation between the order of the multipolar expansion of the inter-particle potential and the resulting minimum-energy clusters.98 In the context of globular proteins, a set of charged patchy particle models was introduced99 to study the adsorption of such units on a polyelectrolyte chain100 or on a polyelectrolyte brush layer.101 These charged patchy models99 have also been used to investigate the effect of multivalent electrolytes on the orientational correlations between the patchy units: it was shown that a careful choice of electrolytes could be used to steer the particle assembly.102 Janus-like dipolar particles and protein-like units have also been modeled to understand how the charge distribution affects the properties of the fluid phase with a particular focus on gas–liquid phase separation.103 Finally, a highly sophisticated model for particles with icosahedral, octahedral, and tetrahedral charge decorations has been put forward to describe the effective interactions between viral capsids.104
Within this broad class of systems, we focus in the following on the results accumulated so far for the most studied IPC systems. We refer to the coarse-grained description of the effective interactions between IPCs that was originally developed for particles with two identical polar patches and an oppositely charged equatorial belt96 and later generalized to characterize colloids with richer surface patterns.105 The model features hard spherical particles with a surface divided into a few extended regions with different properties; the interaction between two IPCs is characterized by three independent sets of parameters: the interaction ranges of the different surface areas, their interaction strengths and their surface extents. These parameters can be related to the physical features of the underlying microscopic system – such as the electrostatic screening of the solvent around the colloids or the charges of the different regions of the particle surface – by developing a suitable description within the framework of the Debye–Hückel theory for dilute electrolytes.106 Thanks to this rigorous derivation, the resulting IPC model is not a toy model despite being characterized by a high degree of computational simplicity.
The distinctive feature of IPC systems is the non-trivial interplay between attractive and repulsive directional interactions: it characterizes the fluid phase107,108 as well as the gas–liquid phase separation109 and it gives rise to very interesting assembly and phase behaviors. In particular, numerical investigations on IPC systems with two identical polar patches have shown that an emerging feature of such systems is the formation of planar aggregates either as monolayers closed to a charged substrate94,95 or as bulk equilibrium phases.109,110
Close to a homogeneously charged substrate, IPCs with two identical patches form assemblies with well-defined translational and orientational order depending on the charge ratio of the different entities involved, the patch size and the interaction range (see Fig. 2).94,95 The features of these assemblies depend on the system parameters and were proven to reversibly respond to changing conditions such as the pH of the solution and the charge of the substrate.95 It is worth noting that the same morphological features observed in simulations have been found in experimental samples of IPCs sedimented on a glass substrate;41 however, while all clusters in the same numerical sample have the same spatial and orientational order, experimental IPCs form different particle arrangements within the same sample, probably due to the patch polydispersity.
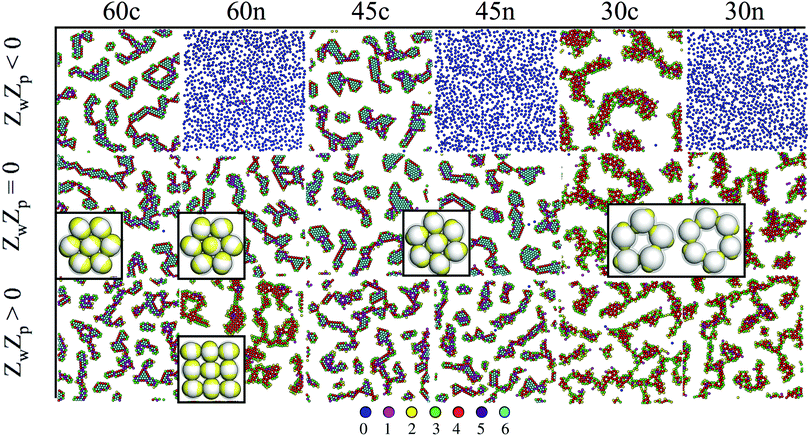 | ||
| Fig. 2 IPCs under planar confinement.94,95 Typical simulation snapshots of several types of IPCs (labelled from left to right as 60c, 60n, 45c, 45n, 30c and 30n, specifying both the patch opening angle and the net particle charge) under confinement between two parallel walls at distance 1.45 (in units of particle diameter); the top wall is always neutral, while the bottom wall can be either neutral (panels in the central row, labelled with ZwZp = 0, where Zw is the charge of a unit square on the bottom wall and Zp is the patch charge) or charged (panels in the top and bottom rows, labelled with ZwZp < 0 and ZwZp > 0, respectively). Particles are colored according to the number of bonded interactions; the corresponding color code is displayed at the bottom. | ||
In the bulk, a tendency towards two-dimensional ordering has been often observed. Three-dimensional structures with two-dimensional order are stabilized by several IPC systems with two identical patches. For overall slightly charged IPCs with relatively extended and long-ranged patches, a crystal formed by parallel monolayers is stable in a wide region of the temperature versus density plane;110 the region of stability of this laminar phase depends on the system parameters, e.g., it expands upon increasing the charge imbalance (that is, on changing the pH of the solution) and/or upon reducing the interaction range (i.e., on changing the salt concentration of the colloidal suspension).109 The formation of a similar lamellar structure can also be observed in a system of overall neutral IPCs. In contrast to the slightly overcharged case, neutral particles self-assemble into a lamellar phase which confines a disordered phase of mobile particles between the monolayers.111 Lamellar phases represent just one of the many assembly scenarios offered by IPCs: depending on the chosen parameters, IPCs with two identical patches can form an even wider zoo of exotic structures, among which there exist porous bulk phases characterized by parallel nano-channels.112 The control over the properties and the stability range of these phases will likely open up possibilities to build three-dimensional lattices with an open and very regular architecture, that might be used, e.g., for drug delivery purposes.
2.2 Patchy proteins
It is generally recognized that the interactions between globular proteins are direction dependent.13,16–22 Such a directionality generally stems from the overall shape of the folded protein, the distribution of hydrophobic residues on the protein surface and the distribution of charged residues. At physiological pH values, this results in a heterogeneous surface charge, with the range of the electrostatic interactions being set by the screening provided by ions in solution.103,113,114 The effect of heterogeneous surface charges and ion condensation on protein–protein interactions has recently been described in ref. 115 by an appropriately developed multipolar coarse-grained model. As pointed out in Section 2.1, this class of proteins is related to charged patchy colloids, and several models are being developed in this respect.100,103 The appropriate modeling of directional interactions caused by charge inhomogeneities can be challenging, in particular with respect to specific ion effects: for instance, by forming salt bridges, multivalent ions have very drastic effects on the effective interactions between proteins in solution to the point of rendering directional charge repulsions attractive.116 More refined models which take into account electric multipoles as well as the distribution of charged, neutral and hydrophobic residues have been developed.14,117The phase behavior of dispersions of proteins is of great interest both from a fundamental point of view and for applications. Since the precise folded structure of a given protein is not known a priori, detailed information on the shape and surface chemistry is not directly available. However, this information can be obtained through neutron or X-ray scattering experiments with crystallized proteins. Unfortunately, even when the knowledge on the architecture of individual proteins is obtained through scattering experiments after successful crystallization, it is not possible to visualize the self-assembly in a protein solution at the single molecule level.121 Consequently, the characterization of the phase behavior of protein solutions is mainly based on interactions with visible light that can be measured with common laboratory equipment and that provide insight into average properties.21,122–124 A recent review of the physics of protein self-assembly in the bulk is given in ref. 14. In general, the study of the phase behavior of protein solutions relies on many simplifications. It is most common for the shape of proteins to be approximated by spheres, with directional interactions being approximated by a set of patches, the number, distribution, extent and range of which are chosen by mapping average properties measured in experiments. The aforementioned parameters have for instance been chosen such that predictions of second-order thermodynamic perturbation theory matched with experimental information on the critical point18 or on the cloud-point (i.e. the temperature at which the solution becomes turbid).125 Within these approaches, the range of the interactions has been found to weakly depend on the salt concentration at high ionic strengths,18 while the strength of the interactions was observed to depend on the nature of the ions.126 Simple patchy models have also been helpful to describe the short-time diffusion of proteins under crowded conditions.127 More complex situations have been recently considered, such as mixtures of different proteins128 and non-spherical shapes.129–131
It is interesting to point out that the folded structure of bovine serum albumin in solution was recently shown to change in response to variations of pH and salt concentration;132 a similar conclusion was previously drawn from simulations on cluster formation in lysozyme solutions.113 It is therefore likely that, at least in some cases, the directional interactions between the proteins depend on the specific conformation in force of the presence of internal degrees of freedom in the proteins. Consequently, these should be considered among the bottom-up systems within the classification proposed in this review (see Section 3). On a similar note, it has been recently shown that proteins undergoing amyloid formation change their internal structure during aggregation, providing another clear example of bottom-up self-assembly.133
In biological environments, several copies of the same protein can self-assemble into multimeric finite-sized assemblies known as homomers,118 which play such an important biological role that their malfunctioning, due to misfolding or misassembly, can lead to the appearance of several diseases.119 Interestingly, the ensemble of observed homomers has been shown to be rather limited, which was related to the patchy nature of the interactions that drive homomer assembly and to the evolutionary processes that lead to homomer formation.118 Protein self-assembly into macroscopic phases, e.g. two-dimensional structures known as s-layers,120 is often based on homomer intermediates and, as such, can be considered as a bottom-up assembly (see Section 3.3).
2.3 Non-spherical patchy colloids
Over the last few decades, the availability of monodisperse non-spherical particles at the nano- and micro-scale134–136 has made it possible to design a vast variety of structures with different symmetries and packing densities.137–139 Shape anisotropy can be realized for instance by making use of different growth potentials of crystal planes,136,140 by embedding polymeric particles in a sacrificial polymer matrix that is then deformed141 or even by swelling polymeric particles in a three-dimensional colloidal crystal.135 Complex spheroidal shapes range from colloidal molecules46,49,142 to more complex colloidal aggregates, such as multipod-like clusters of spheres,143 while even more anisotropic particles range from convex units, such as rods,144 cubes140 and polyhedral particles,135 to concave shapes, such as tetrapods and octapods145,146 or bowl-shaped colloids.147 The particle shape plays an important role in the self-assembly of target structures with tailored properties. A systematic study of the assembly behavior of polyhedral hard particles of many different shapes has, for instance, made it possible to group polyhedra into four categories of organization: liquid crystals, plastic crystals, crystals, and disordered (glassy) phases.138 The same systems can also be mapped according to the coordination number in the fluid phase (i.e., the number of nearest neighbors surrounding each polyhedron in the fluid) and the shape factor (which measures the deviation from a sphere),137 thus providing a roadmap to drive the assembly into the desired direction. On the other side of the spectrum, colloidal branched nanocrystals, like tetrapods or octapods, tend to self-align on a substrate due to their geometry, making them interesting units for technological applications in both two- and three-dimensions.145,146 Finally, the particle shape can also be engineered in order to promote lock-and-key interactions:148–150 shape can be exploited to drive selective lock-and-key binding between colloids, thus realizing a simple mechanism of particle recognition and bonding.Beyond the already rich framework offered by non-spherical particles, the interplay between the anisotropy of the building blocks and well-defined bonding sites on the particle surface might open tantalizing new perspectives.
At the quasi two-dimensional level, the combination of shape- and bond-anisotropy has recently proven to direct the emergence of a rich assembly scenario. A combined numerical and experimental investigation has shown that unconventional long-range ordered assemblies can be obtained for a class of highly faceted planar nanocrystals only when combining the effect of shape anisotropy with directional bonding.151 Numerical investigations have also shown that regular polygonal nanoplates can be designed to assemble into many different Archimedean tilings:152 the competition between shape anisotropy and interaction patchiness was tuned to obtain either close-packed or open tilings, the latter emerging mainly in binary mixtures of different shapes. Moreover, a systematic numerical study of the assembly of convex hard nanoplates combined attractive edge-to-edge interactions with shape transformations:153 results were divided into space filling (not necessarily regular) tilings, porous (periodic) tilings and complex (disordered) tilings, thus providing an important insight into how shape and attractive interactions can be exploited to target specific tiling architectures. The development of heuristic rules for the design of two-dimensional superlattices would allow experimentalists to improve the crystal properties of already available structures as well as to access exotic phases with new interesting features. Progress in the synthesis of anisotropic nanoplates offers indeed many possibilities for the rational design of two-dimensional materials with, for instance, different optical and catalytic properties.154,155 It is worth noting that hard polyhedral tiles decorated with attractive patches can also be used to describe two-dimensional molecular networks:156 numerical investigations on rhombus tilings have for instance identified the mechanisms leading to the emergence of ordered or random phases.157 This study was successively extended by considering model molecules with particular rotational symmetries and studying their self-assembly into network structures equivalent to rhombus tilings.158 Along similar lines, the assembly under planar confinement of patchy rhombi with a fixed geometry – inspired by recently synthesized particles136 – has been investigated,159 focusing on how the number, the type and the position of the patches along the edges of the rhombi influence the tilings (see Fig. 3).
In the bulk, the combination of shape- and patch-induced directional binding has recently provided amazing examples of tunable ordered structures. Binary mixtures of different shapes with mutual attraction induced by isotropically distributed, complementary DNA strands can already exhibit a wide range of exotic extended architectures160–162 (see also Section 3.2): (i) anisotropic polyhedral blocks and spheres, for instance, assemble into complex superlattices that can be tuned by the choice of the DNA shells and the particle size mismatch between the two components of the mixtures;160 (ii) rigid tetrahedral DNA origami cages and spherical nano-particles can form a family of lattices based on the diamond motif.162 When focusing on one-component systems of anisotropic particles decorated with anisotropic bonding patterns, most of the results accumulated so far in the literature deal with Janus-like non-spherical entities – mainly elongated shapes carrying one or at most two patches – assembling into a vast variety of fiber-like structures with diverse applications. Janus nano-cylinders that form vertical, horizontal or even smectic arrays,163,164 ellipsoids with one patch in a Janus-like or “kayak” fashion that form ordered assemblies165 or even field-sensitive colloidal fibers,166 “Mickey Mouse”-shaped colloidal molecules that form tubular aggregates,167 and silica rods coated with gold tips that self-assemble into different multipods168 are just a few examples. The susceptibility of Janus-like anisotropic units to external fields can also be used to drive the assembly into string-like structures.169 Another very interesting example of patchy elongated building blocks is provided by rigid helical units with sticky ends: these colloids can self-assemble into structures with nontrivial topologies, such as links and knots,170,171 some of which have been recently experimentally realized.172
Finally, it is worth noting that the combined approach of complex shapes and bonding surface patches can provide insights into biological processes, such as the self-assembly of clathrin proteins into polyhedral cages173 or the formation of viral capsids.174 We note that the equilibrium assembly of polyhedral protein complexes175–177 is a broad field of investigation and, as such, we refer the interested reader to a very recent review on the topic.178
2.4 Patchy polymers
A large proportion of self-assembling processes in living systems adopt a modular approach based on the hierarchical assembly of simple units into larger heterogeneous objects. In particular, many biopolymers consist of a rather restricted set of different chemical units, called residues, that, once assembled into linear sequences, selectively acquire specific molecular functions and self-assembling properties. The use of a limited set of residues (20 for proteins and only 4 for DNA/RNA) defining a finite alphabet has the advantage that new target structures can be designed (e.g., through evolution) by just changing the order of the elements along the chain. Thus the same alphabet can be used for an efficient recycling of the precious residues: by disassembling chains that do not fulfill their purpose, waste in the form of isolated residues can be efficiently reused for new chains. Incidentally, this is why living organisms can eat each other and synthesize their own proteins from the ingested building blocks.Understanding how the linear information is translated into a three dimensional structure is usually referred to as the “protein folding problem” which will be discussed in Section 3.3. Translating the folding property into a purely artificial system would open up new possibilities for the design of novel materials. The assembly of nano- and micro-scale particles into self-folding strings could enable the cost-effective production of responsive meta-materials with unprecedented spatial control over the single particle positions. Indeed, the possible applications of such materials are extremely diverse: from nanoscale switches and sensors that respond to, for instance, temperature, light or pH, to catalysts (mimicking the spatially defined catalysis of proteins)179–181 and materials with three-dimensional connectivity that can be used, e.g., to optimize charge separation in photovoltaics.182,183
In order to reproduce the protein folding process at the nano- and micro-scale level, patchy particles can prove themselves essential: anisotropically interacting units arranged in strings could play the same role as the residues constituting the proteins, effectively constructing functionalized colloidal chains, the so-called “patchy polymers”184–186 (see panel (a) of Fig. 4). Simulations have shown that control over the folding of particle chains can be obtained by combining three main ingredients:184–186 (i) the availability of chains composed of units interacting through different isotropic potentials, (ii) the control over the particle sequence, and (iii) the presence of directional attractions between the chain units. While the isotropic interactions mimic the chemical flavor of the constituent units along the chain, the directional interactions, induced by, e.g., surface patches, mimic the hydrogen-bonds along the backbone of natural biopolymers. The imprinting of the target structure using a finite alphabet is guaranteed by a reduction of the number of accessible configurations: both hydrogen-bond and patch–patch contact networks (in analogy to the secondary structure in proteins) increase the statistical weight of the configurations that are geometrically compatible with the bond directionality. The generality and versatility of the self-assembly strategy described above has been demonstrated by the successful design and folding of chains made of just two different isotropically interacting units, each decorated with two patches.185 Interestingly, knot-like structures can be chosen as targets for the folding and, in analogy with proteins, such knotted configurations can significantly change the melting temperature of these targets upon cyclization.184 Further work to characterize the relative designability of the knotted topologies is in progress. Recently, the designability properties of linear patchy polymers have been exhaustively explored in terms of alphabet size and number of patches.187 An interesting re-entrant behavior emerged, indicating a “designability window” for the number of patches. The boundaries of the re-entrant region are defined by the number of patches, which should be high enough to reduce the number of statistically relevant compact configurations and low enough to preserve the anisotropic nature of the monomer–monomer directional interactions. This systematic exploration led to the formulation of a simple criterion to predict a priori the designability of different polymer architectures – a criterion that natural proteins also fulfil. This criterion is based on the appearance of a particular peak in the radial distribution function that dominates over the random packing of the patchy units and is thus experimentally accessible.187
The results accumulated so far suggest that designability can be controlled by any strategy that reduces the configurational entropy per monomer, directionality being one example, another example being purely steric constraints.188,189 It would thus be possible to define a general relationship between the configurational entropy per monomer and the alphabet size that controls the boundaries of the designability window, thus serving as a universal guideline to achieve designability. Novel experimentally realizable polymer systems could be conceived using such a guideline.
3 Patchy particles from the bottom-up route
All systems discussed in Section 2 have in common that the particle bonding pattern is permanent and does not change during the interactions with other units. As pointed out in the previous section, the production of patchy units via top-down approaches has some limitations that might hinder the successful assembly of novel materials. Some of these limitations can be overcome by employing molecular building blocks undergoing a hierarchical self-assembly process: the basic idea of the bottom-up route is to use microscopic constituents, such as polymers or biopolymers, that are able to self-assemble into nano- and micro-scale objects, which, in turn, can generate supramolecular assemblies. Bottom-up approaches allow us to obtain precisely defined units, with high yield, precision and monodispersity, once the appropriate sub-units are chosen or designed; the product of the first self-assembly stage, which in the field of proteins is referred to as folding, is a finite structure that successively undergoes a second assembly step. The general strategy relies on the spontaneous emergence of the structure of the intermediate constructs, which stems directly from the microscopic properties of the basic molecular constituents: the latter already contains information about the former. In this section, we focus on systems where, at the level of the intermediate constructs, directional bonding and limited valence emerge; these intermediate objects can thus be referred to as patchy units. The emergence of patchy-particle-like constructs via hierarchical self-assembly yields particles that are different and inherently more complex than their hard counterparts: being a result of the, often reversible, bonding between smaller objects, these patchy units have many internal degrees of freedom and, as a consequence, are intrinsically floppy. Interestingly, softness itself is an emergent trait of this class of particles, and as such can be tuned by changing the microscopic constituents, hence allowing for a systematic study of its role in the dynamics and thermodynamics of soft-matter systems. The presence of inner degrees of freedom in the particles has been proven to play an important role in the determination of the thermodynamics of soft-matter systems,190 going as far as controlling the stability of whole phases.191 In particular, it was shown that patchy systems combining low valence, bond flexibility and soft interactions can stabilize the liquid phase in contrast to the solid one even in the zero-temperature limit, meaning that even at extremely low temperatures the entropic term prevails over the energetic term in the free energy balance of such systems.190 These results were found for patchy models apt to describe associating fluids or DNA-coated colloids with limited valence, but also tetravalent DNA nanostars, i.e. extremely flexible patchy units with four bonding patches, were shown to never crystallize and form instead a thermodynamically stable, fully bonded equilibrium gel.191In recent years, polymer-based macromolecules or nanocomposites (such as mixtures of polymers and colloids) were shown to be extremely powerful and versatile systems for the self-assembly of soft functionalized nanoparticles.26 Janus-like, triblock, striped and multi-patch units can indeed be created by playing with the topology, the geometry and the type of polymeric macromolecules.192–197 Compared to their hard counterparts, soft functionalized nanoparticles from polymer-based systems offer a large and easily accessible playground to direct the design of the desired functionalization. On the other hand, the real time and real space visualization of polymer-based systems through light microscopy is practically impossible because of the small sizes of the forming particles and patches, that are, in turn, limited by the lengths of the polymers. Electron microscopy provides an insight into the structures present in the sample, but the dynamics are hard to follow and one should be always aware of possible artifacts introduced by sample preparation. It should also be noted that, in most cases, the patchiness of the resulting units is frozen in; nonetheless, in principle, these patchy units can be allowed to rearrange by changing the solvent conditions. In Section 3.1, we report several examples of control over the formation of anisotropic units through the specific features of polymeric macromolecules, showing also how the microscopic parameters can influence the emergence of, e.g., gel-, string- or sheet-like structures.192–197 In Sections 3.2 and 3.3, we extend our discussion from polymers to biopolymers, where the control over the self-assembled functionalized units is achieved by making use of distinct alphabets of molecular bricks. Proteins are biopolymers composed of 20 different types of amino acids, the sequence of which determines the way in which they fold and – through their natural conformation – the function they have in nature; DNA molecules are composed of nucleotides of four different types. The interactions between biopolymers such as proteins and DNA are very specific both in direction and in the choice of binding partners. The interactions between DNA monomers for instance are dominated by strongly directional Watson–Crick pairing and have been used in many man-made self-assembling systems. Section 3.2 presents recent advancements related to man-made DNA-based systems, while in Section 3.3, we discuss the progress in predicting the folding of proteins as well as the use of protein–ligand interactions in detail.
3.1 Polymer-based systems
Polymers are macromolecules consisting of a sequence of monomeric units, each with specific chemical properties, linked by means of covalent bonds. Polymeric macromolecules can consist of either a sequence of identical units – homopolymers – or sequences of units interacting selectively with the solvent: solvophobic or solvophilic monomers can be distributed either in groups – block copolymers – or evenly – heteropolymers – along the chain. The selective interactions of the monomeric units with the solvent as well as the physical and topological constraints within each polymer give rise to an intramolecular competition between entropic and enthalpic factors: on the one hand, solvophobic monomers tend to minimize their exposure to the solvent, thus giving rise to effective enthalpic attractions between themselves, while solvophilic monomers tend to maximize their contact with the solvent; on the other hand, the tethering between the various monomers and the finite volume occupied by each of them give rise to an intramolecular entropic repulsion. The interplay between entropic and enthalpic factors drives intramolecular self-assembling processes.A first possibility to obtain nanoparticles with effective directional interactions consists in grafting repulsive polymeric units onto attractive nano-scale colloids. Both experiments198 and simulations199 have shown that these grafted nanoparticles robustly self-assemble into a variety of superstructures that are anisotropic typically observed only in systems of anisotropically interacting units. This result, which stems from the deformability of the polymeric corona, holds for both homogeneously and inhomogeneously grafted units at low and intermediate grafting densities. The characterization of the directional interactions induced by grafting homopolymeric units onto nanoparticles has been theoretically investigated in ref. 200. Both homogeneously and inhomogeneously grafted nanoparticles were shown to qualitatively behave as Janus particles with patches whose size can be predetermined by analytical calculations and appears to be related to the number of grafted homopolymeric chains and to the size ratio between the radius of gyration of the grafted macromolecules and the radius of the nanoparticle. Such an analytical result has been confirmed by extensive simulations performed on colloids functionalized with a low-density homopolymeric grafting. These particles are shown to exclusively belong to the Janus class irrespective of the number of grafted chains, thus rendering it clear that simple homopolymeric units grafted onto a central core might not be able to give rise to functionalized particles with more than one patch.201 In order to reach such a goal it thus appears to be important to add some chemical complexity to the system. Similar to permanently grafted nanoparticles, dendrimeric hydrophobic hosts with condensed hydrophilic polymeric guest molecules were also shown to form aggregates whose architecture is driven by anisotropy. Here the directional interactions depend on the amount of guest molecules on the hosts which in turn is dynamically controlled via the guest molecule concentration.194
A completely different class of patchy units can be obtained by a careful blending of polymeric ingredients only. For instance, Janus-like particles can be obtained by mixing two different phase-separating homopolymers in a solution containing also a non-solvent to both polymers. In this case, the Janus fraction is controlled by the different properties of the two polymers, their molecular weights and the mixing ratios of the various components.192 The assembly scenario can be enriched to include striped and multi-patch particles by linking the two homopolymers together and mixing the resulting diblock copolymer with one of the two original homopolymers.192 The collapse of linear copolymers into particles presenting regions with different levels of hydrophobicity and hydrophilicity had already been shown when copolymeric units had been used to mimic protein like structures.202,203 By exposing linear chains of block copolymers to a solvent that is bad for both parts, it is possible to make the chains collapse into spherical objects. The subsequent phase separation taking place between the two different blocks can be exploited to obtain particles with heterogeneous surfaces.204 The main strength of such an approach is its simplicity, while the size and distribution of the functionalized regions which self-assemble on the collapsed macromolecule are not easily controllable. By playing with both the geometry of the polymeric macromolecules and the composition of the solution, more complex scenarios can emerge: patchy micelles can spontaneously assemble from a binary mixture of diblock copolymers having a common polymeric section, with the patchiness of the system being determined by the solvent quality through the pH.193 Similar results can be obtained by imposing different topological constraints, for instance by binding three homopolymers together. Changing the way in which the three types of polymers are linked together controls the functionality of the system: triblock copolymer chains196 and stars195 have been shown to self-assemble into patchy particles that then form string- and sheet-like superstructures or even open lamellar and cylindrical aggregates depending on the concentration of particular ions (that modifies the solubility of one of the arms), the volumes occupied by the different groups and/or the solvent quality.195,196
Finally, very promising polymeric macromolecules that have been recently shown to self-assemble into soft functionalized units are diblock copolymer stars, also referred to as telechelic star polymers (TSPs).205 Experimental realizations of such macromolecules are, e.g., end-functionalized star polymers.197,206,207 TSPs are obtained by grafting f diblock copolymers, each consisting of a solvophobic and a solvophilic section, onto a central anchoring point: the solvophilic heads form the soft particle core, while the solvophobic tails are exposed to the solvent and form a shell that can either be equally distributed or assembled into distinct regions on the surface. In selective solvents, the intra-star association can lead to the formation of soft patchy units. The number and the size of the resulting patches depend on f, the percentage of attractive monomers in the polymer chains, α, and the solvent properties (temperature, pH, etc.).208–211 In particular, by exploring the single molecule state diagram as a function of f and α, slightly below the Θ-temperature of the solvophobic part, it was shown that such systems self-aggregate into patchy assemblies. The impressive peculiarity of TSP systems is that the stars retain at finite density the valence and the patchiness observed at zero density. Thanks to their robust and flexible architecture, TSPs have been dubbed “soft Legos” possessing the ability to self-assemble at different levels: at the single-molecule level, TSPs order as soft patchy colloids which then, at the supramolecular level, stabilize complex phases that are compatible with the functionalization of the single, self-assembled units. These supramolecular structures include gel-like networks210 and complex crystal structures,209 such as diamond or cubic phases (see Fig. 5). It is worth stressing that the number of functionalized (patchy) regions is completely controlled by the choice of a pre-determined set of chemical and/or physical parameters. Indeed, in addition to the permanent parameters (f, α), the valence of the self-assembled functionalized units can be altered via the solvation conditions, i.e., the chemical composition of the solvent, the pH or temperature,211 thus rendering TSPs fully versatile and tunable flexible self-assembling building blocks. The possibility to tune the number and the equilibrium arrangement of the patches, in combination with the capability of these patchy assemblies to maintain their internal structure at finite density, strongly motivated the development of a coarse-grained model inspired by TSPs and well-suited for the investigation of the bulk behavior of these systems. In particular, the model has been used to elucidate the role of softness and patch rearrangement in the formation of gel networks at a level where both features can be controlled by appropriately chosen parameters.212
3.2 DNA-based systems
Biological systems use DNA to store and retrieve genetic information. The information is encoded in a linear fashion by a four-letter alphabet thanks to the high selectivity provided by the Watson–Crick base pairing. This high selectivity, together with the very different mechanical properties of single- and double-strands, makes DNA an excellent candidate for bottom-up self-assembly.27 Using DNA has a few additional advantages. First of all, nature provides a whole set of enzymes that facilitate working with nucleic acids. Secondly, the cost of synthetic and viral DNA has dropped significantly in the last decade. Lastly, DNA- or RNA-based structures can also be employed as medical tools by virtue of their compatibility with biological matter.213 As a consequence, the use of DNA in materials science and nanotechnology has grown considerably in the last few years.The notion of using DNA as a building block dates back to the 1980s, when N. C. Seeman started working on DNA-based materials.214 On one side, his seminal work spurred the fast development of what is today known as DNA nanotechnology,215 which employs DNA as a tool to build molecular motors,216 logic gates217 and finite-sized objects with pre-designed shapes such as polyhedra,218,219 tubes220,221 or even complicated, irregular structures, e.g., DNA origami,222 which can be used as nano-scaffolds for high precision experiments223–225 or even as drug delivery vectors.213 On the materials science side, the early results obtained by Seeman and others showed that DNA can also be used as a building block for the generation of ordered and disordered bulk phases.27,226–228
DNA-based soft-matter building blocks have been historically divided into two distinct categories: DNA-coated colloids (DNA-CC) and all-DNA supramolecular constructs (all-DNA). Both strategies exploit the selective binding provided by the Watson–Crick mechanism to introduce an effective, temperature-dependent interaction between the basic constituents of the system, although the two schemes are essentially different and have different advantages and disadvantages. However, there exist a few systems which sit in the middle and can be seen as intermediate between DNA-CC and all-DNA systems. Relevant examples are very small particles grafted with very sparse, ultrashort strands229 and mixtures of DNA-CCs and DNA origami.162
However, valency can also be enforced in systems made of uniformly grafted DNA-CC, provided that the DNA strands can diffuse over the surface,240 as suggested by Angioletti-Uberti et al.241 The basic idea revolves around grafting additional non-binding DNA strands onto the particle surface: thanks to the many-body nature of the interaction between DNA-CC, the resulting particle valence is controlled by the interplay between the non-specific repulsion, which depends on the strand length, temperature and salt concentration, and the attraction due to DNA hybridisation. Coarse-grained simulations show that, in contrast to DNA-CC with immobile DNA linkers, these limited-valence DNA-CC can self-assemble into open structures.241
The possibility of going beyond uniformly grafted DNA-CC has been recently demonstrated by the development of techniques aimed at grafting single DNA-strands with specific arrangements on the surface of colloids.242,243 As shown by Halverson and Tkachenko, these directionally functionalized DNA-CC could provide a route to generate error-free mesoscopic structures with high yield.244
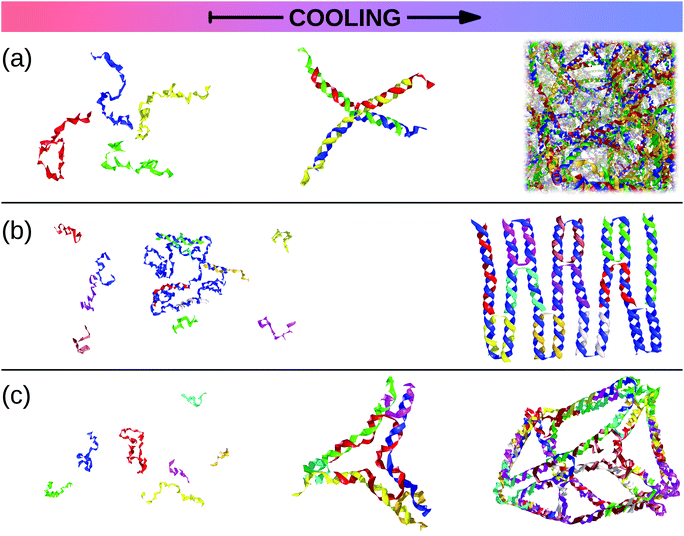 | ||
| Fig. 6 Snapshots taken from oxDNA simulations230 of all-DNA self-assembling systems. As the temperature, T, goes down (from left to right), single strands join to form larger structures. (a) The hierarchical self-assembly of an all-DNA gel: as T decreases, single strands assemble into tetravalent DNA-constructs which, in turn, link with each other to form a physical gel.231,232 (b) A solution of a long scaffold strand (in blue) and short staple strands at high temperature turns into a small DNA origami as T is lowered (courtesy of Ben Snodin). (c) All-DNA tiles can be used as building blocks to assemble more complicated supramolecular structures such as polyhedra or cage-like structures (courtesy of John Schreck).218,219 | ||
This connection between simple anisotropic toy models and DNA constructs has been further strengthened by recent experiments on trivalent and tetravalent DNA nanostars, i.e. DNA constructs with a fixed valence of three and four, respectively. Bellini and co-workers have carried out measurements of the low-density phase diagram and dynamics of these nanostars, providing the first experimental confirmation of the dependence of the size of the gas–liquid instability region on the valence231 and a thorough characterization of the structural and dynamical properties of the equilibrium gel phase.250–252 On the numerical side, accurate coarse-grained simulations and liquid-state theories have been shown to match experimental results,232,253 supporting the experimentally observed thermodynamic stability of the disordered gel with respect to crystallization,191 in line with recent results on toy models of patchy particles.254 In a similar fashion, building on earlier numerical and theoretical work done on toy models,255 mixtures of different DNA constructs have been used to synthesize a material that gels on heating.256
The collection of these results suggests that the phenomenology observed in patchy systems can be reproduced by all-DNA systems, provided that the intrinsic flexibility of DNA is taken into account.191,254
3.3 Biopolymers and proteins
Biopolymers in general, and proteins in particular, provide one of the most spectacular examples of bottom-up self-assembly. The peculiarity of these macromolecules is that they self-assemble at the single molecular level, ending up in a folded state that is completely determined by the sequence of monomers that constitute the polymeric chains. A sub-family of biopolymers has already been discussed in Section 3.2, where it was shown that DNA and RNA can be exploited as tunable self-assembly agents. Here, we focus on the properties of another class of biopolymers: proteins, a system that is the natural inspirer of the patchy polymers discussed in Section 2.4.Proteins are heteropolymers of different length composed of 20 different types of amino acids. Depending on the amino-acid sequence, some proteins can collapse to form a well-defined “native” conformation, while others cannot. The process of forming a compact, native structure is referred to as folding. The folded structure often exposes one or more active regions to the environment: given the highly specific and directional nature of their interactions, these areas can be regarded as patches in the language of colloidal science, as discussed in Section 2.2. The tasks that proteins perform are incredibly diverse. However, they most often involve interactions with other proteins or biomolecules, such as DNA or RNA. These interactions are controlled by the same elements that encode for the native structure of the protein itself. Structure and function are, as a consequence, strongly correlated, and directly dependent on the sequence of amino acids along the protein chain. Hence, unveiling the fundamental properties of proteins is of paramount importance to understand and control the physiology of living organisms at the molecular level. The majority of biochemical reactions in living organisms is based on the activity of proteins.15 Each protein performs a specific set of functions that generally requires folding the chain into specific configurations15,257 or even fluctuating within an ensemble of configurations.258–261 This remarkable property can be exploited in applications either by creating protein-like systems (e.g., the patchy polymers described in Section 2.4) or by creating artificial proteins designed to self-assemble into target architectures. Despite encouraging results, computational protein folding262–269 and protein design270–284 remain a daunting task. The potential applications that could profit enormously from computational protein design can be divided into three main categories: chemistry (e.g., enzyme design179,285–287), materials science282,283,288 and medicine, where computational approaches could significantly contribute to drug design by, for instance, offering new and more powerful delivery methods for existing anti-cancer drugs.3,289
One of the major challenges to design efficient drug delivery vectors is the engineering of the particle functionalization to discriminate between cancerous and healthy tissues. Being present in high concentrations on different typologies of tumor cell membranes, several biomarkers or receptors290–292 would be optimal targets, were it not that they are also present on healthy cells, albeit at lower concentrations. One strategy to overcome this problem relies on multivalency, i.e. the possibility for the same drug delivery vector to bind selectively with many ligands at the same time. The effective binding with the cell membrane becomes thus very sensitive to the concentration of the biomarker. Super-selective multivalent drugs bind preferentially to surfaces rich in target receptors. Multivalent particles are proving to be a promising new direction in nanomedicine,293–298 and are in particular very effective against several types of cancerous cells.293–296,298–306 A key point is that the interaction between the nanoparticle ligands and the target receptors must be both selective and weak, so that, in analogy to Velcro®, the particle only binds to surfaces that have a high concentration of receptors.307,308 Currently, coatings targeting cancers are identified mainly through large trial and error screenings with limited help from computational modelling, and without specific design to control the binding affinity. The key to the realization of velcro-like particles is in the design of both the binding strength and specificity of the ligand–receptor bonds293,307 as well as the control over the geometrical distribution of the ligands on the surface of the nanoparticles. Proteins are an optimal choice as ligands since they offer excellent control over binding selectivity and can be chosen so as to minimize the interference with normal cell function. Unfortunately, among natural proteins it is very hard to select for ligands with low binding strength while maintaining a high selectivity. A computational approach might thus provide such control and could be used to design and test new efficient cancer-targeting drug delivery vectors. A possible strategy to achieve the design of multivalent drug delivery vectors will require a protein design method and a way to control the binding affinity without affecting the specificity towards the target receptors.
Full-atomistic protein models are a very successful approach to the computational modeling of proteins. Such models are detailed representations where all atom–atom interactions, including interactions with the solvent molecules, are explicitly taken into account and are used to infer the equilibrium properties as well as to characterize the protein dynamics. Examples that summarize the current possibility of computer-aided protein design are as follows: the mutation of buried core residues to alter the inner packing of the target proteins272,274–276,310 or to increase protein thermal stability,278 the introduction of residues in order to catalyze specific chemical reactions,311 the synthesis of entirely novel sequences for existing protein structures,273 and, finally, the design of proteins not found in nature.282,312–316 The major drawback of full-atomistic models is that they require massive computational resources, which is the biggest limitation to computational drug design. Moreover, none of the methods developed so far has successfully designed proteins with tuned ligand–receptor interaction strengths.
A direct approach to solving the IFPs would be to use large computer facilities to exhaustively screen sequences capable of folding into a target structure. The enormous number of possible sequences that one would need to test is beyond the available computational power (e.g., a short peptide of just 20 amino acids corresponds to ∼1018 sequences, out of which only a negligible small fraction would fold into the target structure). Shakhnovich et al.317,318 developed a protein design strategy based on the Random Energy Model (REM),319,320 which describes the freezing transition of a heteropolymer in a mean field approach. The validity of the REM solution to the IFPs has been extensively proven using lattice models.318,321–327 Recently, Coluzza328,329 has extended the REM approach off-lattice, introducing the Caterpillar coarse-grained model based exactly on the idea that the proteins are pre-sculpted by molecular features. In the Caterpillar protein model, the amino acids are represented as overlapping spheres anchored along the backbone (see panel (b) of Fig. 4). The model has only transferable parameters that have been adjusted so that the designed sequences refolded to their native structures.329
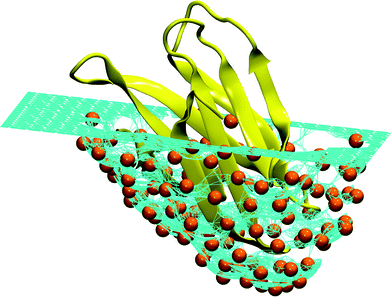 | ||
| Fig. 7 Schematic representation of an ideal pocket designed to reproduce the structure of the human Fas apoptotic inhibitory protein (PDB Id. 3mx7).330 The turquoise surface covering the protein (colored yellow) is made of a mesh of hard particles (colored orange) with the radius equal to the hard core radius of the Caterpillar model (2 Å). When the protein is pushed into the mesh, the hard particles are repelled by the self-avoiding interaction. Different surfaces can be obtained by changing the orientation of the protein and the maximum depth. It is interesting to notice that this procedure is reminiscent of the experimental techniques used to produce molecular moulds.331–334 | ||
4 Conclusions
Self-assembly is a fundamental mechanism that rules nature at the atomic/molecular scale and is nowadays exploited in materials science to build desired structures at the colloidal (nano- or micro-) scale. The spontaneous formation of a target equilibrium architecture is profoundly affected by the thermodynamic balance between entropic and energetic contributions as well as by the aggregation kinetics of the self-assembly process. The interplay between these factors can be to some extent controlled when the self-assembling units possess themselves some additional information for their spontaneous organization. The newest and most successful routes to self-assembled materials rely on anisotropy: extra instructions for the assembly of target materials with desired architectures and properties can be imparted upon the particles if the interactions are no longer merely isotropic but rather depend on the relative positions and orientations of the particles with respect to each other. In this review, we have focused in particular on soft matter systems characterized by a limitation on the number of bonds that each unit is able to form: by virtue of the asymmetry and selectivity of their interaction patterns, particles with limited bonding valence are excellent basic units for the spontaneous assembly of desired structures. We considered a broad range of systems and traced out some of the emerging trends in the design of functionalized particles for the assembly of materials with tailored properties. Contextually, we also proposed some related insights into the mechanisms behind some naturally occurring phenomena such as protein folding and protein crystallization. The topics touched upon in the present review are highly interdisciplinary, involving physics, chemistry, chemical engineering and bio-related sciences, so that a unique framework is hard to be drawn. Among the rich variety of units characterized by limited bonding valence, such as patchy colloids, proteins, polymers and DNA-based systems, we focused on a selection of functionalized building blocks that we believe to be very promising. In particular, we reported in detail on some ingredients of self-assembling systems that might be crucial to gain an ever greater control over the forming structures, such as emerging directionality between charged units, the role of pre-existing bonds between some of the assembling units, the interplay between anisotropic particle shapes and bonding patterns, enhanced fluctuations of the bonding patterns, and/or the control over bond specificity.Acknowledgements
The authors are deeply indebted to C. Dellago, G. Kahl, C. N. Likos and E. Reimhult for fruitful discussions. EB acknowledges support from the Austrian Science Fund (FWF) under Proj. No. M1170-N16 (Lise Meitner Fellowship) and V249-N27 (Elise Richter Fellowship). BC acknowledges support from the Austrian Academy of Sciences (ÖAW) through Grant No. 11723. IC acknowledges support from the FWF under Proj. No. P26253-N27. LR acknowledges support from the European Commission through Marie Skłodowska-Curie Fellowship No. 702298-DELTAS and the FWF through Lise-Meitner Fellowship No. M 1650-N27. PvO acknowledges support from the FWF under Proj. No. P27544-N28.References
- A. N. Shipway, E. Katz and I. Willner, ChemPhysChem, 2000, 1, 18–52 CrossRef CAS PubMed.
- O. D. Velev and E. W. Kaler, Langmuir, 1999, 15, 3693 CrossRef CAS.
- M. Wang and M. Thanou, Pharmacol. Res., 2010, 62, 90–99 CrossRef CAS PubMed.
- T. F. A. de Greef and E. W. Meijer, Nature, 2008, 453, 171 CrossRef CAS PubMed.
- P. Cordier, F. Tournilhac, C. Souliee-Ziakovic and L. Leibler, Nature, 2008, 451, 977 CrossRef CAS PubMed.
- E. Armstrong and C. O'Dwyer, J. Mater. Chem. C, 2015, 3, 6109 RSC.
- G. M. Whitesides and M. Boncheva, Science, 2002, 295, 2418 CrossRef CAS PubMed.
- L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2015, 14, 2 CrossRef CAS PubMed.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407 CrossRef CAS.
- S. C. Glotzer, Science, 2004, 306, 419 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150 CrossRef CAS PubMed.
- E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397 RSC.
- W. Li, B. A. Persson, M. Lund, J. Bergenholtz and M. Z. Oskolkova, J. Phys. Chem. B, 2016, 120, 8953–8959 CrossRef CAS PubMed.
- J. J. McManus, P. Charbonneau, E. Zaccarelli and N. Asherie, Curr. Opin. Colloid Interface Sci., 2016, 22, 73–79 CrossRef CAS.
- A. R. Fersht, Structure and Mechanism in Protein Science, W. H. Freeman and Company, New York, 1999, p. 650 Search PubMed.
- A. Lomakin, N. Asherie and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9465–9468 CrossRef CAS.
- M. Hloucha, J. Lodge, A. Lenhoff and S. Sandler, J. Cryst. Growth, 2001, 232, 195–203 CrossRef CAS.
- C. Gögelein, G. Nägele, R. Tuinier, T. Gibaud, A. Stradner and P. Schurtenberger, J. Chem. Phys., 2008, 129, 085102 CrossRef PubMed.
- D. Fusco and P. Charbonneau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012721 CrossRef PubMed.
- D. Fusco and P. Charbonneau, J. Phys. Chem. B, 2014, 118, 8034–8041 CrossRef CAS PubMed.
- M. K. Quinn, N. Gnan, S. James, A. Ninarello, F. Sciortino, E. Zaccarelli and J. J. McManus, Phys. Chem. Chem. Phys., 2015, 17, 31177–31187 RSC.
- D. J. Audus, F. W. Starr and J. F. Douglas, J. Chem. Phys., 2016, 144, 074901 CrossRef PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- G.-R. Yi, D. J. Pine and S. Sacanna, J. Phys.: Condens. Matter, 2013, 25, 193101 CrossRef PubMed.
- S. Jiang and S. Granick, Langmuir, 2009, 25, 8915–8918 CrossRef CAS PubMed.
- R. L. Marson, T. D. Nguyen and S. C. Glotzer, MRS Commun., 2015, 5, 397–406 CrossRef CAS.
- N. C. Seeman, Nature, 2003, 421, 427–431 CrossRef PubMed.
- R. M. Choueiri, E. Galati, H. Therien-Aubin, A. Klinkova, E. M. Larin, A. Querejeta-Fernandez, L. Han, H. L. Xin, O. Gang, E. B. Zhulina, M. Rubinstein and E. Kumacheva, Nature, 2016, 538, 79 CrossRef CAS PubMed.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- F. Smallenburg, L. Leibler and F. Sciortino, Phys. Rev. Lett., 2013, 111, 188002 CrossRef PubMed.
- M. Lattuada and T. A. Hatton, Nano Today, 2011, 6, 286–308 CrossRef CAS.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed.
- É. Duguet, C. Hubert, C. Chomette, A. Perro and S. Ravaine, C. R. Chim., 2016, 19, 173–182 CrossRef.
- A. B. Pawar and I. Kretzschmar, Langmuir, 2008, 24, 355–358 CrossRef CAS PubMed.
- Z. He and I. Kretzschmar, Langmuir, 2012, 28, 9915–9919 CrossRef CAS PubMed.
- Q. Chen, E. Diesel, J. K. Whitmer, S. C. Bae, E. Luijten and S. Granick, J. Am. Chem. Soc., 2011, 133, 7725–7727 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Langmuir, 2009, 25, 9057–9063 CrossRef CAS PubMed.
- Q. Chen, S. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
- L. Hong, A. Cacciuto, E. Luijten and S. Granick, Nano Lett., 2006, 6, 2510–2514 CrossRef CAS PubMed.
- C.-C. Lin, C.-W. Liao, Y.-C. Chao and C. Kuo, ACS Appl. Mater. Interfaces, 2010, 2, 3185–3191 CAS.
- P. D. J. van Oostrum, M. Hejazifar, C. Niedermayer and E. Reimhult, J. Phys.: Condens. Matter, 2015, 27, 234105 CrossRef CAS PubMed.
- T. Ding, Y. Tian, K. Liang, K. Clays, K. Song, G. Yang and C.-H. Tung, Chem. Commun., 2011, 47, 2429–2431 RSC.
- O. Cayre, V. N. Paunov and O. D. Velev, J. Mater. Chem., 2003, 13, 2445 RSC.
- T. Tigges, D. Hoenders and A. Walther, Small, 2015, 11, 4540–4548 CrossRef CAS PubMed.
- P. Seidel and B. J. Ravoo, Macromol. Chem. Phys., 2016, 217, 1467–1472 CrossRef CAS.
- V. N. Manoharan, M. T. Elsesser and D. J. Pine, Science, 2003, 301, 483–487 CrossRef CAS PubMed.
- Y. Wang, A. D. Hollingsworth, S. K. Yang, S. Patel, D. J. Pine and M. Weck, J. Am. Chem. Soc., 2013, 135, 14064–14067 CrossRef CAS PubMed.
- D. J. Kraft, J. Hilhorst, M. A. P. Heinen, M. J. Hoogenraad, B. Luigjes and W. K. Kegel, J. Phys. Chem. B, 2011, 115, 7175–7181 CrossRef CAS PubMed.
- A. Désert, I. Chaduc, S. Fouilloux, J.-C. Taveau, O. Lambert, M. Lansalot, E. Bourgeat-Lami, A. Thill, O. Spalla, S. Ravaine and E. Duguet, Polym. Chem., 2012, 3, 1130–1132 RSC.
- D. J. Kraft, R. Ni, F. Smallenburg, M. Hermes, K. Yoon, D. A. Weitz, A. van Blaaderen, J. Groenewold, M. Dijkstra and W. K. Kegel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10787–10792 CrossRef CAS PubMed.
- S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578 CrossRef CAS PubMed.
- L. M. Ramrez, S. T. Milner, C. E. Snyder, R. H. Colby and D. Velegol, Langmuir, 2010, 26, 7644–7649 CrossRef PubMed.
- L. M. Ramrez, A. S. Smith, D. B. Unal, R. H. Colby and D. Velegol, Langmuir, 2012, 28, 4086–4094 CrossRef PubMed.
- L. M. Ramrez, C. A. Michaelis, J. E. Rosado, E. K. Pabón, R. H. Colby and D. Velegol, Langmuir, 2013, 29, 10340–10345 CrossRef PubMed.
- A. V. Blaaderen, A. Imhof, W. Hage and A. Vrij, Langmuir, 1992, 8, 1514–1517 CrossRef.
- W. K. Kegel, Langmuir, 2000, 16, 939–941 CrossRef CAS.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef CAS PubMed.
- Z. Wang, H. Liu, S. H. Yang, T. Wang, C. Liu and Y. C. Cao, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12387–12392 CrossRef CAS PubMed.
- S. Gangwal, O. J. Cayre and O. D. Velev, Langmuir, 2008, 24, 13312–13320 CrossRef CAS PubMed.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef PubMed.
- S. K. Smoukov, S. Gangwal, M. Marquez and O. D. Velev, Soft Matter, 2009, 5, 1285–1292 RSC.
- S. Gangwal, A. Pawar, I. Kretzschmar and O. D. Velev, Soft Matter, 2010, 6, 1413–1418 RSC.
- I. Kretzschmar and J. H. Song, Curr. Opin. Colloid Interface Sci., 2011, 16, 84–95 CrossRef CAS.
- H. R. Vutukuri, F. Smallenburg, S. Badaire, A. Imhof, M. Dijkstra and A. van Blaaderen, Soft Matter, 2014, 10, 9110–9119 RSC.
- B. Bharti and O. D. Velev, Langmuir, 2015, 31, 7897–7908 CrossRef CAS PubMed.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882 CrossRef CAS.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef PubMed.
- J. P. K. Doye, A. A. Louis, I.-C. Lin, L. R. Allen, E. G. Noya, A. W. Wilber, H. C. Kok and R. Lyus, Phys. Chem. Chem. Phys., 2007, 9, 2197 RSC.
- M. N. van der Linden, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2012, 136, 054904 CrossRef PubMed.
- A. Reinhardt, F. Romano and J. P. K. Doye, Phys. Rev. Lett., 2013, 110, 255503 CrossRef PubMed.
- S. Roldán-Vargas, F. Smallenburg, W. Kob and F. Sciortino, Sci. Rep., 2013, 3, 2451 CrossRef PubMed.
- L. Rovigatti, V. Bianco, J. M. Tavares and F. Sciortino, J. Chem. Phys., 2017, 146, 041103 CrossRef PubMed.
- D. de las Heras, L. L. Treffenstädt and M. Schmidt, Phys. Rev. E, 2016, 93, 030601 CrossRef PubMed.
- N. A. M. Arajo, C. S. Dias and M. M. T. da Gama, J. Phys.: Condens. Matter, 2017, 29, 014001 CrossRef PubMed.
- E. Bianchi, A. Z. Panagiotopoulos and A. Nikoubashman, Soft Matter, 2015, 11, 3767–3771 RSC.
- R. A. DeLaCruz-Araujo, D. J. Beltran-Villegas, R. G. Larson and U. M. Cordova-Figueroa, Soft Matter, 2016, 12, 4071–4081 RSC.
- M. Wertheim, J. Stat. Phys., 1984, 35, 19 CrossRef; M. Wertheim, J. Stat. Phys., 1984, 35, 35 CrossRef.
- D. de las Heras, J. M. Tavares and M. M. Telo da Gama, Soft Matter, 2011, 7, 5615–5626 RSC.
- J. M. Tavares and P. I. C. Teixeira, Phys. Rev. E, 2017, 95, 012612 CrossRef CAS PubMed.
- S. Sokołowski and Y. V. Kalyuzhnyi, J. Phys. Chem. B, 2014, 118, 9076–9084 CrossRef PubMed.
- B. D. Marshall, D. Ballal and W. G. Chapman, J. Chem. Phys., 2012, 137, 104909 CrossRef PubMed.
- J. M. Tavares, N. G. Almarza and M. M. Telo da Gama, Soft Matter, 2015, 11, 5828–5838 RSC.
- Y. V. Kalyuzhnyi, M. Holovko, T. Patsahan and P. T. Cummings, J. Phys. Chem. Lett., 2014, 5, 4260–4264 CrossRef CAS PubMed.
- B. D. Marshall, Phys. Rev. E, 2016, 94, 012615 CrossRef PubMed.
- A. Bansal, D. Asthagiri, K. R. Cox and W. G. Chapman, J. Chem. Phys., 2016, 145, 074904 CrossRef PubMed.
- R. Fantoni and G. Pastore, Mol. Phys., 2015, 113, 2593–2607 CrossRef CAS.
- E. Bianchi, P. D. J. van Oostrum, C. N. Likos and G. Kahl, Curr. Opin. Colloid Interface Sci., 2017, 30, 8 CrossRef CAS.
- C. N. Likos, R. Blaak and A. Wynveen, J. Phys.: Condens. Matter, 2008, 20, 494221 CrossRef.
- M. Sabapathy, R. Ann Mathews K and E. Mani, Phys. Chem. Chem. Phys., 2017, 19, 13122–13132 RSC.
- M. Sabapathy, Y. Shelke, M. G. Basavaraj and E. Mani, Soft Matter, 2016, 12, 5950–5958 RSC.
- E. Bianchi, C. N. Likos and G. Kahl, ACS Nano, 2013, 7, 4657 CrossRef CAS PubMed.
- E. Bianchi, C. N. Likos and G. Kahl, Nano Lett., 2014, 14, 3412 CrossRef CAS PubMed.
- E. Bianchi, G. Kahl and C. N. Likos, Soft Matter, 2011, 7, 8313 RSC.
- J. M. Dempster and M. O. de la Cruz, ACS Nano, 2016, 10, 5909 CrossRef CAS PubMed.
- R. Hieronimus, S. Raschke and A. Heuer, J. Chem. Phys., 2016, 145, 064303 CrossRef.
- C. Yigit, J. Heyda and J. Dzubiella, J. Chem. Phys., 2015, 143, 064904 CrossRef PubMed.
- C. Yigit, J. Heyda, M. Ballauff and J. Dzubiella, J. Chem. Phys., 2015, 143, 064905 CrossRef PubMed.
- C. Yigit, M. Kanduč, M. Ballauff and J. Dzubiella, Langmuir, 2017, 33, 417 CrossRef CAS PubMed.
- A. I. Abrikosov, B. Stenqvist and M. Lund, Soft Matter, 2017, 13, 4591–4597 RSC.
- M. A. Blanco and V. K. Shen, J. Chem. Phys., 2016, 145, 155102 CrossRef PubMed.
- A. L. Božič and R. Podgornik, J. Chem. Phys., 2013, 138, 074902 CrossRef PubMed.
- M. Stipsitz, E. Bianchi and G. Kahl, J. Chem. Phys., 2015, 142, 114905 CrossRef PubMed.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185 CAS.
- Y. V. Kalyuzhnyi, E. Bianchi, S. Ferrari and G. Kahl, J. Chem. Phys., 2015, 142, 114108 CrossRef PubMed.
- S. Ferrari, E. Bianchi, Y. Kalyuzhnyi and G. Kahl, J. Phys.: Condens. Matter, 2015, 27, 234104 CrossRef PubMed.
- E. G. Noya and E. Bianchi, J. Phys.: Condens. Matter, 2015, 27, 234103 CrossRef PubMed.
- E. G. Noya, I. Kolovos, G. Doppelbauer, G. Kahl and E. Bianchi, Soft Matter, 2014, 10, 8464 RSC.
- S. Ferrari, E. Bianchi and G. Kahl, Nanoscale, 2017, 9, 1956 RSC.
- G. Doppelbauer, Ordered Equilibrium Structures of Patchy Particle Systems, PhD thesis, TU Wien, 2012 Search PubMed.
- H. Y. Chan, V. Lankevich, P. G. Vekilov and V. Lubchenko, Biophys. J., 2012, 102, 1934–1943 CrossRef CAS PubMed.
- A. Kurut, B. A. Persson, T. Åkesson, J. Forsman and M. Lund, J. Phys. Chem. Lett., 2012, 3, 731–734 CrossRef CAS PubMed.
- M. Lund, Colloids Surf., B, 2016, 137, 17–21 CrossRef CAS PubMed.
- F. Roosen-Runge, F. Zhang, F. Schreiber and R. Roth, Sci. Rep., 2014, 4, 7016 CrossRef CAS PubMed.
- A. Šarić, Y. C. Chebaro, T. P. J. Knowles and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17869–17874 CrossRef PubMed.
- E. D. Levy, E. B. Erba, C. V. Robinson and S. A. Teichmann, Nature, 2008, 1262–1265 CrossRef CAS PubMed.
- C. M. Dobson, Nature, 2003, 426, 884–890 CrossRef CAS PubMed.
- D. Pum and U. B. Sleytr, Nanotechnology, 2014, 25, 312001 CrossRef PubMed.
- W. Li, M. Morin, E. Gustafsson, B. A. Persson, M. Lund and M. Z. Oskolkova, Soft Matter, 2016, 12, 9330–9333 RSC.
- C. Ishimoto and T. Tanaka, Phys. Rev. Lett., 1977, 39, 474–477 CrossRef CAS.
- A. George and W. W. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, 50, 361–365 CrossRef CAS PubMed.
- N. J. Greenfield, Nat. Protoc., 2007, 1, 2876–2890 CrossRef PubMed.
- M. Kastelic, Y. V. Kalyuzhnyi, B. Hribar-Lee, K. A. Dill and V. Vlachy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6766–6770 CrossRef CAS PubMed.
- T. Janc, M. Kastelic, M. Bončina and V. Vlachy, Condens. Matter Phys., 2016, 19, 23601 CrossRef.
- S. Bucciarelli, J. S. Myung, B. Farago, S. Das, G. A. Vliegenthart, O. Holderer, R. G. Winkler, P. Schurtenberger, G. Gompper and A. Stradner, Sci. Adv., 2016, 2, e1601432 Search PubMed.
- M. Kastelic, Y. V. Kalyuzhnyi and V. Vlachy, Soft Matter, 2016, 12, 7289–7298 RSC.
- R. Vácha and D. Frenkel, Biophys. J., 2011, 101, 1432–1439 CrossRef PubMed.
- A. Kurut, C. Dicko and M. Lund, ACS Biomater. Sci. Eng., 2015, 1, 363–371 CrossRef CAS.
- W. Li, B. A. Persson, M. Morin, M. A. Behrens, M. Lund and M. Zackrisson Oskolkova, J. Phys. Chem. B, 2015, 119, 503–508 CrossRef CAS PubMed.
- P. S. Sarangapani, S. D. Hudson, R. L. Jones, J. F. Douglas and J. A. Pathak, Biophys. J., 2015, 108, 724–737 CrossRef CAS PubMed.
- R. Vácha, S. Linse and M. Lund, J. Am. Chem. Soc., 2014, 136, 11776–11782 CrossRef PubMed.
- S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–105 CrossRef CAS.
- H. R. Vutukuri, A. Imhof and A. van Blaaderen, Angew. Chem., Int. Ed., 2014, 53, 1–6 CrossRef PubMed.
- K. Kriechbaum, D. A. Cerrón-Infantes, B. Stöger and M. M. Unterlass, Macromolecules, 2015, 48, 8773–8780 CrossRef CAS.
- J. de Graaf and L. Manna, Science, 2012, 337, 417–418 CrossRef PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed.
- B. A. Schultz, P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2015, 9, 2336–2344 CrossRef CAS PubMed.
- L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142 RSC.
- J. A. Champion, Y. K. Katare and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11901–11904 CrossRef CAS PubMed.
- V. Meester, R. W. Verweij, C. van der Wel and D. J. Kraft, ACS Nano, 2016, 10, 4322–4329 CrossRef CAS PubMed.
- A. Désert, J. Morele, J.-C. Taveau, O. Lambert, M. Lansalot, E. Bourgeat-Lami, A. Thill, O. Spalla, L. Belloni, S. Ravaine and E. Duguet, Nanoscale, 2016, 8, 5454–5469 RSC.
- A. Kuijk, D. V. Byelov, A. V. Petukhov, A. van Blaaderen and A. Imhof, Faraday Discuss., 2012, 159, 181–199 RSC.
- K. Miszta, J. de Graaf, G. Bertoni, D. Dorfs, R. Brescia, S. Marras, L. Ceseracciu, R. Cingolani, R. van Roij, M. Dijkstra and L. Manna, Nat. Mater., 2011, 10, 872–876 CrossRef CAS PubMed.
- M. P. Arciniegas, M. R. Kim, J. De Graaf, R. Brescia, S. Marras, K. Miszta, M. Dijkstra, R. Van Roij and L. Manna, Nano Lett., 2014, 14, 1056–1063 CrossRef CAS PubMed.
- M. Marechal, R. J. Kortschot, A. F. Demirörs, A. Imhof and M. Dijkstra, Nano Lett., 2010, 10, 1907–1911 CrossRef CAS PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. J. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
- Y. Wang, Y. Wang, X. Zheng, G. R. Yi, S. Sacanna, D. J. Pine and M. Weck, J. Am. Chem. Soc., 2014, 136, 6866–6869 CrossRef CAS PubMed.
- C. Hubert, C. Chomette, A. Désert, M. Sun, M. Treguer-Delapierre, S. Mornet, A. Perro, E. Duguet and S. Ravaine, Faraday Discuss., 2015, 181, 139–146 RSC.
- X. Ye, J. Chen, M. Engel, J. A. Millan, W. Li, L. Qi, G. Xing, J. E. Collins, C. R. Kagan, J. Li, S. C. Glotzer and C. B. Murray, Nat. Chem., 2013, 5, 466–473 CrossRef CAS PubMed.
- J. A. Millan, D. Ortiz, G. Van Anders and S. C. Glotzer, ACS Nano, 2014, 8, 2918–2928 CrossRef CAS PubMed.
- J. A. Millan, D. Ortiz and S. C. Glotzer, Soft Matter, 2015, 11, 1386–1396 RSC.
- S. Ithurria, M. D. Tessier, B. Mahler, R. P. S. M. Lobo, B. Dubertret and A. L. Efros, Nat. Mater., 2011, 10, 936–941 CrossRef CAS PubMed.
- L. Kavan, J.-H. Yum and M. Grätzel, Nano Lett., 2011, 11, 5501–5506 CrossRef CAS PubMed.
- M. O. Blunt, J. C. Russell, M. D. C. Giménez-López, J. P. Garrahan, X. Lin, M. Schröder, N. R. Champness and P. H. Beton, Science, 2008, 322, 1077–1081 CrossRef CAS PubMed.
- S. Whitelam, I. Tamblyn, P. H. Beton and J. P. Garrahan, Phys. Rev. Lett., 2012, 108, 1–4 CrossRef PubMed.
- S. Whitelam, I. Tamblyn, J. P. Garrahan and P. H. Beton, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- C. Karner, E. Bianchi and C. Dellago, in preparation.
- F. Lu, K. G. Yager, Y. Zhang, H. Xin and O. Gang, Nat. Commun., 2015, 6, 6912 CrossRef CAS PubMed.
- W. Liu, N. A. Mahynski, O. Gang, A. Z. Panagiotopoulos and S. K. Kumar, ACS Nano, 2017, 11, 4950–4959 CrossRef CAS PubMed.
- W. Liu, M. Tagawa, H. L. Xin, T. Wang, H. Emamy, H. Li, K. G. Yager, F. W. Starr, A. V. Tkachenko and O. Gang, Science, 2016, 351, 582–586 CrossRef CAS PubMed.
- B. D. Smith, D. J. Kirby, I. O. Rivera and C. D. Keating, ACS Nano, 2013, 7, 825–833 CrossRef CAS PubMed.
- B. D. Smith, K. A. Fichthorn, D. J. Kirby, L. M. Quimby, D. A. Triplett, P. González, D. Hernández and C. D. Keating, ACS Nano, 2014, 8, 657–670 CrossRef CAS PubMed.
- A. A. Shah, B. Schultz, K. L. Kohlstedt, S. C. Glotzer and M. J. Solomon, Langmuir, 2013, 29, 4688–4696 CrossRef CAS PubMed.
- A. A. Shah, B. Schultz, W. Zhang, S. C. Glotzer and M. J. Solomon, Nat. Mater., 2014, 14, 117–124 CrossRef PubMed.
- J. R. Wolters, G. Avvisati, F. Hagemans, T. Vissers, D. J. Kraft, M. Dijkstra and W. K. Kegel, Soft Matter, 2015, 11, 1067–1077 RSC.
- K. Chaudhary, Q. Chen, J. J. Juárez, S. Granick and J. A. Lewis, J. Am. Chem. Soc., 2012, 134, 12901–12903 CrossRef CAS PubMed.
- C. W. Shields IV, S. Zhu, Y. Yang, B. Bharti, J. Liu, B. B. Yellen, O. D. Velev and G. P. López, Soft Matter, 2013, 9, 9219–9229 RSC.
- G. Polles, D. Marenduzzo, E. Orlandini and C. Micheletti, Nat. Commun., 2015, 6, 6423 CrossRef CAS PubMed.
- G. Polles, E. Orlandini and C. Micheletti, ACS Macro Lett., 2016, 5, 931–935 CrossRef CAS.
- J. J. Danon, A. Krüger, D. A. Leigh, J.-F. Lemonnier, A. J. Stephens, I. J. Vitorica-Yrezabal and S. L. Woltering, Science, 2017, 355, 159–162 CrossRef CAS PubMed.
- W. K. Den Otter, M. R. Renes and W. J. Briels, Biophys. J., 2010, 99, 1231–1238 CrossRef CAS PubMed.
- D. C. Rapaport, Phys. Rev. Lett., 2008, 101, 186101 CrossRef CAS PubMed.
- A. Zlotnick, J. Mol. Biol., 1994, 241, 59–67 CrossRef CAS PubMed.
- A. Zlotnick, J. Mol. Recognit., 2005, 18, 479–490 CrossRef CAS PubMed.
- J. D. Perlmutter, C. Qiao and M. F. Hagan, eLife, 2013, 2, e00632 Search PubMed.
- J. D. Perlmutter and M. F. Hagan, Annu. Rev. Phys. Chem., 2015, 66, 217–239 CrossRef CAS PubMed.
- J. B. Siegel, A. Zanghellini, H. M. Lovick, G. Kiss, A. R. Lambert, J. L. St. Clair, J. L. Gallaher, D. Hilvert, M. H. Gelb, B. L. Stoddard, K. N. Houk, F. E. Michael and D. Baker, Science, 2010, 329, 309–313 CrossRef CAS PubMed.
- S. Gannavaram, S. Sirin, W. Sherman and G. Gadda, Biochemistry, 2014, 53, 6574–6583 CrossRef CAS PubMed.
- S. Sirin, R. Kumar, C. Martinez, M. J. Karmilowicz, P. Ghosh, Y. A. Abramov, V. Martin and W. Sherman, J. Chem. Inf. Model., 2014, 54, 2334–2346 CrossRef CAS PubMed.
- S. H. Mejias, J. Lopez-Andarias, T. Sakurai, S. Yoneda, K. P. Erazo, S. Seki, C. Atienza, N. Martin and A. L. Cortajarena, Chem. Sci., 2016, 7, 4842–4847 RSC.
- S. H. Mejias, A. Aires, P. Couleaud and A. L. Cortajarena, in Advances in Experimental Medicine and Biology, ed. A. L. Cortajarena and T. Z. Grove, Springer International Publishing, Cham, 2016, ch. Protein-ba, pp. 61–81 Search PubMed.
- I. Coluzza, P. D. J. van Oostrum, B. Capone, E. Reimhult and C. Dellago, Phys. Rev. Lett., 2013, 110, 075501 CrossRef PubMed.
- I. Coluzza, P. D. J. van Oostrum, B. Capone, E. Reimhult and C. Dellago, Soft Matter, 2013, 9, 938 RSC.
- I. Coluzza and C. Dellago, J. Phys.: Condens. Matter, 2012, 24, 284111 CrossRef PubMed.
- C. Cardelli, V. Bianco, L. Rovigatti, F. Nerattini, L. Tubiana, C. Dellago and I. Coluzza, Sci. Rep., 2017, 7, 4986 CrossRef PubMed.
- T. Škrbić, A. Badasyan, T. X. Hoang, R. Podgornik and A. Giacometti, Soft Matter, 2016, 12, 4783–4793 RSC.
- T. Škrbić, T. X. Hoang and A. Giacometti, J. Chem. Phys., 2016, 145, 084904 CrossRef PubMed.
- F. Smallenburg, L. Filion and F. Sciortino, Nat. Phys., 2014, 653–657 CrossRef CAS PubMed.
- L. Rovigatti, F. Smallenburg, F. Romano and F. Sciortino, ACS Nano, 2014, 8, 3567–3574 CrossRef CAS PubMed.
- T. Higuchi, A. Tajima, H. Yabu and M. Shimomura, Soft Matter, 2008, 4, 1302–1305 RSC.
- L. Cheng, G. Zhang, L. Zhu, D. Chen and M. Jiang, Angew. Chem., Int. Ed., 2008, 47, 10171–10174 CrossRef CAS PubMed.
- T. M. Hermans, M. A. C. Broeren, N. Gomopoulos, P. van der Schoot, M. H. P. van Genderen, N. A. J. M. Sommerdijk, G. Fytas and E. W. Meijer, Nat. Nanotechnol., 2009, 4, 721–726 CrossRef CAS PubMed.
- A. Hanisch, A. H. Gröschel, M. Förtsch, M. Drechsler, H. Jinnai, T. M. Ruhland, F. H. Schacher and A. H. E. Müller, ACS Nano, 2013, 7, 4030–4041 CrossRef CAS PubMed.
- A. H. Gröschel, A. Walther, T. I. Löbling, F. H. Schacher, H. Schmalz and A. H. E. Müller, Nature, 2013, 503, 247–251 Search PubMed.
- Y. Wang, M. Zhong, J. V. Park, A. V. Zhukhovitskiy, W. Shi and J. A. Johnson, J. Am. Chem. Soc., 2016, 138, 10708–10715 CrossRef CAS PubMed.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed.
- B. Bozorgui, D. Meng, S. K. Kumar and A. Cacciuto, Nano Lett., 2013, 13, 2732–2737 CrossRef CAS PubMed.
- M. Asai, A. Cacciuto and S. K. Kumar, Soft Matter, 2015, 11, 793–797 RSC.
- N. A. Mahynski and A. Z. Panagiotopoulos, J. Chem. Phys., 2015, 142, 074901 CrossRef PubMed.
- A. R. Khokhlov, Conformation-Dependent Design of Sequences in Copolymers II, Springer, Berlin Heidelberg, 2006, vol. 196 Search PubMed.
- A. J. Moreno, F. Lo Verso, A. Arbe, J. A. Pomposo and J. Colmenero, J. Phys. Chem. Lett., 2016, 7, 838–844 CrossRef CAS PubMed.
- J. Zhang, Z.-Y. Lu and Z.-Y. Sun, Soft Matter, 2011, 7, 9944–9950 RSC.
- I. Gârlea, E. Bianchi, B. Capone, L. Rovigatti and C. N. Likos, Curr. Opin. Colloid Interface Sci., 2017, 30, 1 CrossRef.
- M. Pitsikalis, N. Hadjichristidis and J. W. Mays, Macromolecules, 1996, 29, 179 CrossRef CAS.
- D. Vlassopoulos, T. Pakula, G. Fytas, M. Pitsikalis and N. Hadjichristidis, J. Chem. Phys., 1999, 111, 1760 CrossRef CAS.
- F. L. Verso, C. N. Likos, C. Mayer and H. Löwen, Phys. Rev. Lett., 2006, 96, 187802 CrossRef PubMed.
- B. Capone, I. Coluzza, F. LoVerso, C. N. Likos and R. Blaak, Phys. Rev. Lett., 2012, 109, 238301 CrossRef PubMed.
- B. Capone, I. Coluzza, R. Blaak, F. L. Verso and C. N. Likos, New J. Phys., 2013, 15, 095002 CrossRef.
- L. Rovigatti, B. Capone and C. N. Likos, Nanoscale, 2016, 8, 3288–3295 RSC.
- E. Bianchi, B. Capone, G. Kahl and C. N. Likos, Faraday Discuss., 2015, 181, 123–138 RSC.
- S. M. Douglas, I. Bachelet and G. M. Church, Science, 2012, 335, 831–834 CrossRef CAS PubMed.
- N. C. Seeman, J. Theor. Biol., 1982, 99, 237–247 CrossRef CAS PubMed.
- N. C. Seeman, Annu. Rev. Biophys. Biomol. Struct., 1998, 27, 225–248 CrossRef CAS PubMed.
- A. J. M. Wollman, C. Sanchez-Cano, H. M. J. Carstairs, R. A. Cross and A. J. Turberfield, Nat. Nanotechnol., 2013, 9, 44–47 CrossRef PubMed.
- D. Soloveichik, G. Seelig and E. Winfree, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5393–5398 CrossRef CAS PubMed.
- Y. He, T. Ye, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Nature, 2008, 452, 198–201 CrossRef CAS PubMed.
- E. Winfree, F. Liu, L. A. Wenzler and N. C. Seeman, Nature, 1998, 394, 539–544 CrossRef CAS PubMed.
- D. Liu, S. H. Park, J. H. Reif and T. H. LaBean, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 717–722 CrossRef CAS PubMed.
- P. Yin, R. F. Hariadi, S. Sahu, H. M. Choi, S. H. Park, T. H. LaBean and J. H. Reif, Science, 2008, 321, 824–826 CrossRef CAS PubMed.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- A. Rajendran, M. Endo and H. Sugiyama, Angew. Chem., Int. Ed., 2012, 51, 874–890 CrossRef CAS PubMed.
- R. Tsukanov, T. E. Tomov, R. Masoud, H. Drory, N. Plavner, M. Liber and E. Nir, J. Phys. Chem. B, 2013, 117, 11932–11942 CrossRef CAS PubMed.
- P. C. Nickels, B. Wünsch, P. Holzmeister, W. Bae, L. M. Kneer, D. Grohmann, P. Tinnefeld and T. Liedl, Science, 2016, 354, 305–307 CrossRef CAS PubMed.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoffand, Nature, 1996, 382, 607–609 CrossRef CAS PubMed.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901 CrossRef PubMed.
- C. R. Simmons, F. Zhang, J. J. Birktoft, X. Qi, D. Han, Y. Liu, R. Sha, H. O. Abdallah, C. Hernandez, Y. P. Ohayon, N. C. Seeman and H. Yan, J. Am. Chem. Soc., 2016, 138, 10047–10054 CrossRef CAS PubMed.
- J. Largo, F. W. Starr and F. Sciortino, Langmuir, 2007, 23, 5896–5905 CrossRef CAS PubMed.
- J. P. Doye, T. E. Ouldridge, A. A. Louis, F. Romano, P. Šulc, C. Matek, B. E. Snodin, L. Rovigatti, J. S. Schreck and R. M. Harrison, et al. , Phys. Chem. Chem. Phys., 2013, 15, 20395–20414 RSC.
- S. Biffi, R. Cerbino, F. Bomboi, E. M. Paraboschi, R. Asselta, F. Sciortino and T. Bellini, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15633–15637 CrossRef CAS PubMed.
- L. Rovigatti, F. Bomboi and F. Sciortino, J. Chem. Phys., 2014, 140, 154903 CrossRef.
- P. Theodorakis, N. Fytas, G. Kahl and C. Dellago, Condens. Matter Phys., 2015, 18, 22801 CrossRef.
- L. D. Michele and E. Eiser, Phys. Chem. Chem. Phys., 2013, 15, 3115–3129 RSC.
- D. H. Napper, Polymeric stabilization of colloidal dispersions, Academic Pr, 1983, vol. 3 Search PubMed.
- D. Nykypanchuk, M. M. Maye, D. Van Der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed.
- M. M. Maye, M. T. Kumara, D. Nykypanchuk, W. B. Sherman and O. Gang, Nat. Nanotechnol., 2010, 5, 116–120 CrossRef CAS PubMed.
- F. Varrato, L. Di Michele, M. Belushkin, N. Dorsaz, S. H. Nathan, E. Eiser and G. Foffi, Proc. Natl. Acad. Sci. U. S. A., 2012, 19155–19160 CrossRef CAS PubMed.
- L. Feng, R. Dreyfus, R. Sha, N. C. Seeman and P. M. Chaikin, Adv. Mater., 2013, 25, 2779–2783 CrossRef CAS PubMed.
- S. A. van der Meulen and M. E. Leunissen, J. Am. Chem. Soc., 2013, 135, 15129–15134 CrossRef CAS PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Phys. Rev. Lett., 2014, 113, 128303 CrossRef PubMed.
- J.-W. Kim, J.-H. Kim and R. Deaton, Angew. Chem., Int. Ed., 2011, 50, 9185–9190 CrossRef CAS PubMed.
- K. Suzuki, K. Hosokawa and M. Maeda, J. Am. Chem. Soc., 2009, 131, 7518–7519 CrossRef CAS PubMed.
- J. D. Halverson and A. V. Tkachenko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062310 CrossRef PubMed.
- M. Nakata, G. Zanchetta, B. D. Chapman, C. D. Jones, J. O. Cross, R. Pindak, T. Bellini and N. A. Clark, Science, 2007, 318, 1276 CrossRef CAS PubMed.
- G. Zanchetta, T. Bellini, M. Nakata and N. A. Clark, J. Am. Chem. Soc., 2008, 130, 12864–12865 CrossRef CAS PubMed.
- G. Zanchetta, M. Nakata, M. Buscaglia, N. A. Clark and T. Bellini, J. Phys.: Condens. Matter, 2008, 20, 494214 CrossRef.
- C. De Michele, T. Bellini and F. Sciortino, Macromolecules, 2012, 45, 1090–1106 CrossRef CAS.
- C. De Michele, L. Rovigatti, T. Bellini and F. Sciortino, Soft Matter, 2012, 8, 8388 RSC.
- S. Biffi, R. Cerbino, G. Nava, F. Bomboi, F. Sciortino and T. Bellini, Soft Matter, 2015, 11, 3132–3138 RSC.
- F. Bomboi, S. Biffi, R. Cerbino, T. Bellini, F. Bordi and F. Sciortino, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38–64 Search PubMed.
- J. Fernandez-Castanon, F. Bomboi, L. Rovigatti, M. Zanatta, A. Paciaroni, L. Comez, L. Porcar, C. J. Jafta, G. C. Fadda, T. Bellini and F. Sciortino, J. Chem. Phys., 2016, 145, 084910 CrossRef CAS PubMed.
- E. Locatelli, P. H. Handle, C. N. Likos, F. Sciortino and L. Rovigatti, ACS Nano, 2017, 11, 2094–2102 CrossRef CAS PubMed.
- F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554–558 CrossRef CAS.
- S. Roldán-Vargas, F. Smallenburg, W. Kob and F. Sciortino, J. Chem. Phys., 2013, 139, 244910 CrossRef PubMed.
- F. Bomboi, F. Romano, M. Leo, J. Fernandez-Castanon, R. Cerbino, T. Bellini, F. Bordi, P. Filetici and F. Sciortino, Nat. Commun., 2016, 7, 13191 CrossRef CAS PubMed.
- C. B. Anfinsen, Science, 1973, 181, 223–230 CAS.
- P. Tompa, Trends Biochem. Sci., 2002, 27, 527–533 CrossRef CAS PubMed.
- A. L. Fink, Curr. Opin. Struct. Biol., 2005, 15, 35–41 CrossRef CAS PubMed.
- H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208 CrossRef CAS PubMed.
- V. N. Uversky and A. K. Dunker, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804, 1231–1264 CrossRef CAS PubMed.
- C. M. Dobson, A. Šali and M. Karplus, Angew. Chem., Int. Ed., 1998, 37, 868–893 CrossRef.
- A. R. Fersht and V. Daggett, Cell, 2002, 108, 573–582 CrossRef CAS PubMed.
- M. Karplus and J. Kuriyan, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6679–6685 CrossRef CAS PubMed.
- T. R. Sosnick and J. R. Hinshaw, Science, 2011, 334, 464–465 CrossRef CAS PubMed.
- R. Das and D. Baker, Annu. Rev. Biochem., 2008, 77, 363–382 CrossRef CAS PubMed.
- L. Mirny and E. Shakhnovich, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 361–396 CrossRef CAS PubMed.
- J. N. Onuchic and P. G. Wolynes, Curr. Opin. Struct. Biol., 2004, 14, 70–75 CrossRef CAS PubMed.
- V. Tozzini, Curr. Opin. Struct. Biol., 2005, 15, 144–150 CrossRef CAS PubMed.
- P. Bradley, Science, 2005, 309, 1868–1871 CrossRef CAS PubMed.
- O. Dagliyan, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6800–6804 CrossRef CAS PubMed.
- B. I. Dahiyat and S. L. Mayo, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 10172–10177 CrossRef CAS.
- B. I. Dahiyat and S. Mayo, Science, 1997, 278, 82–87 CrossRef CAS PubMed.
- J. R. Desjarlais and T. M. Handel, J. Mol. Biol., 1999, 290, 305–318 CrossRef CAS PubMed.
- J. R. Desjarlais and T. M. Handel, Protein Sci., 1995, 4, 2006–2018 CrossRef CAS PubMed.
- H. W. Hellinga and F. M. Richards, J. Mol. Biol., 1991, 222, 763–785 CrossRef CAS PubMed.
- E. H. Kellogg, O. F. Lange and D. Baker, J. Phys. Chem. B, 2012, 116, 11405–11413 CrossRef CAS PubMed.
- B. Kuhlman and D. Baker, Curr. Opin. Struct. Biol., 2004, 14, 89–95 CrossRef CAS PubMed.
- D. Mandell and T. Kortemme, Nat. Chem. Biol., 2009, 5, 797–807 CrossRef CAS PubMed.
- J. Smadbeck, K. H. Chan, G. A. Khoury, B. Xue, R. C. Robinson, C. A. E. Hauser and C. A. Floudas, PLoS Comput. Biol., 2014, 10, e1003718 Search PubMed.
- A. R. Thomson, A. R. Thomson, C. W. Wood, A. J. Burton, G. J. Bartlett, R. B. Sessions, R. L. Brady and D. N. Woolfson, Science, 2014, 346, 485–488 CrossRef CAS PubMed.
- N. P. King, W. Sheffler, M. R. Sawaya, B. S. Vollmar, J. P. Sumida, I. Andre, T. Gonen, T. O. Yeates and D. Baker, Science, 2012, 336, 1171–1174 CrossRef CAS PubMed.
- N. P. King, J. B. Bale, W. Sheffler, D. E. McNamara, S. Gonen, T. Gonen, T. O. Yeates and D. Baker, Nature, 2014, 510, 103–108 CrossRef CAS PubMed.
- P.-S. Huang, G. Oberdorfer, C. Xu, X. Y. Pei, B. L. Nannenga, J. M. Rogers, F. DiMaio, T. Gonen, B. Luisi and D. Baker, Science, 2014, 346, 481–485 CrossRef CAS PubMed.
- C. B. Eiben, J. B. Siegel, J. B. Bale, S. Cooper, F. Khatib, B. W. Shen, F. Players, B. L. Stoddard, Z. Popovic and D. Baker, Nat. Biotechnol., 2012, 30, 190–192 CrossRef CAS PubMed.
- D. Baker, Protein Sci., 2010, 19, 1817–1819 CrossRef CAS PubMed.
- L. Jiang, E. A. Althoff, F. R. Clemente, L. Doyle, D. Rothlisberger, A. Zanghellini, J. L. Gallaher, J. L. Betker, F. Tanaka, C. F. Barbas, D. Hilvert, K. N. Houk, B. L. Stoddard and D. Baker, Science, 2008, 319, 1387–1391 CrossRef CAS PubMed.
- S. H. Mejias, P. Couleaud, S. Casado, D. Granados, M. A. Garcia, J. M. Abad and A. L. Cortajarena, Colloids Surf., B, 2016, 141, 93–101 CrossRef CAS PubMed.
- U. K. Marelli, F. Rechenmacher, T. R. A. Sobahi, C. Mas-Moruno and H. Kessler, Front. Oncol., 2013, 3, 222 Search PubMed.
- W. E. Evans and M. V. Relling, Nature, 2004, 429, 464–468 CrossRef CAS PubMed.
- W. P. Petros and W. E. Evans, Trends Pharmacol. Sci., 2004, 25, 457–464 CrossRef CAS PubMed.
- S. B. Willingham, J.-P. Volkmer, A. J. Gentles, D. Sahoo, P. Dalerba, S. S. Mitra, J. Wang, H. Contreras-Trujillo, R. Martin, J. D. Cohen, P. Lovelace, F. A. Scheeren, M. P. Chao, K. Weiskopf, C. Tang, A. K. Volkmer, T. J. Naik, T. A. Storm, A. R. Mosley, B. Edris, S. M. Schmid, C. K. Sun, M.-S. Chua, O. Murillo, P. Rajendran, A. C. Cha, R. K. Chin, D. Kim, M. Adorno, T. Raveh, D. Tseng, S. Jaiswal, P. Ø. Enger, G. K. Steinberg, G. Li, S. K. So, R. Majeti, G. R. Harsh, M. Van De Rijn, N. N. H. Teng, J. B. Sunwoo, A. A. Alizadeh, M. F. Clarke and I. L. Weissman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6662–6667 CrossRef CAS PubMed.
- C. B. Calson, P. Mowery, R. M. Owen, E. C. Dykhuizen and L. L. Kiessling, ACS Chem. Biol., 2007, 2, 119–127 CrossRef PubMed.
- J. J. Boniface, J. D. Rabinowitz, C. Wülfing, J. Hampl, Z. Reich, J. D. Altman, R. M. Kantor, C. Beeson, H. M. McConnell and M. M. Davis, Immunity, 1998, 9, 459–466 CrossRef CAS PubMed.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef.
- D. V. Effenterre and D. Roux, Europhys. Lett., 2003, 64, 543–549 CrossRef.
- N. Morel, S. Simon, Y. Frobert, H. Volland, C. Mourton-Gilles, A. Negro, M. C. Sorgato, C. Créminon and J. Grassi, J. Biol. Chem., 2004, 279, 30143–30149 CrossRef CAS PubMed.
- B. E. Collins and J. C. Paulson, Curr. Opin. Chem. Biol., 2004, 8, 617–625 CrossRef CAS PubMed.
- M. E. Davis, J. E. Zuckerman, C. H. J. Choi, D. Seligson, A. Tolcher, C. A. Alabi, Y. Yen, J. D. Heidel and A. Ribas, Nature, 2010, 464, 1067–1070 CrossRef CAS PubMed.
- V. Mani, D. P. Wasalathanthri, A. A. Joshi, C. V. Kumar and J. F. Rusling, Anal. Chem., 2012, 84, 10485–10491 CrossRef CAS PubMed.
- D. T. Wiley, P. Webster, A. Gale and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8662–8667 CrossRef CAS PubMed.
- S. Hauert and S. N. Bhatia, Trends Biotechnol., 2014, 32, 448–455 CrossRef CAS PubMed.
- M. A. Van Dongen, C. A. Dougherty and M. M. Banaszak Holl, Biomacromolecules, 2014, 15, 3215–3234 CrossRef CAS PubMed.
- B. Wang, C. V. Galliford and P. S. Low, Nanomedicine, 2014, 9, 313–330 CrossRef CAS PubMed.
- E. Mahon and M. Barboiu, Org. Biomol. Chem., 2015, 13, 10590–10599 CAS.
- E. Falvo, E. Tremante, A. Arcovito, M. Papi, N. Elad, A. Boffi, V. Morea, G. Conti, G. Toffoli, G. Fracasso, P. Giacomini and P. Ceci, Biomacromolecules, 2016, 17, 514–522 CrossRef CAS PubMed.
- K. D. Schleicher, S. L. Dettmer, L. E. Kapinos, S. Pagliara, U. F. Keyser, S. Jeney and R. Y. H. Lim, Nat. Nanotechnol., 2014, 9, 525–530 CrossRef CAS PubMed.
- F. J. Martinez-Veracoechea and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10963–10968 CrossRef CAS PubMed.
- I. Coluzza, J. Phys.: Condens. Matter, 2017, 29, 143001 CrossRef PubMed.
- R. A. Distasio, O. A. von Lilienfeld and A. Tkatchenko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14791–14795 CrossRef CAS PubMed.
- D. Röthlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Nature, 2008, 453, 190–195 CrossRef PubMed.
- W. F. DeGrado, C. M. Summa, V. Pavone, F. Nastri and A. Lombardi, Annu. Rev. Biochem., 1999, 68, 779–819 CrossRef CAS PubMed.
- S. F. Betz, D. P. Raleigh and W. F. DeGrado, Curr. Opin. Struct. Biol., 1993, 3, 601–610 CrossRef CAS.
- M. Chino, O. Maglio, F. Nastri, V. Pavone, W. F. Degrado and A. Lombardi, Eur. J. Inorg. Chem., 2015, 3371–3390 CrossRef CAS PubMed.
- T. A. Whitehead, A. Chevalier, Y. Song, C. Dreyfus, S. J. Fleishman, C. De Mattos, C. A. Myers, H. Kamisetty, P. Blair, I. A. Wilson and D. Baker, Nat. Biotechnol., 2012, 30, 543–548 CrossRef CAS PubMed.
- B. Kuhlman, G. Dantas, G. C. Ireton, G. Varani, B. L. Stoddard and D. Baker, Science, 2003, 302, 1364–1368 CrossRef CAS PubMed.
- E. I. Shakhnovich, Phys. Rev. Lett., 1994, 72, 3907–3910 CrossRef CAS PubMed.
- A. M. Gutin and E. Shakhnovich, J. Chem. Phys., 1993, 98, 8174–8177 CrossRef CAS.
- B. Derrida, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 2613–2626 CrossRef CAS.
- V. S. Pande, A. Y. Grosberg and T. Tanaka, Rev. Mod. Phys., 2000, 72, 259–314 CrossRef CAS.
- E. I. Shakhnovich and a. M. Gutin, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 7195–7199 CrossRef CAS.
- E. I. Shakhnovich and a. M. Gutin, Protein Eng., 1993, 6, 793–800 CrossRef CAS PubMed.
- I. Coluzza, H. G. Muller and D. Frenkel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 46703 CrossRef CAS PubMed.
- I. Coluzza and D. Frenkel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 51917 CrossRef PubMed.
- I. Coluzza and D. Frenkel, Biophys. J., 2007, 92, 1150–1156 CrossRef CAS PubMed.
- B. M. Rubenstein, I. Coluzza and M. A. Miller, Phys. Rev. Lett., 2012, 108, 1–5 CrossRef PubMed.
- S. Abeln and D. Frenkel, PLoS Comput. Biol., 2008, 4, e1000241 Search PubMed.
- I. Coluzza, PLoS One, 2011, 6, e20853 CAS.
- I. Coluzza, PLoS One, 2014, 9, e112852 Search PubMed.
- F. Nerattini, L. Tubiana, C. Cardelli, V. Bianco and I. Coluzza, in preparation.
- H. F. El-Sharif, H. Yapati, S. Kalluru and S. M. Reddy, Acta Biomater., 2015, 28, 121–127 CrossRef CAS PubMed.
- G. V. Dubacheva, T. Curk, B. M. Mognetti, R. Auzély-Velty, D. Frenkel and R. P. Richter, J. Am. Chem. Soc., 2014, 136, 1722–1725 CrossRef CAS PubMed.
- F. Puoci, G. Cirillo, M. Curcio, F. Iemma, O. I. Parisi, U. G. Spizzirri and N. Picci, Biopolymers, 2010, 548 Search PubMed.
- G. Vasapollo, R. D. Sole, L. Mergola, M. R. Lazzoi, A. Scardino, S. Scorrano and G. Mele, Int. J. Mol. Sci., 2011, 12, 5908–5945 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2017 |