Open Access Article
Open Access ArticleTranslocation dynamics of knotted polymers under a constant or periodic external field†
Vivek
Narsimhan
a,
C. Benjamin
Renner
b and
Patrick S.
Doyle
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: pdoyle@mit.edu
bLiquiglide, 75 Sidney Street, Cambridge, MA 02139, USA
First published on 9th May 2016
Abstract
We perform Brownian dynamics simulations to examine how knots alter the dynamics of polymers moving through nanopores under an external field. In the first part of this paper, we study the situation when the field is constant. Here, knots halt translocation above a critical force with jamming occurring at smaller forces for twist topologies compared to non-twist topologies. Slightly below the jamming transition, the polymer's transit times exhibit large fluctuations. This phenomenon is an example of the knot's molecular individualism since the conformation of the knot plays a large role in the chain's subsequent dynamics. In the second part of the paper, we study the motion of the chain when one cycles the field on and off. If the off time is comparable to the knot's relaxation time, one can adjust the swelling of the knot at the pore and hence design strategies to ratchet the polymer in a controllable fashion. We examine how the off time affects the ratcheting dynamics. We also examine how this strategy alters the fluctuations in the polymer's transit time. We find that cycling the force field can reduce fluctuations near the knot's jamming transition, but can enhance the fluctuations at very high forces since knots get trapped in metastable states during the relaxation process. The latter effect appears to be more prominent for non-torus topologies than torus ones. We conclude by discussing the feasibility of this approach to control polymer motion in biotechnology applications such as sequencing.
1 Introduction
Knots are found everywhere in our daily lives, whether they be fashion accessories or items to fasten two objects together. However, unknown to many people, knots also play an important role in biology. For example, knots in the umbilical cord create complications during child birth,1 and knots in DNA alter the kinetics of transcription,2 so much so that nature has evolved specific enzymes to control the topology of these chains.3–5 Driven by these observations, there has been considerable interest in recent years to understand how these self-entanglements alter the physical properties of polymers at the molecular scale.6–8 By now, we know that knotting in long polymer strands is mathematically inevitable.9,10 This phenomenon leads to drastic changes in the polymer's dynamics (relaxation,11,12 coil-stretch13,14) and its mechanical properties (rupture strength15). We are now at the stage where researchers can test recent theories16–18via single-molecule experiments. For example, researchers can now tie knots into actin filaments19 or DNA20via optical tweezers, and others are able to create knotted conformations via application of an electric field.21,22In this paper, we discuss how knotting on an open, linear chain alters the chain's motion through small pores. This process, known as translocation, has wide ranging applications in biology and biotechnology. Viruses eject their DNA into hosts through small pores in the cell membrane.23,24 Similarly, nanopore sequencing consists of passing DNA through a thin hole via an imposed electric field. If the resulting electric signal is sensitive to chemical detail, this event can be used to read the sequence along the chain's backbone.25–27 This idea, proposed by Deamer and co-workers28–30 and now implemented by Oxford Nanopore,31,32 is a promising next-generation technology as it allows long DNA reads with little to no chemical modification. Its single-molecule nature allows one to sample genetic heterogeneity among cell populations, which is ideal for detecting rare events such as the onset of cancer.
Currently, one limitation facing nanopore sequencing is that DNA moves too quickly through the pore, rendering the electric signal to be noisy.27,30,33 There are several proposals in the literature to address this issue,34–36 most of which involve binding proteins onto DNA to ratchet it through the pore or using exonucleases to hydrolyze the end of the chain one nucleotide at a time.37–39 The idea we present here uses entanglements such as knots to retard the motion of the polymer. The advantage of this technique is that little chemical modification is required and it could be generalized to other polymer systems. As little has been examined on this front, we would like to perform simulations to provide physical insight into this process.
Our paper is divided into two parts. First, we will discuss the translocation dynamics of a knotted polymer under constant field. Previous authors have simulated this process,40,41 finding that knots completely halt translocation above a critical force. Suma et al.41 also examined the effect that topology plays in this process, finding that twist knots jam more easily than torus knots. We verify these effects in our simulation, and we examine another phenomenon that has been unreported thus far. Close to the jamming transition, we find that the translocation speed exhibits large fluctuations because the knot's dynamics are extremely sensitive to its conformation as it enters the pore. These observations are evidence of caging, stick-slip motion, and molecular individualism42–44 of a polymer knot. From a practical standpoint, these results state that there are force regimes where translocation will be difficult to control and thus should be avoided.
The primary contribution to this manuscript comes from the second part of the paper where we study the translocation dynamics of a knotted polymer when the applied field is periodic. We find that by cycling the field on and off at the relaxation time scale of the knot, we can control the swelling of the knot and hence ratchet the polymer through the pore. We examine how the translocation speed varies as a function of the cycle time. We also discuss limitations of this approach to control polymer motion. At large field amplitudes, we observe significant fluctuations in the translocation speed because the knot gets trapped in certain conformations during its relaxation. Remarkably, this effect appears most pronounced for particular chain topologies. We discuss the implication of these results in the conclusion.
We note that the glassy physics of locally-dense, single polymers have been receiving increasing attention in the scientific community. For example, recent experiments shown that collapsed DNA can jam at the pores of viral capsids.45 It is of interest to manipulate these arrested states, and we hope to provide insight into tight, knotted systems here.
2 Methods
Fig. 1a shows the geometry of our Brownian dynamics simulations. We represent a polymer as a linear chain of N beads of diameter b connected by N − 1 rods of length![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The rod length
. The rod length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is equal to the Kuhn length of a polymer, and we vary the bead diameter to alter the roughness along the polymer backbone, which gives rise to friction when segments slide over each other in an entanglement.47 In the main manuscript, we will examine the situation when the bead diameter is equal to the rod length (b =
is equal to the Kuhn length of a polymer, and we vary the bead diameter to alter the roughness along the polymer backbone, which gives rise to friction when segments slide over each other in an entanglement.47 In the main manuscript, we will examine the situation when the bead diameter is equal to the rod length (b = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). In the ESI,† we will briefly discuss results when the beads are not touching (b = 0.8
). In the ESI,† we will briefly discuss results when the beads are not touching (b = 0.8![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., more corrugated landscape) and slightly overlapping (b = 1.5
, i.e., more corrugated landscape) and slightly overlapping (b = 1.5![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., a smoother energy landscape). The model here is the simplest representation of a flexible polymer that captures the essential features of intra-chain friction.48 It should yield order-of-magnitude estimates of jamming forces and time scales while summarizing the major trends in the translocation process. Note: if one were to more accurately determine the jamming behavior of a tightly knotted chain, one likely has to resort to all-atom, explicit solvent simulations to capture all the details of the short-range, intra-chain interactions. This task is computationally intensive and likely cannot be simulated for the time scales of interest here.
, i.e., a smoother energy landscape). The model here is the simplest representation of a flexible polymer that captures the essential features of intra-chain friction.48 It should yield order-of-magnitude estimates of jamming forces and time scales while summarizing the major trends in the translocation process. Note: if one were to more accurately determine the jamming behavior of a tightly knotted chain, one likely has to resort to all-atom, explicit solvent simulations to capture all the details of the short-range, intra-chain interactions. This task is computationally intensive and likely cannot be simulated for the time scales of interest here.
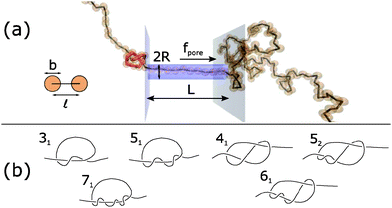 | ||
| Fig. 1 (a) Schematic of Brownian dynamics simulation. A knotted polymer translocates through a pore with a force f(t) per bead. (b) Types of knots simulated (Alexander–Briggs notation46). | ||
In our simulations, we tie a knot at the center of the chain and insert one end of the chain into a cylindrical pore of length L and radius R. Beads inside the pore are subject to a spatially-uniform but time-varying body force f(t) along the pore's axis. This model, albeit simple, is a commonly-used, low-order representation of a polymer electrophoresing through a pore.40,49–51 We simulate a chain of N = 200 beads and set the pore's radius and length to be R = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and L = 10
and L = 10![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . This way, a jammed knot of size 10–20 beads will be much smaller than the polymer chain but larger than pore's diameter, which will allow jamming to occur at sufficiently large forces. Like in previous studies,40,49,52,53 we neglect hydrodynamic interactions between chain segments and set the drag coefficient of each bead to be ζ. Thus, the length and time scale of the problem are the rod size
. This way, a jammed knot of size 10–20 beads will be much smaller than the polymer chain but larger than pore's diameter, which will allow jamming to occur at sufficiently large forces. Like in previous studies,40,49,52,53 we neglect hydrodynamic interactions between chain segments and set the drag coefficient of each bead to be ζ. Thus, the length and time scale of the problem are the rod size ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and its diffusion time td =
and its diffusion time td = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT, where kT is the thermal energy. Typical values for single-stranded DNA are b =
2ζ/kT, where kT is the thermal energy. Typical values for single-stranded DNA are b = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 nm (its nominal width40,41) and td =
= 1 nm (its nominal width40,41) and td = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT ≈ 3πη
2ζ/kT ≈ 3πη![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3/kT ≈ 2.3 ns. To enforce the excluded volume interactions between chain segments, we apply a stiff harmonic potential between overlapping beads with spring constant H = 5000 kT/
3/kT ≈ 2.3 ns. To enforce the excluded volume interactions between chain segments, we apply a stiff harmonic potential between overlapping beads with spring constant H = 5000 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2. Similarly, we localize the chain inside the pore by applying a repulsive harmonic potential on beads that overlap with the pore wall. More details can be found in the ESI,† including how we create the initial conditions.
2. Similarly, we localize the chain inside the pore by applying a repulsive harmonic potential on beads that overlap with the pore wall. More details can be found in the ESI,† including how we create the initial conditions.
In this paper, we vary the body force f(t) in time and see how this parameter affects the velocity of the knotted polymer through the pore. The forces we apply are between f = 1–20 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . If we assume the effective, screened charge across 1 nm of single-stranded DNA is q = −1.25e, these forces correspond to a voltage drop of 0.20–4.1 V across the nanopore, values that have been achieved experimentally.54 See ESI† for more details, which is inspired by the analysis of van Dorp et al.55 The signals we pulse have a off times around 20td ≈ 46 ns, values that have been attained in electroporation studies.56 We also examine what role the chain's topology plays in the translocation dynamics. The knot types we study are in Fig. 1b. The 31, 51, and 71 knots are torus knots, which are knots whose contour can be mapped onto a surface of a torus. The 31, 41, 52, and 61 knots are twist knots, which are created by taking a linear chain, forming a loop with any number of half turns, and then passing one chain end through the loop. We note that the 31 knot is a member of both families.
. If we assume the effective, screened charge across 1 nm of single-stranded DNA is q = −1.25e, these forces correspond to a voltage drop of 0.20–4.1 V across the nanopore, values that have been achieved experimentally.54 See ESI† for more details, which is inspired by the analysis of van Dorp et al.55 The signals we pulse have a off times around 20td ≈ 46 ns, values that have been attained in electroporation studies.56 We also examine what role the chain's topology plays in the translocation dynamics. The knot types we study are in Fig. 1b. The 31, 51, and 71 knots are torus knots, which are knots whose contour can be mapped onto a surface of a torus. The 31, 41, 52, and 61 knots are twist knots, which are created by taking a linear chain, forming a loop with any number of half turns, and then passing one chain end through the loop. We note that the 31 knot is a member of both families.
To measure the boundaries of the knotted region in our simulations, we employ two techniques. The first technique involves projecting the knot onto a plane parallel to the pore axis and then determining the smallest subset of crossings that retains the chain topology via computation of the Alexander polynomial.57,58 Since there are many planes that satisfy this condition, we choose the plane that gives rise to the smallest knot size. When the knot is jammed at the pore wall, we can also use a simpler technique to obtain the knotted boundary. We start one bead into the pore and calculate its number of nearest neighbors, defined as the number of beads within a cutoff radius Rcutoff = 1.2b. We march left until Nneighbors = 2, at which we assign this bead as the left knot boundary. We typically use the simpler technique to calculate the knot's radius of gyration when it is jammed at the pore, although it can only be used in the situation when the knot is relatively tight and its topology is not too complex (as is here).
3 Results – constant force
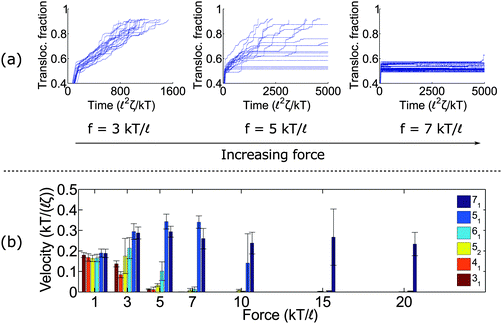
Fig. 2a shows trajectories of a knotted polymer moving through a pore when the body force f is constant in time and the bead diameter is the same as the rod length (b =![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). The y-axis is the fraction of polymer translocated, defined as ϕ = (L0 − s)/L0, where s is the contour of the polymer that has not entered the pore region and L0 is the total length of the polymer. The results plotted here are for the 41 topology – one of the more common knot types observed in bulk and in channels.59 When the knot contacts the pore – as indicated by the bend in the graphs – the polymer slows noticeably as the knot acts an additional source of chain friction. At low applied forces (f = 3 kT/
). The y-axis is the fraction of polymer translocated, defined as ϕ = (L0 − s)/L0, where s is the contour of the polymer that has not entered the pore region and L0 is the total length of the polymer. The results plotted here are for the 41 topology – one of the more common knot types observed in bulk and in channels.59 When the knot contacts the pore – as indicated by the bend in the graphs – the polymer slows noticeably as the knot acts an additional source of chain friction. At low applied forces (f = 3 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), the polymer traverses the pore at a constant speed, albeit slower than the unknotted case. At high forces (f = 7 kT/
), the polymer traverses the pore at a constant speed, albeit slower than the unknotted case. At high forces (f = 7 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), translocation completely halts since the knot jams at the pore entrance. This qualitative behavior has been observed in simulations by Huang et al.,60 Rosa et al.,40 and Suma et al.41 At very high forces, the knot becomes tight and the probability of polymer reptating through its core becomes exponentially small.47
), translocation completely halts since the knot jams at the pore entrance. This qualitative behavior has been observed in simulations by Huang et al.,60 Rosa et al.,40 and Suma et al.41 At very high forces, the knot becomes tight and the probability of polymer reptating through its core becomes exponentially small.47
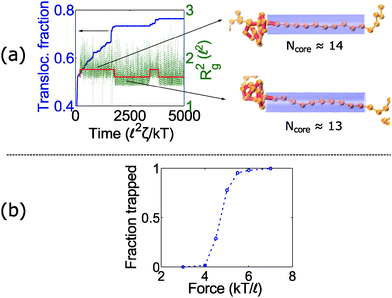
At intermediate forces (f = 5 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), we observe qualitatively different behavior. Some trajectories are completely jammed, others move through the pore at uniform speed, while others exhibit stick-slip motion. In this situation, the configuration of the knot at the pore wall plays a large role in the chain's dynamics. Fig. 3a demonstrates an example of this effect. In this graph, we see a trace of one polymer with a 41 knot moving through a pore. The polymer switches between jammed and unjammed states, and during the transition, the radius of gyration of the knotted region makes distinct hops. The number of monomers in the knotted core changes as well. Results for the other knot topologies (31, 51, 52, 61) are shown in the ESI.† For the most part, we observe a broad distribution in the polymer's transit times when the knot is close to the jamming transition, although for other knot topologies, we see large fluctuations at other force values as well.
), we observe qualitatively different behavior. Some trajectories are completely jammed, others move through the pore at uniform speed, while others exhibit stick-slip motion. In this situation, the configuration of the knot at the pore wall plays a large role in the chain's dynamics. Fig. 3a demonstrates an example of this effect. In this graph, we see a trace of one polymer with a 41 knot moving through a pore. The polymer switches between jammed and unjammed states, and during the transition, the radius of gyration of the knotted region makes distinct hops. The number of monomers in the knotted core changes as well. Results for the other knot topologies (31, 51, 52, 61) are shown in the ESI.† For the most part, we observe a broad distribution in the polymer's transit times when the knot is close to the jamming transition, although for other knot topologies, we see large fluctuations at other force values as well.
Fig. 3b plots the forces at which we observe significant stick-slip behavior for the 41 knot. This figure shows the fraction of time the polymer is jammed over an ensemble of 20–50 runs. When this fraction is O(0.5), stick-slip is significant and hence polymer motion is difficult to control. Although this regime should avoided from a practical standpoint, it is interesting from a physical perspective since it is an example of caging47,61 and molecular individualism42–44 of the knot.
We close this section by graphing the mean translocation speed 〈v〉 as a function of applied force f for several different knot topologies (Fig. 2b). We measure this quantity by fitting each polymer trajectory like in Fig. 2a to a straight line after the knot contacts the pore. We calculate the mean and standard deviation from 20 runs. One observation from these results is that the twist knots (31, 41, 52, and 61) jam much more easily than non-twist knots (51 and 71). This corroborates the observations by Suma et al.,41 and that paper gives an elegant mechanistic explanation for why this discrepancy exists. In short, the twist knots dissipate tension much more easily than non-twist knots, which leads to less force being transmitted to the chain outside the pore. One difference in our graph is that we examine a larger dynamic force range (e.g., we see that the 51 knot eventually jams). We also plot error bars, so one can see what forces lead to large fluctuations relative to the mean (see f = 5 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for the 41 knot, f = 7 kT/
for the 41 knot, f = 7 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for the 52 knot, and f = 10 kT/
for the 52 knot, and f = 10 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for the 51 knot). We note that the values of jamming we obtain in this study are larger than the ones reported by Suma et al.41 This result can be expected as we use nearly hard-sphere repulsions to enforce excluded volume interactions while the other authors use softer intra-chain interactions that allow knots to tighten more easily. We also use a larger pore diameter (R =
for the 51 knot). We note that the values of jamming we obtain in this study are larger than the ones reported by Suma et al.41 This result can be expected as we use nearly hard-sphere repulsions to enforce excluded volume interactions while the other authors use softer intra-chain interactions that allow knots to tighten more easily. We also use a larger pore diameter (R = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as opposed to R = 0.775
as opposed to R = 0.775![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ).
).
In the ESI,† we examine how the roughness of the polymer backbone alters the jamming physics. As expected, knots with a more corrugated backbone (b = 0.8![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., non-touching beads) jam at lower forces than ones with a less corrugated backbone (b =
, i.e., non-touching beads) jam at lower forces than ones with a less corrugated backbone (b = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., touching beads). If the backbone is fairly smooth (b = 1.5
, i.e., touching beads). If the backbone is fairly smooth (b = 1.5![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., overlapping beads), the knots jam at very large forces for certain topologies but fail to jam for other topologies. In the next section, we will see that the corrugation plays a large role in relaxation behavior of the knot – i.e., how the knot swells from its tightened state.
, i.e., overlapping beads), the knots jam at very large forces for certain topologies but fail to jam for other topologies. In the next section, we will see that the corrugation plays a large role in relaxation behavior of the knot – i.e., how the knot swells from its tightened state.
4 Results – pulsed force field
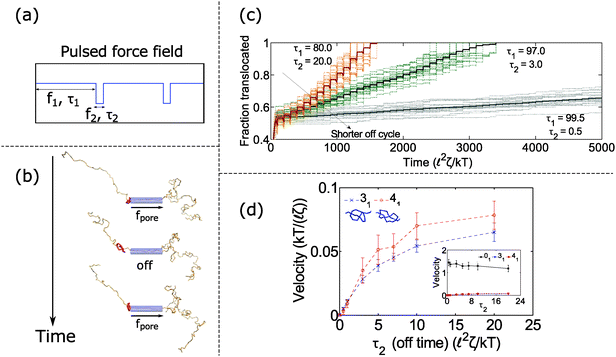
In the previous section, we found that knotted polymers jam at the pore's entrance above a critical force. This observation presents a method to control the motion of the polymer by cycling the applied force. Fig. 4a and b shows the schematic of this idea. We apply force f1 above the jamming transition for time τ1, followed by zero force for time τ2, and then repeat this process ad-infinitum. During the first part of the cycle, the knot jams at the pore entrance and halts the polymer's motion. During the relaxation cycle τ2, the knot swells and diffuses away from the pore. This process introduces slack into the chain, which allows it to ratchet through the pore when the force is turned back on. Thus, by controlling the relaxation dynamics of the chain, one can manipulate the polymer's speed.We demonstrate this claim in Fig. 4c and d. In Fig. 4c, we plot the trajectories of a polymer with a 31 knot under a pulsed field with parameters f1 = 7 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and f2 = 0 kT/
and f2 = 0 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . We vary the time τ2 spent in the off-cycle but keep the total cycle time τ1 + τ2 to be constant (τ1 + τ2 = 100
. We vary the time τ2 spent in the off-cycle but keep the total cycle time τ1 + τ2 to be constant (τ1 + τ2 = 100 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT). The bead size is equal to the rod length (b =
2ζ/kT). The bead size is equal to the rod length (b = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). In the figure, we see that the polymers traverse through the pore in a step-wise fashion with the mean velocity increasing with increasing time spent in the off-cycle. We plot the average translocation speeds of 31 and 41 knots in Fig. 4d, the knots most commonly found in vitro.62 Again, we can tailor the average speed at which polymers move through the pore, and furthermore, these speeds are demonstrably slower than the free chain case (Fig. 4d inset). Translocation speeds for other knot topologies are shown in the ESI.†
). In the figure, we see that the polymers traverse through the pore in a step-wise fashion with the mean velocity increasing with increasing time spent in the off-cycle. We plot the average translocation speeds of 31 and 41 knots in Fig. 4d, the knots most commonly found in vitro.62 Again, we can tailor the average speed at which polymers move through the pore, and furthermore, these speeds are demonstrably slower than the free chain case (Fig. 4d inset). Translocation speeds for other knot topologies are shown in the ESI.†
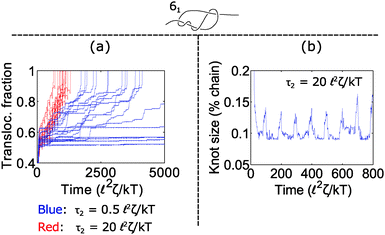
How does cycling the force field affect the fluctuations in the polymer's speed? In some situations, the cycling will reduce the relative fluctuations, while in other situations it will enhance them. We demonstrate the former in Fig. 5. In part (a), we plot trajectories of a polymer with a 61 twist knot when we cycle the force field between f1 = 7 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and f2 = 0 kT/
and f2 = 0 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . We keep the total cycle time constant at τ1 + τ2 = 100
. We keep the total cycle time constant at τ1 + τ2 = 100 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT and vary the time τ2 spent in the off cycle. We note that force f1 for this topology is slightly below the jamming transition and hence leads to large fluctuations when the cycle time τ2 is zero or nearly zero. However, when the off cycle is τ2 = 20
2ζ/kT and vary the time τ2 spent in the off cycle. We note that force f1 for this topology is slightly below the jamming transition and hence leads to large fluctuations when the cycle time τ2 is zero or nearly zero. However, when the off cycle is τ2 = 20 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT, the fluctuations are suppressed and the translocation speed becomes fairly constant. The reason why this phenomenon occurs is that during the off part of the cycle, the knot swells considerably – more than the contour that reptates through the pore during the on cycle (Fig. 5b). Thus, the relaxation dynamics in this case swamp out any fluctuations that rise due to the knot contacting the pore.
2ζ/kT, the fluctuations are suppressed and the translocation speed becomes fairly constant. The reason why this phenomenon occurs is that during the off part of the cycle, the knot swells considerably – more than the contour that reptates through the pore during the on cycle (Fig. 5b). Thus, the relaxation dynamics in this case swamp out any fluctuations that rise due to the knot contacting the pore.
In Fig. 6, we show a situation where the cycling gives rise to the opposite effect – i.e., enhanced fluctuations. In this graph, we show the 31 and 41 knot moving through the pore when we cycle the force field between two values: f = f1 and f2 = 0. We vary the force f1 during the on cycle but keep the cycle times the same at τ1 = 80 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT and τ2 = 20
2ζ/kT and τ2 = 20 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT. The forces we examine are well above the jamming transition for the two knot topologies. When f1 = 7 kT/
2ζ/kT. The forces we examine are well above the jamming transition for the two knot topologies. When f1 = 7 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the polymers ratchet through the pore in a step-wise fashion with a fairly uniform velocity. When the applied force is very large (f1 = 15 kT/
, the polymers ratchet through the pore in a step-wise fashion with a fairly uniform velocity. When the applied force is very large (f1 = 15 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), the 41 knot exhibits large fluctuations in its speed while the dynamics of the 31 knot stays the same. We observe such enhanced fluctuations for the non-torus knot topologies (41, 52, and 61) but have yet to observe these effects for the torus topologies (31, 51, 71) – see ESI† for more details. We offer an explanation for this phenomenon below.
), the 41 knot exhibits large fluctuations in its speed while the dynamics of the 31 knot stays the same. We observe such enhanced fluctuations for the non-torus knot topologies (41, 52, and 61) but have yet to observe these effects for the torus topologies (31, 51, 71) – see ESI† for more details. We offer an explanation for this phenomenon below.
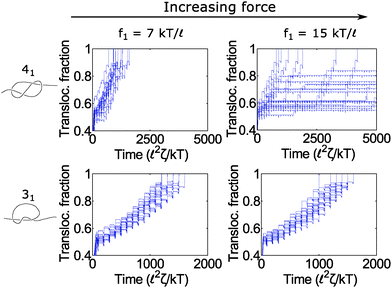 | ||
Fig. 6 Enhanced fluctuations due to cycling at large forces. Top row: Trajectories of a 41-knotted polymer moving through a pore via a force field cycling on and off. The on time is τ1 = 80 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT, and the off time is τ2 = 20 2ζ/kT, and the off time is τ2 = 20 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT. At moderate forces (f1 = 7 kT/ 2ζ/kT. At moderate forces (f1 = 7 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), the polymer ratchets through the pore with a fairly constant velocity. If the force becomes too large (f1 = 15 kT/ ), the polymer ratchets through the pore with a fairly constant velocity. If the force becomes too large (f1 = 15 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), the polymer's speed exhibits large fluctuations. This phenomenon appears primarily for the non-torus knots (41, 52, 61) but not for the torus knots (31, 51, 71) (see ESI† for details). Bottom row: Trajectories of a 31 knot at the same forces. Here we do not observe large fluctuations. In these simulations, the bead size is equal to the rod length (b = ), the polymer's speed exhibits large fluctuations. This phenomenon appears primarily for the non-torus knots (41, 52, 61) but not for the torus knots (31, 51, 71) (see ESI† for details). Bottom row: Trajectories of a 31 knot at the same forces. Here we do not observe large fluctuations. In these simulations, the bead size is equal to the rod length (b = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). ). | ||
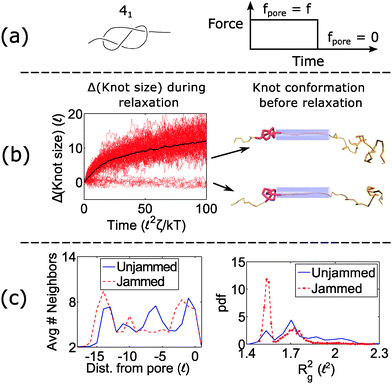
When a knot jams at very large forces, it may become trapped in a metastable state with an escape potential of several kT. To verify this statement, we ran a simulation of a knotted polymer at the pore wall undergoing a step relaxation (Fig. 7a). The initial topology is a 41 knot, and the initial force is f = 15 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., the force at which we observe large fluctuations when we cycle the field as in Fig. 6. When we turn off the field, we see that some trajectories of the 41 knot remain jammed while others swell easily (Fig. 7b). The knot's caging appears to be dependent on how it contacts the pore wall before the field is turned off. In Fig. 7c, we divide all knot trajectories into two populations – one that remains jammed during relaxation and one that remains unjammed. If we plot the average density profile of these two populations before relaxation begins, we see that the two profiles are distinct. We observe a similar distinction for the knot's radius of gyration (Fig. 7c) as well as a simple visual check of the knot's conformation (Fig. 7b). Videos of the step relaxation simulation are in the ESI.†
, i.e., the force at which we observe large fluctuations when we cycle the field as in Fig. 6. When we turn off the field, we see that some trajectories of the 41 knot remain jammed while others swell easily (Fig. 7b). The knot's caging appears to be dependent on how it contacts the pore wall before the field is turned off. In Fig. 7c, we divide all knot trajectories into two populations – one that remains jammed during relaxation and one that remains unjammed. If we plot the average density profile of these two populations before relaxation begins, we see that the two profiles are distinct. We observe a similar distinction for the knot's radius of gyration (Fig. 7c) as well as a simple visual check of the knot's conformation (Fig. 7b). Videos of the step relaxation simulation are in the ESI.†
This caging phenomenon is highly dependent on knot topology and the friction along the polymer backbone. For the case when the bead size is equivalent to the rod length (b = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), we observe that torus topologies (31, 51, 71) relax normally while non-torus ones (41, 52, and 61) fail to unjam at large initial forces (f ≥ 15 kT/
), we observe that torus topologies (31, 51, 71) relax normally while non-torus ones (41, 52, and 61) fail to unjam at large initial forces (f ≥ 15 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). If the polymer backbone is more corrugated (b = 0.8
). If the polymer backbone is more corrugated (b = 0.8![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., non-touching beads), this effect is more pronounced. However, if the polymer's backbone is fairly smooth (b = 1.5
, i.e., non-touching beads), this effect is more pronounced. However, if the polymer's backbone is fairly smooth (b = 1.5![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e., overlapping beads), we find that the knots relax normally even at very large initial forces (f = 40 kT/
, i.e., overlapping beads), we find that the knots relax normally even at very large initial forces (f = 40 kT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). See ESI† for more details.
). See ESI† for more details.
5 Discussion
In this study, we investigate the feasibility of using knots to slow down and control the translocation of polymers through nanopores. Under a constant, external field, we find that:• Knots halt translocation above a critical force
• Twist knots (31, 41, 52, 61) jam more easily than non-twist knots
• For many topologies, polymers experience large fluctuations in their transit times when the knot is slightly below its jamming transition.
These observations show that polymer motion can be drastically altered by the friction created from self-entanglements. This friction is generated by chain segments sliding past each other in the knotted core, and the resistance to this motion depends on the short-range interactions in the knotted region as well as the tension at the pore entrance. The model we employ here is the simplest representation of a flexible chain that captures the essential features of this friction.47 It treats the polymer backbone as an energy landscape corrugated at a monomer length scale, a result borne from recent optical tweezer experiments as the origin of solid friction between polymer filaments.63 Thus, although we do not take into account all the short-range interactions in a polymer like single stranded DNA, we expect our model to capture the generic features of a translocation experiment and give order-of-magnitude estimates for the critical voltages required for jamming.
For the model we choose (the nominal chain width b is approximately equal to the Kuhn step ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), a voltage drop of roughly 1.4 V is needed to jam a 31 or 41 knot of ssDNA along a pore of 2 nm diameter and 10 nm depth. For more complex topologies (51, 61), double the voltage is needed. If experiments show that the transition occurs at a smaller voltage than expected, the energy landscape along the polymer backbone is more corrugated than the model suggests – i.e., there is greater friction due to chains sliding past each other. In general, these experiments can provide insight into how friction arises between chain entanglements, an area that is receiving increasing interest in the polymer physics community as well as in studies with granular, macroscopic chains.64,65 Furthermore, the stick-slip phenomenon observed in this manuscript is fascinating from a physics standpoint as it demonstrates how polymers under the same operating conditions exhibit vastly different dynamics depending on the knot's configuration. It is one of many examples of molecular individualism of a polymer strand42–44 and it shows how topology plays a large role in the polymer's dynamical fluctuations.
), a voltage drop of roughly 1.4 V is needed to jam a 31 or 41 knot of ssDNA along a pore of 2 nm diameter and 10 nm depth. For more complex topologies (51, 61), double the voltage is needed. If experiments show that the transition occurs at a smaller voltage than expected, the energy landscape along the polymer backbone is more corrugated than the model suggests – i.e., there is greater friction due to chains sliding past each other. In general, these experiments can provide insight into how friction arises between chain entanglements, an area that is receiving increasing interest in the polymer physics community as well as in studies with granular, macroscopic chains.64,65 Furthermore, the stick-slip phenomenon observed in this manuscript is fascinating from a physics standpoint as it demonstrates how polymers under the same operating conditions exhibit vastly different dynamics depending on the knot's configuration. It is one of many examples of molecular individualism of a polymer strand42–44 and it shows how topology plays a large role in the polymer's dynamical fluctuations.
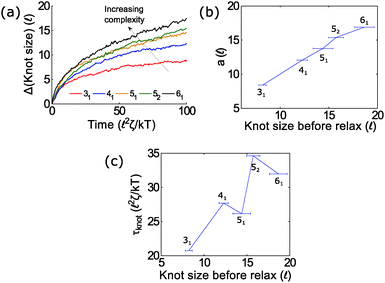
In the second part of the manuscript, we examine the dynamics of a knotted chain when the external field is cycled on and off. If the off time is comparable to the relaxation time of the knot, we can adjust the swelling of the knot and hence ratchet the polymer through the pore. If we perform step relaxation simulations of knots (Fig. 8) and fit the knot size during relaxation to an exponential function y = a[1 − exp(−t/τknot)], we obtain a relaxation time of tknot ≈ 20–35 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2ζ/kT and a change in knot size of a ≈ 8 − 18
2ζ/kT and a change in knot size of a ≈ 8 − 18![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for the topologies studied so far (provided that the knots do not arrest during relaxation). This corresponds to a time scale of tknot ≈ 40–70 ns and a change in knot size of 8–18 nm for single stranded DNA over the time scale studied (200 ns). We expect both of these quantities to increase for more complex topologies. We also expect the knot to swell further at much longer times to a metastable size of ≈140 monomers.17
for the topologies studied so far (provided that the knots do not arrest during relaxation). This corresponds to a time scale of tknot ≈ 40–70 ns and a change in knot size of 8–18 nm for single stranded DNA over the time scale studied (200 ns). We expect both of these quantities to increase for more complex topologies. We also expect the knot to swell further at much longer times to a metastable size of ≈140 monomers.17
When the initial tension on the chain is sufficiently large, the knot can arrest during relaxation. This effect is more pronounced for non-torus topologies than torus ones, and this effect can ultimately lead to large fluctuations in the polymer's transit times through the nanopore (Fig. 6). Again, we note that the forces at which we observe this phenomenon are dependent on the knot's internal friction, which in turn is dependent on the corrugated energy landscape along the polymer backbone. Our model predicts a voltage drop of approximately 3 V is needed across a pore of 2 nm diameter and 10 nm depth to observe the caging of the 41 and 52 knots during relaxation. If the polymer backbone is more corrugated than our model suggests, then this phenomenon will be more prominent. We also note that in some instances, the caging of the knot depends on the geometry of the knot just before it relaxes (Fig. 7c). This observation indicates that the knot's dynamics exhibit memory, which is an interesting topic to examine in the future.
In this work, we do not study how the pore size and the overall chain length alter the dynamics of the knotted polymer. The former is likely to modify the critical force for jamming, while the latter is likely to modify the polymer's speed, especially if the chain is large and long-range hydrodynamic interactions are included. These effects are ripe for future investigation. Additionally, it would be interesting to inspect how the charge relaxation inside the pore alters the knot's dynamics. In most solid state pores, the time scale of charge relaxation is tcap = RsCp = 75 ps to 1 μs,66–68 where Rs is the resistance of the ionic solution and Cp is the pore's capacitance. If tcap > tknot, the knot will remain under tension during charge rearrangement and hence one will have to cycle at a time scale comparable to tcap. Lastly, it is important to extend this study to semi-flexible chains such as double stranded DNA, since many sequencing applications utilize this polymer.
6 Conclusion
In this paper, we study the dynamics of a knotted polymer moving through a pore under an external field. We examine the dynamics when the field is constant in time and when the field periodically switches on and off. We find the latter case can be used to control the knot's swelling at the pore entrance and hence control the polymer's motion through the pore. We discuss how this strategy alters the fluctuations in the polymer's transit times. Cycling the field can reduce fluctuations near the knot's jamming transition, but can increase fluctuations at very large forces as the knot gets trapped in metastable states during relaxation. Although the predictions here have yet to be experimentally tested, we provide some order-of-magnitude estimates of voltages and cycle times where we expect knot jamming and ratcheting dynamics to occur. We also briefly address how the roughness along the polymer backbone alters the frictional dynamics of this system.This study is interesting not only for applications such as nanopore sequencing, but it also provides insight into how self-entanglements give rise to friction in chains, an area of active research in the polymer physics community. This study also describes the relaxation behavior of a tight knot, which to this date has been unreported. This phenomenon may be important in direct optical mapping69 where tight knots in genomic-length DNA appear as false deletions that obscure data analysis.70 Other applications where entangled polymers move through pores include tertiary oil recovery,71 chromatography, and virus-to-cell transmission.72 Lastly, after initial submission of this work, Szymczak performed simulations of knotted proteins moving through pores.73 Molecular motors apply forces in an on–off fashion, which allow these proteins to ratchet through pores in a manner similar to what we observe here.
Acknowledgements
This work is supported by the Singapore-MIT Alliance for Research and Technology (SMART) and National Science Foundation (NSF) grant CBET-1335938. We also thank Prof. Alfredo Alexander-Katz for fruitful discussions regarding this work.References
- W. Camann and J. Marquardt, N. Engl. J. Med., 2003, 349, 159 CrossRef PubMed.
- J. Portugal and A. Rodriguez-Campos, Nucleic Acids Res., 1996, 24, 4890–4894 CrossRef CAS PubMed.
- A. J. Schoeffler and J. M. Berger, Q. Rev. Biophys., 2008, 41, 41–101 CrossRef CAS PubMed.
- J. C. Wang, Annu. Rev. Biochem., 1996, 65, 635–692 CrossRef CAS PubMed.
- J. J. Champoux, Annu. Rev. Biochem., 2001, 70, 369–413 CrossRef CAS PubMed.
- D. Meluzzi, D. E. Smith and G. Arya, Annu. Rev. Biophys., 2010, 39, 349–366 CrossRef CAS PubMed.
- C. Micheletti, D. Marenduzzo and E. Orlandini, Phys. Rep., 2011, 504, 1–73 CrossRef CAS.
- E. Orlandini and S. G. Whittington, Rev. Mod. Phys., 2007, 79, 611 CrossRef CAS.
- D. Sumners and S. Whittington, J. Phys. A: Math. Gen., 1988, 21, 1689 CrossRef.
- E. J. Van Rensburg, D. Sumners, E. Wasserman and S. Whittington, J. Phys. A: Math. Gen., 1992, 25, 6557 CrossRef.
- S. R. Quake, Phys. Rev. Lett., 1994, 73, 3317 CrossRef CAS PubMed.
- P. Y. Lai, Y. J. Sheng and H. K. Tsao, Physica A, 2000, 281, 381–392 CrossRef CAS.
- C. B. Renner and P. S. Doyle, Soft Matter, 2015, 11, 3105–3114 RSC.
- D. Kivotides, S. Wilkin and T. Theofanous, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 041808 CrossRef PubMed.
- A. M. Saitta, P. D. Soper, E. Wasserman and M. L. Klein, Nature, 1999, 399, 46–48 CrossRef CAS PubMed.
- A. Y. Grosberg and Y. Rabin, Phys. Rev. Lett., 2007, 99, 217801 CrossRef PubMed.
- L. Dai, C. B. Renner and P. S. Doyle, Phys. Rev. Lett., 2015, 114, 037801 CrossRef PubMed.
- L. Dai, C. B. Renner and P. S. Doyle, Macromolecules, 2015, 48, 2812–2818 CrossRef CAS.
- Y. Arai, R. Yasuda, K. Akashi, Y. Harada, H. Miyata, K. Kinosita and H. Itoh, Nature, 1999, 399, 446–448 CrossRef CAS PubMed.
- X. R. Bao, H. J. Lee and S. R. Quake, Phys. Rev. Lett., 2003, 91, 265506 CrossRef PubMed.
- J. Tang, N. Du and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16153–16158 CrossRef CAS PubMed.
- C. B. Renner, N. Du and P. S. Doyle, Biomicrofluidics, 2014, 8, 034103 CrossRef PubMed.
- L. F. Liu, L. Perkocha, R. Calendar and J. C. Wang, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 5498–5502 CrossRef CAS.
- R. Matthews, A. A. Louis and J. M. Yeomans, Phys. Rev. Lett., 2009, 102, 088101 CrossRef PubMed.
- S. Chang, S. Huang, J. He, F. Liang, P. Zhang, S. Li, X. Chen, O. Sankey and S. Lindsay, Nano Lett., 2010, 10, 1070–1075 CrossRef CAS PubMed.
- J. Clarke, H. C. Wu, L. Jayasinghe, A. Patel, S. Reid and H. Bayley, Nat. Nanotechnol., 2009, 4, 265–270 CrossRef CAS PubMed.
- C. Dekker, Nat. Nanotechnol., 2007, 2, 209–215 CrossRef CAS PubMed.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770–13773 CrossRef CAS.
- J. J. Kasianowicz, J. W. F. Robertson, E. R. Chan, J. E. Reiner and V. M. Stanford, Annu. Rev. Anal. Chem., 2008, 1, 737–766 CrossRef CAS PubMed.
- D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. Di Ventra, S. Garaj, A. Hibbs, X. Huang, S. B. Jovanovich, P. S. Krstic, S. Lindsay, X. S. Ling, C. H. Mastrangelo, A. Meller, J. S. Oliver, Y. V. Pershin, J. M. Ramsey, R. Riehn, G. V. Soni, V. Tabard-Cossa, M. Wanunu, M. Wiggin and J. A. Schloss, Nat. Biotechnol., 2008, 10, 1146 CrossRef PubMed.
- E. C. Hayden, Nature, 2015, 521, 7550 Search PubMed.
- A. Mikheyev and M. M. Y. Tin, Mol. Ecol. Resour., 2014, 14, 1097–1102 CrossRef CAS PubMed.
- M. Muthukumar, C. Plesa and C. Dekker, Phys. Today, 2015, 68, 40–46 CrossRef CAS.
- B. M. Venkatesan and R. Bahsir, Nat. Nanotechnol., 2011, 6, 615–624 CrossRef CAS PubMed.
- D. Fologea, J. Uplinger, B. Thomas, D. S. McNabb and J. Li, Nano Lett., 2005, 5, 1734–1737 CrossRef CAS PubMed.
- S. W. Kowalczyk, D. B. Wells, A. Aksimentiev and C. Dekker, Nano Lett., 2012, 12, 1038 CrossRef CAS PubMed.
- D. Deamer, Annu. Rev. Biophys., 2010, 39, 79–90 CrossRef CAS PubMed.
- G. M. Cherf, K. R. Lieberman, R. Rashid, C. E. Lam, K. Karplus and M. Akeson, Nat. Biotechnol., 2012, 30, 344 CrossRef CAS PubMed.
- E. A. Manrao, I. M. Derrington, A. H. Laszlo, K. W. Langford, M. K. Hopper, N. Gillgren, M. Pavlenok, M. Niederweis and J. H. Gundlach, Nat. Biotechnol., 2012, 30, 349 CrossRef CAS PubMed.
- A. Rosa, M. Di Ventra and C. Micheletti, Phys. Rev. Lett., 2012, 109, 118301 CrossRef CAS PubMed.
- A. Suma, A. Rosa and C. Micheletti, ACS Macro Lett., 2015, 4, 1420–1424 CrossRef CAS.
- P. G. de Gennes, Science, 1997, 276, 1999–2000 CrossRef CAS PubMed.
- T. Perkins, D. Smith, R. Larson and S. Chu, Science, 1995, 268, 83 CAS.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS PubMed.
- N. Keller, S. Grimes, P. J. Jardine and D. E. Smith, Nat. Phys., 2016 DOI:10.1038/nphys3740.
- D. Rolfsen, Table of knots and links, Appendix C, Publish or Perish Press, 1976 Search PubMed.
- V. Narsimhan, C. B. Renner and P. S. Doyle, ACS Macro Lett., 2016, 5, 123–127 CrossRef CAS.
- A. Ward, F. Hilitski, W. Schwenger, D. Welch, A. W. C. Lau, V. Vitelli, L. Mahadevan and Z. Dogic, Nat. Mater., 2015, 14, 583–588 CrossRef CAS PubMed.
- V. V. Palyulin, T. Ala-Nissilab and R. Metzler, Soft Matter, 2014, 10, 9016 RSC.
- K. Luo, T. Ala-Nissila, S. C. Ying and A. Bhattacharya, Phys. Rev. Lett., 2007, 99, 148102 CrossRef PubMed.
- H. H. Katkar and M. Muthukumar, J. Chem. Phys., 2014, 140, 135102 CrossRef CAS PubMed.
- K. Luo, T. Ala-Nissila, S. C. Ying and R. Metzler, Europhys. Lett., 2009, 88, 68006 CrossRef.
- M. Fyta, S. Melchionna, S. Succi and E. Kaxiras, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036704 CrossRef PubMed.
- J. B. Heng, A. Aksimentiev, C. Ho, P. Marks, P. V. Grinkova, S. Sligar, K. Schulten and G. Timp, Nano Lett., 2005, 5, 1883–1888 CrossRef CAS PubMed.
- S. van Dorp, U. F. Keyser, N. H. Dekker, C. Dekker and S. G. Lemay, Nat. Phys., 2009, 5, 347–351 CrossRef CAS.
- S. J. Beebe and K. H. Schoenbach, J. Biomed. Biotechnol., 2005, 4, 297–300 CrossRef PubMed.
- A. V. Vologodskii, A. V. Lukashin, M. D. Frank-Kamenetskii and V. V. Anshelevich, Zh. Eksp. Teor. Fiz., 1974, 66, 2153–2163 CAS.
- P. Virnau, Phys. Procedia, 2010, 6, 117–125 CrossRef CAS.
- E. Orlandini and C. Micheletti, J. Biol. Phys., 2013, 39, 267–275 CrossRef CAS PubMed.
- L. Huang and D. E. Makarov, J. Chem. Phys., 2008, 129, 121107 CrossRef PubMed.
- L. Huang and D. E. Makarov, J. Phys. Chem. A, 2007, 111, 10338–10344 CrossRef CAS PubMed.
- V. V. Rybenkov, N. R. Cozzarelli and A. V. Vologodskii, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 5307–5311 CrossRef CAS.
- A. Ward, F. Hilitski, W. Schwenger, D. Welch, A. W. C. Lau, V. Vitelli, L. Mahadevan and Z. Dogic, Nat. Mater., 2015, 14, 583–588 CrossRef CAS PubMed.
- A. Belmonte, M. J. Shelley, S. T. Eldakar and C. H. Wiggins, Phys. Rev. Lett., 2001, 87, 114301 CrossRef CAS PubMed.
- E. Ben-Naim, Z. A. Daya, P. Vorobeiff and R. E. Ecke, Phys. Rev. Lett., 2011, 86, 1414 CrossRef PubMed.
- G. Sigalov, J. Comer, G. Timp and A. Aksimentiev, Nano Lett., 2008, 8, 56–63 CrossRef CAS PubMed.
- M. Krems, Y. V. Pershin and M. Di Ventra, Nano Lett., 2010, 10, 2674–2678 CrossRef CAS PubMed.
- R. M. M. Smeets, U. F. Keyser, N. H. Dekker and C. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 417–421 CrossRef CAS PubMed.
- E. T. Dimalanta, A. Lim, R. Runnheim, C. Lamers, C. Churas, D. K. Forrest, J. J. de Pablo, M. D. Graham, S. N. Coppersmith, S. Goldstein and D. C. Schwartz, Anal. Chem., 2004, 76, 5293–5301 CrossRef CAS PubMed.
- J. G. Reifenberger, K. D. Dorfman and H. Cao, Analyst, 2015, 140, 4887–4894 RSC.
- S. Rodriguez, C. Romero, M. L. Sargenti, A. J. Müller, A. E. Sáez and J. A. Odell, J. Non-Newtonian Fluid Mech., 1993, 49, 63–85 CrossRef CAS.
- W. Mothes, N. M. Sherer, J. Jin and P. Zhong, J. Virol., 2010, 84, 8360–8368 CrossRef CAS PubMed.
- P. Szymczak, Sci. Rep., 2016, 6, 21702 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00545d |
| This journal is © The Royal Society of Chemistry 2016 |