Isostructural solid–solid phase transition in monolayers of soft core–shell particles at fluid interfaces: structure and mechanics

Abstract

We have studied the complete two-dimensional phase diagram of a core–shell microgel-laden fluid interface by synchronizing its compression with the deposition of the interfacial monolayer. Applying a new protocol, different positions on the substrate correspond to different values of the monolayer surface pressure and specific area. Analyzing the microstructure of the deposited monolayers, we discovered an isostructural solid–solid phase transition between two crystalline phases with the same hexagonal symmetry, but with two different lattice constants. The two phases corresponded to shell–shell and core–core inter-particle contacts, respectively; with increasing surface pressure the former mechanically failed enabling the particle cores to come into contact. In the phase-transition region, clusters of particles in core–core contacts nucleate, melting the surrounding shell–shell crystal, until the whole monolayer moves into the second phase. We furthermore measured the interfacial rheology of the monolayers as a function of the surface pressure using an interfacial microdisk rheometer. The interfaces always showed a strong elastic response, with a dip in the shear elastic modulus in correspondence with the melting of the shell–shell phase, followed by a steep increase upon the formation of a percolating network of the core–core contacts. These results demonstrate that the core–shell nature of the particles leads to a rich mechanical and structural behavior that can be externally tuned by compressing the interface, indicating new routes for applications, e.g. in surface patterning or emulsion stabilization.

---

1 Introduction

One of the strong suits of soft matter research is the focus on materials that carry both fundamental interest and are highly relevant for applications. In particular, the former often comes about through the investigation of systems whose characteristics are general enough to serve as models for a plethora of materials, including liquids, crystals and glasses, but with the advantage that their structural, dynamical and response properties can be studied at easily accessible length, time and energy scales. The latter is, on the other hand, evident due to the ubiquitous presence of soft materials in a broad range of food, pharmaceutical and chemical formulations, to list a few.

An example of this duality, which has attracted significant recent attention, is the case of microgels. Microgels are cross-linked, swollen polymer particles that can be synthesized out of a variety of different, typically hydrophilic, polymers. There are two main interconnected features that make microgels so interesting: their softness and their responsiveness. Microgels are soft due to the compressibility of the solvated hydrogel network, while their responsiveness comes from changes in the polymer solubility and swelling as a function of the environmental conditions.^1,2 The paradigmatic example is the case of poly(N-isopropylacrylamide) (PNiPAm) microgels, showing a strong temperature-dependent swelling behavior and a volume-phase-transition temperature around 32 °C; the particles are highly swollen and compressible below this temperature, while the polymer chains become more hydrophobic and partially collapse above it, causing particle shrinkage.³ Similarly, co-polymerizing monomers such as methacrylic acid (MAA) with NiPAm during synthesis makes it possible to create pH-responsive particles that swell and are increasingly more deprotonated from low to high pH.⁴ Microgels are synthesized via simultaneous polymerization and cross-linking reactions. Unless special procedures are followed,^5–7 due to the fact that polymerization is typically slower than cross-linking, microgels have a varying degree of cross-linking density across their volume. This effectively leads to the formation of particles with a denser, stiffer core surrounded by looser and softer shells or coronas, also comprising dangling chains.^8,9 We will demonstrate later that the core–shell nature of these particles is at the basis of their phase behavior and mechanical response, in particular when confined at a fluid interface.

The possibility to tune the size of PNiPAm microgels by changing the local temperature has been playing a pivotal role in using them as model systems. It allows local and fine tuning of the suspension's volume fraction in a straightforward manner, and thus of its mechanical properties.¹⁰ This is opposed to the case of hard colloids, where volume fraction effects can only be studied by preparing samples at various concentrations, or by resorting to more complex experiments. The scope and importance of microgel suspensions as models systems has been recently and extensively reviewed.^1,11 Studying microgels has in particular shed significant light, among others, on the concept of fragility in glasses,¹² on the details of the two-dimensional liquid-crystal phase transition¹³ and very recently also on the pathways for martensitic solid–solid phase transitions.¹⁴

From the applications' side,¹⁵ microgels are frequently studied as drug delivery vehicles, where active molecules can be incorporated in the hydrogel network and leaked out at a controlled rate or released by external triggers.^16,17 They also attract particular interest as stabilizers for inorganic nanoparticles allowing the fabrication of responsive hybrid materials,¹⁸ and have been used as substrates for cell culture,^19,20 for the fabrication of micro-lens arrays^21,22 and interferometers,²³ and for surface patterning^24–29 and film formation.³⁰

In addition to these applications, they find increasing use as emulsion stabilizers,³¹ where the effects of softness and responsiveness combine to impart new functionalities to emulsions, including extreme compliance and stability under flow³² or triggered rupture and coalescence.^33,34 The use of microgels as emulsion stabilizers is driven by their strong propensity to adsorb spontaneously at oil–water (o/w) interfaces. As opposed to the case of hard particles, which adsorb and interact at an o/w interface without any deformation,³⁵ it has been extensively reported that microgels can be significantly deformed upon adsorption at a fluid interface.^34,36–40 Adsorption is driven by a reduction of the fluid-interface free energy when the particles sit at the interface, and deformation is driven by the fact that microgels tend to spread to maximize the amount of surface-active polymer chains at the interface. Deformation proceeds until the free energy gain is balanced by internal elasticity;⁴¹ microgels reach therefore effective diameters at the interface that are significantly larger than their size in bulk, depending on the cross-linking ratios,^36,37 but largely independent of other parameters that affect bulk dimensions, such as pH for PNiPAm-co-MAA microgels.³⁸ In particular, previous observations showed that the presence of the afore-mentioned radial gradients of cross-linking density, as well as of some dangling chains at the particle periphery, lead to the accentuation of the core–shell (or core-corona) morphology of the particles after adsorption at a fluid interface.^37,38 Looking at the interface from the top (i.e. removing the oil), the microgels in practice look like “fried eggs” with a less densely cross-linked shell surrounding a more cross-linked, and thus stiffer, core. This morphology has prompted the description of the interactions between the particles at the fluid interface as soft repulsive core–shell interactions, where, depending on the inter-particle distance and surface pressure, different microstructures of the interface have been hypothesized.^37,42 In particular, the existence of both shell–shell and core–core contacts has been assumed, but to date, a systematic visualization of these structures and a thorough study on the transitions between them is still lacking. Additionally, measurements of compression isotherms showed a counterintuitive response in the presence of bulk charges in the microgels, with uncharged particles interacting via the interface at larger inter-particle separations compared to charged systems.⁴³ Furthermore, dilatational elasticity showed an unexpected non-monotonic behavior of the elastic modulus with compression of interfacial microgel monolayers, suggesting that the presence of core–shell interactions couples non-trivially to the interface structure and mechanical properties.^42,44,45 Finally, to date, measuring reliably the shear rheology of microgel-laden interfaces as a function of interface microstructure and compression remains an elusive task, but one of high importance to determine the response of such systems to the mechanical deformations frequently present during processing.

By combining in situ inspection at an o/w interface using freeze-fracture cryo-SEM⁴⁶ with atomic force microscopy (AFM) imaging after deposition on a solid substrate, we have recently demonstrated that we can spread, compress and deposit microgel monolayers from an o/w interface using a Langmuir trough at various surface pressures without altering the monolayer microstructure upon deposition.⁴⁷ This constitutes the starting point of the work presented in this manuscript, where we design a new experiment in which a microgel-laden o/w interface is continuously compressed and the particles are simultaneously deposited on a silicon substrate. This continuous compression/deposition approach makes it possible to transfer, immobilize and visualize the microstructure of the interface upon smoothly varying the surface pressure and the specific area per particle, throughout the complete compression isotherm. We effectively deposit the entire surface pressure/area per particle two-dimensional phase diagram of the microgels confined at the interface onto a solid substrate. Therefore, we can investigate ex situ the structure at the single-particle level and relate it to the macroscopic features of the compression isotherm. Additionally, by performing in situ active microrheology of the monolayers as a function of interface compression using a magnetic microdisk rheometer,^48–50 we obtain a direct link between the interface microstructure and its shear rheology.

Interestingly, we discovered the occurrence of an isostructural solid–solid phase transition in the monolayer between two different hexagonal phases, one where the shells of the particles are in contact and one where the cores enter into physical contact. Both phases have the same hexagonal crystalline symmetry but a different lattice constant, which can be smoothly tuned for the shell–shell contacts by compressing the monolayer. This finding fulfills the predictions of simple theoretical models for soft particles interacting with a repulsive shoulder potential, which were studied in the past,^51,52 but which had so far escaped experimental evidence.

2 Experimental

2.1 Materials

Milli-Q water at neutral pH and n-hexane (Sigma-Aldrich, 99%, as received) were used as the bulk phases in the Langmuir though experiments. The microgels are cross-linked P(NiPAm-co-MAA) particles with N-isopropylacrylamide (NiPAm) as the main monomer and methacrylic acid (MAA) as a comonomer. The content of MAA in the microgels was determined by pH titration to 6.3 ± 0.6 wt%. Details of the microgel synthesis have been previously reported³⁸ and they are produced by standard precipitation polymerization with a surfactant. Dynamic light scattering (Zetasizer, Malvern UK) gives a hydrodynamic radius of the particles of 213 ± 10 nm in Milli-Q water at neutral pH. The microgels were stored as a 1 wt% suspension in Milli-Q water. Before being injected at the water/n-hexane interface in the Langmuir trough, they were further diluted to 0.1 wt% using 50 μL of the microgel stock suspension, 100 μL isopropyl alcohol (Fisher Chemical, 99.97%) and 350 μL Milli-Q water at neutral pH to obtain a water/isopropanol suspension in a ratio of 4 : 1 (v/v). The suspension was mixed with a vortex mixer (Vortex Genie 2) before use. The number of microgels spread at the interface was calculated using the weight of the injected suspension, assuming the particle radius above and a density equal to the one of water (previous measurements on similarly cross-linked microgels gave a polymer density of 1.15 ± 0.5 g cm⁻³ and a polymer content below 20 volume% in the swollen state, leading to an overall density almost identical to the one of water⁸). Silicon wafers were cut into 1 × 2 cm² pieces and were thoroughly cleaned before use. The cleaning procedure included first 15 min ultra-sonication in toluene (Fluka Analytical, 99.7%), followed by 15 min ultra-sonication in isopropanol (Fisher Chemical, 99.97%) and a third ultra-sonication step for 15 min in Milli-Q water. The substrates were subsequently dried in a compressed nitrogen jet and finally cleaned in a UV-Ozone cleaner (UV/Ozone Procleaner Plus, Bioforce Nanosciences) for 30 min to ensure a hydrophilic surface prior to particle deposition.

2.2 Langmuir trough depositions

The microgel particles were transferred to the silicon substrates from a water/n-hexane interface using a KSV5000 Langmuir trough setup, with a custom-made trough allowing depositions at a water–oil interface. The set up is shown in Fig. 1. The trough is made out of a single Teflon block and it has a maximum area of 197.5 cm², which can be compressed down to 57.5 cm². The barriers are made out of Delrin. The sample holder, as installed in Fig. 1, is made out of Teflon and has a Delrin screw that fixes the sample at an angle of 30° relative to the horizontal interface. The surface pressure is measured with a platinum Wilhelmy plate (20 × 10 mm²) attached to a balance.

Fig. 1 Photograph of the Langmuir trough setup for the particle deposition experiments. The silicon wafer is visible in the center of trough and it is connected to the dipper arm with a support at 30° relative to the water/n-hexane interface. The trough was machined out of Teflon and has a slot in the back where the dipper arm can move without disturbing the interface.

Before each experiment all components of the Langmuir trough were thoroughly rinsed with Milli-Q water and ethanol (Fluka Analytical, 99.8%) and then dried in a nitrogen jet and set up as in Fig. 1. The experimental procedure was as follows. The trough was filled with neutral Milli-Q water until reaching the edge corresponding to the oil–water interface with the barriers fully open. The position of the Wilhelmy plate was adjusted so it was immersed for one third under water. The surface pressure value was set to zero. The surface was then compressed by slowly closing the barriers. The presence of contaminants may cause a rise in the surface pressure during this first compression. If the surface pressure with the closed barriers was below 0.2 mN m⁻¹, then the surface was considered as clean. If it was higher than 0.2 mN m⁻¹, then the water surface was aspirated using a 1 mL pipette tip (Tip One) attached to a vacuum pump (Vacuum Brand PC3000) and the compression was repeated after replacing the removed water. As soon as the surface was considered clean the barriers were fully opened. The dipper was moved up until the top edge of the silicon substrate was just below the water surface, 100 mL of n-hexane were carefully added with a clean glass pipette to create the water–oil interface and the surface pressure was zeroed again. The microgel suspension was subsequently spread at the water/n-hexane interface with a 10 μL or 100 μL Hamilton glass syringe to the desired initial amount and left to equilibrate for 5 minutes. At this stage the compression/deposition experiment was started; the barriers and the dipper arm moved simultaneously to a total range of 70 mm per barrier (140 cm² compressed area) with a compression speed of 2.3 mm min⁻¹ while the sample was extracted at a speed of 0.3 mm min⁻¹. Considering a substrate angle of 30°, the compression and dipping speed were adjusted such as the substrate would be just out of the water phase when the compression finished. After 45 min the deposition was complete and the sample had emerged through the hexane surface. The water and hexane were removed by aspiration and the substrate was then carefully released from the sample holder.

2.3 AFM imaging and image analysis

The deposited monolayers were systematically characterized with an AFM (Bruker Icon Dimension). The samples were scanned along the gradient direction and 10 × 10 μm² images were taken every 0.5 or 1 mm to a total of 20/40 images per sample. Nevertheless, the screw used to fix the substrate to the dipping arm did not allow to characterize the whole substrate surface. Scanning along different parallel lines as much as 2 mm apart showed no significant difference in terms of microstructure, emphasizing the spatial homogeneity of the deposition. 512 × 512 pixels² images were scanned in tapping mode with a scanning speed of 0.4 Hz using a Micro Cantilever (Olympus, resonance frequency: 300 kHz, spring constant: 26.1 N m⁻¹). The height images were flattened to remove slight tilt of the sample stage and converted to 8-bit grey-scale for image processing. High-resolution 1 × 1 μm² images of the deposited microgels were also taken at 0.2 Hz using the same cantilevers.

The images were further analyzed using a custom-written particle tracking software built around the Matlab version of the publicly available IDL particle tracking code by Crocker and Grier.⁵³ After locating the center of each particle, a Delaunay triangulation and a Voronoi tessellation were performed, excluding particles close to the edge of the images. The Delaunay triangulation made it possible to count the neighbors of each particle as well as their angles and nearest neighbor distances. The value of the 2D hexagonal order parameter ψ₆ was calculated for each particle using the following formula:

where N_b is the number of nearest neighbors, n is set to 6 and θ_j is the bond angle between the particle and its nearest neighbor j. The area per particle A_p could then be simply calculated by counting the number of particles inside the image divided by its area. Finally, using the surface pressure measured with the Wilhelmy plate plotted against the area per particle measured with the algorithm mentioned above, we were able to produce compression isotherms without making any assumptions on the amount of spread particles.

2.4 Interfacial microdisk rheology

2.4.1 Flow visualization. Since the microgels cannot be directly observed in an optical microscope, we added commercially available, larger polystyrene particles with a diameter of 2.03 μm as tracer particles. The spreading solution consisted of two parts microgel particle suspension (0.1 wt%), five parts polystyrene particles (10%), nine parts isopropyl alcohol and fourteen parts doubly distilled water. The relative fractions of microgels and tracers were chosen to reach an optimal number of tracers at the interface while reaching full coverage of the microgels. The isopropanol leads to the formation of a thin film on top of the water–air interface which allows the particles to arrange in an monolayer while the alcohol evaporates and also diffuses into the water phase. The spreading solution was intensively stirred before we sonicated the suspension for at least 10 minutes and finally stirred again right before spreading onto the interface.

2.4.2 Langmuir trough and magnetic setup. We used a custom-built Langmuir trough to compress the particle monolayer. The trough had an implemented glass slide in the base plate, combined with a light source below the glass and a custom-built microscope above to enable direct observation of the monolayer. The optical line was mounted on motorized micro translators for easy navigation and also featured a motorized zoom lens. Depending on the needs, an objective with different magnifications was mounted. A filter-paper Wilhelmy plate was used to measure the surface pressure continuously. A customized Delrin sample holder, produced by laser cutting, was placed into the trough containing three electromagnets with iron cores in a 90° configuration, as it can be seen in Fig. 2. On the fourth side, a conical opening allowed the microgels to flow toward the center of the electromagnets. At the bottom, a glass slide prevented drift of the monolayer coming from potential convection currents. The micro-rheological measurements were conducted according to a standard procedure.⁴⁹ The single coil (b in Fig. 2) was used to align the magnetic moment of the microdisk perpendicular to the other coils (a and c in Fig. 2), which were connected in series and used to generate the oscillating magnetic field to apply shear to the interface. The full details of the experimental setup can be found elsewhere;⁵⁰ for the purpose of these experiments, the characteristic response time of the magnets was below 1 ms, significantly smaller than the range of frequencies applied in our measurements (0.1–3 Hz).

Fig. 2 Left: Schematics of the custom Langmuir trough with an integrated optical microscope and a Wilhelmy plate. Right: Schematics of the custom sample holder with three electromagnets.

2.4.3 Monolayer preparation. The three coils were placed into the sample holder which was then put into the Langmuir trough. The trough was filled with doubly distilled-water until the water-interface was pinned at the top edge of the sample holder. Using a vacuum pump, we cleaned the interface and adjusted the water level to have a flat interface. The Wilhelmy plate was calibrated by knowing the surface tension of water to be 72.8 mN m⁻¹. Subsequently, the particle suspension was spread at the interface with a 100 μL Hamilton syringe. We formed drops at the syringe tip and by slowly touching the water surface the particles were spread at the interface. A waiting time of 10 seconds was allowed between the deposition of each drop to equilibrate the sample and avoid jamming at the entry of the sample holder. As soon as we reached a non-zero surface pressure by either adding more of the particle suspension or by compressing using the trough barrier, a magnetic micro disk was put on top of the loose monolayer in the center of the sample holder using a plastic pipette tip.

2.4.4 Interfacial micro rheology under compression. A LabView software was used to measure the rheological properties of the microgel monolayer. Sequences of at least 120 images were taken at a frame rate of at least 30 frames per second. The software automatically tracked the holes in the microdisk and a sinusoidal curve was fitted to the disk motion. The applied current, and therefore the applied magnetic field, were also recorded and a second sinusoidal curve was fitted to that data. The rheological properties of the monolayer were calculated from the stress and strain curves. Simultaneously, the image sequence was saved to extract qualitative information on the monolayer behavior under shear, such as slip at the disk edge. Starting from very low surface pressures we conducted frequency and strain sweeps. We increased the surface pressure stepwise by compressing the monolayer as we moved the trough barrier and measured the rheological properties at the different surface pressures, as described in the text.

3 Results and discussion

3.1 Two-dimensional phase diagrams: compression and deposition

In this work we chose to investigate the microstructure of monolayers of N-isopropylacrylamide (NiPAm)-co-methacrylic acid (MAA) microgels P(NiPAm-co-MAA) at water/n-hexane interfaces. These particles have been thoroughly investigated in previous works and we selected them in order to offer a simple benchmark model system, from which we can extract general conclusions on soft repulsive core–shell particles at interfaces. Direct visualization at the interface using cryo-electron microscopy has confirmed the core–shell nature of the particles. The microgels have a total (core + shell) diameter at the interface of 546 ± 50 nm and a core diameter of 355 ± 25 nm.³⁸ These dimensions do not depend on pH, despite the bulk pH-responsiveness of the particles. The surface activity of the co-polymers in the microgel is in fact a very weakly varying function of pH between 3 and 9, which is the experimentally relevant window. Conversely, the mechanical response of microgel monolayers upon compression varies at different values of pH within the same window, highlighting the complex interplay between the different particle properties.⁴³ To fix the experimental conditions, all the experiments reported in this paper were performed using microgel dispersions in Milli-Q water.

Here we present a new strategy to study the microstructure of the interface by means of synchronized and continuous compression/deposition of microgel monolayers in an oil–water Langmuir trough. The idea, schematically described in Fig. 3 and presented in more details in the Materials Section, revolves around the following protocol. After spreading a given amount of microgels at a water/n-hexane interface in a Langmuir trough, the barriers are moved to compress the interface. During the compression, a clean rectangular piece of silicon wafer is lifted through the interface and used as a support to deposit the interfacial microgel monolayer. The compression and deposition rates are synchronized so that the edges of the samples correspond to the maximum and minimum area of the trough, respectively. We have previously demonstrated that this strategy allows for faithful transfer of the arrangement of the microgels from the fluid interface onto a solid substrate.⁴⁷ Here, the particularity of the experiments lies in the fact that the silicon wafer (at an angle of approximately 30° with respect to the interface) crosses the interface while the latter is compressed. This implies that different positions on the substrate correspond to different values of the surface pressure and area per particle at which the particles are deposited. In particular, as the deposition proceeds, particles are deposited at increasing values of surface pressure Π and decreasing values of specific area A_p along the main axis of the sample. In this way, we can continuously and smoothly transfer the interface microstructure during a compression isotherm, and thus immobilize the two-dimensional phase diagram of the microgels onto a solid substrate that can be later investigated ex situ by atomic force microscopy (AFM).

Fig. 3 Schematics of the Langmuir trough setup for particle deposition. Monolayers of microgels adsorbed at the water/n-hexane interface are compressed by the barriers while the particles are continuously transferred onto a silicon substrate. As the compression proceeds, the particle area fraction of the deposited monolayer increases. Each position on the substrate corresponds therefore to different values of surface pressure and specific area of the particles at the interface. In this way, the whole 2D phase diagram of the microgels at the interface can be transferred onto a solid substrate for further analysis.

The results of these experiments are reported in Fig. 4. The figure shows compression isotherms of the microgels, obtained plotting the surface pressure Π, measured with a Wilhelmy plate during compression, versus the particle specific area A_p, locally measured by counting the number of particles per unit area in the AFM images. Each of the data points in the graph corresponds to a different position on the silicon wafer and the different colors refer to different initial amounts of microgels spread at the interface, and thus to different depositions on different substrates. The initial microgel amounts were varied by spreading different volumes of a particle suspension at a known 0.1% weight fraction. The isotherms were composed piece-wise since the dimensions of the trough did not allow the complete compression of the interface. The local microstructure of the monolayer for each particle concentration is obtained by analyzing AFM images systematically taken over the entire substrate every 0.5 mm, following the direction of increasing compression. It is worth noting here that the local measured values of A_p may differ from the estimated ones, based on the amount of microgels injected at the interface. This fact is shown in the inset to Fig. 4, which reports the surface pressure and the area per particle as a function of position on a silicon wafer. The differences may stem from uncertainties in the spreading solution's concentration and from partial loss of particles into the subphase during spreading. The latter is unavoidable in the presence of particle and spreading agent solubility in one of the two bulk phases, as opposed to the case of spreading insoluble monolayers, where all the material is confined at the interface. The filled red dots indicate the estimated area per particle, while the empty symbols show the measured values. Data points after 12 mm on the substrate suffer from edge effects coming from the substrate holder and are discarded from the analysis.

Fig. 4 Surface pressure versus area per particle compression isotherms for the microgels at the water/n-hexane interface. Each data point is obtained plotting Π as a function of the local measured A_p corresponding to different positions on the substrate. Different colors indicate different initial amounts of spread microgels at 0.1 wt%: black-30 μL, red-60 μL, green-95 μL, blue-100 μL, magenta-200 μL, cyan-350 μL and dark blue-950 μL. The arrows point to AFM images showing the microstructure of the transferred monolayers at different values of the surface pressure. The vertical dashed lines define the different regions in the phase diagram as described in the text. All images are 10 × 10 μm². Inset: Area per particle (red) and surface pressure (blue) extracted as a function of position on the silicon substrate. The empty red symbols indicate the measured A_p, while filled symbols represent the calculated A_p. The measured data points terminate before 20 mm and show large scattering at positions greater than 12 mm due to edge effects coming from the sample holder.

The isotherms identify several regimes previously discussed in the literature,^42,47 but here we report a direct insight into the monolayer microstructure and show interesting features of the transitions between the different regions. Representative AFM images of the monolayer in the various regimes are reported next to the isotherm. At low values of surface pressure and area per particle (Region I), the system is in a gas phase, where the particles are on average at distances larger than their diameter at the interface. As the system is compressed, these fluid-like regions start to coexist with clusters of particles in shell–shell contact, but the overall surface pressure remains very low (black data points). As soon as the area per particle corresponds to the size occupied by the microgels at the interface, then all the particles are in shell-to-shell contact and an hexagonal lattice of non-close-packed cores is formed. Experimental data concerning this region have been previously reported in ref. 47, and here we specifically focus on what happens at higher surface pressure. Upon further compression, in fact, the surface pressure rises steeply and the work done onto the system goes into compressing the particle coronas, resulting into a continuous change in the lattice constant of the 2D hexagonal packing (Region II). This region in the phase diagram exists only due to the presence of the soft repulsive shells around the particles; modification of the stiffness and thickness of the shells can allow the modulation of the extent of this region and of the steepness of the surface pressure increase.⁴² If the interface is compressed further, some of the shell–shell contacts start to fail and clusters of particles in core–core contacts start to appear. In this Region III, the surface pressure plateaus and the work done by compressing the interface goes into causing a phase transition between two solid hexagonal crystalline phases with two different lattice constants, corresponding to compressed shell–shell contacts and core–core contacts, respectively. Along the isotherm in Region III, the size of core–core clusters grows until all the monolayer is in the second phase. The close-packed monolayer can also be compressed over a small window of A_p values (Region IV), but very soon the monolayer fails and buckles (Region V). Again, engineering their size and elasticity will make it possible to have different windows of compression of the cores, which would asymptotically disappear for infinitely rigid cores, as in practice obtained by grafting a hydrogel onto solid cores, e.g. silica. We have also proven that the phase transitions between the different regions are reversible by performing continuous deposition during interface expansion (see ESI†). This is an important finding, highlighting once more conceptual differences with hard particles that often irreversibly aggregate upon contact at fluid interfaces.

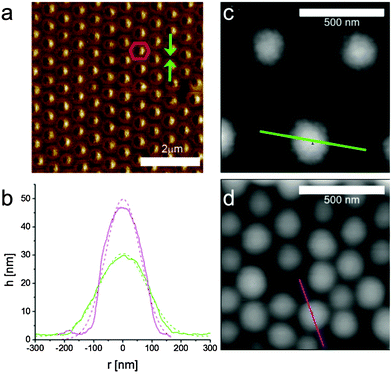
We can gain more insights on the nature of the phase transition by examining the AFM images in more detail. Fig. 5 shows the results of our quantitative image analysis on four representative images across the solid–solid phase transition. Starting at a surface pressure below the phase transition, Fig. 5a displays a rendered AFM image, binarized to identify and locate each particle through a simple Matlab particle-tracking algorithm (see the Methods section for details). After removing the particles close to the image's edges, the center-to-center distances d and angles between all nearest neighboring particles are measured. The probability distribution of d, fitted by a Gaussian, is plotted next to the image and shows one single peak at around 510 nm. In addition, we also overlay the image with a color-coded Voronoi tessellation, which highlights that the vast majority of the particles are in an hexagonal lattice, with few localized defects of particles with 5 and 7 neighbors. If we move to the data in Fig. 5b, which correspond to the beginning of the phase-transition region, we clearly see the appearance of clusters of particles in core–core contacts, which are marked in yellow. The particles within the clusters are also in an hexagonal arrangement and are defined as belonging to the second phase if the area of the triangles connecting the nearest neighbors is below a threshold value. From the image we also clearly see that the clusters of the second phase are disconnected and that their formation melts the lattice of the particles in shell–shell contacts. No preferred orientation of the clusters is found in relation to the compression direction or the orientation of the non-close-packed crystal. This confirms that the transition is triggered by localized failure of shell–shell contacts, i.e. depending on the local microstructure and the detailed particle properties, e.g. uniformity of cross-linking density, etc. At the clusters nucleate, a second peak appears in the distribution of nearest-neighbor distances at a distance corresponding to core–core contacts, while the position of the peak for shell–shell contacts shifts to smaller distances. As the phase transition proceeds further, at some point the clusters of core–core contacts form a percolating network, as shown in Fig. 5c. The peak distance corresponding to core–core contacts does not change, but the height of the peak grows at the expenses of the number of particles in shell–shell contacts. Finally, in Fig. 5d, the phase transition is complete and all the particles are in the second crystalline phase. As it can be evinced from the triangulation, this second phase also has an hexagonal symmetry with local defects.

Fig. 5 Rendered AFM images and corresponding probability distributions of nearest-neighbor distances P(d) for four different points of increasing surface pressure along the compression isotherm. (a) Π = 4.8 mN m⁻¹; (b) Π = 29.3 mN m⁻¹; (c) Π = 30.9 mN m⁻¹; (d) Π = 31.8 mN m⁻¹. The top left (a) and bottom right data (d) correspond to monolayers in the non-close-packed hexagonal and in the close-packed hexagonal phases, respectively. The other two sets (b and c) correspond to two points in the solid–solid phase transition region. We note that the P(d) distributions have a single peak for the single-phase data, while two peaks are present in the phase-coexistence region, characteristic of the lattice spacings in the two phases. The black lines are the data extracted from the corresponding images and the colored lines are Gaussian fits used to extract the data in Fig. 6a. Green: non-close-packed crystal peak; blue: close-packed crystal peak; red: total. The black dots represent the microgel centers found by the image analysis algorithm. The Voronoi polygons are shown for the single-phase images, where green tiles represent particles with 6 neighbors, blue tiles particles with 5 neighbors and red tiles particles with 7 neighbors, respectively. In (a) and (d) the monolayer is in a hexagonal phase with some localized defects. The yellow triangles in the phase-transition images (b and c) highlight neighboring particles that are in the core–core close-packed phase. We see that the cluster size of particles in the close-packed phase grows with increasing surface pressure and that a percolating network of particles in the second phase develops (d). All images are 10 × 10 μm².

The same kind of analysis can be performed on all images that compose the isotherms in Fig. 4 and the data are summarized in Fig. 6. Fig. 6a reports the nearest-neighbor distance as a function of the area per particle in all the regions in the phase diagram. In Regions I and II there is only one preferential value of d, which decreases upon compression. In particular, in Region II, this corresponds to the continuous compression of the shell–shell hexagonal crystal. As soon as the system enters the phase-transition region, we observe the splitting of d into two peaks corresponding to the co-existence of the two phases. The position of the peak of the first phase decreases significantly as the phase transition proceeds, while the position of the second one is weakly dependent on A_p. Interestingly, the error bars, which mark the standard deviation of the Gaussian fits for P(d) are much larger in Region III, indicating that the first lattice is disturbed and that many particles sit at the interface between the two phases. Upon completion of the phase transition, only one peak in P(d) is obtained and in Region IV no appreciable compression takes place before the interface buckles and crosses over to Region 5. Fig. 6b, shows indeed that the percentage of particles in core–core contacts grows smoothly across the phase-transition region. The fact that both solid phases have an hexagonal symmetry is quantitatively confirmed by looking at the hexagonal order parameter ψ₆ as a function of the area per particle. In Fig. 6c, we see that in Region I the average hexagonal order parameter calculated over all the particles in a single AFM image grows until a fully hexagonal phase (ψ₆ close to 1) is formed in Region II. During compression of the first phase, the system stays hexagonal, but the overall hexagonal symmetry of the monolayer is lost upon starting the phase transition, as indicated by a drop of ψ₆ in Region III. A closer look at the distribution of angles between nearest neighbors in Fig. 6d, shows that during the phase transition the distributions broaden but stay peaked at 60°, indicating that the first phase melts, but that the clusters of particles in the second phase still belong to an hexagonal lattice, albeit with a different lattice constant. The broadening of the distribution is directly connected to the emergence of interfaces between the two phases, where particles at the boundary can have a large range of nearest-neighbor angles. As the phase transition completes, the hexagonal order parameter goes back to large values close to unity and the angle distributions return sharply peaked at 60°. Similar findings are also reported when examining the microstructure of the different phases deposited during expansion (see ESI†).

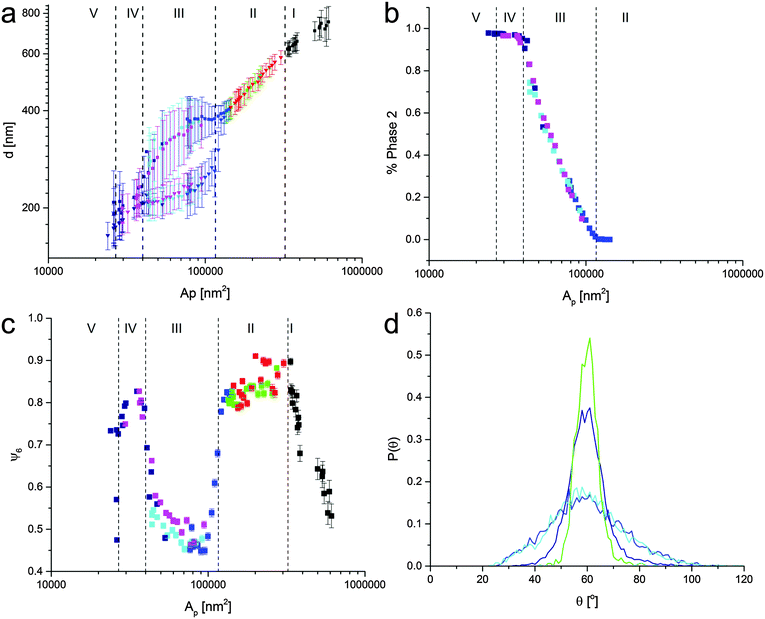Fig. 6 (a) Nearest neighbor inter-particle distance d versus A_p. We notice a split in the values of d in the phase-coexistence region, while a single value is found in Region II and IV. The values are extracted from the data as shown in Fig. 5. (b) Percentage of the second, close-packed hexagonal phase versus A_p, showing the growth of the second phase across the phase transition. (c) Hexagonal order parameter ψ₆ as a function of A_p. High ψ₆ values are visible in the hexagonal-phase regions II and IV, while crystalline order drops in the phase-coexistence region due to melting of the non-close-packed phase by the clusters of the close-packed phase. (d) P(θ) corresponding to the 4 data sets of Fig. 5. The green and dark blue curves correspond the non-close-packed and close-packed hexagonal phases, respectively, and both show a strong peak at 60° while the cyan and blue curves are taken in the phase-coexistence region. Upon entering the phase transition, the distributions become broader but stay peaked at 60°, implying local melting but an overall hexagonal order of the monolayer. The colors of the data correspond to the data sets shown in Fig. 4.

The existence of shell–shell contacts and the structure of the microgels after deposition from the two phases can be examined in detail from the AFM images. Fig. 7a shows an AFM phase image of a microgel monolayer in Region II. Phase imaging is particularly suited to highlight differences in the mechanical properties of different scanned regions and it clearly shows a contrast between the particles, including their shells, and the silicon substrate. The image emphasizes the presence of particle contacts through the soft shells, which are compressed into hexagonal coronas for particles in the crystalline lattice. In the presence of defects, e.g. on the right side of the image, one can clearly see where the shell ends. Fig. 7b shows the particle height profiles extracted from microgels deposited in the first and the second phase, respectively, using the two high-resolution AFM images of Fig. 7c and d. The shape of the deposited and dried particles is approximately Gaussian, the particles are compressed and their height increases in going from the first to the second phase. Similar shapes and height profiles have also been previously reported for dry particles and in liquid.^9,19,54

Fig. 7 (a) AFM phase image of particles in Region II. The presence of compressed, flattened shell–shell contacts (green arrows) as well as shell compression into hexagonal coronas (red hexagon) is visible. (b) Microgel height profiles from high-resolution AFM images in the two different phases. The solid lines are the AFM data and the dashed lines are Gaussian fits. The data correspond to the scan lines on the images (c) and (d) on the right. We observe that the particles are compressed and their height increases in the second phase.

3.2 Monolayer mechanics: interfacial microdisk rheology

After characterizing the structure of the monolayer in the various regions of the 2D phase diagram, we link the microstructure to its shear visco-elastic properties. The measurements were carried out at an air–water interface, rather than at an oil–water interface, due to the construction of our experimental setup; analogous conclusions can nonetheless be drawn, as discussed later.§ The rheology experiments were performed in a custom-made Langmuir trough with a single movable barrier that allowed for simultaneous visualization of the interface (see Fig. 2). In correspondence with the observation window, the interface was funneled into a mm-sized circular well surrounded by three electromagnets. After spreading the microgels at the interface, a 100 μm diameter amphiphilic magnetic disk was inserted at the interface inside the circular aperture and was externally manipulated by means of the electromagnets. The disk could be rotated at the interface in an oscillatory fashion by applying oscillatory fields of known frequency and amplitude, creating a 2D miniaturized version of a 2D large-gap Couette rheometer.⁵⁰ Similar active micro-rheology instruments have been successfully used to measure the interfacial rheology of colloidal and lipid monolayers at fluid interfaces^48,49,56 and here we applied the technique to our microgel-laden fluid interfaces. The rheological response of the interface was measured by tracking the rotation of the microdisk upon the application of a known torque and the strain field of the monolayer could be visualized by adding a small number of tracer particles to the interface (see the Methods section for more details). In particular, we measured frequency and amplitude sweeps as a function of the surface pressure at the interface.

Before performing the rheology experiments, we checked that the compression isotherms at the air–water (a/w) interfaces were analogous to the ones at the water/n-hexane interface and that the same regions were observed. The a/w compression isotherm for the microgels is reported in Fig. 8a. In this case, the area of the trough was large enough to cover the whole isotherm in a single experiment and the data are reported here as a function of the trough area and not of the area per particle. This choice was made in order to avoid the uncertainties and errors associated with the spreading of soluble particles, as previously discussed and as given by the fact that the microstructure of the monolayer could not be deposited from an a/w interface while performing the rheology. Apart from the differences in the values of the surface pressures between a/w and o/w interfaces, the two compression isotherms are indeed analogous, showing the presence of a solid-fluid plateau at low surface pressures, followed by a steep rise corresponding to the compression of the shell–shell crystal and by a pseudo-plateau in the solid–solid phase transition region. After that, another sharp rise in surface pressure was observed before monolayer collapse, corresponding to Regions IV and V in Fig. 4.

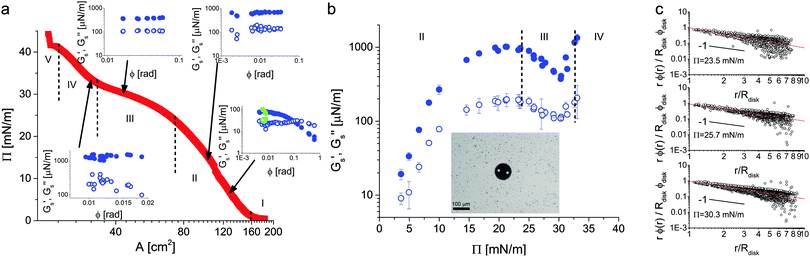Fig. 8 (a) Microgel compression isotherm at the water–air interface showing surface pressure versus trough area. The vertical dashed lines mark the transition between the different regimes identified in Fig. 4. The insets show amplitude sweeps from the microdisk rheometer taken at values of the surface pressure of 6.6, 14.6, 30.1 and 33.1 mN m⁻¹ and a frequency of 0.5 Hz, respectively. The filled symbols correspond to the surface storage modulus, the empty symbols to the surface loss modulus. Green data points show monolayer recovery 2 minutes after yielding. (b) Surface storage and loss moduli as a function of surface pressure measured in the linear regime at a frequency of 0.5 Hz. The larger values of G_s′ over the whole compression isotherm indicate that the material responds elastically to shear deformations. The inset shows the microdisk at the interface in the presence of the tracer particles. (c) Strain profiles as a function of distance from the disk normalized by the strain at the disk edge for three values of the surface pressure and measured from tracer displacements over two consecutive frames. The solid lines are 1/r fits, emphasizing that the rheological response is interface-dominated.

The rheology experiments were then performed as a function of surface pressure and the insets to Fig. 8a report amplitude sweeps taken at 0.5 Hz for some representative values of Π. Starting with the lowest value of 6.6 mN m⁻¹ in the shell–shell hexagonal crystal, we observed that the monolayer was rather weak and presented only a limited linear regime. In any case, the monolayer responded elastically at low strains, measured here from the angular rotation of the disk, and the surface storage modulus G_s′ was larger than the surface loss modulus G_s′′. When leaving the linear regime, as expected, G_s′ decreased until a cross-over was observed at the yield strain, after which the monolayer exhibited shear thinning. Interestingly, the monolayer recovered rather rapidly, as witnessed by a full recovery of the visco-elastic moduli only a couple of minutes after yielding (green symbols).

Upon increasing the surface pressure to 14.6 mN m⁻¹, still within the first crystalline phase, we observed a significant stiffening of the monolayer; both G_s′ and G_s′′ have increased by approximately one order of magnitude. The presence of a linear regime at small strains was confirmed but we could no longer access large strains. The amplitude sweep was in fact limited on the lower end by the accuracy of the setup and at the higher end by the stiffness of the monolayer, which did not allow higher amplitudes with the available range of applicable torques in the setup. We kept compressing and measured the interface visco-elasticity at 30.1 mN m⁻¹ inside the pseudo-plateau corresponding to the phase transition. There we noted that the elastic modulus of the interface had dropped significantly, in spite of the interface maintaining an overall elastic response. Further compression to 33.1 mN m⁻¹, when the phase transition had completed, led to a new increase in the visco-elasticity. The monolayer was actually too stiff for the setup to reach torques corresponding to disk's angular displacements larger than 0.02 radians. In addition to the amplitude sweeps, we also performed frequency sweeps at all the reported surface pressures (see ESI†). In all cases, at the frequency of 0.5 Hz used for the amplitude sweeps, the reported moduli were taken in the small-amplitude, linear elastic region.

The trends exemplified by these measurements can be rationalized by looking at the overall behavior of the surface storage and loss moduli plotted versus Π. The data in Fig. 8b show in fact an initial increase of the visco-elasticity corresponding to a compression of the shell–shell hexagonal lattice; higher compression of the lattice makes it possible to bear greater shear forces. When the system enters the phase coexistence region (between approximately 25 and 31 mN m⁻¹), then the elasticity of the interface starts to saturate. As demonstrated by the AFM images in Fig. 4 and 5, in this region of the phase diagram the nucleation of clusters of particles in core–core contacts partially melts the stress-bearing network of particles in shell–shell contacts. As a consequence of this, the monolayer weakens and its elastic modulus decreases accordingly. This trend continues until the second phase forms a percolating network of particle clusters in core–core contacts, which becomes the stress-bearing entity within the monolayer. At this point the monolayer elasticity increases rapidly due to the higher stiffness of core–core contacts. It is worth emphasizing again that the elastic moduli in the linear regime are always approximately one order of magnitude higher than the viscous moduli, confirming the picture that microgel-laden interfaces exhibit significant interfacial elasticity.

Finally, the fact that our rheological measurements are probing only the interface properties can be confirmed by visualizing the strain profiles of the monolayer by optical tracking of micron-sized polystyrene tracers spread at low area fraction. The data in Fig. 8c show a 1/r decay of the strain field (local azimuthal displacement normalized by the disk azimuthal displacement) as a function of distance from the disk edge, as expected from an elastic response entirely stemming from the interface. Different slopes would indicate partial contributions from the subphase,⁴⁹ which can be excluded in this case. Moreover, the azimuthal monolayer and disk displacements coincide at the disk edge, indicating the absence of slip at the probe boundary.

3.3 Discussion

Our experiments identify two interesting features: the existence of an isostructural solid–solid phase transition in the microgel monolayers and its coupling to the rheological properties of the interface. Solid–solid phase transitions are extremely common in atomic or molecular crystalline materials that exhibit polymorphism under different temperature and pressure conditions. Experimentally identifying and studying the counterpart in colloidal systems has proven a much more difficult and elusive task. Aside from the rich phase behavior seen in two and three dimensions when tuning composition or confinement,^57–61 the most notable examples concern the study of martensitic transitions of colloidal packings under the influence of external fields. In particular, martensitic transitions in charged colloids have been studied under the influence of shear⁶² or electric fields,⁶³ but their investigation in relation to classic thermodynamic transformations remained for many years unexplored. Only very recently Peng et al. managed to use thermo-responsive microgels confined between two flat surfaces to study the kinetics of a martensitic transition triggered by fine tuning of the volume fraction.¹⁴ Remarkably, they found that a two-step nucleation route was followed and that local melting of the crystal and creation of a liquid phase was necessary to enable the transition. Their system was nonetheless quasi-2D and no mechanical properties were measured together with the structural and kinetic characterization. On the other hand, solid–solid phase transitions for colloidal systems have been extensively studied theoretically and by means of numerical simulations. Two models have been mostly investigated using either square-well^64–66 or square-shoulder potentials.^51,52 In both cases, for monodisperse spheres an isostructural phase transition was predicted between two hexagonal lattices with different lattice constants; in particular, the two lattices correspond to an expanded and a collapsed crystal, respectively, where in the latter the particles are in close contact. So far, an experimental observation of such phenomenon was still lacking; in square-well potentials, often gelation prevents accessing the phase transition,⁶⁷ while the observations for repulsive systems have been largely limited to charge-stabilized colloids, i.e. soft repulsive systems with only one length scale in the interaction potential and that irreversibly aggregate if the repulsive barrier is overcome. The use of microgels and of fluid interfaces makes it possible to circumvent these obstacles and to investigate truly two-dimensional models systems interacting only at contact via steric repulsions with two length scales, stemming from the cross-linking density profiles of the particles and their morphology at the interface. The careful choice of the experimental system and the benefits of our continuous monolayer transfer technique finally enabled us to visualize the isostructural solid–solid transition.

The presence of a fluid interface on which the 2D particle system is suspended also enables the study of its mechanical properties without interactions with solid substrates. Previous work on the dilatational rheology of microgel-laden interfaces⁴² also showed that the visco-elastic dilatational moduli are not a monotonically growing function of the surface pressure, but that a maximum is reached at the beginning of the pseudo-plateau, which at the time was hypothesized to correspond to a phase-coexistence region and which we now know corresponds to the onset of the solid–solid phase transition. Dilatational rheology experiments were performed on Gibbs monolayers of spontaneously adsorbed particles and therefore the maximum reachable surface pressures saturated before the dilatational visco-elastic moduli could rise again due to the formation of a percolating network of particles in the second phase. Our experiments demonstrate that similar findings are obtained for the shear rheology and unambiguously link the structure and the mechanics of the interface.

4 Conclusions

Our results show that microgel particles are remarkable model systems, not just to study fundamental physical phenomena in bulk, but also at fluid interfaces, where confinement in 2D makes it possible to access their structural and mechanical properties with unprecedented detail. We studied compression isotherms and demonstrated that the core–shell nature of the particles at the interface enables the presence of transitions between crystalline phases, namely an isostructural solid–solid phase transition between hexagonal lattices. The findings open up a new avenue to study 2D systems where the shape of the potential can be engineered by tuning the architecture of the microgels and their mechanical properties. An even broader parameter space opens if different types of particles are mixed at the interface to combine composition and relative range and stiffness of the interactions. This fact may stimulate the interest of the numerical simulations community to explore such parameter space and direct the design of new particles and interfaces to target specific structures.

The fact that the structure and the rheology of the interface has a non-trivial dependence on compression has also important practical implications in the preparation of microgel-stabilized emulsions. Given mechanical properties of the individual droplets could be thus tuned by controlling the compression state of the interface according to precise emulsification protocols. The possibility to deposit microgel monolayers with fine structural tuning will also have an impact in the applications described in the introduction, namely in the fabrication of substrates with use in optics, sensing, patterning and cell culture.

To conclude, our work has demonstrated a new dimension of the use of microgels as models systems with an eye toward applied implications, which will hopefully foster additional activities in this direction.

Acknowledgements

LI would like to thank David Nelson, Chantal Valeriani, Veronique Trappe and Emanuela Zaccarelli for fruitful discussions. LI acknowledges financial support from the Swiss National Science Foundation grant PP00P2_144646/1. MAFR acknowledges financial support from the COST action: Smart and Green Interfaces (STSM MP1106-14761) and would like to thank Prof. R. Hidalgo-Alvarez, Prof. M. A. Rodriguez-Valverde and Prof. M. A. Cabrerizo-Vilchez for supporting his COST fellowship. KG and WR acknowledge financial support from the German Research Foundation within the Collaborative Research Center SFB985 “Functional Microgels and Microgel Systems”. TMS acknowledges financial support from the U.S. National Science Foundation under grant CBET-1512833. The content of the information does not necessarily reflect the position or the policy of the U.S. Government, and no official endorsement. A portion of this work was performed in the UCSB Nanofabrication Facility, part of the NSF-funded NNIN network, and in the Materials Research Laboratory Central Facilities, which are supported by the NSF Materials Research Science and Engineering Centers Program under Grant DMR 1121053, a member of the NSF-funded Materials Research Facilities Network.

References

1. L. A. Lyon and A. Fernandez-Nieves, Annu. Rev. Phys. Chem., 2012, 63, 25–43.
2. J. A. Bonham, M. A. Faers and J. S. van Duijneveldt, Soft Matter, 2014, 10, 9384–9398.
3. R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33.
4. A. Pich and W. Richtering, Chemical Design of Responsive Microgels, Springer, Berlin Heidelberg, 2011, vol. 234, pp. 1–37.
5. S. Meyer and W. Richtering, Macromolecules, 2005, 38, 1517–1519.
6. X. Wu, R. Pelton, A. Hamielec, D. Woods and W. McPhee, Colloid Polym. Sci., 1994, 272, 467–477.
7. R. Acciaro, T. Gilànyi and I. Varga, Langmuir, 2011, 27, 7917–7925.
8. M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206.
9. S. Höfl, L. Zitzler, T. Hellweg, S. Herminghaus and F. Mugele, Polymer, 2007, 48, 245–254.
10. H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711.
11. P. J. Yunker, K. Chen, M. D. Gratale, M. A. Lohr, T. Still and A. G. Yodh, Rep. Prog. Phys., 2014, 77, 056601.
12. J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83–86.
13. Y. Han, N. Y. Ha, A. M. Alsayed and A. G. Yodh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041406.
14. Y. Peng, F. Wang, Z. Wang, A. M. Alsayed, Z. Zhang, A. G. Yodh and Y. Han, Nat. Mater., 2015, 14, 101–108.
15. G. R. Hendrickson, M. H. Smith, A. B. South and L. A. Lyon, Adv. Funct. Mater., 2010, 20, 1697–1712.
16. M. H. Smith and L. A. Lyon, Acc. Chem. Res., 2012, 45, 985–993.
17. N. M. B. Smeets and T. Hoare, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 3027–3043.
18. M. Karg and T. Hellweg, Curr. Opin. Colloid Interface Sci., 2009, 14, 438–450.
19. S. Schmidt, M. Zeiser, T. Hellweg, C. Duschl, A. Fery and H. Möhwald, Adv. Funct. Mater., 2010, 20, 3235–3243.
20. Y. Xia, X. He, M. Cao, C. Chen, H. Xu, F. Pan and J. R. Lu, Biomacromolecules, 2013, 14, 3615–3625.
21. K. Jongseong, S. Michael J. and L. L. Andrew, J. Am. Chem. Soc., 2004, 126, 9512–9513.
22. K. Jongseong, N. Satish and L. L. Andrew, J. Am. Chem. Soc., 2005, 127, 9588–9592.
23. L. Hu and M. J. Serpe, ACS Appl. Mater. Interfaces, 2013, 5, 11977–11983.
24. A. Burmistrova and R. von Klitzing, J. Mater. Chem., 2010, 20, 3502–3507.
25. S. Tsuji and H. Kawaguchi, Langmuir, 2005, 21, 8439–8442.
26. K. Horigome and D. Suzuki, Langmuir, 2012, 28, 12962–12970.
27. S. Schmidt, T. Hellweg and R. von Klitzing, Langmuir, 2008, 24, 12595–12602.
28. J. Peng, D. Zhao, X. Tang, F. Tong, L. Guan, Y. Wang, M. Zhang and T. Cao, Langmuir, 2013, 29, 11809–11814.
29. M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M. Fernandez-Rodriguez, V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. Voelcker and L. Isa, Nano Lett., 2016, 1, 157–163.
30. T. Still, P. J. Yunker, K. Hanson, Z. S. Davidson, M. A. Lohr, K. B. Aptowicz and A. G. Yodh, Adv. Mater. Interfaces, 2015, 2, 1500371.
31. V. Schmitt and V. Ravaine, Curr. Opin. Colloid Interface Sci., 2013, 18, 532–541.
32. T. Liu, S. Seiffert, J. Thiele, A. R. Abate, D. A. Weitz and W. Richtering, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 384–389.
33. B. Brugger and W. Richtering, Adv. Mater., 2007, 19, 2973–2978.
34. W. Richtering, Langmuir, 2012, 28, 17218–17229.
35. F. Bresme and M. Oettel, J. Phys.: Condens. Matter, 2007, 17, 413101.
36. O. S. Deshmukh, D. van den Ende, M. C. Stuart, F. Mugele and M. H. Duits, Adv. Colloid Interface Sci., 2015, 222, 215–227.
37. M. Destribats, V. Lapeyre, M. Wolfs, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Soft Matter, 2011, 7, 7689–7698.
38. K. Geisel, L. Isa and W. Richtering, Langmuir, 2012, 28, 15770–15776.
39. M. Destribats, V. Lapeyre, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Langmuir, 2012, 28, 3744–3755.
40. B. Brugger, S. Rütten, K.-H. Phan, M. Möller and W. Richtering, Angew. Chem., Int. Ed., 2009, 48, 3978–3981.
41. R. W. Style, L. Isa and E. R. Dufresne, Soft Matter, 2015, 11, 7412–7419.
42. F. Pinaud, K. Geisel, P. Masse, B. Catargi, L. Isa, W. Richtering, V. Ravaine and V. Schmitt, Soft Matter, 2014, 10, 6963–6974.
43. K. Geisel, L. Isa and W. Richtering, Angew. Chem., 2014, 126, 5005–5009.
44. B. Brugger, J. Vermant and W. Richtering, Phys. Chem. Chem. Phys., 2010, 12, 14573–14578.
45. B. Brugger, B. A. Rosen and W. Richtering, Langmuir, 2008, 24, 12202–12208.
46. L. Isa, F. Lucas, R. Wepf and E. Reimhult, Nat. Commun., 2011, 2, 438.
47. K. Geisel, W. Richtering and L. Isa, Soft Matter, 2014, 10, 7968–7976.
48. S. Choi, S. Steltenkamp, J. Zasadzinski and T. Squires, Nat. Commun., 2011, 2, 312.
49. Z. A. Zell, A. Nowbahar, V. Mansard, L. G. Leal, S. S. Deshmukh, J. M. Mecca, C. J. Tucker and T. M. Squires, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3677–3682.
50. Z. A. Zell, V. Mansard, J. Wright, K. Kim, S. Q. Choi and T. M. Squires, J. Rheol., 2016, 141–159.
51. J. M. Kincaid, G. Stell and E. Goldmark, J. Chem. Phys., 1976, 65, 2172–2179.
52. P. Bolhuis and D. Frenkel, J. Phys.: Condens. Matter, 1997, 9, 381.
53. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
54. A. Burmistrova and R. von Klitzing, J. Mater. Chem., 2010, 20, 3502–3507.
55. L. Isa, K. Kumar, M. Müller, J. Grolig, M. Textor and E. Reimhult, ACS Nano, 2010, 4, 5665–5670.
56. I. Buttinoni, Z. A. Zell, T. M. Squires and L. Isa, Soft Matter, 2015, 8313–8321.
57. A. D. Law, D. M. A. Buzza and T. S. Horozov, Phys. Rev. Lett., 2011, 106, 128302.
58. A.-P. Hynninen, J. H. J. Thijssen, E. C. M. Vermolen, M. Dijkstra and A. van Blaaderen, Nat. Mater., 2007, 6, 202–205.
59. M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Nature, 2005, 437, 235–240.
60. D. Ershov, J. Sprakel, J. Appel, M. A. Cohen Stuart and J. van der Gucht, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9220–9224.
61. A. Fortini and M. Dijkstra, J. Phys.: Condens. Matter, 2006, 18, L371.
62. J. A. Weiss, D. W. Oxtoby, D. G. Grier and C. A. Murray, J. Chem. Phys., 1995, 103, 1180–1190.
63. A. Yethiraj, A. Wouterse, B. Groh and A. van Blaaderen, Phys. Rev. Lett., 2004, 92, 058301.
64. P. Bolhuis, M. Hagen and D. Frenkel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 4880–4890.
65. P. Bolhuis and D. Frenkel, Phys. Rev. Lett., 1994, 72, 2211–2214.
66. C. F. Tejero, A. Daanoun, H. N. W. Lekkerkerker and M. Baus, Phys. Rev. Lett., 1994, 73, 752–755.
67. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm03062e

‡ These authors contributed equally to this work.

§ As a side note, depositions are more effectively carried out from water/n-hexane interfaces to minimize the effects of capillary forces during drying.⁵⁵

---