Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The pH-responsive behaviour of poly(acrylic acid) in aqueous solution is dependent on molar mass†
Thomas
Swift
 ab,
Linda
Swanson
a,
Mark
Geoghegan
ab,
Linda
Swanson
a,
Mark
Geoghegan
 *c and
Stephen
Rimmer
*ab
*c and
Stephen
Rimmer
*ab
aDepartment of Chemistry, Brook Hill, University of Sheffield, Sheffield S3 7HF, UK
bSchool of Chemistry and Forensic Sciences, University of Bradford, Richmond Building, Bradford BD7 1DP, UK. E-mail: s.rimmer@bradford.ac.uk
cDepartment of Physics and Astronomy, University of Sheffield, Hounsfield Road, Sheffield S3 7RH, UK. E-mail: mark.geoghegan@sheffield.ac.uk
First published on 29th January 2016
Abstract
Fluorescence spectroscopy on a series of aqueous solutions of poly(acrylic acid) containing a luminescent label showed that polymers with molar mass, Mn < 16.5 kDa did not exhibit a pH responsive conformational change, which is typical of higher molar mass poly(acrylic acid). Below this molar mass, polymers remained in an extended conformation, regardless of pH. Above this molar mass, a pH-dependent conformational change was observed. Diffusion-ordered nuclear magnetic resonance spectroscopy confirmed that low molar mass polymers did not undergo a conformational transition, although large molar mass polymers did exhibit pH-dependent diffusion.
Introduction
The properties of stimulus responsive materials change in response to perturbations in their environment.1,2 A class of stimulus responsive materials which has been extensively studied is that of polyelectrolytes in aqueous media. These generally undergo step changes in chain conformation, passing from open, fully solvated, coils to desolvated globular conformations over a small range of pH. This environmentally stimulated conformational change has given rise to the term “smart” materials. At low molar mass, the chain is expected to form an extended rod-like structure when the polymer is charged, which changes to an open coil conformation for chains longer than the persistence length.3 The uncharged polymer is expected to form a more globular structure for all chain sizes. Here this concept is tested for a model weak polyelectrolyte, poly(acrylic acid) (PAA),4 which is shown not to undergo this rod-to-coil transition with increasing molar mass but rather displays a transition from a relatively pH-independent conformation over typical ranges of pH at low molar mass to a polymer that exhibits a coil-to-globule transition for greater masses.PAA is an important industrial polymer, with a particularly important role in dispersants, where smaller molar mass polymers are regularly used, but larger molecules are less effective.5,6 PAA undergoes a reversible conformational transition (coil-to-globule transition) around pH 5 that is driven by the state of ionization of the carboxylic group,
| RCOOH ⇌ H+ + RCOO−. | (1) |
There are numerous theories considering the size of polyelectrolyte chains1 but the model used the most is the Flory model, which shows that, in the simplest calculation, polyelectrolytes in their most charged state are expected to form rods. This is obtained by minimization of the Helmholtz free energy for partially charged chains,
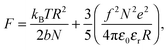 | (2) |
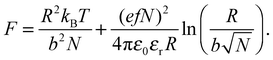 | (3) |
Experimental
A series of poly(acrylic acid) (PAA) samples was synthesized with a range of molar masses using controlled reversible addition-fragmentation chain transfer (RAFT) chemistry, using three separate chain transfer agents. These polymers were dissolved in water at a concentration dependent upon the technique being used to interrogate the samples, and acid or base added to change the pH. Buffer was not used in these experiments in order to avoid charges being shielded.Benzyl-1H-pyrrole-1-carbodithioate (RAFT agent 1) synthesis
Pyrrole (5.00 g, 74.5 mmol) was added dropwise to a rapidly stirring suspension of sodium hydride (1.79 g, 74.5 mmol) in DMSO (80 ml) over 20 min. The solution was then stirred at room temperature for 30 min. The solution was cooled to 5 °C using an ice-water bath before carbon disulfide (5.67 g, 74.5 mmol) was added dropwise. The resultant orange brown solution was stirred at room temperature for 30 min, and then benzyl bromide (12.69 g, 74.5 mmol) was added dropwise. The solution was stirred overnight at room temperature. The mixture was extracted using water (80 ml) and diethyl ether (80 ml), and then the aqueous layer was washed with ether (160 ml) until the entire organic product was extracted. The organic layer was dried over MgSO4 and filtered. The solvent was removed from the mixture by rotary evaporation. The product was purified by flash column chromatography on silica using hexane as the solvent. The RAFT chain transfer agent (CTA) fraction was collected and the solvent removed by rotary evaporation to give 2.4 g (35.1%) of a yellow oil. 1H NMR characterization showed the product to contain the following protons: δ = 4.65 (s, CH2), 6.38 (m, H), 7.40 (m, aromatic H), and 7.75 (m, aromatic H).2-Cyano-2-propyl benzodithioate (RAFT agent 2)
2-Cyano-2-propyl-benzodithioate was purchased from Sigma Aldrich (>97% HPLC) and used with no additional purification.2-{[(Butylsulfanyl)carbonothioyl]sulfanyl}propanoic acid (RAFT agent 3) synthesis
Butanethiol (43.00 g, 0.47 mol) and 20 ml acetone was added dropwise to a 90 ml sodium hydroxide solution (16.0 g, 0.40 mol) at 15 °C. The solution was stirred for 30 min, then cooled to 5 °C, at which temperature 30 ml carbon disulfide was added before being left for a further 30 min. 2-Bromopropionic acid (66.0 g, 0.43 mol) was added, followed by another 30 ml NaOH solution and 25 ml deionized water. This was left to stir for 24 h at room temperature before the orange mixture was extracted using 50 ml concentrated HCl and filtered to extract yellow solid. This was repeatedly washed with cold water, resuspended in a stirring solution, and finally recrystallized in hexane to yield 107.3 g (0.45 mol) of product (a 95% yield). Electrospray ionization time-of-flight mass spectroscopy showed a MH+ peak at 239 Da. 1H Nuclear magnetic resonance (NMR) characterization showed the product to contain the following protons: δ = 3.45 (t, SCH2C), 1.65 (m, CCH2C), 1.45 (m, CCH2C), and 0.90 (t, CH3C). 13C NMR also showed the presence of the following carbon atoms: δ = 205.61 (s, SCSS), 36.23 (s, SCH2C), 30.18 (m, CCH2C), 29.84 (m, CCH2C), 21.97 (s, CCH2C), and 13.22 (s, CH3C).PAA synthesis
RAFT polymerization11–14 was used to synthesize a series of poly(acrylic acid) samples with a range in (number average) molar mass from 6.6 to 63.2 kDa. Most of the samples were copolymerized so that approximately 1% of the monomers contained an acenaphthylene (ACE) unit. Monomers were purified by distillation under reduced pressure. Acrylic acid (5 g), 4,4′-azobis(4-cyanovaleric acid) and ACE were dissolved in 1,4-dioxane and placed in 50 ml ampoules with a quantity of chain transfer agent (1, 2, or 3), as necessary. The polymerization mixtures were degassed via repeated freeze–pump–thawing and heated at 60 °C for 24 h. The polymer was precipitated from dioxane into diethyl ether three times before being freeze-dried from water to leave a white solid. 1H NMR characterization was carried out in D2O (1H: 2.35 (m, CH) and 1.75 (m, CH2); 13C: 41 (CH) and 26 (CH2)) using a Bruker AMX-2 400 spectrometer operating at 400 MHz (1H) or 100 MHz (13C). ACE and one of the three RAFT CTAs were added prior to polymerization depending on requirements. The presence or absence of ACE was confirmed by UV/Vis analysis using a Specord S-600 spectrophotometer (see ESI†), and potentiometric titration was used to show that the presence of ACE had no discernible effect on the ionization of the polymer. Furthermore, the use of three distinct RAFT agents allows us to dismiss any possibility that the polymer end group might affect the results presented in this work.Molar mass determination
Gel permeation chromatography (GPC) was carried out on a tetrahydrofuran-based system. Samples were prepared via a methylation reaction with trimethylsilyldiazomethane then dissolved in tetrahydrofuran (solvent filtered by a 0.45 μm pore). The eluent was passed through 3 × PLgel 10 μm mixed-B LS columns at 1.00 ml min−1 using a Kinesis 307 Gilson Pump. Samples were added via an Anachem 234 auto injector and the refractive index (RI) signal was recorded using an Erma Inc. ERC-7512 RI detector. The system was calibrated using poly(methyl methacrylate) standards.Fluorescence measurements
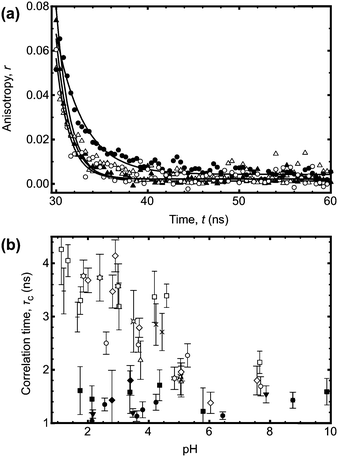
Conformational changes in polymers can be observed using luminescent labelling techniques, by attaching an aromatic label and observing the lifetime and anisotropic response of the excited state.4,13 Excited state lifetime and time resolved anisotropy measurements (TRAMS) were recorded using an Edinburgh Instruments 199 fluorescence spectrometer at λex = 295 nm and λem = 350 nm on dilute solutions of PAA, dissolved in ultrapure water at 1 mg ml−1. The aromatic label (ACE) can be covalently bound to the PAA backbone, giving a direct measure of the polymer segmental motion. Excited state lifetime measurements are calculated assuming that the fluorescent label, or probe, is dispersed in a homogeneous environment, so that the decay of the excited state accurately reflects the sensitivity of the species to the solvent and the conformation of the polymer. Assuming this to be the case, the fluorescence intensity, I(t), can be modelled by a dual exponential decay with time constants τ1 and τ2,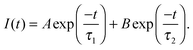 | (4) |
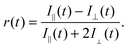 | (5) |
Polymers obtained by RAFT are susceptible to fluorescence quenching,17 but the PAA used here exhibited no luminescence, as determined by steady state measurements (recorded using a Fluoromax-4 spectrofluorometer in ultra-pure water) at these excitation and emission wavelengths, even with the large amounts of chain transfer agent used in the RAFT synthesis.
DOSY NMR
Between 5 and 20 mg of PAA were dissolved in 80 μl D2O. The pH was adjusted by the addition of HCl and NaOH. Sodium carbonate was used to regulate the pH where necessary. Diffusion-ordered NMR spectroscopy (DOSY, sometimes referred to as pulsed-field gradient or spin-echo NMR) experiments were performed on a Bruker Avance III 400 MHz spectrometer at 25 ± 1 °C, with a temperature stabilization time of at least 5 minutes. The samples were not spun. The gradient strength was increased linearly from 2% to 95% over 16 steps. The maximum gradient strength used was 0.535 T m−1. Bipolar rectangular gradients were used with a duration of 2 ms and the gradient recovery delay was 200 μs. Diffusion times were between 0.5 and 1.0 s. The spectrum was phased and baseline corrected before 2D processing via Topspin 2.1.6 software (Bruker).Hydrogen bond calculations
In order to assess the energies of hydrogen bonding between the carboxylic group with itself and with water, small molecule interactions were considered numerically.18 These hydrogen bond energies were calculated using Gaussian 09 (d1). Density functional theory calculations were performed using the M05-2X functional and the 6-311++g** basis set. Solvent (H2O) corrections were applied to monomer energies in the gas phase using single point calculations with the polarizable continuum model. These bond calculations include recognition that a dimer contains two bonds, which mutually reinforce each other, therefore increasing the hydrogen bond energy. The acid–water system may in principle contain two bonds, but the interaction considered is only that between the hydroxyl component of the carboxylic group and the oxygen in the water because this is substantially stronger than the carbonyl (acceptor) on the acid and the hydrogen (donor) on the water, which would not be stable in the gas phase.Results
Excited state lifetimes of P(AA-co-ACE) in dilute aqueous solutions typically decrease from 35 to 25 ns as the pH increases,19 as a result of statistical uncoiling of the polymer backbone. However, as shown in Fig. 1, analysis of low molar mass polymer excited state lifetimes did not show the increase in lifetime at low pH, so that the lifetime of the fluorescent label remained at ∼25 ns.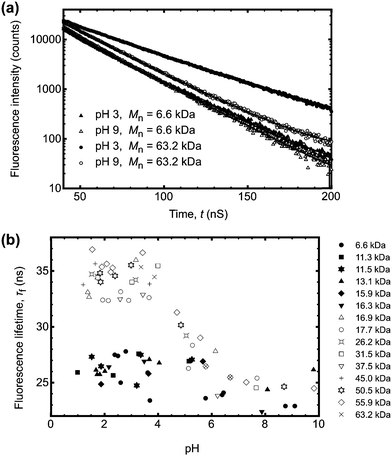 | ||
| Fig. 1 (a) Fluorescence decay for a large and a small molar mass PAA sample at pH 3 and pH 9. The large molar mass sample (63.2 kDa) at pH 3 had a longer lifetime than that revealed in the other three experiments, indicating that it alone had a more collapsed conformation. The solid lines are fits to the data. (b) Complete lifetime data as a function of pH, where τf is the average lifetime obtained from the fits to eqn (4). Open symbols are for molar masses of PAA, where Mn > 16.5 kDa, which exhibited a pH-dependent coil-to-globule transition. Closed symbols represent polymers that did not show a pH-dependent τf. Errors are not shown, but would have been obscured by the symbols. Number average molar masses, Mn, are stated in the legend. | ||
Conversely larger molar mass polymers acted in a manner anticipated for PAA, with a significant increase in lifetime observed at low pH. Thus, these data show that the pH-dependent coil-to-globule transition in PAA is critically dependent on molar mass. This finding was further corroborated by analysis of the equivalent TRAMS data (Fig. 2). It has been shown previously that correlation times of dilute P(AA-co-ACE) decrease as the compacted polymer chain opens into the solvated conformation.20 When protonated the correlation time of low molar mass P(AA-co-ACE) remained fixed across the entire pH range, whilst for high molar mass polymers this increased from ∼2 to ∼4 ns at pH < 5. The lifetime data showed a step change in behaviour as Mn was increased from Mn = 16.3 to 16.9 kDa. Analysis of the anisotropy data was performed via impulse reconvolution which removes the effects of the excitation pulse allowing derivation of fast relaxation processes.13,15
 | ||
| Fig. 2 (a) Impulse reconvolution fits to the anisotropy function for the same samples (and legend) as shown in Fig. 1a. As in Fig. 1a, the large molar mass sample (Mn = 63.2 kDa) showed pH responsive behaviour, with a longer correlation time at pH 3 than the other three samples. The solid lines are fits to the data. (b) Complete correlation time data as a function of pH. The symbols are the same as those in the legend in Fig. 1b. | ||
Both lifetime and anisotropy data suggest the change in behaviour occurs at between 16 and 17 kDa. The results cannot be derived from quenching of the fluorescent ACE group by the (dithioate) end groups, because increased quenching with increasing concentration of the end groups would produce a more gradual change in behaviour than the very narrow molar mass range observed here. Furthermore, it is known that conformational changes in low molar mass acenaphthylene-labelled chains have been observed using fluorescence experiments, albeit for different polymers.21,22 Thus, the experiments described in the present work show a direct effect of molar mass on the pH responsive behaviour of PAA. These PAAs are not generally uniform and the dispersities for those polymers in the region of the transition are: 1.2 (15.9 kDa), 1.6 (16.3 kDa), 1.2 (16.9 kDa), and 1.8 (17.7 kDa). The transition in τc is gradual, as would be expected from disperse samples. The particularly sharp transition in τf is probably due, at least in part, to the dominance of long lifetimes in the data. For example, the integrated area under the pH 3 curve in Fig. 1a for Mn = 63.2 kDa is some 30% larger than that for the pH 9 data.
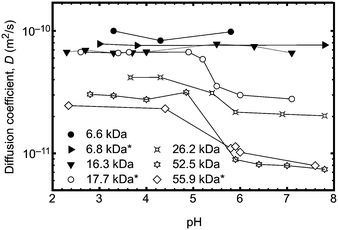
In order to unequivocally eliminate unanticipated problems in the fluorescence experiments, 2D DOSY NMR was employed to examine the conformational change of the poly(acrylic acid) backbone over a wide range of pH. Previously, DOSY NMR has been employed to determine the hydrodynamic radius of polymer samples23 and the diffusion constants of a stimuli responsive polymer (such as PAA) should vary with the conformation of the polymer backbone. An experiment was performed to vary the pH of solutions of seven polymers in D2O. The larger polymers were observed to undergo clear transitions in diffusion constant between pH 4 and 6 (Fig. 3), whilst smaller polymers exhibited no change in size or diffusion constant. These DOSY experiments therefore provide an important independent means of verifying the transition behaviour of the polymer as observed by fluorescence lifetime and TRAMS. In principle it should be possible to obtain the hydrodynamic radius from the diffusion coefficient using the Stokes–Einstein equation, but in this case, the solutions of high molar mass polymers were large enough so that the chains were overlapping; DOSY NMR is not sensitive enough with these polymers to provide single molecule results such as those obtained from the fluorescence experiments. Typically single polymer DOSY NMR is restricted to concentrations less than ∼1 g L−1,24 which is much less than the smallest concentration used here. Nevertheless, the experiments confirm the existence of a molar mass-dependent pH-induced conformational transition.
The direct effect of the ACE label on the pH responsive behaviour of PAA is best determined by potentiometric titration. Sample titration data are shown in Fig. 4a. The pKa obtained from the titration data varied in a narrow range between 4.52 and 4.55, in good agreement with earlier work.25–27 The curves have the same behaviour, and so it can be confirmed that, regardless of the synthetic method, the PAA has the same pH dependence. That the curves are similar for all of the RAFT agents used indicates that their relative hydrophobicities do not significantly change the behaviour of the polymer.
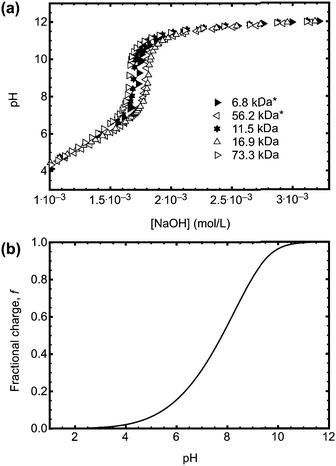 | ||
| Fig. 4 (a) Potentiometric titration data for a series of PAA samples (initially dissolved in water at a concentration of 1 mg ml−1) with and without (*) ACE label. The data shown here are for PAA synthesized using CTA 1 (6.8, 11.5, and 56.2 kDa), 2 (73.3 kDa), and 3 (16.9 kDa). The labelled polymers used different RAFT CTAs. (b) Fractional charge calculated from eqn (6). | ||
Discussion
The conformation of the PAA chain at low pH is not a collapsed structure and remains soluble in water. The collapse of PAA at low pH is similar but much less pronounced than that of poly(methacrylic acid) (PMAA) in that it is solely due to the change in (i.e. loss of) ionization of the acid functional group. PMAA, by contrast, undergoes a transition known as hypercoiling in which it collapses into a tight globule due to the influence of the methyl backbone, which may be observed by a comparison with TRAMS of ACE-labelled PMAA, for which τc covers a greater range (55 ns > τc > 5 ns).15 Lifetime measurements are insensitive to the hypercoiling effect, and ACE-labelled PMAA exhibits similar values28 of τf to those described above.As described in the introduction, the coil-to-globule is anticipated to occur for high molar mass polymers, and this assumption can be tested. However, to determine the point at which the coil-to-globule transition occurs, the fractional number of monomers charged in the chain, f, is needed. The pH dependence of f can be obtained by titration, and an approximate relation for dilute poly(acrylic acid) can be taken from previous work,26
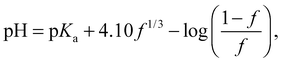 | (6) |
The Bjerrum length multiplied by the square of the number of ionized monomers is equated to the Flory radius at the start of the coil-to-globule transition,1
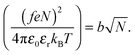 | (7) |
The inability to explain the pH-induced swelling of a model polyacid from a simple consideration of Coulombic effects means that another approach is required. The swelling of a polymer chain under different solvent conditions was first presented by Ptitsyn, Kron, and Eizner,30 in which a simple Flory model for the chain was used. Here the energy of polymer–polymer contacts will be considered as a means to investigate why small chains do not collapse but larger chains do. The swelling, α, of the polymer chain (i.e. the ratio of the radii of gyration of the perturbed to the Θ state) is obtained from the minimization of the Helmholtz free energy of a polymer chain, given by
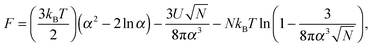 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2) chains, and the second and third terms represent contact energies. Here U is the energy gain of monomer–monomer contacts with respect to contacts between monomers and solvent molecules. The swelling term, α, is found by minimizing eqn (8) to give
α2) chains, and the second and third terms represent contact energies. Here U is the energy gain of monomer–monomer contacts with respect to contacts between monomers and solvent molecules. The swelling term, α, is found by minimizing eqn (8) to give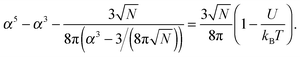 | (9) |
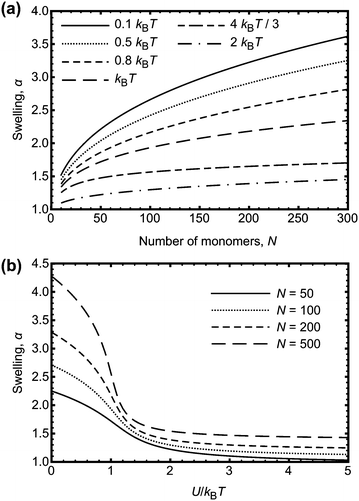 | ||
| Fig. 5 (a) Swelling, α, of a polymer chain as a function of degree of polymerization, N, for different interaction energies, U. (b) Swelling, α, of a polymer chain as a function of U/kBT, for different N. The results are numerical solutions to eqn (9). The experimentally observed behaviour where the swelling decreases with increasing N is not predicted from these calculations. | ||
For hydrogen bonding to take place, the energy of the carboxylic acid dimer must be less than that of the acid with water. The hydrogen bond between a carboxylic acid dimer (of energy −37.6 kJ mol−1) in solution is thus Ucc = −15.4 kBT. A dimer and a hydrogen bond between two water molecules (−13.3 kJ mol−1 or −5.4 kBT) can be compared with two different carboxylic groups hydrogen bonding with water (2Ucw = −11.8 kBT), which leads to a change in energy on the formation of a dimer of U = −9.1 kBT. There are significant approximations here, because, for example, the possibility that the dimer is formed with only one hydrogen bond has been ignored, which would leave one on each carboxylic group free to react with water. Furthermore, only one hydrogen bond between water molecules is assumed, and this is probably not the case in the real systems.
If the interaction energy U were to be a function of N, the result obtained from eqn (9) could perhaps be used to explain the experimental data. One possibility is that an effective energy does increase with degree of polymerization because of hydrogen bonds being located on neighbouring monomers. This is more likely on longer chains than on smaller ones, because there are fewer polymer–polymer contacts on smaller chains. Adjacent monomers are more likely to be involved in hydrogen bonding if the free energy benefit is greater than that for forming hydrogen bonds at random points on the chain. It is not obvious that this is the case; adjacent hydrogen bonds can stabilize crystalline structures, such as for polyurethanes,35 but there are also examples of non-co-operative systems, with hydrogen bonds randomly distributed along the chain.36,37 The effect of neighbouring monomers participating in hydrogen bonding can be considered in the context of Fig. 5b, if it is stated that the larger chains have an increased U to account for a consideration of neighbouring interactions as one contact. Nevertheless, the hydrogen bond energy is too large to change the swelling of the PAA; multiple neighbouring bonds each with an energy gain of −9.1 kBT will not significantly affect the swelling.
There are other examples of mass dependent transitions; for example, it has also been known for many years that there is a molar mass effect in the temperature-induced shape transition of poly(ethylene glycol) in water.38–41 Furthermore, results from fluorescence experiments have hinted that PAA itself exhibits interesting mass-dependent behaviour.42 Viscosity measurements have also tentatively indicated a different behaviour for low molar mass PAA.43
Ultimately, hydrogen bonds are strong, and the presence of such bonding between non-adjacent monomers is likely to cause chain collapse. The models presented above treat interactions as transient contacts but this cannot be the case for hydrogen bonds. A chain with one long-lived monomer–monomer contact is less likely to be able to swell fully. It is also likely that smaller chains will have fewer such contacts. Consider a single chain of size bNν in dilute solution. The probability of a monomer in that chain contacting another monomer in the same chain is proportional to the square of the concentration of that chain,
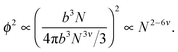 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(U/kBT), where τ is of the order of ps. For U/kBT = 9, this is less than 1 μs. These bonds are long-lived, but cannot be treated as permanent. Any full discussion of the structure of such polymers will need to account for the long lifetime of hydrogen bonds.
exp(U/kBT), where τ is of the order of ps. For U/kBT = 9, this is less than 1 μs. These bonds are long-lived, but cannot be treated as permanent. Any full discussion of the structure of such polymers will need to account for the long lifetime of hydrogen bonds.
Some conformational transitions are molar mass and concentration dependent. For example, poly(N-isopropyl acrylamide) (PNIPAm) has a well-known temperature-dependent conformational transition, with a lower critical solution temperature of 32 °C.44 However, for low molar mass PNIPAm at low concentrations, this transition has been observed to shift to higher temperatures,45 indicating the existence of an activation energy associated with the transition. This effect is not present at greater concentrations.46 Given a molar mass dependence of PNIPAm it is worth considering the same for PAA. Here, it was necessary that the fluorescence measurements were performed in very dilute solution in order to limit the effect of self-quenching,4,47,48 but the DOSY-NMR experiments were performed at concentrations of typically two orders of magnitude greater. The concentrations used for the DOSY-NMR diffusion measurements are listed in Table S4 of the ESI.†
Conclusion
A complete set of poly(acrylic acid) chains was synthesized by RAFT polymerization and fluorescence experiments were used to demonstrate that a pH-induced conformational transition only occurred for chains of a molar mass greater than 16.5 kg mol−1; smaller chains remained solvated. At high pH the correlation time (from TRAMS experiments) and fluorescence lifetime were independent of chain size but at low pH a transition to longer times was only observed for the larger chains. DOSY NMR experiments were also performed to support the conclusions drawn from the fluorescence experiments. Here, the diffusion coefficients of poly(acrylic acid) were measured as a function of pH. For small chains, the diffusion coefficient measured was independent of pH, but for larger chains the diffusion coefficient decreased above a pH of 5. The large molar mass of the polymer above which the conformational transition was observed is particularly surprising. It is possible that the explanation for this phenomenon involves the critical role played by hydrogen bonding in poly(acrylic acid). Small chains are less likely to engage in hydrogen bonding, and it may be that above a critical molar mass, the likelihood of hydrogen bonding in acid solution is sufficient for the chain to undergo a conformational transition from the swollen state at high pH.Acknowledgements
Stella Kritkanu is acknowledged for her help with the Gaussian 09 software. Dr Jianfeng (Peter) Zhu provided invaluable assistance in setting up the DOSY NMR machines. Funding was kindly provided by the Engineering and Physical Sciences Research Council (EPSRC) and SNF (UK) Ltd.References
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS
.
- F. Liu and M. W. Urban, Prog. Polym. Sci., 2010, 35, 3–23 CrossRef CAS
.
-
T. A. Witten and P. A. Pincus, Structured Fluids, Oxford, Oxford, 2004 Search PubMed
.
-
L. Swanson, in Photochemistry and Photophysics of Polymer Materials, ed. N. S. Allen, Wiley, New Jersey, 2010, pp. 41–91 Search PubMed
.
- J. Loiseau, N. Doërr, J. M. Suau, J. B. Egraz, M. F. Llauro, C. Ladavière and J. Claverie, Macromolecules, 2003, 36, 3066–3077 CrossRef CAS
.
- K. R. Rogan, A. C. Bentham, G. W. A. Beard, I. A. George and D. R. Skuse, Prog. Colloid Polym. Sci., 1994, 97, 97–102 CAS
.
- A. Katchalsky and H. Eisenberg, J. Polym. Sci., 1951, 6, 145–154 CrossRef CAS
.
- J. V. M. Weaver, I. Bannister, K. L. Robinson, X. Bories-Azeau, S. P. Armes, M. Smallridge and P. McKenna, Macromolecules, 2004, 37, 2395–2403 CrossRef CAS
.
- W. Kuhn, O. Künzle and A. Katchalsky, Helv. Chim. Acta, 1948, 31, 1994–2037 CrossRef CAS PubMed
.
- T. Pakula, J. Chem. Phys., 1991, 95, 4685–4690 CrossRef CAS
.
- C. Ladavière, N. Dörr and J. P. Claverie, Macromolecules, 2001, 34, 5370–5372 CrossRef
.
- G. Moad, J. Chiefari, Y. K. Chong, J. Krstina, R. T. A. Mayadunne, A. Postma, E. Rizzardo and S. H. Thang, Polym. Int., 2000, 49, 993–1001 CrossRef CAS
.
- I. Soutar, L. Swanson, T. Annable, J. C. Padget and R. Satgurunathan, J. Colloid Interface Sci., 2006, 303, 205–213 CrossRef CAS PubMed
.
- H. Willcock and R. K. O'Reilly, Polym. Chem., 2010, 1, 149–157 RSC
.
- I. Soutar and L. Swanson, Macromolecules, 1994, 27, 4304–4311 CrossRef CAS
.
- I. Soutar, L. Swanson, R. E. Imhof and G. Rumbles, Macromolecules, 1992, 25, 4399–4405 CrossRef CAS
.
- J. P. S. Farinha, P. Relógio, M.-T. Charreyre, T. J. V. Prazeres and J. M. G. Martinho, Macromolecules, 2007, 40, 4680–4690 CrossRef CAS
.
- F. Sterpone, G. Stirnemann, J. T. Hynes and D. Laage, J. Phys. Chem. B, 2010, 114, 2083–2089 CrossRef CAS PubMed
.
- N. J. Flint, R. Haywood, I. Soutar and L. Swanson, J. Fluoresc., 1998, 8, 327–334 CrossRef CAS
.
- J. R. Ebdon, B. J. Hunt, D. M. Lucas, I. Soutar, L. Swanson and A. R. Lane, Can. J. Chem., 1995, 73, 1982–1994 CrossRef CAS
.
- C. K. Chee, S. Rimmer, I. Soutar and L. Swanson, React. Funct. Polym., 2006, 66, 1–11 CrossRef CAS
.
- C. K. Chee, S. Rimmer, I. Soutar and L. Swanson, Soft Matter, 2011, 7, 4705–4714 RSC
.
- W. Li, H. Chung, C. Daeffler, J. A. Johnson and R. H. Grubbs, Macromolecules, 2012, 45, 9595–9603 CrossRef CAS PubMed
.
- A. Chen, D. H. Wu and C. S. Johnson Jr, J. Am. Chem. Soc., 1995, 117, 7965–7970 CrossRef CAS
.
- D. F. Anghel, V. Alderson, F. M. Winnik, M. Mizusaki and Y. Morishima, Polymer, 1998, 39, 3035–3044 CrossRef CAS
.
- R. Arnold, J. Colloid Sci., 1957, 12, 549–556 CrossRef CAS
.
- M. Mandel, Eur. Polym. J., 1970, 6, 807–822 CrossRef CAS
.
- L. Ruiz-Pérez, A. Pryke, M. Sommer, G. Battaglia, I. Soutar, L. Swanson and M. Geoghegan, Macromolecules, 2008, 41, 2203–2211 CrossRef
.
- H. Li, B. Liu, X. Zhang, C. Gao, J. Shen and G. Zou, Langmuir, 1999, 15, 2120–2124 CrossRef CAS
.
- O. B. Ptitsyn, A. K. Kron and Y. Y. Eizner, J. Polym. Sci., Part C: Polym. Symp., 1968, 16, 3509–3517 CrossRef
.
- T. M. Birshtein and V. A. Pryamitsyn, Macromolecules, 1991, 24, 1554–1560 CrossRef CAS
.
- G. Graziano, Int. J. Biol. Macromol., 2000, 27, 89–97 CrossRef CAS PubMed
.
- M. Nakata, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 5770–5775 CrossRef CAS
.
- D. Yang and Q. Wang, ACS Macro Lett., 2013, 2, 952–954 CrossRef CAS
.
- J. Mattia and P. Painter, Macromolecules, 2007, 40, 1546–1554 CrossRef CAS
.
- H. Eisenberg and G. Felsenfeld, J. Mol. Biol., 1967, 30, 17–37 CrossRef CAS PubMed
.
- P. J. M. Stals, M. A. J. Gillissen, T. F. E. Paffen, T. F. A. de Greef, P. Lindner, E. W. Meijer, A. R. A. Palmans and I. K. Voets, Macromolecules, 2014, 47, 2947–2954 CrossRef CAS
.
- Y. C. Bae, S. M. Lambert, D. S. Soane and J. M. Prausnitz, Macromolecules, 1991, 24, 4403–4407 CrossRef CAS
.
- E. E. Dormidontova, Macromolecules, 2002, 35, 987–1001 CrossRef CAS
.
- G. N. Malcolm and J. S. Rowlinson, Trans. Faraday Soc., 1957, 53, 921–931 RSC
.
- S. Saeki, N. Kuwahara, M. Nakata and M. Kaneko, Polymer, 1976, 17, 685–689 CrossRef CAS
.
- J. Seixas de Melo, T. Costa, A. Francisco, A. L. Macanita, S. Gago and I. S. Gonçalves, Phys. Chem. Chem. Phys., 2007, 9, 1370–1385 RSC
.
- P. J. Kay and F. E. Treloar, Makromol. Chem., 1974, 175, 3207–3223 CrossRef CAS
.
- H. G. Schild, Prog. Polym. Sci., 1992, 17, 163–249 CrossRef CAS
.
- E. I. Tiktopolu, V. N. Uvesky, V. B. Lushchik, S. I. Klenin, V. E. Bychkova and O. B. Ptitsyn, Macromolecules, 1995, 28, 7519–7524 CrossRef
.
- Y. Zhang, S. Furyk, L. B. Sagle, Y. Cho, D. E. Bergbreiter and P. S. Cremer, J. Phys. Chem. C, 2007, 111, 8916–8924 Search PubMed
.
- Q. Hao, W. Lei, X. Xie, M. Xia, F. Wang and X. Yang, Polym. Chem., 2011, 2, 1085–1090 RSC
.
- D. J. Kiserow, Y. Itoh and S. E. Webber, Macromolecules, 1997, 30, 2934–2940 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Characterization of the poly(acrylic acid) samples, further experimental information, and tables of results. See DOI: 10.1039/c5sm02693h |
| This journal is © The Royal Society of Chemistry 2016 |