Celebrating Soft Matter's 10th Anniversary: Sequential phase transitions in thermoresponsive nanoemulsions

Abstract

We report the coexistence of stress-bearing percolation with arrested phase separation in a colloidal system of thermoresponsive nanoemulsions spanning a broad range of volume fractions (0.10 ≤ ϕ ≤ 0.33) and temperatures (22 °C ≤ T ≤ 65 °C). Here, gelation is driven by short-range interdroplet polymer bridging at elevated temperatures. Direct visualization of the gel microstructure shows that nanoemulsions undergo a homogenous percolation transition prior to phase separation. Rheological characterization shows that both the percolated and the phase separated structures are capable of supporting a significant amount of elastic stress. As the system is heated, the sequential onset of these phase transitions is responsible for the unusual two-step increase in the linear viscoelasticity of the gels. In addition, we find that slowing the heating rate significantly reduces the elasticity of the gels at high temperatures. Our results suggest that the formation of metastable gelled states not only depends on the attraction strength and volume fraction of the system, but is also sensitive to the rate at which the attraction strength is increased.

---

Introduction

Colloids can bond and form a sample-spanning network – known as a gel – when a sufficiently strong attraction is present. Aggregation is commonly induced with colloid-polymer depletion interactions,¹ thermoreversible adhesive polymers,² and screened electrostatics.³ The microscopic interactions of individual colloids collectively contribute to the overall structure and dynamics of a colloidal gel, which ultimately give rise to its macroscopic viscoelastic properties.⁴ In these attraction-driven systems, the strength of the interparticle attraction, U_a, determines the bond lifetime, τ_B. Strong, permanent bonds in which U_a ≫ k_BT (k_B is the Boltzmann constant and T is the temperature) are linked to τ_B ≫ τ_E, where τ_E is the experimentally accessible timescale. These irreversible chemical gels display characteristic fractal structures.⁵ Their ideal gel transition and growth is well-described by classical percolation theory.^6–8 Although the percolation threshold has also been calculated for weakly gelling systems (U_a ∼ k_BT and τ_B ∼ τ_E),³³ a space-spanning interconnected network of a sufficiently long lifetime is necessary for transient gels to bear a significant load.⁹

Weak colloidal gels can typically support their own weights before the onset of delayed sedimentation.^10–12 Colloids residing within dense regions are thought to be caged by excluded volume, leading to local jamming and dynamical arrest.^13–16 The definition of gelation is not universal and varies depending on the specific interactions that drive dynamical arrest. For example, the onset of homogenous percolation is masked by liquid–gas spinodal decomposition in depletion gels.¹⁴ In contrast, percolation and phase separation compete in the arrest of thermoreversible adhesive hard spheres (AHS), depending on the volume fraction.^17–19 Although a full description of the assembly kinetics is necessary to classify the gelation mechanism,²⁰ the observed microstructure can provide some general guidelines. Broadly speaking, gels formed by homogenous percolation are fractal in nature, similar to irreversible gels. The microstructure of a gel undergoing liquid–gas phase separation tends to be highly heterogeneous and has thick strands interspersed with void regions.^14,21 Their characteristic domain size is dependent on the thermodynamics and kinetics of the gelation process. When the attraction strength is increased, phase separation is arrested to the point where the domains become smaller than that seen at the gel transition.²² Because of the load-bearing capability of these space-spanning networks, definitions of the gel point can also be made when the linear viscoelastic moduli of the sample increase beyond a critical value.²³

Recently, we developed a thermoresponsive nanoemulsion system where gelation is driven by interdroplet bridging of difunctional polymer end groups.²⁴ Unlike depletion gels, these nanoemulsions allow us to study the effect of the heating rate on gelation. Earlier studies involved the use of small angle neutron scattering to probe the microstructure and dynamics of gels formed under a specific set of volume fractions and temperatures.^25,26 Although the existence of homogenous percolation and arrested phase separation for two different samples were shown, a more general phase space and the transition between the two states remains unclear. Here, we use confocal microscopy to directly visualize the microstructure of nanoemulsions spanning a broad range of volume fractions (0.10 ≤ ϕ ≤ 0.33) and temperatures (22 °C ≤ T ≤ 65 °C), and compare our results to rheological measurements in which the heating rate varies between 0.5 °C min⁻¹ and 10 °C min⁻¹. Surprisingly, we find that thermogelling nanoemulsions exhibit a two-step increase in their elasticity across the range of volume fractions tested. The sequential phase transitions are in agreement with structures observed with confocal microscopy that represent long-lived percolated and phase separated states. We discuss a rationale for the observed phase behavior in nanoemulsions with respect to the mechanism of percolation and phase separation in thermoreversible AHS systems.

Methods

Nanoemulsion synthesis and gelation

The experimental system consists of monodisperse poly(dimethyl siloxane) (PDMS, viscosity, η = 5 cP) oil droplets (2a = 42 ± 6 nm, polydispersity between 17% and 35%) suspended in a continuous phase of the crosslinker poly(ethylene glycol) diacrylate (PEGDA, M_n = 700 g mol⁻¹, R_g ∼ 9 Å estimated from PEG at room temperature^27,28) with 200 mM of the surfactant sodium dodecyl sulfate (SDS). Nanoemulsions are generated with a range of volume fractions (ϕ = 0.10, 0.15, 0.20, 0.25, 0.33). A pre-emulsion is first generated by placing a 50 mL centrifuge tube containing the constituents on a vortex mixer for 30 seconds, or until the sample is thoroughly mixed. The pre-emulsion is then passed through a high pressure homogenizer (Emulsiflex-C3, AVESTIN) at a pressure of 18 000 psi for a total of 20 passes.²⁵ The sample is chilled to 4 °C in between each pass and is stored at 4 °C until further use. We measure the diameter of the droplets, 2a, using dynamic light scattering (DLS) after diluting samples with an appropriate solvent (33 vol% PEGDA in DI water) to ϕ = 0.002 (DynaPro NanoStar, Wyatt Technology). The value of 2a = (42 ± 6) nm holds across all ϕ. The range of the attraction is estimated at ξ = R_g/a ∼ 0.04 ± 0.01 at room temperature. The zeta potential of the PDMS droplets, ζ = (−55 ± 27) mV, is measured from the electrophoretic mobility of PDMS droplets (Zetasizer Nano, Malvern Instruments). These samples are diluted to ϕ = 0.01 with the same solvent used in the DLS measurements.

When the temperature is raised beyond a critical value, the difunctional end groups on the PEGDA molecules increasingly partition into the oil phase, and the molecules serve as bridges between droplets (Fig. S1, ESI†). Small amounts of a fluorescent lipophilic dye and an ultraviolet (UV)-sensitive photoinitiator are added to lock the gel microstructure in place for confocal laser scanning microscopy (CLSM). The dye and photoinitiator does not affect the thermogelling behavior (Fig. S2–S4, ESI†).

Confocal microscopy and image processing

We use confocal laser scanning microscopy (CLSM) to visualize gelled structures that are locked in place. We incorporate a fluorescent lipophilic dye (PKH26) and a UV-sensitive photoinitiator (2-hydroxy-2-methylpropiophenone, or Darocur) at 1 vol% each into the nanoemulsions. The mixture is passed through a 1.5 μm nylon filter to remove any coalesced droplets, and 250 μL of the sample is placed in a glass chamber with a #1.5 coverslip (Nunc LabTek II, Thermo Scientific). Thermogelation is induced by heating the sample-containing chamber from room temperature (T = 22 °C) to a range of temperatures (T = 30–65 °C) in an oven for 10 minutes. Assuming that the nanoemulsions heat up with a constant heat transfer coefficient close to that of water, we find that samples heat up nearly instantaneously in the oven (minimum heating rate of >100 °C s⁻¹). The heated sample is removed from the oven and immediately placed under a 2 mW UV light source for 1 minute to ensure complete crosslinking. Deionized water is added to the top of the cured organohydrogels to reduce evaporation.

We use an inverted confocal laser scanning microscope (Nikon A1R) equipped with a resonant scanner head and fitted with a 60× oil immersion objective (numerical aperture = 1.4) to capture the 2D images of the crosslinked nanoemulsions. Images used for structural analysis have dimensions of 30.7 μm × 30.7 μm with a pixel size of 60 nm, and images shown in Fig. 1 have dimensions of 15.4 μm × 15.4 μm with a pixel size of 30 nm. A fast Fourier Transform (FFT) is applied to the 2D images using the image processing software ImageJ (NIH). The radially averaged scattered light intensity of the FFT images, I(q), is obtained using a radial profile plugin to ImageJ.²⁹ Here, q represents the wave vector that is equivalent to inverse length in real space.

Fig. 1 Direct visualization of thermoresponsive nanoemulsions. Representative 2D CLSM images of nanoemulsions at various volume fractions (ϕ) and temperatures (T). Samples are fluorescently dyed and heated to T for 10 minutes. The microstructure is then rapidly locked in place with a UV-sensitive photoinitiator. Scale bars = 3 μm.

Rheological characterization

We use rheological measurements to characterize the viscoelastic moduli of a broad range of nanoemulsions as the temperature is increased at a rate of 2.0 °C min⁻¹. Small amplitude oscillatory rheology is performed on a stress-controlled rheometer (AR-G2, TA Instruments). Pure nanoemulsions are passed through a 1.5 μm nylon filter and loaded onto a Peltier plate. An aluminum 2° cone-and-plate geometry (diameter = 60 mm) is lowered to the gap distance of 58 μm while rotating at an angular frequency, ω = 0.5 rad s⁻¹, to minimize the formation of bubbles at the interface. The nanoemulsions are subjected to a preshear (ω = 20 rad s⁻¹) for 30 seconds, and allowed to quiescently equilibrate for 1 minute prior to the application of a temperature ramp. The temperature of the Peltier plate is increased from T = 22 °C to 70 °C at a rate of 2 °C min⁻¹, a fixed angular frequency of ω = 20 rad s⁻¹, and a fixed strain, γ = 0.05% (within the linear regime of the material). Dynamical arrest within the nanoemulsions is characterized at various T using small oscillatory measurements, where we measure the frequency-dependent response (1 rad s⁻¹ ≤ ω ≤ 100 rad s⁻¹) at γ = 0.05%. An additional set of experiments with variable heating rates (0.5 °C min⁻¹ to 10 °C min⁻¹) is performed on nanoemulsions with ϕ = 0.25. The linear viscoelastic moduli, G′ and G′′, are monitored over the duration of the temperature ramp experiment. We verify the absence of slip by repeating the same temperature ramp experiment (for nanoemulsions at ϕ = 0.25 at a heating rate of 1 °C min⁻¹) with a layer of 600 grit sandpaper adhered to the geometry.

Results and discussion

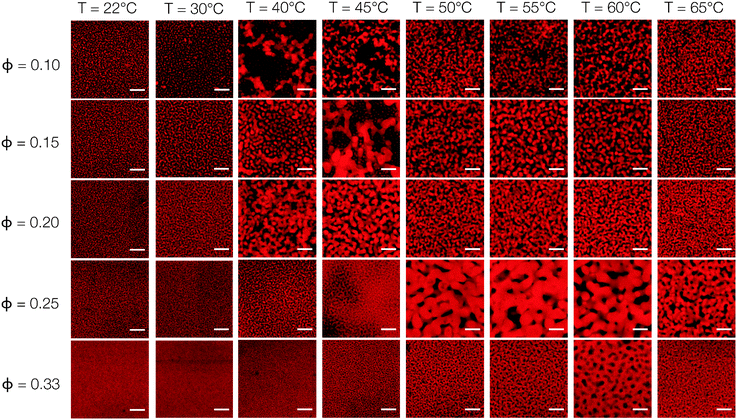
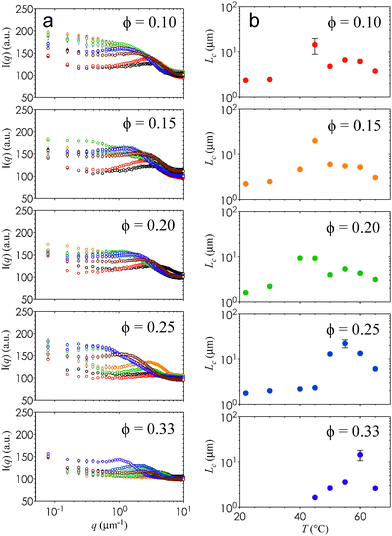
Fig. 1 is a panel of representative CLSM images that provides visual evidence of the sequential phase transitions of the nanoemulsions. We illustrate the difference between an ungelled nanoemulsion, a fractal-like percolated structure, and a spinodal-like phase separated network with arrested kinetics in Fig. 2. At T = 22 °C, nanoemulsions exist mostly as dispersed droplets and mobile clusters. Because of the intrinsic resolution limits imposed by the wavelength of the emitted light and the numerical aperture of the microscope objective, individual droplets are observed as Airy disks for ϕ = 0.10–0.25 and a homogenous image is seen at ϕ = 0.33. As temperature is increased, a finely percolated structure begins to emerge for systems at ϕ = 0.15–0.33, while fluid clusters are seen in the sample at ϕ = 0.10. Nanoemulsions with ϕ = 0.10, 0.15, and 0.20 show a distinctive phase transition at T = 40 °C, where droplets form thick strands that are characteristic of the onset of liquid–gas phase separation. The thickest strands seen here are ∼2 μm in width. Because of the visual clarity of this phase transition, we define the critical temperature observed from CLSM as T_c. Samples of higher ϕ phase separate at higher T_c. Snapshots of nanoemulsions close to T_c show striking signs of dynamical heterogeneity where mobile clusters coexist with colloid-rich strands, as well as density fluctuations that precede phase separation of the percolated structure (Fig. S5, ESI†). The thickness of the strands in all of the nanoemulsions is seen to decrease as T is further increased to 65 °C, implying that the phase separation becomes arrested.²² The attraction strength in our system increases with the temperature in our system unlike experiments on adhesive hard spheres.³⁰ We note that the thermogelation from an increase in attraction strength occurs at elevated temperatures, and overcomes the corresponding increase in colloidal mobility.

Fig. 2 Representative CLSM images of a nanoemulsion (ϕ = 0.33) as it transitions from the ungelled to gelled states. (a) An ungelled sample at T = 22 °C, (b) a fractal-like percolated structure formed at T = 55 °C, and (c) a spinodal-like network formed by arrested phase separation at T = 65 °C. Scale bars = 5 μm.

The homogenous percolation at low T and the arrested phase separation at higher T are quantified by the characteristic length scale, L_c, of the gels. The value of L_c is obtained from a FFT applied to the raw 2D images. The ensemble-averaged intensities of the FFT images, I(q), are shown as a function of T for different ϕ in Fig. 3(a). We define q_m as the local maximum in I(q). The characteristic length scales of the gels, L_c = 2π/q_m, are plotted in Fig. 3(b). Here, the temperature-dependent transition from percolation to phase separation shown in Fig. 1 is quantified by a gradual increase in L_c for T ≤ T_c, followed by a sharp jump at T = T_c, and finally by a gradual decrease beyond T_c. The decrease in L_c with increasing kinetic arrest is a generic feature of non-equilibrium gels.²²

Fig. 3 Quantification of characteristic gel length scales. (a) The radially-averaged scattered intensity, I(q), is plotted as a function of q for ϕ = 0.10, ϕ = 0.15, ϕ = 0.20, ϕ = 0.25, and ϕ = 0.33. Samples heated to different temperatures are plotted as open circles: T = 22 °C (black), T = 30 °C (red), T = 40 °C (orange), T = 45 °C (green), T = 50 °C (teal), T = 55 °C (blue), T = 60 °C (purple), and T = 65 °C (brown). Error bars are generated from 3 independent measurements. (b) The value of L_c is plotted as a function of T for the different values of ϕ. Error bars are generated from 3 independent measurements.

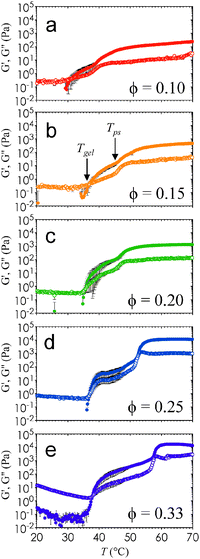
It is interesting that L_c increases by nearly an order of magnitude at T_c, and that this difference is much more pronounced at high ϕ. This change in L_c, combined with the observed increase in the thickness of the interconnected strands, imply that the elastic and viscous moduli, G′ and G′′, of these nanoemulsions will depend on ϕ and T. As expected, G′ attains a plateau value at high T (Fig. 4) that is commensurate with the increase in stress-bearing capability brought on by the kinetic arrest and high droplet loading. In addition, Fig. 4 shows that G′ and G′′ display two characteristic phase transition temperatures, T_gel and T_ps. Here, T_gel is defined as the temperature at which G′ = G′′,²³ and T_ps is the temperature of the inflexion point in G′ at T > T_gel. The existence of T_gel and T_ps, in conjunction with the two distinct types of gel microstructure from Fig. 2, provides consistent evidence that the onset of homogenous percolation followed consequently by phase separation is responsible for the two-step increase in G′. The dynamics of both the percolated and the phase separation structures are arrested (Fig. S6, ESI†).

Fig. 4 Viscoelastic response of nanoemulsions as a function of T. The elastic and viscous moduli, G′ (closed symbols) and G′′ (open symbols), are obtained from temperature ramping (rate of 2 °C min⁻¹) small amplitude oscillatory rheological measurements. Here, G′ and G′′ are plotted as a function of T for (a) ϕ = 0.10, (b) ϕ = 0.15, (c) ϕ = 0.20, (d) ϕ = 0.25, and (e) ϕ = 0.33. Error bars are generated from 3 independent samples.

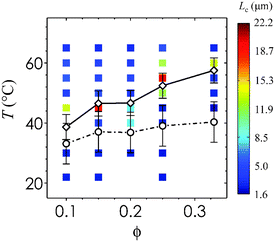
To provide a direct comparison between the gel microstructure and our rheological data, we overlay T_gel and T_ps on a plot containing the values of L_c for each state point. Fig. 5 is a diagram that illustrates the effect of ϕ and T on the characteristic length scale of the thermogelling nanoemulsions. The percolation transition T_gel persists across the range of ϕ tested, and this threshold is passed before the phase separation transition T_ps. Error bars indicate the variation in T_gel and T_ps when heating rate is varied from 0.5 °C min⁻¹ to 10 °C min⁻¹ in the rheological measurements. The two transitions are most distinct from each other at high ϕ. The fact that we are able to distinguish them in Fig. 5 suggests that gels can arise from percolation prior to the onset of phase separation. This is distinctly different from the case of depletion gels in which phase separation, not percolation, drives dynamical arrest.¹⁴ Nanoemulsion gelation is driven by a short-range interaction similar to that of thermoreversible AHS (aggregation in AHS is induced by a collapse in the polymer brushes below a critical temperature¹⁸). There is a very narrow range (∼2 °C) of temperatures for which the gel transition occurs in AHS. The broader range of gelation temperatures in our nanoemulsion system could explain the unusual two-step change in G′ when crossing the percolation threshold into the liquid–gas coexistence region: the first increase in G′ corresponds to the formation of a sample-spanning fractal network capable of supporting stress, and the second increase corresponds to the spinodal-like structures that develops with phase separation. Our results support observations in the AHS literature that stable gels can arise by percolation, and provide evidence that substantial elasticity in nanoemulsions (0.10 ≤ ϕ ≤ 0.33) is generated by the formation of a percolating network. Further increase in the attraction strength then introduces arrested liquid–gas phase separation.

Fig. 5 Phase behavior of thermoresponsive nanoemulsions. The values of L_c from CLSM images (filled squares with color given in inset legend) from direct observations of the phase boundary, as well as T_gel (open black circles connected by dashed-dotted black line) and T_ps (open black diamonds connected by solid black line) from rheological measurements. Lines are drawn to guide the eye. Here, T_gel is indicative of the percolation transition and T_ps represents the phase separation transition. Error bars represent the standard deviations reported from the range of heating rates tested on nanoemulsions at ϕ = 0.25, applied across all ϕ.

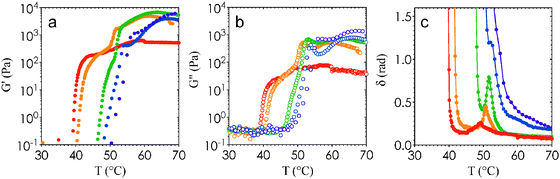
A lack of two-step gelation in previous studies on the same system suggests that percolation is sensitive to differences in droplet sizes and hence interaction range (∼15% difference between^24,25 and this work). In addition, we acknowledge that the heating rates are different between our microscopy and rheology measurements. For direct visualization experiments, we place samples in a hot oven where heating is nearly instantaneous even with the lowest temperature differences (sample heating rate is >100 °C s⁻¹ when ΔT = 13 °C). In contrast, the samples are heated at a rate of 2 °C min⁻¹ over the duration a temperature ramp experiment in the rheometer. To explore these differences in heating protocols, we analyze the effect of heating rate on the temperature-dependent rheology of nanoemulsions at ϕ = 0.25. Fig. 6(a) and (b) show that as the heating rate is increased, T_gel and T_ps both shift to higher temperatures. We note here that when the heating rate is increased from 0.5 °C min⁻¹ to 10 °C min⁻¹, the change in T_gel and T_ps is about ±5 °C and within the experimental window of T_c from microscopy measurements. Plotting the ratio of the loss and storage moduli as δ = tan⁻¹(G′′/G′) show that local peaks appear at intermediate heating rates, corresponding to an increase in the liquid-like behavior of the gels (Fig. 6(c)). More remarkable is the almost complete disappearance of the local peak in δ at a heating rate of 0.5 °C min⁻¹, and a high-T plateau in G′ that is an order of magnitude lower than that of gels formed with higher heating rates (∼10² Pa versus ∼10³ Pa, see Fig. 6a).

Fig. 6 Effect of heating rate on viscoelastic properties of gels. The values of (a) G′, (b) G′′, and (c) δ are plotted as a function of T for nanoemulsions (ϕ = 0.25) heated at a rate of 0.5 °C min⁻¹ (red), 1 °C min⁻¹ (orange), 2 °C min⁻¹ (green), 5 °C min⁻¹ (blue), and 10 °C min⁻¹ (purple).

The rheological measurements in Fig. 6 show that the ramp rate plays an important role in the final gel microstructure. Experimental work on AHS have shown that a low ramp rate is necessary to reduce hysteresis, and that the transient microstructure is highly sensitive to the path to gelation.¹² The competition between percolation and phase separation is well-known in AHS,¹⁷ and their competing kinetics could be responsible for the significant microstructural differences observed at various heating rates. Nevertheless, the ability to control the heating rate provides a unique method to study the route taken towards gelation, unlike depletion-induced colloidal gels in which the rate of change of the attraction strength cannot be varied.^14,21

We have shown here that the gelation of thermoresponsive nanoemulsions can be manipulated by changing the temperature, the heating rate, and the volume fraction of the oil droplets. Adjusting these tuning parameters allow us to generate nanoemulsion gels with well-defined network morphology. This type of thermoresponsive self-assembly could be used to engineer microporous materials, such as metallic bijel templates³¹ and hydrogel scaffolds that facilitate wound healing.³² Further experimental and simulation work to understand the rate-dependent phenomena of thermogelation would provide a guiding framework to design these types of multiphase materials.

Acknowledgements

The authors thank the group of Gareth McKinley for usage of the AR-G2 rheometer, the Koch Institute Microscopy Core for usage of the CLSM, and the Biophysical Instrumentation Facility at MIT for usage of the DLS. This work is supported by the Institute for Collaborative Biotechnologies through grant W911NF-09-0001 from the U.S. Army Research Office. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred. This work was supported in part by the MRSEC Program of the National Science Foundation under award number DMR-1419807.

References

1. S. M. Ilett, A. Orrock, W. C. K. Poon and P. N. Pusey, Phys. Rev. E, 1995, 51, 1344.
2. H. Verduin and J. K. G. Dhont, J. Colloid Interface Sci., 1995, 172, 425.
3. E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Dover Publications, 1999.
4. J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, 2012.
5. P. Meakin, Phys. Rev. Lett., 1983, 51, 1119.
6. T. A. Witten and L. M. Sander, Phys. Rev. Lett., 1981, 47, 1400.
7. J. C. Phillips, J. Non-Cryst. Solids, 1979, 34, 153.
8. M. F. Thorpe, J. Non-Cryst. Solids, 1983, 57, 355.
9. F. Sciortino, et al. , Comput. Phys. Commun., 2005, 169, 166.
10. S. Manley, J. M. Skotheim, L. Mahadevan and D. A. Weitz, Phys. Rev. Lett., 2005, 94, 218302.
11. L. Starrs, W. C. K. Poon, D. J. Hibberd and M. M. Robins, J. Phys.: Condens. Matter, 2002, 14, 2485.
12. J. M. Kim, J. Fang, A. P. R. Eberle, R. Castañeda-Priego and N. J. Wagner, Phys. Rev. Lett., 2013, 110, 208302.
13. V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811.
14. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499.
15. S. Manley, H. M. Wyss, K. Miyazaki, J. C. Conrad, V. Trappe, L. J. Kaufman, D. R. Reichman and D. A. Weitz, Phys. Rev. Lett., 2005, 95, 238302.
16. P. N. Segrè, V. Prasad, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2001, 86, 6042.
17. M. A. Miller and D. Frenkel, Phys. Rev. Lett., 2003, 90, 135702.
18. A. P. R. Eberle, R. Castañeda-Priego, J. M. Kim and N. J. Wagner, Langmuir, 2012, 28, 1866.
19. N. E. Valadez-Pérez, Y. Liu, A. P. R. Eberle, N. J. Wagner and R. Castañeda-Priego, Phys. Rev. E, 2013, 88, 060302.
20. A. Zaccone, H. H. Winter, M. Siebenbürger and M. Ballauff, J. Rheol., 2014, 58, 1219.
21. C. J. Dibble, M. Kogan and M. J. Solomon, Phys. Rev. E, 2006, 74, 041403.
22. J. C. Conrad, H. M. Wyss, V. Trappe, S. Manley, K. Miyazaki, L. J. Kaufman, A. B. Schofield, D. R. Reichman and D. A. Weitz, J. Rheol., 2010, 54, 421.
23. H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367.
24. M. E. Helgeson, S. E. Moran, H. Z. An and P. S. Doyle, Nat. Mater., 2012, 11, 344.
25. M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122.
26. Y. Gao, J. Kim and M. E. Helgeson, Soft Matter, 2015, 11, 6360.
27. K. Devanand and J. C. Selser, Macromolecules, 1991, 24, 5943.
28. H. Lee, R. M. Venable, A. D. MacKerell Jr and R. W. Pastor, Biophys. J., 2008, 95, 1590.
29. Y. Gao and M. E. Helgeson, Opt. Express, 2014, 22, 10046.
30. A. P. R. Eberle, N. J. Wagner and R. Castañeda-Priego, Phys. Rev. Lett., 2011, 106, 105704.
31. M. N. Lee and A. Mohraz, Adv. Mater., 2010, 22, 4836.
32. D. R. Griffin, W. M. Weaver, P. O. Scumpia, D. Di Carlo and T. Segura, Nat. Mater., 2015, 14, 737.
33. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01581b

---