Slow magnetization dynamics in a series of two-coordinate iron(II) complexes†
Joseph M.
Zadrozny
a,
Mihail
Atanasov
*bc,
Aimee M.
Bryan
d,
Chun-Yi
Lin
d,
Brian D.
Rekken
d,
Philip P.
Power
*d,
Frank
Neese
*b and
Jeffrey R.
Long
*a
aDepartment of Chemistry, University of California, Berkeley, California 94720, USA. E-mail: jrlong@berkeley.edu
bMax-Planck Institut für Chemische Energiekonversion, Stifstr. 32-34, D-45479 Mülheim an der Ruhr, Germany. E-mail: mihail.atanasov@cec.mpg.de; frank.neese@cec.mpg.de
cInstitute of General and Inorganic Chemistry, Bulgarian Academy of Sciences, Acad Georgi Bontchev Str. 11, 1113 Sofia, Bulgaria
dDepartment of Chemistry, University of California, Davis, California 95616, USA. E-mail: power@chem.ucdavis.edu
First published on 25th October 2012
Abstract
A series of two-coordinate complexes of iron(II) were prepared and studied for single-molecule magnet behavior. Five of the compounds, Fe[N(SiMe3)(Dipp)]2 (1), Fe[C(SiMe3)3]2 (2), Fe[N(H)Ar′]2 (3), Fe[N(H)Ar*]2 (4), and Fe(OAr′)2 (5) feature a linear geometry at the FeII center, while the sixth compound, Fe[N(H)Ar#]2 (6), is bent with an N–Fe–N angle of 140.9(2)° (Dipp = C6H3-2,6-Pri2; Ar′ = C6H3-2,6-(C6H3-2,6-Pri2)2; Ar* = C6H3-2,6-(C6H2-2,4,6-Pri2)2; Ar# = C6H3-2,6-(C6H2-2,4,6-Me3)2). Ac magnetic susceptibility data for all compounds revealed slow magnetic relaxation under an applied dc field, with the magnetic relaxation times following a general trend of 1 > 2 > 3 > 4 > 5 ≫ 6. Arrhenius plots created for the linear complexes were fit by employing a sum of tunneling, direct, Raman, and Orbach relaxation processes, resulting in spin reversal barriers of Ueff = 181, 146, 109, 104, and 43 cm−1 for 1–5, respectively. CASSCF/NEVPT2 calculations on the crystal structures were performed to explore the influence of deviations from rigorous D∞h geometry on the d-orbital splittings and the electronic state energies. Asymmetry in the ligand fields quenches the orbital angular momentum of 1–6, but ultimately spin–orbit coupling is strong enough to compensate and regenerate the orbital moment. The lack of simple Arrhenius behavior in 1–5 can be attributed to a combination of the asymmetric ligand field and the influence of vibronic coupling, with the latter possibility being suggested by thermal ellipsoid models to the diffraction data.
Introduction
In the presence of axial magnetic anisotropy (D), the MS levels of a system with total spin S will split under zero magnetic field according to the Hamiltonian Ĥ = DŜz2. If D is negative, the two ±MS levels of maximal projection along the z-axis are degenerate and form a bistable ground state. Reversing the moment by converting −MS to +MS then requires traversal of a spin-inversion barrier, U = S2|D| (or U = (S2 − 1/4)|D| for non-integer S), where the system passes through the MS = 0 (or MS = ±1/2 for non-integer S) levels at the height of the barrier. The existence of this energy barrier can lead to the slow relaxation of the magnetic moment at low temperatures upon removal from a polarizing dc field. An important manifestation of this barrier is a magnetic hysteresis that is molecular in origin, as first observed for the compound Mn12O12(CH3CO2)16(H2O)4.1Molecules exhibiting such behavior are known as single-molecule magnets, and have been invoked as possible media for high-density information storage,2 quantum computing,3 and magnetic refrigeration.4 A significant effort has therefore been dedicated to the preparation and study of new systems in search of a better understanding of the various phenomena that influence single-molecule magnet behavior. These studies have led to the discovery of slow magnetic relaxation in a variety of polynuclear coordination clusters5 as well as in mononuclear lanthanide,6 actinide,7 and, most recently, transition metal complexes.8 Synthetic efforts have occurred in tandem with theoretical studies, with the latter showing the magnitude of D to decrease with increasing S, implying that the overarching goal of the discovery a single-molecule magnet with a large U should not be pursued solely in terms of maximizing S.9
Mononuclear transition metal complexes provide a fertile new platform for research in the field. Experimental techniques for characterizing their electronic structures are well established,10 and ligand field theory provides chemists with an intuitive framework for tuning the electronic properties by ligand and/or metal ion variation.11
Several classes of first-row transition metal complexes lend themselves to bearing large magnetic anisotropies. Octahedral complexes of cobalt(II) have long been known12 to display significant magnetic anisotropy as result of the orbital angular momentum of the t2g5eg2 electron configuration. This behavior extends to complexes with lower coordination numbers, for which the 3d orbital energy splittings are reduced. For example, iron(II) complexes of coordination numbers 4 and 3 have been characterized as having the magnetic signatures of orbital angular momentum.13 Furthermore, recent studies on the trigonal pyramidal iron(II) complexes [(tpaR)Fe]− have presented the ability to systematically enhance the magnetic anisotropy of the S = 2 center via increasing the electron donating abilities of the tris(pyrrolyl-α-methyl)amine ligand.8a,b Together, these observations suggest that the common principles of molecular inorganic chemistry can be utilized in the search for and design of systems with large magnetic relaxation barriers.
In our study of mononuclear transition metal single-molecule magnets, we have deliberately targeted complexes with low-coordination numbers. Here, the low coordination number supports the preparation, via appropriate ligand choice, of local coordination geometries with one principal axis of rotation of order greater than 2. This will engender orbital degeneracies that, when coupled with the appropriate number of d-electrons, produce orbital angular momentum conducive to a large magnetic anisotropy.
Although many are known,14 paramagnetic two-coordinate transition metal complexes have yet to be evaluated in detail as potential single-molecule magnets. Of particular interest are complexes displaying a rigorously linear L–M–L geometry with local D∞h symmetry at the metal center. Here, the ligand field splits the energies of the d-orbitals as (dxy, dx2–y2) < (dxz, dyz) < dz2, with the (dxz, dyz), and dz2 orbital energies being destabilized by π and σ-metal–ligand interactions, respectively. In contrast, the (dxy, dx2–y2) orbitals have δ symmetry with respect to the axial ligands and are thus not engaged in bonding. Consequently, for a d6 metal center, such as iron(II), we can expect a large first-order contribution to the orbital angular momentum that will not be quenched through a Jahn–Teller distortion.15 There are many two-coordinate complexes of iron(II) known,16 some with rigorously linear L–M–L geometries.16e,f,j,k,l,m Importantly, magnetic and spectroscopic measurements on a select few have revealed the signatures of large magnetic anisotropies.16g,j,m
Herein, we report the first detailed characterization of the magnetization dynamics for a series of homoleptic, two-coordinate iron(II) complexes of varying ligand-field donor strength, which indeed behave as single-molecule magnets. In particular, we explore the direct current (dc) and alternating current (ac) susceptibility and magnetization data for the six iron(II) complexes depicted in Fig. 1, each featuring two sterically encumbering ligands. All compounds display slow magnetic relaxation under an applied field, and the trends observed in relaxation behavior are explored using first-principles calculations within the context of ligand field theory.
![Structures of the two-coordinate iron(ii) complexes analyzed in this study: Fe[N(SiMe3)(Dipp)]2 (Dipp = C6H3-2,6-Pri2) (1), Fe[C(SiMe3)3]2 (2),16e,f Fe[N(H)Ar′]2 (Ar′ = C6H3-2,6-(C6H3-2,6-Pri2)2) (3), Fe[N(H)Ar*]2 (Ar* = C6H3-2,6-(C6H2-2,4,6-Pri3)2) (4),16m Fe(OAr′)2 (5),16l and Fe[N(H)Ar#]2 (Ar# = C6H3-2,6-(C6H2-2,4,6-Me3)2) (6).16m Orange, cyan, red, blue, and gray spheres represent Fe, Si, O, N, and C atoms, respectively; H atoms have been omitted for the sake of clarity.](/image/article/2013/SC/c2sc20801f/c2sc20801f-f1.gif) | ||
| Fig. 1 Structures of the two-coordinate iron(II) complexes analyzed in this study: Fe[N(SiMe3)(Dipp)]2 (Dipp = C6H3-2,6-Pri2) (1), Fe[C(SiMe3)3]2 (2),16e,f Fe[N(H)Ar′]2 (Ar′ = C6H3-2,6-(C6H3-2,6-Pri2)2) (3), Fe[N(H)Ar*]2 (Ar* = C6H3-2,6-(C6H2-2,4,6-Pri3)2) (4),16m Fe(OAr′)2 (5),16l and Fe[N(H)Ar#]2 (Ar# = C6H3-2,6-(C6H2-2,4,6-Me3)2) (6).16m Orange, cyan, red, blue, and gray spheres represent Fe, Si, O, N, and C atoms, respectively; H atoms have been omitted for the sake of clarity. | ||
Experimental section
General considerations
All manipulations were performed with the use of modified Schlenk techniques or in a Vacuum Atmospheres glove box under N2 or Ar. Solvents were dried and collected using a Grubbs-type solvent purification system17 (Glass Contour) and degassed by using the freeze–pump–thaw method. Unless otherwise stated, all materials were obtained from commercial sources and used as received. The compound [Fe(N(SiMe3)2)2]2 was prepared by a modified literature procedure18 from ‘activated,’ anhydrous FeCl2, which was obtained from finely powdered FeCl2·4H2O by following a similar dehydration procedure as previously reported for MnCl2.19 The compounds LiN(SiMe3)(Dipp), LiN(H)Ar*, LiN(H)Ar′, LiN(H)Ar# and HOAr′ were prepared according to literature procedures,16m,20 as was Fe[C(SiMe3)3]2 (2).16fSynthesis of Fe[N(SiMe3)(Dipp)]2 (1)
To a slurry of FeCl2 (0.70 g, 5.6 mmol) in ca. 10 mL of diethyl ether was added a solution of LiN(SiMe3)(Dipp) (3.0 g, 12 mmol) in 50 mL of diethyl ether at 0 °C. The dark brown reaction mixture was allowed to warm to room temperature and stirred for 18 h. All volatile materials were removed in vacuo and the residue was extracted with hexanes. This extract was filtered via a cannula and the dark brown filtrate was concentrated and refrigerated at −18 °C overnight to afford large, brown crystals of 1 (1.8 g, 58 %). M.p.: 209–211 °C. UV-Vis (hexane): λmax (εM, M−1 cm−1) 344 (6200) nm. IR (Nujol): νFe–N, 400 cm−1. Anal. calcd for C30H52FeN2Si2: C, 65.19; H, 9.48; N, 5.07. Found: C, 66.01; H, 9.25; N, 4.95%.Synthesis of Fe[N(H)Ar′]2 (3)
To a slurry of FeCl2 (0.12 g, 0.96 mmol in 10 mL of diethyl ether) at 0 °C was added a slurry of LiN(H)Ar′ (0.81 g, 1.9 mmol in 60 mL of diethyl ether) dropwise over 30 min. The resultant pale orange slurry was allowed to warm to room temperature and stirred for 3 days, during which time the solution darkened to red. All volatile components were removed in vacuo and the residue was extracted with hexanes (70 mL) and filtered via cannula. The solution was concentrated to ca. 40 mL and stored at −18 °C for 2 days to produce X-ray quality orange-red crystals of 3 (0.31 g, 36%). M.p.: 196-198 °C. 1H NMR (600 MHz, C6D6, 298 K): δ 7.31 (br, s, p-C6H3-2,6-Pri2), 7.22 (br, s, m-C6H3-2,6-Pri2), 6.99 (br, s, m-C6H3-2,6-Pri2), 6.83 (br, s, p-C6H3-2,6-Pri2), 2.95 (br, S, –CHMe2), 2.88 (br, s, N–H), and 1.17 (br, d, CHCH3) ppm. UV-Vis (hexanes): λmax (εM, M−1 cm−1) 449 (1190), 424 (1240), 323 (3200), and 298 (9400) nm. IR (Nujol): νN–H 3345 and νFe–N 385 cm−1. Anal. calcd for C60H76FeN2 : C, 81.79; H, 8.69; N, 3.18. Found: C, 82.64; H, 8.86; N, 2.90%.Synthesis of Fe[N(H)Ar*]2 (4)
This compound was prepared by an alternative route to a reported procedure.16m To a slurry of FeCl2 (0.25 g, 2.0 mmol) in 10 mL of diethyl ether at 0 °C was added a solution of LiN(H)Ar* (2.0 g, 4.0 mmol in 45 mL of diethyl ether) slowly over 20 min. The resultant red solution was stirred at 0 °C for 30 min then allowed to warm to room temperature and stirred for a further 3 days. All volatile components were removed in vacuo and the residue was extracted with hexanes (80 mL) and filtered via cannula. The solution was concentrated to ca. 30 mL and stored at −18 °C for 3 days to produce red crystals of 4 (0.86 g, 41%). Compound identity was confirmed via single-crystal X-ray analysis.Synthesis of Fe(OAr′)2 (5)
This compound was prepared by an alternative route to the reported procedure.16l Solid [Fe(N(SiMe3)2)2]2 (1.1 g, 1.5 mmol) was dissolved in diethyl ether (ca. 20 mL) with rapid stirring. This solution was cooled to −78 °C, and a solution of HOAr′ (2.5 g, 6.0 mmol) in diethyl ether (ca. 30 mL) was added dropwise via cannula to afford a green solution that slowly turned brown after several days of stirring. Diethyl ether was removed under reduced pressure and the resulting brown solid was extracted with 40 mL of hexanes. The extract was filtered through diatomaceous earth (Celite 545) and concentrated to ca. 15 mL under reduced pressure. This solution yielded yellow crystals of 5 (0.60 g, 23%) after storage overnight at −18 °C. The identity of the compound was confirmed by UV-Vis spectroscopy, X-ray crystallography, and elemental analysis.Synthesis of Fe[N(H)Ar#]2 (6)
This compound was prepared by an alternative route to the reported procedure.16m The reagent H2NAr# (3.8 g, 12 mmol) was treated with a 2.5 M solution of n-BuLi (5 mL, 13 mmol) in hexanes to generate a solution of LiN(H)Ar#, which was then added dropwise to a slurry of FeCl2 (0.76 g, 6.0 mmol) in ca. 20 mL of diethyl ether chilled to 0 °C. The solution was allowed to warm to room temperature and allowed to stir for 3 days, becoming dark red in the process. All volatile components were removed in vacuo and the orange residue was extracted with 40 mL of hot toluene and filtered through diatomaceous earth using a filter stick. The solution was concentrated to ca. 30 mL and stored at ca. −18 °C for 3 days to produce red crystals of 6 (3.2 g, 79%). This yield represents a significant improvement over the previously reported transamination method (39%).16m Compound identity was confirmed by single crystal X-ray analysis.Magnetic measurements
Magnetic susceptibility data were collected using a Quantum Design MPMS-XL SQUID magnetometer. Measurements for all compounds were performed on finely ground microcrystalline powders restrained in a frozen eicosane matrix within a vacuum-sealed fused silica tube. Loading of the powders into the fused silica tube was performed under an inert atmosphere. Dc susceptibility measurements were collected in the temperature range 2–300 K under a dc field of 1 kOe. Dc magnetization data were obtained in the temperature range 1.8–5 K under dc fields of 1, 2, 3, 4, 5, 6, and 7 T. Ac susceptibility measurements were obtained in a variety of temperature ranges under a 4 Oe ac field oscillating at frequencies of 0.06–1488 Hz and under applied dc fields from 0 to 5 kOe. Dc magnetic susceptibility data were corrected for diamagnetic contributions from the sample holder and eicosane, as well as for the core diamagnetism of each sample (estimated using Pascal's constants).21Single-crystal X-ray diffraction
Crystals suitable for X-ray diffraction were covered in a thin layer of hydrocarbon oil, mounted on a glass fiber attached to a copper pin, and placed under an N2 cold stream. Data for 1 and 3 were collected at 90 K on a Bruker SMART 1000 diffractometer and Bruker APEX diffractometer equipped with a Bruker APEX-II CCD using Mo Kα radiation (λ = 0.71073 Å), respectively. Absorption corrections were applied using SADABS.22 Crystal structures were solved by direct methods and refined by full-matrix least-squares procedures in SHELXTL.23 All non-H atoms were refined anisotropically, while all H-atoms were placed at calculated positions and refined using a riding model. The data obtained for 3 were best modelled assuming a partial occupancy of the Fe atom and cocrystallization with the protonated ligand H2NAr′. Cocrystallization was verified by infrared spectroscopy, which indicated a slight presence of free-amine N–H stretches. Full crystallographic tables for 1 and 3 are presented in the ESI (see Tables S1 and S2†).All other physical measurements
1H NMR data were obtained on a Varian Inova 600 MHz spectrometer. All 1H NMR spectra are referenced to an external standard of tetramethylsilane (δ = 0). IR spectra were recorded as Nujol mulls between KBR plates on a Perkin Elmer 1430 spectrophotometer. UV-Vis spectra were recorded on dilute hexane solutions in 3.5 mL quartz cuvettes using a HR2000 CG-UVNIR spectrometer with Ocean Optics DH2000 light source. Melting points were measured on samples sealed under N2 in glass capillaries with a Mel-Temp II apparatus and are uncorrected. Combustion analyses were performed by Columbia Analytical Services.Computational details
Electronic multiplets and their magnetic sublevels are highly sensitive probes to small structural variations governed by their surroundings in the crystalline phase.24 Thus, a complete theoretical account of all of the subtle influences of small distortions that occur due to crystal packing is not feasible. For this reason, ground- and excited-state energies and wave functions were calculated using geometries obtained directly from the X-ray crystal structures (see Fig. 1). Since positions of hydrogen atoms from such data are subject to large error-bars their coordinates have been optimized using DFT by freezing out the non-hydrogen atoms core and allowing H-atom relaxation only. The Complete-Active-Space Self-Consistent-Field (CASSCF) module of ORCA (to account for static correlation) together with N-Electron Valence Perturbation Theory (NEVPT2)25,26 (to account for dynamic correlation) were used to perform the calculations, in a manner detailed elsewhere.24bNon-truncated complexes 1–6 were used throughout in the calculations. It is worth emphasizing that this is essential to obtain realistic results. For the correlated calculations, basis sets of TZVP quality alongside with the corresponding auxiliary sets (TZVP/C) were used.26 In this set of calculations, only the metal d-orbitals were included in the active space.
Spin–orbit coupling (SOC) was taken into account using quasi-degenerate perturbation theory.27 In a 5E orbitally degenerate ground state SOC occurs in first order of perturbation theory, but generally to second order for orbitally non-degenerate states with S > 1/2. This leads to mixing of states which differ in their spin by ΔS = ±1, 0. Through this mixing, SOC reintroduces some orbital angular momentum into the electronic ground state that is otherwise quenched through low-symmetry. In a first step, non-relativistic multireference CASSCF wave functions in the form given by eqn (1) are calculated within the Born–Oppenheimer (BO) approximation; the upper indices SS stand for a many-particle wavefunction (configuration state function, CSF) with a spin quantum number S and spin projection quantum number MS = S.
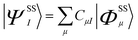 | (1) |
SOC lifts the (2S + 1) degeneracy of the total spin S ĤBO eigenfunctions. Thus, the basis for the SOC treatment are the |ΨISS > states, in which I extends to all states calculated in the first step of the procedure and MS = −S, …, +S labels all members of a given term. Matrix elements of SOC over the |ΨISMs > basis functions are easily generated making use of the Wigner–Eckart theorem, since all (2S + 1) term components share the same spatial part of the wavefunction.28 In this way, the SOC and Zeeman interactions are accounted for accurately. Specifically, the Zeeman interaction can be accounted for by diagonalization of the matrix representation of Ĥ = ĤBO + ĤSOC + Ĥz in the |ΨISMs > basis (eqn (2)).
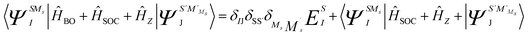 | (2) |
The complete manifold of 5 quintet and 45 triplet states were included in the calculations and SOC was accounted for by the mean field (SOMF) Hamiltonian.29 Evaluation of the matrix elements of the orbital momentum operators between the |ΨISMs > basis functions was done in terms of one-electron matrix elements within the MO basis. This procedure carries us beyond the perturbative regime and accounts for strong SOC effects to all orders. Test calculations also included the 50 singlet states but did not change the results. Similar to the procedures followed in the closely related CASSCF/CASPT2 methodology with inclusion of SOC,30 matrix elements were calculated using the state averaged CASSCF wavefunctions and NEVPT2 corrections were only included in the diagonal elements of the QDPT matrix.
Results and discussion
Syntheses and structures
With the exception of 5, all compounds were synthesized via simple salt elimination reactions, as shown in Scheme 1. The standard procedure involved slow addition of either an ether or THF solution of a freshly prepared lithium salt of LiN(C6H3-2,6-Pri2)(SiMe3), LiC(SiMe3)3, or LiN(H)Ar′,*,# to one of freshly dehydrated FeCl2 that was chilled to −78 or 0 °C. In the cases of 1, 2, and 4, the color change of the reaction mixture was immediate, whereas the less bulky aryl amide (as used in the synthesis of 3) darkened upon slow warming to room temperature.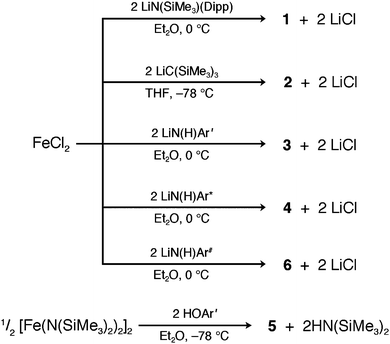 | ||
| Scheme 1 Synthetic routes to 1–6. | ||
The syntheses of 3, 4 and 6 presented here differ from the previously published transamination method, which treated [Fe(N(SiMe3)2)2]2 with 2 equiv. of the respective primary amine.16m In light of the recent publication of the cobalt(II) and nickel(II) analogues of 4 and 6, which were obtained via salt elimination in good yields,31 compounds 3, 4 and 6 were synthesized analogously, with yields nearly double those of the transamination results.
Complex 5 was synthesized through the reaction of [Fe(N(SiMe3)2)2]2 with two equivalents of the respective bulky phenol ligand. Here, an ether solution of the ligand was added slowly to an ether solution of [Fe(N(SiMe3)2)2]2 at −78 °C, and upon warming to room temperature, the resulting solution slowly changed from green to brown after several days of stirring. Overall, the process is similar to the transamination approach used to prepare 4 and 6 in previous studies. This route differs from the previously reported synthetic route to 5, accomplished via O2 insertion into the Fe–C bonds of the diaryl complex Fe(Ar′)2.16l
All solutions were stirred for ca. 3 days to ensure completeness of the reaction, and, upon workup, the products were obtained as crystals and characterized by single-crystal X-ray analysis. The structures of 1–6 are illustrated in Fig. 1, and some important interatomic distances and angles are listed in Table 1. For compounds 1–5, the Fe atom resides on a crystallographic inversion center, resulting in strictly linear L–Fe–L moieties. Compound 6, in contrast, exhibits a bent coordination geometry, with an N–Fe–N angle of 140.9(2)° and local C2v symmetry at the Fe atom.
| 1b | 2 | 3b | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| a Denotes zero error because the Fe atom lies on a special position. b Full crystal tables can be found in the ESI.† | ||||||
| Fe–L (Å) | 1.853(1) | 2.045(5) | 1.893(1) | 1.902(1) | 1.947(1) | 1.911(3) |
| L–Fe–L (°) | 180a | 180a | 180a | 180a | 180a | 140.9(2) |
| Fe⋯Fe (Å) | 8.823(2) | 8.925(4) | 10.894(2) | 11.696(1) | 11.156(1) | 9.297(2) |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
C2/c | P21/n | P21/n | P21/n |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
As observed in the crystal structures, Fe–N and Fe–O distances are in general shorter than those found for iron(II) complexes with higher coordination numbers. While this could indicate greater Fe–L covalency for the lower coordinate species, there are no ionic radii for 2-coordinate metal ions published,32 so a strict comparison of bond distances to the sums of ionic radii is not possible. Covalent radii for Fe, N, C, and O have been reported as 1.16, 0.71, 0.75, and 0.63 Å, respectively,33 which provide Fe–N, Fe–C, and Fe–O distances of 1.87, 1.91, and 1.79 Å, respectively. The numbers compare reasonably well with the observed distances, although the differences from the calculated values hint at the influence of steric repulsion in determining the Fe–L bond distances in this class of compounds. The Fe–N distances in 1, 3, 4, and 6 (1.8532(13), 1.8937(18), 1.9017(14), and 1.911(3) Å, respectively) are comparable to those reported for Fe[N(SiMe2Ph)2]2 (1.903(7) Å), Fe[N(SiMePh2)2]2 (1.917(2) Å), Fe[N(C6H2-2,4,6-Me3)B(C6H2-2,4,6-Me3)2]2 (1.938(2) Å) and Fe[N(t-Bu)2]2 (1.879(2) Å).16a,b,c,j Complex 1 has an unusually short Fe–N bond, while, 2, which possesses significant steric bulk adjacent to the metal center, displays a Fe–C distance of 2.045(5) Å—much greater than the simple difference in size between N and C atoms. In addition, it should be noted that the origin of the planar Fe[N((Cipso)(Si))]2 array of C2h symmetry in 1 may be due to a combination of packing and Fe–N π-bonding effects.
In the crystalline state, the metal atoms are well separated from one another in all of the structures, with the closest Fe⋯Fe separation being 8.823(4) Å, as observed in 1 (see Table 1). None of the structures exhibit hydrogen bonding contacts that would encourage significant long-range magnetic interactions. Interactions between the π-clouds of the aromatic ligands are other possible mediators of long-range magnetic coupling, and such interactions presumably require close contacts between the carbon atoms of co-facial aromatic moieties. Only the structures of 1, 4, and 6 suggest any possible π interactions of this type. While portions of the ligands of 1 and 4 have the necessary alignment for π-stacking, the rings are rather well separated with minimum C⋯C distances of 4.766(11) and 5.696(2) Å, respectively. In contrast, portions of the ligands of complex 6 do possess the necessary alignment together with a relatively short C⋯C contact of 3.203(6) Å.
Thermal ellipsoid plots from the structures of 1–5 feature significant anisotropic displacement parameters perpendicular to the L–Fe–L axis (see Fig. S1†). Dynamic vibronic behavior could explain this observation, as a result of Renner–Teller coupling. This possibility will be further explored in the accompanying manuscript.15 Another possible explanation is that 1–5 are slightly bent and disorder about the special position gives the illusion of a linear structure accompanied by vibronic activity. Differentiation between these two cases would be possible by variable temperature diffraction experiments, which are beyond the scope of this paper, thus, our references to the thermal ellipsoids are, at this point, speculative. We note, however, that 6, which is not situated on a position of inversion symmetry, also shows thermal ellipsoids of the necessary orientation to suggest vibronic activity.
Static magnetic properties
Variable-temperature dc magnetic susceptibility data for compounds 1–6 indicate high-spin (S = 2) iron(II) centers with varying magnitudes of magnetic anisotropy (see Fig. 2). Landé g-values were extracted from the values of χMT at room temperature, and provide a more quantitative measure of the magnetic anisotropy by the magnitude of their deviation from the isotropic value of g = 2.0023. As listed in Table 2, the values obtained range from 2.53 to 1.96 and follow the order: 2 > 1 > 3 > 4 > 5 > 6. Notably, the g-values observed for linear complexes 1–5 are in general greater than the isotropic value, while 6, which possesses a bent L–Fe–L angle, has a g-value slightly below 2.0023.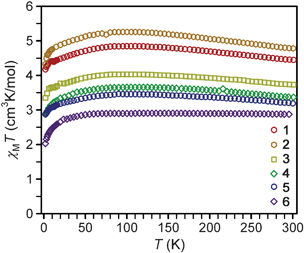 | ||
| Fig. 2 Variable temperature magnetic susceptibility data collected on restrained microcrystalline samples of 1–6 under an applied dc field of 1 kOe. The expected spin-only value of χMT for S = 2 is 3.0 cm3 K mol−1. | ||
| Compound | g | P σ | M sat (μB) |
|---|---|---|---|
| a Determined from χMT at 300 K. b Degree of non-superimposability; see ESI† for details regarding this parameter. c Saturation magnetization, as determined from magnetization data collected at 1.8 K and 7 T. | |||
| 1 | 2.44 | 0.029 | 3.00 |
| 2 | 2.53 | 0.027 | 3.24 |
| 3 | 2.23 | 0.013 | 2.74 |
| 4 | 2.13 | 0.062 | 2.14 |
| 5 | 2.06 | 0.005 | 2.06 |
| 6 | 1.96 | 0.135 | 1.93 |
As the temperature is lowered, compounds 1–5 exhibit an increase in the χMT value, reaching a maximum near 100 K. After this maximum, there is a gradual decrease in χMT as the temperature is lowered, eventually reaching a minimum at 2 K. The extent of the increase in χMT at the maximum relative to the 300 K value is largest for 1 and 2, but somewhat less pronounced in 3–5. In contrast, complex 6 displays a relatively constant χMT value at higher temperatures. In the absence of magnetic anisotropy or exchange coupling, the magnetic moment of a transition metal ion will display Curie behavior, with χMT remaining invariant with temperature at a magnitude corresponding to the Curie constant. Alternatively, systems that possess magnetic anisotropy can be expected to display some temperature dependence for χMT which reflects the changing Boltzmann populations of their respective low-lying magnetic states.34 The rise in χMT as the temperature decreases from 300 to 100 K thus also likely mirrors the presence of magnetic anisotropy. The low temperature maxima, however, are atypical for a χMT plot of a complex with spin-only magnetic anisotropy (D), where a monotonic decrease in χMT with decreasing T is instead the common observation.12 Contrastingly to 1–5, the data for complex 6 do not show such a rise, likely due to quenching of the magnetic anisotropy by the bent N–Fe–N angle. At the lowest temperatures, all plots display a monotonic decrease in χMT. Such a decrease is perhaps also attributable to magnetic anisotropy, but could also be due to long-range antiferromagnetic interactions between molecules (possibly via π–π interactions in 1, 4, and 6) and/or magnetic saturation (the Zeeman effect) at the very lowest temperatures.
Low-temperature magnetization data for 1–6 reveal saturation at Msat = 3.00, 3.24, 2.74, 2.14, 2.06, and 1.93 μB, respectively (see Fig. S2–S7†). These values are much lower than the 4 μB that would be expected for a spin-only S = 2 center. Such differences are typical for a measurement of randomly oriented highly anisotropic species. Previous magnetization studies16g,m of 2, 4, and 6 afforded higher values of Msat (5.82, 4.79, and 3.40 μB, respectively) than observed here. Differing sample restraints, as well as the observation of O2 contamination in the previous measurements, may be influencing the absolute magnitudes of these values, but the general trend observed, as well as the shapes of the χMT plots for 2 and 4, are at least consistent with the results reported here.
The field and temperature dependence of low-temperature magnetization data can be fit to quantify the axial (D) and transverse (E) magnetic anisotropies of a compound. To probe these values, variable-temperature magnetization data were collected for 1–6 at applied dc fields of 1, 2, 3, 4, 5, 6, and 7 T (see Fig. S2–S7†). In general, isotropic systems will produce a set of variable-temperature magnetization data at one field (termed an isofield line) that will be superimposable with the Brillouin function12 for a given S and g. Further, isofield lines collected at different fields for an isotropic system will all be superimposable upon the same Brillouin function when plotted versus H/T. In contrast, anisotropic moments can produce isofield lines that are non-superimposable with a single Brillouin-like curve. Complexes 1–4 and 6 all produce non-superimposable isofield lines consistent with the latter case, confirming dominant magnetic anisotropy. Complex 5, in contrast, produces isofield lines that are superimposable to a single line, although not to the Brillouin curve (see ESI†). The degree to which the magnetization were superimposable to a Brillouin like curve was quantified by the index Rσ, which represents an error with respect to the derived curve (further details are again provided in the ESI†). Complexes 1–4 and 6 display Rσ values of greater than 0.13, signaling non-superimposability, while 5 has a smaller Rσ of 0.005, indicating a high degree of superimposability of the isofield lines. This parameter does not follow any apparent trend across the series of complexes. Complex 5, which is a linear molecule and should be expected to be highly anisotropic, produces isofield lines that seem to suggest isotropic behavior. In contrast, 6, which is bent and expected to be approximately isotropic, instead shows a large Rσ, suggesting the presence of significant magnetic anisotropy.
In an attempt to quantify the magnetic anisotropy of complexes 1–6, ANISOFIT 2.0 (ref. 35) was used to try and fit the magnetization data employing a Hamiltonian incorporating the axial (D) and transverse anisotropy (E) of an S = 2 center:
| Ĥ = DŜz2 + E(Ŝx2 − Ŝy2) + gisoμβSH | (3) |
No acceptable fits were possible with this model for the entire series of compounds. Here, an untenable assumption of the model Hamiltonian is probably the cause. A description of the system with D and E assumes that the ground magnetic states are characterized as spin-only and that any anisotropy is due to the interaction between the ground spin-only state and unpopulated excited states. For a rigorously linear L–Fe–L angle, however, the ground state is expected to display a significant unquenched orbital component to its magnetization. Upon bending, this orbital component is expected to be quenched, making it somewhat surprising that the data obtained for 6 could not be fit using eqn (3). The second assumption made by the model Hamiltonian is that g is isotropic. Linear iron(II) complexes have been shown both experimentally and theoretically to possess highly anisotropic g-tensors as result of their orbital moments.16m,36
Taken together, the results from the χMT and magnetization data indicate that the two-coordinate iron(II) complexes 1–6 all have highly anisotropic magnetic moments. The inability to fit the magnetization data, as well as the shapes of the χMT plots, further suggest that the magnetic anisotropies of these compounds cannot be attributed to spin-only phenomena.
Dynamic magnetic properties
Ac magnetic susceptibility measurements were performed for complexes 1–6 to probe the low-temperature magnetic relaxation behavior of the highly anisotropic magnetic moments. Within the frequency range 0.1–1500 Hz, all of the compounds were found to display fast magnetic relaxation under zero applied dc field. This is likely attributable to ground state magnetic tunneling, as usually observed for mononuclear iron(II) systems.8a–d We note, however, that slow magnetic relaxation has been previously observed for compound 2 under zero applied dc field using Mössbauer spectroscopy,16g which probes magnetic relaxation on a much faster time scale. For all complexes, application of a small dc field slows the magnetic relaxation sufficiently to afford a nonzero signal in the out-of-phase ac susceptibility (χM′′) (see Fig. 3, 4, and S8–S13†). For complexes 1–5, well-resolved peaks appear in the plots of χM′′ versus ac field switching frequency, with maxima that shift in frequency with applied dc field strength. In contrast, only tails of peaks at high frequency are apparent for 6 under an applied dc field, and the magnetic relaxation never slowed enough for the peak maxima to fall within the frequency range of our magnetometer. Fits of the frequency dependence of the in-phase (χM′) and out-of-phase (χM′′) ac susceptibility to a generalized Debye model37 were performed to determine the dc field dependence of the magnetic relaxation time (τ) for the complexes (see Fig. 3, 4, and S8–S13†). For each compound, τ increases from H = 0 Oe to a maximum value at some field strength denoted Hτ,max (see Table 3). At dc fields greater than this value, the relaxation time begins to decrease again. For 1 and 2, τ begins to increase again when Hdc is roughly 1 kOe greater than Hτ,max. The τ values observed for complexes 3, 4, and 5, however, continue to decrease at these higher dc field strengths.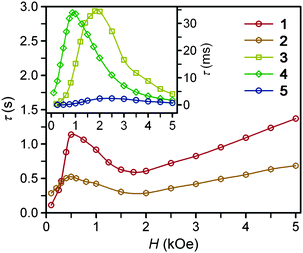 | ||
| Fig. 3 Field dependence of the magnetic relaxation time, τ, at 2 K for restrained microcrystalline samples of 1–5. | ||
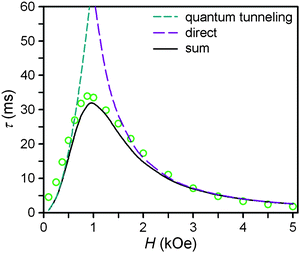 | ||
| Fig. 4 Field dependence of the magnetic relaxation time, τ, at 2 K for a restrained microcrystalline sample of 4. The dashed cyan and purple lines correspond to the contributions to the relaxation time from the zero-field tunneling and direct relaxation processes, as discussed in the text. The solid black line corresponds to the weighted sum of the two processes. | ||
| Compound | H τ,max (Oe) | τ (s) at 2 K | AH 2 , (s−1 K−1) | B 1 (s−1) | B 2 (T−2) | C (s−1 K−5) | τ 0 (s) | U eff (cm−1) |
|---|---|---|---|---|---|---|---|---|
| a Obtained at Hdc = Hτ,max. b Determined from fitting the H-dependence of τ for 1–5. c Calculated with H = Hτ,max, where Hτ,max is in units of Teslas. d Parameters for Raman exponent n = 5. e Parameters for Raman exponent n = 4; C is in units of s−1 K−4. | ||||||||
| 1 | 500 | 1.14 | 0.12 | 40.02 | 22933 | 0.003 | 1 × 10−11 | 181 |
| 2 | 500 | 0.52 | 0.265 | 3.35 | 570 | 0.005 | 4 × 10−9 | 146 |
| 3 | 1800 | 0.035 | 9.04 | 8.92 × 1012 | 1.72 × 1013 | 0.011 | 5 × 10−9 | 109 |
| 4 | 875 | 0.034 | 6.00 | 220 | 1560 | 0.473e | 4 × 10−8e | 104e |
| 5 | 2500 | 0.002 | 122.5 | 4.89 × 1012 | 3.94 × 1011 | 0.152 | 3 × 10−7 | 43 |
At zero applied dc field, fast spin-reversal between the ±MS levels occurs via resonant quantum-mechanical tunneling processes, which can be mediated by transverse anisotropy (E), dipolar interactions, or nuclear hyperfine coupling, any of which can serve to mix the ground ±MS levels.38 Upon application of a dc magnetic field, however, the degeneracy of the ground ±MS levels is split, reducing the degree of mixing and mitigating the quantum tunnelling process. Slow magnetic relaxation is therefore induced, as the moments now have to traverse a thermal activation barrier in order to reverse direction. At higher fields, however, magnetic relaxation can become fast again by the emergence of a separate spin-reversal pathway, the direct relaxation process,39 which can occur between the non-degenerate ±MS levels, provided the corresponding energy of the transition can be released as a phonon. Quantum tunnelling and direct moment reversal processes, which allow the spin to flip without traversing the energy barrier, display different dependences upon the strength of the applied dc field. Eqn (4) was employed to model the field dependence of τ for 1–5, in a manner analogous to that previously utilized for a polynuclear single-molecule magnet.40 In this expression, the first term represents the direct process, while the second corresponds to the zero-field tunnelling process. The competition between these two spin reversal pathways gives rise to the maxima displayed in Fig. 3 and 4.
The maxima in Fig. 3 suggest two field-dependent regimes for the slow magnetic relaxation: lower dc field, where resonant quantum tunnelling is suppressed and therefore moment reversal becomes slow, and higher dc field, where direct relaxation becomes dominant and spin reversal again becomes rapid (see Fig. 4 and S14†). Approximate fits to the data for compounds 3–5 can be obtained using eqn (4), yielding values for A, B1, and B2, as enumerated in Table 3. In contrast, the τ versus H plots for 1 and 2 are complicated by the rise in τ with H values greater than 2 kOe, which cannot be modelled using eqn (4). The
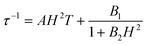 | (4) |
The temperature dependence of the relaxation time provides an invaluable experimental probe of the processes responsible for spin reversal in a magnetic system. The magnetic relaxation times for 1–6 were therefore evaluated by measuring the frequency dependences of χM′ and χM′′ over a range of temperatures (see Fig. 5 and S15–S24†). These data were then used to construct the Arrhenius plots in Fig. 6. For 1–5, the magnetic relaxation times are approximately temperature-independent at very low temperatures and then become increasingly temperature dependent above 5 K. An absence of temperature dependence for τ suggests that the spin reversal occurs due to a quantum tunneling process that does not require the input or release of energy to proceed. Temperature dependence of τ, however, signifies that the spin reversal process requires the exchange of energy with lattice vibrations. In particular, an exponential temperature-dependence indicates that absorption of phonons is promoting the moments of the complexes from the ground state to the height of the energy barrier. This “over-barrier” spin reversal pathway (Orbach relaxation41) will produce a linear plot of ln(τ) versus 1/T, where the slope corresponds to the effective spin reversal barrier, Ueff, and the y-intercept yields the inverse of the attempt relaxation time, τ0−1. In contrast, when τ is proportional to T or Tn, “through-barrier” direct (n = 1) and Raman (n ≥ 4) spin reversal processes39,41 are presumed operative. Unlike an Orbach relaxation process, these latter two processes produce curvature in an Arrhenius plot. Thus, in Fig. 6 we see evidence of significant direct and Raman spin-reversal processes. To quantitatively compare the respective influences of the above three relaxation processes, the temperature-dependent relaxation time profiles of 1–5 were fit as a sum of the contributions of the quantum tunneling, direct, Orbach, and Raman relaxation mechanisms. The expression used to model the data in Fig. 6, for example, is given as eqn (5).
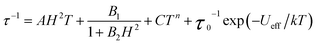 | (5) |
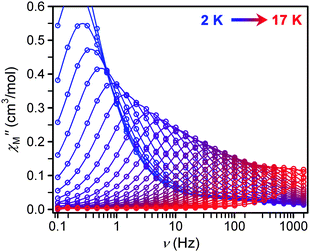 | ||
| Fig. 5 Frequency dependence of χM′′ for 1 as a function of temperature under a 500 Oe dc field from 2 to 17 K in 0.5 K intervals. | ||
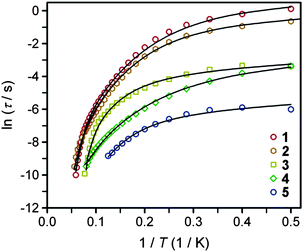 | ||
| Fig. 6 Arrhenius plots of the temperature dependences of τ for compounds 1–5. Black lines represent fits to multiple relaxation processes, as discussed in the text. | ||
In view of the many unknowns in eqn (5), we sought to avoid possibly meaningless fits as result of overparameterization. The field-dependent τ data for 1–5, which were successfully modeled using eqn (4), were relatively insensitive to the inclusion of the Orbach and Raman terms in eqn (5). In contrast, inclusion of the Orbach and Raman processes in modeling the temperature dependence of τ proved essential for describing the relaxation behavior at the lowest temperatures. Thus, the values of A, B1, and B2 were taken from fits to the data presented in Fig. 3, and were then used in modeling the Arrhenius plots. Values of C, τ0 and Ueff were then obtained from the best fit of the Arrhenius plots (see Table 3). In the course of fitting attempts, we noticed that the Raman exponent, n, best fit 1, 2, 3, and 5 with the value of 5, as expected for integer-spin systems with low-lying excited states,41c while n = 4 afforded a much better fit for compound 4. In line with the decreasing relaxation times at 2 K from 1 to 5, the value of Ueff decreases across the series. The contributions of the direct and Raman processes also increase from 1 to 5, as evidenced by increasing magnitudes of A and C. The physical significance of the coefficients A and C is not easily intuited, as both values depend on variables such as the crystal density, the speed of sound in the solid, and the strength of the interaction of the spin system with the phonons.41a,b At a most basic level, the increase in A and C across 1 to 5 is a reflection of an increasing prevalence of a through-barrier spin-reversal mechanism under the applied fields, and is also manifest in the drop in τ at 2 K from 1 to 5. Significantly, the Ueff values of as high as 181 cm−1 obtained for 1–4 are the largest yet observed for mononuclear iron(II) complexes, with the previous record corresponding to 100 cm−1 for [(C5Me5)Fe(2,6-Pri2-C6H3)].8c We further note that the values of τ0 obtained are in the typical range observed for single-molecule magnets.
Ligand field description of D∞h iron(II) complexes
In the absence of intermolecular interactions, slow magnetic relaxation in mononuclear complexes is governed by the lowest energy magnetic states that stem from their respective electronic configurations. To better understand the magnetic relaxation in these complexes, we therefore explored the electronic structures 1–6 by computational methods. Under a local D∞h ligand field, the d orbital energies split into δg (dxy, dx2–y2), πg (dxz, dyz), and σg+ (dz2) sets. The characters of these sets with respect to the ligand orbitals are non-bonding, π-antibonding, and σ-antibonding, respectively. Hence, they are listed in order of increasing energy if the ligand is capable of π- and σ-donation. The ordering of the πg and σg+ energies can invert if there is prominent s–d mixing for the metal orbitals. In either case, the pair of δg orbitals remains lowest in energy and non-bonding. A high-spin d6 ion in this coordination environment is therefore expected to have a large magnetic anisotropy as result of the triply occupied δg set and the resulting first-order contribution to the orbital angular momentum.For a d6 ion in D∞h geometry, the (δg)3(πg)2(σg+)1 electronic configuration yields a ground 5Δ state characterized by an unquenched orbital angular momentum with ML = 2. One-electron excitations from the δg to the πg and σg+ orbitals, respectively, generate the electronic configurations responsible for the 5Π and 5Σ excited states. The 5Π state possesses orbital angular momentum (ML = 1), while the 5Σ+ state does not. Spin–orbit coupling serves to split the 5Δ ground state into spin–orbit coupled MJ sublevels with energies dictated by the strength of the spin–orbit coupling constant of the iron(II) center (ζ ≈ 400 cm−1 for the free Fe2+ ion).10–12 This splitting of the MJ energies is similar to the divergence of the energies of MS sublevels under the action of a negative D, whereby the ±MJ sublevels with maximal projection along the z-axis constitute a bistable ground state. In this case the magnitude of the spin reversal barrier, U, is governed by ζ, and the calculated value is U = 2ζ. Given the fact that ζ is much greater than even the largest reported D values,42–44 a simple ligand field description of compounds 1–5 predicts that they should have very large spin reversal barriers, on the order of 800 cm−1.
The foregoing description of the electronic structure has been successfully applied to the interpretation of the UV-Vis absorption spectra of metal dihalide complexes in the gas phase,45 where the MX2 geometries are purported to be linear on the basis of a variety of spectroscopic evidence.46 Here, the lone pairs of the chloride ions are related by symmetry and interact indistinguishably with the d orbitals of the metal ion, providing ideal D∞h symmetry. We took this model as a starting point for assessing the ligand fields of the linear iron(II) complexes and, ultimately, for understanding the origins of the slow magnetic relaxation.
Ligand field description of linear iron(II) complexes with lower-symmetry ligand fields
For the linear complexes investigated here, we hypothesized that the varying orientations of the lone pairs of the ligand donor atoms could disrupt the rigorous axial symmetry of the L–Fe–L moiety, leading to an asymmetry in the x and y directions (the z direction here is defined as the L–Fe–L axis). This lower-symmetry ligand field could relax the symmetry-required nonbonding character of the δg (dxy, dx2–y2) orbitals by allowing mixing between the (dxy, dx2–y2) orbitals and the dxz, dyz, and dz2 orbitals. The dxy and dx2–y2 orbitals resulting from this interaction could have enough dxz, dyz, or dz2 character such that their respective interactions with the asymmetric ligand field would split the (dxy, dx2–y2) orbital degeneracy and quench the associated orbital angular momentum.First-principles computational techniques were utilized to study the effect of the xy-asymmetry on the low-energy electronic structures of complexes 1–5. Calculations were also performed on 6 to study the effect of the bent L–Fe–L angle, and on another known linear two-coordinate Fe(II) complex, Fe[N(t-Bu)2]2,16j for comparison. Monoconfigurational DFT methods were avoided owing to the orbital degeneracy of the 5Δ ground state of the linear, 3d6 FeII center. Instead, CASSCF and NEVPT2 methods were employed with the ORCA electronic structure package.26
The 3d6 configurations of the FeII centers in complexes 1–6 and Fe[N(t-Bu)2]2 each give rise to 5 quintet states with NEVPT energies, computed using the crystal structure geometries, as depicted in Fig. 7. Further details on these calculations can be found in the subsequent paper.15 For the present system, the five lowest energy states are mapped onto d-orbital energies, provided one takes the ground dxy orbital as an energy reference point. Thus, the energies given in Fig. 7 represent not only the splitting of the multi-electron states in the lower-symmetry ligand field, but also that of the d orbitals. In the following discussion, we refer to the state labels primarily, but also list the orbital labels, as done in Fig. 7.
![Calculated quintet energy states of 1–6 and Fe[N(t-Bu)2]2 with structures taken from X-ray diffraction data. The symmetry labels correspond to D3 point group notation. As discussed in the text, the energies of the depicted quintet states can be mapped to d-orbital energies. The orbitals corresponding to each quintet state are labeled in parentheses.](/image/article/2013/SC/c2sc20801f/c2sc20801f-f7.gif) | ||
| Fig. 7 Calculated quintet energy states of 1–6 and Fe[N(t-Bu)2]2 with structures taken from X-ray diffraction data. The symmetry labels correspond to D3 point group notation. As discussed in the text, the energies of the depicted quintet states can be mapped to d-orbital energies. The orbitals corresponding to each quintet state are labeled in parentheses. | ||
The ground states of all complexes are S = 2 quintet (hereafter given in D3 symmetry notation, as would apply to complex 2) states with energies that are 15200–20600 cm−1 lower than the first 3A excited states. Fe–L σ- and π-interactions, resulting from the non-rigorous D∞h symmetry, split the degeneracy of the 5E(dxy) and 5E(dx2–y2) states. The splitting is just 90 cm−1 for 2, and increases to 235 cm−1 for 3 and 369 cm−1 for 4, and becomes as large as 1188 cm−1 for the bent complex 6. The splittings of 158 and 218 cm−1 for complexes 1 and 5, respectively, are intermediate between those of 2 and 3, such that a monotonic increase across the series is not observed. Interestingly, the splitting of 766 cm−1 for the 5E(dxy) and 5E(dx2–y2) states in Fe[N(t-Bu)2]2 is large compared to that of the other linear compounds, and second only to the bent complex 6. Also of note is that the 5A(dz2) state is in the same energy range as the 5E(dxz) and 5E(dyz) states.
As depicted in Fig. 8, spin–orbit coupling splits the 5E(dxy) ground state into five pairs of spin–orbit coupled magnetic sublevels, corresponding to different linear combinations of the spin and orbital angular momenta. The asymmetric ligand field in turn splits these pairs. However, for all complexes included in this study, such splitting of the spin–orbit coupled states by asymmetric π-interactions is negligible, except for the 2E state (MS = 0, ML = 2), shown in red in Fig. 8, which is highly sensitive to the low symmetry of the ligand field. Complexes 1 and 2 display the smallest splitting of the 2E state, and this splitting increases across the series, becoming very large for 6 and Fe[N(t-Bu)2]2. Additionally, in moving across the series, the energy separation between the ground 1E sublevels (blue in Fig. 8) and the first excited {1A1, 1A2} sublevels (purple in Fig. 8) decreases from 191 cm−1 for 1 to 122 cm−1 for 6.
![Spin–orbit coupled splitting of the ground 5E state, calculated for complexes 1–6 and Fe[N(t-Bu)2]2. Symmetry labels are according to D3 notations. Energies are given as numerical values in the following paper.15](/image/article/2013/SC/c2sc20801f/c2sc20801f-f8.gif) | ||
| Fig. 8 Spin–orbit coupled splitting of the ground 5E state, calculated for complexes 1–6 and Fe[N(t-Bu)2]2. Symmetry labels are according to D3 notations. Energies are given as numerical values in the following paper.15 | ||
The ab initio results are readily interpreted starting from the D∞h electronic structure and considering the xy-asymmetry and the spin–orbit coupling as perturbations on the ligand field states. In contrast to ideal D∞h symmetry, we see in Fig. 7 that the non-rigorous axial symmetry imposed by the lone pairs of the ligand donor atoms of 1–5 and Fe[N(t-Bu)2]2 relaxes the non-bonding character of the δg (dxy, dx2–y2) orbitals, causing them to split in energy. This is expected to quench the orbital angular momentum of the compounds. This would in turn minimize the magnetic anisotropy, promoting faster magnetic relaxation times. A dramatic example of this effect occurs in 6, where the bent L–Fe–L angle strongly splits the δg orbitals, and as result 6 displays the fastest magnetic relaxation times of the series at low temperature. We emphasize again that the 5A(dz2) state (5Σ+ in D∞h notation) is comparable in energy to the 5E(dxz) and 5E(dyz) states (5Π in D∞h notation). This is a direct manifestation of s–d mixing which serves to weaken the antibonding character of the FeII 3dz2 orbital. This could, in part, contribute to the relatively short Fe–N bond distances observed in the crystal structures of 1–5 compared with higher-coordination number complexes, where in the latter case electrons occupy strongly antibonding orbitals.
In comparison with the spin–orbit coupling, the influence of the ligand field asymmetry is relatively weak. Here, by virtue of a suitably weak ligand field, the electronic structures of these 3d transition metal complexes are similar to those observed for many lanthanide and 5d transition metal complexes, where the spin–orbit coupling is comparable with or stronger than the influence of the ligand field.
Correlation of ab initio results with relaxation dynamics
The magnetic properties of mononuclear transition metal complexes are by and large dictated by the relative energy spacings of the lowest lying magnetic sublevels in addition to the angular momenta associated with each of these sublevels. As the surrounding ligand field strongly influences the energies and spins of the sublevels of a transition metal complex, it is expected that the ligands, through their electron donating/withdrawing abilities and/or their spatial arrangement, are predominantly responsible for the magnetic properties of the complex. In both the experimental8a,b and theoretical24a,b studies of the magnetic properties of the [(tpaR)Fe]− series of complexes, the magnetic anisotropies and spin reversal barriers were found to correlate to the Lewis basicity of the tpaR ligand. This same observation is not present here, where the magnetic behaviors do not appear to follow a trend based on the ligand-field strength of the donor atoms. For example, 3 and 4, which should have nearly identical ligand field strengths, exhibit different relaxation behaviors, and the ab initio results indicate a significant difference in the relative energy spacings of their low lying magnetic sublevels. Additionally, 3 and 5, which are the same except for their respective NH and O donor moieties, possess similar splitting in Fig. 8, yet their respective relaxation behaviors are very different. Rigorous axial symmetry about the iron could be envisioned to enhance the slow magnetic relaxation, but 2, which has relatively high D3d molecular symmetry, is not a better SMM than 1, which is of lower C1 symmetry. Furthermore, the computational results indicate that there is not a large energetic difference in the spin–orbit coupled sublevels between 1 and 2, which seems to downplay the importance of symmetry in dictating the magnetic relaxation properties for these compounds, if only the spacings of the sublevels present in Fig. 8 are directing the low temperature magnetization dynamics. We note, however, that 2 shows slow magnetic relaxation at zero field in the Mossbauer spectrum, while 4, 6, and Fe[N(t-Bu)2]2 only do so under modest applied dc fields, suggesting that symmetry may have greater influence on the magnetization dynamics at zero applied dc field.The spin reversal barriers of mononuclear systems often appear to correlate to the energy requirement for excitation to the first excited MS or MJ sublevel.6a,g,j,8b,47 In the present series of complexes, therefore, the ab initio results predict Ueff values corresponding to the excitation from the 1E ground state to the {A1, 1A2} set of states depicted in Fig. 8. Complex 1 does not deviate far from the predicted behavior, and possesses a Ueff (181 cm−1) in reasonable agreement with the energy separation between its ground and first-excited spin–orbit coupled state (191 cm−1). Across the series, this separation appears to decrease, thus, if dominant Orbach spin reversal invoking the first excited spin–orbit coupled state were observed for all compounds, one would expect the observed Ueff values to follow the trend 1 > 2 > 5 > 3 > 4 > 6. While Ueff indeed decreases across the series in qualitative agreement with the ab initio results, it does so at a quicker pace than the gap between the 1E and {A1, 1A2} states. Thus, factors other than simply the 1E to {A1, 1A2} energy gap are influencing the barrier magnitude involved in the Orbach process.
One such factor could be the dynamic vibrational activity of the iron(II) coordination sphere in the crystalline state. A bent L–Fe–L angle strongly influences the energies of the magnetic sublevels as demonstrated in the ab initio results for 6, where a bent L–Fe–L angle yields the largest splitting of the dxy and dx2–y2 orbitals and hence the strongest quenching of the orbital angular momentum. If dynamic activity were occurring, its subtle effects could easily be overlooked, given that the L–Fe–L angles are linear as depicted in the crystal structures. A preliminary inspection of the thermal ellipsoids of 1–5 suggests that dynamic movement in the crystalline state may be present. As shown in Fig. S1,† all structures feature thermal ellipsoids for the Fe atom with significant anisotropic displacement oriented away from the L–Fe–L axis, suggestive of dynamic bending vibrations. As evidenced by complex 6, which in this context represents a snapshot of a complex with a high degree of distortion, a bent L–Fe–L angle is accompanied by fast magnetic relaxation.
Given the Ueff predictions from the ab initio computations (191, 196, 178, 161, 185, and 82 cm−1 for 1–6 respectively) one may expect Arrhenius plots of 1–5 to be indicative of dominant Orbach relaxation and very large spin reversal barriers. Hypothetically, such behavior would be expected at zero applied dc field, in the absence of the zero-field tunneling process and possible vibronic influences. An applied dc field, however, is required to observe slow magnetic relaxation for all complexes, and, as evidenced by our analysis, while the applied field disrupts the tunnelling process, it also enhances the direct process. Thus, all compounds produce highly curved Arrhenius plots from the influence of spin reversal relaxation pathways other than the Orbach process. Over most of the temperatures of the measurements (<20 K, kT = 13.9 cm−1), phonons of the necessary energy for excitation to the first excited MJ sublevels are likely very scarce. Thus, spin reversal by thermally activated relaxation mechanisms (Orbach) can be expected to be less favorable than the field-induced direct relaxation processes, as well as multi-phonon relaxation processes (Raman), neither of which require relatively high-energy phonons for spin-reversal. The foregoing argument implies that there may be a limit to the energy separation between the ground and first excited MJ levels if one is to observe Orbach relaxation behavior under applied dc fields. If the separation is above this limit, faster relaxation mechanisms take over since the first excitation requires much more energy than is available from phonons. This is a key observation, because many efforts to produce mononuclear transition metal single-molecule magnets with larger barriers have been guided by the belief that increasing the energy of the first excitation would necessarily result in larger magnetic relaxation barriers.
The direct and Raman relaxation processes, which may be interfering with the observation of the Orbach process under an applied field, are highly dependent upon the interactions between the spins and the vibrational structure of the lattice. Such interactions are mediated by the coupling between the orbital moment of the FeII center and the phonons, as evidenced by the calculations and magnetic data. Our results also indicate that the coupling of the orbital moment to the FeII spin is strong. By invoking a transitive relationship, this means that the moments of the studied molecules are strongly coupled to the phonon system. Thus, the influence of the spin–orbit coupling on the slow magnetic relaxation under an applied dc field is bilateral. On one hand, the spin–orbit coupling overrides the deleterious quenching effects of the ligand field, resulting in sustained magnetic anisotropy, despite the deviation of the ligand field from rigorous D∞h symmetry. Adversely, the spin–orbit coupling bolsters the coupling of the spins to the lattice phonons and promotes other faster magnetic relaxation processes. Ultimately, this means that the same effect responsible for generating the large magnetic anisotropy is also facilitating fast magnetic relaxation under an applied field.
Conclusions
Taken together, the foregoing results demonstrate how two-coordinate iron(II) complexes can provide a fruitful platform for the study of slow magnetic relaxation in highly anisotropic systems. Direct- and alternating-current magnetic susceptibility measurements confirmed the existence of substantial magnetic anisotropy, with the latter indicating very slow relaxation times for 1–5 at low temperature. Importantly, the field and temperature dependences of the magnetic relaxation times were modelled to yield Ueff values ranging from 181 cm−1 for 1 to 43 cm−1 for 5. Partial quenching of the magnetic anisotropy across the series of compounds can be attributed to non-axial symmetry of the L–Fe–L moieties, though this quenching is mostly cancelled due to the relative strength of the orbital angular momentum compared to the ligand field. The inability to observe a strong temperature dependence for the relaxation time, indicative of dominant Orbach relaxation, across the series has been attributed to either far more efficient direct and Raman relaxation processes, or the influence of vibronic coupling. This ambiguity highlights the need for more detailed studies into the relaxation processes of mononuclear systems and the various factors that influence them. A study of this nature is presented as a companion paper to this work.15Acknowledgements
This research was supported by NSF grants CHE-1111900 and CHE-0948417. We thank Tyco Electronics and NSF for fellowship support of J.M.Z. and A.M.B., respectively, and Dr A. M. LaPointe, Dr M. E. Fasulo, and E. R. Hosler for informative discussions.Notes and references
- (a) R. Sessoli, L. Hui, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804 CrossRef CAS; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (c) D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194 CrossRef CAS.
- (a) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS; (b) A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef; (c) P. C. E. Stamp and A. Gaita-Ariño, J. Mater. Chem., 2009, 19, 1718 RSC.
- F. Torres, J. M. Hernández, X. Bohigas and J. Tejada, J. Appl. Phys. Lett., 2000, 77, 3248 CrossRef CAS.
- (a) J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729 CrossRef CAS; (b) S. Accorsi, A. L. Barra, A. Caneschi, G. Chastanet, A. Cornia, A. C. Fabretti, D. Gatteschi, C. Mortalò, E. Olivieri, F. Parenti, P. Rosa, R. Sessoli, L. Sorace, W. Wernsdorfer and L. Zobbi, J. Am. Chem. Soc., 2006, 128, 4742 CrossRef CAS; (c) C.-F. Wang, J.-L. Zuo, B. M. Bartlett, Y. Song, J. R. Long and X.-Z. You, J. Am. Chem. Soc., 2006, 128, 7162 CrossRef CAS; (d) J. Martínez-Lillo, D. Armentano, G. De Munno, W. Wernsdorfer, M. Julve, F. Lloret and J. Faus, J. Am. Chem. Soc., 2006, 128, 14218 CrossRef; (e) C.-I. Yang, W. Wernsdorfer, G.-H. Lee and H.-L. Tsai, J. Am. Chem. Soc., 2007, 129, 456 CrossRef CAS; (f) C. J. Milios, A. Vinslava, P. A. Wood, S. Parsons, W. Wernsdorfer, G. Christou, S. P. Perlepes and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 8 CrossRef CAS; (g) C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 2754 CrossRef CAS; (h) E. J. Schelter, F. Karadas, C. Avendano, A. V. Prosvirin, W. Wernsdorfer and K. R. Dunbar, J. Am. Chem. Soc., 2007, 129, 8139 CrossRef CAS; (i) D. E. Freedman, D. M. Jenkins, A. T. Iavarone and J. R. Long, J. Am. Chem. Soc., 2008, 130, 2884 CrossRef CAS; (j) D. Yoshihara, S. Karasawa and N. Koga, J. Am. Chem. Soc., 2008, 130, 10460 CrossRef CAS; (k) P.-H. Lin, T. J. Burchell, R. Clérac and M. Murugesu, Angew. Chem., Int. Ed., 2008, 47, 8848 CrossRef CAS; (l) P.-H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489 CrossRef CAS; (m) J. M. Zadrozny, D. E. Freedman, D. M. Jenkins, T. D. Harris, A. T. Iavarone, C. Mathionière, R. Clérac and J. R. Long, Inorg. Chem., 2010, 49, 8886 CrossRef CAS; (n) S. Karasawa and N. Koga, Inorg. Chem., 2011, 50, 5186 CrossRef CAS; (o) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef CAS; (p) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS.
- (a) N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and S. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS; (b) N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and S. Kaizu, J. Phys. Chem. B, 2004, 108, 11265 CrossRef CAS; (c) N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650 CrossRef CAS; (d) M. A. AlDamen, S. Cardona-Serra, J.-M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874 CrossRef CAS; (e) M. A. AlDamen, S. Cardona-Serra, J.-M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467 CrossRef CAS; (f) S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448 CrossRef CAS; (g) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730 CrossRef CAS; (h) M. Jeletic, P.-H. Lin, J. J. Le Roy, I. Korobkov, S. I. Gorelsky and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 19286 CrossRef CAS; (i) H. L. C. Feltham, Y. Lan, F. Klöwer, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Chem.–Eur. J., 2011, 17, 4362 CrossRef CAS; (j) G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606 CrossRef CAS.
- (a) J. D. Rinehart and J. R. Long, J. Am. Chem. Soc., 2009, 131, 12558 CrossRef CAS; (b) J. D. Rinehart, K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7572 CrossRef CAS; (c) N. Magnani, C. Apostolidis, A. Morgenstern, E. Colineau, J.-C. Griveau, H. Bolvin, O. Walter and R. Caciuffo, Angew. Chem., Int. Ed., 2011, 50, 1696 CrossRef CAS; (d) M. A. Antunes, L. C. J. Pereira, I. C. Santos, M. Mazzanti, J. Marçalo and M. Almedia, Inorg. Chem., 2011, 50, 9915 CrossRef CAS.
- (a) D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224 CrossRef CAS; (b) W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowksi, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115 CrossRef CAS; (c) D. Weismann, Y. Sun, Y. Lan, G. Wolmershauser, A. K. Powell and H. Sitzmann, Chem.–Eur. J., 2011, 17, 4700 CrossRef CAS; (d) P.-H. Lin, N. C. Smythe, S. L. Gorelsky, S. Maguire, N. J. Henson, I. Korobkov, B. L. Scott, J. C. Gordon, R. T. Baker and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 15806 CrossRef CAS; (e) T. Jurca, A. Farghal, P.-H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814 CrossRef CAS; (f) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732 CrossRef CAS.
- (a) F. Neese and E. I. Solomon, Inorg. Chem., 1998, 37, 6568 CrossRef CAS; (b) O. Waldmann, Inorg. Chem., 2007, 46, 10035 CrossRef CAS; (c) F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229 RSC.
- R. S. Drago, Physical Methods For Chemists, Surfside Scientific Publishers, Gainesville, 1992 Search PubMed.
- B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Applications, John Wiley & Sons, New York, 2000 Search PubMed.
- O. Kahn, Molecular Magnetism, John Wiley & Sons, New York, 1993 Search PubMed.
- (a) H. Andres, E. L. Bominaar, J. M. Smith, N. A. Eckert, P. L. Holland and E. Münck, J. Am. Chem. Soc., 2002, 124, 3012 CrossRef CAS; (b) C. V. Popescu, M. T. Mock, S. A. Stoian, W. G. Dougherty, G. P. A. Yap and C. G. Riordan, Inorg. Chem., 2009, 48, 8317 CrossRef CAS.
- P. P. Power, Chem. Rev., 2012, 112, 3482 CrossRef CAS and references therein.
- The orbital angular momentum can be highly influenced by subtle, dynamic distortions of the L–Fe–L moiety. Such distortions may be minor enough that they would not appear via a bent L-Fe-L angle in the crystal structure. These influences are explored in full in a companion paper: M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2012 10.1039/C2SC21394J.
- (a) R. A. Bartlett and P. P. Power, J. Am. Chem. Soc., 1987, 109, 7563 CrossRef CAS; (b) H. Chen, R. A. Bartlett, H. V. R. Dias, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 1989, 111, 4338 CrossRef CAS; (c) H. Chen, R. A. Bartlett, M. M. Olmstead, P. P. Power and S. C. Shoner, J. Am. Chem. Soc., 1990, 112, 1048 CrossRef CAS; (d) H. Müller, W. Seidel and H. Görls, Angew. Chem., Int. Ed. Engl., 1995, 34, 325 CrossRef; (e) T. Viefhaus, W. Schwarz, K. Hübler, K. Locke and J. Weidlein, Z. Anorg. Allg. Chem., 2001, 627, 715 CrossRef CAS; (f) A. M. LaPointe, Inorg. Chim. Acta, 2003, 345, 359 CrossRef CAS; (g) W. M. Reiff, A. M. LaPointe and E. Witten, J. Am. Chem. Soc., 2004, 126, 10206 CrossRef CAS; (h) T. Nguyen, A. Panda, M. M. Olmstead, A. F. Richards, M. Stender, M. Brynda and P. P. Power, J. Am. Chem. Soc., 2005, 127, 8545 CrossRef CAS; (i) H. Y. Au-Yeung, C. H. Lam, C.-K. Lam, W.-Y. Wong and H. K. Lee, Inorg. Chem., 2007, 46, 7695 CrossRef CAS; (j) W. M. Reiff, C. E. Schulz, M.-H. Whangbo, J. I. Seo, Y. S. Lee, G. R. Potratz, C. W. Spicer and G. S. Girolami, J. Am. Chem. Soc., 2009, 131, 404 CrossRef CAS; (k) A. E. Ashley, A. R. Cowley, J. C. Green, D. R. Johnston, D. J. Watkin and D. L. Kays, Eur. J. Inorg. Chem., 2009, 2547 CrossRef CAS; (l) C. Ni and P. P. Power, Chem. Commun., 2009, 5543 RSC; (m) W. A. Merrill, T. A. Stich, M. Brynda, G. J. Yeagle, J. C. Fettinger, R. De Hont, W. M. Reiff, C. E. Schulz, R. D. Britt and P. P. Power, J. Am. Chem. Soc., 2009, 131, 12693 CrossRef; (n) H. Lei, J.-D. Guo, J. C. Fettinger, S. Nagase and P. P. Power, J. Am. Chem. Soc., 2010, 132, 17399 CrossRef CAS.
- A. B. Pangborn, M. A. Giardello, R. H. Grubbs, K. R. Rosen and F. J. Timmens, Organometallics, 1996, 15, 518 CrossRef.
- R. A. Andersen, K. Faegiri Jr, J. C. Green, A. Haaland, M. F. Lappert, W. Leung and K. Rypdal, Inorg. Chem., 1988, 27, 1782 CrossRef CAS.
- B. Horvath, R. Möseler and E. G. Horvath, Z. Anorg. Allg. Chem., 1979, 450, 165 CrossRef CAS.
- (a) Y. W. Chao, P. A. Wexler and D. E. Wigley, Inorg. Chem., 1989, 28, 3860 CrossRef CAS; (b) D. K. Kennepohl, S. Brooker, G. M. Sheldrick and H. W. Roesky, Chem. Ber., 1991, 124, 2223 CrossRef CAS; (c) J. Li, H. Song, C. Cui and J.-P. Cheng, Inorg. Chem., 2008, 47, 3468 CrossRef CAS.
- Though these constants are located in a variety of references, the following is an exceptional collection of almost all necessary values for the calculations: G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- G. Sheldrick, SADABS, Madison, WI, 1996 Search PubMed.
- SHELXTL P.C. v. 5.1, Siemens Analytical X-ray Instruments Inc., Madison, WI, 1994 Search PubMed.
- (a) E. Cremades and E. Ruiz, Inorg. Chem., 2011, 50, 4016 CrossRef CAS; (b) M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Inorg. Chem., 2011, 50, 7640 Search PubMed; (c) D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297 CrossRef CAS; (b) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS; (d) C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef.
- F. Neese and F. Wennmohs, ORCA; version 2.8, An ab initio, DFT, and semiempirical SCF-MO package with contributions from U. Becker, D. Ganyushin, A. Hansen, D. G. Liakos, C. Kollmar, S. Kossman, T. Petrenko, C. Reimann, C. Riplinger, K. Sivalingam, E. Valeev and B. Wezisla, Lehrstuhl fur theoretische Chemie, Bonn, Germany, 2010 Search PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 34107 CrossRef.
- R. McWeeny, Methods of Molecular Quantum Mechanics, Academic Press, London, 1992 Search PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef.
- B. O. Roos and P.-Å. Malmqvist, Phys. Chem. Chem. Phys., 2004, 6, 2919 RSC.
- A. M. Bryan, W. A. Merrill, W. M. Reiff, J. C. Fettinger and P. P. Power, Inorg. Chem., 2012, 51, 3366 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186 CrossRef.
- M. Kotani, J. Phys. Soc. Jpn., 1949, 4, 293 CrossRef CAS.
- M. P. Shores, J. J. Sokol and J. R. Long, J. Am. Chem. Soc., 2002, 124, 2279 CrossRef CAS.
- D. Dai and M.-H. Whangbo, Inorg. Chem., 2005, 44, 4407 CrossRef CAS.
- (a) K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS; (b) C. J. F. Böttcher, Theory of Electric Polarisation, Elsevier, New York, 1952 Search PubMed; (c) S. M. J. Aubin, Z. M. Sun, L. Pardi, J. Krzystek, K. Folting, L. C. Brunel, A. L. Rheingold, G. Christou and D. N. Hendrickson, Inorg. Chem., 1999, 38, 5329 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef CAS.
- R. Carlin, Magnetochemistry, Springer-Verlag, Berlin, 1986 Search PubMed.
- A. Fort, A. Rettori, J. Villain, D. Gatteschi and R. Sessoli, Phys. Rev. Lett., 1998, 80, 612 CrossRef CAS.
- (a) R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 458 CrossRef CAS; (b) R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 485 CrossRef CAS; (c) M. B. Walker, Can. J. Phys., 1968, 46, 1347 CrossRef CAS.
- D = −70 cm−1, (Ph4P)2[Co(SPh)4]: (a) K. Fukui, H. Ohya-Nishiguchi and N. Hirota, Bull. Chem. Soc. Jpn., 1991, 64, 1205 CrossRef CAS; (b) K. Fukui, N. Kojima, H. Ohya-Nishiguchi and N. Hirota, Inorg. Chem., 1992, 31, 1338 CrossRef CAS; (c) K. Fukui, H. Masuda, H. Ohya-Nishiguchi and H. Kamada, Inorg. Chim. Acta, 1995, 238, 73 CrossRef CAS.
- |D| = 76 cm−1, [(HL)2Fe6(NCMe)6](PF6)3: Q. Zhao, T. D. Harris and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 8293 CrossRef CAS.
- D ≈ 70 cm−1, Mixed-valence di-ruthenium tetracarboxylate complexes: (a) J. Telser and R. S. Drago, Inorg. Chem., 1984, 23, 3114 CrossRef CAS; (b) J. Telser and R. S. Drago, Inorg. Chem., 1985, 24, 4765 CrossRef; (c) F. D. Cukiernik, A. M. Giroud-Godquin, P. Maldivi and J. C. Marchon, Inorg. Chim. Acta, 1994, 215, 203 CrossRef CAS; (d) M. Handa, Y. Sayama, M. Mikuriya, R. Nukada, L. Hiromitsu and K. Kasuga, Bull. Chem. Soc. Jpn., 1998, 71, 119 CrossRef CAS; (e) R. Jimenez-Apraricio, F. A. Urbanos and J. M. Arrieta, Inorg. Chem., 2001, 40, 613 CrossRef; (f) T. E. Vos, Y. Liao, W. W. Shum, J.-H. Her, P. W. Stephens, W. M. Reiff and J. S. Miller, J. Am. Chem. Soc., 2004, 126, 11630 CrossRef CAS.
- (a) J. T. Hougen, G. E. Leroi and T. C. James, J. Chem. Phys., 1960, 34, 1670 CrossRef; (b) C. W. DeKock and D. M. Gruen, J. Chem. Phys., 1966, 44, 4387 CrossRef CAS.
- M. Hargittai, Chem. Rev., 2000, 100, 2233 CrossRef CAS and references therein.
- J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Chem. Commun., 2012, 112, 3927 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Full crystallographic data for 1 and 3, additional magnetic data, and additional figures. CCDC 888342 and 888343. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2sc20801f |
| This journal is © The Royal Society of Chemistry 2013 |
