Adsorption of core-shell nanoparticles at liquid–liquid interfaces†
Lucio
Isa
*a,
Esther
Amstad
a,
Konrad
Schwenke
b,
Emanuela
Del Gado
b,
Patrick
Ilg
c,
Martin
Kröger
c and
Erik
Reimhult
ad
aLaboratory for Surface Science and Technology, Department of Materials, ETH Zürich, Wolfgang-Pauli-Strasse 10, 8093, Zürich, Switzerland. E-mail: lucio.isa@mat.ethz.ch; Fax: +41 (0)44 633 10 27; Tel: +41 44 633 63 76
bMicrostructure and Rheology, Institute for Building Materials, Department of Civil, Geomatic and Environmental Engineering, ETH Zürich, Schafmattstrasse 6, 8093, Zürich, Switzerland
cPolymer Physics, Department of Materials, ETH Zürich, Wolfgang-Pauli-Strasse 10, 8093, Zürich, Switzerland
dDepartment of NanoBiotechnology, University of Natural Resources and Life Sciences (BOKU) Vienna, Muthgasse 11, 1190, Vienna, Austria
First published on 2nd August 2011
Abstract
The use of nanoparticles as building blocks for the self-assembly of functional materials has been rapidly increasing in recent years. In particular, two-dimensional materials can be effectively self-assembled at liquid interfaces thanks to particle localization and mobility at the interface in combination with tailoring of specific interactions. Many recent advances have been made in the understanding of the adsorption and assembly at liquid interfaces of small hydrophobic nanoparticles stabilized by short-chain rigid dispersants but the corresponding studies on core-shell nanoparticles sterically stabilized by extended hydrophilic polymer brushes are presently missing. Such particles offer significant advantages in terms of fabrication of functional, responsive and bio-compatible materials. We present here a combination of experimental and numerical data together with an intuitive and simple model aimed at elucidating the mechanisms governing the adsorption of iron oxide nanparticles (5–10 nm) stabilized by low molecular weight poly(ethylene glycol) (1.5–10 kDa). We show that the adsorption dynamics and the structure of the final assembly depend on the free energy of the particles at the interface and discuss the thermodynamics of the adsorption in terms of the polymer solubility in each phase.
1 Introduction
The extraordinary properties of inorganic nanoparticles (NPs) are exploited in an increasing number of technological applications, including biosensing,1 therapeutics2–5 and diagnostics.3,6 NPs can also be used as “additives” to improve the performance of existing materials7 (e.g. thermal conductivity,8 mechanical stability9 or energy transfer9), or to impart new functions to them (e.g. magnetic10,11 or triggered release12,13). In parallel, vast efforts have been recently made in order to synthesize and fabricate NPs of controlled shape and functionality14,15 and to understand how they interact16 with the aim to direct their assembly into complex structures.17A particularly suited way to assemble NPs in a controlled way is to exploit their self-assembly at liquid–liquid or liquid–air interfaces (SALI).18 Surface-active NPs adsorb and localize at interfaces, thus offering the possibility of easily assembling two-dimensional (2-D) materials for the fabrication of capsules,19 ultra-thin cross-linked membranes20–24 and free-standing metal films.25 The reason for particle trapping at liquid–liquid interfaces has been extensively discussed in the literature26,27 and hinges upon a free energy gain for the system due to the removal of interfacial area between two fluids when a particle resides at the interface.28 The energy gain depends on particle size and wetting properties and on the interfacial tension between the two phases γ0. Neutrally wetting conditions lead to the highest adsorption energy since they maximize the particle cross-sectional area at the interface. For this reason several strategies have been developed to tune the wettability of NPs, either by exchanging ligands on the particle to achieve the right surface chemistry,19 by changing the solvent composition (e.g. by adding ethanol)25,29 or by controlling the pH.30 Despite vertical trapping at the interface, NPs still retain lateral mobility which, under the right circumstances, allows for the assembly of highly spatially uniform structures.31,32 Moreover, at the interface additional inter-particle interactions are present,27,33,34i.e. electrostatic, capillary and solvation, which are absent in the bulk and which contribute to determine the structure of interfacial assemblies. All the aforementioned points highlight the flexibility of SALI as a route to fabricate 2-D NP-based materials. Of particular interest is to obtain 2-D materials with controlled NP content and spatial organization. In this respect, the use of expanded, solvated shells makes it also possible to assemble responsive membranous materials, for which the polymer matrix, the NP internal structure and inter-particle distance can be controlled over a large range of distances by applying external stimuli. Such membranes enable the true combination of the best features of polymer chemistry and physical properties of NPs. Moreover, many well-studied polymer brushes are hydrophilic and exhibit controlled biomolecular interactions; for these reasons such materials are highly relevant for biomedical and biotechnological applications.
Experimental studies on NP-SALI have almost exclusively dealt with “hard” NPs, stabilized by short chain, rigid dispersants. Most of these systems consist of hydrophobic particles modified by alkyl self-assembled monolayers. The most advanced examples have been demonstrated by Emrick, Russell and co-workers20,35 and Möhwald and co-workers.19,36 However, the unknown stability of the dispersant anchoring groups at the interface combined with limited hydrophobic shell thickness and homogeneity is likely to lead to aggregation at the oil–water interface and precludes the possibility of obtaining particle spacings larger than 1–2 nm. Regarding water soluble NPs, the very limited available examples include 2 nm Au NPs functionalized with short chain alkyl-oligo(ethylene glycol) thiols,23 8–40 nm charge-stabilized, citrate-capped Au NPs29 and tobacco mosaic virus.37 However, in the first case the use of only four ethylene glycol units led to weak stability and very short inter-particle separations. Citrate NPs were found to aggregate in 2-D domains and the charge stabilization was not sufficient to produce homogeneous monolayers as in the case of larger colloids.28 Finally, virus particles offer tremendous monodispersity, shape and functional control as well as high structural order,22 but do not possess the chemical or physical (optical, magnetic, mechanical) properties to perform the functions offered by inorganic nano-sized objects.
The limitations put forth above can be overcome by using core-shell NPs, where the shell comprises grafted, osmotically repulsive, hydrophilic polymers of controlled molecular weight (Fig. 1). The presence of the polymer shell has multiple functions. It above all provides colloidal stability to the particles in the aqueous phase. For this purpose it is crucially important that the polymer is irreversibly grafted to the particle cores at high density via a suitable anchoring group. The thickness of the polymer shell also determines the separation between the particle cores in close-packed assemblies. Moreover, the free end of the polymers can be functionalized to carry specific binding or cross-linking groups for targeting or in situpolymerization and dyes for fluorescent tagging. Finally, the choice of polymers responsive to external stimuli (e.g. temperature or pH) can be exploited to actuate the assembled structures.
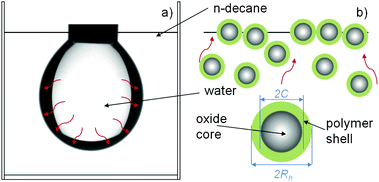 | ||
| Fig. 1 Schematic representation of the pendant drop geometry (a) and of the adsorption process for core-shell NPs (b). The red arrows schematically represent diffusion of NPs from the bulk aqueous phase towards the liquid–liquid interface. NP core (C) and hydrodynamic radius (Rh) in water are highlighted. Upon reaching the interface, the NPs are adsorbed and their separation at close packing is determined by the thickness of the hydrated polymer shell, as it will be discussed further in the text. | ||
In addition to application-driven advantages, SALI of core-shell NPs presents questions of high fundamental scientific interest. In core-shell NP-SALI the lowering of the interfacial energy by particle adsorption no longer depends only on the size and wetting properties of the core but also on the solubility of the organic polymer shell in the two solvents. The study of these effects is in its infancy. Numerical simulations have started to address the shell conformation for individual particles at liquid–liquid interfaces, but the studies are still limited to relatively short dispersants.38,39 Preliminary experimental studies have highlighted a link between polymer molecular weight and colloidal stability at the interface.40
We focus here on SALI of iron oxide NPs, which find numerous applications due to their magnetic properties and good biocompatibility,41 including diagnostics42 and therapeutics, e.g. hyperthermia.4,5 Single-core iron oxide NPs can be sterically stabilized by a dense poly(ethylene glycol) (PEG) shell bound to the NP surface by a stable anchor via a simple “grafting to” approach.43–47 We have recently demonstrated that particles of superior stability are obtained using PEG anchored with nitrocatechols43,48 and thus all the results shown in this paper were obtained using Fe3O4 NPs stabilized by PEG-nitroDOPA shells of different thickness.
This work is triggered by the experimental observation of a complex adsorption behavior for iron oxide-PEG NPs at the water/n-decane interface (Fig. 1). Based on such observation, we have developed a set of experiments, simulations and theoretical models, which provide a comprehensive approach to decipher the adsorption behavior of soft sterically stabilized core-shell NPs. The experimental characterization is preceded by a short description of the particle synthesis and stabilization procedure. We later move to time-resolved interfacial tension measurements which capture the collective NP behavior at the interface and then attempt to gain microscopic insight by looking at the hydration of PEG brushes in the two solvents used. The “macroscopic-to-microscopic” approach is also followed in the presented numerical and modeling results, aimed at integrating and shedding light on the experimental data. Numerical studies unravel the different adsorption regimes as a function of particle interfacial binding energy and allow for the characterization of the interface coverage and the size distribution of adsorbed NPs. In addition to the collective NP adsorption behavior studied in the numerical simulations, we have also elaborated a simple theoretical model to explore further the effects of the polymer shell on the adsorption of individual NPs at liquid–liquid interfaces. The model is based on a Flory-type theory for a polymer brush grafted on a spherical colloid which sees an interface between two liquids with different qualities and gives as an output, aside from brush heights, the equilibrium position for a core-shell NP relative to the interface and corresponding free energy gain.
2 Results and discussion
2.1 Experimental results
| PEG molecular weight (Mw/kDa] | Synthesis temperature (T/°C) | Core radius (C/nm) | Hydrodynamic radius (Rh/nm) |
|---|---|---|---|
| 1.5 | 150 | 2.1 ± 0.1 | 10 ± 2.5 |
| 5 | 150 | 2.1 ± 0.1 | 13 ± 3 |
| 10 | 150 | 2.1 ± 0.1 | 14 ± 2 |
| 1.5 | 180 | 4.8 ± 0.3 | 12 ± 1 |
| 5 | 180 | 4.8 ± 0.3 | 14 ± 2.5 |
| 10 | 180 | 4.8 ± 0.3 | 16 ± 2.5 |
Fig. 2 shows the normalized interfacial tension γ′ = γ/γ0 as a function of time for two iron oxide core sizes and three PEG molecular weights, where γ0 = 53.2 mN m−1 is the interfacial tension of the pure water/n-decane interface.51 Analogously to what was reported in preliminary studies,40,52 we observe that the bulk concentration c and the PEG molecular weight have a strong influence on the adsorption kinetics. As the concentration of the NP suspension increases we observe that the initial value of γ′ decreases; this is due to the fact that as the droplet is formed, a given number of particles (increasing with concentration) is already adsorbed at the interface leading to a value of γ < γ0 above a size-dependent bulk concentration. Additionally, we observe that the interfacial tension decreases faster for more concentrated suspensions. This is expected as the adsorption rate scales with bulk concentration. Moreover, for all particles γ′ plateaus (more or less markedly depending on the size) at high concentrations and long times to a saturation value γ∞ which is independent of c. But what perhaps is the most striking feature of Fig. 2 is the complex shape of the time dependence of γ′, which appears to be an exclusive of core-shell NPs. Such complex behavior is absent for “harder” objects which show a smooth γ decay with time.53,54 Upon increasing particle size and bulk concentration, different adsorption regimes appear. Starting from the smallest particles with core radius C = 2.1 nm and stabilized by PEG 1500, we observe that by the increasing bulk concentration c, the γ′ versus time curve initially decays smoothly (c < 1 × 10−6 mol) but then develops shoulders which correspond to transitions in the adsorption rates. A similar but more pronounced behavior is observed for the PEG molecular weight and larger core radius C = 4.8 nm. As the thickness of the PEG shell increases and thus the size of the NPs, the presence of a plateau in γ′ at intermediate times becomes evident. Moreover with increasing c the plateau shows up at increasingly shorter times and for the highest concentrations a second, long-time plateau is observed. The latter also manifests itself at shorter times for higher concentrations and the value of the long-time, asymptotic interfacial tension γ∞ becomes independent of c, corresponding to a saturation of the interface. The numerical simulations reported in Section 2.2 have the specific aim to elucidate further the nature of these complex adsorption regimes.
 | ||
| Fig. 2 Normalized interfacial tension γ′ ≡ γ/γ0versus time at the water n-decane interface for particles of various PEG molecular weights and core sizes. The different symbols indicate the following concentrations on NP aqueous suspensions: (filled triangle) 2 × 10−7 mol; (filled square) 1 × 10−6 mol; (open square) 2 × 10−6 mol; (filled circle) 1 × 10−5 mol; (open circle) 2 × 10−5 mol. | ||
In order to exclude the possibility that the reduction in the interfacial tension is coming from free polymer and to confirm that the complex adsorption behavior is stemming from the presence of composite, soft NPs, we have also performed PDT experiments on pure PEG aqueous solutions. Fig. 3 shows γ as a function of time for NPs coated by PEG 5000 and C = 2.1 and 4.8 nm and for free PEG 5000 chains. At the concentration used (c = 1 × 10−5 mol) the free polymer very rapidly saturates the water/n-decane interface while the core-shell NPs show the complex behavior reported in Fig. 2. The PEG molecular weight has a strong influence on the asymptotic long-time interfacial tension γfpc∞ of the free polymer chains (fpc) (inset to Fig. 3), while this dependence is not observed for the core-shell NPs.
 | ||
| Fig. 3 Interfacial tension γ versus time at the water n-decane interface for particles coated by PEG 5000 with C = 2.1 nm (red squares) and C = 4.8 nm (green filled circles) and of non-tethered PEG 5000 (blue triangles) at 1 × 10−5 mol concentration (particles and free polymer chains, respectively). Inset: long-time interfacial tension γfpc∞ of the free polymer chains (fpc) versus PEG molecular weight at the water n-decane interface. The solid line is a fit from eqn (8) with eqn (7). | ||
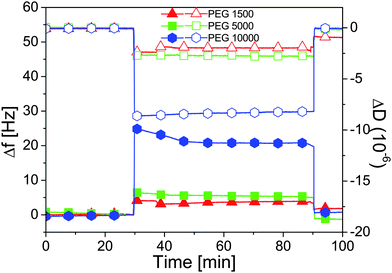 | ||
| Fig. 4 Frequency shifts Δf (filled symbols) and dissipation ΔD (open symbols) measured with QCM-D as a function of time on adsorbed brushes of PEG-nitroDOPA of various molecular weights. At t = 30 min, Millipore water is exchanged with n-decane and we note the correspondent increase in Δf and decrease in ΔD stemming from partial collapse of the polymer chains. At t = 90 min, the solvent is changed back to Millipore water and the baselines are recovered showing the reversibility of the collapse. | ||
To quantify the amount of collapse it is also necessary to measure the absolute hydrated mass of the PEG-nitroDOPA films. However, the protocol for functionalization of TiO2 surfaces with a stable PEG brush cannot be performed in situ in our QCM-D setup (see Section 3.1 for details). Furthermore, the density and density profile of PEG brushes on the planar TiO2 and on the Fe3O4 NP surfaces are expected to differ significantly.57,12 A quantitative extension of the results presented here to the collapse of PEG shells on NPs at the water/n-decane interface is therefore not meaningful, but we nonetheless note that a significant collapse is observed in n-decane and that, as expected, the absolute collapse is higher for thicker brushes (higher PEG molecular weight). For these reasons we decided to carry out a modeling study which, upon the existence of the evidence of at least a partial collapse of the polymer shell, is aimed to elucidate the role that polymer solubility has on the free energy of individual core-shell NPs at liquid interfaces (Section 2.3).
2.2 Numerical simulations results
To adsorb/desorb particles we use a Grand-Canonical Monte Carlo (MC) scheme where the Metropolis rate is given by the energy difference upon adsorption/desorption of a particle randomly chosen from the distribution specified above, the temperature T and the number of adsorbed particles.60 The energy gain for a particle i to be adsorbed onto the interface is taken to be −ΔEi = ΔE0(σi/σ)2, where ΔE0 is determined by the solvent pair (water/n-decane in this case), the particle surface chemistry and size.28 Note that this expression assumes naked (non-coated) particles centered at the interface. The contribution of the core-shell nature of our NPs will be discussed in Section 2.3. The adsorption/desorption rates are fixed by ΔEi, the number N of particles at the interface and the change ΔUi in the interaction energy on the surface upon adsorption/desorption of particle i.60 In the simulations we consider ΔE0 from 1.0kBT to 100kBT, where kB is Boltzmann’s constant; the experimental values for our system are higher (see Section 2.4), but ΔE0 = 50kBT already starts to capture some essential features of systems with irreversible adsorption at the interface over the simulation time window considered here.
We perform Δ steps of Molecular Dynamics (MD) between two MC cycles to mimic the particle dynamics at the interface, using velocity Verlet with a step 0.002 and fixing the temperature T = 1.0 via velocity rescaling.61 The unit time is 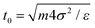 . The data presented here correspond to Δ = 10 MD steps. In the following, we use the MD time as the lapsing time of the numerical experiments and we qualitatively compare the different regimes detected in the simulations to the ones observed in the adsorption experiments. A quantitative matching of the numerical time with the physical time will be performed in future work.
. The data presented here correspond to Δ = 10 MD steps. In the following, we use the MD time as the lapsing time of the numerical experiments and we qualitatively compare the different regimes detected in the simulations to the ones observed in the adsorption experiments. A quantitative matching of the numerical time with the physical time will be performed in future work.
Finally, we assume that the particle density close to the interface scales with the bulk concentration c. This corresponds to a higher rate of adsorption attempts (as described by the MC cycle). Hence, in a first simple approximation, in order to account for concentration effects, we consider each MC cycle to be limited to N0 attempts and therefore assume an attempt rate N0/Δ: increasing values of N0 correspond to increasing concentration. Here we varied N0 between 10 and 104.
 | ||
| Fig. 5 Snapshots of the 2-D simulation box after 0.8 t0 for ΔE0 = 1kBT (left) and ΔE0 = 100kBT (right), leading to a surface coverage Φ of ≃ 0.26 and ≃ 0.8, respectively. The color code indicates the potential energy. | ||
The number and size of particles adsorbed at the interface determine the reduction of the interfacial tension; in particular, the normalized interfacial tension γ′ = γ/γ0 reported in Fig. 2 is linearly related to Φ(t) viaeqn (6). Fig. 6 shows 1 − Φ(t) as a function of time for different ΔE0§. The surface coverage obtained at the end of the simulation increases monotonically upon increasing ΔE0. For low adsorption energies ΔE0 < 10kBT, the system reaches an equilibrium surface coverage over the simulation time window: particles are continuously adsorbed and desorbed but the surface coverage value does not change. The permanence time on the surface of a particle of σi = 1.0σ is typically ≃10t0 for ΔE0 = 1kBT. The permanence time increases with ΔE0 and at the largest ΔE0 hardly any particle is desorbed; for ΔE0 ≳ 20kBT, the adsorption curves show an evolution towards higher surface coverage without reaching a steady state within the simulation time frame.
 | ||
| Fig. 6 1 − Φ (related to γ′ = γ/γ0viaeqn (6)) versus simulation time for different adsorption energy strengths ΔE0 from numerical simulations of NP adsorption in the simulation box. | ||
An interesting feature of the curves in Fig. 6 which also appears in the experimental data, is the complex behavior of 1 − Φ(t) at intermediate times (∼0.2t0 < t < 10t0) for the largest adsorption energies. The observed intermediate plateau in 1 − Φ(t) corresponds to the fact that, after a first rapid filling of the surface, adsorption is blocked until a sufficiently large void becomes available. Once the particles which were adsorbed in the initial filling have had time to rearrange, particles equal to or smaller than the available void can be adsorbed and thus increase further the surface coverage. At small adsorption energies ΔE0 ≤ 1kBT the system smoothly evolves towards its equilibrium distribution, with a progressive increase of the mean radius ( ) and a corresponding decrease of the polydispersity (δ(t) = (〈σ2(t)〉 − 〈σ(t)〉2)/〈σ(t)〉2, where
) and a corresponding decrease of the polydispersity (δ(t) = (〈σ2(t)〉 − 〈σ(t)〉2)/〈σ(t)〉2, where 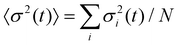 ) at the interface towards “optimal” values where particles are continuously adsorbed and desorbed (Fig.7). For larger adsorption energies 10kBT ≳ ΔE0 ≳ 20kBT, desorption events become rare and a new type of adsorption dynamics sets in: higher surface coverage is attained upon adsorbing relatively larger particles, as compared to the case of lower ΔE0. The system eventually evolves towards the steady state upon decreasing the mean radius and polydispersity on the surface only at much longer times. Finally, for even larger adsorption energies ΔE0 ≥ 50kBT, the system gets stuck in a regime characterized by the irreversible adsorption of particles of any size. The mean radius of the particles at the interface keeps decreasing due to the fact that at longer times only smaller and smaller particles can fill the space left by the irreversibly trapped particles and therefore the polydispersity does not decrease and remains, in the simulations window, very different from the “optimal” values attained in the equilibrium regime of small ΔE0.
) at the interface towards “optimal” values where particles are continuously adsorbed and desorbed (Fig.7). For larger adsorption energies 10kBT ≳ ΔE0 ≳ 20kBT, desorption events become rare and a new type of adsorption dynamics sets in: higher surface coverage is attained upon adsorbing relatively larger particles, as compared to the case of lower ΔE0. The system eventually evolves towards the steady state upon decreasing the mean radius and polydispersity on the surface only at much longer times. Finally, for even larger adsorption energies ΔE0 ≥ 50kBT, the system gets stuck in a regime characterized by the irreversible adsorption of particles of any size. The mean radius of the particles at the interface keeps decreasing due to the fact that at longer times only smaller and smaller particles can fill the space left by the irreversibly trapped particles and therefore the polydispersity does not decrease and remains, in the simulations window, very different from the “optimal” values attained in the equilibrium regime of small ΔE0.
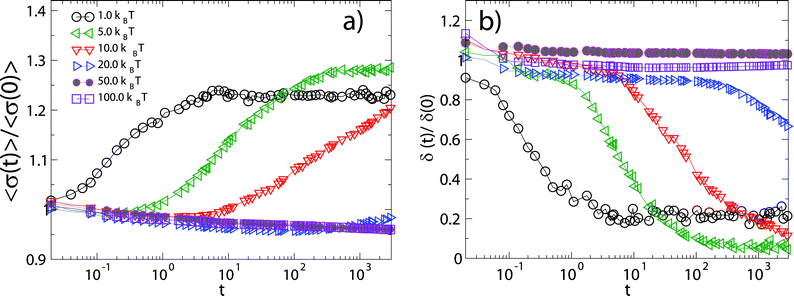 | ||
| Fig. 7 Average size (a) and relative fluctuation (b) of the particle radius in the simulation box versus simulation time for different adsorption energy strengths ΔE0 (here normalized with their initial values). | ||
These observations are summarized in Fig. 8. In particular we observe that the maximum attained NP surface coverage grows monotonically with ΔE0 and so does the long-time polydispersity for large adsorption energies. For small adsorption energies ΔE0 the adsorption process is dominated by the “optimal” size selection, which is more effective upon increasing ΔE0, hence the final attained polydispersity accordingly decreases and is smaller than the one of the parent distribution. For large ΔE0 instead, the adsorption dynamics is controlled by the persistence of larger particles at the interface and the irreversible progressive space filling which corresponds to a polydispersity close to the initial one.
 | ||
| Fig. 8 Long-time interfacial surface coverage Φ (left axis) and polydispersity of the adsorbed particle distribution (right axis) extracted from simulations as a function of adsorption energy ΔE0. The values refer to t1 ≃ 1.0 × 103τ0. | ||
To study the effect of bulk concentration of the initial NP suspension on the adsorption process, we fix ΔE0 = 100kBT and vary N0. In Fig. 9 we plot 1 − Φ(t) as a function of time. The numerical data show remarkable similarities to the experimental findings. The short-time value of 1 − Φ(t) decreases with increasing N0, in agreement with the picture where a large number of particles is rapidly adsorbed in the first stages of the experiments at higher initial concentrations, as indicated by the decrease of the initial values of γ (Fig. 2). Moreover, for N0 ≲ 102 a lower surface coverage is obtained over the same simulation time window and 1 − Φ(t) does not show the plateau discussed before. This is also qualitatively consistent with the experimental observations of Fig. 2 and suggests that, for sufficiently diluted suspensions, the adsorption kinetics leads to a continuous increase of the surface coverage without being much affected by the inter-particle interactions at the interface. For N0 ≳ 103, we note the appearance of the adsorption plateau at intermediate times and a saturation value of the final coverage which is only weakly dependent on N0 within the simulation time window, in analogy to what is reported in Fig. 2 as a function of the bulk concentration c.
 | ||
| Fig. 9 1 − Φ as a function of simulation time for systems with a different number of attempts to adsorb/desorb particles and ΔE0 = 100kBT. | ||
Overall, in spite of the rather crude assumptions, the simple model and simulation approach described above seem to capture the qualitatively most striking features of the PDT experiments. The results of the preliminary numerical studies presented here suggest that cooperative processes (i.e., the creation of space sufficient for the adsorption of new particles) are relevant and significantly affect the adsorption kinetics.
However, a more detailed representation of the experimental system would take into account the active role played by the polymer shell in determining the position of the NP relative to the interface, the corresponding reduction of interfacial area and the binding energy. In the following we therefore propose a Flory-type theory to account for the effect of the liquid–liquid interface on the polymer chains attached to the surface of the colloidal particle.
2.3 Modeling results: a Flory-type theory for polymer brush on colloids at liquid–liquid interfaces
 | ||
| Fig. 10 Schematic representation of a core-shell NP at a liquid–liquid interface highlighting all the quantities necessary for the derivation of the theoretical model. | ||
A simple form of the elasticity entropy is given by  as function of brush height R, where R0 is the size of an ideal chain with N spherical monomers of size a. The molecular interpretation of these quantities depends on the polymer model used. We will later employ a wormlike chain model for quantitative comparisons with the experimental results.
as function of brush height R, where R0 is the size of an ideal chain with N spherical monomers of size a. The molecular interpretation of these quantities depends on the polymer model used. We will later employ a wormlike chain model for quantitative comparisons with the experimental results.
In a mean-field approximation, the interaction between polymer chains is taken into account by62,63
 | (1) |
So far, we have followed the classical Flory theory in each solventi for which the equilibrium polymer size Req in some simple geometries is known63¶. In the following, we extend the theory to a curved surface and consider additional contributions arising from the presence of a liquid–liquid interface. Our approach to describe the brush tethered to the NP core (also known as Alexander brush for the case of tethering to a planar surface,62i.e. infinite core) does not allow us to calculate the density profile within the polymer layer, or a corresponding effective interaction potential. The former can however be derived following the self-consistent field approach reviewed and extended to branched polymers in.64 For the purpose of the following arguments, the precise knowledge of the density profile is not required.
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ) = π[(C2 − z2)1/2 +
) = π[(C2 − z2)1/2 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ]2 where,
]2 where, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ≡ (R1 + R2)/2 is an effective shell thickness within the plane of the interface. The free energy contribution thus becomes F12(z) = −γ0A12(z,
≡ (R1 + R2)/2 is an effective shell thickness within the plane of the interface. The free energy contribution thus becomes F12(z) = −γ0A12(z,![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ). Except for the interface region, the polymers contribute with a free energy fi per chain, i.e. in total n1(z)f1 + n2(z)f2, where ni(z) is the number of polymers on the surface of the core exposed to solventi. We have implicitly assumed that the chains are predominantly exposed to either solvent 1 or 2. This description becomes unsuitable in the limit of vanishing core, C = 0 (to be discussed separately below).
). Except for the interface region, the polymers contribute with a free energy fi per chain, i.e. in total n1(z)f1 + n2(z)f2, where ni(z) is the number of polymers on the surface of the core exposed to solventi. We have implicitly assumed that the chains are predominantly exposed to either solvent 1 or 2. This description becomes unsuitable in the limit of vanishing core, C = 0 (to be discussed separately below).
We assume homogeneous coating, where Σ is the area per polymer, i.e. the inverse grafting density. Given these approximations, the free energy of the coated NP at the interface is given by
F(z) = n1(z)f1(Req1) + n2(z)f2(Req2)−γ0A12(z,![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) eq) eq) | (2) |
As mentioned above, we obtain the equilibrium size of the polymerReqi in the two solvents by minimizing separately fi(R). We thus assume that the polymer size is unaffected by the presence of the interface. We expect this to be a good approximation for dense brushes sufficiently far from the interface, but this becomes questionable close to the interface, where the shell can be deformed.38,39 Moreover, the definition of an effective shell thickness ![[R with combining macron]](https://www.rsc.org/images/entities/char_0052_0304.gif) at the interface is also neglecting such shell deformations. For the minimization of fi(R), explicit expressions for the available volume are needed. By purely geometric arguments, the available volume per chain of given size R is
at the interface is also neglecting such shell deformations. For the minimization of fi(R), explicit expressions for the available volume are needed. By purely geometric arguments, the available volume per chain of given size R is 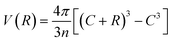 . The total number of tethered chains is the sum n = 4πC2/Σ = n1(z) + n2(z) and, for homogeneous coating, the number of tethered polymers in solvent 1 and 2 is n1(z) = 2πC(C + z)/Σ and n2(z) = 2πC(C − z)/Σ, respectively.
. The total number of tethered chains is the sum n = 4πC2/Σ = n1(z) + n2(z) and, for homogeneous coating, the number of tethered polymers in solvent 1 and 2 is n1(z) = 2πC(C + z)/Σ and n2(z) = 2πC(C − z)/Σ, respectively.
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) eq = (Req1 + Req2)/2, is taken as the effective shell thickness at the interface (Fig. 10). Therefore the cross-sectional area taken up by a single particle at the interface|| is A12(z,
eq = (Req1 + Req2)/2, is taken as the effective shell thickness at the interface (Fig. 10). Therefore the cross-sectional area taken up by a single particle at the interface|| is A12(z,![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ) = πσ20 with
) = πσ20 withσ0 = (C2 − z2eq)1/2 + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) eq. eq. | (3) |
For particles sitting preferentially in the solvent with highest quality (1), σ0 does not represent the true distance between the centers of two touching particles.** This distance is instead
| σ = C + Req1, | (4) |
In order to compare these two distances, we need to minimize F(z), eqn (2), with respect to z to obtain the equilibrium height zeq of the coated NP center from the liquid–liquid interface. The maximum and minimum values of zeq correspond to NPs that are fully immersed in solvent 1 and 2, respectively. An analytic expression for zeq is not available in closed form and it has to be evaluated numerically.††
With all the relevant quantities at hand, the binding energy of a single core–shell NP coated by n chains is obtained as the difference between (i) the free energy at its equilibrium position zeq within the interface, and (ii) the free energy of the same NP dissolved in the best of the two solvents,
 | (5) |
Given a macroscopic surface area δA, at saturation coverage Φ (we assume 2-D close-packing Φ = 0.91 of equally-sized particles), the number of NPs at the interface is ΦδA/πσ2 and the related reduction of macroscopic surface tension is −ΔE times the number of NPs, divided by δA, in agreement with the approach of Du and co-workers.54 Accordingly, we extract the asymptotic long-time interfacial tension γ∞ (as measured in experiments) from the energy gain, eqn (5), and the equilibrium NP radius, eqn (4), via
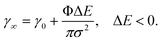 | (6) |
 | (7) |
| C | M w /kDa | N | R 0/nm | γ fpc∞/mN m−1 | Σ/a2 | n | R eq1/nm | R eq2/nm | σ/nm | z eq/nm | σ 0/nm | ΔE/kBT | γ ∞ /mN m−1 | γ ∞/γ0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.1 | 1.5 | 35 | 1.39 | 36.5 | 2 | 271 | 3.18 | 2.82 | 5.28 | 1.29 | 4.65 | −643 | 25.7 | 0.48 |
| 2.1 | 5 | 115 | 2.72 | 32.3 | 2.5 | 216 | 6.82 | 5.22 | 8.92 | 1.9 | 6.91 | −1705 | 27.7 | 0.52 |
| 2.1 | 10 | 230 | 3.9 | 31.5 | 5 | 108 | 8.94 | 5.58 | 11.04 | 1.91 | 8.14 | −2419 | 29.5 | 0.56 |
| 4.8 | 1.5 | 35 | 1.39 | 36.5 | 2 | 1414 | 3.95 | 3.66 | 8.75 | 2.83 | 7.68 | −1501 | 29.8 | 0.56 |
| 4.8 | 5 | 115 | 2.72 | 32.3 | 2.5 | 1131 | 8.91 | 7.44 | 13.71 | 4.52 | 9.78 | −3274 | 32.4 | 0.61 |
| 4.8 | 10 | 230 | 3.9 | 31.5 | 5 | 565 | 11.65 | 8.24 | 16.45 | 4.58 | 11.39 | −4629 | 32.8 | 0.62 |
The model is also able to predict the size, free energy gain and corresponding interfacial tension reduction for single free polymer chains (fpc) at the interface. A single chain of size R gains, when absorbed at the interface, an amount of free energy that is proportional to the area occupied by its N monomers, ΔFfpc = −γfpcNπa2. The values of γfpc are related to the values of γfpc∞ reported in the inset to Fig. 3 as a function of PEG molecular weight. Following the same approach of eqn (6), let us consider the total free energy for a layer of total area δA saturated by ΦδA/πR20 ideal polymers (at 2-D close-packing, Φ ≈ 0.91). The corresponding interfacial tension is γfpc∞ = −Ftotal/δA = −ΦΔFfpc/πR20 + (1 − Φ)γ0. Replacing ΔFfpc this reads
 | (8) |
The predictions for the size σ of the PEG–coated NPs in water are also in reasonable agreement with the Rh values quoted in Table 1 using the specified core radii C and Σ as reported in Table 2. Assuming Σ as a weakly increasing function of Mw is consistent with preliminary experimental evidence (see Section 2.1.1). Such result is a consequence of adsorbing the polymer in a fully collapsed state on a highly curved surface. This approach, however, underestimates the hydrodynamic radii for the low molecular weight PEG particles (Mw = 1.5 kDa), even assuming the surface area per polymer to be Σ≃a2. In this respect the deviations are most likely stemming from neglecting important factors in the conformation and density profile of the brushes arising from the topology of the NP surface (e.g. high curvature and nanoscale roughness). Finally, in order to calculate the interfacial quantities of interest as ΔE from eqn (5) or the surface tension γ∞ from eqn (6), the solvent quality τ2 has to be specified. Table 2 summarizes these values for a simple choice, τ2 = −0.2.‡‡ By looking at the values of the trapping energy at the interface we immediately see that they are much larger than the highest |ΔE0| = 100kBT used in the numerical simulations. As commented in Section 2.2 this calls for a refinement of the interaction potential for more detailed studies, but at the same time enforces the arguments by which our experiments are described by irreversible trapping at the interface. Moreover we see that the Flory model is able to yield values of the saturation interfacial tension which are in the range of the data in Fig. 2. However, the model predicts a weak dependence of γ∞ on the PEG Mw which is not observed in the experiments. Once more, these minor differences can be expected given the strong approximations made in the model which does not take into account the real Σ(Mw), the details of brush properties and the presence of polydispersity in the particle sizes.
These observations are further explored in Fig. 11 where three relevant energy differences are reported as a function σ and τ2. F(zeq)+γ0π(C + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) eq)2is the free energy difference at the interface between a coated NP and “naked” one with the same size. We observe that the addition of a polymer shell rapidly makes interfacial adsorption more energetically favorable as a function of σ; moreover, for solvents 2 of higher quality, having a polymer brush is also energetically beneficial due to positive solvation contributions. F(zeq) − F(0) represents the error one makes in calculating the free energy by assuming a fixed particle at z = 0 and neglecting the energy penalty paid by the polymer shell exposed to solvent 2. We observe, as one would intuitively expect, that this difference rapidly increases with σ for poor solvents, while the z = 0 approximation is accurate for τ1≈τ2 and/or small σ. i.e. low PEG Mw for a fixed core size. Finally, we note that solvent quality strongly affects how ΔE scales with particle size σ. For τ1 ≈ τ2 one has zeq ≈ 0 and thus σ ≈ σ0 which as a consequence gives ΔE ≈ −γ0σ2, as it can be observed at the front of Fig. 11. This quadratic dependence is consistent with the observations reported for hard, “naked” particles;28,54 in this regime, the behavior of our coated core-shell NPs is well described by an effective representation which neglects the actual role of the polymer shell in the energy balance. However, for poor solvents, the quadratic dependence is lost due to the fact that the contributions coming from the solvation of each portion of the shells exposed to the different solvents become increasingly different and σ is no longer describing the particle size at the interface. The details of ΔE(σ) depend on the specific choices of the parameters in the Flory model (e.g.Σ(Mw)), but it is anyway worth noting that the NP behavior becomes qualitatively different.
eq)2is the free energy difference at the interface between a coated NP and “naked” one with the same size. We observe that the addition of a polymer shell rapidly makes interfacial adsorption more energetically favorable as a function of σ; moreover, for solvents 2 of higher quality, having a polymer brush is also energetically beneficial due to positive solvation contributions. F(zeq) − F(0) represents the error one makes in calculating the free energy by assuming a fixed particle at z = 0 and neglecting the energy penalty paid by the polymer shell exposed to solvent 2. We observe, as one would intuitively expect, that this difference rapidly increases with σ for poor solvents, while the z = 0 approximation is accurate for τ1≈τ2 and/or small σ. i.e. low PEG Mw for a fixed core size. Finally, we note that solvent quality strongly affects how ΔE scales with particle size σ. For τ1 ≈ τ2 one has zeq ≈ 0 and thus σ ≈ σ0 which as a consequence gives ΔE ≈ −γ0σ2, as it can be observed at the front of Fig. 11. This quadratic dependence is consistent with the observations reported for hard, “naked” particles;28,54 in this regime, the behavior of our coated core-shell NPs is well described by an effective representation which neglects the actual role of the polymer shell in the energy balance. However, for poor solvents, the quadratic dependence is lost due to the fact that the contributions coming from the solvation of each portion of the shells exposed to the different solvents become increasingly different and σ is no longer describing the particle size at the interface. The details of ΔE(σ) depend on the specific choices of the parameters in the Flory model (e.g.Σ(Mw)), but it is anyway worth noting that the NP behavior becomes qualitatively different.
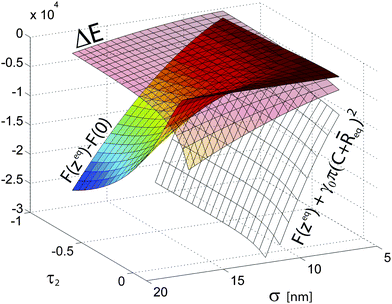 | ||
Fig. 11 Three relevant energy differences as a function σ and τ2 for core-shell NPs. The values of τ2 terminate at 0.13 = τ1. ΔE represents the trapping energy at the interface; F(zeq) − F(0) represents the error made in calculating the free energy assuming a particle forcefully centered at the interface; F(zeq) + γ0π(C + ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) eq)2 is the free energy difference at the interface between a coated NP and “naked” one the same hydrodynamic radius σ. eq)2 is the free energy difference at the interface between a coated NP and “naked” one the same hydrodynamic radius σ. | ||
2.4 Discussion
The combination of experimental data and numerical and modeling results lends itself to the discussion of several interesting issues. It is a noteworthy fact that our very simple simulation approach reproduces several qualitative features of our experiments and also confirms other experimental observations. In particular the occurrence of size selection at interfaces has been previously observed experimentally in the ΔE0 = 3–6kBT range for CdSe NPs, where the larger ones are preferentially adsorbed at the expenses of the smaller ones.35 The structure of the interfacial assembly also resembles the data reported from X-ray reflectivity measurements of 3 and 5 nm CdSe NPs at the water/toluene which highlight a highly dense, liquid-like monolayer.69 Moreover, the numerical study also suggests that cooperative processes become relevant for the adsorption kinetics. In this respect, the soft repulsion and the stability against aggregation provided by the thick PEG shells appear to be key ingredients in the unique manifestation of plateaus in the adsorption kinetics. The absence of the former and the presence of attraction and aggregation at the interface is bound to create a dense percolating particle network in which collective rearrangements and thus the adsorption kinetics are frozen.70The knowledge on the individual NP adsorption behavior gained with our simple Flory model is also remarkable. The main conclusion of the modeling approach lies in the acknowledgement that the adsorption energy is dominated by the solvation of the polymer shell. As a result a non-quadratic scaling of the trapping energy for core-shell NPs is predicted away from neutral solvation conditions as opposed to the case of “naked” particles.28,54 This fact stems from the complex and unique interplay between the reduction of the interfacial area between the two liquids when a NP sits at the interface and the free energy of the polymer brushes exposed to the two solvents as a function of polymer molecular weight and solvent quality. As a consequence, away from the conditions of equally good solvents, the particle is not centered at the interface and two separate length scales develop and determine the adsorption and the interactions between NPs at the interface. In particular, the three-dimensional character of the problem can no longer be neglected and we need one length scale σ which determines excluded volume interactions and establishes core-to-core separations and another one σ0 which takes into account the effective particle size at the interface. The excluded volume interactions, and thus inter-particle separation, are not necessarily determined at the interface plane, as for steric hindrance between icebergs floating on water. Conversely, σ0 will determine viscous forces and motion of the NPs at the interface.71 These facts can be implemented in the numerical simulations, especially upon gaining more detailed experimental information on the polymer grafting density as a function of Mw and of the conformation of the NPs at the interface, for instance by employing in situX-ray reflectometry. In this case, the knowledge of the shell solvation and polymer density profile could be used as an input parameter to obtain an accurate interaction potential for the numerical simulations and it could also be explicitly used in our Flory-model to estimate the effect of solvent quality, polymer molecular weight and core radius.
Finally, due to the evidence of very large trapping energies at the interface, it is necessary to clarify the nature of the measured interfacial tension γ. Following the arguments presented by Clegg and co-workers,72 this quantity is indeed conceptually different from the “classical” interfacial tension defined for soluble, surface-active molecules, e.g.surfactants and lipids. Soluble molecules at the interface coexist in thermodynamical equilibrium with others in the bulk and can thus adsorb to and desorb from the interface determining an equilibrium surface coverage and consequently an equilibrium interfacial tension which is independent of interface area but which depends on the bulk concentration. The situation is different for our NPs; given the large ΔE, particles in practice do not desorb once adsorbed and the surface coverage keeps growing until a saturated monolayer is formed, as also confirmed by our numerical simulations. Therefore the asymptotic long-time, steady state values of the interfacial tension become independent of the bulk concentration and what is measured in a tensiometry experiment is then an “effective” interfacial tension which is a direct measure of the number of adsorbed particles per unit area times ΔE, as presented in eqn (6). As seen in Section 2.2, the reversibility of particle binding plays also a fundamental role on the kinetics of the adsorption.
3 Experimental
3.1 Material and methods
3.1.1.1 Materials. Fe(ac)2 (batch 517933, Lot 03901JJ, purity ≥ 99.99%), NaCl, KSO4 and N-morpholinopropane sulfunic acid (MOPS) were purchased from Sigma-Aldrich, DOPA, from Acros and PEG(1.5)-NHS, PEG(5)-NHS and PEG(10)-NHS from Jemkem. nitroDOPA was synthesized adapting the protocol reported by Napolitano et al.73 by exchanging dopamine with DOPA.48PEG-nitroDOPA was synthesized as described previously.48
3.1.1.2 Synthesis and stabilization. Iron oxide cores with radii between 2 and 5 nm were synthesized by a non-aqueous non-gel method. In brief, 1 mmol Fe(ac)2 was dissolved in 5 ml benzylalcohol. The dispersion was heated to 70 °C using an oil bath and kept at this temperature for 1 h to dissolve the precursor. Using the oil bath as an energy source, NPs were nucleated and grown for 24 h under constant magnetic stirring at temperatures between 150 and 180 °C, depending on the targeted core size. NPs were washed twice with ethanol. As-synthesized NPs were stabilized with PEG-nitroDOPA. 6 mg PEG nitroDOPA was dissolved in 0.5 ml ethanol before 5 mg iron oxide NPs dispersed in ethanol at a NP concentration of ≃ 10 mg ml−1 were added. PEG-nitroDOPA was adsorbed on iron oxide NPs for 24 h at 50 °C under constant mechanical stirring (Thermomixer comfort, Vaudaux-Eppendorf, Switzerland). Stabilized nanoparticles were purified by dialysis and Sephadex column separation (Sephadex G-75). Purified NPs were freeze-dried and dispersed in Millipore water (R = 18.2 M Ω, TAC ≤ 6 ppb) at a concentration of 1 mmol.
4 Conclusions
In this paper we have shown a combination of experimental, numerical and theoretical results aimed at deepening our understanding of the adsorption behavior of composite, core-shell NPs at liquid interfaces. Our findings highlight the fact that the presence of a polymer brush on the NP surface leads to a complex behavior, absent for hard objects, in the collective interfacial adsorption kinetics and in the free energy of individual particles at the interface. Concluding, we highlight once more the simplicity of our measurements, simulations and models which nonetheless led to significant new insights. The study of complex objects at liquid–liquid interfaces, like core-shell NPs, is still in its infancy and we therefore expect further rapid advances of the field to take place in the near future.5Acknowledgements
The authors acknowledge Prof. N. D. Spencer and Prof. M. Textor for support. LI acknowledges financial support from MC-IEF- 2009-252926. EA and ER acknowledge financial support from COST Action D43. KS and EDG are supported by the SNSF (Grant No. PP002_126483/1). MK is supported by SNSF (Grant No. SCOPES IZ73Z0-128169).References
- W. Zhao, M. A. Brook and Y. F. Li, ChemBioChem, 2008, 9, 2363–2371 CrossRef CAS.
- S. Lal, S. E. Clare and N. J. Halas, Acc. Chem. Res., 2008, 41, 1842–1851 CrossRef CAS.
- C. Sun, J. S. H. Lee and M. Q. Zhang, Adv. Drug Delivery Rev., 2008, 60, 1252–1265 CrossRef CAS.
- M. J. Pittet, F. K. Swirski, F. Reynolds, L. Josephson and R. Weissleder, Nat. Protoc., 2006, 1, 73–79 CrossRef CAS.
- M. Namdeo, S. Saxena, R. Tankhiwale, M. Bajpai, Y. M. Mohan and S. K. Bajpai, J. Nanosci. Nanotechnol., 2008, 8, 3247–3271 CrossRef CAS.
- J. H. Lee, Y. M. Huh, Y. Jun, J. Seo, J. Jang, H. T. Song, S. Kim, E. J. Cho, H. G. Yoon, J. S. Suh and J. Cheon, Nat. Med., 2006, 13, 95–99 CrossRef.
- A. C. Balazs, T. Emrick and T. P. Russell, Science, 2006, 314, 1107–1110 CrossRef CAS.
- J. Xie, C. Xu, N. Kohler, Y. Hou and S. Sun, Adv. Mater., 2007, 19, 3163 CrossRef CAS.
- M. F. Bedard, D. Braun, G. B. Sukhorukov and A. G. Skirtach, ACS Nano, 2008, 2, 1807–1816 CrossRef CAS.
- D. A. Gorin, S. A. Portnov, O. A. Inozemtseva, Z. Luklinska, A. M. Yashchenok, A. M. Pavlov, A. G. Skirtach, H. Mohwald and G. B. Sukhorukov, Phys. Chem. Chem. Phys., 2008, 10, 6899–6905 RSC.
- X. Zhao, J. Kim, C. A. Cezar, N. Huebsch, K. Lee, K. Bouhadir and D. J. Mooney, Proc. Natl. Acad. Sci. U. S. A., 2010, 108, 67–72 CrossRef.
- E. Amstad, J. Kohlbrecher, E. Müller, T. Schweizer, M. Textor and E. Reimhult, Nano Lett., 2011, 11, 1664–1670 CrossRef CAS.
- A. S. Angelatos, B. Radt and F. Caruso, J. Phys. Chem. B, 2005, 109, 3071–3076 CrossRef CAS.
- M. Grzelczak, J. Perez-Juste, P. Mulvaney and L. M. Liz-Marzan, Chem. Soc. Rev., 2008, 37, 1783–1791 RSC.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS.
- M. Grzelczak, J. Vermant, E. M. Furst and L. Liz-Marzan, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS.
- A. Boeker, J. He, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231–1248 RSC.
- H. W. Duan, D. Y. Wang, N. S. Sobal, M. Giersig, D. G. Kurth and H. Mohwald, Nano Lett., 2005, 5, 949–952 CrossRef CAS.
- Y. Lin, H. Skaff, A. Boker, A. D. Dinsmore, T. Emrick and T. P. Russell, J. Am. Chem. Soc., 2003, 125, 12690–12691 CrossRef CAS.
- H. Skaff, Y. Lin, R. Tangirala, K. Breitenkamp, A. Boker, T. P. Russell and T. Emrick, Adv. Mater., 2005, 17, 2082 CrossRef CAS.
- J. T. Russell, Y. Lin, A. Boker, L. Su, P. Carl, H. Zettl, J. B. He, K. Sill, R. Tangirala, T. Emrick, K. Littrell, P. Thiyagarajan, D. Cookson, A. Fery, Q. Wang and T. P. Russell, Angew. Chem., Int. Ed., 2005, 44, 2420–2426 CrossRef CAS.
- E. Glogowski, R. Tangirala, J. B. He, T. P. Russell and T. Emrick, Nano Lett., 2007, 7, 389–393 CrossRef CAS.
- P. Arumugam, D. Patra, B. Samanta, S. S. Agasti, C. Subramani and V. M. Rotello, J. Am. Chem. Soc., 2008, 130, 10046 CrossRef CAS.
- H. Xia and D. Wang, Adv. Mater., 2008, 20, 4253–4256 CrossRef CAS.
- B. S. Binks and T. S. Horozov, Colloidal particles at liquid interfaces, Cambridge University Press, Cambridge, 2006 Search PubMed.
- F. Bresme and M. Oettel, J. Phys.: Condens. Matter, 2007, 19, 413101 CrossRef.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572 CrossRef CAS.
- F. Reincke, S. G. Hickey, W. K. Kegel and D. Vanmaekelbergh, Angew. Chem., Int. Ed., 2004, 43, 458–462 CrossRef CAS.
- F. Reincke, W. K. Kegel, H. Zhang, M. Nolte, D. Y. Wang, D. Vanmaekelbergh and H. Mohwald, Phys. Chem. Chem. Phys., 2006, 8, 3828–3835 RSC.
- Y. K. Park, S. H. Yoo and S. Park, Langmuir, 2007, 23, 10505–10510 CrossRef CAS.
- Y. K. Park and S. Park, Chem. Mater., 2008, 20, 2388–2393 CrossRef CAS.
- M. Oettel and S. Dietrich, Langmuir, 2008, 24, 1425–1441 CrossRef CAS.
- F. Bresme, H. Lehle and M. Oettel, J. Chem. Phys., 2009, 130, 214711 CrossRef.
- Y. Lin, H. Skaff, T. Emrick, A. D. Dinsmore and T. P. Russell, Science, 2003, 299, 226–229 CrossRef CAS.
- H. W. Duan, D. A. Wang, D. G. Kurth and H. Mohwald, Angew. Chem., Int. Ed., 2004, 43, 5639–5642 CrossRef CAS.
- J. B. He, Z. W. Niu, R. Tangirala, J. Y. Wan, X. Y. Wei, G. Kaur, Q. Wang, G. Jutz, A. Boker, B. Lee, S. V. Pingali, P. Thiyagarajan, T. Emrick and T. P. Russell, Langmuir, 2009, 25, 4979–4987 CrossRef CAS.
- K. A. Tay and F. Bresme, J. Am. Chem. Soc., 2006, 128, 14166–14175 CrossRef CAS.
- A. S. Almusallam, Phys. Chem. Chem. Phys., 2008, 10, 3099–3107 RSC.
- L. Isa, E. Amstad, M. Textor and E. Reimhult, Chimia, 2010, 64, 145–149 CrossRef CAS.
- R. Weissleder, D. D. Stark, B. L. Engelstad, B. R. Bacon, C. C. Compton, D. L. White, P. Jacobs and J. Lewis, Am. J. Roentgenol., 1989, 152, 167–173 CAS.
- J. H. Lee, Q. Wu and W. Park, Opt. Lett., 2009, 34, 443–445 CrossRef CAS.
- E. Amstad, S. Zurcher, A. Mashaghi, J. Y. Wong, M. Textor and E. Reimhult, Small, 2009, 5, 1334–1342 CrossRef CAS.
- C. J. Xu, K. M. Xu, H. W. Gu, R. K. Zheng, H. Liu, X. X. Zhang, Z. H. Guo and B. Xu, J. Am. Chem. Soc., 2004, 126, 9938–9939 CrossRef CAS.
- J. Xie, C. Xu, N. Kohler, Y. Hou and S. Sun, Adv. Mater., 2007, 19, 3163 CrossRef CAS.
- H. W. Gu, Z. M. Yang, J. H. Gao, C. K. Chang and B. Xu, J. Am. Chem. Soc., 2005, 127, 34–35 CrossRef CAS.
- J. H. Gao, G. L. Liang, J. S. Cheung, Y. Pan, Y. Kuang, F. Zhao, B. Zhang, X. X. Zhang, E. X. Wu and B. Xu, J. Am. Chem. Soc., 2008, 130, 11828–11833 CrossRef CAS.
- E. Amstad, T. Gillich, I. Bilecka, M. Textor and E. Reimhult, Nano Lett., 2009, 9, 4042–4048 CrossRef CAS.
- E. Amstad, A. U. Gehring, H. Fischer, V. V. Nagaiyanallur, G. Haehner, M. Textor and E. Reimhult, J. Phys. Chem. C, 2011, 115, 683–691 CAS.
- D. B. Thiessen, D. J. Chione, C. B. McCreary and W. B. Krantz, J. Colloid Interface Sci., 1996, 177, 658–665 CrossRef CAS.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS.
- E. Amstad, L. Isa and E. Reimhult, Chimia, 2010, 64, 826–826 CrossRef CAS.
- S. Kutuzov, J. He, R. Tangirala, T. Emrick, T. P. Russell and A. Boker, Phys. Chem. Chem. Phys., 2007, 9, 6351–6358 RSC.
- K. Du, E. Glogowski, T. Emrick, T. P. Russell and A. D. Dinsmore, Langmuir, 2010, 26, 12518–12522 CrossRef CAS.
- M. Rodahl, F. Hook, A. Krozer, P. Brzezinski and B. Kasemo, Rev. Sci. Instrum., 1995, 66, 3924–3930 CrossRef CAS.
- M. T. Muller, X. P. Yan, S. W. Lee, S. S. Perry and N. D. Spencer, Macromolecules, 2005, 38, 3861–3866 CrossRef.
- B. Malisova, S. Tosatti, M. Textor, K. Gademann and S. Zurcher, Langmuir, 2010, 26, 4018–4026 CrossRef CAS.
- E. Reimhult, C. Larsson, B. Kasemo and F. Hook, Anal. Chem., 2004, 76, 7211–7220 CrossRef CAS.
- F. Hook, B. Kasemo, T. Nylander, C. Fant, K. Sott and H. Elwing, Anal. Chem., 2001, 73, 5796–5804 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic press, 2002 Search PubMed.
- M. Allen and D. Tildesley, Computer Simulation of Liquids, Oxford Science Publications, 1987 Search PubMed.
- P.-G. De Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1988 Search PubMed.
- M. Kröger, O. Peleg and A. Halperin, Macromolecules, 2010, 43, 6213–6224 CrossRef.
- A. Halperin, M. Kröger and E. Zhulina, Macromolecules, 2011, 44, 3622–3638 CrossRef CAS.
- R. M. and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, England, 2003 Search PubMed.
- L. Livadaru, R. R. Netz and H. J. Kreuzer, J. Chem. Phys., 2003, 118, 1404–1416 CrossRef CAS.
- A. Halperin and M. Kröger, Langmuir, 2009, 25, 11621–11634 CrossRef CAS.
- K. Devanand and J. C. Selser, Macromolecules, 1991, 24, 5943–5947 CrossRef CAS.
- Y. Lin, A. Boker, H. Skaff, D. Cookson, A. D. Dinsmore, T. Emrick and T. P. Russell, Langmuir, 2005, 21, 191–194 CrossRef CAS.
- E. Sanz, K. A. White, P. S. Clegg and M. E. Cates, Phys. Rev. Lett., 2009, 103, 255502 CrossRef.
- T. M. Fischer, P. Dhar and P. Heinig, J. Fluid Mech., 2006, 558, 451–475 CrossRef.
- P. S. Clegg, E. M. Herzig, A. B. Schofield, S. U. Egelhaaf, T. S. Horozov, B. P. Binks, M. E. Cates and W. C. K. Poon, Langmuir, 2007, 23, 5984–5994 CrossRef CAS.
- A. Napolitano, M. Dischia, C. Costantini and G. Prota, Tetrahedron, 1992, 48, 8515–8522 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: ESI contains an .avi movie of a pendant drop tensiometry experiment and additional QCM-D and numerical simulation data. See DOI: 10.1039/c1sm05407d |
| ‡ Nitrocatechol-PEG in this molecular weight range has been shown to form brushes when adsorbed on TiO2.57 |
| § From eqn (6), it follows that γ/γ0 = 1 − Φ only if one assumes γ0 = ΔE/πσ2 but the shape of the curve is not affected by the choice of γ0. |
| ¶ For the case of a planar brush, V(R) ∼ R, while for a free polymer chain in solution, V(R) ∼ R3 |
| || For a particle to be considered at the interface, we assume |zeq| ≤ C. |
| ** We emphasize that the following discussion is not dependent on this particular choice of σ0 but is valid for any chosen effective size at the interface. |
| †† However, as long as ϕ ≪ 1, a scaling analysis can be trivially performed for Reqi ≪ C and Reqi ≫ C, corresponding to the limiting cases of a planar brush and non–tethered chains. Interactive online facility available at http://www.complexfluids.ethz.ch/colloids |
| ‡‡ The results for γ∞ are anyway only weakly dependent on the precise value of τ2. |
| This journal is © The Royal Society of Chemistry 2011 |
