Design of stiff, tough and stretchy hydrogel composites via nanoscale hybrid crosslinking and macroscale fiber reinforcement†
Shaoting
Lin
a,
Changyong
Cao
a,
Qiming
Wang
a,
Mark
Gonzalez
a,
John E.
Dolbow
b and
Xuanhe
Zhao
*ac
aDepartment of Mechanical Engineering and Materials Science, Duke University, Durham, NC 27708, USA. E-mail: zhaox@mit.edu
bDepartment of Civil and Environmental Engineering, Duke University, Durham, NC 27708, USA
cSoft Active Materials Laboratory, Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 30th June 2014
Abstract
Hydrogels' applications are usually limited by their weak mechanical properties. Despite recent great progress in developing tough hydrogels, it is still challenging to achieve high values of stretchability, toughness and modulus all together in synthetic hydrogels. In this paper, we designed highly stretchable, tough, yet stiff hydrogel composites via a combination of nanoscale hybrid crosslinking and macroscale fiber reinforcement. The hydrogel composites were constructed by impregnating a 3D-printed thermoplastic-fiber mesh with a tough hydrogel crosslinked both covalently and ionically. The hydrogel composites can achieve a fracture energy of over 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2, a modulus of over 6 MPa, and can be stretched over 2.8 times even in the presence of large structural defects. The enhancement of toughness in the new hydrogel composites relies on multiple pairs of toughening mechanisms which span over multiple length scales. A theoretical model is further developed to predict the toughness and modulus of the hydrogel composites and guide the design of future materials.
000 J m−2, a modulus of over 6 MPa, and can be stretched over 2.8 times even in the presence of large structural defects. The enhancement of toughness in the new hydrogel composites relies on multiple pairs of toughening mechanisms which span over multiple length scales. A theoretical model is further developed to predict the toughness and modulus of the hydrogel composites and guide the design of future materials.
1. Introduction
Most synthetic hydrogels are compliant and fragile with examples ranging from Jell-O to contact lenses.1–3 Increasing the stiffness of synthetic hydrogels usually leads to deterioration of their toughness and stretchability.4 On the other hand, natural hydrogels such as load-bearing tissues can be stiff, tough and stretchy – a combination of properties that enables their robustness under mechanical loads. For example, articular cartilages, albeit containing ∼70% water, have toughnesses over 1000 J m−2, moduli over 1 MPa, and are capable of sustaining stretches over 2 times.5,6 Designing new synthetic hydrogels that can match or exceed the mechanical performance of natural hydrogels is of critical importance to a wide range of applications spanning the regeneration of load-bearing tissues, to antifouling coatings, to swellable packers in oil and gas recovery.7–9 Over the last few decades, various types of hydrogels with enhanced mechanical properties have been developed such as double-network hydrogels,10 hybrid-crosslinking hydrogels,11–15 hydrogels with crystalline domains,16,17 and fiber-reinforced hydrogels.18–21 Despite the great promise, it is still challenging for existing hydrogels to achieve the combination of high toughness, high stiffness, and stretchability of articular cartilages.1–3 For example, double-network and hybrid-crosslinked hydrogels exhibit impressive toughnesses over 1000 J m−2, but their moduli are usually low – on the order of a few kilopascals.10–12 Recently developed fiber-reinforced hydrogels can be relatively stiff, but they are not as deformable as cartilages.19,20 While highly stretchable and resilient hydrogels have also been synthesized, their toughnesses and moduli are generally inferior to those of cartilages.22–24In addition, the general principle for the design of tough hydrogels3 is to implement mechanisms for dissipating mechanical energy and maintaining high elasticity. However, existing tough hydrogels usually rely on a single pair of toughening mechanisms (see Table 1).1–3,13 If either of the mechanisms becomes invalid under mechanical or environmental loads, the hydrogel will lose its high toughness. For example, tough hydrogels that rely on long-chain networks to maintain high elasticity and reversible crosslinking to dissipate mechanical energy will become weak and/or brittle, if the reversible crosslinkers in them are eliminated.12
Here, we report a novel hydrogel that contains around 80% water but can achieve an extremely high toughness (>30 kJ m−2), a high modulus (>6 MPa), and can be stretched over 2.8 times even in the presence of large structural defects. Moreover, the new hydrogel innovatively integrates multiple toughening mechanisms across multiple length scales to make it more robust under mechanical and environmental loads than existing tough hydrogels (Table 1). At the nanoscale, we interpenetrate a physically crosslinked short-chain polymer network with a chemically crosslinked long-chain network to form a tough hydrogel with hybrid crosslinking.12 The reversible crosslinking of physical crosslinkers dissipates mechanical energy in the hydrogel under deformation, while the long-chain network maintains the high elasticity. At the macroscale, we construct a thermoplastic-elastomer fiber mesh with 3D printing and infuse the hydrogel into the mesh. The stiff yet stretchy fibers lead to a high modulus for the composite at moderate deformation. Under large deformations, the plastic deformation and fracture of fibers significantly dissipate mechanical energy while the stretchy hydrogel can still maintain the integrity of the composite (Table 1).
2. Experimental details
2.1 Fabrication of a fiber mesh by 3D printing
A fiber mesh was constructed by printing a thermoplastic Flex EcoPLA (Formfutura, Netherland) with a 3D printer MakerBot Replicator 2 (MakerBot, US). The heating temperature was set to 230 °C and the printing resolution was fixed at 0.2 mm. The extruding speed while printing was controlled at 150 mm s−1. The resultant fiber mesh consists of 4–8 layers of fibers overlapped in orthogonal directions. The radius of the fiber can be tuned from 100 μm to 400 μm, and the distance between adjacent fibers in the same layer can be tuned from 1 mm to 8 mm.2.2 Fabrication of the fiber-reinforced hydrogel
A pre-gel solution of alginate and polyacrylamide was prepared by mixing 4.1 mL 4.8% alginate (Sigma, A2033) and 5.5 mL 18.7% acrylamide (Sigma, A8887). We added 377 μL of 0.2 g per 100 ml N,N-methylenebisacrylamide (Sigma, 146072) as the crosslinker for polyacrylamide and 102 μL of 0.2 M ammonium persulphate (Sigma, 248614) as a photo initiator for polyacrylamide. After degassing in the pre-gel solution in a vacuum chamber, we added 200 μL of 1 M calcium sulphate (Sigma, C3771) as the crosslinker for alginate and 8.2 μL N,N,N′,N′-tetramethylethylenediamine (Sigma, T7024-50M) as the crosslinking accelerator for polyacrylamide. Thereafter, the pre-gel solution was infused into the printed fiber mesh and the composite was subjected to ultraviolet light for 60 minutes with 8 W power and 254 nm wavelength to cure the gel. The resultant fiber-reinforced hydrogel was sealed with parafilm for 12 hours to let Ca2+ diffuse homogeneously throughout the gel.2.3 Fabrication of the artificial intervertebral disc
A stretchy fiber mesh representing the stiff annulus fibrosus was fabricated by layer-by-layer 3D printing. Thereafter, the alginate–polyacrylamide hydrogel was synthesized based on the aforementioned process. The stretchy fiber mesh was placed in a plastic mould and then alginate–polyacrylamide hydrogel was poured into the mould and infused into the stretchy fiber mesh. The resultant artificial intervertebral disc was cured in a UV oven for 60 minutes and was then left in a humid box for 1 day to stabilize the reaction.3. Results
3.1 Experimental results
Fig. 1 shows the fabrication process and multiscale structure of the stretchy-fiber-reinforced tough hydrogel. In brief, a fiber mesh was constructed by printing a thermoplastic elastomer Flex EcoPLA (Formfutura, Netherland) into layers of fibers. The fibers within the same layers are parallel to one another, while fibers in adjacent layers are orthogonal to one another. Fibers of adjacent layers were bonded together during the curing of the thermoplastic elastomer. Thereafter, a pre-gel solution of alginate and polyacrylamide (PAAm) was infused into the printed fiber mesh and cured to form the fiber-reinforced hydrogel (see Experimental details). Fig. S1† shows the volume fraction of the fiber mesh in the hydrogel. We denote the radius of the fiber as R, the distance between two adjacent fibers in a layer along the applied force as δ∥, and the distance between two adjacent fibers in a layer perpendicular to the applied force as δ⊥. Considering the configuration of the fiber mesh, the area fraction of fibers along the applied force can be calculated as A∥ = πR/(4δ∥), the area fraction of fibers perpendicular to the applied force as A⊥ = πR/(4δ⊥), and the volume fraction of fibers in the fiber-reinforced hydrogel as Vf = A∥ + A⊥ (Fig. S1†).The pure-shear test was used to measure the fracture energy, stiffness, and critical stretch of the fiber-reinforced hydrogel (Fig. S2†).25–27 In brief, two identical pieces of the fiber-reinforced hydrogel were fabricated with the same thickness T, width W and high H, where W ≫ H ≫ T. Both pieces of samples were clamped along their long edges with rigid plates. A notch was introduced into the first sample, which was then gradually pulled to a critical stretch λc until a crack began to propagate. Thereafter, the second sample without notch was uniformly stretched to the same stretch as λc, with nominal stress s recorded as a function of the stretch λ. Based on the measured data, the fracture energy of the gel can be calculated as25,26
 | (1) |
 | (2) |
Fig. 2a and Video S1† show the deformation and fracture processes of a fiber-reinforced hydrogel (A∥ = 1.93%, A⊥ = 4.07%) with a notch under the pure-shear test. Since both the hydrogel and the fiber mesh are relatively stretchable, the tip of the notch is blunted as the sample is gradually deformed28 (Fig. 2a). Meanwhile, the fiber and the hydrogel matrix begin to detach from each other under subsequent deformation, owing to their weak adhesion (Fig. 2a). As the stretch further increases, fibers in a segment perpendicular to the notch plane begin to fracture. To be conservative, we regard the stretch when the first fiber begins to fracture as the critical stretch of the fiber-reinforced hydrogel, λc, to measure and calculate its fracture energy (Fig. S2† and 2). However, it should be noted that even after all the fibers in the segment are fractured, the remaining hydrogel can still be highly stretched, maintaining the integrity of the composite (Fig. 2a). Therefore, the fracture process of the fiber-reinforced alginate–PAAm hydrogel is distinctly different from those of traditional fiber-reinforced composites, where fibers usually bridge the cracked matrices.29,30 In the current study, conversely, the fibers are first fractured, while the highly stretchable hydrogel matrix maintains the integrity of the sample (Fig. 2a).
Then, in Fig. 3a we plot the stress–stretch curve of the un-notched alginate–PAAm hydrogel reinforced with stretchy thermoplastic-elastomer fibers (A∥ = 1.93%, A⊥ = 4.07%). The critical stretches obtained from the notched samples are marked on the curves as crosses. For comparison, we also measure the stress–stretch curves of two control samples: the alginate–PAAm hydrogel without fiber reinforcement, and the hydrogel reinforced with rigid but relatively brittle PLA (polylactic acid, MakerBot, US) fibers. As shown in Fig. 3a, the hydrogel reinforced with thermoplastic-elastomer fibers can indeed provide relatively high values of the modulus (1.4 MPa), toughness (8554 J m−2) and stretchability (λc ≈ 2.80 for the notched sample). In comparison, the hydrogel reinforced with brittle PLA fibers has a high modulus but relatively low toughness (967 J m−2), because the stiff but brittle fibers are fractured at a very low stretch (λc ≈ 1.09 for the notched sample). On the other hand, the hydrogel without fiber reinforcement is highly stretchable (λc ≈ 19 for the notched sample) but its modulus is very low (70.0 kPa). Therefore, the design of stiff, tough and stretchy hydrogels in the current study relies on a combination of the stiff yet stretchy fiber mesh and the tough hydrogel matrix. Furthermore, the strengthening of the composite indeed relies on multiple mechanisms across multiple length scales (Fig. 1a and Table 1).
We further vary the area fraction of stretchy thermoplastic-elastomer fibers along the direction of the applied force (A∥ = 0.94–7.69%), while maintaining the area fraction of orthogonal fibers constant (A⊥ = 4.07%). From Fig. 3b it can be seen that as the fiber density increases, the modulus and yield stress of the composite increase, and the critical stretch maintains in the range of 2.8 to 3.8. The yield stretch of the thermoplastic-elastomer fiber mesh is ∼1.4, below which the fiber-reinforced hydrogel can be repeatedly stretched and un-stretched multiple cycles without inducing permanent deformation or damage of the sample (Fig. 3c). Hysteresis loops can also be observed on the loading–unloading curves over multiple cycles, potentially due to viscoelasticity of the thermoplastic-elastomer fibers and reversible crosslinking in the hydrogel matrix. The repeated hysteresis loop over multiple loading–unloading cycles is a critical character of anti-fatigue hydrogels.15,31,32
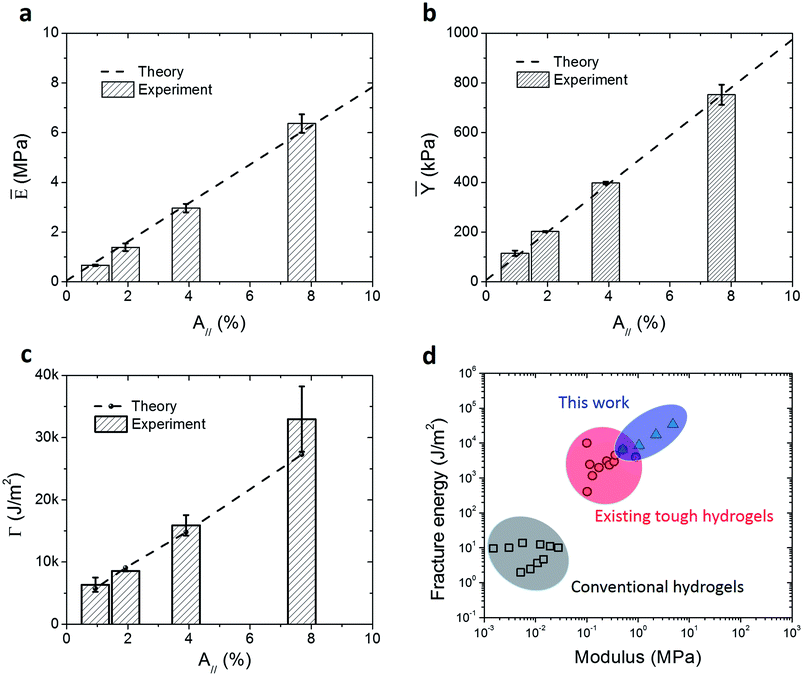
The measured modulus, yield stress, and fracture energy of the alginate–PAAm hydrogel reinforced with various densities of fiber meshes are shown in Fig. 5. As the area fraction of fibers along the applied force A∥ increases from 0.94% to 7.69%, the plane-strain Young's modulus of the composite increases from 0.66 to 6.37 MPa, the yield stress from 115 to 753 kPa, and the fracture toughness from 6360 to 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2, while the critical stretch remains relatively constant, in the region as 2.8–3.8.
000 J m−2, while the critical stretch remains relatively constant, in the region as 2.8–3.8.
3.2 Theoretical models
While the fiber-reinforced hydrogel has orthotropic mechanical properties, the current study is focused on the properties along the applied-force direction. When the fiber-reinforced hydrogel is stretched in a pure-shear test (inset in Fig. 2a), the majority of the hydrogel matrix undergoes plane-strain tension, and the fibers along the applied force undergo uniaxial tension. Therefore, the plane-strain Young's modulus of the composite hydrogel can be predicted as| Ē = A∥Ef + (1 − A∥)Ēg | (3) |
Similarly, the plane-strain yield (nominal) stress of the fiber-reinforced hydrogel can be predicted as
 | (4) |
 is the nominal stress in an un-notched pure hydrogel under the pure shear test at the yield stretch of the fiber λYf ≈ 1.4 (Fig. S3b†).
is the nominal stress in an un-notched pure hydrogel under the pure shear test at the yield stretch of the fiber λYf ≈ 1.4 (Fig. S3b†).
Fracture energy of fiber-reinforced materials generally consists of contributions from the fiber mesh, the matrix, and friction between the matrix and fibers. In the current study, since the fibers debond from the hydrogel at moderate deformation, we neglect the fracture energy due to friction between fibers and the hydrogel matrix. Furthermore, in measuring the fracture energy, we regard the stretch when the crack begins to propagate in the fiber mesh as the critical stretch, λc. Therefore, the fracture energy of the fiber-reinforced hydrogel is a summation of the fracture energy of the fiber mesh and the work done to stretch the hydrogel matrix to λc in the pure shear test, i.e.
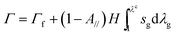 | (5) |
 | (6) |
 is the work of extension of a single fiber in the fiber mesh, δ⊥ gives a typical length scale of the fiber mesh, and α is a function of δ∥/δ⊥ and the constitutive law of a single fiber. The curve of sfvs. λf of a single fiber is shown in Fig. S3b,† where the fracture stretch of a single fiber λcf and the work of extension
is the work of extension of a single fiber in the fiber mesh, δ⊥ gives a typical length scale of the fiber mesh, and α is a function of δ∥/δ⊥ and the constitutive law of a single fiber. The curve of sfvs. λf of a single fiber is shown in Fig. S3b,† where the fracture stretch of a single fiber λcf and the work of extension  have been measured to be 5 and 51
have been measured to be 5 and 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 J m−3, respectively.
700 J m−3, respectively.
From eqn (5) and (6), we can see that the fracture energy of the fiber-reinforced hydrogel can be predicted based on the measured stress vs. stretch relationship of a pure hydrogel and a single fiber (Fig. S3†), given the non-dimensional parameter α. In order to calculate α, we construct a finite-element model of a notched fiber mesh, which undergoes the pure-shear test, using the software package ABAQUS 6.10. The fiber meshes of different geometries (i.e., δ∥/δ⊥ = 0.5, 1, 2, 4; and H/δ⊥ = 3, 5, 7, 9, 11) are modeled with beam elements. Following the experimental setup, one edge of the model is fixed and the opposite edge of the model is subjected to a prescribed vertical displacement. Mesh insensitivity of the model is verified by uniformly reducing the element sizes: no significant change in the calculated structural response is observed. Since unloading of the fiber mesh is not considered in the model,33 the elastoplastic fiber can be taken as a hyperelastic material that follows the stress vs. stretch relationship shown in Fig. S3b.†
In the calculation, as the stretch in the fiber segment right in front the notch reaches λcf (i.e., the fiber segment begins to fracture), and the stretch of the fiber mesh is recorded as the critical stretch, λc (Fig. 2b). Considering the pure-shear test, the fracture energy of the fiber mesh can also be calculated as  . Further considering eqn (6), we can express the non-dimensional parameter α as
. Further considering eqn (6), we can express the non-dimensional parameter α as
 | (7) |
4. Discussion and conclusion
In Fig. 5a–c, we compare the measured Young's modulus, yield stress, and fracture energy of the fiber-reinforced hydrogel with the theoretical predictions from eqn (3)–(6). It can be seen that the theoretical and experimental results consistently match for various fiber concentrations. In addition, from the experimental and theoretical results, we can see that the modulus, yield stress, and fracture energy of the fiber-reinforced hydrogel increase almost linearly with the area fracture of fibers along the applied-force direction, A∥. While increasing the modulus of conventional hydrogels usually corresponds to a reduction in toughness, the fiber reinforcement allows for an increase in the modulus, toughness and yield stress. Furthermore, the critical stretch for crack propagation in the fiber mesh is over 2.8, higher than the critical stretches of the existing fiber-reinforced hydrogels and cartilages.19,20In Fig. 5d, we further compare the fracture energies and moduli of various types of synthetic hydrogels reported in the literature.2,13 It can be seen that the fracture energy of conventional hydrogels is usually below 100 J m−2, with moduli below 100 kPa. Tough hydrogels that rely on a single pair of toughening mechanisms can reach fracture energies up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2 and moduli up to 1 MPa (Fig. 5d and Table 1). By comparison, the stretchy-fiber-reinforced hydrogel developed in the current study can reach a fracture energy over 33
000 J m−2 and moduli up to 1 MPa (Fig. 5d and Table 1). By comparison, the stretchy-fiber-reinforced hydrogel developed in the current study can reach a fracture energy over 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2 and a modulus over 6 MPa.
000 J m−2 and a modulus over 6 MPa.
We then discuss the robustness of hydrogels under environmental loads. Since the stretchy-fiber-reinforced hydrogel integrated multiple pairs of toughening mechanisms (Table 1), it can still maintain its high toughness even when some of the mechanisms become invalid. For example, we soak the fiber-reinforced PAAm–alginate hydrogel in 2% EDTA (ethylenediamine tetraacetic acid) (in 1 M NaOH, which is 1 Normality NaOH) to chelate Ca2+ in the hydrogel matrix, which eliminates the dissipation mechanism of reversible crosslinking (Fig. S4a†). However, since the viscoelasticity and plasticity of the fiber mesh can still dissipate the mechanical energy under deformation, the resultant fiber-reinforced hydrogel without Ca2+ can still reach an impressively high modulus of ∼6.7 MPa and a toughness of ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2 (Fig. S4a† and Table 1). In comparison, we also soak a PAAm–alginate hydrogel without fiber reinforcement in 2% EDTA (ethylenediamine tetraacetic acid) (in 1 M NaOH). Due to the loss of the only dissipation mechanism in the hydrogel, the resultant hydrogel indeed becomes weaker with a fracture energy reduced from 9000 J m−2 to 400 J m−2 (Fig. S4b† and Table 1).
000 J m−2 (Fig. S4a† and Table 1). In comparison, we also soak a PAAm–alginate hydrogel without fiber reinforcement in 2% EDTA (ethylenediamine tetraacetic acid) (in 1 M NaOH). Due to the loss of the only dissipation mechanism in the hydrogel, the resultant hydrogel indeed becomes weaker with a fracture energy reduced from 9000 J m−2 to 400 J m−2 (Fig. S4b† and Table 1).
In addition, the fiber-reinforced hydrogel can be easily printed and cast into various shapes for potential applications in biomedical and robotic areas.3,8,34,35 For example, in Fig. S5a,† we demonstrate an artificial intervertebral disc made of the fiber-reinforced hydrogel. The inner part of the artificial intervertebral disc consists of a pure PAAm–alginate hydrogel to approximate the relatively compliant nucleus pulposus, which is surrounded by the fiber-reinforced hydrogel to approximate the relatively stiff annulus fibrosus. We further compare the force vs. displacement curves of artificial intervertebral discs made of the fiber-reinforced hydrogel, PAAm–alginate and PAAm hydrogels without fiber reinforcement (Fig. S5b†). It can be seen that, by using the stretchy-fiber reinforcement, we can indeed tune the overall stiffness of the artificial intervertebral disc over a wide range, while maintaining the high toughness of the hydrogel.
In this paper, we integrate nanoscale hybrid crosslinking and macroscale fiber reinforcement to develop a novel hydrogel with an unprecedented set of mechanical properties including a high toughness (>33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2), a high modulus (>6 MPa), and a high stretchability (>2.8 with a notch). Theoretical and computational models are further developed to predict the mechanical properties and guide the design of the new hydrogels. The combined experimental and theoretical results show that the toughness, modulus and yield stress of the new hydrogel can be uniformly increased by rational design of the stretchy-fiber mesh and the tough hydrogel matrix. Due to the multi-scale multi-mechanism strengthening, the new hydrogel is more robust against mechanical and environmental loads than conventional tough hydrogels. In addition, the fiber mesh can be printed into various shapes with commercially available 3D printers, on which the tough hydrogel matrix can be cast. The combined theoretical and experimental study opens up new avenues to both fundamental understanding and practical applications of hydrogels with extraordinary properties.
000 J m−2), a high modulus (>6 MPa), and a high stretchability (>2.8 with a notch). Theoretical and computational models are further developed to predict the mechanical properties and guide the design of the new hydrogels. The combined experimental and theoretical results show that the toughness, modulus and yield stress of the new hydrogel can be uniformly increased by rational design of the stretchy-fiber mesh and the tough hydrogel matrix. Due to the multi-scale multi-mechanism strengthening, the new hydrogel is more robust against mechanical and environmental loads than conventional tough hydrogels. In addition, the fiber mesh can be printed into various shapes with commercially available 3D printers, on which the tough hydrogel matrix can be cast. The combined theoretical and experimental study opens up new avenues to both fundamental understanding and practical applications of hydrogels with extraordinary properties.
Acknowledgements
This work was supported by NSF CAREER Award CMMI-1253495, ONR YIP Award N00014-14-1-0528, NSF Grant CMMI-1200515, and NSF MRSEC DMR-1121107.References
- Y. Tanaka, J. P. Gong and Y. Osada, Prog. Polym. Sci., 2005, 30, 1–9 CrossRef CAS PubMed.
- S. Naficy, H. R. Brown, J. M. Razal, G. M. Spinks and P. G. Whitten, Aust. J. Chem., 2011, 64, 1007–1025 CrossRef CAS.
- X. H. Zhao, Soft Matter, 2014, 10, 672–687 RSC.
- H. J. Kong, E. Wong and D. J. Mooney, Macromolecules, 2003, 36, 4582–4588 CrossRef CAS.
- N. Simha, C. Carlson and J. Lewis, J. Mater. Sci.: Mater. Med., 2004, 15, 631–639 CrossRef CAS.
- V. C. Mow, M. H. Holmes and W. Michael Lai, J. Biomech., 1984, 17, 377–394 CrossRef CAS.
- J. S. Temenoff and A. G. Mikos, Biomaterials, 2000, 21, 431–440 CrossRef CAS.
- P. Shivapooja, Q. M. Wang, B. Orihuela, D. Rittschof, G. P. Lopez and X. H. Zhao, Adv. Mater., 2013, 25, 1430–1434 CrossRef CAS PubMed.
- M. Hirakawa, M. Nakamura, S. Obayashi, S. Takemori and H. Tanaka, Google Patents, EP0179937/B1, 1986 Search PubMed.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS PubMed.
- K. J. Henderson, T. C. Zhou, K. J. Otim and K. R. Shull, Macromolecules, 2010, 43, 6193–6201 CrossRef CAS.
- J. Y. Sun, X. H. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- J. Li, W. R. K. I. Illeperuma, Z. Suo and J. J. Vlassak, Macro Lett., 2014, 3, 520–523 CrossRef CAS.
- M. Guo, L. M. Pitet, H. M. Wyss, M. Vos, Y. W. D. Patricia and E. W. Meijer, J. Am. Chem. Soc., 2014, 136, 6969–6977 CrossRef CAS PubMed.
- Y.-n. Sun, G.-r. Gao, G.-l. Du, Y.-j. Cheng and J. Fu, Macro Lett., 2014, 3, 496–500 CrossRef CAS.
- N. A. Peppas and E. W. Merrill, J. Biomed. Mater. Res., 1977, 11, 423–434 CrossRef CAS PubMed.
- J. Yang, C.-R. Han, X.-M. Zhang, F. Xu and R.-C. Sun, Macromolecules, 2014, 47, 4077–4086 CrossRef CAS.
- F. T. Moutos, L. E. Freed and F. Guilak, Nat. Mater., 2007, 6, 162–167 CrossRef CAS PubMed.
- A. Agrawal, N. Rahbar and P. D. Calvert, Acta Biomater., 2013, 9, 5313–5318 CrossRef CAS PubMed.
- I. Liao, F. T. Moutos, B. T. Estes, X. Zhao and F. Guilak, Adv. Funct. Mater., 2013, 23, 5833–5839 CrossRef CAS PubMed.
- D. G. Strange, K. Tonsomboon and M. L. Oyen, J. Mater. Sci.: Mater. Med., 2014, 1–10 Search PubMed.
- J. Cui, M. A. Lackey, A. E. Madkour, E. M. Saffer, D. M. Griffin, S. R. Bhatia, A. J. Crosby and G. N. Tew, Biomacromolecules, 2012, 13, 584–588 CrossRef CAS PubMed.
- M. Tan, T. Zhao, H. Huang and M. Guo, Polym. Chem., 2013, 4, 5570–5576 RSC.
- H. Kamata, Y. Akagi, Y. Kayasuga-Kariya, U.-i. Chung and T. Sakai, Science, 2014, 343, 873–875 CrossRef CAS PubMed.
- R. S. Rivlin and A. G. Thomas, J. Polym. Sci., 1953, 10, 291–318 CrossRef CAS PubMed.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CrossRef CAS.
- T. Baumberger, C. Caroli and D. Martina, Nat. Mater., 2006, 5, 552–555 CrossRef CAS PubMed.
- C.-Y. Hui, A. Jagota, S. Bennison and J. Londono, Proc. R. Soc. London, Ser. A, 2003, 459, 1489–1516 CrossRef.
- B. Budiansky, J. W. Hutchinson and A. G. Evans, J. Mech. Phys. Solids, 1986, 34, 167–189 CrossRef.
- C. M. Landis, I. J. Beyerlein and R. M. McMeeking, J. Mech. Phys. Solids, 2000, 48, 621–648 CrossRef.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- T. Bai, P. Zhang, Y. Han, Y. Liu, W. Liu, X. Zhao and W. Lu, Soft Matter, 2011, 7, 2825–2831 RSC.
- X. H. Zhao, J. Mech. Phys. Solids, 2012, 60, 319–332 CrossRef CAS PubMed.
- P. Calvert, Adv. Mater., 2009, 21, 743–756 CrossRef CAS PubMed.
- E. Palleau, D. Morales, M. D. Dickey and O. D. Velev, Nat. Commun., 2013, 4, 2257 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm01039f |
| This journal is © The Royal Society of Chemistry 2014 |