Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
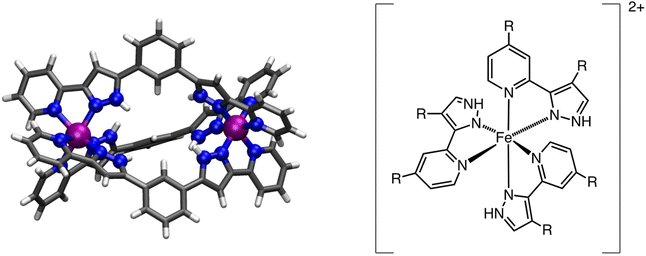
Tuning the spin-crossover properties of [Fe2] metal–organic cages†
Laia
Navarro
 ,
Arnau
Garcia-Duran
,
Arnau
Garcia-Duran
 and
Jordi
Cirera
and
Jordi
Cirera
 *
*
Departament de Química Inorgànica i Orgànica and Institut de Recerca de Química Teòrica i Computacional, Universitat de Barcelona, Diagonal 645, 08028, Barcelona, Spain. E-mail: jordi.cirera@qi.ub.es
First published on 23rd July 2024
Abstract
A computational study on the interplay between ligand functionalization and guest effects on the transition temperature (T1/2) in the [Fe2(L1R)3]@X (L1 = 1,3-bis-(3-(pyridin-2-yl)-1H-pyrazol-5-yl)benzene, X = H−, F−, Cl−, Br−, I− and [BF4]−, R = H, F, or CH3) family of metal–organic cages (MOCs) is presented. Our results indicate that ligand functionalization with electron-donating or electron-withdrawing groups can significantly impact the T1/2 as expected, while the guest effect in lowering the T1/2 has a linear correlation with the increasing guest size. More importantly, small guests can move away from the center of the cavity, thus enhancing the two-step characteristic of the transition. All the data can be understood by analyzing the underlying electronic structure of the studied systems in terms of the relevant d-based molecular orbitals. These results can help in the rational design of new MOCs that can operate as sensors at specific temperatures, thus accelerating the discovery of new SCO devices with tailored properties.
1. Introduction
Spin-crossover (SCO) complexes are a class of molecular based materials that can access two alternative electronic states close in energy by means of an external stimulus.1–3 The change in the electronic configuration of the metal center, which can be triggered using temperature, pressure or electromagnetic radiation, introduces profound changes in the physical properties of the system, ranging from changes in color, bond lengths and geometries, and magnetic properties.4–6 Thus, this dual behavior makes such systems perfect candidates as molecular level switches, and therefore, there has been a lot of interest in the study and design of new SCO based materials for data storage, display devices, and sensors, among other nanotechnological applications.7–16 The phenomenon, reported for the first time in 1931,17 appears when the ligand field around the metal center generates an intermediate situation, thus allowing the metal center to access two alternative electronic states. Following this idea, a more rigorous approach was used by Orgel,18 which introduced the concept of spin-equilibrium, and finally, the thermodynamic basis of this phenomenon was introduced.19 Since then, major developments in the field have taken place and have been reviewed in the literature.2,4,20–30 SCO usually occurs for Fe(II) metal centers with six nitrogen donor atoms, but due to the intense research in the field, other metals and oxidation states (CrII, MnIII, MnII, FeIII, CoII and NiII) as well as coordination numbers, donor atoms, and geometries have also been reported.31–35 Much in the same way, more complex SCO molecules with an increasing number of metal centers up to 2D and 3D extended systems have also been reported over the last few years.36–42When thermally induced, the SCO process is controlled by the corresponding change in the Gibbs free energy (ΔG = ΔH − T·ΔS), which has the corresponding enthalpic and entropic terms.19,43 At the molecular level, the enthalpic term accounts mostly for the electronic energy difference between the two alternative spin-states, with a small vibrational contribution.44 The entropic term, on the other hand, is made out of molecular vibrations, with a small contribution from the degeneracy of the spin-state of the metal centers.45 Because both terms are positive, raising the temperature leads to a particular point in which both ΔH and T·ΔS are equal, thus making ΔG zero. The particular temperature at which this occurs is known as the transition temperature (T1/2), and it is defined as the temperature at which we have equal populations of both spin-states. This parameter is key in the physical characterization of SCO systems, and much interest is devoted to the rational design of new SCO-type materials that can operate at pre-designed T1/2.
Discrete polynuclear SCO systems have raised a lot of interest due to their potential application in multifunctional devices.12,46,47 The number of systems exhibiting SCO with more than one metal center has been increasing over the last few years significantly.48–51 Because both metal centers can undergo spin-transition, thus leading to multistep SCO transitions, and, in some cases, such molecules can serve as host systems for small guest molecules, one can envision the use of such coordination compounds in nanoscale-based sensor devices.52 Recently, a new family of metal–organic cages (MOCs) with two FeII metal centers that exhibit SCO behavior has been reported. In such systems, the bis-chelating ligand 1,3-bis-(3-(pyridin-2-yl)-1H-pyrazol-5-yl)benzene (L1) is used to generate an FeII dinuclear species that can encapsulate different anionic species (Cl−, Br− and I−) or even coordination compounds.53–55
More importantly, the SCO properties of such systems can be tuned by the guest species, shifting the value of T1/2 as a function of the guest nature, which makes such molecules perfect candidates for sensing applications.53 However, the origin of the host–guest interaction in tuning the T1/2 is not very well understood, which somehow limits the potential use of such systems as molecular level sensors. For this reason, we decided to computationally study the [Fe2(L1R)3]@X (X = H−, F−, Cl−, Br−, I− and BF4−, R = H, F, or CH3) family to analyse in detail the origin of such tuning behaviour as well as the impact that the guest molecule and ligand functionalization has on the overall electronic structure of the system and its implications on the single-step or two-step transition exhibited by some of these dinuclear systems. Because of their balance between computational cost and accuracy, Density Functional Theory (DFT) methods have been used as an appealing approach for the computational study of spin-crossover systems. These include specific reparameterizations,56 benchmarking,57,58 use of double hybrids59 and screening across different exchange/correlation approximations.60–65 DFT methods have also been used to study SCO systems within periodic boundary conditions, using the SCAN functional or DFT+U methods.66,67 It is precisely because of their performance that DFT methods can be used for larger systems, including dinuclear68,69 or higher nuclearity systems.70 In this work, electronic structure calculations at the Density Functional Theory (DFT) level have been used to model the T1/2 in [Fe2(L1R)3]4+ (R = H, F, or CH3) systems, as well as the effects that different guest molecules have on tuning such quantity. First, we will present the used methodology and the results, which will be discussed in terms of the local electronic structure of the metal centers and the nature of the guest molecule. Finally, conclusions will be outlined.
2. Computational details
All density functional theory (DFT) calculations have been carried out using the Gaussian 16 (revision B.01) electronic structure suite.71 All calculations have been converged to 10−8 for the density matrix elements, and the corresponding vibrational analysis has been done to ensure they are minimum values along the potential energy surface. A triple-ζ basis set with polarization functions (TZVP) was employed for all the elements72 since TZVP offers a good compromise between the computational cost and accuracy. The exchange correlation functional TPSSh has been used for all systems,73,74 since it has been recently reported as the most accurate one towards spin-state energy gaps in d4 to d7 transition metal ions.58 Yet, the calculation of these energies using DFT methods is a challenging problem.57,58,60 Thus, a benchmark study on the mononuclear [Fe(L2R)3]2+ (L2 = 3-(2-pyridyl)pyrazole) system, which properly mimics the coordination environment of the dinuclear cage, was performed. The results show that only TPSSh and OPBE,75,76 which has shown also to be a proper method of choice to compute spin-state energy gaps,60,77 were the only exchange/correlation functionals that provided the correct spin-state energy gap (see Table S1 in the ESI†). Finally, the TPSSh functional, a hybrid version of the TPSS74 meta-GGA functional with 10% of exact exchange Hartree–Fock, was chosen due to its overall performance towards SCO systems. Also, TPSSh has shown its proficiency in connecting the observed trends in T1/2 with the underlying electronic structure of the system, which is key if one would like to make a rational design of new SCO systems with tailored properties. The different spin topologies were generated using the fragments option of the G16 code.To compute the transition temperatures and the thermochemistry data, we used an in-house Python code that builds on the Slichter and Drickamer model78 applied to dinuclear species.47 Among the different theoretical frameworks to study such multi-step spin-crossover transition in mononuclear systems, which includes elastic interactions79,80 or microscopic Ising-like models,81 the Slichter and Drickamer approach was quite convenient in terms of software implementation. The model also has proved its applicability to dinuclear systems before.47,69 The program provides the populations of the [HS–HS], [HS–LS], and [LS–LS] species by computing the ΔG at each temperature according to the following expression:
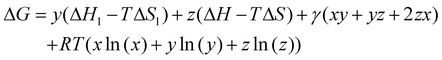 | (1) |
| x + y + z = 1 | (2) |
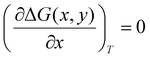 | (3) |
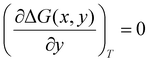 | (4) |
This improves previous approaches to solve this model that had to assume an average ΔS value for the transition from [LS–LS] to [HS–LS] and from [HS–LS] to [HS–HS], because from our calculation, the entropy changes associated with each process can be extracted individually. Therefore, the code provides us with the molar fraction of each spin-state as a function of temperature, which in turn allows us to compute the corresponding transition temperatures (see S3 in the ESI†). From this analysis, it is possible to see if the transition should occur in one step or two steps and extract the corresponding transition temperatures for each system. Obviously, in our case, we had to set up γ to zero because no intermolecular interactions have been accounted for. The code also allows us to work on fitting mode, being capable of extracting the ΔH, ΔS, W and γ for experimental values by fitting the experimental magnetic moment vs. the temperature curve. The code is available on request to the authors.
To study the d-MO energy gap in the low-spin systems (S = 0), n-electron valence perturbation theory (NEVPT2)82 calculations were performed using the Orca 4.0 computer code.83 In these calculations, we employed the def2TZVPP basis set, including the corresponding auxiliary basis set for the correlation and Coulomb fitting. The active space contains the 5 d-orbitals of the metal and 6 electrons, and the ab initio ligand-field theory (AILFT)84 approach was employed to extract and compute the splitting between the antibonding and non-bonding sets of d-based MOs.
3. Results
The first part of this study was devoted to checking if it was possible to model the empty metal–organic cage [Fe2(L1)3]4+ (L1 = 1,3-bis(3-(pyridin-2-yl)-1H-pyrazol-5-yl)benzene) using electronic structure methods. The system under study has three potential spin-state configurations: both metals in the high-spin state ([HS–HS]), one metal in the high-spin state and one in the low-spin state ([HS–LS]) and both metals in the low-spin state ([LS–LS]). The results from our calculations show that, indeed, the computational methodology used reproduces the correct spin-state order of energies, that is, [LS–LS] is the most stable configuration, followed by the [HS–LS] and, finally, the [HS–HS] spin state (see Table 1). The computed T1/2 values are larger than the experimental values, a fact that has been systematically observed for the TPSSh functional when computing such quantity for SCO systems,58,69,85,86 but in any case, they fell within a reasonable range of values (Table 1). It is important to notice here that the electronic stabilization of the intermediate spin-state ([HS–LS]) is, partially, responsible for the two-step or single-step behaviour in dinuclear Fe(II) SCO systems. In fact, this can be quantified using the W and ρ parameters. If the ΔH[HS–LS]/[LS–LS] (ΔH1) does not lie right at half the value of the ΔH[HS–HS]/[LS–LS] (ΔH), the intermediate spin state can be stabilized or destabilized.47,68 The [HS–LS] spin state will be stabilized if the ΔH[HS–LS]/[LS–LS] lies below the half value of the ΔH[HS–HS]/[LS–LS]. In that context, W is defined as W = ΔH1 − 1/2·ΔH. Thus, W can take positive (the [HS–LS] spin state is destabilized) or negative (the [HS–LS] spin state is stabilized) values. The associated ρ parameter is defined as ρ = 2·W/ΔH and quantifies the stabilization of the intermediate spin-state. Therefore, for systems in which ρ < 0, a two-step transition is expected, and two transition temperatures have been computed.47| ([Fe2(L1)3]@X)3+ | ΔH | ΔH1 | ΔH2 | W | ρ | T 1/2 |
|---|---|---|---|---|---|---|
| — | 17.79 | 8.94 | 8.85 | 0.04 | 0.00 | 502 |
| H− | 15.84 | 5.84 | 10.00 | −2.08 | −0.26 | 301, 608 |
| F− | 15.21 | 5.27 | 9.94 | −2.33 | −0.31 | 288, 563 |
| Cl− | 14.20 | 6.68 | 7.52 | −0.42 | −0.06 | 372 |
| Br− | 12.62 | 6.06 | 6.55 | −0.24 | −0.04 | 337 |
| I− | 9.95 | 4.68 | 5.27 | −0.30 | −0.06 | 263 |
| [BF4]− | 10.52 | 5.12 | 5.40 | −0.14 | −0.03 | 285 |
After being able to study the parent system [Fe2(L1)3]4+, we decided to explore how chemical modifications of the L1 ligand would affect the ligand field around the metal center. To model this, we reduced the system size to only one metal center with three L2 ligands (L2 = 3-(2-pyridyl)pyrazole), which properly mimics the coordination environment of the parent system and allows us to more quickly study the effects of ligand functionalization over the Fe(II) metal ion. As shown in Fig. 1, the R groups of the L2 ligand have been modelled as R = –H, –CH3, –OCH3, –F and –Cl. For this particular case, with only one metal center, the only possible transition is from the low-spin (S = 0) to the high-spin (S = 2) state. Results for the thermochemistry data and computed transition temperatures are listed in Table 2. As can be seen from the data, functionalization of the R groups does indeed have a strong impact on the ligand field, and thus, over the T1/2. The computed data for that mononuclear system is in good agreement with the available data for R = H.87 The effects of the functionalization of the para position of the pyridyl ring or the pyrazine ring have been intensively studied by different authors and for different systems88–92 as well as for Fe(III) SCO complexes.93,94 For this reason, we investigated the effects of only functionalizing the pyridyl ring or the pyrazole ring (see S4 in the ESI†). A close inspection of this data shows that the para functionalization of the pyridyl ligand correlates with the electronegativity of the atom attached to the para position, that is, the more electronegative the atom is, the more we reduce the electron density on the N atom, reducing its sigma donor abilities (inductive effect) and thus making the antibonding interaction less antibonding (i.e., we reduce the ligand field around the metal center), an effect that has been also observed for other systems.89,92 This is the reason why functionalization with more electronegative atoms leads to a lower T1/2, but functionalization with a methyl group has very little effect with respect to the hydrogen atom (see S4 in the ESI†). Because this substituent is in the para position, very low resonance effects are expected. However, functionalization of the pyrazole ring has larger resonant effects, thus correlating with the σm Hammett parameters better than with the electronegativity of the substituent (see S4 in the ESI†). This makes the electron donating groups (EDG), such as methyl, increase the ligand field around the metal center (i.e., increase the T1/2), while electron withdrawing groups (EWG), such as fluorine, have the opposite effect. This effect is much more pronounced than in the pyrazole group, and methyl functionalization of this ring significantly increases T1/2, as compared with the much subtle effect that the methyl functionalization of the pyridyl group has on such a quantity.
| [Fe(L2R)3]2+ | ΔH | ΔS | T 1/2 |
|---|---|---|---|
| –F | 7.13 | 17.496 | 408 |
| –H | 9.45 | 18.577 | 509 |
| –OCH3 | 8.84 | 16.917 | 523 |
| –Cl | 9.39 | 17.643 | 532 |
| –CH3 | 11.13 | 17.933 | 621 |
From the above, it was clear that the thermochemistry of [Fe2(L1)3]4+ can be tuned by modifying the L1 ligand. To explore this effect, two new systems were computed, [Fe2(L1F)3]4+ and [Fe2(L1CH3)3]4+, using the substituents that generate the lowest and highest spin-state energy gaps for the [Fe(L2R)3]2+ molecule. As can be seen from Table 1, the effect is fully transferable to the dinuclear system and, as expected, an increasing trend in the T1/2 is observed ([Fe2(L1F)3]4+ < [Fe2(L1H)3]4+ < [Fe2(L1CH3)3]4+).
Finally, it has been experimentally reported that different guest molecules are able to tune the T1/2 in these types of MOCs. Thus, we proceed to compute the thermochemistry and transition temperatures for the ([Fe2(L1R)3]@X)3+ systems (R = –F, –CH3, X = H−, F−, Cl−, Br−, I− and [BF4]−). Results are summarized in Tables 1, 3 and 4.
| ([Fe2(L1F)3]@X)3+ | ΔH | ΔH1 | ΔH2 | W | ρ | T 1/2 |
|---|---|---|---|---|---|---|
| — | 12.98 | 6.53 | 6.45 | 0.04 | 0.01 | 368 |
| H− | 11.13 | 3.45 | 7.68 | −2.11 | −0.38 | 178, 436 |
| F− | 10.50 | 2.87 | 7.63 | −2.38 | −0.45 | 149, 451 |
| Cl− | 9.46 | 4.24 | 5.22 | −0.49 | −0.10 | 250 |
| Br− | 8.00 | 3.76 | 4.24 | −0.24 | −0.06 | 219 |
| I− | 5.53 | 2.49 | 3.04 | −0.28 | −0.10 | 154 |
| [BF4]− | 6.26 | 3.00 | 3.25 | −0.12 | −0.04 | 177 |
| ([Fe2(L1CH3)3]@X)3+ | ΔH | ΔH1 | ΔH2 | W | ρ | T 1/2 |
|---|---|---|---|---|---|---|
| — | 22.63 | 11.33 | 11.30 | 0.01 | 0.00 | 688 |
| H− | 22.70 | 10.06 | 12.64 | −1.29 | −0.11 | 662 |
| F− | 22.16 | 9.51 | 12.65 | −1.57 | −0.14 | 665 |
| Cl− | 20.98 | 9.97 | 11.00 | −0.51 | −0.05 | 593 |
| Br− | 18.98 | 9.07 | 9.92 | −0.42 | −0.04 | 587 |
| I− | 15.96 | 7.50 | 8.46 | −0.48 | −0.06 | 511 |
| [BF4]− | 15.52 | 7.26 | 8.26 | −0.50 | −0.06 | 486 |
4. Discussion
The analysis of the results presented above allows us to extract some trends in the interplay between ligand functionalization and guest effects over the transition temperature in the [Fe2(L1R)3]4+ systems.The first thing one can observe is that the functionalization of the L1R ligand can effectively shift the T1/2 value to larger or smaller values, depending on the nature of the R group. Electron-withdrawing (EWG) groups shift the T1/2 to lower values, while electron-donating (EDG) groups have the opposite effect, as has been observed in other systems with this type of functionalization.88,95,96 It can clearly be seen from Tables 1, 3 and 4 that the observed trend in ΔH, that is, [Fe2(L1CH3)3]4+ > [Fe2(L1H)3]4+ > [Fe2(L1F)3]4+ (ΔH of 22.63, 17.79 and 12.98 kcal mol−1 respectively), reflects the effect that the L1 functionalization has on the metal center ligand field. Although we only explored the limiting cases, the potential fine-tuning effects of the ligand functionalization cannot be overlooked, because one can clearly tune up or down the T1/2 playing with the EWG or EDG characteristic of the substituents.88,95,96
The second systematic effect that can be observed from the computed data is that larger guests shift to lower values of the T1/2. This trend, which has also been reported experimentally,53,54,97 remains constant, regardless of L1 functionalization, and the calculations reproduce the available experimental data (see S2 in the ESI†).54 Moreover, it is possible to get a linear dependence of the T1/2 as a function of the ionic radii of the guest molecule (Fig. 2 and Table 5), which clearly shows that the larger the guest, the smaller the T1/2. The decrease in T1/2 associated with larger guests is consistent, regardless of the functionalization of L1, as can be seen from the fitting expressions in Fig. 2. Because there are different sets of anionic radii, we analyzed if the correlation persists in all cases. Indeed, the trend is reproduced with other sets of radii used for the correlation (see S5 in the ESI†).
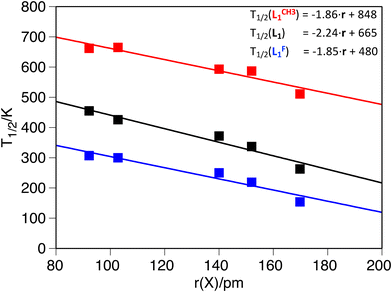 | ||
| Fig. 2 Computed transition temperature as a function of the guest radius: L1F (blue, R2 = 0.93), L1H (black, R2 = 0.95) and L1CH3 (red, R2 = 0.92). All temperatures in K and radii in pm. | ||
To further analyze the origin of such effects, we computed the magnitude of the d-based molecular orbitals using the Ab Initio Ligand-Field Theory (AILFT) approach to process the output from NEVPT2 calculations on the low-spin optimized geometries of the [Fe2(L1R)3]4+ systems (see S7 and S8 in the ESI†). From such calculations, one can observe the ligand-field splitting between the antibonding and non-bonding d-based molecular orbitals, which are 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651, 16
651, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 and 15
167 and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 cm−1 for the [Fe2(L1CH3)3]4+, [Fe2(L1)3]4+ and [Fe2(L1F)3]4+ systems, respectively. More importantly, a close inspection of the optimized geometries reveals that the average Fe–N bond length is, essentially, independent of the L1 functionalization, thus indicating that the tuning effect of the R group over the T1/2 has a purely electronic effect. However, when guest molecules are inserted, it is possible to get a clear correlation between the enlargement of the Fe–N bond lengths and the size of the guest molecule (see S11 in the ESI†). Larger guests force the system to expand from the inside, pretty much like pumping a balloon that fits inside the cavity, making the Fe–N bond lengths larger (0.015 Å bond length increases from an empty system to the iodine one), thereby weakening the ligand-field around the metal center. This reduction in the splitting among the d-based MOs, which can be quantified and shows a significant decrease between the [Fe2(L1)3]4+ and ([Fe2(L1)3]@I)3+ systems (16
835 cm−1 for the [Fe2(L1CH3)3]4+, [Fe2(L1)3]4+ and [Fe2(L1F)3]4+ systems, respectively. More importantly, a close inspection of the optimized geometries reveals that the average Fe–N bond length is, essentially, independent of the L1 functionalization, thus indicating that the tuning effect of the R group over the T1/2 has a purely electronic effect. However, when guest molecules are inserted, it is possible to get a clear correlation between the enlargement of the Fe–N bond lengths and the size of the guest molecule (see S11 in the ESI†). Larger guests force the system to expand from the inside, pretty much like pumping a balloon that fits inside the cavity, making the Fe–N bond lengths larger (0.015 Å bond length increases from an empty system to the iodine one), thereby weakening the ligand-field around the metal center. This reduction in the splitting among the d-based MOs, which can be quantified and shows a significant decrease between the [Fe2(L1)3]4+ and ([Fe2(L1)3]@I)3+ systems (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 and 15
167 and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 cm−1, respectively), is responsible for the decrease in the corresponding T1/2, because the smaller the gap, the lower the energy that the system requires to undergo the transition (Table 5).
401 cm−1, respectively), is responsible for the decrease in the corresponding T1/2, because the smaller the gap, the lower the energy that the system requires to undergo the transition (Table 5).
The [BF4]− anion, with its unique tetrahedral shape, adopts a special arrangement within the cavity (see S12 in the ESI†). One of the fluorine atoms orients itself towards one metal center, thus displacing the B from the center of the cavity. Because it lacks the spherical shape, defining the radii for this guest is not trivial. However, an estimation can be done by using the average B–F bond length as surveyed in the Cambridge Structural Database (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 fragments),99 which returns a value of 137 pm. Adding the covalent radii for the fluorine atom (57 pm)100 provides an overall estimated radii of 193.8 pm. This also allows the inclusion of this anion in the correlations, which leads to the same trends, as shown in Fig. 2 (see S12 in the ESI†). The estimated radii for the [BF4]− anion, which place it as the largest across the tested guests, should lead to the smallest T1/2 in all cases. However, this is only observed for the ([Fe2(L1CH3)3]@X)3+ family, an effect that can be attributed to the special arrangement that the guest adopts inside the cavity (see S12 in the ESI†).
272 fragments),99 which returns a value of 137 pm. Adding the covalent radii for the fluorine atom (57 pm)100 provides an overall estimated radii of 193.8 pm. This also allows the inclusion of this anion in the correlations, which leads to the same trends, as shown in Fig. 2 (see S12 in the ESI†). The estimated radii for the [BF4]− anion, which place it as the largest across the tested guests, should lead to the smallest T1/2 in all cases. However, this is only observed for the ([Fe2(L1CH3)3]@X)3+ family, an effect that can be attributed to the special arrangement that the guest adopts inside the cavity (see S12 in the ESI†).
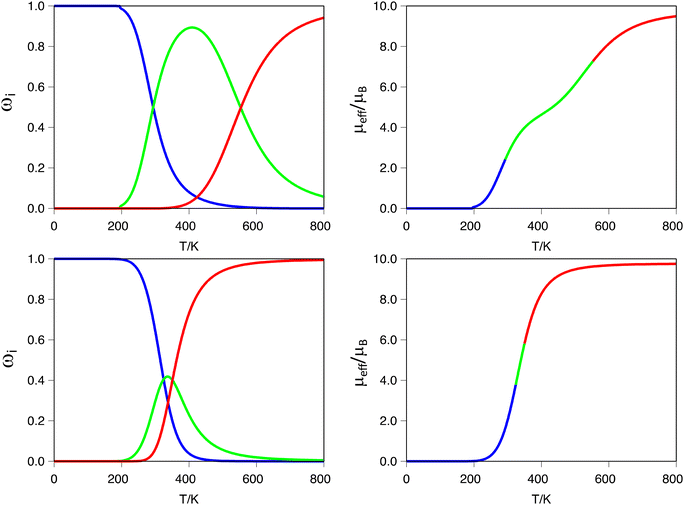
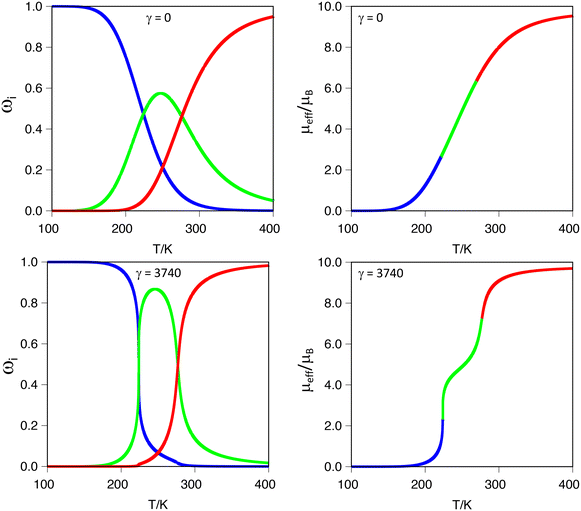
A more interesting effect is observed in terms of the guest induced two-step behavior. As can be seen from Tables 1, 3 and 4, the smallest guests (H− and F−) are the ones that generate the larger negative values for the ρ term, which quantifies the tendency of a dinuclear system to exhibit a two-step transition. To trace back the origin of such effects, we carefully analyzed the electronic structures and geometries of the systems [Fe2(L1R)3]@F3+ (R = H, F and CH3). The first thing that one can notice is that small guest molecules do not stick to the center of the cavity, rather they move closer to one of the Fe(II) metal centers. This asymmetry is not observed for larger guest molecules, for whom actually the distance to both Fe(II) metal centers is equivalent. The fact that the guest molecule lies closer to one of the metal centers has implications in tuning its electronic structure and making it more prone to undergo the SCO transition. The calculated d-MO splitting is, on average, 330 cm−1 smaller for the metal center that is closer to the guest molecule. Moreover, regardless of the fact that bond lengths are, on average, equal for both metal centers, the coordination sphere of the metal closer to the guest molecule is more distorted, as can be seen using the corresponding Continuous Shape Measures (CShM) for the octahedron (see S8 in the ESI†).101 Thus, the slight distortion that the guest introduces in the coordination environment of the metal center seems to be enough to stress the two-step nature of the SCO transition. Obviously, once the guest remains at the center of the cavity, this effect is lost, and the transition tends to move towards a single step one, as can be seen in the same analysis for the [Fe2(L1R)3]@Br3+ systems, for which the bromine atom is located at the midpoint between the two iron metal centers. In such cases, both metals are geometrically equivalent, and the small differences that enhance the two-step transition become less pronounced. This means that even though we can compute two transition temperatures, the difference between these two values becomes small, and the transition curve shows a single step characteristic. This effect is illustrated in Fig. 3 for the ([Fe2(L1)3]@X)3+ (X = F− or Br−) systems. As can be seen in the figure, the ([Fe2(L1)3]@F)3+ system clearly exhibits the shape of a two-step transition, because the [HS–LS] spin-state gains enough stability through a certain range of temperatures. On the other hand, for the ([Fe2(L1)3]@Br)3+ system, even though one can determine two transition temperatures, they are so close that the magnetic moment curve resolves into a single step one, making it effectively impossible to determine the two values for T1/2 from that plot. This is also illustrated by the significant difference in the ρ value between both systems (Table 1, ρ = −0.31 and −0.06 for F− or Br−, respectively). It is important to notice here that even with relatively large negative values of ρ, in the absence of cooperativity (γ = 0), the magnetic moment curve exhibits a single step, as can be seen, for instance, for the ([Fe2(L1CH3)3]@F)3+ system, which despite having a ρ value of −0.14 exhibits a single step transition (see S10 in the ESI†).
It is important to stress that ρ values below −0.20 produce a marked two-step transition when modelling the magnetic moment as a function of temperature. However, in all our cases, the γ value is set to zero because we cannot model the intermolecular interactions through our calculations. Using our code, as described in the computational details, we tested the effects of increasing intermolecular interactions, that is, using γ values between zero and γc (defined as 2·R·ΔH/ΔS)78 on systems with ρ values in the range −0.20 < ρ < −0.05. The results show that by increasing γ values, the curve becomes sharper and the two-step characteristic more pronounced. In Fig. 4, this effect is illustrated for the ([Fe2(L1F)3]@Cl)3+ system, with a ρ = −0.10 (Table 3) in the limit cases. As can be seen in the figure, γ = 0 produces a single step transition, while the γc (the largest tested) features a two-step transition. The effect of gamma is, therefore, increasing the slope (i.e., the rate) at which each spin-state appears/disappears, as can be seen in Fig. 4 by comparing the thermal dependence of each spin-state population as a function of the gamma value. Intermediate gamma values have also been tested, showing the increasing tendency towards a two-step transition that larger γ values induce in the magnetic moment curve (see S9 in the ESI†). It is also important to notice that increasing the γ factor does not alter the crossing points between different spin-state populations, i.e., does not change the values of the corresponding transition temperatures, which only depends on the thermochemistry (ΔH, ΔS and W) of the system. This feature of our software can be of great help when fitting experimental data, thus allowing us to entangle the cooperativity from electronic contributions to the two-step characteristic of the transition.
5. Conclusions
In this work, a computational approach to calculate the T1/2 in dinuclear [Fe2(L1R)]4+ (R = –H, –F or –CH3) systems has been presented. This computational approach, based on the TPSSh exchange/correlation functional, allows for the calculation of the corresponding thermochemical quantities within some methodological error, which in turn allows us to outline trends in the T1/2 based on the underlying electronic structure of the studied system. As expected, functionalization of the ligand with electron withdrawing groups reduces the gap between the non-bonding and antibonding sets of orbitals for each Fe(II) metal center, thus lowering the T1/2, while the opposite is observed when the electron donating groups are used to functionalize the ligand, as has been observed for other spin-crossover systems.88,95,96 A much more interesting effect is observed when guest molecules are inserted into these metal–organic cages, leading to ([Fe2(L1)3]@X)3+ systems (X = H−, F−, Cl−, Br−, I− and [BF4]−). Our calculations showed that there is a linear dependence of the T1/2 on the size of the guest molecule. In fact, the larger the guest, the lower the T1/2, a trend that is constant for all the studied ligands. This implies that there is an interplay between the ligand functionalization, which allows for a larger degree of change in the T1/2, and the guest molecule size, which lowers T1/2 in a much softer way. More importantly, small guests (H− and F− in particular) can move away from the center of the cavity, thus generating small differences between the two Fe(II) metal sites. This effect stresses the two-step characteristic of the transition for such systems, an effect that is not observed for the empty systems, which always display single-step transitions. The computed thermochemical quantities allow us to extract the populations of each spin-state species as a function of temperature. From these results, the electronic influence on having a single-step or a two-step transition can easily be analyzed in terms of the W and ρ quantities, as well as the calculation of the different T1/2. Our data indicate that only for ρ < −0.20, a clear two-step transition is observed despite the fact that two transition temperatures can be computed. For ρ > −0.20, the [HS–LS] species is not able to generate the two-step shape in the magnetic moment curve, leading to a single-step transition. This can be, however, enhanced if large cooperativity is present in the system.Thus, from our results, the interplay between ligand functionalization and host/guest interactions in tuning the T1/2 can be outlined, thus providing insight into the rational design of new dinuclear systems that can undergo spin-transition at specific temperatures.
Data availability
Data for this article are available from ioChem-DB[1] through the following link: https://iochem-bd.bsc.es/browse/handle/100/322091.[1] M. Álvarez-Moreno, C. de Graaf, N. Lopez, F. Maseras, J. M. Poblet, C. Bo, J. Chem. Inf. Model. 2015, 55, 95.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
J. C. thanks the Spanish MICINN for the Ramón y Cajal research contract (RYC2018-024692-I) and the Spanish MICINN research grant (PID2020-115165GB-I00). J. C., A. G.-D. and L. N. is thankful to the Spanish Structures of Excellence María de Maeztu program (CEX2021-001202-M). L. N. is grateful for the PREDOCS-UB 2022 grant. A. G.-D is grateful for the FPI grant (CEX2021-001202-M).References
- P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds III, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, vol. 235 Search PubMed.
- P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 RSC.
- Y. Garcia and P. Gütlich, in Beilstein Journal of Organic Chemistry, 2013, vol. 9, pp. 49–62 Search PubMed.
- H. A. Goodwin, Coord. Chem. Rev., 1976, 18, 293–325 CrossRef CAS.
- E. König, G. Ritter, J. Waigel and H. A. Goodwin, J. Chem. Phys., 1985, 83, 3055–3061 CrossRef.
- P. Gütlich and A. Hauser, Coord. Chem. Rev., 1990, 97, 1–22 CrossRef.
- O. Kahn, J. Kröber and C. Jay, Adv. Mater., 1992, 4, 718–728 CrossRef CAS.
- O. Sato, Nat. Chem., 2016, 8, 644–656 CrossRef CAS PubMed.
- G. Ke, C. Duan, F. Huang and X. Guo, InfoMat, 2020, 2, 92–112 CrossRef CAS.
- Z.-S. Yao, Z. Tang and J. Tao, Chem. Commun., 2020, 56, 2071–2086 RSC.
- M. Deumal, S. Vela, M. Fumanal, J. Ribas-Arino and J. J. Novoa, J. Mater. Chem. C, 2021, 9, 10624–10646 RSC.
- M. A. Halcrow, Spin–Crossover Materials, Wiley, Oxford, UK, 2013 Search PubMed.
- H. Li and H. Peng, Curr. Opin. Colloid Interface Sci., 2018, 35, 9–16 CrossRef CAS.
- G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 1703862 CrossRef PubMed.
- G. Molnár, L. Salmon, W. Nicolazzi, F. Terki and A. Bousseksou, J. Mater. Chem. C, 2014, 2, 1360–1366 RSC.
- B. Schneider, S. Demeshko, S. Neudeck, S. Dechert and F. Meyer, Inorg. Chem., 2013, 52, 13230–13237 CrossRef CAS PubMed.
- L. Cambi and L. Szegö, Berichte der Dtsch. Chem. Gesellschaft (A B Ser.), 1931, 64, 2591–2598 Search PubMed.
- L. E. Orgel, J. Chem. Soc., 1952, 4756 RSC ; Proc. 10th Solvay Conference in Chemistry, Brussels (1956).
- O. Kahn, Molecular Magnetism, VCH, 1993 Search PubMed.
- E. König, Coord. Chem. Rev., 1968, 3, 471–595 CrossRef.
- E. Konig, G. Ritter and S. K. Kulshreshtha, Chem. Rev., 1985, 85, 219–234 CrossRef CAS.
- H. Toftlund, Coord. Chem. Rev., 1989, 94, 67–108 CrossRef CAS.
- J. A. Real, A. B. Gaspar, V. Niel and M. C. Muñoz, Coord. Chem. Rev., 2003, 236, 121–141 CrossRef CAS.
- A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313 RSC.
- M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119 RSC.
- G. Aromí, L. A. Barrios, O. Roubeau and P. Gamez, Coord. Chem. Rev., 2011, 255, 485–546 CrossRef.
- M. C. Muñoz and J. A. Real, Coord. Chem. Rev., 2011, 255, 2068–2093 CrossRef.
- J. Tao, R.-J. Wei, R.-B. Huang and L.-S. Zheng, Chem. Soc. Rev., 2012, 41, 703–737 RSC.
- A. B. Gaspar and M. Seredyuk, Coord. Chem. Rev., 2014, 268, 41–58 CrossRef CAS.
- K. Senthil Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176–205 CrossRef CAS.
- Y. Garcia and P. Gütlich, Thermal Spin Crossover in Mn(II), Mn(III), Cr(II) and Co(III) Coordination Compounds, in Topics in Current Chemistry: Spin Crossover in Transition Metal Compounds II, Springer, Berlin, Heidelberg, 2004, vol. 234 Search PubMed.
- J. Olguín, Coord. Chem. Rev., 2020, 407, 213148 CrossRef.
- Y. Homma and T. Ishida, Chem. Mater., 2018, 30, 1835–1838 CrossRef CAS.
- H. Ma, J. L. Petersen, V. G. Young, G. T. Yee and M. P. Jensen, J. Am. Chem. Soc., 2011, 133, 5644–5647 CrossRef CAS PubMed.
- G. Alcover-Fortuny, C. de Graaf and R. Caballol, Phys. Chem. Chem. Phys., 2015, 17, 217–225 RSC.
- M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4767–4771 CrossRef CAS PubMed.
- S. M. Neville, G. J. Halder, K. W. Chapman, M. B. Duriska, B. Moubaraki, K. S. Murray and C. J. Kepert, J. Am. Chem. Soc., 2009, 131, 12106–12108 CrossRef CAS PubMed.
- J. Cirera, Rev. Inorg. Chem., 2014, 34, 199–216 CAS.
- C. Bartual-Murgui, L. Salmon, A. Akou, N. A. Ortega-Villar, H. J. Shepherd, M. C. Muñoz, G. Molnár, J. A. Real and A. Bousseksou, Chem. – Eur. J., 2012, 18, 507–516 CrossRef CAS PubMed.
- C. Bartual-Murgui, A. Akou, C. Thibault, G. Molnár, C. Vieu, L. Salmon and A. Bousseksou, J. Mater. Chem. C, 2015, 3, 1277–1285 RSC.
- G. J. Halder, C. J. Kepert, B. Moubaraki, K. S. Murray and J. D. Cashion, Science, 2002, 298, 1762–1765 CrossRef CAS PubMed.
- S. Cobo, G. Molnár, J. A. Real and A. Bousseksou, Angew. Chem., Int. Ed., 2006, 45, 5786–5789 CrossRef CAS PubMed.
- W. Nicolazzi and A. Bousseksou, C. R. Chim., 2018, 21, 1060–1074 CrossRef CAS.
- L. F. Lindoy and S. E. Livingstone, Coord. Chem. Rev., 1967, 2, 173–193 CrossRef CAS.
- A. Bousseksou, J. J. McGarvey, F. Varret, J. A. Real, J.-P. Tuchagues, A. C. Dennis and M. L. Boillot, Chem. Phys. Lett., 2000, 318, 409–416 CrossRef CAS.
- J. R. Galán-Mascarós, G. Aromí and M. Darawsheh, C. R. Chim., 2018, 21, 1209–1229 CrossRef.
- J. A. Real, H. Bolvin, A. Bousseksou, A. Dworkin, O. Kahn, F. Varret and J. Zarembowitch, J. Am. Chem. Soc., 1992, 114, 4650–4658 CrossRef CAS.
- J. Olguín and S. Brooker, Coord. Chem. Rev., 2011, 255, 203–240 CrossRef.
- Y. Sunatsuki, R. Kawamoto, K. Fujita, H. Maruyama, T. Suzuki, H. Ishida, M. Kojima, S. Iijima and N. Matsumoto, Coord. Chem. Rev., 2010, 254, 1871–1881 CrossRef CAS.
- B. Weber, Coord. Chem. Rev., 2009, 253, 2432–2449 CrossRef CAS.
- M. Nihei, T. Shiga, Y. Maeda and H. Oshio, Coord. Chem. Rev., 2007, 251, 2606–2621 CrossRef CAS.
- S.-L. Yang, X. Zhang, Q. Wang, C. Wu, H. Liu, D. Jiang, R. Lavendomme, D. Zhang and E.-Q. Gao, JACS Au, 2023, 3, 2183–2191 CrossRef CAS PubMed.
- M. D. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Chem. Commun., 2017, 53, 569–572 RSC.
- M. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Chem. – Eur. J., 2016, 22, 8635–8645 CrossRef CAS PubMed.
- M. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Angew. Chem., 2018, 130, 13697–13701 CrossRef.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- K. P. Jensen and J. Cirera, J. Phys. Chem. A, 2009, 113, 10033–10039 CrossRef CAS PubMed.
- J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105 CrossRef CAS PubMed.
- S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772–774 CrossRef CAS PubMed.
- M. Swart, J. Chem. Theory Comput., 2008, 4, 2057–2066 CrossRef CAS PubMed.
- S. Zein, S. A. Borshch, P. Fleurat-Lessard, M. E. Casida and H. Chermette, J. Chem. Phys., 2007, 126, 014105 CrossRef PubMed.
- C. Rong, S. Lian, D. Yin, B. Shen, A. Zhong, L. Bartolotti and S. Liu, J. Chem. Phys., 2006, 125, 174102 CrossRef PubMed.
- A. Fouqueau, S. Mer, M. E. Casida, L. M. Lawson Daku, A. Hauser, T. Mineva and F. Neese, J. Chem. Phys., 2004, 120, 9473–9486 CrossRef CAS PubMed.
- A. Fouqueau, M. E. Casida, L. M. L. Daku, A. Hauser and F. Neese, J. Chem. Phys., 2005, 122, 044110 CrossRef PubMed.
- L. M. Lawson Daku, A. Vargas, A. Hauser, A. Fouqueau and M. E. Casida, ChemPhysChem, 2005, 6, 1393–1410 CrossRef PubMed.
- J. Cirera and E. Ruiz, J. Phys. Chem. A, 2020, 124, 5053–5058 CrossRef CAS PubMed.
- S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2020, 22, 4938–4945 RSC.
- S. Zein and S. A. Borshch, J. Am. Chem. Soc., 2005, 127, 16197–16201 CrossRef CAS PubMed.
- J. Cirera and E. Ruiz, J. Mater. Chem. C, 2015, 3, 7954–7961 RSC.
- A. Moneo-Corcuera, D. Nieto-Castro, J. Cirera, V. Gómez, J. Sanjosé-Orduna, C. Casadevall, G. Molnár, A. Bousseksou, T. Parella, J. M. Martínez-Agudo, J. Lloret-Fillol, M. H. Pérez-Temprano, E. Ruiz and J. R. Galán-Mascarós, Chem, 2023, 9, 377–393 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. C. 01, 2016 Search PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. M. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Swart, A. W. Ehlers and K. Lammertsma, Mol. Phys., 2004, 102, 2467–2474 CrossRef CAS.
- C. P. Slichter and H. G. Drickamer, J. Chem. Phys., 1972, 56, 2142–2160 CrossRef CAS.
- P. Gütlich, Y. Garcia and H. Spiering, in Magnetism: Molecules to Materials, Wiley, 2004, pp. 271–344 Search PubMed.
- A. Hauser, J. Jeftić, H. Romstedt, R. Hinek and H. Spiering, Coord. Chem. Rev., 1999, 190–192, 471–491 CrossRef CAS.
- A. Bousseksou, J. Nasser, J. Linares, K. Boukheddaden and F. Varret, J. Phys. I, 1992, 2, 1381–1403 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327 CrossRef.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
- J. Cirera and F. Paesani, Inorg. Chem., 2012, 51, 8194–8201 CrossRef CAS PubMed.
- J. Cirera and E. Ruiz, Inorg. Chem., 2016, 55, 1657–1663 CrossRef CAS PubMed.
- L. S. Harimanow, K. H. Sugiyarto, D. C. Craig, M. L. Scudder and H. A. Goodwin, Aust. J. Chem., 1999, 52, 109 CrossRef CAS.
- L. J. Kershaw Cook, R. Kulmaczewski, R. Mohammed, S. Dudley, S. A. Barrett, M. A. Little, R. J. Deeth and M. A. Halcrow, Angew. Chem., Int. Ed., 2016, 55, 4327–4331 CrossRef CAS PubMed.
- H.-C. Liang, Y. Pan, H.-L. Zhu, Y.-S. Meng, C.-H. Liu, T. Liu and Y.-Y. Zhu, Inorg. Chem. Front., 2022, 9, 2343–2352 RSC.
- A. Kimura and T. Ishida, Inorganics, 2017, 5, 52 CrossRef.
- K. Nakano, N. Suemura, K. Yoneda, S. Kawata and S. Kaizaki, Dalton Trans., 2005, 740 RSC.
- J. G. Park, I.-R. Jeon and T. D. Harris, Inorg. Chem., 2015, 54, 359–369 CrossRef CAS PubMed.
- B. Dey, A. Mondal and S. Konar, Chem. – Asian J., 2020, 15, 1709–1721 CrossRef CAS PubMed.
- B. Dey, S. Mehta, A. Mondal, J. Cirera, E. Colacio and V. Chandrasekhar, ACS Omega, 2022, 7, 39268–39279 CrossRef CAS PubMed.
- L. Navarro and J. Cirera, Inorg. Chem. Front., 2023, 10, 250–258 RSC.
- D. Vidal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2023, 25, 12490–12499 RSC.
- R. A. Bilbeisi, S. Zarra, H. L. C. Feltham, G. N. L. Jameson, J. K. Clegg, S. Brooker and J. R. Nitschke, Chem. – Eur. J., 2013, 19, 8058–8062 CrossRef CAS PubMed.
- J. Liu, W. H. E. Schwarz and J. Li, Chem. – Eur. J., 2013, 19, 14758–14767 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832 RSC.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01213e |
| This journal is © The Royal Society of Chemistry 2024 |