Growth of nano-domains in Gd–CeO₂ mixtures: hybrid Monte Carlo simulations

Abstract

Hybrid Monte Carlo (HMC) simulations are used to study the growth of Gd-rich domains in Gd doped CeO₂, and we probe the conductivity of the resulting and other configurations by molecular dynamics. Previous work has been restricted to the dilute defect limit, assumptions of particular cluster formation, and neglect of all temperature effects. Our methods suffer none of these restrictions. Even at low concentrations Gd³⁺ segregates into domains. We have examined the local environment of the Gd³⁺ ions using radial distribution functions and Steinhardt order parameters. The observed structure is consistent with the formation of cubic C-type (Gd₂O₃) domains, rather than the monoclinic B-type or pyrochlore clusters which have been suggested previously. In addition, previous detailed pair distribution function analysis of the solid solution has indicated different local cation environments from those from a Rietveld analysis – overall our results support the former analysis rather than the latter. At the elevated temperatures (1000 K) of the simulations there is no particular preference for vacancy and dopant cations to be located at second neighbour sites, an issue long discussed for this and similar systems. Both calculated and experimental conductivities show a similar variation with composition, passing through a maximum with increasing Gd concentration. The conductivities of the configurations generated in the hybrid Monte Carlo simulations are lower than those of configurations generated independently in which the Gd ions are distributed at random. The HMC thermally generated Gd nano-domains capture oxygen vacancies, reduce oxygen vacancy mobility and block diffusion paths.

---

1 Introduction

CeO₂ is a technologically important material, abundant and with rich defect- and nano-chemistries.¹ In particular gadolinium doped ceria (GDC), Gd_xCe_1−xO_2−x/2, has been proposed as an intermediate temperature solid oxide fuel cell (SOFC) electrolyte,² and consequently has been the subject of numerous experimental and theoretical studies. The efficiency of a SOFC is linked to the ionic conductivity and the conductivity of CeO₂ can be enhanced by doping with a cation with a different charge to that of Ce. Here Gd³⁺ replaces Ce⁴⁺:

For every two Gd³⁺ dopants introduced, an oxygen vacancy is created and eqn (1) implies that the ionic conductivity should increase steadily with dopant concentration and thus proportional to the concentration of oxygen vacancies. However the actual behaviour is considerably more complex and the experimental conductivity of GDC is not a simple function of the dopant concentration, but passes through a maximum at approximately 10–20% Gd, above which the conductivity starts to decrease.² The conductivity is also a function of the thermal history of the sample. Zhang et al., for instance, have compared the conductivity of sintered pellets and samples aged at 1273 K for 3 to 8 days.³ For compositions x ≥ 0.2 they observed a marked decrease in conductivity for the aged samples and attributed this to the formation of micro-domains. The experimental conductivity is often further complicated by the presence of grain boundaries; the dc conductivity will also include contributions from grain boundaries, and production of an optimum electrolyte has to involve optimisation of the microstructure.

This paper concentrates on the properties of the bulk material. The variation of the conductivity with Gd concentration has long been thought to be due to interactions between the dopant cations and oxygen vacancies and the formation of associated clusters. This is a challenging problem for both experiment and theory and has received significant and continuing attention due to the importance of understanding the mechanisms of conductivity and potential improvement in the performance of SOFC. High resolution transmission electron microscopy (HRTEM) carried out by Mori and Drennan⁴ concluded the conducting properties are strongly influenced by the micro-domain size in the grain; the larger the microdomains the lower the conductivity and the authors suggested the domains may have a distorted pyrochlore structure. From extended X-ray adsorption fine structure (EXAFS) spectra, probing the local structure around cations, Ohashi et al.⁵ suggested the association of two Gd ions and one oxygen vacancy in heavily doped solutions with vacancies located around both Gd and Ce. XAFS studies in ref. 6 and 7 concluded that metal–oxygen bond lengths increase with decreasing Gd content. Deguchi et al.⁸ used EXAFS to examine the coordination of dopant cations and suggested that 1–2 Gd³⁺ ions surround each oxygen vacancy and small such clusters are distributed in the ceria lattice at random, with no tendency of the Gd³⁺ ions to cluster together. Chen and Navrotsky⁹ combined calorimetry and X-ray diffraction, and in line with Deguchi et al.⁸ propose the same neutral trimers as the main associated defects and speculate on the importance of local site distortion. In contrast Banerji et al. interpreted their experimental Raman spectra in terms of the formation of regions with the Gd₂O₃ crystal structure (called C-type) in which the dopant metal atoms are 6-coordinate to oxygen and the fluorite (F-type) Raman mode gradually disappears when x increases beyond 0.2.¹⁰ The C-type Gd₂O₃ structure is closely related to that of fluorite requiring the removal of two oxygen atoms from every eight in an ordered fashion. A different ordering of vacancies gives rise to the pyrochlore structure – oxygen vacancies are all at next-nearest neighbour positions to Gd³⁺ and the coordination number of dopant cations is 8. The absence of clustering of Gd³⁺ is questioned¹¹ by energy filtering transmission electron microscopy which has identified segregation of Gd³⁺ to nano-sized domains even for x = 0.1. The size of these domains increased with increasing x and the analysis of Ye et al.¹¹ who also revise the earlier conclusions of ref. 4, suggests a C-type rather than pyrochlore structure for the domains. The measured electrical conductivity led the authors to speculate that the conductivity is inversely proportional to their size.¹¹ More recent microscopy (HRTEM, energy-filtering TEM (EFTEM) and selected-area electron diffraction (SAED)) have confirmed the existence of defect clusters with ordered structures in GDC.¹²

In parallel there has been substantial computational work to try and resolve some of the issues raised by these different experimental conclusions. For methodological reasons to which we return below direct contact between experiment and theory is not straightforward. Thus, early studies have concentrated on point defect calculations and energy minimisation using interatomic potentials for particular clusters in the dilute limit rather than solid solutions with finite dopant concentrations. These studies have also been restricted to the static limit, i.e., 0 K and neglecting vibrational contributions to the energy. Minervini et al.¹³ using such methods examined different arrangements of isolated dimers and trimers and concluded that location of the Gd³⁺ at nearest neighbour† (NN) or next-nearest neighbour (NNN) positions to the oxygen vacancies to were very similar in energy. More recent ab initio DFT+U calculations however have indicated the nearest neighbour arrangement is lower in energy.^14,15 Ye et al. have used the same computational approach as Minervi et al.,¹³ with a different set of interatomic potentials, for larger, but still isolated, defect clusters with up to six vacancies and associated dopant cations.¹⁶ In their most stable clusters containing more than three oxygen vacancies, each vacancy has two Gd³⁺ cations in the next-nearest neighbour site common to both, in a C-type consistent structure. However, similar studies by Li et al.^17,18 favour nearest rather than next-nearest neighbours. Lower energy clusters than those in ref. 16 have been reported subsequently by Li et al.¹⁹

Again using the same computational methods, Wang et al.²⁰ suggest that dopant concentration limits the size of the nano-domains, such that at lower Gd concentrations GDC favours small pyrochlore-type clusters but C-type nano-domains at higher concentration and suggest the maximum in the conductivity vs. concentration plot is linked to the formation of the latter. In a related study Wang et al.²¹ conclude from calculated (dilute limit) defect energies that monoclinic B-type extended defect structures within the CeO₂ lattice are less stable than C-type. Wang and Cormack have more recently also investigated the relationship between bulk strain and defect structure in GDC and proposed that the next nearest neighbour type associations are preferred under zero or tensile applied strains, while nearest neighbour type defect associations become more favourable under compression.²²

Evidence for the presence of extended defects locally has come from an experimental Pair Distribution Function (PDF) Analysis by Scavini et al.²³ However, as Fig. 4 of ref. 18 shows, there are major differences in the variation of the interatomic metal–metal and metal–oxygen interatomic distances determined by Rietveld analysis, PDF and EXAFS. We return to this discrepancy later in this paper. Most recently Scavini et al.²⁴ conclude that on the subnanometre scale all GDC solid solutions can be described as biphasic containing ‘droplets’ of CeO₂ and Gd₂O₃; for x ≤ 0.25 the average structure is that of fluorite, which turns into C-type at larger x and they view these changes as a percolation-driven phase transition.

Thus in spite of a large number of experimental and computational studies, the nature and role of extended defect clusters in GDC and how these vary with composition are far from being clarified. A study providing a complete description of both local and micro-structure is required. Moreover, the atomistic simulations described above employed energy minimisation in the static limit (i.e., at 0 K, ignoring vibrational terms). Absolute and relative defect binding energies can strongly vary with temperature; Raman spectroscopy of GDC at elevated temperatures indicates that oxygen vacancies dissociate from clusters stable at lower temperatures.²⁵ Indeed, the number of configurations and the size of the defect clusters explored in previous computational studies are limited and this in turn has restricted the contact between theory and experiment.

In this paper we report hybrid Monte Carlo (HMC) simulations, which combine Monte Carlo and molecular dynamics techniques in order to explore phase space efficiently. These are an appropriate method to remove almost all of these limitations. Simulation cells containing many thousand atoms are feasible, and we can examine finite concentrations of dopants rather than solely clusters in the dilute limit. Temperature effects are included automatically. Thus here we present, to our knowledge, the first HMC study of grossly non-stoichiometric GDC.

2 Computational method

2.1 Monte Carlo simulations

The properties of solid state materials, especially, ionic compounds, have been investigated using either supercell or point defect calculations.²⁶ However, these methods are not readily extended to disordered systems containing a finite impurity or defect content, thereby restricting simulations to end-member compounds and excluding studies of many naturally occurring minerals and ceramics of industrial importance. Standard Monte Carlo (MC) and molecular dynamics (MD) is unable to overcome kinetic energy barriers to sufficiently sample all necessary configurations. In previous papers we have described MC methods that exchange cation positions in order to sample multiple configurations and calculate the thermodynamic and solubility limits of ionic materials.^27–31 However, even with MC swaps the sampling of configurations will be very poor due to the different size and charge of the cations. It is necessary to resort to a different strategy, i.e. some form of relaxation must be provided. We also demonstrated, in a previous paper, that a simple relaxation (energy minimisation) is not sufficient and vibrational effects must be included within the calculation.²⁷ Unfortunately these effects were not included in previous calculations.

The HMC approach we have developed is related to that used in the modelling of polymers and biomolecules.^32–34 The technique has been applied previously to such problems as the enthalpies of mixing of binary oxides^27,29 and non-convergent ordering of cations in olivine and phase transitions.¹⁹ During one HMC cycle, one of three options is chosen at random, with equal probability. The first of these is a short molecular dynamics (MD) simulation (140 steps and a timestep of 1.0 fs) in the microcanonical ensemble. The last configuration is accepted or rejected by comparing its energy with the energy of the starting configuration and using the standard Metropolis algorithm.³⁵ The Metropolis approach requires that a trial move from the original state (o) to a new state (n) is accepted with the probability,

P_(o→n) = exp{−β[U_n − U_o]}

where U_n and U_o are the energies of the new and original states and β is 1/kT. At the start of each MD run, velocities are chosen anew at random from a Maxwellian distribution. In the second, which is only applicable to the solid solution, a short MD run follows a random exchange of Ce and Gd ions. Again, the difference in energy between the previous configuration and that immediately after the MD simulation is used in the Metropolis algorithm. Since the MD technique is used to update the positions of the ions it not possible to track the location of the vacancies and it was not feasible to swap the position of a vacancy with an oxygen ion. However, in GDC the oxygen ions are mobile at 1000 K and can move to the most energetically favourable position. The third option is a random change of the volume/shape of the box, which again is accepted or rejected using the Metropolis algorithm. Enthalpy and structural data were averaged over a period of 150 000 cycles, prior to which an equilibration period of 150 000 cycles was undertaken.

We stress that our method does not involve the use of an approximate parameterised Hamiltonian. Not only does parameterisation of, for example, an Ising-type Hamiltonian become increasingly difficult beyond binary or pseudobinary mixtures, but it can average out local effects due to ion clustering and association, and such methods cannot readily be extended to include the effects of lattice vibrations and pressure. The HMC technique permits an efficient sampling of different configurations and takes explicit account both of ionic relaxation near impurity ions and thermal effects.

For consistency with previous calculations,^16–22 the potential parameters used were those developed in ref. 13. A 20.0 Å cutoff for the potentials was employed.

2.2 Order parameters

To examine the nature of the local order more closely we have evaluated averaged local (Steinhardt) bond order parameters.³⁶ These are often used to distinguish different crystalline structures and polytopes, (e.g.ref. 37), to characterise non-stoichiometry at interfaces³⁸ and very recently the disorder induced by radiation damage and subsequent healing in ceramics.³⁹ These parameters are translationally and rotationally invariant, i.e., independent of the reference frame specifying the crystal structure.

A cation i (Gd or Ce) is selected from the structure. A set of even-order spherical harmonics⁴⁰Q_lm are calculated: for each vector r which connects this atom i to those within a specified primary cut-off distance,

Q_lm(r) = Y_lm(θ(r), ϕ(r)) (2)

θ and ϕ are polar angles which define the orientation of r. Here we set the primary cut-off to 3.2 Å, which restricts contributions to Q_lm from only nearest oxygen neighbours.

The average value of Q_lm over the N_b neighbours within the cut-off distance is thus

We now average, for a given l, over all possible values of m to obtain Q_l(i), which is rotationally invariant,

To assign local structures surrounding individual atoms, we use the average of Q_l(i) over all atoms i located within 8 Å, the secondary cut-off, of one of the atoms in the simulation cell. The region around each atom i defines a secondary sphere and so we obtain finally Q_l for each such sphere. Lechner and Dellago⁴¹ in their study of soft particle systems use a similar method but first find the mean of the Q_lm. While this final averaging to obtain the Q_l invariably reduces the spatial resolution, it makes it easier in practice to distinguish different structures, and tests showed that 8 Å was the optimum secondary radius to achieve this aim. In this paper we use Q₂ (l = 2) and Q₈ (l = 8).

2.3 Molecular dynamics

In order to compare with experimental conductivity measurements calculation of the ionic diffusion is required. This cannot be achieved using the HMC technique and we have chosen to use molecular dynamics simulations. Atomic configurations obtained from the HMC were used as starting points for the simulations. The MD simulations, with the DL_POLY package,⁴² were undertaken in the isothermal–isobaric ensemble using Nosé–Hoover dynamics to control the temperature (1000 K) and pressure (1 atmosphere). The oxygen diffusion constant, D, was calculated from the mean squared displacements following the procedure in ref. 43:

The ionic conductivity, σ, can then be obtained from the Nernst–Einstein relationship; note this is strictly only valid for dilute systems but in practice is often used also for solid solutions at the concentrations considered in this paper.

where z_ie is the charge of species i, and c is the concentration of defects – here oxygen vacancies, which we assume is the only species responsible for the conductivity.

3 Results

3.1 Hybrid Monte Carlo

The simulations of Ce_1−xGd_xO_2−x/2 (GDC) used a cubic 8 × 8 × 8 simulation cell of CeO₂ containing the appropriate number of dopant cations and oxygen vacancies according to eqn (1) (i.e. for x = 0.05 the number of Gd ions and oxygen vacancies are 102 and 61 respectively). HMC runs were undertaken on simulation cells ranging in composition from x = 0.0 to x = 1.0. Thus all calculations were performed on simulation cells of between 6144 and 5120 ions (depending on dopant concentration) and at 1000 K.

We first present data for the pure end member oxides (CeO₂ and Gd₂O₃) as this provides a platform to discuss the results for the CeO₂/Gd₂O₃ mixtures. CeO₂ has the fluorite structure (space group Fm3̄m) in which all cation positions are symmetrically equivalent as are those of the anions. All the Ce–O and Ce–Ce (i.e. next nearest cation neighbours) distances are identical (Table 1).¹⁰ In contrast, in the C-type structure adopted by Gd₂O₃ there are two distinct cation and two distinct anion sites (M1 and M2 for the cations, O1 and O2 for the anions, respectively). The M1 site has six Gd–O bonds of the same length, but the M2 is environment is less symmetric, giving rise to a range of bond lengths (Table 2)^10,44,45 and this distortion also gives rise to a range of Gd–Gd distances. In our simulations the automatic calculation of bond lengths is straightforward and an appropriate vehicle for their presentation is the radial distribution function (RDF). We have calculated the RDFs for HMC simulations and to obtain average bond lengths we have fitted these to one or two Gaussians, as appropriate. In Fig. 1 we display the cation–cation RDFs for CeO₂ and Gd₂O₃. As expected from the experimental data in Table 1 the M–M RDF for CeO₂ has a single peak. This is in contrast to Gd₂O₃ where two peaks are observed (consistent with the bond lengths in Table 2) and this distinction can be used to interpret the structure of CeO₂/Gd₂O₃ solid solutions as discussed below. The lattice parameter and bond lengths determined from X-ray diffraction are compared with data determined using HMC simulations in Tables 1 and 2. Our simulations have a slightly greater lattice parameter than experiment (0.7% difference), which, in part, can be attributed to the higher temperature of the simulation than experiment.

Table 1 Comparison of calculated and experimental structures of CeO₂. The experimental data are from Scavini et al. in ref. 23. a refers to the cubic lattice parameter. The calculated bond lengths were obtained from fitting the RDF's with a single Gaussian. All distances are in Å

	Experiment	Calculated
a	5.405	5.442
Ce–O	2.341	2.325
Ce–Ce	3.822	3.824
O–O	2.703	2.685

---

Table 2 Comparison of calculated and experimental Gd₂O₃ structures. The experimental data are from Scavini et al. in ref. 23. a refers to the cubic lattice parameter. The calculated Gd–O and O–O bond lengths were obtained from fitting the RDF's with a single Gaussian whilst the Gd–Gd distances were obtained by fitting to two Gaussians. All distances are in Å. Note the experimental data were collected at 90 K while the HMC simulations were undertaken at 1000 K

	Experiment	Calculated
a	10.808	10.870
Gd(M1)–O	2.349	2.291
Gd(M2)–O	2 × 2.255	2.291
	2 × 2.314
	2 × 2.412
Gd–Gd	M1–M2 × 6 3.590	3.592/4.034
	M1–M2 × 6 4.068
	M2–M1 × 2 3.590
	M2–M1 × 2 4.068
	M2–M2 × 4 3.605
	M2–M2 × 4 4.082
O–O		2.976

---

Fig. 1 Calculated cation–cation radial distribution functions (RDFs) for the nearest cation neighbours in (a) CeO₂ and (b) Gd₂O₃. The red lines in figures (a) and (b) are fitted Gaussians.

We now examine the change in lattice parameter as a function of composition. The solubility limit of Gd in CeO₂ has been investigated using X-ray diffraction and reported by Bevan et al. to exceed 40%.⁴⁶ This has been disputed by Chen and Navrotsky who observed additional peaks in their diffraction patterns due to C-type phase at 39% and the lattice parameter varies linearly with Gd content only up to 30.5%.⁹ Chen and Navrotsky interpret these diffraction data to infer that at x ≤ 0.2 the structure is fluorite, while for 0.2 < x < 0.4 there is a two phase region of fluorite and C-type and for x > 0.4 a C-type solid solution. Comparison of our calculations and experiment is difficult; not only were our calculations run at 1000 K but the data can be interpreted assuming several possible models. Thus in ref. 9 the authors have presented data that has been analysed within the above constraints and so for x > 0.4 split the fluorite and C-type lattice parameters. Indeed, Scavini et al. concluded that diffraction data could not be correctly interpreted using average structural models but required a biphasic model even for x = 0.125.²³ Unfortunately, making a direct comparison with the biphasic model interpretation of the experimental data is not possible as we are only able to determine the lattice parameters from the simulation cell vectors and cannot identify individual components in the same manner as XRD which operates over a much longer length scale. For the sake of comparison we compare our calculated values with experimental data defined as the fluorite cell parameter (i.e. half the C-type parameter) (Fig. 2). The calculated values are greater than the experimental values by less than 1%. Both experimental and calculated values exhibit a strong positive deviation from Vegard's law, i.e. from ideal solid solution behaviour. The calculated values form a slightly asymmetric curve with a maximum at x = 0.6.

Fig. 2 The calculated lattice parameter defined as the fluorite cell parameter, as explained in the text. The experimental data are from Chen and Navrotsky,⁹ Scavini et al.,²³ Grover et al.,⁴⁵ and Kennedy and Avdeev.⁴⁴

We turn to analyse trends in bond lengths and compare those determined using EXAFS and in a detailed pair distribution function (PDF) and Rietveld analysis by Scavini and co-workers.²³ We commence with the cation–oxygen (i.e. nearest neighbour) bond lengths. The variation of the Ce–O (Fig. 3) and of the Gd–O (Fig. 4) bond lengths reproduce the observed EXAFS trends although underestimated by the current potential model. For the end-member compounds the difference in the average bond lengths for Ce–O and Gd–O are 0.5% and 2% respectively. The contraction in cation–oxygen bond lengths with Gd content is in contrast to the lattice parameter in which increases with Gd³⁺ concentration. The average O–O bond distances obtained from our simulations is presented in Table 3 and exhibit a gradual increase as the number of Gd³⁺ ions increases. We stress that the relatively high temperature of the simulations and the distortion of octahedra associated with the formation of interfaces produces a wide range of O–O distances that can only be interpreted in terms of a simple average. Moreover, experimental O–O bond lengths for GDC do the best of our knowledge have not been reported in the literature so no comparison is possible. However, there are O–O distances for Ce_1−xY_xO_2−x/2 (YDC) from powder diffraction experiments⁴⁷ demonstrating a similar trend and the data has been analysed using three distinct O–O bond lengths. The initial increase in the unit cell volume and subsequent decrease has been rationalised in terms of the relative importance of the O–O and cation–O bond lengths.^23–25 The M–M distances, as discussed earlier, are a key marker of the local environment around the Ce⁴⁺ and Gd³⁺ ions. In Scavini et al.²³ there are significant differences depending on the assumptions made to refine the data (i.e. whether the data was analysed using either the Rietveld or PDF methods). The Rietveld refinement for x = 0 can be reconciled with a single NNN distance consistent with the fluorite structure. As x increased the distance splits at x_Gd = 0.25 into short and long distances (Fig. 5). In contrast, in PDF analysis the longer M–M distance decreases slightly as x_Gd increases and is present at x_Gd < 0.25. Our results, and the EXAFS experiments in ref. 8 (also shown in Fig. 5), tend to support the PDF analysis. Indeed, for the short M–M distance our results are in excellent agreement with experiment and for the long M–M distance are intermediate between those of the PDF and EXAFS results. Even in the Ce–Ce RDF's (not shown) for x_Gd = 0.05 we observe a splitting of the peaks into two distinct distances. Our results do not support the formation of small pyrochlore-type clusters as suggested by Wang et al.²⁰ since the Gd–Gd RDF for pyrochlore Gd₂O₃ does not show the splitting we see in Fig. 1b.

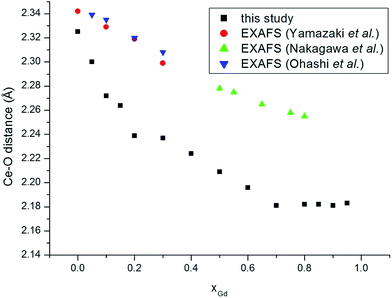Fig. 3 Ce–O distances as a function of composition for Gd_xCe_1−xO_2−x/2. The experimental data are from Ohashi et al.,⁵ Nakagawa et al.,⁶ and Yamazaki et al.⁷

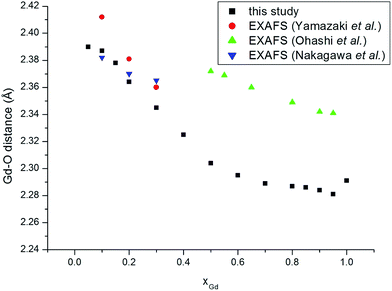Fig. 4 Gd–O distances as a function of composition for Gd_xCe_1−xO_2−x/2. Experimental data are from Ohashi et al.,⁵ Nakagawa et al.,⁶ and Yamazaki et al.⁷

Table 3 The average O–O bond length calculated using the hybrid Monte Carlo method

Composition x of GdxCe1−xO2−x/2	O–O distance (Å)
0.00	2.685
0.05	2.695
0.10	2.701
0.15	2.721
0.20	2.735
0.30	2.753
0.40	2.750
0.50	2.796
0.60	2.818
0.70	2.850
0.80	2.898
0.85	2.921
0.90	2.940
0.95	2.957
1.00	2.976

---

Fig. 5 The M–M distances as a function of composition. The PDF and Rietveld analysis are from ref. 23 and the EXAFS data from ref. 8.

Although we cannot make direct comparison with the XRD lattice parameters, we are able to examine snapshots of the structure and in particular the distribution of the cations. Several authors have postulated that the ionic conductivity is related to the trapping of vacancies around clusters of Gd³⁺ defects.⁴⁸ Thus, in order to demonstrate the clustering of Gd³⁺ ions we have removed all the Ce⁴⁺ and O²⁻ ions in Fig. 6 to display only the Gd³⁺ ions and where any two Gd are nearest (cation) neighbours to each other a “bond” has been inserted (this “bond” is only for graphical purposes and there no other inference as to physical interaction) – we call these associated Gd³⁺ ions. In addition, we have calculated both the average ratio of isolated to the total number of Gd³⁺ ions (Fig. 7a) and total number (Fig. 7b) of isolated Gd³⁺ ions (i.e. an isolated Gd³⁺ ion is where there are no Gd³⁺ ions as nearest cation neighbours). At x = 0.05 approximately half of the Gd³⁺ ions are isolated, the remaining Gd³⁺ ions have at least one Gd³⁺ ion as a nearest (cation) neighbour (Fig. 6a).

Fig. 6 Snapshots of the Gd distribution obtained from hybrid Monte Carlo simulations for (a) x_Gd = 0.05, (b) x_Gd = 0.10, (c) x_Gd = 0.15, (d) x_Gd = 0.20 and (e) x_Gd = 0.30. The “bonds” are used to demonstrate that a Gd ion has another Gd ion as its nearest cation neighbour.

Fig. 7 (a) The ratio of isolated Gd³⁺ (N_isolated) to the total number of Gd³⁺ (N_total) ions averaged over the simulation. (b) The average total number of isolated Gd³⁺ ions (N_total) obtained from the simulations.

We have already referred to a number of computational studies which have demonstrated the favourable formation of vacancy-dopant clusters in doped ceria.^16–22 These calculations were performed at 0 K and for the potential model employed in this study the difference in defect binding energy between these combinations¹³ is relatively low for Gd, as discussed above. In contrast our calculations were run at 1000 K and so explore a wider range of defect combinations without any a priori assumptions. As x increases to 0.10 while the total number of isolated Gd³⁺ ions increases (Fig. 6b and 7), the fraction of isolated Gd³⁺ ions decreases. Further increases in Gd content cause a dramatic decrease in both the average ratio and absolute total of isolated Gd³⁺ ions. Indeed, at x = 0.2 there appears to be the formation of a network consisting largely of Gd³⁺ ions and by x = 0.3 few isolated Gd³⁺ ions remain.

To obtain more information on local structure in the solid solution, Q₂ and Q₈ Steinhardt signatures were calculated with Gd at the centre of the primary sphere and separately also with Ce from 50–100 snapshots from the equilibrated hybrid Monte Carlo runs at 1000 K on bulk CeO₂, bulk cubic Gd₂O₃ and on each composition. All individual curves are normalised such that the area under each curve is one. For Gd and Ce these are collected together in Fig. 8 for the compositions x = 0.1, x = 0.2, x = 0.4 and x = 0.8; other compositions are consistent with these results. The signatures for each composition are distinct and there is an evident shift from the CeO₂ end-member towards the other end-member, Gd₂O₃, as the Gd content increases. The change in peak position with composition is not linear. The width of the signatures reflects the variation in local environments for both Gd and Ce, which are reflected in the O–Gd–O and O–Ce–O angles respectively. It is evident from Fig. 8 that CeO₂ and Gd₂O₃ produce distinct features in the Steinhardt order parameters that reflect the average local environment of the Ce⁴⁺ and Gd³⁺ cations. The order parameters are dissimilar to those of other oxide structures such as the pyrochlore Gd₂Ce₂O₇ (for which the Q₂ and Q₈ peaks are narrower and at 0.15 and 0.40 respectively) and corresponding defective fluorite and the signatures can be employed as an indication of the local environment of the cations in the Gd_xCe_1−xO_2−x/2 mixtures. Starting from the CeO₂ end member, as Gd/O dopants/vacancies are created the order parameters of both Ce⁴⁺ and Gd³⁺ are positioned close to that of the CeO₂ end-member, reflecting local environments similar to that in CeO₂. The fluorite framework dominates. The further introduction of Gd causes a local distortion of both cations. The widths of the signatures for Gd³⁺ are broader than for Ce⁴⁺ indicating that the range of angles around the Gd³⁺ ions is much greater than that around the Ce⁴⁺ ions, reflecting the larger Ce–O bond strength. As more Gd³⁺ ions are added the probability distributions become progressively more similar to that of Gd₂O₃. In addition, the width of the Gd³⁺ peak decreases, whilst that of the Ce⁴⁺ gradually increases. The structure becomes more similar to that of Gd₂O₃.

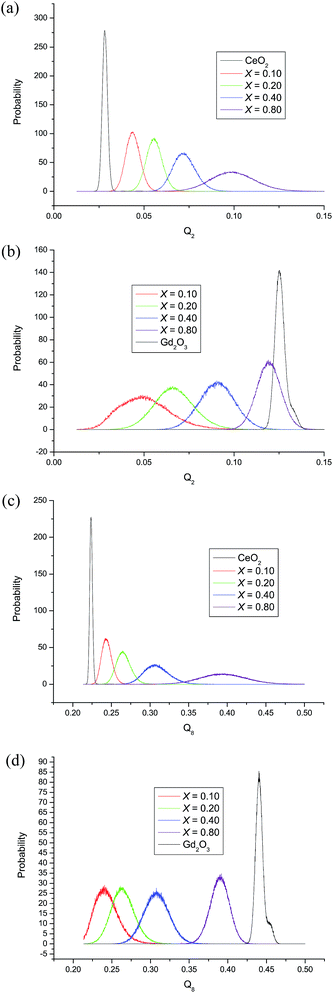Fig. 8 Probability distributions of the order parameters obtained from the hybrid Monte Carlo simulations. (a) Q₂ for Ce, (b) Q₂ for Gd, (c) Q₈ for Ce and (d) Q₈ for Gd.

To investigate further the sensitivity of the order parameter analysis to different arrangements of the Gd and the oxygen vacancies we have also analysed separately the results of optimised supercells of the same composition and size but which were not generated in the HMC runs. These included: (A) cells in which the Gd, and independently the oxygen vacancies, are distributed at random; (B) cells in which all the Gd ions and oxygen vacancies are distributed around the centre of the cell, forming one discrete nano-domain, or nano-crystallite of Gd₂O₃. Two different such examples for (B) were examined, in which the interfaces of the nanocrystallite were {100}, and {111} respectively. Fig. 9 displays the Q₂ and Steinhardt signature for all these cases. None of these match the signatures from the HMC; it is rather hard to judge but (A) is closer than (B) to the HMC. Almost all the signatures are wider than those in Fig. 8 from the HMC, showing a greater spread of angles and more distorted environments in the artificially constructed cells. For the (B) cells the signatures are further away from the Gd₂O₃ signature than those of the HMC plots, even with increasing Gd concentration, which must be a consequence of the different boundaries (interfaces) separating Gd and Ce rich regions. Q₈ plots show the same variations. Overall these results suggest the formation of smaller nanodomains of Gd₂O₃ in the HMC simulations with a greater uniformity of Gd environments.

Fig. 9 Probability distributions of Q₂ Ce parameters for structures generated by HMC, randomisation of cation and anion sublattices, [111] surface nanodomain and [100] surface nanodomain for Gd concentrations of (a) 10%, (b) 40% and (c) 80%.

3.2 Conductivity

Previous experimental and theoretical research, as discussed in the introduction, has identified a complex relationship between the atomic configuration and the ionic conductivity and the formation of Gd-rich domains reduces the ionic conductivity. In ref. 3 the conductivity was measured in freshly sintered (1873 K for 5 hours) material and in samples that had been aged for up to 8 days (heating at 1273 K). The ratio of the conductivity of the aged and sintered samples demonstrated that for x < 0.2 the aged samples had the greater conductivity whilst for x > 0.2 the aged samples had significant lowering of the conductivity. This observation was explained by the precipitation and coarsening of these domains during the ageing process.³ To test this hypothesis and the influence of Gd-rich domains on the ionic conductivity, we have undertaken MD simulations, as described in Section 2.3, using different cation configurations as starting points for the simulations. We have assumed that the sintered sample can be represented by a random configuration of cations (and vacancies) and the aged samples by configurations obtained from the HMC simulations (representative configurations were taken from the later stages of the calculations). The ratio of the oxygen ion conductivity obtained from the random, σ_random, and HMC, σ_HMC, configurations is presented in Fig. 10. Our results are in good agreement with the experimental results of ref. 3 and the calculated conductivity of the HMC configurations is greatly reduced for x ≥ 0.15. This is the composition at which we observe the formation of a network of Gd-rich ions. Despite the significant approximations in our calculations, our results suggest that the growth of Gd-rich domains have significant impact on the conductivity of GDC.

Fig. 10 The ratio of ionic conductivity obtained from HMC starting configurations, σ_HMC, and those obtained from random configurations of cations, σ_random. The ionic conductivity is assumed to be entirely from oxygen ion diffusion.

4 Conclusions

Hybrid Monte Carlo calculations have been performed to examine the thermodynamic equilibrium properties of Gd doped ceria. In particular, HMC simulations are capable of providing efficient sampling of configurations where large differences in size of the cations/anions. Unlike previous calculations^13,17–22 our work includes the effect of temperature on defect associations and the HMC technique allows exploration of a large number of configurations with different cation arrangements. We make no assumptions as to the formation of any particular clusters, and temperature and effects are included automatically and we are not restricted to the dilute limit. It is worth stressing our HMC simulations do not take into account any kinetic factors, which are undoubtedly important in the fabrication of experimental samples and their behaviour over long time scales.

Visualisation of the positions of cations obtained from the simulations reveal that the Gd³⁺ ions start to form domains even at low concentrations (x_Gd ≈ 0.1). Moreover, we have demonstrated that Gd³⁺ rich domains are established when x_Gd reaches approximately 0.2. This is in contrast to the solubility limits of Gd³⁺ in CeO₂ reported by Bevan et al. where solid solution systems greater than 40% Gd were observed.⁴⁶ We stress that the hybrid Monte Carlo technique explores equilibrium thermodynamic properties. This is in contrast to many experiments are unlikely to have been carried out under equilibrium because of the very long annealing times necessary.

MD simulations have been used to calculate the ionic conductivity on the representative structures obtained from the HMC. The results of these calculations and those in which the positions of the ions are randomised support the hypothesis that a Gd³⁺ rich network reduces ionic conductivity. Moreover, we propose that the growth in the network of Gd³⁺ ions is the main driver in the reduction of the conductivity of GDC. Overall our results are consistent with percolation theory arguments;⁴⁹ as the Gd concentration increases the Gd₂O₃ nanodomains restrict the diffusion paths and decrease the mobility of oxygen vacancies. Fig. 6 shows that by x = 0.3 few isolated Gd³⁺ ions remain and this is close to the site percolation threshold of 0.311 for a cubic lattice, and where Scavini et al. suggest a percolation-driven phase transition takes place.²⁴

We have analysed both the RDF's and Steinhardt order parameters to examine the local environment around the cations, and both are consistent with the formation of Gd₂O₃-like regions. The calculated cation–cation RDF's lend support to the interpretation of powder diffraction data using PDF's rather than the more standard Rietveld analysis of the data.¹⁰ The calculated RDF's are also in reasonable agreement with data obtained from EXAFS experiments.^7,8

The shorter than expected cation–oxygen bond length suggests that these potentials are too strong and may have influenced previous simulations concerned with defect binding. Further work will improve the efficiency of the technique so that we can study much larger simulation cells to observe growth of domain structure in materials.

5 Acknowledgements

The SCARF computing resources were provided by STFC's e-Science facility.

References

1. C. Sun, H. Li and L. Chen, Energy Environ. Sci., 2012, 5, 8475.
2. B. C. H. Steele, Solid State Ionics, 2000, 129, 95.
3. T. S. Zhang, J. Ma, L. B. Kong, S. H. Chan and J. A. Kilner, Solid State Ionics, 2004, 170, 209.
4. T. Mori and J. Drennan, J. Electroceram., 2006, 17, 749.
5. T. Ohashi, S. Yamazaki, T. Tokunaga, Y. Arita, T. Matsui, T. Harami and K. Kobayashi, Solid State Ionics, 1998, 113–115, 559.
6. T. Nakagawa, T. Osuki, T. A. Yamamoto, Y. Kitauji, M. Kano, M. Katsura and S. Emura, J. Synchrotron Radiat., 2001, 8, 740.
7. S. Yamazaki, T. Matsui, T. Sato, Y. Arita and T. Nagasaki, Solid State Ionics, 2002, 154–155, 113.
8. H. Deguchi, H. Yoshida, T. Inagaki and M. Horiuchi, Solid State Ionics, 2005, 176, 1817.
9. W. Chen and A. Navrotsky, J. Mater. Res., 2006, 21, 3242.
10. A. Banerji, V. Grover, V. Sathe, S. K. Deba and A. K. Tyagi, Solid State Commun., 2009, 149, 1689.
11. F. Ye, T. Mori, D. R. Ou, J. Zou, G. Auchterlonie and J. Drennan, Solid State Ionics, 2008, 179, 827.
12. Z.-P. Li, T. Mori, F. Ye, D. R. Ou, J. Zou and J. Drennan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180201.
13. L. Minervini, M. O. Zacate and R. W. Grimes, Solid State Ionics, 1999, 339–349, 116.
14. P. P. Dholabhai, J. B. Adams, P. Crozier and R. Sharma, Phys. Chem. Chem. Phys., 2010, 12, 7904.
15. S. Grieshammer, B. O. H. Grope, J. Koettgen and M. Martin, Phys. Chem. Chem. Phys., 2014, 16, 9974.
16. F. Ye, T. Mori, D. R. Ou, A. N. Cormack, R. J. Lewis and J. Drennan, Solid State Ionics, 2008, 179, 1962.
17. Z.-P. Li, T. Mori, J. Zou and J. Drennan, Phys. Chem. Chem. Phys., 2012, 14, 8369.
18. Z.-P. Li, T. Mori, J. Zou and J. Drennan, Mater. Res. Bull., 2013, 48, 807.
19. Z.-P. Li, T. Mori, F. Ye, D. R. Ou, J. Zou and J. Drennan, J. Chem. Phys., 2011, 134, 224708.
20. B. Wang, R. J. Lewis and A. N. Cormack, Acta Mater., 2011, 59, 2035.
21. B. Wang, R. J. Lewis and A. N. Cormack, Solid State Ionics, 2011, 182, 8.
22. B. Wang and A. N. Cormack, J. Phys. Chem. C, 2013, 117, 146.
23. M. Scavini, M. Coduri, M. Allieta, M. Brunelli and C. Ferrero, Chem. Mater., 2012, 24, 1338.
24. M. Scavini, M. Coduri, M. Allieta, P. Masala, S. Cappelli, C. Oliva, M. Brunelli, F. Orsini and C. Ferrero, IUCrJ, 2015, 511, 2.
25. S. A. Acharya, V. M. Gaikwad, V. Sathe and S. K. Kulkarni, Appl. Phys. Lett., 2014, 104, 113508.
26. C. R. A. Catlow and W. C. Mackrodt, Computer Simulation of Solids, Springer-Verlag, Berlin, 1982.
27. J. A. Purton, G. Barrera, N. L. Allan and J. D. Blundy, J. Phys. Chem. B, 1998, 102, 5202.
28. M. Y. Lavrentiev, N. L. Allan, G. D. Barrera and J. A. Purton, J. Phys. Chem. B, 2001, 105, 3594.
29. J. A. Purton, N. L. Allan and J. D. Blundy, Chem. Commun., 1999, 707.
30. J. A. Purton, M. Y. Lavrentiev and N. L. Allan, J. Mater. Chem., 2005, 15, 785.
31. J. A. Purton, J. C. Crabtree and S. C. Parker, Mol. Simul., 2013, 39, 1240.
32. S. Duane, A. D. Kennedy, B. J. Pendelton and D. Roweth, Phys. Lett. B, 1987, 195, 216.
33. B. Mehlig, D. W. Heermann and B. M. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 679.
34. M. E. Clamp, P. G. Baker, C. J. Stirling and A. Brass, J. Comput. Chem., 1994, 15, 838.
35. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087.
36. P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784.
37. D. Moroni, P. R. ten Wolde and P. G. Bolhuis, Phys. Rev. Lett., 2005, 94, 235703.
38. A. L. S. Chua, N. A. Benedek, L. Chen, M. W. Finnis and A. P. Sutton, Nat. Mater., 2010, 9, 418.
39. A. Archer, H. R. Foxhall, N. L. Allan, D. S. D. Gunn, J. H. Harding, I. T. Todorov, K. P. Travis and J. A. Purton, J. Phys.: Condens. Matter, 2014, 26, 485011.
40. P. M. Morse and H. Feshbach, Methods of Theoretical Physics, McGraw-Hill, New York, 1953.
41. W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707.
42. W. Smith, T. R. Forrester and I. T. Todorov, The DL_POLY Classic User Manual, Daresbury Laboratory, 2010.
43. M. Kilo, C. Argirusis, G. Borchardt and R. A. Jackson, Phys. Chem. Chem. Phys., 2003, 5, 2219.
44. B. J. Kennedy and M. Avdeev, Aust. J. Chem., 2011, 64, 119.
45. V. Grover, S. N. Achary and A. K. Tyagi, J. Appl. Crystallogr., 2003, 36, 1082.
46. D. J. M. Bevan, W. W. Barker, R. L. Martin and T. C. Parks, Rare Earth Research, ed. L. Eyring, Gordon & Breach, New York, 1965.
47. M. Coduri, M. Scavini, M. Allieta, M. Brunelli and C. Ferrero, Chem. Mater., 2013, 25, 4278.
48. J. A. Kilner, Faraday Discuss., 2007, 134, 9.
49. M. Meyer, N. Nicoloso and V. Jaenisch, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5961.

---

Footnote

† We use, following the literature, NN throughout this paper to refer to a cation at a nearest neighbour position to an oxygen vacancy and NNN to refer to a cation at a next-nearest (cation) position to an oxygen vacancy.

---