Heavily Eu₂O₃-doped yttria-aluminoborate glasses for red photoconversion with a high quantum yield: luminescence quenching and statistics of cluster formation

Abstract

We report on the photoluminescence (PL) properties of heavily Eu₂O₃ doped Y₂O₃–Al₂O₃–B₂O₃ glasses as a high-gain red-emitting material for photoconversion. A UV-to-red conversion efficiency of up to 60% is achieved in this material. Concentration quenching is related to the formation of –{Eu–O–Me–O–Eu}– (Me = B, Y, Al) and –{Eu–O–Eu}– linkages in the first and second coordination shell, respectively, of Eu³⁺. For a quantitative consideration, we employ a statistical approach to estimate the number of those species as a function of europium concentration. In this way, a crossover composition is obtained at a dopant concentration of ∼3 mol% of Eu₂O₃ where further addition of europium directly increases the number of –{Eu–O–Eu}–. In the latter species, the critical distance for concentration quenching of PL is achieved so that for concentrations above the crossover, PL quantum efficiency decreases. This observation is confirmed experimentally through lifetime analyses as well as direct measurements of internal quantum efficiency. The proposed tool can now be used to predict and optimize cluster formation and concentration quenching in rare-earth doped glasses.

---

Introduction

Inorganic materials doped with trivalent europium have been of strong interest for photo-conversion due to the 4f⁶ electronic configuration of Eu³⁺ which results in the characteristic red photoluminescence (PL) with often high quantum efficiency.¹ In detail, the PL spectrum of Eu³⁺ usually exhibits a variety of sharp PL lines in the orange to red spectral region arising from the intra-configurational parity-forbidden 4f⁶ → 4f⁶ electronic transitions from the non-degenerated ⁵D₀ level to the ground levels of ⁷F_{J(J = 0, 1, 2, 3 and 4)}.^1–4 While the band energy of these f–f transitions is usually not dependent on ligand field strength and, hence, the host material, the electric-dipole allowed transition of Eu³⁺:⁵D₀ → ⁷F₂ depends strongly on local symmetry. As a consequence, this transition can be used to probe the local structure in the considered host material. For this, the relative PL intensity ratio R of the electric- and magnetic-dipole-allowed transitions (usually denoted asymmetry ratio) is calculated, R = I_ED/I_MD. For example, a high value of R reflects low ligand symmetry and high bond covalency of the Eu³⁺ species.^5–7 The intrinsic excitation bands of Eu³⁺ are located in the near-ultraviolet spectral range (NUV), i.e., between ∼360 and 420 nm, and in the blue (∼464 nm). However, the parity-forbidden nature of Eu³⁺ absorption results in only low absorption cross section. Enhancing the Eu³⁺ doping concentration in the host material is one way to overcome this problem, but only as far as concentration quenching of photoluminescence can be avoided. This results in a trade-off between absorption efficiency, quantum efficiency and re-absorption.⁸ In particular, glasses with a high quantum yield of photoluminescence are desirable for applications where high transparency for light other than the excitation light is required to enable visually transparent emitters.⁸ Such target applications are, for example, luminescent concentrators,^9–11 bulk spectral converters for photochemical¹² or photovoltaic solar energy harvesting,^13,14 or three-dimensional luminescent displays.¹⁵ Compared to (single-) crystalline hosts, glasses provide the major advantage of facile processing into almost any size and shape.

In the present study, we consider the borate system of Y₂O₃–Al₂O₃–B₂O₃ (YAB).¹⁶ On the one hand, borate glasses generally offer a comparably high solubility for rare-earth ions.^8,17 In addition to this, the crystalline YAl₃(BO₃)₄ is known as an excellent nonlinear optical crystal and host for various rare-earth dopants (e.g., Nd³⁺ and Yb³⁺).^18,19 However, especially the incongruent melting of the constituting oxides strongly complicates the synthesis of single-crystalline YAl₃(BO₃)₄, which puts a limit on possible applications. On the other hand, due to the similarity of ionic radii (0.90 vs. 0.947 Å), the octahedral site of Y³⁺ can readily be occupied by Eu³⁺.²⁰ While there are no clear data available, in the glassy matrix, we expect a 6 to 8-fold coordination situation for both Y³⁺ and Eu³⁺, with a tendency to lower coordination with higher Y/Eu content.^21,22 Due to the supposedly less symmetric environment of the Y³⁺/Eu³⁺-sites, however, we also expect that the red emission band at ∼612 nm will be more dominant in the PL spectrum of Eu³⁺-doped yttria-aluminoborate glasses.^23–25 Finally, rare earth species (e.g., Eu³⁺) tend to be better dispersed in glasses as compared to crystals, which may be advantageous with respect to dopant concentration and concentration quenching of PL.²⁶

Experimental section

Precursor glasses were chosen at an excess of B₂O₃versus (Eu, Y, Al)₂O₃ as compared to the stoichiometric YAl₃(BO₃)₄, and also at an excess of (Eu³⁺,Y³⁺) over the Al³⁺-ion with higher-field strength in order to ensure facile glass formation and high rare-earth content. Nominal compositions (mol%) were (20−x)Y₂O₃–20Al₂O₃–60B₂O₃–xEu₂O₃ (YAB–xEu with x = 0, 0.25, 0.5, 1, 2, 4, 8 and 20). Corresponding mixtures of Y₂O₃ (99.99%), Al₂O₃ (99.9%), H₃BO₃ (99.9%) and Eu₂O₃ (99.999%) were prepared in batches of ∼30 g and melted conventionally in alumina crucibles at 1400 °C for 2 h in air. Melts were poured into preheated stainless steel moulds and annealed at 600 °C for 2 h to obtain stress-free glass slabs. These were subsequently cut into disks of ∼30 × 20 × 5 mm³ and polished on both sides for further characterization.

UV-vis absorption spectra were recorded with a double-beam photospectrometer (Cary 5000) over the spectral range of 300 to 700 nm with a step size of 1 nm. Static photoexcitation (PLE) and luminescence (PL) spectra and dynamic decay curves of Eu³⁺-related PL were collected with a high-resolution spectrofluorometer (Horiba Jobin Yvon Fluorolog FL3-22). PLE spectra were corrected over the lamp intensity with a silicon photodiode. PL spectra were corrected by the spectral response of the employed photomultiplier tube. Absorbance, internal (η_IQE) and external quantum efficiency (η_EQE) were obtained through measuring excitation and emission spectra on samples and a blank reference with a BaSO₄-coated integration sphere. The values of absorbance (a), η_IQE and η_EQE were then determined as follows:

a = (∫E_R − ∫E_S)/∫E_R (1)

η_IQE = (∫L_S − ∫L_R)/(∫E_R−∫E_S) (2)

η_EQE = η_IQEa (3)

In eqn (1)–(3), ∫L_S and ∫L_R are the integrated PL intensities with and without the sample, and ∫E_R and ∫E_S are the integrated intensities of excitation light without and with the sample in the integration sphere, respectively. CIE 1931 (Commission International de I'Eclairage) chromaticity coordinates were determined by integrating the PL spectra. All analyses were performed at room temperature.

Results and discussion

Fig 1a shows the UV-vis optical absorption spectra of YAB–xEu glasses for various concentrations of Eu₂O₃. For Eu³⁺-doped samples, seven characteristic absorption bands of Eu³⁺ with maxima at 362, 376, 394, 414, 465, 532 and 579 nm arising from the intrinsic 4f ↔ 4f transitions of Eu³⁺ from the ground state ⁷F₀ to the labeled excited states can be identified, as illustrated schematically in the energy level diagram of Eu³⁺ (inset of Fig. 1a).^8,26,27 The increased intensity of absorption bands of Eu³⁺ with Eu₂O₃ concentration especially in the UV region results in a shift of the absorption edge to longer wavelength, which is reflected by the changing visual color of the samples from colorless to dark orange with increasing Eu₂O₃ concentration (Fig. 1e). Fig. 1b present PLE spectra of YAB–xEu glasses by monitoring Eu³⁺ PL at 612 nm. In full agreement with the absorption bands of Eu³⁺ (Fig. 1a), six typical PLE lines of Eu³⁺ peaking at 318, 362, 376, 394, 414 and 464 nm are observed. They are assigned to the aforementioned transitions of Eu³⁺ from the ground state ⁷F₀ to the labeled excited states (Fig. 1b).²⁵ The sharp PLE line at 394 nm (Eu³⁺:⁷F₀ → ⁵L₆) which shows the strongest intensity is chosen as the PLE wavelength to record the following PL spectra (Fig. 1c).

Fig. 1 (a) UV-vis absorption spectra of YAB–xEu glasses as a function of Eu₂O₃ doping concentration. Room temperature (b) PLE (λ_em = 612 nm), (c) PL (λ_ex = 394 nm) and (d) normalized PL (λ_ex = 394 nm; normalized to the PL peak at 612 nm) spectra of YAB–xEu dependent on Eu₂O₃ doping concentration (labels: doping concentration of Eu₂O₃ in mol%). (e and f): Photographs of YAB–xEu glasses in sunlight (e) and under UV-A irradiation (f). The inset of (a) shows the energy levels of Eu³⁺. The insets of (b) and (c) show the PL peak intensity at 612 nm and PLE peak intensity at 394 nm of Eu³⁺versus the doping concentration of Eu₂O₃, respectively. The inset in (c) is a photograph of YAB–8Eu under irritation with a 532 nm laser diode. The inset of (d): zoom at the spectral region of 400 to 550 nm. The drawn lines in the inset of (b) and (c) are a guide to the eye.

Six characteristic PL lines of Eu³⁺ peaking at 578, 591, 612, 652, 700 and 748 nm are observed. These bands are attributed to the 4f⁶ ↔ 4f⁶ transitions of Eu³⁺ from the lowest excited state ⁵D₀ to the ground state multiplet of ⁷F_{J (J = 0, 1, 2, 3, 4 and 5)}.²⁵ The intensity of all Eu³⁺ PL lines increases linearly with increasing Eu₂O₃ concentration up to x = 2. A plateau is found for further increasing concentration up to x ≤ 8 mol%, reflecting the interplay of the negative effect of beginning concentration quenching and the positive effect of further increasing absorbance on PL intensity. Strong quenching is found for the sample doped with 20 mol% Eu₂O₃. This observation is confirmed through dynamic PL analyses. The decay curves of Eu³⁺ PL (at 612 nm) follow a single-exponential function for all studied dopant concentrations. The effective emission lifetime τ_1/e of Eu³⁺ remains at a constant value of ∼1.90 ms up to x = 2. For a higher doping concentration up to x = 8, it decreases to ∼1.35 ms, and decreases more for x = 20, i.e., to ∼0.092 ms (Fig. 2a). This indicates that concentration quenching sets-in at a concentration of ∼x = 2: at this concentration, the distance between neighbouring Eu³⁺-species becomes critical so that energy transfer and non-radiative relaxation may occur. As previously noted, unfortunately, clear data on Eu³⁺ (or Y³⁺) coordination in the considered glass are not available. For a first approximation, we may assume two principle coordination environments, i.e., 6-fold and 8-fold which are typically found for Eu³⁺ in oxide glasses.^22,28,29

Fig. 2 (a) Decay kinetics of the Eu³⁺:⁵D₀ → ⁷F₂ emission at 612 nm as a function of Eu₂O₃ doping concentration under excitation at 394 nm. (b) Variation of the effective lifetime τ_1/e (λ_em = 612 nm and λ_ex = 394 nm) as a function of doping concentration.

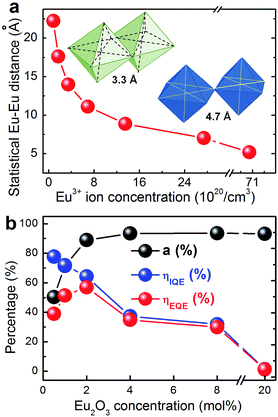
At room pressure, the minimum Eu–Eu-distance for corner-sharing polyhedra through a linear Eu–O–u group corresponds to twice the Eu–O-distance which is about 2.34 Å in Eu₂O₃, i.e., ∼4.7 Å. For edge-sharing, it is ∼3.3 Å (inset of Fig. 3a). A somewhat higher Eu–O distance would occur in 8-fold oxygen coordinated Eu³⁺, i.e., ∼2.4 Å, corresponding to ∼4.8 and ∼3.4 Å for corner and edge-sharing groups, respectively.²² A first estimate of the average statistical distance between all Eu³⁺ species can be obtained directly from the volumetric ion concentration. This is illustrated in Fig. 3a. In this consideration, the critical average Eu–Eu distance at which the onset of notable concentration quenching is observed corresponds to ∼11.1 Å for x = 2. Even though we are considering a glassy lattice, however, it is clear that within the length scale regime of <20 Å, the average value of interionic distances has only little meaning because the mid- and short-range structure is more and more specified. That is, within the first and second coordination shell, the distribution of potential Eu–Eu distances converges around two values which correspond to the bridging species of –{Eu–O–Eu}– (first coordination shell, Fig. 4b) and –{Eu–O–Me–O–Eu}– (second coordination shell, Fig. 4a, with Me = B, Y, Al according to the chemical composition of the considered glass). If we neglect the potential impact of local chemical heterogeneity (preferential ion clustering, dynamic heterogeneity, etc.), the speciation into either of the two configurations is given by the probability at which they occur in the glass lattice. For the –{Eu–O–Eu}– species, this probability is approximately,

P_Eu–Eu = 1 − (1 − x/100)^CN_Eu (4)

Fig. 3 (a) Average statistical Eu³⁺–Eu³⁺ distance as a function of volumetric ion concentration of Eu³⁺. The inset of (a) exemplarily shows edge and corner-sharing octahedral [EuO₆] species through a linear Eu–O–Eu group. The labels indicate the corresponding minimum Eu–Eu-distance. (b) Variation of absorbance (a), internal quantum efficiency (η_IQE) and external quantum efficiency (η_EQE) of red PL of Eu³⁺ under excitation at 394 nm in YAB–xEu glasses versus the doping concentration of Eu₂O₃. The drawn lines in the insets of (a) and (b) are a guide to the eye.

Fig. 4 (a and b) Schematic illustration of the –{Eu–O–Eu}– and –{Eu–O–Me–O–Eu}– (Me = B, Y, Al) linkages in the first and second coordination shell, repectively, of the Eu³⁺ ion. (c) Probability of cluster speciation P_Eu–Eu and P_Eu–Me–Eu, and sum of (P_Eu–Eu + P_Eu–Me–Eu), calculated for the two extremes of coordination number (six and eight) as a function of Eu₂O₃ concentration. The drawn lines in (c) are a guide to the eye.

with the Eu-coordination number CN_Eu and assuming an infinitely large ensemble of atoms. For the –{Eu–O–Me–O–Eu}– species, i.e., for having no Eu-neighbour on the first coordination shell but one on the second, it is

P_Eu–Me–Eu = (1 − P_Eu–Eu)(1 − (1 − x/100)^{(CN_Av−1)CN_Eu}. (5)

In eqn (5), CN_Av is the average coordination number of the cation species on the first coordination shell. As an approximation, we use ^IVB, ^VIAl and ^VIY and average according to the glass composition and the value of x. The result of this calculation is shown in Fig. 4c. As the accurate average coordination number of Eu³⁺ is not known for the present glass system beyond that it lies between six and eight, we plot data for ^VIEu and ^VIIIEu. We also plot the sum of P_Eu–Eu and P_Eu–Me–Eu as a measure of at least how many of the Eu species are found within the first or second coordination shells of each other. That is, when this sum approaches unity, each Eu has at least one Eu within its first or second coordination shell. At the nominal Eu₂O₃ dopant concentration of ∼3 mol%, we find a compositional crossover where the statistical number of –{Eu–O–Me–O–Eu}– species starts to decrease in favour of –{Eu–O–Eu}–. Interestingly, this crossover composition corresponds well to the observed onset of notable concentration quenching. At the crossover point, we may assume that about 60% of the Eu species lie within ∼10 Å of each other, and about 25% are first-shell neighbours which lie within ∼4.7 Å of each other.

This observed correlation confirms that the Eu–Eu linkages form mostly statistically with no notable contribution of selective cluster formation or even phase separation. At the crossover composition, newly added Eu₂O₃ does not contribute anymore to the number of –{Eu–O–Me–O–Eu}– or farther separated Eu species which act as efficient luminescence centers. Instead, from this composition onwards, every Eu-ion which is added to the material increases the number of –{Eu–O–Eu}– in which the critical interaction distance for PL quenching is achieved. Hence, notable PL quenching is observed for higher dopant concentrations. We believe that this approach can be used to predict and optimize the concentration quenching properties of similar photoluminescent glasses.

As expected, the PL spectra are dominated by the electronic-dipole allowed transition of Eu³⁺:⁵D₀ → ⁷F₂ at 612 nm for all samples which suggests an environment of lower symmetry for the Eu³⁺ species. As already noted, the intensity of the electronic-dipole allowed transition is strongly dependent on the symmetry of the local environment while the magnetic-dipole allowed transition of Eu³⁺:⁵D₀ → ⁷F₁ is independent of symmetry. Here, we obtain an asymmetry ratio of R ∼ 3.55, which is a relatively high value.^5–8 This confirms the distortion of local symmetry in YAB glasses. Expectedly, R does not notably depend on the Eu³⁺ concentration x, which reflects the very similar structural role of Y³⁺ and Eu³⁺.^30,31

As already noted, there is no notable variation in the intensity ratios of all emission peaks. The corresponding CIE 1931 chromaticity coordinates of all sample are (∼0.650 ± 0.003, ∼0.349 ± 0.001), close to the NTSC standard red of (0.670, 0.330). For illustration, we show photographs of the samples UV-A light (Fig. 1f) and under local excitation with a green laser beam (532 nm, Fig. 1c). Besides the PL lines from the lowest excited state of Eu³⁺, ⁵D₀, the PL lines which originate from higher lying levels such as ⁵D₁ are very weak or even absent in all samples (inset of Fig. 1d). This is due to the relatively high maximum phonon energy of the considered borate glass system (∼1400 cm⁻¹).^32–34 The forbidden transition of Eu³⁺:⁵D₀ → ⁷F₀ at 580 nm can be observed in all samples. Noteworthily, Eu²⁺-related photoluminescence cannot be observed in any of the samples.

The absorbance (a), internal quantum efficiency (η_IQE) and external quantum efficiency (η_EQE) are reported in Fig. 3b. For x = 0.5 mol%, we obtain a value of η_IQE of ∼80%. In correspondence with PL lifetime observations, this value decreases to ∼32% for a Eu₂O₃ concentration of 8 mol%. In parallel, the absorbance increases, which leads to the observed plateau in the emission intensity. The absorbance at 394 nm is ∼50% for x = 0.5, and increases to ∼94% for x = 4. The quantum yield therefore increases from ∼40% to ∼60% for a Eu₂O₃ concentration of up to 2 mol%. At higher concentration, it commences to decrease (Fig. 3b). This means that at the optimal Eu₂O₃ doping concentration of ∼2 mol%, about two thirds of the incoming photons are absorbed and re-emitted through Eu³⁺ photoluminescence in the red spectral range.

Conclusions

In conclusion, heavily Eu₂O₃ doped Y₂O₃–Al₂O₃–B₂O₃ represents a high-gain red-emitting material for UV-to-red photoconversion with a conversion efficiency of up to 60%. We related concentration quenching to the occurrence of –{Eu–O–Me–O–Eu}– (Me = B, Y, Al) and –{Eu–O–Eu}– entities in the first and second coordination shell, respectively, of Eu³⁺. For a quantitative consideration, we proposed a statistical approach to estimate the number of those species as a function of europium concentration. In this way, a crossover was found for a dopant concentration of ∼3 mol% of Eu₂O₃ where further addition of europium directly increases the number of –{Eu–O–Eu}– in which the critical distance for concentration quenching of PL is achieved. This observation is confirmed experimentally through lifetime analyses as well as quantum efficiency measurements. The proposed tool can now be used to predict and optimize cluster formation and concentration in rare-earth doped glasses.

Acknowledgements

Parts of this work have been supported financially by the German Science Foundation through its priority program 1594 (grant no. WO1220/10-1). The authors further acknowledge financial support from the Department of Education of Guangdong Province (Grant no. 2013gjhz0001).

Notes and references

1. G. Blasse and B. C. Grabmaier, Luminescent materials, Springer-Verlag, 1994.
2. G. Gao, N. Da, S. Reibstein and L. Wondraczek, Opt. Express, 2010, 18, A575–A583.
3. G. Gao, S. Reibstein, M. Peng and L. Wondraczek, J. Mater. Chem., 2011, 21, 3156–3161.
4. D. K. Williams, B. Bihari, B. M. Tissue and J. M. McHale, J. Phys. Chem. B, 1998, 102, 916–920.
5. J. C. Boyer, F. Vetrone, J. A. Capobianco, A. Speghini and M. Bettinelli, J. Phys. Chem. B, 2004, 108, 20137–20143.
6. Z. Qi, C. Shi, W. Zhang, W. Zhang and T. Hu, Appl. Phys. Lett., 2002, 81, 2857–2859.
7. C.-H. Yan, L.-D. Sun, C.-S. Liao, Y.-X. Zhang, Y.-Q. Lu, S.-H. Huang and S.-Z. Lu, Appl. Phys. Lett., 2003, 82, 3511–3513.
8. G. Gao and L. Wondraczek, J. Mater. Chem. C, 2013, 2, 691–695.
9. A. Goetzberger and W. Greube, Appl. Phys., 1977, 14, 123–139.
10. H. Lin, D. Hou, L. Li, Y. Tao and H. Liang, Dalton Trans., 2013, 42, 12891–12897.
11. B. Tian, B. Chen, Y. Tian, X. Li, J. Zhang, H. Zhong, L. Cheng, S. Fu, H. Zhong, Y. Wang, X. Zhang, H. Xia and R. Hua, J. Mater. Chem. C, 2013, 1, 2338–2344.
12. L. Wondraczek, M. Batentschuk, M. A. Schmidt, R. Borchardt, S. Scheiner, B. Seemann, P. Schweizer and C. J. Brabec, Nat. Commun., 2013, 4, 2047.
13. X. Huang, S. Han, W. Huang and X. Liu, Chem. Soc. Rev., 2012, 42, 173–201.
14. M. Peng and L. Wondraczek, J. Mater. Chem., 2009, 19, 627–630.
15. E. Downing, L. Hesselink, J. Ralston and R. Macfarlane, Science, 1996, 273, 1185–1189.
16. H. L. Rutz, D. E. Day and C. F. Spencer, J. Am. Ceram. Soc., 1990, 73, 1788–1790.
17. G. Gao and L. Wondraczek, Opt. Mater. Express, 2013, 3, 633–644.
18. D. R. S. Santos, C. N. Santos, A. S. S. de Camargo, W. F. Silva, W. Q. Santos, M. V. D. Vermelho, N. G. C. Astrath, L. C. Malacarne, M. S. Li, A. C. Hernandes, A. Ibanez and C. Jacinto, J. Chem. Phys., 2011, 134, 124503.
19. A. Brenier, D. Jaque and A. Majchrowski, Opt. Mater., 2006, 28, 310–323.
20. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
21. O. Bouty, J. M. Delaye and S. Peuget, Procedia Chem., 2012, 7, 540–547.
22. Y. Shimizugawa, N. Umesaki, J. Qiu and K. Hirao, J. Synchrotron Radiat., 1999, 6, 624–626.
23. R. Balda, J. Fernández, J. L. Adam and M. A. Arriandiaga, Phys. Rev. B: Condens. Matter, 1996, 54, 12076–12086.
24. P. Babu and C. K. Jayasankar, Phys. B, 2000, 279, 262–281.
25. A. Ivankov, J. Seekamp and W. Bauhofer, J. Lumin., 2006, 121, 123–131.
26. H. Deters, J. F. de Lima, C. J. Magon, A. S. S. de Camargo and H. Eckert, Phys. Chem. Chem. Phys., 2011, 13, 16071–16083.
27. G. Gao and L. Wondraczek, Opt. Mater. Express, 2014, 4, 476–485.
28. S. Iftekhar, B. Pahari, K. Okhotnikov, A. Jaworski, B. Stevensson, J. Grins and M. Edén, J. Phys. Chem. C, 2012, 116, 18394–18406.
29. T. Murata, Y. Moriyama and K. Morinaga, Sci. Technol. Adv. Mater., 2000, 1, 139–145.
30. A. A. Reddy, S. Das, S. Ahmad, S. S. Babu, J. M. F. Ferreira and G. V. Prakash, RSC Adv., 2012, 2, 8768–8776.
31. G. Gao and L. Wondraczek, J. Mater. Chem. C, 2013, 1, 1952–1958.
32. C. Xu, Y. Li, Y. Huang, Y. M. Yu and H. J. Seo, J. Mater. Chem., 2012, 22, 5419–5426.
33. B. S. Richards, Sol. Energy Mater. Sol. Cells, 2006, 90, 1189–1207.
34. G. Jia, M. Yang, Y. Song, H. You and H. Zhang, Cryst. Growth Des., 2009, 9, 301–307.

---