 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comparative cost and qualitative analysis for the transportation of green energy carriers†
Tom
Kroon
 *b,
Amir
Fattahi
*b,
Amir
Fattahi
 ad,
Francesco
Dalla Longa
ad,
Francesco
Dalla Longa
 ab,
J. Chris
Slootweg
ab,
J. Chris
Slootweg
 b and
Bob
van der Zwaan
b and
Bob
van der Zwaan
 abc
abc
aTNO, Energy and Materials Transition (TES), Amsterdam, The Netherlands
bVan 't Hoff Institute for Molecular Sciences (HIMS), University of Amsterdam, Amsterdam, The Netherlands. E-mail: t.kroon@uva.nl
cSchool of Advanced International Studies (SAIS), Johns Hopkins University, Bologna, Italy
dCopernicus Institute of Sustainable Development, Utrecht University, Utrecht, The Netherlands
First published on 26th February 2025
Abstract
Green energy carriers play a pivotal role in the transition towards the pervasive use of variable renewable electricity, as they allow for efficient storage, transportation, and utilization of excess electricity generated in specific regions and/or over different time frames. In this paper, we analyze the cost-optimality of transporting eight liquid or gaseous green energy carriers, including H2, via pipelines and shipping, over distances from 250 to 3000 km. To provide a more comprehensive deployability evaluation beyond purely cost-based criteria, we introduce several novel concepts that allow comparing green energy carriers on the basis of safety, applicability, and end-use characteristics. Our study reveals that H2 exhibits significantly higher costs compared to other energy carriers across both transportation modes. For a pipeline and shipping distance of 250 km, we calculate H2 transportation costs of 1.4 and 8.1 m€ per PJ, respectively, while for alternative carriers costs range from 0.1 to 0.7 and 0.2 to 3.1 m€ per PJ. For a distance of 3000 km, H2 transportation costs through pipeline and shipping are estimated at 18.6 and 10.3 m€ per PJ, respectively, whereas for alternative carriers the cost ranges from 1.2 to 7.6 and 0.3 to 4.0 m€ per PJ. An integration of additional selection criteria, however, implies that the practical deployability differs significantly across different green energy carriers, and that no one-to-one relationship exists between deployability and transportation costs.
1. Introduction
To mitigate climate change, the Paris Agreement aims at limiting the global temperature rise to 1.5 °C above pre-industrial levels.1–3 Achieving this goal necessitates a global shift from a fossil fuel-dependent society, to one driven by renewable and sustainable energy ensuring a decrease in greenhouse gas (GHG) emissions across the economy.4–6 The energy sector accounted for 73.2% of global GHG emissions in 2020, which underscores the urgency of embracing renewable electricity as well as other green alternatives.7 However, renewable electricity presents its own costly challenges due to regional and temporal generation constraints, hence conversion routes (i.e. power to X) for efficient electricity storage and transportation are required. One such alternative is the transformation of renewable electricity into synthetic H2 and H-based fuels, i.e. so-called green energy carriers (GEC). These “green” carriers are termed such because they are produced using clean, renewable energy sources, mitigating GHG emissions. GECs are expected to play an important role in reaching global climate control targets thanks to their efficiency, favorable costs, broad applicability, and safety aspects.8–10 The possibility to produce GECs at low cost in regions with a favorable climate (i.e. high solar irradiance and strong winds) and relatively low demand, followed by export to places where renewable resources are scarce and demand is high, makes these carriers particularly attractive. Europe, for example, could potentially benefit from GECs imports to bolster its energy independence,11,12 especially since the fragility of its energy supply recently became apparent.13In recent years, the prominent GEC – green H2 – has received unprecedented attention in both the scientific and the policy discourse, thanks to its large gravimetric energy carrying capacity and carbon-emission free nature.14–16 Nevertheless, large-scale H2 deployment presents some difficulties stemming from its chemical properties such as its low volumetric density at ambient temperatures, low temperatures required for a gas-to-liquid phase change and corrosive effect on existing steel-pipeline infrastructure.17,18
Its energy intensive production and transport processes further exemplify challenges faced, demanding substantial investments to maintain a viable green H2 supply chain.9,19,20 Because of this, several liquid GECs, collectively labeled liquid organic hydrogen carriers (LOHCs), are being considered as an alternative way to efficiently transport H2. LOHCs can be stored at ambient temperatures while maintaining high volumetric density values.21,22
In addition to further exploration of the chemical properties of LOHCs, extensive research is also being conducted on their economics. This particular research is driven by the desire to achieve cost-optimality in key aspects of the supply chain, such as production sites and transport modes, among others.9,21 In a comparative analysis conducted by the International Energy Agency (IEA) in 2019, the transportation costs of H2 and other GECs were examined for both carbon-neutral shipping and pipeline usage. The study assessed the feasibility of utilizing H2, ammonia as hydrogen carrier (HC) and the toluene–methylcyclohexane cycle employed as a LOHC, for transportation purposes. In addition to the latter two, several other promising candidates – namely, synthetic green methanol, ethanol and methane, as well as formic acid – have been identified and subjected to chemical and economic evaluation.8,10,22
Another added benefit of HCs and LOHCs is that they are considered potential ‘drop-in’ solutions, allowing seamless utilization or conversion of existing infrastructure to support an particular HC or LOHC supply chain, prompting further research on this feature.23,24 However, these examples of the growing body of available literature on GECs, predominantly emphasize their usage for enhancing green H2 supply chains, leaving a notable absence of detailed information on cost-effective energy carrying potential and end-use avenues. For example, Niermann et al. conducted a study on various GECs utilized as LOHCs for long-distance transport and long-term storage of hydrogen, without addressing possible end-use characteristics.25 Furthermore, Wijayanta et al. stated the cost-effective option of directly using GECs, yet kept its primary focus on the transportation cost of pure hydrogen.26 Lastly, Genge et al. evaluated and summarized 30 different GEC studies all focused on HC effectiveness.27 Thus, analyzing this gap could unveil additional pathways for the enhancement of climate-neutral energy carrier supply chains.
Our study evaluates eight liquid or gaseous GECs, including H2, calculating their respective energy transportation costs, with additional assessment on safety, applicability, and end-use features. Our findings provide comparative insight into the GEC performance in energy transport focusing on both carbon-neutral shipping and pipeline usage.
Section 2 describes the methodology we use for our analysis in detail. This is followed by its application for calculating transportation costs of the eight GECs that we selected (Section 3). In Section 4 we discuss our findings and cast them in a broader perspective, followed by a presentation of our overall conclusions and recommendations for the policy making scene (Section 5).
2. Methodology
Following the calculation pathway employed by the IEA,28 we have devised a similar framework for estimating GEC levelized energy transportation costs (ETC) in million € (2023) per Petajoule [m€ per PJ].28 In current literature, the predominant use of [$ per kg H2] and [€ per kg H2] as primary output units limits a comprehensive understanding of specific GEC transport costs, as it focuses on the transported H2 tonnage rather than the overall amount of energy being transported.9,10,19,29,30 By choosing to characterize various LOHCs in terms of levelized costs of energy, i.e. adopting the [m€ per PJ] unit, we are able to consolidate all ETC estimates into a single, unified value, facilitating comparative analysis. In addition to cost analysis, we evaluate GEC performance through four new scoring concepts. In this section, we elaborate our GEC selection (Section 2.1), followed by elucidating the key parameters and calculation procedures of the ETC framework (Section 2.2). Subsequently, we introduce our comprehensive scoring scheme (Section 2.3) and conclude by presenting three illustrative transportation scenarios for the import of GECs into Europe from different locations (Section 2.4).2.1 The GEC selection
For our analysis we have selected the following GECs: hydrogen (H2), ammonia (NH3), methanol (MeOH), ethanol (EtOH), synthetic methane (CH4), toluene–methylcyclohexane (TMCH), synthetic paraffinic kerosene (SPK) and formic acid (FA), all being produced using carbon containing building blocks i.e. CO2 and CO, and renewable energy sources such as solar panels, wind turbines, and biomass burners.31,32 Our selection criteria are based on the GECs scientific significance, popularity, economic performance and chemical properties (Table A1, Appendix I†), with the latter factor greatly influencing the required supply chain infrastructure and safety measurements. Drawing from commonalities between these chemical characteristics, we divide the eight GECs into three groups: group 1 (G1) including H2 and CH4, group 2 (G2) comprising of NH3, MeOH and EtOH and group 3 (G3) containing TMCH, SPK and FA. The groups are utilized to solve the problem of missing GEC data, requiring chemical extrapolation to fill in these voids. For instance, unknown MeOH values are derived by extrapolating known NH3 data based on chemical properties. The first GEC in each group has known values, while subsequent carriers necessitate chemical extrapolation.9 Additionally, specific GEC information for both chosen modes of transport, i.e. carbon-neutral shipping (s) and pipeline utilization (p), is lacking as well. This is solved by associating each of the groups to an established s- and p-supply chain, such as natural gas for G1 and oil for G2 & G3, which again requires data extrapolation to tailor our ETC framework.24,33,34 In Appendix I, Table A1† shows the relevant chemical properties of the GEC selection, integrated into our ETC framework for both modes of transportation. For a more detailed overview of the selected GECs and their industrial applications we refer to SI & SII.†2.2 The ETC framework
To calculate the pipeline and shipping ETC (p- and s-ETC, respectively) for each GEC, we modified the computation method used by the IEA,28 calibrating our framework by accurately recalculating their reported values in [$ (2017) per kg H2]. Building upon this groundwork, we perform chemical extrapolation (i.e. mass, energy and H2 density) as well as economic inflation and currency conversion. These processes are aimed at tailoring the ETC framework, ultimately yielding levelized energy costs ([m€ per PJ]) as our primary output. Fig. 1 illustrates a schematic representation of the GEC supply chain components adopted in our adjusted ETC framework. For both modes of transportation, conversion to and production of a GEC (B) determines the main GEC-input into our system in [kt GEC per year], greatly influencing the potential ETC for a given transportation distance (TD) in [km]. In the context of p-ETC (C), we examine two critical components, C1, representing the necessary number of compressor or pump stations (CP-stations) for pipeline operation, and C2, indicating the average distance between these CP-stations. Transitioning to s-ETC (D), our attention shifts to maritime infrastructure, where we encounter three pivotal elements, D1, denoting the count of export terminals, D2, representing the fleet size of ships required, and D3, indicating the number of import terminals essential for a well-functioning transport network. Segments A and E, representing, respectively, renewable energy generation local distribution and end-use options, are beyond the scope of this study and disregarded from our ETC pathway. Due to the exclusion of the latter we refer to the supply chain of interest as the transport chain.Similar to the IEA,9 each segment contributes to the total capital required for constructing and operating the transport chains. By determining the type and total number of each required component for a chosen TD, we can calculate and annuitize the capital expenditures (CAPEX). Subsequently, we add operation and maintenance expenditures (OPEX) to obtain the total yearly transport chain cost and find the average cost per kilometer in [€ per km].9 The segments shown in Fig. 1, facilitate us to formulate eqn (1.1) for a given TD, which represents the main equation for the p- and s-ETC frameworks:
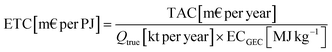 | (1.1) |
| TAC [m€ per year] = (AF [per year] × total CAPEX [m€]) + total OPEX [m€ per year] | (1.2) |
In this study, the TD [km] is the pivotal factor influencing all other terms featured in each equation. We analyze the p- and s-ETC across a TD range of 250–3000 km to identify the optimal transportation mode for these specific distances.9 The TD strongly impacts all integrated parameters within the ETC framework such as energy usage, applicable losses, CP-stations, pipelines, export/import terminals, and ships, thereby exerting a significant influence on the total annual costs value. Due to the strong dependence of total annual costs on a given TD, we have devised a second output unit, [m€ per TJ per km]. The unit is obtained by dividing the main output unit by the given TD, followed by a unit conversion, allowing us to closely monitor potential cost gradient changes. For our GEC p- and s-ETC results, we utilize and plot the two output units [m€ per PJ] and [m€ per TJ per km], respectively, to provide a clear overview of potential economic breakeven points, capital function minimums, and cost gradient dynamics.
| Subgroup | Base GEC | Transport mode | Base GEC-input | Extrapolated GEC-input [kt GEC per year] |
|---|---|---|---|---|
| a N.B. reminder p- = pipeline utilization & s- = shipping; the chemical conversions applied for p- = base GEC-input/(GEC hydrogen content/2) & for s- = 0.125 × ship capacity. | ||||
| G1 | H2 | p- | 340 kt H2 per year | 340 |
| s- | 520 kt H2 per year | 520 | ||
| G2 | NH3 | p- | 240 kt H2 per year | 2800 |
| s- | 12.5% ship capacity | 6625 | ||
| G3 | TMCH | p- | 800 kt H2 per year | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 230 |
| s- | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 kt TMCH per year 500 kt TMCH per year |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
||
| Transport-chain component | CAPEX | OPEX |
|---|---|---|
| a N.B. costs are adjusted for inflation (2023) and currency conversion ($ → €); Reminder G1 = H2 & CH4, G2 = NH3, MeOH & EtOH, and G3 = TMCH, SPK & FA; NA = not available. | ||
| Pipeline C/P-station | Eqn (3), Appendix II | NA |
| 9.64 m€ | 4% of CAPEX | |
| Export terminal | G1: 303 m€ | 4% of CAPEX |
| G2: 71 m€ | ||
| G3: 44 m€ | ||
| Ship | G1: 431 m€ | 4% of CAPEX |
| G2: 89 m€ | ||
| G3: 79 m€ | ||
| Import terminal | G1: 335 m€ | NA |
| G2: 101 m€ | ||
| G3: 37 m€ | ||
Due to loss factors in the various GEC groups, such as leakage (G1) [% per km] and energy usage (G1, G2, and G3), whereby each operational CP-station consumes a certain percentage of the transported GEC [% per km CP] (Table A3, Appendix III†), GEC-input [kt per year] is not equal to GEC-output [kt per year].33 Alongside these potential losses we are required to factor in the main GEC-inputs [kt per year] (Fig. 1B), which are presented in Table 1 to maintain clarity.28 It is these values in Table 1 that serve as the basis for conducting the chemical extrapolation, allowing data customization for each specific GEC. Subsequently, the true GEC throughput gives us the ability to calculate the number of CP-stations required to facilitate an operational p-transport chain (eqn (7) and (8), Appendix III†).33,34
To derive the TAC [m€ per year] (eqn (1.2)), we evaluate pipeline CAPEX [m€ per km], CP-station CAPEX [m€ per station], and OPEX [% CAPEX per year], with the initial step involving the annuitization of combined CAPEX (eqn (3), Appendix II†).28 The number of required CP-stations relates to the TD [km], average CP-station spacing [km] and maximum CP-station GEC throughput [kt per year] (eqn (7) and (8), Appendix III†).33,34
For s-ETC, the loss factors include boil-off rates (G1) [% per day], flash-rates (G1) [%], and fuel usage (G2 & G3) [PJ per year]. While the p- and s-loss factors differ, both result in the GEC-input [kt per year] being unequal to the GEC output [kt per year].28 Due to the changing numbers of export/import terminals and ships required to facilitate an operational transport chain, the fluctuating loss factors affect the true GEC throughput (eqn (10)–(13.3), Appendix IV†). For consistency, we included the used base GEC-input value in Table 1.28
To calculate the TAC [m€ per year] (eqn (1.2)), we assess the CAPEX [m€ per unit] of ships and export/import terminals, along with the OPEX [% CAPEX per year] for export and shipping (with the absence of import OPEX in the IEA report being addressed in Section 4). Similar to p-ETC, the initial step involves annuitizing the combined CAPEX (eqn (3), Appendix II†).28 Importantly, the number of export/import terminals required, as well as the number of ships, strongly depends on the GEC-input in [kt per year], TD in [km], ship's speed in [km h−1], ship capacity in [tGEC], export/import terminal capacity in [tGEC] and minimal required GEC storage [days] (eqn (14.1)–(14.3), Appendix IV†).28 An adjustment in one or each of these terms, significantly influences the TAC.
2.3 Qualitative criteria
To expand beyond quantitative results, we have developed and employed four distinct scoring tools to assess qualitative criteria. These criteria are used to assess each GEC in terms of safety, where we consider the chemical hazards and required transport conditions. Additionally, we evaluate versatility by examining potential applications. We assess ease-of-use to gauge how well studied and integrable the GEC is. Below we introduce and elaborate the hazard score (H-score), rigidity score (R-score) and energy transportation cost score (ETC-score). Finally, all scores are combined into the main transport performance score (TP-score). | (2) |
The TP-score enables us to look beyond cost-efficiency and reveals the genuine energy transport performance of each GEC, as detailed in the following section. For additional TP-score details we refer to SV.†
2.4 Scenarios
For a selected TD, a final TP-score will be computed for each of the p- and s-GECs, offering a comprehensive overview of costs, safety, applicability and end-use advantages associated with each GEC. We characterize these costs and scores for a whole range of TDs between 250 and 3000 km. Additionally we devised three transport scenarios for importing GECs into Europe, based on actual distances between Mediterranean export and import harbors, with their pertinent data outlined in Table 3. The outcomes from these scenarios will offer some real-world insights into the energy transport capabilities of each GEC.| Scenario | Export harbor | Import harbor | Transport distance [km] |
|---|---|---|---|
| a N.B. p- = pipeline utilization & s- = shipping; distances within in scenarios differ between export to import harbor due to pipelines being directly connected and shipping being confined to commercial shipping lanes. | |||
| 1 | Sfax (TUN) | Milazzo (ITA) | p-557 |
| s-717 | |||
| 2 | Algiers (DZA) | Milazzo (ITA) | p-1084 |
| s-1219 | |||
| 3 | Alexandria (EGY) | Milazzo (ITA) | p-1551 |
| s-2091 | |||
3. Results
In Fig. 2 (left plot), we present our G1 total p- and s-ETC comparison estimates. Initially, at a TD of 250 km, pipeline utilization emerges as the most economical option, with p-H2 and p-CH4 yielding ETC values of 1.39 and 0.19 m€ per PJ, respectively. However, as the TD increases, we observe a significant divergence in cost trends between the two modes of transportation for H2. Specifically, while the cost trend for p-H2 remains almost linear, its s-H2 counterpart exhibits a polynomial character, resulting in a break-even point of 10.50 m€ per PJ at 1900 km. For CH4, while the p-CH4 trend is again linear, its slope is much smaller than that of p-H2, and its costs remain below those for s-CH4, with no cost intersection throughout the examined TD range. Furthermore, in the TD range of 2000–2500 km, we observe a notable decrease in ETC for s-H2 and a slight decrease for s-CH4. This feature is attributed to an increase in fleet size (i.e. n ship + 1), necessary to maintain the transport chain. Despite the additional capital investment required, the ETC reduction is attributable to the increased GEC throughput achievable with a larger fleet, compared to the capacity limitations of a single vessel. | ||
| Fig. 2 G1 p- & s-ETC comparison [250–3000 km]: total ETC (left) [m€ per PJ] and km specific ETC (right) [m€ per TJ per km]. | ||
Fig. 2 (right plot) shows our G1 km specific p- and s-ETC projections in terms of m€ per TJ per km. At the starting TD of 250 km, both s-H2 and s-CH4 exhibit significantly higher average costs per km per TJ compared to their p-counterparts. Furthermore, it is worth noting the substantial starting cost of s-H2, which exceeds the predetermined y-axis range. Similar to the left plot, the intersection point for H2 occurs at 1900 km, with a value of 5.58 m€ per TJ per km, while no intersection is observed for CH4. Within the TD range of 2000–2500 km, a constant cost decrease is observed. Additionally, the trend for both s-GECs remain polynomial, consistently with the left plot. Interestingly, the right plot reveals a deviation from linear p-GECs characteristics, providing further insight into the cost dynamics across different modes of transportation and energy carriers.
In Fig. 3 (left plot), we display our G2 total p- and s-ETC comparison estimates. At a TD of 250 km, pipeline utilization emerges as the most cost-effective option for all three GECs, with p-NH3, p-MeOH, and p-EtOH exhibiting ETC values of 0.69, 0.51, and 0.38 m€ per PJ, respectively. However, as the distances increase, intersection points are rapidly reached: 1.16 m€ per PJ for NH3 at 450 km, 1.10 m€ per PJ for MeOH at 580 km, and 0.81 m€ per PJ for EtOH at 570 km. Notably, the cost slope for each p-GEC is much higher than that of their s-GEC counterparts, with both transportation mediums displaying a roughly linear trend. The G2 s-ETC decrease, located in the 1500–2500 km TD range, are again attributed to the need for a larger fleet size to maintain the transport chain.
 | ||
| Fig. 3 G2 – ETC comparison projection [250–3000 km]: main ETC (left) [m€ per PJ] and km specific ETC (right) [m€ per TJ per km]. | ||
Fig. 3 (right plot) depicts the difference between our G2 km specific p- and s-ETC projections. As observed in Fig. 2 (right plot), at the initial TD of 250 km, the average cost per km of transporting 1 TJ is notably higher for all s-GECs compared to their p-GEC counterparts, although the cost intersections are quickly reached. Additionally, within this TD range, it becomes evident that for all the s-GECs, the lines tend to converge around the 3000 km mark. Furthermore, the trend for the p-GECs no longer appear linear but slightly polynomial, exhibiting a similar trend yet differing cost values.
In Fig. 4 (left plot), we illustrate the comparison of our G3 total p- and s-ETC calculations. Pipeline utilization emerges as the most cost-effective option for all three GECs at the starting TD of 250 km, with p-TMCH, p-SPK, and p-FA yielding ETC values of 0.64, 0.11, and 0.54 m€ per PJ, respectively. However, as the TD increases, cost intersections for all three GECs occur in rapid succession, with values of 1.21 m€ per PJ for TMCH at 495 km, 0.20 m€ per PJ for SPK at 490 km, and 1.20 m€ per PJ for FA at 620 km. Although the intersection distances are closely situated, the ETC of SPK is notably lower compared to the other two. Additionally, consistent with previous Fig. 2 and 3, the steep cost slope for each p-GEC contrasts significantly with the shallow cost growth of the s-GEC counterparts. Furthermore, both transportation mediums exhibit seemingly linear functions. Interestingly, instead of a s-ETC decrease, G3 shows the line flattening within a 2000–3000 km TD range. While the need for a larger fleet size remains, its impact is significantly reduced compared to G1 and G2. This indicates that G3 maintains more consistent costs once additional capital requirements are integrated.
 | ||
| Fig. 4 G3 – ETC comparison projection [250–3000 km]: total ETC (left) [m€ per PJ] and km specific ETC (right) [m€ per TJ per km]. | ||
Fig. 4 (right plot) presents our varying G3 km specific p- and s-ETC estimates. Similar to the previous right plots (Fig. 2 and 3), at the starting distance of 250 km, the average cost per km of transporting 1 TJ is significantly higher for all s-GECs compared to their counterparts, yet the cost intersections are quickly reached. Furthermore and similar to G2, the trend for the p-GECs no longer appear linear but slightly polynomial, exhibiting similar trends yet differing cost values.
In Fig. 5 (top panel), the ETC-scores for all GECs are illustrated for a TD of 1000 km. GECs within the [0–0.2] score interval are considered the best-performing and are depicted in green, with SPK scoring the lowest among both s- and p-variants. The next interval, [0.2–0.4], is shaded light green, indicating GECs with high-performance which are capable of reaching the optimal range with only slight improvements required. The plot also shows the low-performing ([0.6–0.8], orange) and poorest-performing ([0.8–1.0], red) intervals, with only H2 falling within the latter two. Moreover, s-H2 scores a value of 1 due to its function as the highest value benchmark required for eqn (17) (Appendix V†). The ranking in the plot is based on scores from lowest to highest and is maintained in subsequent segments to visualize the alternating ETC-scores for varying TDs.
Fig. 5 (middle panel), notable changes are observed across all intervals for a TD of 2000 km. The most significant difference is the marked increase of p-H2 to the highest score of 1, placing it in the poorest-performing range, alongside s-H2, which is no longer the least favorable at 0.961. Additionally, p-TMCH and p-NH3 have seen an increase in score, moving from the high-to intermediate-performance interval [0.4–0.6|yellow]. Lastly, slight deviations are noted within the best-performing interval, with s-EtOH being the only outlier demonstrating no change. In Fig. 5 (bottom panel) portrays the most significant changes among all segments, characterized by notable shifts in ETC scores for a TD of 3000 km. The most prominent change is the advancement of s-H2 into the intermediate-performance interval, substantially reducing the difference in ETC-scores compared to other intermediate GECs such as p-TMCH and p-NH3. Aside from s-H2, no additional interval changes have occurred, with only minor scoring adjustments noted. However, one outlier worth mentioning is s-CH4, which transitioned from the higher part of the high-performance interval to the lower part. Overall, focusing on the normalized ETC data reveals various interval changes and indicates growing performance for GECs with increasing TDs.
In Fig. 6 we present the TP-score of all the GECs, based on the ranking from Fig. 5 (top panel) and for a TDs of 1000 km (top panel), 2000 km (middle panel) and 3000 km (bottom panel). Interestingly, the TP-score reveals greater variation among intervals and larger differences in scores compared to Fig. 5. Despite several GECs still falling within the high-performance interval at the 1000 km TD, the intermediate- and low-performance intervals are more populated. Notably, s-EtOH [0.186] remains within the best-performance range, while s-H2 is the sole GEC in the poorest-performance interval, scoring a 1.
In Fig. 6 (middle panel), as the TD increases to 2000 km, we observe a notable migration of intervals from low- to poorest-performance for p-TMCH and p-H2. Additionally, p-MeOH enters the intermediate-performance interval. Despite an overall score increase for all GECs compared to a TD of 1000 km, their respective rankings remain consistent. However, one exception is p-CH4 [0.359], which surpasses its closely neighboring s-MeOH [0.346].
In Fig. 6 (bottom panel), the TP-score at a TD of 3000 km exhibits the highest diversity among all segments. Notably, s-EtOH continues to be the only GEC present in the best-performance range, while only s-SPK, MeOH, FA and p-EtOH remain in the top half of the high-performance interval. Both the intermediate- and poorest-performance intervals expand by one GEC each, with p-H2 now achieving the highest score of 1. Importantly, while s-H2 remains in the poorest-performance interval, it is surpassed by both p-TMCH and p-NH3, suggesting that increased TDs favors s-H2 over various p-GECs. Consequently, the TP-score, as depicted in eqn (2), reveals intriguing differences compared to the ETC data in Fig. 5, prompting us to utilize our tool for real-life scenarios.
Fig. 7 illustrates the TP-score, derived from averaging the combined results of all Mediterranean scenarios, ranking the GEC based on their performance. For the detailed results of all three scenarios we refer to SIV.† Notably, s-EtOH stands out as the only GEC present in the best-performance interval, followed by seven GECs utilizing both transportation mediums, within the high-performance region. Additionally, three intermediate- and four low-performance GECs are observed, with variations in transportation medium. Particularly noteworthy is p-H2, which achieves a TP-score of 0.636, indicating an increasing favorability for H2 in these real-life situations. However, s-H2 stands out with a score of 1, signifying its status as the poorest-performance option when all parameters are considered in these scenarios.
 | ||
| Fig. 7 Mediterranean scenario TP-score ranking [1–16] for all GEC, their respective transportation medium and phase. | ||
4. Discussion
Our ETC calculations reveal that H2 does not emerge as the clear best-performing GEC, contrary to what might have been expected given its popularity and extensive study.9,16,20,29 While H2 holds significant potential in industrial decarbonization, our comprehensive analysis demonstrates its substantially high ETC compared to seven alternative GECs, utilized directly as energy carriers rather than as LOHCs. These findings offer a different perspective on Europe's transition efforts towards a H-based society, suggesting that H2 may not be the most cost-effective energy transportation option when compared directly with other GECs.Our study does not propose a definitive solution for achieving the targets outlined in the Paris Agreement but aims to provide valuable insights into green energy transport cost-efficiency. By potentially reducing the required capital investments for sustaining GEC transport chains,1 the use of alternative GECs could be exploited to boost energy security. For instance, in the context of a prospective energy partnership between Europe and North Africa, economically viable GEC transport chains could leverage existing or repurposed infrastructure to enhance energy security.12 Numerous studies confirm that promising GECs used as LOHCs have demonstrated improved cost-efficiency in transport chains.8,10,22 However, the costly H2 conversion and reconversion steps can be eliminated for some GECs, such as ammonia, as they can be used directly in end-use applications. In addition, a review of the literature reveals that transport research predominantly focuses on H2 as end product.25–27 However, literature on the direct utilization of GECs is not completely absent. For example, Sánchez et al. demonstrated that for long-distance supply chains (>3000 km), the direct use of NH3 and MeOH is more cost-effective than employing H2.38 Moreover, Blanco et al. concluded that “A progressive introduction of these green liquid fuels will be necessary to achieve a 100% renewable energy system in all areas” referring to the cost-effective direct use of NH3 and MeOH, as means to support hard-to-electrify sectors.39 Therefore, we recommend that an comprehensive analysis of the whole supply chain, including production and end-use applications for all evaluated GECs, would be a valuable extension to this research, as it was beyond the direct scope of this study. In terms of energy transport, other GECs demonstrate a better performance compared to H2. Hence, in this paper, we therefore emphasize that focusing solely on H2 transport overlooks the potential benefits of many other GECs with respect to their energy carrying potential, positioning our findings as complementary insights.
To obtain our ETC results, the G1, G2, and G3 cost values presented in Fig. 2–4, respectively, are derived from values extracted from literature.28,33 In Chapter 2, we utilized these values following the calculation framework developed by the IEA.28 On the one hand, this allowed us to offer more in-depth insights into aspects left unaddressed by the IEA report, such as safety, applicability and, end-use features, while remaining within the same cost dataset. On the other hand, using these fixed cost values limited our insight into the transportation data of MeOH, EtOH, CH4, SPK, and FA, which were not examined by the IEA. Ideally, the base cost data of our ETC framework should be altered for each different GEC and transport scenario (i.e. cost of dedicated specific GEC pipeline or shipping transport chain). Furthermore, while GEC production costs were beyond this study's scope, their potential impact on our findings cannot be overlooked. We recommend that future research, conducted by us or others, expand upon our work by analyzing the full supply chain, and establishing specific base cost values for a more comprehensive GEC assessment.
Similarly to the used cost values, the ETC results for G1, G2, and G3 in Fig. 5 are calculated using known (i.e. H2, NH3 and TMCH) or chemical extrapolated (i.e. MeOH, EtOH, CH4, SPK and FA) GEC-inputs obtained from the IEA report and outlined in Table 1 (Section 2.2). However, it is important to note that resolving the need for chemical extrapolation by integrating GEC-specific input data, will influence the ETC estimates. To put this into perspective, we estimate that doubling the GEC-input will directly correlate with a twofold increase in GEC performance (i.e. significant cost reduction and improved transport efficiency). Thus using our equation framework presented in Appendix II–IV,† complemented by additional GEC data, could yield more accurate ETC estimates. Further expansion of the ETC framework can enhance its accuracy, enabling a more precise cost-optimal assessment for both our selected GECs and additional ones.
We justified the viability of our ETC framework by following the IEA calculation pathway, replicating their estimates and precisely mirroring their data integration steps.28 This process highlighted the absence of certain data points. As outlined in Section 2.2.2, there is no mention of OPEX costs related to import terminals in the s-transport chain. To keep alignment with the IEA approach, these OPEX costs were therefore neglected. Additionally, in Table 1 (Section 2.2), there is an absence of base GEC-input for G2, which was substituted by estimating a certain percentage based on the known input values. Importantly, the GEC-input for G3 was derived from reconversion values (X to H2), presented by the IEA. Such a method could have been applied to G2,28 however, it was decided to employ these two distinct approaches to gain additional methodological insight. Thus, to enhance precision in our analysis, future studies should investigate and establish the real GEC-input values of our selected GECs, among others, or opt for one of our two approaches.
The arbitrary nature of the H- and R-scores could raise questions about the legitimacy of the results. While quantifying qualitative data enabled the formulation of the TP-score, it is important to note that the criteria for these scores were predetermined by the authors. To maintain simplicity, all three factors in eqn (2), ETC-, H-, and R-score, are given equal weight. However, this may not accurately reflect the true importance of each factor in determining GEC favorability. Future studies, based on literature reviews and/or empirical data, could lead to adjusted scoring weights. For instance, these adjustments could see a prioritization of cost over technological advancements in determining GEC performance.
Building on this, we calculated the p- and s-TP-score for three Mediterranean cities and ports.36,37 Each scenario corresponded to a specific TD presented in Table 3 (Section 2.4), highlighting the discrepancy between using international shipping lanes and the required pipeline length. Importantly, these TDs are not inherently the most efficient transport trajectories, suggesting that refining transport routes could yield further improvements in TP-scores. Noteworthy, pipelines between Europe and North Africa may offer greater efficiency for routes not covered in our scenarios, such as Spain to Morocco and Egypt to Turkey or Greece. Conversely, shipping could offer a cost-effective solution for GEC transport beyond the Mediterranean. As depicted in Fig. 2–4 (Section 3), approaching a TD of 3000 km significantly favors shipping as the preferred method of transportation. We recommend further investigation into the integration of GECs on an industrial scale within the existing infrastructure. If feasible, the new GEC transport evaluation should utilize an updated ETC framework incorporating all the previously mentioned aspects.
Lastly, while the absence of production costs is necessary to solely evaluate energy transport costs, it cannot be entirely disregarded. We initially excluded consideration of GEC production costs since they are perceived as lying outside of the transport chain (Fig. 1, Section 2.2). Certain regions boast significantly more favorable and efficient locations for GEC production compared to Europe. We specifically addressed North Africa, which stands out due to its abundance of sunlight (strong solar radiation), which, together with its proximity to Europe, makes it a particularly promising candidate for low-cost GEC trade.11,12,24 Additional region-specific techno-economic studies are needed to expand the scope of the presented research, ultimately assessing the ETC of the entire GEC supply chain.
5. Conclusions and policy implications
In the present paper, we calculated the transportation costs for a set of liquid and gaseous molecules, focusing on their role as energy carriers rather than as hydrogen carriers. Our analysis of energy transportation via pipeline and carbon-neutral shipping for eight GECs, including green H2, over distances ranging from 250 to 3000 km, yields several novel insights, which we deem useful to further investigate the potential role of power to X routes in the transition to a climate-neutral energy system.To properly investigate and to account for any missing data, our GECs selection was divided into three groups. G1 includes H2 and CH4, G2 contains NH3, MeOH, and EtOH, and G3 comprises of TMCH, SPK, and FA, with the GECs being matched together based on similarities in chemical properties and transport conditions. For the first mentioned molecule in each group, supply chain data was readily available and obtained from existing literature, which was then chemically extrapolated to the other GECs within the same group.
Our ETC (G1) pipeline versus shipping results depicted a breakeven point around 1900 km for H2, whereas CH4 did not reach such a point. Evaluation of H2 transportation highlighted both the benefits (i.e. high energy density and carbon-emission free) and drawbacks (i.e. low volumetric density and cryogenic temperatures required) of its physical chemical properties, significantly influencing its ETC. Additionally, for nearly any given energy transport scenario, other GECs (G2 and G3) proved more suitable, as evidenced by the ranked TP-score obtained from our Mediterranean scenarios. Furthermore, GECs (G2 and G3) exhibit breakeven points between 450 and 620 km, indicating significant potential for cost-efficiency improvements with respect to H2. Consequently, we conclude that H2 is not the best-performing GEC based on its ETC. However, it is important to note that there is no one-size-fits-all solution, as, within the scope of our study, ETC estimates are not the sole determinant for GEC performance. To stylistically take this into account, we propose a scoring system (TP-score) that integrates cost estimates with qualitative features, allowing us to look beyond the ETC calculations.
For all our devised GEC groups (G1, G2, and G3), pipeline utilization consistently proved economically advantageous for short distances [250–620 km], as the construction cost of pipelines and CP-stations did not exceed those of export/import terminals and ships. However, as transportation distances increased, shipping became cost-competitive, leading to breakeven points favoring this mode for all but one GEC, within G1, G2, and G3.
The only exception was CH4, which did not reach a breakeven point favoring shipping. The absence of this cost intersection can be attributed to the marginal cost increase in CH4 pipeline construction compared to the substantial expenses associated with shipping infrastructure. Therefore, facilitating the production of green CH4 at strategically favorable locations (i.e. high solar radiation) and subsequent pipeline transport could offer a viable alternative for energy transportation.
Furthermore, our calculations revealed that across all examined transportation distances, shipped EtOH stood out as the best-performing GEC. Its relative affordability, minimal safety-risks, and applicational versatility, position it as the preferred choice for energy transportation. Notably, EtOH transported by ship exhibited the lowest cost-performance ratio, with its transportation via pipeline ranked second as well. These result reinforce EtOH's position as the most cost-effective GEC. Despite H2 exhibiting a notably high TP-score for both pipeline and shipping transportation, increased distances led to a considerable cost reduction for shipped H2 compared to other GECs. Thus, while currently not the best-performing GEC, future cost-reductions could enhance the economic deployability of shipped H2. In addition, MeOH displayed a low TP-score for both pipeline and shipping transportation, placing it in the high-performance category, which is consistent with findings in the literature.
In conclusion, our evaluation of alternative GECs across their respective chemical properties, ETC calculations, and TP-scores indicated promising cost reductions for medium transport distances [1000–3000 km], compared to H2-focused transport. Within this context, EtOH emerged as the best-performing GEC, offering low cost, robust energy carrying capacity, minimal safety risks, and applicational versatility. This positions EtOH as our recommended GEC, particularly in enhancing Europe's energy security through strengthened trade relations with North Africa. Our Mediterranean scenarios corroborated these findings, with multiple GECs achieving low TP-scores, confirming their high- to best-performance. Hence, while H2 currently dominates energy discussions, it is crucial to recognize other promising green energy carriers for shaping our energy future.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. F., F. D. L. and B. v. d. Z. thank the Ministry of Economic Affairs and Climate Policy of the Netherlands for its continued financial support of research on the international dimensions of the energy transition and climate change mitigation, and the energy security dimensions thereof in particular. The views expressed in this paper are exclusively those of the authors.References
- UNFCCC, The Paris Agreement, United Nations Framework Convention on Climate Change, 2018, [cited 2021 Nov 14], Available from: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement Search PubMed.
- IPCC, Climate change widespread, rapid, and intensifying, IPCC, 2021, [cited 2022 Nov 22], Available from: https://www.ipcc.ch/2021/08/09/ar6-wg1-20210809-pr/ Search PubMed.
- IPCC, Global Warming of 1.5 °C: An IPCC Special Report on Impacts of Global Warming of 1.5 °C above Pre-industrial Levels in Context of Strengthening Response to Climate Change, Sustainable Development, and Efforts to Eradicate Pover. Glob. Warm 15 °C, 2018, pp. 1–24, Available from: https://www.cambridge.org/core/product/identifier/9781009157940%23prf2/type/book_part.
- EC. European Commision, The European Green Deal, 2019, [cited 2024 Mar 19], Available from: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en.
- IPCC, Summary for Policymakers, Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, 2022, vol. 2022, pp. 1–52, DOI:10.1017/9781009157926.001.
- IEA, World Energy Balances: Overview, World, 2019, [cited 2023 May 25], Available from: https://www.iea.org/reports/world-energy-balances-overview/world Search PubMed.
- H. Ritchie and M. Roser, CO2 and Greenhouse Gas Emissions, Our World Data, 2020 May 11, [cited 2023 May 24], Available from: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions Search PubMed.
- B. S. Crandall, T. Brix, R. S. Weber and F. Jiao, Techno-Economic Assessment of Green H2 Carrier Supply Chains, Energy Fuels, 2022, 37(2), 1441–1450, DOI:10.1021/acs.energyfuels.2c03616.
- IEA, The Future of Hydrogen, The International Energy Agency, Paris, 2019, Available from: https://www.iea.org/reports/the-future-of-hydrogen, Licence: CC BY 4.0 Search PubMed.
- D. D. Papadias, J. K. Peng and R. K. Ahluwalia, Hydrogen carriers: Production, transmission, decomposition, and storage, Int. J. Hydrogen Energy, 2021, 46(47), 24169–24189, DOI:10.1016/j.ijhydene.2021.05.002.
- F. Dalla Longa and B. van der Zwaan, Autarky penalty versus system cost effects for Europe of large-scale renewable energy imports from North Africa, Energy Strategy Rev., 2024, 51, 101289, DOI:10.1016/j.esr.2023.101289.
- B. van der Zwaan, S. Lamboo and F. Dalla Longa, Timmermans' dream: An electricity and hydrogen partnership between Europe and North Africa, Energy Policy, 2021, 159, 112613, DOI:10.1016/j.enpol.2021.112613.
- REPowerEU, REPowerEU: A plan to rapidly reduce dependence on Russian fossil fuels and fast forward the green transition, 2022, [cited 2024 Mar 19], Available from: https://ec.europa.eu/commission/presscorner/detail/en/IP_22_3131.
- IRENA, Hydrogen: a Renewable Energy Perspective, Irena, 2019, p. , p. 52, Available from: https://irena.org/publications/2019/Sep/Hydrogen-A-renewable-energy-perspective%0Awww.irena.org Search PubMed.
- K. T. Møller, T. R. Jensen, E. Akiba and Li H. wen, Hydrogen – A sustainable energy carrier, Prog. Nat. Sci.: Mater. Int., 2017, 27(1), 34–40, DOI:10.1016/j.pnsc.2016.12.014.
- IRENA, Global Hydrogen Trade to Meet the 1.5°C Climate Goal: Part I – Trade Outlook for 2050 and Way Forward, 2022, p. , p. 114, Available from: https://www.irena.org/publications/2022/Jul/Global-Hydrogen-Trade-Outlook Search PubMed.
- NCBI, Hydrogen|H2|CID 783, PubChem, 2023, [cited 2023 May 23], Available from: https://pubchem.ncbi.nlm.nih.gov/compound/Hydrogen#section=Boiling-Point Search PubMed.
- M. F. Shehata and A. M. El-Shamy, Hydrogen-based failure in oil and gas pipelines a review, Gas Sci. Eng., 2023, 115, 204994, DOI:10.1016/j.jgsce.2023.204994.
- L. G. Di, T. Giwa, A. Okunlola, M. Davis, T. Mehedi and A. O. Oni, et al., Large-scale long-distance land-based hydrogen transportation systems: A comparative techno-economic and greenhouse gas emission assessment, Int. J. Hydrogen Energy, 2022, 47(83), 35293–35319, DOI:10.1016/j.ijhydene.2022.08.131.
- IRENA, Global Hydrogen Trade to Meet the 1.5 °C Climate Goal: Part III – Green Hydrogen Supply Cost and Potential, International Renewable Energy Agency, Abu Dhabi, 2022 Search PubMed.
- M. Raab, S. Maier and R. U. Dietrich, Comparative techno-economic assessment of a large-scale hydrogen transport via liquid transport media, Int. J. Hydrogen Energy, 2021, 46(21), 11956–11968, DOI:10.1016/j.ijhydene.2020.12.213.
- M. Niermann, A. Beckendorff, M. Kaltschmitt and K. Bonhoff, Liquid Organic Hydrogen Carrier (LOHC) – Assessment based on chemical and economic properties, Int. J. Hydrogen Energy, 2019, 44(13), 6631–6654, DOI:10.1016/j.ijhydene.2019.01.199.
- S. Timmerberg and M. Kaltschmitt, Hydrogen from renewables: Supply from North Africa to Central Europe as blend in existing pipelines – Potentials and costs, Appl. Energy, 2019, 237, 795–809, DOI:10.1016/j.apenergy.2019.01.030.
- B. van der Zwaan, K. Schoots, R. Rivera-tinoco and G. P. J. Verbong, The cost of pipelining climate change mitigation: an overview of the economics of CH4 , CO2 and H2 transportation, Appl. Energy, 2011, 88(11), 3821–3831, DOI:10.1016/j.apenergy.2011.05.019.
- M. Niermann, S. Drünert, M. Kaltschmitt and K. Bonhoff, Liquid organic hydrogen carriers (LOHCs)-techno-economic analysis of LOHCs in a defined process chain, Energy Environ. Sci., 2019, 12(1), 290–307, 10.1039/C8EE02700E.
- A. T. Wijayanta, T. Oda, C. W. Purnomo, T. Kashiwagi and M. Aziz, Liquid hydrogen, methylcyclohexane, and ammonia as potential hydrogen storage: Comparison review, Int. J. Hydrogen Energy, 2019, 44(29), 15026–15044, DOI:10.1016/j.ijhydene.2019.04.112.
- L. Genge, F. Scheller and F. Müsgens, Supply costs of green chemical energy carriers at the European border: A meta-analysis, Int. J. Hydrogen Energy, 2023, 48(98), 38766–38781, DOI:10.1016/j.ijhydene.2023.06.180.
- IEA, IEA G20 Hydrogen Report: Assumptions, The International Energy Agency, Paris, 2019 Search PubMed.
- IRENA, Global Hydrogen Trade to Meet the 1.5°C Climate Goal: Part II – Technology Review of Hydrogen Carriers, 2022, Available from: https://www.irena.org/publications/2022/Apr/Global-hydrogen-trade-Part-II Search PubMed.
- C. Kim, Y. Lee, K. Kim and U. Lee, Implementation of Formic Acid as a Liquid Organic Hydrogen Carrier (LOHC): Techno-Economic Analysis and Life Cycle Assessment of Formic Acid Produced via CO2 Utilization, Catalysts, 2022, 12(10), 1113, DOI:10.3390/catal12101113.
- NCBI, PubChem, PubChem, 2023, [cited 2024 Mar 20], Available from: https://pubchem.ncbi.nlm.nih.gov/.
- J. R. Rostrup-nielsen, Syngas in perspective, Catal. Today, 2002, 71(3–4), 243–247, DOI:10.1016/S0920-5861(01)00454-0.
- ETSAP, Oil and Natural Gas Logistics, IEA ETSAP – Technol Br, 2011, (August), vol. 7, Available from: https://iea-etsap.org/E-TechDS/PDF/P03_oilgaslogistics_PS_revised_GSOK2.pdf Search PubMed.
- S. Baufumé, F. Grüger, T. Grube, D. Krieg, J. Linssen and M. Weber, et al., GIS-based scenario calculations for a nationwide German hydrogen pipeline infrastructure, Int. J. Hydrogen Energy, 2013, 38(10), 3813–3829, DOI:10.1016/j.ijhydene.2012.12.147.
- NCBI, Pubchem: GHS Classification. PubChem, 2023, [cited 2023 May 23], Available from: https://pubchem.ncbi.nlm.nih.gov/ghs/ Search PubMed.
- Ports.com, Sea route & distance, Ports.com, 2024, [cited 2023 Jun 29], Available from: http://ports.com/sea-route/.
- DC. Distance Calculator, Distance Calculator, 2024, [cited 2023 Jun 29], Available from: https://www.distancecalculator.net/.
- A. Sánchez, E. C. Blanco and M. Martín, Comparative assessment of methanol and ammonia: Green fuels vs. hydrogen carriers in fuel cell power generation, Appl. Energy, 2024, 374, 124009, DOI:10.1016/j.apenergy.2024.124009.
- E. C. Blanco, A. Sánchez, M. Martín and P. Vega, Methanol and ammonia as emerging green fuels: Evaluation of a new power generation paradigm, Renew. Sustain. Energy Rev., 2023, 175, 113195, DOI:10.1016/j.rser.2023.113195.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4se00959b |
| This journal is © The Royal Society of Chemistry 2025 |



