Progress in computational methods and mechanistic insights on the growth of carbon nanotubes

Abstract

Carbon nanotubes (CNTs), as a promising nanomaterial with broad applications across various fields, are continuously attracting significant research attention. Despite substantial progress in understanding their growth mechanisms, synthesis methods, and post-processing techniques, two major goals remain challenging: achieving property-targeted growth and efficient mass production. Recent advancements in computational methods driven by increased computational resources, the development of platforms, and the refinement of theoretical models, have significantly deepened our understanding of the mechanisms underlying CNT growth. This review aims to comprehensively examine the latest computational techniques that shed light on various aspects of CNT synthesis. The first part of this review focuses on progress in computational methods. Beginning with atomistic simulation approaches, we introduce the fundamentals and advancements in density functional theory (DFT), molecular dynamics (MD) simulations, and kinetic Monte Carlo (kMC) simulations. We discuss the applicability and limitations of each method in studying mechanisms of CNT growth. Then, the focus shifts to multiscale modeling approaches, where we demonstrate the coupling of atomic-scale simulations with reactor-scale multiphase flow models. Given that CNT growth inherently spans multiple temporal and spatial scales, the development and application of multiscale modeling techniques are poised to become a central focus of future computational research in this field. Furthermore, this review emphasizes the growing role played by machine learning in CNT growth research. Compared with traditional physics-based simulation methods, data-driven machine learning approaches have rapidly emerged in recent years, revolutionizing research paradigms from molecular simulation to experimental design. In the second part of this review, we highlight the latest advancements in CNT growth mechanisms and synthesis methods achieved through computational techniques. These include novel findings across fundamental growth stages, i.e., from nucleation to elongation and ultimately termination. We also examine the dynamic behaviors of catalyst nanoparticles and chirality-controlled growth processes, emphasizing how these insights contribute to advancing the field. Finally, in the concluding section, we propose future directions for advancements of computational approaches toward deeper understanding of CNT growth mechanisms and better support of CNT manufacturing.

---

Sili Deng

Prof. Sili Deng is the Class of 1954 Career Development Associate Professor in Mechanical Engineering at Massachusetts Institute of Technology. She received her doctoral degree in Mechanical and Aerospace Engineering from Princeton University and postdoctoral training at Stanford University in Mechanical Engineering. She joined MIT as an Assistant Professor in 2019. Her research focuses on energy conversion and storage, specifically, the fundamental understanding of combustion and emissions, physics-informed data-driven modeling of reacting flows, carbon-neutral energetic materials, and flame synthesis of materials for catalysis and energy storage.

---

1 Introduction

Carbon nanotubes (CNTs) are one of the most promising nanomaterials, and decades of research have continuously revealed their application potential in various fields, including electronic devices, energy and chemical engineering, and construction materials.^1–4 The broad applications of carbon nanotubes are closely related to their unique physicochemical properties, such as electrical conductivity,⁵ thermal stability,⁶ optical properties⁷ and mechanical strength.⁸ The distinctive properties originate from the versatile configurations of CNTs. This unique two-dimensional material features varying diameters and chirality, and can be categorized into single-wall carbon nanotubes (SWCNTs) and multi-wall carbon nanotubes (MWCNTs).⁹ Under different manufacturing processes, the length of a CNT can extend from several nanometers up to centimeters, even decimeters.¹⁰ Although various breakthroughs in CNT performance and synthesis methods have been reported in the literature, achieving low-cost, large-scale, and high-quality synthesis of CNTs for widespread use in diverse downstream applications remains a challenge that both researchers and industry are striving for.^11–13 A core issue in the field of carbon nanotube research is how we can achieve property-oriented fabrication. A comprehensive and in-depth response to this question must delve into the molecular mechanisms of carbon nanotube growth, specifically, the mechanisms leading to the growth of certain types of CNTs and the influence of fabrication conditions on the governing mechanisms.

It should be acknowledged that there are many unclear key issues regarding the growth details of CNTs. Even for the most direct influencing factors, such as temperature, atmosphere, and catalyst type, we still cannot provide consistent descriptions and comprehensive explanations.¹⁸ The fundamental challenge in exploring the mechanisms of CNT growth lies in the inherent complexity of the carbon nanotube growth process.¹⁹ In Fig. 1, we show a schematic diagram demonstrating the growth and synthesis process of CNTs from microscopic to macroscopic perspectives. During the catalytic growth of CNTs, several fundamental processes will simultaneously occur on the catalyst surface, including (1) the decomposition of carbon sources, (2) the removal of carbon atoms by etching agents, (3) the diffusion of carbon atoms, and (4) the integration of these atoms into the CNT wall. These processes are crucial across all three key stages of CNT growth, namely the nucleation of the graphitic cap, tube wall elongation, and growth termination. Each stage involves extensive migration and conversion of numerous chemical species across the gas phase, solid phase, and the tube–catalyst interfaces. These characteristics inherently distinguish the catalytic synthesis of CNTs from other typical heterogeneous catalytic reactions, such as the water–gas shift reaction²⁰ and methane oxidation.²¹ During CNT growth, the catalyst surface not only facilitates the decomposition of reactants and provides a platform for intermediate diffusion, but also serves as a “carbon sink”. As the growth process progresses, the scale of the carbon nanotube can far exceed that of the catalyst nanoparticles, introducing highly complex multi-scale diffusion and reaction phenomena throughout the catalytic process.²²

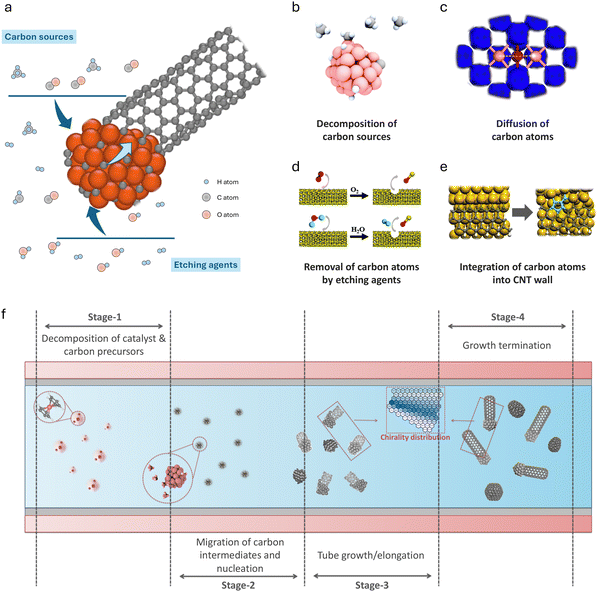Fig. 1 Growth and synthesis process of carbon nanotubes from microscopic to macroscopic perspectives. (a) Schematic of CNT growth from the perspective of a single catalyst nanoparticle. (b) Decomposition of carbon sources.¹⁴ (c) Diffusion of carbon atoms.¹⁵ (d) Removal of carbon atoms by etching agents.¹⁶ (e) Integration of carbon atoms into the CNT wall.¹⁷ (f) Multiple conversion stages of CNT synthesis from the perspective of a CVD reactor.

Although experimental investigations provide valuable information on the behavior of catalysts,²³ reaction conditions,²⁴ and precursor species,²⁵ computational exploration has always played a critical role in unraveling the complex mechanisms behind CNT synthesis, attracting constant attention from researchers of various backgrounds.^26–28 Particularly, the growth of CNTs involves multiple sub-processes and a complex reaction network. The variety of synthesis techniques and numerous influencing factors add significant challenges to elucidating the mechanisms.²⁹ Many conversion processes that are difficult to thoroughly characterize experimentally can be explored through theoretical calculations, which provide rich insights from the scale of individual atoms to the reactor level.³⁰ Moreover, computational modeling not only supplements and explains experimental results but also unveils previously undiscovered directions for elucidating underlying mechanisms. Early theoretical studies mainly focused on atomistic details of nanotube formation, especially the early-stage mechanisms.^31,32 These works have illuminated many important aspects, like the impact of catalyst type,³³ the dynamics of carbon atom diffusion,³⁴ and the influence of precursors.³⁵ However, due to various limitations, early theoretical and computational studies on CNT growth were largely constrained by both temporal and spatial scales, making it difficult to comprehensively observe the entire CNT growth process using computational methods,³⁶ let alone directly guide industrial-scale synthesis.

In recent years, the rapid development of computational resources and the continuous maturation of computational platforms and software have led to significant advancements in computational chemistry.³⁷ These improvements have brought us enhanced efficiency and quantitative accuracy, providing more detailed theoretical insights than early methods. For example, data-driven machine learning techniques are increasingly being integrated into computational chemistry.³⁸ When combined with approaches such as molecular dynamics (MD) simulations, these methods achieve significant computational acceleration while maintaining high accuracy.³⁹ Meanwhile, there is a growing urgency for multiscale simulations, particularly in translating reaction information obtained at the static molecular scale to dynamic/operando scenarios⁴⁰ and to simulations at the reactor scale.⁴¹ These new computational methods are vital for supporting the scaled-up and controlled production of CNTs. Some combined and multiscale models have been developed that more accurately capture the complexity of the CNT growth process and that of other related carbonaceous materials, especially by integrating ab initio mechanical calculations with larger-scale models to simulate growth on large timescales.^42–44 Although these methods are still in the early stages, we believe that they will ultimately fundamentally change the paradigm of using computational chemistry to study the CNT growth process. By revealing important reaction mechanisms at the microscopic scale and guiding the massive and property-targeted synthesis of CNTs at the macroscopic scale, these computational advancements hold great promise for the future of nanomaterials research and industrial applications.

Over the past decade, a wealth of review articles has provided researchers with comprehensive insights into various aspects of CNT growth, including synthesis methods, growth mechanisms, and applications. Notably, the works by Zhang et al.,⁴⁵ Yang et al.,⁹ and Rathinavel et al.⁴⁶ have extensively covered the advancements in CNT synthesis techniques, elucidating the fundamental principles and practical developments in the field. Specialized reviews focusing on CVD synthesis methods, such as those by Pang et al.,⁴⁷ Zhang et al.,⁴⁸ Hou et al.,²⁹ Singh et al.,⁴⁹ and Sehrawat et al.,⁵⁰ have thoroughly examined technological innovations, influencing factors, pre- and post-treatment processes, and developing trends. In the realm of selective CNT growth, some notable reviews, including the works by C. Liu et al.,⁵¹ B. Liu et al.,⁵² He et al.,⁵³ Qiu and Ding,¹⁸ and Zhao et al.,²³ have summarized progress in chirality-controlled synthesis, catalyst design, and understanding growth mechanisms. As for computational approaches, early works often focused on static structures or the dynamics of cap formation. For instance, the works by Page et al.²⁶ in 2015 and by Amara and Bichara⁵⁴ in 2017 have thoroughly reviewed the computational methods and insights gained from molecular simulations, highlighting how these studies contribute to understanding the nucleation and growth dynamics of CNTs. In addition, there are some reviews addressing specific aspects of CNT growth, such as the dynamic behavior of catalysts observed through environmental transmission electron microscopy by Zhao et al.,²³ modeling of base versus tip growth modes by Chen et al.,⁵⁵ and the role played by sulfur in CVD synthesis by Bogdanova et al.⁵⁶ This review does not extensively introduce foundational concepts in heterogeneous catalysis, first-principles calculations, or machine learning. For readers seeking background knowledge on computational methods widely used in heterogeneous catalysis—including electronic structure calculations, first-principles microkinetic modeling, and catalyst design/discovery—we recommend the comprehensive reviews by Shambhawi et al.³⁷ and Chen et al.³⁰ Additionally, for a broader perspective on machine learning applications in catalysis research, we direct readers to the insightful summaries by Margraf et al.³⁸ and Mou et al.⁵⁷

Despite the abundance of literature on CNT growth, there is a noticeable gap concerning comprehensive reviews on computational methods and recent computational findings in this field, especially when compared with the existing works on experimental insights and manufacturing techniques. Recent years have witnessed groundbreaking advancements in computational chemistry—from multiscale modeling frameworks that bridge atomic-scale dynamics to reactor-scale synthesis, to machine learning-driven tools that accelerate discovery and enable predictive design. These developments now allow researchers to address longstanding challenges in CNT growth, such as chirality-selective synthesis and defect control, with unprecedented precision. However, the rapid evolution of these methods has yet to be systematically synthesized into a cohesive resource for the CNT research community. Given the rapid advancements in theoretical and computational techniques in recent years, it is essential to consolidate and evaluate how these methods have contributed to our understanding of CNT growth mechanisms. Therefore, the aim of this review is to present the latest progress in computational methods and their applications in CNT growth research, offering a timely and focused perspective that complements existing experimental reviews and provides new insights into the theoretical underpinnings of CNT synthesis.

In Fig. 2, we present a schematic representation of the main content of this work. In this progress-focused review, we prioritize how transformative advancements in computational methods, from classical atomistic approaches to emerging machine learning frameworks, have enabled paradigm-shifting insights into CNT growth mechanisms. The review is organized along two complementary dimensions:

• Vertical progression: we begin with foundational approaches detailed in Sec. 2 and progressively transition to the most cutting-edge tools discussed in Sec. 4, thereby tracing the evolution of computational methods in this field.

• Horizontal linkage: as illustrated in Fig. 2, every methodological advancement presented on the left side of the schematic directly underpins specific mechanistic insights on the right side.

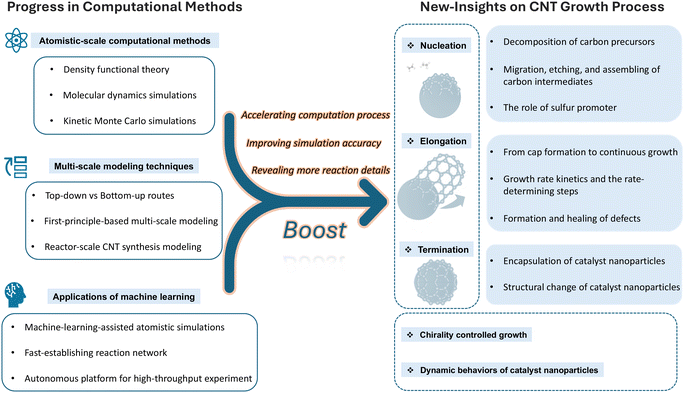Fig. 2 Schematic representation of the main content of this work, highlighting the core concept that progress in computational methods will boost new insights into the CNT growth process.

Specifically, the review begins by outlining the foundational principles and applicable challenges addressed by major atomistic-scale computational tools in Sec. 2. This includes an in-depth look at quantum chemistry and density functional theory methods, molecular dynamics simulations, and kinetic Monte Carlo modeling. These tools provide the groundwork for understanding the intricate processes involved in CNT synthesis. Following this is a critical area of discussion in Sec. 3, multiscale modeling, where we examine both bottom-up and top-down strategies and their implications for reactor-scale synthesis of CNTs. This section assesses how these approaches integrate different scales of modeling to enhance the accuracy and applicability of predictions in practical synthesis scenarios. Significant emphasis is then placed on the evolution and integration of machine learning techniques within this field in Sec. 4. We evaluate how machine learning facilitates heterogeneous catalysis, expedites first-principles calculations, enriches molecular dynamics simulations, and serves as a novel platform for interpreting experimental data. Additionally, this section explores the capability of machine learning to guide experimental investigations, thereby bridging theoretical predictions with practical applications. Furthermore, this review provides detailed insights into the CNT growth process as elucidated by computational studies in Sec. 5. It covers the entire spectrum from nucleation to growth termination, with a special focus on the latest research in chirality-controlled growth and the dynamic behaviors of catalyst nanoparticles. These discussions are pivotal for understanding the mechanistic underpinnings and variability in CNT synthesis. In concluding, we will highlight how these advanced computational methods can be leveraged to gain deeper mechanistic insights into CNT growth, potentially driving further innovations and enhancements in CNT synthesis technologies.

2 Fundamentals and advancements of atomistic computational methods

Advancements in atomistic-scale computational methods form a crucial foundation that allows computational chemistry to effectively reveal the underlying mechanisms of CNT growth.³⁷ We must acknowledge that experimental characterizations have provided rich and detailed empirical insights into surface catalytic processes, such as the morphology of catalysts⁵⁸ and the organization of carbon structures.⁵⁹ However, they are inevitably limited by reaction conditions and characterization techniques. Relying solely on experimental approaches is insufficient to fully support our understanding and control of the CNT synthesis process.⁶⁰ Theoretical and computational analysis, from electronic structures to thermodynamics and kinetics, offers a more comprehensive and profound understanding of the mechanisms involved.²⁶ Additionally, predictive analysis of unexplored conditions, from catalyst design to reaction condition control, requires theoretical exploration based on models extracted from experiments.

In this section, we will initially focus on three core atomistic-scale computational chemistry techniques, namely quantum chemistry and DFT calculations, molecular dynamics simulations, and kinetic Monte Carlo simulations. We will introduce the fundamental concepts and the significance of these methods in studying CNT growth based on recent literature.

2.1 Quantum chemistry and DFT methods

Quantum mechanical calculations have become fundamental in reaction chemistry, providing deep insight into the electronic structures and properties of atoms, molecules, and materials.⁶¹ Among the earliest quantum mechanical approaches, Hartree–Fock (HF) methods utilize a self-consistent field approach for approximating electronic structures by treating electrons as non-interacting entities within a mean field. However, HF methods have limitations in capturing electron correlation effects, leading to the development of more sophisticated techniques.⁶² Notably, density functional theory (DFT) offers a practical framework for electronic structure calculations. This method simplifies the computational process by focusing on electron density rather than solving the Schrödinger equation for wave functions.⁶³ The efficiency and versatility of DFT make it particularly useful for studying complex catalytic systems and a broad spectrum of other phenomena. In the context of CNT-related computational research, almost all the quantum chemical calculations are performed based on DFT and its simplified or approximated forms. Fig. 3 illustrates the basic process of studying CNT growth-related problems using quantum chemical methods. In Table 1, we list the computational platforms, molecular systems, and research targets of selected papers using DFT calculations to study the CNT growth process.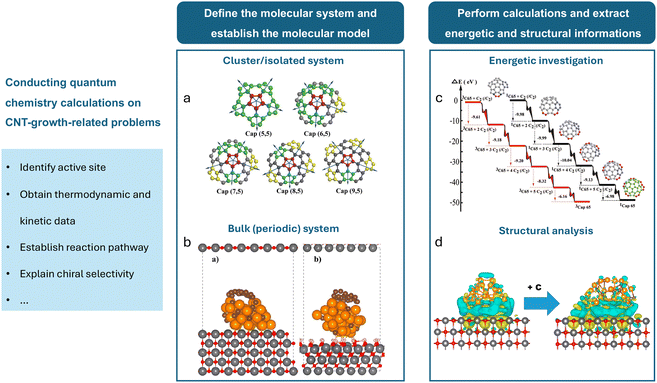

Fig. 3 Fundamental process of studying CNT growth-related problems using quantum chemical methods. After defining the problem, the major steps involve defining the molecular system, establishing the molecular model, performing calculations, and extracting energetic and structural information. The molecular system primarily includes (a) cluster/isolated systems⁶⁵ and (b) bulk/periodic systems.⁶⁹ (c) An example of using DFT for energetic investigation, showing the potential energy surfaces during the formation of the (6,5) cap by the continuous addition of C2 dimers to its edge.⁶⁵ (d) An example of using DFT for structural analysis, demonstrating the charge density difference analysis before and after carburization and the addition of a graphene fragment for a MgO(100)-supported 32-atom Cu nanoparticle.⁶⁹

Table 1 Computational platforms, molecular systems, and research targets in selected papers using DFT to study CNT growth

Author and year	Platform	Molecular system	Research target
Ding et al. (2007)^33	VASP	Four distinct model systems were selected: a (5,0) zigzag nanotube bonded to an M13 cluster, a (3,3) armchair nanotube bonded to the same M13 cluster, a larger (5,5) armchair nanotube bonded to an M55 cluster, and a (10,0) zigzag nanotube bonded to an M55 cluster. The metal M in these clusters represents Fe, Co, Ni, Cu, Pd, or Au. The icosahedral configuration was chosen for the metal particles	The authors calculated the adhesion strengths between SWCNTs and the catalyst particles to show from which they grow needs to be strong to support nanotube growth
Wang et al. (2010)^65	Gaussian 03	The armchair carbon cap (5,5) was selected as a starting point, and both singlet and triplet PESs of single C atom and C2 dimers reacting with the caps (n,5) were calculated (where n = 5, 6, 7, 8, and 9). The calculations were conducted under catalyst-free conditions	The authors established potential energy surfaces SWCNT growth by single C atom and C2 dimer addition to explain chirality selection induced by different carbon intermediates
Yuan et al. (2011)^68	VASP	A stepped catalyst surface accommodating a graphene edge was adopted to represent part of the CNT–catalyst interface, examining the catalyst–AM graphene edge interaction. The efficiency of Fe, Co, and Ni, in CNT growth was compared. The process of incorporating two dissociated carbon atoms into a new 6-membered ring (6MR) of the tube wall was investigated	To study the energy barriers of incorporating C atoms into the CNT wall through the CNT–catalyst interface
Eveleens et al. (2016)^66	Gaussian 09	Caps with 0° ≤ θ ≤ 30° [(5,5), (6,5), (7,4), (8,3), (9,2), (10,1), and (11,0)] were considered. The authors did not include a catalyst interface in the model system	To demonstrate how ammonia-derived etchant radicals (H, NH, and NH2) can be used to promote particular (n,m) chirality SWCNT caps CVD growth. The adsorption energies of these radicals with different caps were calculated
Didar and Balbuena (2017)^69	VASP	The study examined unsupported Cu nanoparticles with 38 atoms (from the face-centered cubic crystal), 55 atoms (from the icosahedral crystal), and 68 atoms (from the fcc crystal). Cu nanoparticles of 32 and 38 atoms supported on MgO substrates were analyzed. Two MgO facets, the (100) and the more active oxygen-terminated (111) facet, were studied	To study unsupported and MgO-supported Cu nanoparticles as potential catalysts for the growth of CNTs. The charge density difference before and after carburization and the addition of graphene fragments were analyzed
Kimura et al. (2018)^67	Gaussian 09	Cap models with similar diameters (6.6 to 8.4 Å) and (n,m) chiralities (5,5), (6,5), (7,4), (8,3), (9,2), (10,1), and (11,0) were considered. The carbon atoms at the cap edge were terminated by hydrogen atoms. Metal catalysts and support were neglected	To study how water-based etchant radicals (OH and H) may enhance the chiral selectivity during CVD growth using CNT cap models. The reaction energies of different radicals and cap models with different chiralities were compared
Wu et al. (2022)^76	VASP	Very short (6, 5) and (7, 5) capped tubes which contain only 70 × 2C atoms were initially selected to calculate the curvature energy, and then C atoms were gradually added from 70 × 2 to 206 × 2. To calculate the interface formation free energy, models with a 3-layer Co slab with (0001) surface (bottom layer fix during the relaxation), and (6, 5), (7, 5) tubes with H termination at both tube ends	To elucidate the mechanism of the chirality selectivity at different growth temperatures by considering the competition between the SWCNT–catalyst interfacial energy and the SWCNT curvature energy during the SWCNT nucleation stage
Orbán and Höltzl (2024)^74	GPAW	Acetylene and ethylene binding at different sites of Fen (n = 3 − − 10, 13, 55)	Comparing the adsorption of acetylene and ethylene on iron clusters and nanoparticles representing the nascent phase of CNT growth by FCCVD and studying the effect of sulfur
Shiina et al. (2024)^70	VASP	To calculate the energy of the CNT on the Ni3 Sn (0001) surface, a four-layer slab model with 3 × 3 periodicity was used in a hexagonal supercell (a = 15.885 Å, c = 30 Å). The armchair CNT, three times the length of its unit cell, had one end terminated with hydrogen atoms	To examine the structural matching between (6,6) CNTs and Ni3 Sn catalyst towards chiral-selective growth, the authors calculated the lowest binding energy for different structures with different chiralities and locations of bonds

---

When performing quantum chemistry calculations on the CNT catalytic growth system, it is essential to clearly define the type of system to be studied, construct an appropriate molecular model, and select a suitable computational platform. In general, the nature of the systems studied in CNT growth include cluster/isolated system and bulk/periodic system.⁶⁴ In cluster calculations, where a small group of atoms or molecules is isolated, precise electronic structure descriptions are essential.^65–67 This is often adopted in some early works or in scenarios that do not consider the catalyst surface. Gaussian-type orbitals (GTOs) are commonly employed as the basis set due to their effectiveness in modeling isolated systems. Software such as Gaussian, ORCA, and GAMESS is frequently utilized for these types of calculations, offering robust functionalities tailored to the needs of cluster or isolated molecule studies. Conversely, in bulk or periodic system calculations, the focus shifts to extended structures like crystals and surfaces, where periodic boundary conditions play a critical role.^33,68–70 This is a more commonly adopted way in CNT growth-related investigations. For these systems, plane-wave basis sets coupled with pseudopotentials or projector-augmented wave (PAW) potentials are standard. This combination efficiently handles electron–ion interactions and is particularly adept at capturing the periodicity inherent in crystal lattices. Tools such as VASP, Quantum Espresso, and CASTEP are widely used for periodic DFT calculations, providing specialized capabilities to tackle the complexities of extended systems.

However, there are still some unresolved questions regarding whether to use periodic or cluster systems to study heterogeneous catalytic processes.⁷¹ A typical scenario involves CNT growth under the tangential mode, where CNTs have diameters similar to those of corresponding catalyst nanoparticles.⁷² In situ observations by Yang et al.⁵⁸ confirm that a VSS (Vapor–Solid–Solid) growth process generally follows a perpendicular mode, while a VLS (Vapor–Liquid–Solid) growth process adopts a tangential mode. Therefore, it is quite common and theoretically more appropriate to use cluster models for calculations for VLS growth, although current computational works do not clearly make this distinction.

The primary functions of DFT calculations can be categorized into two main types: (1) obtaining the energies of stable structures or transition states to aid in the analysis of thermodynamic and kinetic characteristics of reaction processes; (2) conducting electronic structure analyses of specific systems to ascertain the properties of active sites and elucidate the mechanisms underlying reaction pathways. Both functions play crucial roles in research related to the growth of CNTs, as summarized in Table 1.

For instance, in terms of energy calculations, Eveleens et al.⁶⁶ demonstrated how ammonia-derived etchant radicals (H, NH, and NH₂) promote specific (n, m) chirality CNT caps during the CNT synthesis process. They calculated the chemical reactivity of these etchant radical species with SWCNTs by determining the adsorption energies between the cap and the etchant species. Zhang et al.⁷³ analyzed the formation energy of SWCNTs on catalyst surfaces across various CNT groups and the tungsten carbide (WC) catalyst, successfully demonstrating the symmetry matching between nanotubes and solid catalysts that leads to chiral-selective nucleation. Orbán and Höltzl⁷⁴ explored the adsorption of acetylene and ethylene on iron clusters and nanoparticles, considering the effects of sulfur. They calculated binding energies for numerous adsorption configurations and iron particles of varying sizes.

From a structural analysis perspective, Gomez-Ballesteros and Balbuena⁷⁵ investigated the structure and dynamics of metallic and carburized catalytic Ni nanoparticles. Their analysis of electronic distribution revealed that the addition of carbon atoms to the carburized nanoparticles enhances the attraction between Ni and C, as evidenced by a slight increase in the magnitude of average charges. Didar and Balbuena⁶⁹ conducted charge density difference analysis before and after carburization and the addition of a graphene fragment on Cu nanoparticles. Their findings highlighted how the interaction between the cluster and the metal–oxide interface could influence catalytic activity.

Although DFT has been instrumental in providing accurate insights into catalytic reactions, the extensive computational demands of DFT still pose significant challenges. Transitioning state calculations pose another obstacle, particularly in heterogeneous catalysis and the CVD synthesis of CNTs. These scenarios often involve large atomic systems with multiple reaction sites and potential pathways, complicating the full exploration of the potential energy surface (PES). The effort to determine PES minima is feasible, yet identifying maxima, or saddle points, is markedly more computationally intensive.³⁸ Consequently, there are only very limited research works that have actually touched the PES of carbon incorporation into the CNT wall on catalysts surface.⁶⁸

The speed of DFT calculations also remains a bottleneck, hindering its application for comprehensive and rapid analyses necessary in high-throughput studies. Using the Density Functional based Tight Binding method (DFTB) and similar approximate computational approaches allows for results to be obtained two to three orders of magnitude faster, making DFTB a widely used tool in CNT-related computational studies for rapidly generating datasets over an extended period.^44,77,78 However, without appropriate benchmarking, the accuracy of DFTB can be significantly compromised, presenting a trade-off between computational speed and accuracy.⁷⁹ Recent advances in machine learning offer promising developments in predicting transition states rapidly, significantly reducing the time and computational resources required. As noted in recent literature,^80–82 leveraging ML in this capacity could be a pivotal direction for future research, enhancing the scalability and applicability of DFT in real-world catalytic design and optimization.

2.2 Molecular dynamics simulation

Ab initio methods such as DFT require substantial computational resources even for small systems at ground-state (0 K) conditions. Consequently, molecular dynamics (MD) is often used as a more practical and computationally efficient alternative, especially when exploring the dynamic behavior of the system under a given condition. MD models particle interactions using classical mechanics by solving Newton's equations of motion over time. The particles, often representing individual atoms, are time-stepped, incrementally accounting for accelerations and decelerations due to interatomic forces. The velocity-Verlet algorithm is often used to conduct the trajectory updating process. These forces are typically determined using empirically parameterized potential fields, which, while less accurate than DFT, enable the simulation of significantly larger systems. However, even with the reduced computational expense, many millions of atoms and tens of millions of timesteps are often required to reach time and length scales of practical use. As such, MD simulations are considered stiff and are often deployed with immense computational resources. Additional simplifications to the atomistic system are used to decrease expense, such as artificially decreasing the system atom count, accelerating the interaction rate to reduce the overall simulation time, and under-representing the environment surrounding the system. These simplifications accumulate into errors and limit the validity of the simulations. Modern computational advancements like machine learning have reduced this computational burden, as discussed in Sec. 4.

For application to CNT growth, a mechanistic understanding necessitates an atomic-level insight into the system's energetics and dynamics, thus making MD a popular choice. Catalysts, substrates, and other relevant subsystems can consist of hundreds or thousands of atoms, and the nanotubes themselves can theoretically grow without limit. Additionally, the CNT growth processes must involve chemical reactions as carbon evolves from a component of precursor species into a nanotube structure, in addition to the adsorption processes of precursors onto catalysts. The high computational cost resulting from the complex system and the need for a dynamic representation of the growth process at an atomistic scale makes higher fidelity methods like DFT infeasible and MD a widely favored approach for simulating CNT growth. A classic approach to conducting CNT growth simulations in molecular dynamics is presented in Fig. 4. Once the molecular system is established, carbon supply rates must be selected. Carbon supply rates have been historically accelerated due to computational limitations, leading to inaccurate CNT formation trends, as discussed in Sec. 5.2. Following this, inter-atomic potentials must be constructed to best approximate the interactions in the system. Careful attention must be paid to applying potentials which can capture covalent bonding between C atoms accurately and can accurately capture long-range effects. When running the simulation, atomic clusters must first be equilibrated before supplying carbon and conducting a longer run. Upon completion, atom locations, trajectories, and termination events may be gathered to extract larger trends, such as key transition events, growth pathways, and defect formation, among others. Additionally, Table 2 outlines select research works using MD simulations in chronological order, including their molecular system (i.e., atomic configurations, carbon supply rates, and total atom counts), the bond potentials, and their research targets.

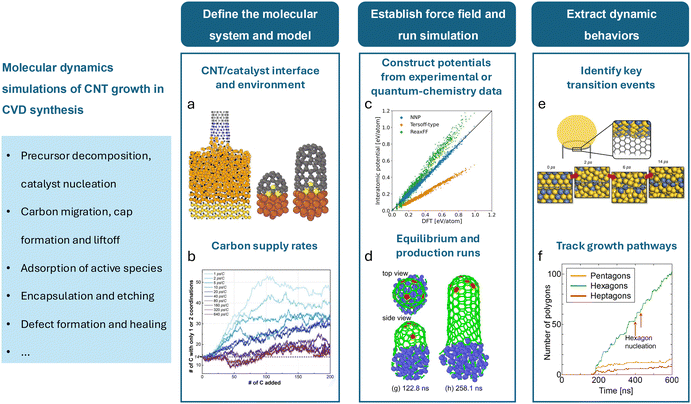Fig. 4 General procedure for conducting MD simulations of catalytic CNT growth. (a) A sample CNT/catalyst system and its environment; (left) a growing CNT under strain attached to a larger catalyst,⁸³ (right) CNT cap liftoff and growth in a system with sulfur.⁸⁴ (b) A chart from ref. 85 describing the strong influence of the carbon supply rate on CNT growth kinetics. (c) A comparison of classical and neural network-based force fields with quantum-chemistry calculations from ref. 86. (d) CNT cap formation and liftoff demonstrated during a production simulation.⁸⁶ (e) The congregation of the high-activity metals in an alloy catalyst around the growing end of a CNT.⁸⁷ (f) A tally of five-, six-, and seven-member rings in a growing CNT lattice.⁸⁸

Table 2 Molecular systems, bond potentials, and research contents of selected Molecular Dynamics (MD) studies applied to CNT growth simulations

Author and year	Molecular system	Bond potentials	Research target
a This study conducted alternating MD and uniform-acceptance force-based Monte-Carlo (UFMC) steps to allow for relaxation of the CNT.
Shibuta and Maruyama (2003)^89	C–metal clusters, 756 total atoms (500 C and 256 Ni catalyst). Carbons were supplied all at once randomly in a cube surrounding the catalyst	Brenner potential for C–C, custom potential for metal-C and metal–metal interactions. LJ for intermolecular C–C in the precursors	To study of nucleation and growth process in HiPco environments.^90
Ding et al. (2004)^91	CNT growth on FeC nanoparticle accounting for precipitated C (CP) and dissolved C (CD). The maximum C supply rate was one every 100 picoseconds for a total of 50 Fe atoms and ∼500 C for 20 ns total simulation time	Brenner potential for CP–CP and Lennard-Jones for any CD–CP and CD–CD interactions. Johnson potential for CD–Fe	To demonstrate VLS growth in floating catalyst CVD at realistic temperature ranges
Zhao et al. (2005)^92	CNT growth on a supported Ni catalyst with up to 80 atoms. The carbon supply rate was between 6 and 25 picoseconds for an estimated ∼5 ns resulting in ∼250 total C atoms	Modified REBO for C–C interactions. A Morse-type potential represents metal–metal and metal–carbon interactions	To observe the nucleation process on Ni nanoclusters in CVD environments
Neyts et al. (2011)^93 ^a	Over 400 atoms total consisting of 32 Ni and 381 C. Carbon supplied every two picoseconds.	ReaxFF universally. LJ between carbon atoms of different clusters to aid in the addition of carbon to the catalyst.	Demonstrate a hybrid MD and UFMC simulation technique to grow CNTs with definable chirality.
Yoshikawa et al. (2019)^88	CVD synthesis on a 60-mer Co or Fe system. C injection method was constructed to allow sufficient catalyst and CNT relaxation and maintain a specified C pressure	Tersoff-type potentials for metal-to-metal and metal-to-C bonds, modified Brenner/Tersoff potentials for bound carbon atoms, and LJ potentials for long-range interactions with C	To attempt to grow CNTs of definable chirality by modulating carbon supply rate and to demonstrate the influence of chirality on the growth mechanism
Qiu and Ding (2022)^85	72-Atom Nickel catalyst with 200 carbon atoms added at feeding rates up to 640 ps^−1	Ab initio accurate MD using DFT for detailed simulations and an empirical potential energy surface for feeding rate studies	To determine if more realistic carbon supply rates result in a cleaner catalyst surface
Hedman et al. (2024)^44	Sized 53 clusters of Fe catalyst with C supplied every 500 ps	Deep Potential^94 machine learning force field trained using DFTB	To model CNT growth with more physically realistic C supply rates. To capture the process of defect growth and healing and generate statistics of the process
Kohata et al. (2024)^86	Maximum 120-mer Fe catalysts. C was supplied at a rate limited to ensure 8 maximum free C atoms in the domain	Deep Potential^94 machine learning force field trained using DFT	To model CNT growth with more physically realistic C supply rates. To model the dynamic rearrangement of edge configurations and to model edge defect growth and healing

---

Various classical MD potentials have been used for carbon nanotubes. Their accuracy depends on the quality of their parameters and the physical phenomena are captured by their formulation. Ab initio molecular dynamics (AIMD) computes quantum-accurate potential fields in conjunction with MD particle field tracking. These methods are highly computationally prohibitive for many applications. Classical interatomic potentials, such as the Abell⁹⁵ and Tersoff⁹⁶ models, offer computationally inexpensive force calculations whose formulation is constructed to account for the physics of covalent bond orders.

Two classical force field methods extend the bond-order concept and are most commonly used in reactive molecular dynamics studies: AIREBO and ReaxFF. Reactive Empirical Bond Order (REBO), introduced by Brenner,⁹⁷ was previously a significant tool during initial CNT growth modeling but has since been shown to be inaccurate.²⁶ CNT simulations with REBO potentials demonstrate fewer bond formation and dissociation events primarily resulting from non-local events such as π-conjugational effects.⁹⁸ This results from its limited quantum and Van der Waals interaction. Therefore, dynamic variations of system electronegativity are not representative.²⁶ Adaptive Intermolecular REBO (AIREBO) improves this model⁹⁹ by accounting for torsion and nonbonded interactions. Tight binding approaches are also an extension of this approach. ReaxFF extends the models of Abell and Tersoff to include a summation of various additional bond energy contributions, including Van der Waals, coulombic, valence, and other effects. Like REBO, ReaxFF considers the bond order, where the influences of local chemical environments are accounted for in covalent bonds.¹⁰⁰ This allows for appropriate modeling of the sp² hybridized structure that is the basis of the carbon-nanotube lattice. ReaxFF also considers a much longer-range distance of interactions than AIREBO. Many ReaxFF models have been built for accurate combustion kinetic modeling,¹⁰¹ and the model has also been applied to catalytic systems, with successful modeling of the chemisorption process and surface reactions.¹⁰² Since 2010, ReaxFF has been used for CNT growth simulations as well. Neyts et al.⁹³ applied ReaxFF to show both tip and root growth of CNTs. The improvements in computational efficiency allowed for a more realistic carbon deposition rate onto the catalysts compared with DFTB simulations. Significant differences can be found in results from AIREBO and ReaxFF. Orekhov et al.¹⁰³ found that during simulations of carbon nanoparticle formation with AIREBO, nanoparticles formed from gas phase mixtures at extremely high temperatures, while for ReaxFF, no graphitization appeared even at lower temperatures. Recently, studies have determined that many bond-order potentials, like the Tersoff potential, result in zigzag-type chiralities more than observed in experiments.^86,104

Several outstanding problems exist in the current state of MD simulation for CNT growth. Atomic simulations have historically struggled to match experimental results primarily due to two reasons: inaccurate computational time scales and misrepresentation of the potential field.^26,105 These result from the disparate simulation time scales. Sufficiently small time steps (of order 1 femtosecond) must be taken to accurately integrate the equations of motion of an atomic system, and these simulations must be conducted for up to microseconds of simulation time to adequately model the growing nanotube. This imposes immense computational expense, resulting in researchers artificially inflating carbon supply rates to the overall physical time required to create a realistic nanotube. High carbon addition rates relative to experiments have been a well-recognized issue in CNT MD studies for a while.⁹³ These computational limitations have resulted in artifacts in the defect healing process of nanotubes⁴⁴ and the reaction kinetic process at the catalyst interface.⁸⁷ Additionally, existing potential fields are sometimes inaccurate or insufficiently constructed for given conditions, such as for sulfer-aided CNT growth as shown by ref. 106.

2.3 Kinetic Monte Carlo and microkinetic modeling

At atomic scales, DFT and MD offer unparalleled accuracy and resolution to understand material synthesis by resolving the interactions between individual atoms. However, at the larger scale with operando conditions, the system involves a great number of atoms under relatively high temperatures, making DFT and MD computationally impractical. Meanwhile, the system is still far from being able to be described by continuum models. It turns out that, at this scale, microkinetic models that replace the explicit modeling of atom–atom interactions with kinetics governed by ODEs or stochastic processes governed by stochastic differential equations (SDEs) are more suitable to link atomic-scale events with macroscopic properties.^30,107 The microkinetic models including mean-field micro-kinetics model (MF-MKM) and kinetic Monte Carlo (kMC) effectively describe the evolution of species concentrations and reaction rates over time without explicitly simulating individual atomic interactions.

This simplification is justified by the statistical averaging that emerges naturally at large scales, where the behavior of materials can be described by macroscopic quantities like concentrations, temperature, and pressure.^108,109 The law of large numbers ensures that fluctuations at the atomic level average out, leading to predictable behavior that can be captured by continuum models. Additionally, reaction kinetics models allow for integration with process engineering tools and real-world industrial constraints, enabling efficient optimization of synthesis processes while avoiding the computational expense of atomistic simulations.

MF-MKM is a computational approach that models the surface coverage by different species using an ODE equation set. This method naturally adopts mean-field approximation and skips the detailed neighboring information on the heterogeneous catalyst surface to the benefit of ODE-level calculation speed. It adopts mean-field approximation by mapping the catalytic outcome of surface reactions onto reactivity descriptors, for example, adsorption energies of key intermediates or their derivatives for the description of the heterogeneous catalytic processes.¹¹⁰ However, a typical CNT growth process needs to be considered in a more accurate way for the purpose of discerning different mechanical properties or chiralities, because there are clustered tube–catalyst interfaces that cannot be treated as mean-field. Meanwhile, for a complex process, MF-MKMs are typically hard to parametrize; although there is an attempt to quantitatively optimize MF-MKM parameters, MF-MKMs are still limited by the inherent mean-field treatment on describing complex catalytic behaviors.^111,112 Therefore, MF-MKM is barely utilized to study the growth of CNTs.

Conversely, kMC offers a more detailed representation by incorporating spatial inhomogeneities, correlations in the distribution of reactants on the catalytic surface, and detailed configuration–active sites pair information. Unlike MF-MKMs, kMC utilizes defined lattices to track the positions of each adsorbate, effectively mirroring atomistic models and preserving the nature of discrete active sites. Despite the complexity and the intensive nature of probing reaction mechanisms manually, the adoption of kMC is growing, supported by the availability of efficient and user-friendly kMC codes within the heterogeneous catalysis modeling community, such as Zacros,¹¹³ kmclib,¹¹⁴ kmos,¹¹⁵ MoCKA,¹¹⁶ MonteCoffee,¹¹⁷ and SuSMoST.¹¹⁸

Basics of kMC for heterogeneous catalysis include defining lattice structure, enumeration of elementary steps, parametrization, and sampling configurational update^107,119 The parametrization procedure is: (1) elementary steps, (2) DFT energy calculation, (3) intrinsic kinetic database, and (4) kMC for the events simulation. The configurational update is a stochastic process based on Boltzmann law, assigning a higher probability of state transition to critical events with lower energy barrier, and vice versa.

Narrowing down from general heterogeneous catalysis to carbon-based nanomaterial, graphene growth is a field closely associated with CNT growth. The adoption of kMC in this field serves as a system-specific approximation to make graphene growth simulations computationally feasible after deriving energetics from the calculation of electronic structures. By feeding kMC simulations with first-principles parameters, we can directly simulate the growth process and thus understand the growth mechanisms.⁶⁰

In parallel with the success in graphene growth modeling, kMC was applied to CNT growth; some examples are listed in Fig. 5. Also, in Table 3, we list the kMC simulation descriptions and research targets of selected papers using kMC calculations to study the CNT growth process. By simplifying the elongation process of CNTs as graphene growth on metal surfaces, Li et al.¹²⁵ concluded that CNT growth is dominated by surface growth, through the analysis of the activity of the Ni catalyst controlled by the balance of C atoms nucleation on the surface, C and C3 surface diffusion, and addition into the CNT wall at the edge of the CNT–Ni interface. Furthermore, similar to first-principles kMC graphene growth, first-principles calculations are also adopted for appropriate parametrization for kMC simulation of CNT growth directly. Apart from using graphene as a substitute for CNT, primarily in the study of CNT kMC is suitable for the simulation of the tube's growing edge, given the predefined lattice of the edge, termed the on-lattice approach. The chemical potential calculation for the incorporation of carbon atoms in a predefined tube lattice is proposed to account for the controlled growth kinetics determined by the interface energy and temperature.¹²¹ The experimental value can also be incorporated into the kMC model with the predefined lattice in this work,¹²² where kMC demonstrates fluctuations of the tube/catalyst interface between different orientations with respect to the tube axis, leading to different growth regimes, evidenced by in situ measurements of the growth kinetics of individual tubes. kMC can be used to solve the theoretical master equation for relatively large CNT edge structures as a sampling approach. By constructing a 5-vertex simplified Glauber dynamics model for the reactive CNT edge, studies^123,126 have numerically simulated the growth kinetics by kMC equipped with a BKL update algorithm to qualitatively investigate the different growth regimes under different carbon source pressures and temperatures.

Fig. 5 Kinetic Monte Carlo application on CNT growth. (a) kMC events for simplified CNT growth on CNT–Ni interface.¹²⁰ (b) Scheme for semi-grand canonical kMC on a predefined CNT lattice.¹²¹ (c) Modeling the difference of growing rate due to the fluctuations of tube/catalysts surface by kMC on chirality-defined lattices.¹²² (d) 5-Vertex model for CNT growing edge (excluded 1,2,3 from 8-vertex model) as lattice model for kMC.¹²³ (e) The abundance simulated by kMC for CNT growth on zeolite MFI nanosheet-supported Co nanoparticles showed good agreement with experiment results.¹²⁴

Table 3 Simulation description, and research targets in selected papers using kMC to study CNT growth. The computational platforms are not specified since most kMC simulations were carried out using in-house codes

Author and year	Simulation description	Research target
Li et al. (2015)^125	Flattened CNT growth on Ni surface with DFT energy calculation and accelerated kMC algorithm	Investigate the rate determining process among C atoms nucleation, surface diffusion and addition to the CNT wall
Carpena et al. (2020)^124	Hybrid off-lattice kMC on freestanding Co nanoparticles	Investigate the nucleation and growth of CNT on Co nanoparticles influenced by the presence of zeolite MFI nanosheets, to guide the direction for the growth of thermodynamically unfavorable CNTs
Förster et al. (2021)^121	kMC simulation on CNT lattice with predefined chirality	Investigate how interface energy and temperature determines the controlled chirality growth kinetics
Zounmenou et al. (2022)^123	5-Vertex model, solved by kMC algorithm and BKL update algorithm	Study the growth kinetics and surface roughness of a hexagonal SWCNT with zero chiral angle
Förster et al. (2023)^122	kMC simulation on CNT lattice with predefined chirality, and with different number of armchair/zigzag sites	Compare the growth rate difference brought by fluctuating tube/catalyst interface structure and different growth regimes
Adda et al. (2024)^126	Kinetic 5-vertex model, solved by kMC algorithm and BKL update algorithm	Investigate hexagon-islands formation on growing SWCNT, with C atoms adsorption and migration processes taken into account

---

The kMC algorithm can be designed for more complex CNT growth conditions, where the interaction between tube lattice and catalyst can be taken into account by the off-lattice approach.¹²⁴ To understand the observed chirality distribution of SWCNTs on zeolite MFI nanosheet-supported Co nanoparticles, the authors used a hybrid off-lattice kMC model describing the kinetics of nucleation and growth of nanotubes on freestanding particles so that the addition of carbon atoms and the resulting CNT configurations reflected the actual energy landscape determined by DFT calculations. By this flexible design, the resulting model could guide the direction for the growth of thermodynamically unfavorable, small-diameter CNTs.

Although kMC has achieved good simulation results, it still has some drawbacks. kMC generally utilizes a probabilistic model on an atomic level. This averages out the particle–particle interaction to critical stochastic events by a predefined event table to speed up the simulation, which in turn hinders kMC's ability to capture the complete dynamics on a dynamically evolving substrate.¹²⁷ It is also limited by constraints on the CNT structure, such as the predefined CNT edges discussed in a number of studies.^{121–123,126} To make kMC compatible with MD for the exploration of CNT growth dynamics and further leverage the unique advantage of its speed, there are some challenges for kMC modeling as summarized in a recent kMC method review:¹⁰⁷ scheduling and executing elementary events, treating complicated energetic models of non-ideal adlayers, treating large surface domains with distributed simulations, treating event frequency disparity, steady-state detection, sensitivity analysis and uncertainty quantification, and coupling with larger scales.

In the future, especially in the parametrization stage, it is expected that faster substitutes, other than those derived from calculation results of electronic structures, can be applied for kMC research in CNT growth. Atomic-level features from MD can be used to guide kMC parametrization.¹²⁸ Colossal fast-converging kMC data can be treated as a surrogate model for data-driven complex kMC parametrization.¹²⁹ Combining diffusion-only kMC and implicit lattice kMC in phenomenological form, Chen et al.¹³⁰ proposed a new scheme to deal with the timescale disparity problem in kMC simulations. To take into account non-ideal adlayers during parametrization, there are also options, such as cluster expansion Hamiltonian (CEH),^110,131 for modeling lateral adsorbate interactions effects and integrating them into kMC efficiently.

3 Multiscale modeling for CNT growth

In the field of heterogeneous catalysis, modeling the complicated relationships between material structure and function presents considerable challenges due to the diverse length and time scales involved. Despite the fact that atomic-scale simulations have offered fundamental understandings, we must go beyond larger spatial and temporal scales to attain a comprehensive perspective.

The effectiveness of a catalyst hinges on the atomic structure and composition at the active sites.¹³² These structural and compositional features are highly sensitive to variations in local concentrations, temperatures, or external environment, all influenced by ongoing chemical reactions and the dynamics of heat and mass transfer within the reactor. Consequently, there is a complex and dynamic interplay between the microscopic mechanisms of chemical conversion and the broader meso- to macroscopic conditions under which these reactions take place.³⁰

The growth of CNTs serves as a prime example of a heterogeneous catalytic process, characterized by the multi-scale nature of the involved physicochemical processes.¹³³ Unlike conventional thermal catalytic reactions involving small-molecule gases,¹³⁴ the synthesis of CNTs via heterogeneous catalysis encompasses multi-scale heat and mass transfer and chemical reactions between the catalyst surface and the reaction environment. The dimensions of the main product, carbon nanotubes, often match or exceed the size of the catalyst particles during the nucleation phase and can grow several magnitudes larger as the process continues.¹³⁵ Therefore, understanding the mechanisms of CNT growth at the microscopic level, as well as controlling the synthesis conditions at the macroscopic level, necessitates the integration of multi-scale modeling approaches.

3.1 Bottom-up and top-down multiscale modeling

Before delving into the advancements in multiscale modeling research, it is essential to introduce the two fundamental approaches for multiscale simulation routes: bottom-up and top-down.¹³²

Bottom-up multiscale modeling is grounded in first-principles methods through quantum mechanical calculations. In general, this approach begins with a quantum mechanical description of the electronic structure of materials, emphasizing the reactive chemistry and charge transport at the atomic scale. Subsequently, first-principles microkinetic models can be constructed, either through mean-field rate equations or spatially resolved kinetic Monte Carlo simulations. These models are utilized to describe the progression of chemical reactions on catalyst surfaces. Through hierarchical couplings, this method integrates detailed atomic-scale descriptions into larger scale models, transitioning from electron behavior to reaction dynamics within reactors or electrochemical cells.¹³⁸

Meanwhile, top-down multiscale modeling starts at the macroscopic scale and aims to incorporate influences from smaller scales, often relying more on empirical data and observed phenomena.¹³⁹ This approach prioritizes a broader understanding of system behavior over atomic-level specifics by incorporating various scales of interaction. Top-down models are typically employed to complement bottom-up approaches, particularly in scenarios where macroscopic data can refine or validate the detailed models developed from the bottom-up methodology.

For multiscale modeling, the challenge lies in accurately characterizing the molecular-level system description. Errors in models can arise from two main sources: (1) inherent model limitations, such as the omission of a reaction or an active site, and (2) inaccuracies in the physics or computations, such as errors in the estimated kinetic parameters for an elementary reaction step.¹⁴⁰ Presently, the distinction between bottom-up and top-down approaches has become less clear, with integrated methods often being more effective. Accurate modeling typically results from a synergy between these two approaches. To be effective, these models and simulations must strike a balance between chemical and physical accuracy and practical usability, sometimes necessitating compromises on microscopic details for broader applicative value.

Both bottom-up and top-down multiscale modeling are crucial for the growth and synthesis process of CNTs. This is because we aim not only to understand the reaction mechanisms that achieve property-specific growth of CNTs but also to control all influencing factors to realize mass production in industrial-scale reactors. Fig. 6 illustrates the different levels of multiscale modeling in catalytic CNT synthesis, which can conceptually be divided into four levels. At level 1, the focus is on the active site and electronic structure, which are fundamental to heterogeneous catalytic reactions. It involves exploring the interactions between various catalyst structures and reactants at an atomic scale to identify the chemical nature of active sites or phases. At level 2, the task is to establish a model of the surface structure and elementary processes, often referred to as developing a micro-kinetic model in general heterogeneous catalysis research.¹⁴⁰ The challenge at this level is the dynamic nature of catalyst surfaces and their constant evolution. For CNT synthesis, the different carbon intermediates and the chirality of the cap/tube–catalyst interface can significantly influence the reaction pathways. At level 3, the target expands to the scale of entire nanoparticle catalysts and their interactions, since a prerequisite for surface chemical reactions is the effective diffusion of reactants and intermediates to the active sites.²⁶ In CNT catalysis, understanding how nanoparticles form, evolve, and how carbon atoms diffuse is crucial for quantitatively analyzing the transformation processes, as individual nanoparticles typically act as units of catalytic activity. Finally, level 4 involves scaling up to the reactor scale, integrating macroscopic flow, heat and mass transfer with surface chemical reactions to calculate the final product distribution, and optimizing reactor design and operating conditions.⁵⁰ This scale ultimately connects theory with application, representing the final step in transforming catalytic theory into practical catalytic products.

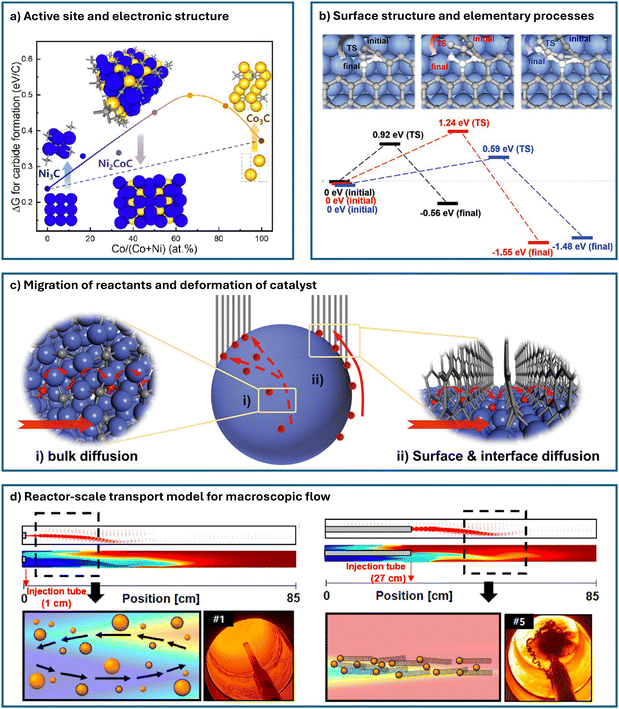Fig. 6 Different levels of multi-scale modeling in catalytic CNT synthesis. (a) Level-1: active site and electronic structure. The figure shows carbide formation energy for pure metal and alloy catalysts of different composition ratios.¹⁵ (b) Level-2: surface structure and elementary processes. The figure demonstrates energy barriers of C2 (black), C3 (red), and C4 (blue) chains transforming into a new hexagon at the K site of the CNT–catalyst interface.⁸⁵ (c) Level-3: migration of reactants and deformation of catalyst. The figure describes the two possible routes for carbon supply during MWCNT growth from a Co catalyst.¹³⁶ (d) Level-4: reactor-scale transport model for macroscopic flow. The figure depicts fluid dynamics simulation at different injection depths of FCCVD reactor. Digital images are taken downstream of the reactor and show collection of CNTs.¹³⁷

Despite years of accumulated research and progress in theoretical and computational studies related to CNTs, bridging these scales with current research capabilities and computational methods is still insufficient. Whether establishing fundamental reaction pathways or coupling reactions with transport on a macroscopic scale, these efforts are still in the early stages and not yet adequate to support industrial production needs. Current research trends suggest that a gradual integration of both top-down and bottom-up approaches is necessary to truly translate the vast amount of fundamental research on CNTs into practical theoretical guidance and quantitative analysis for production processes.

3.2 First-principles-based multiscale modeling on CNT growth

First-principles-based multiscale modeling is increasingly utilized to predict the properties of CNT-based materials.¹⁴¹ Here we take a recent work by Venkatesan et al.¹⁴² as an example. They established an atomistically informed multiscale modeling framework to evaluate the enhancement of mechanical properties in unidirectional fiber-reinforced polymer composites, featuring a radially grown CNT architecture, as shown in Fig. 7(a). Molecular dynamics simulations are employed to explore damage phenomena in matrix-fertile regions and the intricate interactions across various constituent phases at the fiber/matrix interface enhanced by radially grown CNTs. Nanoscale properties are leveraged to develop submicroscale constitutive models, which inform the microscale properties of each constituent. The computational homogenization of the microscale representative unit cell enables the prediction of overall composite properties based on the constituent properties of the epoxy matrix, fibers, and the CNT-reinforced interphase region. The elastic properties of a unidirectional composite lamina with radially grown CNT architecture are derived through microscale homogenization, while the onset of damage is indicated by submicroscale constitutive damage models.

Fig. 7 Recent computational studies on first-principles-based multiscale modeling on CNT growth. (a) The atomistically informed multiscale modeling framework to evaluate the enhancement of mechanical properties in unidirectional fiber-reinforced polymer composites.¹⁴² (b) Energy barriers at 0 K from nudged elastic band calculations for different carbon diffusion pathways on fcc Ni: through the Ni bulk (1), on the (4 × 4) Ni(111) surface. (c) Model of a Ni particle configuration and diffusion mechanism. The nickel carbide carbon concentration increases.¹⁴³ (d) The SWCNT population distributions (y-axis) calculated as a product of nucleation probability (dotted) and the growth rate (dashed) shown for near ZZ (green) and near-AC (orange) chiralities.¹⁴⁴ (e) kMC modeling of growth instabilities. This figure shows the sharp growth rate changes for (13, 9) and (12, 10) tubes, associated with growth rate changes. Slower growth rates correspond to large fractions of zigzag edge atoms, faster ones to large fractions of armchair atoms.¹²²

However, analyzing the reaction mechanisms and growth processes of CNTs is considerably more complex than property prediction. While comprehensive multiscale simulations bridging multiple scales remain challenging, the strategies and philosophies of first-principles-based multiscale modeling have been extensively applied in recent research, indicating significant potential for further exploration in the growth processes of CNTs.

Gili et al.¹⁴³ investigated the growth mechanism of multiwalled carbon nanotubes on nickel nanoparticles supported by a combination of in situ synchrotron XRD, DFT, and MD simulations. They highlighted the challenges with DFT calculations, which are confined to short time scales (several femtoseconds) and small atomic groups (a few to 100 atoms) due to their high computational demands. These scales are insufficient to accurately describe the expansion of the nickel lattice influenced by changes in temperature and varying carbon-to-nickel ratios. To address these limitations, they employed ReaxFF reactive force field models, which are based on ab initio calculations, enabling the reproduction of first-principles calculation behaviors more effectively over larger scales. Initially, the DFT calculations were used to study the adsorption and diffusion processes on various nickel surfaces. This step was crucial to test the theoretical approaches and assess the quality of the reactive force fields used, as shown in Fig. 7(b). Furthermore, the ReaxFF approach allowed for a more comprehensive analysis of different carbon concentrations within the bulk unit cells compared with the ab initio DFT calculations. By integrating these models with experimental observations, Gili et al. proposed a mechanism for carbon precipitation during CNT growth, as shown in Fig. 7(c). The proposed model graphically represents the composition changes in a nickel particle during the CNT formation process, combining both experimental and modeling insights. It suggests that the initial metallic nickel particle catalyzes the decomposition of methane. The generated carbon species subsequently dissolve within the nickel particle, forming three distinct bulk carbides. This conceptual framework helps in understanding the dynamic interactions and transformations occurring during the CNT growth on nickel catalysts.

Turaeva et al.¹⁴⁴ developed an extended model for chirality selection in SWCNTs. This model, applied throughout all stages of the SWCNT growth process—adsorption, decomposition, diffusion, and incorporation—marks the first instance these steps were collectively utilized to achieve chirality selection in SWCNT populations. In their model, the abundance of specific types of SWCNTs produced during the CVD process is dictated by the interaction between thermodynamic nucleation and kinetic growth factors. Molecular dynamics calculations revealed that SWCNTs with achiral edges establish low-energy, tight contacts, whereas chiral tubes exhibit a higher free interface energy, which is roughly proportional to the number of kinks present. The nucleation probability is influenced by the free energy of the critical nucleus, which increases linearly with the chiral angle starting from the achiral values. The role played by catalysts in the chirality-selective growth of SWCNTs is twofold: they stimulate the adsorption and decomposition of carbon precursors and the nucleation of nanotubes with tight low-energy contacts on one hand, and promote the diffusion and incorporation of carbon atoms into the growing nanotube on the other hand. The researchers demonstrated that the distribution of the population based on chirality, defined by the product of nucleation probability and growth rate, exhibits a volcano-shaped curve, as shown in Fig. 7(d). This model aligns well with experimental studies and corroborates findings that there is a predominance of near-armchair or near-zigzag SWCNTs. However, it is important to note that while this study illustrates the necessity of integrating multiscale simulations to quantitatively describe property-targeted CNT synthesis, the researchers did not perform these simulations themselves. Instead, they consolidated model parameters. Future research should aim to harmonize and integrate simulations across different scales within a unified framework to ensure the completeness and consistency of the model, making it broadly applicable.

In recent research, Förster et al.¹²² introduced a model that categorizes and enumerates reactive sites along different types of tube edges, which was developed through atomic-scale kMC simulations. These simulations were informed by key parameters derived from experimental data analysis. The team identified two distinct growth regimes, characterized by rapid shifts in growth rates, as is shown in Fig. 7(e). In the first regime, the edge atoms at the interface are predominantly armchair, and they fluctuate around an average height that progressively ascends during growth. In the second regime, the edge atoms are primarily zigzag (highlighted in green), with incoming dimers needing to ascend from lower positions and randomly choosing either a clockwise or anticlockwise direction to integrate into the tube structure. They discussed the potential of using DFT calculations to determine the formation energies of different tube/catalyst interfaces for calibrating the interface energy in their kMC simulations. However, they cautioned against straightforward extrapolation of these DFT results, which are typically calculated for simple interfaces, to a more complex mix of armchair and zigzag edge atoms while maintaining a constant total number of edge atoms. This could result in misleading interpretations. Consequently, the research accepted that interfaces of armchair tubes with iron, cobalt, and nickel catalysts are less stable than those with zigzag configurations. This assumption leads to the inference that the average interface energy in the second regime is lower than that in the first. This work highlights a significant challenge in current research using first-principles-based multiscale modeling on CNT growth: the substantial computational resources required at each simulation scale. Although integrating multiscale simulations could potentially yield more comprehensive results, often the necessity to simplify specific scales limits researchers to focusing on phenomena observable within the constraints of available computational resources.

We believe that as computational tools continue to improve and processing power increases, multiscale simulations based on first principles will gain more prominence and application in research related to the growth mechanisms of CNTs. Currently, there are still many critical issues that have not been clearly explained:

• Impact of catalyst surface heterogeneity: the influences of the heterogeneity of catalyst surfaces on reaction pathways, thermodynamics (especially selectivity), and kinetics are unclear. It is crucial to investigate the roles played by carbon solubility and the use of sulfur as a promoter in these processes.

• Tube–nanoparticle interactions: there is a need for theoretical studies to explore instabilities at the interfaces between tubes and nanoparticles and to understand how these instabilities impact growth selectivity. Despite the importance of these interactions, simulations that cover large temporal and spatial scales necessary to replicate these phenomena are still lacking.

• Lack of a micro-kinetic model for CNT growth: the growth of carbon nanotubes involves complex interactions among catalysts, conditions, and products, presenting a complicated problem that currently lacks a comprehensive micro-kinetic model. To establish a detailed reaction mechanism, it is essential to utilize multiscale simulations that focus on primary processes and omit extraneous information.

3.3 Multiscale modeling towards reactor-scale CNT synthesis

Top-down multiscale models provide a systematic framework for linking the macroscopic processing parameters (e.g., temperature, pressure, flow rate, reactor dimensions) to the microscopic or atomistic processes (e.g., catalytic dissociation, nucleation, growth kinetics) that govern CNT growth. This integration across multiple length and time scales has proved particularly valuable for optimizing CNT production¹⁴⁵ and guiding experimental design.¹⁴⁶ While bottom-up approaches provide detailed insights into atomistic mechanisms, top-down, experiment-driven simulations are indispensable when bridging fundamental growth physics and the larger scales. Common approaches use computational fluid dynamics (CFD) and other continuum models, and are usually guided by empirically determined parameters—e.g., chemical reaction rate equations in an ODE system, diffusion coefficients, and wall deposition rates. The key goal of top-down models is to account for global phenomena, such as the impact of recirculation zones, the method of precursor supply, and thermal gradients that bottom-up models cannot capture.

However, there is a known coupling of smaller-scale physics with larger-scale observables,¹⁴⁷ so the accurate modeling of small-scale influences cannot be compromised in these simulations. Atomistic modeling to capture these effects accurately is not computationally feasible, and while overly simplified representations can easily produce experimentally valid results with parameter tuning, they fail to reveal the coupling between the scales in interpretable ways. Therefore, the primary difficulty in top-down modeling lies in creating submodels that can accurately capture small-scale intricacies with a reasonable computational cost. Key sub-models for CVD reactors include the decomposition of precursors,¹⁴⁸ the nucleation of nanocatalysts,¹⁴⁹ tube–tube interaction,^147,150 chirality-dependent growth of carbon nanotubes,^151,152 catalyst poisoning,¹⁵³ and the action of etching agents,¹⁴ among others. The fidelity of all submodels will detail the physics ingrained in the model and play an essential role in determining the accuracy of the simulation as a whole.

Here, we outline recent progress in top-down multiscale modeling for various CNT reactor configurations. We emphasize the submodels used, their validity, and how they aided the conclusions of the study. We outline the trends and deficiencies of these works, showing where future work can improve (Table 4).

Table 4 Sample top-down large scale simulation studies for various CNT reactor configurations

Author and year	Reactor configuration	Model description	Reaction mechanism	Research target
Grujicic et al. (2002)^145,154	Axisymmetric SCCVD	2-D, steady state, accounting for boundary layer development and two-way coupling of gas/wall effects	13 gas species with 34 gas-phase reactions. 12 surface species with 19 reactions	To optimize CNT yield with minimal amorphous carbon
Kuwana et al. (2005)^155	Axisymmetric SCCVD	2-D steady CFD in cylindrical coordinates. Eulerian particles	Simplified one-step model of ferrocene decomposition with no influence on the surrounding fluid	To model ferrocene decomposition and the deposition of iron particles to the reactor wall
Lysaght and Chiu (2008)^156	Axisymmetric SCCVD	3-D, steady state with wall heating. Carbonaceous species to catalyst surfaces phase impingement rates calculated	6 gas phase and 14 surface phase reactions	To optimize CNT growth by demonstrating the rate-limiting regimes for growth, the influence of wall temperatures, and the influence of the active site model
Hosseini et al. (2009)^157	SCCVD	Time-dependent, multi-phase CFD model including transport, reactions, and thermal radiation	13 gas-phase species and 60 reactions. 13 surface species and 19 reactions accounting for CNT and amorphous carbon formation	To determine the influence of temperature, flow rate, and mixture composition on CNT growth for reactor optimization
Moraveji et al. (2011)^158	Fluidized Bed Reactor	Multi-phase model considering particle-fluid heat, mass, and momentum transfer	No reactions present	The determination of optimal inflow temperatures and velocities for CNT production using just inert, multiphase CFD
Bedewy et al. (2014)^159	CNT Forest	Continuum model accounting for diffusion of active species, consisting of micropillars of nanotubes	Puretzky model^153 with accounting for catalyst overcoating with a carbonaceous layer	To explain the nonuniformity of CNT micropillar heights and the energy barrier of vertically aligned growth
Oh et al. (2020)^160	FCCVD	Inert CFD investigation, discounting any CNT-producing reactions. Simplified turbulence modeling included	Inert simulation	To investigate the influence of rotational flow and feed ratios in the reactor
Kaushal et al. (2023)^161	FCCVD	2-D steady state simulation. Surface-to-surface radiation.	Reactions from Kuwana et al.^155	To demonstrate optimal use of a heating rod in FCCVD.
Andalouci et al. (2023)^162	PECVD	0-D model accounting for detailed chemistry and 2-D model. 2-D CFD model including transport and advection	134 species and 471 gas-phase reactions for 1-D model. A reduced 23 species and 100 reactions for the 2-D model	To determine optimal oxygen content for optimal CNT growth

---

Several examples highlight the value of top-down modeling for supported catalyst CVD (SCCVD) systems. Even from early works, emphasis has been placed on accurately capturing the chemical kinetic rates in catalysis. Grujicic et al.^145,154 conducted a 2-D simulation with 34 gas-phase reactions and 19 surface reactions accounting for adsorption at both the substrate impurity layer and to the catalyst. Their model obtained similar CNT growth rates as seen in experiments while providing a reasonably detailed steady-state representation of the axisymmetric system but neglected all growth termination mechanisms. Bedewy et al.¹⁵⁹ created a micro-scale model for CNT forest growth, utilizing the Puretzky chemical kinetic model¹⁵³ for growth and catalyst encapsulation rates alongside a 2-D diffusion model for active species transport. This combination of submodels allowed them to demonstrate that spatial variations in micropillar height stem from active species diffusion within the pillars, influenced by temperature and pressure. Furthermore, they predicted the minimum concentration of active species needed to transition the ensemble of CNTs from tangled to vertically aligned, providing a route toward CNT production uniformity. More recently, Gakis et al.¹⁶³ used CFD to model supported catalyst CVD reactors of CNTs, shown in Fig. 8(a). Their model–which incorporates fluid dynamics, heat transfer, species transport, and reaction kinetics (including catalyst particle nucleation, growth, and deactivation)—revealed that the experimentally observed carbon deposition on the top surface of their reactors likely stemmed from elevated temperatures and byproduct partial pressures. They attributed these unfavorable thermodynamic conditions to recirculation and further showed how chemical kinetic rates evolve across different temperature regimes. Their computational approach validated well against adjacent experiments when comparing CNT mass deposition as a function of reactor temperature and time. Contributions of macroscopic thermal-fluid effects on CNT growth have also been caused by thermal radiation. Dong et al.¹⁶⁴ constructed a CFD model of a horizontal CVD reactor with porcelain-boat-supported catalysts, as presented in Fig. 8(b). They included radiant heat transfer, which dominates conductive heat transfer and ultimately caused distinct pressure differences, leading to vortex formation, a detriment to CNT growth. Furthermore, they analyzed the influence of inflow velocity on vortex formation. They determined that the vortices reduced residence times in the reactor and redirected precursor flow upwards, away from the catalyst surface, further inhibiting CNT formation.

Fig. 8 Select works demonstrating top-down multiscale modeling for CVD reactors. (a) Impurities collecting along a reactor surface alongside temperature and pressure plots from computational models from ref. 163. (b) Velocity vectors showing radiation-driven recirculation zones around catalyst surfaces.¹⁶⁴ (c) Sock formation in FCCVD visualized with Fe catalyst mass fractions at varying working fluid flow rates.¹⁶⁵ (d) A pathline map from CFD (bottom) compared with a digital photo (top) at the end section of an FCCVD reactor.¹⁴⁶

Top-down modeling has also aided the progress in FCCVD research. Recently, Sehrawat et al.⁵⁰ conducted a review of FCCVD literature, highlighting parametric variations of flow rates, precursor compositions, S/Fe ratios, and more. As a trend, computational studies are better able to reveal macroscopic influences of reactor configurations, revealing underlying reasons behind observations made during experiments. Gökstorp and Juniper¹⁶⁵ applied CFD to investigate the effects of flow rate, peak temperature, and ferrocene mass fraction on nanoparticle formation within an FCCVD reactor, as shown in Fig. 8(c). Their results revealed that as the flow rate or ferrocene mass fraction increases, the iron particle mass fraction shifts away from the reactor's centerline, likely explaining how CNTs form the hollow, sock-like aerogel commonly observed in experiments. The model matches experimental data well at high temperatures but struggles to capture all dynamics at lower temperatures. The study provides insights into optimizing the FCCVD process for better control of CNT growth and improved material properties. Trends obtained from macroscopic models like these enable comparison between reactor configurations and ultimately optimization of the overall design. Rashid et al.¹⁶⁶ compared flow patterns in vertical and horizontal FCCVD reactors and found that the horizontal reactor configurations contained recirculation zones where catalyst coalescence and deactivation were occurring, reducing reactor yield. Adverse influences of flow recirculation were also demonstrated by Yu et al.¹⁴⁶ for the FCCVD reactor presented in Fig. 8(d). Their experiments demonstrated a 20× improvement of CNT quality can be achieved under laminar flow conditions, and they explained their observations using CFD. Similar to what Gakis observed for SCCVD reactions,¹⁶³ recirculation in the flow stream caused pyrolysis bi-product formation and the accumulation of impurities along the reactor walls. They determined that turbulence is effective at colliding catalysts with carbon precursors, but it also inhibited catalyst nucleation and enabled bi-product formation. Meanwhile, a smaller diameter and larger flow rate reactor will reduce buoyancy-driven recirculation, leading to a more uniform flow field and improving CNT quality. At the walls, Oh et al.¹⁶⁰ captured the influence of a highly conductive material like alumina on reducing wall temperature variation, as seen in experiments, which helped explain the resulting straightening of the flow. Even in plug-flow conditions, where flow exists in a fully developed state, such as in work by Hoecker et al.,¹⁶⁷ fluid simulations helped reveal the existence of measurable thermophoretic forces, where the hotter walls result in a radial thermal gradient, driving particles toward the reactor centerline. Finally, Gakis et al.¹⁴⁹ extended their previous SCCVD work to model FCCVD reactors, including the influences of ferrocene decomposition and iron nanoparticle collisions and coalescence in their model within the Eulerian reference frame.¹⁴⁹ Slower velocities near the walls resulted in larger nanoparticles, and higher flow temperatures resulted in faster ferrocene decomposition and catalyst nucleation. Their results are excellent compared with experiments; however, their model neglects the agglomeration of carbon impurities on the growing nanotube, a potential source of error. The inclusion of tube collision rates¹⁵⁰ and catalyst surface etching might also make their model more descriptive.

The benefits of top-down modeling are not isolated just to SCCVD and FCCVD configurations. Gao et al.¹⁶⁸ reviewed progress in the utilization of computation to assist in the research of fluidized bed reactors. They emphasized the benefit of comprehending and optimizing the processes involved in CNT growth through particle–fluid system simulations. However, simulating these reactors poses significant challenges due to the complex interplay between fluid and particle dynamics, the irregular flow patterns generated by bubble movement, and the intricate nature of the coupled chemical reactions. In particular, they highlighted the importance of improvements to drag force models, a major mode of momentum transfer given the relative densities of the fluid and the gas phases, due to its influence on bubble dynamics and the fluidization process. Additionally, flame-assisted methods have seen use of multi-scale modeling. Safaei et al.¹⁶⁹ used models developed for diamond-CVD to investigate the kinetics of growth of CNTs in sooty conditions. They determined the carbon bulk diffusion rate is insufficient to predict the carbon nanotube growth regions in the flame due to the presence of soot contamination. Instead, the ratio of carbon bulk diffusion rate to soot nucleation rate is a more appropriate indicator as it qualitatively measures the dominance of carbon nanotube growth to soot formation.

These challenges underscore the complexities of top-down multi-scale modeling for CNT growth, particularly when interpreting experimental observations. For example, Rodiles et al.¹⁷⁰ demonstrated that ceramic reactor tube walls can catalyze hydrocarbon precursors, doubling yield in mullite compared with alumina. Yet, this effect is seldom captured in existing models. Water-assisted CVD (supergrowth)¹⁷¹ similarly defies many current kinetic and reactor-scale predictions by abruptly terminating.¹⁷² Meanwhile, other processes such as flame synthesis,¹⁷³ CoMoCat,¹⁷⁴ HiPco,^90,175 and deep injection¹³⁷ each present unique chemical environments and catalyst dynamics, giving rise to macroscale behaviors that are not yet fully captured by existing computational models. Developing models that accurately represent the physics behind these enhancements is crucial for guiding reactor design modifications and improving performance. Toward that end, emerging techniques—such as CFD-based adjoint optimization¹⁷⁶—are increasingly integrated into modern simulation frameworks and have demonstrated success in other reactor contexts. By embedding more detailed physics into continuum-scale computations, researchers can automate parameter searches to optimize yield, purity, and other critical metrics of CNT growth.

Overall, top-down multiscale modeling could see significant improvement. Platforms like COMSOL Multiphysics and Ansys Fluent are highly accessible, enabling reactor-scale simulations for a broad range of researchers; however, these tools often fall short of modeling the intricate mechanisms underlying CNT growth. To date, simulations have typically relied on simplifying assumptions, such as global chemical kinetics, steady-state conditions, or the exclusion of complex factors like wall effects, growth promoters, and etching agents. These limitations stem from both the computational demands of detailed models and the lack of sufficient work dedicated to developing such models. Experiments focused on characterizing the output CNT often rely on extracting samples from reactors before conducting measurements. Direct, in situ experimental observation of the CNT growth process is limited. As such, there is limited insight into reaction mechanisms, kinetics, and intermediate species, which are lost during off-line measurements and where computational methods prove valuable.

As experimental techniques progress, computational models must advance in parallel to reflect the integrated and dynamic nature of CNT growth processes. Researchers should focus on creating submodels informed by both experimental data and computational insights, enabling a more accurate representation of the underlying physics at finer scales. Chirality-specific growth kinetics models, soot production in reaction kinetics, catalyst reactivation, or CNT agglomeration, have either never been adequately simulated or are neglected. This includes incorporating detailed heterogeneous catalysis chemistry, refining grid resolutions, and accounting for phenomena like conjugate heat transfer, which are critical for bridging top-down and bottom-up multiscale modeling approaches to provide holistic CNT reactor modeling.

Weller et al.¹⁷⁷ made a notable contribution by consolidating experimental data from FCCVD reactors into a consistent parameter space for comparison. Their analysis uncovered global trends across diverse experimental configurations, providing a useful framework for unified comparison. Computational models should aim to replicate these trends and, more importantly, uncover the mechanisms driving them—mechanisms that cannot be fully elucidated through measurements alone. Furthermore, well-validated models have the potential to explore untested regimes beyond the experimental parameter space, offering insights for reactor optimization. With growing computational capabilities and advancements in machine learning, achieving these goals is becoming increasingly feasible.

4 Development and application of machine learning methods

Physics-based computational methods, whether at the atomic scale or the reactor scale, inevitably come with extremely high computational costs if rich information and sufficient resolution are desired. In contrast, data-driven machine learning methods represent an entirely new paradigm. Particularly in accelerating large-scale computations and uncovering hidden features, they open up new pathways for studying the behavior of complex systems.¹⁸¹ In the broader heterogeneous catalysis field, the application of machine learning is becoming more and more promising for solving existing challenges, to narrow and bridge the gap created by the dynamic, mechanistic and chemostructural complexities inherent to the reactive interfaces of practical relevance.⁵⁷

In this section, we categorize three major aspects in which ML is becoming promising in CNT growth research, which are atomistic simulations, establishing reaction networks, and autonomous platforms for high-throughput experiments. Fig. 9 synthesizes methodologies and examples from three categories. Leveraging the evidence of recent ML-related computation progress from neighboring fields including computational catalysis,⁵⁷ computational quantum chemistry,¹⁸² and computational molecule discovery,¹⁸³ we introduce potential next-step research areas for further ML involvement in the CNT growth field.

Fig. 9 An overview for development and application of machine learning methods for CNT growth and examples. (a) First-principles calculation accelerated by machine learning as discussed in Sec. 4.1.1. DFT Hamiltonian is predicted through crystal graph neural networks with vertices v_i and edges e_ij on the right.¹⁷⁸ (b) Machine learning-aided molecular dynamics as discussed in Sec. 4.1.2. Simulated process of the healing of a pentagon colored in blue with DeepCNT-22 MLFF.⁴⁴ (c) Swift construction of reaction network as discussed in Sec. 4.2. Chemical reaction neural network¹⁷⁹ that enables autonomous discovery of elementary reactions from experimental species’ trajectories. (d) Experimental parametric surrogate models as discussed in Sec. 4.3.2. Experimental and predicted growth rates convergence given the increasing number of surrogate model guided experiments.¹⁸⁰

4.1 Machine-learning-assisted atomistic simulations

For a long time, the key factor limiting the application of atomistic simulation methods in heterogeneous catalysis systems has been the computational efficiency for complex systems. However, the operando catalytic system is an even more complex system to model but is generally needed for high-performance catalysts.^184,185 In order to reveal the nature of active sites, unravel reaction pathways and ultimately accelerate catalyst discovery, this field is in great need of strong computational advancements. The concerns like computational resources and complex chemistry for computational heterogeneous catalysis also apply for CNT growth.^87,186,187 For a field like CNT growth where much uncertainty remains about the detailed growth mechanism, the need for precision of atomistic simulations is especially stressed, otherwise unrealistic phenomena would be observed in computational studies.¹⁰⁴ The fidelity of resolved energetics is crucial for confidence in the concluded growth mechanisms as well, so that the derived mechanisms are more likely to enable further research on process engineering and rational catalyst design for CNT growth.

In the early computational research about CNT growth, researchers mostly still used highly reduced catalyst–substrate reaction systems and conducted studies within very limited spatiotemporal scales and empirical interatomic potentials, primarily because the computational resources were insufficient to meet the requirement of larger systems (∼100 atoms) and longer timescales (∼1 ms) to take into account ‘slow’ processes like defect healing. In recent years, with the enrichment of computational resources (e.g., GPUs) and the rapid development of machine learning methods and especially their widespread application in scientific research, our computational capabilities for complex systems have made a qualitative leap forward. There are abundant computational works with ab initio accuracy, elevated simulation speed, and considerable operational system size, for us to further understand the growth mechanism of CNT by machine learning-aided atomistic simulations.

We explain how ML aids the atomistic simulations in three common tasks relevant to computational modeling of CNT growth: acceleration of first-principles (1p) calculation, machine learning-aided molecular dynamics (ML-aided MD), and transition state search.

4.1.1 Acceleration of first-principles calculation. First-principles calculation is limited to the scope of solving electronic structures. Especially for catalysis, electronic structure determines how atoms bond in a catalyst and the material grown on it. Understanding bonding helps explain catalyst stability, material strength, and chemical behavior between the catalyst and growing material.¹⁸⁸ Electronic structure also provides insight into how defects alter a material's properties, creating active sites, and influencing the surface adsorption ability and charge transfer ability, which in total determine the catalytic performances.¹⁸⁹

In the case of CNT research, we are facing great catalyst design demands, and need to deal with the combination of different CNT edges and environment variables,⁶⁶ which creates huge numbers of combinations to calculate. An efficient protocol for first-principles calculation can serve as the first step toward the fast, high-throughput computational modeling of CNT growth in the near future.

On a hardware level, first-principles calculation is currently possible on the GPU platform, making the best use of the progress in GPU sources in recent years. For example, GPU4PySCF¹⁹⁰ is a GPU-accelerated and Python-based quantum calculation package that supports calculations involving DFT and other quantum chemistry protocols, making it a versatile tool for researchers in the field.

Primarily, machine learning models can accelerate the first-principles energy calculation with errors on par with or lower than those of hybrid DFT, and neural network-based ML models can potentially offer greater accuracy if trained on explicitly electron-correlated quantum or experimental data suggested by early research.¹⁹¹ Almost every neural network model is GPU-friendly, which is promising for speeding up the calculation given a rational strategy for implementation. PauliNet uses neural network models to replace parts of the HF theory that solves the electronic structure, which in turn captures the complex correlations and electronic motion that HF alone cannot fully address.¹⁹² DeepH uses deep graph neural networks to predict the Hamiltonian of DFT.¹⁷⁸ The equivariance of electronic structures is a very useful inductive bias for first-principles calculations, which paves the way for large-scale adoption of equivariant neural networks when people are working with ML-aided first-principles calculations. For example, atomic and virtual orbital-based charge density prediction is implemented with a high-capacity equivariant neural network,¹⁹³ and symmetries in the covariant transformation of DFT Hamiltonian matrix can be significantly accelerated by E(3)-equivariant neural networks.^194–196 Large-scale accurate tight-binding electronic simulations are also achieved through symmetry-preserving descriptors and neural network models trained on ab initio electronic bands.¹⁹⁷

Lastly, since the training of neural network-based models requires ample high-quality first-principles data, there are also calls for researchers to work on the data collection process.⁸¹ This review focuses on using ML for atomistic modeling in chemistry. This approach diverges from conventional data-driven ML by emphasizing methods that start with a scientific question to guide the collection of data and model design rather than relying on large, curated databases, which are often lacking in chemistry. Key aspects of this science-driven approach include the use of chemical and physical priors to enhance data efficiency and the importance of appropriate model evaluation and error estimation. To address the data utilization efficiency problem, a multi-fidelity transfer learning method for quantum chemical calculations is proposed to make better use of current datasets.¹⁹⁸

4.1.2 Machine learning-aided molecular dynamics. The ML-aided MD is based on machine learning force field (MLFF) or machine learning interatomic potential (MLIP) implemented on GPUs. The development of MLFFs and MLIP is motivated by several key factors that address limitations in traditional computational methods used in molecular simulations and materials science: accuracy and efficiency, scalability, cost reduction, automation and integration with high-throughput workflows, and addressing the complexity of potential energy surfaces. Thanks to the expressibility of neural networks, MLFF or MLIP can embed first-principled calculation results with minimal loss in the MD simulation. With the acceleration provided by GPU implementation, ML-aided MD also reliably extends the simulation time and length scale to a realistic scale to offer more insights for theory development. In general, ML-aided MD can serve as a powerful tool in various complex physicochemical systems to revisit the major scientific problems that have remained controversial owing to the limitations of previous computational methods.¹⁹⁹ It is able to revolutionize computational chemistry and materials science by providing a powerful tool that balances accuracy, efficiency, and scalability.^200–202

The quality of MLFF or MLIP has been rapidly growing over the years. The current state-of-the-art MLFFs generally adopt equivariant neural networks structures.^203–205 For large-scale MDs, a coarse-grained method²⁰⁶ or multiscale approach²⁰⁷ can also be incorporated in the ML-aided MD framework. To take into account more physics to simulate the experimental conditions, for the external electric field, there are some MLFFs that allow electronic degrees of freedom and nonlocal effects.^208,209 Unsupervised methods based on physics laws are also under exploration.²¹⁰ More recently, people have been looking into the attention-based modeling approach without SE-3 equivariant inductive bias as well.²¹¹

Up to now, there are quite a few examples of ML-aided MD for nano-structure growth applications. One of them is ML-aided MD simulation for growing graphene on liquid copper. Rein et al.²¹² reported on a combined experimental and computational study of the kinetics of graphene growth during chemical vapor deposition on a liquid copper catalyst. Large-scale free energy simulations are enabled by an efficient machine-learning moment tensor potential trained to density functional theory data, which enables a reliable sampling of the liquid state. The simulation provides quantitative energy barriers for key atomic-scale growth processes, which essentially consists of a practical model for operando condition graphene growth on liquid copper.

For large-scale simulations, it is common to come across certain configurations that are not included in the datasets for MLFF training, because relying only on the configuration-averaged metric for selecting new structures during deposition simulation could omit structures that exhibit significant variations only in the local areas surrounding the deposited atom. To enhance the efficiency and effectiveness of MLFF, the on-the-fly training of deposition processes with a well-defined selection protocol is required. This motivates research about active learning, which is an emergent methodology that develops the MLFF model with a changing training set based on current simulation stages.²¹³

Utilizing a synergistic approach of molecular dynamics and time-stamped force-biased Monte Carlo (tfMC) methods, along with Gaussian Approximation Potential (GAP) as the base model of MLIP, a selection strategy for the training set based on smooth overlap of atomic positions (SOAP), and an automated screening, fitting, and validation procedure, Zhang et al.⁴³ performed fully dynamic simulations of graphene growth on Cu(111) to capture the microscopic processes in the substrate-catalyzed growth. By extending the model to Cr(110), Ti(001), and oxygen-contaminated Cu(111), their results agreed well with experimental observations, proving that this framework is well suited for practical and efficient substrates design for carbon nanostructures synthesis.

In the case of CNT research, the importance of simulating CNT growth over long timescales lies in capturing the slow, atomic-level processes that govern their formation, such as the gradual addition of carbon atoms and defect healing. Traditional MD simulations struggle with these timescales due to computational constraints, making it challenging to study the continuous growth of long CNTs and understand how factors like temperature and carbon supply rate affect defect formation and chirality. Meanwhile, traditional potential shows unrealistic characteristics of growth dynamics,¹⁰⁴ which suggests that the field is in great need of accurate potentials. Finally, the size of the atomic system can be very large considering the modeling of a real catalyst particle, which also requires the computational model to be properly scalable.

The CNT growth research community is making the way toward efficiency, accuracy, and scalable MD simulation. For example, Hedman et al.⁴⁴ utilized MLFF for CNT growth simulation, and the workflow is summarized in Fig. 10. This work is among the newest computational works following this line,^91,214,215 from which readers can clearly see how computational advances help the development of CNT theory. The authors presented DeepCNT-22, a machine learning force field to drive molecular dynamics simulations through which they unveil the mechanisms of CNT formation thoroughly, from nucleation to growth including defect formation and healing. Notably, the training of this force field DeepCNT22 has integrated an active learning scheme on-the-fly to optimize the ergodicity of carbon nanostructures encountered during simulation.

Fig. 10 Flow chart for the procedure of ML-aided MD.⁴⁴ (a) Generate diverse atomic configurations from GAP-20 dataset and randomly perturbed nanostructures and label configurations with energies and forces using dispersion-corrected DFT. (b) Use active learning to identify underrepresented configurations during preliminary simulations. Iteratively refine the training set and retrain MLFF to minimize prediction errors. (c) Use MLFF for MD simulations of CNT growth. Iterate simulations until representative configurations and growth processes are captured. (d) Deploy the trained MLFF (DeepCNT-22) in large-scale MD simulations. Explore atomistic details of CNT growth, including nucleation and defect dynamics. (e) Perform statistical analysis on defects and growth dynamics. Evaluate configurational entropy and stochastic influences on CNT growth.

Contemporary work⁸⁶ also investigated the defect-free chirality-definable SWCNT growth with dynamic rearrangement of edge configurations which matches the appearance of entropy-driven edge instability predicted from the nanotube–catalyst interfacial energy, enabled by a neural network-based interatomic potential. The ability to simulate over extended periods provides critical insights into growth stages, catalyst interactions, and the kinetics of atom incorporation that are not observable in shorter simulations or at unrealistic growth rates.

The studies^44,86 that leverage MLFF or MLIP for CNT growth highlight the potential of machine learning in extending the reach of MD simulations, enabling the study of complex materials over practical and experimentally relevant timescales. This capability is crucial for advancing the manufacturing processes of high-quality CNTs and other nanostructures, pushing the boundaries of materials science and nanotechnology.

4.1.3 Transition state search and generation. The transition state for elementary reactions provides critical insights into the reaction mechanism, energy barriers, and kinetics. It is also an essential component of downstream computational approaches, e.g., kMC, to evaluate the heterogeneous catalysis process and especially CNT growth.

Conventional approaches for generating transition states require expensive PES explorations and need post-processing to locate the exact structure. With the development of deep learning potentials, people have made use of them to derive appropriate transition states.²¹⁶ There are more attempts to generate reliable transition states skipping the process of PES evaluation. Pattanaik et al.²¹⁷ employed a graph neural network (GNN) to predict a distance matrix for the transition state based on the geometries of reactants and products. This matrix is then optimized to generate the final 3D coordinates of the TS. The model incorporates a rigorous quantum mechanics workflow to ensure that the predicted TS accurately corresponds to the intended reactants and products. Furthermore, Duan et al.⁸⁰ introduced an object-aware SE(3) equivariant diffusion model called OA-ReactDiff, which is also designed to generate accurate 3D transition state (TS) structures given reactant and product only. The approach significantly reduces the computational time typically required for TS search from hours to seconds while maintaining high accuracy. This method shows promise for constructing large reaction networks, especially those with unknown mechanisms, by efficiently generating TS structures with minimal computational resources. Following the previous work, they²¹⁸ also introduced React-OT, which uses optimal transport theory to generate transition state (TS) structures from reactants and products. This model is even faster than OA-ReactDiff because it reduces the time needed for step-by-step denoising inherited in diffusion-based models.

While current works employing kMC for CNT growth generally rely on conventional approaches for transition state search,^{121–124,126} in the future the dynamic tube–catalyst interfaces, dynamic catalyst surfaces and larger atom systems would require more efficient ways in the search of transition states. The above frontier may be promising for dealing with the predictable complexity.

4.2 Swift construction of reaction network

Elementary reaction networks are crucial for the upscaling of the CNT growth simulation system at the atomic level to the industrial scale, as mentioned in section 2.3. Although Gakis et al.¹⁶³ provided a simplified reaction network of elementary reactions in the gas phase and on catalyst surfaces, a comprehensive mechanism incorporating elementary reactions is currently lacking in existing research. However, such a mechanism is essential for multiscale modeling and engineering applications. Therefore, this represents a significant gap and an important direction for future research. ML methods can do automated exploration and optimization loops for the establishment of a reaction network in this upscaling procedure.

Margraf et al.³⁸ addressed the challenges of sparse experimental data and the uncertainties of computational models, highlighting how machine learning can assist in inferring effective kinetic rate laws and exploring complex reaction networks computationally. Neural networks can be modeled with strictly embedded law of mass action¹⁷⁹ to explore the reaction network based on species trajectories. There is also a sparse data-driven symbolic regression model²¹⁹ for the same task of deriving kinetic mechanisms from species trajectories to derive micro-kinetics in homogeneous reactors.

Especially for a heterogeneous catalytic surface, micro-kinetics can be inferred and optimized by ML-based optimization procedures. The wealth of experimental and theoretical data can be consistently combined into a micro-kinetic model that reveals mixed growth kinetics that, in contrast to the situation at solid Cu, is partly controlled by precursor attachment alongside precursor availability.²¹²

For the prevalent micro-kinetic models MF-MKM and kMC, we list exemplary cases where inference and optimization of parameters are conducted. Data-driven methods can be of help to correct MF-MKM parameters to increase its adaptability facing complex scenarios.¹¹² kMC's formula relies on accurate and comprehensive micro-kinetics of elementary events. Data-driven approaches can be applied for the optimization and acquisition of these critical events in kMC.¹²⁹ Deep learning methods also help the large-scale parameter optimization for kMC simulation.²²⁰

4.3 Autonomous platforms for high-throughput experiments

Automating high-throughput experiments to discover new catalysts or molecules and select optimal production conditions is a highly influential area, and it is becoming within touch in the age of artificial intelligence.¹⁸³

Especially regarding CNT growth research, surging demand for selectivity and high performance for CNT growth requires numerous combinations of synthesis components including catalysts, chirality, etching agents, temperature, pressure, etc. In order to optimize targeting of synthesis protocols in this parametric space, high-throughput experiments for CNT are definitely worth researching.

ML techniques have already advanced the development of heterogeneous catalysts by automating data generation, processing, and interpretation.⁸² We classify two kinds of research that can contribute to the construction of autonomous platforms for CNT growth: property prediction models for rational catalyst design and surrogate models that project experimental parametric space to product distributions.

4.3.1 Property prediction models. Rational catalyst design requires the validation of generated candidates. Yet, the generated candidates’ number is still huge for current high-throughput experimental platforms, thus we need a generalizable property prediction model that gives generated candidates a virtual screening without the expensive 1p calculations, even when adopting ML to mitigate the efficiency problem as mentioned in Sec. 4.1.1. Serving as a rough estimation, the property prediction models using conventional computational approaches are problem-specific and confirmatory in nature, which means that ML methods can achieve significant speed increases for a given loss of accuracy or generalizability. Indeed, ML models have also been evolving towards being more transferable and exploratory to be as accurate as possible and extensible for more systems in recent years.³⁷

In heterogeneous catalysis systems, ML-enabled property prediction models have been applied for the evaluation of solid catalyst and reaction energy barriers. For the catalyst performance, ML property prediction models can be constructed in a statistical way due to their superior properties compared with the conventional statistical approaches. Guan et al.⁸² established key relationships between the features of materials and targeted catalytic performance, activity, selectivity, and stability through ML. These advances have resulted in the development of efficient design or screening guidelines for solid-state catalysts with targeted properties. For energetics analysis of reactions involved in catalytic systems, to deal with the complexity of molecular spaces, the need for quality data, and the difficulty of choosing appropriate ML models, Singh et al.¹⁸¹ explored better feature engineering and feature learning methods tailored to various catalytic reactions, such as asymmetric hydrogenation and cross-coupling reactions. The study emphasized the use of transfer learning and deep neural networks to handle small data scenarios, making it a promising strategy for the energetics prediction for various reactions.

However, most applications of machine learning in heterogeneous catalysis thus far have used black-box models to predict computable physical properties (descriptors), such as adsorption or formation energies, that can be related to catalytic performance (that is, activity or stability). Researchers²²¹ are seeking to use interpretable ML to bridge the gap between high predictive accuracy and meaningful scientific insights as well. They also show that interpretable property prediction models can guide physics-informed efficient dataset generation for other tasks like ML-aided 1p calculation.

Similar ML-enabled property prediction models have been applied to predict carbon nanotube properties. Ji et al.²²² proposed an ML model that maps the catalyst composition to the end CNT product. To train the model, they presented a high-throughput strategy to investigate the statistical patterns in catalyst activity and selective growth of SWCNTs using Co/Pt/Mo ternary catalysts. Therefore a phase diagram for the composition of ternary alloy could be derived from experiment results and could guide rational alloy catalyst design for CNT growth. For CNT forest's mechanical property prediction, Hajilounezhad et al.²²³ used simulated microscopic images as training data to establish CNTNet, a deep learning model that classifies CNT forest properties and predicts their mechanical performance, such as stiffness and buckling load, with high accuracy. By utilizing image-based features, CNTNet surpasses traditional linear regression models in predicting forest properties without requiring detailed physical input data, paving the way for rapid, high-throughput material discovery and optimization in CNT forest synthesis.

For CNT systems, more ML-enabled property prediction models are expected for rational catalyst design, and we expect that some of the fundamental tasks such as edge reactivity prediction can also be achieved with the descriptor-to-property paradigm.

4.3.2 Experimental parametric surrogate models. Besides the complexity in the catalyst itself, the parametric space of the experimental space is very complicated. Synthesis of CNT in labs is actually a highly complex process that is defined by numerous tunable parameters including catalyst composition, temperature, carbon supply rate, etc. To explore this highly dimensional parametric space and optimize towards desired CNT production distributions, an efficient surrogate model is greatly needed. ML-based surrogate modeling for mapping from the experimental parametric space to yield can quantify the impact of high-dimensional experimental conditions, so as to help the ultimate goal of autonomous platforms for CNT growth research.^224,229 A comprehensive surrogate model surely opens the possibility for modern data science techniques to be applied in the CNT growth field.

With rich experimental efforts, researchers have been summarizing their data for the goal of finding the optimal condition for CNT synthesis in recent years, and some of the examples are listed in Fig. 11. Lin et al.²²⁵ developed a machine-learning model based on data from over 600 real experiments and performed 16 000 virtual experiments to explore potential methods to overcome the challenges of simultaneously achieving high growth efficiency and high crystallinity in SWCNT forests. The surrogate model is suitable for importance tests for different influencing conditions, where the reactivity and concentration of the carbon feedstock are identified as playing a critical role in balancing the crystallinity–height trade-off. The results from real validation experiments confirmed the machine-learning model's predictions, leading to a 48% increase in SWCNT growth efficiency while maintaining high crystallinity. Krasnikov et al.²²⁴ employed the dataset of 369 points, comprising synthesis parameters (catalyst amount, temperature, feed of carbon sources) and corresponding carbon nanotube characteristics (yield, quality, structure, optoelectrical figure of merit), to train a surrogate model for their experimental setting, and will be using it for future explorations.

Fig. 11 Experimental parametric surrogate models for CNT growth. (a) ANN surrogate model prediction quality of resistance of carbon nanotube aerosol increases with the enlargement of dataset size.²²⁴ (b) Plot of virtual experiment data with prediction points beyond the boundary highlighting the successful access to the inaccessible region through inset strategy extrapolated from surrogate model.²²⁵ (c) The ARES response surface constructed for yield prediction given temperature difference and time difference of non-isothermal control.²²⁶ (d) An illustration of the close-loop experimental scheme on the ARES platform with Bayesian optimization to update the existing dataset and plan new experiments.²²⁷ (e) The ARES response surface constructed for yield prediction by multi-stage data collection and jump detection algorithm.²²⁸

We noticed that there is already a mature and highly assembled platform for CNT growth called ARES,¹⁸⁰ which was originally designed for high-throughput experiments for CNT growth parametric space exploration. Autonomous Research System (ARES) is an autonomous research robot capable of first-of-its-kind closed-loop iterative materials experimentation. Besides a highly efficient surrogate model for experimental parametric space, ARES is also equipped with advances in autonomous robotics and in situ techniques. Because of its completeness, it is able to design, execute, and analyze its own experiments orders of magnitude faster than current research methods. ARES platform-based studies have achieved good results in diameter control²³⁰ and high-throughput catalyst design²³¹ for CNT growth, and non-isothermal controlled growth.²²⁶ Meanwhile, the formulation of this surrogate model allows advanced data science approaches’ application including closed-loop Bayesian optimization of CNT growth rate,²²⁷ and the jump regression method for discontinuity in the parametric space.^228,232

5 New insights into the CNT growth process from computational approaches

After decades of relentless research by many scientists, we have gained a profound understanding of the growth mechanisms of CNTs. Although there are still many contentious details regarding the reactions, recent studies continue to provide new insights, especially with the aid of continuously advancing computational methods. Before delving into the latest advancements in the growth mechanisms of carbon nanotubes, we first briefly clarify a few pairs of key concepts.

• Substrate-supported catalyst chemical vapor deposition (SCCVD) and floating catalyst chemical vapor deposition (FCCVD)

SCCVD and FCCVD are two primary techniques for synthesizing CNTs.²⁹ SCCVD uses catalysts positioned on a substrate within a controlled temperature environment.²³³ This method allows for precise control over the growth kinetics, quality, and morphology of CNTs, making it ideal for producing aligned CNTs that are bound to substrates. FCCVD, on the other hand, facilitates the continuous production of CNTs.⁵⁰ In this method, catalyst precursors decompose within a high-temperature reactor, creating floating nanoparticles that catalyze the growth of CNTs in the gas phase. While SCCVD offers superior control over specific characteristics of individual CNTs, FCCVD is better suited for the continuous, large-scale production of CNTs and excels in generating diverse macroscopic structures.

• Vapor–liquid–solid (VLS) and vapor–solid–solid (VSS) growth modes

VLS and VSS are differentiated by the physical state of the catalysts.²³ VLS mode typically occurs at higher temperatures or with low-melting-point catalysts.²³⁴ The catalyst remains in a liquid state. This liquidity facilitates carbon diffusion through the surface, subsurface, and bulk of the catalyst, driven by a carbon concentration gradient. However, the fluid nature of the catalyst can complicate the control over specific chiralities during CNT nucleation due to catalyst reconstruction. Conversely, VSS mode utilizes solid catalysts, which are more common at lower temperatures or with materials that have higher melting points.²³⁵ In this mode, carbon diffusion mainly occurs on the catalyst surface, and the solid state helps maintain a crystalline structure throughout the growth process. The stability of the solid catalyst in VSS growth promotes epitaxial relationships between the catalyst and the growing CNTs, potentially enhancing control over chirality during nucleation.

• Tip growth mode and base growth mode

In base growth mode, typically observed with catalysts on flat surfaces such as SiO₂/Si, quartz, sapphire, or MgO, a strong particle–support interaction securely anchors the catalyst to the substrate.⁵⁵ This setup allows the growing CNTs to be pushed upward, facilitating enhanced control over catalyst morphology and CNT nucleation/growth kinetics. This control often leads to more selective chirality distributions of CNTs. In contrast, tip growth mode is observed when the particle–support interaction is weaker, which allows the catalyst particle to detach from the substrate and move with the growing tip of the CNTs.²³⁶ This mode generally results in a broader range of chirality distributions.

• Perpendicular growth mode and tangential growth mode

These two modes are primarily differentiated by how the nanotube's diameter relates to that of the catalyst particle.²³ In tangential growth, the diameter of the CNTs closely matches that of the catalyst particle. The nanotube wall grows tangentially to the catalyst surface, a condition that is favored under near-equilibrium situations and typically occurs when growth times are extended. This mode is also associated with catalysts that have low carbon solubility. Conversely, perpendicular growth produces CNTs with diameters significantly smaller than that of the catalyst particle, with the nanotube wall growing perpendicular to the catalyst surface. This mode involves higher energy barriers and is driven by kinetic effects, typically occurring in the early stages of growth or with catalysts that have high carbon solubility.

The following sections present recent advances in the study of CNT growth mechanisms, with a particular focus on computational works, while also covering studies that integrate experimental and simulation methods. Sec. 5.1, 5.2, and 5.3 examine the nucleation, elongation, and termination stages by their order in typical CNT growth, summarizing the latest insights into the internal mechanisms driving these critical conversion stages. Subsequently, Sec. 5.4 delves into chirality-controlled CNT growth, highlighting the underlying causes of chiral selectivity at different stages of CNT growth. In Sec. 5.5, the focus shifts to the dynamic properties and active sites of catalysts, a cornerstone of modern heterogeneous catalysis research. While much of the theoretical analysis in earlier CNT growth studies has been conducted on relatively static catalyst surfaces, future research will increasingly emphasize catalyst dynamics to identify effective strategies for regulating the synthesis process.

5.1 Nucleation stage

The nucleation stage is the initial stage of CNT growth and has traditionally been the focus of intense theoretical research.²³⁷ This focus is partly because nucleation is a prerequisite for all subsequent transformation processes and has a crucial impact on the diameter and chirality of the CNTs. Additionally, compared with later stages, nucleation is relatively simpler to study, which aligns with the computational resources and methods available. Extensive experimental and theoretical studies, particularly in situ observations and MD simulations, have helped establish a preliminary framework for understanding the nucleation process of CNT growth.²³⁸

In general, nucleation involves three fundamental steps: (1) decomposition of precursors, dissolution of carbon atoms, and formation of metal carbide; (2) formation of carbon chains and carbon islands; (3) aggregation of carbon islands and formation of a “cap”. However, many reaction details remain unclear in existing research, leaving several seemingly fundamental experimental observations without comprehensive explanations.⁹ For example, the effects of different carbon precursors or the role played by etching agents are still not fully understood.⁵⁰ Many recent computational works continue to focus on key issues during the nucleation phase, achieving further progress in this area.

5.1.1 Decomposition of carbon precursors and formation of catalyst nanoparticles. The synthesis of CNTs employs a diverse range of carbon precursors, including hydrocarbons, alcohols, and carbon monoxide.³¹ Numerous experimental studies have demonstrated that these precursors significantly influence growth dynamics.^29,239 However, existing theoretical and computational research has not adequately addressed the impact of precursor selection. A widely accepted theory posits that catalysts primarily facilitate precursor decomposition by substantially lowering the activation energy compared with non-catalytic conditions.⁵³ Consequently, precursor decomposition is often not considered the rate-limiting step in CNT growth¹⁹ and neglected in theoretical and computational studies. For instance, in the growth simulation via MD, atomic carbon was often directly added into the system as the only carbon source.²⁴⁰ However, this perspective has several limitations.

Firstly, from a broader perspective of the reactor system rather than the localized viewpoint of microscopic growth, the decomposition process of the precursor cannot be overlooked. Under low-temperature or low-concentration conditions, carbon precursors may primarily decompose on the catalyst surface. However, as FCCVD is becoming a key industrial production method for CNTs,⁵⁰ the predominance of catalyst-mediated precursor decomposition in large-scale, high-temperature multiphase reactors is questionable. In these systems, catalysts (e.g., Fe nanoparticles) are formed through the high-temperature homogeneous transformation of precursors like ferrocene. This environment also exposes carbon precursors to high temperatures, potentially leading to significant homogeneous decomposition.¹³⁷ Meanwhile, the specific carbon intermediates that directly participate in the growth of CNTs are also not definitively identified in current research. It remains unresolved whether carbon atoms or dimers are the direct participants in CNT growth.²⁴¹ This uncertainty raises the question of whether optimal precursor–catalyst combinations can be selected to produce the most suitable direct intermediates for efficient CNT growth. These considerations highlight the need for a more comprehensive understanding of carbon precursor effects in CNT synthesis.

Although these issues currently lack a complete theoretical explanation, some of the latest computational works have provided new insights. These studies continue to push the boundaries of our understanding, suggesting that a re-evaluation of traditional models and assumptions may be necessary to fully grasp the complexities of CNT synthesis.

Khalilov et al.²⁴² employed the hybrid MD/kMC technique to simulate the nucleation and subsequent growth of SWCNTs, emphasizing the critical role played by both carbon and non-carbon species from oxygen-containing hydrocarbons in these processes. Their atomistic simulations revealed that non-carbon species significantly influence both the nucleation and growth stages. The research team delineated three primary types of growth contributors: those originating from the decomposition of the feedstock, those involved in rehydroxylation, and those contributing to the etching of the growing CNT, as shown in Fig. 12(a). These findings suggest that competition among these processes determines which species in the three primary types become predominant in the growth of the CNTs. The study also highlighted the dynamic role played by hydrogen and oxygen atoms. Specifically, the incorporation of these atoms into the growing tube was found to either increase or decrease the tube's diameter. For instance, reactive hydrogen atoms were observed to rapidly attach to carbon sheets or cap-ends, diminishing the adhesion between the carbon structure and the catalyst. This interaction causes the carbon cap to expand by reducing its rim diameter, allowing the carbon sheet to partially cover the catalyst surface. This nuanced understanding of CNT growth mechanisms offers valuable insights into the influence of varied atomic species on the structural characteristics of carbon nanotubes.

Fig. 12 Recent computational works on the decomposition of carbon precursors and formation of catalyst nanoparticles. (a) Schematics of three types of carbon contributors during CNT growth, together with the ratio of different types of carbon atoms to other carbon species.²⁴² (b) Trajectory analysis of the MD simulations of ferrocene decomposition in a vacuum versus a H₂ atmosphere performed at 2000 K. Left: molar percentage of Fe in the formed clusters; right: changes in the total number of Fe–C bonds in the simulation cell.¹⁴ (c) Energy profile of the rate-limiting step in: Route I without Cl introduction, Route I with Cl introduction, and Route II with Cl introduction. Compared with the acetone decomposition without Cl introduction, the Cl-modulated reactions have lower ΔG and activation energy (E_a), leading to an elevated concentration of reactive carbon.²⁴³

Lei et al.¹⁴ recently conducted a computational study focusing on the formation of catalyst particles through MD simulations. They highlighted that at the high temperatures typical of FCCVD, iron nanoparticles are likely in a liquid state, lacking distinct crystal facets, which contrasts with many earlier studies that examined carbon precursor decomposition on well-defined crystal planes of solid metals. Hydrogen plays a crucial role in removing carbon produced during the decomposition of ferrocene by preventing catalyst poisoning and enabling the subsequent nucleation and growth of CNTs, as shown in Fig. 12(b). They examined the catalytic role played by liquid Fe nanoparticles in breaking down methane into precursor blocks ready for CNT growth. They focused on methane dissociation over a liquid Fe₅₅ cluster. During simulation, one in five methane molecules was completely dissociated into one carbon and four adsorbed hydrogen atoms (H*), while another methane molecule partially broke down into CH₃ and H*. These decomposition products remained strongly bound to the catalyst surface due to chemical interactions. At high hydrogen coverage, hydrogen could desorb from the cluster (Fe₄₁H₄₀) as H₂, whereas at reduced hydrogen coverage, methane would continue to dissociate (CH₄ → CH₃ + H*) on Fe₄₁H₄₀. They concluded that methane dissociation occurs only on Fe particles with low to moderate hydrogen coverage, as high levels of surface hydrogen inhibit the dehydrogenation process. Moreover, their computational results indicated that the liquid-state Fe nanoparticles encountered a rate-limiting barrier of about 0.9 eV when catalyzing methane dehydrogenation, ultimately facilitating the formation of C₂ dimers essential for subsequent CNT growth.

Hu et al.²⁴³ recently introduced a novel chlorine (Cl) and water-assisted lengthening technique in FCCVD to influence the interactions between CNTs and enhance the mechanical properties of macroscopic fibers. They performed DFT calculations to analyze the decomposition of carbon sources like acetone and ethanol. Their findings indicated that the C–C bond in acetone is particularly prone to breaking during gas phase pyrolysis due to its low bond overlap population and inherent weakness, leading to a sequence of dehydrogenation reactions that supply precursors for CNT growth, as shown in Fig. 12(c). Their thermodynamic analysis showed that the chlorine atoms interact with acetone, weakening the C–C bonds through electron redistribution, dramatically lowering the overall ΔG for complete pyrolysis to 5.11 eV. This reduction in the required reaction heat facilitates an easier breakdown of the carbon source. From a kinetic point of view, the activation energy (E_a) needed for the key acetone pyrolysis step (CH₃ CO → CH₃ + CO) was initially the same as the reaction heat (ΔE, 1.37 eV). However, when chlorine is involved in the reaction (CH₃CO + Cl → CH₃Cl + CO), the E_a and ΔE_a drop to 0 and −2.44 eV, respectively, making the reaction spontaneous and exothermic. Similarly, the E_a for the reaction with chlorine (CH₂CO + Cl → CH₂Cl + CO) is also very low at 0.06 eV. Thus, the introduction of methylene chloride to release chlorine in the gas phase not only enhances the formation of activated carbon species necessary for rapid CNT growth but also lowers the energy barriers for carbon source decomposition, optimizing the production process for high-quality CNT.

5.1.2 Migration, etching, and assembling of carbon intermediates. After the carbon precursors decompose into carbon atoms and intermediate dimers, the processes of nucleation on the catalyst surface requires both migration and assembling of these intermediates. The mechanism of carbon migration has been a subject of long-standing debate, encompassing several theories such as bulk migration, sub-surface, and surface migration.²³ Various studies have documented these mechanisms through experimental observations or theoretical analyses. The fundamental challenge is that both the type of catalyst and the nature of the carbon source can significantly influence the migration process.²⁴⁴ On the other hand, the complexity of the assembling process lies in its dynamic nature, requiring simulations over longer time scales to comprehensively assess the behavior of carbon atoms on the catalyst surface. This level of analysis has been challenging for many earlier studies. Recently, advances in computational methods have provided deeper insight into the assembling process, improving our understanding of how carbon atoms interact and consolidate on the catalyst surface to form structures.

Wang et al.¹³⁶ demonstrated using ETEM and DFT calculations that the active catalytic phase for MWCNT growth is Co₃C. This finding led them to reevaluate the mechanisms of carbon migration in the growth process of VLS, as shown in Fig. 13(a) and (b). Their calculations aligned with previous studies, indicating that carbon diffusion through solid cobalt has an activation energy of 1.35 eV, supporting rapid carbon atom diffusion at the temperatures required for MWCNT growth. However, the diffusion dynamics differ significantly in a solid Co₃C nanoparticle, where interstitial sites are occupied by carbon atoms, making vacancy diffusion the primary carbon transport method. Their detailed analysis revealed that the activation energies for carbon vacancy diffusion along the three orthogonal axes of the orthorhombic Co₃C crystal are considerably high at 2.63, 2.45, and 2.62 eV, respectively. Consequently, the researchers concluded that the growth of the outermost walls of MWCNTs is likely facilitated by surface diffusion of carbon atoms, which has a much lower activation energy of approximately 0.68 eV. This ensures a rapid supply of carbon atoms. Addressing the challenge of carbon supply to the inner walls of MWCNTs, which are typically obstructed by the outer walls, they further proposed an interface diffusion mechanism. At the modeled CNT–Co₃C catalyst interface, the activation energies for carbon diffusion were notably lower at 0.53 eV at the zigzag edge–Co₃C interface and 0.94 eV at the armchair edge–Co₃C interface. These values are significantly lower than those for bulk diffusion, suggesting an efficient route for inner wall growth.

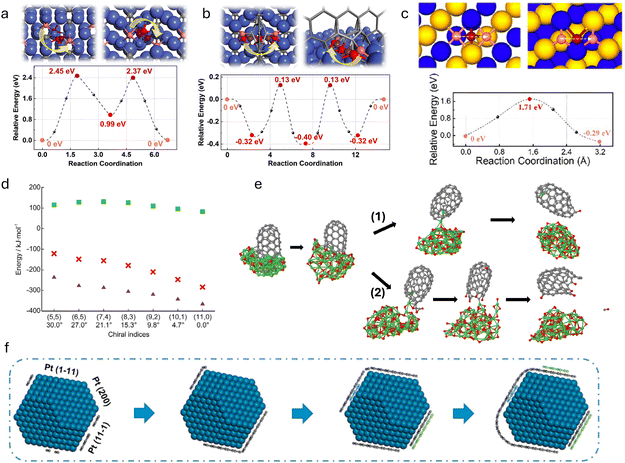Fig. 13 Recent computational works on the migration, etching, and assembling of carbon intermediates. (a) Top and side views of the bulk diffusion process and the minimum energy path (MEP) along the b-axis. (b) Top and perspective views of the interface diffusion process between a zigzag CNT edge and the Co₃C (001) surface and the corresponding MEP.¹³⁶ (c) Bulk diffusion barrier of atomic carbon in the Ni–Co alloy. The initial and final positions of the C atom are denoted with pink, and that of the transition state is shown in red. The large sphere in (e) represents a homogeneous Ni–Co alloy metal particle.¹⁵ (d) Average ΔE_OH (red cross), E_def (green squares), and E_int (purple triangles) of cap-OH at the edge carbon atoms.⁶⁷ (e) Two scenarios of the detachment of small CNTs. (1) CNT detachment as a fullerene in both the OH and O cases and (2) detachment of an O-terminated CNT in the O case.²⁴⁵ (f) Atomic models illustrating the evolution of the graphene layers in facet-selective growth of graphene on Pt nanocrystals.²⁴⁶

Fan et al.¹⁵ identified bulk diffusion as the primary mechanism for carbon transport when using a Ni–Co alloy catalyst. During in situ imaging, they observed that the catalyst particles predominantly remained in a pure metallic phase without transitioning to any significant carbide phase. In this case, carbon atoms, generated from the decomposition of ethylene at the catalyst's surface, predominantly undergo bulk diffusion, as shown in Fig. 13(c). This process was supported by DFT calculations, which confirmed that bulk diffusion is more energy efficient than surface diffusion. They noted that single-metal catalysts tend to form carbides where carbon diffusion is mostly restricted to slower surface and interface mechanisms, likely limiting growth rates. In contrast, the Ni–Co alloy presents a significant advantage; it increases the resistance to carbide formation, thus maintaining a metallic state that supports rapid bulk diffusion of carbon. This characteristic notably enhances the efficiency of the Ni–Co alloy catalyst over its monometallic counterparts for applications requiring efficient carbon transport.

The influence of etching agents on the growth of CNTs has been a significant focus of research. Studies have shown that varying etching agents, such as hydrogen, steam, and even ammonia, can markedly affect the yield and quality of CNTs.²⁹ Despite this, the specific effects of these agents on the growth mechanisms, particularly their impact on the chirality distribution of CNTs, have been less explored.

Kimura et al.⁶⁷ analyzed the chiral-selective etching effects of OH radicals, originating from water or alcohol additives, on the growth of carbon nanotubes at the edge carbon atoms. Their DFT calculations revealed a chirality-dependent reactivity at the edges of SWCNT caps. While the overall reactivity of the carbon atoms in each cap showed little variation with SWCNT chirality, the reactivity at the edge carbons increased with a decreasing chiral angle. Energy decomposition analysis clarified that this reactivity trend is driven by the interaction energy between the reactive species and the caps, indicating that etching reaction energies are influenced by SWCNT chirality, as shown in Fig. 13(d). This suggests that etchants can be used for chirality-controlled growth of SWCNTs by selecting appropriate additive species.

Eveleens and Page²⁴⁷ demonstrated through non-equilibrium quantum chemical MD simulations how chemical etchants can differently influence the SWCNT nucleation mechanism on Fe and Ni catalysts. The interaction between carbon and the catalyst surface is stronger with Fe than with Ni, which results in a higher carbon desorption rate and chemical potential on Ni. Additionally, Ni more effectively activates adsorbed C–H and N–H bonds compared with Fe. However, due to the relative strengths of Ni–H and Fe–H interactions, the hydrogen chemical potential is consistently lower on Ni, leading to faster carbon chain growth and SWCNT nucleation on Ni catalysts. Ammonia, in particular, effectively drives carbon species from the Ni surface, more so than from iron, influencing how it etches active carbon species during nucleation and growth.

Sompel et al.²⁴⁵ recently compared hydrogen etching with OH etching in plasma-assisted nucleation of CNTs using integrated MD/kMC simulations. Contrary to the initial hypothesis, the effects of oxidation were found to differ significantly from hydrogenation etching, as shown in Fig. 13(e). Hydrogen radicals destroy the carbon structure while leaving the nanocluster intact. In contrast, oxygen radicals saturate the nanocluster, causing the carbon structure to dissociate from the cluster but remain largely intact. This demonstrates that the addition of OH radical results in the removal of CNT from the nanocluster while preserving the carbon structure, highlighting the nuanced effects of different etching agents on CNT growth and structure.

Computational research on nucleation faces challenges, particularly concerning the growth mechanisms on dynamic catalytic surfaces and the development of general design strategies. With advancements in machine learning, we now have more sophisticated tools to simulate the complex carbon assembly processes. Zhang et al.⁴³ employed a combination of MD and time-stamped force-biased kMC methods, enhanced by the Gaussian Approximation Potential, to dynamically simulate graphene growth on Cu(111) surfaces. Traditional kMC simulations on static metal surfaces may miss crucial reaction processes, and ab initio MD simulations are often limited by their short timescales, unable to capture complete reaction pathways involving Cu atoms. Their results accurately replicate key subprocesses, including the preferred diffusion of carbon monomers/dimers, as well as chain or ring formations leading to edge-passivated Cu-aided graphene growth.

Recent theoretical studies also revealed new insights into the early stages of CNT growth, such as the nucleation process not necessarily starting from the cap formation. Ma et al.²⁴⁶ reported atomic-resolved nucleation of SWCNTs on truncated octahedral Pt catalysts under atmospheric pressure. They found that graphene layers initially formed on the (111) surfaces, then merged to form an annular belt and a hemispherical cap, followed by SWCNT elongation. To understand the selective coverage of graphene layers on different Pt nanoparticle facets, formation energies of various graphene islands on Pt (111) and (200) surfaces were calculated in three distinct modes: on-terrace, metal-terminated, and H-terminated. The H-terminated mode was found to be energetically preferred. They proposed that SWCNT nucleation on faceted Pt nanoparticles occurs through the assembly of graphene layers formed during the early stages, differing from the traditional one-step nucleation process. The facet-dependent formation indicates that the coverage of graphene on all (111) facets is a necessary step to create a closed carbon network over the (200) surfaces, suggesting a selective growth mechanism based on particle size and surface orientation. This model proposes that the nucleation of SWCNTs involves assembling graphene layers rather than extending a single graphene island, explaining why graphene extends only to (111) surfaces and not both (200) and (111) surfaces.

5.1.3 The role played by sulfur promoter. Sulfur has long been utilized as a promoter in the synthesis of CNTs.²⁴⁸ Without sulfur, there is a significantly higher probability of deactivation of catalyst nanoparticle due to carbon encapsulation. A generally accepted theory is that S lowers the activation energy for the nucleation of CNTs and also lowers the nucleation barrier of the catalyst nanoparticles.²⁴⁹ Yet understanding its precise effects remains elusive. A recent review by Bogdanova et al.⁵⁶ provides a comprehensive overview of the multifaceted role played by sulfur in the synthesis of CNT. The review highlights several key impacts of sulfur, including:

1. Reduction of the melting point of catalyst particles, which enhances their diffusion rate and surface reconstruction, thereby increasing catalytic activity.

2. Decrease in carbon solubility in liquid iron and the surface tension of Fe–C–S alloys, which enhances carbon diffusion on the surface and fosters CNT growth.

3. Enlargement of CNT diameters through the formation of Fe–S nucleation sites for synthesizing specific types of CNTs influenced by the sulfur-to-iron (S/Fe) ratio.

The review also delineates the role played by sulfur at three distinct levels: catalyst particle, catalytic process, and the resulting carbon nanotube. Despite these insights, many aspects of sulfur's influence on CNT growth still require further investigation.

In recent computational research, Orbán and Höltzl⁷⁴ investigated how acetylene and ethylene adsorb onto iron clusters and nanoparticles, specifically focusing on Fe₁₃ and Fe₅₅. They discovered that sulfur's presence predominantly reduces the adsorption strength near the adsorbate, indicating that the impact of sulfur is largely steric rather than electronic, which plays a more minor role. Their findings further revealed that a dense coverage of sulfur on the surface substantially diminishes both the number and strength of available adsorption sites. This reduction significantly affects the catalytic activity of the iron clusters or nanoparticles. Such an effect can encourage the growth of catalyst nanoparticles while preventing carbon encapsulation. This prevention is crucial as it can lead to early deactivation of the catalyst during the nucleation stage of CNTs in the FCCVD method. Moreover, as the process progresses and temperatures increase, sulfur tends to evaporate from the surfaces of these catalyst nanoparticles. Consequently, its influence on CNT growth decreases in the later stages.

In recent experimental studies, researchers have uncovered findings that have yet to be fully theoretically explored. For example, Vazquez-Pufleau et al.²⁴⁹ examined the influence of sulfur in controlling the morphology and aggregation of CNTs by synthesizing a broad spectrum of sulfur-to-carbon (S/C) ratios. They observed that the quantity of carbon reaching the catalyst and subsequently forming CNTs remains constant, irrespective of the sulfur content in the catalyst. This suggests that the rate-limiting step in CNT formation is not at the catalyst/promoter interface but rather in the transport of carbonaceous active precursors to the catalyst, possibly due to their diffusion in the gas phase or decomposition kinetics. Simultaneously, Sharma et al.²⁵⁰ recently conducted experimental studies that revealed the significant impact of additives (such as chlorine and sulfur) on the tube diameter, wall thickness, and catalyst phase filling. Introducing a small amount of sulfur during synthesis has shown potential in precisely adjusting the catalyst phase and achieving high-pressure phases (γ-Fe) within the CNT structure.

In summary, although many researchers acknowledge the critical role played by sulfur, particularly in the FCCVD process, there is still a substantial gap in computational and theoretical studies related to the mechanisms of the action of sulfur.

5.2 Elongation stage

The elongation stage is a critical step in the sustained growth of CNTs, directly influencing their structural quality and production efficiency. Although nucleation requires overcoming a substantial energy barrier during cap formation and lift-off, the subsequent growth stage proceeds with a considerably lower activation energy. Continuous growth requires the assimilation of carbon into an existing tube structure. However, this growth is not inherently stable; defects and changes in chirality can occur as the structure grows. Theoretical studies suggest that achieving steady-state growth is not guaranteed, and growth characteristics depend on complex interactions between gas-phase precursors, nanocatalysts, and environmental conditions.¹⁰⁵ For efficient and high-quality CNT production, sustaining rapid elongation over prolonged periods with high purity is essential. To address these needs, research has focused on several key challenges. These challenges center around capturing the influence of catalyst and environmental conditions, adequately defining the CNT growth kinetics, and identifying how defects form and heal during this process. Key metrics of interest during the CNT elongation stage include nanotube growth rate, catalyst efficiency, and defect lifetimes. This section reviews relevant literature on the elongation process, which occurs after cap lift-off and before growth termination, addressing the challenges and mechanisms that govern this stage.

5.2.1 From cap formation to continuous growth. Upon completion of the cap formation, the process of cap formation to the lifting off of the tube is the initial step in continuous CNT growth. Ding et al.²⁵¹ addressed this central step using DFT. They evaluated the interfacial energy at the edge of the catalyst as a function of the contact angle to identify the ultimate reason why liftoff is energetically favorable. Their analysis revealed that higher contact angles, facilitated by the lift-off of the graphitic cap, were shown to significantly decrease interfacial energy by as much as 6–9 eV nm⁻¹. This reduction helps to overcome van der Waals forces between the cap and the catalyst, ultimately promoting CNT growth. Their study also incorporated the presence of metal step-edges at the interface, showing that CNT lift-off can be more energetically favorable at varying carbon concentrations and particle diameters. The interplay between adhesion strength, curvature energy, and interfacial energy, all as functions of contact angle, can identify the diameter, chirality, and growth mode of the CNT. The researchers employed MD simulations to validate their results and demonstrated excellent agreement with their DFT calculations. These simulations confirmed that both diluted particles within the catalyst weaken adhesion strength and that larger contact angles reduce adhesive energy, thereby increasing the likelihood of CNT growth.

Although modifying contact angles and interfacial energies is crucial, catalyst crystallinity also influences whether or not CNTs continue to grow. Also along these lines, Wang et al.¹³⁶ conducted ETEM and DFT to analyze the behavior of Co nanoparticles as catalysts, demonstrating that specific crystal structures and faceted planes of cobalt nanoparticles are critical for determining whether the nanotube growth will initiate, continue, or stop. Nanoparticles in the carbon-rich Co₂C phase are found to be active for SWCNT growth, while those in the Co₃C phase are more likely to be inactive or deactivated. Additionally, they demonstrated the work of adhesion between the nanotube and catalyst surface plays a crucial role, where a disparity in the work of adhesion between different planes is necessary to achieve nanotube lift-off and continued growth.

Beyond the specific crystal structure, catalyst composition often plays a decisive role in achieving robust and sustained nanotube growth. Qiu and Ding⁸⁷ explored why metallic alloy catalysts have been more effective for CNT production than pure metals. With ab initio MD, they followed the trajectories of small-scale alloy nanocatalysts’ subcomponents around growing nanotubes. They discovered that during the early stages of CNT growth, the more active metal component of the alloy would congregate around the growing CNT edge at a measurable rate. The high-affinity metals would then attract carbon, resulting in an increased rate of overall carbon supply to the growing nanotube. Simultaneously, the less active metal accumulated at increasing concentrations away from the CNT edge, preventing graphitic encapsulation of the nano-particle and extending the catalyst's lifetime for CNT growth. Classical MD simulations corroborate this theory for larger-scale catalysts containing tens of thousands of atoms by also showing the same congregation around the growing CNT edge. It is noted that this effect does not apply to metal carbides, as the bond will reduce the carbide's affinity to the nanotube, counteracting the observed effect.

5.2.2 Growth rate kinetics and the rate-determining steps of tube elongation. After beginning continuous growth elongation, a key question is identifying which step in the assembly process dictates the overall growth rate. In CVD, the CNT growth process can be described as seven overlapping processes: decomposition process of the particulate precursors, molecular transport of the decomposed species from the surrounding fluid to the surface of the catalyst, adsorption of the precursor to the active sites of the catalyst, non-CNT reactions on the surface of the catalyst, carbon diffusion on or in the nanocatalyst towards the growing nanotube, carbon integrating into the growing CNT lattice, and finally desorption of particles back into the bulk gases.

Various studies have established kinetic mechanisms of CNT formation using experiments.^{153,154,156,252–254} Page et al.²⁶ summarized the literature before 2015 on FCCVD for CNT production, revealing disagreement on the determined rate-limiting steps between experiments in different groups. They concluded that the rate-limiting step may vary depending on temperature ranges, pressures, and types of catalysts. Commonly, it was found that carbon precursors’ decomposition and carbon assembly into molecules or atoms were common bottlenecks. Recent efforts have continued this line of work, such as Novikov et al.,²⁵⁵ who have established new methods for kinetic model development in aerosol floating catalyst CVD.

Subsequent studies have attempted to unveil the continuous growth process steps using atomistic simulations. Förster et al.¹²¹ conducted semi-grand canonical kMC to provide chirality-specific trends of SWCNT growth, focusing on how the carbon nanotube–catalyst interface energy and synthesis conditions influence growth rates. The simulations reveal the non-monotonic trend of chiral angle selectivity as a function of interfacial energy, E_Z, between the catalyst and the nanotube. Near-zigzag configurations grow fastest at low interfacial energies, while at higher E_Z, the trend shifts towards faster-growing near-armchair configurations. The study identifies conditions under which selective growth of certain chiral angles can be achieved, essential for synthesizing SWCNTs with desired electronic properties. Specifically, the available active sites can act as a rate-limiter under specific conditions. However, the study only applies when the rate-limiting influence is the energy barrier associated with the carbon incorporation into the tube and that there is always a readily available carbon supply, which may not be the case. Yamanaka et al.⁸³ postulated that the rate-limiting growth was C–C bond formation and investigated using MD simulations. The MD simulations focused on the interaction between CNTs and cementite (Fe₃C) nanoparticles, specifically examining the effects of tensile strain and temperature on CNT growth. The results showed that at temperatures above 1273 K, the carbon atoms within the cementite diffuse well, supporting CNT growth at high speeds. In contrast, at 1073 K, CNT growth is hindered by insufficient carbon supply. The chiral CNTs demonstrated the most stable growth at a pull-up speed of 1 mm s⁻¹, which is the fastest ever observed in FCCVD, while armchair and zigzag CNTs exhibited slower growth. At 1473 K, CNT growth produced defect rings due to high fluidity in the cementite structure. The study concluded that higher temperatures above the melting point of cementite enhance carbon diffusion, but too high of a temperature can introduce defects, impacting CNT quality. Other studies have focused on the barrier of the carbon diffusion process. Unlike bulk diffusion, subsurface diffusion always has a lower energy barrier because of the smaller elastic response in nanoparticle subsurface.⁶⁸

Several general models have been constructed to model the growth process by integrating various modeling approaches with experiments. In early studies, the barrier for carbon atom incorporation into the tube wall was thought to be very low because of the SWCNT open end's high activity and the reaction's exothermicity. Ding et al.¹⁵¹ then demonstrated the screw dislocation theory, which hypothesizes that growth rates should be proportional to the chiral angle. Their results compared well with some, but not all, experiments.¹⁰⁵ Further validation came from recent work from Qiu and Ding,⁸⁵ who used DFT/MD to show that unclean catalyst–nanotube interfaces observed in simulations are just an artifact of short annealing times relative to experiments due to computational expense. The transition state theory says that the annealing time is of order 2 μs, while MD simulations currently run for a max of 100 ns. Their models also show that the catalyst–CNT interface is clean, meaning it has well-defined active sites or that no extraneous carbon chains are attached. While this has been hypothesized by screw dislocation theory and known from experiments, it has not been directly observed through molecular dynamics and Monte Carlo simulations. They attest to the high annealing rates, up to six orders of magnitude too fast, in simulations compared with experiments imposed by computational limitations. Yuan et al.⁶⁸ reasoned that the experimental validity of the screw dislocation theory suggested that the carbon incorporation into the CNT wall was the threshold step, as opposed to the decomposition of feedstock or the diffusion of C to the CNT active sites. They used DFT to calculate energy barriers of incorporating dimer C atoms into SWCNT walls for Fe, Co, and Ni, and found that the incorporation of the second C into an exposed armchair-type CNT was, in fact, the limiting barrier. The carbon atom insertion had an energy barrier of 1.85 eV for a Fe catalyst. In comparison, carbon feedstock decomposition had a barrier of less than 1.5 eV, and carbon atom diffusion was less than 1.2 eV. He et al.¹⁹ extended the screw-dislocation model to account for the role played by etching. According to their model, in an etching-free environment, the SWCNT's growth rate ultimately depends on the ratio of the accessible catalyst surface to the tube diameter and the feedstock pressure and not the number of active sites on the CNT. If they are in an etching-rich environment, growth rates only become dependent on the number of active sites, and their model collapses to the screw-dislocation theory. They validated their model against the literature and with their own experiments, obtaining good agreement. In more recent work, Otsuka et al.¹⁵² combined experiments and modeling to develop a universal chemical kinetic model that decomposes the growth rates of nanotubes into the adsorption and removal of carbon atoms on the catalysts. They classified nanotube growth into five regimes depending on the carbon source pressure P_C and the etching agent pressure P_E, as shown in Fig. 14. At low P_E, there is the homogeneous rate regime, where growth rates are limited by the carbon supply rate, and hence are independent of CNT chirality. The randomly dispersed regime is identified in the regime where both P_C and P_E are low, a condition commonly found in in situ electron microscopy studies. In the metallicity selective regime, CNTs of metallic chirality are grown less due to low P_C/P_E ratios. Even lower P_C/P_E ratios result in the shrinking regime, where nanotubes are found to have greater shrinkage rates than growth rates. Lastly, the chirality-selective regime is found at high etchant pressures and P_C/P_E ratios. This regime corresponds to the chirality-specific growth rates elucidated from the screw-dislocation theory.¹⁵¹ Ultimately, their approach revealed the various causes of rate limitations given the conditions in the experiment, finally explaining why some previous studies observed chirality-independent growth rates in etching-free environments,⁵³ while others demonstrated growth rates that depend on the number of active sites.¹⁵¹ It should be noted, however, that growth rates alone do not dictate the output distribution of chiralities from a reactor. The chirality-varying rates of nucleation, termination, and defect evolution, may result in the non-uniform chirality distributions often observed experimentally.

Fig. 14 Universal chemical kinetic model of CNT growth identified by ref. 152. (a) Growth rates, γ, and, (b) relative dominance of growth to etchant kinetic constants, S_g/e, identified alongside the various growth regimes based on etchant pressure P_E and carbon precursor pressure P_C in the universal kinetic model.

Larger-scale, multidimensional studies have also been used to connect chemical kinetic theories to reactor-scale trends. Gakis et al.¹⁶³ applied continuum-scale models of FCCVD with a global reaction mechanism to determine the rate-limiting steps in CNT growth. They modeled gas-phase reactions using a single-step reaction defining the generation of carbon impurities. Catalysis is initiated through a single-step acetylene adsorption process, followed by decomposition into smaller species and carbon that eventually either assimilates into the tube or develops an impurity layer on the catalyst surface. Their models elucidated the influence of heating on the flow recirculation regions, including how it generates unwanted gas-phase species like polycyclic aromatic hydrocarbons, which evolve to condensed phase deposition on the reactor walls. Their results showed that carbon diffusion through the catalyst was the rate-limiting step for CNT growth. They identified a low-temperature regime, where reactor yield is limited by impurity formation from surface reactions, and a high-temperature regime, where direct gas-phase deposition to the catalyst generates impurity layers. While their model does a good job connecting reactor-scale dynamics to the smaller-scale growth processes, it is important to note that their studies consider CNTs to be a homogeneous carbon sink, independent of chirality, and their representations of gas-phase and catalytic reactions with global models are fairly simplified. Thus a determination of rate-limitation under these configurations is incomplete, but at least gives an additional piece of the overall puzzle of the influence of larger scale effects on CNT growth. Andalouci et al.¹⁶² used a 0-D and a 2-D model, with the computational methods described in Fig. 15, to assess oxygen's effects on gas-phase species and key reactions in plasma-enhanced CVD of CNTs. Their 0-D model included a considerable 134 species and 471 gas-phase reactions, and their 2-D model incorporated a reduced 23 species with 100 reaction model, but included transport and advection. Experiments were conducted by varying the oxygen flow rate in the H₂CH₄ mixture, and the modeling results were compared with experimental outcomes, showing good agreement. The study highlights how oxygen species such as H₂O, OH, CO, and atomic oxygen affect the CNT growth, providing insight into optimum oxygen content for enhanced vertical CNT growth in PECVD reactors. Lin et al.²²⁵ found that key factors, such as the reactivity and concentration of the carbon feedstock, play a critical role in balancing the crystallinity–height trade-off. The results from validation experiments confirmed the machine-learning model's predictions, leading to a 48% increase in SWCNT growth efficiency while maintaining high crystallinity.

Fig. 15 Description of computational methods used for the combined 0-D and 2-D modeling approach from ref. 162. 0-D models include a detailed gas and surface chemistry mechanism; the 2-D models incorporate a reduced mechanism but account for the diffusion and advection of the surrounding flow-field.

5.2.3 Mechanisms of formation and healing of defects. During continuous growth, perfect carbon assembly into a graphitic CNT wall is not guaranteed. Defects may form, which are defined as abnormalities in the hexagonal structure. These often manifest as non-6-sided rings in the CNT lattice, such as pentagons or heptagons. Several common defect types are 5–7 defects, Stone–Wales defects, and vacancies.²⁵⁶ Within CNT growth, 5- and 7-member rings may become metastable, remaining embedded in the tube despite their thermodynamic infavorability.²⁵⁷ Using atomistic models, one can elucidate the process of emerging defects and their conversion rate to hexagons. Simulations have previously demonstrated that the process of defect healing occurs over long time scales. These time periods, in combination with the short time-step sizes required in atomistic simulations, make defect-free nanotubes hard to grow in MD.²¹⁵ As a result, changes in chirality can occur during simulated growth. Until recently, this computational limitation has been a common theme in CNT growth simulations.^44,88,215

A long-standing issue in atomistic research of CNT growth is that CNTs obtained via molecular dynamics simulations often have irregular shapes and contain numerous defects. At the same time, CNTs produced experimentally possess surprisingly highly ordered and defect-free structures.²¹⁵ Experimental studies have shown defects in FCCVD processes occur every 10 μm in direct-spun samples, independent of chirality.²⁵⁸ Modeling efforts to unveil this process in CNT formation have demonstrated much higher rates of defect formation, leading to CNTs with no definable chirality.⁸⁹ Before the past decade, the lack of computational resources inhibited the dynamic study of the defect-healing process in the growth process due to both the substantially high timescale involved and the computational expense associated with modeling atomic interactions with high accuracy. Previously, biasing methods were introduced to artificially reduce defects in CNTs to make them more appropriately match experiments. Yoshikawa et al.⁸⁸ demonstrated MD simulations of defect-free SWCNTs, that is, chirality-definable SWCNTs, under the optimized carbon supply rate and temperature. The near-zigzag SWCNTs grew via a kink-running process, in which bond formation between a carbon atom at a kink and a neighboring carbon chain led to the forming of a hexagon with a new kink at the SWCNT edge. Defects, including pentagons and heptagons, were sometimes formed but effectively healed into hexagons on metal surfaces. Wang et al.²⁵⁷ conducted reactive MD for simulating the interaction between carbon atoms and nickel catalysts to observe the process of CNT ring formation from the carbon chain to assimilation within the tube. The research identified two primary pathways for the formation of six-membered carbon rings. The first pathway involves the direct incorporation of carbon chains on the catalyst surface, while the second involves the formation of non-six-membered rings (like pentagons) that eventually transform into stable hexagonal rings. Despite the first path resulting in a stable configuration more quickly, most hexagonal rings form through the second path due to intermediate states reducing overall activation energies. Specifically, the final hexagonal structure is most likely to emerge from a pentagon shape after defect-healing because the activation energy is lower than direct hexagonal formation. The study provides valuable insights into the kinetics of ring formation, offering a clearer understanding of defect formation and healing during CNT growth.

Most recently, the development of MLFFs have enabled drastic improvement of MD simulation computing cost, significantly aiding in providing more realistic annealing times. Hedman et al.⁴⁴ applied their ML-aided MD simulation to model CNT growth with long overall growth periods. The ML acceleration enabled them to quantify defect formation frequency and time for defect healing. It was found that most defects healed within a nanosecond, quite a bit shorter than estimated in previous analyses.²¹⁵ The authors demonstrated that defects form stochastically at the tube–catalyst interface. However, under low growth rates and high temperatures, these heal before becoming incorporated into the tube wall, allowing CNTs to grow defect-free to seemingly unlimited lengths. Similarly, Kohata et al.⁸⁶ applied MLFFs for their MD simulations and observed defects healed very rapidly compared with previous simulations. Their simulations demonstrated a consistent six pentagons were maintained during CNT growth, and the number of heptagons never breached one. Additionally, edge defects, primarily caused by vacancies, were shown to be healed via adatom diffusion, enabling smooth SWCNT growth. However, even with ML acceleration, Kohata et al. still noted that their growth rates were two orders of magnitude higher than experiments, suggesting significant room for improvement in making MD growth simulations more physically realistic.

5.3 Termination stage

Understanding the termination mechanisms in CNT growth is crucial for optimizing synthesis conditions and tailoring nanotube properties at the production scale. Growth termination, defined as the point at which the formation of CNTs ceases, occurs due to various factors such as catalyst sintering, feedstock depletion, or the accumulation of amorphous carbon on the catalyst surface. These processes result from an intricate coupling of various elements from the reactor scale to the nanoscale, including gas-phase kinetics, precursor decomposition, catalyst–substrate interaction, and catalyst surface dynamics.

Significant advancements have been achieved in observing and analyzing termination mechanisms in CNT growth through experimental innovations. Techniques such as in situ methods and TEM have provided unprecedented insight into nanoscale processes during CVD synthesis. Overall, experimental studies have revealed the two common methods of growth cessation in CVD are due to the saturation of active sites due to the encapsulation of the catalysts²⁵⁹ and catalyst sintering.²⁶⁰ For the former, etchants such as water vapor, hydrogen, and oxygen have been used to prevent impurity layers from forming and improve CNT growth efficiency.⁹ Xu et al.²⁵⁹ conducted TEM on extracted samples from their in their ferrocene, xylene, and acetylene CVD system and directly observed nanoparticle growth termination due to carbon encapsulation. For the latter, Ostwald ripening has been shown to cause sudden termination of growth²⁶¹ but can be resolved through additives.²⁶⁰

However, many aspects remain poorly understood, particularly regarding the prevalence of each termination mechanism. CVD forests have been shown to have both an exponential decay in growth rates,²⁶² which may correspond to a reduction in carbon diffusion²⁶² and a sudden termination process,^153,263 which may correspond to catalyst sintering, encapsulation, or burning.^264,265 Stadermann et al.²⁶⁶ demonstrated in their studies that the nanotube growth rate remains relatively stable until it encounters a sudden and permanent termination. The authors provide a detailed quantitative model suggesting that this abrupt halt is caused by two key factors: the progressive buildup of amorphous carbon deposits on the surface of the catalyst particles and the transfer of carbon atoms to the edge of the growing nanotube. These processes disrupt the delicate balance required for continued growth, leading to an irreversible termination. Other termination mechanisms may also play a role. Zhang et al.²⁶⁷ applied environmental TEM to Co/MgO catalyst-grown CNTs and attributed growth termination to both the necking and a broadening of the tube–catalyst interface. They observed nanotube growth with insufficient carbon supply rates, resulting in nanotube growth rates of a slow 0.1 nm s⁻¹, which they believe led to defect formation. Additionally, previously unobserved mechanisms were shown, such as catalysts eating existing nanotubes and double-nucleation.

Overall, several unsolved problems remain in the study of CNT termination mechanisms: the cause and frequency of each termination mechanism, the selectivity of CNT chirality and diameter, the influence of reactor conditions, and potential routes for mitigating termination.²⁶¹ Direct experimental observation under conditions of production-scale reactors is still limited. As such, efforts have been made to determine the exact mechanisms of CNT termination with computation. This section explores the key termination mechanisms in CNT growth and highlights how modeling approaches have elucidated the underlying processes.

5.3.1 Growth termination by the encapsulation of catalysts. The process of catalyst poisoning, or encapsulation, due to the poisoning of unwanted molecules or amorphous/graphitic carbon is known to be a primary mechanism of CNT growth termination. Here, the carbon surface is covered in unwanted adsorbants or impurities, which ultimately surround the entire particle, preventing further carbon adsorption and CNT growth. Modeling this dynamic effect atomistically has been difficult, as MD simulations would require simulating from nucleation to termination, which requires considerable computational time. Additionally, encapsulation may be caused by environmental conditions,²⁵⁵ catalyst and substrate configurations,¹⁴⁹ and catalyst surface dynamics. Thus, parametric variations spanning these large configurational spaces add to the complexity and computational cost, inhibiting the investigation of all the possible routes of encapsulation. Despite this limitation, recent efforts have been applied to reveal experimental observations atomistically, and some multi-scale studies using kinetic models have achieved representations that are comparable to experiments.

Reactor-scale modeling has been a successful technique employed to model the process of deactivation. Jiang et al.²⁶⁸ introduced the substrate interception and direction strategy (SIDS), a new technique for producing ultra-long CNTs with high yield using a modified floating catalyst method. Their approach involved capturing the passing CNTs at the edge of a substrate, enabling their growth into a flying kite tip-growth mode along the streamlined direction of the flow. The authors also employed CFD to verify this assumption and to reveal further details about their new configuration. Using this method, they obtained growth rates comparable to those of previous studies for ultra-long CNTs but with two orders of magnitude higher aerial densities than previously reported, resulting in much higher yields. Gakis et al.¹⁶³ included an analysis of catalyst deactivation in their combined experimental and reacting-CFD study of a SCCVD reactor. Their models show that for reactor temperatures below 750 °C, the competition of carbon diffusion and carbon impurities formed directly on the surface of the catalyst from adsorbed hydrocarbon species are more likely to be the drivers of catalyst deactivation. In contrast, at higher temperatures, the direct formation of carbon impurities from gas-phase acetylene is the primary driver. They observed an increased rate of C diffusion through the catalyst in the first regime, resulting in decreased surface coverage, concomitant decreased impurity layer growth, and increased catalyst lifetime, as shown in Fig. 16. Further increases in temperature in the second regime result in excessive deposition of gas-phase carbon onto the surface as impurities. A comparison of CNT mass deposition with experiments validated the model and confirmed the existence of the two temperature regimes. Still, as discussed by the authors, there remains the possibility that the process of catalyst sintering was the primary driver of the second regime and the falloff of CNT mass production observed in the experiment. A more detailed reaction mechanism and atomistic simulations might provide a clearer answer. Additional work by the authors focused on floating catalyst CVD¹⁴⁹ applied a similar model but accounting for nanoparticle collision and coalescence, resulting in an excellent comparison to the experiment. In the case of floating catalysts, the decomposition of iron precursor ferrocene and subsequent nucleation of nanocatalyst was highly coupled to temperature and flow velocities. Carbon deposition saturating catalyst active sites also inhibited iron nucleation, limiting nanoparticle sizes even under high-temperature conditions.

Fig. 16 Quantitative analysis of catalyst surface coverage and lifetimes from ref. 163. (a) The catalyst surface coverage for their horizontal CVD reactor as a function of time for various temperatures. (b) The catalyst lifetime with respect to the reactor temperatures. (c) The CNT mass deposition as a function of the catalyst lifetime.

Etching agents have been shown to be effective countermeasures that improve CNT yield and inhibit catalyst deactivation.²⁶⁹ Etchants are chemicals that act on the surface of the catalysts, stripping unwanted elements, such as extraneous molecules, back into the surroundings. This etching process can provide a means of regulating the degree of coverage on the surface, extending the lifetime of the nanoparticles. To this end, atomistic simulations have been effective at elucidating the dynamics of the etching process. In their studies of the role played by sulfur, Orbán and Höltzl⁸⁴ used DFT to show that sulfur not only reduces the binding strength between the growing carbon cap and the iron nanoparticles to help carbon cap lift-off, as discussed in section 5.1, but also inhibits catalyst deactivation, allowing for longer, sustained growth. In this case, sulfur was demonstrated to be an effective surrounding etchant at removing surface impurities on the catalyst. Later, they explored the adsorption behavior of acetylene and ethylene on floating iron catalysts during the initial stages of CNT growth in FCCVD⁷⁴ with DFT. They tested various adsorption configurations on iron clusters and evaluated sulfur's effect on adsorption. Their key finding was that sulfur coverage significantly weakens the adsorption of both acetylene and ethylene and inhibits the buildup of graphitic carbon at lower temperatures, preventing carbon encapsulation. At higher temperatures, sulfur then evaporates from the surface, enabling CNT formation and growth. Overall, sulfur was shown to prevent catalyst deactivation during the early stages of CVD by reducing carbon encapsulation, while high sulfur content could slow carbon cap formation, preventing catalyst deactivation for the higher-temperature later stages in reactors. Yadav et al.²⁷⁰ and Lei et al.¹⁴ also applied DFTB simulations and revealed that hydrogen in the environment could act as an etching agent to strip amorphous carbon from catalyst surfaces, preventing catalyst encapsulations. Kimura et al.⁶⁷ further demonstrated this effect with water-based radicals OH and H. Hu et al.²⁴³ also applied DFT to investigate why environmental Cl and H₂O in the medium extends CNT lengths by 731% in their reactors. They showed that H₂O was enabling the etching process and extending catalyst lifetimes, and that Cl greatly facilitates the decomposition of precursors.

5.3.2 Growth termination by structural change of catalysts. Another common route for catalyst deactivation is the sintering of particles, in which multiple smaller particles merge into a single larger particle. Sintering can proceed through two primary mechanisms: Ostwald ripening (OR) and particle migration and coalescence (PMC).²⁷¹ OR involves the direct transfer of molecules from one catalyst particle to another, while PMC arises from the Brownian motion of particles that eventually collide and merge. Both processes are thermodynamically favorable; when small particles unite into a larger one, the total surface-area-to-volume ratio decreases, improving the system's overall stability. Because a cluster's surface is at a higher energy state than its interior, coalescence helps minimize the free energy at equilibrium. In practice, both OR and PMC occur simultaneously, resulting in an overall aggregation of catalysts over time. This process has been extensively studied in the field of heterogeneous catalysis, as summarized in several reviews.^272,273 In carbon nanotube synthesis, this process is known to impede CNT output in substrate-supported conditions. In their experimental study, Navas et al.²⁶¹ applied in situ Raman spectroscopy to observe the growth termination process of CNTs directly. They deduced that OR dominated for small-diameter tubes and carbon poisoning for larger-diameter tubes. Additionally, OR has also been observed directly through in situ TEM.^274,275

While the influence of sintering can be observed experimentally, quantum chemistry has been used to describe the process in more detail. Börjesson et al.²⁷⁶ used DFT to demonstrate the termination of CNT growth in vertically aligned forests due to OR. They demonstrated that under nanotube-free conditions, there is greater stability in one large catalyst than two smaller ones. As a result, there is a trend of smaller particles merging into larger ones. However, when CNTs are attached at the ends of the catalysts, there must be cleavage of one nanotube from its catalyst before the particles can converge. This cleavage process acts as an energy barrier to particle sintering. Thus, the combined decrease in energy from agglomerating the particles must be greater than the energy barrier associated with the cleavage of the nanotube on the smaller catalyst. It was found that different chiralities of nanotubes exhibited different energy barriers, resulting in chirality-selective OR. Breaching into larger scales, Wang et al.²⁷⁷ developed a modeling framework that combines DFT, kMC, and machine learning methods (see Fig. 17). They then applied this model to the heterogeneous catalysis Pd–Co system commonly found in catalytic converters. First, they used DFT data to train Hamiltonian machine learning models capable of rapidly predicting the energy of a given atomic configuration. An active learning loop retrained the Hamiltonian iteratively based on newly discovered low-energy structures, as shown in Fig. 17(a). These models were then integrated into a kMC algorithm, Fig. 17(c), to obtain timescales and size distributions, and they were coupled to a cluster genetic algorithm to identify the lowest-energy structures, Fig. 17(b). By applying this framework, the authors obtained adequate modeling of lattice structure and adsorption sites (see Fig. 17(d)–(f)), gaining mechanistic insights into the sintering of Pd catalysts and estimations of the timescales for sintering at various temperatures. They determined that sintering can happen at room temperature and occurs from both single and multi-atom diffusion. The adsorption process of CO actively modified the catalyst structure, exposing more surface area adjacent to the substrate interface where CO is more readily adsorbed. Although the approach was not applied to CVD conditions, it effectively harnesses quantum chemistry for structural exploration and rate predictions while circumventing computational bottlenecks—and could, therefore, be adapted for carbon nanotube growth.

Fig. 17 The multi-scale modeling framework developed by Wang et al. to study the sintering of Pd catalysts at various conditions.²⁷⁷ (a) An iteratively trained ML-based Hamiltonian calculation. (b) Structure optimization using Monte-Carlo based approach. (c) Structure dynamics evaluated using kMC – gray: C, red: O, light yellow: Ce, cyan: Pd. (d) Visualization of Pd on CeO₂ catalyst. (e) Lattice of the bare Pd sites. (f) Lattice of the Pdn–CO. CO adsorption sites are denoted by type as top, bridge, or hollow and the corresponding neighboring Pd layer numbers.

Several works have also included termination effects from coalescence in computational studies bridging larger scales. Gakis et al. modeled catalyst sintering¹⁶³ in their reacting-CFD simulations of SCCVD. They later extended their model to FCCVD conditions.¹⁴⁹ There, they showed that lower near-wall velocities and higher flow temperatures resulted in the collision of and subsequent coalescence of nanoparticles. Meanwhile, increased carbon precursor supply to the flow increased the coverage of catalyst active sites, decreasing the availability of iron nanoparticles to converge. This reduced nanoparticle size and decreased overall CNT generation, which aligned with experiments. These results demonstrate the coupling between the encapsulation of the catalyst with amorphous or graphitic carbon and the coalescence of the catalysts themselves.

Overall, the computational modeling of growth termination in CNT synthesis remains an underexplored area, particularly regarding mechanisms like catalyst poisoning and sintering. While many studies have focused on the nucleation and elongation phases, the precise termination mechanisms, which are crucial for determining CNT quality and yield, have not received comparable attention. Recent advances in machine learning have raised the possibility of bridging this gap by extending the effective timescale of MD simulations and reducing the computational cost of incorporating a more detailed catalyst environment, including adsorbing species and interactions between adjacent catalysts. These innovations offer promising avenues to more accurately model catalyst deactivation processes, providing deeper insights into the termination dynamics that ultimately dictate CNT growth behavior.

5.4 Chirality-controlled growth

Chirality is very important for specific applications of CNT such as electronics, optoelectronics, and biomedical imaging, owing to CNT's tunable semiconductivity or metallic behaviors depending on its chirality. To control the chirality with the guidance from the modeling side, researchers have developed some theories to understand the phenomena of selective growth of CNTs.

Chirality is primarily assigned during the nucleation stage.^91,281 After nucleation, reactor-scale production of chirality-pure nanotubes may be achieved by modulating the rates at which different chiralities grow and terminate. Thus, even if chiralities are uniformly distributed and fixed after the initial nanotube nucleation stage, the overall production output may be controlled, resulting in a high purity of reactor production overall. As overviewed in Sec. 5.2.2, various kinetic growth theories, such as the screw-dislocation model,¹⁵¹ the universal kinetic model developed by Otsuka et al.,¹⁵² and kMC predictions by Förster et al.¹²¹ suggest methods in which this may be achieved.

Early work captures the difference in CNT growth rate of various chiralities by computational models.²⁸² According to the structural observation of carbon nanotubes as a stack of carbon rings, the screw-dislocation of crystal growth is adapted to CNT growth very early.¹⁵¹ For chiral CNTs, a screw dislocation provides a non-barrier path for the sequential accretion of carbon atoms along the spiral ladder of tube lattice while the addition of a whole ring has a large energy barrier; thus the growth rate should be proportional to the magnitude of the Burgers vector of such dislocation and ultimately the chiral angle,²⁸³ which in short suggests overall dominance of near-armchair chirality.

To understand clearly the growth rate dependence, one study²⁸⁴ suggests that both kinetic and thermodynamic aspects of CNT growth should be considered, and summarizes the selective growth as a competition between energetic preference towards achiral and the faster growth kinetics of chiral CNTs. This work also extends to the kinetic side to take into account thermal fluctuation-induced screw dislocations. In general, the combination of thermodynamic and kinetic aspects results in a growth rate preference on the near-zigzag chiralities.

The concept of screw dislocation theory is also extended to take into account the etching agent-dependent growth on solid catalyst particles,¹⁹ or chirality assignment on liquid catalysts,¹⁸ or chemisorption strength of precursors on the catalyst surface.¹⁴⁴ In the future, screw-dislocation theory can be further modified by adjusting the preconditions of the current model¹⁸ one by one, such as adjusting the concentration level of etching agents, and modeling lifetimes and nucleation probabilities of different chiralities in detail.

Besides all the variations of screw-dislocation theory, researchers²⁷⁸ also analyzed the chirality-controlled growth by Diels–Alder chemistry. Diels–Alder cycloaddition from a ring-like structure has inspired researchers to control the chirality by providing chirality-defined templates, and ample energy analysis was provided.²⁸⁵ In the future, it is expected that Diels–Alder chemistry can be integrated with screw-dislocation theory to provide a unified growth mechanism.

Since selective etching strategy is mostly related to the termination stage, and commonly molecular seeding and catalyst design strategies both play a role in the nucleation stage, here instead of categorizing research into methods proposed in ref. 18, we categorize the attempts to control chiralities based on the intervention stage during growth, which are nucleation, elongation, and termination. In Fig. 18, we list the elements of screw-dislocation theory and Diels–Alder chemistry, and chirality control strategies during nucleation, elongation, and termination stages.

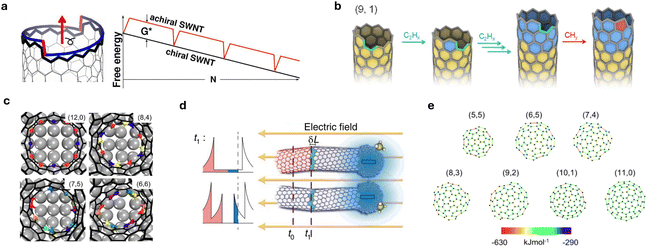Fig. 18 Models for chirality-controlled CNT growth. (a) The (n,2) chirality CNT tube has 2 dislocations, where the addition of carbon atom does not require the free energy difference G* on the right, as demonstrated in screw-dislocation theory.¹⁵¹ (b) Atomic illustration of chirality-dependent SWCNT growth via Diels–Alder cycloaddition processes on (9,1) chirality CNT edge.²⁷⁸ (c) The optimized structures of (12,0), (8,4), (7,5), and (6,6) SWCNTs on a WC(100) surface to demonstrate the symmetry matching of tube and catalyst surface in nucleation stage.²⁷⁹ (d) Chiralities shift in elongation stage, controlled by the external electric field induced electrostatic energy difference between m-SWCNT (top) and s-SWCNT (bottom) at time t₁.²⁸⁰

We also noted that diameter or curvature of carbon nanotubes is critical in applications such as catalysis by inducing localized electric field to tune the activity of catalysts,^286,287 and semiconductors by tuning bandgap that determines electrical properties.²⁵⁷ However, simulation towards phenomena induced by different curvature is hard. We are hopeful that the methodology development in chirality-controlled CNT growth can benefit this field as well.

5.4.1 Chirality control in nucleation stage. Experimentally, years of development of catalyst design guided by symmetry matching²⁸⁸ has offered up to 97% (14,4) CNT with W₆Co₇,²⁸⁹ 92% (12,6) CNT with W₆Co₇,²⁹⁰ 90% (12,6) CNT with Mo₂C,⁷³ and 96% (6,5) CNT with NiSnFe⁷⁰ by direct synthesis as exemplary cases. Besides structural matching, to explain the selectivity of (12,6) on W₆Co₇/Mo₂C and (8,4) on WC catalysts, authors²⁷⁹ have explored in two more directions: how kinetics eliminates undesired chirality during growth and how the catalyst particle size further narrows down candidate chiralities, which extends more possibility to control the chirality from the nucleation stage. Recent results⁴⁴ revealed that defect formation and tube–catalyst interface configuration shift very often occur during the nucleation stage, which could potentially be a new direction for chirality control during the nucleation stage.

It is also possible to skip the nucleation stage by providing predefined chirality segments as molecular seeding. Liu et al.²⁷⁸ experimented with prepared molecular seeds to clone their chirality and observed that different chiralities have different growth rates and active lifetimes, which in turn determines the portion of each chirality in the final product. Additionally, they explained the growth rates as being proportional to the number of active sites on the reactive edge by Diels–Alder chemistry. This approach isolated elongation and termination from nucleation to better observe the difference of growth rate and active lifetime of nanotubes, respectively.

5.4.2 Chirality control in the elongation stage. The nucleation probability is combined with growth rate to determine a final chirality distribution of nanotubes.²⁸⁴ A natural methodology is to make the nucleation probability of single chirality equal to 1; that is to say, use a chirality-defined segment of CNTs and start continual growth with this. Based on this, molecular seeding was considered as the way to control chirality.^278,291,292 However, molecular seeding or cloning methods are faced with common challenges in efficiency, purity, precise control of the tube structure and seed supply.⁹

Meanwhile, the concept that CNTs are able to grow with well-defined chiralities was not validated in atomistic simulation for a significant amount of time.^93,215 This indicates that there is some space for manipulating the chirality or diameter of carbon nanotubes during the growth process. We categorize existing attempts to change chirality during elongation into three methods: temperature, feedstock, and external fields.

The concept of the possibility of changing chirality during growth can find evidence in an early paper⁹³ adopting hybrid ReaxFF and force-biased kMC to show that the self-healing process can happen along with the chirality shift during the elongation phase. Firstly, the influence of environmental temperature during elongation has been studied.²⁹³ Experimentally, in one study,²⁸⁸ researchers successfully shifted the chirality along the elongation process by setting the temperature to be periodically changing so that an energetically preferred SWCNT–catalyst interface could be built up.

Yakobson and Bets²⁹⁴ also pointed out that the chirality can be controlled by precisely manipulating feedstock supply heights. This strategy is based on growth rate differences across different chiralities. Using prospective experiments guided by the strategy, this strategy can also discover the intrinsic functional relationship between the growth speed of each CNT type and its chirality by moving the localized reaction zone; only those chiralities that are able to keep up will still grow.

The elongation process can also be controlled by periodically changing the external electric field.^257,280,295 Wang et al.²⁸⁰ demonstrated that the electro-renucleation approach twists the chirality of the CNTs to produce nearly defect-free semiconducting CNTs horizontally aligned on the substrate with less than 0.1% residual metallic CNT. DFT calculation indicates that when the negative electric field is applied, the renucleation energy barrier of m-CNT to s-CNT (m → s) is lower than that of m-CNT to m-CNT (m → m); and the barrier of s-CNT to s-CNT (s → s) is lower than that of s-CNT to m-CNT (s → m), so that the shifted chiralities remain semiconducting. Recently a new method based on EEF, low work function electrode and high permittivity environment to control the chirality has been proposed as remote contact catalysis,²⁵⁷ which further enlarges the energy difference between s- and m-SWCNTs with mild EEF intensity and achieves 99.92% semiconducting CNTs selectivity and a narrow diameter range. The presence of an external electric field opens a new route for the synthesis of CNTs and is surely worth exploration given that its theoretical upper limit, as suggested in ref. 257, is well beyond the large-scale electronic fabrication requirement.

5.4.3 Chirality control in the termination stage. The lifetime of the growing nanotubes influences the abundance of the chirality in the final product because the final grown product relies on the multiplication amount of nucleated CNTs and lifetime of each CNT. The termination of CNT growth is highly influenced by the encapsulation of the catalyst and dysfunction of catalysts. In order to control the exposed active sites on the catalyst surface, researchers¹⁸ used sufficient feedstock and gradually increased the feedstock; (2n,n) selectivity can be enhanced without etchant's presence.

Originally the etchant was used to remove amorphous carbon on the catalyst surfaces to maximize the utility of catalyst particles.¹⁷¹ However, experimental evidence indicates it reshapes the chirality distribution.²⁹⁶ Etchants like water, ammonia, or acetone are found to act differently with CNTs with various chiralities,^66,67,297 so that adding an etchant in the growth environment is an approach for controlled growth during the termination stage. DFT computation is suitable for the study of etchant effects by providing an accurate reactivity evaluation of CNT edges.

The catalyst particles are prone to clustering together and breaking favorable surfaces for catalytic growth possibly due to a phenomenon named Ostwald ripening. Borjesson et al.²⁷⁶ explained chirality-specific Ostwald ripening using results from DFT calculations. They confirmed that the energetically favorable convergence of particles is inhibited by a CNT–catalyst cleavage event that must occur in the smaller particle. The adhesion energy of zigzag CNTs to the catalyst is stronger than the adhesion energy of armchair CNTs, and therefore zigzag CNTs have a more significant barrier to Ostwald ripening. The authors identified regimes where Ostwald ripening would occur for armchair CNTs and not zigzag CNTs, resulting in the termination of growth of any absorbed catalysts of armchair CNTs and the continued growth of any remaining zigzag CNTs. Even for the remaining armchair CNTs, their larger catalyst clusters would solidify, potentially terminating growth anyway.

5.5 Dynamic behaviors and active sites of catalyst nanoparticles

Heterogeneous catalysts often exhibit structural transformations that directly influence their catalytic activity.²⁹⁸ These active structures may dynamically interconvert among multiple configurations with low energy barriers. Operando characterization techniques have been instrumental in elucidating the dynamic atomic and electronic structures of these catalysts under actual working conditions, enhancing our understanding of interfacial behaviors and catalytic mechanisms.¹³⁸ Despite these advancements, theoretical models capable of simulating these operando conditions accurately remain underdeveloped. Existing models often oversimplify these conditions, and are still unable to fully reflect the complexity of the catalytic processes accurately.²⁹⁹ Addressing this challenge requires a multiscale computational approach that integrates various physical and chemical methodologies to develop a comprehensive operando model.

In the specific context of CNT synthesis, significant interactions at the tube–nanoparticle and nanoparticle–substrate interfaces introduce dynamic effects that are crucial during the synthesis process.²³ Numerous in situ characterizations of catalysts have documented the dynamic evolution of catalyst nanoparticles under various conditions and types of catalysts.³⁰⁰ Historically, theoretical research did not adequately address these dynamic effects.^36,68,284 However, recent shifts in research focus now spotlight the structural dynamics of the catalyst nanoparticles themselves. Contemporary theoretical investigations employ a range of approaches for deeply analyzing these dynamics. In this section, we discuss these recent advancements, highlighting the interplay between carbon incorporation and the dynamic structural changes of the catalyst, as well as the identification of active sites in the CNT growth process.

5.5.1 Mutual impacts between carbon incorporation and dynamic catalyst structure. There are multiple factors that trigger the dynamic evolution of catalyst structures, including temperature-driven restructuring of surfaces and interfaces, gas environment-driven restructuring, surface reaction-driven restructuring of catalyst surfaces, and restructuring driven by strong metal–support interactions.²⁹⁹ CNT growth via CVD is a typical thermo-catalytic process, characterized by complex atmospheres and potential metal–support interactions, which all contribute to the structure and phase transformation of the catalyst.²⁹ Among these factors, current research mostly focuses on the interactions between carbon nanotubes and the growth interfaces of catalyst nanoparticles. This is partly due to the strength and significant impact of these interactions, and also because modeling other factors involves simulations on a larger scale, which are comparatively more challenging.

Firstly, during the interaction between the tube/cap and the nanoparticle, not only does the shape of the catalyst itself undergo significant changes, but the structure of the carbon caps also varies compared with their stand-alone optimized structures. For example, Wang et al.³⁰² employed spin-polarized DFT calculations to study the interaction between a fully relaxed Ni₅₅ metal cluster and nanotubes with different chiral indices during the early stage of growth. Their calculations revealed that the carbon–carbon bond length at the end-edges of the nanotubes changes significantly compared with that of free-standing carbon caps. In contrast, the C−C bond length of the non-edge carbon atoms undergoes only minor changes. The increase in the C−C bond length at the end-edge indicates that these sites become more reactive when interacting with the Ni cluster. Additionally, they found that Ni atoms closest to the Ni−C interface deviate from their original positions, likely due to the stronger Ni−C interaction compared with the Ni−Ni interaction.

In addition to configurational changes, the interaction between nanoparticles and CNTs significantly alters the electronic distribution within the cluster, thereby affecting the reactivity of key sites. For example, Gomez-Ballesteros and Balbuena⁷⁵ utilized DFT and MD simulations on model metallic and carburized Ni clusters. Their results clearly revealed that carburized Ni nanoparticles exhibit dynamic evolution during the pre-growth and growth stages of CNTs. In the absence of a substrate, the nanocatalyst fails to maintain a defined faceted structure. Most importantly, a charge transfer process occurs from surface Ni atoms and rim C atoms to the interfacial region between the growing nanotube and the nanoparticle, as shown in Fig. 19(a). This transfer creates an electron-rich interfacial area and electron-depleted zones near the nanotube rim, potentially facilitating continued growth and defect healing. Surface Ni atoms in carburized nanoparticles are positively charged, while those in pure nanoparticles remain neutral, suggesting that carburized nanoparticles may provide a more reactive environment for nanotube growth. Additionally, Wang et al.³⁰² also found that electronic charges are primarily depleted from the Ni atoms closest to the Ni−C interface toward the end-edge carbon atoms of carbon caps. The charge transfer at the Ni₅₅−Cap interfaces exhibits patterns associated with the end-edge structure of carbon caps. Their HOMO–LUMO gap becomes negligible, suggesting that SWCNT growth would be much more efficient on Ni clusters as compared with growth without a metal catalyst.

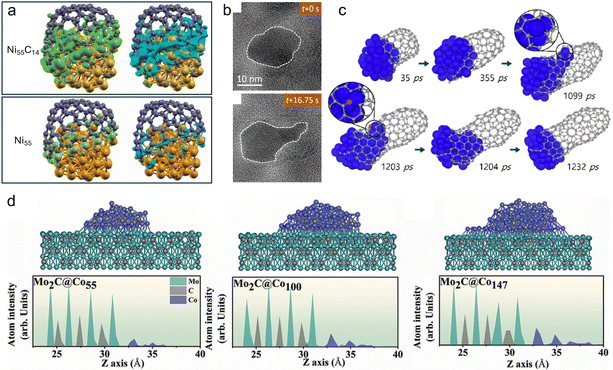Fig. 19 Recent computational works on the dynamic catalyst structure. (a) Charge density difference analysis for Ni₅₅C₁₄ and Ni₅₅ nanoparticles in contact with a nanotube cap with chiral indexes (9,6).⁷⁵ Green regions correspond to electron accumulation. Blue regions correspond to electron depletion. (b) Sequential TEM images showing periodic elongation/contraction of the catalytic particle.¹⁵ (c) Trajectory of the MD simulation of CNT growth showing the elongation/contraction dynamics of the catalyst particle due to the formation and healing of a single-vacancy defect in the CNT wall.¹⁵ (d) Atomic distribution ofMo₂C@Co₅₅, Mo₂C@Co₁₀₀, and Mo₂C@Co₁₄₇ during deposition of the C atoms. The green, grey, and blue spheres represent the Mo, C, and Co atoms, respectively. The results show that a drastic structural fluctuation of the NPs occurs during the nucleation of SWCNTs.³⁰¹

The intrinsic reasons behind the dynamic structural evolution of catalyst nanoparticles have recently become a focal point for researchers. This issue is crucial, not only for understanding the core mechanisms involved, but also for guiding the design of more stable catalysts in engineering applications. Fan et al.¹⁵ conducted in situ structural characterization and theoretical calculations of alloy catalysts, specifically a Ni–Co alloy, during the growth process of CNTs, as shown in Fig. 19(b) and (c). They proposed that the cyclic generation and healing of defects in the CNT wall offer a plausible explanation for the observed dynamics of the particle structure during experimental observations. More specifically, the MD simulations showed that interaction between several Ni atoms and a single-vacancy defect in the tube wall leads to the “elongation” of the catalyst particle as the tube grows. Conversely, when the defect is repaired by the addition of a carbon atom, the catalyst particle reverts to a spherical shape. DFT calculations further revealed that the appearance of a defect site in the graphitic wall increases the binding energy between the catalyst and the graphitic wall by approximately 3–7 eV per defect site. This strong interaction prompts the “elongation” of the catalyst particle concurrent with tube growth. The presence of the catalyst facilitates the supply of carbon to the defective site, effectively healing the defect and significantly reducing the binding energy between the catalyst and the tube wall. Once the defects in the tube wall are healed, the binding between the wall and the metal particle weakens, falling below the particle deformation energy, thus initiating particle contraction.

Chen and colleagues have explored an alternative perspective on the dynamic evolution of catalyst particles in recent computational works.^301,303 They examined the initial stages of CNT growth using Mo nanoparticles.³⁰³ They discovered that these nanoparticles alternate between solid and semi-liquid phases during the gradual deposition of carbon atoms, even though the deposition temperature remained well below the melting point of the nanoparticles. They proposed that this transformation was driven by the elastic strain within the nanoparticles, which could be influenced by the presence of carbon atoms. This means that the formation of a semi-liquid phase in Mo₅₅CN NPs is an intrinsic mechanism for dynamic structural evolution in these catalysts. Furthermore, by analyzing the evolution mechanism of solid Co nanoparticles during the nucleation process of SWCNTs through MD simulations,³⁰¹ they observed significant structural fluctuations in the nanoparticles as shown in Fig. 19(d). This fluctuation was attributed to elastic strain energy, and further findings suggested that the surface energy of the nanoparticles can be altered by the presence of a carbon gradient between the subsurface and interior of the nanoparticle. Adjusting the carbon feeding rate could reduce this carbon gradient. These insights provide opportunities to develop solid catalysts with stable structures during the nucleation reaction by modifying experimental parameters.

Although the recent studies summarized here do not cover every significant issue, they clearly demonstrate the research community's focus on this topic. With the ongoing development of computational resources and the continuous improvement of computational methods, we anticipate that future computational chemistry research will provide deeper insights into the growth processes of CNTs from the perspective of catalyst dynamics. A key issue to be addressed is how to integrate additional factors such as the atmosphere (especially etching agents and carbon sources), temperature, and other environmental conditions into the computational framework. This integration is crucial for elucidating the actual synthesis processes and guiding the development of targeted synthetic techniques.

5.5.2 Identification of active sites in the CNT growth process. While the general role played by metal catalyst nanoparticles in the growth of CNTs is broadly understood, the microscopic mechanisms and crucial active sites remain unclear.²⁴⁴ A significant point of contention in the field is whether the active state of the catalyst is metallic or carbide, as experimental results have shown conflicting outcomes.

Yang et al.⁹ provided a comprehensive summary of various experimental studies and concluded that carbon-feeding conditions play a crucial role in determining the nature of the active catalyst species during CNT growth. Depending on the conditions of the CVD process, even the same metal can exhibit different active states. For instance, cobalt catalysts demonstrate variable behavior under different conditions. They may remain in a metallic state,³⁰⁴ convert into cobalt carbides (like Co₂C or Co₃C),²⁶⁷ or form mixed structures such as Co–Co₂C or Co–Co₃C,³⁰⁵ depending on the growth conditions and the types of support materials used. The impact of carbon-feeding conditions is particularly pronounced. The specific species of active catalyst can be significantly influenced by how the carbon is supplied in the CVD process. Environmental factors such as the gaseous atmosphere, e.g., using CO versus C₂H₂ as the carbon source,³⁰⁶ also play a critical role in determining the catalyst structures and compositions during the growth of CNTs. These insights highlight the complex interplay of factors that control the catalytic activity and the structural evolution of metal nanoparticles in nanotube synthesis.

The identification of active sites in the catalysis process for CNT growth remains elusive, with dynamic changes and fluctuations in the structure of catalyst nanoparticles playing a crucial role. Besides the experimental evidence, recent studies have increasingly utilized theoretical approaches to analyze in greater detail the relationship between active sites and the mechanisms of CNT growth.

Wang et al.¹³⁶ conducted an in situ TEM study that pinpointed orthorhombic Co₃C as the active phase of the cobalt catalyst for CNT growth. To evaluate the stability of Co₃C relative to Co₂C and metallic Co under CNT growth conditions, they investigated the free energies of these phases across varying temperatures and carbon chemical potentials using DFT calculations, as shown in Fig. 20(a). Their findings revealed that Co₃C and Co₂C exhibit similar stabilities at lower temperatures. However, as the temperature increases, the stability of the Co₃C phase grows more rapidly than that of the Co₂C phase. Consequently, they determined that the active catalytic phase is likely a fully carbonized cobalt carbide with an orthorhombic Co₃C structure. Furthermore, their calculations showed that in the orthorhombic Co₃C crystal structure, the activation energies for carbon vacancy diffusion are significantly higher than those for the bulk diffusion of carbon atoms through a liquid metal particle. This observation challenges the traditional VLS growth theory. They thus suggested an alternative mechanism where carbon atoms are primarily supplied through surface and interface diffusion, providing a new understanding of the CNT growth process.

Fig. 20 Recent computational works on the active site of CNT growth. (a) Phase diagram of cobalt carbides at different temperatures and relative chemical potentials of carbon (Δμ_C). The vertical dashed lines correspond to the carbon chemical potentials in graphite and SWCNTs with diameters of 2, 1, and 0.678 nm.¹³⁶ (b) Carbide formation energy for pure metal and alloy catalysts of different composition ratios. While the Ni–Co alloy preserves its metallic state under reaction conditions, the Ni or Co may transform to the carbide phases under the chemical potentials of the CNT growth.¹⁵ (c) Top view of the bulk diffusion process and the minimum energy path (MEP) in a Co₃W₃C solid NP; (d) top view of the surface diffusion process and the corresponding MEP in the [−110] direction for Co₃W₃C (111) plane.³⁰⁷

In contrast to previous findings, Fan et al.¹⁵ reported distinct discoveries in their work with alloy catalysts. They hypothesized that carbon atoms, produced from the dissociation of ethylene at the catalyst's exposed surface, predominantly diffuse through the bulk of the catalyst. This bulk diffusion results in the formation of cone-shaped graphene layers at the catalyst's rear surface. Their hypothesis was supported by DFT calculations, which confirmed that bulk diffusion is a more energy-efficient process compared with surface diffusion. In situ TEM observations during the growth of CNF and CNT showed that the Ni–Co alloy catalyst primarily remains in a metallic state, rather than converting to carbides. DFT calculations also demonstrated higher energy requirements for carbide formation, both monometallic and bimetallic phases, in Ni–Co alloys compared with their monometallic equivalents. Additionally, their calculations revealed that the activation energies for hydrocarbon decomposition on surfaces of Co, Ni, Ni₂Co, and Co₃C were relatively similar, ranging from 0.47 to 0.68 eV. This suggests that the metallic alloy does not inherently possess higher catalytic activity for feedstock decomposition than its monometallic or carbide counterparts. Instead, the primary advantage of using a Ni–Co alloy catalyst over monometallic catalysts lies in its ability to increase the barrier for carbide formation. This feature promotes faster bulk diffusion of carbon while in the metallic state of the alloy catalyst, leading to more efficient growth of CNTs.

In addition to the catalysts with significant dynamic structural changes previously mentioned, Wang et al.³⁰⁷ also recently conducted research on a structurally stable solid-state catalyst, specifically a Co–W–C solid alloy, to study its active sites for catalyzing the growth of CNTs. The active phase of the Co–W–C catalyst was identified as a single-phase cubic η-carbide phase, which remained stable during the CNT growth process. Based on this identification, the diffusion process was theoretically investigated, building on the experimentally determined phase structure of the active catalyst nanoparticles, as indicated in Fig. 20(c) and (d). It is important to note that they did not theoretically demonstrate the mechanism of formation of this active site structure; instead, they further calculated and analyzed the mechanisms of carbon diffusion based on experimental observations. In the solid carbide catalyst, bulk diffusion occurs through vacancy diffusion, and the activation energy for carbon diffusion is as high as 2.67 eV, which poses challenges for supporting CNT growth. The researchers used the (111) plane as a representative plane for estimating the activation energy of surface diffusion in their DFT calculations. The calculated results revealed that the activation energy for carbon surface diffusion on the (111) plane of the solid catalyst is 1.47 eV in the [−110] direction and 1.66 eV in the [−1−12] direction, ensuring an adequate supply of carbon atoms for the growth of CNTs.

Drawing from both existing experimental studies and recent theoretical advancements, a fundamental conclusion that emerges is that the types of active sites involved in the catalysis of CNT growth by metal catalysts are closely linked to the reaction conditions. The catalyst structure is subject to continuous fluctuations, making the actual CNT synthesis process microscopically highly unstable. It is therefore challenging to summarize the thermodynamic properties and kinetic characteristics of these processes with a single definitive figure. At least from a theoretical modeling perspective, these properties should be derived from statistical averages that take into account the dynamic evolution of the catalyst structure, rather than being based on an ideal, static lattice structure. This approach acknowledges the complexity and variability inherent in real-world catalytic processes.

6 Summary and future directions

The continuous advancement of computational methods has enabled significant progress in understanding the growth mechanisms of CNTs, addressing various theoretical and practical challenges. As highlighted by the numerous recent studies summarized in this review, innovative computational tools have provided new insights and reshaped our comprehension of classic models in this field. The development of these new computational methods can be summarized into three key functions.

• Accelerating computation process: advanced algorithms and high-performance computing have significantly reduced computational time, leveraging simplified methods such as DFTB³⁰⁸ and combined MD-kMC approaches,³⁰⁹ enabling the simulation of complex systems that were previously computationally prohibitive. Currently, the acceleration achieved through the integration of machine learning methods is particularly noteworthy.⁴⁴ With the support of data-driven approaches, many challenges that traditional methods struggle to address now hold the promise of groundbreaking advancements.

• Improving simulation accuracy: enhanced theoretical models and more precise computational methods have significantly improved the predictive accuracy of simulations, yielding results that closely align with experimental observations. In particular, incorporating the dynamic structures of catalysts and integrating experimental evidence for more accurate modeling of active sites have greatly enhanced our understanding of microscopic transformation processes.

• Revealing more reaction details: high-fidelity simulations have revealed complex reaction pathways and intermediate states during CNT growth, providing deeper insights into the underlying mechanisms. Compared with earlier studies, which largely focused on energy comparisons of static structures or dynamic analyses of cap formation, recent theoretical and computational research has begun to address critical reaction details, such as formation and evolution of catalyst nanoparticles,¹⁴ carbon diffusion mechanisms,¹³⁶ and autonomous defect healing.⁸⁵ These advancements are pivotal for a comprehensive understanding of CNT growth mechanisms.

From an application perspective, achieving chirality-controlled growth for high-quality CNT products and ensuring the economic and stable mass production of CNTs remain challenging. Existing computational methods, while advanced, still exhibit significant shortcomings and require further enhancement to meet these industrial demands. The current progress inspires confidence in overcoming these challenges. We outline several important directions for the future development of computational methods in CNT research, providing guidance for researchers.

• Establishing multiscale simulation systems: developing multi-scale models that bridge molecular-level mechanisms with reactor-scale simulations is crucial. Unlike most heterogeneous catalytic reactions, CNT growth lacks a microkinetic model suitable for larger-scale simulations due to its unique complexity and the historical focus on single-scale studies. Integrating molecular dynamics with continuum models will facilitate the translation of atomic-scale interactions into macroscopic phenomena, enabling more accurate and predictive reactor-scale models. In addition, we emphasize the importance of bridging the gap with experiments by integrating empirical data and validation, which will refine the models and ensure they faithfully capture real-world behavior.

• Incorporating dynamic catalyst structures and operando properties: integrating the dynamic nature of catalyst structures and their operando properties into computational models will yield parameters that more accurately reflect real synthesis conditions.³¹⁰ This approach involves accounting for the nature of active sites, the formation and dynamic evolution of catalysts, particle–substrate interactions in SCCVD, particle–particle interactions in FCCVD, and the influence of environmental factors on catalyst surface properties and macroscopic reaction characteristics. Such comprehensive models will enhance our understanding of catalyst behavior under realistic conditions.

• Developing comprehensive DFT databases and machine learning force fields: establishing extensive DFT databases that include various catalyst systems, including metal catalysts, alloy catalysts, and complex-based catalysts, is essential.³¹¹ Coupling these databases with universal machine learning force fields can significantly accelerate the exploration of CNT growth processes over extended timescales. ML techniques can expedite transition state searches and long-time dynamics simulations, as demonstrated in recent studies.^71,312,313 This acceleration enables the investigation of phenomena that are otherwise inaccessible due to computational limitations.

• Integrating generative artificial intelligence for catalyst design: leveraging generative AI models in catalyst design, in conjunction with the latest experimental advancements, offers a promising pathway to develop catalysts with superior chirality control, stability, and efficiency.³¹⁴ Such models can predict optimal catalyst compositions and structures, enhancing the selectivity and yield of CNT synthesis processes. This integration of AI and experimental data paves the way for rational catalyst design, accelerating the discovery of high-performance catalysts.

We are optimistic that the advancement of both computational methods and experimental approaches will continue to drive progress in CNT synthesis. These developments will enable CNTs to play an increasingly significant role in addressing future challenges across various fields, including energy, chemical engineering, environmental science, and medicine. The ongoing integration of cutting-edge computational techniques will not only deepen our fundamental understanding, but also facilitate the practical realization of CNT-based technologies.

Author contributions

L.W.: conceptualization, methodology, writing—original draft. N.T.: resources, visualization, writing—original draft. Z.C.: resources, visualization, writing—original draft. S.D.: funding acquisition, supervision, project administration, writing—review and editing.

Abbreviations

CNT	Carbon nanotube
SWCNT	Single-walled carbon nanotube
MWCNT	Multi-walled carbon nanotube
NP	Nano-particles
CVD	Chemical vapor deposition
SCCVD	Supported catalyst chemical vapor deposition
FCCVD	Floating catalyst chemical vapor deposition
PECVD	Plasma-enhanced chemical vapor deposition
ML	Machine learning
AI	Artificial intelligence
MLFF	Machine learning force field
GNN	Graph neural network
MLIP	Machine learning inter-atomic potential
GPU	Graphics processing unit
GAP	Gaussian approximation potential
PES	Potential energy surface
MD	Molecular dynamics
UFMC	Uniform-acceptance force-based Monte-Carlo
LJ	Lennard-Jones
AIMD	Ab initio molecular dynamics
1p	First principles
DFT	Density functional theory
PAW	Projector-augmented wave
GTO	Gaussian-type orbitals
HF	Hartree–Fock
DFTB	Density functional tight binding
kMC	kinetic Monte-Carlo
MF-MKM	Mean-field micro-kinetics model
CFD	Computational fluid dynamics
ODE	Ordinary differential equation
TEM	Transmission electron microscopy
ETEM	Environmental transmission electron microscopy
SEM	Scanning electron microscopy
XRD	X-Ray diffraction
VLS	Vapor–liquid–solid
VSS	Vapor–solid–solid
OR	Ostwald ripening
PMC	Particle migration and coalescence
ARES	Autonomous research system
SIDS	Substrate intersection and direction strategy
TS	Transition state
C	Carbon
Cl	Chlorine
Co	Cobalt
Fe	Iron
H	Hydrogen
Mo	Molybdenum
Ni	Nickel
Pd	Palladium
S	Sulfur
Sn	Tin
W	Tungsten

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work is supported by The Kavli Foundation and the Carbon Hub. LW acknowledges the financial support from the International Post-doctoral Fellowship Program of the Biomass Energy Research Center, Shanghai Jiao Tong University.

References

1. Z. Xie, E. Huang, S. Garg, S. Hwang, P. Liu and J. G. Chen, Nat. Catal., 2024, 7, 98–109.
2. K. J. Hughes, K. A. Iyer, R. E. Bird, J. Ivanov, S. Banerjee, G. Georges and Q. A. Zhou, ACS Appl. Nano Mater., 2024, 7, 18695–18713.
3. H. Ijaz, A. Mahmood, M. M. Abdel-Daim, R. M. Sarfraz, M. Zaman, N. Zafar, S. Alshehery, M. M. Salem-Bekhit, M. A. Ali and L. B. Eltayeb, et al., Inorg. Chem. Commun., 2023, 111020.
4. Y. Wu, X. Zhao, Y. Shang, S. Chang, L. Dai and A. Cao, ACS Nano, 2021, 15, 7946–7974.
5. X. Zhang, W. Lu, G. Zhou and Q. Li, Adv. Mater., 2020, 32, 1902028.
6. B. Kumanek and D. Janas, J. Mater. Sci., 2019, 54, 7397–7427.
7. A. H. Brozena, M. Kim, L. R. Powell and Y. Wang, Nat. Rev. Chem., 2019, 3, 375–392.
8. K. W. Kayang, A. H. Banna and A. N. Volkov, Langmuir, 2022, 38, 1977–1994.
9. F. Yang, M. Wang, D. Zhang, J. Yang, M. Zheng and Y. Li, Chem. Rev., 2020, 120, 2693–2758.
10. R. Zhang, Y. Zhang and F. Wei, Acc. Chem. Res., 2017, 50, 179–189.
11. Z. He, C. Zhang, Z. Zhu, Y. Yu, C. Zheng and F. Wei, Adv. Funct. Mater., 2024, 34, 2408285.
12. S. K. Soni, B. Thomas and V. R. Kar, Mater. Today Commun., 2020, 25, 101546.
13. L. W. Taylor, O. S. Dewey, R. J. Headrick, N. Komatsu, N. M. Peraca, G. Wehmeyer, J. Kono and M. Pasquali, Carbon, 2021, 171, 689–694.
14. J. Lei, K. V. Bets, E. S. Penev and B. I. Yakobson, J. Phys. Chem. Lett., 2023, 14, 4266–4272.
15. H. Fan, L. Qiu, A. Fedorov, M.-G. Willinger, F. Ding and X. Huang, ACS Nano, 2021, 15, 17895–17906.
16. Z. Wang, Q. Zhao, L. Tong and J. Zhang, J. Phys. Chem. C, 2017, 121, 27655–27663.
17. S. Lv, Q. Wu, Z. Xu, T. Yang, K. Jiang and M. He, Carbon, 2022, 192, 259–264.
18. L. Qiu and F. Ding, Acc. Mater. Res., 2021, 2, 828–841.
19. M. He, X. Wang, S. Zhang, H. Jiang, F. Cavalca, H. Cui, J. B. Wagner, T. W. Hansen, E. Kauppinen and J. Zhang, et al., Sci. Adv., 2019, 5, eaav9668.
20. E. Baraj, K. Ciahotnỳ and T. Hlinčík, Fuel, 2021, 288, 119817.
21. N. F. Dummer, D. J. Willock, Q. He, M. J. Howard, R. J. Lewis, G. Qi, S. H. Taylor, J. Xu, D. Bethell and C. J. Kiely, et al., Chem. Rev., 2022, 123, 6359–6411.
22. L. Mleczko and G. Lolli, Angew. Chem., Int. Ed., 2013, 52, 9372–9387.
23. X. Zhao, S. Sun, F. Yang and Y. Li, Acc. Chem. Res., 2022, 55, 3334–3344.
24. L. S. Salah, N. Ouslimani, D. Bousba, I. Huynen, Y. Danlée and H. Aksas, J. Nanomater., 2021, 2021, 4972770.
25. E. M. Khabushev, D. V. Krasnikov, A. E. Goldt, E. O. Fedorovskaya, A. P. Tsapenko, Q. Zhang, E. I. Kauppinen, T. Kallio and A. G. Nasibulin, Carbon, 2022, 189, 474–483.
26. A. J. Page, F. Ding, S. Irle and K. Morokuma, Rep. Prog. Phys., 2015, 78, 36501.
27. G. P. Gakis, S. Termine, A.-F. A. Trompeta, I. G. Aviziotis and C. A. Charitidis, Chem. Eng. J., 2022, 445, 136807.
28. P. Sharma, V. Pavelyev, S. Kumar, P. Mishra, S. Islam and N. Tripathi, J. Mater. Sci.: Mater. Electron., 2020, 31, 4399–4443.
29. P.-X. Hou, F. Zhang, L. Zhang, C. Liu and H.-M. Cheng, Adv. Funct. Mater., 2022, 32, 2108541.
30. B. W. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2020, 121, 1007–1048.
31. J.-P. Tessonnier and D. S. Su, ChemSusChem, 2011, 4, 824–847.
32. G. D. Nessim, Nanoscale, 2010, 2, 1306–1323.
33. F. Ding, P. Larsson, J. A. Larsson, R. Ahuja, H. Duan, A. Rosén and K. Bolton, Nano Lett., 2008, 8, 463–468.
34. S. Naha and I. K. Puri, J. Phys. D: Appl. Phys., 2008, 41, 065304.
35. D. A. Gomez-Gualdron, J. M. Beetge, J. C. Burgos and P. B. Balbuena, J. Phys. Chem. C, 2013, 117, 10397–10409.
36. Z. Xu, T. Yan, G. Liu, G. Qiao and F. Ding, Nanoscale, 2016, 8, 921–929.
37. Shambhawi, O. Mohan, T. S. Choksi and A. A. Lapkin, Catal. Sci. Technol., 2024, 14, 515–532.
38. J. T. Margraf, H. Jung, C. Scheurer and K. Reuter, Nat. Catal., 2023, 6, 112–121.
39. K. Wan, J. He and X. Shi, Adv. Mater., 2024, 36, 2305758.
40. Y. Nian, X. Huang, M. Liu, J. Zhang and Y. Han, ACS Catal., 2023, 13, 11164–11171.
41. C. Li, J. Xu, T. Qiu, Z. Sun, H. Zhang and W. Ge, Chem. Eng. J., 2023, 455, 140745.
42. D. Zhang, L. Peng, X. Li, P. Yi and X. Lai, J. Am. Chem. Soc., 2020, 142, 2617–2627.
43. D. Zhang, P. Yi, X. Lai, L. Peng and H. Li, Nat. Commun., 2024, 15, 344.
44. D. Hedman, B. McLean, C. Bichara, S. Maruyama, J. A. Larsson and F. Ding, Nat. Commun., 2024, 15, 4076.
45. R. Zhang, Y. Zhang and F. Wei, Chem. Soc. Rev., 2017, 46, 3661–3715.
46. S. Rathinavel, K. Priyadharshini and D. Panda, Mater. Sci. Eng., B, 2021, 268, 115095.
47. J. Pang, A. Bachmatiuk, I. Ibrahim, L. Fu, D. Placha, G. S. Martynkova, B. Trzebicka, T. Gemming, J. Eckert and M. H. Rümmeli, J. Mater. Sci., 2016, 51, 640–667.
48. Q. Zhang, N. Wei, P. Laiho and E. I. Kauppinen, Single-Walled Carbon Nanotubes: Preparation, Properties and Applications, 2019, pp. 99–128.
49. M. Vir Singh, A. Kumar Tiwari and R. Gupta, ChemistrySelect, 2023, 8, e202204715.
50. M. Sehrawat, M. Rani, S. Sharma, S. Bharadwaj, B. G. Falzon and B. P. Singh, Carbon, 2024, 219, 118747.
51. C. Liu and H.-M. Cheng, J. Am. Chem. Soc., 2016, 138, 6690–6698.
52. B. Liu, F. Wu, H. Gui, M. Zheng and C. Zhou, ACS Nano, 2017, 11, 31–53.
53. M. He, S. Zhang, Q. Wu, H. Xue, B. Xin, D. Wang and J. Zhang, Adv. Mater., 2019, 31, 1800805.
54. H. Amara and C. Bichara, Single-Walled Carbon Nanotubes: Preparation, Properties and Applications, 2019, 1–23.
55. X. Chen, X. Pang and C. Fauteux-Lefebvre, Carbon Trends, 2023, 12, 100273.
56. A. R. Bogdanova, D. V. Krasnikov and A. G. Nasibulin, Carbon, 2023, 210, 118051.
57. T. Mou, H. S. Pillai, S. Wang, M. Wan, X. Han, N. M. Schweitzer, F. Che and H. Xin, Nat. Catal., 2023, 6, 122–136.
58. F. Yang, H. Zhao, R. Li, Q. Liu, X. Zhang, X. Bai, R. Wang and Y. Li, Sci. Adv., 2022, 8, eabq0794.
59. M. Choe, H. Chung, W. Kim, Y. Jang, Z. Wang and Z. Lee, Carbon, 2024, 219, 118843.
60. Z. Qiu, P. Li, Z. Li and J. Yang, Acc. Chem. Res., 2018, 51, 728–735.
61. S. Ahn, M. Hong, M. Sundararajan, D. H. Ess and M.-H. Baik, Chem. Rev., 2019, 119, 6509–6560.
62. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943.
63. E. S. Kryachko and E. V. Ludena, Phys. Rep., 2014, 544, 123–239.
64. P. Makkar and N. N. Ghosh, RSC Adv., 2021, 11, 27897–27924.
65. Q. Wang, M.-F. Ng, S.-W. Yang, Y. Yang and Y. Chen, ACS Nano, 2010, 4, 939–946.
66. C. A. Eveleens, Y. Hijikata, S. Irle and A. J. Page, J. Phys. Chem. C, 2016, 120, 19862–19870.
67. R. Kimura, Y. Hijikata, C. A. Eveleens, A. J. Page and S. Irle, J. Comput. Chem., 2019, 40, 375–380.
68. Q. Yuan, H. Hu and F. Ding, Phys. Rev. Lett., 2011, 107, 156101.
69. B. Rahmani Didar and P. B. Balbuena, J. Phys. Chem. C, 2017, 121, 7232–7239.
70. S. Shiina, T. Murohashi, K. Ishibashi, X. He, T. Koretsune, Z. Liu, W. Terashima, Y. K. Kato, K. Inoue and M. Saito, et al., ACS Nano, 2024, 18, 23979–23990.
71. Q. Zhao, Y. Xu, J. Greeley and B. M. Savoie, Nat. Commun., 2022, 13, 4860.
72. M. He, Y. Magnin, H. Jiang, H. Amara, E. I. Kauppinen, A. Loiseau and C. Bichara, Nanoscale, 2018, 10, 6744–6750.
73. S. Zhang, L. Kang, X. Wang, L. Tong, L. Yang, Z. Wang, K. Qi, S. Deng, Q. Li and X. Bai, et al., Nature, 2017, 543, 234–238.
74. B. Orbán and T. Höltzl, Inorg. Chem., 2024, 63, 13624–13635.
75. J. L. Gomez-Ballesteros and P. B. Balbuena, Phys. Chem. Chem. Phys., 2015, 17, 15056–15064.
76. Q. Wu, L. Qiu, L. Zhang, H. Liu, R. Ma, P. Xie, R. Liu, P. Hou, F. Ding and C. Liu, et al., Chem. Eng. J., 2022, 431, 133487.
77. Y. Ohta, Y. Okamoto, S. Irle and K. Morokuma, ACS Nano, 2008, 2, 1437–1444.
78. Y. Wang, X. Gao, H.-J. Qian, Y. Ohta, X. Wu, G. Eres, K. Morokuma and S. Irle, Carbon, 2014, 72, 22–37.
79. M. Gruden, L. Andjeklović, A. K. Jissy, S. Stepanović, M. Zlatar, Q. Cui and M. Elstner, J. Comput. Chem., 2017, 38, 2171–2185.
80. C. Duan, Y. Du, H. Jia and H. J. Kulik, Nat. Comput. Sci., 2023, 3, 1045–1055.
81. J. T. Margraf, Angew. Chem., Int. Ed., 2023, 62, e202219170.
82. Y. Guan, D. Chaffart, G. Liu, Z. Tan, D. Zhang, Y. Wang, J. Li and L. Ricardez-Sandoval, Chem. Eng. Sci., 2022, 248, 117224.
83. A. Yamanaka, R. Jono, S. Tejima and J.-i. Fujita, Sci. Rep., 2024, 14, 5625.
84. B. Orbán and T. Höltzl, Dalton Trans., 2022, 51, 9256–9264.
85. L. Qiu and F. Ding, Small, 2022, 18, 2204437.
86. I. Kohata, R. Yoshikawa, K. Hisama, C. Bichara, K. Otsuka and S. Maruyama, arXiv, 2024, preprint, arXiv:2302.09264,  DOI:10.48550/arXiv.2302.09264.
87. L. Qiu and F. Ding, Phys. Rev. Lett., 2019, 123, 256101.
88. R. Yoshikawa, K. Hisama, H. Ukai, Y. Takagi, T. Inoue, S. Chiashi and S. Maruyama, ACS Nano, 2019, 13, 6506–6512.
89. Y. Shibuta and S. Maruyama, Chem. Phys. Lett., 2003, 382, 381–386.
90. M. J. Bronikowski, P. A. Willis, D. T. Colbert, K. A. Smith and R. E. Smalley, J. Vac. Sci. Technol., A, 2001, 19, 1800–1805.
91. F. Ding, K. Bolton and A. Rosen, J. Phys. Chem. B, 2004, 108, 17369–17377.
92. J. Zhao, A. Martinez-Limia and P. B. Balbuena, Nanotechnology, 2005, 16, S575.
93. E. C. Neyts, A. C. Van Duin and A. Bogaerts, J. Am. Chem. Soc., 2011, 133, 17225–17231.
94. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
95. G. C. Abell, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 31, 6184–6196.
96. J. Tersoff, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 6991–7000.
97. D. W. Brenner, Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 42, 9458–9471.
98. G. Zheng, S. Irle, M. Elstner and K. Morokuma, J. Phys. Chem. A, 2004, 108, 3182–3194.
99. S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486.
100. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
101. Q. Mao, M. Feng, X. Z. Jiang, Y. Ren, K. H. Luo and A. C. T. van Duin, Prog. Energy Combust. Sci., 2023, 97, 101084.
102. J. E. Mueller, A. C. T. van Duin and W. A. Goddard, III, J. Phys. Chem. C, 2010, 114, 4939–4949.
103. N. Orekhov, G. Ostroumova and V. Stegailov, Carbon, 2020, 170, 606–620.
104. Y. Liu, A. Dobrinsky and B. I. Yakobson, Phys. Rev. Lett., 2010, 105, 235502.
105. H. Amara and C. Bichara, Top. Curr. Chem., 2017, 375, 55.
106. R. Cruz-Silva, A. Morelos-Gomez, J. L. Fajardo-Diaz, J. Ryota, T. Morita, T. Yamaki, H. Otake, S. Tejima and M. Endo, Appl. Catal. O: Open, 2024, 191, 206933.
107. M. Pineda and M. Stamatakis, J. Chem. Phys., 2022, 156, 120902.
108. E. Mola, I. Irurzun, J. Vicente and D. King, Surf. Rev. Lett., 2003, 10, 23–38.
109. D. N. Theodorou, Ind. Eng. Chem. Res., 2010, 49, 3047–3058.
110. T. Mou, X. Han, H. Zhu and H. Xin, Curr. Opin. Chem. Eng., 2022, 36, 100825.
111. M. Andersen, C. P. Plaisance and K. Reuter, J. Chem. Phys., 2017, 147, 152705.
112. H. Tian and S. Rangarajan, J. Phys. Chem. C, 2021, 125, 20275–20285.
113. J. Nielsen, M. d'Avezac, J. Hetherington and M. Stamatakis, J. Chem. Phys., 2013, 139, 224706.
114. M. Leetmaa and N. V. Skorodumova, Comput. Phys. Commun., 2014, 185, 2340–2349.
115. M. J. Hoffmann, S. Matera and K. Reuter, Comput. Phys. Commun., 2014, 185, 2138–2150.
116. L. Kunz, F. M. Kuhn and O. Deutschmann, J. Chem. Phys., 2015, 143, 044108.
117. M. Jørgensen and H. Grönbeck, J. Chem. Phys., 2018, 149, 044108.
118. S. S. Akimenko, G. D. Anisimova, A. I. Fadeeva, V. F. Fefelov, V. A. Gorbunov, T. R. Kayumova, A. V. Myshlyavtsev, M. D. Myshlyavtseva and P. V. Stishenko, J. Comput. Chem., 2020, 41, 2084–2097.
119. M. Stamatakis, J. Phys.: Condens. Matter, 2014, 27, 013001.
120. J. Li, Ph.D. thesis, University of Waterloo, Waterloo, 2014.
121. G. D. Förster, T. D. Swinburne, H. Jiang, E. Kauppinen and C. Bichara, AIP Adv., 2021, 11, 045306.
122. G. D. Förster, V. Pimonov, H.-N. Tran, S. Tahir, V. Jourdain and C. Bichara, ACS Nano, 2023, 17, 7135–7144.
123. F. Zounmenou, R. Hontinfinde and F. Hontinfinde, Phys. A, 2022, 594, 127013.
124. J. Carpena-Núñez, R. Rao, D. Kim, K. V. Bets, D. N. Zakharov, J. A. Boscoboinik, E. A. Stach, B. I. Yakobson, M. Tsapatsis and D. Stacchiola, et al., Small, 2020, 16, 2002120.
125. J. Li, E. Croiset and L. Ricardez-Sandoval, J. Catal., 2015, 326, 15–25.
126. J. Adda, J. Kple and F. Zounmenou, et al., World J. Condens. Matter Phys., 2024, 14, 77–95.
127. J. Dong, L. Zhang, B. Wu, F. Ding and Y. Liu, J. Phys. Chem. Lett., 2021, 12, 7942–7963.
128. V. Dufour-Décieux, R. Freitas and E. J. Reed, J. Phys. Chem. A, 2021, 125, 4233–4244.
129. I. Kouroudis, M. Gößwein and A. Gagliardi, J. Phys. Chem. A, 2023, 127, 5967–5978.
130. Z. Chen, H. Wang, N. Q. Su, S. Duan, T. Shen and X. Xu, ACS Catal., 2018, 8, 5816–5826.
131. F. Hess, J. Comput. Chem., 2019, 40, 2664–2676.
132. A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, Nat. Catal., 2019, 2, 659–670.
133. R. Huang, Results Phys., 2024, 56, 107220.
134. R. Schlögl, Angew. Chem., Int. Ed., 2015, 54, 3465–3520.
135. Y. Bai, H. Yue, J. Wang, B. Shen, S. Sun, S. Wang, H. Wang, X. Li, Z. Xu and R. Zhang, et al., Science, 2020, 369, 1104–1106.
136. Y. Wang, L. Qiu, L. Zhang, D.-M. Tang, R. Ma, Y. Wang, B. Zhang, F. Ding, C. Liu and H.-M. Cheng, ACS Nano, 2020, 14, 16823–16831.
137. S.-H. Lee, J. Park, J. H. Park, D.-M. Lee, A. Lee, S. Y. Moon, S. Y. Lee, H. S. Jeong and S. M. Kim, Carbon, 2021, 173, 901–909.
138. A. Rajan, A. P. Pushkar, B. C. Dharmalingam and J. J. Varghese, Iscience, 2023, 26, 107029.
139. F. X. Zhu and L. Xu, Chem. Eng. Sci., 2022, 254, 117619.
140. S. Matera, W. F. Schneider, A. Heyden and A. Savara, ACS Catal., 2019, 9, 6624–6647.
141. A. Zarei and A. Farazin, J. Comput. Appl. Mech., 2024, 55, 462–472.
142. K. R. Venkatesan and A. Chattopadhyay, J. Aerosp. Eng., 2020, 33, 04020084.
143. A. Gili, L. Schlicker, M. F. Bekheet, O. Görke, D. Kober, U. Simon, P. Littlewood, R. Schomäcker, A. Doran and D. Gaissmaier, et al., ACS Catal., 2019, 9, 6999–7011.
144. N. Turaeva, Y. Kim and I. Kuljanishvili, Nanoscale Adv., 2023, 5, 3684–3690.
145. M. Grujicic, G. Cao and B. Gersten, Appl. Surf. Sci., 2002, 191, 223–239.
146. G. Yu, P. Han, H. Yi, J. Zhao, S. Hou, Z. Yan, J. Liu, H. Li, H. Zheng and C. Zhou, Diamond Relat. Mater., 2024, 145, 111093.
147. R. Qiao, X. Qiu and A. Boies, Langmuir, 2024, 40, 21460–21475.
148. A. Khrabry, I. D. Kaganovich, Y. Barsukov, S. Raman, E. Turkoz and D. Graves, Int. J. Hydrogen Energy, 2024, 56, 1340–1360.
149. G. P. Gakis, T. A. Chrysoloras, I. G. Aviziotis and C. A. Charitidis, Chem. Eng. Sci., 2024, 295, 120204.
150. A. M. Boies, C. Hoecker, A. Bhalerao, N. Kateris, J. de La Verpilliere, B. Graves and F. Smail, Small, 2019, 15, 1900520.
151. F. Ding, A. R. Harutyunyan and B. I. Yakobson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 2506–2509.
152. K. Otsuka, R. Ishimaru, A. Kobayashi, T. Inoue, R. Xiang, S. Chiashi, Y. K. Kato and S. Maruyama, ACS Nano, 2022, 16, 5627–5635.
153. A. A. Puretzky, D. B. Geohegan, S. Jesse, I. N. Ivanov and G. Eres, Appl. Phys. A, 2005, 81, 223–240.
154. M. Grujicic, G. Cao and B. Gersten, J. Mater. Sci., 2003, 38, 1819–1830.
155. K. Kuwana and K. Saito, Carbon, 2005, 43, 2088–2095.
156. A. C. Lysaght and W. K. S. Chiu, Nanotechnology, 2008, 19, 165607.
157. M. R. Hosseini, N. Jalili and D. A. Bruce, AIChE J., 2009, 55, 3152–3167.
158. M. K. Moraveji, F. S. Sokout and A. Rashidi, Int. Commun. Heat Mass Transfer, 2011, 38, 984–989.
159. M. Bedewy, B. Farmer and A. J. Hart, ACS Nano, 2014, 8, 5799–5812.
160. E. Oh, H. Cho, J. Kim, J. E. Kim, Y. Yi, J. Choi, H. Lee, Y. H. Im, K.-H. Lee and W. J. Lee, ACS Appl. Mater. Interfaces, 2020, 12, 13107–13115.
161. A. Kaushal, R. Alexander, D. Mandal, J. B. Joshi and K. Dasgupta, Chem. Eng. J., 2023, 452, 139142.
162. A. Andalouci, I. Hinkov, O. Brinza, A. Kane, C. Porosnicu, A. H. Barry, S. M. Chérif and S. Farhat, Plasma Chem. Plasma Process., 2023, 43, 757–786.
163. G. P. Gakis, S. Termine, A.-F. A. Trompeta, I. G. Aviziotis and C. A. Charitidis, Chem. Eng. J., 2022, 445, 136807.
164. Q. Dong, C. Gao, W. Bai, L. Wang, D. Chu and Y. He, Phys. E, 2025, 165, 116074.
165. F. K. A. Gökstorp and M. P. Juniper, Catalysts, 2020, 10, 1383.
166. S. A. Rashid, M. Z. A. Rashid, M. A. Musa and S. H. Othman, Asia–Pac. J. Chem. Eng., 2013, 8, 254–261.
167. C. Hoecker, F. Smail, M. Bajada, M. Pick and A. Boies, Carbon, 2016, 96, 116–124.
168. C. Gao, D. Chu, Q. Dong, X. Zhao, X. Zhang, W. Bai and Y. He, Chem. Eng. J., 2024, 488, 151017.
169. B. Safaei, H. C. How and G. Scribano, Int. J. Environ. Sci. Technol., 2023, 20, 1–10.
170. X. Rodiles, V. Reguero, M. Vila, B. Alemán, L. Arévalo, F. Fresno, V. A. d. l. P. O'Shea and J. J. Vilatela, Sci. Rep., 2019, 9, 9239.
171. K. Hata, D. N. Futaba, K. Mizuno, T. Namai, M. Yumura and S. Iijima, Science, 2004, 306, 1362–1364.
172. X. Wang, Y. Feng, H. E. Unalan, G. Zhong, P. Li, H. Yu, A. I. Akinwande and W. I. Milne, Carbon, 2011, 49, 214–221.
173. L. Yuan, K. Saito, C. Pan, F. A. Williams and A. S. Gordon, Chem. Phys. Lett., 2001, 340, 237–241.
174. B. Kitiyanan, W. E. Alvarez, J. H. Harwell and D. E. Resasco, Chem. Phys. Lett., 2000, 317, 497–503.
175. P. Nikolaev, M. J. Bronikowski, R. Bradley, F. Rohmund, D. T. Colbert, K. A. Smith and R. E. Smalley, Chem. Phys. Lett., 1999, 313, 91–97.
176. G. K. W. Kenway, C. A. Mader, P. He and J. R. R. A. Martins, Prog. Aerosp. Sci., 2019, 110, 100542.
177. L. Weller, F. R. Smail, J. A. Elliott, A. H. Windle, A. M. Boies and S. Hochgreb, Carbon, 2019, 146, 789–812.
178. H. Li, Z. Wang, N. Zou, M. Ye, R. Xu, X. Gong, W. Duan and Y. Xu, Nat. Comput. Sci., 2022, 2, 367–377.
179. W. Ji and S. Deng, J. Phys. Chem. A, 2021, 125, 1082–1092.
180. P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, npj Comput. Mater., 2016, 2, 1–6.
181. S. Singh and R. B. Sunoj, Acc. Chem. Res., 2023, 56, 402–412.
182. L. Fiedler, N. A. Modine, K. D. Miller and A. Cangi, Phys. Rev. B, 2023, 108, 125146.
183. B. A. Koscher, R. B. Canty, M. A. McDonald, K. P. Greenman, C. J. McGill, C. L. Bilodeau, W. Jin, H. Wu, F. H. Vermeire and B. Jin, et al., Science, 2023, 382, eadi1407.
184. J. W. Frenken and I. Groot, Operando research in heterogeneous catalysis, Springer, 2017, vol. 222.
185. L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Chem. Soc. Rev., 2018, 47, 8307–8348.
186. E. Pigos, E. S. Penev, M. A. Ribas, R. Sharma, B. I. Yakobson and A. R. Harutyunyan, ACS Nano, 2011, 5, 10096–10101.
187. C. Wirth, S. Hofmann and J. Robertson, Diamond Relat. Mater., 2009, 18, 940–945.
188. J. R. Pankhurst, P. Iyengar, A. Loiudice, M. Mensi and R. Buonsanti, Chem. Sci., 2020, 11, 9296–9302.
189. E. Pastor, M. Sachs, S. Selim, J. R. Durrant, A. A. Bakulin and A. Walsh, Nat. Rev. Mater., 2022, 7, 503–521.
190. X. Wu, Q. Sun, Z. Pu, T. Zheng, W. Ma, W. Yan, X. Yu, Z. Wu, M. Huo, X. Li, et al., arXiv, 2024, preprint, arXiv:2404.09452,  DOI:10.48550/arXiv.2404.09452.
191. F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264.
192. J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897.
193. X. Fu, A. Rosen, K. Bystrom, R. Wang, A. Musaelian, B. Kozinsky, T. Smidt and T. Jaakkola, arXiv, 2024, preprint, arXiv:2405.19276,  DOI:10.48550/arXiv.2405.19276.
194. X. Gong, H. Li, N. Zou, R. Xu, W. Duan and Y. Xu, Nat. Commun., 2023, 14, 2848.
195. Z. Tang, H. Li, P. Lin, X. Gong, G. Jin, L. He, H. Jiang, X. Ren, W. Duan and Y. Xu, Nat. Commun., 2024, 15, 8815.
196. Y. Wang, H. Li, Z. Tang, H. Tao, Y. Wang, Z. Yuan, Z. Chen, W. Duan and Y. Xu, arXiv, 2024, preprint, arXiv:2401.17015,  DOI:10.48550/arXiv.2401.17015.
197. Q. Gu, Z. Zhouyin, S. K. Pandey, P. Zhang, L. Zhang and W. E, Nat. Commun., 2024, 15, 6772.
198. M. Cui, K. Reuter and J. T. Margraf, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-9734b.
199. P. Hou, Y. Tian and X. Meng, Chem. – Eur. J., 2024, 30, e202401373.
200. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186.
201. H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184.
202. J. Zeng, D. Zhang, D. Lu, P. Mo, Z. Li, Y. Chen, M. Rynik, L. Huang, Z. Li and S. Shi, et al., J. Chem. Phys., 2023, 159, 054801.
203. O. T. Unke, M. Stöhr, S. Ganscha, T. Unterthiner, H. Maennel, S. Kashubin, D. Ahlin, M. Gastegger, L. Medrano Sandonas and J. T. Berryman, et al., Sci. Adv., 2024, 10, eadn4397.
204. S. Gong, Y. Zhang, Z. Mu, Z. Pu, H. Wang, Z. Yu, M. Chen, T. Zheng, Z. Wang, L. Chen, et al., arXiv, 2024, preprint, arXiv:2404.07181,  DOI:10.48550/arXiv.2404.07181.
205. J. T. Frank, O. T. Unke, K.-R. Müller and S. Chmiela, Nat. Commun., 2024, 15, 6539.
206. X. Fu, T. Xie, N. J. Rebello, B. Olsen and T. S. Jaakkola, Transactions on Machine Learning Research, 2023.
207. X. Fu, A. Musaelian, A. Johansson, T. Jaakkola and B. Kozinsky, arXiv, 2023, preprint, arXiv:2310.13756,  DOI:10.48550/arXiv.2310.13756.
208. O. T. Unke, S. Chmiela, M. Gastegger, K. T. Schütt, H. E. Sauceda and K.-R. Müller, Nat. Commun., 2021, 12, 7273.
209. K. Joll, P. Schienbein, K. M. Rosso and J. Blumberger, Nat. Commun., 2024, 15, 8192.
210. W. Jin, X. Chen, A. Vetticaden, S. Sarzikova, R. Raychowdhury, C. Uhler and N. Hacohen, bioRxiv, 2023, 2023–2012.
211. E. Qu and A. S. Krishnapriyan, arXiv, 2024, preprint, arXiv:2410.24169,  DOI:10.48550/arXiv.2410.24169.
212. V. Rein, H. Gao, H. H. Heenen, W. Sghaier, A. C. Manikas, C. Tsakonas, M. Saedi, J. T. Margraf, C. Galiotis and G. Renaud, et al., ACS Nano, 2024, 18, 12503–12511.
213. M. Kulichenko, B. Nebgen, N. Lubbers, J. S. Smith, K. Barros, A. E. Allen, A. Habib, E. Shinkle, N. Fedik and Y. W. Li, et al., Chem. Rev., 2024, 13681–13714.
214. M. A. Ribas, F. Ding, P. B. Balbuena and B. I. Yakobson, J. Chem. Phys., 2009, 131, 224501.
215. Z. Xu, T. Yan and F. Ding, Chem. Sci., 2015, 6, 4704–4711.
216. E. C.-Y. Yuan, A. Kumar, X. Guan, E. D. Hermes, A. S. Rosen, J. Zádor, T. Head-Gordon and S. M. Blau, Nat. Commun., 2024, 15, 8865.
217. L. Pattanaik, J. B. Ingraham, C. A. Grambow and W. H. Green, Phys. Chem. Chem. Phys., 2020, 22, 23618–23626.
218. C. Duan, G.-H. Liu, Y. Du, T. Chen, Q. Zhao, H. Jia, C. P. Gomes, E. A. Theodorou and H. J. Kulik, arXiv, 2024, preprint, arXiv:2404.13430,  DOI:10.48550/arXiv.2404.13430.
219. G. Ducci, M. Kouyate, K. Reuter and C. Scheurer, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-jgprs.
220. H. Shang, X. Chen, X. Gao, R. Lin, L. Wang, F. Li, Q. Xiao, L. Xu, Q. Sun, L. Zhu, F. Wang, Y. Zhang and H. Song, SC21: International Conference for High Performance Computing, Networking, Storage and Analysis, 2021, pp. 1–14.
221. J. A. Esterhuizen, B. R. Goldsmith and S. Linic, Nat. Catal., 2022, 5, 175–184.
222. Z.-H. Ji, L. Zhang, D.-M. Tang, Y.-M. Zhao, M.-K. Zou, R.-H. Xie, C. Liu and H.-M. Cheng, Carbon, 2023, 210, 118073.
223. T. Hajilounezhad, R. Bao, K. Palaniappan, F. Bunyak, P. Calyam and M. R. Maschmann, npj Comput. Mater., 2021, 7, 134.
224. D. V. Krasnikov, E. M. Khabushev, A. Gaev, A. R. Bogdanova, V. Y. Iakovlev, A. Lantsberg, T. Kallio and A. G. Nasibulin, Carbon, 2023, 202, 76–82.
225. D. Lin, S. Muroga, H. Kimura, H. Jintoku, T. Tsuji, K. Hata, G. Chen and D. N. Futaba, ACS Nano, 2023, 17, 22821–22829.
226. R. Rao, J. Carpena-Nunez and B. Maruyama, ChemRxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2023-fzv07.
227. J. Chang, P. Nikolaev, J. Carpena-Núñez, R. Rao, K. Decker, A. E. Islam, J. Kim, M. A. Pitt, J. I. Myung and B. Maruyama, Sci. Rep., 2020, 10, 9040.
228. C. Park, P. Qiu, J. Carpena-Núñez, R. Rao, M. Susner and B. Maruyama, IISE Trans., 2022, 55, 111–128.
229. L. Wang, R. Deng, R. Zhang, Y. Luo and S. Deng, Chem. Eng. J., 2024, 499, 156435.
230. R. Rao, J. Carpena-Núñez, P. Nikolaev, M. A. Susner, K. G. Reyes and B. Maruyama, npj Comput. Mater., 2021, 7, 157.
231. B. M. Everhart, R. Rao, P. Nikolaev, T.-W. Liu, D. A. Gómez-Gualdrón, B. Maruyama and P. B. Amama, Chem. Mater., 2022, 34, 4548–4559.
232. R. Waelder, C. Park, A. Sloan, J. Carpena-Núñez, J. Yoho, S. Gorsse, R. Rao and B. Maruyama, Carbon, 2024, 228, 119356.
233. Y. Chen and J. Zhang, Acc. Chem. Res., 2014, 47, 2273–2281.
234. E. Kukovitsky, S. L′vov and N. Sainov, Chem. Phys. Lett., 2000, 317, 65–70.
235. F. Yang, X. Wang, M. Li, X. Liu, X. Zhao, D. Zhang, Y. Zhang, J. Yang and Y. Li, Acc. Chem. Res., 2016, 49, 606–615.
236. A. Gohier, C. Ewels, T. Minea and M. Djouadi, Carbon, 2008, 46, 1331–1338.
237. L. S. Lobo, Carbon, 2017, 114, 411–417.
238. M. Moors, H. Amara, T. Visart de Bocarmé, C. Bichara, F. Ducastelle, N. Kruse and J.-C. Charlier, ACS Nano, 2009, 3, 511–516.
239. J. Barnard, C. Paukner and K. Koziol, Nanoscale, 2016, 8, 17262–17270.
240. K. Hisama, R. Yoshikawa, T. Matsuo, T. Noguchi, T. Kawasuzuki, S. Chiashi and S. Maruyama, J. Phys. Chem. C, 2018, 122, 9648–9653.
241. V. Jourdain and C. Bichara, Carbon, 2013, 58, 2–39.
242. U. Khalilov, C. Vets and E. C. Neyts, Nanoscale Horiz., 2019, 4, 674–682.
243. Z. Hu, X. Sun, X. Zhang, X. Jia, X. Feng, M. Cui, E. Gao, L. Qian, X. Gao and J. Zhang, J. Am. Chem. Soc., 2024, 146, 11432–11439.
244. A. J. Page, Y. Ohta, S. Irle and K. Morokuma, Acc. Chem. Res., 2010, 43, 1375–1385.
245. P. Van de Sompel, U. Khalilov and E. C. Neyts, J. Phys. Chem. C, 2021, 125, 7849–7855.
246. R. Ma, L. Qiu, L. Zhang, D.-M. Tang, Y. Wang, B. Zhang, F. Ding, C. Liu and H.-M. Cheng, ACS Nano, 2022, 16, 16574–16583.
247. C. A. Eveleens and A. J. Page, J. Phys. Chem. C, 2019, 123, 10622–10629.
248. M. Motta, A. Moisala, I. Kinloch and A. Windle, J. Nanosci. Nanotechnol., 2008, 8, 2442–2449.
249. M. Vazquez-Pufleau, R. F. Torres, L. Arevalo, N. Abomailek and J. J. Vilatela, Carbon Trends, 2024, 15, 100355.
250. M. Sharma, R. Bhatia and I. Sameera, Chem. Phys. Lett., 2024, 847, 141358.
251. L. P. Ding, B. McLean, Z. Xu, X. Kong, D. Hedman, L. Qiu, A. J. Page and F. Ding, J. Am. Chem. Soc., 2022, 144, 5606–5613.
252. K. Voelskow, M. J. Becker, W. Xia, M. Muhler and T. Turek, Chem. Eng. J., 2014, 244, 68–74.
253. H. Ma, L. Pan and Y. Nakayama, Carbon, 2011, 49, 854–861.
254. C. T. M. Kwok, B. J. Reizman, D. E. Agnew, G. S. Sandhu, J. Weistroffer, M. S. Strano and E. G. Seebauer, Carbon, 2010, 48, 1279–1288.
255. I. V. Novikov, D. V. Krasnikov, E. M. Khabushev, V. S. Shestakova, Y. E. Matyushkin and A. G. Nasibulin, Carbon, 2024, 217, 118589.
256. Q. Yuan, Z. Xu, B. I. Yakobson and F. Ding, Phys. Rev. Lett., 2012, 108, 245505.
257. J. Wang, X. Zheng, G. Pitner, X. Ji, T. Zhang, A. Yao, J. Zhu, T. Palacios, L.-J. Li and H. Wang, et al., J. Am. Chem. Soc., 2024, 146, 33064–33074.
258. J. S. Bulmer, T. S. Gspann, J. S. Barnard and J. A. Elliott, Carbon, 2017, 115, 672–680.
259. Y. Xu, Y. Ma, Y. Liu, S. Feng, D. He, P. Haghi-Ashtiani, A. Dichiara, L. Zimmer and J. Bai, J. Phys. Chem. C, 2018, 122, 6437–6446.
260. P. B. Amama, C. L. Pint, L. McJilton, S. M. Kim, E. A. Stach, P. T. Murray, R. H. Hauge and B. Maruyama, Nano Lett., 2009, 9, 44–49.
261. H. Navas, M. Picher, A. Andrieux-Ledier, F. Fossard, T. Michel, A. Kozawa, T. Maruyama, E. Anglaret, A. Loiseau and V. Jourdain, ACS Nano, 2017, 11, 3081–3088.
262. D. N. Futaba, K. Hata, T. Yamada, K. Mizuno, M. Yumura and S. Iijima, Phys. Rev. Lett., 2005, 95, 56104.
263. E. R. Meshot and A. J. Hart, Appl. Phys. Lett., 2008, 92, 113107.
264. L. Zhang, M. He, T. W. Hansen, J. Kling, H. Jiang, E. I. Kauppinen, A. Loiseau and J. B. Wagner, ACS Nano, 2017, 11, 4483–4493.
265. S. Maruyama, E. Einarsson, Y. Murakami and T. Edamura, Chem. Phys. Lett., 2005, 403, 320–323.
266. M. Stadermann, S. P. Sherlock, J.-B. In, F. Fornasiero, H. G. Park, A. B. Artyukhin, Y. Wang, J. J. De Yoreo, C. P. Grigoropoulos, O. Bakajin, A. A. Chernov and A. Noy, Nano Lett., 2009, 9, 738–744.
267. L. Zhang, M. He, T. W. Hansen, J. Kling, H. Jiang, E. I. Kauppinen, A. Loiseau and J. B. Wagner, ACS Nano, 2017, 11, 4483–4493.
268. Q. Jiang, F. Wang, R. Li, B. Li, N. Wei, N. Gao, H. Xu, S. Zhao, Y. Huang, B. Wang, W. Zhang, X. Wu, S. Zhang, Y. Zhao, E. Shi and R. Zhang, Nano Lett., 2023, 23, 523–532.
269. N. Yoshihara, H. Ago and M. Tsuji, J. Phys. Chem. C, 2007, 111, 11577–11582.
270. M. D. Yadav and K. Dasgupta, Ind. Eng. Chem. Res., 2021, 60, 2187–2196.
271. T. W. Hansen, A. T. DeLaRiva, S. R. Challa and A. K. Datye, Acc. Chem. Res., 2013, 46, 1720–1730.
272. X. Duan, Y. Han, B. Zhu and Y. Gao, Mater. Today Catal., 2023, 3, 100032.
273. M. Rahmati, M.-S. Safdari, T. H. Fletcher, M. D. Argyle and C. H. Bartholomew, Chem. Rev., 2020, 120, 4455–4533.
274. M. Bedewy, B. Viswanath, E. R. Meshot, D. N. Zakharov, E. A. Stach and A. J. Hart, Chem. Mater., 2016, 28, 3804–3813.
275. S. M. Kim, C. L. Pint, P. B. Amama, D. N. Zakharov, R. H. Hauge, B. Maruyama and E. A. Stach, J. Phys. Chem. Lett., 2010, 1, 918–922.
276. A. Börjesson and K. Bolton, ACS Nano, 2011, 5, 771–779.
277. Y. Wang, J. Kalscheur, Y.-Q. Su, E. J. M. Hensen and D. G. Vlachos, Nat. Commun., 2021, 12, 5430.
278. B. Liu, J. Liu, X. Tu, J. Zhang, M. Zheng and C. Zhou, Nano Lett., 2013, 13, 4416–4421.
279. X. Wang and F. Ding, J. Phys. Chem. Lett., 2019, 10, 735–741.
280. J. Wang, X. Jin, Z. Liu, G. Yu, Q. Ji, H. Wei, J. Zhang, K. Zhang, D. Li and Z. Yuan, et al., Nat. Catal., 2018, 1, 326–331.
281. A. G. Tefera and M. D. Mochena, Carbon, 2014, 67, 198–202.
282. H. Dumlich and S. Reich, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 085421.
283. F. Ding and B. I. Yakobson, 2010 3rd International Nanoelectronics Conference (INEC), 2010, p. 168.
284. V. I. Artyukhov, E. S. Penev and B. I. Yakobson, Nat. Commun., 2014, 5, 4892.
285. E. H. Fort and L. T. Scott, J. Mater. Chem., 2011, 21, 1373–1381.
286. J. Su, C. B. Musgrave III, Y. Song, L. Huang, Y. Liu, G. Li, Y. Xin, P. Xiong, M. M.-J. Li and H. Wu, et al., Nat. Catal., 2023, 6, 818–828.
287. B. Wang, M. Wang, Z. Fan, C. Ma, S. Xi, L.-Y. Chang, M. Zhang, N. Ling, Z. Mi and S. Chen, et al., Nat. Commun., 2024, 15, 1719.
288. Q. Zhao, Z. Xu, Y. Hu, F. Ding and J. Zhang, Sci. Adv., 2016, 2, e1501729.
289. F. Yang, X. Wang, J. Si, X. Zhao, K. Qi, C. Jin, Z. Zhang, M. Li, D. Zhang and J. Yang, et al., ACS Nano, 2017, 11, 186–193.
290. F. Yang, X. Wang, D. Zhang, J. Yang, D. Luo, Z. Xu, J. Wei, J.-Q. Wang, Z. Xu and F. Peng, et al., Nature, 2014, 510, 522–524.
291. J. Liu, C. Wang, X. Tu, B. Liu, L. Chen, M. Zheng and C. Zhou, Nat. Commun., 2012, 3, 1199.
292. J. Tomada, T. Dienel, F. Hampel, R. Fasel and K. Amsharov, Nat. Commun., 2019, 10, 3278.
293. H.-B. Li, A. J. Page, S. Irle and K. Morokuma, J. Phys. Chem. Lett., 2013, 4, 3176–3180.
294. B. I. Yakobson and K. V. Bets, Sci. Adv., 2022, 8, eadd4627.
295. Z. Liu, J. Wang, K. Zhang, X. Gao, P. Liu, Q. Li, L. Zhang, S. Fan, J. Kong and K. Jiang, J. Am. Chem. Soc., 2021, 143, 17607–17614.
296. B. Liu, H. Jiang, A. V. Krasheninnikov, A. G. Nasibulin, W. Ren, C. Liu, E. I. Kauppinen and H.-M. Cheng, Small, 2013, 9, 1379–1386.
297. S. Y. Moon and W. S. Kim, Chem. Commun., 2019, 55, 13888–13891.
298. X. Shi, X. Lin, R. Luo, S. Wu, L. Li, Z.-J. Zhao and J. Gong, JACS Au, 2021, 1, 2100–2120.
299. F. Tao and M. Salmeron, Science, 2024, 386, eadq0102.
300. R.-H. Xie, L. Zhang, R. Ma, X.-Y. Jiao, D.-M. Tang, C. Liu and H.-M. Cheng, Nano Res., 2023, 16, 12781–12787.
301. X. Chen, H. Duan and B. Cao, Small, 2024, 20, 2310543.
302. Q. Wang, H. Wang, L. Wei, S.-W. Yang and Y. Chen, J. Phys. Chem. A, 2012, 116, 11709–11717.
303. X. Chen, H. Duan and B. Cao, Carbon, 2023, 211, 118106.
304. M. He, H. Jiang, B. Liu, P. V. Fedotov, A. I. Chernov, E. D. Obraztsova, F. Cavalca, J. B. Wagner, T. W. Hansen and I. V. Anoshkin, et al., Sci. Rep., 2013, 3, 1460.
305. Y. Kohigashi, H. Yoshida, Y. Homma and S. Takeda, Appl. Phys. Lett., 2014, 105, 073108.
306. P. A. Lin, J. L. Gomez-Ballesteros, J. C. Burgos, P. B. Balbuena, B. Natarajan and R. Sharma, J. Catal., 2017, 349, 149–155.
307. Y. Wang, L. Qiu, L. Zhang, D.-M. Tang, R. Ma, C.-L. Ren, F. Ding, C. Liu and H.-M. Cheng, Sci. Adv., 2022, 8, eabo5686.
308. B. McLean, I. Mitchell and F. Ding, Carbon, 2022, 191, 1–9.
309. D. Just, A. Dzienia, K. Milowska, A. Mielańczyk and D. Janas, Mater. Horiz., 2024, 11, 758–767.
310. B. Roldán Cuenya and M. A. Bañares, Chem. Rev., 2024, 124, 8011–8013.
311. S. Röcken and J. Zavadlav, npj Comput. Mater., 2024, 10, 69.
312. S. Choi, Nat. Commun., 2023, 14, 1168.
313. P. Kang, E. Trizio and M. Parrinello, Nat. Comput. Sci., 2024, 4, 451–460.
314. A. Lazaridou, L. R. Smith, S. Pattisson, N. F. Dummer, J. J. Smit, P. Johnston and G. J. Hutchings, Nat. Rev. Chem., 2023, 7, 287–295.

---

Footnote

† These authors contributed equally to this work.

---