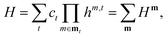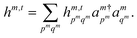DOI:
10.1039/D3SC01984E
(Edge Article)
Chem. Sci., 2023,
14, 7733-7742
Optimizing the number of measurements for vibrational structure on quantum computers: coordinates and measurement schemes
Received
17th April 2023
, Accepted 7th June 2023
First published on 29th June 2023
Abstract
One of the primary challenges prohibiting demonstrations of practical quantum advantages for near-term devices amounts to excessive measurement overheads for estimating relevant physical quantities such as ground state energies. However, with major differences between the electronic and vibrational structures of molecules, the question of how the resource requirements of computing anharmonic, vibrational states can be reduced remains relatively unexplored compared to its electronic counterpart. Importantly, bosonic commutation relations, distinguishable Hilbert spaces and vibrational coordinates allow manipulations of the vibrational system that can be exploited to minimize resource requirements. In this work, we investigate the impact of different coordinate systems and measurement schemes on the number of measurements needed to estimate anharmonic, vibrational states for a variety of three-mode (six-mode) molecules. We demonstrate an average of 3-fold (1.5-fold), with up to 7-fold (2.5-fold), reduction in the number of measurements required by employing appropriate coordinate transformations, based on an automized construction of qubit Hamiltonians from a conventional vibrational structure program.
I. Introduction
The simulation of many-body quantum systems on quantum computers is a promising candidate to achieve computational advantages in both academic and practical applications.1–4 However, current quantum devices are subject to noise and errors to a degree that restricts the available computational resources. While practical quantum advantages are yet to be demonstrated, hybrid quantum-classical algorithms such as the variational quantum eigensolver (VQE) are expected to provide such demonstrations.5–9 The electronic structure problem on quantum computers has in recent years been investigated greatly while the vibrational structure problem remains relatively unexplored.10–13 Importantly, it has been suggested that classically intractable vibrational structure problems may be solved on quantum computers prior to their electronic equivalents.10 Estimating eigenstates of many-body Hamiltonians using the VQE requires the sampling of expectation values of Pauli operators with a trial state. However, it has been shown empirically that the estimation of the electronic ground state of small molecules to chemical accuracy requires infeasible runtimes due to sampling overhead, which is called the measurement problem.14,15 Different measurement schemes have been employed to reduce the sampling overhead, including the grouping of Pauli products into mutually commuting sets,16–25 classical shadow tomography,26–29 low-rank factorizations of the electronic Hamiltonian30 and algebraic approaches.31 Current studies have however only investigated electronic Hamiltonians. The impact of measurement schemes on the measurement problem therefore remains relatively unexplored in the context of vibrational structure.14 In contrast to the two-body electronic Hamiltonian, the many-body vibrational Hamiltonian contains up to N-body coupling terms between the vibrational modes and depends on the choice of vibrational coordinates. The choice of coordinate system impacts the vibrational interactions and may be exploited to obtain approximate mode decoupling. Such a decoupling affects the distribution of small and large terms, which in favorable cases decreases the importance of high-mode coupling terms. This can be seen as better decoupling of coordinates and fewer very important terms, but as all terms are effected, this does not necessarily imply optimal variances. In this paper, we investigate the impact of different measurement schemes and coordinate systems on the number of measurements needed to estimate the ground state of a variety of three- and six-mode molecules. The runtime of a ground state calculation depends on the number of measurements required to estimate the ground state energy, which is determined by the variance of the Hamiltonian. We therefore study the required number of measurements and demonstrate an average of 3-fold (1.5-fold), with up to 7-fold (2.5-fold), reduction in this number using appropriate coordinate transformations. These results are obtained using state of the art vibrational structure potential energy surfaces (PESs) and anharmonic wave function computations and an automized construction of qubit Hamiltonians from a conventional vibrational structure program.
II. Background
II.A Sampling expectation values
Consider a qubit Hamiltonian  where hi denotes matrix elements and
where hi denotes matrix elements and| |  | (1) |
denotes a product of Pauli operators. In the VQE, the ground state energy functional is estimated as the expectation value of the Hamiltonian with a trial state |ψ(θ)〉,| |  | (2) |
To reduce the number of measurements, the Hamiltonian may be grouped into mutually commuting sets
| |  | (3) |
such that

Each set,
Hα, may be rotated into a diagonal basis and the operators of the set measured simultaneously. Let
mα denote the number of measurements required to estimate the energy contribution from
Hα and

the total number of measurements. By optimizing {
mα} the number of measurements required for a given precision
ε reads
| |  | (4) |
if
mα are optimally allocated for each group.
18 With the total number of measurements depending on the variance of each group, the measurements may be optimized by optimizing the total group variances.
II.B Measurement schemes
Qubit-space measurement schemes group mutually commuting Pauli products into measurable sets according to either qubit-wise commutativity (QWC) or full commutativity (FC).16–18,20,21,24,32 In the QWC scheme, the Pauli products commute locally for each qubit subspace, whereas the FC scheme only requires commutativity of the full tensor products. It is important to note that the commutativity scheme alone (i.e. QWC or FC) does not define an algorithm for grouping operator terms. For definiteness, we consider the sorted insertion (SI) approach18,22 in combination with QWC or FC and denote the resulting algorithms as SI/QWC and SI/FC, respectively. In the SI approach one starts by ordering the operator terms (Pauli strings) in decreasing order according to the absolute value of their coefficients. The term with the largest coefficient is added to the first group. The algorithm then iterates through the remaining terms, which are added to the first group if they commute (in the QWC or FC sense) with all other terms in that group. When all terms have been checked, the algorithm starts over by generating a second group and so on until no terms are left. Despite its simplicity, the SI algorithm has been demonstrated to outperform recent classical shadow tomographic methods.18 Thus, the SI algorithm will be used in this work.
The qubit-wise commutativity of two terms implies that the terms commute fully, although the converse is not true. In that sense, QWC can be said to form a subset of FC. It should however be kept in mind that the algorithms SI/QWC and SI/FC will generally produce different groupings of a given set of operator terms.
After grouping the operator terms, each group is diagonalized. In the QWC case, the diagonalization can be performed using only one-qubit gates, while the FC case will generally require both one- and two-qubit gates. The QWC scheme thus has a prima facie advantage in terms of circuit depth. For electronic Hamiltonians it has however been shown that this advantage is outweighed by other factors making the FC scheme preferable18,19 in that case.
III. Vibrational structure
III.A Vibrational Hamiltonian and potential energy surfaces
Consider a molecule with M vibrational modes described by a set of mass-weighted normal coordinates (NCs) (or other orthogonal coordinates) qm. Neglecting the Coriolis and pseudopotential terms of the Watson operator,33,34 the vibrational Hamiltonian reads| |  | (5) |
where the potential in principle contains terms coupling up to M modes simultaneously. The PES, i.e. the vibrational potential, may be obtained using a variety of methods, e.g. using Taylor expansion or the adaptive density-guided approach (ADGA).35 A Taylor expansion of the PESs around the equilibrium geometry provides the PESs in an economical form but suffers from the limited reliability of such expansions including limited radius of convergence and high risk of providing a variationally unbound potential. In contrast, the ADGA is a robust and accurate black-box procedure, which builds the potential according to the need as determined from a vibrational calculation. The ADGA uses very inexpensive vibrational self-consistent field densities to iteratively sample the surface in a physically motivated way. The PES construction is thereby independent of the following correlated vibrational wave function computation, which is our main focus. After generating the PESs, the vibrational Hamiltonian may be transformed into a qubit Hamiltonian using existing encoding algorithms.11–13
III.A.1 Vibrational coordinates.
A standard choice of coordinates is NCs which provide excellent first order insights into the vibrations of stiff molecules close to their equilibrium structures. The benefit of NCs for stiff molecules close to their equilibrium structures is that they decouple the Hamiltonian to second order in distortions from the equilibrium structure. However, the use of NCs does not suppress higher-order terms (in fact, the contrary might be true away from equilibrium). This motivates the search for other types of coordinates that ensure some degree of decoupling of the Hamiltonian. Such coordinates include various kinds of curvilinear coordinates (e.g. bond angles and lengths or polyspherical coordinates), which are often deemed chemically relevant. These coordinates typically reduce the couplings in the potential energy at the price of increasing the coupling level and overall complexity of the kinetic energy. To avoid this latter complication, we focus on rectilinear coordinates that are derived from NCs by orthogonal transformations. All such coordinates are uniquely defined by a rectangular matrix Q with orthogonal columns that contains expansion coefficients in terms of mass weighted Cartesian displacements (see Appendix A). They include optimized coordinates36,37 obtained by minimizing the vibrational self-consistent field (VSCF) energy for a given PES and localized coordinates38 obtained by applying some localization scheme to a set of NCs. A pragmatic and inexpensive compromise is offered by the so-called hybrid optimized and localized coordinates (HOLCs),39 which minimize a cost function including an energy term and a localization term:| |  | (6) |
here, Q is varied over matrices that are related to the normal coordinate matrix QNC by orthogonal transformations. The energy term E(Q) is taken to be the VSCF energy for a second-order Taylor approximation of the PES. This energy depends on the choice of coordinates, as indicated. The localization term (penalty term) L(Q) can be defined in various ways (we use the simple localization scheme described in ref. 39; see Appendix A for details). We note that setting wL = 0 yields NCs, while a large value of wL yields very localized (but not necessarily meaningful) coordinates. We emphasize the fact that, as was mentioned in the introduction, approximate decoupling of the Hamiltonian does not necessarily provide optimal variances.
III.A.2 Distinguishability of vibrational modes.
Since vibrational modes are distinguishable (in constrast to electrons), the vibrational Hilbert space factorizes into distinguishable one-mode subspaces. This factorization allows for further grouping schemes that are not accesible to electronic Hamiltonians. To see this, we write the vibrational Hamiltonian as| |  | (7) |
The sum runs over sets of modes 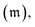 which we denote as mode combinations (MCs), and the set of all MCs
which we denote as mode combinations (MCs), and the set of all MCs  is referred to as the mode combination range (MCR). The operator
is referred to as the mode combination range (MCR). The operator 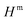 is the sum of all terms that act non-trivially on the modes contained in
is the sum of all terms that act non-trivially on the modes contained in  Consider, for example, the operators
Consider, for example, the operators  and
and  Since the MCs (0,1) and (2,3,4) are disjoint (non-overlapping), the operators commute trivially. However, operators within the same MC do not generally commute. We thus propose the following grouping scheme: first, non-overlapping MCs are combined into larger batches of terms. Then, each such batch is grouped in a trivially parallel fashion using either SI/QWC or SI/FC. The resulting algorithms are denoted as SI/QWC/MCR and SI/FC/MCR, respectively. Although the MC logic does not solve the grouping problem on its own, it provides a sensible scheme that cheaply divide the problem into batches of subproblems (see Appendix B for an example).
Since the MCs (0,1) and (2,3,4) are disjoint (non-overlapping), the operators commute trivially. However, operators within the same MC do not generally commute. We thus propose the following grouping scheme: first, non-overlapping MCs are combined into larger batches of terms. Then, each such batch is grouped in a trivially parallel fashion using either SI/QWC or SI/FC. The resulting algorithms are denoted as SI/QWC/MCR and SI/FC/MCR, respectively. Although the MC logic does not solve the grouping problem on its own, it provides a sensible scheme that cheaply divide the problem into batches of subproblems (see Appendix B for an example).
Note that the MC based commutativity is included in QWC and FC but that the concrete algorithms (SI/QWC/MCR and SI/FC/MCR) will generally result in different groups compared to SI/QWC and SI/FC.
IV. Computational details
A total of 18 molecules were considered, including nine triatomic (three-mode) systems and nine tetratomic (six-mode) systems. All electronic structure calculations were performed at the CCSD(F12*)(T)/cc-pVDZ-F12 level40,41 of theory as implemented in the Turbomole42 program suite. The geometry of each molecule was optimized using numerical gradients, after which a numerical Hessian was computed and used to generate NCs and HOLCs with a series of localization parameters, wL. Coordinate generation was performed using the MidasCpp program,43 which was also used to construct electronic PESs with the ADGA algorithm for each coordinate set as well as VSCF and full vibrational configuration interaction (FVCI) computations. Following the PES construction, VSCF calculations were carried out in large B-spline bases. The resulting VSCF modals were then used as a basis in conventional FVCI calculations. We studied the convergence of the FVCI energy in terms of the number of VSCF modals and found that four (three) modals recovered a large fraction of the FVCI correlation energy for the three-mode (six-mode) systems (see Appendix C for details). These bases were therefore chosen as a good balance between accuracy and CPU-time for the variance computations, which is the computational bottleneck of our locally developed Python3 code for this purpose. Having determined appropriate basis sizes, the Hamiltonians were represented in a suitable format, a process that is fully automatized within MidasCpp (see Appendix D for a few considerations in this regard). The Hamiltonian and the FVCI wave functions were finally transformed to a qubit representation and the variance computed using the aforementioned variance code. A direct encoding was used due to its simplicity. We note that several encoding methods other than the direct mapping have been studied. In particular, compact encodings allow a reduction in the number of qubits which, depending on the problem, either decrease or increase circuit depths.11 In this preliminary study, however, we focus on the direct mapping. For each molecule and coordinate system, the measurement groups were generated using the SI/QWC, SI/FC, SI/QWC/MCR and SI/FC/MCR algorithms as described in Sections II.B and III.A.2 respectively.
V. Results
We initially consider the SI/QWC and SI/FC algorithms for each molecule and each set of coordinates. Selecting the smaller of the two variances (SI/QWC or SI/FC), Fig. 1 and 2 are obtained. Almost all molecules exhibit the largest variances for strongly localized coordinates with localization parameter wL = 1.0 × 10−3. Such behaviour is not surprising, since strongly localized coordinates are not necessarily physically meaningful. Localization of coordinates yields a smaller variance for some of the molecules but not all, and as such no choice of coordinates is systematically better than the others.
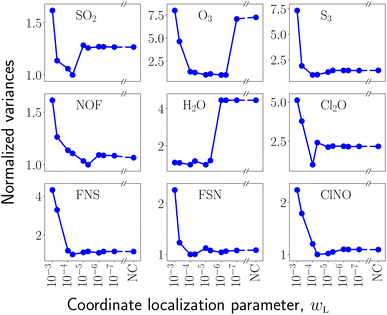 |
| | Fig. 1 Variances of the three-mode molecules normalized relative to the minimum variance for all coordinate systems. For each coordinate system, the variance depicted is the optimal variance considering both the SI/QWC and SI/FC algorithms. Each HOLC coordinate system is represented by its localization parameter wL and NC refers to normal coordinates (equivalent to wL = 0). Note the broken first axis that places the NC data points alongside the HOLC data. | |
 |
| | Fig. 2 Variances of the three-mode molecules normalized relative to the minimum variance for all coordinate systems. For each coordinate system, the variance depicted is the optimal variance considering both the SI/QWC and SI/FC algorithm. Each HOLC coordinate system is represented by its localization parameter wL and NC refers to normal coordinates (equivalent to wL = 0). Note the broken first axis that places the NC data points alongside the HOLC data. | |
V.A Invariance and reductions
To further estimate the impact of coordinate transformations, two ratios are studied. Using the data displayed in Fig. 1 and 2 the lowest and highest variance is calculated for each molecule with wL = 1.0 × 10−3 excluded as it is vastly inferior for most of the molecules. The first ratio compares the lowest and highest of these variances,| |  | (8) |
while the second ratio compares the variance of NCs to the minimum variance,| |  | (9) |
That is for NOF the ratio r is that of the variances at wL = 5.0 × 10−3 and wL = 5.0 × 10−5, as these are the maximum and minimum variances for the molecule when excluding the consistently unfavourable wL = 1.0 × 10−3 data point. Likewise rNC is variance ratio of NCs to wL = 5.0 × 10−5.
If rNC > 1, NCs provide a larger variance compared to HOLCs and thus HOLCs are preferential. In contrast, if rNC = 1, NCs provide a smaller variance compared to HOLCs and thus NCs are preferential. r therefore serves as a measure of the overall impact on variance of coordinate transformation, whereas rNC measures the extent to which HOLCs improve the variance compared to NCs. These reductions measures are depicted in Fig. 3 and 4.
 |
| | Fig. 3 The ratio for the three-mode molecules between the variances of the worst and best choice of coordinates [eqn (8)] in blue diamonds, along with the ratio between the variances of the optimal choice of coordinates and NCs [eqn (9)] in black dots. All coordinate systems are compared excluding the localization parameter wL = 1.0 × 10−3 since these coordinates were inferior for all molecules. | |
 |
| | Fig. 4 The ratio for the six-mode molecules between the variances of the worst and best choice of coordinates [eqn (8)] in blue diamonds, along with the ratio between the variances of the optimal choice of coordinates and NCs [eqn (9)] in black dots. All coordinate systems are compared excluding the localization parameter wL = 1.0 × 10−3 since these coordinates were inferior for all molecules. | |
The mean reduction for the three-mode (six-mode) molecules is around 3 (1.5) with relatively large standard deviations. The largest improvements for the three-mode (six-mode) molecules amounts to around a 7-fold (2.5-fold) reduction. Meanwhile, some of the molecules exhibit approximate invariance under reasonable coordinate transformations (r close to 1).
V.B Molecular symmetry
We see no clear pattern relating to point group symmetry as exemplified by the molecules O3 and S3. Despite being extremely similar with respect to symmetry and structure, they behave quite differently with respect to the computed variances (see Fig. 1, 3 and 5). These results highlight the complexity of the interdependence between the choice of coordinates, the details of the PES and the vibrational structure of the molecule.
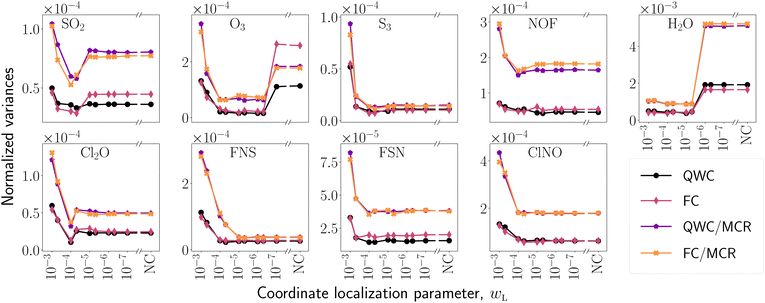 |
| | Fig. 5 Variances of the three-mode molecules for each grouping scheme (Sections II.B and III.A.2). The HOLC coordinate systems are defined by their localization parameter wL, with NC denoting normal coordinates (equivalent to wL = 0). Note the broken first axis that places the NC data points alongside the HOLC data. All grouping schemes employ sorted insertion with the commutator schemes indicated in the legend. In general, using sorted insertion for all terms (not using MCR grouping) produces the smallest variances and the discrepancy between commutativity schemes is small. | |
V.C SI/QWC and SI/FC schemes
To study the SI/QWC and SI/FC schemes, the variances were calculated for each measurement scheme which is depicted in Fig. 5 and 6. In contrast to a corresponding electronic structure study,18 no commutativity scheme systematically outperforms the other across molecules and coordinates. In particular, no appreciable return on investment is observed for the additional circuit depth of FC compared to QWC. The vibrational operators are very different from their electronic counterparts with the electronic Hilbert space spanned by spin-orbitals and the vibrational Hilbert space of modal basis functions. This might explain the difference in relative performance of the SI/QWC and SI/FC algorithms when comparing vibrational and electronic structure.
 |
| | Fig. 6 Variances of the six-mode molecules for each grouping scheme (Sections II.B and III.A.2). The HOLC coordinate systems are defined by their localization parameter wL, with NC denoting normal coordinates (equivalent to wL = 0). Note the broken first axis that places the NC data points alongside the HOLC data. All grouping schemes employ sorted insertion with the commutator schemes indicated in the legend. In general, using sorted insertion for all terms (not using MCR grouping) produces the smallest variances and the discrepancy between commutativity schemes is small. | |
In Fig. 5 there are some significant differences in the performance of the two commutativity schemes, e.g. SO2 and O3, is observed for the three-mode systems. This is however not observed for the six-mode systems (Fig. 5), which might be due to a peculiarity of the three-mode Hilbert space. With three modes there is a single MC in the MCR that contains a vast majority of all terms in the Hamiltonian. For the six-mode systems the number of terms are more evenly distributed among the MCs, which may explain the different observed behaviours of the commutativity schemes as operators from two non-overlapping MCs commute (see Section III.A.2).
V.D Vibrational heuristics for sorting
From Fig. 5 and 6 it is clear that SI/QWC and SI/FC outperform SI/QWC/MCR and SI/FC/MCR. SI/QWC and SI/FC thus seem to be the best options, which in some sense is not surprising. The MCR methods essentially divide the set of all Hamiltonian terms into smaller subsets, in a chemically motivated fashion. The SI algorithm then sorts these subsets in order to obtain the final groups, hence the sorting is restricted, meaning that the sorting has less flexibility. For larger molecules this might however be an advantage if the sorting overhead becomes significant due to the non-linear scaling of sorting algorithms. This scaling implies that in general sorting of multiple small sets is faster than the sorting of one large set. Additionally, the sorting of smaller sets is trivially parallelizable in contrast to a single sorting of the full set. As seen for S3 and FNS the MCR methods has the potential to yield groupings of comparable variance to plain SI hence it is possible that the MCR methods might yield a faster overall time to solution for large molecules. For the three-mode systems the vast majority of terms are contained within the MC  hence the potential speed-up in group generation is negligible in this case. However, for larger molecules, the number of combinations of higher-order terms increase rapidly.
hence the potential speed-up in group generation is negligible in this case. However, for larger molecules, the number of combinations of higher-order terms increase rapidly.
V.E Measurement numbers
Using the SI/QWC variances with the optimal choice of coordinates, for each molecule, the number of measurements for estimating a single energy evaluation are shown in Fig. 7 and 8. These measurement numbers are calculated using eqn (4) with an error of ε = 1μEh corresponding to relevant accuracy for vibrational structure. The number of measurements required for both the three-mode and six-mode molecules falls in the order of magnitude range 107 to 108. That the measurement numbers for the three- and six-mode systems are so close on average is somewhat surprising considering the size of Hilbert space or the number of operator terms in the Hamiltonian. The dimensions of the Hilbert space are| |  | (10) |
whereas the number of second quantized terms (in the format of Appendix D) for a three-mode coupled Hamiltonian is| |  | (11) |
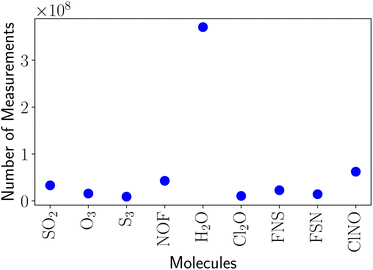 |
| | Fig. 7 The number of measurements for estimating a single energy evaluation for each of the three-mode benchmark molecules using the SI/QWC sorting scheme. The three-mode bases includes 4 modals per mode. | |
 |
| | Fig. 8 The number of measurements for estimating a single energy evaluation for each of the six-mode benchmark molecules using the SI/QWC sorting scheme. The six-mode bases include 3 modals per mode. | |
It should, however, be recalled that the three-mode systems are dominated by a single three-mode coupling with many terms while the six-mode systems have a comparatively large number of mode couplings that each contribute a relatively small number of terms. This impacts the grouping of terms after the qubit transformation and, in turn, the variances and measurement numbers. The general structures of the two Hilbert spaces are thus quite different, and a naive argument based on the size of the Hilbert space or the number of operator terms alone is not sufficient.
VI. Conclusion
In this work, we have presented different vibrational coordinates that provide reductions in measurements for quantum computations of anharmonic vibrational wave functions using realistic potential energy surfaces (PESs). It was shown that an average of 3-fold (1.5-fold), with up to 7-fold (2.5-fold), reductions may be achieved by appropriately transforming the vibrational coordinates for three-mode (six-mode) molecules. One must emphasize the size of the molecules which were used in the benchmarks. Localized coordinates are generally favourable for relatively large molecules for which delocalized interactions may be negligible. Thus, localized coordinates should be further investigated in the context of larger systems to investigate the performance for larger molecules. Contrary to what has been observed for electronic structure, we see no systematic reduction in variance using the sorted insertion with full commutativity (SI/FC) scheme compared to the sorted insertion with qubit-wise commutativity (SI/QWC) scheme. Such differences between electronic and vibrational structure may arise due to the different commutation relations (fermionic/bosonic). Additionally, the Hilbert spaces differ in structure, with the electronic Hilbert space spanned by spin-orbitals and the vibrational Hilbert space spanned by modal basis functions. Combining the sorted insertion (SI) algorithm with the grouping of non-overlapping interaction terms in the mode combination range (MCR) algorithm (Section III.A.2) does not provide better groupings compared to the plain SI algorithm. They are however still interesting because the sorting of multiple sets is trivially parallelizable which might be useful if the sorting overhead becomes significant, e.g. for large molecules.
These results agree with previous conclusions for electronic structure where minimizing the total number of groups does not necessarily provide optimal variances.
VII. Appendix A: details on coordinates
For an N-atomic molecule we introduce a 3N dimensional column vector d containing the Cartesian displacements from the equilibrium geometry. We likewise introduce a 3N × 3N diagonal matrix G of atomic masses,| | | G = diag(M1, M1, M1,…, MN, MN, MN). | (A1) |
A set of mass weighted displacements is then defined as d′ = G1/2d and forms the basis for further coordinates q via an orthogonal transformation Q:
Normal coordinates correspond to the choice of Q that diagonalizes the mass weighted Hessian:
where
Λ is the vector of eigenvalues and
F is the unweighted Hessian. Six eigenvectors (five for linear molecules) have zero eigenvalues and correspond to the overall rotation and translation of the molecule. These eigenvectors are not included in
Q. New rectilinear coordinates
Q′ can be obtained by performing orthogonal transformations of the
Q matrix:
here,
L is an
M ×
M orthogonal matrix, where
M = (3
N − 6) (non-linear molecules) or
M = (3
N − 5) (linear molecules). In the hybrid optimized and localized coordinate (HOLC) algorithm,
39L is parametrized through Jacobi sweeps. The algorithm optimizes
L such that the following cost function is minimized:
| | | f(Q′) = wEE(Q′) + wLL(Q′). | (A5) |
The energy term E(Q′) is taken as the vibrational self-consistent field (VSCF) energy on a second-order approximate PES, while we use an atomic localization term:
| |  | (A6) |
| |  | (A7) |
VIII. Appendix B: MCR grouping for five-mode systems
For a five-mode system with one-, two-, and three-mode couplings in the Hamiltonian, the grouping based on the MCR may be obtained by grouping disjoint two- and three-body couplings along with one-body couplings. The two- and three-body couplings yield {H(i,j,k) + H(m,n)|(m, n)⊄(i, j, k)} while the one-body couplings yield {H(i)}. An example is presented in the following:
| • S0 = {H(0,1,2), H(3,4)} |
| • S1 = {H(1,2,3), H(0,4)} |
| • S2 = {H(2,3,4), H(0,1)} |
| • S3 = {H(0,2,3), H(1,4)} |
| • S4 = {H(0,3,4), H(1,2)} |
| • S5 = {H(0,1,4), H(2,3)} |
| • S6 = {H(1,3,4), H(0,2)} |
| • S7 = {H(0,1,3), H(2,4)} |
| • S8 = {H(0,2,4), H(1,3)} |
| • S9 = {H(0), H(1), H(2), H(3), H(4)} |
The terms commute since their mode couplings are disjoint. The terms also exhibit maximal mode coupling since all modes are active in the terms. However, the operators for each mode coupling within an MCR do not mutually commute and must be diagonalized. Using the SI algorithm, each MCR group may be decomposed into subgroups which mutually commute. The MCR grouping for the three- and six-mode molecules studied in this work are generated analogously to the five-mode system. Due to the more complex combinations for the six-mode system, however, we present the example of a five-mode system for simplicity.
IX. Appendix C: modal basis set convergence
In order to test the convergence of the modal basis set dimensions, we calculate full vibrational configuration interaction (FVCI) ground state correlation energies for up to ten (eight) modals per mode for the three-mode (six-mode) systems. The results are presented in Fig. 9 and 10. As can be seen, a large fraction of the ground state correlation energies is recovered for four (three) modals per mode for the three-mode (six-mode) systems.
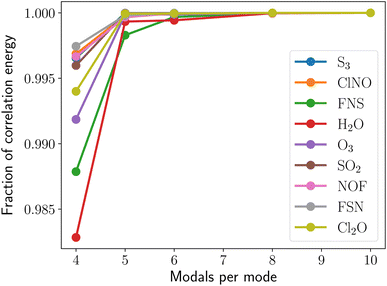 |
| | Fig. 9 Convergence of the correlation energy with respect to the modal basis set size for the three-mode molecules. The displayed fraction is relative to the 10 modal computation for each molecule. | |
 |
| | Fig. 10 Convergence of the correlation energy with respect to the modal basis set size for the six-mode molecules. The displayed fraction is relative to the 8 modal computation for each molecule. | |
X. Appendix D: operator format
The Hamiltonian for the vibrational problem is usually represented in a sum-of-products (SOP) form,| | 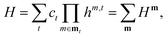 | (D1) |
where ct is the coefficient for the term indexed by t. Any given term includes a product of one-mode operators hm,t for a set of modes mt. The one-mode operators can be written as| | 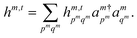 | (D2) |
The SOP format covers most practically relevant cases such as Taylor expanded potentials and more elaborate polynomial representations such as those generated by the adaptive density-guided approach (ADGA) algorithm.35 When designing algorithms for classical computers, it is extremely beneficial to keep the operator in the SOP form and never expand the products of one-mode operators. However, for the purpose of transforming the Hamiltonian into qubit format, we expand all product into simple strings of creating and annihilation operators. As an elementary example, consider the terms pertaining to a given two-mode combination,
| |  | (D3) |
This example is readily generalized to terms containing more modes. A trivial but important point is that the number of coefficients in eqn (D3) does not depend on the number of terms in the SOP expansion in eqn (D1).
Data availability
The code related to the study is available upon reasonable request to the authors.
Author contributions
All authors contributed to drafting and revising the manuscript. The theory was developed by MM, RBJ, MGH and OC. The numerical computations were carried out by MM, RBJ and MGH. The project was supervised by OC and NTZ.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
O. C. acknowledges support from the Independent Research Fund Denmark through grant number 1026-00122B. The authors acknowledge funding from the Novo Nordisk Foundation through grant NNF20OC0065479. PES calculations were performed at the Centre for Scientific Computing Aarhus (CSCAA).
References
- A. J. Daley, I. Bloch, C. Kokail, S. Flannigan, N. Pearson, M. Troyer and P. Zoller, Practical quantum advantage in quantum simulation, Nature, 2022, 607, 667–676 CrossRef CAS PubMed.
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry, Nat. Commun., 2023, 14, 1952 CrossRef CAS PubMed.
-
V. E. Elfving, B. W. Broer, M. Webber, J. Gavartin, M. D. Halls, K. P. Lorton and A. Bochevarov, How will quantum computers provide an industrially relevant computational advantage in quantum chemistry?, arXiv, 2020, preprint, arXiv:2009.12472 [physics, physics:quant-ph], DOI:10.48550/arXiv.2009.12472.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated quantum computation of molecular energies, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, A Quantum Computing View on Unitary Coupled Cluster Theory, Chem. Soc. Rev., 2022, 51, 1659–1684 RSC.
- R. Babbush, D. W. Berry, I. D. Kivlichan, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, Exponentially more precise quantum simulation of fermions in second quantization, New J. Phys., 2016, 18, 033032 CrossRef.
- R. Babbush, D. W. Berry, Y. R. Sanders, I. D. Kivlichan, A. Scherer, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, Exponentially more precise quantum simulation of fermions in the configuration interaction representation, Quantum Science and Technology, 2017, 3, 015006 CrossRef.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New J. Phys., 2016, 18, 023023 CrossRef.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and L. Jeremy, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- N. P. D. Sawaya, F. Paesani and D. P. Tabor, Near- and long-term quantum algorithmic approaches for vibrational spectroscopy, Phys. Rev. A, 2021, 104, 062419 CrossRef CAS.
- N. P. D. Sawaya, T. Menke, T. H. Kyaw, S. Johri, A. Aspuru-Guzik and G. G. Guerreschi, Resource-efficient digital quantum simulation of d-level systems for photonic, vibrational, and spin-s Hamiltonians, npj Quantum Inf., 2020, 6, 1–13 CrossRef.
- S. McArdle, A. Mayorov, X. Shan, S. Benjamin and X. Yuan, Digital quantum simulation of molecular vibrations, Chem. Sci., 2019, 10(22), 5725–5735 RSC.
- P. J. Ollitrault, A. Baiardi, M. Reiher and I. Tavernelli, Hardware Efficient Quantum Algorithms for Vibrational Structure Calculations, Chem. Sci., 2020, 11(26), 6842–6855 RSC.
-
J. F. Gonthier, M. D. Radin, C. Buda, E. J. Doskocil, C. M. Abuan and J. Romero, Identifying challenges towards practical quantum advantage through resource estimation: the measurement roadblock in the variational quantum eigensolver, arXiv (Tech. Rep.), 2020, preprint, arXiv:2012.04001, arXiv [quant-ph], DOI:10.1103/PhysRevResearch.4.033154.
- G. Wang, D. E. Koh, P. D. Johnson and Y. Cao, Minimizing estimation runtime on noisy quantum computers, PRX Quantum, 2021, 2, 010346 CrossRef.
- A. Zhao, A. Tranter, W. M. Kirby, S. F. Ung, A. Miyake and P. Love, Measurement reduction in variational quantum algorithms, Phys. Rev. A, 2020, 101, 062322 CrossRef CAS.
- V. Verteletskyi, T.-C. Yen and A. F. Izmaylov, Measurement Optimization in the Variational Quantum Eigensolver Using a Minimum Clique Cover, J. Chem. Phys., 2020, 152, 124114 CrossRef CAS PubMed.
- T.-C. Yen, A. Ganeshram and A. F. Izmaylov, Deterministic improvements of quantum measurements with grouping of compatible operators, non-local transformations, and covariance estimates, npj Quantum Inf., 2023, 9, 14 CrossRef.
-
Z. P. Bansingh, T.-C. Yen, P. D. Johnson and A. F. Izmaylov, Fidelity overhead for non-local measurements in variational quantum algorithms, arXiv, 2022, preprint, arXiv:2205.07113 [physics, physics:quant-ph], DOI:10.48550/arXiv.2205.07113.
-
T.-C. Yen, V. Verteletskyi and A. F. Izmaylov, Measuring all compatible operators in one series of a single-qubit measurements using unitary transformations, arXiv (Tech. Rep.), 2020, preprint, arXiv:1907.09386 [physics, physics:quant-ph], DOI:10.48550/arXiv.1907.09386.
- I. Hamamura and T. Imamichi, Efficient evaluation of quantum observables using entangled measurements, npj Quantum Inf., 2020, 6, 1–8 CrossRef.
- O. Crawford, B. v. Straaten, D. Wang, T. Parks, E. Campbell and S. Brierley, Efficient quantum measurement of Pauli operators in the presence of finite sampling error, Quantum, 2021, 5, 385 CrossRef.
-
S. Choi, T.-C. Yen and A. F. Izmaylov, Improving quantum measurements by introducing ”ghost” Pauli products, arXiv, 2022, preprint, arXiv:2208.06563 [physics, physics:quant-ph], DOI:10.48550/arXiv.2208.06563.
- A. F. Izmaylov, T.-C. Yen and I. G. Ryabinkin, Revising the measurement process in the variational quantum eigensolver: is it possible to reduce the number of separately measured operators?, Chem. Sci., 2019, 10, 3746–3755 RSC.
-
A. F. Izmaylov, T.-C. Yen, R. A. Lang and V. Verteletskyi, Unitary partitioning approach to the measurement problem in the Variational Quantum Eigensolver method, arXiv (Tech. Rep.), 2019, preprint, arXiv:1907.09040 [physics, physics:quant-ph], DOI:10.48550/arXiv.1907.09040.
-
C. Hadfield, S. Bravyi, R. Raymond and A. Mezzacapo, Measurements of Quantum Hamiltonians with Locally-Biased Classical Shadows, arXiv, 2020, preprint, arXiv:2006.15788 [quant-ph], DOI:10.48550/arXiv.2006.15788.
- H.-Y. Huang, R. Kueng and J. Preskill, Efficient Estimation of Pauli Observables by Derandomization, Phys. Rev. Lett., 2021, 127, 030503 CrossRef CAS PubMed.
-
C. Hadfield, Adaptive Pauli Shadows for Energy Estimation, arXiv, 2021, preprint, arXiv:2105.12207 [quant-ph], DOI:10.48550/arXiv.2105.12207.
-
B. Wu, J. Sun, Q. Huang and X. Yuan, Overlapped grouping measurement: A unified framework for measuring quantum states, arXiv, 2021, preprint, arXiv:2105.13091 [quant-ph], DOI:10.48550/arXiv.2105.13091.
- W. J. Huggins, J. McClean, N. Rubin, Z. Jiang, N. Wiebe, K. B. Whaley and R. Babbush, Efficient and Noise Resilient Measurements for Quantum Chemistry on Near-Term Quantum Computers, npj Quantum Inf., 2021, 7, 23 CrossRef.
- T.-C. Yen and A. F. Izmaylov, Cartan Subalgebra Approach to Efficient Measurements of Quantum Observables, PRX Quantum, 2021, 2, 040320 CrossRef.
-
A. Jena, S. Genin and M. Mosca, Pauli Partitioning with Respect to Gate Sets, arXiv, 2019, preprint, arXiv:1907.07859 [quant-ph], DOI:10.48550/arXiv.1907.07859.
- J. K. Watson, Simplification of the molecular vibration-rotation hamiltonian, Mol. Phys., 1968, 15, 479–490 CrossRef CAS.
- J. K. Watson, The vibration-rotation hamiltonian of linear molecules, Mol. Phys., 1970, 19, 465–487 CrossRef CAS.
- M. Sparta, D. Toffoli and O. Christiansen, An adaptive density-guided approach for the generation of potential energy surfaces of polyatomic molecules, Theor. Chem. Acc., 2009, 123, 413–429 Search PubMed.
- K. Yagi, M. Keçeli and S. Hirata, Optimized coordinates for anharmonic vibrational structure theories, J. Chem. Phys., 2012, 137, 204118 CrossRef PubMed.
- B. Thomsen, K. Yagi and O. Christiansen, Optimized coordinates in vibrational coupled cluster calculations, J. Chem. Phys., 2014, 140, 154102 CrossRef.
- C. R. Jacob and M. Reiher, Localizing normal modes in large molecules, J. Chem. Phys., 2009, 130, 084106 CrossRef PubMed.
- E. L. Klinting, C. König and O. Christiansen, Hybrid Optimized and Localized Vibrational Coordinates, J. Phys. Chem. A, 2015, 119, 11007–11021 CrossRef CAS PubMed.
- C. Hättig, D. P. Tew and A. Köhn, Communications: Accurate and efficient approximations to explicitly correlated coupled-cluster singles and doubles, CCSD-F12, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B–Ne, and Al–Ar, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
-
Turbomole V7.5, TURBOMOLE GmbH Search PubMed.
-
D. G. Artiukhin, O. Christiansen, I. H. Godtliebsen, E. M. Gras, W. Győrffy, M. B. Hansen, M. B. Hansen, E. L. Klinting, J. Kongsted, C. König, D. Madsen, N. K. Madsen, K. Monrad, G. Schmitz, P. Seidler, K. Sneskov, M. Sparta, B. Thomsen, D. Toffoli, A. Zoccante, M. G. Højlund, N. M. Høyer and A. B. Jensen, MidasCpp, 2022 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc,
Rasmus
Berg Jensen
*abc,
Rasmus
Berg Jensen
 bc,
Mads
Greisen Højlund
bc,
Mads
Greisen Højlund
 c,
Nikolaj
Thomas Zinner
c,
Nikolaj
Thomas Zinner
 ab and
Ove
Christiansen
ab and
Ove
Christiansen
 *ac
*ac
 where hi denotes matrix elements and
where hi denotes matrix elements and


 Each set, Hα, may be rotated into a diagonal basis and the operators of the set measured simultaneously. Let mα denote the number of measurements required to estimate the energy contribution from Hα and
Each set, Hα, may be rotated into a diagonal basis and the operators of the set measured simultaneously. Let mα denote the number of measurements required to estimate the energy contribution from Hα and  the total number of measurements. By optimizing {mα} the number of measurements required for a given precision ε reads
the total number of measurements. By optimizing {mα} the number of measurements required for a given precision ε reads



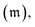 which we denote as mode combinations (MCs), and the set of all MCs
which we denote as mode combinations (MCs), and the set of all MCs  is referred to as the mode combination range (MCR). The operator
is referred to as the mode combination range (MCR). The operator 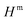 is the sum of all terms that act non-trivially on the modes contained in
is the sum of all terms that act non-trivially on the modes contained in  Consider, for example, the operators
Consider, for example, the operators  and
and  Since the MCs (0,1) and (2,3,4) are disjoint (non-overlapping), the operators commute trivially. However, operators within the same MC do not generally commute. We thus propose the following grouping scheme: first, non-overlapping MCs are combined into larger batches of terms. Then, each such batch is grouped in a trivially parallel fashion using either SI/QWC or SI/FC. The resulting algorithms are denoted as SI/QWC/MCR and SI/FC/MCR, respectively. Although the MC logic does not solve the grouping problem on its own, it provides a sensible scheme that cheaply divide the problem into batches of subproblems (see Appendix B for an example).
Since the MCs (0,1) and (2,3,4) are disjoint (non-overlapping), the operators commute trivially. However, operators within the same MC do not generally commute. We thus propose the following grouping scheme: first, non-overlapping MCs are combined into larger batches of terms. Then, each such batch is grouped in a trivially parallel fashion using either SI/QWC or SI/FC. The resulting algorithms are denoted as SI/QWC/MCR and SI/FC/MCR, respectively. Although the MC logic does not solve the grouping problem on its own, it provides a sensible scheme that cheaply divide the problem into batches of subproblems (see Appendix B for an example).



 hence the potential speed-up in group generation is negligible in this case. However, for larger molecules, the number of combinations of higher-order terms increase rapidly.
hence the potential speed-up in group generation is negligible in this case. However, for larger molecules, the number of combinations of higher-order terms increase rapidly.