Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Universality class of the motility-induced critical point in large scale off-lattice simulations of active particles†
Claudio
Maggi
 *ab,
Matteo
Paoluzzi
*ab,
Matteo
Paoluzzi
 c,
Andrea
Crisanti
c,
Andrea
Crisanti
 bd,
Emanuela
Zaccarelli
bd,
Emanuela
Zaccarelli
 bd and
Nicoletta
Gnan
bd and
Nicoletta
Gnan
 *bd
*bd
aNANOTEC-CNR, Institute of Nanotechnology, Soft and Living Matter Laboratory -Piazzale A. Moro 2, I-00185, Roma, Italy. E-mail: claudio.maggi@cnr.it
bDipartimento di Fisica, Università di Roma “Sapienza”, I-00185, Roma, Italy
cDepartamento de Fìsica de la Matèria Condensada, Universitat de Barcelona, C. MartìFranquès 1, 08028 Barcelona, Spain
dCNR-ISC, Institute of Complex Systems, Roma, Italy. E-mail: nicoletta.gnan@cnr.it
First published on 10th February 2021
Abstract
We perform large-scale computer simulations of an off-lattice two-dimensional model of active particles undergoing a motility-induced phase separation (MIPS) to investigate the system's critical behaviour close to the critical point of the MIPS curve. By sampling steady-state configurations for large system sizes and performing finite size scaling analysis we provide exhaustive evidence that the critical behaviour of this active system belongs to the Ising universality class. In addition to the scaling observables that are also typical of passive systems, we study the critical behaviour of the kinetic temperature difference between the two active phases. This quantity, which is always zero in equilibrium, displays instead a critical behavior in the active system which is well described by the same exponent of the order parameter in agreement with mean-field theory.
Introduction
One of the pillars of statistical physics is the concept of universality in critical phenomena. In equilibrium systems, close to a second-order phase transition, universality can be ultimately attributed to the divergence of the correlation length of the order parameter. The behavior of this growing length-scale is found to be independent of the microscopic details of the systems but is determined only by few specific features, i.e. the spatial dimensionality and the symmetries of the order parameter as firstly hypothesized by Kadanoff.1 Depending on these parameters it is possible to trace back the critical behaviour of disparate systems within few groups, called universality classes.One of the biggest challenges of recent years is to transfer the vast knowledge acquired on the universal behaviour of equilibrium systems into active matter physics. Active matter represents a peculiar class of non-equilibrium systems where the elementary units or agents are self-propelled objects capable of converting energy into systematic movement.2,3 The interacting agents are often complex biological objects that exhibit self-organized behavior on large scales giving rise to many diverse living materials.4 In particular, self-propulsion can trigger a feedback between motility and local density causing an effective attractive interaction between active particles.5 This attractive force can cause a phase separation in active fluids, remarkably similar to the gas–liquid coexistence in equilibrium systems, which is called Motility-Induced Phase Separation (MIPS).6 Since MIPS is a very general feature of active dynamics it might play a role also in biological systems. For instance, it has been recently observed that multicellular aggregates of Myxococcus xanthus might take advantage of density-motility feedback for developing large scale collective behaviors that have been well described by MIPS.7
In equilibrium physics the standard gas–liquid coexistence ends with a critical point that belongs to the Ising universality class.8,9 A natural question is whether or not the MIPS curve ends in a critical point and whether there is a region close to phase separation in which the active critical behaviour can be traced back to a specific universality class. Effective equilibrium approaches,10,11 and field-theoretic computations12 have previously pointed to the Ising universality class. Concerning numerical simulations, although numerous works have addressed the properties of phase-separated MIPS states,13–20 the study of the critical region and the determination of the critical properties still remains challenging and controversial. In particular it has been shown that active Brownian particles in two-dimensions (2d) display some critical exponents deviating considerably from the Ising ones.21 Differently on-lattice simulations of an active model have shown results in agreement with the Ising universality class12 and suggested that off-lattice simulations have been performed far from the scaling regime due to the small size of the systems. However, more recent simulations of the same lattice model have shown a deviation of the order parameter exponent from the Ising value.22 Since it is not a priori clear if these models lie in the same universality class, one must rely on large-scale computer simulations which are often a necessary tool to understand possible discrepancies between off-lattice and on-lattice critical exponents. This has been the case, for example, for Heisenberg fluids at equilibrium.23,24
In this work, we report results of large-scale off-lattice simulations of Active Ornstein–Uhlenbeck Particles (AOUPs) at criticality. Performing Finite-Size-Scaling (FSS) analysis, we show that the system's critical exponents agree with the Ising universality class. We also show that the kinetic temperature difference between the two phases, emerging at criticality, displays a critical behavior which is well described by the exponent of the order parameter in agreement with mean-field theory combined with a small-τ expansion of the AOUPs model.
Model and methods
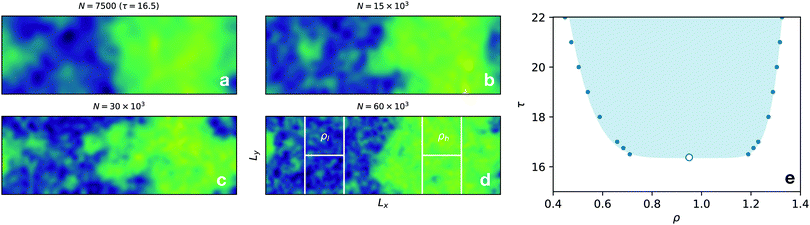
We consider a system composed of N self-propelled AOUP particles in 2d.25,26 This model is perhaps the simplest active particle model (due to the linearity of the process producing the “active noise”) which has led to numerous novel theoretical developments.11,27–31 It has been shown27 that AOUPs exhibit MIPS for large values of the persistence time of the activity, as also displayed in Fig. 1(a–d). The equations of motion of AOUPs read| ṙi = μ(ψi + Fi) | (1) |
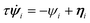 | (2) |
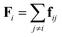 is the conservative force acting on the particle. We consider two-body interactions, i.e., fij = −∇riϕ(rij), with rij = |ri − rj| and we use a simple inverse power-law potential ϕ(r) = (r/σ)−12/12 with a cut-off at r = 2.5σ. Here σ represents the diameter of the particle and is set to 1. In eqn (2)τ is the persistence time of the active force and η is a standard white noise source, i.e. 〈ηαi(t)〉 = 0 and
is the conservative force acting on the particle. We consider two-body interactions, i.e., fij = −∇riϕ(rij), with rij = |ri − rj| and we use a simple inverse power-law potential ϕ(r) = (r/σ)−12/12 with a cut-off at r = 2.5σ. Here σ represents the diameter of the particle and is set to 1. In eqn (2)τ is the persistence time of the active force and η is a standard white noise source, i.e. 〈ηαi(t)〉 = 0 and 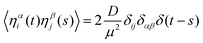 , where the greek indices indicate Cartesian components. Here D is the diffusivity of the non-interacting particles and μ is the particles mobility (set to one in simulations). In the absence of deterministic forces eqn (1) and (2) yield32,33 〈ṙ2〉 = 2v2 = 2D/τ, allowing to express the diffusivity as D = v2τ, i.e. as function of v which is the (axial) free root-mean-squared velocity. In all simulations we fix v = 1 and increase τ from small to large values to observe the transition as shown by the schematic phase diagram in Fig. 1(e). Eqn (1) and (2) have been integrated numerically using the Euler scheme with a time step Δt = 10−3 up to Nt = 109 time steps for the largest system size which is adequate to observe full relaxation of the density auto-correlation function as shown in the ESI.† In addition we start each simulation from a random initial configuration and we perform up to Ne = 108 preparation steps which guarantee that all runs reach the steady-state, even close to the critical point. We perform averages over several independent runs and errors reported represent twice the standard error of the mean (see the ESI† for details on the error estimation).
, where the greek indices indicate Cartesian components. Here D is the diffusivity of the non-interacting particles and μ is the particles mobility (set to one in simulations). In the absence of deterministic forces eqn (1) and (2) yield32,33 〈ṙ2〉 = 2v2 = 2D/τ, allowing to express the diffusivity as D = v2τ, i.e. as function of v which is the (axial) free root-mean-squared velocity. In all simulations we fix v = 1 and increase τ from small to large values to observe the transition as shown by the schematic phase diagram in Fig. 1(e). Eqn (1) and (2) have been integrated numerically using the Euler scheme with a time step Δt = 10−3 up to Nt = 109 time steps for the largest system size which is adequate to observe full relaxation of the density auto-correlation function as shown in the ESI.† In addition we start each simulation from a random initial configuration and we perform up to Ne = 108 preparation steps which guarantee that all runs reach the steady-state, even close to the critical point. We perform averages over several independent runs and errors reported represent twice the standard error of the mean (see the ESI† for details on the error estimation).
The active particles move in a rectangular box of size Lx × Ly with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio (Lx = 3Ly) and periodic boundary conditions. The simulated system sizes are N = (7.5, 15, 30, 60) × 103. To avoid spurious effects due to the presence of an interface21,34 we compute the quantities of interest only in four sub-boxes of size L = Ly/2 centered on the dense and dilute phases. These boxes are located at x = Lx/2 ± Lx/4 and at y = Ly/2 ± Ly/4. To ensure that these positions coincide with the locations of the dense and dilute phases, as in ref. 21, for each configuration we first find the center of mass of the system along x (with periodic boundaries35), and we shift all particles so that the x-coordinate of the center of mass coincides with x = 3Lx/4 as shown in Fig. 1(d). We stress that the method also works at the critical point if the two phases are distinguishable enough. This is typically the case when the critical order parameter distribution shows two peaks as in many Ising36 and Lennard–Jones systems.37 This technique has been successfully applied to the 2d Ising model21 and to the lattice active model.12
3 ratio (Lx = 3Ly) and periodic boundary conditions. The simulated system sizes are N = (7.5, 15, 30, 60) × 103. To avoid spurious effects due to the presence of an interface21,34 we compute the quantities of interest only in four sub-boxes of size L = Ly/2 centered on the dense and dilute phases. These boxes are located at x = Lx/2 ± Lx/4 and at y = Ly/2 ± Ly/4. To ensure that these positions coincide with the locations of the dense and dilute phases, as in ref. 21, for each configuration we first find the center of mass of the system along x (with periodic boundaries35), and we shift all particles so that the x-coordinate of the center of mass coincides with x = 3Lx/4 as shown in Fig. 1(d). We stress that the method also works at the critical point if the two phases are distinguishable enough. This is typically the case when the critical order parameter distribution shows two peaks as in many Ising36 and Lennard–Jones systems.37 This technique has been successfully applied to the 2d Ising model21 and to the lattice active model.12
All simulations are performed at a fixed density ρ = 0.95 by varying accordingly the box size Lx = 3Ly = (3N/ρ)1/2. This value approximately corresponds to the critical density estimated for the smallest investigated system size, which is found to be ρc = 0.953(0.037) (errors from fit are given in brackets, see the ESI† for details on the estimation of ρc).
Results
Although finite systems cannot develop any diverging correlation length, the finite-size scaling hypothesis allows us to systematically study the critical properties away from the thermodynamic limit.38 Using the finite-size scaling ansatz, we assume that a generic observable![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) near the critical point behaves as
near the critical point behaves as 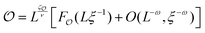 , where ζ
, where ζ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is the critical exponent associated with the observable
is the critical exponent associated with the observable ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) , F
, F![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is a universal finite-size scaling function and ω is the power of the (subleading) correction-to-scaling exponent.38 Here ν is the exponent associated with the divergence of the correlation length ξ as the control parameter is varied across the transition. In our active particle system the relaxation time of the noise τ is the control parameter, therefore we assume ξ ∼ (τ − τc)−ν. Using this and ignoring sub-leading corrections we get
is a universal finite-size scaling function and ω is the power of the (subleading) correction-to-scaling exponent.38 Here ν is the exponent associated with the divergence of the correlation length ξ as the control parameter is varied across the transition. In our active particle system the relaxation time of the noise τ is the control parameter, therefore we assume ξ ∼ (τ − τc)−ν. Using this and ignoring sub-leading corrections we get ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = Lζ
= Lζ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) /νG
/νG![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (L1/ν(τ − τc)) (where G
(L1/ν(τ − τc)) (where G![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is a universal scaling function). This implies that, if the correct τc, ν and ζ
is a universal scaling function). This implies that, if the correct τc, ν and ζ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) are known, all values of
are known, all values of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) measured for different sizes should collapse onto each other when L−ζ
measured for different sizes should collapse onto each other when L−ζ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) /ν
/ν![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is plotted as a function of L1/ν(τ − τc).
is plotted as a function of L1/ν(τ − τc).
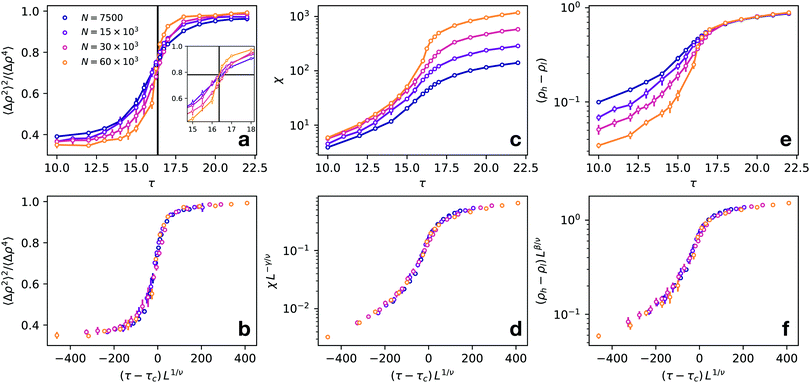
A particularly interesting observable is the fourth order cumulant of density fluctuations 〈Δρ2〉2/〈Δρ4〉 (the Binder parameter39–41), where brackets indicate averages over configurations and over sub-boxes. The density fluctuations are computed in the four L × L sub-boxes described above, specifically 〈Δρ2〉 = 〈(Nb/L2 − 〈Nb/L2〉)2〉 where Nb is the number of particles found in one single sub-box. For the Binder parameter we expect ζ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 0 and thus it should be size-independent at τ = τc.
= 0 and thus it should be size-independent at τ = τc.
Exploiting this property we locate τc = 16.361(0.058) and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = [〈Δρ2〉2/〈Δρ4〉]τ=τc = 0.781(0.017) as the intersection of the data for N = 15 × 103 and N = 60 × 103 (Fig. 2(a)). We chose to use these two sizes because N = 60 × 103 is the largest simulated size and N = 15 × 103 is two times smaller in linear size. The estimated value of
= [〈Δρ2〉2/〈Δρ4〉]τ=τc = 0.781(0.017) as the intersection of the data for N = 15 × 103 and N = 60 × 103 (Fig. 2(a)). We chose to use these two sizes because N = 60 × 103 is the largest simulated size and N = 15 × 103 is two times smaller in linear size. The estimated value of ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 0.781(0.017) is lower than the corresponding value found in the triangular lattice gas (
= 0.781(0.017) is lower than the corresponding value found in the triangular lattice gas (![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 0.8321(0.0023), see the ESI† for discussion on the triangular lattice), but it is close to that found in the active lattice model12 (
= 0.8321(0.0023), see the ESI† for discussion on the triangular lattice), but it is close to that found in the active lattice model12 (![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ≈ 0.75). Note that τc = 16.36 is approximately the value at which cumulants of all sizes cross as shown in the inset of Fig. 2(a) where we report a magnification of the main panel in a small τ-interval around τc (see the ESI† for a systematic study of the crossing points). Fig. 2(b) shows a good data collapse of the cumulant data-points with the Ising exponent ν = 1. A direct way21 to determine ν is to consider the size dependence of the slope of the cumulants at τ = τc, this method yields ν = 1.03(0.10) as shown in the ESI.†
≈ 0.75). Note that τc = 16.36 is approximately the value at which cumulants of all sizes cross as shown in the inset of Fig. 2(a) where we report a magnification of the main panel in a small τ-interval around τc (see the ESI† for a systematic study of the crossing points). Fig. 2(b) shows a good data collapse of the cumulant data-points with the Ising exponent ν = 1. A direct way21 to determine ν is to consider the size dependence of the slope of the cumulants at τ = τc, this method yields ν = 1.03(0.10) as shown in the ESI.†
Next we test the scaling of the susceptibility χ = 〈(Nb − 〈Nb〉)2〉/〈Nb〉 (shown in Fig. 2(c)). Fig. 2(d) shows that the scaling is very good using the Ising critical exponent γ = 7/4. In the ESI† we also show that if we fit directly the size-dependent values of χ at τc, we obtain γ = 1.84(0.20) which is compatible with the Ising γ. Note also that the χ in Fig. 2(c) does not show the typical peak as in the Ising model. This is due to the fact that the χ is obtained here by averaging the values of Nb in both the dense and dilute phases. In the ESI† we show that the χ (computed in the same way) for the lattice gas displays a similar s-shaped curve as a function of the inverse temperature and scales with γ = 7/4. Furthermore, in Fig. 2(e) we consider the density difference between the boxes centered in the high and low-density phases (ρh − ρl) (see Fig. 1(d)), which corresponds to the order parameter of the system. Note that this quantity is on average greater than zero since, even in the homogeneous phase, since the density around the center of mass for a given configuration is expected to be larger than the density in the low-density sub-boxes. We find that this quantity displays a good scaling with the Ising exponent β = 1/8 = 0.125 (Fig. 2(f)). It is worth stressing that in the thermodynamic limit, the order parameter would be different from zero only for τ > τc. It is, however, expected that for finite systems, a smooth variation of the order parameter could also be found below τc and that this should scale with the appropriate exponent. We have also checked that (ρh − ρl), computed as in the active system, scales with β = 0.125 in the case of the 2d equilibrium lattice gas for temperatures above the critical temperature (see the ESI† for details). A direct fit of the size-dependent critical (ρh − ρl) gives β = 0.113(0.055), which is compatible with the Ising β. To improve the accuracy of the β estimate we apply a finer technique finding the value of the exponent which optimizes the data collapse (see the ESI† for details on β estimation). This yields β = 0.133(0.022).
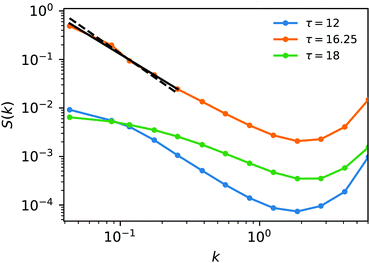
Next we test if our results are consistent with the Ising exponent η = 1/4 which controls the decay of the static structure factor S(k) near the critical point, i.e. S(k) ∼ k−2+η. To this aim we compute 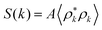 where ρk is the Fourier transform of the density fluctuations and the normalization factor A is chosen so that S(0) = 〈ΔNb2〉/〈Nb〉. To avoid the interface and focus only on the bulk phase we compute the S(k) for particles in the dilute phase considering only those particles having |x − Lx/4| < L/2, i.e. all particles in the left sub-boxes in Fig. 1(d). As shown in Fig. 3 the resulting S(k) close to criticality becomes fairly linear in the double log scale at low k. The data at low k are well fitted by the power law k−2+η with η = 1/4 (full line) which is appreciably different from the mean-field decay S(k) ∼ k−2 (dashed line). A direct power-law fit of these points gives 2 − η = 1.709(0.090) and η = 0.290(0.090) which are compatible with the Ising values 2 − η = 1.75 and η = 0.25.
where ρk is the Fourier transform of the density fluctuations and the normalization factor A is chosen so that S(0) = 〈ΔNb2〉/〈Nb〉. To avoid the interface and focus only on the bulk phase we compute the S(k) for particles in the dilute phase considering only those particles having |x − Lx/4| < L/2, i.e. all particles in the left sub-boxes in Fig. 1(d). As shown in Fig. 3 the resulting S(k) close to criticality becomes fairly linear in the double log scale at low k. The data at low k are well fitted by the power law k−2+η with η = 1/4 (full line) which is appreciably different from the mean-field decay S(k) ∼ k−2 (dashed line). A direct power-law fit of these points gives 2 − η = 1.709(0.090) and η = 0.290(0.090) which are compatible with the Ising values 2 − η = 1.75 and η = 0.25.
Up to this point, we have discussed quantities which display a critical behavior also in equilibrium fluids. We now show an observable that is zero in equilibrium while it exhibits a singular behavior in the active case. Since in active systems the instantaneous velocities are coupled to positions,27 whenever MIPS occurs, dense regions of slow particles coexist with dilute regions of fast ones.20 We then consider the average squared speed of particles in the dense and dilute sub-boxes that we indicate, respectively, with 〈|ṙ|2〉h and 〈|ṙ|2〉l. The quantity 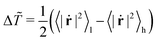 can be seen as the (effective) kinetic temperature difference between the two phases and its behavior is shown in Fig. 4(a). As expected Δ
can be seen as the (effective) kinetic temperature difference between the two phases and its behavior is shown in Fig. 4(a). As expected Δ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) decreases, as the two phases progressively mix upon lowering τ. By combining mean-field theory with a small-τ approximation of the AOUP model we have derived the scaling Δ
decreases, as the two phases progressively mix upon lowering τ. By combining mean-field theory with a small-τ approximation of the AOUP model we have derived the scaling Δ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ∼ (τ − τc)κ (see Appendix A). Moreover these approximations lead to the identification of the exponent κ of Δ
∼ (τ − τc)κ (see Appendix A). Moreover these approximations lead to the identification of the exponent κ of Δ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) with the exponent β of the order parameter. Indeed we find a good data collapse for Δ
with the exponent β of the order parameter. Indeed we find a good data collapse for Δ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) if we use the exponents κ = β = 1/8 and ν = 1 (Fig. 4(b)). A direct estimate of the exponent gives κ = 0.122(0.022) satisfying κ = β within the errors (see the ESI† for details).
if we use the exponents κ = β = 1/8 and ν = 1 (Fig. 4(b)). A direct estimate of the exponent gives κ = 0.122(0.022) satisfying κ = β within the errors (see the ESI† for details).
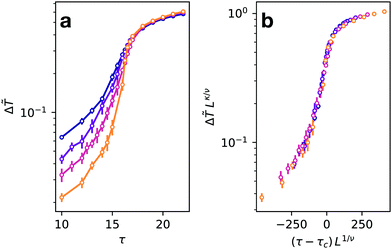 | ||
| Fig. 4 (a) Kinetic temperature difference between the dilute and dense phases plotted as a function of τ (different colors indicate different system sizes, legends are the same as Fig. 2(a)). (b) Data of (a) scaled with the exponents ν = 1 and κ = β = 1/8. | ||
Conclusions
In this article, we have studied the critical properties of an active system undergoing MIPS in two spatial dimensions. Performing large-scale numerical simulations on GPU we have demonstrated that the critical behavior of the system agrees well with the Ising universality class. The importance of simulating large system sizes is worth stressing since previous studies on ABPs have reported different values of the critical exponents.21 Although it has been speculated12 that the limited sizes employed did not allow the observation of the scaling regime, it is true that similar sizes have been exploited for the study of critical passive attractive liquids, providing numerical results compatible with the Ising universality class.34 We instead suspect that for those sizes another correlation length, different from the critical one, may interfere with the scaling behaviour of the active system. A recent work42 has shown that the dense phase formed by active particles undergoing MIPS is made of a mosaic of hexatic micro-domains. We find that, at the critical point, the hexatic correlation length is comparable with the size of the sub-boxes employed for the FSS analysis when the system is small (N = 3750), justifying the choice of larger system sizes (see the ESI† for discussion). Indeed for a size as small as N = 3750 we find that the crossing point of the Binder cumulant is observed at quite low values, although a reasonable scaling is found. Although we expect that the microscopic dynamical details of the model (ABPs or AOUPs) should not affect the universality class of the system, large-scale simulations of critical ABPs are necessary to further clarify this issue.Our large-scale simulation results are also consistent with recent works taking into account non-integrable active terms in a field-theoretical framework.43 These models, in some parameter range, may show micro-phase separation instead of a full MIPS and must be included in a different (non-Ising) universality class. Differently when parameters allow for a full MIPS the extra terms in these active field-theories are irrelevant (in a renormalization group sense) and the system belongs to the Ising universality class. On the other hand, far from criticality, these non-equilibrium contributions could produce significant differences with respect to an equilibrium gas–liquid phase separation.20,44–47 Within this context it would be interesting to understand how one could make the active critical point unstable43 by altering the microscopic interactions and/or the dynamics.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A
Derivation of the exponent identity κ = β
To derive the exponent identity κ = β we considered an AOU particle in d = 1 and subjected it to an external potential Φ(x). It is known33,48 that for small τ the velocity distribution of the particle is a zero-centered Gaussian with variance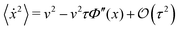 | (A.1) |
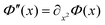 is the potential curvature. We now assume that the total potential curvature Φ experienced by the probe particle in x is generated by the interactions with other particles:
is the potential curvature. We now assume that the total potential curvature Φ experienced by the probe particle in x is generated by the interactions with other particles: 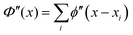 , where ϕ′′(x − xi) is the second derivative of the pair interaction potential. This can be rewritten as
, where ϕ′′(x − xi) is the second derivative of the pair interaction potential. This can be rewritten as 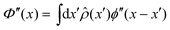 where the integral extends over all space, and we have introduced the density field
where the integral extends over all space, and we have introduced the density field 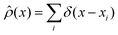 . By ignoring density fluctuations (mean-field approximation) we set
. By ignoring density fluctuations (mean-field approximation) we set ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x) = ρ = constant and we obtain
(x) = ρ = constant and we obtain 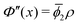 , where
, where 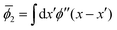 is the mean potential curvature which is assumed to be positive. By using this in eqn (1) and neglecting higher order corrections we get 〈ẋ2〉 = v2(1 − τ
is the mean potential curvature which is assumed to be positive. By using this in eqn (1) and neglecting higher order corrections we get 〈ẋ2〉 = v2(1 − τ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2ρ). We now consider the difference between the averaged squared speed in the low and high density phases, i.e.
2ρ). We now consider the difference between the averaged squared speed in the low and high density phases, i.e.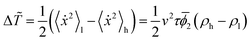 . If we now assume that (ρh − ρl) ∼ (τ − τc)β near the critical point we have:
. If we now assume that (ρh − ρl) ∼ (τ − τc)β near the critical point we have:Δ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ∼ (τ − τc)κ ∼ (τ − τc)κ | (A.2) |
Acknowledgements
MP acknowledges financial support from the H2020 program and from the Secretary of Universities and Research of the Government of Catalonia through Beatriu de Pinós program Grant No. 2018 BP 00088.References
- L. Kadanoff, Critical behavior, universality and scaling in critical phenomena, 1971 Search PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- A. Klopper, Nat. Phys., 2018, 14, 645 Search PubMed.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- G. Liu, A. Patch, F. Bahar, D. Yllanes, R. D. Welch, M. C. Marchetti, S. Thutupalli and J. W. Shaevitz, Phys. Rev. Lett., 2019, 122, 248102 CrossRef CAS.
- H. B. Callen, Thermodynamics and an Introduction to Thermostatistics, 1998 Search PubMed.
- C. Domb, Phase transitions and critical phenomena, Elsevier, 2000 Search PubMed.
- M. Paoluzzi, C. Maggi and A. Crisanti, Phys. Rev. Res., 2020, 2, 023207 CrossRef CAS.
- M. Paoluzzi, C. Maggi, U. Marini Bettolo Marconi and N. Gnan, Phys. Rev. E, 2016, 94, 052602 CrossRef CAS.
- B. Partridge and C. F. Lee, Phys. Rev. Lett., 2019, 123, 068002 CrossRef CAS.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- A. Patch, D. Yllanes and M. C. Marchetti, Phys. Rev. E, 2017, 95, 012601 CrossRef.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- D. Levis, J. Codina and I. Pagonabarraga, Soft Matter, 2017, 13, 8113–8119 RSC.
- A. Patch, D. M. Sussman, D. Yllanes and M. C. Marchetti, Soft Matter, 2018, 14, 7435–7445 RSC.
- S. Hermann, P. Krinninger, D. de las Heras and M. Schmidt, Phys. Rev. E, 2019, 100, 052604 CrossRef CAS.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS.
- S. Mandal, B. Liebchen and H. Löwen, Phys. Rev. Lett., 2019, 123, 228001 CrossRef CAS.
- J. T. Siebert, F. Dittrich, F. Schmid, K. Binder, T. Speck and P. Virnau, Phys. Rev. E, 2018, 98, 030601 CrossRef CAS.
- F. Dittrich, T. Speck and P. Virnau, 2020, arXiv preprint arXiv:2010.08387.
- M. Nijmeijer and J. Weis, Phys. Rev. Lett., 1995, 75, 2887 CrossRef CAS.
- I. Mryglod, I. Omelyan and R. Folk, Phys. Rev. Lett., 2001, 86, 3156 CrossRef CAS.
- C. Maggi, U. M. B. Marconi, N. Gnan and R. Di Leonardo, Sci. Rep., 2015, 5, 10742 CrossRef.
- G. Szamel, E. Flenner and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062304 CrossRef.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef.
- S. Dal Cengio, D. Levis and I. Pagonabarraga, Phys. Rev. Lett., 2019, 123, 238003 CrossRef CAS.
- L. L. Bonilla, Phys. Rev. E, 2019, 100, 022601 CrossRef CAS.
- R. Wittmann, U. M. B. Marconi, C. Maggi and J. M. Brader, J. Stat. Mech.: Theory Exp., 2017, 2017, 113208 CrossRef.
- U. M. B. Marconi, M. Paoluzzi and C. Maggi, Mol. Phys., 2016, 114, 2400–2410 CrossRef CAS.
- G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012111 CrossRef.
- U. M. B. Marconi, N. Gnan, M. Paoluzzi, C. Maggi and R. Di Leonardo, Sci. Rep., 2016, 6, 23297 CrossRef CAS.
- M. Rovere, P. Nielaba and K. Binder, Z. Phys. B: Condens. Matter, 1993, 90, 215–228 CrossRef.
- L. Bai and D. Breen, J. Graph. Tools, 2008, 13, 53–60 CrossRef.
- J. A. Plascak and P. Martins, Comput. Phys. Commun., 2013, 184, 259–269 CrossRef CAS.
- J. J. Potoff and A. Z. Panagiotopoulos, J. Chem. Phys., 1998, 109, 10914–10920 CrossRef CAS.
- D. J. Amit and V. Martin-Mayor, Field Theory, the Renormalization Group, and Critical Phenomena: Graphs to Computers Third Edition, World Scientific Publishing Company, 2005 Search PubMed.
- K. Binder, Z. Phys. B: Condens. Matter, 1981, 43, 119–140 CrossRef.
- M. Rovere, D. Hermann and K. Binder, Europhys. Lett., 1988, 6, 585 CrossRef.
- M. Rovere, D. W. Heermann and K. Binder, J. Phys.: Condens. Matter, 1990, 2, 7009 CrossRef.
- C. B. Caporusso, P. Digregorio, D. Levis, L. F. Cugliandolo and G. Gonnella, 2020, arXiv preprint arXiv:2005.06893.
- F. Caballero, C. Nardini and M. E. Cates, J. Stat. Mech.: Theory Exp., 2018, 2018, 123208 CrossRef.
- R. Wittkowski, A. Tiribocchi, J. Stenhammar, R. J. Allen, D. Marenduzzo and M. E. Cates, Nat. Commun., 2014, 5, 4351 CrossRef CAS.
- C. Nardini, É. Fodor, E. Tjhung, F. Van Wijland, J. Tailleur and M. E. Cates, Phys. Rev. X, 2017, 7, 021007 Search PubMed.
- R. Singh and M. E. Cates, Phys. Rev. Lett., 2019, 123, 148005 CrossRef CAS.
- E. Tjhung, C. Nardini and M. E. Cates, Phys. Rev. X, 2018, 8, 031080 CAS.
- D. Martin, J. O'Byrne, M. E. Cates, É. Fodor, C. Nardini, J. Tailleur and F. van Wijland, 2020, arXiv preprint arXiv:2008.12972.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02162h |
| This journal is © The Royal Society of Chemistry 2021 |