Open Access Article
Open Access ArticleLarge-scale comparison of 3d and 4d transition metal complexes illuminates the reduced effect of exchange on second-row spin-state energetics†
Aditya
Nandy‡
 ab,
Daniel B. K.
Chu‡
ab,
Daniel B. K.
Chu‡
 a,
Daniel R.
Harper
ab,
Chenru
Duan
ab,
Naveen
Arunachalam
a,
Daniel R.
Harper
ab,
Chenru
Duan
ab,
Naveen
Arunachalam
 a,
Yael
Cytter
a and
Heather J.
Kulik
a,
Yael
Cytter
a and
Heather J.
Kulik
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu; Tel: +1-617-253-4584
bDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 10th August 2020
Abstract
Density functional theory (DFT) is widely used in transition-metal chemistry, yet essential properties such as spin-state energetics in transition-metal complexes (TMCs) are well known to be sensitive to the choice of the exchange–correlation functional. Increasing the amount of exchange in a functional typically shifts the preferred ground state in first-row TMCs from low-spin to high-spin by penalizing delocalization error, but the effect on properties of second-row complexes is less well known. We compare the exchange sensitivity of adiabatic spin-splitting energies in pairs of mononuclear 3d and 4d mid-row octahedral transition-metal complexes. We analyze hundreds of complexes assembled from four metals in two oxidation states with ten small monodentate ligands that span a wide range of field strengths expected to favor a variety of ground states. We observe consistently lower but proportional sensitivity to exchange fraction among 4d TMCs with respect to their isovalent 3d TMC counterparts, leading to the largest difference in sensitivities for the strongest field ligands. The combined effect of reduced exchange sensitivities and the greater low-spin bias of most 4d TMCs means that while over one-third of 3d TMCs change ground states over a modest variation (ca. 0.0–0.3) in exchange fraction, almost no 4d TMCs do. Differences in delocalization, as judged through changes in the metal–ligand bond lengths between spin states, do not explain the distinct behavior of 4d TMCs. Instead, evaluation of potential energy curves in 3d and 4d TMCs reveals that higher exchange sensitivities in 3d TMCs are likely due to the opposing effect of exchange on the low-spin and high-spin states, whereas the effect on both spin states is more comparable in 4d TMCs.
1. Introduction
Approximate density functional theory (DFT) is widely used in studying the catalytic1–6 and materials7–13 properties of open-shell transition-metal complexes.14 The well-localized d or f electrons of open-shell transition-metal centers impart unique properties but also can lead to a significant number of low-energy spin and oxidation states that are challenging to describe on equal footing using approximate electronic structure methods. For DFT in particular, presently available exchange–correlation (xc) approximations suffer from one- and many-electron self-interaction errors,15–19 commonly referred to as delocalization error20–22 (DE).The high earth abundance and prevalence of 3d transition metals in enzymatic systems has motivated the widespread study16,23–41 of electronic structure method accuracy in first-row transition-metal complexes. For 3d transition-metal chemistry, DE can lead to pronounced errors in calculated bond dissociation energies,16,23–27 barrier heights,28,29 and properties of the density30–33 within a given spin state as well as the relative energetic ordering of spin states.29,34–41 While in some cases, it is possible to use higher accuracy methods such as correlated wavefunction theory, such methods have their own challenges in open-shell transition-metal complex (TMC) property prediction accuracy42–45 and remain cost-prohibitive for large-scale discovery of new TMCs.46–51
Although less earth abundant than 3d metals, 4d transition metals often form catalysts with superior catalytic activity and turnover number (e.g., Ru52–54 for water oxidation and Mo55 for hydrogen evolution) and are excellent photosensitizers.56 Despite this importance of 4d transition metals, comparatively less is known about the relative accuracy of electronic structure methods for these TMCs.57–59 While we can anticipate that there should be some transferable observations between 3d and 4d metals, a more detailed understanding of the relationship between 3d and 4d TMC sensitivity to method choice is needed.
Broadly, the need to balance cost and accuracy has motivated a number of strategies aimed at efficiently eliminating DE in approximate DFT by recovering the derivative discontinuity60 lacking from pure (i.e., generalized gradient approximation or GGA) functionals.15,61–66 Approaches have included self-interaction67–69 and closely related DFT+U70–73 corrections, tailoring higher order terms in the xc functional,37,40,45,74–85 or incorporating an admixture32,33,86–102 of Hartree–Fock (HF) exchange globally or with range-separation in a GGA. All such strategies generally behave similarly in TMCs by decreasing covalency33 or dative bonding32,103–105 and localizing density away from the metal.30,37 Functional tuning for either 3d or 4d transition-metal chemistry is challenged106 both by the limited availability of reference data and the highly system- and property-specific nature of optimal functional choice,29,35–37,107–112 although physically motivated tuning approaches have been developed for select cases.113–115 Still, tuning the global amount of HF exchange (i.e., aHF) in a GGA hybrid remains one of the most widely used approaches to improving approximate DFT errors.
For 3d midrow, octahedral TMCs, it is well known that the ground state is highly sensitive to the fraction of HF exchange due to the near-degeneracy of multiple spin states in these complexes36,82,116–119 as well as the close relationship between spin-state stabilization and DEs in approximate DFT.30,111 Pure, semi-local GGA functionals120,121 consistently stabilize overly-delocalized,18,30 strongly covalent states,33 tending to favor the increased bonding in low-spin (LS) over high-spin (HS) states.29,39,70,77,122–125 This manifestation of DE leads GGAs to predict incorrect ground states as well as relative energies14,124,125 between spin states (e.g., adiabatic HS to LS spin splitting, ΔEH–L). Hybrid functionals counteract35–37,118,126–129 the bias for LS states, but the appropriate fraction of HF exchange is strongly system dependent.35–37,108–111,130 For 3d TMCs, conflicting proposals of low (as little as aHF = 0.0)35,117,131,132 and high (aHF = 0.4–0.5)31,36,40,133,134 fractions have been recommended, but 4d TMCs do not have similar heuristics.
In this work we apply our pragmatic approach of understanding the linearized29–31,37,39 exchange sensitivity of spin-splitting energies35–37,108,117,131,132 simultaneously to 3d and 4d TMC spin-state energetics. In 3d TMCs, this spin-state ordering exchange sensitivity is correlated to the ligand field strength of coordinating ligands,37,108 with bare ions exhibiting reduced sensitivities39 in comparison to strong-field ligands. For common ligands in mid-row, 3d TMCs, this exchange sensitivity can be significant, leading to a change in ΔEH–L on the order of 10–20 kcal mol−1 for a change in HF exchange from aHF = 0.15 (e.g. in B3LYP*132) to aHF = 0.25 (e.g., in PBE0135). While the form of the pure GGA xc being tuned (e.g., BLYP vs. PBE) can influence ΔEH–L, the HF exchange sensitivity has been shown to be invariant to GGA choice in 3d TMCs.37,39,40 These strong relationships between chemical structure and method sensitivity in 3d TMCs have enabled the development of machine learning models to predict exchange sensitivity and exchange-dependent properties, enlarging understanding of how changes in functional definition can influence large-scale discovery efforts.136–139
Although these relationships have been established and fruitfully applied for 3d TMCs, the sensitivity of second-row (i.e., 4d) TMCs to HF exchange is not well known. In this work, we carry out a large-scale study of hundreds of mononuclear octahedral TMCs to understand broad relationships among first- and second-row spin-state ordering and exchange sensitivity. In Section 2, we describe how we construct a data set in which both the 3d and an isovalent 4d metal complex's properties and sensitivity to exchange are known for mid-row transition metals in low-, intermediate-, and high-spin states. In Section 3, we discuss our results on quantifying distinct behavior in ground state preference and sensitivity to HF exchange fraction for the second-row complexes. We identify sources for this difference by noting distinct effects of exchange on each spin state's potential energy surface in 3d and 4d TMCs. Finally, in Section 4, we provide our conclusions.
2. Computational details
a. Data set construction
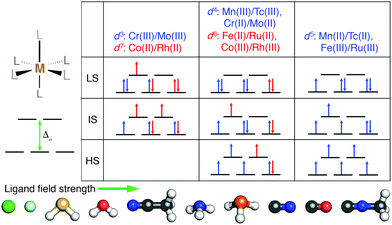
We studied the effect of HF exchange on the spin-state ordering of octahedral TMCs with a single mid-row transition-metal center. We compared properties of TMCs comprised of first-row (i.e., 3d valence) Cr, Mn, Fe, and Co to second-row (i.e., 4d valence) Mo, Tc, Ru, and Rh (Fig. 1). In all cases, we calculated properties of metal centers in formal M(II) or M(III) oxidation states to ensure differences in spin state correspond to differences in d orbital occupations (Fig. 1). The TMCs were evaluated in up to three spin states: low-spin (LS), intermediate-spin (IS), and high-spin (HS), where we defined the IS and HS states as those that differ from the LS state (i.e., with ls unpaired electrons) by two more (i.e., ls + 2) or four more (i.e., ls + 4) unpaired electrons, respectively. We then computed the gas phase, adiabatic spin-splitting energy: between the LS and HS states, ΔEH–L, as well as between the IS state and either the HS or the LS state (i.e., ΔEH–I and ΔEI–L). The nominally d3 Cr(III)/Mo(III) and d7 Co(II)/Rh(II) were evaluated only in LS doublet and IS quartet spin multiplicities (i.e., also the highest accessible spin state), and only ΔEI–L was computed (Fig. 1). The d5 metals (i.e., Mn(II)/Tc(II) or Fe(III)/Ru(III)) were studied in LS doublet, IS quartet, and HS sextet states (Fig. 1). Analogously, d4 (i.e., Mn(III)/Tc(III) or Cr(II)/Mo(II)) and d6 (i.e., Fe(II)/Ru(II) or Co(III)/Rh(III)) metals were calculated in LS singlet, IS triplet, and HS quintet states (Fig. 1).We calculated properties of complexes formed from combinations of ten small, monodentate ligands that spanned ligand field strengths and coordinating element identities. Negatively charged halides (Cl− and F−) ions are known140 to have among the weakest field strengths, while several others (i.e., phosphine, carbonyl, and cyanide) have among the highest field strengths (Fig. 1). Intermediate behavior is expected of the remaining (i.e., water, ammonia, hydrogen sulfide, acetonitrile, and methyl isocyanide) ligands (Fig. 1). In addition to homoleptic complexes, heteroleptic complexes were formed from up to two ligands (i.e., L1 and L2). Both M(L1)4(L2)2 TMCs with the two minority L2 ligands either trans (i.e., aligned 180° in the TMC) or cis (i.e., 90° in the TMC) were studied along with M(L1)5(L2) TMCs.
b. Electronic structure calculations
Calculations on mononuclear, octahedral TMCs studied in this work followed an established protocol.141,142 All initial structures were generated using molSimplify,48,143,144 which employs OpenBabel145,146 as a backend for ligand structure generation. These calculations were automated and checked for fidelity with molSimplify automatic design (mAD).119,141 All TMCs were geometry optimized with DFT using a development version of TeraChem.147,148 For the geometry optimizations, the standard B3LYP149–151 global hybrid functional was employed along with modified forms in which the Hartree–Fock exchange fraction (aHF) was varied from its default value of 0.20 to as low as aHF = 0.00 (i.e., a pure BLYP GGA) or as high as aHF = 0.30 in increments of 0.05 while holding the LDA/GGA exchange ratio fixed.37,136 As in 3d TMCs,37,39,40 sensitivities from aHF variations using PBE as the GGA xc functional are comparable on a representative 4d TMC (ESI,† Table S1). All calculations employed the LANL2DZ152 effective core potential for transition metals and the 6-31G* basis for all other atoms. Only singlet calculations were carried out in a spin-restricted formalism, with all other spin multiplicities carried out unrestricted. Level shifting153 was employed to aid self-consistent field (SCF) convergence with the majority spin and minority spin virtual orbitals each shifted by 0.25 Ha. The default SCF convergence threshold of 3 × 10−5 for the largest component of the DIIS vector was employed. Geometry optimizations were carried out in translation rotation internal coordinates154 using the L-BFGS algorithm to default tolerances for the gradient of 4.5 × 10−4 Hartree Bohr−1 and energy difference between steps of 10−6 Hartree. Geometric properties from a representative case optimized with a larger triple-ζ basis set and the resulting exchange sensitivities preserves trends (ESI,† Table S1).For the mAD calculation workflow, calculations were run for 24-hour increments and resubmitted for up to five additional runs. At each resubmission, mAD applies loose geometric criteria141 and abandons any calculations that fail these checks (ESI,† Table S2). In this workflow, the B3LYP (aHF = 0.20) geometry optimization was carried out first. If the B3LYP geometry optimization converged, we used the converged structure and wavefunction to initialize geometry at the adjacent increased (i.e., 0.25) and decreased (i.e., 0.15) aHF values, as in prior work.136 If these calculations converged, their structures and wavefunctions were then used for the next adjacent (e.g., increased to 0.30 or decreased to 0.10) aHF value geometry optimizations. However, if an optimization failed to converge, the next aHF value was not attempted.
For all converged calculations, automated data fidelity checks were employed based on refinements of prior geometric141 and electronic structure criteria141,142,155 (ESI,† Table S2). Specifically, complexes were retained if their structure was deemed to be intact based on tighter geometric criteria than were employed during the optimization (ESI,† Table S3). The electronic structure criteria required that the deviation of the Ŝ2 expectation value from its anticipated value (i.e., S(S + 1)) was below 1 and the Mulliken metal atomic spin density was within 1 μB of the total spin of the molecule (ESI,† Table S3).
Linearized exchange sensitivities, S, were obtained from linear fits of the dependence of the relevant property (e.g., ΔEH–L) on aHF. The resulting sensitivity (e.g., S(ΔEH–L)) is reported as the change in property over the range from aHF = 0.0 to 1.0, which we refer to as HFX as in prior work.29,37,136 As long as a single, qualitatively consistent electronic state has been converged over all points, this linear approximation is known to be good for a range of properties, both energetic (e.g., spin splitting29,35–37,131,136 and reaction energies29,156) and electronic30,31,157 in nature. To ensure that linearized exchange sensitivities could be quantitatively obtained from collected data points, we applied a series of constraints and filtering steps; this procedure and its results are detailed in ESI,† Table S4. All raw data, resulting R2 values, computed sensitivities, and reasons for eliminating points or sensitivities are provided in the ESI.†
Potential energy curves (PECs) of 3d Fe(II) and 4d Ru(II) in LS singlet and HS quintet states were obtained for homoleptic complexes of He atoms and CO ligands also using TeraChem and B3LYP/LACVP* with modified aHF values. These PECs were obtained by rigidly shifting all six He atom (CO) ligands from distances as short as 1.70 Å (1.80 Å) to as long as 2.90 Å (2.80 Å) in 0.01 Å (0.02 Å) increments, with calculations at longer bond lengths starting from the converged wavefunction at the shorter bond lengths. The He atom was selected following recent work43 that showed it is a representative weak field ligand, and a single He atom is simpler to translate during PEC evaluation than a typical non-linear weak-field ligand (i.e., H2O or NH3). The CO bond length was fixed to 1.125 Å, its value in relaxed TMCs. These calculations were repeated for aHF fractions increasing from 0.0 to 0.45 in increments of 0.05, with wavefunctions always initializing from shorter bond lengths and lower aHF values. All total energies and computed sensitivities are provided in the ESI.†
3. Results and discussion
a. Ligand field sensitivity trends in homoleptic TMCs
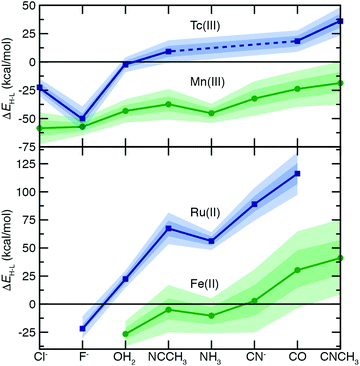
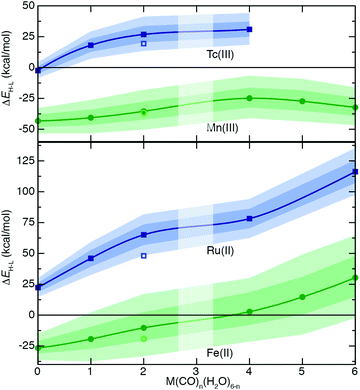
To understand the extent to which previous observations35–38,40,126,131 in first-row transition metals are likely to be generalizable to the second row, we first compared spin-splitting properties for a subset of homoleptic complexes. Depending on the field strength of the ligand, 3d Fe(II) TMCs are known to favor distinct ground states.140 For example, d6 Fe(II) TMCs with intermediate-field nitrogen-coordinating ligands commonly exhibit spin crossover (SCO)158 phenomena by changing from an LS singlet to HS quintet state with increasing temperature. The ΔEH–L for these complexes is sensitive to HF exchange fraction, becoming more negative with increasing aHF. The combination of this physical phenomenon with sensitivity to DFT functional parameters means that different aHF values can predict the same complex to have either an LS or HS ground state.35–38,40,126,131Indeed, for the complexes studied in this work, homoleptic complexes of Fe(II) with acetonitrile or cyanide have near-degenerate LS and HS states when evaluated with B3LYP and thus are predicted to be LS with lower HF exchange (i.e., aHF = 0.1) but HS with higher fractions (i.e., aHF = 0.3, Fig. 2). Consistent with prior observations,36,37,136 the magnitude of this typically negative exchange sensitivity, S, generally increases with field strength. This means that a hexa-carbonyl Fe(II) complex that is strongly LS with B3LYP can become HS with higher exchange fractions (ca. aHF = 0.4), whereas weak-field hexa-aqua Fe(II) is uniformly HS for all aHF values (Fig. 2).
In comparison to their first-row counterparts, the isovalent 4d Ru(II) TMCs are considerably low-spin shifted, with almost all Ru(II) complexes strongly favoring LS states over HS states except for the weakest field (i.e., hexa-fluoride) cases (Fig. 2). The Ru(II) homoleptic complexes also exhibit uniformly reduced exchange sensitivities (Fig. 2). Thus, complexes with modest B3LYP ΔEH–L values (e.g., hexa-aqua Ru(II), ca. 25 kcal mol−1) are not predicted to change their ground state with varied aHF in contrast to Fe(II) homoleptic complexes (Fig. 2). Despite these differences, qualitative trends with ligand field strength appear preserved from Fe(II) to Ru(II), with increasing exchange sensitivity apparent with increasing ligand field (Fig. 2).
Given the strong LS shift of 4d Ru(II) TMCs with respect to their 3d Fe(II) TMC counterparts, we identified d4 Tc(III) as a possible metal/oxidation state where TMCs could be expected to favor HS or LS states depending on field strength (Fig. 2). The 4d Tc(III) singlet LS and quintet HS states are in fact close in energy with B3LYP for weak-field (i.e., hexa-aqua) and intermediate-field (i.e., hexa-acetonitrile) complexes (Fig. 2). The isovalent Mn(III) complexes are comparatively HS shifted, with only the homoleptic methyl-isocyanide with a pure BLYP (i.e., aHF = 0.0) GGA coming close to spanning the LS–HS transition (Fig. 2). The exchange sensitivity of all Mn(III) homoleptic TMCs is reduced with respect to the Fe(II) TMCs but follows a consistent trend of increasing with increasing ligand field strength (Fig. 2). Consistent with 3d/4d observations from Fe(II)/Ru(II), Tc(III) homoleptic TMCs have reduced exchange sensitivity compared to isovalent Mn(III) (Fig. 2). This means that even though a number of 4d Tc(III) TMCs have modest B3LYP ΔEH–L (<25 kcal mol−1) values, the only ground state assignment change for Tc(III) in this series would be for the B3LYP HS hexa-aqua complex to become LS when aHF is 0.1 or less (Fig. 2). Overall, reduced exchange sensitivities in these 4d TMCs (i.e., whether with Ru(II) or Tc(III)) would require the B3LYP ΔEH–L to be within ±10 kcal mol−1 as opposed to ±25 kcal mol−1 for comparable 3d TMCs for the 4d TMC spin-state preference to change with HF exchange.
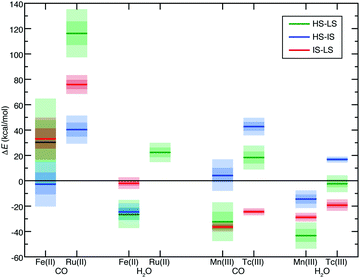
Both d6 Fe(II)/Ru(II) and d4 Mn(III)/Tc(III) TMCs have an IS triplet state. We thus also calculated the IS state to obtain ΔEH–I and ΔEI–L as well as their sensitivities (i.e., S(ΔEH–I) and S(ΔEI–L)) for select homoleptic TMCs. We identified hexa-carbonyl TMCs as representative strong-field complexes and hexa-aqua as representative weak-field complexes (Fig. 3). All 4d TMCs favor IS states over HS states with B3LYP (i.e., ΔEH–I > 0) unlike the isovalent 3d TMCs (Fig. 3). Spin-state orderings change with aHF due to high S for several of the 3d TMCs (i.e., HS–IS/HS–LS Fe(II)(CO)6, IS–LS Fe(II)(H2O)6, and HS–IS Mn(III)(CO)6) but only one of the 4d TMCs (i.e., HS–LS Tc(III)(H2O)6) in part due to the reduced exchange sensitivity of 4d TMCs (Fig. 3).
For all spin-splitting energies, the hexa-aqua exchange sensitivities are lower than those for hexa-carbonyl in both 3d and 4d TMCs (Fig. 3). As can be expected,39,40S(ΔEH–I) and S(ΔEI–L) are reduced with respect to S(ΔEH–L), with S(ΔEI–L) consistently the smallest of the three (Fig. 3). The trend holds across the over 150 pairs of 3d/4d heteroleptic or homoleptic TMCs for which all three spin-state energies have been evaluated. On average, S(ΔEI–L) and S(ΔEH–I) values are 38% and 62% of S(ΔEH–L), respectively (ESI,† Table S5). That is, when the 4d TMC S value is reduced with respect to its 3d TMC counterpart, this reduction is proportional across both spin states and ligand chemistry.
b. Global comparison of 3d and 4d TMCs
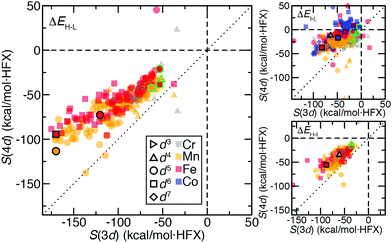
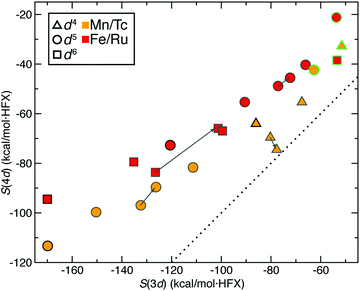
We next expanded our comparison of HS–LS energies and their sensitivities to include heteroleptic complexes for an overall set of more than 200 d4–d6 TMC pairs. Over all of these 3d/4d TMC pairs, the 4d S(ΔEH–L) was consistently reduced with respect to that for 3d TMCs (Fig. 4). The largest (i.e., most negative) 3d S(ΔEH–L) values are larger than those of 4d TMCs by around 50 kcal mol−1 HFX−1 (i.e., around 40% larger, ESI,† Table S6). For each 3d metal/oxidation state, average exchange sensitivities also vary, i.e., highest for Mn(II) or Fe(II) and lowest for Cr(II), with similar trends for the isovalent 4d metal/oxidation states (ESI,† Table S6). The overall reduced sensitivities of 4d TMCs become more apparent the larger the 3d TMC S values are (Fig. 4). Based on prior analysis36,37,136 and our observations on homoleptics, this should mean that strong-field 3d TMCs are much more sensitive to HF exchange than 4d TMCs while weak-field 3d and 4d TMCs complexes have more similar exchange sensitivity (Fig. 4). Indeed, the sensitivities of the prototypical strong-field hexa-carbonyl and weak-field hexa-aqua homoleptics largely reside at extremes of the overall relationship between 3d and 4d TMC S values (Fig. 4).There are a few noteworthy exceptions where the 4d TMC S exceeds that of its 3d TMC counterpart, namely: (i) in weak-field, hexafluoro complexes of Mn(III)/Tc(III) (S(3d) ca. −35 vs. S(4d) −50 to −70 kcal mol−1 HFX−1) and (ii) in stronger fields (e.g., Mn(II)(NCCH3)4(CNCH3)2) where the 3d TMC sensitivity is typical but the Tc(II) value is among the largest evaluated for 4d TMCs (ESI,† Table S7). The strong net negative charge on the halide complexes also results in other types of outliers: Ru(III) hexafluoride and a Cl−-containing Mo(II) complex are the only two 4d TMC cases for which the S(ΔEH–L) is weakly (ca. 20–45 kcal mol−1 HFX−1) positive (ESI,† Table S8). In both 4d TMCs, the corresponding 3d TMC still has a negative, albeit small S value (ESI,† Table S8).
Trends for the 2-electron ΔEH–I are largely consistent with those for the 4-electron ΔEH–L. Although overall S(ΔEH–I) values for both 3d and 4d TMCs are lower than S(ΔEH–L), 3d TMC sensitivities nearly always exceed their 4d TMC values (Fig. 4 and ESI,† Table S6). The 3d/4d metal/oxidation states with the highest average S(ΔEH–L) (i.e., Mn(II)/Tc(II) and Fe(II)/Ru(II)) also have the highest S(ΔEH–I) values (ESI,† Table S6). On average, best-fit lines relating S(4d) vs. S(3d) for ΔEH–L and ΔEH–I have comparable ratios of change in S(4d) per change in S(3d) of 0.55 and 0.65, respectively (ESI,† Table S6). As in the case of ΔEH–L, a small number of 4d TMC ΔEH–I sensitivities exceed their 3d TMC counterparts and typically correspond to Mn(II) complexes with strong-field equatorial ligands (CO or NCCH3) expected to have strong Jahn–Teller distortion (ESI,† Table S7).
We also analyzed 2-electron ΔEI–L pair trends, which additionally include d3 Cr(III)/Mo(III) and d7 Co(II)/Rh(II) TMCs in their doublet LS and quartet IS states (see Fig. 1). As in the other two cases of spin-splitting energetics, 4d TMCs exhibit reduced exchange sensitivity with respect to 3d TMCs (Fig. 4 and ESI,† Table S6). For the d3/d7 TMCs for which only ΔEI–L is defined, S(4d)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(3d) ratios from best-fit lines of 0.42 for d3 and 0.64 for d7 are consistent with the ratios observed in d4–d6 TMCs (ESI,† Table S6). Several more 4d TMC outliers that are close to parity are observed, typically Mn(III)/Tc(III) complexes with equatorial chlorides or Cr(II)/Mo(II) complexes with equatorial ammonia ligands (Fig. 4 and ESI,† Table S7). Far more positive 4d TMC sensitivities are observed for several Rh(III) complexes with a range of weak- and strong-field ligands (ESI,† Table S9). A handful of 3d TMCs (e.g., in Fe(II) complexes with CN− ligands) also have positive sensitivities, but the equivalent, isovalent Ru(II) TMCs have weakly negative sensitivities (ESI,† Table S9). These observations on ΔEI–L are distinct from ΔEH–L and ΔEH–I where only one cis Mo(II)(NH3)4(Cl−)2 complex had positive 4d TMC sensitivities for both quantities (ESI,† Table S8).
S(3d) ratios from best-fit lines of 0.42 for d3 and 0.64 for d7 are consistent with the ratios observed in d4–d6 TMCs (ESI,† Table S6). Several more 4d TMC outliers that are close to parity are observed, typically Mn(III)/Tc(III) complexes with equatorial chlorides or Cr(II)/Mo(II) complexes with equatorial ammonia ligands (Fig. 4 and ESI,† Table S7). Far more positive 4d TMC sensitivities are observed for several Rh(III) complexes with a range of weak- and strong-field ligands (ESI,† Table S9). A handful of 3d TMCs (e.g., in Fe(II) complexes with CN− ligands) also have positive sensitivities, but the equivalent, isovalent Ru(II) TMCs have weakly negative sensitivities (ESI,† Table S9). These observations on ΔEI–L are distinct from ΔEH–L and ΔEH–I where only one cis Mo(II)(NH3)4(Cl−)2 complex had positive 4d TMC sensitivities for both quantities (ESI,† Table S8).
c. Analysis of a heteroleptic complex series
Given the diversity of TMC chemistry in these larger data sets, we simplified our analysis to understand the extent to which trends in ΔE and S(ΔE) were additive in a narrower subset of representative 3d and 4d TMC complexes. To assess the additive nature of ligand contributions, we chose a subset of the data consisting of homoleptic complexes of a weak-field ligand (H2O), the homoleptic complexes of a strong-field ligand (CO), and the heteroleptic complexes with both ligands present. In addition to their differing field strengths, H2O and CO were chosen for their neutral charge, eliminating the need to compare TMCs of differing net charge. For a fixed metal, oxidation state, and principal quantum number, the full set can contain up to six mixed H2O/CO complexes between the homoleptic hexa-aqua and hexa-carbonyl limits. This includes two cases where a single ligand of the minority type is in the complex (i.e., 5 + 1: (CO)5(H2O) or (H2O)5(CO)) as well as four cases where two ligands of the alternate type are included in either a cis (i.e., equatorial/axial adjacent) or trans (i.e., axial) conformation (e.g., (CO)4(H2O)2 or (H2O)4(CO)2). Although the exchange sensitivity of homoleptic 3d TMCs has been widely studied,35–37,118,126–129 the expected exchange sensitivity of heteroleptic TMCs is not well established for either 3d or 4d TMCs.There is a smooth, nearly monotonic increase in ΔEH–L with increasing number of strong-field CO ligands for Fe(II) or Ru(II) complexes (Fig. 5). For the Fe(II) TMCs, B3LYP LS states become stabilized over HS states for four or more CO ligands, whereas all Ru(II) complexes are uniformly LS (Fig. 5). The trend of increasing ΔEH–L with increasing CO number is largely consistent between Ru(II) and Fe(II), but B3LYP ΔEH–L for Ru(II) is more sensitive to the number of CO ligands (Fig. 5). Interestingly, the only exception to the monotonic trend is the trans (H2O)4(CO)2 isomer, with an ΔEH–L closer to that for the mono-carbonyl complexes (Fig. 5 and ESI,† Tables S10, S11). The cis (H2O)2(CO)4 isomer has been filtered from the dataset, prohibiting broader conclusions about cis/trans isomers (see ESI†). For the Fe(II) TMCs, all mixed H2O/CO complexes span the LS/HS transition between aHF = 0.0 and 0.4 (Fig. 5). While Fe(II) TMC S values are significantly larger than for Ru(II) TMCs, both 3d and 4d complexes appear to have a monotonic increase in sensitivity with the addition of more strong-field ligands (Fig. 5 and ESI,† Table S12).
For the series of d4 Mn(III)/Tc(III) TMCs, reduced overall ligand field dependence of both ΔEH–L and S is observed with respect to Fe(II)/Ru(II) TMCs (Fig. 5 and ESI,† Tables S10, S12). The 3d Mn(III) TMCs are uniformly HS-favored regardless of aHF value (Fig. 5). Both ΔEH–L and S values appear to reach a maximum for Mn(III) complexes once all four equatorial ligands are CO with no effect of added CO axial ligands (Fig. 5). This likely occurs both because of the reduced ligand field sensitivity of Mn(III) and non-monotonic geometric changes for the most CO-saturated Mn(III) complexes (see ESI† data). Overall trends are consistent between Tc(III) and Mn(III), although the 4d TMCs are again marked by reduced S values with respect to the isovalent 3d TMCs (Fig. 5). Given the reduced sensitivities of 4d TMCs, only the homoleptic aqua Tc(III) complex spans the LS-to-HS transition, whereas even the modest ΔEH–L (<15 kcal mol−1) in the mono-carbonyl Tc(III) complex remains LS-favored over all aHF values (Fig. 5). Across an expanded series of TMCs with more metals (i.e., d5 Fe(III)/Ru(III) and Mn(II)/Tc(II)), addition of strong-field carbonyl ligands has a largely monotonic, linearly increasing effect on S values starting from the lower extreme of homoleptic hexa-aqua TMCs and moving toward the upper extreme of hexa-carbonyl TMCs (Fig. 6 and ESI,† Table S12). The most significant deviations in S between 3d/4d TMC pairs occurs for the Fe(II)/Ru(II) cases (i.e., up to a 60 kcal mol−1 HFX−1 difference) but remains substantial for most metals, excluding only the low-S Mn(III)/Tc(III) pairs (Fig. 6). Over this broad set, we confirm the cis (H2O)4(CO)2 complexes have significantly higher sensitivities for both 3d and 4d metals than their trans counterparts, with the exception of Mn(III)/Tc(III) (Fig. 6).
We also analyzed this ligand series for ΔE and S(ΔE) trends in the 2-electron HS–IS and IS–LS spin state splitting. For ΔEH–I, increasing the number of CO ligands shifts the B3LYP preference from HS to IS for most 3d metals (i.e., excluding only Mn(III) and Fe(II)), but the 4d TMC preference remains uniformly IS regardless of complex composition (ESI,† Tables S13 and S14). Although S(ΔEH–I) is lower than S(ΔEH–L), the 3d TMC spin-state preference can still shift depending upon aHF value (e.g., trans Fe(II)(H2O)4(CO)2 is IS-favoring for aHF = 0.15 but HS for B3LYP, ESI,† Table S13). The relationships of 3d and 4d TMC S(ΔEH–I) values are similar to that for S(ΔEH–L): (i) the smallest and largest S magnitudes are typically bounded by the homoleptic hexa-aqua and hexa-carbonyl complexes, respectively, and (ii) mixed complexes with more CO ligands have larger sensitivities especially in 3d versus 4d TMCs (ESI,† Fig. S1 and Table S15). For ΔEI–L, multiple d3 Cr(III)/Mo(III) and d7 Co(II)/Rh(II) complexes could also be compared in their LS doublet and IS quartet (i.e., ls + 2) states (ESI,† Tables S16 and S17). Reduced exchange sensitivity for IS–LS pairs mean that few ground state assignments change in either 3d or 4d TMCs with change in functional (ESI,† Table S15). Across all metals, the trend of increasing deviation of 3d and 4d S values with increasing ligand field strength is consistent with HS–LS and HS–IS behavior for mixed-ligand complexes, but non-monotonic behavior with CO ligand number is observed and several of the Rh(III) complexes have positive S(ΔEI–L) values (ESI,† Fig. S2). The S values are also relatively comparable and modest for early d3 Cr(III)/Mo(III) and d4 Mn(III)/Tc(III) complexes (ESI,† Fig. S2).
As a possible explanation for the distinct behavior of IS–LS spin splitting trends among complexes, we considered differences in closed-shell LS states (i.e., for d4 and d6) and open-shell ones (i.e., for d5) but observe no significant difference (ESI,† Fig. S2). The greater variability is likely due to noise in evaluating the lower IS–LS S values, in line with prior observations,29,136 and the larger range of metals and oxidation states. Despite some differences for IS–LS in comparison to HS–IS or HS–LS spin-splitting energies, the ligand series analysis suggests overall that there are consistently greater differences in the effect of exchange on 3d compared to 4d TMCs that grow with ligand field strength.
d. Effect of exchange on spin-state ordering
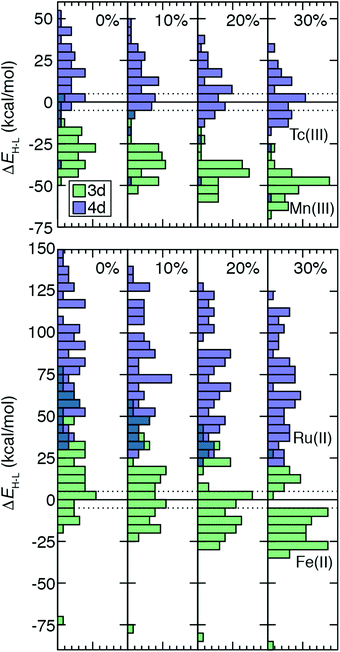
TMC spin-state splitting sensitivities depend both on row (3d vs. 4d) and electron configuration (e.g., d4vs. d6) of the metal atom as well as on the strength of the ligand field. The combined effect of these differences can be further understood by evaluating how the distribution of ΔEH–L shifts with HF exchange fraction. For this comparison, we chose 64 Fe(II)/Ru(II) and 51 Tc(III)/Mn(III) metal/oxidation state pairs where 3d TMCs and 4d TMCs span the HS–LS transition, respectively (Fig. 7). For Fe(II) TMCs, increasing HF exchange from a pure GGA to 30% has a strong effect on the distribution of ΔEH–L values (Fig. 7). Because complexes with strong-field ligands have more negative sensitivities than complexes with weak-field ligands, the width of the Fe(II) ΔEH–L distribution decreases monotonically from aHF = 0.0 (−75 to 80 kcal mol−1) to aHF = 0.3 (−90 to 30 kcal mol−1, Fig. 7). We note that a complex with |ΔEH–L| ≤ 5 kcal mol−1 could be a spin crossover (SCO) complex. Using this definition, the number of potential Fe(II) SCOs is maximal for moderate, aHF = 0.1–0.2 exchange and decreases again at higher exchange values (Fig. 7). From aHF = 0.0 to 0.3, the population of HS-favored Fe(II) TMCs also increases dramatically from 12 to 49 of 64 complexes (Fig. 7 and ESI,† Table S18).The isovalent Ru(II) TMCs span nearly as wide a range for aHF = 0.0 (30 to 150 kcal mol−1) as the 3d TMCs, but none are HS at any exchange fraction (Fig. 7 and ESI,† Table S18). Modest differences in exchange sensitivity across Ru(II) complexes have a limited effect on the shape of the distribution in comparison to Fe(II) TMCs (Fig. 7). The range of the Ru(II) ΔEH–L distribution for aHF = 0.3 (20 to 125 kcal mol−1) is reduced, but this reduction (12%) is smaller than was observed for the Fe(II) TMCs (19%).
For the Tc(III)/Mn(III) isovalent pairs, the 4d TMCs have a more even distribution of HS and LS ground states (Fig. 7). This is particularly true (18 LS and 33 HS) at aHF = 0.3, while LS is generally favored by Tc(III) TMCs (44 LS and 7 HS) at aHF = 0.0, and all aHF values have a significant number of potential Tc(III) HS–LS SCOs (Fig. 7 and ESI,† Table S18). In contrast to Fe(II), most (49 of 51) Mn(III) TMCs are HS even for aHF = 0.0, and all are significantly HS (i.e., outside of the SCO region) for aHF = 0.1 and higher (Fig. 7 and ESI,† Table S18). The Mn(III) ΔEH–L values span a smaller range than the Fe(II) TMCs, meaning that even though the width of the Mn(III) ΔEH–L distribution narrows only slightly with increasing HF exchange (aHF = 0.0: −50 to 5 kcal mol−1vs. aHF = 0.3: −25 to −70 kcal mol−1), this 18% reduction is roughly comparable to that for Fe(II) (Fig. 7). For the Tc(III) ΔEH–L distribution, there is no change in the width due to sensitivities of outliers in the distribution tails (Fig. 7). Nevertheless, both Tc(III) and Mn(III) distributions become more peaked at intermediate values of the ΔEH–L range, and the effect of aHF on the shape of both distributions is more modest than for Fe(II) but more significant than for Ru(II) TMCs (Fig. 7).
Over all 3d/4d metal/oxidation state pairs for which ΔEH–L was calculated, trends are similar to those observed for Fe(II)/Ru(II) and Tc(III)/Mn(III) (ESI,† Table S18). The HS–LS preference of 3d TMCs is highly sensitive to exchange, with an even number of LS-favoring vs. HS-favoring 3d TMCs at aHF = 0.0 becoming predominantly (90%) HS at aHF = 0.3 or higher (ESI,† Table S18). The 4d TMCs almost exclusively favor LS states at aHF = 0.0, and a much smaller number (i.e., 28) of TMCs, typically with Tc(III) and to a lesser extent Tc(II) or Mo(II), becoming HS-favored at aHF = 0.3 (ESI,† Table S18). Thus, based on this analysis, the 4d TMC LS-bias with respect to 3d TMCs combined with reduced exchange sensitivity also makes the 4d TMC HS/LS preferences significantly less sensitive to aHF values.
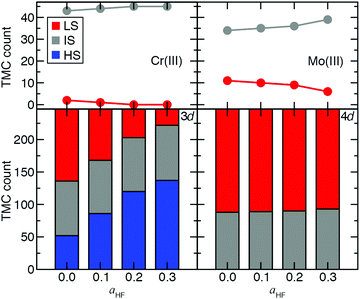
Ultimately, to quantify the effect of HF exchange on 3d/4d TMC ground state (GS) assignment, we extended the comparison of spin-state energetics to include IS states. There are 155 d4–d6 3d/4d TMC pairs for which all three (i.e., HS, IS, and LS) spin states and the spin-splitting energy sensitivities are computed. We combine these pairs with the 92 d3 or d7 3d/4d TMC pairs for which only two states were accessible (i.e., IS and LS), and their energies are computed. Over this 247-complex set, significant differences in the sensitivity of GS assignment to aHF are apparent between 3d and 4d TMCs (Fig. 8). Namely, the number of HS ground states rises from around one in five at aHF = 0.0 to over half at aHF = 0.3 for 3d TMCs, whereas none of the 4d TMCs have a HS GS at any aHF value (Fig. 8 and ESI,† Tables S19, S20). The proportion of IS states remains roughly constant for 3d TMCs over this range, although their identities shift with added exchange to predominantly d3/d7 TMCs (i.e., excluding only two Mn(III) and one Cr(II) complex, ESI,† Table S19). The 4d TMCs differ from 3d TMCs because most have either an IS (ca. 35%) or LS (ca. 65%) GS, with almost no change in this distribution with aHF value (Fig. 8 and ESI,† Table S19). While all 3d metal/oxidation states have at least one GS change from aHF = 0.0 to 0.3, only a small number (i.e., 5 of 45) of d3 Mo(III) 4d TMCs change from LS to IS over this range (Fig. 8 and ESI,† Table S19). This change in GS is somewhat larger than for the Cr(III) TMCs, which are all IS for aHF = 0.2 or above (Fig. 8 and ESI,† Table S19). The d4 Mo(II) and Tc(III) TMCs favor IS ground states exclusively, whereas most of the 3d isovalent Cr(II) or Mn(III) TMCs are HS-favoring especially with increasing aHF values (ESI,† Table S19). Thus, overall 4d TMC GS assignment is significantly less likely to be affected by a change in functional than an equivalent 3d TMC although the sensitivity of predicted energies to exchange fraction is only on average reduced by around one third from the first- to second-row TMCs.
e. Relationships between energetic sensitivity and structure
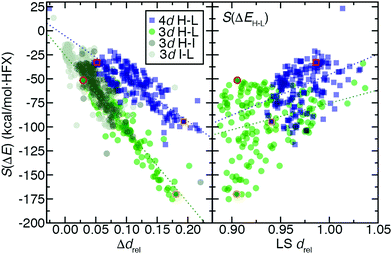
In 3d TMCs, increasing spin multiplicity typically leads to longer metal–ligand bond lengths as antibonding states become preferentially occupied over states with bonding character, and this effect is more significant with increasing ligand field. Bond lengths do not change significantly with aHF value,138 and thus structural differences between spin states are also invariant. To determine if structural differences between 3d and 4d TMC pairs could explain distinct exchange sensitivities due to increased diffuseness of the 4d orbitals, we compared the B3LYP structures (i.e., metal–ligand bond lengths) of isovalent complexes. In both 3d and 4d TMCs, increasing spin multiplicity leads to longer metal–ligand bond lengths, consistent with our expectations, but bond lengths differ primarily due to the different sizes of 3d and 4d metals (ESI,† Fig. S3 and Table S21).As in previous work,138 we facilitate comparison by focusing on relative metal–ligand bond lengths, drel:
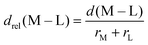 | (1) |
For 3d TMCs, the drel difference, Δdrel, between HS and LS states is well correlated (R2 = 0.86) with S(ΔEH–L) values (Fig. 9 and ESI,† Table S24). The Fe(II)(CO)6 Δdrel is among the largest, consistent with the large magnitude (ca. −175 kcal mol−1 HFX−1) of its S(ΔEH–L), while Mn(III)(H2O)6 has both a much lower S(ΔEH–L) (ca. −50 kcal mol−1 HFX−1) and Δdrel of 0.04 (Fig. 9). In line with these observations, the overall largest HS–LS Δdrel values are observed for the cases with the most positive ΔEH–L values (ESI,† Fig. S7). As with HS–LS, a similar relationship can be observed for S(ΔE) and Δdrel for the 3d TMC HS–IS or IS–LS splittings (ESI,† Fig. S8 and Table S24). In fact a single good correlation (R2 = 0.81) can be fit through all three sets of S(ΔE) and Δdrel values for 3d TMCs (Fig. 9 and ESI,† Fig. S8 and Table S24). Taken together with our prior findings,29 these observations suggest that increasing aHF penalizes the delocalized, highly bonded lower-spin states more strongly than higher-spin states. When this bonding difference is larger, the sensitivity to aHF is also higher.
For the second-row transition metals, there is also a good correlation (R2 = 0.71) between S(ΔE) and Δdrel for the HS–LS states of the 4d TMCs (Fig. 9 and ESI,† Fig. S9, Table S24). The slope of the relationship however is reduced with respect to the value for 3d TMCs (Fig. 9 and ESI,† Table S24). Indeed, Δdrel values across all spin-state pairs in 4d TMCs are as large as those for the 3d TMCs. Thus, more diffuse 4d orbitals do not change Δdrel value trends and cannot be used to explain the reduced exchange sensitivity of 4d TMCs (ESI,† Fig. S4). A weaker, but somewhat unified, relationship can be observed between the LS state drel, which is generally longer in some but not all 4d TMCs, and S(ΔEH–L) across both 3d and 4d TMCs (Fig. 9 and ESI,† Table S24, Fig. S4).
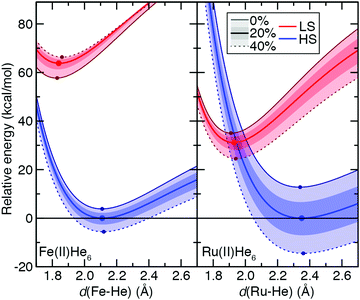
To understand the origins of this relationship, we obtained potential energy curves (PECs) with varied metal–ligand bond length and varied aHF values for 3d Fe(II) and 4d Ru(II) TMCs in their quintet HS and singlet LS states. We contrasted homoleptic helium-atom 3d/4d complexes as a simplified example of the weak-field limit with strong-field, hexa-carbonyl 3d/4d TMCs, in which we rigidly displaced the CO ligands (see Section 2). The closed-shell He atoms act as very weak field ligands, with the 3d/4d TMCs both strongly favoring the HS state over the LS state (B3LYP ΔEH–L: Fe(II) ca. −64 kcal mol−1 and Ru(II) ca. −31 kcal mol−1, Fig. 10 and see ESI,† Table S25). The S(ΔEH–L) values are both small and comparable (Fe(II): −47 vs. Ru(II): −43 kcal mol−1 HFX−1), consistent with small S(ΔEH–L) values (hexa-aqua Fe(II): −53 vs. Ru(II): −38 kcal mol−1 HFX−1) from other weak-field TMCs (ESI,† Tables S12 and S25). Despite these comparable exchange sensitivities, the dependence on aHF of individual PECs of Ru(II) and Fe(II) TMCs is distinct (Fig. 10). Both HS and LS Ru(II)(He)6 PECs are stabilized with increasing aHF, but the HS relative energy is more sensitive to exchange (Fig. 10). For Fe(II)(He)6, on the other hand, the HS PEC is stabilized with increasing aHF while the LS is destabilized (Fig. 10). For individual LS or HS states, Ru(II) TMCs PECs have higher sensitivities than the Fe(II) counterparts (Fig. 10 and ESI,† Table S25). The negative S(ΔEH–L) for Fe(II)(He)6 arises from additive sensitivities of the HS and LS states, while for Ru(II)(He)6 the simultaneous LS and HS stabilization leads to a comparable net S(ΔEH–L) (Fig. 10 and ESI,† Table S25).
The He complexes are weakly bound, with the small covalent radius of the He atom leading to a very long estimated drel values in LS states for both 3d and 4d TMCs (Fe(II): drel = 1.08 vs. Ru(II): drel = 1.11) despite moderate absolute bond lengths of 1.84 and 1.93 Å, respectively (Fig. 10 and ESI,† Tables S21, S25). The HS states are even more weakly bound, with large Δdrel values of 0.16 for Fe(II) and 0.24 for Ru(II), and these observations are insensitive to aHF (Fig. 10 and ESI,† Table S25). Since we can obtain the exchange sensitivity over a wide range of M–He bond lengths in these TMCs, we also evaluated the extent to which S values vary at points away from equilibrium (Fig. 10). The vertical HS–LS sensitivity evaluated at the LS geometry for Ru(II) or Fe(II) is comparable to that for the adiabatic case, despite the fact that the LS–HS ordering is inverted at the LS geometry for Ru(II) but unchanged for Fe(II) (Fig. 10 and ESI,† Table S25). When stretched to the HS geometry, the S values decrease significantly for both Ru(II) and Fe(II) (Fig. 10 and ESI,† Table S25).
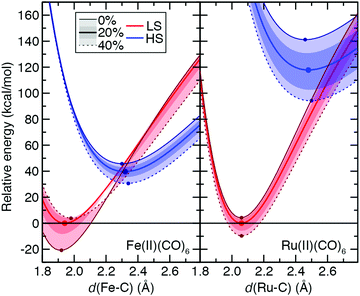
While the ground state preferences for model strong-field complexes of both Fe(II) and Ru(II) are uniformly LS (B3LYP ΔEH–L: Fe(II) ca. 30 kcal mol−1 and Ru(II) ca. 116 kcal mol−1), the exchange sensitivity trends are comparable to the weak-field He case (Fig. 11 and ESI,† Table S26). That is, larger total energy sensitivity in the HS Ru(II) PEC still leads to a lower overall S(ΔEH–L) magnitude compared to Fe(II) because exchange destabilizes the LS 3d TMC while weakly stabilizing the LS 4d TMC (Fig. 11 and ESI,† Table S26). The only significant distinction observed for the strong-field CO ligands is that S for each PEC and the splitting is much more dependent on bond length, with the effect of significantly reducing (>50%) S values for vertical spin-state energetics with respect to adiabatic S(ΔEH–L) values (Fig. 11 and ESI,† Table S26).
From the set of all 3d/4d TMC pairs, over 25 3d TMCs have positive sensitivities of the LS total energies whereas only one of the 4d TMCs does (ESI,† Table S27). While average sensitivities of the total energy with respect to aHF are higher for both states in 4d TMCs, they are more likely to be similar in magnitude between LS and HS states. Thus, distinct geometric and electronic structure of the LS states of 3d TMCs likely contributes to their higher exchange sensitivity (ESI,† Table S27).
4. Conclusions
We have carried out a comprehensive study of the extent to which established trends in 3d TMC exchange sensitivity and spin-state ordering have analogies in equivalent, isovalent 4d TMCs. From ten ligands covering a wide range of ligand field strengths, we generated hundreds of homoleptic and heteroleptic TMCs with a range of mid-row M(II)/M(III) 3d and 4d metal centers to interpret both 4-electron (i.e., HS–LS) and 2-electron (i.e., HS–IS or IS–LS) spin-splitting energies and sensitivities. We observed consistently increasing exchange sensitivity of ΔEH–L with increasing ligand field in both 3d and 4d homoleptic TMCs. Over the larger data set, we made a number of surprising observations:(1) Strong-field ligand effects were found to be additive in heteroleptics for both ΔEH–L and S(ΔEH–L). Similar trends were observed for HS–IS and IS–LS spin-state energetics, albeit with all magnitudes and ligand field sensitivities reduced.
(2) The 4d TMC exchange sensitivities were consistently smaller in magnitude than the equivalent 3d TMC sensitivities for all metals and oxidation states considered, and this deviation between 3d and 4d TMCs increased with increasing ligand field strength.
(3) Despite 4d TMC energetics being less sensitive than their 3d TMC counterparts, variations by as much as 10 kcal mol−1 per 10% change in HF exchange were still observed, which could have a significant effect on energetic predictions.
(4) Combined with the significant LS-shifting of 4d TMCs with respect to their equivalent 3d TMCs, the reduced 4d TMC exchange sensitivity led to a much lower likelihood of change in spin-state ordering than for their 3d TMC counterparts. While over the range of aHF = 0.0 to 0.3 many 3d TMCs changed ground states from LS to IS or HS states, a very small number of 4d TMCs shifted from LS to IS and none were HS.
(5) Delocalization does not explain the reduced exchange sensitivity of 4d TMCs. The 3d and 4d bond length differences between spin states were comparably large but could not explain the reduced sensitivity of 4d TMCs.
(6) Analysis of PECs of representative complexes indicated the higher spin-splitting exchange sensitivities of 3d TMCs is likely due to the opposing effects of exchange on the two spin states, despite higher exchange-sensitivity of the total energy in 4d TMCs.
Overall, we find that while spin-state energetics of 4d TMCs are roughly two-thirds as sensitive as those of 3d TMCs, this study suggests it is unlikely for HF exchange tuning to alter ground state predictions for 4d TMCs. This does not guarantee that common DFT functionals are always capable of predicting the ground state spin but does suggest that conventional tuning approaches that work in 3d TMCs to reproduce experimental spin state ordering will not be applicable in 4d TMCs.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge primary support by the Office of Naval Research under grant numbers N00014-17-1-2956 and N00014-18-1-2434 (for D. H., N. A., and C. D.) and the National Science Foundation under grant number CBET-1704266 (for A. N.). This work was also supported by the Department of Energy under grant number DE-SC0018096 (for Y. C. and D. B. K. C.). A. N. was partially supported by a National Science Foundation Graduate Research Fellowship under Grant #1122374. This work was carried out in part using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund and an AAAS Marion Milligan Mason Award, which supported this work. The authors thank Adam H. Steeves for providing a critical reading of the manuscript.References
- H. Schwarz, Ménage-À-Trois: Single-Atom Catalysis, Mass Spectrometry, and Computational Chemistry, Catal. Sci. Technol., 2017, 7, 4302–4314 RSC.
- D. Schröder, S. Shaik and H. Schwarz, Two-State Reactivity as a New Concept in Organometallic Chemistry, Acc. Chem. Res., 2000, 33, 139–145 CrossRef PubMed.
- S. Shaik, D. Danovich, A. Fiedler, D. Schröder and H. Schwarz, Two-State Reactivity in Organometallic Gas-Phase Ion Chemistry, Helv. Chim. Acta, 1995, 78, 1393–1407 CrossRef CAS.
- T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Incorporation of Redox-Inactive Cations Promotes Iron Catalyzed Aerobic C–H Oxidation at Mild Potentials, Chem. Sci., 2018, 9, 2567–2574 RSC.
- W. A. Hoffert, M. T. Mock, A. M. Appel and J. Y. Yang, Incorporation of Hydrogen-Bonding Functionalities into the Second Coordination Sphere of Iron-Based Water-Oxidation Catalysts, Eur. J. Inorg. Chem., 2013, 3846–3857 CrossRef CAS.
- M. Foscato and V. R. Jensen, Automated in Silico Design of Homogeneous Catalysts, ACS Catal., 2020, 10, 2354–2377 CrossRef CAS.
- A. Bousseksou, G. Molnár and G. Matouzenko, Switching of Molecular Spin States in Inorganic Complexes by Temperature, Pressure, Magnetic Field and Light: Towards Molecular Devices, Eur. J. Inorg. Chem., 2004, 4353–4369 CrossRef CAS.
- S. Decurtins, P. Gütlich, C. Köhler, H. Spiering and A. Hauser, Light-Induced Excited Spin State Trapping in a Transition-Metal Complex: The Hexa-1-Propyltetrazole-Iron (II) Tetrafluoroborate Spin-Crossover System, Chem. Phys. Lett., 1984, 105, 1–4 CrossRef CAS.
- A. Hauser, Light-Induced Spin Crossover and the High-Spin → Low-Spin Relaxation, Spin Crossover in Transition Metal Compounds II, Springer, 2004, pp. 155–198 Search PubMed.
- D. A. Reed, D. J. Xiao, M. I. Gonzalez, L. E. Darago, Z. R. Herm, F. Grandjean and J. R. Long, Reversible CO Scavenging via Adsorbate-Dependent Spin State Transitions in an Iron (II)–Triazolate Metal–Organic Framework, J. Am. Chem. Soc., 2016, 138, 5594–5602 CrossRef CAS PubMed.
- T. Groizard, N. Papior, B. Le Guennic, V. Robert and M. Kepenekian, Enhanced Cooperativity in Supported Spin-Crossover Metal–Organic Frameworks, J. Phys. Chem. Lett., 2017, 8, 3415–3420 CrossRef CAS PubMed.
- S. M. Neville, G. J. Halder, K. W. Chapman, M. B. Duriska, B. Moubaraki, K. S. Murray and C. J. Kepert, Guest Tunable Structure and Spin Crossover Properties in a Nanoporous Coordination Framework Material, J. Am. Chem. Soc., 2009, 131, 12106–12108 CrossRef CAS PubMed.
- S. Hedström, S. Chaudhuri, N. T. La Porte, B. Rudshteyn, J. F. Martinez, M. R. Wasielewski and V. S. Batista, Thousandfold Enhancement of Photoreduction Lifetime in Re (Bpy)(CO) 3 via Spin-Dependent Electron Transfer from a Perylenediimide Radical Anion Donor, J. Am. Chem. Soc., 2017, 139, 16466–16469 CrossRef PubMed.
- C. J. Cramer and D. G. Truhlar, Density Functional Theory for Transition Metals and Transition Metal Chemistry, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Many-Electron Self-Interaction Error in Approximate Density Functionals, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, Density Functionals That Are One- and Two- Are Not Always Many-Electron Self-Interaction-Free, as Shown for H2+, He2+, LiH+, and Ne2+, J. Chem. Phys., 2007, 126, 104102 CrossRef PubMed.
- R. Haunschild, T. M. Henderson, C. A. Jiménez-Hoyos and G. E. Scuseria, Many-Electron Self-Interaction and Spin Polarization Errors in Local Hybrid Density Functionals, J. Chem. Phys., 2010, 133, 134116 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Insights into Current Limitations of Density Functional Theory, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- T. Schmidt and S. Kümmel, One- and Many-Electron Self-Interaction Error in Local and Global Hybrid Functionals, Phys. Rev. B, 2016, 93, 165120 CrossRef.
- M.-C. Kim, E. Sim and K. Burke, Understanding and Reducing Errors in Density Functional Calculations, Phys. Rev. Lett., 2013, 111, 073003 CrossRef PubMed.
- X. Zheng, M. Liu, E. R. Johnson, J. Contreras-García and W. Yang, Delocalization Error of Density-Functional Approximations: A Distinct Manifestation in Hydrogen Molecular Chains, J. Chem. Phys., 2012, 137, 214106 CrossRef PubMed.
- E. R. Johnson, A. Otero-de-la-Roza and S. G. Dale, Extreme Density-Driven Delocalization Error for a Model Solvated-Electron System, J. Chem. Phys., 2013, 139, 184116 CrossRef PubMed.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, Spurious Fractional Charge on Dissociated Atoms: Pervasive and Resilient Self-Interaction Error of Common Density Functionals, J. Chem. Phys., 2006, 125, 194112 CrossRef PubMed.
- A. D. Dutoi and M. Head-Gordon, Self-Interaction Error of Local Density Functionals for Alkali–Halide Dissociation, Chem. Phys. Lett., 2006, 422, 230–233 CrossRef CAS.
- T. Bally and G. N. Sastry, Incorrect Dissociation Behavior of Radical Ions in Density Functional Calculations, J. Phys. Chem. A, 1997, 101, 7923–7925 CrossRef CAS.
- Y. Zhang and W. Yang, A Challenge for Density Functionals: Self-Interaction Error Increases for Systems with a Noninteger Number of Electrons, J. Chem. Phys., 1998, 109, 2604–2608 CrossRef CAS.
- J. J. Determan, K. Poole, G. Scalmani, M. J. Frisch, B. G. Janesko and A. K. Wilson, Comparative Study of Nonhybrid Density Functional Approximations for the Prediction of 3d Transition Metal Thermochemistry, J. Chem. Theory Comput., 2017, 13, 4907–4913 CrossRef CAS PubMed.
- B. G. Johnson, C. A. Gonzales, P. M. W. Gill and J. A. Pople, A Density Functional Study of the Simplest Hydrogen Abstraction Reaction. Effect of Self-Interaction Correction, Chem. Phys. Lett., 1994, 221, 100–108 CrossRef CAS.
- T. Z. H. Gani and H. J. Kulik, Unifying Exchange Sensitivity in Transition Metal Spin-State Ordering and Catalysis through Bond Valence Metrics, J. Chem. Theory Comput., 2017, 13, 5443–5457 CrossRef CAS PubMed.
- T. Z. H. Gani and H. J. Kulik, Where Does the Density Localize? Convergent Behavior for Global Hybrids, Range Separation, and DFT+U, J. Chem. Theory Comput., 2016, 12, 5931–5945 CrossRef CAS PubMed.
- F. Liu and H. J. Kulik, Impact of Approximate DFT Density Delocalization Error on Potential Energy Surfaces in Transition Metal Chemistry, J. Chem. Theory Comput., 2020, 16, 264–277 CrossRef PubMed.
- M. Srebro and J. Autschbach, Does a Molecule-Specific Density Functional Give an Accurate Electron Density? The Challenging Case of the Cucl Electric Field Gradient, J. Phys. Chem. Lett., 2012, 3, 576–581 CrossRef CAS PubMed.
- J. Autschbach and M. Srebro, Delocalization Error and “Functional Tuning” in Kohn–Sham Calculations of Molecular Properties, Acc. Chem. Res., 2014, 47, 2592–2602 CrossRef CAS PubMed.
- H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach, Phys. Rev. Lett., 2006, 97, 103001 CrossRef PubMed.
- G. Ganzenmüller, N. Berkaïne, A. Fouqueau, M. E. Casida and M. Reiher, Comparison of Density Functionals for Differences between the High- (T2g5) and Low- (A1g1) Spin States of Iron(II) Compounds. IV. Results for the Ferrous Complexes [Fe(L)(‘NHS4’)], J. Chem. Phys., 2005, 122, 234321 CrossRef PubMed.
- A. Droghetti, D. Alfè and S. Sanvito, Assessment of Density Functional Theory for Iron (II) Molecules across the Spin-Crossover Transition, J. Chem. Phys., 2012, 137, 124303 CrossRef CAS.
- E. I. Ioannidis and H. J. Kulik, Towards Quantifying the Role of Exact Exchange in Predictions of Transition Metal Complex Properties, J. Chem. Phys., 2015, 143, 034104 CrossRef.
- S. R. Mortensen and K. P. Kepp, Spin Propensities of Octahedral Complexes from Density Functional Theory, J. Phys. Chem. A, 2015, 119, 4041–4050 CrossRef CAS PubMed.
- E. I. Ioannidis and H. J. Kulik, Ligand-Field-Dependent Behavior of Meta-GGA Exchange in Transition-Metal Complex Spin-State Ordering, J. Phys. Chem. A, 2017, 121, 874–884 CrossRef CAS PubMed.
- F. Liu, T. Yang, J. Yang, E. Xu, A. Bajaj and H. J. Kulik, Bridging the Homogeneous-Heterogeneous Divide: Modeling Spin and Reactivity in Single Atom Catalysis, Front. Chem., 2019, 7, 219 CrossRef CAS PubMed.
- O. S. Siig and K. P. Kepp, Iron(II) and Iron(III) Spin Crossover: Toward an Optimal Density Functional, J. Phys. Chem. A, 2018, 122, 4208–4217 CrossRef CAS PubMed.
- Q. M. Phung, C. Martín-Fernández, J. N. Harvey and M. Feldt, Ab Initio Calculations for Spin-Gaps of Non-Heme Iron Complexes, J. Chem. Theory Comput., 2019, 15, 4297–4304 CrossRef CAS PubMed.
- M. Feldt, Q. M. Phung, K. Pierloot, R. A. Mata and J. N. Harvey, Limits of Coupled-Cluster Calculations for Non-Heme Iron Complexes, J. Chem. Theory Comput., 2019, 15, 922–937 CrossRef PubMed.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, Toward Highly Accurate Spin State Energetics in First-Row Transition Metal Complexes: A Combined CASPT2/Cc Approach, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS PubMed.
- S. Vancoillie, H. Zhao, M. Radon and K. Pierloot, Performance of CASPT2 and DFT for Relative Spin-State Energetics of Heme Models, J. Chem. Theory Comput., 2010, 6, 576–582 CrossRef CAS PubMed.
- J. K. Nørskov and T. Bligaard, The Catalyst Genome, Angew. Chem., Int. Ed., 2013, 52, 776–777 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1, 011002 CrossRef.
- KulikGroup molSimplify & molSimplify Automatic Design. https://github.com/hjkgrp/molsimplify, accessed June 1, 2020.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz, H. Tribukait, C. Amador-Bedolla, C. J. Brabec, B. Maruyama, K. A. Persson and A. Aspuru-Guzik, Accelerating the Discovery of Materials for Clean Energy in the Era of Smart Automation, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- S. Curtarolo, G. L. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The High-Throughput Highway to Computational Materials Design, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- D. J. Durand and N. Fey, Computational Ligand Descriptors for Catalyst Design, Chem. Rev., 2019, 119, 6561–6594 CrossRef CAS PubMed.
- S. W. Gersten, G. J. Samuels and T. J. Meyer, Catalytic Oxidation of Water by an Oxo-Bridged Ruthenium Dimer, J. Am. Chem. Soc., 1982, 104, 4029–4030 CrossRef CAS.
- H.-W. Tseng, R. Zong, J. T. Muckerman and R. Thummel, Mononuclear Ruthenium (II) Complexes That Catalyze Water Oxidation, Inorg. Chem., 2008, 47, 11763–11773 CrossRef CAS PubMed.
- R. Zong and R. P. Thummel, A New Family of Ru Complexes for Water Oxidation, J. Am. Chem. Soc., 2005, 127, 12802–12803 CrossRef CAS PubMed.
- D. Merki and X. Hu, Recent Developments of Molybdenum and Tungsten Sulfides as Hydrogen Evolution Catalysts, Energy Environ. Sci., 2011, 4, 3878–3888 RSC.
- S. Zakeeruddin, M. K. Nazeeruddin, P. Pechy, F. Rotzinger, R. Humphry-Baker, K. Kalyanasundaram, M. Grätzel, V. Shklover and T. Haibach, Molecular Engineering of Photosensitizers for Nanocrystalline Solar Cells: Synthesis and Characterization of Ru Dyes Based on Phosphonated Terpyridines, Inorg. Chem., 1997, 36, 5937–5946 CrossRef CAS.
- V. Jonas and W. Thiel, Theoretical Study of the Vibrational Spectra of the Transition Metal Carbonyls M (CO) 6 [M= Cr, Mo, W], M (CO) 5 [M= Fe, Ru, Os], and M (CO) 4 [M= Ni, Pd, Pt], J. Chem. Phys., 1995, 102, 8474–8484 CrossRef CAS.
- M. P. Waller, H. Braun, N. Hojdis and M. Bühl, Geometries of Second-Row Transition-Metal Complexes from Density-Functional Theory, J. Chem. Theory Comput., 2007, 3, 2234–2242 CrossRef CAS PubMed.
- M. L. Laury and A. K. Wilson, Performance of Density Functional Theory for Second Row (4 D) Transition Metal Thermochemistry, J. Chem. Theory Comput., 2013, 9, 3939–3946 CrossRef CAS.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- O. A. Vydrov, G. E. Scuseria and J. P. Perdew, Tests of Functionals for Systems with Fractional Electron Number, J. Chem. Phys., 2007, 126, 154109 CrossRef PubMed.
- W. Yang, Y. Zhang and P. W. Ayers, Degenerate Ground States and a Fractional Number of Electrons in Density and Reduced Density Matrix Functional Theory, Phys. Rev. Lett., 2000, 84, 5172–5175 CrossRef CAS PubMed.
- J. P. Perdew and M. Levy, Physical Content of the Exact Kohn-Sham Orbital Energies: Band Gaps and Derivative Discontinuities, Phys. Rev. Lett., 1983, 51, 1884–1887 CrossRef CAS.
- L. J. Sham and M. Schlüter, Density-Functional Theory of the Energy Gap, Phys. Rev. Lett., 1983, 51, 1888–1891 CrossRef.
- E. Sagvolden and J. P. Perdew, Discontinuity of the Exchange-Correlation Potential: Support for Assumptions Used to Find It, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 012517 CrossRef.
- P. Mori-Sanchez and A. J. Cohen, The Derivative Discontinuity of the Exchange-Correlation Functional, Phys. Chem. Chem. Phys., 2014, 16, 14378–14387 RSC.
- A. Zunger and A. J. Freeman, Ground- and Excited-State Properties of LiF in the Local-Density Formalism, Phys. Rev. B: Solid State, 1977, 16, 2901–2926 CrossRef CAS.
- M. R. Pederson, R. A. Heaton and C. C. Lin, Density-Functional Theory with Self-Interaction Correction: Application to the Lithium Molecule, J. Chem. Phys., 1985, 82, 2688–2699 CrossRef CAS.
- M. R. Pederson, A. Ruzsinszky and J. P. Perdew, Communication: Self-Interaction Correction with Unitary Invariance in Density Functional Theory, J. Chem. Phys., 2014, 140, 121103 CrossRef PubMed.
- H. J. Kulik, Perspective: Treating Electron over-Delocalization with the DFT+U Method, J. Chem. Phys., 2015, 142, 240901 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band Theory and Mott Insulators - Hubbard-U Instead of Stoner-I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-Functional Theory and Strong-Interactions - Orbital Ordering in Mott-Hubbard Insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA + U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- L. Wilbraham, C. Adamo and I. Ciofini, Communication: Evaluating Non-Empirical Double Hybrid Functionals for Spin-State Energetics in Transition-Metal Complexes, J. Chem. Phys., 2018, 148, 041103 CrossRef PubMed.
- J. L. Bao, L. Gagliardi and D. G. Truhlar, Self-Interaction Error in Density Functional Theory: An Appraisal, J. Phys. Chem. Lett., 2018, 9, 2353–2358 CrossRef CAS PubMed.
- B. G. Janesko, Reducing Density-Driven Error without Exact Exchange, Phys. Chem. Chem. Phys., 2017, 19, 4793–4801 RSC.
- L. Wilbraham, P. Verma, D. G. Truhlar, L. Gagliardi and I. Ciofini, Multiconfiguration Pair-Density Functional Theory Predicts Spin-State Ordering in Iron Complexes with the Same Accuracy as Complete Active Space Second-Order Perturbation Theory at a Significantly Reduced Computational Cost, J. Phys. Chem. Lett., 2017, 8, 2026–2030 CrossRef CAS PubMed.
- C. Waitt, N. M. Ferrara and H. Eshuis, Thermochemistry and Geometries for Transition-Metal Chemistry from the Random Phase Approximation, J. Chem. Theory Comput., 2016, 12, 5350–5360 CrossRef CAS PubMed.
- F. Furche and J. P. Perdew, The Performance of Semilocal and Hybrid Density Functionals in 3d Transition-Metal Chemistry, J. Chem. Phys., 2006, 124, 044103 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, Validation of Exchange−Correlation Functionals for Spin States of Iron Complexes, J. Phys. Chem. A, 2004, 108, 5479–5483 CrossRef CAS.
- K. P. Jensen and J. Cirera, Accurate Computed Enthalpies of Spin Crossover in Iron and Cobalt Complexes, J. Phys. Chem. A, 2009, 113, 10033–10039 CrossRef CAS.
- S. Ye and F. Neese, Accurate Modeling of Spin-State Energetics in Spin-Crossover Systems with Modern Density Functional Theory, Inorg. Chem., 2010, 49, 772–774 CrossRef CAS PubMed.
- M. Swart, Accurate Spin-State Energies for Iron Complexes, J. Chem. Theory Comput., 2008, 4, 2057–2066 CrossRef CAS PubMed.
- B. G. Janesko, E. Proynov, J. Kong, G. Scalmani and M. J. Frisch, Practical Density Functionals Beyond the Overdelocalization–Underbinding Zero-Sum Game, J. Phys. Chem. Lett., 2017, 8, 4314–4318 CrossRef CAS.
- T. Stein, L. Kronik and R. Baer, Prediction of Charge-Transfer Excitations in Coumarin-Based Dyes Using a Range-Separated Functional Tuned from First Principles, J. Chem. Phys., 2009, 131, 244119 CrossRef.
- S. Refaely-Abramson, R. Baer and L. Kronik, Fundamental and Excitation Gaps in Molecules of Relevance for Organic Photovoltaics from an Optimally Tuned Range-Separated Hybrid Functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144 CrossRef.
- L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Functionals, J. Chem. Theory Comput., 2012, 8, 1515–1531 CrossRef CAS PubMed.
- J. D. Gledhill, M. J. G. Peach and D. J. Tozer, Assessment of Tuning Methods for Enforcing Approximate Energy Linearity in Range-Separated Hybrid Functionals, J. Chem. Theory Comput., 2013, 9, 4414–4420 CrossRef CAS PubMed.
- A. Karolewski, L. Kronik and S. Kümmel, Using Optimally Tuned Range Separated Hybrid Functionals in Ground-State Calculations: Consequences and Caveats, J. Chem. Phys., 2013, 138, 204115 CrossRef PubMed.
- H. Sun and J. Autschbach, Influence of the Delocalization Error and Applicability of Optimal Functional Tuning in Density Functional Calculations of Nonlinear Optical Properties of Organic Donor–Acceptor Chromophores, ChemPhysChem, 2013, 14, 2450–2461 CrossRef CAS PubMed.
- T. Körzdörfer and J.-L. Brédas, Organic Electronic Materials: Recent Advances in the DFT Description of the Ground and Excited States Using Tuned Range-Separated Hybrid Functionals, Acc. Chem. Res., 2014, 47, 3284–3291 CrossRef PubMed.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Combining Long-Range Configuration Interaction with Short-Range Density Functionals, Chem. Phys. Lett., 1997, 275, 151–160 CrossRef CAS.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A Long-Range Correction Scheme for Generalized-Gradient-Approximation Exchange Functionals, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- J. Toulouse, F. Colonna and A. Savin, Long-Range-Short-Range Separation of the Electron-Electron Interaction in Density-Functional Theory, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 062505 CrossRef.
- R. Baer and D. Neuhauser, Density Functional Theory with Correct Long-Range Asymptotic Behavior, Phys. Rev. Lett., 2005, 94, 043002 CrossRef PubMed.
- O. A. Vydrov and G. E. Scuseria, Assessment of a Long-Range Corrected Hybrid Functional, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- E. Livshits and R. Baer, A Well-Tempered Density Functional Theory of Electrons in Molecules, Phys. Chem. Chem. Phys., 2007, 9, 2932–2941 RSC.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Development of Exchange-Correlation Functionals with Minimal Many-Electron Self-Interaction Error, J. Chem. Phys., 2007, 126, 191109 CrossRef PubMed.
- U. Salzner and R. Baer, Koopmans’ Springs to Life, J. Chem. Phys., 2009, 131, 231101 CrossRef PubMed.
- T. Tsuneda, J.-W. Song, S. Suzuki and K. Hirao, On Koopmans’ Theorem in Density Functional Theory, J. Chem. Phys., 2010, 133, 174101 CrossRef.
- A. Mahler, B. G. Janesko, S. Moncho and E. N. Brothers, When Hartree-Fock Exchange Admixture Lowers DFT-Predicted Barrier Heights: Natural Bond Orbital Analyses and Implications for Catalysis, J. Chem. Phys., 2018, 148, 244106 CrossRef PubMed.
- B. Pritchard and J. Autschbach, Theoretical Investigation of Paramagnetic NMR Shifts in Transition Metal Acetylacetonato Complexes: Analysis of Signs, Magnitudes, and the Role of the Covalency of Ligand–Metal Bonding, Inorg. Chem., 2012, 51, 8340–8351 CrossRef CAS PubMed.
- T. Duignan and J. Autschbach, Impact of the Kohn-Sham Delocalization Error on the 4f Shell Localization and Population in Lanthanide Complexes, J. Chem. Theory Comput., 2016, 12(7), 3109–3121 CrossRef CAS PubMed.
- T. Duignan, J. Autschbach, E. Batista and P. Yang, Assessment of Tuned Range Separated Exchange Functionals for Spectroscopies and Properties of Uranium Complexes, J. Chem. Theory Comput., 2017, 13(8), 3614–3625 CrossRef CAS PubMed.
- W. Jiang, N. J. DeYonker, J. J. Determan and A. K. Wilson, Toward Accurate Theoretical Thermochemistry of First Row Transition Metal Complexes, J. Phys. Chem. A, 2011, 116, 870–885 CrossRef PubMed.
- K. A. Moltved and K. P. Kepp, The Metal Hydride Problem of Computational Chemistry: Origins and Consequences, J. Phys. Chem. A, 2019, 123, 2888–2900 CrossRef CAS.
- D. N. Bowman and E. Jakubikova, Low-Spin Versus High-Spin Ground State in Pseudo-Octahedral Iron Complexes, Inorg. Chem., 2012, 51, 6011–6019 CrossRef CAS.
- D. M. Smith, M. Dupuis and T. Straatsma, Multiplet Splittings and Other Properties from Density Functional Theory: An Assessment in Iron–Porphyrin Systems, Mol. Phys., 2005, 103, 273–278 CrossRef CAS.
- M. Bruschi, L. De Gioia, G. Zampella, M. Reiher, P. Fantucci and M. Stein, A Theoretical Study of Spin States in Ni-S4 Complexes and Models of the [NiFe] Hydrogenase Active Site, JBIC, J. Biol. Inorg. Chem., 2004, 9, 873–884 CrossRef CAS PubMed.
- P. Verma, Z. Varga, J. E. Klein, C. J. Cramer, L. Que and D. G. Truhlar, Assessment of Electronic Structure Methods for the Determination of the Ground Spin States of Fe (II), Fe (III) and Fe (IV) Complexes, Phys. Chem. Chem. Phys., 2017, 19, 13049–13069 RSC.
- G. N. Simm and M. Reiher, Systematic Error Estimation for Chemical Reaction Energies, J. Chem. Theory Comput., 2016, 12, 2762–2773 CrossRef CAS PubMed.
- T. Stein, J. Autschbach, N. Govind, L. Kronik and R. Baer, Curvature and Frontier Orbital Energies in Density Functional Theory, J. Phys. Chem. Lett., 2012, 3, 3740–3744 CrossRef CAS PubMed.
- J. H. Skone, M. Govoni and G. Galli, Self-Consistent Hybrid Functional for Condensed Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195112 CrossRef.
- T. Shimazaki and Y. Asai, First Principles Band Structure Calculations Based on Self-Consistent Screened Hartree–Fock Exchange Potential, J. Chem. Phys., 2009, 130, 164702 CrossRef PubMed.
- D. C. Ashley and E. Jakubikova, Ironing out the Photochemical and Spin-Crossover Behavior of Fe(II) Coordination Compounds with Computational Chemistry, Coord. Chem. Rev., 2017, 337, 97–111 CrossRef CAS.
- M. Reiher, Theoretical Study of the Fe (Phen) 2 (NCS) 2 Spin-Crossover Complex with Reparametrized Density Functionals, Inorg. Chem., 2002, 41, 6928–6935 CrossRef CAS PubMed.
- E. A. Bleda, C. Trindle and Z. Altun, Studies on Spin State Preferences in Fe(II) Complexes, Comput. Theor. Chem., 2015, 1073, 139–148 CrossRef CAS.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9, 1064–1071 CrossRef CAS PubMed.
- K. Burke, Perspective on Density Functional Theory, J. Chem. Phys., 2012, 136, 150901 CrossRef PubMed.
- A. D. Becke, Perspective: Fifty Years of Density-Functional Theory in Chemical Physics, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- J. P. Janet, Q. Zhao, E. I. Ioannidis and H. J. Kulik, Density Functional Theory for Modelling Large Molecular Adsorbate-Surface Interactions: A Mini-Review and Worked Example, Mol. Simul., 2017, 43, 327–345 CrossRef CAS.
- R. J. Deeth and N. Fey, The Performance of Nonhybrid Density Functionals for Calculating the Structures and Spin States of Fe (II) and Fe (III) Complexes, J. Comput. Chem., 2004, 25, 1840–1848 CrossRef CAS PubMed.
- D. Coskun, S. V. Jerome and R. A. Friesner, Evaluation of the Performance of the B3LYP, PBE0, and M06 DFT Functionals, and DBLOC-Corrected Versions, in the Calculation of Redox Potentials and Spin Splittings for Transition Metal Containing Systems, J. Chem. Theory Comput., 2016, 12, 1121–1128 CrossRef CAS PubMed.
- T. F. Hughes and R. A. Friesner, Correcting Systematic Errors in DFT Spin-Splitting Energetics for Transition Metal Complexes, J. Chem. Theory Comput., 2011, 7, 19–32 CrossRef CAS PubMed.
- K. P. Kepp, Theoretical Study of Spin Crossover in 30 Iron Complexes, Inorg. Chem., 2016, 55, 2717–2727 CrossRef CAS PubMed.
- S. Zein, S. A. Borshch, P. Fleurat-Lessard, M. E. Casida and H. Chermette, Assessment of the Exchange-Correlation Functionals for the Physical Description of Spin Transition Phenomena by Density Functional Theory Methods: All the Same?, J. Chem. Phys., 2007, 126, 014105 CrossRef PubMed.
- K. Boguslawski, C. R. Jacob and M. Reiher, Can DFT Accurately Predict Spin Densities? Analysis of Discrepancies in Iron Nitrosyl Complexes, J. Chem. Theory Comput., 2011, 7, 2740–2752 CrossRef CAS PubMed.
- P. Milko and M. A. Iron, On the Innocence of Bipyridine Ligands: How Well Do DFT Functionals Fare for These Challenging Spin Systems?, J. Chem. Theory Comput., 2014, 10, 220–235 CrossRef CAS PubMed.
- E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, Characterization of Synthetic Oxomanganese Complexes and the Inorganic Core of the O2-Evolving Complex in Photosystem II: Evaluation of the DFT/B3LYP Level of Theory, J. Inorg. Biochem., 2006, 100, 786–800 CrossRef CAS PubMed.
- M. Reiher, O. Salomon and B. A. Hess, Reparameterization of Hybrid Functionals Based on Energy Differences of States of Different Multiplicity, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- O. Salomon, M. Reiher and B. A. Hess, Assertion and Validation of the Performance of the B3LYP* Functional for the First Transition Metal Row and the G2 Test Set, J. Chem. Phys., 2002, 117, 4729–4737 CrossRef CAS.
- A. Fouqueau, S. Mer, M. E. Casida, L. M. Lawson Daku, A. Hauser, T. Mineva and F. Neese, Comparison of Density Functionals for Energy and Structural Differences between the High- [5t2g:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (T2g)4(Eg)2] and Low- [1a1g:
(T2g)4(Eg)2] and Low- [1a1g:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (T2g)6(Eg)0] Spin States of the Hexaquoferrous Cation [Fe(H2O)6]2+, J. Chem. Phys., 2004, 120, 9473–9486 CrossRef CAS PubMed.
(T2g)6(Eg)0] Spin States of the Hexaquoferrous Cation [Fe(H2O)6]2+, J. Chem. Phys., 2004, 120, 9473–9486 CrossRef CAS PubMed. - A. Fouqueau, M. E. Casida, L. M. Lawson Daku, A. Hauser and F. Neese, Comparison of Density Functionals for Energy and Structural Differences between the High-[5t2g:(T2g) 4 (Eg) 2] and Low-[1a1g:(T2g) 6 (Eg) 0] Spin States of Iron (II) Coordination Compounds. II. More Functionals and the Hexaminoferrous Cation,[Fe (NH3) 6]2+, J. Chem. Phys., 2005, 122, 044110 CrossRef PubMed.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Janet and H. J. Kulik, Predicting Electronic Structure Properties of Transition Metal Complexes with Neural Networks, Chem. Sci., 2017, 8, 5137–5152 RSC.
- H. J. Kulik, Making Machine Learning a Useful Tool in the Accelerated Discovery of Transition Metal Complexes, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1439 CAS.
- M. G. Taylor, T. Yang, S. Lin, A. Nandy, J. P. Janet, C. Duan and H. J. Kulik, Seeing Is Believing: Experimental Spin States from Machine Learning Model Structure Predictions, J. Phys. Chem. A, 2020, 124, 3286–3299 CrossRef CAS PubMed.
- J. P. Janet, F. Liu, A. Nandy, C. Duan, T. Yang, S. Lin and H. J. Kulik, Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry, Inorg. Chem., 2019, 58, 10592–10606 CrossRef CAS PubMed.
- R. Tsuchida, Absorption Spectra of Co-ordination Compounds. I, Bull. Chem. Soc. Jpn., 1938, 13, 388–400 CrossRef CAS.
- A. Nandy, C. Duan, J. P. Janet, S. Gugler and H. J. Kulik, Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry, Ind. Eng. Chem. Res., 2018, 57, 13973–13986 CrossRef CAS.
- C. Duan, J. P. Janet, F. Liu, A. Nandy and H. J. Kulik, Learning from Failure: Predicting Electronic Structure Calculation Outcomes with Machine Learning Models, J. Chem. Theory Comput., 2019, 15, 2331–2345 CrossRef CAS PubMed.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, molSimplify: A Toolkit for Automating Discovery in Inorganic Chemistry, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- KulikGroup molSimplify Documentation, http://molsimplify.mit.edu, accessed June 1, 2020.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An Open Chemical Toolbox, J. Cheminf., 2011, 3, 33 Search PubMed.
- N. M. O'Boyle, C. Morley and G. R. Hutchison, Pybel: A Python Wrapper for the Openbabel Cheminformatics Toolkit, Chem. Cent. J., 2008, 2, 5 CrossRef PubMed.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- Petachem, http://www.petachem.com, accessed June 1, 2020.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- V. R. H. Saunders and I. Hillier, A “Level-Shifting” Method for Converging Closed Shell Hartree-Fock Wave Functions, Int. J. Quantum Chem., 1973, 7, 699–705 CrossRef.
- L.-P. Wang and C. Song, Geometry Optimization Made Simple with Translation and Rotation Coordinates, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A Quantitative Uncertainty Metric Controls Error in Neural Network-Driven Chemical Discovery, Chem. Sci., 2019, 10, 7913–7922 RSC.
- Q. Zhao and H. J. Kulik, Stable Surfaces That Bind Too Tightly: Can Range Separated Hybrids or DFT+U Improve Paradoxical Descriptions of Surface Chemistry?, J. Phys. Chem. Lett., 2019, 10, 5090–5098 CrossRef CAS PubMed.
- Q. Zhao and H. J. Kulik, Where Does the Density Localize in the Solid State? Divergent Behavior for Hybrids and DFT + U, J. Chem. Theory Comput., 2018, 14, 670–683 CrossRef CAS PubMed.
- P. Gütlich, Spin Crossover in Iron (II)-Complexes, Metal Complexes, Springer, 1981, pp. 83–195 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of calculation criteria, filtering steps, and eliminated complexes; statistics of sensitivities and relative sensitivities for different spin-splitting energies; sensitivities of pairs of 3d and 4d TMCs including outliers for different spin splittings; spin splitting and sensitivity properties of CO/H2O complexes; ground state preference and HS vs. LS preference for 3d and 4d TMCs vs. exchange fraction; absolute averaged M–L distances for LS and HS states; covalent radii for computing relative distances; histograms and statistics of relative distances; comparison of equatorial and axial relative distances; relationship between relative distances and exchange sensitivity; properties of potential energy curves for hexa-helium and hexa-carbonyl complexes; and total energy sensitivities of HS and LS states in 239 TMC pairs (PDF). Structures and total energies of all 3d and 4d TMCs studied in this work; reasons complexes or sensitivities were not included in the data set; individual metal–ligand bond lengths for all converged complexes at all exchange fractions; total energy sensitivities in HS–LS pairs of TMCs; individual metal–ligand bond lengths for B3LYP and the relative metal–ligand bond length calculation for all pairs of 3d/4d TMCs; spin splitting values and sensitivities for all pairs of 3d/4d TMCs; total energies and analysis of sensitivities for PECs of Fe(II)/Ru(II) homoleptic TMCs in LS and HS states with CO and He atom ligands (ZIP). See DOI: 10.1039/d0cp02977g |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2020 |