Surfactant-induced wetting dynamics in the context of hypersaline desalination for membrane distillation

Abstract

Amongst different desalination technologies to tackle freshwater demand, membrane distillation (MD) is promising in that it can effectively treat hypersaline feed or reverse osmosis reject and further improve freshwater recovery while simultaneously reducing the amount of liquid discharge. However, wetting of the membrane pores by surfactant compromises the separation efficiency since MD relies on maintaining a stable air gap in the membrane pore. The kinetics of surfactant-induced wetting for a hydrophobic membrane applied in MD technology have been shown to depend only on bulk surfactant concentration and vapour flux. In this study, we examine the decoupled effect of salt concentration and bulk surfactant concentration and its relation to surfactant-induced wetting. Even at low surfactant concentration (0.1 mM sodium dodecyl sulphate), the concentration of salt (sodium chloride) can significantly affect the wetting dynamics. In particular, high salt concentrations (above 1.2 M or 70 g L⁻¹ NaCl) can notably accelerate wetting, and thereby render MD unsuitable for such feeds. On the other hand, surfactant concentrations well above the critical micelle concentration (CMC) are tested with low salt concentration, and the results reveal that hydrophobic PVDF membranes perform quite stably without any significant loss in salt removal efficiency. A mathematical framework that captures ionic strength and surfactant activity is also proposed to predict different membrane wetting regimes. These findings point to the need for coupling bulk surfactant concentration with salt concentration to predict surfactant-induced wetting more accurately. These results also open an avenue for an alternative mechanism that complements the existing understanding of surfactant-induced wetting.

---

Raju Kumar Gupta

We are delighted to join Nanoscale Horizons in celebrating its 10th anniversary and are excited to share our recent findings in the field of membrane distillation for desalination as part of this special collection. Over the past few years, I have had the privilege of witnessing the journal's steadfast commitment to publishing high-quality research in my capacity as a member of its Editorial Advisory Board. It is truly a great pleasure to contribute our first article to the journal as it marks this significant milestone. Once again, a heartfelt congratulations to Nanoscale Horizons and best wishes as the journal strives to advance the frontiers of nanoscale science!

---

New concepts

The concept of salting out of the surfactant phase was applied to understand surfactant-induced wetting dynamics in the context of hypersaline feeds for membrane distillation technology. A mathematical framework that incorporates ionic strength and surfactant activity was proposed to predict and understand different membrane wetting regimes. Salting out of the surfactant leads to a rapid loss in separation efficiency. We demonstrate that both background electrolyte concentration and surfactant concentration contribute to accelerated surfactant-induced wetting. The traditional understanding of surfactant-induced wetting does not account for the background electrolyte concentration or ionic strength. Hence, experiments that consider salting-out of the surfactant phase and its ability to accelerate wetting are rare or absent. Given that membrane distillation technology is highly suited for hypersaline feeds, novel membranes for membrane distillation must prove competent even when surfactant precipitation occurs at high salinity. This also calls for improved surface chemistry modifications along with tight pore size control in the range of a few nanometres to overcome this issue.

Introduction

Membrane distillation (MD) technology is considered to have great potential for treating hypersaline feedwater.^1–3 However, the intrusion of feed into the pores of a hydrophobic membrane compromises its separation performance in MD technology. Surfactants are a class of culprits that can induce wetting in MD. Most novel membranes for MD applications are subjected to surfactant-induced wetting.^4–7 The purpose of this experiment is to determine the concentration of surfactant up to which the membrane remains unwet. This concentration indirectly denotes the effectiveness of chemical modification (such as lowering of surface energy) made to the membrane. For instance, Wang et al.⁷ showed that their membrane in its unmodified state could remain unwet only up to a concentration of 0.1 mM sodium dodecyl sulphate (SDS). However, after modification with fluoroalkyl silane, it could remain unwetted up to 0.4 mM SDS.

It is generally understood that wetting induced by surfactant is transient, in contrast to water miscible solvents such as alcohols, where it is abrupt and rapid.⁸ The difference in mechanism and a kinetic model for wetting have been illustrated by Wang et al.^9,10 In principle, in the case of surfactant-induced wetting, almost instantaneous adsorption of the surfactant onto the membrane pore deters the wetting frontier from progressing any further. Thus, the kinetics is controlled by diffusion and advection of surfactant molecules from the bulk.

However, the above treatment of surfactant-induced wetting assumes that the salt present in the feed does not interfere with the adsorption, diffusion or advection kinetics of the surfactant. This assumption may not be accurate, as many studies^11–13 indicate that the kinetics of adsorption at the air–water interface is a function of salt concentration. Among them, Qazi et al.¹¹ reported a decrease in the equilibrium surface tension and critical micelle concentration (CMC) of an ionic surfactant in the presence of high concentration NaCl (5 M). In a slightly different context, recent studies^14,15 indicate evidence for partitioning (or salting-out) of water-soluble organic molecules upon mixing with saline underground water in porous underground networks. These reports together provide a compelling basis for the influence of salt concentration on surfactant-induced wetting dynamics in MD. At present, there is a lack of understanding on the decoupled influence of salt concentration and surfactant concentration in MD literature. Although Han et al.¹⁶ in their work observe that the combined presence of NaCl and SDS can accelerate wetting, the individual contribution or the associated mechanism does not receive sufficient attention. Another recent study¹⁷ shows how different cations (such as Na⁺, Mg²⁺, Al³⁺, Ca²⁺ and K⁺) affect wetting dynamics differently. However, the concentration of both salt and surfactant was maintained constant in these experiments. This lack of a decoupled understanding has led most, if not all, experimental studies to ignore the background electrolyte concentration and consider only surfactant concentration during wetting studies. This has also resulted in the notion that surfactant concentration is the sole contributor to wetting. Thus, a systematic and comprehensive decoupled experimental MD study supported by dynamic surface tension, water contact angle and optical microscopy measurements is presented to fill this gap.

Most researchers use 0.6 M NaCl (35 g L⁻¹ NaCl) or lower,^16,18–24 and some, 1 M NaCl,²⁵ along with the surfactant (usually, SDS) as the starting point for these wetting experiments. This salt concentration helps mimic real seawater or brackish water conditions and aids in the detection of wetting when it happens via electrical conductivity measurements. One of the only existing works that deviates from the above trend is a work by Ma et al.²⁶ employing a hypersaline feed (5 M NaCl) and surfactant concentration close to the CMC (8 mM). However, in their work, the authors do not discuss the impact of salt concentration or provide insights into the underlying mechanism of surfactant-induced wetting under such harsh conditions.

In this work, we have kept the surfactant concentration constant while varying the background electrolyte (NaCl) concentration in order to study the role, if any, of salt concentration in surfactant-induced wetting dynamics. In the second set of experiments, we try to understand the sole effect of the surfactant by keeping the salt concentration at a minimum. The results from these experiments are interpreted in the light of water chemistry and membrane-surfactant interactions and aimed at a better understanding of surfactant-induced wetting dynamics. We also attempt to tailor an existing dimensionless number for our system to account for the effect of salt concentration and surfactant activity to predict wetting dynamics for different scenarios.

We use SDS as our surfactant in all our experiments since most research articles use SDS as their model surfactant for wetting-induced studies.

Results and discussion

Characterization of different feed liquids

The wetting of membrane pores is described using the liquid entry pressure (LEP) equation derived by applying a force balance at the triple phase boundary between the feed and the membrane (eqn (1)),²⁷where γ_L is the surface tension of the feed, cos θ₀ is the intrinsic contact angle between the feed and the membrane, β accounts for the deviation from a perfect cylindrical pore, and r is the equivalent pore radius.

A low surface tension feed, such as a surfactant solution, implies a decrease in γ_L and cos θ₀. The dynamic surface tension of different salt concentrations with 0.1 mM SDS was carried out at 25 °C (Fig. 1A).

Fig. 1 (A) Dynamic surface tension measurements for different combinations of salt concentrations with 0.1 mM SDS, (B) comparison of optical microscope images with and without SDS addition for different NaCl concentrations (60 g L⁻¹, 100 g L⁻¹ and 200 g L⁻¹). The latter images of SDS addition with 100 g L⁻¹ and 200 g L⁻¹ reveal a separated phase that is absent in all others, (C) schematic showing surfactant molecules in the bulk for lower salt concentrations (10 g L⁻¹ and 60 g L⁻¹) while they precipitate out for higher salt concentrations (100 g L⁻¹ and 200 g L⁻¹).

While pure SDS (0.1 mM) has a surface tension close to that of water, the addition of salt is seen to significantly alter surface tension. This change in surface tension is attributed to surfactant molecules packing in greater numbers and density at the air–water interface, losing to competition for solvent molecules with sodium chloride.¹¹ While the surface tension steadily decreases upon addition of salt up to 60 g L⁻¹, the rate of decrease in surface tension is minimal beyond this point. This is suggestive of a CMC-like behaviour^13,28 where the surface tension lowers to a point up to the CMC and does not change thereafter. Though CMC can be lowered by the addition of a salt for an ionic surfactant, we hypothesise that another phenomenon may be at work here, too. High salt concentrations drastically reduce the solubility of SDS, an amphiphilic molecule. This is because sodium and chloride ions end up being solvated more easily than SDS molecules by the solvent (water), leaving little or no room for the solubilization of SDS. Thus, SDS molecules, severely dehydrated, salt out of the bulk into a different phase, a process known as salting-out.^29,30 While both lowering of the CMC and salting-out may refer to surfactant molecule packing at the air–water interface, the latter refers to a phase separation-like phenomenon as shown in the optical microscopy images (Fig. 1B). Qazi et al.,³¹ in their work, report precipitation (or salting-out) of SDS around 0.5 M NaCl (for 8–10 mM SDS). While CMC refers to the concentration at which surfactant molecules can favourably aggregate to form micelles in the bulk (or sometimes at the interface), salting-out is explicitly an interfacial phenomenon occurring due to high background electrolyte concentration and should not be confused with classical bulk crystallization. Thus, we conclude that salting-out or precipitation^31,32 of surfactant molecules to the water–air interface, in addition to a decrease in CMC, is the reason why the surface tension reaches a value of ∼29 mN m⁻¹ at high NaCl concentrations (>70 g L⁻¹).

The unusual curve for 200 g L⁻¹ NaCl in Fig. 1A in comparison to other salt concentrations is because SDS molecules in the bulk cannot easily adsorb at the air–water interface due to constantly colliding with sodium chloride ions (∼3400 mM NaCl as compared to 0.1 mM SDS). Thus, surface tension decreases much more slowly in comparison to other concentrations. The equilibrium surface tension, thus may be reached only at very long durations of measurement. Contact angle measurements over time (600 s) for the same set of concentrations as above were carried out (SI, Fig. S2). The trend is similar to that of dynamic surface tension as a result of surfactant molecules adsorbing at the air–water interface, decreasing surface tension and the apparent contact angle. Images captured from optical microscopy (Fig. 1B) also suggest the appearance of a separated phase at salt concentrations greater than 60 g L⁻¹. For salt concentrations 60 g L⁻¹ and below, the optical images were clear with no visible phase separation with or without SDS. Having concluded that salt concentration can significantly alter the surface tension of 0.1 mM SDS, we carried out MD experiments to understand the implications of these results.

Wetting studies for different salt concentrations at 0.1 mM SDS

Salt concentrations varying from 10 g L⁻¹ to 200 g L⁻¹ NaCl were tested with 0.1 mM SDS in the first set of MD experiments. Physical properties of the PVDF membrane used for all the MD experiments are tabulated in Table 1. While 10 g L⁻¹ (0.17 M) NaCl mimicked brackish water or low salinity feed, 200 g L⁻¹ (3.4 M) NaCl represented hypersaline concentration, for which desalination using MD technology is considered to hold significant potential. We further considered 35 g L⁻¹ or 0.6 M mimicking seawater salinity and 60 g L⁻¹ (1 M) NaCl since several studies use this concentration to simulate elevated RO reject salinity.^7,25,33

Table 1 Physical properties of the PVDF membrane

Average surface pore size (µm)	Roughness (nm)	Water contact angle (°)	LEP (bar)
a The water contact angle is lower than the usual hydrophobic angle of 90° since the membranes were fabricated using pure water as a non-solvent, leading to quick phase inversion and a resulting smooth top surface.
0.1 ± 0.05	0.12 ± 0.03	87.8 ± 0.3^a	2 ± 0.2

---

We observe that among the different salt concentrations (Fig. 2A), only 200 g L⁻¹ surfactant solution experienced a sudden failure, while others experienced transient wetting or stable rejection (>99.9%) throughout the run of 200 min duration. Intuitively, one may assume that wetting propensity would be higher for the 60 g L⁻¹ feed owing to a much lower surface tension than 10 g L⁻¹ (52.8 vs. 30.8 mN m⁻¹). However, we observe that the hydrophobic membrane responds to both feeds in a similar way.

Fig. 2 (A) Normalized flux and salt rejection plotted against time for MD experiments carried out at different NaCl concentrations (10 g L⁻¹, 35 g L⁻¹, 60 g L⁻¹ and 200 g L⁻¹) by maintaining the surfactant concentration at 0.1 mM SDS, (inset) magnified view of the salt removal efficiency for 10 g L⁻¹, 35 g L⁻¹ and 60 g L⁻¹; (B) normalized flux and salt removal efficiency plotted against time for MD experiments carried out at different NaCl concentrations (70 g L⁻¹, 90 g L⁻¹ and 100 g L⁻¹) by maintaining the surfactant concentration at 0.1 mM SDS. For each data point in (A) and (B), the average value is plotted. Error bars represent standard deviation arising from three independent measurements (n = 3) and (C) pictorial comparison of the membranes used for two different feed concentrations (0.1 mM SDS with 70 g L⁻¹ and 0.1 mM SDS with 100 g L⁻¹).

While most membranes tested for MD applications report failure at 0.3 or 0.4 mM SDS,^20,23,24 we show that even at 0.1 mM SDS, the membrane may fail, subject to the background electrolyte concentration. The inset in Fig. 2A reveals that, regardless of feed concentration, some degree of wetting does take place. However, this is minimal and not threatening towards separation efficiency.

It is to be noted that during the duration of the experiments (200 min), the feed concentration was maintained by adding the appropriate amount of vapour that condensed on the permeate side periodically. In any case, the small vapour permeation rate compared (∼3 mL every 10 min) to the volume of the feed (800 mL) ensured that any significant feed concentration did not occur.

Having observed an abrupt loss in separation (almost alcohol-like) for 200 g L⁻¹ feed, we suspected whether such a phenomenon occurred only for hypersaline (>60 g L⁻¹) conditions. More specifically, it was desired to find the salt concentration where there would be a transition from stable rejection or transient wetting to abrupt wetting. Thus, we tailored our next set of experiments to test this hypothesis.

As with previous experiments, SDS concentration was kept at 0.1 mM. We started by testing 70 g L⁻¹ NaCl (Fig. 2B) and, having noticed a stable rejection for the same, we next tested 90 g L⁻¹ NaCl. This time, there was a visible increase in conductivity around 60 min (Fig. 2B). We further tested 100 g L⁻¹ NaCl and noticed a similar rise in conductivity at around 40 min of the run. Thus, we notice a transition from stable rejection to abrupt wetting at around 90 g L⁻¹ NaCl for 0.1 mM SDS. Upon visually comparing the two membranes (Fig. 2C), one subjected to 0.1 mM SDS with 70 g L⁻¹ and the other to 0.1 mM SDS with 100 g L⁻¹, it is clear how the latter is thoroughly wetted as a consequence of feed intrusion. The difference in membrane surface hydrophilization for the case where wetting happens gradually versus abruptly is shown through dynamic contact angle measurements and surface free energy analysis (Fig. S1 and Table S1). In the case of 100 g L⁻¹ + 0.1 mM SDS, the water contact angle diminishes from 89.8° to 44.7° due to adsorption by SDS on the membrane surface, while in the case of 60 g L⁻¹ + 0.1 mM SDS, it only reduces from 88.8° to 76.2° (Fig. S1). Therefore, it can be concluded that the degree of surface hydrophilization was greater in the case where wetting was abrupt and rapid. Furthermore, pre-wetting measurements also show a slight decline in contact angle (from 88.4° to 80.6°), which can be ascribed to evaporation of the water droplet. This trend is more clearly brought out by surface free energy analysis, with the surface energy being the lowest before wetting (29 ± 2.6 mJ m⁻²) and the highest for the membrane wet by 100 g L⁻¹ NaCl + 0.1 mM SDS feed (36.8 ± 1.0 mJ m⁻², Table S1).

We gather from the above set of experiments that a feed solution with high ionic strength (hypersaline) may lead to much faster wetting and thus can be more threatening for the MD process when surfactants are involved. The underlying reason for such an occurrence for hypersaline feeds could be traced back to a well-known phenomenon, usually applied for protein purification/separation³⁴ and previously discussed, salting-out. As illustrated in Fig. 1C, when the ionic strength of the feed is very high (1.54 M, 90 g L⁻¹ NaCl), SDS molecules can no longer remain in the bulk and salt-out into a different phase. Velioğlu et al.³⁵ conclude from molecular dynamics simulations that the presence of NaCl can increase PVDF–SDS affinity by interfering with the SDS–water network. Once phase separated, most of the SDS molecules tend to be present at the wetting frontier rather than the bulk. As a result, the surface tension at the wetting frontier does not increase and remains low as SDS molecules readily adsorb throughout the length of the pore while simultaneously hydrophilizing the pore. This allows the incoming highly concentrated feed (the second phase) to proceed via an expanding Poiseuille-driven flow to the permeate side, resulting in loss of rejection as measured through ion conductivity. Wang et al.⁹ pointed out a Poiseuille-driven model for alcohol wetting and a simplified adsorption model for surfactant-induced wetting. According to the adsorption model for surfactant-induced wetting, SDS molecules almost instantaneously adsorb onto the pore walls, thus increasing the surface tension of the wetting frontier. This deters further wetting until surfactant molecules are replenished from the bulk and again adsorbed onto a fresh part of the pore. This cycle continues until the wetting front reaches the permeate side and a rise in conductivity is noted. However, in all their experiments, salt concentration was maintained at 35 g L⁻¹ (0.6 M) and was not accounted for in the model. Yet we see that at elevated salinity, the simplified adsorption model may not hold true and that an expanding Poiseuille-driven flow that predicts faster kinetics may be more accurate.

Wetting studies for different salt concentrations at 0.2 mM SDS

If the phenomenon of salting-out is indeed responsible for an abrupt loss in rejection, we may encounter a similar instance of wetting at lower salt concentrations, given a higher bulk surfactant concentration. In other words, given that the solvent (here, water) can solubilize only so many ions, a higher number of surfactant ions (higher bulk concentration) may fail to solubilize for the same amount of salt concentration.

To this end, experiments similar to those in the previous section were carried out (Fig. 3) by doubling the concentration of SDS (0.2 mM). While 10 g L⁻¹ and 35 g L⁻¹ showed stable performance, an abrupt loss in separation efficiency was observed in the case of the 60 g L⁻¹ feed. In the earlier set of experiments with 0.1 mM SDS, a similar loss in separation efficiency was not noticed until 90 g L⁻¹. Thus, we conclude that both the surfactant concentration and salinity (or ionic strength) contribute towards accelerated membrane wetting via the salting-out effect. This is in sharp contrast to most previous reports that blamed the surfactant concentration alone for wetting.

Fig. 3 Normalized flux and salt rejection plotted against time for MD experiments carried out at different NaCl concentrations (10 g L⁻¹, 35 g L⁻¹ and 60 g L⁻¹) by maintaining the surfactant concentration at 0.2 mM SDS. For each data point, the average value is plotted. Error bars represent standard deviation arising from three independent measurements (n = 3).

Role of bulk surfactant concentration

We used surfactant concentrations significantly higher than the CMC of SDS (20 mM and 40 mM) to understand the role of bulk surfactant concentration towards surfactant-induced wetting dynamics. In order to facilitate immediate detection via conductivity measurements, the exact feed concentration was 20 mM SDS along with 2 g L⁻¹ NaCl and 40 mM SDS along with 1 g L⁻¹ NaCl. One would expect almost immediate wetting at such elevated concentrations. Interestingly, as shown in Fig. 4A, almost no wetting was observed as evidenced by conductivity measurements. A visual comparison between the two membranes indicated that 40 mM SDS managed to wet some pores, though not fully. These experiments indicate that, unlike the prevailing belief that discourages the use of MD technology for high surfactant concentrations, one may be able to apply MD technology for high bulk surfactant concentrations, provided the salinity is low.

Fig. 4 (A) Normalized flux, (B) change in conductivity for MD experiments with feed concentration 20 mM SDS with 2 g L⁻¹ NaCl and 40 mM SDS with 1 g L⁻¹ NaCl. The initial conductivity in both experiments was 3 µS cm⁻¹, and (C) schematic comparison of how the wetting frontier propagates in the absence of the salting-out effect vs. how it propagates when salting-out happens. For each data point, the average value is plotted. Error bars represent the standard deviation arising from two (n = 2) independent measurements.

Predicting the accelerated wetting regime

The competition between the ionic strength of the feed and the surfactant activity can be conveniently analysed through the dimensionless parameter, Bond number (Bo), widely applied in fluid mechanics. Bo estimates the ratio of gravitational stress to capillary or surface tension stress and is given by eqn (2):where Δρ is the density difference (kg m⁻³), g is the acceleration due to gravity (m s⁻²), L is the characteristic length (m), and γ is the equilibrium surface tension (mN m⁻¹).

To apply the Bo number analysis to our system, a droplet is first created (6 µL) and then gently placed on top of a pristine PVDF membrane. The radius of the contact line at the membrane-droplet interface is noted and is taken to be the characteristic length, L. Bo numbers for solutions of different ionic strength for different surfactant concentrations are plotted in Fig. 5 after feeding other relevant parameters into the equation. We use the 0.1 mM SDS dataset as a representative one to explain the similar trend exhibited across all three surfactant concentrations.

Fig. 5 Variation of Bond number with NaCl concentration for different SDS concentrations. Bo* refers to the critical Bo number and marks the transition from a gradual-wetting regime to accelerated-wetting regime. For each data point, the average value is plotted. Error bars represent standard deviation arising from three independent measurements (n = 3). The dotted lines are only a visual guide and do not represent any fitting.

For moderate salinities, the surface tension gradually decreases (as shown in Fig. 1A) with increasing salinity. As a result, Bo number increases linearly as shown in Fig. 5. However, when salting-out occurs, almost all the SDS molecules are pushed to the interface and we obtain the highest Bo number (corresponding to ∼1.7 M NaCl for 0.1 mM SDS) since surface tension stresses are weakest and gravity can deform the droplet significantly resulting in a higher characteristic length (L). However, at very high salinities (>1.5–1.7 M), non-ideal behaviour such as ion-pairing and ion-crowding becomes significant.^36,37 As a result, the salting-out of SDS molecules does not show the same signature (equilibrium surface tension and droplet-membrane contact line length) at such high ionic strength. As a result, the Bo number goes down. Since the Bo number is highest when salting-out occurs, this salinity (or salt concentration) provides an initial estimate for the case of accelerated wetting. Any salt concentration higher than this will also cause salting-out to occur, leading to accelerated wetting. As surfactant concentration increases, the maximum Bo number (or critical Bo number, Bo*) is attained at a lower NaCl concentration, consistent with our experimental findings. We define Bo* as the value corresponding to the NaCl concentration above which rapid wetting occurs. However, it would be incorrect to assume that this trend would continue, as the NaCl concentration corresponding to Bo* reduces by ∼40% upon moving from 0.1 mM to 0.2 mM and reduces by approximately the same amount on moving from 0.2 mM to 0.5 mM SDS. Further increase in surfactant concentration is not expected to lower the NaCl concentration corresponding to Bo* significantly. In other words, whatever the concentration of SDS, the MD membrane remains in the gradually wetting regime as long as the salt concentration is below a threshold. This, again, is experimentally validated via experiments under the ‘Role of bulk surfactant concentration’ section. This is also consistent with a report by Qazi et al.,³² where precipitation or salting-out of SDS was reported at 35 g L⁻¹ for SDS concentrations as high as 8–10 mM.

For most wetting-related MD studies in the literature, the SDS concentration varies from 0.1 mM to 0.4 mM SDS.^24,38–40 In this range, it would be sufficient to estimate the Bo number for different salt concentrations to obtain the curve and determine the salt concentration corresponding to Bo* for predicting the transition from a gradual-wetting regime to a flow-dominated wetting regime.

Conclusions

In this work, we studied surfactant-induced wetting for MD technology by decoupling the role of salt concentration and bulk surfactant concentration, and the experimental results allow us to conclude the following:

• At hypersaline concentrations (>1.2 M or 70 g L⁻¹ NaCl), almost immediate wetting is observed at 0.1 mM SDS. Thus, unlike low salt concentrations, surfactants present in hypersaline streams require special attention.

• Salting-out or phase separation of surfactant molecules into the air–water interface (wetting frontier) takes place when the feed is of high ionic strength. This allows the salted-out surfactant molecules to hydrophilize the length of the pore via adsorption, leading to water bridging.

• At higher bulk surfactant concentrations, salting-out can occur for lower salt concentrations and thus, both parameters must be taken into account for correctly predicting the kinetics of surfactant-induced wetting.

• MD membranes may be able to withstand high surfactant concentrations without loss in separation efficiency as long as the ionic strength of the feed is kept below a minimum threshold. Such applications may include brackish water laden with surfactant.

• Bo number analysis for various SDS–NaCl combinations helped predict the transition from a gradual-wetting regime to an accelerated-wetting regime. This analysis could also predict that below a certain salt concentration, one would not have to worry about accelerated wetting.

In light of the results presented in this study, future novel membranes for MD applications must be designed to withstand wetting when surfactant precipitation occurs, either due to elevated salinity or high bulk surfactant concentration, pushing MD technology's ability to deal with a variety of feedwater chemistries.

Materials & methods

Materials

Polyvinylidene difluoride (PVDF, 44080, Thermo Scientific) powder was used for casting all the membranes in this work and dimethyl formamide (DMF, ≥99%, Merck) was used for dissolution of PVDF powder. Other laboratory grade reagents such as sodium chloride (NaCl, ≥99%, Merck), and sodium dodecyl sulphate (SDS, ≥99%, Sigma-Aldrich) were used as such without further purification. De-ionized water with a conductivity less than 5 µS cm⁻¹ was procured from an in-house facility at IIT Kanpur for casting membranes and preparing feed and permeate solutions. Non-woven fabric upon which the membranes were cast was procured from Permionics, Gujarat, India (air permeability: 2.5 cm³ psi⁻¹ cm⁻² and thickness: 90–100 µm).

Fabrication of the membranes

The dope solution for casting was prepared by first mixing a certain amount (4.2 g) of PVDF with DMF at 60 °C for 6 h to get a polymer dope solution of 21% (wt%) PVDF concentration. We chose this as our concentration based on previous studies that recommend a sufficient working LEP for MD experiments.²⁷ The dope solution was then left undisturbed at ambient conditions for at least 12 hours to ensure complete removal of air bubbles, after which it was ready for casting. During casting, the non-woven fabric was stuck to the glass plate using an adhesive at the edges. It was then impregnated with DMF by pipetting out ∼1 mL on one end of the fabric and then allowing the doctor blade to run across the fabric. This was followed by adjusting the doctor blade to 200 µm thickness and pouring a certain amount of dope solution. Once cast, the membrane was dipped in water (non-solvent) maintained at 25 °C. This protocol was carefully followed across all membrane preparations for this study to ensure uniform pore size distribution and thickness across different batches.

Membrane characterization

The top surface of the membrane was examined by a field emission scanning electron microscope (FE-SEM, TESCAN, MIRA3). Since PVDF is non-conductive, the membrane sample was sputter-coated with a 10 nm thick Au layer before imaging. The average surface pore size was estimated from high magnification FE-SEM images using ImageJ (National Institutes of Health, USA, 64-bit). Dynamic surface tension of different feed solutions and static contact angle measurements of the membrane were carried out using a contact angle goniometer (DMo-601, Kyowa). The dynamic surface tension of a liquid sample was measured by the pendant drop method. According to this method, surface tension is derived by fitting the shape of the droplet to the Laplace equation. A period of 600 seconds was usually sufficient for most systems to reach their equilibrium surface tension. For contact angle measurements, samples measuring approximately 2.5 cm × 2.5 cm were cut, cleaned in ethanol, dried and loaded onto the goniometer stage. Measurements were carried out using the sessile drop method by dispensing a 6 µL droplet onto the surface of the membrane. Surface free energy measurements of the membranes were determined by the Owens, Wendt, Rabel and Kaelble (OWRK) model using water and di-iodomethane as test liquids. The roughness of the membranes was measured over a 10 µm × 10 µm area using atomic force microscopy (AFM, MFP-3D, Asyum Research) in tapping mode. The minimum LEP of the membranes was tested by a setup developed in-house. All characterization data reported represent the average of three independent measurements along with their standard deviation (or error bars), except for dynamic surface tension measurements, where two data points were collected for each test liquid and averaged. An optical microscope (Leica, DM750M) was used to visualize liquids (approx. 2 mL) dropped onto a clean and dry glass slide. These measurements were carried out to observe any phase separation or precipitation of surfactant molecules, especially in systems having high ionic strength.

Membrane distillation (MD) experiments

The membranes were tested for their performance in a direct contact membrane distillation (DCMD) module with the hot feed and cold distillate being recirculated using peristaltic pumps. The hot side was maintained at 60 °C (±1 °C) and the cold side at 20 °C (±1 °C). The effective membrane area inside the MD module was 20 cm². The inlet and outlet pressures at both the hot and cold ends never exceeded 0.1 bar. The flux and rejection were calculated according to the formula:

where, 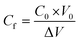, Δw refers to the increment in weight in the distillate side (litre) and this is taken to be the same as the weight in kilograms since the density of water is approximated as 1 kg per litre, A_m is the effective membrane area (m²), Δt is the time interval between the collection of two successive readings (hours), C_d is the concentration of the distillate stream (molar), C_f is the concentration of the feed side (molar), C₀ is the initial concentration of the feed (molar) and is a known value, V₀ is the initial volume of the feed (L) and ΔV refers to the amount of distillate that has passed from the feed to the cold side since the start of the run (L).

For surfactant-induced wetting experiments, initially the whole system was flushed with de-ionized water for 30 min, and then the temperature was allowed to stabilize on both the hot and cold sides. Once the temperatures were stabilized, the flux values were noted for the first 10 min to account for pure water flux, and then the surfactant-containing salt solution (pre-heated) was added to the existing feed to make up the exact feed concentration. Increase in weight and salt conductivity on the permeate end, and temperatures were monitored every minute.

Accuracy of primary measurements

Primary measurement	Accuracy
Weighing balance for computing flux measurements	0.01 g
Conductivity meter for calculation of salt rejection	0.01 µS cm^−1
Thermocouple probes for temperature measurements	0.1 °C
Weighing balance for measuring chemicals (required to prepare feed solution)	0.0001 g

Author contributions

Joel Parayil Jacob: writing – original draft, investigation, methodology, data curation, conceptualization. Raju Kumar Gupta: writing – review and editing, investigation, supervision, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data pertaining to this study have been presented in this manuscript or the supplementary information (SI).

Supplementary information: hydrophilization of membranes due to SDS adsorption, SEM image of the membrane used in this work, contact angle measurements of different salt concentrations with 0.1 mM SDS and dynamic surface tension measurements of different SDS concentrations. See DOI: https://doi.org/10.1039/d5nh00535c.

Acknowledgements

The authors acknowledge the support from the Department of Science and Technology, Government of India (Project – FIST/2023640) and are grateful to Post Graduate Research Laboratory of the Department of Chemical Engineering, IIT Kanpur, for providing access to FESEM equipment. The authors would also like to thank Mr Benament Paul and Ms Bhavika Gupta for their help in carrying out some of the experiments.

References

1. R. Zhao, F. Meng, Q. Wu, Z. Zhong, Y. Liu, R. Yang, A. Li, H. Liu, Y. Lu, Z. Zhang, Q. Li, H. Zhao, J. Li, L. Han and K. Zuo, Environ. Sci. Technol., 2024, 58, 14929–14939.
2. R. Shevate, D. R. Flores, P. Taheri, D. A. Musale and D. L. Shaffer, ACS ES&T Water, 2023, 3, 3407–3417.
3. K. L. Hickenbottom and T. Y. Cath, J. Membr. Sci., 2014, 454, 426–435.
4. X. Yang, N. Zhang, J. Zhang, W. Liu, M. Zhao, S. Lin and Z. Wang, Environ. Sci. Technol., 2023, 57, 15725–15735.
5. Y. Chen, K. J. Lu, W. Gai and T. S. Chung, Environ. Sci. Technol., 2021, 55, 7654–7664.
6. C. Wang, Y. Qiu, G. Wang, L.-F. Ren and J. Shao, Water Res., 2025, 271, 122985.
7. W. Wang, X. Du, H. Vahabi, S. Zhao, Y. Yin, A. K. Kota and T. Tong, Nat. Commun., 2019, 10, 3220.
8. T. Horseman, Y. Yin, K. S. S. Christie, Z. Wang, T. Tong and S. Lin, ACS ES&T Eng., 2021, 1, 117–140.
9. Z. Wang, Y. Chen, X. Sun, R. Duddu and S. Lin, J. Membr. Sci., 2018, 559, 183–195.
10. Z. Wang, Y. Chen and S. Lin, J. Membr. Sci., 2018, 564, 275–288.
11. M. J. Qazi, S. J. Schlegel, E. H. G. Backus, M. Bonn, D. Bonn and N. Shahidzadeh, Langmuir, 2020, 36, 7956–7964.
12. S. Tiwari, S. Namsani and J. K. Singh, J. Mol. Liq., 2022, 360, 119498.
13. S. G. Woolfrey, G. M. Banzon and M. J. Groves, J. Colloid Interface Sci., 1986, 112, 583–587.
14. H. M. Hort, C. E. Robinson, A. H. Sawyer, Y. Li, R. Cardoso, S. A. Lee, D. Roff, D. T. Adamson and C. J. Newell, Groundwater, 2024, 62, 860–875.
15. C. Yin, C.-G. Pan, S.-K. Xiao, Q. Wu, H.-M. Tan and K. Yu, Environ. Pollut., 2022, 300, 118957.
16. L. Han, Y. Z. Tan, T. Netke, A. G. Fane and J. W. Chew, J. Membr. Sci., 2017, 539, 284–294.
17. M. Lou, X. Fang, S. Huang, J. Li, Y. Liu, G. Chen and F. Li, Desalination, 2022, 532, 115739.
18. P. J. Lin, M. C. Yang, Y. L. Li and J. H. Chen, J. Membr. Sci., 2015, 475, 511–520.
19. A. Ghodsi and H. Fashandi, Sep. Purif. Technol., 2024, 348, 127744.
20. Q. Wu, J. Zhou, Y. Li, L. Zhang, X. Wang and X. Lu, Sep. Purif. Technol., 2024, 335, 126145.
21. Q. Ding, K. Dong, X. Si, T. Xiao and X. Yang, J. Membr. Sci., 2024, 701, 122794.
22. Q. Wu, X. Wang, Y. Li, J. Zhou, Z. Liu, M. Sun, X. Lu and C. Wu, Surf. Interfaces, 2024, 51, 104546.
23. M. Lou, S. Huang, X. Zhu, J. Chen, X. Fang and F. Li, J. Membr. Sci., 2024, 697, 122494.
24. P. Zhang, S. Xiang, R. R. Gonzales, Z. Li, Y.-H. Chiao, K. Guan, M. Hu, P. Xu, Z. Mai, S. Rajabzadeh, K. Nakagawa and H. Matsuyama, J. Membr. Sci., 2024, 693, 122338.
25. C. Coolidge, A. M. H. Alhadidi, W. Wang and T. Tong, J. Membr. Sci. Lett., 2024, 4, 100077.
26. Y. Ma, Z. Yu, X. Fu, T. Qiu, N. Zhao, H. Liu, Z. Huang and K. Liu, Nano Lett., 2024, 24, 4202–4208.
27. M. S. El-Bourawi, Z. Ding, R. Ma and M. Khayet, J. Membr. Sci., 2006, 285, 4–29.
28. A. Chatterjee, S. P. Moulik, S. K. Sanyal, B. K. Mishra and P. M. Puri, J. Phys. Chem. B, 2001, 105, 12823–12831.
29. A. M. Hyde, S. L. Zultanski, J. H. Waldman, Y. L. Zhong, M. Shevlin and F. Peng, Org. Process Res. Dev., 2017, 21, 1355–1370.
30. M. El Haber, C. Ferronato, A. Giroir-Fendler, L. Fine and B. Nozière, Sci. Rep., 2023, 13, 20672.
31. A. Kharlamova, F. Boulogne, P. Fontaine, S. Rouzière, A. Hemmerle, M. Goldmann and A. Salonen, Langmuir, 2024, 40, 84–90.
32. M. J. Qazi, R. W. Liefferink, S. J. Schlegel, E. H. G. Backus, D. Bonn and N. Shahidzadeh, Langmuir, 2017, 33, 4260–4268.
33. S. Kalam, A. Dutta, X. Du, X. Li, T. Tong and J. Lee, Desalination, 2024, 573, 117195.
34. K. C. Duong-Ly and S. B. Gabelli, in Methods in Enzymology, ed. J. Lorsch, Academic Press, 2014, vol. 541, pp. 85–94.
35. S. Velioğlu, L. Han and J. W. Chew, J. Membr. Sci., 2018, 551, 76–84.
36. L. Wang, A. Morita, N. M. North, S. M. Baumler, E. W. Springfield and H. C. Allen, J. Phys. Chem. B, 2023, 127, 1618–1627.
37. N. F. A. van der Vegt, K. Haldrup, S. Roke, J. Zheng, M. Lund and H. J. Bakker, Chem. Rev., 2016, 116, 7626–7641.
38. L. Meng, X. Chen, T. Cai, X. Tong and Z. Wang, Water Res., 2024, 263, 122176.
39. D. Hou, Z. Yuan, M. Tang, K. Wang and J. Wang, J. Membr. Sci., 2020, 595, 117495.
40. S. Xie, Y. Chen, D. Feng and Z. Wang, Adv. Mater. Technol., 2023, 8, 2201426.

---