Acoustic metamaterials for remote manipulation of large objects in water†
Dajun
Zhang
and
Chu
Ma
 *
*
Department of Electrical and Computer Engineering, University of Wisconsin–Madison, 1415 Engineering Drive, Madison, WI 53706, USA. E-mail: chu.ma@wisc.edu
First published on 23rd April 2025
Abstract
Acoustic metamaterials have recently been applied to assist in the remote manipulation of objects in air, showing remarkable potential to alleviate the constraints of non-metamaterial-based acoustic manipulation methods in terms of object size and the force degree of freedom. To extend this approach to underwater manipulation, in this work, we develop a new type of underwater acoustic metamaterial based on a metal–resin composite, offering submillimeter scale feature resolution and high acoustic impedance contrast with water. By designing the surface patterns of the metamaterial, we demonstrate the remote acoustic manipulation of in-water large objects (>20 wavelengths) with 3D translational and rotational degrees of freedom. We then proposed two methods, surface pattern superimposition and frequency multiplexing, to integrate different manipulation forces within a single metamaterial patch. Additionally, we demonstrate more examples of complex object manipulation using multiple metamaterial patches and transducers, such as multi-object, multi-path, non-invasive, and 3D underwater manipulation. Our metamaterial-assisted remote underwater acoustic manipulation will have broad applications in underwater robot actuation, vehicle transportation, manufacturing, drug delivery and minimally invasive surgery.
New conceptsAcoustic wave scattering from a thin layer of metamaterial coated on an object's surface can generate radiation forces with tailored spatial distributions, enabling remote object manipulation. While this concept was demonstrated in air, it has not been extended to liquid environments due to the lack of underwater metamaterials with high acoustic impedance contrast with water and high fabrication resolution at the same time. Our work addresses this challenge by developing a new metamaterial fabrication technique using soft lithography of a metal–resin composite. The fabricated metamaterial enables the excitation of various actuation forces in water. Novel designs of the metamaterials are further developed to enable the simultaneous excitation of multiple forces from one single metamaterial layer, offering unprecedented maneuvering complexity and flexibility. Different from existing in-water acoustic manipulation systems that only work for objects comparable or smaller than the wavelength, our metamaterial-assisted system achieves 3D multi-path, multi-object, and non-invasive manipulation of objects larger than 20 times the wavelength. Our work will provide a new way to reduce the weight, complexity, and operational limitations of underwater robots and vehicles. Additionally, the metamaterial fabrication technique will benefit other underwater acoustic applications, such as underwater sensing, communication, biomedical diagnostics, therapy, and drug delivery. |
1. Introduction
Acoustic metamaterials1–4 are composite structures formed by unit cells with subwavelength sizes and exotic properties that do not exist in natural forms, e.g., negative mass density5 and/or bulk modulus,6–8 negative refractive index9,10 and negative Poisson's ratio.11,12 Acoustic metamaterials provide a variety of novel wave manipulation functionalities, e.g., phase/amplitude engineering,13–15 super-resolution imaging,9,16,17 impedance matching,18,19 invisibility cloaking,20,21 sound absorption,22,23 unidirectional transparency, and nonreciprocal propagation.24–26 These functions have offered powerful tools to solve the challenges in applications such as noise control, communications, medical diagnosis, and non-destructive testing.Recently, acoustic metamaterials were applied to assist remote manipulation of large objects (i.e., objects greater than at least twice the wavelength) using acoustic waves.27 When an acoustic wave is reflected by the object's surface, the exchange of momentum between the reflected and incident waves results in an acoustic radiation force on the object. By coating the object with a thin layer of acoustic metamaterial, the radiation force's spatial distribution can be controlled with subwavelength precision. Without the assistance of metamaterials, acoustic waves can only manipulate objects smaller or comparable to their wavelength. For example, particles can be tapped by acoustic standing waves at wave nodes and antinodes,28–32 or at the potential wells generated by either a transducer array33,34 or a hologram.35,36 If the size of the object is large, the acoustic radiation force generated by the diffraction of a wave by the object has the magnitude and direction dependent on the object's surface shape and material properties, making it difficult to levitate and precisely manipulate the object. Only the levitation of large objects in particular symmetric shapes, such as spheres and flat plates, was previously demonstrated37–41 without metamaterials. In contrast, acoustic metamaterials enable the manipulation of large objects with arbitrary sizes and shapes, by shaping the acoustic radiation force with subwavelength-sized surface patterns.
While metamaterial-assisted acoustic manipulation provides an intriguing prospect for large-object manipulation, it has only been demonstrated to manipulate an object in air.27 To expand this approach to underwater manipulation, creating underwater acoustic metamaterials is a necessary but challenging step, mainly because of the small acoustic impedance contrast between water and most of the materials used in existing metamaterial construction, such as polymer-based resins42 and soft materials.43 This small contrast cannot provide the required modulation to the acoustic radiation force for object manipulation. Metals or ceramics are viable material choices considering their relatively large acoustic impedance compared to water,44,45 however, the fabrication capability of these two cannot provide sufficient resolution or shape complexity needed by metamaterials, not to mention the high cost.46–49 The development of a low-cost, high-resolution solution to create underwater metamaterials will not only advance the remote acoustic manipulation, but also has immense potential for applications of acoustic metamaterials in underwater sensing, communication, biomedical diagnosis, and therapy.50,51
In this work, we developed a new type of underwater acoustic metamaterial by fabricating subwavelength surface patterns using a metal–resin composite. Using the fabricated underwater metamaterial patches, we demonstrated remote acoustic manipulation of large objects in water with 3D translational and rotational degrees of freedom. We then developed two methods, surface pattern superimposition and frequency multiplexing, to achieve different manipulation functions within a single metamaterial patch. Additionally, we demonstrated more complex examples of multi-object, multi-path, non-invasive, and 3D underwater manipulation using multiple patches/transducers. Our metamaterial-assisted remote underwater acoustic manipulation has broad applications in underwater robot control and vehicle transportation, underwater assembly, drug delivery and minimally invasive surgery.
2. Results and discussion
2.1. Fabrication and characterization of underwater acoustic metamaterials
To achieve the required high acoustic impedance contrast with water, acoustic metamaterials are fabricated using a metal–resin composite created by mixing iron granules with epoxy resin (see details in the Experimental Section). The iron granules have sizes in the range of 5–250 μm, which are smaller than the acoustic wavelength we are using (500–1500 μm for 1–3 MHz). Microscopic pictures of the metal–resin composite with different mass ratios of iron fillings are shown in Fig. 1(a). The measured density ρ and acoustic wave speed c of the composite are shown in Fig. 1(b). Because of the density difference between the iron granules (∼7800 kg m−3) and resin (∼1500 kg m−3), the equivalent density of the composite increases as the mass ratio of the iron granules increases. The acoustic speed inside the composite remains roughly the same as the iron mass ratio increases. As a result, the acoustic impedance (Z = ρc) increases from 2.89 MPa S m−3 to 13.8 MPa S m−3 as the iron mass ratio increases from 0% to 80%, leading to the increase of the acoustic reflection coefficient (|R| = (Zmixture − Zwater)/(Zmixture + Zwater)) from 0.3 to 0.8, as depicted in Fig. 1(c). More details regarding the acoustic property measurement are presented in Note S1 (ESI†).Fig. 1(d) illustrates the steps to fabricate a metamaterial patch. Details of the fabrication process can be found in the Experimental Section. One fabricated sample with 80% iron granule mass ratio is pictured in Fig. 1(e). The 20 mm × 20 mm × 2 mm sample works for 1 MHz acoustic waves. It has surface patterns with a height ranging from 0 to 0.75 mm. This fabrication method can realize ∼50 micrometre fabrication resolution. Our underwater metamaterials have the advantages of high spatial feature resolution, large acoustic impedance contrast with water, as well as low fabrication cost, promising for underwater and biomedical applications even beyond acoustic manipulation.
2.2. Design and demonstration of acoustic manipulation functions: pushing, rotating, following
As illustrated in Fig. 2(a), a metamaterial patch is attached to the bottom surface of the object that is floating on the water. The patch has a surface pattern with varying extrusion height. The height gradient corresponds to the phase gradient of the reflected wave from the surface. The momentum exchange of the waves with the metamaterial surface generates an acoustic radiation force Fr on the object, whose direction and magnitude depend on the phase gradient. In an underwater environment, the other forces on the object are gravity Fg and buoyancy Fb, both in the z direction in the coordinate system shown in Fig. 2(a).The incident acoustic beam is perpendicular to the metamaterial surface, emitted by an acoustic transducer with a center frequency of 1 MHz located 30 mm away from the metamaterial surface. We characterized the incident beam profile using a needle transducer and plotted the acoustic wave intensity along and perpendicular to the beam direction in Fig. 2(c) and (d). More details of acoustic beam characterization are in the Experimental Section. Fig. 2(d) shows that the incident acoustic beam has a width of around 3 mm at the Z0 = 30 mm position.
The metamaterial surface patterns are designed to realize three basic manipulation functions: pushing, rotating, and following (Movie S1 (ESI†)). Combinations of these basic functions can realize more complex 3-D object manipulation.
| hpushing = mod(tan(α)·x, λ/2) | (1) |
To gain insight into the pushing mechanism, we experimentally measure the acoustic radiation force in the z-direction, Frz, as a function of the reflection angle α. In underwater manipulation, the mass and volume of an object determine the magnitude of the buoyancy and gravity forces. At force equilibrium, the Frz should equal the difference between the buoyancy and gravity. The experimental measurement of Frz is performed in the following way: as the object is floated on the water surface, the immersion volume change of the object after the acoustic beam is turned on is proportional to Frz. By constraining the object's xy-plane movement by a 3D printed ring-shape structure (left structure in Fig. S4 (ESI†)) and measuring its immersion volume change (ΔV), the Frz can be calculated by Frz = ρwater·g·ΔV, where g = 9.8 N kg−1 and ρwater = 997 kg m−3 (Fig. S5(a) and Note S2 (ESI†)). In the Frz measurements presented in Fig. 3(a), the same transducer input power of 3 W is applied and the acoustic wave reflection angle α varies from 0° to 60°. At each angle α, the measurement is repeated 20 times. The results indicate that the larger the reflection angle α, the smaller the Frz. We also calculate the xy-direction and z-direction acoustic radiation forces, Frx and Frz, based on the theory of acoustic radiation force52 and COMSOL modelling of the acoustic field distribution after the incident beam is reflected by the metamaterial patch (see more details in the Experimental Section and Note S3 (ESI†)). The normalized forces Frx/max(Frz) and Frz/max(Frz) from the calculations are also plotted in Fig. 3(a). A similar decreasing trend as in experimental measurements is observed in the Frzvs. α plot. At the same time, the calculated Frx increases with α. The angle between the direction of the acoustic radiation force and the +z direction can be calculated by arctan(Frx/Frz), which shows an increasing trend as the α become larger (shown in Fig. S7(e) (ESI†)). In Fig. S5(b) (ESI†), we presented the measured Frz as a function of the transducer input power, showing that the magnitude of Frz increases linearly with the transducer input power. We have also plotted the required Frz as a function of the total mass and water-immersed volume of the object in Fig. S6(a) (ESI†). In addition to the mass and size of the object, the lateral size of the metamaterial patch also impacts the acoustic radiation force in both vertical and horizontal directions. On one hand, when using a focused ultrasound beam as in our experiments, the acoustic radiation force reaches its maximum at a specific transducer power as long as the lateral size of the metamaterial patch is slightly larger than the focal spot. On the other hand, a larger patch enables longer actuation time when the object moves, resulting in larger accumulative effects on the object's motion. A larger metamaterial patch is also heavier. In Fig. S6(b) (ESI†), we show the additional z-direction radiation forced needed because of the metamaterial patch as a function of the patch size.
| hrotating = mod(RN·φ·λ/4π, λ/2), | (2) |
 | (3) |
The acoustic radiation force at any point of the metamaterial surface has a z-component, Frz that is perpendicular to the surface, and a transverse component, Frxy, that is along the radial direction and points to the center of the surface. We name Frxy the trapping force as it determines the capability of the metamaterial to trap and make the object following the transducer. The angle θ determines the ratio between Frxy and Frz. When the center of the acoustic beam and the center of the surface pattern overlap, the forces on the object are balanced because of the axial symmetry. As the acoustic beam center begins to move off the surface pattern center, for example to the left, the right-pointing force will become larger than the left-pointing one. The object will be forced to move left, following the movement of the acoustic beam center. In Fig. 2(g), we demonstrate that the object follows the transducer center and moves along an S-shape trajectory (also shown in Movie S1, ESI†).
To illustrate the relationship between the angle θ of the metamaterial surface pattern and the strength of the trapping force in the “following” function, we measured the largest speed change, Δvmax, of the object that the transducer can induce as a function of θ. An illustration of the measurement setup is in Fig. S5(c) (ESI†). The object is originally static while the transducer speed changes from 0 to Δvmax (acceleration). With the fixed transducer input power and object total weight, the increased angle θ in metamaterial design increases the Δvmax, which is due to the larger trapping force generated by the metamaterial (shown in Fig. 3(c)). We also show that with a fixed transducer input power, the Δvmax decreases with the object total weight (Fig. S5(d) (ESI†)). This is because the acceleration decreases with the object mass.
2.3. Multifunctional design of a single metamaterial patch
In the above designs, a single metamaterial patch supports one manipulation function. Multifunctional design expands the manipulation capability provided by a single patch, thereby reducing the overall system complexity and manufacturing cost. Here we develop two mechanisms for multifunctional manipulation that are complementary to each other: surface pattern superimposition and frequency multiplexing.| hpushing_rotating = mod(tan(α)·x + RN·φ·λ/4π, λ/2) | (4) |
The angle α is set as 45° and RN is set as 0.5. When an acoustic beam is incident onto the patch, the acoustic radiation force in the xy plane has two components: one along the x-direction and another rotating clockwise. Hence, the acoustic wave will push the object to move along a curved trajectory (Movie S2 (ESI†)).
In another example, we combine the “following” and “rotating” patterns (as shown in Fig. 4(b)) as:
 | (5) |
The angle θ is set to 45° and RN is set to 0.3. After turning on the acoustic incident beam, the object follows the movement of the beam and rotates clockwise at the same time (see Fig. 4(b) and Movie S2 (ESI†)).
Our first example demonstrates the switching between two pushing directions using incident acoustic beams at 1 MHz and 3 MHz. We set the reflection angle as α1 = −20° for 1 MHz, and α3 = 40° for 3 MHz. The combined surface pattern distribution (Fig. 4(c)) is:
| hmultiplexing_pushing = mod(x·tan(α1), λ1/2) + mod(x·tan(α3), λ3/2) | (6) |
In our second example, we demonstrate the switching between clockwise and counterclockwise rotation using 1-MHz and 3-MHz acoustic beams. The surface pattern is the combination of the following two designs: (1) the surface pattern superimposition of the “following” and “rotating” functions at 1 MHz, and (2) the “rotating” function at 3 MHz:
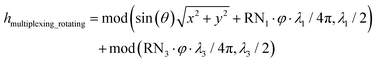 | (7) |
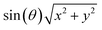 provides the trapping force to stabilize the object above the transducer.
provides the trapping force to stabilize the object above the transducer.
2.4. Demonstration of complex underwater object manipulation
Our single- and multi-functional metamaterial patches enable many application scenarios for underwater acoustic object manipulation. We have already shown examples using a single patch, such as pushing, rotating, following, simultaneous following and rotating, simultaneous pushing and rotating, and frequency multiplexing of different functions. In this section we demonstrate several more complex scenarios that require the cooperation of more than one patch and transducer pair. The results are presented in Fig. 5 and Movie S3 (ESI†). | ||
| Fig. 5 Demonstration of complex object manipulation functions enabled by more than one metamaterial patches and transducers. (a) Multi-object manipulation. (b) Multi-path manipulation. (c) Non-invasive manipulation inside a tube. (d) 3D manipulation in water. The experiment videos are shown in Movie S3 (ESI†). | ||
3. Conclusions
In this study, we developed an acoustic metamaterial to tailor the acoustic radiation force for multi-degree-of-freedom manipulation of large objects (>20 wavelengths) in water. The metamaterial fabricated through soft lithography of iron-resin mixtures have the advantages of large acoustic impedance contrast with water, sub-millimeter spatial feature resolution, and low fabrication cost, which are highly demanded in underwater applications of metamaterials, including sensing, communication, and actuation. In our work, we explored its application in enabling underwater acoustic remote manipulation of large objects. We developed basic manipulation functions including pushing, rotating, and following. We also developed two methods, surface pattern superimposition and frequency multiplexing, to combine different basic manipulation functions onto a single metamaterial patch, such as pushing and rotating, rotating and following, left and right pushing, and clockwise and counterclockwise rotating. Furthermore, we demonstrated application-driven examples of complex underwater object manipulation by the collaboration of more than one metamaterial patches and transducers.In our metamaterial-assisted remote acoustic manipulation, the size of the object is no longer limited by the acoustic wavelength. We can exert controllable forces on underwater objects with sizes much larger than the used acoustic wavelength, which was difficult in previously established acoustic manipulation approaches based on standing waves or acoustic pressure gradients. As acoustic wave can penetrate through materials non-invasively, our system can also be used to manipulate objects inside containers and behind obstacles. In future studies, the metamaterial patches can be made soft and conformable to different object surface shapes. The metamaterial structure can be designed so that the manipulation function is switchable with different incident wave angles or wavefront shapes. The metamaterial can also be made of reconfigurable materials, so that the manipulation function can be changed with environmental stimuli. Moreover, we can attach multiple patches at different locations of the object, each implementing a different movement. Feedback control through imaging of the object position and trajectory can be added to the system to generate more stable object motion, and also enable real-time motion planning. Our work will have broad applications in the control of underwater robots and unmanned vehicles, underwater assembly, minimally invasive surgery, and drug delivery.
4. Experimental section
4.1. Metamaterial fabrication and characterization
The metamaterial patches were fabricated through a soft lithography process. First, a resin base (Formlabs Clear Resin) was fabricated by a 3D printer (Form 3, Formlabs Inc.). Then the resin base was immersed into PDMS liquid (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio, Sylgard 186 Silicone Elastomer Kit). After heating at 80 degrees for 60 minutes, the PDMS mold with inversed patterns was separated from the resin base. The metal–resin mixture, prepared by mixing iron granules (Bulk Iron Filings, by American Heritage Industries) with resin gel (Epoxy crystal clear Resin Kit, PIXISS) at pre-designed weight ratios, was then filled into the PDMS mold. After 12 hours of curing at room temperature, the ready-to-use metamaterial patch was separated from the PDMS mold. The metamaterial patches used in the experiments are shown in Fig. S1 (ESI†).
1 volume ratio, Sylgard 186 Silicone Elastomer Kit). After heating at 80 degrees for 60 minutes, the PDMS mold with inversed patterns was separated from the resin base. The metal–resin mixture, prepared by mixing iron granules (Bulk Iron Filings, by American Heritage Industries) with resin gel (Epoxy crystal clear Resin Kit, PIXISS) at pre-designed weight ratios, was then filled into the PDMS mold. After 12 hours of curing at room temperature, the ready-to-use metamaterial patch was separated from the PDMS mold. The metamaterial patches used in the experiments are shown in Fig. S1 (ESI†).
We also fabricated 4 cm × 4 cm × 1 cm samples with different iron filling weight ratios to measure the acoustic properties. The density of these samples was calculated using the mass and volume, and acoustic velocities of the used 1 MHz and 3 MHz acoustic waves were measured through the wave transmission experiment (more in the Note S1 (ESI†)).
4.2. Acoustic field simulation and acoustic radiation force calculation
The spatial distribution of an acoustic field generated by the reflection of an acoustic beam by a metamaterial patch is simulated using the Pressure Acoustics module in COMSOL Multiphysics 6.0. The acoustic radiation force exerted on the object was calculated using the following equation:52,53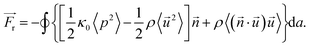 | (8) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) are the acoustic pressure and acoustic velocity of the wave. The integration is performed along a boundary enclosing the object. More details of the simulation and acoustic radiation force calculation are given in Note S3 and Fig. S7 (ESI†).
are the acoustic pressure and acoustic velocity of the wave. The integration is performed along a boundary enclosing the object. More details of the simulation and acoustic radiation force calculation are given in Note S3 and Fig. S7 (ESI†).
4.3. Acoustic manipulation experiments
The materials of the objects used in the experiments include wood, wax, 3D-printed resin, plastic foam, and PDMS. The metamaterial patch was fixed on an object and was placed at the focal spot of a high-intensity focused ultrasound (HIFU) transducer (focal length: 30 mm). Two HIFU transducers, TQ20-1030 and TQ20-3030 from Siansonic Inc., are used to generate 1-MHz and 3-MHz beams, respectively. The HIFU transducers are controlled by a function generator (AFG3022C, Tektronix Inc.) and a power amplifier (AD1006, T&C Power Conversion) to specify the frequency and power of the incident beam. A needle hydrophone (Precision Acoustics NH0075) mounted on a 3D translation stage was used to characterize the field distribution of the beam (Fig. S3 (ESI†)). More details of the metamaterial patches, objects, and input power of the transducer are listed in Table S1 (ESI†).Author contributions
D. Z. and C. M. proposed the project and conceived the idea. D. Z. designed and carried out the experiments. D. Z. and C. M. analyzed the data and wrote the manuscript. C. M. supervised the project.Data availability
The data supporting the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation under Grant No. 2328096.Notes and references
- S. A. Cummer, J. Christensen and A. Alù, Nat. Rev. Mater., 2016, 1, 16001 CrossRef.
- H. Ge, M. Yang, C. Ma, M.-H. Lu, Y.-F. Chen, N. Fang and P. Sheng, Natl. Sci. Rev., 2018, 5, 159–182 CrossRef CAS.
- J. Liu, H. Guo and T. Wang, Crystals, 2020, 10, 305 CrossRef CAS.
- G. Ma and P. Sheng, Sci. Adv., 2016, 2, e1501595 CrossRef PubMed.
- S. H. Lee, C. M. Park, Y. M. Seo, Z. G. Wang and C. K. Kim, Phys. Lett. A, 2009, 373, 4464–4469 CrossRef CAS.
- N. Fang, D. Xi, J. Xu, M. Ambati, W. Srituravanich, C. Sun and X. Zhang, Nat. Mater., 2006, 5, 452–456 CrossRef CAS PubMed.
- S. H. Lee, C. M. Park, Y. M. Seo, Z. G. Wang and C. K. Kim, Phys. Rev. Lett., 2010, 104, 054301 CrossRef PubMed.
- M. Yang, G. Ma, Z. Yang and P. Sheng, Phys. Rev. Lett., 2013, 110, 134301 CrossRef PubMed.
- N. Kaina, F. Lemoult, M. Fink and G. Lerosey, Nature, 2015, 525, 77–81 CrossRef CAS PubMed.
- Z. J. Wong, Y. Wang, K. O’Brien, J. Rho, X. Yin, S. Zhang, N. Fang, T.-J. Yen and X. Zhang, J. Opt., 2017, 19, 084007 CrossRef.
- S. Babaee, J. Shim, J. C. Weaver, E. R. Chen, N. Patel and K. Bertoldi, Adv. Mater., 2013, 25, 5044–5049 CrossRef CAS PubMed.
- X. Hou and V. V. Silberschmidt, in Mechanics of Advanced Materials: Analysis of Properties and Performance, ed. V. V. Silberschmidt and V. P. Matveenko, Springer International Publishing, Cham, 2015, pp. 155–179 Search PubMed.
- Y. Li, C. Shen, Y. Xie, J. Li, W. Wang, S. A. Cummer and Y. Jing, Phys. Rev. Lett., 2017, 119, 035501 CrossRef PubMed.
- B. Xie, K. Tang, H. Cheng, Z. Liu, S. Chen and J. Tian, Adv. Mater., 2017, 29, 1603507 CrossRef PubMed.
- Y. Xie, W. Wang, H. Chen, A. Konneker, B.-I. Popa and S. A. Cummer, Nat. Commun., 2014, 5, 5553 CrossRef CAS PubMed.
- J. Zhu, J. Christensen, J. Jung, L. Martin-Moreno, X. Yin, L. Fok, X. Zhang and F. J. Garcia-Vidal, Nat. Phys., 2011, 7, 52–55 Search PubMed.
- M. Molerón and C. Daraio, Nat. Commun., 2015, 6, 8037 Search PubMed.
- G. D’Aguanno, K. Q. Le, R. Trimm, A. Alù, N. Mattiucci, A. D. Mathias, N. Aközbek and M. J. Bloemer, Sci. Rep., 2012, 2, 340 Search PubMed.
- Y. Xie, A. Konneker, B.-I. Popa and S. A. Cummer, Appl. Phys. Lett., 2013, 103, 201906 CrossRef.
- H. Chen and C. T. Chan, J. Phys. D: Appl. Phys., 2010, 43, 113001 CrossRef.
- S. Zhang, C. Xia and N. Fang, Phys. Rev. Lett., 2011, 106, 024301 CrossRef PubMed.
- J. Mei, G. Ma, M. Yang, Z. Yang, W. Wen and P. Sheng, Nat. Commun., 2012, 3, 756 CrossRef PubMed.
- M. Yang, C. Meng, C. Fu, Y. Li, Z. Yang and P. Sheng, Appl. Phys. Lett., 2015, 107, 104104 CrossRef.
- C. Shi, M. Dubois, Y. Chen, L. Cheng, H. Ramezani, Y. Wang and X. Zhang, Nat. Commun., 2016, 7, 11110 CrossRef CAS PubMed.
- X. Zhu, H. Ramezani, C. Shi, J. Zhu and X. Zhang, Phys. Rev. X, 2014, 4, 031042 Search PubMed.
- R. Fleury, D. Sounas and A. Alù, Nat. Commun., 2015, 6, 5905 CrossRef PubMed.
- M. Stein, S. Keller, Y. Luo and O. Ilic, Nat. Commun., 2022, 13, 6533 CrossRef CAS PubMed.
- H. M. Hertz, J. Appl. Phys., 1995, 78, 4845–4849 CrossRef CAS.
- X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109 CrossRef CAS PubMed.
- D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686 CrossRef CAS PubMed.
- J. Li, C. Shen, T. J. Huang and S. A. Cummer, Sci. Adv., 2021, 7, eabi5502 CrossRef CAS PubMed.
- V. M. Jooss, J. S. Bolten, J. Huwyler and D. Ahmed, Sci. Adv., 2022, 8, eabm2785 CrossRef CAS PubMed.
- A. Marzo and B. W. Drinkwater, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 84–89 CrossRef CAS PubMed.
- A. Marzo, S. A. Seah, B. W. Drinkwater, D. R. Sahoo, B. Long and S. Subramanian, Nat. Commun., 2015, 6, 8661 CrossRef CAS PubMed.
- K. Melde, A. G. Mark, T. Qiu and P. Fischer, Nature, 2016, 537, 518–522 CrossRef CAS PubMed.
- Z. Ma, A. W. Holle, K. Melde, T. Qiu, K. Poeppel, V. M. Kadiri and P. Fischer, Adv. Mater., 2020, 32, 1904181 CrossRef CAS PubMed.
- M. A. B. Andrade, A. L. Bernassau and J. C. Adamowski, Appl. Phys. Lett., 2016, 109, 044101 CrossRef.
- M. A. B. Andrade, F. T. A. Okina, A. L. Bernassau and J. C. Adamowski, J. Acoust. Soc. Am., 2017, 141, 4148–4154 CrossRef PubMed.
- S. Zhao and J. Wallaschek, Arch. Appl. Mech., 2011, 81, 123–139 CrossRef.
- D. Foresti, M. Nabavi, M. Klingauf, A. Ferrari and D. Poulikakos, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12549–12554 CrossRef CAS PubMed.
- C. E. M. Démoré, P. M. Dahl, Z. Yang, P. Glynne-Jones, A. Melzer, S. Cochran, M. P. MacDonald and G. C. Spalding, Phys. Rev. Lett., 2014, 112, 174302 CrossRef PubMed.
- L. J. Tan, W. Zhu and K. Zhou, Adv. Funct. Mater., 2020, 30, 2003062 CrossRef CAS.
- H. Lim, H. S. Kim, R. Qazi, Y. Kwon, J. Jeong and W. Yeo, Adv. Mater., 2020, 32, 1901924 CrossRef CAS PubMed.
- C. W. Cushing, P. S. Wilson, M. R. Haberman, C. Shen, J. Li, S. A. Cummer, Z. J. Tan, C. Ma, H. Du and N. X. Fang, J. Acoust. Soc. Am., 2021, 149, 1829–1837 CrossRef CAS PubMed.
- H. Li, Z. D. Deng and T. J. Carlson, Sens. Lett., 2012, 10, 679–697 CrossRef CAS.
- Y. Bi, H. Jia, Z. Sun, Y. Yang, H. Zhao and J. Yang, Appl. Phys. Lett., 2018, 112, 223502 CrossRef.
- M. Y. Wang, M. Thevamaran, M. S. Mattei, B. G. Hacha, G. A. Mazzei Capote, Z. Yu, T. Osswald, R. H. Goldsmith, D. J. Thoma and C. Ma, Appl. Phys. Lett., 2022, 120, 141702 CrossRef CAS.
- Y.-X. Shen, Y.-G. Peng, F. Cai, K. Huang, D.-G. Zhao, C.-W. Qiu, H. Zheng and X.-F. Zhu, Nat. Commun., 2019, 10, 3411 CrossRef PubMed.
- C. Shen, C. Rohde, C. W. Cushing, J. Li, Z. J. Tan, H. Du, X. Peng, P. S. Wilson, M. R. Haberman, N. X. Fang and S. A. Cummer, Adv. Eng. Mater., 2023, 25, 2201294 CrossRef CAS.
- E. Dong, P. Cao, J. Zhang, S. Zhang, N. X. Fang and Y. Zhang, Natl. Sci. Rev., 2023, 10, nwac246 CrossRef CAS PubMed.
- J. Zhang, B. Hu and S. Wang, Appl. Phys. Lett., 2023, 123, 010502 CrossRef CAS.
- H. Bruus, Lab Chip, 2012, 12, 1014 Search PubMed.
- M. Settnes and H. Bruus, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016327 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00048c |
| This journal is © The Royal Society of Chemistry 2025 |




