Unraveling the myths and mysteries of photon avalanching nanoparticles

Abstract

Photon avalanching (PA) nanomaterials exhibit some of the most nonlinear optical phenomena reported for any material, allowing them to push the frontiers of applications ranging from nanoscale imaging and sensing to optical computing. But PA remains shrouded in mystery, with its underlying physics and limitations misunderstood. Photon avalanching is not, in fact, an avalanche of photons, at least not in the same way that snowballs beget more snowballing in an actual avalanche. In this focus article, we dispel these and other common myths surrounding PA in lanthanide-based nanoparticles and unravel the mysteries of this unique nonlinear optical effect. We hope that removing the misconceptions surrounding avalanching nanoparticles will inspire new interest and applications that harness the giant nonlinearity of PA across a broad range of scientific fields.

---

Artiom Skripka

Dr Artiom Skripka is an Assistant Professor in the Department of Chemistry at Oregon State University. His research focuses on nonlinear emitters, including lanthanide-doped nanoparticles, for applications ranging from bioimaging and sensing to optical computing. Currently, Dr Skripka is developing novel host materials for lanthanide dopants and studying the nontrivial energy exchange pathways between them. His previous efforts in this area have yielded methods for imprinting photon avalanches onto linear emitters and led to the discovery of intrinsic optical bistability in photon avalanching nanocrystals.

Emory M. Chan

Dr Emory Chan is a Staff Scientist at the Molecular Foundry, a U.S. Department of Energy nanoscience user facility at Lawrence Berkeley National Laboratory. Dr Chan's research interests include the accelerated, high-throughput synthesis of nanomaterials with complex compositions, such as semiconductor nanoparticle heterostructures tailored for solid state lighting and biological imaging. He also investigates nanomaterials that host complex energy transfer networks, such lanthanide-doped upconverting nanoparticles for lasing and super-resolution imaging. Towards this end, Dr Chan has developed robotic workflows that increase the reproducibility and throughput of colloidal nanoparticle synthesis while also enabling machine-learning guided experimentation.

---

1. Introduction

When one thinks of photon avalanching (PA) in a material, one might envision a photon stimulating the emission of additional photons, which each go on to stimulate even more photons in an optical feedback loop (Fig. 1, left). While this cartoon image may be useful for illustrating the general nonlinearity of PA, the aforementioned process more accurately describes amplified spontaneous emission or lasing than PA.^1,2 Confusingly, photon avalanching is not actually an avalanche of photons. Unlike a real avalanche, in which snow cascading down a mountain stimulates even more falling snow in a nonlinear chain reaction, the photons emitted by PA materials do not feed back into the production of more photons. Instead, PA is a feedback loop of excited ions begetting more excited ions, or absorption begetting more absorption (Fig. 1, right).³

Fig. 1 Photon avalanches are not avalanches of photons, but rather, avalanches in the population of excited ions (promoted by avalanches of photon absorption).

Why do these misconceptions persist? For one, “excited state population avalanching” and “absorption avalanching” do not capture the imagination quite like an avalanche of photons does. PA may also be misunderstood because it is a relatively esoteric phenomenon that, until recently, was the subject of relatively little research activity outside a small community of scientists studying lanthanide-doped bulk crystals and other nonlinear optical materials.⁴ The recent observation of true PA in lanthanide (Ln³⁺)-doped nanoparticles has sparked newfound interest in PA, especially since these colloidal, solution-processable avalanching nanoparticles (ANPs) have demonstrated applications in “super-resolution” imaging (with <100 nm resolution and <1 Å localization accuracies),^5,6 nanoscale temperature⁷ and pressure sensing,⁸ and in optical memory⁹ and logic.¹⁰ It is possible that, in the excitement surrounding these groundbreaking applications and the giant nonlinearity of PA (sometimes exceeding that of a 100-photon process^9,11), fundamental aspects and important nuances of PA get overlooked. While several recent and historical reviews have comprehensively discussed the mechanism and application of PA materials^3,12 and nanoparticles,^4,13,14 there is a strong need to clarify frequently misunderstood yet essential concepts.

In this Focus Article, we dispel 11 common myths and answer 8 longstanding questions about PA nanomaterials to remove the shroud of mystery surrounding these uniquely nonlinear systems. In the process, we highlight the essential features of the PA mechanism and use them to explain the unique but sometimes contradictory behavior of PA materials. The case studies presented here will explore why PA may be simultaneously underappreciated as an optical phenomenon and also unlikely to live up to its more extreme hype due to nuances that may not be readily apparent. Ultimately, untangling the confusion surrounding PA nanomaterials will allow a broader range of scientists to fully exploit the potential of ANPs and develop a wide range of applications that can leverage the extreme nonlinearity of these materials.

2. The mysteries of ANPs

As provocative as their name is, the composition and behavior of PA materials remain an enigma to many scientists. Here, we first address some of the mysteries of ANPs before we explore myths about their behavior.

Mystery #1: What is a photon avalanching nanoparticle?

ANPs are nanocrystals – typically 4–100 nm in diameter and doped with Ln³⁺ ions (Fig. 2a) – that upconvert low-energy photons to higher-energy ones. The defining characteristic of these and other PA materials is their extremely nonlinear optical behavior, which originates from a positive feedback loop of photophysical interactions (e.g., energy transfer) between Ln³⁺ ions. The nonlinear behavior is most clearly manifested in the emission intensity (I_em), which scales with the excitation power density (P_ex) as I_em ∼ P^N_ex (Fig. 2b), where N signifies the order of the nonlinearity.⁴ While N = 1 for conventional fluorophores and N = 2 for two-photon emitters, the first experimentally confirmed ANPs, based on Tm³⁺:NaYF₄ nanocrystals, exhibited N as high as 31.⁵ This unprecedented nonlinearity, equivalent to a 31-photon process, made these ANPs some of the most nonlinear materials reported at the time, and the first single nanomaterials to exhibit PA. Later work revealed that ANPs doped with different combinations of lanthanide ions (e.g., Yb³⁺/Pr³⁺, with Tm,³⁺ Er³⁺, or Ho³⁺), strategically partitioned across heterostructures with multiple concentric shells,¹⁵ could achieve even higher nonlinearities of 41,¹⁶ 46,¹⁷ and even 60.¹⁸ Most recently, Tm³⁺- or Nd³⁺-doped ANPs with alternative host matrices (e.g., NaLuF₄,¹¹ KMgF₃,¹⁹ KPb₂Cl₅)²⁰ have been reported in some cases to exhibit step-like optical responses that imply nonlinearities greater than 100.^9,11

Fig. 2 Avalanching nanoparticles. (a) Schematic of a lanthanide-doped photon avalanching nanoparticle. (b) Output light intensity vs. input excitation intensity, showing on a linear scale the nonlinearity N of the emission from avalanching nanoparticles (20–100) compared to conventional, 2-photon, and 5-photon emitters.

Mystery #2: Why is such high nonlinearity useful?

The high nonlinearity of ANPs has immense implications beyond the spectral conversion applications (Fig. 3a) that are commonly associated with nonlinear optical materials.²¹ For N = 30, doubling P_ex theoretically increases the emission intensity by 2³⁰, or one billion times, although in actual experiments, the saturation of Tm³⁺:NaYF₄ ANPs resulted in “only” a 10⁴-fold increase.⁵ When N = 100, the same 10⁴-fold enhancement can be achieved with only a 10% increase in P_ex. Thus, the absorption of a small number of additional photons produces a disproportionate response of upconverted photons – a form of an avalanche.

Fig. 3 Uses for highly nonlinear systems. (c) Adapted from Torii et al.,²² Copyright 2012, with permission from Elsevier.

To understand why such nonlinearity is useful, we look towards other nonlinear systems. PA is a chain reaction in which excited ions beget excited ions, making it analogous to an autocatalytic reaction A + B → 2A in which species A catalyzes the production of more of itself.²³ Since the rate of increase in the concentration of A over time t (dA/dt) is proportional to A, the solution to this differential rate equation (DRE) dictates that A exponentially increases over time. The population of species A is thus auto-amplified due to the positive feedback of A begetting more A. Such amplification (Fig. 3b) is observed in many other nonlinear systems in everyday life, including the feedback that occurs when a microphone is placed too close to a speaker, compounding interest (“it takes money to make money”), ripening fruit (“one bad apple spoils the barrel”), and social and telecommunications networks growing exponentially because bigger networks have more value (people want to be friends with people who have a lot of friends).

The greatest utility of nonlinearity is that it enables the encoding of complex behavior, which is valuable because life is rarely simple and linear. Nonlinear interactions in nature are often encoded as positive or negative feedback loops that stimulate or inhibit a process, respectively. In developmental biology, it has been hypothesized that autocatalytic reaction–diffusion networks and nonlinear gene regulation networks use such feedback to pattern organisms,²² e.g. into Turing patterns (Fig. 3c),^24–26 spots/stripes (Fig. 3d),^27,28 and to segment vertebrae and exoskeletons.^29,30 These nonlinear networks can also evolve dynamically in time to explain Circadian rhythms and the oscillation of predator and prey populations (e.g., the Lotka–Volterra model,³¹ Fig. 3e).²³ In principle, nonlinear systems can be designed to mimic biology and convert homogeneous systems into complex patterns that vary over time and space. Already, electronics and optics are designed to leverage the nonlinear interactions of components to produce amplifiers that convert analog signals into digital ones (Fig. 3f).³² Such amplification motifs can be combined in complex circuits to build oscillators, bistable switches, and memory elements (Fig. 3g).³³ In optics, nonlinearities are observed not only in parametric nonlinear optical materials,²¹ but also in saturable absorbers that are used to turn continuous wave excitation into pulsed radiation (passive mode-locking).³⁴ Nonlinear changes in refractive indices also lead to lensing and self-focusing.³⁵ In machine learning, nonlinear activation functions built into neural networks allow them to model and predict complex, high-dimensional behavior (Fig. 3h).³⁶ Thus, the question is not whether nonlinearity is useful, but whether the nonlinearity of ANPs can be harnessed in ways similar to the applications listed above.

Mystery #3: Why would you want nonlinearity on the nanoscale?

Reducing the dimensions of nonlinear materials to the nanometer scale has several key benefits.^21,35 Nanoscale materials have size- and shape-dependent properties due to confinement effects and due to their high surface-area-to-volume ratios.³⁷ Nanostructures can confine and enhance electromagnetic fields, leading to strong light–matter interactions that may further enhance nonlinear processes or increase their efficiency.³⁸ The optical properties of nanomaterials can be precisely tuned by controlling their size, shape, and composition, enabling optimization of nonlinear responses for specific applications. For colloidal nanoparticles, such as ANPs, their dispersibility enables applications such as biological labeling, which require materials to be suspended in solution, and they facilitate low-cost solution-phase fabrication for technological applications. Nanoscale dimensions allow nonlinear materials to be densely integrated into devices that match the length scales of current and future device fabrication nodes. The small size and solution processability of nanomaterials allow them to be combined into complex composites that have emergent properties that are not linear combinations of their components.^39,40 By leveraging these nanoscale advantages, researchers can create more efficient and compact nonlinear optical devices, access new nonlinear phenomena, and expand the applications of nonlinear optics in fields ranging from telecommunications to biomedicine.

3. The mythical origins of PA in nanoparticles

Many myths about PA arise due to the lack of understanding of its origins and assumptions connecting it to other nonlinear materials, as we discuss below:

Myth #1: PA occurs through (1) a parametric nonlinear optical process or (2) delocalized excitonic states

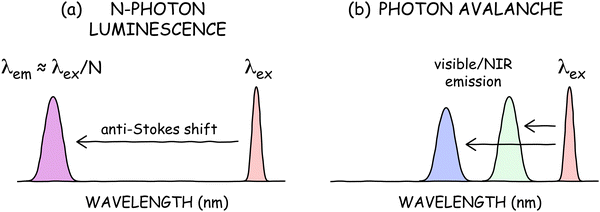
PA is sometimes mistaken for a parametric nonlinear optical process such as second harmonic generation (SHG) or sum frequency generation (SFG) (Fig. 4a) or for a non-parametric process in which multiple photons are absorbed simultaneously (Fig. 4b). Unlike these processes, PA is a step-wise non-parametric process most commonly observed in the ladder-like 4f^N excited states of trivalent lanthanide ions (Fig. 4c).⁴ Due to the shielding of the 4f valence orbitals by filled 5s and 5p orbitals, these excited states are highly localized, unlike the excitons in semiconductor quantum dots (QDs, Fig. 4b). This localization benefits ANPs by giving them high environmental stability and long excited-state lifetimes. Although QDs can also exhibit multiphoton emission, the fact that upconversion in ANPs and other upconverting nanoparticles (UCNPs) occurs through real, long-lived states rather than virtual states means that Ln³⁺ upconversion is at least six orders of magnitude more efficient than the multiphoton emission from QDs or parametric nonlinear optical processes like SFG.⁴¹

Fig. 4 Origins of photon avalanching. Photon avalanche does not occur through a parametric process (a), virtual states (dashed horizontal lines), or via delocalized states in semiconductors (b). PA occurs through a step-wise process in the real, localized states (solid horizontal lines) of lanthanide ions (c). Energy level diagrams show electronic transitions associated with photon absorption and radiative relaxation (black vertical arrows), as well as the incident excitation radiation (red wavy arrows) and upconverted emission (blue wavy arrows).

Myth #2: ANPs must have incredibly short emission wavelengths and low quantum yields if they involve 30+ photons

In multiphoton absorption or SHG, the conservation of energy results in an emission wavelength of λ_em ⋍ λ_ex/N, where λ_ex is the excitation wavelength (Fig. 5a). Thus, a common misconception is that ANPs should have incredibly short wavelength emission, e.g., λ_ex/30 = 35 nm for a Tm³⁺-doped ANP with a typical N of 30 and λ_ex = 1064 nm. In reality, such ANPs emit at 800 nm or visible wavelengths (Fig. 5b) despite their large nonlinearities. This modest anti-Stokes shift and decoupling of λ_em from N is beneficial for applications because extreme ultraviolet (UV) emission would preclude many technological and biological imaging applications. The small anti-Stokes shifts also simplify optics, since few optical materials are transparent and stable to such extreme UV radiation.

Fig. 5 PA does not require large anti-Stokes shifts. High-order (N) multi-photon processes (a) typically result in large anti-Stokes shifts in which the emission wavelength λ_em ⋍ λ_ex/N. In photon avalanching (b), however, λ_em is less coupled to λ_ex, resulting in small anti-Stokes shifts and visible or near infrared (NIR) emission.

A related misconception is that ANPs should have very low quantum yields if they involve 30+ photons. At typical avalanching threshold powers, a 30-photon absorption process or 30th harmonic generation would have exceedingly low efficiency due to the requirement that 30 photons interact simultaneously. Although it is impractical to directly measure the absolute quantum yield of ANPs due to their high nonlinearities and power requirements, calculations have indicated that ANPs can theoretically reach quantum yields as high as ∼40% at avalanching powers, which would be several times greater than the highest measured efficiencies of conventional UCNPs.^42,43 These high theoretical efficiencies indicate that ANP nonlinearities of 30 do not actually imply the involvement of 30 photons, especially because the theoretical maximum of a 30-photon process would be 3.33%.

Mystery #4: Why are photon avalanches so bad, they are good?

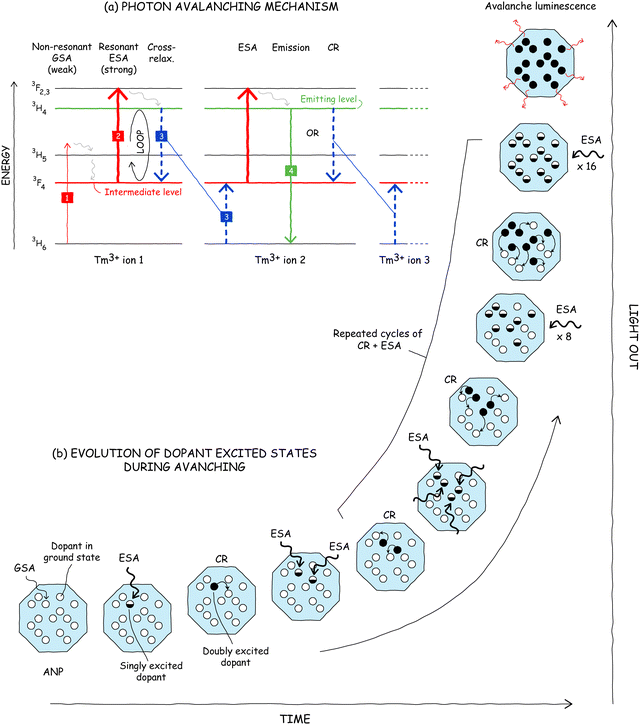
Highly nonlinear (“good”) PA requires three key components: (1) non-resonant or “bad” ground state absorption, (2) resonant excited state absorption, and (3) cross-relaxation energy transfer (Fig. 6a).^5,12 Below, we discuss how these features combine to realize the mechanism of PA. The pathway begins with step 1 in Fig. 6a, in which the absorption of a photon by an ion (e.g., Tm³⁺) in its ground state populates, after some vibrational relaxation, an intermediate state. This ground state absorption (GSA) is unlikely (and therefore slow) because it is non-resonant: the excitation energy (1064 nm for Tm³⁺), does not match the energy difference between the initial and final states of the optical transition, thus requiring the assistance of a phonon provided by the surrounding crystal. How is any emission observed if it is so hard to absorb light? The answer partially lies in the fact that PA materials also must have a resonant excited state absorption step (ESA, step 2) that originates from the intermediate level populated by the initial GSA step. However, one may ask how substantial ESA can be when the inefficient GSA step is a bottleneck in any serial GSA + ESA upconversion process.

Fig. 6 Mechanism of PA in lanthanide ions, shown for thulium(III). (a) Transitions between 4f^N manifolds (horizontal lines) include absorption (red arrows), cross-relaxation energy transfer (CR, blue dashed arrows), photon emission (green arrows), and multi-phonon relaxation (gray wavy arrows). (b) Step-by-step illustration of the evolution of dopant excited states during avalanching. Hollow, half-filled, and black-filled circles represent dopant ions in their ground, singly excited, and doubly excited states, respectively. Upconverted luminescence (red wavy arrows) occurs via radiative transitions from the doubly excited state.

A critical enabling feature of PA is a cross-relaxation step (CR, step 3) in which a doubly excited dopant ion (e.g., Tm³⁺ ion 1 in Fig. 6a) donates part of its energy – via multipole–multipole (e.g. Förster) or Dexter energy transfer (ET) – to a neighboring ion in its ground state (Tm³⁺ ion 2), producing two ions in their intermediate state. Due to the resonant ESA, these two singly excited ions can both undergo rapid ESA to their doubly excited states and then cross-relax with their neighbors again to result in four singly excited ions. This ESA + CR “energy loop”⁴⁴ can cycle repeatedly, in principle doubling the population of the intermediate level with every iteration (Fig. 6b). This positive feedback loop, which exponentially amplifies the emission intensity over time, is the engine that gives rise to the extreme nonlinearity of PA.

Additional conditions required for avalanching. Avalanching is not necessarily observed in every nanoparticle with energy levels that can foster weak GSA, strong ESA, and CR. Even ANPs do not avalanche under all conditions – they have little to no emission at excitation below a characteristic threshold power. The main factor that determines whether avalanching can occur in an ANP is whether the CR can outcompete alternate relaxation processes that depopulate the emitting and intermediate levels. High CR rates are generated in ANPs by increasing the dopant concentration, since the rate of any type of ET increases rapidly as the distance R between interacting ions decreases (e.g., scaling as R⁻⁶ for Förster dipole–dipole ET). CR is also promoted by proper alignment of energy levels: the energy lost by the donor species (e.g., a Tm³⁺ ion in its ³H₄ excited state in the top half of step 3 of Fig. 6a) should be close in magnitude to energy gained by the acceptor to maximize coupling, although there should be overall a slight loss of energy (via phonon emission) to suppress the reverse energy transfer process.

In a nanoparticle with suitable dopant electronic structure, the critical conditions for achieving avalanching are: (1) a sufficiently high excitation power to seed the population of the intermediate state via GSA and drive ESA; (2) high dopant concentration so that CR rates are significantly faster than the relaxation of intermediate and emitting levels, and (3) slow overall relaxation rate of the intermediate state (including radiative and non-radiative pathways) to further minimize competition with the ESA + CR energy loop. Under these conditions, avalanching commences at a threshold excitation power at which the ESA rate equals the relaxation rate of the intermediate state.^45,46 Above this threshold, the ESA + CR energy loop populates the intermediate level faster than it is depopulated, resulting in nonlinear gain in the population under repeated looping, i.e., avalanching.

Myth #3: Photon avalanches are avalanches of photons

Now that we know the mechanism of PA, we can fully unravel why PA is not an avalanche of photons. While PA has a positive feedback loop of ESA + CR, photon emission is not a part of this loop. The emitted photons are not the same wavelength as the absorbed photons, so emission cannot feed back into more absorption, not like stimulated emission in lasers stimulates more emission. Instead, photons emitted by ANPs are rare side products that just happen to be enhanced by the increased population of the emitting level (e.g., step 4 in Fig. 6a).

The reason why PA emission exhibits high nonlinearity, even though it is not a key component of the feedback loop, is that the emitting level is fed by ESA from the intermediate level, which is the critical hub of the ESA + CR feedback loop. The heavy population of the intermediate level during this loop induces more ESA and CR, which in turn further populates the intermediate level. Thus, PA is really an avalanche in the population of this intermediate excited state (Fig. 1), i.e., excited ions beget more excited ions, with the occasional emission of a photon on the side. Another way to think about PA is that the absorption of incident light leads to more absorption (ESA) due to the increased population of the absorbing intermediate species. Whether you think of PA as a population avalanche or an absorption avalanche, unraveling this myth is not just a semantic exercise. Identifying the actual nonlinear process and its engaged energy levels is key to being able to manipulate and enhance the properties of ANPs, as we discuss below.

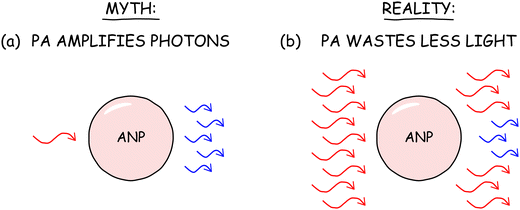
Myth #4: ANPs output more light than they receive

A related myth is that the giant nonlinearity of PA allows ANPs to amplify photon emission such that the power of their emission is higher than the power of light incident upon them (Fig. 7a). This, of course, would violate the laws of thermodynamics. In reality, ANPs and other PA materials do not even come close to exceeding the theoretical limits for such external quantum efficiency (EQE). Ln³⁺ ions, with their parity-forbidden 4f → 4f optical transitions and practical limits on doping levels, absorb an almost insignificant fraction of the photons incident upon a nanoparticle. In order to reach 100% EQE (or even 50% EQE, the theoretical maximum for a two-photon process), each lanthanide ion would have to emit many photons for each absorbed photon just to make up for all of the incident photons that are not absorbed.

Fig. 7 Photon avalanches do not amplify the number of photons incident upon them (red arrows), as depicted in (a). Compared to pre-avalanching conditions, ANPs under avalanching conditions (b) dramatically absorb more pump photons due to the nonlinear amplification of intermediate excited state populations during avalanching, resulting in a nonlinear increase in the overall number of emitted photons (blue arrows).

If the emission of ANPs increases nonlinearly with power, one might expect that the light output would eventually exceed the input power, but this would never happen for several reasons. First, the nonlinear increase of absorption and emission does not occur indefinitely. Absorbing ANP states become depleted with a sufficiently high excitation flux, reducing the probability of absorption and decreasing N.

Even if absorption did not saturate, the total PA emission power can never exceed the absorbed photon power because PA is an avalanche of absorption. The emission increases nonlinearly precisely because the absorption explodes nonlinearly. As shown in Fig. 6b, each excited ion is generated by the absorption of a different photon. When eight singly excited ions undergo ESA and CR to produce eight more singly excited ions, an additional eight photons are required – there is no free lunch.

By amplifying absorption, PA enables ANPs to waste less of the vast number of photons that would normally transmit untouched through the ANP (Fig. 7b). Thus, an underappreciated reality of ANPs is that they do not amplify photons or create them out of thin air – instead, the ANPs better utilize the incident photons, particularly those that are not absorbed under non-avalanching conditions.

Myth #5: You can improve PA by enhancing ground state absorption

In the PA mechanism described above, weak GSA (step 1 in Fig. 6a) is the bottleneck under sub-threshold pump powers, so it might seem reasonable to assume that more nonlinear PA or lower PA thresholds could be achieved by making the GSA step more resonant (e.g., by using excitation with a second laser or by using a sensitizing species). However, doing so would simply convert the system into a conventional two-step, GSA + ESA upconversion pathway in which strong GSA populates the intermediate level, followed by strong ESA from that level. While this system may indeed be brighter than the equivalent ANP at low powers, the nonlinearity would collapse, approaching N ∼ 2. This reduced N highlights the fact that the extreme nonlinearity of ANPs is a direct consequence of the terrible GSA in the PA mechanism. The emission of ANPs is virtually non-existent at low, sub-threshold P_ex because the non-resonant GSA cannot populate the intermediate level before ions relax to their ground state. Only at threshold powers is the intermediate state population high enough to initiate the PA that allows the ANPs to emit appreciable amounts of light. Since the nonlinearity of the optical response describes the relative increase of the emission between different excitation powers, high N is only possible with low emission at low P_ex, which is realized through non-resonant GSA. As the GSA becomes more resonant, it becomes harder to achieve the same level of enhancement at incrementally higher powers, reducing N. So, if one were interested in maximizing nonlinearity, one would want to decrease rather than increase the amount of GSA.

In fact, one of the three classic criteria for PA is that the ratio of ESA vs. GSA cross sections (ESA/GSA) must be greater than or equal to 10⁴.^41,47 Thus, to maximize nonlinearity, one would want to make GSA as non-resonant as possible, which historically has been accomplished by cooling PA materials to cryogenic temperatures to minimize phonon-assisted absorption.

Mystery #5: how can you tell whether a material is really avalanching?

Mechanistically, we recognize PA as an energy-looping process that rapidly amplifies the number of excited states in ANPs, eliciting more ESA.⁴⁸ Yet, experimentally determining if a material follows this PA mechanism is less obvious. How does one determine whether a nanoparticle is avalanching, and how do we distinguish it from other possible mechanisms of photon upconversion, such as GSA + ESA or energy transfer upconversion (ETU)?⁴¹

To meet the classic definition of PA, a material's optical response must meet three strict criteria: (1) a clear threshold, (2) ESA/GSA > 10⁴, and (3) a slow-down of rise times. We discuss these three requirements below:

1. The optical response must exhibit a clear threshold. An avalanching system exhibits a threshold excitation power (P_th) above which the emission intensity of the material is amplified nonlinearly.^48,49 However, determining this threshold value, or even the presence of a threshold, is sometimes not trivial. To find the threshold, one typically measures the power-dependent profile of the PA emission intensity (Fig. 8a), plotted as log(I_em) vs. log(P_ex). While most multiphoton processes like ETU or two-photon emission exhibit linear traces (in log–log scaling) with slopes equal to N before they saturate at high powers, avalanching and energy-looping nanoparticles⁴⁴ exhibit “S-shaped” curves that can be divided into three regimes: pre-avalanching, avalanching, and saturation. The transition from the pre-avalanching to the avalanching regime marks the threshold of PA, P_th (Fig. 8b, left). We can determine P_th by extrapolating linear fits of pre-avalanching and avalanching regimes in the log(I_em) vs. log(P_ex) curves. The intersection of these lines indicates the P_th above which ANPs undergo PA.

Fig. 8 Experimental determination of PA. (a) Representative “S-shape” of the log(I_em) vs. log(P_ex) plot of PA materials, sub-divided into pre-avalanching, avalanching, and saturation regimes. (b) True PA materials exhibit clear threshold behavior (P_th), dominant excited state absorption (ESA/GSA > 10⁴), and elongated rise times near P_th. (c) Materials with high nonlinearities (N > 10) and intensity amplification ratios (Δ_av > 500) are generally regarded as photon avalanching.

2. ESA/GSA > 10⁴. As discussed previously, strong ESA and weak GSA are necessary conditions for PA, typically met in ANPs when ESA/GSA > 10⁴. Due to the complexity of lanthanide photophysical networks,⁵⁰ the ESA and GSA cross-sections are impractical for most scientists to measure directly. Instead, one can fit the power-dependent emission profile of an ANP sample with a differential rate equation model (see Lee et al.,⁵ for example) in which the cross-sections for ESA and GSA are adjustable fit parameters (Fig. 8b, center). One can then compare the ESA/GSA ratios of the rates or cross-sections (the literature is often ambiguous about which values to compare; cross-sections are often reported, but rates may be more relevant to PA).

3. Rise times become longer near the avalanching threshold. The most difficult criterion to meet, and the least reported, is that the luminescence rise times become dramatically longer near P_th – as high as hundreds of milliseconds compared to hundreds of microseconds for most lanthanide-doped nanoparticles.^5,51 Rise times are determined by acquiring the time-resolved luminescence of an ANP sample and measuring the time that the luminescence takes to reach steady state after excitation begins (Fig. 8b, right). For practical purposes, rise times are reported as the t_1/2 or t_90%, the time taken to reach 50 or 90% of steady state intensity, respectively. We elaborate on the origins and misconceptions of this strange “slowing down” of rise times in Myth #6.

Practical considerations when determining avalanching. While the three avalanching criteria listed above are specific, their evaluation can be clouded by real-world experimental constraints. One of the greatest issues with analyzing ANP intensity curves is that the luminescence in the pre-avalanching regime is extraordinarily dim and can go undetected if it is obscured by detector noise. Thus, long integration times should be used to minimize noise in the pre-avalanching region. Furthermore, the fitting of N from slopes of log(I_em) vs. log(P_ex) curves is highly sensitive to the background intensity due to the log scaling. The background intensity must be carefully and objectively subtracted from the measured intensities. Also, to obtain a reliable N value, as many consecutive data points as possible should be used to fit log(I_em) vs. log(P_ex) curves, and it is preferable to confirm the obtained N value from multiple independent measurements. Random fluctuations in emission intensity or pump power may accentuate changes between neighboring data points and lead to overestimating N at small sample sizes.

Alternate evidence for avalanching. A sample is definitely considered to be avalanching if it meets the three criteria delineated above (Fig. 8b). However, finding the threshold, developing DRE models for unknown systems, and measuring rise times can be challenging and time-consuming. Recent publications have proposed more phenomenological metrics for avalanching that allow one to assess avalanching behavior based on how steeply its emission intensity scales with pump power. Although there is no strictly defined N value above which the material is said to be avalanching, a soft criterion for avalanching when N > 10 can be found and has historically been used in the ANP literature (Fig. 8c, left).^5,10,15

To further corroborate PA in materials with N > 10, Lee et al.⁵ also define a Δ_av measure as a ratio of emission intensity when the pump intensity is increased from the threshold to twice the threshold value, Δ_av = I_em(2P_th)/I_em(P_th), where I(P) is the emission intensity at pump intensity P (Fig. 8c, right). The authors find that Δ_av of 500 is a reasonable minimum to classify a system as avalanching, while the most nonlinear ANPs in their study (N = 31.6) exhibited Δ_av above 10⁴. Nanoparticles that exhibit both N > 10 and Δ_av > 500 are highly likely to be classified as ANPs. The advantage of using N and Δ_av to roughly assess potential PA materials is that the values can be determined quickly using just the power-dependent intensity profiles. Thus, they can be used to prescreen samples for more involved rise time and rate equation analysis (Fig. 8b).

Excluding alternate nonlinear optical processes. Even if a nanoparticle exhibits high nonlinearity, how do we know this nonlinearity does not originate from or induce another nonlinear process like lasing, amplified spontaneous emission (ASE)/superluminescence (SL), or superfluorescence (SF)? Lasing and ASE can be easily distinguished from PA based on their power-dependent spectral line shapes, such as the emergence of sharp lasing modes that narrow with increasing pump power. The nonlinear nature of energy looping has been hypothesized to promote population inversion and enable the low threshold lasing observed with microsphere cavities coated with Tm³⁺-doped energy looping nanoparticles (N ∼ 3).^1,2 No modes or spectral shifts have been observed in experimental ANP spectra, however, suggesting that the nonlinearities for those ANPs are not strongly correlated with lasing or ASE. To distinguish SF from PA, SF can be readily identified by its characteristic shortening of decay lifetimes and rise delay times to nanoseconds (<2.5 ns) as the pump power is increased.^52–55 The long μs–ms decay lifetimes of ANPs,^6,9 as well as their elongated rise times near avalanching thresholds,⁵ strongly suggest that SF does not play a role in the ANP systems reported thus far.

Finally, some materials may exhibit most but not all of the PA criteria listed above. These nanoparticles can be and are often categorized as PA-like or energy-looping. However, regardless of classification, the excitation mechanism via ESA + CR differentiates PA from other upconversion processes. And regardless of its mechanism, the nonlinearity of a material ultimately determines its utility.

Myth #6: Photophysical kinetics slow down near avalanching thresholds

The unusual mechanism of PA leads to some truly head-scratching and seemingly contradictory photophysics, most notably the oft-repeated belief that PA kinetics “slow down” near avalanching thresholds. It is true that the PA luminescence rise times lengthen dramatically in this regime (to 600 ms for Tm³⁺-doped ANPs,⁵ shown in Fig. 9a). However, it does not necessarily follow that the photophysical kinetics slow down. In fact, this is one of the greatest myths of ANPs.

Fig. 9 Photophysical kinetics do not slow down near PA thresholds. (a) Elongation of PA luminescence rise times for Tm³⁺:NaYF₄ ANPs, adapted from Lee et al.⁵ (b) Time-resolved luminescence traces below, near, and above PA thresholds, showing faster kinetics in parallel with longer rise times. Adapted from unpublished simulations performed for Skripka et al.⁹

To understand the origins of misconception, we must dive deeper into why rise times increase. In a normal UCNP, rise times tend to be relatively long (100 μs–10 ms, comparable to luminescence decay lifetimes) due to the multi-step upconversion process. Ions must establish sufficient intermediate state populations before they can be excited again to the emitting levels. This population build-up can only occur so fast given the forbidden transitions of lanthanide ions.

How do dynamics get even slower for ANPs? They don’t. In fact, the rate at which ANP luminescence rises actually gets faster as the pump power is increased near the avalanching threshold (Fig. 9b). The PA time traces in Fig. 9b, simulated for Nd³⁺:KPb₂Cl₅ ANPs,⁹ show that the population of the intermediate ⁴I_11/2 excited state of Nd³⁺ rises faster over time as the power is increased from sub-threshold pump powers to above the avalanching threshold. Despite these faster kinetics, the rise times (indicated by the dashed vertical lines in Fig. 9b) still get longer near the threshold.

To unravel this ball of contradictions, one can visualize dopant ions as buckets that hold water, where the water represents energy. In a conventional two-level fluorophore, the bucket size is roughly fixed. For a given flow rate (i.e., excitation power), a smaller bucket would mean a shorter filling time (i.e., rise time).

The trick to understanding the contradiction of ANPs is that their buckets are not fixed size! In our analogy, filling the buckets with water makes them increase in volume faster than the flow rate can catch up with it, leading to longer and longer filling times. The same thing happens for ANPs – every time a singly excited ion absorbs a photon (as in Fig. 6b), the ESA + CR energy looping cycle produces two singly excited ions that can each absorb photons. This increased capacity to absorb photons increases the population at which the excited states will stabilize in their steady state (the plateau in the curves in Fig. 6b). Since PA is an avalanche of absorption, the population of absorbing species and the capacity of the ANPs to absorb photons increase nonlinearly over time. As a result, the rise time elongates significantly near the avalanching threshold because this population ceiling rises faster than the system can approach it, even with increased kinetics.

When the excitation power density exceeds the avalanching threshold (red trace in Fig. 9b), the high nonlinearity of the system means that the exponentially increasing population of the intermediate level quickly saturates at such a high level that it cannot increase significantly with additional laser power. Our bucket's volume (or capacity to absorb more photons) stops increasing and now fills faster as the flow rate (laser power) increases. As is typical with conventional UCNPs, the rise time now decreases as the power is increased above the PA threshold. Thus, the rise times of ANPs are the longest around the PA threshold, even though the overall photophysics become faster monotonically with increasing excitation power.

4. Applications

Mystery #6: What are ANPs good for?

Now that we know ANPs work, how can their unique photophysics be exploited? The initial and killer application of ANPs has been their use as probes for imaging below the diffraction limit of the excitation radiation (Fig. 10a), as we discuss in more detail in Myths #7 and #8.^5,6,11,56 The giant nonlinearities of ANPs enable standard scanning confocal microscopes to essentially perform N-photon microscopy (with N > 26) and resolve features as fine as 33 nm.^5,18 The less intuitive photoswitching properties of ANPs allow them to be localized using stochastic localization microscopy with localization accuracies less than 1 Å.⁶ In the future, the <100 nm emission point spread functions afforded by the nonlinear response of ANPs may be exploited in lithography⁵⁷ and 3D printing to create structures with unprecedented resolutions at depth (Fig. 10b),⁵⁸ pending the demonstration of ANPs with highly nonlinear emission in the UV region.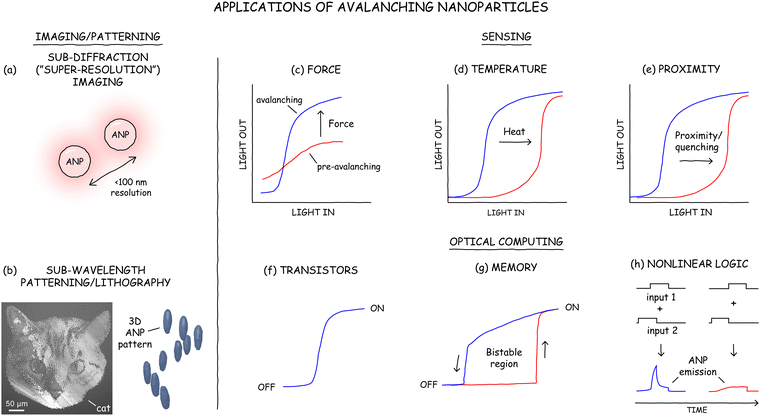

Fig. 10 ANP applications in imaging (a), patterning and lithography (b); sensors for force (c), temperature (d), and proximity to quenching molecules (e); and components for optical computing, including transistors (f), memory (g), and nonlinear logic (h). (b) Adapted with permission from Pan et al.,⁵⁷ copyright 2024 American Chemical Society, and Lee et al.⁶ (c) Adapted from Fardian-Melamed et al.⁸ (d) Adapted from Szalkowski et al.,⁵⁹ Copyright 2021, with permission from Elsevier. (e) Inspired by Majak et al.⁶⁰ (g) Adapted from Skripka et al.⁹ (h) Adapted from Bednarkiewicz et al.¹⁰

The extreme nonlinearity of these nanocrystals also makes them exquisitely sensitive to external perturbations, which is beneficial in detecting minute changes in temperature,^7,59 pressure,⁸ or chemical environment (Fig. 10c–e). For example, Bednarkiewicz and coworkers have explored the distance-dependent quenching of ANP luminescence by small-molecule quenchers for molecular rulers or biological assays.^60,61 However, the sensitivity of ANPs is a double-edged sword. The effects of unaccounted phenomena, e.g., a slight temperature change when sensing pressure, are nonlinearly amplified, disrupting the delicate balance of PA and introducing artifacts into measurements. Thus, although sensing applications are likely to benefit from the unique properties of ANPs, a deeper and broader understanding of PA processes is needed to reliably extract measured quantities.

The ability of ANPs to toggle between their non-luminescent and luminescent states, either through persistent photoswitching⁶ or through dynamic bistability,⁹ inspires their use as optical switches, memory, analog-to-digital converters, or tiny signal integrators for reservoir computing¹⁰ and photonic neural networks³⁶ (see Fig. 10f–h, and Mystery #7).^9,10 As research into ANPs is still in its infancy, more novel applications will surely be developed as we continue to innovate in the ANP space and increase our understanding of their properties.

Myth #7: Confocal imaging with PA enables breaking of the resolution limit

The signature application for ANPs has been imaging below the diffraction limit of the pump excitation wavelength, achieving resolutions as low as 33 nm^11,17 using only a simple scanning confocal microscope. The simplicity of such photon avalanche single-beam super-resolution imaging (PASSI⁵¹) is that it does not require the complex optical setups of super-resolution techniques such as stimulated emission depletion (STED) or complex post-processing of the data required for techniques such as photoactivated localization microscopy (PALM⁶²), stochastic optical reconstruction microscopy (STORM⁶³), or structured illumination microscopy (SIM). In contrast, PASSI involves scanning a diffraction-limited excitation spot across a field of ANPs and detecting the emission only when an ANP is almost directly in the center of the beam spot (Fig. 11).

Fig. 11 (a) Point spread functions (PSF) of a diffraction-limited beam spot Airy pattern (top) and the emission profile from an ANP with N = 30. (b) Resolution vs. N, illustrating how PA confocal imaging occurs at actual resolution, rather than exceeding it. Dashed lines show resolution for N = 30. All FWHM and resolution values are shown for excitation at 1064 nm and NA = 1.4.

A common myth about ANPs is that their nonlinearity gives them the ability to be imaged below their theoretical resolution limit, i.e., with “super-resolution” (as PASSI acronym erroneously suggests). In conventional imaging with linear emitters, the diffraction-limited resolution can be considered as the full-width at half maximum (FWHM) of the point spread function (PSF) of the excitation beam spot, i.e., an Airy disk. According to the Abbe resolution equation, the FWHM is 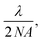which for an excitation wavelength λ of 1064 nm and a numerical aperture (NA) of 1.4 equals 387 nm (Fig. 11a, top).

Sub-diffraction imaging with ANPs leverages the giant nonlinearity of PA along with the fact that a diffraction-limited excitation spot is more intense in its center than on its edges. For an ANP with N = 30, a point on the Airy disk with half the maximum excitation intensity theoretically would excite 0.5³⁰ or 1 billionth of the emission intensity at the center of the beam spot (accounting for typical saturation of PA in ANPs, realistically this contrast is more like 1/10 000th of the maximum intensity). In this scenario, the intensity of the emission PSF is half of its peak value where the excitation beam intensity is 97.7% of its maximum, meaning that the FWHM of the emission of an ANP will be dramatically smaller than for a linear emitter. For λ = 1064 nm and NA = 1.4, the FWHM resolution would be 71 nm (Fig. 11a, bottom) compared to the 387 nm diffraction limit. With ANP nonlinearities now reported to exceed 100, such ANPs have been imaged with resolutions as low as 33 nm,¹¹ with theoretical limits smaller than 20 nm.

So why is it a myth that ANPs break the resolution limit? The misconception lies in the fact that ANPs do not break the resolution limit, but rather, they lower it. In fact, all multiphoton microscopy methods, even with N as low as 2, will result in finer resolution than single-photon microscopy at the same excitation wavelength. When the Abbe resolution equation is modified for nonlinear microscopy, the resolution is calculated to be (Fig. 11b). Importantly, this equation describes the FWHM of the emission profile, such that two ANPs separated by this distance can be resolved. Thus, PASSI acquires images at the actual optical resolution, i.e., the FWHM of the emission PSF, but this resolution itself moves to smaller distances as N increases. This is not the same as super-resolution, like stochastic localization microscopy techniques (PALM, STORM) that localize individual features within the emission PSF. However, PASSI is not the only mode of sub-diffraction imaging available to ANPs, as we discuss in the next myth.

Myth #8: ANPs do not photobleach (which would be detrimental for high resolution imaging)

Lanthanide-doped UCNPs are renowned for their exceptional photostability,⁶⁴ making them valuable for single-particle imaging and long-term studies. Unlike organic dyes, which readily photobleach,^62,63 and unlike quantum dots, which blink intermittently,⁶⁵ conventional UCNPs like Yb³⁺/Tm³⁺:NaYF₄ emit at a constant intensity even under hours of continuous excitation at irradiances exceeding 10⁶ W cm⁻² (Fig. 12a, left).

Fig. 12 (a) ANPs photodarken under high-intensity excitation (several times the avalanching threshold power), unlike conventional UCNPs, which are stable over hours of continuous high-power excitation. (b) The photobrightening (PB) and photodarkening (PD) of ANPs can be harnessed for sub-diffraction-limited localization microscopy (INPALM) with <1 Å localization accuracy. Scale bar for scanning electron microscopy overlay: 20 nm. All panels adapted from Lee et al.⁶

Given their incredibly similar compositions, it would be logical to assume that ANPs have similar photostabilities to UCNPs. Surprisingly, this inference would be incorrect! When excited at high irradiances – several times the avalanching threshold power but still within typical pump powers used for UCNPs – ANPs like NaYF₄:8% Tm³⁺ abruptly photodarken,⁶ losing their intensity (Fig. 12a, right).

Such photodarkening would seem to make ANPs a poor choice for imaging, particularly when tracking single nanoparticles with confocal microscopy (PASSI). Fortunately, photodarkened ANPs can be subsequently restored to their previous “bright” state by exciting them with higher energy light (400–940 nm for Tm³⁺-doped ANPs photodarkened by 1064 nm excitation).⁶ At intermediate intensities, this photobrightening process is not complete, such that only a random subset of ANPs is returned to their bright state. Importantly, ANPs can be photobrightened and photodarkened over more than 1000 cycles – so many that the maximum number of cycles has not been established.

This ability to photodarken and stochastically photobrighten ANPs is reminiscent of stochastic localization microscopy methods like PALM⁶² or STORM,⁶³ in which all of the organic dyes are bleached and then a subset is randomly activated. These techniques can image finer than the diffraction-limited resolution by activating a small enough fraction of emitters that are unlikely to have emitting neighbors within their emission PSF, thereby allowing localization of their single-molecule emission spots.

ANPs have been leveraged in a similar manner for super-resolution localization microscopy using a technique called indefinite NIR PA localization microscopy (INPALM⁶), whose step-by-step process is shown in Fig. 12b. During INPALM imaging, an ensemble of nanoparticles is fully photodarkened by a high-powered excitation source, and then a small fraction of the ANPs is photobrightened by using an intermediate dose of a second laser. The centroids of the emission spots of those bright single ANPs are then localized, and the particles are subsequently photodarkened. A second set of ANPs is photobrightened and localized, and this process is repeated many times until each nanoparticle has a large set of localization coordinates. Finally, two-dimensional (2D) Gaussians are used to fit localization points for each ANP, generating a centroid and uncertainty for each ANP. Using INPALM, ANPs have been imaged with localization accuracies finer than 1 Å. Due to this accuracy, the centroids of 35 nm ANPs can be determined even when the nanocrystals are touching. INPALM has a major advantage over stochastic localization methods that use organic dyes, since ANPs can be cycled indefinitely without photobleaching like organic dyes. This is important because the localization accuracy is inversely proportional to the square root of the number of photons collected, suggesting that the accuracy of INPALM has no theoretical limit.

Thus, while ANPs do photodarken, their ability to recover their emission and be cycled indefinitely allows them to access a second mode of sub-diffraction imaging. And unlike PASSI, INPALM does in fact break the resolution limit.

Mystery #7: How do some ANPs live two parallel lives? Do they remember their past lives?

Nonlinear networks can exhibit memory, lag, or echo in their response to external inputs, often due to the different scaling laws of competing processes (see, for example, the lag between the predator and prey populations in Fig. 3e). UCNPs, made out of thousands of interacting Ln³⁺ ions,⁵⁰ are no exception, with ANPs elevating these phenomena to a new level.

Recently, we found that Nd³⁺:KPb₂Cl₅ ANPs²⁰ can live parallel lives: the same nanocrystal can appear dark (no luminescence) or bright (emitting light) under identical excitation wavelengths and pump powers.⁹ Their current state – dark or bright – is determined by the history of pump power, as if these ANPs can “remember” the preceding laser power and respond in one of the two ways. Such response is called optical bistability and is characterized by power-dependent luminescence hysteresis (Fig. 10g). In Nd³⁺:KPb₂Cl₅ ANPs, optical bistability arises from competition between two opposing forces: PA and phonon relaxation. Vibrational properties of the KPb₂Cl₅ host and low temperatures reduce phonon assistance to electronic transitions, like GSA, requiring higher powers to switch these ANPs on. However, once these ANPs do emit, a rapid population of excited states via energy looping can outcompete multiphonon relaxation (energy dissipation as heat), maintaining the bright state of ANPs even below the switch-on threshold. Think of it as riding a bike. At first, getting the bike moving takes a lot of effort because you have to push the pedals really hard. But once the bike is moving, the bike has inertia and keeps moving even after pedaling ceases. Of course, eventually the bike will stop.

Bistable ANPs eventually switch off but at lower laser powers than were required to switch them on. Since the photoluminescence in optically bistable ANPs vanishes without a laser pump, their memory is volatile. Observing luminescence hysteresis and being able to switch these ANPs from a dark to a bright state opens opportunities to use them as nanoscale switches and memories for optical computing.^66,67

Classic Tm³⁺:NaYF₄ ANPs can also remember, so to speak, their not-so-distant past. The population of the Tm³⁺ energy-looping intermediate state, which facilitates ESA, could be dynamically controlled by time-gating pump laser pulses.¹⁰ If two excitation pulses overlap in time, the intermediate state is populated, and ANPs emit light (Fig. 10h). However, if the delay between pulses is longer than the lifetime of the intermediate state, the ANPs do not emit light. Such behavior resembles signal integration by biological synapses and could be used in optical reservoir computing. This type of computing, leveraged in machine learning, utilizes a non-linear system as a reservoir, just like Ln³⁺-doped ANPs, to process information inputs without requiring system training (only the outputs need to be trained), accelerating computation and reducing costs.

5. Limitations of ANPs

Myth #9: ANPs are ready for prime time

The ANP literature may imply that ANPs are ready to be integrated into applications, but there are a number of downsides to these unique materials – some that may be easy to overcome and some that may never be overcome. Areas in which ANPs still need to improve relative to other fluorophores include their low brightness and quantum yields and their moderately high-power requirements (kW cm⁻²). In fact, quantitative brightnesses of ANPs are relatively unexplored and still must be measured, as both quantum yield and ESA cross-sections have only been derived numerically using simplified rate equation models. The exquisite nonlinearity of ANPs makes them particularly sensitive to small fluctuations in their excitation powers or to attenuation of the excitation due to scattering and refraction in their local environment. This sensitivity can make applications difficult to calibrate, especially when considering that ANP brightness and avalanching thresholds can vary due to slight differences in ANP size,⁶⁸ composition, shell thickness,⁴⁵ and even excitation beam profile.⁶⁸ Finally, the photodarkening of ANPs leveraged for super-resolution imaging can be problematic for applications that do not require photoswitching. Future research is required to ameliorate these drawbacks. However, some of these issues can already be addressed by existing technology. For example, the photodarkening of ANPs can be counteracted by subsequent photobrightening. And as we discuss below, some of the perceived drawbacks of ANPs are myths, while others further reveal hidden truths about the dark sides of ANPs.

Myth #10: You can change the color or excitation wavelength of ANPs by introducing different dopants into existing ANP systems

Imaging, display, and sensing applications of ANP may require a library of probes with different emission or excitation wavelengths. Such spectral diversity is critical for cases in which multiple species are being tracked simultaneously, and spectral breadth is important, for example, for extending excitation wavelengths into NIR and SWIR windows in which photons have the lowest attenuation in highly scattering media such as tissue.^69–71

ANPs are relatively new materials, so it is no surprise that they are only available in a handful of emission and excitation wavelengths. Because ANPs are strictly driven via ESA, the laser wavelength must be carefully tuned to maximize ESA and minimize GSA, as is the case of 1064 nm excitation for Tm³⁺ or Nd³⁺ and 852 nm for Pr³⁺ ions.^17,44,51,72 Deviating from these wavelengths eliminates PA or, at the very least, reduces the nonlinearities of ANPs. Due to these and other constraints, it is challenging to expand the library of the currently known avalanching systems (Tm³⁺, Nd³⁺, Yb/Pr³⁺). Thus, there is a need to be able to modify the emission wavelengths of these existing ANPs.

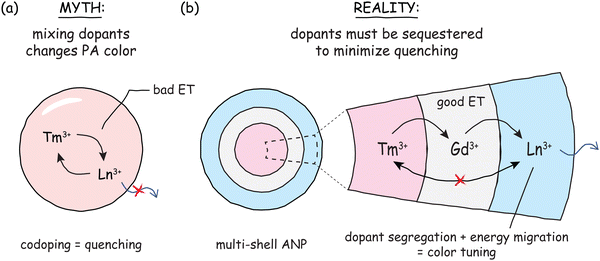
To change the emission or excitation bands of Ln³⁺-doped UCNPs, one typically mixes different sensitizing or emitting dopants and changes their concentrations.⁷³ Therefore, it might be reasonable to assume that one could introduce other dopants into known ANPs to induce them to emit at different wavelengths. However, these traditional methods for spectral tailoring do not readily translate to ANPs since adding even the tiniest amounts of codopants is often detrimental to PA.⁶⁰ Codopants act as energy sinks, depopulating excited states involved in absorption or emission pathways, usually through processes like CR that funnel energy to lower energy states (the “bad ET” in Fig. 13a), without the benefit of energy looping. Due to the extreme nonlinearity of PA, even small perturbations can have outsized influence on the nonlinearity and intensity of homogeneously codoped ANPs.

Fig. 13 (a) Codoping ANPs homogeneously with multiple lanthanide ions often leads to quenching of emission due to deleterious energy transfer (ET) between dopants. (b) Segregating dopants in different domains of multi-shell heterostructures allows energy to be transferred from absorbing to emitting dopants without deleterious ET and quenching.

Fortunately, there is a workaround for introducing other ions in ANPs. To ensure that incompatible ions do not share the same space, one can synthesize Ln³⁺-doped nanocrystal heterostructures with multiple layers, like layers of an onion, with each layer having unique dopants and a unique role (Fig. 13b).^74,75 In such core/shell UCNPs, a third dopant is incorporated in both the core and the shell(s) as a bridge to migrate excitation energy from the light-absorbing ion to the light-emitting ion without them interacting directly.⁷⁶ Unlike the deleterious ET in homogeneously codoped nanoparticles, the resonant energy transfer shown in Fig. 13b occurs through the excited states of ions like Gd³⁺ that cannot cross-relax (due to lack of intermediate energy levels), allowing energy to be directed quickly away from ions where avalanching and CR can occur and delivered efficiently to ions that emit the desired wavelengths.

This concept of energy migration has been successfully applied to several core/shell ANPs. The excitation energy, captured by the “PA engine” of Tm³⁺ ions (or the Yb³⁺/Pr³⁺ couple), migrates through a sublattice of Gd³⁺ or Yb³⁺ ions to excite non-PA ions like Eu³⁺ or Tb³⁺, located in a different domain of the same nanocrystal.^15–18 The same concept has been applied to excite external emitters¹⁵ such as CdS/CdSe/CdS quantum dot heterostructures.^77–79 Through energy migration, the giant nonlinearities of ANPs can be preserved and imprinted on the energy-accepting ions to emit nonlinearly at different colors.

Taking the long path of energy migration does come with a cost, including inadvertently increasing the avalanching threshold, reducing the nonlinearity, or reducing the emission intensity. Nonetheless, these first demonstrations show great promise in creating multicolor libraries of ANPs and transforming ordinarily linear emitters into highly nonlinear ones.

In addition to core/shell engineering, the same PA ions may have different emission colors when introduced in host materials with different properties. For example, orange PA emission was generated in low-phonon-energy Nd³⁺:KPb₂Cl₅ ANPs,²⁰ while blue emission was reported in tetragonal Tm³⁺:LiYF₄ ANPs, which have different Ln³⁺ site symmetry to hexagonal Tm³⁺:NaYF₄ ANPs.⁶⁸

General ANP design strategies for improving avalanching behavior. Beyond color tuning, the various ANP design strategies discussed in the debunking of this myth can be used more generally to improve many other avalanching properties, such as nonlinearity, PA threshold, and luminescence intensity. In addition to varying, mixing, and partitioning dopants to tune excitation and emission wavelengths,^15,17,44 dopant concentrations can be modulated to optimize the rates of CR and ET critical to avalanching pathways. Additionally, researchers have explored varying the dimensions and morphologies of ANPs,⁶⁸ the thicknesses of passivating shells,⁴⁵ and the phonon energy of host matrices²⁰ to reduce non-radiative pathways that can compete with energy looping. A salient example of several of these strategies can be found in the discovery process for the first reported ANPs:⁵ to observe avalanching, we needed to (1) identify dopants that could undergo energy looping (Tm³⁺),⁴⁴ (2) increase Tm³⁺ levels to relatively high concentrations (8–100%) to enhance CR, and (3) grow thick, 4.0–8.5 nm undoped shells to suppress surface quenching.⁵ These strategies for designing and optimizing the structure of ANPs largely track with those for tuning the properties of UCNPs and are discussed in more detail in recent reviews.^{4,13,14,80,81}

Myth #11: The slow rise times of PA mean that ANPs cannot be used for video-rate imaging

One consequence of the slow rise times of ANPs is that they limit the scanning speed of raster-based imaging methods. An ANP with a rise time greater than half a second would require pixel dwell times at least that long just to be able to view the ANP at its maximum intensity. In fact, demonstrations of the two different modes of deeply subwavelength imaging (PASSI and INPALM) routinely used integration times and photobrightening/darkening times from 0.5 s⁵ to as long as 8 s.⁶ Is the resolution gain of PASSI or INPALM worth sacrificing imaging speed? For biologists studying live cells and the dynamic world inside them, the answer might be “no.” Spending 0.5 s or more on every pixel might mean missing out on important cellular events.

Several promising solutions to this problem have been proposed or demonstrated. The first relies on the fact that the laser beams have approximately Gaussian beam profiles with widths much larger than the size of individual ANPs. This means that the outer edges of the beam spot have non-zero intensities, resulting in the weak excitation of ANPs in that region. Because the power on the periphery is below the PA threshold, these ANPs barely emit, so they don’t contribute to the signal of the ANPs being imaged in the center of the beam spot. But the excited state population of the ANPs on the edges of the beam is primed – they are pre-avalanching. In our previous analogy of filling buckets with water, the Gaussian laser beam is a shower head that sprays water over a wide radius. So, as we fill one bucket in the center and move to the next in line, the next one is already partially filled, such that it will take less time to top it off (Fig. 14). Similarly, the edge of the laser beam primes the ANPs around the ones currently being imaged, reducing rise times and drastically improving imaging speeds when the center of the beam moves over the primed ANPs.⁵

Fig. 14 Although the long rise times of ANPs may appear to preclude rapid scanning for video-rate imaging, the actual rise times for ANPs directly under the excitation beam are shorter because they have been previously primed by excitation on the edges of the beam spot when the beam is focused on a nearby ANP.

To further increase imaging speeds, we can use multiple lasers to create complex illumination patterns. We can imagine irradiation schemes where priming is done by a second, low-power laser either preceding the main beam or illuminating the entire sample. This second beam would prime next-in-line ANPs right to the avalanching threshold so that when our scanning beam comes around, ANPs emit without much delay. The potential of priming has been demonstrated in both Tm³⁺ ANPs⁵ and for KPb₂Cl₅:Nd³⁺ ANPs that are optically bistable (Mystery #7).⁹ These bistable ANPs were primed by a wavelength resonant with their ESA below P_th and then exposed to a short pulse of a second beam – resonant with GSA. These initially dark, non-emitting ANPs underwent instability crossing and became bright, emitting even after the second laser was turned off. Such a fast and direct photoswitching of ANPs illustrates how Ln³⁺ ions, with their multiple excited states, enable various priming strategies.

A final approach that can be used in conjunction with the first two is splitting excitation beams into parallel focused beams. Such beam spot arrays can quickly map an entire sample using far fewer scan steps than single-point scanning. With the aid of CCDs for two-dimensional acquisition and photon localization to extract the positions of ANPs, Lee et al. demonstrated that a hexagonal lattice of Gaussian beam spots can theoretically image a 2 × 2 μm area with 80-nm resolution using only 25 scan steps.⁵

With these advances and discoveries, slow rise times of PA do not prevent us from acquiring fast, possibly video-rate, high-resolution images with ANPs. We are not limited by the rise times of ANPs when raster scanning samples because our Gaussian beam primes nanocrystals in its vicinity, and implementing multi-beam irradiation may help reduce imaging times even further.

6. The future

Mystery #8: Where do ANPs go from here?

Surface engineering. If ANPs are not quite ready for widespread application, where does their near-term future lie? As suggested above, there are fundamental issues with ANPs that need to be addressed through basic research. For example, imaging applications – many of them in the biological realm – require a deeper understanding of how surface effects^45,60 influence the highly sensitive PA process, which may be quenched by ET to ligands and solvents. Super-resolution imaging and sensing in cells and tissue may require the development of new inorganic and polymeric coatings and ligands, particularly those with lower molecular weight, low vibration energies,⁸² resistance to oxidative degradation,⁸³ and those that enable robust coupling with biological species like antibodies.⁸⁴ Increasing the absorption rates of ANPs without disrupting their ESA/GSA ratio may require the development of innovative approaches to sensitize these transitions with dyes,^85–87 transition metals, or by coupling the transitions strategically to resonant waveguide gratings⁸⁸ or plasmon modes.⁸⁹

Understanding photodarkening and photobrightening. Further research is also required to understand the origins of photodarkening (PD) and photobrightening (PB) of ANPs, which is not seen in conventional UCNPs. Although it has been proposed that PD and PB processes are related to the respective generation and annihilation of color centers in the NaYF₄ host matrix⁶ (following reported mechanisms in bulk materials⁹⁰), deeper investigations are needed to confirm or identify the actual defects and mechanism. For INPALM microscopy, such models may be used to learn how to speed up the PD/PB processes to increase scan rates and reduce laser powers, while increased mechanistic understanding may also provide a path to suppress PD for PASSI and sensing applications for which PD is a nuisance. A critical roadblock to understanding the origins of PD/PB is our limited ability to visualize such defects directly. Progress in this area may require advances in electron microscopy, such as automation of low-dose and phase-contrast techniques,⁹¹ ultrasensitive detectors,⁹² tomography/pytochraphy,⁹³ and in situ methods, particularly those that couple with laser excitation.^94–96 Advanced X-ray techniques such as X-ray absorption spectroscopy⁹⁷ (e.g., EXAFS) and pump–probe methods under free electron lasers⁹⁸ may also provide structural insight into the steady state or transient formation of defects. Scanning tunneling microscopy may provide the most direct insight into the location and electronic structure of defects in thin ANPs,⁹⁹ while techniques borrowed from the persistent luminescence nanomaterials community may elucidate thermodynamic properties and design rules for such defects.¹⁰⁰ Control experiments will be required to examine whether PD and defects are a consequence of a specific synthetic method or host matrix, or if other preparations and materials have increased or suppressed PD.

Implementing ANPs in the real world. Many of the proof-of-concept demonstrations or predictions for ANPs, such as sub-diffraction imaging and pattering,^5,6 pressure sensing,⁸ UV disinfection,¹⁰¹ and optical computing,¹⁰ have not found their way yet into real-world applications. While there are a handful of examples of sub-wavelength imaging of ANPs of fixed cells,¹⁷ imaging and sensing with ANPs still need to be demonstrated on live cells to monitor physiologically relevant processes in a way that provides insight into current biological problems, with performance that matches or exceeds state-of-the-art techniques. And while the exquisite temperature sensitivity of ANPs has been theoretically predicted, sub-wavelength PA nanothermometry has yet to be demonstrated experimentally, even though such nanometer-resolution thermometry has been demonstrated for single UCNPs,^102–104 even in live cells and organelles.¹⁰⁵

Finally, the greatest challenge and opportunity for ANPs is developing new applications for nanoscale PA that have yet to be envisioned. These may include anti-counterfeiting labels,¹⁰⁶ since high-order nonlinear processes are more challenging to invert than linear or low-order processes.¹⁰⁷ The complexity of PA responses, including their power-dependent lifetimes and emission intensities, convoluted with the wide encoding space of heterostructures, make them difficult to reverse engineer and useful for physical unclonable functions,¹⁰⁸ such as those resistant to quantum computing attacks.¹⁰⁹

Optical networks and computing. The development of ANPs is an important milestone for our long-term vision of building highly integrated, nanoscale optical circuits. Amplifiers are key components in the electronic circuits and biological reaction networks that we seek to mimic with ANPs, particularly since the positive feedback of PA provides the nonlinear behavior that enables complex outputs.⁵⁰ Optical nonlinearities are generally sought-after in photonic integrated circuits, e.g., powering activation functions for deep neural networks³⁶ or performing analog-to-digital signal conversion (as in Fig. 3f and h). Hence, ANPs, with their giant nonlinearities and small sizes that can facilitate very-large-scale integration, provide a pathway for general-purpose optical computing, with the ANPs acting as components in larger optical logic circuits. For example, memory could be implemented with bistable ANPs, while the addition of waveguides or energy migration relays would establish interconnects. Notably, the relatively minor anti-Stokes shift between excitation and emission lines of ANPs helps to cascade signals over many interconnected nanocrystals. The emission of one ANP could serve as an input to excite a neighboring ANP, which would emit to excite its neighbor, and so on. Such signal cascading is impossible, or at the very least impractical, in materials whose nonlinearities derive from parametric processes or multi-photon absorption.

Alternatively, single ANPs could themselves be engineered as self-contained optical circuits that reproduce the behavior of canonical electronic and biochemical networks. To complete this vision, however, optical motifs for other major components besides positive feedback loops must be developed. For example, optical Turing patterns (Fig. 3d) would require optical motifs that can mimic the amplification, inhibition, and diffusion processes in the network diagram shown in Fig. 3c.²² In ANPs, this could be accomplished via processes such as PA, cross-relaxation ET, and resonant energy migration, respectively. These elements would be encoded as doped domains within core/shell ANP heterostructures (as in migrating PA motifs^15,17), in barcode nanorods,^110,111 or more complex branched heterostructures.¹¹² In practice, however, numerous components that do not have equivalents in the UCNP world still remain to be developed, and integrating existing components can face challenges such as alignment of energy levels. Ultimately, the development of such libraries of optical motifs will allow lanthanide-doped nanostructures to serve as circuit boards on which such motifs can be modularly connected via iterative chemical synthesis^113,114 to build complex nanoscale optical circuits.

Complex ANPs through machine learning and automated discovery. If the future of ANPs is complex heterostructures that serve as optical breadboards, how will these intricate ANP compositions, with their large number of parameters, be optimized? Computational modeling will be important for identifying the best compositions for motifs and their optimal assembly into larger networks.

Differential rate equation models are the most common way to understanding ANP results (e.g., extracting novel pathways for avalanching^44,50,115) and are a key tool for performing high-throughput in silico screening of a wide range of ANP compositions, since hundreds of thousands of DREs can be solved at the rate of ∼1 min per composition.^44,69,73 However, rate equation models have drawbacks that limit them to moderate doping levels and the simplest ANP geometries (e.g. those with a single doped domain and concentric, core/shell heterostructures).¹¹⁶ These limitations arise in part from the fact that the DREs are typically assembled manually, inherently biasing the results towards the subset of interactions included in the model. Even when their construction is automated, DREs must be restricted in their complexity in order to limit calculation times, like constraining the number of energy levels and transitions considered. DREs commonly use estimates for the thousands of rate constants (e.g., using Judd–Ofelt theory¹¹⁷ or literature values of related materials) since most are difficult to measure precisely. The required number of transition rate constants is significantly reduced by assuming that they are independent of doping level, population, and excitation power. These are oversimplifications, particularly at the high doping or alloying used for many ANPs^5,8 and UCNPs,¹¹⁸ which would be expected to change lattice spacings and interatomic distances, altering transition rates. Most DRE models also assume a homogeneously doped bulk material, and the most erroneous models use ET rates calculated with a single, average distance between dopants. In reality, the stochastic doping at discrete lattice coordinates in finite-size crystals results in an uneven distribution of distances between dopants and localized regions of high or low doping. Finally, because energy can migrate or “diffuse” rapidly between dopants via resonant ET, DRE models must assume whether their systems are in the migration-limited or fast migration regime,^115,119 asymptotic cases that are rarely accurate for all excited states. These assumptions and compromises rapidly break down for the complex core/shell heterostructures currently being investigated for multi-color ANPs.

Unlike DREs, kinetic Monte Carlo (kMC) models allow for simulation of complex heterostructures because they operate on atomically specified geometries and dopant distributions.^{50,75,120,121} A major challenge for kMC modeling, however, is their computational expense – one simulation of a large, multi-shell nanoparticle of the diameter required to encode a complex network (>30 nm) can require weeks or months of computational time even on high-performance computing clusters.¹²² The large number of simulations required to optimize such structures would make kMC screening impractical.

To overcome this challenge, ANP heterostructures in the future can be optimized by machine learning (ML) models trained on simulation data, as was recently demonstrated for UCNP heterostructures.^75,122 Active learning approaches^123–125 such as Bayesian Optimization can be used to iteratively and efficiently search through compositional space spanned by as many as seven dimensions, such as those that describe the concentrations and dimensions of triply doped core/shell UCNPs.⁷⁵ However, for the even higher number of parameters required for the most complex heterostructures, deep learning models such as convolutional neural networks can be more efficient, as we demonstrated with heterogeneous graph neural networks (GNNs) that model UCNPs with up to 10 core or shell domains.¹²² These deep learning approaches do require large simulation datasets for training – 6000–30 000 structures in the case of the SUNSET databases used to train GNNs.¹²² Such ML-guided approaches may also aid other areas of ANP research, such as searching for ligands that enhance ANP emission.^82,126 Because the use of ML to accelerate ANP and UCNP research is in its infancy,^75,127–135 we may look towards ML-guided approaches^124,125 for accelerating the discovery of other nanomaterials¹³⁶ like quantum dots and perovskites.^123,137,138 Such data-driven techniques can also guide experimental campaigns, particularly when used in conjunction with high-throughput automated workflows.^73,80,139 Future approaches may leverage ML models that combine multiple data streams – experimental, theoretical, and literature-based data – to autonomously guide robotic synthesis^140–142 and optical characterization of the most promising ANP candidates and those that help refine existing understanding.

7. Conclusions

In this focus article, we have dispelled some of the largest misconceptions and most common questions about photon avalanching nanoparticles that we hear as we share our ANP research. Some of these questions are as fundamental as what goes in an ANP and why its nonlinearity is useful, while common myths center around the origins of PA and how PA can be enhanced. We have explored the truly puzzling contradictions of PA – that its rise times get longer as its kinetics get faster, and that ANP imaging can sometimes break the resolution limit without achieving super-resolution. Understanding the true nature of ANPs, including the limitations described here, may allow researchers to design brighter, more stable ANPs with a variety of colors and faster responses – helping these materials to meld their unique nonlinearity properties with real-world demands.

Perhaps the greatest mystery of ANPs is what new properties and applications will emerge in the future. Similar to the repeated branching illustrated in pictorial representations of PA, ANPs have continually and consistently revealed novel behavior and intriguing use-cases at every turn. To illustrate how ANPs are the gift that keeps on giving, we conclude this focus article by describing our journey in ANP research and how it continually branched and fed back upon itself. In 2014, in search of UCNPs that could be excited through brain, we and our collaborators computationally predicted and experimentally verified energy looping in Tm³⁺-doped nanoparticles.⁴⁴ While not sufficiently nonlinear to be classified as ANPs, these “ELNPs” inspired our long-term vision of nonlinear optical networks.⁵⁰ This vision led to the development of highly Tm³⁺-doped ANPs that met the strict criteria for PA outlined in Fig. 8b⁵ and the demonstration of sub-wavelength imaging (PASSI, as predicted by Bednarkiewicz et al.⁵¹). During this ANP research, our collaborators coincidentally observed photodarkening in the same nanoparticles, leading to the development of INPALM.⁶ In ostensibly separate research, our efforts to make brighter UCNPs with low-phonon-energy hosts²⁰ led to the observation of PA-driven intrinsic optical bistability in Nd³⁺-doped KPb₂Cl₅ ANPs, which exhibit nonlinearities greater than 100.⁹

What are the lessons to be learned from our journey? First, computational predictions were essential since conventional UCNP thinking would not have suggested such strange and contradictory materials. Second, in every step of this journey, each small advance has led to a chain reaction of further advances that have revealed new insight into lanthanide-doped avalanching nanomaterials. Finally, many of our discoveries were serendipitous, defying the idealized scientific myth of intentionality. Synergistic collaborations, cutting-edge techniques, and open minds were critical for amplifying seemingly minor observations into grand hypotheses and scientific outcomes. We hope that disproving the myths presented here and unraveling the mysteries of ANPs will similarly amplify research in ANPs and their applications and continue the chain reaction of novel discoveries for these peculiar and nonlinear nanoparticles.

Data availability

No original data was generated for this Focus Article. Data may be available from the original sources cited within this article.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. A. S. is grateful for startup funds from Oregon State University.

References

1. A. Fernandez-Bravo, K. Yao, E. S. Barnard, N. J. Borys, E. S. Levy, B. Tian, C. A. Tajon, L. Moretti, M. V. Altoe, S. Aloni, K. Beketayev, F. Scotognella, B. E. Cohen, E. M. Chan and P. J. Schuck, Nat. Nanotechnol., 2018, 13, 572–577.
2. Y. Liu, A. Teitelboim, A. Fernandez-Bravo, K. Yao, M. V. P. Altoe, S. Aloni, C. Zhang, B. E. Cohen, P. J. Schuck and E. M. Chan, ACS Nano, 2020, 14, 1508–1519.
3. M.-F. Joubert, Opt. Mater., 1999, 11, 181–203.
4. M. Szalkowski, A. Kotulska, M. Dudek, Z. Korczak, M. Majak, L. Marciniak, M. Misiak, K. Prorok, A. Skripka, P. J. Schuck, E. M. Chan and A. Bednarkiewicz, Chem. Soc. Rev., 2025, 54, 983–1026.
5. C. Lee, E. Z. Xu, Y. Liu, A. Teitelboim, K. Yao, A. Fernandez-Bravo, A. M. Kotulska, S. H. Nam, Y. D. Suh, A. Bednarkiewicz, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2021, 589, 230–235.
6. C. Lee, E. Z. Xu, K. W. C. Kwock, A. Teitelboim, Y. Liu, H. S. Park, B. Ursprung, M. E. Ziffer, Y. Karube, N. Fardian-Melamed, C. C. S. Pedroso, J. Kim, S. D. Pritzl, S. H. Nam, T. Lohmueller, J. S. Owen, P. Ercius, Y. D. Suh, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2023, 618, 951–958.
7. Z. Korczak, M. Dudek, M. Majak, M. Misiak, Ł. Marciniak, M. Szalkowski and A. Bednarkiewicz, Low Temp. Phys., 2023, 49, 322.
8. N. Fardian-Melamed, A. Skripka, B. Ursprung, C. Lee, T. P. Darlington, A. Teitelboim, X. Qi, M. Wang, J. M. Gerton, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2025, 637, 70–75.
9. A. Skripka, Z. Zhang, X. Qi, B. Ursprung, P. Ercius, B. E. Cohen, P. J. Schuck, D. Jaque and E. M. Chan, Nat. Photonics, 2025, 19, 212–218.
10. A. Bednarkiewicz, M. Szalkowski, M. Majak, Z. Korczak, M. Misiak and S. Maćkowski, Adv. Mater., 2023, 35, 2304390.
11. X. Liu, J. Chen, C. Liu, S. Xi, S. T. Tan, Q. He and L. Liang, Res. Square, 2024 DOI:10.21203/rs.3.rs-4183918/v1.
12. M. F. Joubert, S. Guy, B. Jacquier and C. Linarés, Opt. Mater., 1994, 4, 43–49.
13. C. Liu, X. Zhang, X. Chen and L. Liang, Nano Lett., 2024, 24, 15489–15500.
14. J. Huang, G. Wei, H. Wei and B. Zhou, ACS Appl. Opt. Mater., 2024, 2, 1841–1853.
15. A. Skripka, M. Lee, X. Qi, J.-A. Pan, H. Yang, C. Lee, P. J. Schuck, B. E. Cohen, D. Jaque and E. M. Chan, Nano Lett., 2023, 23, 7100–7106.
16. C. Wang, Z. Wen, R. Pu, B. Pan, B. Wang, K. Zheng, Y. Du and Q. Zhan, Adv. Mater., 2024, 36, e2307848.
17. Y. Liang, Z. Zhu, S. Qiao, X. Guo, R. Pu, H. Tang, H. Liu, H. Dong, T. Peng, L.-D. Sun, J. Widengren and Q. Zhan, Nat. Nanotechnol., 2022, 17, 524–530.
18. C. Wang, Z. Wen, R. Pu and Q. Zhan, Laser Photonics Rev., 2024, 18, 2400290.
19. M. Zhang, P. Huang, W. Zheng, X. Song, X. Shang, W. Zhang, D. Yang, X. Yi and X. Chen, Nano Lett., 2023, 23, 8576–8584.
20. Z. Zhang, A. Skripka, J. C. Dahl, C. Dun, J. J. Urban, D. Jaque, P. J. Schuck, B. E. Cohen and E. M. Chan, Angew. Chem., Int. Ed., 2023, 62, e202212549.
21. J. K. Zaręba, M. Nyk and M. Samoć, Adv. Opt. Mater., 2021, 9, 2100216.
22. K. U. Torii, Trends Cell Biol., 2012, 22, 438–446.
23. S. N. Semenov, L. J. Kraft, A. Ainla, M. Zhao, M. Baghbanzadeh, V. E. Campbell, K. Kang, J. M. Fox and G. M. Whitesides, Nature, 2016, 537, 656.
24. A. M. Turing, Philos. Trans. R. Soc., B, 1952, 237, 37–72.
25. I. Lengyel and I. R. Epstein, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 3977–3979.
26. N. Tompkins, N. Li, C. Girabawe, M. Heymann, G. B. Ermentrout, I. R. Epstein and S. Fraden, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4397.
27. A. Blagodatski, A. Sergeev, M. Kryuchkov, Y. Lopatina and V. L. Katanaev, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10750–10755.
28. Q. Ouyang and H. L. Swinney, Nature, 1991, 352, 610–612.
29. H. Meinhardt, in Current Topics in Developmental Biology, ed. S. Schnell, P. K. Maini, S. A. Newman and T. J. Newman, Academic Press, 2008, vol. 81, pp. 1–63.
30. R. Sheth, L. Marcon, M. F. Bastida, M. Junco, L. Quintana, R. Dahn, M. Kmita, J. Sharpe and M. A. Ros, Science, 2012, 338, 1476–1480.
31. A. J. Lotka, J. Phys. Chem., 1910, 14, 271–274.
32. H. S. Otto, J. Sci. Instrum., 1938, 15, 24.
33. S.-Y. Yun, J.-K. Han and Y.-K. Choi, Nano Lett., 2024, 24, 2751–2757.
34. J. Du, Q. Wang, G. Jiang, C. Xu, C. Zhao, Y. Xiang, Y. Chen, S. Wen and H. Zhang, Sci. Rep., 2014, 4, 6346.
35. Y.-X. Zhang and Y.-H. Wang, RSC Adv., 2017, 7, 45129–45144.
36. M. Miscuglio, A. Mehrabian, Z. Hu, S. I. Azzam, J. George, A. V. Kildishev, M. Pelton and V. J. Sorger, Opt. Mater. Express, 2018, 8, 3851–3863.
37. E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592.
38. H. Yu, Y. Peng, Y. Yang and Z.-Y. Li, npj Comput. Mater., 2019, 5, 45.
39. M. A. Firestone, S. C. Hayden and D. L. Huber, MRS Bull., 2015, 40, 760–767.
40. X. Li, X. Liu and X. Liu, Chem. Soc. Rev., 2021, 50, 2074–2101.
41. F. Auzel, Chem. Rev., 2004, 104, 139–174.
42. C. Homann, L. Krukewitt, F. Frenzel, B. Grauel, C. Würth, U. Resch-Genger and M. Haase, Angew. Chem., Int. Ed., 2018, 57, 8765–8769.
43. F. Li, L. Tu, Y. Zhang, D. Huang, X. Liu, X. Zhang, J. Du, R. Fan, C. Yang, K. W. Krämer, J. Marques-Hueso and G. Chen, Nat. Photonics, 2024, 18, 440–449.
44. E. S. Levy, C. A. Tajon, T. S. Bischof, J. Iafrati, A. Fernandez-Bravo, D. J. Garfield, M. Chamanzar, M. M. Maharbiz, V. S. Sohal, P. J. Schuck, B. E. Cohen and E. M. Chan, ACS Nano, 2016, 10, 8423–8433.
45. K. W. C. Kwock, C. Lee, A. Teitelboim, Y. Liu, K. Yao, S. B. Alam, B. E. Cohen, E. M. Chan and P. J. Schuck, J. Phys. Chem. C, 2021, 125, 23976–23982.
46. S. Guy, M. F. Joubert and B. Jacquier, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 8240–8248.
47. P. Goldner and F. Pelle, Opt. Mater., 1996, 5, 239–249.
48. M. F. Joubert, S. Guy and B. Jacquier, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10031–10037.
49. F. Auzel and Y. Chen, J. Lumin., 1995, 65, 45–56.
50. A. Teitelboim, B. Tian, D. J. Garfield, A. Fernandez-Bravo, A. C. Gotlin, P. J. Schuck, B. E. Cohen and E. M. Chan, J. Phys. Chem. C, 2019, 123, 2678–2689.
51. A. Bednarkiewicz, E. M. Chan, A. Kotulska, L. Marciniak and K. Prorok, Nanoscale Horiz., 2019, 4, 881–889.
52. M. Zhou, P. Huang, X. Shang, R. Zhang, W. Zhang, Z. Shao, S. Zhang, W. Zheng and X. Chen, Nat. Commun., 2024, 15, 9880.
53. K. Huang, K. K. Green, L. Huang, H. Hallen, G. Han and S. F. Lim, Nat. Photonics, 2022, 16, 737–742.
54. L. E. MacKenzie, arXiv, 2024, preprint, arXiv:2412.12891 DOI:10.48550/arXiv.2412.12891.
55. B. Russ and C. N. Eisler, Nanophotonics, 2024, 13, 1943–1951.
56. C. Liu, B. Pan, B. Wang, Q. Zhao, Y. Ni, H. Wu, Z. Luo, T. Chen and Q. Zhan, Optica, 2024, 11, 1324.
57. J. A. Pan, A. Skripka, C. Lee, X. Qi, A. L. Pham, J. J. Woods, R. J. Abergel, P. J. Schuck, B. E. Cohen and E. M. Chan, J. Am. Chem. Soc., 2024, 146, 7487–7497.
58. S. N. Sanders, T. H. Schloemer, M. K. Gangishetty, D. Anderson, M. Seitz, A. O. Gallegos, R. C. Stokes and D. N. Congreve, Nature, 2022, 604, 474–478.
59. M. Szalkowski, M. Dudek, Z. Korczak, C. Lee, Ł. Marciniak, E. M. Chan, P. J. Schuck and A. Bednarkiewicz, Opt. Mater.: X, 2021, 12, 100102.
60. M. Majak, M. Misiak and A. Bednarkiewicz, Mater. Horiz., 2024, 11, 4791–4801.
61. A. Bednarkiewicz, E. M. Chan and K. Prorok, Nanoscale Adv., 2020, 2, 4863–4872.
62. E. Betzig, G. H. Patterson, R. Sougrat, O. W. Lindwasser, S. Olenych, J. S. Bonifacino, M. W. Davidson, J. Lippincott-Schwartz and H. F. Hess, Science, 2006, 313, 1642–1645.
63. M. J. Rust, M. Bates and X. Zhuang, Nat. Methods, 2006, 3, 793–796.
64. S. Wu, G. Han, D. J. Milliron, S. Aloni, V. Altoe, D. V. Talapin, B. E. Cohen and P. J. Schuck, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10917.
65. X. Wang, X. Ren, K. Kahen, M. A. Hahn, M. Rajeswaran, S. Maccagnano-Zacher, J. Silcox, G. E. Cragg, A. L. Efros and T. D. Krauss, Nature, 2009, 459, 686–689.
66. P. L. McMahon, Nat. Rev. Phys., 2023, 5, 717–734.
67. D. A. B. Miller, Nat. Photonics, 2010, 4, 3–5.
68. M. Dudek, M. Szalkowski, M. Misiak, M. Ćwierzona, A. Skripka, Z. Korczak, D. Piątkowski, P. Woźniak, R. Lisiecki, P. Goldner, S. Maćkowski, E. M. Chan, P. J. Schuck and A. Bednarkiewicz, Adv. Opt. Mater., 2022, 10, 2201052.
69. X. Qi, C. Lee, B. Ursprung, A. Skripka, P. J. Schuck, E. M. Chan and B. E. Cohen, J. Am. Chem. Soc., 2024, 146, 29292–29296.
70. M. P. Hansen and D. S. Malchow, Proc. SPIE, Thermosense XXX, SPIE, 2008, vol. 6939, pp. 94–104.
71. F. Cao, L. Liu and L. Li, Mater. Today, 2023, 62, 327–349.
72. S. Kück, A. Diening, E. Heumann, E. Mix, T. Sandrock, K. Sebald and G. Huber, J. Alloys Compd., 2000, 300–301, 65–70.
73. E. M. Chan, G. Han, J. D. Goldberg, D. J. Gargas, A. D. Ostrowski, P. J. Schuck, B. E. Cohen and D. J. Milliron, Nano Lett., 2012, 12, 3839–3845.
74. X. Li, Z. Guo, T. Zhao, Y. Lu, L. Zhou, D. Zhao and F. Zhang, Angew. Chem., Int. Ed., 2016, 55, 2464–2469.
75. X. Xia, E. Sivonxay, B. A. Helms, S. M. Blau and E. M. Chan, Nano Lett., 2023, 23, 11129–11136.
76. F. Wang, R. Deng, J. Wang, Q. Wang, Y. Han, H. Zhu, X. Chen and X. Liu, Nat. Mater., 2011, 10, 968–973.
77. I. Rreza, H. Yang, L. Hamachi, M. Campos, T. Hull, J. Treadway, J. Kurtin, E. M. Chan and J. S. Owen, ACS Appl. Mater. Interfaces, 2021, 13, 12191–12197.
78. L. S. Hamachi, H. Yang, I. Jen-La Plante, N. Saenz, K. Qian, M. P. Campos, G. T. Cleveland, I. Rreza, A. Oza, W. Walravens, E. M. Chan, Z. Hens, A. C. Crowther and J. S. Owen, Chem. Sci., 2019, 10, 6539–6552.
79. H. Yang, L. S. Hamachi, I. Rreza, W. Wang and E. M. Chan, Chem. Mater., 2019, 31, 4173–4183.
80. E. M. Chan, Chem. Soc. Rev., 2015, 44, 1653–1679.
81. G. Chen, H. Qiu, P. N. Prasad and X. Chen, Chem. Rev., 2014, 114, 5161–5214.
82. J.-A. Pan, X. Qi and E. M. Chan, Nanoscale Horiz., 2025, 10, 596–604.
83. M. Jaugstetter, X. Qi, E. M. Chan, M. Salmeron, K. R. Wilson, S. Nemšák and H. Bluhm, ACS Nano, 2025, 19, 418–426.
84. C. C. S. Pedroso, V. R. Mann, K. Zuberbühler, M.-F. Bohn, J. Yu, V. Altoe, C. S. Craik and B. E. Cohen, ACS Nano, 2021, 15, 18374–18384.
85. X. Wang, C. Jiang, Z. Wang, B. E. Cohen, E. M. Chan and G. Chen, Nano Lett., 2023, 23, 7001–7007.
86. D. J. Garfield, N. J. Borys, S. M. Hamed, N. A. Torquato, C. A. Tajon, B. Tian, B. Shevitski, E. S. Barnard, Y. D. Suh, S. Aloni, J. B. Neaton, E. M. Chan, B. E. Cohen and P. J. Schuck, Nat. Photonics, 2018, 12, 402–407.
87. X. Wu, Y. Zhang, K. Takle, O. Bilsel, Z. Li, H. Lee, Z. Zhang, D. Li, W. Fan, C. Duan, E. M. Chan, C. Lois, Y. Xiang and G. Han, ACS Nano, 2016, 10, 1060–1066.
88. T.-T. Le-Vu, J.-R. Chang, V.-D. Pham, J.-Y. Lin, H.-C. Kan, S.-W. Kuo and C.-C. Hsu, ACS Appl. Nano Mater., 2025, 8, 427–437.
89. A. Fernandez-Bravo, D. Wang, E. S. Barnard, A. Teitelboim, C. Tajon, J. Guan, G. C. Schatz, B. E. Cohen, E. M. Chan, P. J. Schuck and T. W. Odom, Nat. Mater., 2019, 18, 1172–1176.
90. C. Lee and P. J. Schuck, Annu. Rev. Phys. Chem., 2023, 74, 415–438.
91. A. J. Pattison, C. C. S. Pedroso, B. E. Cohen, J. C. Ondry, A. P. Alivisatos, W. Theis and P. Ercius, Nanotechnology, 2024, 35, 015710.
92. P. Ercius, I. J. Johnson, P. Pelz, B. H. Savitzky, L. Hughes, H. G. Brown, S. E. Zeltmann, S.-L. Hsu, C. C. S. Pedroso, B. E. Cohen, R. Ramesh, D. Paul, J. M. Joseph, T. Stezelberger, C. Czarnik, M. Lent, E. Fong, J. Ciston, M. C. Scott, C. Ophus, A. M. Minor and P. Denes, Microsc. Microanal., 2024, 30, 903–912.
93. S. M. Ribet, G. Varnavides, C. C. S. Pedroso, B. E. Cohen, P. Ercius, M. C. Scott and C. Ophus, Appl. Phys. Lett., 2024, 124, 240601.
94. Y. Han, L. Wang, K. Cao, J. Zhou, Y. Zhu, Y. Hou and Y. Lu, Chem. Rev., 2023, 123, 14119–14184.
95. S. B. Alam, G. Soligno, J. Yang, K. C. Bustillo, P. Ercius, H. Zheng, S. Whitelam and E. M. Chan, Langmuir, 2022, 38, 7168–7178.
96. S. B. Alam, J. Yang, K. C. Bustillo, C. Ophus, P. Ercius, H. Zheng and E. M. Chan, Nanoscale, 2020, 12, 18606–18615.
97. E. M. Chan, M. A. Marcus, S. Fakra, M. ElNaggar, R. A. Mathies and A. P. Alivisatos, J. Phys. Chem. A, 2007, 111, 12210–12215.
98. E. A. Schriber, D. W. Paley, R. Bolotovsky, D. J. Rosenberg, R. G. Sierra, A. Aquila, D. Mendez, F. Poitevin, J. P. Blaschke, A. Bhowmick, R. P. Kelly, M. Hunter, B. Hayes, D. C. Popple, M. Yeung, C. Pareja-Rivera, S. Lisova, K. Tono, M. Sugahara, S. Owada, T. Kuykendall, K. Yao, P. J. Schuck, D. Solis-Ibarra, N. K. Sauter, A. S. Brewster and J. N. Hohman, Nature, 2022, 601, 360–365.
99. S. Barja, S. Refaely-Abramson, B. Schuler, D. Y. Qiu, A. Pulkin, S. Wickenburg, H. Ryu, M. M. Ugeda, C. Kastl, C. Chen, C. Hwang, A. Schwartzberg, S. Aloni, S.-K. Mo, D. Frank Ogletree, M. F. Crommie, O. V. Yazyev, S. G. Louie, J. B. Neaton and A. Weber-Bargioni, Nat. Commun., 2019, 10, 3382.
100. K. Huang, N. Le, J. S. Wang, L. Huang, L. Zeng, W.-C. Xu, Z. Li, Y. Li and G. Han, Adv. Mater., 2022, 34, 2107962.
101. E. Z. Xu, C. Lee, S. D. Pritzl, A. S. Chen, T. Lohmueller, B. E. Cohen, E. M. Chan and P. J. Schuck, Opt. Mater.: X, 2021, 12, 100099.
102. A. D. Pickel, A. Teitelboim, E. M. Chan, N. J. Borys, P. J. Schuck and C. Dames, Nat. Commun., 2018, 9, 4907.
103. J. D. Kilbane, E. M. Chan, C. Monachon, N. J. Borys, E. S. Levy, A. D. Pickel, J. J. Urban, P. J. Schuck and C. Dames, Nanoscale, 2016, 8, 11611–11616.
104. Z. Ye, B. Harrington and A. D. Pickel, Sci. Adv., 2024, 10, eado6268.
105. X. Di, D. Wang, Q. P. Su, Y. Liu, J. Liao, M. Maddahfar, J. Zhou and D. Jin, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2207402119.
106. X. Liu, Y. Wang, X. Li, Z. Yi, R. Deng, L. Liang, X. Xie, D. T. B. Loong, S. Song, D. Fan, A. H. All, H. Zhang, L. Huang and X. Liu, Nat. Commun., 2017, 8, 899.
107. W. Meier and O. Staffelbach, Nonlinearity Criteria for Cryptographic Functions, in Advances in Cryptology – EUROCRYPT ’89, ed. J.-J. Quisquater and J. Vandewalle, Springer-Verlag, Berlin Heidelberg, 1990, pp. 549–562.
108. M. R. Carro-Temboury, R. Arppe, T. Vosch and T. J. Sørensen, Sci. Adv., 2018, 4, e1701384.
109. M. Kumar and P. Pattnaik, in 2020 IEEE High Performance Extreme Computing Conference (HPEC), 2020, pp. 1–9 DOI:10.1109/HPEC43674.2020.9286147.
110. S. Wen, Y. Liu, F. Wang, G. Lin, J. Zhou, B. Shi, Y. D. Suh and D. Jin, Nat. Commun., 2020, 11, 6047.
111. Y. Zhang, L. Zhang, R. Deng, J. Tian, Y. Zong, D. Jin and X. Liu, J. Am. Chem. Soc., 2014, 136, 4893–4896.
112. D. J. Milliron, S. M. Hughes, Y. Cui, L. Manna, J. Li, L.-W. Wang and A. Paul Alivisatos, Nature, 2004, 430, 190–195.
113. S. Mehra, E. M. Chan and A. Salleo, J. Mater. Chem. C, 2015, 3, 7172–7179.
114. S. Mehra, A. Bergerud, D. J. Milliron, E. M. Chan and A. Salleo, Chem. Mater., 2016, 28, 3454–3461.
115. E. M. Chan, D. J. Gargas, P. J. Schuck and D. J. Milliron, J. Phys. Chem. B, 2012, 116, 10561–10570.
116. S. J. W. Vonk, J. J. E. Maris, A. J. H. Dekker, J. W. de Wit, T. P. van Swieten, A. Cocina and F. T. Rabouw, ACS Nano, 2024, 18, 28325–28334.
117. B. M. Walsh, Advances in Spectroscopy for Lasers and Sensing, Springer, 2006, pp. 403–433.
118. B. Tian, A. Fernandez-Bravo, H. Najafiaghdam, N. A. Torquato, M. V. P. Altoe, A. Teitelboim, C. A. Tajon, Y. Tian, N. J. Borys, E. S. Barnard, M. Anwar, E. M. Chan, P. J. Schuck and B. E. Cohen, Nat. Commun., 2018, 9, 3082.
119. B. Di Bartolo, Energy Transfer Processes in Condensed Matter, Plenum Press, New York, 1983.
120. L. Zichi, D. Barter, E. Sivonxay, E. W. C. Spotte-Smith, R. S. Mohanakrishnan, E. M. Chan, K. A. Persson and S. M. Blau, J. Open Source Software, 2024, 9, 7244.
121. M. J. J. Mangnus, J. Zom, T. A. J. Welling, A. Meijerink and F. T. Rabouw, ACS Nanosci. Au, 2022, 2, 111–118.
122. E. Sivonxay, L. Attia, E. W. C. Spotte-Smith, B. Lengeling, X. Xia, D. Barter, E. Chan and S. Blau, ChemRxiv, 2024, preprint DOI:10.26434/chemrxiv-2024-1dw4q.
123. M. A. Kim, Q. Ai, A. J. Norquist, J. Schrier and E. M. Chan, ACS Nano, 2024, 18, 14514–14522.
124. V. Shekar, G. Nicholas, M. A. Najeeb, M. Zeile, V. Yu, X. Wang, D. Slack, Z. Li, P. W. Nega, E. M. Chan, A. J. Norquist, J. Schrier and S. A. Friedler, J. Chem. Phys., 2022, 156, 064108.
125. Z. Li, P. W. Nega, M. A. N. Nellikkal, C. Dun, M. Zeller, J. J. Urban, W. A. Saidi, J. Schrier, A. J. Norquist and E. M. Chan, Chem. Mater., 2022, 34, 756–767.
126. H. Xu, S. Han, R. Deng, Q. Su, Y. Wei, Y. Tang, X. Qin and X. Liu, Nat. Photonics, 2021, 15, 732–737.
127. F. Yang, Y. Wang, X. Jiang, B. Lin and R. Lv, ACS Comb. Sci., 2020, 22, 285–296.
128. W. Wang, K. Chen, X. Ma and J. Guo, Fundam. Res., 2023, 3, 544–556.
129. J. Wang, Z. Jiang, Y. Wei, W. Wang, F. Wang, Y. Yang, H. Song and Q. Yuan, ACS Nano, 2022, 16, 3300–3310.
130. H. Liu, Z. Ju, X. Hui, W. Li and R. Lv, Nanoscale, 2024, 16, 16697–16705.
131. J. Liao, J. Zhou, Y. Song, B. Liu, J. Lu and D. Jin, J. Phys. Chem. Lett., 2021, 12, 10242–10248.
132. Z. Yi, H. Gao, X. Ji, X.-Y. Yeo, S. Y. Chong, Y. Mao, B. Luo, C. Shen, S. Han, J.-W. Wang, S. Jung, P. Shi, H. Ren and X. Liu, J. Am. Chem. Soc., 2021, 143, 14907–14915.
133. Y. Wen, W.-Y. Liu, J.-H. Wang, Y.-L. Yu and S. Chen, Anal. Chem., 2023, 95, 12152–12160.
134. H. Wen, X. Xu, S. Cheong, S.-C. Lo, J.-H. Chen, S. L. Y. Chang and C. Dwyer, Nanoscale Adv., 2021, 3, 6956–6964.
135. J. L. Mejia-Mendez, E. E. Reza-Zaldívar, A. Sanchez-Martinez, O. Ceballos-Sanchez, D. E. Navarro-López, L. Marcelo Lozano, J. Armendariz-Borunda, N. Tiwari, D. A. Jacobo-Velázquez, G. Sanchez-Ante and E. R. López-Mena, J. Nanobiotechnol., 2024, 22, 687.
136. H. Tao, T. Wu, M. Aldeghi, T. C. Wu, A. Aspuru-Guzik and E. Kumacheva, Nat. Rev. Mater., 2021, 6, 701–716.
137. J. C. Dahl, S. Niblett, Y. Cho, X. Wang, Y. Zhang, E. M. Chan and A. P. Alivisatos, J. Am. Chem. Soc., 2023, 145, 23076–23087.
138. J. C. Dahl, X. Wang, X. Huang, E. M. Chan and A. P. Alivisatos, J. Am. Chem. Soc., 2020, 142, 11915–11926.
139. E. M. Chan, C. Xu, A. W. Mao, G. Han, J. S. Owen, B. E. Cohen and D. J. Milliron, Nano Lett., 2010, 10, 1874–1885.
140. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241.
141. A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Sci. Adv., 2020, 6, eaaz1708.
142. H. S. Stein and J. M. Gregoire, Chem. Sci., 2019, 10, 9640–9649.

---