Open Access Article
Open Access ArticleA general graph neural network based implicit solvation model for organic molecules in water†
Paul
Katzberger
 and
Sereina
Riniker
and
Sereina
Riniker
 *
*
Department of Chemistry and Applied Biosciences, ETH Zürich, Vladimir-Prelog-Weg 2, 8093, Zürich, Switzerland. E-mail: sriniker@ethz.ch
First published on 19th June 2024
Abstract
The dynamical behavior of small molecules in their environment can be studied with classical molecular dynamics (MD) simulations to gain deeper insight on an atomic level and thus complement and rationalize the interpretation of experimental findings. Such approaches are of great value in various areas of research, e.g., in the development of new therapeutics. The accurate description of solvation effects in such simulations is thereby key and has in consequence been an active field of research since the introduction of MD. So far, the most accurate approaches involve computationally expensive explicit solvent simulations, while widely applied models using an implicit solvent description suffer from reduced accuracy. Recently, machine learning (ML) approaches that provide a probabilistic representation of solvation effects have been proposed as potential alternatives. However, the associated computational costs and minimal or lack of transferability render them unusable in practice. Here, we report the first example of a transferable ML-based implicit solvent model trained on a diverse set of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular structures that can be applied to organic small molecules for simulations in water. Extensive testing against reference calculations demonstrated that the model delivers on par accuracy with explicit solvent simulations while providing an up to 18-fold increase in sampling rate.
000 molecular structures that can be applied to organic small molecules for simulations in water. Extensive testing against reference calculations demonstrated that the model delivers on par accuracy with explicit solvent simulations while providing an up to 18-fold increase in sampling rate.
1 Introduction
Classical molecular dynamics (MD) is a widely used approach that employs Newton's equation of motion to provide insights into the dynamical processes of molecules, ultimately allowing rationalization of experimental findings and supporting drug discovery in general (for examples see ref. 1–3). Much progress has been made in efficiently exploring the conformational space of molecules in a given environment. The development of specialized hardware,4 highly parallelized algorithms,5 and enhanced sampling methods6 continues to push the frontier of accessible timescales. A key aspect of exploring the correct conformational space of a molecule is solvation effects. To capture the local solvation effects correctly, the solvent molecules around a molecule (typically in their thousands) are typically modelled explicitly in the simulation. However, this explicit treatment of solvation results in a large number of degrees of freedom in the system, which is computationally expensive (computational cost per simulation step scales between O(N) and O(N2) where N is the number of atoms). The larger number of degrees of freedom leads additionally to a more rugged free-energy surface, which decreases the effective sampling rate further.7 Hence, the majority of the computational cost is spent on solvent–solvent interactions, which are typically not of interest per se.The alternatives to this approach are implicit solvent methods, which model the mean effect of a given environment on the solute in a probabilistic fashion.7 Most of these implicit solvents rely on continuum approaches where the effect of an equidispersed medium on a given molecule is calculated. While many of them are indeed much faster than their explicit counterpart, the major drawback of these methods is that they do not describe the local solvation effects correctly. Based on recent successes of applying machine learning (ML) in the field of chemistry,8 ML-based approaches have been developed to learn the effects of a given environment (solvent) on a solute.9–13 These models are either too slow and/or not sufficiently transferable between different molecules to be practically usable in MD simulations, leaving explicit solvent simulations as the only reliable solution for generating accurate conformational ensembles in solution.
In this work, we showcase a novel ML-based implicit solvent model using a graph neural network (GNN) that is applicable to diverse small organic molecules, achieving the accuracy of explicit-solvent simulations but in a fraction of the time. To the best of our knowledge this is the first instance of a truly transferable ML-based implicit solvent method covering a vast organic chemical space while achieving high accuracy. The approach is validated against explicit solvent reference simulations by comparing predicted mean forces of an external test set as well as by performing prospective MD simulations. To highlight the substantial improvements over state-of-the-art implicit solvents, the commonly used GB-Neck2 implicit solvent14 is taken as a point of reference.
1.1 Background
Standard implicit solvent models largely rely on estimating the mean energies and forces of a given environment exerted on a solute by modeling the solvent as a continuum. For instance, the polar contribution of the solvation free energy can be calculated by the effect of a dielectric continuum on the solute. Examples of such approaches would be Poisson–Boltzmann (PB),15 fast analytical continuum treatments of solvation (FACTS),16 or generalised Born (GB) methods.17 Similarly, the non-polar contribution is typically modeled as a linear function of a molecule's surface area.18 These simplifications are likely responsible for the inability of these kinds of models to accurately describe local solvation effects. This is most pronounced in cases where the discrete nature of the solvent molecules yields a density distribution that diverges from a continuum description at the solute–solvent interface. Examples for this behavior can be found in previous studies,12,19 as well as in the Results section of this work.ML approaches have also been applied to model the effects of a given solvent environment on molecules.9–13 While these models are indeed capable of reproducing desired effects (e.g., reproduction of conformational ensembles or free-energy profiles) and dramatically outperform the standard implicit solvent methods in reproducing explicit solvent reference calculations, they currently have two major limitations for practical usability. First, even though much smaller systems were studied (i.e., only the molecule of interest and not a solvated box) these ML based approaches were considerably slower than the explicit solvent reference. As the rather young field of ML potentials (i.e., the broader field of applying ML models to describe the Hamiltonian in MD simulations) develops further, we expect this issue to be reduced as many of the optimisations for classical MD developed over the last half century still need to be introduced for these applications (e.g., parallel evaluation of all parts of the Hamiltonian or usage of pairlist algorithms).20 The second issue and hence the truly limiting one is, however, that the ML models are currently either not or only partially transferable from one molecular system to the next. In practice, this means that the current ML approaches need to be re-trained every time a new system or class of systems is studied (including generation of suitable training data), rendering them impractical for most common applications.
Recently, we developed a GNN that utilized a Δ-ML scheme for modeling solvation effects, which showed promising transferability within a relatively narrow set of similar small peptides.12 In this methodology, a three layer GNN was inserted into the functional form of the classical GB-Neck2 implicit solvent14 model. The rationale behind this approach is that while the forces exerted on a solute estimated by a continuum are not accurate, they provide the GNN with a good starting point. Specifically, the long-range effects are already well represented by the classical implicit solvent, and the GNN needs to learn only a correction for the short-range (local) effects.
In the work presented here, the functional form of the GNN model was further refined by introducing an additional separate term accounting for the non-polar interactions that does not rely on the generalized Born radii as commonly used in GBSA models or in our previous model,12
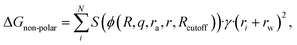 | (1) |
It should be noted that even though this functional form has experimental as well as theoretical foundations, the incorporation of the GNN renders it a numerical potential. While the prediction of the GNN represents the fraction of an atom that is accessible by the solvent, its numerical values do not necessarily correspond to the analytical solution. Both scalings in the polar and non-polar parts of the GNN architecture are related to the level of screening exerted from intramolecular atoms. To allow for synergistic effects as well as to introduce a certain level of flexibility, a multitask approach was chosen where the GNN predicts two instead of one value per atom (i.e., for each atom a scaling factor for the polar and the non-polar part of the solvation free energy is predicted). During training, both terms are fit together, further diluting the direct correlation between the classical functional form and the resulting potential. The GNN model is trained on a diverse data set consisting of 369![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 small molecules (molecular weight <500 Da) designed to cover a large fraction of the organic chemical space.21 For each molecule, the mean forces exerted by the solvent environment are calculated for up to nine conformations leading to 3
486 small molecules (molecular weight <500 Da) designed to cover a large fraction of the organic chemical space.21 For each molecule, the mean forces exerted by the solvent environment are calculated for up to nine conformations leading to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208
208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 data points in total. The employed approach shares similarities with the average solvent environment configuration (ASEC)22,23 approach, which was recently applied by Yao et al.24 for the training of an ML potential.
720 data points in total. The employed approach shares similarities with the average solvent environment configuration (ASEC)22,23 approach, which was recently applied by Yao et al.24 for the training of an ML potential.
A substantial benefit of explicit solvent simulations is that they work for any solvent (given corresponding force-field parameters). Currently, ML-based solvent models need to be trained on a specific solvent in order to accurately describe it. In this study, the focus lies on developing a replacement for explicit water simulations. The aqueous environment is not only one of the most studied but also one of the most computationally expensive solvents, as water has a high atomic density. In addition, its ability to form multiple hydrogen bonds makes it especially challenging for implicit solvents to describe the local solvation effects.
2 Results and discussion
2.1 Timings and external test set
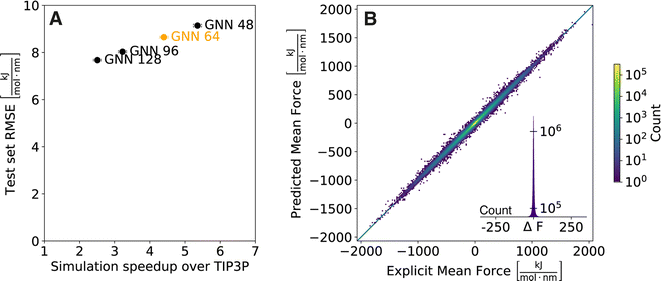
As computational efficiency is crucial for practical usability (i.e., the implicit solvent model must be faster than explicit-solvent simulations, which is not achieved by many of the proposed ML models11–13), we first investigated the effect of the complexity of the GNN architecture on simulation speed. For this, we varied the number of parameters in the GNN (i.e., the size of the hidden layers in the multi-layer perceptrons (MLPs)) from 128 to 96, 64, and 48 when training on our set of 369![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 diverse small molecules with molecular weight <500 Da. The prediction accuracy of the four GNN architectures was compared on an external test set containing 1000 compounds with molecular weight ranging from 500 Da to 700 Da (see Table S1 in the ESI† for a compilation of the test-set performance assessed by the most common metrics). Current neural network implementations are focused on optimising parallel operations rather than consecutive ones. For MD applications, this is problematic as the foundations of MD rely on fast consecutive evaluations of the Hamiltonian. To utilise the full potential of current graphics processing unit (GPU) models as well as to follow good MD practices,25 we simulated multiple replicates of a molecule at once and compared the cumulative simulation times with explicit solvent TIP3P simulations (Fig. 1A). A summary of absolute timings for the different solvent models is shown in the ESI (Table S2†). An almost linear relationship between the simulation speed and the test set RMSE can be observed, which is to be expected as the larger number of parameters allows the model to increase accuracy at the cost of more computations when evaluated. Importantly, all four GNN architectures provide a significant speed-up over the explicit-solvent simulations (i.e., by factors of 2.5, 3.2, 4.4, and 5.4, respectively). While the test set RMSE increases with decreasing hidden layer size, it is noteworthy that the relative error increment between the architectures remains low (e.g., the relative difference in test set RMSE for the model with a hidden size of 128 versus 64 is only 13%). A key aspect of implicit solvent models is that they can provide comparable insights at lower computational cost. Following this argument, we decided to use in the following the GNN with a hidden layer size of 64 as it reduces computational cost by 4.4-fold while still achieving high accuracy on the external test set (Fig. 1B).
486 diverse small molecules with molecular weight <500 Da. The prediction accuracy of the four GNN architectures was compared on an external test set containing 1000 compounds with molecular weight ranging from 500 Da to 700 Da (see Table S1 in the ESI† for a compilation of the test-set performance assessed by the most common metrics). Current neural network implementations are focused on optimising parallel operations rather than consecutive ones. For MD applications, this is problematic as the foundations of MD rely on fast consecutive evaluations of the Hamiltonian. To utilise the full potential of current graphics processing unit (GPU) models as well as to follow good MD practices,25 we simulated multiple replicates of a molecule at once and compared the cumulative simulation times with explicit solvent TIP3P simulations (Fig. 1A). A summary of absolute timings for the different solvent models is shown in the ESI (Table S2†). An almost linear relationship between the simulation speed and the test set RMSE can be observed, which is to be expected as the larger number of parameters allows the model to increase accuracy at the cost of more computations when evaluated. Importantly, all four GNN architectures provide a significant speed-up over the explicit-solvent simulations (i.e., by factors of 2.5, 3.2, 4.4, and 5.4, respectively). While the test set RMSE increases with decreasing hidden layer size, it is noteworthy that the relative error increment between the architectures remains low (e.g., the relative difference in test set RMSE for the model with a hidden size of 128 versus 64 is only 13%). A key aspect of implicit solvent models is that they can provide comparable insights at lower computational cost. Following this argument, we decided to use in the following the GNN with a hidden layer size of 64 as it reduces computational cost by 4.4-fold while still achieving high accuracy on the external test set (Fig. 1B).
2.2 Prospective molecular dynamics simulations
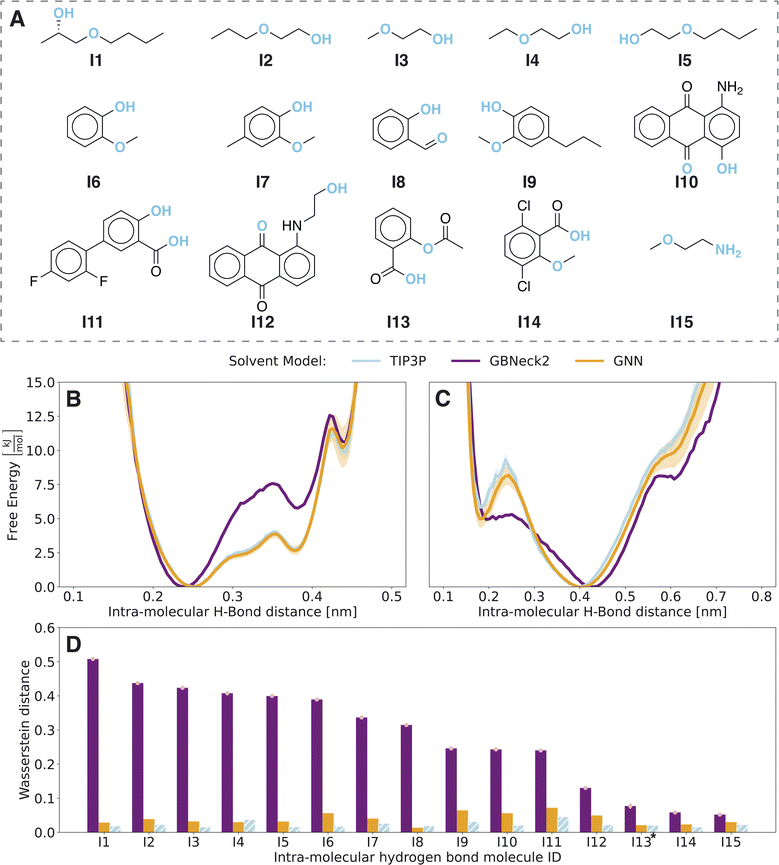
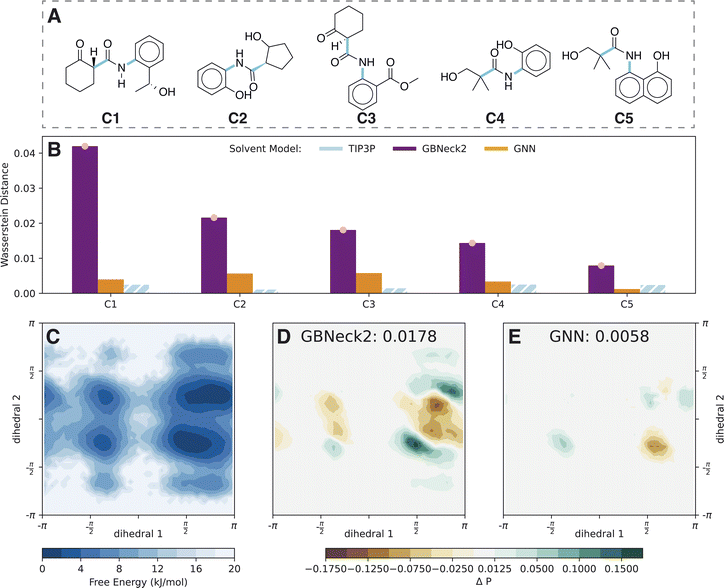
The low RMSE on the external test set indicates that the model is transferable between different sets of compounds. However, recently it was discovered that accurate force predictions on a test set do not necessarily correlate with accurate and stable simulations.26 Hence, the GNN is further evaluated by performing prospective MD simulations of compounds not included in the training set. While we trained three models per architecture with different initialisation to assess the variance in the previous section, a single GNN is used to carry out the simulations, mimicking how the approach would be used in practice. To be conservative, we chose the model with the highest external test set RMSE for this. Note that we have repeated the computational experiments with the other two models and the results are qualitatively equivalent (see Fig. S14–S21 in the ESI†).For a quantitative assessment, the underlying probability distributions of the free-energy profiles of the implicit solvent models (Fig. S3 in the ESI†) were compared to the TIP3P reference using the Wasserstein distance28 (Fig. 2D). The Wasserstein distance has its origins in optimal transport and calculates the cost of transforming one probability distribution into another, i.e., the lower the distance the more similar the two distributions are. To exclude differences due to finite sampling, we checked the convergence of the Wasserstein distance (see Fig. S3 in the ESI†). Compounds I8 and I13 showed non-converged results and hence both simulations were elongated by 10-fold. Even with the extended simulation time, these issues persisted for compound I13 with respect to a second intramolecular hydrogen bond of the carboxy group. For a fair comparison, the free-energy profiles and corresponding probability distributions were only analyzed for the more populated state of intramolecular hydrogen bonds within the carboxy group of distance <0.27 nm. To assess the variance within explicit-solvent simulations, the reference TIP3P simulation was divided into two parts and the Wasserstein distance between the first half and the second half of the simulation was calculated (blue bars in Fig. 2D). For all molecules in set I, the GNN approach outperforms the GB-Neck2 model with significantly smaller Wasserstein distances.
A good example for the observed differences is compound C3, for which the 2D probability distribution along the two central torsional angles is shown in Fig. 3C. The difference plots in probability distributions are shown in Fig. 3D and E for the GB-Neck2 and GNN models, respectively. While there are only minor differences for the GNN, the GB-Neck2 model systematically shifts the distribution of dihedral 2 closer to 0 rad. In addition, the asymmetric nature of the two global minima is only captured by the GNN model.
2.3 Effective sampling rates
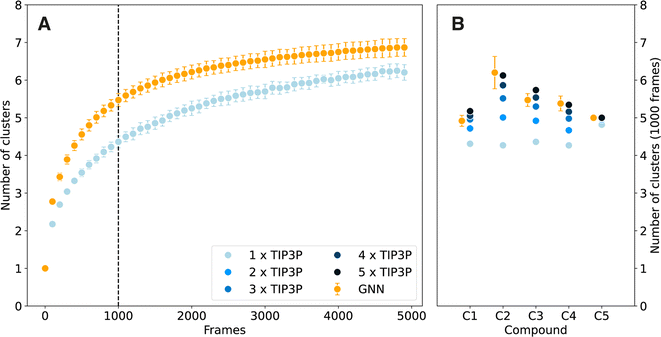
The analyses above indicate that the GNN model is capable of generating results on par with TIP3P explicit solvation, making it a valuable tool to study solvation effects in water at lower computational costs. In addition to a (dramatic) reduction of the number of degrees of freedom in the system with implicit solvation, the effective sampling rate of such a simulation should be higher due to a smoothing of the free-energy surface. In order to study and quantify this effect, the speed at which the conformational space is explored was compared for the GNN and TIP3P simulations of set C. For this, the conformations were clustered for each compound using the energy based clustering (EBC) algorithm,29 and the number of unique clusters found after a given number of simulation frames (write-out frequency every 100 simulation steps) served as a metric for sampling speed. The clustered free-energy surfaces as well as the cluster assignments are shown in Fig. S5–S9 in the ESI.† For all five compounds, the GNN simulations visit more clusters within the same number of frames as the TIP3P explicit solvent model. This is shown for compound C3 in Fig. 4A and for compounds C1, C2, C4, and C5 in Fig. S10–S13 in the ESI.† The difference in the effective sampling rate of the GNN relative to the TIP3P model can be quantified by artificially increasing the speed of the TIP3P simulations (i.e., an effective speed-up by factors of 2, 3, 4, and 5 was achieved by constructing new trajectories considering every second, third, fourth, and fifth frame of the TIP3P simulation, respectively). Fig. 4B summarizes these results for the five compounds, showing the average number of visited clusters after 1000 frames (indicated by the vertical dashed line in Fig. 4A). The achieved effective sampling speed-up for the GNN implicit solvent model over the reference TIP3P simulations ranges from a factor of 3 to 5 depending on the studied system. Interestingly, the increase in effective sampling rate is highest for compounds C2 and C4, which feature the largest barriers to cross. This observation is in line with the findings by Anandakrishnan et al.,30 who observed that implicit solvent simulations exhibit a higher increase in effective sampling rate compared to explicit solvent simulations as the magnitude of the conformational flexibility increases. This may present a further benefit of the GNN approach as overcoming the highest energy transitions faster is especially desirable. In this context, it is noteworthy that this increase in effective sampling rate by approximately a factor of 4 is on top of the lower computational cost of the GNN (by a factor of 4.4). As the two factors are multiplicative, an overall increase in sampling speed of approximately 18-fold is achieved.3 Conclusions
In this study, we presented a novel ML approach to learn the mean solvation energies and forces exerted on small molecules by water using a GNN trained on a large dataset of mean explicit solvent forces containing 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208
208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 data points for chemically diverse organic molecules. The resulting ML model reaches the accuracy of explicit solvent reference simulations both in terms of reproducing reference forces of an external test set as well as conformational sampling in prospective MD simulations. The high transferability and an overall effective sampling speed-up of 18-fold compared to explicit solvent simulations allow the GNN to be used in practice as a general ML-based implicit solvent model for small organic molecules, the first of its kind. The approach is easy to use as it can be integrated into the commonly used OpenMM software package for MD simulation and only requires default OpenMM functions for parametrizing novel compounds. All data and source code are made freely available. In the future, we will employ the GNN in practical applications and expand the approach to other solvents as well as force-field representations (e.g., polarizable force fields).
720 data points for chemically diverse organic molecules. The resulting ML model reaches the accuracy of explicit solvent reference simulations both in terms of reproducing reference forces of an external test set as well as conformational sampling in prospective MD simulations. The high transferability and an overall effective sampling speed-up of 18-fold compared to explicit solvent simulations allow the GNN to be used in practice as a general ML-based implicit solvent model for small organic molecules, the first of its kind. The approach is easy to use as it can be integrated into the commonly used OpenMM software package for MD simulation and only requires default OpenMM functions for parametrizing novel compounds. All data and source code are made freely available. In the future, we will employ the GNN in practical applications and expand the approach to other solvents as well as force-field representations (e.g., polarizable force fields).
4 Methods
4.1 Molecular dynamics simulations
Starting coordinates for molecules were generated using the ETKDG conformer generator31 as implemented in the RDKit.32 The OpenFF 2.0.0 force field33 was used to parametrize the compounds. All simulations were carried out using the OpenMM (version 8.0.0) simulation program.34 For the explicit solvent simulations, the solutes were solvated with the TIP3P water model35 in a box with a padding of 1 nm using the PACKMOL program.36 Energy minimization was performed using the L-BFGS algorithm37 with a tolerance of 10 kJ mol−1 nm−1. The SETTLE38 and CCMA39 algorithms were used to constrain all bonds involving hydrogens for water and intramolecular bonds, respectively. All simulations were carried out under Langevin dynamics using the LFMiddle discretization scheme,40 a Monte Carlo barostat with a reference pressure of 1 bar, a reference temperature of 300 K, and a time step of 2 fs. Explicit solvent simulations were performed with a particle mesh Ewald (PME) correction41 above a non-bonded cutoff of 1 nm.4.2 Generation of the training and test sets
The molecules for the training set were taken from the DASH dataset.21 The external test set was generated by drawing 1000 compounds at random from the QMUGS dataset42 ensuring a molecular weight between 500 Da and 700 Da. The generation of the forces follows the general procedure described in ref. 12. For each molecule, three conformers were generated using the ETKDG conformer generator31 as implemented in the RDKit.32 These conformations were solvated and an explicit solvent simulation of 500 ps length was performed under NPT conditions. From this simulation, snapshots were extracted after 180 ps, 340 ps, and 500 ps. These snapshots served as starting coordinates for new simulations of 200 ps length where the solute was positionally restrained. For each solute atom, the forces exerted by the solvent on the solute were averaged (write-out frequency of 200 fs). The mean forces were not further modified (e.g., to make them translationally invariant). Note that not all compounds could be parametrized using the OpenFF force field and some simulations were unstable. Those compounds were excluded from the study as no mean forces could be extracted. The final data set is available at the ETH Research Collection (https://www.research-collection.ethz.ch/handle/20.500.11850/667722).4.3 Graph neural networks
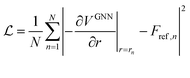
The core of the GNN was implemented as described in ref. 12 with the addition of the multitask SA term shown in eqn (1). During optimization, a random selection of 95% of all data points were used for training and the remaining 5% for validation. The GNN was trained for 30 epochs with a batch size of 32 and an exponentially decaying learning rate starting at 0.0005 and decaying to 0.000005. Gradients were clipped using a maximum norm of 1.0 and a norm type of 2. The Adam optimiser43 was chosen for optimizing the network with the mean squared error (MSE) between the predicted forces and the explicit solvent reference forces Fref as a loss function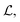
 | (2) |
4.4 Prospective molecular dynamics simulations
The OpenMM-Torch package (version 1.0, https://github.com/openmm/openmm-torch) was used to introduce the GNN on top of the vacuum Hamiltonian. The non-bonded forces were re-implemented using the OpenMM-Custom Forces classes for running multiple replicates of the system in parallel using one GNN. For the benchmarking of the GNN speed, compound C3 was simulated with a replica size of 256 to optimize the simulation speed on the RTX 3090 GPU. The prospective simulations were carried out in 128 replicates to also allow the usage of GPUs with lower VRAM such as the RTX 1080TI or the RTX 2080TI. Note that while the replicates are of the same molecule in this study, they do not need to be and also 128 different molecules could be studied in one go. Explicit solvent TIP3P and GB-Neck2 simulations were performed for 500 ns. GNN simulations of each replicate for the molecules in set I and set C were carried out for 5 ns and 10 ns, respectively.4.5 Data analysis
For analyzing the trajectories, MDTraj (version 1.9.7)44 was used. The probability distributions for intramolecular hydrogen bond pairs or torsional angles were calculated by a histogram analysis. The free-energy profiles were than estimated using direct counting. For the atom–atom distances, a Jacobian correction factor of 4πr2 was applied.45 The Wasserstein distances were calculated using the Python Optimal Transport library46 and the SciPy library47 for two-dimensional and one-dimensional distributions, respectively.Data and software availability
The code used to perform this study is open source and available on GitHub (https://github.com/rinikerlab/GNNImplicitSolvent). The training and test sets for the GNN are freely available at the ETH Research Collection (https://www.research-collection.ethz.ch/handle/20.500.11850/667722). Trajectories are available upon reasonable request from the corresponding author.Author contributions
P. K.: conceptualization, data generation and curation, methodology, software, validation, visualization, writing – original draft. S. R.: conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank ETH Zurich for financial support (Research Grant No. ETH-50 21-1), Philippe H. Hünenberger for interesting discussions, and Felix Pultar for reviewing the provided data and code.References
- T. Hansson, C. Oostenbrink and W. F. van Gunsteren, Curr. Opin. Struct. Biol., 2002, 12, 190–196 CrossRef CAS.
- J. Mortier, C. Rakers, M. Bermudez, M. S. Murgueitio, S. Riniker and G. Wolber, Drug Discovery Today, 2015, 20, 686–702 CrossRef CAS.
- J. B. Metternich, P. Katzberger, A. S. Kamenik, P. Tiwari, R. Wu, S. Riniker and R. Zenobi, J. Phys. Chem. A, 2023, 127, 5620–5628 CrossRef CAS.
- D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. A. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346 CrossRef CAS.
- T.-S. Lee, D. S. Cerutti, D. Mermelstein, C. Lin, S. LeGrand, T. J. Giese, A. Roitberg, D. A. Case, R. C. Walker and D. M. York, J. Chem. Inf. Model., 2018, 58, 2043–2050 CrossRef CAS.
- A. S. Kamenik, S. M. Linker and S. Riniker, Phys. Chem. Chem. Phys., 2022, 24, 1225–1236 RSC.
- B. Roux and T. Simonson, Biophys. Chem., 1999, 78, 1–20 CrossRef CAS.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS.
- S. S. Mohamed Mahmoud, G. Esposito, G. Serra and F. Fogolari, Bioinformatics, 2020, 36, 1757–1764 CrossRef.
- D. Horvath, G. Marcou and A. Varnek, J. Chem. Inf. Model., 2020, 60, 2951–2965 CrossRef CAS.
- Y. Chen, A. Krämer, N. E. Charron, B. E. Husic, C. Clementi and F. Noé, J. Chem. Phys., 2021, 155, 084101 CrossRef CAS.
- P. Katzberger and S. Riniker, J. Chem. Phys., 2023, 158, 204101 CrossRef CAS.
- J. Airas, X. Ding and B. Zhang, ACS Cent. Sci., 2023, 9, 2286–2297 CrossRef CAS.
- H. Nguyen, D. R. Roe and C. Simmerling, J. Chem. Theory Comput., 2013, 9, 2020–2034 CrossRef CAS.
- N. A. Baker, Curr. Opin. Struct. Biol., 2005, 15, 137–143 CrossRef CAS.
- U. Haberthür and A. Caflisch, J. Comput. Chem., 2007, 29, 701–715 CrossRef.
- C. W. Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127–6129 CrossRef.
- M. Schaefer and M. Karplus, J. Phys. Chem., 1996, 100, 1578–1599 CrossRef CAS.
- E. J. M. Lang, E. G. Baker, D. N. Woolfson and A. J. Mulholland, J. Chem. Theory Comput., 2022, 18, 4070–4076 CrossRef CAS.
- R. Galvelis, A. Varela-Rial, S. Doerr, R. Fino, P. Eastman, T. E. Markland, J. D. Chodera and G. D. Fabritiis, J. Chem. Inf. Model., 2023, 63, 5701–5708 CrossRef CAS.
- M. T. Lehner, P. Katzberger, N. Maeder, C. C. G. Schiebroek, J. Teetz, G. A. Landrum and S. Riniker, J. Chem. Inf. Model., 2023, 63, 6014–6028 CrossRef CAS.
- M. L. Sanchez, M. A. Aguilar and F. J. O. del Valle, J. Comput. Chem., 1997, 18, 313–322 CrossRef CAS.
- D. M. Nikolaev, M. Manathunga, Y. Orozco-Gonzalez, A. A. Shtyrov, Y. O. G. Martínez, S. Gozem, M. N. Ryazantsev, K. Coutinho, S. Canuto and M. Olivucci, J. Chem. Theory Comput., 2021, 17, 5885–5895 CrossRef CAS.
- S. Yao, R. Van, X. Pan, J. H. Park, Y. Mao, J. Pu, Y. Mei and Y. Shao, RSC Adv., 2023, 13, 4565–4577 RSC.
- B. Knapp, L. Ospina and C. M. Deane, J. Chem. Theory Comput., 2018, 14, 6127–6138 CrossRef CAS.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. Jaakkola, Forces are not Enough: Benchmark and Critical Evaluation for Machine Learning Force Fields with Molecular Simulations, arXiv, 2022, preprint, arXiv:2210.07237, DOI:10.48550/arXiv.2210.07237.
- D. L. Mobley and J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 711–720 CrossRef CAS.
- L. N. Vaserstein, Probl. Peredachi Inf., 1969, 5, 64–72 Search PubMed.
- M. Thürlemann and S. Riniker, J. Chem. Phys., 2023, 159, 024105 CrossRef.
- R. Anandakrishnan, A. Drozdetski, R. C. Walker and A. V. Onufriev, Biophys. J., 2015, 108, 1153–1164 CrossRef CAS.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS.
- Open-source cheminformatics toolkit, 2022.09.1 (Q3 2022) Release, 2022, http://www.rdkit.org, accessed: April 12, 2024.
- S. Boothroyd, P. K. Behara, O. C. Madin, D. F. Hahn, H. Jang, V. Gapsys, J. R. Wagner, J. T. Horton, D. L. Dotson, M. W. Thompson, J. Maat, T. Gokey, L.-P. Wang, D. J. Cole, M. K. Gilson, J. D. Chodera, C. I. Bayly, M. R. Shirts and D. L. Mobley, J. Chem. Theory Comput., 2023, 19, 3251–3275 CrossRef CAS.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- P. Eastman and V. S. Pande, J. Chem. Theory Comput., 2010, 6, 434–437 CrossRef CAS.
- Z. Zhang, X. Liu, K. Yan, M. E. Tuckerman and J. Liu, J. Phys. Chem. A, 2019, 123, 6056–6079 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- C. Isert, K. Atz, J. Jiménez-Luna and G. Schneider, Sci. Data, 2022, 9, 273 CrossRef CAS.
- D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, arXiv, 2014, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS.
- D. R. Herschbach, H. S. Johnston and D. Rapp, J. Chem. Phys., 1959, 31, 1652–1661 CrossRef CAS.
- R. Flamary, N. Courty, A. Gramfort, M. Z. Alaya, A. Boisbunon, S. Chambon, L. Chapel, A. Corenflos, K. Fatras, N. Fournier, L. Gautheron, N. T. Gayraud, H. Janati, A. Rakotomamonjy, I. Redko, A. Rolet, A. Schutz, V. Seguy, D. J. Sutherland, R. Tavenard, A. Tong and T. Vayer, J. Mach. Learn. Res., 2021, 22, 1–8 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc02432j |
| This journal is © The Royal Society of Chemistry 2024 |