Tuning the magnetic properties of van der Waals materials by intercalation

Abstract

Recent advances in low-dimensional spintronic devices have resulted in an increased demand for layered van der Waals materials with tunable magnetic properties. To this end, intercalation – the insertion of a guest species in the van der Waals gap between the planes of the host material – proves to be a versatile tool. In this review, we discuss various forms of intercalation that allow for tuning the magnetic properties of van der Waals materials. We focus on alkali metal, transition metal and molecule intercalation, and provide an extensive overview of current research efforts. Furthermore, we highlight typical challenges that materials scientists face in this field, and provide suggestions for future research directions.

---

1 Introduction

Since the discovery of graphene in 2004,¹ two-dimensional (2D) materials have gathered a lot of interest from the solid-state community.^2–6 In particular, magnetic van der Waals (vdW) materials were sought after, as these could provide a platform for studying magnetism in the 2D limit, when cleaved to monolayer thickness, and could find applications in spintronic devices.^6,7 The first example of long-range magnetic order observed in an atomically thin material was introduced in 2016 by Lee et al., who reported stable antiferromagnetic order in a monolayer of FePS₃, observed through Raman measurements.⁸ This was quickly followed in 2017 by the direct observation of spontaneous magnetization in single layer Cr₂Ge₂Te₆⁹ and CrI₃.^10,11

In addition to studying magnetism in the 2D limit by means of exfoliation, magnetic vdW materials form the ideal template to develop low-dimensional spintronic applications.¹² In these low-dimensional devices, the interlayer magnetic coupling is of utmost importance to the magnetic properties. However, it remains a challenge to not only understand, but also manipulate this magnetic coupling between neighbouring layers to achieve desired properties for these spin-based electronic applications. In recent years, numerous candidate magnetic vdW materials have been reported, including those based on transition metal halides,^13–16 transition metal chalcogenides,^17–19 transition metal phosphorus chalcogenides,^20–22 and metal oxy- and chalcohalides.^23–27 Despite this rapidly growing library of magnetic vdW materials, relatively few layered materials with room temperature magnetic order have been reported, despite this being a requirement for several applications.^28,29

Therefore, there is a crucial need for tuning the magnetic properties of vdW materials, enabling novel magnetic ordering above room temperature, and expanding the library of magnetic materials. Materials chemists will play a pivotal role in this development, by providing the tools to tune magnetism in vdW materials.

Among strategies to modify the properties of vdW materials, intercalation has become one of the most widely used.^30,31 In general, intercalation of layered materials is the post-synthetic, reversible process of inserting a foreign ion, atom or molecule in the vdW gap between the layers of the host lattice, as schematically illustrated in Fig. 1.^32,33 Intercalation is exploited in a wide range of energy storage technologies, spanning from batteries to supercapacitors,^34–40 and is a powerful tool for modifying the properties of the host material.³⁰ The insertion of an intercalant into the interlayer gap, i.e. the vdW gap, results in an increased interlayer distance, generally reducing the interlayer interaction and making the material “more 2D”. The introduction of a new species also typically results in doping of the host lattice, and new interaction pathways in the material. Consequently, intercalation is a powerful and versatile tool for tuning the properties of materials. For example, intercalation has been used to tune and/or induce superconductivity,^41–47 charge density waves,^47–49 and to tune the bandgap,^50–52 thermoelectric properties,^53–56 and increasingly, the magnetic properties of vdW materials.

Fig. 1 Schematic illustration of intercalation of vdW materials. The purple spheres represent the intercalants. Upon intercalation, the interlayer distance d₁ increases (d₂ > d₁).

In this review, we focus on tuning the magnetic properties of vdW materials by means of intercalation by highlighting current advances and provide challenges for materials scientists to enhance the field. First, we will discuss common forms of intercalation to tune the magnetic properties of materials, sorted by intercalant type. After that, we will provide challenges for materials scientists and suggestions for future research directions.

2 Types of intercalants

A wide range of intercalants have been used to tune the magnetic properties of vdW materials, ranging from simple monovalent cations to complex intercalants endowing the intercalated host lattice with new properties. In Table 1, we list several examples of such magnetic vdW materials that are tuned by means of intercalation. Note that the table only contains experimental data. Here we will discuss the three most common forms of intercalation currently used to tune magnetic properties in vdW materials: alkali metal intercalation, transition metal intercalation and molecule intercalation. For each method, we will start by briefly outlining the chemical process of intercalation, followed by its effect on the magnetic properties of the vdW materials.

Table 1 Examples of tunable magnetic properties observed in vdW materials by means of different intercalation methods

Compound	Method^a	Order^b	T c (K)	Ref.
a Chemical (Chem.), electrochemical (E. chem.), ion exchange (ion exch,) and as grown from the elements (AS). b Ferromagnetic (FM), antiferromagnetic (AFM), ferrimagnetic (FiM) and chiral helimagnetic (CHM). c (approximate) magnetic ordering temperature. d This range in Tc depends on the exact amount of Fe in the compound.
Fe2GeTe3	—	FM	220–230^d	57 and 58
LixFe2GeTe3	E. chem.	FM	300	58
(TBA)xFe2GeTe3	E. chem.	FM	300	59
Cr2Ge2Te6	—	FM	67	9
NaxCr2Ge2Te6	Chem.	FM	240	60
(TBA)xCr2Ge2Te6	E. chem.	FM	208	61
NiPS3	—	AFM	155	62
(TBA)0.25NiPS3	E. chem.	FiM	78	63
[Co(Cp)2]0.25NiPS3	Ion exch.	FiM	98	63
NbS2	—	—	—
Fe0.25NbS2	AS	AFM	145	64
Fe0.33NbS2	AS	AFM	45	65
Cr0.33NbS2	AS	CHM	127	16, 66 and 67
TaS2	—	—	—
Fe0.25TaS2	AS	FM	160	68 and 69
Fe0.33TaS2	AS	FM	38	68 and 70
Cr0.33TaS2	AS	CHM	142	71
CrTe2	—	FM	310	72
Cr2Te3 (Cr1.33Te2)	AS	FM	180	73
Cr3Te4 (Cr1.5Te2)	AS	FM	320	73 and 74
CrI3	—	FM	61	10, 11 and 75
CrSBr	—	AFM	132	26, 27 and 76

---

2.1 Alkali metal intercalation

Alkali metals are typically intercalated using chemical or electrochemical methods. Of the chemical procedures, the most widely used methods are low-temperature intercalation using an alkali metal ammonium solution,^60,77–80 and high-temperature intercalation using organometallic reagents.^81–87 Of the organometallic reagents, n-butyllithium (n-BuLi) is the most commonly used Li⁺ intercalant for its high reduction potential.^80–83 Intercalation using n-BuLi is typically realised by immersing the vdW material in stoichiometric n-BuLi hexane under inert atmosphere, and stirring at 100 °C for around 2–3 days. The relatively long reaction time, need for inert atmosphere, and highly flammable nature of n-BuLi motivated chemists to look for alternatives to this method. To this end, Li-intercalation has also been achieved using lithium borohydride (LiBH₄),⁸⁴ naphthalenide lithium (Nap-Li),⁸⁸ and pyrene lithium (Py-Li).⁸⁵ Note that other alkali metals have been intercalated with various degrees of success using analogous organometallic compounds.^88,89

Electrochemical intercalation can be achieved using an electrochemical cell with a metal anode (e.g. Li) and the host vdW material as cathode, separated by an ionically conducting electrolyte.^58,90–94 The electrochemical intercalation process allows for controlling the intercalation by adjusting the magnitude and polarity of the applied voltage as well as the duration. Moreover, deintercalation can be readily realised by applying the opposite bias, allowing for precise control of the degree of intercalation. The voltage window in which intercalation can occur is determined by the host compound, the electrolyte and the concentration of the intercalant. At more extreme voltages, decomposition can occur. Furthermore, depending on the precise reaction, high degrees of intercalation may only be achieved in an inert atmosphere, requiring a more complex method than chemical intercalation techniques.

2.1.1 Charge doping through alkali metal intercalation. Of the three different types of intercalants discussed in this review, alkali metals are generally the least complex. Alkali cations do not induce magnetic order in nonmagnetic vdW materials, but can be used to tune the magnetic properties of magnetic vdW materials.^{58,60,83,95–100} Notably, in most cases, intercalation is found to increase the T_C of the material.

The strength of alkali metal intercalation is exemplified by the work of Deng et al., who reported intercalation-dependent ferromagnetism in few-layer Fe₃GeTe₂,⁵⁸ one of the most promising materials for spintronic applications due to its metallicity. Note that Fe₃GeTe₂ is prone to Fe deficiency and often written as Fe_3-xGeTe₂ instead, but we will here use Fe₃GeTe₂ to indicate this family of compounds, as often done in literature as well. Deng et al. demonstrated that while the T_C of Fe₃GeTe₂ decreases drastically when the number of layers is reduced (see Fig. 2(a)), intercalation with Li gives rise to a sharp increase in T_C, even exceeding that of the bulk sample. This was achieved by intercalating trilayer Fe₃GeTe₂ crystal flakes with Li ions through an ionic gate configuration, where a gate voltage V_g was used to intercalate the Li ions into the flakes, akin to charging in Li-ion batteries. As shown in Fig. 2(b), Li intercalation using a small V_g causes a decrease in T_C, but a sharp increase up till room temperature is observed for optimal V_g. Intercalating beyond this point again decreases the T_C.⁵⁸

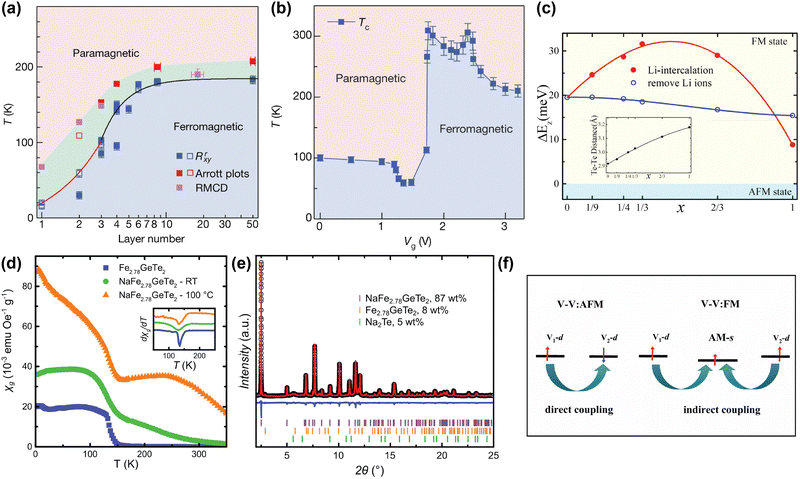Fig. 2 (a) Magnetic phase diagram of Fe₃GeTe₂ as function of number of layer and temperature. T_C values determined from anomalous Hall measurements (R^r_xy), Arrott plots, and refractive magnetic circular dichroism (RMCD), are displayed in blue, red and magenta respectively.⁵⁸ (b) Magnetic phase diagram of trilayer Fe₃GeTe₂ flakes as function of gate voltage (V_g) and temperature. A higher V_g corresponds to a higher degree of Li intercalation. The T_C values were determined from temperature-dependent anomalous Hall measurements, extrapolated to zero.⁵⁸ (c) Calculated interlayer magnetic coupling energy (ΔE_z) in Li_xFe₃GeTe₂ bilayers as function of intercalation level x. The inset displays the calculated interlayer distance between the two interfacial Te sublayers.⁹⁵ (d) Temperature dependence of the specific magnetic susceptibility χ_g of pristine Fe_2.78GeTe₂ (blue squares), Na-intercalated Fe_2.78GeTe₂ (green circles), and Na-intercalated Fe_2.78GeTe₂ annealed at 100 °C (orange triangles), measured at 0.01 T. The inset shows the derivative of χ_g, indicating a T_C of ∼140 K for all three samples.⁹⁶ (e) Rietveld refinement of NaFe_2.78GeTe₂ (λ = 0.412852 Å), including reflections of unreacted Fe_2.78GeTe₂ (orange) and Na₂Te (green).⁹⁶ (f) Schematic plot of the change in the magnetic exchange mechanism from direct (left) to indirect (right) exchange, in alkali-intercalated VS₂ and VSe₂.⁹⁷ Reproduced from ref. 97. Reproduced from ref. 58 with permission from Springer Nature, copyright 2018. Reprinted from ref. 95, with the permission of AIP Publishing, copyright 2021. Reprinted with permission from ref. 96. Copyright 2021 American Chemical Society.

This remarkable find was supported by first-principle calculations from Huang et al., who suggested that with increasing amount of Li intercalation in Fe₃GeTe₂, and the associated electron doping of the host lattice, the ferromagnetic interlayer coupling is increased.⁹⁵ However, past a certain doping concentration, this interlayer coupling decreases again (see Fig. 2(c)). This is hypothesised to result from two competing factors: firstly, the intercalated Li ions allow for hopping of charge carriers, resulting in an indirect exchange between the Fe₃GeTe₂ layers that strengthens the interlayer coupling. This becomes particularly apparent at low intercalant concentrations; secondly, at high Li concentrations, the electron transfer from the Li ions to the Fe₃GeTe₂ layers fills the previously unfilled 3d orbitals of the Fe ions, thereby reducing the ferromagnetic coupling.⁹⁵

Although Huang et al. were able to model the experimentally observed T_C-increase of Fe₃GeTe₂ upon Li intercalation, reported by Deng et al., the observed initial decrease of T_C is not consistent with this model.^58,95 Shen et al. further investigated this observation by calculating the effect of the electron doping on Fe₃GeTe₂ monolayers using first-principle calculations.¹⁰¹ At low levels of electron doping, they observed a decrease in T_C from 159 K in undoped Fe₃GeTe₂ to 93 K, whereas at higher doping, the T_C increases to 175 K. They hypothesise that the electron doping might tune frustrated intralayer exchange interactions, resulting in the observed evolution of T_C.¹⁰¹ However, as their calculations were performed on monolayer Fe₃GeTe₂, no interlayer interactions or intercalants were included, making it difficult to directly compare these findings to the results reported by Deng et al.

Interestingly, Khan et al. recently reported on how electron doping by intercalation of alkali metals can also result in a magnetically-disordered compound.⁶⁰ They inhomogeneously intercalated Cr₂Ge₂Te₆ with Na ions, resulting in a magnetically frustrated state around 35 K, which is not present in pristine Cr₂Ge₂Te₆. They argue that electron doping through intercalated Na ions alters the ionic states of some of the Cr³⁺ ions into Cr²⁺, resulting in a double exchange mechanism.⁶⁰ The authors also hypothesise that since Cr²⁺ is a Jahn–Teller active ion, its substitution for Cr³⁺ leads to local distortions, increasing local anisotropy and possibly enhancing the spin glass behaviour.

2.1.2 Structural effects of alkali metal intercalation. Besides the possible charge doping described above, alkali metal intercalation also has a strong effect on the structure of the host material and can cause decomposition. For example, Weber et al. explored the structural effects of Na intercalation in Fe₃GeTe₂.⁹⁶ They used Na instead of Li, as it is easier to detect using X-ray diffraction methods. In contrast to Deng et al., who intercalated Fe₃GeTe₂ electrochemically, Weber et al. used metallic sodium and benzophenone (Ph₂CO) to intercalate Na into Fe₃GeTe₂. As a result, they found that the Fe₃FeTe₂ layers become heavily charge-doped and strained via chemical pressure, yet retain their crystal structure. Surprisingly, in great contrast to the Li intercalation discussed above, the intercalation with Na does not affect the ordering temperature, maintaining it at ∼140 K (see Fig. 2(d)). The main difference with pristine Fe₃GeTe₂ is that the intercalated samples displayed magnetisation above T_C, and even at room temperature. This was attributed to the presence of the defects after Na intercalation. Synchrotron radiation measurements revealed that intercalation had caused some decomposition of the host lattice, resulting in the formation of Na₂Te and amorphous Fe_2-xGe phases (see Fig. 2(e)). As a result, they concluded that the nonzero magnetisation at 300 K could be explained by the presence of ferromagnetic Fe₂Ge, as well as undetected Fe.⁹⁶ The authors noted that despite the heavy charge doping of 6.95 × 10¹⁴ e⁻ cm⁻² per Fe₃GeTe₂ layer, this did not result in any significant change in T_C, in sharp contrast to other studies on alkali metal intercalation of Fe₃GeTe₂. The reason for this could be the difference in intercalation-induced strain in the structure, caused by Li and Na, as intercalation does not only affect the spin density through electron doping, but also the inter- and intralayer bond length and angles, thereby also affecting the magnetic exchange interactions.^90,96

Alkali metal intercalation studies typically limit themselves to the use of Li and Na as intercalants, as the larger K and Rb would further increase the interlayer distance, decreasing the interlayer coupling. However, in certain cases, the larger vdW gap created by intercalation of larger alkali metals is beneficial for the magnetic properties of the host lattice, especially in those that contain competing interlayer and intralayer interactions. Intercalation with alkali metals can then tip the balance between these two interactions to favour the intralayer interaction, which can in turn change the type of magnetic order.^{17,97,102,103} An example to illustrate this is VX₂ (X = S, Se), which is paramagnetic in the bulk, but DFT calculations predicted that it exhibits ferromagnetic intralayer ordering in the monolayer limit.^102,103 This prediction was experimentally verified for VSe₂ by Bonilla et al.¹⁷ In more general terms, these VX₂ (X = S, Se) systems have direct exchange between the layers that can result in antiferromagnetic coupling, but by intercalation of a large alkali metal such as K or Rb, the interlayer coupling can be switched from antiferromagnetic to ferromagnetic.⁹⁷ The explanation for this is that when alkali metals are introduced into the vdW gap, their s-orbitals can become slightly magnetised by the surrounding magnetic ions through Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions (see Fig. 2(f)). This slight magnetisation then enables the indirect interlayer coupling mediated by the alkali metal ions.

2.2 Transition metal intercalation

Unlike alkali metals, which are exclusively intercalated as cations, transition metals can be intercalated as zerovalent or as cationic species. The intercalation of zerovalent atoms is typically referred to as atom intercalation, to distinguish it from ion intercalation.

A large number of zerovalent transition metals and post-transition metals (Ag, Au, Bi, Co, Cr, Cu, Fe, Ge, Hg, In, Mo, Mn, Ni, Os, Pb, Pd, Pt, Rh, Ru, Sb, Sn, W)^104–113 have been intercalated into vdW compounds, using a variety of reactions, including disproportionate redox reactions,^104–107 decomposition of coordination compounds,^{104–106,109} stannous chloride (SnCl₂) reduction,¹⁰⁴ hydrazine reduction,¹⁰⁷ and liquid metal immersion.^110,111 Electrochemical intercalation of transition metals is not as widely reported as chemical methods, as moving heavy metals electrochemically is much more difficult compared to moving alkali metals.

As charge transfer is often hypothesised to contribute to any change in magnetic properties of transition-metal-intercalated vdW materials, ion intercalation is often used. Note that aside from the chemical post-synthetic methods listed above, and possible solid state reactions between the host material and elemental intercalants,¹¹⁴ transition metal intercalated materials are often synthesised from their constituent elements.^66,69 While this technically does not qualify as a form of intercalation, the obtained products can be regarded as ‘intercalated products’. Therefore, we purposely chose to include these materials in this review.

Note that despite the large range of possibilities, transition metal intercalation with the aim of tuning the magnetic properties has almost exclusively focused on 3d metals, especially Fe and Cr, due to their strong magnetic moments.

2.2.1 Tuning magnetism by self-intercalation of magnetic vdW materials. Besides the intercalation of foreign atoms into the vdW gap, the intercalation of native atoms, i.e. those that are already present in the vdW material, is particularly interesting. The power of such self-intercalation is well demonstrated by CrTe₂. By intercalating Cr atoms into the vdW gap between the CrTe₂ layers, different chromium telluride compounds with chemical formula Cr_1+δ Te₂ (0 < δ ≤ 1) are formed (see Fig. 3(a)). This class of materials consists of a broad range of phases,^72,115–119 and shows a variety of interesting magnetic properties, including skyrmions,¹²⁰ biskyrmions,¹²¹ the magnetocaloric effect,¹²² and large anomalous Hall effect.^123,124 As shown in Fig. 3(b), a monotononic positive relationship between T_C and the Cr content has been established.^{72,117,125–128} Alongside this increase in T_C, a reorientation or isotropisation of magnetic anisotropy was reported. In CrTe₂, all spins are aligned ferromagnetically and out-of-plane with respect to the CrTe₂ layers. When self-intercalated, the magnetic moments of the intercalated Cr atoms tend to align antiferromagnetically with respect to the host layers, inducing noncollinearity (see Fig. 3(c)).^129,130 In general, the magnetic properties are mainly governed by a competition between antiferromagnetic Cr–Cr direct exchange and ferromagnetic Cr–Te–Cr superexchange.¹³¹ This self-intercalation introduces more spins into the system, enhancing the superexchange. Note that besides the introduction of additional spins, intercalation also leads to the formation of Cr–Te–Cr bonds, that have a bond angle of ∼132°, which is significantly larger than those of ∼90° in the host lattice, further enhancing the ferromagnetic coupling.¹³²

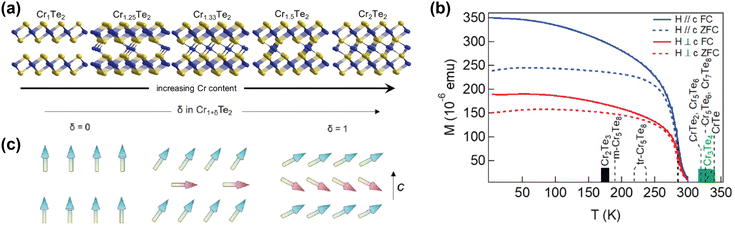Fig. 3 Self-intercalation of CrTe₂. (a) Crystal structures of CrTe₂ (Cr₁Te₂), Cr_1.25Te₂ (Cr₅Te₈), Cr_1.33Te₂ (Cr₂Te₃), Cr_1.5Te₂ (Cr₃Te₄) and Cr₂Te₂ (CrTe).⁷³ (b) Temperature-dependent magnetisation of Cr_1.5Te₂, also showing the ordering temperatures of various intercalation levels of CrTe₂.⁷³ (c) Schematic drawing of the expected evolution of the ground-state magnetic configuration of Cr_1+δTe₂, with the arrows indicating the local spins.¹³³ Reprinted with permission from ref. 73. Copyright 2021 American Chemical Society. Reprinted with permission from ref. 133. Copyright 2020 by the American Physical Society.

Computational studies have also shown that the magnetic properties of CrI₃ and FeCl₂, materials which have garnered a lot of interest from the solid state physics community,^{10,11,134–139} can be tuned using self-intercalation.¹⁴⁰ The self-intercalation of Cr into CrI₃ induces charge transfer from the intercalated Cr ions to the Cr atoms in the host lattice, changing the formal oxidation state of the latter from +3 in pristine CrI₃ to +2.67 in Cr-intercalated CrI₃.¹⁴⁰ This charge transfer induces a double exchange, resulting in an increased ferromagnetic coupling in Cr-intercalated CrI₃ compared to pristine CrI₃.¹⁴⁰

Similarly, the self-intercalation of Fe into FeCl₂ bilayers has shown to alter the interlayer coupling by charge transfer from the intercalated Fe ions to the host lattice.¹⁴¹ Pristine FeCl₂ exhibits strong ferromagnetic intralayer coupling, but antiferromagnetic interlayer coupling, both in its bulk form as in bilayer systems.^142,143 DFT calculations revealed that the interlayer coupling could be switched from antiferro- to ferromagnetic upon self-intercalation with Fe ions, as the intercalated ions donate charge to the host lattice, resulting in a mixed-valence system. This is responsible for altering the interlayer exchange mechanism from superexchange to double exchange, which favours antiparallel alignment.¹¹² Notably, this even occurs at low levels of Fe intercalation, as the charge transfer from intercalated Fe ions is larger at low concentrations. However, despite the ferromagnetic interlayer coupling not being dependent on the degree of intercalation, the magnetic anisotropy is strongly affected by the concentration of the intercalated Fe ions. For ≤25% Fe intercalation in FeCl₂, the magnetic anisotropy is directed in-plane, whereas for >25% Fe intercalation, the anisotropy switches to out-of-plane.¹⁴¹

2.2.2 Inducing magnetism by transition metal intercalation of nonmagnetic vdW materials. Aside from tuning inherent magnetic order in vdW materials, intercalation with transition metals is also suitable for inducing magnetic order in nonmagnetic host lattices. Good examples of this are the Fe and Cr intercalation of TaS₂ and NbS₂.^{66,69,71,144–147} At certain intercalant concentrations, crystallographic superlattices form by a periodic ordering of the intercalants in the octahedral interstitial sites. As shown in Fig. 4(a), superlattices form in Fe_xMS₂ and Cr_xMS₂ with M = Nb or Ta, for x = 1/4 and x = 1/3.¹⁴⁴ Due to the distances and bonding motifs between the intercalants in these materials, direct exchange and superexchange are not expected to contribute to the magnetic ordering. The RKKY interactions are considered to be the dominant exchange interaction driving the magnetic ordering.^148,149 Because Fe_xNbS₂, Fe_xTaS₂, Cr_xNbS₂ and Cr_xTaS₂ are all metallic, it is hypothesised that the localised Fe or Cr 3d electrons couple to the delocalised electrons in the conduction band. However, other studies suggest that the magnetic properties of these compounds are effected by the electronic structure in a manner that cannot be explained by just RKKY theory.^150,151

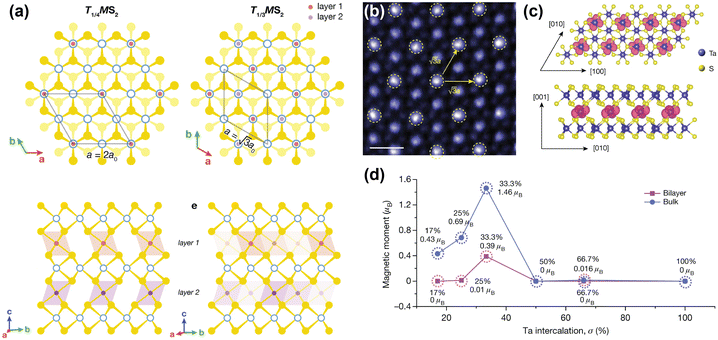Fig. 4 Inducing magnetic order through transition metal intercalation. (a) Superlattices of Fe_xMS₂ and Cr_xMS₂ with M = Nb or Ta, for x = 1/4 and x = 1/3.¹⁴⁴ (b) Atomic-resolution STEM–ADF (scanning transmission electron microscopy – angular dark field) image of self-intercalated Ta₇S₁₂, showing the superstructure of the intercalated Ta ions. The scale bar corresponds to 0.5 nm.¹⁵² (c) Top view (top) and side view (bottom) of the spin density isosurface of the intercalated Ta in Ta₇S₁₂.¹⁵² (d) Calculated magnetic moments as a function of Ta intercalation (σ) in TaS₂.¹⁵² Reprinted with permission from ref. 144. Copyright 2022 American Chemical Society. Reproduced from ref. 152 with permission from Springer Nature, copyright 2020.

Although Fe_xNbS2 and Fe_xTaS₂ are isostructural and isoelectronic, they exhibit different magnetic behaviours. For x < 0.4, Fe_xTaS₂ orders ferromagnetically whereas Fe_xNbS₂ orders antiferromagnetically, with an easy-axis along the c-axis. The magnetic properties of these intercalated species are very sensitive to small changes in composition, especially around the superlattice stoichiometry x = 1/3. At this stoichiometric x, the structures exhibit strong magnetic transitions,^{69,70,153,154} whereas off-stoichiometric Fe_xTaS₂ shows broadened magnetisation switching and large magnetoresistance,^68,155 and off-stoichiometric Fe_xNbS₂ shows spin glass behaviour and resistive switching.^145,153 The Fe stoichiometry affects the spacing between the magnetic intercalants, thereby altering the magnetic exchange interactions and spatial symmetry of these materials. At high intercalation amounts (x > 0.4), antiferromagnetic exchange interactions dominate,¹¹⁴ while at low intercalation amounts (0.2 ≤ x ≤ 0.4) long-range ferromagnetic ordering is observed.^68,156 The Curie temperature for Fe_xTaS₂ is at its maximum for x = 1/4, for which T_C ≈ 160 K, whereas for x = 1/3, T_C ≈ 38 K, demonstrating the clear difference in magnetic behaviour as a function of Fe content. In contrast to Fe_xTaS₂, Fe_xNbS₂ exhibits antiferromagnetic order at both x = 1/4 and x = 1/3, with T_N ≈ 145 K and T_N ≈ 45 K, respectively.^64,65 Most notably, the triangular sublattice formed by the intercalants results in the antiferromagnetic ground state being frustrated. These frustrated exchange interactions play an essential role in the formation of the off-stoichiometric spin glass phases.^157,158

Unlike their Fe-intercalated counterparts, Cr_xTaS₂ and Cr_xNbS₂ have their easy-axis in the ab-plane. The lack of inversion symmetry in these systems enables a Dzyaloshinskii–Moriya (DM) interaction that competes with the ferromagnetic ordering, resulting in spin-canting. As a result, both Cr_1/3TaS₂ and Cr_1/3NbS₂ exhibit chiral magnetic states.^66,159–161 The relative strength of this DM interaction increases when exchanging Nb for Ta, because of the increased spin–orbit coupling imparted by Ta compared to Nb. Consequently, the period of the chiral helimagnetic ground state, which is proportional to the ratio between the ferromagnetic exchange and DM interactions, is smaller in Cr_1/3TaS₂ compared to Cr_1/3NbS₂.^71,162 Thus, the interplay between different magnetic interactions results in these compounds having rich magnetic phase diagrams.^67,144,163

A remarkable find was made by Zhao et al., who reported that self-intercalation of Ta, a nonmagnetic intercalant, in nonmagnetic TaS₂ and TaSe₂ can induce magnetic ordering at certain stoichiometries.¹⁵² By intercalating 1/3 of Ta in TaS₂ (i.e. Ta₇S₁₂), a ferromagnetic state was observed. Herein, the intercalated Ta atoms form a superlattice similar to those reported for Fe_1/3MS₂ and Cr_1/3MS₂ (M = Nb, Ta), in which the intercalated Ta atoms bond with six S atoms to from octahedral units (see Fig. 4(b)). DFT calculations showed that this additional bonding induces a charge transfer from the octahedrally-coordinated intercalated Ta atoms to the prismatically-coordinated Ta atoms of the host lattice. This induces a spin-split band close to the Fermi level, and causes a ferromagnetic ground state to form.¹⁵² Hybridisation of the Ta 5d_z² orbital with the spin-up band of the 5d_x²−y² orbital of the intercalated Ta causes the formation of this ferromagnetic ground state, where the magnetic moments are localised on the 5d orbitals of the intercalated Ta ions (see Fig. 4(c) and (d)).¹⁵² Moreover, by intercalating 2/3 of Ta in TaSe₂ (i.e. Ta₈Se₁₂), a Kagome lattice forms, which stabilises charge-density waves. Temperature-dependent Hall measurements revealed an anomalous Hall effect below 15 K, confirming the presence of ferromagnetic order.¹⁵² This example again demonstrates the richness of induced physical phenomena that can be achieved by transition metal intercalation.

Furthermore, we note that despite the various reports on transition metal intercalation in transition metal dichalcogenides, little work has focused on intercalation of transition metals in other vdW magnets.

2.3 Molecule intercalation

In contrast to the above-mentioned alkali metal and transition metal intercalation, the use of molecular intercalants to tune the magnetic properties of vdW materials is relatively unexplored. However, molecules provide a particularly versatile platform for altering the properties of the host compound by means of intercalation, especially by tailoring the interlayer distance and charge density.¹⁶⁴

There are a few common methods employed to intercalate small molecules into vdW materials. The preferred method for alkylammonium cations is intercalation through electrochemical intercalation.^{59,61,63,165,166} For other molecular intercalants, a variety of chemical methods have typically been reported.^167–171 Another method of intercalation is post-intercalation ion exchange, in which the host compound is first intercalated with another, easy-to-intercalate intercalant that is then replaced by the desired intercalant.^63,172

2.3.1 Alkylammonium cation intercalation. As molecules are typically much larger than monoatomic intercalants, they tend to increase the interlayer distance much more. To this end, alkylammonium cations have been widely investigated.^{59,61,63,165,166} Wang et al. intercalated Cr₂Ge₂Te₆ with tetrabutylammonium (TBA) cations, which increased the interlayer distance from 6.8 Å to 16.48 Å, consistent with inserting a single TBA cation layer of ∼10 Å, without significantly influencing the in-plane lattice parameters.⁶¹ Moreover, as shown in Fig. 5(a), they observed a massive increase in T_C from 67 K in pristine Cr₂Ge₂Te₆ to 208 K in the TBA-intercalated compound. Besides this significant increase in T_C, TBA intercalation also changed the intrinsic magnetocrystalline anisotropy, reorienting the easy-axis from the c-axis in pristine Cr₂Ge₂Te₆ to lie in the ab-plane. In pristine Cr₂Ge₂Te₆, the spins mainly interact through 90° superexchange interactions via the Cr 3d_z² and Te 5p orbitals.^61,173,174 This results in weak ferromagnetic interlayer coupling and the easy-axis aligning with the c-axis due to spin–orbit coupling. DFT calculations on TBA-intercalated Cr₂Ge₂Te₆ showed that after intercalation, the Cr₂Ge₂Te₆ layers become electron-doped by the intercalant. These extra electrons were calculated to occupy the previously empty Cr 3d_xy and 3d_yz orbitals, resulting in a major density of state contribution near the Fermi level. As a result, the conducting electrons in the Cr 3d_xy and 3d_yz orbitals enable double exchange between the electron-doped Cr ions and the surrounding Cr ions that in combination with spin–orbit coupling causes the switch of the easy-axis.⁶¹

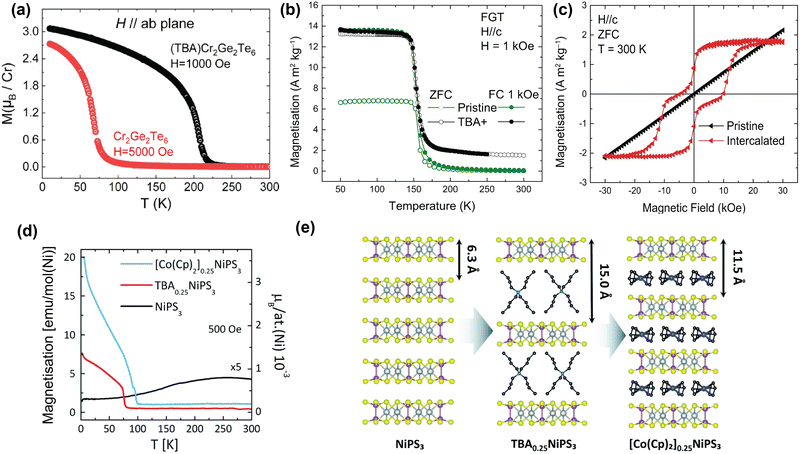Fig. 5 TBA intercalation in magnetic vdW materials. (a) Temperature-dependent magnetisation of pristine Cr₂Ge₂Te₆ and TBA-intercalated Cr₂Ge₂Te₆ with H applied parallel to the ab-plane.⁶¹ (b) Temperature-dependent magnetisation of pristine Fe₃GeTe₂ (green) and TBA-intercalated Fe₃GeTe₂ (black). Reproduced from ref. 59. (c) Room-temperature, field-dependent magnetisation of pristine Fe₃GeTe₂ (black) and TBA-intercalated Fe₃GeTe₂ (red). Reproduced from ref. 59. (d) Temperature-dependent magnetisation of pristine NiPS₃ (black), TBA_0.25NiPS3 (red), and [Co(Cp)₂]_0.25NiPS3 (blue), measured in the ab-plane.⁶³ (e) Scheme of the intercalation of TBA cations in NiPS₃, and the subsequent cation exchange with Co(Cp)₂⁺.⁶³ Reprinted with permission from ref. 61. Copyright 2019 American Chemical Society. Reprinted from ref. 63 with permission from the Royal Society of Chemistry, copyright 2022.

In contrast, recent work by the Singamaneni group did not find any switching of the easy-axis upon intercalation of Cr₂Ge₂Te₆ with TBA.¹⁶⁶ They did, however, observe a similar change in exchange mechanism from superexchange to double exchange, as well as a previously reported semiconductor-to-metal ground state transition upon TBA intercalation.¹⁶⁶ This means that further work might be necessary to come to a clear conclusion regarding the easy-axis anisotropy.

In addition to TBA intercalation in Cr₂Ge₂Te₆, earlier work by the same group showed that TBA intercalation in Fe₃GeTe₂ results in a negligible change in T_C (see Fig. 5(b)).⁵⁹ Despite TBA not affecting T_C of Fe₃GeTe₂,^{57,59,175,176} it was suggested that charge transfer induced by intercalation results in the observation of room-temperature ferromagnetism.⁵⁹ As shown in Fig. 5(c), this room-temperature ferromagnetism manifests itself as a ferromagnetic ‘wasp-waisted’ hysteresis loop, which can be indicative of competition between two different phases of different coercivities, in this case caused by antiferromagnetic exchange related to the antiferromagnetic interlayer coupling.⁵⁹

As shown in Fig. 5(d), intercalation of TBA into NiPS₃ to form TBA_0.25NiPS3, on the other hand, supresses the intrinsic antiferromagnetic order (T_N = 155 K) and instead induces ferrimagnetic order below ∼78 K.⁶³ This change in magnetic ordering was argued to be caused by reducing Ni²⁺ cations in the host lattice to zerovalent Ni atoms, as a consequence of the electron doping by TBA. This reduction is accompanied by a displacement of the Ni ions from an octahedral to a tetrahedral coordination site, as confirmed by Raman measurements.⁶³ Since this only happens to a fraction of the Ni ions, the antiferromagnetic order is only partially suppressed, giving rise to the observed ferrimagnetic ordering.

Tezze et al. also reported on a substitution of the TBA cations with (Co(Cp)₂⁺) through a non-redox cation exchange, utilizing the increased interlayer distance.⁶³ This exchange intercalation is illustrated in Fig. 5(e). The formed [Co(Cp)₂]_0.25NiPS₃ also displays ferrimagnetic order, with an ordering temperature of ∼98 K (see Fig. 5(d)). Note that this cation exchange could be applied more universally and provides a great template for studying molecular effects on the magnetic properties of the host lattice at a constant doping level.

2.3.2 Co-intercalation. The sizable increase in vdW gap between layers, induced by molecule intercalation, opens the door for simultaneous co-intercalation of multiple intercalants. It was reported that co-intercalation aides in the intercalation of cations using metal ammonium solutions,^77–79 although in these reactions the ammonium deintercalates again, leaving only the metal cations behind as intercalants. Co-intercalation of Li⁺ and ammonia has shown to greatly enhance the interlayer spacing in Bi₂Se₃,¹⁷⁷ and increase the superconducting transition temperature in FeSe,⁴⁶ but in this review we focus on tuning the magnetic properties of vdW materials and give an example of co-intercalation below.

Li et al. reported on co-intercalation of TBA cations with Co into the vdW gap of TaS₂, introducing ferromagnetic long-range order whilst maintaining the superconductive properties of 2H-TaS₂.¹⁷⁸ Intercalation of the TBA cations increased the vdW gap, and simultaneously allowed for surface modification by the Co ions, resulting in a TaS₂ organic–inorganic superlattice. The Co ions integrated into the basal plane of the TaS₂ layers, either by replacing Ta ions or by adsorbing into hollow sites in the layer, as shown in Fig. 6(a).

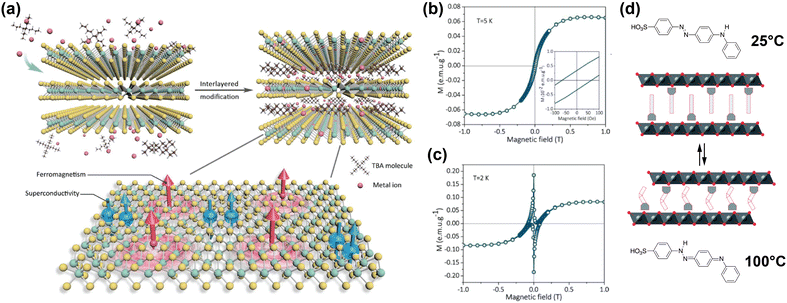Fig. 6 (a) Schematic illustration of co-intercalation of TBA and Co ions in TaS₂, creating an organic–inorganic superlattice with superconducting and ferromagnetic regions in a single atomic layer. Adapted from Li et al.¹⁷⁸ (b), (c) Isothermal field-dependent magnetisation of Co and TBA-intercalated TaS₂ superlattice, at 5 K and 2 K.¹⁷⁸ (d) Schematic illustration of 4(4-anilinophenylazo)benzenesulfonate intercalated CoAl layered double hydroxides. The intercalant reversibly switches between the two isomers displayed at high and low temperatures, changing the interlayer distance. Reproduced from ref. 171. Reproduced from ref. 178 with permission from John Wiley and Sons, copyright 2020.¹⁷¹

The hysteresis loops shown in Fig. 6(b) and (c) reveal the presence of ferromagnetism at 5 K and both ferromagnetism and superconducting diamagnetism arising from the host lattice at 2 K.¹⁷⁸ DFT calculations showed that the integration of the Co ions introduced spin polarisation through orbital-specific hybridisation of the Co 3d orbitals with the Ta 5d and S 3p orbitals. The ferromagnetic coupling between the Co sites was also shown to be stronger than the antiferromagnetic coupling, resulting in the observed ferromagnetism. Because the majority spin density is localised on the Co sites, ferromagnetic coupling occurs through RKKY interactions, as the local magnetic moment could polarise the surrounding conduction electrons.¹⁷⁸

2.3.3 Molecule-derived functionality for tunable magnetic materials. Besides acting like a spacer or electron dopant, other properties of molecular intercalants can also be transferred to the host lattice. In this way, molecular intercalation opens a pathway for exploring tunable magnetic systems with molecule-derived functionality, e.g. by using thermoresponsive, photoswitchable or chiral molecules, allowing for additional functionalisation of these materials.^168,171,179

One example of this was reported by Abellán et al., who reported the intercalation of CoAl double hydroxide with 4(4-anilinophenylazo)benzenesulfonate; a thermoresponsive molecule which switches between two isomers depending on the temperature.¹⁷¹ Because the two isomers have different lengths, the interlayer distance of the intercalated compound can be reversibly switched between ∼25.9 Å and ∼25.1 Å by changing the temperature from 25 °C to 100 °C and back (see Fig. 6(d)).

3 Materials chemistry challenges and opportunities

As described in the introduction, there is a large interest from the physics community in tuning the magnetic properties of vdW materials. The specific expertise of materials chemists is essential to enhance the field, not only by their ability to synthesise new compounds and perform (novel) intercalation reactions, but also by their characterisation toolkit necessary to study the produced materials in great detail. However, this comes with a number of challenges. In this section, we highlight the key challenges related to tuning magnetic properties of vdW materials by means of intercalation, and give directions for future research, calling on materials chemists to join this versatile field of research.

3.1 Determination of crystal structure and composition

To understand the effects of intercalation on the magnetic properties of the host lattice, a good understanding of any structural changes induced by intercalation is required. There are a variety of characterisation techniques that could be used to identify features of successful intercalation.^{32,104–107,180,181} The increased interlayer spacing obtained upon intercalation can be observed using X-ray diffraction (XRD) techniques, as peaks originating from the lateral planes normal to the stacking direction are expected to shift to lower angles. Moreover, this increased interlayer spacing can typically be observed using electron microscopy techniques. Lateral (scanning) transmission electron microscopy ((S)TEM) provides a sophisticated means to directly observe the increased layer spacing, and accurately determine the magnitude of this expansions.

The presence of both heavier elements, such as Te or I, found in a lot of magnetic vdW materials (e.g. CrI₃, Fe₃GeTe₂ and Cr₂Ge₂Te₆), together with lighter elements such as Li poses a challenge for structural characterization using X-ray diffraction. In the presence of heavy elements that scatter X-rays strongly, the weak signal from the light intercalant species is diminished. Neutron scattering is the technique of choice to overcome this problem, as neutrons are sensitive to lighter elements as well.^182,183 However, neutron scattering comes with additional challenges such as the need for large sample masses, typically in the order of grams, and access to large, international user facilities.

The structure determination using X-ray diffraction can also be complicated by defects in the material. Particularly noteworthy defect are stacking faults – discontinuities in the stacking patterns of layered materials. These microstructural defects complicate structure determination, even at low concentration, because they affect both the intensities and shapes of the diffraction peaks in a non-trivial manner. This can make separating the contribution of stacking faults from other factors, such as occupational disorder and vacancies, very difficult. Moreover, it is crucial to mention that intercalated compounds can exhibit challenges with respect to their stability. Air-stability is often an issue, especially when small organic molecules are intercalated. This could lead to decomposition of the product. Furthermore, intercalation can also lead to exfoliation. While this can be used as a way to obtain monolayer products,¹⁸⁴ it also causes stability issues when searching for intercalated products.

Intercalants can also form superlattices.^{104,105,107,108,144,152} These can be directly captured using (S)TEM techniques,¹⁵² or indirectly using selected area electron diffraction (SAED).^{104,107,152,155} The formation of superstructures also results in additional Bragg peaks in the diffraction patterns,^{32,104–107,113,185} and are often found in certain materials with more than 5% intercalation.^{105–107,113,186} Because defective superlattices are not necessarily apparent through X-ray diffraction alone, correlation of the magnetic (and electronic) properties using composition-determining techniques might be necessary.

Additional information about the structure of the intercalated material can be obtained through Raman scattering. Intercalation does not necessarily result in the observation of additional peaks with respect to the pristine host material, but an intercalated superlattice may reconstruct the Brillouin zone, giving rise to new phonons that may or may not be Raman active.³² The shifting of Raman peaks can be indicative of vibrational stiffening or softening due to electronic contributions from the intercalant. Raman scattering is especially useful in structure determination of molecular intercalation,^59,63 as, in principle, no new Raman peaks are expected from metallic intercalants.

Aside from determining the changes to the host lattice, accurately determining the stoichiometry of the intercalated compound is of paramount importance, as magnetic properties are often highly sensitive to the degree of intercalation.^{58,64,68,144,152,153} Notably, not all studies investigate the precise composition by elemental analysis techniques, despite the fact that defective superlattices may not be apparent from diffraction. A precise report of composition and its correlation with magnetic and electronic properties may greatly improve the reproducibility.

Commonly available techniques to study the composition are energy-dispersive X-ray spectroscopy (EDX), X-ray fluorescence spectroscopy (XFS), X-ray photoelectron spectroscopy (XPS), energy electron loss spectroscopy (EELS) and inductively-coupled plasma analysis (ICP). However, these techniques may not always be sensitive enough to accurately determine concentrations of lighter elements. The development of muon elemental analysis, which is sensitive to problematic light elements such as Li, could be an outcome.^187,188

Electron microscopy can also be used to directly observe the intercalants. This is typically done through high-angle annular dark-field STEM. In practise this is done almost exclusively for transition metal intercalants,^152,178 as the combination of light intercalant elements, such as Li or C and H present in organic molecules, and heavier elements typically present in the host lattice, results in low contrast due to the difference in scattering intensities between these different elements. This typically causes the lighter elements to be indistinguishable from the background noise. Techniques such as annular bright field STEM have allowed for the direct imaging of elements as light as hydrogen in other material systems, but require extremely thin samples (<10 nm) to do so.¹⁸⁹ Molecular intercalants pose additional challenges in atomic resolution (S)TEM imaging due to the dynamics of the molecular intercalants and the potential for structural rearrangements.

Another crucial challenge is sample inhomogeneity. Intercalation typically starts at the edge of the vdW host material, before extending to the center of the flake with increasing intercalation time or amount.^51,190,191 Moreover, optical microscopy studies have shown that diffusion within a single flake starts from the thick part of the flake and moves into the thin part.¹⁹¹In situ far-field optical techniques, including photoluminescence (PL) and Raman spectroscopy have been used to monitor electrochemical intercalation dynamics, but the light diffraction limit makes it difficult to exactly detect the distribution of intercalants with nanoscale resolution.³¹ Using in situ TEM, the alkali-intercalation process was successfully probed with sub-nanoscale resolution, but the observed area was too small to be representative of the sample as a whole and determine its kinetics accurately. In addition, sample preparation for in situ TEM measurements is a relatively complex and involved process.

3.2 Characterisation of magnetic properties

Determining the magnetic properties and magnetic structure of intercalated vdW materials is a non-trivial task. When assessing the magnetic properties of a sample, magnetic susceptibility measurements are often performed using SQUID magnetometry^{60,61,120,128,146,150,155,170,172} or vibrating-sample magnetometry (VSM).^{59,63,68,70,125} These techniques work well for bulk intercalated materials, but become problematic for few-layer samples. The same holds true for neutron scattering experiments that could be used to determine the magnetic ground state spin structure as well as its dynamics.^126,129 As mentioned above, this requires large sample volumes and it cannot be used to determine spin structures of few-layer samples. Therefore, several other characterization techniques might be required. These techniques can be divided into optical techniques, electrical techniques, and electron microscopy techniques.

Optical spectroscopy is a powerful tool that can distinguish various types of magnetic ordering.¹⁹² A lot of pioneering work on 2D magnetism relied on the use of optical techniques.^8–11,193 The most commonly used optical techniques are based on the magneto-optical Kerr effect (MOKE), which measures changes in polarisation of the interaction between linearly polarised light and magnetism, and on magnetic circular dichroism (MCD), which measures the difference in absorption towards left- and right-handed light when incident polarised light passes through the sample under an external magnetic field.^{58,121,132,192} By measuring the polarisability or signal strength of the reflected light, MOKE can produce magnetisation curves. As the signal strength is proportional to the magnetisation, hysteresis loops can be obtained. The high spatial resolution also allows for obtaining information about domains and magnetisation processes.¹⁹² MCD allows for determining the magnetic state of a material by observing changes in amplitude and phase of the outgoing light. Limited by the measurement setup, MOKE and MCD are very sensitive to the magnetisation of a sample, but can only recognise out-of-plane magnetisation for few layer materials.

Electrical measurements on intercalated vdW materials typically take the form of Hall measurements.^58,146,152 In ferromagnetic materials, both the normal Hall effect (NHE) and the anomalous Hall effect (AHE) exist, with the former being sensitive to the external magnetic field, and the latter dependent on the magnetisation of the sample. In vdW systems, the Hall resistance R_xy can be written as

R_xy = R₀B_z + R_sM_z (1)

where the first term denotes the normal Hall resistance, and the second term the anomalous Hall resistance. B_z and M_z denote the out-of-plane components of the applied magnetic field and magnetisation of the sample, respectively. R₀ and R_s are constants used to describe the strength of the NHE and AHE, respectively. In itinerant ferromagnets like Fe₃GeTe₂, the NHE is negligibly weak compared to the AHE due to the metallic conductivity, allowing for straightforward characterisation of the ferromagnetism through AHE measurements.⁵⁸ In these cases, R_xy is proportional to M_z, meaning that magnetisation can directly be obtained through measuring R_xy. Since most vdW magnets, as well as their intercalated counterparts, are insulators, in-plane transport measurements are almost impossible on many of these materials.

Aside from providing structural information, electron microscopy techniques can also be used to provide magnetic information about a sample, e.g. through Lorentz transmission electron microscopy (L-TEM). In L-TEM, when the electron beam passes through the sample, it is deflected by the Lorentz force of the intrinsic magnetic field of the sample. The detection of this beam then results in focusing and under-focusing which appear as black-and-white areas on a 2D map. This allows for the detection of exotic magnetic textures, and has been used to identify chiral helimagnetism⁷¹ and skyrmions¹²⁰ in intercalated vdW materials.

3.3 Future research directions

Based on the plethora of intercalation possibilities that can be exploited to tune the magnetic properties of vdW materials and the challenges that are associated with this, as highlighted in this review, we propose several directions for future research.

The number of vdW materials that have been successfully intercalated to tune their magnetic properties is relatively small compared to the rapidly increasing library of (magnetic) vdW materials. Given the topical nature of vdW materials research, more and more candidates for intercalation become rapidly available, while there simultaneously is a demand for materials with specific magnetic properties that can for example be implemented in spintronic applications.^6,7 Therefore, materials chemists can play a crucial role in expanding the playing field by employing various types of intercalants, such as those described in Section 2. This would give rise to magnetically-tunable materials with desired properties. For example, the tuning of magnetic properties through transition-metal intercalation has a strong focus on 3d metals. With an increasing interest in exotic magnetic states originating from strong spin–orbit coupling,¹⁹⁴ the door is open for the exploration of intercalation of 4d, 5d, or possibly 4f metals. Work by Koski and co-workers has shown that a good number of heavy metals can be readily intercalated,¹⁰⁴ but its relation to the magnetic properties is currently understudied.

Looking forward to spintronic applications, vdW materials play an essential role for hosting magnons, which form a key research direction within this field. However, investigation of magnons into intercalated vdW materials so far has been limited mainly to intercalated graphite.^195–197 With the ever expanding library of (magnetic) vdW materials, and the broad range of intercalation possibilities highlighted in this review, new host lattices can be employed. Techniques such as Brillouin scattering (for acoustic magnons), Raman scattering (for optical magnons) and inelastic neutron scattering would need to be employed to successfully characterise magnons in these materials.

Until now, molecular intercalation has mainly focussed on the use of the intercalant as a dopant or spacer, with very little work utilizing other aspects of the versatile template that molecular intercalation forms. The use of molecule-derived functionalities could allow for responsive magnetic systems. These systems could, depending on the stimulus, tune their magnetic properties. This could be done by using thermoresponsive, photoswitchable, or chiral molecules.^168,171,179 With molecular machines and more complex forms of soft matter gathering a lot of interest, one can envision complex, stimuli-responsive materials with reversibly tunable magnetic interactions.

Another relatively underexplored area is that of using multiple functionalities of intercalants in one system. For example, Chen et al. successfully intercalated dual elements into Be₂Se₃, resulting in the formation of superlattices.¹⁰⁷ This could form a platform for complex novel magnetic structures that can further expand the field of magnetic-property tuning by means of chemical intercalation. As demonstrated by Li et al., co-functionality can extend beyond the need of two similar intercalants, as combining multiple families of intercalants opens up the avenue for new types of intercalated compounds that combine their functionalities into a single host lattice.¹⁷⁸

Moreover, a lot of intercalated vdW materials are not (air) stable. For these materials to be used in device application, this barrier needs to be overcome. This can be done either by formation of air stable intercalants, or by exploring methods to encapsulating the intercalated products. So far, this has barely been explored.

Another research direction that would require enhanced efforts is the understanding of the intercalation process. Especially with regards to the dynamics of intercalation, a lot is still left unknown. To this end, several in situ studies have been performed, using optical microscopy,¹⁹⁰ and X-ray and neutron scattering techniques.¹⁷⁷ Understanding the dynamics can give us insights into the intercalation process and inhomogeneity, allowing for a better prediction of the formed intercalation products and their properties.

Aside from using intercalation to tune the (magnetic) properties of vdW materials, intercalation has also been employed to exfoliate layered materials. Compared to other top-down exfoliation techniques, such as micromechanical cleavage¹ and direct liquid exfoliation,¹⁹⁸ intercalation-based exfoliation results in high yields of exfoliation and is applicable to a wide range of vdW materials.^184,199 A recent review by Yang et al. extensively describes several intercalation-based exfoliation strategies and provides a great overview of the status quo. We therefore refer the reader to this review for additional information and future research directions along the line of exfoliation.¹⁸⁴

4 Conclusion

VdW materials have gained a lot of interest from the solid-state community, and there is a specific interest in vdW materials with tunable magnetic properties. In this review, we have provided a comprehensive overview of the most common forms of intercalation reactions that are used to achieve this goal. While alkali metal intercalation is potentially the most studied form of interclation, we also pinpointed the various exotic changes observed by transition metal intercalation. Moreover, we discussed how molecule intercalation embodies a rather versatile, yet underexplored, area in the field. Furthermore, we have highlighted the most common materials chemistry challenges and opportunities that could enhance the field. These challenges are based on accurately determining the materials structure and composition, as well as on characterising the magnetic properties. In this review we proposed future research directions along the lines of exploring other forms of intercalation, e.g. heavy-metal intercalation, molecule intercalation and intercalating multiple functionalities into a single host lattice, as well as for investigating air-stabilty and understanding the intercalation mechanism in more detail. We are certain that the expertise of materials chemists is crucial to enhance this field.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

MEK acknowledges the research program “Materials for the Quantum Age” (QuMat) for financial support. This program (registration number 024.005.006) is part of the Gravitation program financed by the Dutch Ministry of Education, Culture and Science (OCW).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669,  DOI:10.1126/science.1102896.
2. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425,  DOI:10.1038/nature12385.
3. G. Fiori, F. Bonaccorso, G. Iannaccone, T. Palacios, D. Neumaier, A. Seabaugh, S. K. Banerjee and L. Colombo, Nat. Nanotechnol., 2014, 9, 768–779,  DOI:10.1038/nnano.2014.207.
4. J. G. Park, J. Phys.: Condens. Matter, 2016, 28, 301001,  DOI:10.1088/0953-8984/28/30/301001.
5. S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033,  DOI:10.1038/natrevmats.2017.33.
6. N. Samarth, Nature, 2017, 546, 216–218,  DOI:10.1038/546216a.
7. K. S. Burch, D. Mandrus and J. G. Park, Nature, 2018, 563, 47–52,  DOI:10.1038/s41586-018-0631-z.
8. J. U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C. H. Park, J. G. Park and H. Cheong, Nano Lett., 2016, 16, 7433–7438,  DOI:10.1021/acs.nanolett.6b03052.
9. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269,  DOI:10.1038/nature22060.
10. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273,  DOI:10.1038/nature22391.
11. B. Huang, G. Clark, D. R. Klein, D. MacNeill, E. Navarro-Moratalla, K. L. Seyler, N. Wilson, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao, P. Jarillo-Herrero and X. Xu, Nat. Nanotechnol., 2018, 13, 544–548,  DOI:10.1038/s41565-018-0121-3.
12. S. Yang, T. Zhang and C. Jiang, Adv. Sci., 2021, 8, 2002488,  DOI:10.1002/advs.202002488.
13. H. Wang, V. Eyert and U. Schwingenschlögl, J. Phys.: Condens. Matter, 2011, 23, 116003,  DOI:10.1088/0953-8984/23/11/116003.
14. T. Kong, K. Stolze, E. I. Timmons, J. Tao, D. Ni, S. Guo, Z. Yang, R. Prozorov and R. J. Cava, Adv. Mater., 2019, 31, 1808074,  DOI:10.1002/adma.201808074.
15. B. Zhang, Y. Zeng, Z. J. Zhao, D. P. Qiu, T. Zhang and Y. L. Hou, Rare Met., 2022, 41, 2921–2942,  DOI:10.1007/s12598-022-02004-2.
16. S. Mondal, A. Midya, M. M. Patidar, V. Ganesan and P. Mandal, Appl. Phys. Lett., 2020, 117, 2300333,  DOI:10.1063/5.0019985.
17. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M. H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293,  DOI:10.1038/s41565-018-0063-9.
18. B. Li, Z. Wan, C. Wang, P. Chen, B. Huang, X. Cheng, Q. Qian, J. Li, Z. Zhang, G. Sun, B. Zhao, H. Ma, R. Wu, Z. Wei, Y. Liu, L. Liao, Y. Ye, Y. Huang, X. Xu, X. Duan, W. Ji and X. Duan, Nat. Mater., 2021, 20, 818–825,  DOI:10.1038/s41563-021-00927-2.
19. Y. Zhang, J. Chu, L. Yin, T. A. Shifa, Z. Cheng, R. Cheng, F. Wang, Y. Wen, X. Zhan, Z. Wang and J. He, Adv. Mater., 2019, 31, 1900056,  DOI:10.1002/adma.201900056.
20. G. Le Flem, R. Brec, G. Ouvard, A. Luisy and P. Segransan, J. Phys. Chem. Solids, 1982, 43, 455–461,  DOI:10.1016/0022-3697(82)90156-1.
21. Y. Peng, S. Ding, M. Cheng, Q. Hu, J. Yang, F. Wang, M. Xue, Z. Liu, Z. Lin, M. Avdeev, Y. Hou, W. Yang, Y. Zheng and J. Yang, Adv. Mater., 2020, 32, 2001200,  DOI:10.1002/adma.202001200.
22. Y. J. Sun, Q. H. Tan, X. L. Liu, Y. F. Gao and J. Zhang, J. Phys. Chem. Lett., 2019, 10, 3087–3093,  DOI:10.1021/acs.jpclett.9b00758.
23. T. Zhang, Y. Wang, H. Li, F. Zhong, J. Shi, M. Wu, Z. Sun, W. Shen, B. Wei, W. Hu, X. Liu, L. Huang, C. Hu, Z. Wang, C. Jiang, S. Yang, Q. M. Zhang and Z. Qu, ACS Nano, 2019, 13, 11353–11362,  DOI:10.1021/acsnano.9b04726.
24. W. Wang, R. Sun, S. He, Z. Jia, C. Su, Y. Li and Z. Wang, 2D Mater., 2021, 8, 015027,  DOI:10.1088/2053-1583/abc5cf.
25. J. Klein, T. Pham, J. D. Thomsen, J. B. Curtis, T. Denneulin, M. Lorke, M. Florian, A. Steinhoff, R. A. Wiscons, J. Luxa, Z. Sofer, F. Jahnke, P. Narang and F. M. Ross, Nat. Commun., 2022, 13, 5420,  DOI:10.1038/s41467-022-32737-8.
26. K. Lee, A. H. Dismukes, E. J. Telford, R. A. Wiscons, J. Wang, X. Xu, C. Nuckolls, C. R. Dean, X. Roy and X. Zhu, Nano Lett., 2021, 21, 3511–3517,  DOI:10.1021/acs.nanolett.1c00219.
27. M. E. Ziebel, M. L. Feuer, J. Cox, X. Zhu, C. R. Dean and X. Roy, CrSBr: An Air-Stable, Two-Dimensional Magnetic Semiconductor, Nano Lett., 2024, 4319–4329,  DOI:10.1021/acs.nanolett.4c00624.
28. X. Zhang, Q. Lu, W. Liu, W. Niu, J. Sun, J. Cook, M. Vaninger, P. F. Miceli, D. J. Singh, S. W. Lian, T. R. Chang, X. He, J. Du, L. He, R. Zhang, G. Bian and Y. Xu, Nat. Commun., 2021, 12, 2492,  DOI:10.1038/s41467-021-22777-x.
29. G. Zhang, F. Guo, H. Wu, X. Wen, L. Yang, W. Jin, W. Zhang and H. Chang, Nat. Commun., 2022, 13, 5067,  DOI:10.1038/s41467-022-32605-5.
30. M. Rajapakse, B. Karki, U. O. Abu, S. Pishgar, M. R. K. Musa, S. M. Riyadh, M. Yu, G. Sumanasekera and J. B. Jasinski, npj 2D Mater. Appl., 2021, 5, 30,  DOI:10.1038/s41699-021-00211-6.
31. Y. Li, H. Yan, B. Xu, L. Zhen and C. Y. Xu, Adv. Mater., 2021, 33, 2000581,  DOI:10.1002/adma.202000581.
32. M. S. Dresselhaus, Intercalation in layered materials, NATO ASI Series, Subseries B, Physics, Plenum Press, New York, 1987.
33. W. Müller-Warmuth and R. Schöllhorn, Progress in Intercalation Research, ed. W. Müller-Warmuth and R. Schöllhorn, Springer, Netherlands, Dordrecht, 1994, vol. 17 DOI:10.1007/978-94-011-0890-4.
34. M. S. Whittingham, Science, 1976, 192, 1126–1127,  DOI:10.1126/science.192.4244.1126.
35. W. B. Johnson and W. L. Worrell, Synth. Met., 1982, 4, 225–248,  DOI:10.1016/0379-6779(82)90015-7.
36. D. Li, D. L. Danilov, L. Gao, Y. Yang and P. H. L. Notten, J. Electrochem. Soc., 2016, 163, A3016–A3021,  DOI:10.1149/2.0821614jes.
37. M. Winter, B. Barnett and K. Xu, Chem. Rev., 2018, 118, 11433–11456,  DOI:10.1021/acs.chemrev.8b00422.
38. Y. Gu, Y. Katsura, T. Yoshino, H. Takagi and K. Taniguchi, Sci. Rep., 2015, 5, 12486,  DOI:10.1038/srep12486.
39. V. Augustyn, J. Come, M. A. Lowe, J. W. Kim, P. L. Taberna, S. H. Tolbert, H. D. Abruña, P. Simon and B. Dunn, Nat. Mater., 2013, 12, 518–522,  DOI:10.1038/nmat3601.
40. M. R. Lukatskaya, B. Dunn and Y. Gogotsi, Nat. Commun., 2016, 7, 12647,  DOI:10.1038/ncomms12647.
41. Y. Koike, H. Suematsu, K. Higuchi and S. Tanuma, Solid State Commun., 1978, 27, 623–627,  DOI:10.1016/0038-1098(78)90457-X.
42. T. E. Weller, M. Ellerb, S. S. Saxena, R. P. Smith and N. T. Skipper, Nat. Phys., 2005, 1, 39–41,  DOI:10.1038/nphys0010.
43. J. T. Ye, Y. J. Zhang, R. Akashi, M. S. Bahramy, R. Arita and Y. Iwasa, Science, 2012, 338, 1193–1196,  DOI:10.1126/science.1228006.
44. Y. Saito, Y. Kasahara, J. Ye, Y. Iwasa and T. Nojima, Science, 2015, 350, 409–413,  DOI:10.1126/science.1259440.
45. N. Z. Wang, M. Z. Shi, C. Shang, F. B. Meng, L. K. Ma, X. G. Luo and X. H. Chen, New J. Phys., 2018, 20, 023014,  DOI:10.1088/1367-2630/aaa8a7.
46. M. Burrard-Lucas, D. G. Free, S. J. Sedlmaier, J. D. Wright, S. J. Cassidy, Y. Hara, A. J. Corkett, T. Lancaster, P. J. Baker, S. J. Blundell and S. J. Clarke, Nat. Mater., 2013, 12, 15–19,  DOI:10.1038/nmat3464.
47. E. Morosan, H. W. Zandbergen, B. S. Dennis, J. W. Bos, Y. Onose, T. Klimczuk, A. P. Ramirez, N. P. Ong and R. J. Cava, Nat. Phys., 2006, 2, 544–550,  DOI:10.1038/nphys360.
48. C. Pettenkofer and W. Jaegermann, Phys. Rev. B, 1994, 50, 8816–8823,  DOI:10.1103/PhysRevB.50.8816.
49. K. E. Wagner, E. Morosan, Y. S. Hor, J. Tao, Y. Zhu, T. Sanders, T. M. Mcqueen, H. W. Zandbergen, A. J. Williams, D. V. West and R. J. Cava, Phys. Rev. B, 2008, 78, 104520,  DOI:10.1103/PhysRevB.78.104520.
50. M. Wang and K. J. Koski, ACS Nano, 2015, 9, 3226–3233,  DOI:10.1021/acsnano.5b00336.
51. F. Xiong, H. Wang, X. Liu, J. Sun, M. Brongersma, E. Pop and Y. Cui, Nano Lett., 2015, 15, 6777–6784,  DOI:10.1021/acs.nanolett.5b02619.
52. L. Quan, H. Zhang, H. Wei, Y. Li, S. O. Park, D. Y. Hwang, Y. Tian, M. Huang, C. Wang, M. Wang, S. K. Kwak, F. Qin, H. X. Peng and R. S. Ruoff, ACS Appl. Mater. Interfaces, 2020, 12, 16841–16848,  DOI:10.1021/acsami.0c02301.
53. E. Guilmeau, Y. Bréard and A. Maignan, Appl. Phys. Lett., 2011, 99, 052107,  DOI:10.1063/1.3621834.
54. R. Matsumoto, Y. Okabe and N. Akuzawa, J. Electron. Mater., 2015, 44, 399–406,  DOI:10.1007/s11664-014-3409-6.
55. G. Zhu, J. Liu, Q. Zheng, R. Zhang, D. Li, D. Banerjee and D. G. Cahill, Nat. Commun., 2016, 7, 13211,  DOI:10.1038/ncomms13211.
56. J. S. Kang, M. Ke and Y. Hu, Nano Lett., 2017, 17, 1431–1438,  DOI:10.1021/acs.nanolett.6b04385.
57. A. F. May, S. Calder, C. Cantoni, H. Cao and M. A. McGuire, Phys. Rev. B, 2016, 93, 014411,  DOI:10.1103/PhysRevB.93.014411.
58. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99,  DOI:10.1038/s41586-018-0626-9.
59. H. Iturriaga, L. M. Martinez, T. T. Mai, A. J. Biacchi, M. Augustin, A. R. Hight Walker, M. F. Sanad, S. T. Sreenivasan, Y. Liu, E. J. Santos, C. Petrovic and S. R. Singamaneni, npj 2D Mater. Appl., 2023, 7, 56,  DOI:10.1038/s41699-023-00417-w.
60. S. Khan, E. S. Y. Aw, L. A. V. Nagle-Cocco, A. Sud, S. Ghosh, M. K. B. Subhan, Z. Xue, C. Freeman, D. Sagkovits, A. Gutierrez-Llorente, I. Verzhbitskiy, D. M. Arroo, C. W. Zollitsch, G. Eda, E. J. G. Santos, S. E. Dutton, S. T. Bramwell, C. A. Howard and H. Kurebayashi, arXiv, 2023 DOI:10.48550/arXiv.2312.17554.
61. N. Wang, H. Tang, M. Shi, H. Zhang, W. Zhuo, D. Liu, F. Meng, L. Ma, J. Ying, L. Zou, Z. Sun and X. Chen, J. Am. Chem. Soc., 2019, 141, 17166–17173,  DOI:10.1021/jacs.9b06929.
62. P. A. Joy and S. Vasudevan, Phys. Rev. B, 1992, 46, 5425,  DOI:10.1103/PhysRevB.46.5425.
63. D. Tezze, J. M. Pereira, Y. Asensio, M. Ipatov, F. Calavalle, F. Casanova, A. M. Bittner, M. Ormaza, B. Martín-García, L. E. Hueso and M. Gobbi, Nanoscale, 2022, 14, 1165–1173,  10.1039/d1nr07281a.
64. O. Gorochov, A. Le Blanc-Soreau, J. Rouxel, P. Imbert and G. Jehanno, Philos. Mag. B, 1981, 43, 621–634,  DOI:10.1080/01418638108222164.
65. Y. Yamamura, S. Moriyama, T. Tsuji, Y. Iwasa, M. Koyano, S. Katayama and M. Ito, J. Alloys Compd., 2004, 383, 338–341,  DOI:10.1016/j.jallcom.2004.04.045.
66. T. Miyadai, K. Kikuchi, H. Kondo, S. Sakka, M. Arai and Y. Ishikawa, J. Phys. Soc. Jpn., 1983, 52, 1394–1401,  DOI:10.1143/JPSJ.52.1394.
67. H. Han, L. Zhang, D. Sapkota, N. Hao, L. Ling, H. Du, L. Pi, C. Zhang, D. G. Mandrus and Y. Zhang, Phys. Rev. B, 2017, 96, 094439,  DOI:10.1103/PhysRevB.96.094439.
68. C. W. Chen, S. Chikara, V. S. Zapf and E. Morosan, Phys. Rev. B, 2016, 94, 054406,  DOI:10.1103/PhysRevB.94.
69. E. Morosan, H. W. Zandbergen, L. Li, M. Lee, J. G. Checkelsky, M. Heinrich, T. Siegrist, N. P. Ong and R. J. Cava, Phys. Rev. B, 2007, 75, 104401,  DOI:10.1103/PhysRevB.75.104401.
70. S. Mangelsen, J. Hansen, P. Adler, W. Schnelle, W. Bensch, S. Mankovsky, S. Polesya and H. Ebert, J. Phys. Chem. C, 2020, 124, 24984–24994,  DOI:10.1021/acs.jpcc.0c07711.
71. C. Zhang, J. Zhang, C. Liu, S. Zhang, Y. Yuan, P. Li, Y. Wen, Z. Jiang, B. Zhou, Y. Lei, D. Zheng, C. Song, Z. Hou, W. Mi, U. Schwingenschlögl, A. Manchon, Z. Q. Qiu, H. N. Alshareef, Y. Peng and X. X. Zhang, Adv. Mater., 2021, 33, 2101131,  DOI:10.1002/adma.202101131.
72. D. C. Freitas, R. Weht, A. Sulpice, G. Remenyi, P. Strobel, F. Gay, J. Marcus and M. Núñez-Regueiro, J. Phys.: Condens. Matter, 2015, 27, 176002,  DOI:10.1088/0953-8984/27/17/176002.
73. A. L. Coughlin, D. Xie, X. Zhan, Y. Yao, L. Deng, H. Hewa- Walpitage, T. Bontke, C. W. Chu, Y. Li, J. Wang, H. A. Fertig and S. Zhang, Nano Lett., 2021, 21, 9517–9525,  DOI:10.1021/acs.nanolett.1c02940.
74. M. Yamaguchi and T. Hashimoto, J. Phys. Soc. Jpn., 1972, 32, 635–638,  DOI:10.1143/JPSJ.32.635.
75. M. A. McGuire, H. Dixit, V. R. Cooper and B. C. Sales, Chem. Mater., 2015, 27, 612–620,  DOI:10.1021/cm504242t.
76. O. Gisser, W. Paul and H. G. Kahle, J. Magn. Magn. Mater., 1990, 92, 129,  DOI:10.1016/0304-8853(90)90689-N.
77. W. Rüdorff, Angew. Chem., Int. Ed. Engl., 1959, 71, 487–491,  DOI:10.1002/ange.19590711504.
78. R. B. Somoano, V. Hadek and A. Rembaum, J. Chem. Phys., 1973, 58, 697–701,  DOI:10.1063/1.1679256.
79. J. A. Woollam and R. B. Somoano, Mater. Sci. Eng., 1977, 31, 289–295,  DOI:10.1016/0025-5416(77)90048-9.
80. P. Palvadeau, L. Coïc, J. Rouxel and J. Portier, Mater. Res. Bull., 1978, 13, 221–227,  DOI:10.1016/0025-5408(78)90226-X.
81. M. B. Dines, Mater. Res. Bull., 1975, 10, 287–292,  DOI:10.1016/0025-5408(75)90115-4.
82. D. W. Murphy, J. Di Salvo Francis, G. W. Hull and J. V. Waszczak, Inorg. Chem., 1976, 15, 17–21,  DOI:10.1021/ic50155a005.
83. C. Berthier, Y. Chabre and M. Minier, Solid State Commun., 1978, 28, 327–332,  DOI:10.1016/0038-1098(78)90434-9.
84. H.-L. Tsai, J. Heising, J. L. Schindler, C. R. Kannewurf and M. G. Kanatzidis, Chem. Mater., 1997, 21, 879–882,  DOI:10.1021/cm960579t.
85. X. Zhu, Z. Su, C. Wu, H. Cong, X. Ai, H. Yang and J. Qian, Nano Lett., 2022, 22, 2956–2963,  DOI:10.1021/acs.nanolett.2c00148.
86. A. M. Ferrenti, S. Klemenz, S. Lei, X. Song, P. Ganter, B. V. Lotsch and L. M. Schoop, Inorg. Chem., 2020, 59, 1176–1182,  DOI:10.1021/acs.inorgchem.9b02856.
87. G. Villalpando, A. M. Ferrenti, R. Singha, X. Song, G. Cheng, N. Yao and L. M. Schoop, ACS Nano, 2022, 16, 13814–13820,  DOI:10.1021/acsnano.2c01858.
88. J. Zheng, H. Zhang, S. Dong, Y. Liu, C. Tai Nai, H. Suk Shin, H. Young Jeong, B. Liu and K. Ping Loh, Nat. Commun., 2014, 5, 2995,  DOI:10.1038/ncomms3995.
89. A. I. Smith, H. V. Wladkowski, Z. H. Hecht, Y. She, S. Kattel, P. I. Samarawickrama, S. R. Rich, J. R. Murphy, J. Tian, J. F. Ackerman, W. D. Rice, E. B. Hulley and B. M. Leonard, Chem. Mater., 2020, 32, 10482–10488,  DOI:10.1021/acs.chemmater.0c03270.
90. Y. Yu, F. Yang, X. F. Lu, Y. J. Yan, Y. H. Cho, L. Ma, X. Niu, S. Kim, Y. W. Son, D. Feng, S. Li, S. W. Cheong, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2015, 10, 270–276,  DOI:10.1038/nnano.2014.323.
91. Y. Guo, R. B. Smith, Z. Yu, D. K. Efetov, J. Wang, P. Kim, M. Z. Bazant and L. E. Brus, J. Phys. Chem. Lett., 2016, 7, 2151–2156,  DOI:10.1021/acs.jpclett.6b00625.
92. Y. Wu, J. He, J. Liu, H. Xing, Z. Mao and Y. Liu, Nanotechnology, 2019, 30, 035702,  DOI:10.1088/1361-6528/aaea3b.
93. D. K. Bediako, M. Rezaee, H. Yoo, D. T. Larson, S. Y. Zhao, T. Taniguchi, K. Watanabe, T. L. Brower-Thomas, E. Kaxiras and P. Kim, Nature, 2018, 558, 425–429,  DOI:10.1038/s41586-018-0205-0.
94. L. Oakes, R. Carter, T. Hanken, A. P. Cohn, K. Share, B. Schmidt and C. L. Pint, Nat. Commun., 2016, 7, 11796,  DOI:10.1038/ncomms11796.
95. X. Huang, J. Xu, R. Zeng, Q. Jiang, X. Nie, C. Chen, X. Jiang and J. M. Liu, Appl. Phys. Lett., 2021, 119, 012405,  DOI:10.1063/5.0051882.
96. D. Weber, A. H. Trout, D. W. McComb and J. E. Goldberger, Nano Lett., 2019, 19, 5031–5035,  DOI:10.1021/acs.nanolett.9b01287.
97. H. M. Ahamd and J. Zhou, AIP Adv., 2020, 10, 045323,  DOI:10.1063/1.5139061.
98. R. Basnet, D. Ford, K. Tenbarge, J. Lochala and J. Hu, J. Phys.: Condens. Matter, 2022, 34, 434002,  DOI:10.1088/1361-648X/ac8a81.
99. D. Wu, Y. Zhao, Y. Yang, L. Huang, Y. Xiao, S. Chen and Y. Zhao, Nanomaterials, 2022, 12, 1420,  DOI:10.3390/nano12091420.
100. A. Kabiraj and S. Mahapatra, J. Phys. Chem. C, 2020, 124, 1146–1157,  DOI:10.1021/acs.jpcc.9b09477.
101. Z.-X. Shen, X. Bo, K. Cao, X. Wan and L. He, Phys. Rev. B, 2021, 108, 085102,  DOI:10.1103/PhysRevB.103.085102.
102. Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, ACS Nano, 2012, 6, 1695–1701,  DOI:10.1021/nn204667z.
103. H. R. Fuh, B. Yan, S. C. Wu, C. Felser and C. R. Chang, New J. Phys., 2016, 18, 113038,  DOI:10.1088/1367-2630/18/11/113038.
104. M. Wang, D. Williams, G. Lahti, S. Teshima, D. D. Aguilar, R. Perry and K. J. Koski, 2D Mater., 2018, 5, 045005,  DOI:10.1088/2053-1583/aacfc2.
105. K. J. Koski, C. D. Wessells, B. W. Reed, J. J. Cha, D. Kong and Y. Cui, J. Am. Chem. Soc., 2012, 134, 13773–13779,  DOI:10.1021/ja304925t.
106. K. J. Koski, J. J. Cha, B. W. Reed, C. D. Wessells, D. Kong and Y. Cui, J. Am. Chem. Soc., 2012, 134, 7584–7587,  DOI:10.1021/ja300368x.
107. K. P. Chen, F. R. Chung, M. Wang and K. J. Koski, J. Am. Chem. Soc., 2015, 137, 5431–5437,  DOI:10.1021/jacs.5b00666.
108. J. P. Motter, K. J. Koski and Y. Cui, Chem. Mater., 2014, 26, 2313–2317,  DOI:10.1021/cm500242h.
109. Y. Gong, H. Yuan, C. L. Wu, P. Tang, S. Z. Yang, A. Yang, G. Li, B. Liu, J. Van De Groep, M. L. Brongersma, M. F. Chisholm, S. C. Zhang, W. Zhou and Y. Cui, Nat. Nanotechnol., 2018, 13, 294–299,  DOI:10.1038/s41565-018-0069-3.
110. E. W. Ong, M. J. McKelvy, G. Ouvrard, W. S. Glaunsinger and V. Dreele, Chem. Mater., 1992, 4, 14–17,  DOI:10.1021/cm00019a006.
111. M. V. Sidorovw, M. J. Mckelvy, R. Sharma and W. S. Glaunsinger, J. Solid State Chem., 1998, 141, 330–337,  DOI:10.1006/jssc.1998.7929.
112. Z. Li, D. Li, H. Wang, P. Chen, L. Pi, X. Zhou and T. Zhai, Small Methods, 2021, 5, 2100567,  DOI:10.1002/smtd.202100567.
113. M. Wang, I. Al-Dhahir, J. Appiah and K. J. Koski, Chem. Mater., 2017, 29, 1650–1655,  DOI:10.1021/acs.chemmater.6b04918.
114. H. Narita, H. Ikuta, H. Hinode, T. Uchida, T. Ohtani and M. Wakihara, J. Solid State Chem., 1994, 108, 148–151,  DOI:10.1006/jssc.1994.1022.
115. X. Sun, W. Li, X. Wang, Q. Sui, T. Zhang, Z. Wang, L. Liu, D. Li, S. Feng, S. Zhong, H. Wang, V. Bouchiat, M. Nunez Regueiro, N. Rougemaille, J. Coraux, A. Purbawati, A. Hadj-Azzem, Z. Wang, B. Dong, X. Wu, T. Yang, G. Yu, B. Wang, Z. Han, X. Han and Z. Zhang, Nano Res., 2020, 13, 3358–3363,  DOI:10.1007/s12274-020-3021-4.
116. Y. Liu and C. Petrovic, Phys. Rev. B, 2017, 96, 134410,  DOI:10.1103/PhysRevB.96.134410.
117. Y. Liu and C. Petrovic, Phys. Rev. B, 2018, 98, 195122,  DOI:10.1103/PhysRevB.98.195122.
118. Y. Liu, M. Abeykoon, E. Stavitski, K. Attenkofer and C. Petrovic, Phys. Rev. B, 2019, 100, 245114,  DOI:10.1103/PhysRevB.100.245114.
119. A. L. Coughlin, D. Xie, Y. Yao, X. Zhan, Q. Chen, H. Hewa- Walpitage, X. Zhang, H. Guo, H. Zhou, J. Lou, J. Wang, Y. S. Li, H. A. Fertig and S. Zhang, ACS Nano, 2020, 14, 15256–15266,  DOI:10.1021/acsnano.0c05534.
120. R. Saha, H. L. Meyerheim, B. Göbel, B. K. Hazra, H. Deniz, K. Mohseni, V. Antonov, A. Ernst, D. Knyazev, A. Bedoya-Pinto, I. Mertig and S. S. P. Parkin, Nat. Commun., 2022, 13, 3965,  DOI:10.1038/s41467-022-31319-y.
121. B. Li, X. Deng, W. Shu, X. Cheng, Q. Qian, Z. Wan, B. Zhao, X. Shen, R. Wu, S. Shi, H. Zhang, Z. Zhang, X. Yang, J. Zhang, M. Zhong, Q. Xia, J. Li, Y. Liu, L. Liao, Y. Ye, L. Dai, Y. Peng, B. Li and X. Duan, Mater. Today, 2022, 57, 66–74,  DOI:10.1016/j.mattod.2022.04.011.
122. X. H. Luo, W. J. Ren and Z. D. Zhang, J. Magn. Magn. Mater., 2018, 445, 37–43,  DOI:10.1016/j.jmmm.2017.08.078.
123. M. Huang, S. Wang, Z. Wang, P. Liu, J. Xiang, C. Feng, X. Wang, Z. Zhang, Z. Wen, H. Xu, G. Yu, Y. Lu, W. Zhao, S. A. Yang, D. Hou and B. Xiang, ACS Nano, 2021, 15, 9759–9763,  DOI:10.1021/acsnano.1c00488.
124. B. Tang, X. Wang, M. Han, X. Xu, Z. Zhang, C. Zhu, X. Cao, Y. Yang, Q. Fu, J. Yang, X. Li, W. Gao, J. Zhou, J. Lin and Z. Liu, Nat. Electron., 2022, 5, 224–232,  DOI:10.1038/s41928-022-00754-6.
125. L. Z. Zhang, X. D. He, A. L. Zhang, Q. L. Xiao, W. L. Lu, F. Chen, Z. Feng, S. Cao, J. Zhang and J. Y. Ge, APL Mater., 2020, 8, 031101,  DOI:10.1063/1.5143387.
126. A. F. Andresen, E. Zeppezauer, T. Boive, B. Nordström and C. Brändén, Acta Chem. Scand., 1970, 24, 3495–3509,  DOI:10.3891/acta.chem.scand.24-3495.
127. J. Dijkstra, H. H. Weitering, C. F. van Bruggen, C. Haas and R. A. de Groot, J. Phys.: Condens. Matter, 1989, 1, 9141–9161,  DOI:10.1088/0953-8984/1/46/008.
128. K. Lukoschus, S. Kraschinski, C. Näther, W. Bensch and R. K. Kremer, J. Solid State Chem., 2004, 177, 951–959,  DOI:10.1016/j.jssc.2003.09.041.
129. T. Hamasaki, T. Hashimoto, Y. Yamaguchi and H. Watanabe, Solid State Commun., 1975, 16, 895–897,  DOI:10.1016/0038-1098(75)90888-1.
130. S. Polesya, S. Mankovsky, D. Benea, H. Ebert and W. Bensch, J. Phys.: Condens. Matter, 2010, 22,  DOI:10.1088/0953-8984/22/15/156002.
131. H. Y. Lv, W. J. Lu, D. F. Shao, Y. Liu and Y. P. Sun, Phys. Rev. B, 2015, 92, 214419,  DOI:10.1103/PhysRevB.92.214419.
132. J. Zhong, M. Wang, T. Liu, Y. Zhao, X. Xu, S. Zhou, J. Han, L. Gan and T. Zhai, Nano Res., 2022, 15, 1254–1259,  DOI:10.1007/s12274-021-3633-3.
133. Y. Fujisawa, M. Pardo-Almanza, J. Garland, K. Yamagami, X. Zhu, X. Chen, K. Araki, T. Takeda, M. Kobayashi, Y. Takeda, C. H. Hsu, F. C. Chuang, R. Laskowski, K. H. Khoo, A. Soumyanarayanan and Y. Okada, Phys. Rev. Mater., 2020, 4, 114001,  DOI:10.1103/PhysRevMaterials.4.114001.
134. D. R. Klein, D. Macneill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernández-Rossier and P. Jarillo-Herrero, Science, 2018, 360, 1218–1222,  DOI:10.1126/science.aar3617.
135. Y. Liu, L. Wu, X. Tong, J. Li, J. Tao, Y. Zhu and C. Petrovic, Sci. Rep., 2019, 9, 13599,  DOI:10.1038/s41598-019-50000-x.
136. N. Ubrig, Z. Wang, J. Teyssier, T. Taniguchi, K. Watanabe, E. Giannini, A. F. Morpurgo and M. Gibertini, 2D Mater., 2020, 7, 015007,  DOI:10.1088/2053-1583/ab4c64.
137. D. A. Wahab, M. Augustin, S. M. Valero, W. Kuang, S. Jenkins, E. Coronado, I. V. Grigorieva, I. J. Vera-Marun, E. Navarro-Moratalla, R. F. Evans, K. S. Novoselov and E. J. Santos, Adv. Mater., 2021, 33, 2004138,  DOI:10.1002/adma.202004138.
138. Y. Feng, X. Wu, L. Hu and G. Gao, J. Mater. Chem. C, 2020, 8, 14353–14359,  10.1039/d0tc04156d.
139. C. Xu, C. Carnahan, H. Zhang, M. Sretenovic, P. Zhang, D. Xiao and X. Ke, Phys. Rev. B, 2023, 107, L060404,  DOI:10.1103/PhysRevB.107.L060404.
140. Y. Guo, N. Liu, Y. Zhao, X. Jiang, S. Zhou and J. Zhao, Chin. Phys. Lett., 2020, 37, 107506,  DOI:10.1088/0256-307X/37/10/107506.
141. R. Li, J. Jiang, H. Bai and W. Mi, J. Mater. Chem. C, 2022, 10, 14955–14962,  10.1039/d2tc03228g.
142. I. S. Jacobs, S. Roberts and P. E. Lawrence, J. Appl. Phys., 1965, 36, 1197–1198,  DOI:10.1063/1.1714167.
143. X. Zhou, B. Brzostowski, A. Durajski, M. Liu, J. Xiang, T. Jiang, Z. Wang, S. Chen, P. Li, Z. Zhong, A. Drzewínski, M. Jarosik, R. Szczésniak, T. Lai, D. Guo and D. Zhong, J. Phys. Chem. C, 2020, 124, 9416–9423,  DOI:10.1021/acs.jpcc.0c03050.
144. L. S. Xie, S. Husremovíc, O. Gonzalez, I. M. Craig and D. K. Bediako, J. Am. Chem. Soc., 2022, 144, 9525–9542,  DOI:10.1021/jacs.1c12975.
145. E. Maniv, R. A. Murphy, S. C. Haley, S. Doyle, C. John, A. Maniv, S. K. Ramakrishna, Y. L. Tang, P. Ercius, R. Ramesh, A. P. Reyes, J. R. Long and J. G. Analytis, Nat. Phys., 2021, 17, 525–530,  DOI:10.1038/s41567-020-01123-w.
146. J. G. Checkelsky, M. Lee, E. Morosan, R. J. Cava and N. P. Ong, Phys. Rev. B, 2008, 77, 014433,  DOI:10.1103/PhysRevB.77.014433.
147. N. L. Nair, E. Maniv, C. John, S. Doyle, J. Orenstein and J. G. Analytis, Nat. Mater., 2020, 19, 153–157,  DOI:10.1038/s41563-019-0518-x.
148. K. T. Ko, K. Kim, S. B. Kim, H. D. Kim, J. Y. Kim, B. I. Min, J. H. Park, F. H. Chang, H. J. Lin, A. Tanaka and S. W. Cheong, Phys. Rev. Lett., 2011, 107, 247201,  DOI:10.1103/PhysRevLett.107.247201.
149. Y. Togawa, Y. Kousaka, K. Inoue and J. I. Kishine, J. Phys. Soc. Jpn., 2016, 85, 112001,  DOI:10.7566/JPSJ.85.112001.
150. N. J. Ghimire, M. A. McGuire, D. S. Parker, B. Sipos, S. Tang, J.-Q. Yan, B. C. Sales and D. Mandrus, Phys. Rev. B, 2013, 87, 104403,  DOI:10.1103/PhysRevB.87.104403.
151. N. Sirica, P. Vilmercati, F. Bondino, I. Pis, S. Nappini, S. K. Mo, A. V. Fedorov, P. K. Das, I. Vobornik, J. Fujii, L. Li, D. Sapkota, D. S. Parker, D. G. Mandrus and N. Mannella, Commun. Phys., 2020, 3, 65,  DOI:10.1038/s42005-020-0333-3.
152. X. Zhao, P. Song, C. Wang, A. C. Riis-Jensen, W. Fu, Y. Deng, D. Wan, L. Kang, S. Ning, J. Dan, T. Venkatesan, Z. Liu, W. Zhou, K. S. Thygesen, X. Luo, S. J. Pennycook and K. P. Loh, Nature, 2020, 581, 171–177,  DOI:10.1038/s41586-020-2241-9.
153. E. Maniv, N. L. Nair, S. C. Haley, S. Doyle, C. John, S. Cabrini, A. Maniv, S. K. Ramakrishna, Y.-L. Tang, P. Ercius, R. Ramesh, Y. Tserkovnyak, A. P. Reyes and J. G. Analytis, Sci. Adv., 2021, 7, eabd8452,  DOI:10.1126/sciadv.abd8452.
154. A. Little, C. Lee, C. John, S. Doyle, E. Maniv, N. L. Nair, W. Chen, D. Rees, J. W. Venderbos, R. M. Fernandes, J. G. Analytis and J. Orenstein, Nat. Mater., 2020, 19, 1062–1067,  DOI:10.1038/s41563-020-0681-0.
155. W. J. Hardy, C. W. Chen, A. Marcinkova, H. Ji, J. Sinova, D. Natelson and E. Morosan, Phys. Rev. B, 2015, 91, 054426,  DOI:10.1103/PhysRevB.91.054426.
156. M. Eibschütz, S. Mahajan, F. J. Disalvo, G. W. Hull and J. V. Waszczak, J. Appl. Phys., 1981, 52, 2098–2100,  DOI:10.1063/1.329629.
157. M. Koyano, H. Watanabe, Y. Yamamura, T. Tsuji and S. Katayama, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 2000, 341, 33–38,  DOI:10.1080/10587250008026113.
158. T. Tsuji, Y. Yamamura, M. Koyano, S. Katayama and M. ito, J. Alloys Compd., 2001, 317, 213–216,  DOI:10.1016/S0925-8388(00)01329-3.
159. T. Moriya and T. Miyadai, Solid State Commun., 1982, 42, 209–212,  DOI:10.1016/0038-1098(82)91006-7.
160. K. Du, F.-T. Huang, J. Kim, S. J. Lim, K. Gamage, J. Yang, M. Mostovoy, J. Garlow, M.-G. Han, Y. Zhu and S.-W. Cheong, Proc. Natl. Acad. Sci. USA, 2021, 118, e2023337118,  DOI:10.1073/pnas.2023337118.
161. D. Obeysekera, K. Gamage, Y. Gao, S. W. Cheong and J. Yang, Adv. Electron. Mater., 2021, 7, 2100424,  DOI:10.1002/aelm.202100424.
162. Y. Togawa, T. Koyama, K. Takayanagi, S. Mori, Y. Kousaka, J. Akimitsu, S. Nishihara, K. Inoue, A. S. Ovchinnikov and J. Kishine, Phys. Rev. Lett., 2012, 108, 107202,  DOI:10.1103/PhysRevLett.108.107202.
163. C. Zhang, Y. Yuan, M. Wang, P. Li, J. Zhang, Y. Wen, S. Zhou and X. X. Zhang, Phys. Rev. Mater., 2019, 3, 114403,  DOI:10.1103/PhysRevMaterials.3.114403.
164. J. M. Pereira, D. Tezze, M. Ormaza, L. E. Hueso and M. Gobbi, Adv. Phys. Res., 2023, 2, 2200084,  DOI:10.1002/apxr.202200084.
165. M. Mi, X. Zheng, S. Wang, Y. Zhou, L. Yu, H. Xiao, H. Song, B. Shen, F. Li, L. Bai, Y. Chen, S. Wang, X. Liu and Y. Wang, Adv. Funct. Mater., 2022, 32, 2112750,  DOI:10.1002/adfm.202112750.
166. S. Samanta, H. Iturriaga, T. T. Mai, A. J. Biacchi, R. Islam, A. R. HightWalker, M. F. Sanad, C. Phatak, R. Siebenaller, E. Rowe, M. A. Susner, F. Xue and S. R. Singamaneni, arXiv, 2023 DOI:10.48550/arXiv.2312.01270.
167. R. Clément, J. J. Girerd, I. Morgenstern-Badarau, J. Rouxel, B. E. Taylor, J. Steger, A. Wold and J. Solid, Inorg. Chem., 1980, 19, 2852–2854,  DOI:10.1021/ic50211a079.
168. S. Bénard, A. Léaustic, E. Rivière, R. Yu and P. Clément, Chem. Mater., 2001, 13, 3709–3716,  DOI:10.1021/cm011019j.
169. X. Ma, L. Zhang, C. Xu, Q. Dong, R. I. Walton, Z. Li, S. Honglong, C. Genfu, H. Jiangping and Y. Huaxin, Chem. Commun., 2022, 56, 4603–4606,  10.1039/D0CC00636J.
170. P. Fuentealba, V. Paredes-Garcia, D. Venegas-Yazigi, I. D. Silva, C. J. Magon, R. Costa De Santana, N. Audebrand, J. Manzur and E. Spodine, RSC Adv., 2017, 7, 33305–33313,  10.1039/c7ra05089e.
171. G. Abellán, J. L. Jordá, P. Atienzar, M. Varela, M. Jaafar, J. Gómez-Herrero, F. Zamora, A. Ribera, H. García and E. Coronado, Chem. Sci., 2015, 6, 1949–1958,  10.1039/c4sc03460k.
172. A. Léaustic, J. P. Audiè, D. Cointereau, R. Clément, L. Lomas, F. Varret and H. Constant-Machado, Chem. Mater., 1996, 8, 1954–1961,  DOI:10.1021/cm960059y.
173. G. T. Lin, H. L. Zhuang, X. Luo, B. J. Liu, F. C. Chen, J. Yan, Y. Sun, J. Zhou, W. J. Lu, P. Tong, Z. G. Sheng, Z. Qu, W. H. Song, X. B. Zhu and Y. P. Sun, Phys. Rev. B, 2017, 95, 245212,  DOI:10.1103/PhysRevB.95.245212.
174. Y. Sun, R. C. Xiao, G. T. Lin, R. R. Zhang, L. S. Ling, Z. W. Ma, X. Luo, W. J. Lu, Y. P. Sun and Z. G. Sheng, Appl. Phys. Lett., 2018, 112, 072409,  DOI:10.1063/1.5016568.
175. A. Milosavljevíc, A. Šolajíc, S. Djurdjíc-Mijin, J. Pešíc, B. Višíc, Y. Liu, C. Petrovic, N. Lazarevíc and Z. V. Popovíc, Phys. Rev. B, 2019, 99, 214304,  DOI:10.1103/PhysRevB.99.214304.
176. Y. Liu, J. Li, J. Tao, Y. Zhu and C. Petrovic, Sci. Rep., 2019, 9, 13233,  DOI:10.1038/s41598-019-49654-4.
177. M. E. Kamminga, S. J. Cassidy, P. P. Jana, M. Elgaml, N. D. Kelly and S. J. Clarke, Dalton Trans., 2021, 50, 11376–11379,  10.1039/d1dt00960e.
178. Z. Li, X. Zhang, X. Zhao, J. Li, T. S. Herng, H. Xu, F. Lin, P. Lyu, X. Peng, W. Yu, X. Hai, C. Chen, H. Yang, J. Martin, J. Lu, X. Luo, A. H. Castro Neto, S. J. Pennycook, J. Ding, Y. Feng and J. Lu, Adv. Mater., 2020, 32, 1907645,  DOI:10.1002/adma.201907645.
179. Q. Qian, H. Ren, J. Zhou, Z. Wan, J. Zhou, X. Yan, J. Cai, P. Wang, B. Li, Z. Sofer, B. Li, X. Duan, X. Pan, Y. Huang and X. Duan, Nature, 2022, 606, 902–908,  DOI:10.1038/s41586-022-04846-3.
180. M. S. Whittingham, Prog. Solid State Chem., 1978, 12, 41–99,  DOI:10.1016/0079-6786(78)90003-1.
181. T. Yajima, M. Koshiko, Y. Zhang, T. Oguchi, W. Yu, D. Kato, Y. Kobayashi, Y. Orikasa, T. Yamamoto, Y. Uchimoto, M. A. Green and H. Kageyama, Nat. Commun., 2016, 7,  DOI:10.1038/ncomms13809.
182. V. F. Sears, Neutron News, 1992, 3, 26–37,  DOI:10.1080/10448639208218770.
183. A. Rauch and W. Waschkowski, Neutron Data Booklet, Old City, 2nd edn, 2003.
184. R. Yang, Y. Fan, L. Mei, H. S. Shin, D. Voiry, Q. Lu, J. Li and Z. Zeng, Nat., Synth., 2023, 2, 101–118,  DOI:10.1038/s44160-022-00232-z.
185. M. Wang and K. J. Koski, J. Phys.: Condens. Matter, 2016, 28, 494002,  DOI:10.1088/0953-8984/28/49/494002.
186. Y. R. Li, A. S. Poyraz, X. Hu, M. Cuiffo, C. R. Clayton, L. Wu, Y. Zhu, E. S. Takeuchi, A. C. Marschilok and K. J. Takeuchi, J. Electrochem. Soc., 2017, 164, A2151–A2158,  DOI:10.1149/2.1431709jes.
187. A. D. Hillier, D. M. Paul and K. Ishida, Microchem. J., 2016, 125, 203–207,  DOI:10.1016/j.microc.2015.11.031.
188. A. D. Hillier, S. J. Blundell, I. McKenzie, I. Umegaki, L. Shu, J. A. Wright, T. Prokscha, F. Bert, K. Shimomura, A. Berlie, H. Alberto and I. Watanabe, Nat. Rev. Methods Primers, 2022, 2(4) DOI:10.1038/s43586-021-00089-0.
189. S. De Graaf, J. Momand, C. Mitterbauer, S. Lazar and B. J. Kooi, Sci. Adv., 2020, 6, eaay4312,  DOI:10.1126/sciadv.aay4312.
190. M. Azhagurajan, T. Kajita, T. Itoh, Y. G. Kim and K. Itaya, J. Am. Chem. Soc., 2016, 138, 3355–3361,  DOI:10.1021/jacs.5b11849.
191. F. Li, J. Zou, L. Cao, Z. Li, S. Gu, Y. Liu, J. Zhang, H. Liu and Z. Lu, J. Phys. Chem. C, 2019, 123, 5067–5072,  DOI:10.1021/acs.jpcc.8b09898.
192. K. F. Mak, J. Shan and D. C. Ralph, Nat. Rev. Phys., 2019, 1, 646–661,  DOI:10.1038/s42254-019-0110-y.
193. B. Zhou, Y. Wang, G. B. Osterhoudt, P. Lampen-Kelley, D. Mandrus, R. He, K. S. Burch and E. A. Henriksen, J. Phys. Chem. Solids, 2019, 128, 291–295,  DOI:10.1016/j.jpcs.2018.01.026.
194. A. J. Browne, A. Krajewska and A. S. Gibbs, J. Mater. Chem. C, 2021, 9, 11640–11654,  10.1039/d1tc02070f.
195. H. Zabel and S. M. Shapiro, Phys. Rev. B, 1987, 36, 7292,  DOI:10.1103/PhysRevB.36.7292.
196. K. Sugihara, K. Kobayashi and H. Oshima, J. Phys. Soc. Jpn., 1990, 59, 2865–2874,  DOI:10.1143/JPSJ.59.2865.
197. D. G. Wiesler, H. Zabel and S. M. Shapiro, Z. Phys. B: Condens. Matter, 1994, 93, 277–297,  DOI:10.1007/BF01312698.
198. J. N. Coleman, M. Lotya, A. O’neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571,  DOI:10.1126/science.1194975.
199. Z. Lin, Y. Liu, U. Halim, M. Ding, Y. Liu, Y. Wang, C. Jia, P. Chen, X. Duan, C. Wang, F. Song, M. Li, C. Wan, Y. Huang and X. Duan, Nature, 2018, 562, 254–258,  DOI:10.1038/s41586-018-0574-4.

---