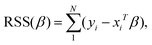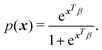Open Access Article
Open Access ArticleMachine learning for carbon dot synthesis and applications
Ali Nabi
Duman
 *a and
Almaz S.
Jalilov
*a and
Almaz S.
Jalilov
 *b
*b
aDepartment of Mathematics and Statistics, University of Houston-Downtown, Houston, USA. E-mail: dumana@uhd.edu
bDepartment of Chemistry and Interdisciplinary Research Center for Advanced Materials, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia. E-mail: jalilov@kfupm.edu.sa
First published on 29th July 2024
Abstract
One of the hottest topics in nanoparticles research right now is carbon dots (CDs). In order to be used in applications like medical imaging and diagnostics, pharmaceutics, optoelectronics, and photocatalysis, CDs must be synthesized with carefully controlled properties. This is often a tedious task due to the fact that nanoparticle syntheses frequently involve multiple chemicals and are carried out under complex experimental conditions. The emerging data-driven methods from artificial intelligence (AI) and machine learning (ML) provide promising tools to go beyond the time-consuming and laborious trial-and-error approach. In this review, we focus on the recent uses of ML accelerating exploration of the CD chemical space. Future applications of these methods address the current limitations in CD synthesis expanding the potential uses of these intriguing nanoparticles.
Almaz Jalilov obtained his PhD in Chemistry from the University of Wisconsin. After postdoctoral positions in Northwestern University and Rice University, he joined King Fahd University of Petroleum and Minerals, where he is now an Associate Professor of Chemistry, and his research interest includes physical organic chemistry and materials chemistry with an emphasis on the mechanism-based design of carbon nanoparticles for sustainable energy and catalysis. |
Ali Nabi Duman received a PhD from the University of British Columbia in 2010. He has been an Assistant Professor of Mathematics at King Fahd University of Petroleum and Minerals from 2015 to 2023. In 2023, he joined the University of Houston-Downtown, where he is now an Assistant Professor of Data Science. His research focuses on topological data analysis with applications in neuroimaging, microscopy and genomics. |
1 Introduction
Due to their distinctive advantages, such as simple synthesis, long-term photo- and colloidal stability, biocompatibility, biodegradability, non-/low toxicity, low cost, tunable photoluminescence, and good dispersibility, carbon-based nanomaterials, particularly carbon dots (CDs), have been one of the most studied materials in recent years.1–8 These favorable characteristics make CDs useful for applications in biosensing and bioimaging,9–11 cancer research,12 drug delivery,13 visible light communication,14,15 and optoelectronic devices.16–19 A base carbon core with chemical functional groups attached or modified on the surface makes up the core–shell-like structure of CDs. The surface generally consists of some common functional groups, such as amino, epoxy, carbonyl, aldehyde, hydroxyl, and carboxylic acid, while the carbon core structure consists of sp2 and sp3 carbon atoms.20–22 The additional molecular structures which are essential to their features make CDs extremely complex.CDs can be synthesized by utilizing bottom-up or top-down methods.16,23 In the top-down methods, large carbon materials are cut into small carbon structures smaller than 10 nm. The demanding physical procedures to break down the carbon materials (e.g., graphite, graphene oxide, carbon nanotubes, activated carbon, soot) involve laser ablation, arc discharge and nanolithography under unfavorable conditions such as strong oxidants, concentrated acids, and high temperatures.24–33 The more adaptable and accessible bottom-up methods usually include ultrasound synthesis, chemical oxidation, room temperature method, and hydrothermal and solvothermal processing of relatively small molecular precursors.34 Although these methods may include high temperatures/pressures, long reaction times, or toxic solvents, the use of microwaves in solvothermal synthesis partially solves these issues by reducing the reaction time and the amount of solvents.35–40 The room temperature method is another advantageous technique because it does not require complicated machinery or harsh synthesis conditions, making it environmentally friendly and sustainable.41–43 Hence, the simple setup, low cost and accessibility to a wide variety of precursors make bottom-up methods more favorable over top-down methods.
CDs can be divided into four main classes according to their carbon core structure, surface functionalities, and performance features: (i) graphene quantum dots (GQDs), (ii) carbon nanodots (CNDs), (iii) carbon quantum dots (CQDs), and (iv) carbonized polymer dots (CPDs).44,45 GQDs are usually synthesized by using a top-down approach, while preparation of CNDs and CQDs is mainly done by using bottom-up methods.46–48 A variety of models (e.g. polycyclic aromatic hydrocarbons, molecular fluorophores, or sp2/sp3 hybrid spherical structures) are used to explain the different structures of CDs.49–52
Due to the necessary high temperatures during bottom-up synthesis of CDs, multiple reaction pathways occur while forming a considerable amount of by-products. Along with the irregular mass transfer, low reproducibility is also common as reported in earlier studies.35,53 One solution to optimize the target properties is to scan large experimental synthesis conditions including the reaction temperature, the mass of precursor, ramp rate, and reaction time. However, the high complexity of the extracted data, repetitive experimental procedures, and the lack of predictability make this scan very time-consuming to achieve ideal results. For example, it is still unclear how CQDs emit their fluorescence because it is a very complicated process. It is customary to analyze the pH-dependent photoluminescence (PL) spectra of CQDs at a fixed excitation and ignore all other potential excitations; however, this method only allows for the extraction of a portion of the available data.39,54–60 On the other hand, the complexity of data analysis methods can rise along with the number of PL measurements. Similarly, current CDs reported in the literature were frequently prepared optimally by controlling one reaction parameter and fixing the other reaction factors, while not considering the complex relationship between reaction parameters during CD synthesis. Therefore, there is a need to employ methods that accelerate the screening of the necessary parameters in order to create CDs with enhanced features and applications.
Quantum mechanics methods such as density functional theory (DFT) provide a reliable computational solution to search a reasonably designed parameter space.61,62 These semi-empirical approaches can be used to explore the electronic structure and chemical reactivity of CDs.63–67 Density-functional-based tight binding (DFTB) is another semi-parametric method which approximates DFT in a tight binding framework.68–71 DFTB requires fewer empirical parameters and is computationally more efficient than DFT. The mechanism of graphene formation and single-walled carbon nanotube nucleation are examples studied using DFTB.72,73 However, these semi-empirical methods are computationally too costly for a large search space. The alternative approaches to reduce the entire search space include optimization and gradient based algorithms. The accuracy and computational performance of these methods depend on the initially determined parameters; hence, they might return different results from the different initial values and potentially end up in local minima.
Data-driven approaches based on machine learning (ML) algorithms provide an alternative to the abovementioned computational methods for the description of the structure and properties of CDs. As a branch of artificial intelligence, ML employs statistical and probabilistic methods to learn from a given dataset by optimizing performance measures for particular tasks.74,75 Certain methods have the ability to detect the relationship (correlations/inference) between input variables and the target variable. Instead of screening the entire parameter space, ML methods learn the hidden patterns using a limited amount of data. These trained algorithms are later generalized to predict the target variables from previously unseen input variables. As a result of increasing amount of experimental data and accessible computational power, ML has successful applications in a variety of fields including image/speech recognition, cancer research, chemical synthesis, and protein structure prediction.76–84
In materials science, ML has attracted a lot of interest in applications such as materials discovery, materials structure/property prediction, performance optimization, and acceleration of the protocols for nanoparticle synthesis.85–95 Using ML, the reaction parameters and their effects on the nanoparticle synthesis can be revealed objectively,96,97 and the synthesis process can be made more efficient by choosing appropriate evaluation criteria including shape, size, polydispersity, and surface chemistry.98 ML accelerates not only the experimental protocols but also the search of new semiconductor, metal, carbon-based, and polymeric nanoparticles with superior features requiring low computational cost.8 The large amount of data needed for ML algorithms can be obtained using computational or experimental methods. Numerous databases such as the Materials Project, Automatic Flow for Materials Discovery, Open Quantum Materials Database, Novel Materials Discovery make it possible to access data of a lot of materials in addition to using computer simulations to generate it.
In particular, the use of ML in the field of CD has generated a lot of interest in research in recent years. The proper adjustment of a variety of variables, including precursors, temperature, and reaction time, is necessary for the successful preparation of CDs. It is simple to use these elements as input parameters in ML, which is trained with the available experimental data and generates accurate new predictions. Therefore, the addition of ML can aid in the relationship between precursors and desired properties, which may result in the formation of a design principle for further study and significantly shorten the synthesis cycle and lower the cost of CDs.
Many outstanding reviews on the applications of computational and ML methods to the nanoparticle synthesis have been published.98–106 Although some of them focus on CD synthesis, they partially cover the development of ML methods along with the experimental techniques.99 The more general reviews include CDs as a subcategory of nanoparticles,98,100 quantum dots,103,104 and graphene-based101,105 or polymer-based106 materials. Theoretical methods such as quantum mechanics and/or molecular mechanics approaches applied to CDs are also available in the literature.102 To the best of our knowledge, a thorough review of ML applications specifically for CD synthesis is lacking. In this review, we outline the primary ML algorithms in the context of CD research, discuss recent studies on ML applications for CD synthesis, and enumerate potential future directions for this rapidly expanding field of study (Table 1).
| ML models | Input | Output | Samples | Ref. |
|---|---|---|---|---|
| MLR, poly. reg. | Microstructural features | Thermoelectric performance | 322 | 107 |
| Lin. reg., poly. reg. | Synthesis process parameters | UV-visible and PL spectra | 44 | 108 |
| MLR, KNN | Synthesis process parameters | PLQY, PL peak position | 227 | 109 |
| MLR | PL characteristics | Temperature sensing accuracy | 121 | 110 |
| Random forest | Reaction parameters | Emission wavelength, Stokes shift, PLQY | 480 | 111 |
| Log. reg., KNN, SVM | CD fluorescence sensor array | Protein classification | 48 | 112 |
| CNN | Synthesis process parameters | Spectral properties and FL colors | 170 | 113 |
| ANN | Synthesis process parameters | Color classification, emission wavelength | 407 | 114 |
| ANN | CDs fluorescence variation maps | Amino acid classification | 90 | 115 |
| Multilayer perceptron | Synthesis process parameters | PLQY | 30 | 116 |
| CNN | Emission/PL decay data of CDs | Ethanol content prediction | 597 | 117 |
| XGBoost | Synthesis process parameters | PLQY | 391 | 82 |
| XGBoost | Synthesis process parameters | PLQY | 467 | 118 |
| PCA, XGBoost | Synthesis process parameters | FL intensity, emission centers | 400 | 119 |
| XGBoost | Reaction parameters of CD catalysts | Failure/success of oxidation of C–H bonds | 652 | 120 |
| GBDT | Biochar preparation parameters | Fluorescence quantum yield | 480 | 121 |
| Random forest | Precursor combinations | PL wavelength intensity | 202 | 122 |
| Random forest, GA | Synthesis process parameters | Corrosion inhibition efficiency | 102 | 123 |
| PCA, MCR, NMF | Wavelengths, pH | Unsupervised clustering | 401 | 124 |
| LDA, SVM | CD fluorescence sensor array | Tetracycline classification | 92 | 125 |
2 Linear regression
Numerous machine learning algorithms have been devised for diverse learning scenarios, encompassing unsupervised, semi-supervised, and supervised learning. In scientific and engineering contexts, supervised learning, also known as predictive modeling, is widely favored. Of all the supervised learning methods, linear regression is the most fundamental, having been extensively studied and applied due to its simplicity and high interpretability. Given input variables x = (x1,…,xp), the output variable y is predicted by| y = xTβ. |
The most common objective function to determine the coefficients β is the residual sum of squares:
Applying multiple linear regression (MLR), Armida et al. explored the relationship between the size, dimensionality, concentration, doping and other microstructural features of carbon dots and their thermoelectric performance.107 The conversion efficiency of a thermoelectric material is quantified by the thermoelectric figure of merit, ZT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the absolute temperature. MLR is performed for each ZT, σ, T and κ using 10 input variables characterizing size, dimensionality, concentration, doping and other features. The results revealed a strong negative relationship between functionalization and S, as well as a strong positive relationship between the type of carbon nanostructures and σ. Polynomial regression highlighted significant impacts of six input parameters on the Seebeck coefficient, electric conductivity σ and thermal conductivity κ, while no combination of parameters significantly affected thermoelectricity ZT.
Zhang et al. utilized linear and polynomial regression models to investigate the core synthesis process parameters of B,N-GQDs (synthesis temperature, H2O2 additional volume, and synthesis time).108 The models are trained using the optical properties of B,N-GQDs derived from UV-visible and PL spectra (i.e. 675/500 peak intensity ratio and PLQY). While the authors employed other complex models such as bagging regression, random forest regression, LASSO regression, and ridge regression, the highest R2-score is obtained using the polynomial model of degree 7 (R2 = 0.9860). Polynomial and linear regression models pointed out that high H2O2 additional volume, low synthesis temperature, and appropriate synthesis time in the selected process conditions contribute to achieving a high 675/500 peak intensity ratio (see Fig. 1).
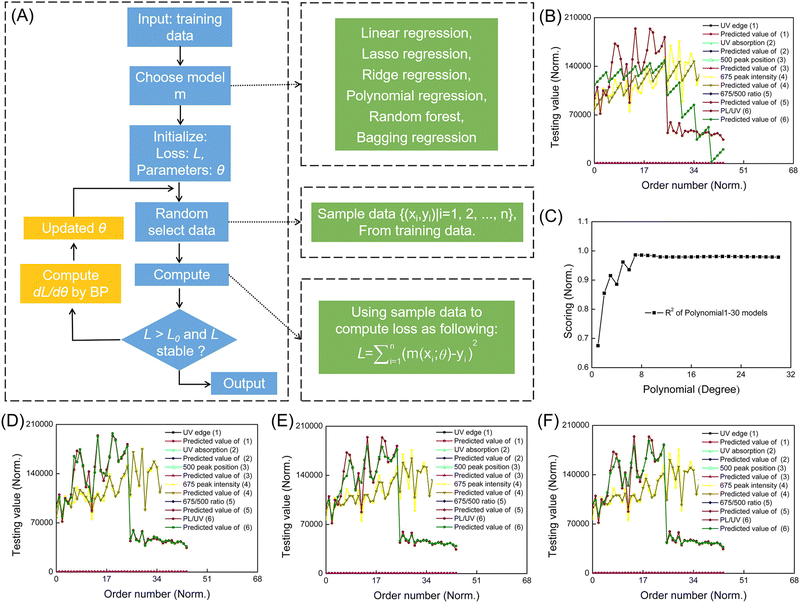 | ||
| Fig. 1 Machine learning-assisted evaluation of B,N-GQDs. (A) Schematic of machine learning-assisted evaluation of the optical properties of B,N-GQDs. Optical properties of B,N-GQDs in varied synthesis conditions and the corresponding predicted value sets with (B) linear regression, (C) polynomials 1–30, (D) polynomial regression 7, (E) bagging regression, and (F) random forest regression. The R2 scores of linear regression, polynomial regression 7, bagging regression, and random forest regression models are 0.6751, 0.9860, 0.9473, and 0.9469, respectively. Reprinted with permission from ref. 108. Copyright 2022 American Chemical Society. | ||
Tuchin et al. analysed a dataset on the synthesis parameters and optical characteristics of carbon dots focusing on their optical behavior within the red and near-infrared wavelengths.109 A predictive model using multiple linear regression has been developed to forecast the spectral attributes of these carbon dots. The validity of this model was confirmed by comparing its predictions with the actual optical properties observed in carbon dots synthesized in three distinct laboratories.
Doring et al. applied a multiple linear regression model that combines steady-state and time-resolved luminescence data from carbon dots to enhance temperature sensing accuracy to 0.54 K.110 This research illustrates the significant advancements in temperature sensing using optical probes through multidimensional machine learning techniques.
Several machine learning algorithms are dedicated to classification tasks. Logistic regression considered under the umbrella of a generalized linear model is specifically designed for predicting probabilities associated with discrete (categorical) variables. The probability p(x) of a sample belonging to a particular category is expressed as
3 Artificial neural networks
Linear models excel when a linear connection exists between input and output variables; however, their accuracy diminishes in the presence of nonlinear interactions between variables. Artificial neural networks (ANNs) are employed to surmount these constraints. ANNs are characterized by multiple hidden layers, excluding input and output layers. Each hidden layer consists of numerous neurons, employing linear regression with a nonlinear activation function. Notably, the hidden layers feature complete connectivity between the neurons of adjacent layers. It is proven that any continuous function can be approximated by ANNs with one hidden layer. Convolutional neural networks (CNNs) stand as a prevalent architecture within artificial neural networks (ANNs), finding particular application in the analysis of images and videos. At the heart of the CNN lies the convolution layer, featuring multiple convolution filters. Each filter undergoes convolution with the input from the preceding layer, producing feature maps subsequently utilized as the input for the following layer. The streamlined interconnection between layers contributes to the computational efficiency of CNNs, enabling them to outperform basic ANN models, particularly in tasks such as image classification.ANNs have found applications in various carbon dot studies. Wang et al. have used a convolutional neural network (CNN) model tailored for predicting the optical characteristics of carbon dots such as spectral properties and fluorescence (FL) colors under ultraviolet (UV) irradiation.113 The model is trained with CD synthesis features (precursor, mass, temperature, solvent, and reaction time) from 170 prototypical studies. The output layer is a feature vector that indicates spectral properties and FL color under UV irradiation. Subsequently, CDs with distinct emission properties were synthesized, and their experimental data were compared with the predicted outcomes from the trained model. These synthesized CDs were employed in cell imaging, demonstrating good performance. These findings suggest that the implementation of CNNs can assist researchers in achieving effective CD design without the need for extensive manual processes. Within the same study, alternative classification models, such as support vector machines, K-nearest neighbors, random forests, decision trees, and extreme gradient boosting, demonstrated inferior performance compared to CNNs. These outcomes underscore the significant potential of CNNs in guiding the synthesis of CDs.
Senanayake et al. conducted a parallel study, employing ANNs, to characterize the influence of synthesis parameters on and make predictions for the emission color and wavelength of CDs.114 The machine analysis indicated that the selection of the reaction method, purification method, and solvent is more closely correlated with CD emission characteristics compared to factors like reaction temperature or time, which are often adjusted in experimental settings. A total of 407 data examples were gathered from the literature, with 379 of them constituting the training database. The remaining 28 data examples were reserved as an external test set to validate the model. The color prediction from the classification model, which does not include reaction temperature and time as features, attained a training accuracy value of 0.94. The accuracy of emission prediction is enhanced from MAE = 38.4 to 25.8 when a combination of both classification and regression methods is employed. To overcome the limitations associated with a small dataset in an ANN model, the authors used an ANN k-ensemble model which outperformed XGBoost, K-nearest neighbor (KNN), and support vector machine (SVM). The hybrid models employed a two-step approach: initially, a classification model was utilized to predict the color, and subsequently this predicted color (combined with the actual color during training) served as an input to predict the emission wavelength using a regression machine learning model. The tools developed in this study, particularly the hybrid models, are expected to be valuable in predicting the emission of novel carbon dots (CDs). This approach allows for the selection of promising reaction examples from the model, streamlining the synthesis of CDs with specific colors and significantly reducing the effort required in the optimization process.
In another classification problem, Tuccito et al. employed CD fluorescence as a nanochemosensor to detect different amino acids.115 The modification of CD surfaces can alter fluorescence properties, including emission intensity and excitation and emission wavelengths. In this study, carboxyl groups on nanoparticle surfaces were activated and subsequently reacted with various amino acids. The nanochemosensors demonstrated the ability to distinguish between amino acids within a mixture, showcasing their potential in complex amino acid analyses. ANNs were trained with fluorescence variation maps of activated CDs to predict if the amino acid is alanine (ALA) or not alanine. The resulting model had 0.8 sensitivity and 0.91 specificity. These discoveries will contribute to the advancement of cost-effective nanochemosensors for investigating specific diseases that are presently diagnosed through basic amino acid detection methods.
In a regression task, Pudza et al. applied multilayer perceptron (MLP) to predict the photoluminescent quantum yield (PLQY) of fluorescent carbon dots synthesized from tapioca powder.116 The training data (n = 30) were collected from the experiments. MLP trained with temperature, time, dosage and the solvent ratio predicted the PLQY with high accuracy. The optimization and prediction processes have yielded sustainable, efficient, and reliable fluorescent carbon dots. This approach not only saves energy within a manageable timeframe but also reduces the required dosage while maintaining an optimal quality output.
Doring et al. applied CNNs and deep neural networks on the emission/PL decay data of CDs to improve ethanol content determination in ethanol/water mixtures (n = 578) as well as in alcohol-containing beverages (n = 19).117 The models are trained by PL excitation/emission maps, PL decay spectra, and extracted features (i.e. PL intensities, PL peak positions, and PL lifetimes) to predict the ethanol content. The utilization of time-resolved spectral information (PL decays and lifetimes) as the input for CNNs enables more accurate prediction of ethanol content compared to steady-state emission data. Using entire optical spectra, namely PL decays and PL excitation/emission maps, advanced deep learning models demonstrated their applicability in the analysis of beverages. In contrast to CNN models with only a few predictor variables, which struggled due to autofluorescence of the beverages, advanced deep learning models enabled better predictions of ethanol content. Although CDs serve as excellent candidates for showcasing deep learning in optical sensing, the methods outlined in this study hold promise for enhancing chemical sensing across a range of luminescent materials (see Fig. 2).
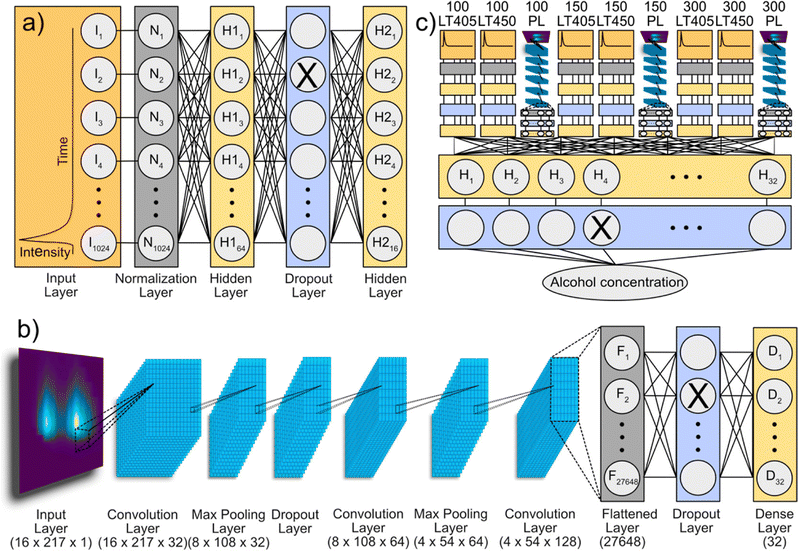 | ||
| Fig. 2 Multi-channel deep learning model: (a) structure of the PL decay channel. The input layer takes 1024 intensity integers as the input. After normalization, data are passed through a dense layer (64 neurons), a dropout layer (dropout = 0.01), and a second dense layer (16 neurons). (b) Structure of the PL map channel. The input layer takes a 16 × 217 × 1 matrix as the input. It is passed through a series of convolution, maximum pooling, and dropout layers before it is flattened and fed through another dropout layer and dense layer (32 neurons). (c) Example of a multi-channel model with 9 inputs. The respective input data are passed through either a PL decay channel or a PL map channel. These channels are concatenated before being passed through a dense layer (32 neurons) and a dropout layer (dropout = 0.3) to predict the ethanol concentration as the target variable. Reprinted with permission from ref. 117. Copyright 2022 American Chemical Society. | ||
4 Gradient boosting
Traditional gradient boosting techniques have long served as stalwarts in the realm of machine learning, providing a robust framework for constructing powerful predictive models. The foundational concept behind gradient boosting involves the sequential training of weak learners, such as decision trees, with each subsequent learner aiming to correct errors made by the ensemble of preceding ones. This iterative process enables the algorithm to progressively refine its predictive accuracy, making gradient boosting a popular choice for regression and classification tasks. Despite its success, traditional gradient boosting is not without its limitations. The absence of explicit regularization mechanisms can lead to overfitting, especially in the presence of noisy or high-dimensional datasets. Recognizing these challenges, the advent of extreme gradient boosting (XGBoost) marked a significant evolution in the field, addressing these limitations and introducing innovations that have propelled it to the forefront of machine learning algorithms.126Extreme gradient boosting (XGBoost), a powerful ensemble learning algorithm, has emerged as a dominant force in the realm of machine learning, demonstrating remarkable success across various domains. Developed as an extension of traditional gradient boosting techniques, XGBoost has garnered widespread popularity due to its efficiency, scalability, and superior predictive performance. At its core, XGBoost operates by sequentially training a series of weak learners, typically decision trees, and iteratively refining their predictive capabilities. Unlike traditional gradient boosting, XGBoost incorporates a regularization term and employs a second-order Taylor expansion to optimize the objective function, enhancing its ability to capture complex patterns within the data.
One of the defining features of XGBoost is its versatility, making it applicable to both regression and classification tasks. The algorithm excels in handling large datasets and high-dimensional feature spaces, showcasing robustness in the face of noisy or missing data. Moreover, XGBoost provides a comprehensive set of hyperparameters that can be fine-tuned to accommodate diverse modeling scenarios, fostering adaptability to different applications. The success of the algorithm is further underscored by its ability to balance bias and variance, mitigating overfitting and ensuring generalizability across unseen data. As a result, XGBoost has become a method of choice in various fields, ranging from finance and healthcare to image processing and natural language processing, showcasing its broad utility and effectiveness in extracting meaningful patterns from complex datasets.
XGBoost has demonstrated considerable efficacy in numerous CD studies. Han et al. reported a machine learning-assisted approach for synthesizing highly fluorescent CDs using a hydrothermal route.82 XGBoost outperformed multilayer perceptron, support vector machine, and Gaussian process regressor in predicting the QY using five input variables: the volume of ethylenediamine, the mass of precursor, reaction temperature, ramp rate and reaction time. The data were collected from 391 experiments with different combinations of growth parameters, and respective QYs ranged from 0 to 1. XGBoost unveiled a noteworthy correlation between outstanding optical properties and the mass of the precursor and the volume of the alkaline catalyst. This observation aligns well with experimental findings. The methodology introduced in this study serves as a foundational step toward the advancement of artificial intelligence techniques for the analysis and optimization of material preparation methods (see Fig. 3).
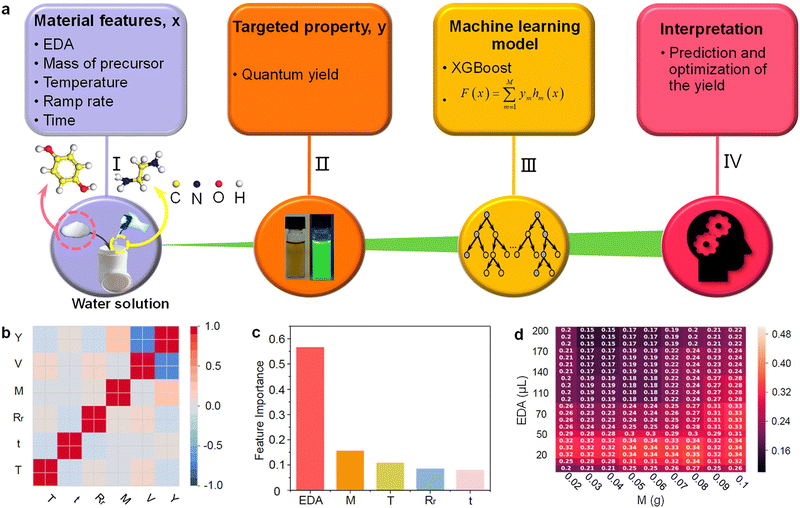 | ||
| Fig. 3 Application of ML for guided synthesis of CDs. (a) Design framework for the guided synthesis of CDs with a large QY based on ML and hydrothermal experiments. (b) The heat map of the Pearson correlation coefficient matrix among the selected features of hydrothermally grown CDs. (c) Feature importance retrieved from XGBoost-R that learns from the full data set. The most important features are EDA and M. (d) Predictions from the trained model, which is represented by the matrix formed by the two most important features. Reprinted with permission from ref. 82. Copyright 2020 American Chemical Society. | ||
Tang et al. developed a regression model to improve the PLQY of carbon quantum dots (CQDs) grown through hydrothermal methods.118 Six hydrothermal parameters were identified as input features: the pH value (pH), reaction temperature (T), reaction time (t), the mass of precursor A (M), ramp rate (Rr), and solution volume (V). A total of 467 experimental records were used with different growth parameters and respective PLQYs ranged from 0 to 1. In order to best infer the PLQY from the features, several regression algorithms are evaluated with nested cross validation, including XGBoost regressor, support vector machine regressor, and Gaussian process regressor. XGBoost demonstrates superior performance, surpassing the other algorithms by a significant margin, as indicated by its R2 value of 0.8402. The most critical factor influencing the PLQY is shown to be the pH value, with reaction temperature and reaction time following closely in significance. The trained XGBoost model is then employed to predict the PLQY for a vast array of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 555
555![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 potential synthesis conditions generated from various combinations. Eleven synthesis conditions are recommended by the model attributed to their highest predicted PLQY. Subsequent experiments conducted in the laboratory yielded a remarkably high photoluminescence quantum yield (PLQY) of 55.5%. This achievement is particularly noteworthy given the ultra-low heteroatom doping precursor ratio employed, making it one of the highest reported PLQY values under such conditions. The findings support the promising potential of ML in optimizing and expediting the material synthesis process. This endorsement suggests that ML has the capability to facilitate the development of advanced inorganic materials, contributing to practical applications through reduced processing time and enhanced material properties.
840 potential synthesis conditions generated from various combinations. Eleven synthesis conditions are recommended by the model attributed to their highest predicted PLQY. Subsequent experiments conducted in the laboratory yielded a remarkably high photoluminescence quantum yield (PLQY) of 55.5%. This achievement is particularly noteworthy given the ultra-low heteroatom doping precursor ratio employed, making it one of the highest reported PLQY values under such conditions. The findings support the promising potential of ML in optimizing and expediting the material synthesis process. This endorsement suggests that ML has the capability to facilitate the development of advanced inorganic materials, contributing to practical applications through reduced processing time and enhanced material properties.
Hong et al. utilized the XGBoost model for predicting the maximum fluorescence (FL) intensity and emission centers of CDs synthesized under room temperature conditions using p-benzoquinone (PBQ) and ethylenediamine (EDA) as starting materials.119 They successfully synthesized a variety of CDs with tailored optical properties. These CDs were effectively employed for applications such as detecting Fe3+, facilitating sustained drug release, enabling whole-cell imaging, and contributing to the preparation of poly(vinyl alcohol) (PVA) films. The input dataset comprises four hundred types of CDs prepared under different reaction conditions, encompassing the mass of p-benzoquinone (VEDA), volume of ethylenediamine (VEDA), reaction duration, and solvent types. For output, the predicted target variables are the FL intensity and the location of emission centers. Principal component analysis (PCA) was employed to create new variables characterized by relative independence. Subsequently, PC1 and PC2 were utilized as novel input features for the training of the model. XGBoost showed superior performance compared to K-nearest neighbor, decision trees, random forest, support vector machine and convolutional neural networks. Leveraging the significant features and parameters (i.e. VEDA and MPBQ) extracted from the XGBoost model, the authors successfully fabricated a series of novel carbon dots (CDs) with customizable fluorescence (FL) intensity and emission center properties. This study demonstrates that the XGBoost algorithm, as a machine learning approach, is effective in identifying crucial factors in CD synthesis. It provides chemists with a rapid and reliable means to access optimal reaction parameters for synthesizing desired CDs (see Fig. 4).
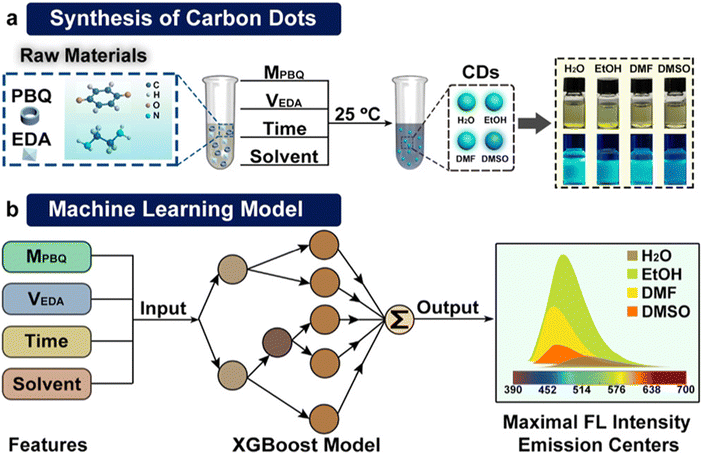 | ||
| Fig. 4 Schematic illustration of machine learning guiding the synthesis of CDs. (a) Synthetic process of CDs. (b) Prediction of CD optical properties using machine learning models. Reprinted with permission from ref. 119. Copyright 2022 American Chemical Society. | ||
Using ML, Wang et al. successfully predicted and synthesized metal-free CD homogeneous catalysts for the oxidation of C–H bonds.120 The dataset for cyclohexane oxidation was compiled from literature sources and laboratory notebooks, comprising a total of 652 entries. This dataset consists of 113 positive samples (17.3%) and 539 negative samples (82.7%). The boundary between success and failure in this context is characterized by achieving a 10% conversion of cyclohexane and a 70% selectivity towards the production of adipic acid (AA). The input features are selected as O (content of oxygen), Mw (weight-average molecular weight of the nonmetal catalyst), G (O2 or not), p (homogeneous catalysis or heterogeneous catalysis), T (catalytic temperature), P (pressure), and t (reaction time). Out of the four classical models considered (multilayer perceptron, naive Bayes, SVM, and XGBoost), the XGBoost model was chosen due to its high performance. The analysis of feature importance derived from the XGBoost model indicates that the molecular weight (Mw) takes precedence over other features. The order of importance follows Mw, followed by O, T, P, and t. Subsequently, the established XGBoost model is employed to apply the unexplored conditions, predicting the probability of success or failure. All predictions align with the actual outcomes of “success” in the conducted true experiments, affirming the accuracy of the model. This study distinctly illustrates a novel approach to C–H bond activation, employing metal-free CDs as quasi-homogeneous catalysts.
Chen et al. explored the relationship between biochar preparation parameters and the fluorescence quantum yield of CDs in biochar, employing six machine learning models including decision trees (DT), random-forest (RF), gradient-boosting decision-trees (GBDT), extra-trees (ET), K-nearest-neighbor (KNN) regression, and XGBoost, where the dataset consisted of 480 samples.121 The input parameters for the biochar production experiment were determined, encompassing the type of farm waste, as well as characteristics such as cellulose, hemicellulose, lignin, ash, moisture, nitrogen (N), carbon (C), and carbon-to-nitrogen ratio (C/N) contents of the samples. Additionally, parameters related to the pyrolysis process, including pyrolysis temperature (T) and residence time (t), were considered. The GBDT model had the best performance among the other models, as GBDT exhibit resilience to missing values and outliers, are less susceptible to the impact of extreme values, and demonstrate effectiveness in handling high-dimensional sparse data. It was identified that four features, namely, pyrolysis temperature, residence time, nitrogen (N) content, and carbon-to-nitrogen (C/N) ratio, had the most significant impact on enhancing the accuracy of QY predictions. The methodology introduced in this study can serve as a foundation for the advancement of new techniques leveraging artificial intelligence for the analysis and prediction of CDs generated in the process of biochar production.
5 Random forest
Random forest (RF), a versatile and robust machine learning algorithm, has emerged as a cornerstone in data-driven decision-making across diverse scientific and industrial domains. Born out of the ensemble learning paradigm, this algorithm is particularly well-suited for applications where the accuracy and reliability of predictions are paramount. The metaphorical “forest” comprises a multitude of decision trees, each contributing its unique insights to the collective wisdom of the algorithm. As a result, random forest is known for its resilience against overfitting and its ability to produce accurate and stable predictions. The integration of random forest algorithms in the study of carbon dots opens up new avenues for predicting and understanding their behavior.Chen et al. explored the relationship between reaction parameters and the photoluminescence characteristics of CDs, achieving controllable synthesis of multi-color CDs with the aid of ML.111 Five input parameters are used, including varied precursor types and quantities such as p-phenylenediamine with urea, p-phenylenediamine with citric acid, and diverse solvent types (anhydrous ethanol, water, and N,N-dimethylformamide), along with reaction time and temperature. 270 experiments with different parameter combinations are conducted to feed the ML algorithms. The 3D fluorescence spectra (maximum emission wavelength, Stokes shift) and fluorescence quantum yield were used as the output variables. The RF model demonstrated superior predictive performance compared to other models, including extreme gradient boosting (XGBoost), light gradient boosting machine (LGBM), ridge regression (ridge), least absolute shrinkage and selection operator (LASSO), and support vector regression (SVR), specifically in predicting the maximum emission wavelength, the fluorescence quantum yield and the Stokes shift of multicolor CDs. The authors also implemented a computer algorithm for ranking importance, utilizing a method to calculate the significance of features. The outcomes revealed that the solvent was the primary factor influencing the maximum emission wavelength of multicolor CDs. The key determinant influencing the fluorescence quantum yield was identified to be the precursor ratio and the precursor type was the main influencing factor of the Stokes shift.
Xing et al. employed RF to facilitate the synthesis of CDs with predictable photoluminescence (PL).122 In contrast to treating the precursors as constants, the variables in this context involve randomly chosen 202 combinations of precursors, specifically three-precursor combinations of 24 precursors. The wavelengths of the peaks with the strongest intensity and the longest wavelength under excitation wavelengths of 365 and 532 nm were used as output parameters. The other reaction parameters were fixed to 200 °C and 10 h. The RF model demonstrated the highest performance among the six models including KNN, AdaBoost, bagging, DT, RF and SVM. It is shown that, utilizing prediction data that encompass the entire precursor combination space, the screening of CDs with specific PL wavelength features can be conducted much more effectively than through random trials.
He et al. established an RF regression model for corrosion inhibitors based on hydrothermally synthesized CDs to predict the inhibition efficiency.123 This model unveils the relationship between different synthesis parameters and the inhibition efficiency of the CDs. The dataset was created by combining 102 data points on CD synthesis and inhibition efficiency, drawing from reported studies and the authors’ own experimental findings. Typical input parameters such as CD concentration in HCl, precursor type and quantity, solvent type and volume, and reaction time and temperature were selected. The inhibition efficiencies of CDs, calculated through potentiodynamic polarization (PDP), served as the output variable in the analysis. Utilizing the feature importance derived from the RF model, critical factors in the synthesis of CD-based corrosion inhibitors were identified. The concentration of CDs in HCl emerges as the most influential factor affecting the inhibitory behaviors of the synthesized CDs, followed by N atomic content and reaction time. Additionally, the synthesis route is intelligently optimized using the genetic algorithm (GA), which is an optimization technique inspired by natural selection and genetics, utilizing a population-based approach with genetic operators to iteratively evolve solutions for a given problem. Successful controlled preparation of CD-based corrosion inhibitors was achieved. By identifying and filtering out unsatisfactory synthesis conditions, this approach significantly enhances the synthetic efficiency of CD-based corrosion inhibitors (see Fig. 5).
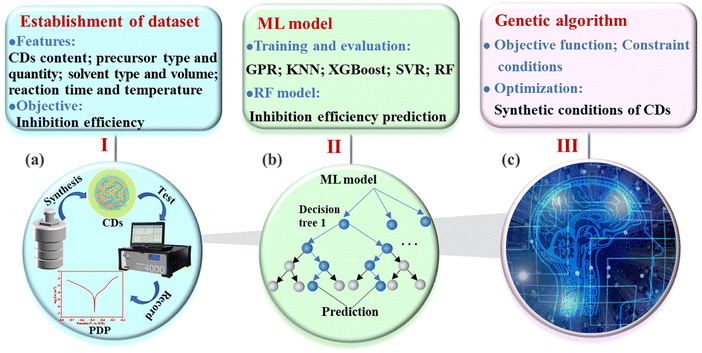 | ||
| Fig. 5 Application of ML for controlled synthesis of CD-based corrosion inhibitors: (a) establishment of the dataset; (b) modelling for inhibition efficiency prediction; and (c) synthetic optimization of CDs. Reprinted with permission from ref. 123. Copyright 2023 Elsevier. | ||
6 Other ML algorithms
Here we mention other ML algorithms used in CD studies. Dager et al. detailed the production of monodisperse carbon quantum dots (C-QDs) through a single-step thermal decomposition procedure employing fennel seeds.124 They employed ML techniques such as PCA (see ref. 127 for more details on PCA), multivariate curve resolution (MCR),128 and sparse non-negative matrix factorization (NMF)129 to assess the PL of synthesized C-QDs with a focus on addressing two key questions: (i) the ability of ML to classify pH-dependent PL measurements, including spectra obtained at different pH levels and excitation wavelengths, and its capacity to suggest optimal excitation wavelengths for a comprehensive pH-dependent study; and (ii) whether ML can aid in identifying the source of the PL mechanism, considering that multiple PL measurements at varying pH levels and excitation wavelengths may activate different types of surface states. PL data were obtained through excitations at wavelengths of 200, 220, 240, 260, 280, 300, 320, and 340 nm, corresponding to pH values of 3, 5, 7, 9, 11, and 13. A total of forty-eight (48) PL measurements were conducted, each representing a single spectrum for 401 data points acquired in the spectral range of 300–750 nm. PCA, MCR, and NMF were employed to identify the underlying mechanisms contributing to the PL behavior of the synthesized C-QDs.Xu et al. used linear discriminant analysis (LDA)130 and support vector machine (SVM)131 to analyze multidimensional data of a CD-based sensor array fabricated for the detection and differentiation of four tetracyclines (TC), including tetracycline (TC), oxytetracycline (OTC), doxycycline (DOX), and metacycline (MTC).125 A training data set comprising a matrix of 2 CDs, 4 TCs, and 5 replicates was created through the utilization of I/I0 values. The reliability of the established fluorescence sensor array was confirmed by studying 52 unknown samples. At a concentration of 1.0 μM, four different TCs can be effectively clustered by SVM and LDA. Furthermore, the sensor array demonstrates the capability to effectively differentiate between individual TCs as well as binary mixtures of TCs and DOXs. The utilization of SVM presents an innovative option for array sensing systems in handling diverse data sets. The research illustrates the potential of the fluorescence sensor array in environmental monitoring and quantifying antibiotics (see Fig. 6).
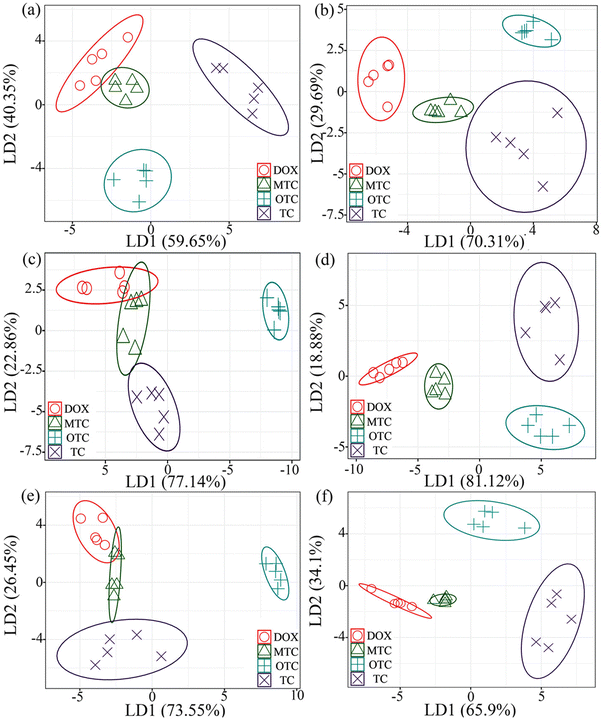 | ||
| Fig. 6 Two-dimensional LDA score plot of the fluorescence sensor array for the discrimination of the four TCs at different concentrations: (a) 1.0 μM; (b) 10 μM; (c) 25 μM; (d) 50 μM; (e) 100 μM; and (f) 150 μM (QR-CDs, 13.3 μg mL−1; CPC-CDs, 60 μg mL−1). Reprinted with permission from ref. 125. Copyright 2020 Elsevier. | ||
7 Summary and future perspectives
This comprehensive review explores the latest advancements in utilizing machine learning for CDs. We provide a concise summary of prevalent ML algorithms and examine recent research employing ML models for the prediction of the properties of CDs. ML models were employed to investigate the parameter space of CD experiments and generate optimal input parameters for CDs. By leveraging the optimal parameters derived from ML for various CD challenges, one can explore design strategies aimed at achieving high-performing CDs. While ML models are frequently perceived as “black box” models, the identified strategies can offer novel insights into enhancing the performance of CDs in various applications.While artificial neural networks and gradient boosting algorithms have shown superior performance in several studies, research indicates that the optimal machine learning model can vary, even under identical input and target feature conditions. Hence, future research is needed to understand the performance, either theoretically or numerically, of various ML applications for CDs. Although achieving the true optimal experimental parameters remains a challenge in the field, there is optimism that ML will play a promising role in addressing this problem in the future. A promising avenue for enhancement involves establishing a more comprehensive model that incorporates both synthesis process-related and chemistry-related features.
The median of the sample size in the studies covered in this review is 357. For the gradient boosting algorithms, this number is 467. To enhance the accuracy and applicability of the ML approach, future endeavors should focus on collecting high-quality data for refining and updating the currently employed models. This continual improvement is crucial for advancing the development of more efficient CD synthesis strategies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
ASJ thanks the Deanship of Research Oversight and Coordination, King Fahd University of Petroleum and Minerals (KFUPM) for funding this work through project INAM2206.References
- K. Ghosal and A. Ghosh, Carbon dots: The next generation platform for biomedical applications, Mater. Sci. Eng. C Mater. Biol. Appl., 2019, 96, 887–903 CrossRef CAS PubMed.
- A. Sharma and J. Das, Small molecules derived carbon dots: synthesis and applications in sensing, catalysis, imaging, and biomedicine, J. Nanobiotechnol., 2019, 17, 92 CrossRef PubMed.
- L. Xiao and H. Sun, Novel properties and applications of carbon nanodots, Nanoscale Horiz., 2018, 3, 565–597 RSC.
- G. Ragazzon, A. Cadranel, E. V. Ushakova, Y. Wang, D. M. Guldi, A. L. Rogach, N. A. Kotov and M. Prato, Optical processes in carbon nanocolloids, Chem, 2021, 7, 606–628 CAS.
- L. Pan, S. Sun, A. Zhang, K. Jiang, L. Zhang, C. Dong, Q. Huang, A. Wu and H. Lin, Truly Fluorescent Excitation-Dependent Carbon Dots and Their Applications in Multicolor Cellular Imaging and Multidimensional Sensing, Adv. Mater., 2015, 27, 7782–7787 CrossRef CAS PubMed.
- D. Benetti, E. Jokar, C.-H. Yu, A. Fathi, H. Zhao, A. Vomiero, E. WeiGuang Diau and F. Rosei, Hole-extraction and photostability enhancement in highly efficient inverted perovskite solar cells through carbon dot-based hybrid material, Nano Energy, 2019, 62, 781–790 CrossRef CAS.
- B. Wang, G. I. N. Waterhouse and S. Lu, Carbon dots: mysterious past, vibrant present, and expansive future, Trends Chem., 2023, 5, 76–87 CrossRef CAS.
- J. Peng, et al., Graphene Quantum Dots Derived from Carbon Fibers, Nano Lett., 2012, 12, 844–849 CrossRef CAS PubMed.
- C. Rizzo, F. Arcudi, L. Orevic, N. T. Dintcheva, R. Noto, F. D’Anna and M. Prato, Nitrogen-Doped Carbon Nanodots-Ionogels: Preparation, Characterization, and Radical Scavenging Activity, ACS Nano, 2018, 12, 1296–1305 CrossRef CAS PubMed.
- S. K. Misra, I. Srivastava, I. Tripathi, E. Daza, F. Ostadhossein and D. Pan, Macromolecularly “Caged”Carbon Nanoparticles for Intracellular Trafficking via Switchable Photoluminescence, J. Am. Chem. Soc., 2017, 139, 1746–1749 CrossRef CAS PubMed.
- X. Xu, K. Zhang, L. Zhao, C. Li, W. Bu, Y. Shen, Z. Gu, B. Chang, C. Zheng, C. Lin, H. Sun and B. Yang, Aspirin-Based Carbon Dots, a Good Biocompatibility of Material Applied for Bioimaging and Anti-Inflammation, ACS Appl. Mater. Interfaces, 2016, 8, 32706–32716 CrossRef CAS PubMed.
- T. H. Kim, J. P. Sirdaarta, Q. Zhang, E. Eftekhari, J. John, D. Kennedy, I. E. Cock and Q. Li, Selective toxicity of hydroxyl-rich carbon nanodots for cancer research, Nano Res., 2018, 11, 2204–2216 CrossRef CAS.
- S. Li, et al., Targeted tumour theranostics in mice via carbon quantum dots structurally mimicking large amino acids, Nat. Biomed. Eng., 2020, 4, 704–716 CrossRef CAS PubMed.
- S. Mei, X. Liu, W. Zhang, R. Liu, L. Zheng, R. Guo and P. Tian, High-Bandwidth White-Light System Combining a Micro-LED with Perovskite Quantum Dots for Visible Light Communication, ACS Appl. Mater. Interfaces, 2018, 10, 5641–5648 CrossRef CAS PubMed.
- Z. Zhou, P. Tian, X. Liu, S. Mei, D. Zhou, D. Li, P. Jing, W. Zhang, R. Guo, S. Qu and A. L. Rogach, Hydrogen Peroxide-Treated Carbon Dot Phosphor with a Bathochromic-Shifted, Aggregation-Enhanced Emission for Light-Emitting Devices and Visible Light Communication, Adv. Sci., 2018, 5, 1800369 CrossRef PubMed.
- M. Semeniuk, Z. Yi, V. Poursorkhabi, J. Tjong, S. Jaffer, Z.-H. Lu and M. Sain, Future Perspectives and Review on Organic Carbon Dots in Electronic Applications, ACS Nano, 2019, 13, 6224–6255 CrossRef CAS PubMed.
- H. Tetsuka, A. Nagoya, T. Fukusumi and T. Matsui, Molecularly Designed, NitrogenFunctionalized Graphene Quantum Dots for Optoelectronic Devices, Adv. Mater., 2016, 28, 4632–4638 CrossRef CAS PubMed.
- F. Arcudi, V. Strauss, L. Orevic, A. Cadranel, D. M. Guldi and M. Prato, Porphyrin Antennas on Carbon Nanodots: Excited State Energy and Electron Transduction, Angew. Chem., Int. Ed., 2017, 56, 12097–12101 CrossRef CAS PubMed.
- T. Yuan, T. Meng, P. He, Y. Shi, Y. Li, X. Li, L. Fan and S. Yang, Carbon quantum dots: an emerging material for optoelectronic applications, J. Mater. Chem. C, 2019, 7, 6820–6835 RSC.
- Y. Li, H. Shu, X. Niu and J. Wang, Electronic and Optical Properties of EdgeFunctionalized Graphene Quantum Dots and the Underlying Mechanism, J. Phys. Chem. C, 2015, 119, 24950–24957 CrossRef CAS.
- H. Abdelsalam, H. Elhaes and M. A. Ibrahim, Tuning electronic properties in graphene quantum dots by chemical functionalization: Density functional theory calculations, Chem. Phys. Lett., 2018, 695, 138–148 CrossRef CAS.
- B. Wang, J. Yu, L. Sui, S. Zhu, Z. Tang, B. Yang and S. Lu, Rational Design of MultiColor-Emissive Carbon Dots in a Single Reaction System by Hydrothermal, Adv. Sci., 2021, 8, 2001453 CrossRef CAS PubMed.
- Y. Choi, Y. Choi, O.-H. Kwon and B.-S. Kim, Carbon Dots: Bottom-Up Syntheses, Properties, and Light-Harvesting Applications, Chem. – Asian J., 2018, 13, 586–598 CrossRef CAS PubMed.
- Y. Dong, C. Chen, X. Zheng, L. Gao, Z. Cui, H. Yang, C. Guo, Y. Chi and C. M. Li, One-step and high yield simultaneous preparation of single- and multi-layer graphene quantum dots from CX-72 carbon black, J. Mater. Chem., 2012, 22, 8764–8766 RSC.
- Y. Li, Y. Hu, Y. Zhao, G. Shi, L. Deng, Y. Hou and L. Qu, An Electrochemical Avenue to Green-Luminescent Graphene Quantum Dots as Potential Electron-Acceptors for Photovoltaics, Adv. Mater., 2011, 23, 776–780 CrossRef CAS PubMed.
- Y.-P. Sun, et al., Quantum-Sized Carbon Dots for Bright and Colorful Photoluminescence, J. Am. Chem. Soc., 2006, 128, 7756–7757 CrossRef CAS PubMed.
- R. L. Calabro, D.-S. Yang and D. Y. Kim, Liquid-phase laser ablation synthesis of graphene quantum dots from carbon nano-onions: Comparison with chemical oxidation, J. Colloid Interface Sci., 2018, 527, 132–140 CrossRef CAS PubMed.
- J. Xu, S. Sahu, L. Cao, P. Anilkumar, K. N. Tackett II, H. Qian, C. E. Bunker, E. A. Guliants, A. Parenzan and Y.-P. Sun, Carbon Nanoparticles as Chromophores for Photon Harvesting and Photoconversion, Chem. Phys. Chem., 2011, 12, 3604–3608 CrossRef CAS PubMed.
- X. Xu, R. Ray, Y. Gu, H. J. Ploehn, L. Gearheart, K. Raker and W. A. Scrivens, Electrophoretic Analysis and Purification of Fluorescent Single-Walled Carbon Nanotube Fragments, J. Am. Chem. Soc., 2004, 126, 12736–12737 CrossRef CAS PubMed.
- X. Li, H. Wang, Y. Shimizu, A. Pyatenko, K. Kawaguchi and N. Koshizaki, Preparation of carbon quantum dots with tunable photoluminescence by rapid laser passivation in ordinary organic solvents, Chem. Commun., 2011, 47, 932–934 RSC.
- J. Lee, K. Kim, W. I. Park, B.-H. Kim, J. H. Park, T.-H. Kim, S. Bong, C.-H. Kim, G. Chae, M. Jun, Y. Hwang, Y. S. Jung and S. Jeon, Uniform Graphene Quantum Dots Patterned from Self-Assembled Silica Nanodots, Nano Lett., 2012, 12, 6078–6083 CrossRef CAS PubMed.
- L. A. Ponomarenko, F. Schedin, M. I. Katsnelson, R. Yang, E. W. Hill, K. S. Novoselov and A. K. Geim, Chaotic Dirac Billiard in Graphene Quantum Dots, Science, 2008, 320, 356–358 CrossRef CAS PubMed.
- Y. Weng, Z. Li, L. Peng, W. Zhang and G. Chen, Fabrication of carbon quantum dots with nano-defined position and pattern in one step via sugar-electron-beam writing, Nanoscale, 2017, 9, 19263–19270 RSC.
- S. Y. Lim, W. Shen and Z. Gao, Carbon quantum dots and their applications, Chem. Soc. Rev., 2015, 44, 362–381 RSC.
- T. V. de Medeiros, J. Manioudakis, F. Noun, J.-R. Macairan, F. Victoria and R. Naccache, Microwave-assisted synthesis of carbon dots and their applications, J. Mater. Chem. C, 2019, 7, 7175–7195 RSC.
- F. Arcudi, L. Orevic and M. Prato, Design, Synthesis, and Functionalization Strategies of Tailored Carbon Nanodots, Acc. Chem. Res., 2019, 52, 2070–2079 CrossRef CAS PubMed.
- K. Suzuki, L. Malfatti, M. Takahashi, D. Carboni, F. Messina, Y. Tokudome, M. Takemoto and P. Innocenzi, Design of Carbon Dots Photoluminescence through Organo-Functional Silane Grafting for Solid-State Emitting Devices, Sci. Rep., 2017, 7, 5469 CrossRef PubMed.
- R. C. So, J. E. Sanggo, L. Jin, J. M. A. Diaz, R. A. Guerrero and J. He, GramScale Synthesis and Kinetic Study of Bright Carbon Dots from Citric Acid and Citrus japonica via a Microwave-Assisted Method, ACS Omega, 2017, 2, 5196–5208 CrossRef CAS PubMed.
- W. U. Khan, D. Wang, W. Zhang, Z. Tang, X. Ma, X. Ding, S. Du and Y. Wang, High Quantum Yield Green-Emitting Carbon Dots for Fe() Detection, Biocompatible Fluorescent Ink and Cellular Imaging, Sci. Rep., 2017, 7, 14866 CrossRef PubMed.
- B. B. Chen, Z. X. Liu, W. C. Deng, L. Zhan, M. L. Liu and C. Z. Huang, A large-scale synthesis of photoluminescent carbon quantum dots: a self-exothermic reaction driving the formation of the nanocrystalline core at room temperature, Green Chem., 2016, 18, 5127–5132 RSC.
- T. Li, W. Shi, S. E, Q. Mao and X. Chen, Green preparation of carbon dots with different surface states simultaneously at room temperature and their sensing applications, J. Colloid Interface Sci., 2021, 591, 334–342 CrossRef CAS PubMed.
- L. Branzi, G. Lucchini, E. Cattaruzza, N. Pinna, A. Benedetti and A. Speghini, The formation mechanism and chirality evolution of chiral carbon dots prepared via radical assisted synthesis at room temperature, Nanoscale, 2021, 13, 10478–10489 RSC.
- P. Zhao, X. Li, G. Baryshnikov, B. Wu, H. Agren, J. Zhang and L. Zhu, One-step solvothermal synthesis of high-emissive amphiphilic carbon dots via rigidity derivation, Chem. Sci., 2018, 9, 1323–1329 RSC.
- S. Zhu, Y. Song, X. Zhao, J. Shao, J. Zhang and B. Yang, The photoluminescence mechanism in carbon dots (graphene quantum dots, carbon nanodots, and polymer dots): current state and future perspective, Nano Res., 2015, 8, 355–381 CrossRef CAS.
- C. Xia, S. Zhu, T. Feng, M. Yang and B. Yang, Evolution and Synthesis of Carbon Dots: From Carbon Dots to Carbonized Polymer Dots, Adv. Sci, 2019, 6, 1901316 CrossRef CAS PubMed.
- K. Hola, Y. Zhang, Y. Wang, E. P. Giannelis, R. Zboril and A. L. Rogach, Carbon dots—Emerging light emitters for bioimaging, cancer therapy and optoelectronics, Nano Today, 2014, 9, 590–603 CrossRef CAS.
- J. Lu, J.-x Yang, J. Wang, A. Lim, S. Wang and K. P. Loh, One-Pot Synthesis of Fluorescent Carbon Nanoribbons, Nanoparticles, and Graphene by the Exfoliation of Graphite in Ionic Liquids, ACS Nano, 2009, 3, 2367–2375 CrossRef CAS PubMed.
- S. H. Jin, D. H. Kim, G. H. Jun, S. H. Hong and S. Jeon, Tuning the Photoluminescence of Graphene Quantum Dots through the Charge Transfer Effect of Functional Groups, ACS Nano, 2013, 7, 1239–1245 CrossRef CAS PubMed.
- M. A. Sk, A. Ananthanarayanan, L. Huang, K. H. Lim and P. Chen, Revealing the tunable photoluminescence properties of graphene quantum dots, J. Mater. Chem. C, 2014, 2, 6954–6960 RSC.
- B. Zhi, et al., Multicolor polymeric carbon dots: synthesis, separation and polyamidesupported molecular fluorescence, Chem. Sci., 2021, 12, 2441–2455 RSC.
- M. Fu, F. Ehrat, Y. Wang, K. Z. Milowska, C. Reckmeier, A. L. Rogach, J. K. Stolarczyk, A. S. Urban and J. Feldmann, Carbon Dots: A Unique Fluorescent Cocktail of Polycyclic Aromatic Hydrocarbons, Nano Lett., 2015, 15, 6030–6035 CrossRef CAS PubMed.
- N. V. Tepliakov, E. V. Kundelev, P. D. Khavlyuk, Y. Xiong, M. Y. Leonov, W. Zhu, A. V. Baranov, A. V. Fedorov, A. L. Rogach and I. D. Rukhlenko, sp2–sp3-Hybridized Atomic Domains Determine Optical Features of Carbon Dots, ACS Nano, 2019, 13, 10737–10744 CrossRef CAS PubMed.
- T. T. Meiling, R. Schurmann, S. Vogel, K. Ebel, C. Nicolas, A. R. Milosavljević and I. Bald, Photophysics and Chemistry of Nitrogen-Doped Carbon Nanodots with High Photoluminescence Quantum Yield, J. Phys. Chem. C, 2018, 122, 10217–10230 CrossRef CAS.
- N. R. Pires, C. M. W. Santos, R. R. Sousa, R. C. M. D. Paula, P. L. R. Cunha and J. P. A. Feitosa, Novel and Fast Microwave-Assisted Synthesis of Carbon Quantum Dots from Raw Cashew Gum, J. Braz. Chem. Soc., 2015, 26, 1274–1282 CAS.
- N. Parvin and T. K. Mandal, Synthesis of a highly fluorescence nitrogen-doped carbon quantum dots bioimaging probe and its in vivo clearance and printing applications, RSC Adv., 2016, 6, 18134–18140 RSC.
- J. Zhang, X. Chen, Y. Li, S. Han, Y. Du and H. Liu, A nitrogen doped carbon quantum dot-enhanced chemiluminescence method for the determination of Mn2+, Anal. Methods, 2018, 10, 541–547 RSC.
- X. Liu, J. Pang, F. Xu and X. Zhang, Simple Approach to Synthesize AminoFunctionalized Carbon Dots by Carbonization of Chitosan, Sci. Rep., 2016, 6, 31100 CrossRef CAS PubMed.
- Y. Dong, L. Wan, J. Cai, Q. Fang, Y. Chi and G. Chen, Natural carbon-based dots from humic substances, Sci. Rep., 2015, 5, 10037 CrossRef CAS PubMed.
- M. Xue, Z. Zhan, M. Zou, L. Zhang and S. Zhao, Green synthesis of stable and biocompatible fluorescent carbon dots from peanut shells for multicolor living cell imaging, New J. Chem., 2016, 40, 1698–1703 RSC.
- X. Guo, H. Zhang, H. Sun, M. O. Tade and S. Wang, Green Synthesis of Carbon Quantum Dots for Sensitized Solar Cells, ChemPhotoChem, 2017, 1, 116–119 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. O. Dral and T. Clark, Semiempirical UNO–CAS and UNO–CI: Method and Applications in Nanoelectronics, J. Phys. Chem. A, 2011, 115, 11303–11312 CrossRef CAS PubMed.
- A. V. Vorontsov and E. V. Tretyakov, Determination of graphene's edge energy using hexagonal graphene quantum dots and PM7 method, Phys. Chem. Chem. Phys., 2018, 20, 14740–14752 RSC.
- J. J. P. Stewart, Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- M. F. Budyka, Semiempirical study on the absorption spectra of the coronene-like molecular models of graphene quantum dots, Spectrochim. Acta, Part A, 2019, 207, 1–5 CrossRef CAS PubMed.
- J. T. Margraf, V. Strauss, D. M. Guldi and T. Clark, The Electronic Structure of Amorphous Carbon Nanodots. The, J. Phys. Chem. B, 2015, 119, 7258–7265 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- G. Seifert, Tight-Binding Density Functional Theory: An Approximate KohnSham DFT Scheme, J. Phys. Chem. A, 2007, 111, 5609–5613 CrossRef CAS PubMed.
- G. Seifert, D. Porezag and T. Frauenheim, Calculations of molecules, clusters, and solids with a simplified LCAO-DFT-LDA scheme, Int. J. Quantum Chem., 1996, 58, 185–192 CrossRef CAS.
- A. F. Oliveira, G. Seifert, T. Heine and H. A. Duarte, Density-functional based tightbinding: an approximate DFT method, J. Braz. Chem. Soc., 2009, 20, 1193–1205 CrossRef CAS.
- A. J. Page, H. Yamane, Y. Ohta, S. Irle and K. Morokuma, QM/MD Simulation of SWNT Nucleation on Transition-Metal Carbide Nanoparticles, J. Am. Chem. Soc., 2010, 132, 15699–15707 CrossRef CAS PubMed.
- T. Lei, W. Guo, Q. Liu, H. Jiao, D.-B. Cao, B. Teng, Y.-W. Li, X. Liu and X.-D. Wen, Mechanism of Graphene Formation via Detonation Synthesis: A DFTB Nanoreactor Approach, J. Chem. Theory Comput., 2019, 15, 3654–3665 CrossRef CAS PubMed.
- V. Botu and R. Ramprasad, Adaptive machine learning framework to accelerate ab initio molecular dynamics, Int. J. Quantum Chem., 2015, 115, 1074–1083 CrossRef CAS.
- T. M. Mitchell, Machine learning, McGraw-hill New York, 1997; vol. 1 Search PubMed.
- D.-M. Koh, N. Papanikolaou, U. Bick, R. Illing, C. E. Kahn, J. Kalpathi-Cramer, C. Matos, L. Martí-Bonmatí, A. Miles, S. K. Mun, S. Napel, A. Rockall, E. Sala, N. Strickland and F. Prior, Artificial intelligence and machine learning in cancer imaging, Commun. Med., 2022, 2, 133 CrossRef PubMed.
- E. Cambria, B. White and N. L. P. Jumping, Curves: A Review of Natural Language Processing Research [Review Article]. Computational Intelligence Magazine, IEEE Comput. Intell. Magaz., 2014, 9, 48–57 Search PubMed.
- C. Jin, H. Yu, J. Ke, P. Ding, Y. Yi, X. Jiang, X. Duan, J. Tang, D. T. Chang, X. Wu, F. Gao and R. Li, Predicting treatment response from longitudinal images using multi-task deep learning, Nat. Commun., 2021, 12, 1851 CrossRef CAS PubMed.
- S. Kalasin, P. Sangnuang and W. Surareungchai, Lab-on-Eyeglasses to Monitor Kidneys and Strengthen Vulnerable Populations in Pandemics: Machine Learning in Predicting Serum Creatinine Using Tear Creatinine, Anal. Chem., 2021, 93, 10661–10671 CrossRef CAS PubMed.
- D. Kiyasseh, T. Zhu and D. Clifton, A clinical deep learning framework for continually learning from cardiac signals across diseases, time, modalities, and institutions, Nat. Commun., 2021, 12, 4221 CrossRef CAS PubMed.
- Y. Xie, C. Zhang, X. Hu, C. Zhang, S. P. Kelley, J. L. Atwood and J. Lin, Machine Learning Assisted Synthesis of Metal–Organic Nanocapsules, J. Am. Chem. Soc., 2020, 142, 1475–1481 CrossRef CAS PubMed.
- Y. Han, B. Tang, L. Wang, H. Bao, Y. Lu, C. Guan, L. Zhang, M. Le, Z. Liu and M. Wu, Machine-Learning-Driven Synthesis of Carbon Dots with Enhanced Quantum Yields, ACS Nano, 2020, 14, 14761–14768 CrossRef CAS PubMed.
- X. Wang, B. Wang, H. Wang, T. Zhang, H. Qi, Z. Wu, Y. Ma, H. Huang, M. Shao, Y. Liu, Y. Li and Z. Kang, Carbon-Dot-Based White-Light-Emitting Diodes with Adjustable Correlated Color Temperature Guided by Machine Learning, Angew. Chem., Int. Ed., 2021, 60, 12585–12590 CrossRef CAS PubMed.
- A. W. Senior, et al., Improved protein structure prediction using potentials from deep learning, Nature, 2020, 577, 706–710 CrossRef CAS PubMed.
- J. Im, S. Lee, T.-W. Ko, H. W. Kim, Y. Hyon and H. Chang, Identifying Pb-free perovskites for solar cells by machine learning. npj Computational, Materials, 2019, 5, 37 Search PubMed.
- H. Jin, H. Zhang, J. Li, T. Wang, L. Wan, H. Guo and Y. Wei, Discovery of Novel TwoDimensional Photovoltaic Materials Accelerated by Machine Learning. The, J. Phys. Chem. Lett., 2020, 11, 3075–3081 CrossRef CAS PubMed.
- D. K. Pradhan, S. Kumari, E. Strelcov, D. K. Pradhan, R. S. Katiyar, S. V. Kalinin, N. Laanait and R. K. Vasudevan, Reconstructing phase diagrams from local measurements via Gaussian processes: mapping the temperature-composition space to confidence, npj Comput. Mater., 2018, 4, 23 CrossRef.
- J. Timoshenko, D. Lu, Y. Lin and A. I. Frenkel, Supervised Machine-Learning-Based Determination of Three-Dimensional Structure of Metallic Nanoparticles, J. Phys. Chem. Lett., 2017, 8, 5091–5098 CrossRef CAS PubMed.
- K. Takahashi and L. Takahashi, Creating Machine Learning-Driven Material Recipes Based on Crystal Structure, J. Phys. Chem. Lett., 2019, 10, 283–288 CrossRef CAS PubMed.
- Q. Zhou, S. Lu, Y. Wu and J. Wang, Property-Oriented Material Design Based on a Data-Driven Machine Learning Technique, J. Phys. Chem. Lett., 2020, 11, 3920–3927 CrossRef CAS PubMed.
- H. Sahu and H. Ma, Unraveling Correlations between Molecular Properties and Device Parameters of Organic Solar Cells Using Machine Learning, J. Phys. Chem. Lett., 2019, 10, 7277–7284 CrossRef CAS PubMed.
- D. Li, X. Li, Y. Zhang, L. Sun and S. Yuan, Four Methods to Estimate Minimum Miscibility Pressure of CO2-Oil Based on Machine Learning, Chin. J. Chem., 2019, 37, 1271–1278 CrossRef CAS.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. AspuruGuzik and Y. Jung, Inverse Design of Solid-State Materials via a Continuous Representation, Matter, 2019, 1, 1370–1384 CrossRef.
- Z. Yao, B. Śanchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Inverse design of nanoporous crystalline reticular materials with deep generative models, Nat. Mach. Intell., 2021, 3, 76–86 CrossRef.
- Y. Ma, T. Jin, R. Choudhury, Q. Cheng, Y. Miao, C. Zheng, W. Min and Y. Yang, Understanding the Correlation between Lithium Dendrite Growth and Local Material Properties by Machine Learning, J. Electrochem. Soc., 2021, 168, 090523 CrossRef CAS.
- J. Zhu, Z. Ren and C. Lee, Toward Healthcare Diagnoses by Machine-Learning-Enabled Volatile Organic Compound Identification, ACS Nano, 2021, 15, 894–903 CrossRef CAS PubMed.
- H. Tao, T. Wu, M. Aldeghi, T. C. Wu, A. Aspuru-Guzik and E. Kumacheva, Nanoparticle synthesis assisted by machine learning, Nat. Rev. Mater., 2021, 6, 701–716 CrossRef.
- B. Bartolomei, J. Dosso and M. Prato, New trends in nonconventional carbon dot synthesis, Trends Chem., 2021, 3, 943–953 CrossRef CAS.
- C.-T. Chen and G. X. Gu, Mach. Learn. Compos. Mater., 2019, 9, 556–566 CAS.
- M. Huang, Z. Li and H. Zhu, Recent Advances of Graphene and Related Materials in Artificial Intelligence, Adv. Intell. Syst., 2022, 4, 2200077 CrossRef.
- M. Langer, M. Paloncýová, M. Medveď, M. Pykal, D. Nachtigallová, B. Shi, A. J. Aquino, H. Lischka and M. Otyepka, Progress and challenges in understanding of photoluminescence properties of carbon dots based on theoretical computations, Appl. Mater. Today, 2021, 22, 100924 CrossRef.
- N. Munyebvu, E. Lane, E. Grisan and P. D. Howes, Accelerating colloidal quantum dot innovation with algorithms and automation, Mater. Adv., 2022, 3, 6950–6967 RSC.
- J. Peng, R. Muhammad, S.-L. Wang and H.-Z. Zhong, How Machine Learning Accelerates the Development of Quantum Dots? †, Chin. J. Chem., 2021, 39, 181–188 CrossRef CAS.
- M. Tamtaji, A. Tyagi, C. Y. You, P. R. Galligan, H. Liu, Z. Liu, R. Karimi, Y. Cai, A. P. Roxas, H. Wong and Z. Luo, Singlet Oxygen Photosensitization Using Graphene-Based Structures and Immobilized Dyes: A Review, ACS Appl. Nano Mater., 2021, 4, 7563–7586 CrossRef CAS.
- M.-X. Zhu, T. Deng, L. Dong, J.-M. Chen and Z.-M. Dang, Review of machine learningdriven design of polymer-based dielectrics, IET Nanodielectrics, 2022, 5, 24–38 CrossRef.
- S. A. Armida, D. Ebrahimibagha, M. Ray and S. Datta, Assessing thermoelectric performance of quasi 0D carbon and polyaniline nanocomposites using machine learning, Adv. Compos. Mater., 2023, 1–23 Search PubMed.
- Q. Zhang, Y. Tao, B. Tang, J. Yang, H. Liang, B. Wang, J. Wang, X. Jiang, L. Ji and S. Li, Graphene Quantum Dots with Improved Fluorescence Activity via Machine Learning: Implications for Fluorescence Monitoring, ACS Appl. Nano Mater., 2022, 5, 2728–2737 CrossRef CAS.
- V. S. Tuchin, E. A. Stepanidenko, A. A. Vedernikova, S. A. Cherevkov, D. Li, L. Li, A. Döring, M. Otyepka, E. V. Ushakova and A. L. Rogach, Optical Properties Prediction for Red and Near-Infrared Emitting Carbon Dots Using Machine Learning, Small, 2024, 2310402 CrossRef CAS PubMed.
- A. Döring, Y. Qiu and A. L. Rogach, Improving the Accuracy of Carbon Dot Temperature Sensing Using Multi-Dimensional Machine Learning, ACS Appl. Nano Mater., 2024, 7, 2258–2269 CrossRef.
- J. Chen, J. B. Luo, M. Y. Hu, J. Zhou, C. Z. Huang and H. Liu, Controlled Synthesis of Multicolor Carbon Dots Assisted by Machine Learning, Adv. Funct. Mater., 2023, 33, 2210095 CrossRef CAS.
- S. Pandit, T. Banerjee, I. Srivastava, S. Nie and D. Pan, Machine Learning-Assisted Array-Based Biomolecular Sensing Using Surface-Functionalized Carbon Dots, ACS Sens., 2019, 4, 2730–2737 CrossRef CAS PubMed.
- X.-Y. Wang, B.-B. Chen, J. Zhang, Z.-R. Zhou, J. Lv, X.-P. Geng and R.-C. Qian, Exploiting deep learning for predictable carbon dot design, Chem. Commun., 2021, 57, 532–535 RSC.
- R. D. Senanayake, X. Yao, C. E. Froehlich, M. S. Cahill, T. R. Sheldon, M. McIntire, C. L. Haynes and R. Hernandez, Machine Learning-Assisted Carbon Dot Synthesis: Prediction of Emission Color and Wavelength, J. Chem. Inf. Model., 2022, 62, 5918–5928 CrossRef CAS PubMed.
- N. Tuccitto, L. Fichera, R. Ruffino, V. Cantaro, G. Sfuncia, G. Nicotra, G. T. Sfrazzetto, G. Li-Destri, A. Valenti, A. Licciardello and A. Torrisi, Carbon Quantum Dots as Fluorescence Nanochemosensors for Selective Detection of Amino Acids, ACS Appl. Nano Mater., 2021, 4, 6250–6256 CrossRef CAS.
- M. Yahaya Pudza, Z. Zainal Abidin, S. Abdul Rashid, F. Md Yasin, A. S. Noor and M. A. Issa, Sustainable Synthesis Processes for Carbon Dots through Response Surface Methodology and Artificial Neural Network, Processes, 2019, 7, 704 CrossRef.
- A. Döring, Y. Qiu and A. L. Rogach, Utilizing Deep Learning to Enhance Optical Sensing of Ethanol Content Based on Luminescent Carbon Dots, ACS Appl. Nano Mater., 2022, 5, 11208–11218 CrossRef.
- B. Tang, Y. Lu, J. Zhou, T. Chouhan, H. Wang, P. Golani, M. Xu, Q. Xu, C. Guan and Z. Liu, Machine learning-guided synthesis of advanced inorganic materials, Mater. Today, 2020, 41, 72–80 CrossRef CAS.
- Q. Hong, X.-Y. Wang, Y.-T. Gao, J. Lv, B.-B. Chen, D.-W. Li and R.-C. Qian, Customized Carbon Dots with Predictable Optical Properties Synthesized at Room Temperature Guided by Machine Learning, Chem. Mater., 2022, 34, 998–1009 CrossRef CAS.
- X. Wang, S. Chen, Y. Ma, T. Zhang, Y. Zhao, T. He, H. Huang, S. Zhang, J. Rong, C. Shi, K. Tang, Y. Liu and Z. Kang, Continuous Homogeneous Catalytic Oxidation of C–H Bonds by Metal-Free Carbon Dots with a Poly(ascorbic acid) Structure, ACS Appl. Mater. Interfaces, 2022, 14, 26682–26689 CrossRef CAS PubMed.
- J. Chen, M. Zhang, Z. Xu, R. Ma and Q. Shi, Machine-learning analysis to predict the fluorescence quantum yield of carbon quantum dots in biochar, Sci. Total Environ, 2023, 896, 165136 CrossRef CAS PubMed.
- C. Xing, G. Chen, X. Zhu, J. An, J. Bao, X. Wang, X. Zhou, X. Du and X. Xu, Synthesis of carbon dots with predictable photoluminescence by the aid of machine learning, Nano Res., 2024, 17, 1984–1989 CrossRef CAS.
- H. He, S. E, L. Ai, X. Wang, J. Yao, C. He and B. Cheng, Exploiting machine learning for controlled synthesis of carbon dots-based corrosion inhibitors, J. Cleaner Prod., 2023, 419, 138210 CrossRef CAS.
- A. Dager, T. Uchida, T. Maekawa and M. Tachibana, Synthesis and characterization of Mono-disperse Carbon Quantum Dots from Fennel Seeds: Photoluminescence analysis using Machine Learning, Sci. Rep., 2019, 9, 14004 CrossRef PubMed.
- Z. Xu, Z. Wang, M. Liu, B. Yan, X. Ren and Z. Gao, Machine learning assisted dual-channel carbon quantum dots-based fluorescence sensor array for detection of tetracyclines, Spectrochim. Acta, Part A, 2020, 232, 118147 CrossRef CAS PubMed.
- T. Chen and C. Guestrin XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA, 2016; pp 785–794.
- O. A. Maslova, G. Guimbretière, M. R. Ammar, L. Desgranges, C. Jégou, A. Canizarès and P. Simon, Raman imaging and principal component analysis-based data processing on uranium oxide ceramics, Mater. Charact., 2017, 129, 260–269 CrossRef CAS.
- J. Felten, H. Hall, J. Jaumot, R. Tauler, A. de Juan and A. Gorzśas, Vibrational spectroscopic image analysis of biological material using multivariate curve resolution–alternating least squares (MCR-ALS), Nat. Protoc., 2015, 10, 217–240 CrossRef CAS PubMed.
- M. Shiga, K. Tatsumi, S. Muto, K. Tsuda, Y. Yamamoto, T. Mori and T. Tanji, Sparse modeling of EELS and EDX spectral imaging data by nonnegative matrix factorization, Ultramicroscopy, 2016, 170, 43–59 CrossRef CAS PubMed.
- P. Yan, X. Li, Y. Dong, B. Li and Y. Wu, A pH-based sensor array for the detection and identification of proteins using CdSe/ZnS quantum dots as an indicator, Analyst, 2019, 144, 2891–2897 RSC.
- L.-L. Li, X. Zhao, M.-L. Tseng and R. R. Tan, Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm, J. Cleaner Prod., 2020, 242, 118447 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |