CoTeO₄ – a wide-bandgap material adopting the dirutile structure type

Abstract

High-quality crystals of CoTeO₄ were grown by application of chemical vapor transport reactions in closed silica ampoules, starting from polycrystalline material in a temperature gradient 640 °C → 580 °C with TeCl₄ as transport agent. Crystal structure analysis of CoTeO₄ from single crystal X-ray data revealed a dirutile-type structure with Co^II and Te^VI atoms at crystallographically distinct sites, each with point group symmetry 1̄. The statistical significance and accuracy of the previously reported structural model based on powder data with the ordered arrangement of Co and Te cations was noticeably improved. CoTeO₄ does not undergo a structural phase transition upon heating, but decomposes stepwise (Co₂Te₃O₈ as intermediate phase) to Co₃TeO₆ as the only crystalline phase stable above 770 °C. Temperature-dependent magnetic susceptibility and dielectric measurements suggest antiferromagnetic ordering at ∼50 K. Optical absorption spectroscopy and computational studies reveal wide-band semiconductive behavior for CoTeO₄. The experimentally determined band gap of ∼2.42 eV is also found for CdS, which is frequently used in photovoltaic systems but is hazardous to the environment. Hence, CoTeO₄ might be a possible candidate to replace CdS in this regard.

---

Introduction

Complex Te-based metal oxides represent an attractive class of multifunctional materials based on a rich versatility with respect to their crystal structures and composition diagrams. This includes the capability to exist in two stable oxidation states in an oxidic environment, i.e. in form of Te^IV (resulting compounds are named oxidotellurates(IV)) and Te^VI (oxidotellurates(VI)).¹ For instance, some of these Te-based oxides have interesting physical properties due to their low dielectric losses in the microwave range and show potential applications in the field of low-temperature co-fired ceramic technology.² The renewed interest in transition metal oxidotellurates(VI) with formula type A₃TeO₆ (A is a divalent transition metal) is related to their interesting optical^3,4 and low-temperature magnetic properties,^5–8 including magnetic field induced spontaneous electric polarization in Co₃TeO₆.^9–14 Stimulated by these properties, Co₃TeO₆ has also been investigated in the high-pressure regime.^15,16

For synthesis of polycrystalline Co₃TeO₆ in its ambient-pressure form, solid-state reactions between suitable precursor materials are usually applied. In this regard, the growth reaction mechanism of Co₃TeO₆ has been studied in detail,¹⁷ revealing that CoTeO₄ is an intermediate product during the ceramic route for preparation of Co₃TeO₆. Although CoTeO₄ has been reported more than forty years ago,¹⁸ its structural and physical properties were not investigated in much detail. The first structure report was based on powder X-ray data and revealed a crystal structure derived from rutile (TiO₂).¹⁹ However, the original structure model was subsequently corrected on basis of high-resolution synchrotron X-ray data from nanocrystalline material.²⁰

We became interested in CoTeO₄ due to the interesting physical properties associated with inorganic materials adopting the rutile structure type or MM′′O₄ and MM₂′′O₆ derivatives thereof.²¹ For example, rutile-type compounds have been widely investigated for photocatalytic activities.^22,23 TiO₂ is also known for its incipient ferroelectric property because of its large static dielectric permittivity that shows strong frequency dependence associated with a soft (A_2u) mode behavior.²⁴ Moreover, rutile-type FeTiNbO₆ was reported to be a multiferroic material.²⁵ In the context of structure–property relationships, it is of paramount importance to have available both a reliable crystal structure model for computational studies and highly crystalline material for measurement/determination of physical properties related to long-range order and correlated phenomena. However, the reported crystal structure model of CoTeO₄ is not very accurate – which lies in the nature of structure refinements from powder data. Thus, improving the crystal structure model of CoTeO₄ is highly desirable, preferably on basis of single-crystal X-ray diffraction data. The same is true for the few reported findings regarding physical properties of CoTeO₄, which were determined from products with poor crystallinity.^19,20 Hence, advancements and complementary results are also expected in this area. Considered from this point of view, single crystal growth of CoTeO₄ with subsequent structure analysis as well as preparation of material with high crystallinity for determination of physical properties were the main reasons for a reinvestigation.

We report here the results of crystal growth studies, crystal structure elucidation, physical properties and theoretical calculations of CoTeO₄.

Experimental

Preparation of polycrystalline material

Stoichiometric amounts of Te(OH)₆ (5.500 g, 24 mmol) and Co(NO₃)₂(H₂O)₆ (6.970 g, 24 mmol) were thoroughly mixed and ground in an agate mortar. The mixture was heated in a porcelain crucible within three hours from room temperature to 300 °C and left at this temperature for twelve hours to expel water and oxides of nitrogen. The resulting black solid was ground again and heated within three hours to 550 °C, and left with another intermediate grinding step for two days. Powder X-ray diffraction of the light-brown solid revealed a single-phase product, however with poor crystallinity (Fig. 1). The crystallinity was significantly increased by heating the as-obtained powder in an evacuated and sealed silica ampoule at 600 °C for further 20 days (Fig. 1), resulting in an amber-colored polycrystalline material.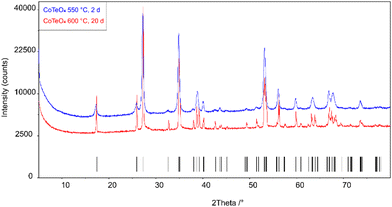

Fig. 1 X-ray powder diffraction patterns of single-phase CoTeO₄ tempered for 2 days at 550 °C and for 20 days at 600 °C. Tick marks represent the position of Bragg reflections.

Crystal growth

Crystals were grown by using chemical vapor transport reactions.²⁶ In a typical batch, 500 mg of polycrystalline CoTeO₄ and 50 mg TeCl₄ as transport agent were loaded in a silica ampoule (diameter 1 cm, length 12 cm) that was subsequently evacuated and sealed with an oxyhydrogen torch. The ampoule was placed in a horizontal two-zone furnace, applying a temperature gradient of 640 °C (source region) → 580 °C (sink region), and heated for 20 days. The grown crystals aggregated into intergrown species up to 3 mm in length with a nearly black color (Fig. 2). The streak of the crystals is dark-brown; the powder obtained by grinding the crystals is red-brown.

Fig. 2 Crystal aggregates of CoTeO₄. The distance between the scale bars is 1 mm.

Single crystal diffraction

The large crystal aggregates were broken into small amber-coloured pieces. Specimen of good optical quality were pre-selected under a polarizing microscope, embedded in perfluorinated polyether and mounted on MiTeGen MicroLoops®. X-ray diffraction data were recorded on a Bruker APEX-II diffractometer, equipped with monochromatized Mo-K_α radiation, using ω- and φ-scans. The collection strategy was chosen (APEX3)²⁷ to comprise the complete reciprocal sphere up to high angles and with high redundancy. After integration of the intensity data, a semi-empirical absorption correction (SADABS)²⁸ was performed. The crystal structure was solved by using SHELXT²⁹ and refined by using SHELXL.³⁰ The monoclinic unit-cell in space group P2₁/c was chosen with unique axis b and cell choice 1.³¹ Atomic coordinates were adapted to demonstrate the symmetry-relationship to the rutile aristotype in a concise way.³² The CoTeO₄ crystal under investigation showed a small contribution (8.7%) of a second domain that was correspondingly processed for the final data reduction (TWINABS).²⁷ The final refinement is based on a HKLF5-type file containing reflections from the first domain and overlapping reflections.

Numerical details of the data collection and structure refinement are compiled in Table 1. Selected bond lengths are given in Table 2, together with results of bond valence sum (BVS) calculations³³ using the parameters of Brese and O’Keeffe.³⁴ Further details of the crystal structure investigations may be obtained from the joint CCDC/FIZ Karlsruhe online deposition service: https://www.ccdc.cam.ac.uk/structures/by by quoting the deposition number specified at the end of Table 1.

Table 1 Data collection and refinement details

Formula	CoTeO4
M r	250.53
Temp./°C	25
Crystal dimension/mm^3	0.10 × 0.10 × 0.012
Crystal color	Brown
Crystal form	Plate
Space group, no.	P21/c, 15
Formula units Z	2
a/Å	5.5635(12)
b/Å	4.6675(10)
c/Å	5.5424(12)
β/°	112.321(6)
V/Å^3	133.14(5)
μ/mm^−1	16.975
X-ray density/g cm^−3	6.25
θ min–θmax/°	3.960–46.631
h	−11 to 10
k	0 to 9
l	0 to 11
Independent reflections	1243
Observed reflections (I > 2σ(I))	1073
T min; Tmax	0.4871; 0.7492
No. of parameters	33
R1 (F^2 > 2σ(F^2))	0.0168
wR2(F^2 all)	0.0450
GOF	1.082
CSD number	2265144

---

Table 2 Selected bond lengths/Å, bond valence sums (BVS)/valence units and distortion parameters calculated on basis of the current single crystal (SC) study and the previous high-resolution synchrotron powder study²⁰

Bond lengths			Current SC study	Synchrotron powder study
Co1–	O2	2×	2.0619(11)	1.967
	O2	2×	2.0812(11)	1.984
	O1	2×	2.1163(11)	2.188
Average			〈2.087〉	〈2.046〉
Te1–	O2	2×	1.8619(11)	1.939
	O1	2×	1.9625(10)	2.101
	O1	2×	1.9667(10)	1.963
Average			〈1.930〉	〈1.992〉
BVS
Co1			2.07	2.38
Te1			5.85	4.87
O1			2.02	1.52
O2			1.88	2.09
Polyhedral volume/Å^3		[CoO6]	11.641	10.997
		[TeO6]	9.493	10.519
Quadratic elongation		[CoO6]	1.027	1.029
		[TeO6]	1.007	1.012
Angle variance/°^2		[CoO6]	92.95	86.83
		[TeO6]	19.99	31.81

---

Laboratory powder X-ray diffraction (PXRD)

PXRD measurements were performed on a PANalytical X’Pert II Pro type PW 3040/60 diffractometer (Cu-K_α radiation, Bragg–Brentano geometry, X’Celerator detector) or on a Bruker D8 Advance diffractometer (Cu-K_α radiation, Bragg–Brentano geometry, LynxEye detector). Analyses of the powder diffraction data were carried out with the Highscore+ software suite³⁵ or the DIFFRACT plus software.³⁶ Results of the Rietveld analyses are given in the electronic ESI† (Tables S1–S3 and Fig. S1).

Synchrotron powder X-ray diffraction (SPXRD)

The in situ synchrotron powder X-ray diffraction (SPXRD) measurements were carried out at the Brockhouse High Energy Wiggler Beamline, Canadian Light Source (CLS), Canada. The experimental heating apparatus consisted of a flow-cell furnace³⁷ composed of a quartz capillary cell, capable of holding the sample in vacuum/inert gases atmosphere and surrounded by a helical coil connected to a source of electric current for controllable heating rate and natural convection cooling on the beam path. A thermocouple inserted into the capillary was used to monitor the temperature of the sample. A 2D PerkinElmer detector, 200 × 200 μm² pixel size and 40 × 40 cm² in area, was placed downstream of the powders in Kapton capillary, allowing data acquisition in a Debye–Scherrer/transmission mode. SPXRD patterns were acquired using a monochromatic focused beam of 30 keV. The calibrated X-ray wavelength and sample-to-detector distance from an Ni calibrant was λ = 0.4087 Å and 481.29 mm, respectively. An exposure time of 0.2 s was used and a total of 150 snapshots were acquired to ensure good data statistics. Obtained raw 2D diffraction patterns were integrated along each ring by the GSAS-II software.³⁸ Then, the resulting 1D HE-SXRD profiles were analyzed using Rietveld refinement analysis³⁹ in the 2θ range from 2 to 30°.

Simultaneous thermal analysis (STA)

Complementary STA measurements made use of thermogravimetry/differential thermal analysis (TG/DTA) coupled with mass spectrometry (MS). STA measurements were performed with a ∼50 mg sample on a NETZSCH STA 449 C Jupiter system in the temperature range 30 → 900 °C (corundum crucibles, flowing argon atmosphere (40 ml min⁻¹), heating rate 10 °C min⁻¹) coupled with a quadrupol mass analyzer (QMS) Aeolos by using a silica capillary kept at 250 °C. The measured mass signals were 2 (H₂), 12 (C), 14 (N), 15 (CH₃), 16 (CH₄, O), 17 (OH), 18 (H₂O), 28 (N₂, CO), 32 (O₂), 44 (CO₂) and 40 (Ar). A base line correction of the TG curve was carried out by measuring the empty crucible prior to the measurement.

Chemical composition analysis

The Co:Te cationic ratio in the CoTeO₄ single-crystals was determined from energy-dispersive X-ray spectroscopy (EDS) data, obtained using a ZEISS Leo 1550 field emission scanning electron microscope (SEM) equipped with an Aztec energy dispersive X-ray detector for spectroscopic analysis. Two single crystals were mounted onto conducting carbon tape, and EDS point analysis was performed using 20 kV on 11 spots per crystal. The oxidation states of the ions in CoTeO₄ was determined using X-ray photoelectron spectroscopy (XPS), conducted using an Ulvac-Phi Quantera II spectrometer with monochromatic Al-Kα radiation (1486.7 eV). Samples were mounted electrically floating, and measured under constant charge neutralisation using low energy electrons and Ar⁺.⁴⁰ The binding energy scale was referenced using the O 1s peak at 530.0 eV.

Measurements of physical properties

Selected crystal aggregates of CoTeO₄ (as grown by chemical transport reactions) were used for measurements of physical properties.

The heat capacity data of a crystal aggregate was recorded as a function of temperature and magnetic fields using a Bluefors dilution refrigerator equipped with a superconducting magnet and a differential membrane-based nanocalorimeter.⁴¹ The dc- and ac-magnetic properties of a crystal aggregate were measured using a superconducting quantum interference device (SQUID) magnetometer from Quantum Design Inc. The magnetization M of the sample was recorded both as a function of temperature T at a fixed applied magnetic field, and as a function of magnetic field H at fixed temperature.

The dielectric properties of the sample were characterized using an Agilent E4980A Precision LCR Meter. The two-electrode configuration was achieved by applying silver paint on the opposite surfaces of a chosen crystal aggregate and attaching copper wires to each surface. The sample was mounted on a custom-made probe in a Physical Property Measurement System (PPMS) from Quantum Design Inc. The capacitance of the sample was measured as a function of temperature and magnetic field for various frequencies (100 Hz to 2 MHz).

Optical absorption spectroscopy

Unpolarized optical absorption spectra of CoTeO₄ were recorded in the near ultraviolet (UV), visible (Vis), and near-infrared (NIR) spectral ranges between 32 000 and 5500 cm⁻¹ (3.97 to 0.68 eV) at a measuring spot of 50 μm in diameter, using a Bruker Hyperion 1000 microscope attached to a Bruker Vertex 80 FTIR spectrometer. To account for the strongly different absorption intensities in the NIR compared to the Vis and UV ranges, two crystal fragments with thicknesses of 30 and 5 μm, respectively, were investigated, using appropriate combinations of light sources (tungsten or xenon lamp), beam splitters (CaF₂-NIR or CaF₂-ViS/UV), and detectors (InGaAs-, Si- or GaP-diodes) to cover the desired spectral range. Hence, the full spectrum is combined from three partial spectra (32 000 to 18 000 cm⁻¹: spectral resolution 40 cm⁻¹, averaged from 512 scans; 18 000 to 10 000 cm⁻¹: resolution 20 cm⁻¹, 256 scans; 10 000 to 5500 cm⁻¹: resolution 10 cm⁻¹, 128 scans), which were aligned in absorbance for perfect match, if necessary, and calculated to linear absorption coefficient α (cm⁻¹).

Computational investigations

Density functional theory (DFT) calculations on CoTeO₄ were performed with the Wien2k code,⁴² which is based on the all electron full-potential Augmented-Plane-Wave (APW) method. Starting with the experimentally determined single-crystal structural data, the free positions of the O atoms were optimized (ESI,† Table S2) both at the level of generalized gradient approximation (PBE-GGA)⁴³ and also PBE+U (with U = 4.08 or 5.44 eV for Co 3d states).⁴⁴ We adopted an antiferromagnetic order, splitting the two symmetry-related Co atoms in the unit cell into spin-up and spin-down. The electronic structure, the band gap and the absorption spectra were calculated with different functionals (PBE+U, TB-mBJ,⁴⁵ TB-mBJ+U⁴⁶ and a YS-PBE0 hybrid functional,⁴⁷ which is closely related to the well-known HSE-functional).⁴⁸ The calculations were initialized with “-prec 2”, resulting into atomic spheres of 2.04, 1.84 and 1.58 Bohr for Co, Te and O, respectively, a plane wave cutoff parameter RK_max = 7.5 and a 15 × 16 × 15 k-mesh. Besides the usual valence states, also Co-3s,3p and Te-4p,4d states were treated as band states using local orbitals.

The optical properties have been calculated using the OPTIC module⁴⁹ of WIEN2k. The imaginary part of the dielectric function ε₂ has been obtained from the direct transitions including the corresponding dipole matrix elements, and via a Kramers–Kronik transformation the real part of ε is calculated. Once these quantities are known, the other optical properties (e.g. the absorption) follow from well-known relations.

Results and discussion

The crystal structure of CoTeO₄ has previously been determined from laboratory PXRD data in space group P2₁/n.‡ In the corresponding model,¹⁹ the Co and Te atoms equally occupy the same general site (4 e), and the two oxygen atoms likewise are situated on a general site each. Due to the mixed (Co,Te) occupancy, the resulting M–O bond lengths spread largely from 1.792(5) to 2.209(2) Å for the resulting [MO₆] octahedron, which is too short for a typical Co^II–O bond (mean 2.108 Å for coordination number (CN) = 6)⁵⁰ and too long for a typical Te^VI–O bond (mean 1.923 Å for CN = 6).⁵¹ In general, it appears unlikely that a divalent cation (for Co^II the ionic radius is 0.745 Å for high-spin configuration)⁵² shares the same site with a highly charged Te^VI atom (0.56 Å).⁵² §

The current crystal structure refinement of CoTeO₄ based on single-crystal X-ray data clearly revealed that the previous model¹⁹ is incorrect. In fact, Co and Te are situated on two distinct sites, 2 a and 2 d, respectively, each with site symmetry 1̄. The resulting bond lengths (Table 2) are in the characteristic ranges and comply with the expected mean bond lengths given above.

A recent structure determination of CoTeO₄ based on high-resolution synchrotron radiation from nanocrystalline material²⁰ likewise revealed the inaccuracy of the original structure model,¹⁹ and two distinct Co and Te positions were refined, similar to our model based on single-crystal data. However, the Co and Te atoms are swapped on respective Wyckoff positions, i.e. 2 b for Co and 2 c for Te, which corresponds to a shift of 1/2 0 0 in the unit cell. In comparison with the model derived from synchrotron data, our current redetermination reveals more satisfactory bond valence sums (close to the expected values of 2, 6 and 2 for Co, Te and O atoms), all atoms with anisotropic displacement parameters, standard uncertainties for the atomic coordinates, and shows considerable improvement in terms of higher precision and accuracy regarding bond lengths and angles (Table 2; ESI,† Tables S1–S3).

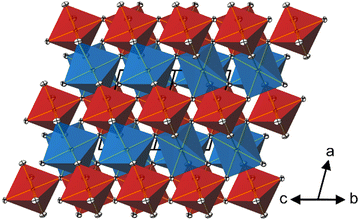
CoTeO₄ crystallizes in a dirutile-type structure and is isotypic with LiCo^IIIF₄,⁵⁴ LiMn^IIIF₄⁵⁵ and Cu^IIU^VIO₄.⁵⁶ Baur has described the relation of these cation-ordered dirutile structures (abbreviated as CUU) to the rutile structure (RUT) in detail.²¹ The symmetry-relationship³² between the rutile aristotype and the CUU hettotype of CoTeO₄ is graphically represented in Fig. 3 in form of a Bärnighausen tree.⁵⁷ In a first step, a translationengleiche (t2) symmetry reduction takes place from the rutile structure⁵⁸ to the CaCl₂ structure,⁵⁹ followed by a subsequent t2 symmetry reduction to the CuF₂ structure.⁶⁰ In the last step, an isomorphe (i2) symmetry reduction with a doubling of the unit cell occurs due to the cation ordering of Co^II and Te^VI in the CoTeO₄ structure.

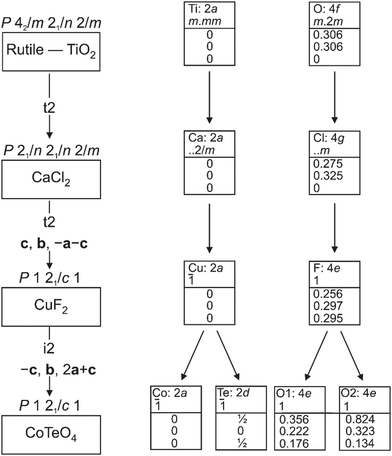Fig. 3 Bärnighausen tree showing the symmetry relationship between the rutile aristotype and the CoTeO₄ hettotype.

In the crystal structure of CoTeO₄, [CoO₆] octahedra share common corners, forming ¹_∝[CoO_2/2O_4/1] chains running along [011]. The Co–O bond lengths are similar (Table 2), leading to a far smaller octahedral distortion⁶¹ (Table 2) than in the isotypic congeners.²¹ Adjacent ¹_∝[CoO_2/2O_4/1] chains are joint at the same height (at x = 0) through additional corner-sharing, resulting in a cobalt(II) oxide layer ²_∝[CoO_4/2O_2/2] extending parallel to (100). The same kind of connection occurs for the [TeO₆] octahedra to form a ²_∝[TeO_4/2O_2/2] tellurium oxide layer (at x = 1/2). Common corners and edges link the two alternating layers into the tri-periodic structure. Edge-sharing occurs between alternating [CoO₆] and [TeO₆] octahedra in rows parallel to [101] (Fig. 4). Like in the rutile aristotype, the oxygen atoms coordinate to three positively charged atoms, viz. O1 to two Te and one Co, and O2 to two Co and one Te.

Fig. 4 Projection of the dirutile-type crystal structure of CoTeO₄ along [01̄1]. [CoO₆] octahedra are given in blue, [TeO₆] octahedra in red. Displacement ellipsoids are drawn at the 90% probability level.

The shortest distances between the cations (Co^II⋯Te^VI; Co^II⋯Co^II; Te^VI⋯Te^VI) are all greater than 3.0 Å (Co^II⋯Te^VI ∼ 3.09 Å; Co^II⋯Co^II ∼3.62 Å; Te^VI⋯Te^VI ∼3.62 Å), precluding any bonding interactions between them as observed for rutile-type VO₂ and its monoclinic polymorph where V⋯V separations of 2.85 Å and alternating short (2.62 Å) and long (3.17 A) separations, respectively, are observed.⁶² In CoTeO₄, interatomic Co⋯Te distances monotonically increase with heating in the region of existence of this phase (Fig. 5–7(a)).

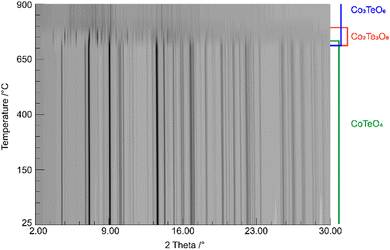Fig. 5 Temperature-dependent SPXRD in situ study of CoTeO₄ using a wavelength of 0.4087 Å. The existence range of present phases is indicated on the right.

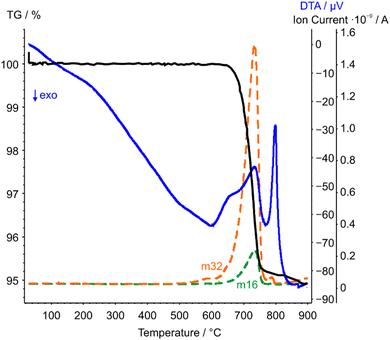Fig. 6 STA-MS measurement curves of CoTeO₄ (TG curve black, DTA curve blue). Only the mass signals (dashed lines) with significant intensities with respect to the ion current are displayed.

Fig. 7 (a) Evolution of unit-cell parameters with temperature; (b) dependence of eigenvalues of the thermal expansion; (c) three-dimensional surface of the thermal expansion tensor for CoTeO₄ (500 °C data).

Thermal behavior

CoTeO₄ shows no temperature-induced structural phase transition from room-temperature to the end of its stability range at ∼700 °C. According to Singh et al.,¹⁷ intermediately formed CoTeO₄ (starting from Co₃O₄/TeO₂ mixtures) becomes unstable above 700 °C and successively transforms to Co₃TeO₆. In contrast to this ex situ study, our current temperature-dependent in situ SPXRD study is based on single-phase CoTeO₄ (Fig. 5). Although under atmospheric conditions the final product at 900 °C is likewise single-phase Co₃TeO₆, the temperature-dependent SPXRD study clearly revealed spiroffite-type Co₂Te₃O₈⁶³ as an intermediate phase that is present between the decomposition of CoTeO₄ at ∼700 °C and the formation of Co₃TeO₆⁶⁴ at ∼770 °C (Fig. 5).

Hence, the overall decomposition can be formulated by eqn 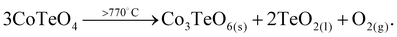(1):

Above 700 °C, TeO₂ suggested as a decomposition product, shows no reflections, because it either forms as an amorphous phase or is already molten (melting point 733 °C).⁶⁵

The complementary STA-MS measurement (Fig. 6) reveals an onset for the CoTeO₄ decomposition at 665 °C in the TG curve (end point 747 °C), with an overall mass loss of 4.8% (theory according to eqn (1): 4.3%). The observed masses of the released gases (m = 16, 32) correspond solely to oxygen, underpinning the decomposition reaction formulated in eqn (1). The two endothermic effects in the DTA signal with onsets and peak maxima at 677/733 °C and 782/799 °C indicate the decomposition of CoTeO₄ under formation of Co₂Te₃O₈, and the subsequent decomposition of Co₂Te₃O₈ under formation of Co₃TeO₆, respectively. The decomposition/formation temperatures determined from temperature-dependent SPXRD and STA-MS data differ due to different placements of thermocouples for temperature control, and different heating rates and atmospheres applied in the two measurement procedures (slow heating and holding times, atmospheric conditions for PXRD versus fast heating times, Ar atmosphere for STA-MS).

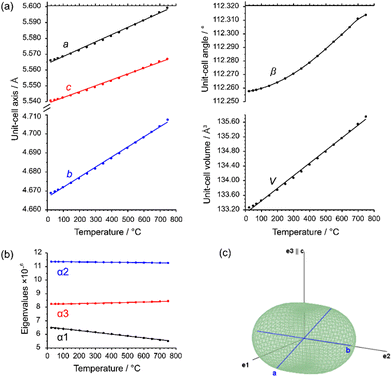
The evolution of unit-cell parameters with temperature of dirutile-type CoTeO₄ is depicted in Fig. 7(a) and shows a linear increase of the unit-cell volume from room temperature up to the end of its stability region. On basis of the formalism in the infinitesimal temperature limit introduced by Paufler and Weber,⁶⁶ the TEV software⁶⁷ has been used for calculation of the components of the thermal expansion tensor αij. For the definition of the second rank tensor within the TEV program, the following orthogonalized coordinate system was used: e3 is parallel to c, e2 is parallel to b* and e1 = e2 × e3. The resulting symmetrical tensor has six independent components (α11, α22, α33, α12, α13, α23). Owing to the symmetry restrictions of the monoclinic crystal system with unique axis b, the components α12 and α23 are zero. The regression curves for description of unit-cell parameters and the temperature-dependent numerical values for the four tensor components of CoTeO₄ are compiled in Table S4 in the ESI.† After transformation to principal axes, the tensor can be simplified and is described by only three independent components (α1, α2, α3). The dependence on temperature of these eigenvalues is shown in Fig. 7(b). Whereas each individual expansion coefficient shows only subtle changes with temperature, the expansion coefficient α2 has about twice the absolute value of the smallest eigenvalue α1, making the thermal expansion in CoTeO₄ anisotropic. The representation of the tensor and its anisotropy in form of a surface in three-dimensional space is exemplified in Fig. 7(c) for the 500 °C data. It can be seen that the strongest expansion is along the b axis that exactly coincides with eigenvalue α2 and the corresponding eigenvector. The lowest expansion is perpendicular to this direction.

Chemical composition

The elemental composition as determined by EDS is in very good agreement with the nominal one, yielding the chemical formula of Co_1.01(1)Te_0.99(1)O₄ (ESI;† Table S5 and Fig. S2).

For pristine crystals, a significant surface contamination by carbon was revealed by XPS measurements (see ESI,† Fig. S3), most probably caused by immersing the crystals in acetone for selection. The surface contamination significantly decreased after temperature annealing (500 °C for two hours) in air. The XPS spectra suggest that cobalt and tellurium are solely present as Co^II and Te^VI, respectively. The high-resolution core-level binding energy revealed well-resolved chemical states corresponding to Co 2p, Te 3d, O 1s (and C 1s) levels (ESI,† Fig. S3). The core level XPS spectrum of Co 2p consist of a large peak at 780.3 eV and a broad satellite approximately 6 eV from the main peak, as expected for Co^II but not for Co^III.⁶⁸ The Te 3d core level spectrum consist of two major peaks located at 576.0 and 586.4 eV, consistent with Te^VI.⁶⁹

Caloric properties

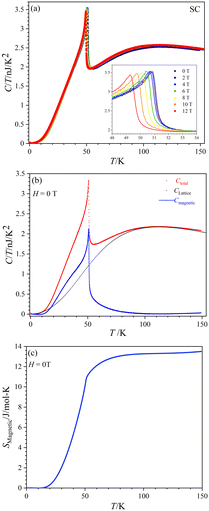
Fig. 8(a) displays the total specific heat (C) divided by temperature (T) of a CoTeO₄ crystal measured in different magnetic fields (0 ≤ H ≤ 12 T) over a broad temperature range from 0.1 to 151 K. The position of the sharp peak is shifted from 50.9 K to 49.2 K by an increase of the applied magnetic field from 0 to 12 T (see inset), however without significant changing in the C/T value. This behavior suggests that the system undergoes an antiferromagnetic (AFM) phase transition.

Fig. 8 (a) C/T vs. T curves of CoTeO₄ in the range 0 ≤ H ≤ 12 T. Inset in (a) represents the zoom view of peak maxima. (b) Magnetic (blue) and lattice (black) contributions of C/T vs. T for H = 0 T. (c) S_magneticvs. T for H = 0 T.

Fig. 8(b) shows the calculated magnetic specific heat (C_magnetic, blue color) of CoTeO₄ at zero magnetic field, after subtracting from the total specific heat (C_total, red color) the high temperature lattice contributions (C_lattice, black color) estimated from a Debye model. Moreover, the magnetic entropy (S_magnetic) was calculated from C_magnetic using the following equation, 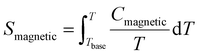, as shown in Fig. 8(c), which reveals a sharp release of the magnetic entropy near the transition temperature.

A gradual increase of the magnetic entropy is observed in the high temperature region, with the magnitude (13 J mol⁻¹ K⁻¹) being higher than the spin-only value of 11.51 J mol⁻¹ K⁻¹ (R ln(2S + 1)) of Co^II (3d⁷, S = 3/2). Such discrepancy might have an intrinsic origin, related to the orbital component of the Co^II moments. However, we cannot exclude that it could also originate from the determination of C_lattice, as well as uncertainties on the volume of the investigated crystal.

Magnetic susceptibilities

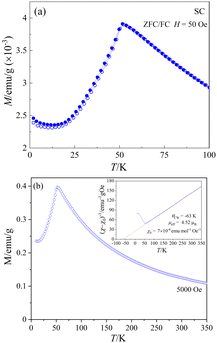
Fig. 9(a) shows the temperature-dependent dc-magnetization measured as a function of temperature under zero-field-cooled (ZFC) and field-cooled (FC) conditions in an external dc-magnetic field, H = 50 Oe. Both ZFC and FC curves show a peak maximum around 51.6 K and no divergence in the entire temperature region, indicating the onset of AFM long-range ordering, in agreement with the sharp peak observed near 50.9 K in the heat capacity data (Fig. 8). The linear M(H) curves measured at different temperatures below the magnetic transition provides further evidence of typical AFM behavior (see ESI,† Fig. S4) at low temperatures. Fig. 9(b) shows the M(T) data measured at 5 kOe under ZFC condition. The inset of Fig. 9(b) shows the temperature dependence of the corresponding inverse of the susceptibility (χ − χ₀)⁻¹ where χ = M/H and χ₀ is a background contribution. The high temperature susceptibility data from 70 K to 300 K was fitted to the Curie–Weiss (CW) law, χ = C/(T − θ_CW) + χ₀, where C and θ_CW represents the Curie constant and Curie–Weiss temperature, respectively.

Fig. 9 (a) ZFC/FC M vs. T curves of CoTeO₄ for H = 50 Oe; (b) M(T) under H = 5 kOe. Inset in (b) shows (χ − χ₀)⁻¹vs. T and linear Curie–Weiss fit in the range 70 ≤ T ≤ 300 K. The obtained parameters are indicated in the Figure.

The straight-line fitting of the inverse susceptibility vs. temperature data yields C = 2.47 emu K mol⁻¹ Oe⁻ and θ_CW = −63 K. The negative sign and the value of θ_CW indicates AFM interactions and relatively weak frustration effects.⁷⁰ The effective paramagnetic moment μ_eff calculated from C (= N_Aμ_eff²/3k_B) is 4.52 μ_B per Co. This value is considerably greater than the spin-only value of μ_spin = 3.87 μ_B for high-spin Co^II cations (3d⁷, S = 3/2), indicating an unquenched orbital moment, e.g. stemming from an unevenly occupied degenerate t_2g-state of the central Co^II cation in the coordination polyhedron. Similar values of μ_eff for Co^II in an oxidic environment were also observed in various system such as Co₃TeO₆ (4.70 μ_B),¹¹ Sr₂CoWO₆ (5.2 μ_B),⁷¹ or Ba₂CoO₂Cu₂S₂ (4.45 μ_B).⁷²

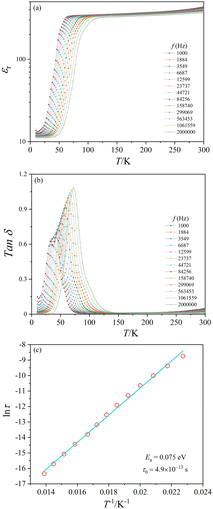
Dielectric properties

The present crystal aggregates have relatively small sizes. Nonetheless, dielectric measurements were attempted. The temperature dependence of the relative dielectric constant (ε_r) and the dielectric loss (Tan δ) of CoTeO₄ at variable frequencies (1 kHz ≤ H ≤ 2 MHz) and in zero magnetic field is shown in Fig. 10. ESI,† Fig. S5 shows ε_r(T) and Tan δ(T) for 1.06 MHz at 0 and 10 kOe magnetic fields, and ESI,† Fig. S6 displays ε_rvs. f and Tan δ vs. f plots of CoTeO₄ crystals at different temperatures.

Fig. 10 (a) ε_rvs. T plots and (b) Tan δ vs. T plots of CoTeO₄ crystal aggregates at selected frequencies and in zero magnetic field. (c) ln τ vs. 1/T plot; scattered symbols are the peak maxima of Tan δ and the solid line is the least-squares straight line fit according to an Arrhenius equation.

The value of the dielectric constant reveals a relatively weak temperature (T) and frequency (f) dependence while decreasing the sample temperature from room temperature down to 100 K, followed by a sharp decrease of approximately 90% until the temperature decreases to 50 K. Below 50 K, the ε_r value is almost constant. The shift of the ε_r value to higher temperature with increasing frequency in the temperature range of 50 K < T < 100 K indicates a relaxor-like behavior. The sharp increase of the dielectric loss peak around 55 K (Fig. 10(b)) is consistent with the decrease of the dielectric constant. Fig. 10(b) shows also that the Tan δ peak shifts to higher temperature with increasing frequency, which corresponds to a thermally activated relaxation process. The peak maxima of the Tan δ curve can be plotted using an Arrhenius equation: τ = τ₀ exp(E_a/k_BT), where τ = 1/2πf and k_B is the Boltzmann constant (Fig. 10(c)). The straight-line fitting gives the activation energy, E_a ≈ 0.07 eV, and the relaxation time, τ₀ ≈ 4.9 × 10^−13+/−1 s.

DFT calculations and electronic structure

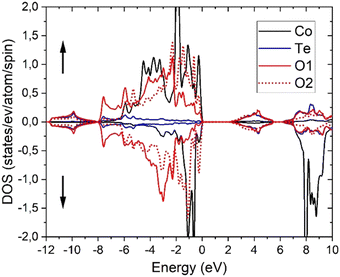
As generally accepted and therefore expected,^44,46 PBE calculations are not suitable for the correlated Co-3d electrons as can be seen from the fact that it would lead to a metallic state and rather short Co–O and large Te–O equilibrium distances (ESI,† Table S3). Therefore, the atomic positions of oxygen were also relaxed using PBE+U and, as evident from Tables S2 and S3 (ESI†), a much better agreement with the experimental single crystal results is obtained from the latter calculations. Using the relaxed PBE+U (4.08) structure, PBE+U, TB-mBJ, TB-mBJ+U and YS-PBE0 hybrid-DFT calculations yield a material with semiconductive behavior with direct band gaps at Γ of 0.61, 1.31, 2.14 and 1.60 eV, respectively. Similarly, the obtained spin magnetic moments vary with the DFT approximation as 2.70, 2.76, 2.82 and 2.70 μ_B, while plain PBE would get a significantly smaller moment of 2.50 μ_B. These values are similar as in CoO (2.72 μ_B with TB-mBJ)⁷³ and indicative for Co^II ions with significant covalent interactions with oxygen atoms. On the other hand, the orbital moment remains smaller (0.15 μ_B with PBE+U) than in CoO.⁷⁴ The density of states (DOS) comprises basically four parts (Fig. 11 for TB-mBJ+U calculations). The lowest one, between −12 and −8 eV consists mainly of bonding Te-s–O-sp states, followed by the main valence band of predominantly Co-3d and O-2p states together with a small Te-6p contribution. The Co-3d states are spin-splitted, leading to a Co^II high-spin state with fully occupied majority (spin-up) states but only partially occupied spin-down bands. The O-2p states of the two different oxygen atoms in the structure are strongly shifted in energy with O2 being less ionic (see also the BVS values in Table 2) due to two Co and only one Te nearest neighbors (nn), while the O1 site has two Te and only one Co nn. This correlates with an about 1 eV XPS core level shift of the O-1s states with O2 states at larger binding energies. The first conduction band states are mainly derived from antibonding Te-6p–O-2p states followed by the Co-3d spin-down bands. The detailed bandwidth and the possible separation of those four band regions depend crucially on the specific choice of the DFT approximation.

Fig. 11 Spin-polarized partial DOS of CoTeO₄ in the TB-mBJ+U (4.08 eV) approximation.

Optical spectroscopy and computational investigation

The brownish color of CoTeO₄ is rather unusual for Co^II-containing oxidic compounds, which usually appear with a pinkish color (in octahedral coordination) or bluish color (in tetrahedral coordination).⁷⁵Fig. 12 shows the unpolarized optical absorption spectrum of CoTeO₄. It is characterized on the one hand by comparatively weak absorption features within the NIR spectral region, on the other hand by an absorption edge strongly ascending within the visible spectral range towards the UV region.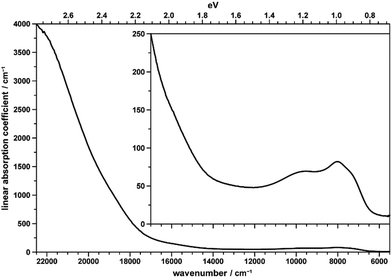

Fig. 12 Unpolarized absorption spectrum of a thin CoTeO₄ crystal. The inset shows the data on the smaller y-range.

The NIR absorption bands (inset in Fig. 12) correspond to the first spin-allowed crystal field transition of high-spin Co^II in octahedral coordination, i.e.⁴T_1g(F) → ⁴T_2g(F), split by the distortion of the [CoO₆] polyhedron from ideal cubic symmetry, with components located around 7200 (shoulder), 7970, and 9750 cm⁻¹. The second spin-allowed, but – as two-electron jump in the strong field limit – electronically forbidden and thus weak ⁴T_1g(F) → ⁴A_2g(F) transition, might be spotted roughly around 15 900 cm⁻¹, within the onset of the absorption edge (see inset in Fig. 12). Finally, the third and usually most intense ⁴T_1g(F) → ⁴T_1g(P) crystal field transition is located around 18 750 cm⁻¹ within the ascent of the absorption edge, thus slightly reducing its slope up to ∼20 000 cm⁻¹; quite evidently, for ⁴T_1g(P) no low-symmetry band splitting could be extracted. The observed approximate crystal field transition energies correspond to a comparatively high crystal field strength parameter of ∼875 cm⁻¹,⁷⁶ in agreement with the rather small average Co–O distance of 2.087 Å in CoTeO₄; the interelectronic repulsion parameter Racah B is ∼800 cm⁻¹.

The strong increase of the absorption edge towards higher energies, roughly setting in around 17 500 cm⁻¹, is responsible for the brownish color of CoTeO₄.

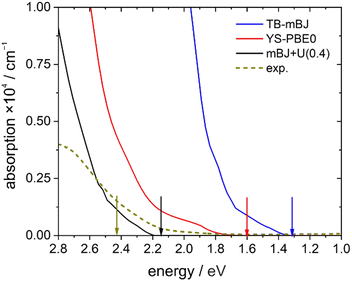
A direct comparison between the experimental absorption spectrum and the different DFT calculations revealed that the TB-mBJ+U (4.08 eV) functional fits best to the onset and slope of the experimental absorption curve, followed by hybrid functional (YS-PBE0) calculations (Fig. 13). From such a comparison one would estimate that the TB-mBJ+U calculation results in a slightly too large band gap, while the YS-PBE0 gap is too small. This is in contrast to the band gaps derived directly from the DFT calculations and the experimental Tauc-plot, see below.

Fig. 13 Onset of the unpolarized theoretical absorption spectrum (TB-mBJ, YS-PBE0, TB-mBH+U (4.08) functionals) in comparison with the experimental (exp.) data. The arrows mark the corresponding band gaps.

Assuming a direct bandgap (as found in the DFT calculations), a Tauc plot⁷⁷ applied to the linearly increasing absorption above ∼20 000 cm⁻¹ (i.e. the region not affected by the ⁴T_1g(P) crystal field band) reveals an experimental band gap of 2.42 eV (Fig. 14), a value also found for CdS,⁷⁸ which is one of the most promising photovoltaic materials available for low-cost high-efficiency solar cells.⁷⁹ In that regard, CoTeO₄ might replace the environmentally hazardous CdS in photovoltaic devices.

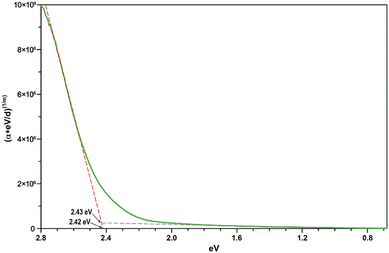Fig. 14 Direct bandgap Tauc plot derived from the unpolarized transmission spectrum of CoTeO₄ using a crystal plate with a thickness of ∼5 μm.

The experimentally found band gap (2.42 eV) from the Tauc-plot (Fig. 14) is slightly larger than the TB-mBJ+U gap (2.14 eV), while the YS-PBE0 hybrid-DFT gap (1.60 eV) and in particular TB-mBJ or PBE+U calculations yield significantly smaller gaps (Fig. 13). This is not unreasonable since it is well documented that both TB-mBJ and hybrid-DFT functionals yield reasonable band gaps for sp semiconductors,^80–82 but their effect on transition metal 3d states might be too small.^46,83 On the other hand, a Hubbard-U correction for the 3d states yield the desired splitting between occupied and unoccupied 3d bands, but since the sp states of the main group elements are not affected, the resulting band gap might still be too small and only a combination of TB-mBJ+U yields reasonable band gaps in transition metal oxides.

Conclusions

Chemical vapor transport reactions with TeCl₄ as transport were employed to grow CoTeO₄ crystals in the millimeter range. High-quality crystals grown this way were used for the determination of the chemical composition, for crystal structure refinement and measurement of physical properties. The current single-crystal X-ray data clearly showed that the originally reported structure model for dirutile-type CoTeO₄¹⁹ is incorrect. The refined crystal structure model in the centrosymmetric space group P2₁/c excludes the prospect of using this material as a polar dielectric. Thermal analysis and temperature-dependent synchrotron diffraction studies revealed that CoTeO₄ does not undergo a temperature-dependent structural phase transition in the stability field from room temperature up to 700 °C, and current pressure-dependent Raman spectroscopy studies⁸⁴ likewise showed no structural phase transition of CoTeO₄ up to pressures of ∼10 GPa. Heat capacity and magnetic susceptibility measurements indicated an antiferromagnetic ordering of CoTeO₄ at ∼50 K, in the vicinity of which dielectric relaxation is observed. Neutron diffraction measurement for determination of the magnetic structure of CoTeO₄ are planned in near future. Optical absorption spectroscopy on a thin single-crystal plate was used to experimentally determine the band gap. Complementary computational studies on the basis of different DFT models showed that the TB-mBJ+U functional resulted in a band gap of 2.14 eV that matches best the experimentally found value of 2.42 eV, whereas the experimental absorption spectrum edge is in the middle of the TB-mBJ+U and the YS-PBE0 hybrid calculations.

Author contributions

Matthias Weil: conceptualization, investigation, data curation, project administration, resources, supervision, validation, writing – original draft, writing – review and editing; Prativa Pramanik: investigation, data curation; Pierfrancesco Maltoni: investigation; Rebecca Clulow: investigation; Andreas Rydh: investigation; Manfred Wildner: investigation, data curation; Peter Blaha: investigation, data curation, writing – original draft; Graham King: investigation, data curation; Sergey A. Ivanov: conceptualization, writing – original draft; Roland Mathieu: investigation, data curation, project administration, resources, supervision, writing – original draft, writing – review and editing; Harishchandra Singh: investigation, data curation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Erik Lewin for his help with the XPS measurements and analyses. We also thank Christian Gierl-Mayer for his help for the STA measurements. R. C. acknowledges the SSF contract number EM-16-0039 and Åforsk contract 22-92. We acknowledge Myfab Uppsala for providing facilities and experimental support. Myfab is funded by the Swedish Research Council (2019-00207) as a national research infrastructure. The authors acknowledge the X-ray centre of TU Wien for providing free access to single crystal and powder X-ray diffraction instruments, and TU Wien Bibliothek for financial support through its Open Access Funding Program. P. P. and R. M. thank Stiftelsen Olle Engkvist Byggmästare (grant no. 207-0427) for financial support. R. C. acknowledges the SSF contract number EM-16-0039. Research conducted by S. A. I. was carried out with the financial support of the RSF (grant 22-13-00122). Part of the research described in this work was performed at the Canadian Light Source, a national research facility of the University of Saskatchewan, which is supported by the Canada Foundation for Innovation (CFI), the Natural Sciences and Engineering Research Council (NSERC), the National Research Council (NRC), the Canadian Institutes of Health Research (CIHR), the Government of Saskatchewan, and the University of Saskatchewan. EU/Interreg Aurora/Sustainable Hydrogen project is also acknowledged for financial support.

Notes and references

1. A. G. Christy, S. J. Mills and A. R. Kampf, A review of the structural architecture of tellurium oxycompounds, Mineral. Mag., 2018, 80, 415–545.
2. M. T. Sebastian, H. Wang and H. Jantunen, Low temperature co-fired ceramics with ultra-low sintering temperature: a review, Curr. Opin. Solid State Mater. Sci., 2016, 20, 151–170.
3. A. Bhim, J. Gopalakrishnan and S. Natarajan, Exploring the Corundum Structure as a Host for Colored Compounds – Synthesis, Structures, and Optical Studies of (MM′)₃TeO₆ (M = Mg, Mn, Co, Ni, Zn; M′ = Mg, Mn, Co, Ni, Cu), Eur. J. Inorg. Chem., 2018, 2277–2284.
4. D. Reichartzeder, M. Wildner, M. Weil, S. A. Ivanov, A. Stash and Y. S. Chen, Crystal chemistry, optical spectroscopy and crystal field calculations of Co₃TeO₆ and solid solutions Co_3−xZn_xTeO₆, Eur. J. Inorg. Chem., 2018, 4221–4233.
5. N. V. Golubko, V. Yu Proidakova, G. M. Kaleva, S. A. Ivanov, A. V. Mosunov, S. Yu Stefanovich, N. V. Sadovskaya, E. D. Politova and P. Nordblad, Synthesizing and investigating the structure and phase transitions in A₃TeO₆ (A—Mn, Co, Ni) oxides, Bull. Russ. Acad. Sci.: Phys., 2010, 74, 724–726.
6. I. Živković, K. Prša, O. Zaharko and H. Berger, Ni₃TeO₆—a collinear antiferromagnet with ferromagnetic honeycomb planes, J. Phys.: Condens. Matter, 2010, 22, 056002.
7. S. A. Ivanov, P. Nordblad, R. Mathieu, R. Tellgren, C. Ritter, N. V. Golubko, E. D. Politiva and M. Weil, New type of incommensurate magnetic ordering in Mn₃TeO₆, Mater. Res. Bull., 2011, 46, 1870–1877.
8. R. Mathieu, S. A. Ivanov, P. Nordblad and M. Weil, Enhancement of antiferromagnetic interaction and transition temperature in M₃TeO₆ systems (M = Mn, Co, Ni, Cu), Eur. Phys. J., 2013, B 86, 361.
9. J. Fernández-Catalá, H. Singh, S. Wang, H. Huhtinen, P. Paturi, Y. Bai and W. Cao, Hydrothermal Synthesis of Ni₃TeO₆ and Cu₃TeO₆ Nanostructures for Magnetic and Photoconductivity Applications, ACS Appl. Nano Mater., 2023, 6, 4887–4897.
10. S. A. Ivanov, R. Tellgren, C. Ritter, P. Nordblad, R. Mathieu, G. André, N. V. Golubko, E. D. Politova and M. Weil, Temperature-dependent multi-k magnetic structure in multiferroic Co₃TeO₆, Mater. Res. Bull., 2012, 47, 63–72.
11. M. Hudl, R. Mathieu, S. V. Ivanov, M. Weil, V. Carolus, T. Lottermoser, M. Fiebig, Y. Tokunaga, Y. Taguchi, T. Tokura and P. Nordblad, Complex magnetism and magnetic-field-driven electrical polarization of Co₃TeO₆, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180404.
12. W.-H. Li, C.-W. Wang, D. Hsu, C.-H. Lee, C.-M. Wu, C.-C. Chou, H.-D. Yang, Y. Zhao, S. Chang, J. W. Lynn and H. Berger, Interplay between the magnetic and electric degrees of freedom in multiferroic Co₃TeO₆, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 094431.
13. C.-H. Lee, E. Batsaikhan, M.-H. Ma, W.-H. Li, C.-W. Wang, C.-M. Wu, H.-D. Yang, J. W. Lynn and H. Berger, Charge transfer enhanced magnetic correlations in type-II multiferroic Co₃TeO₆, J. Chin. Chem. Soc., 2021, 68, 395–402.
14. H. Singh, H. Ghosh, T. V. Chandrasekhar Rao, G. Sharma, J. Saha and S. Patnaik, Short range ferromagnetic, magneto-electric, and magneto-dielectric effect in ceramic Co₃TeO₆, J. Appl. Phys., 2016, 119, 044104.
15. E. Solana-Madruga, C. Aguilar-Maldonado, C. Ritter, M. Huvé, O. Mentré, J. P. Attfield and Á. M. Arévalo-López, Complex magnetism in Ni₃TeO₆-type Co₃TeO₆ and high-pressure polymorphs of Mn_3−xCo_xTeO₆ solid solutions, Chem. Commun., 2021, 57, 2511–2514.
16. E. Selb, T. Buttlar, O. Janka, M. Tribus, S. G. Ebbinghaus and G. Heymann, Multianvil high-pressure/high-temperature synthesis and characterization of magnetoelectric HP-Co₃TeO₆, J. Mater. Chem. C, 2021, 9, 5486–5496.
17. H. Singh, A. K. Sinha, S. M. Gupta, M. N. Singh and H. Ghosh, Insight into the Growth Reaction Mechanism of Ceramic Co₃TeO₆: Synchrotron Structural and Thermal Analysis., J. Am. Ceram. Soc., 2016, 99, 3443–3448.
18. J. Sikač and L. Jenšovský, The preparation and properties of cobalt(II) tellurates, Collect. Czech. Chem. Commun., 1980, 45, 2489–2498.
19. J. Isasi, New MM’O₄ oxides derived from the rutile type: synthesis, structure and study of magnetic and electronic properties, J. Alloys Compd., 2001, 322, 89–96.
20. A. K. Patel, M. R. Panda, E. Rani, H. Singh, S. S. Samatham, A. Nagendra, S. N. Jha, D. Bhattacharyya, K. G. Suresh and S. Mitra, Unique Structure-Induced Magnetic and Electrochemical Activity in Nanostructured Transition Metal Tellurates Co_1–xNi_xTeO₄ (x = 0, 0.5, and 1), ACS Appl. Energy Mater., 2020, 3, 9436–9448.
21. W. H. Baur, The rutile type and its derivatives, Crystallogr. Rev., 2007, 13, 65–113.
22. A. Fujishima and K. Honda, Electrochemical photolysis of water at a semiconductor electrode, Nature, 1972, 238, 37–38.
23. N. Kumada, N. Koike, K. Nakanome, S. Yanagida, T. Takei, A. Miura, E. Magome, C. Moriyoshi and Y. Kuroiwa, Synthesis of rutile-type solid solution Ni_1−xCo_xTi(Nb_1−yTa_y)₂O₈ (0 ≤ x ≤ 1, 0 ≤ y ≤ 1) and its optical property, J. Aust. Ceram. Soc., 2017, 5, 284–289.
24. C. Lee, P. Ghosez and X. Gonze, Lattice dynamics and dielectric properties of incipient ferroelectric rutile, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13379–13387.
25. S. Wang, Y.-D. Hou, M.-P. Zheng, H.-Y. Ge, M.-K. Zhu and H. Yan, Room-temperature dielectric relaxation and magnetic properties in rutile-type FeTiNbO₆, Mater. Res. Bull., 2013, 48, 3098–3102.
26. M. Binnewies, R. Glaum, M. Schmidt and P. Schmidt. Chemical Vapour Transport Reactions. De Gruyter, Berlin, Germany, 2012.
27. APEX3, SAINT and TWINABS, Bruker AXS Inc., Madison, Wisconsin, USA, 2016.
28. L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination, J. Appl. Crystallogr., 2015, 48, 3–10.
29. G. M. Sheldrick, SHELXT-Integrated space-group and crystal-structure determination, Acta Crystallogr., 2015, A71, 3–8.
30. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., 2015, C71, 3–8.
31. International Tables for Crystallography, Space-group symmetry, ed. M. I. Aroyo, Wiley, 2016, vol. A.
32. U. Müller. Symmetry Relationships between Crystal Structures, Oxford University Press, Okford, United Kingdom, 2013.
33. I. D. Brown, The Chemical Bond in Inorganic Chemistry: The Bond Valence Model, Oxford University Press, Oxford, United Kingdom, 2002.
34. N. E. Brese and M. O’Keeffe, Bond-valence parameters for solids, Acta Crystallogr., 1991, B47, 192–197.
35. T. Degen, M. Sadki, E. Bron, U. König and G. Nénert, The HighScore suite, Powder Diffract., 2014, 29, S13–S18.
36. Diffract-Plus, Bruker AXS, Karlsruhe, Germany, 2020.
37. P. J. Chupas, K. W. Chapman, C. Kurtz, J. C. Hanson, P. L. Lee and C. P. Grey, A versatile sample-environment cell for non-ambient X-ray scattering experiments, J. Appl. Crystallogr., 2008, 41, 822–824.
38. B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549.
39. H. M. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2, 65–71.
40. P. E. Larson and M. Kelly, A. Surface charge neutralization of insulating samples in X-ray photoemission spectroscopy, J. Vac. Sci. Technol., A, 1998, 16, 3483–3489.
41. S. Tagliati, V. M. Krasnov and A. Rydh, Differential Membrane-Based Nanocalorimeter for High-Resolution Measurements of Low-Temperature Specific Heat, Rev. Sci. Instrum., 2012, 83, 055107.
42. P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, WIEN2k: An APW + lo program for calculating the properties of solids, J. Chem. Phys., 2020, 152, 074101.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A. Sawatzky, Density-functional theory and NiO photoemission spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929–16934.
45. F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102, 226401.
46. H. Jiang, Band gaps from the Tran-Blaha modified Becke-Johnson approach: A systematic investigation, J. Chem. Phys., 2013, 138, 134115.
47. F. Tran and P. Blaha, Implementation of screened hybrid functionals based on the Yukawa potential within the LAPW basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235118.
48. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106.
49. C. Ambrosch-Draxl and J. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175, 1–14.
50. O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: results for the transition metals and quantification of the factors underlying bond-length variation in inorganic solids, IUCrJ, 2020, 7, 581–629.
51. O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: results for the non-metals and discussion of lone-pair stereoactivity and the polymerization of PO₄, Acta Crystallogr., 2018, B74, 79–96.
52. R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., 1976, A32, 751–767.
53. M. Weil, M. Shirkhanlou and T. Stürzer, Phase formation studies of lead(II) copper(II) oxotellurates: the crystal structures of dimorphic PbCuTeO₅, PbCuTe₂O₆, and [Pb₂Cu₂(Te₄O₁₁)](NO₃)₂. 2019, Z. Anorg. Allg. Chem., 2018, 645, 347–353.
54. P. Lacorre, J. Pannetier, F. Averdunk, R. Hoppe and G. Ferey, Crystal and magnetic structures of LiCoF₄: The first compound with a dirutile structure, J. Solid State Chem., 1989, 79, 1–11.
55. K.-H. Wandner and R. Hoppe, Der erste Di-Rutil-Vertreter: LiMnF₄. (Mit einer Bemerkung über LiCoF₄), Z. Anorg. Allg. Chem., 1987, 546, 113–121.
56. S. Siegeland and H. R. Hoekstra, The crystal structure of copper uranium tetroxide, Acta Crystallogr., 1968, B24, 967–970.
57. H. Bärnighausen, Group-Subgroup Relations between Space Groups: A useful Tool in Crystal Chemistry, Math. Commun., 1989, 9, 139–175.
58. W. H. Baur and A. A. Khan, Rutile-type compounds. IV. SiO₂, GeO₂ and a comparison with other rutile-type structures, Acta Crystallogr., 1971, B27, 2133–2139.
59. A. K. van Bever and W. Nieuwenkamp, Die Kristallstruktur von Calciumchlorid, CaCl₂, Z. Kristallogr., 1935, 90, 374–376.
60. P. Fischer, W. Hälg, D. Schwarzenbach and H. Gamsjäger, Magnetic and crystal structure of copper(II) fluoride, J. Phys. Chem. Solids, 1974, 35, 1683–1689.
61. K. Robinson, G. V. Gibbs and P. H. Ribbe, Quadratic elongation: a quantitative measure of distortion in coordination polyhedra, Science, 1971, 172, 567–570.
62. D. B. Rogers, R. D. Shannon, A. W. Sleight and J. L. Gillson, Crystal Chemistry of Metal Dioxides with Rutile-Related Structures, Inorg. Chem., 1969, 8, 841–849.
63. C. R. Feger, G. L. Schimek and J. W. Kolis, Hydrothermal Synthesis and Characterization of M₂Te₃O₈ (M = Mn, Co, Ni, Cu, Zn): A Series of Compounds with the Spiroffite Structure., J. Solid State Chem., 1999, 143, 246–253.
64. R. Becker, M. Johnsson and H. Berger, A new synthetic cobalt tellurate: Co₃TeO₆, Acta Crystallogr., 2006, C62, i67–i69.
65. Handbook of Chemistry and Physics, ed. R. C. Weast, 63rd edn, CRC Press, Boca Raton, Florida, USA, 1982, B-155.
66. P. Paufler and Z. Weber, On the determination of linear thermal expansion coefficients of triclinic crystals using X-ray diffraction, Eur. J. Mineral., 1999, 11, 721–730.
67. T. Langreiter and V. Kahlenberg, TEV—A Program for the Determination of the Thermal Expansion Tensor from Diffraction Data, Crystals, 2015, 5, 143–153.
68. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. St. C. Smart, Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Cr, Mn, Fe, Co and Ni, Appl. Surf. Sci., 2011, 257, 2717–2730.
69. T. Sarkar, S. V. Ivanov, M. Weil, R. Clulow, E. Lewin and R. Mathieu, Compositional Dependence of the Magnetic State of Co_3−xZn_xTeO₆ Solid Solutions, J. Alloys Compd., 2021, 884, 161111.
70. A. P. Ramirez, Strongly Geometrically Frustrated Magnets, Annu. Rev. Mater. Sci., 1994, 24, 453–480.
71. M. C. Viola, M. J. Martínez-Lope, J. A. Alonso, J. L. Martínez, J. M. De Paoli, S. Pagola, J. C. Pedregosa, M. T. Fernández-Díaz and R. E. Carbonio, Structure and Magnetic Properties of Sr₂CoWO₆: An Ordered Double Perovskite Containing Co²⁺ (HS) with Unquenched Orbital Magnetic Moment, Chem. Mater., 2003, 15, 1655–1663.
72. C. F. Smura, D. R. Parker, M. Zbiri, M. R. Johnson, Z. A. Gál and S. J. Clarke, High-Spin Cobalt(II) Ions in Square Planar Coordination: Structures and Magnetism of the Oxysulfides Sr₂CoO₂Cu₂S₂ and Ba₂CoO₂Cu₂S₂ and Their Solid Solution, J. Am. Chem. Soc., 2011, 133, 2691–2705.
73. F. Tran, G. Baudesson, J. Carrete, G. K. H. Madsen, P. Blaha, K. Schwarz and D. J. Singh, Shortcomings of meta-GGA functionals when describing magnetism, Phys. Rev. B, 2020, 102, 024407.
74. F. Tran, P. Blaha, K. Schwarz and P. Novák, Hybrid exchange-correlation energy functionals for strongly correlated electrons: Applications to transition-metal monoxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155108.
75. K. Nassau, The Physics and Chemistry of Color, Wiley Interscience Publication, 2nd edn, 1983, p.454.
76. M. Wildner, M. Andrut and C. Z. Rudowicz, Optical absorption spectroscopy in geosciences. Part I: Basic concepts of crystal field theory, in Spectroscopic methods in mineralogy. EMU Notes in Mineralogy, ed. A. Beran and E. Libowitzky, 2004, vol. 6, pp.93–143.
77. J. Tauc, R. Grigorovici and A. Vancu, Optical Properties and Electronic Structure of Amorphous Germanium, Phys. Status Solidi B, 1966, 15, 627–637.
78. S. M. Sze, Physics of Semiconductor Device, Wiley Interscience Publication, 1981, pp.848–849.
79. J. Wang and M. Isshiki, II–IV Semiconductors for Optoelectronics: CdS, CdSe, CdTe, in Springer Handbook of Electronic and Photonic Materials. Springer Handbooks, ed. S. Kasap and P. Capper, Springer, Boston, MA, 2006.
80. F. Tran, J. Doumont, L. Kalantari, A. W. Huran, M. A. L. Marques and P. Blaha, Semilocal exchange-correlation potentials for solid-state calculations: Current status and future directions, J. Appl. Phys., 2019, 126, 110902.
81. F. Tran, S. Ehsan and P. Blaha, Assessment of the GLLB-SC potential for solid-state properties and attempts for improvement, Phys. Rev. Mater., 2018, 2, 023802.
82. F. Tran and P. Blaha, Importance of the Kinetic Energy Density for Band Gap Calculations in Solids with Density Functional Theory, J. Phys. Chem. A, 2017, 121, 3318–3325.
83. Q. Wang, H. Ma, B. Ni, Y. Li, S. Huang, W. Lin and Y. Zhang, Validation of Density Functional Theory Methods for Predicting the Optical Properties of Cu-Based Multinary Chalcogenide Semiconductors, J. Phys. Chem. C, 2022, 126, 4684–4697.
84. P. Pramanik, F. Eder, M. Weil, S. A. Ivanov, P. Maltoni, R. Miletich, T. Edvinsson and R. Mathieu. Vibrational properties of monoclinic CoTeO₄. In preparation.

---

Footnotes

† Electronic Supplementary Information (ESI) available: X-ray diffraction measurements and Rietveld refinements of CoTeO₄, optimized atomic coordinates from DFT calculations, bond lengths and angles for different experimental studies and DFT optimization, numerical data of regression curves and coefficients of the thermal expansion tensor, energy dispersive spectroscopy measurements, surface images of selected CoTeO₄ aggregates, X-ray photoemission spectra, magnetic measurements (M vs. H), temperature-dependence of dielectric properties. CCDC 2265144. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ma01106b

‡ The given cell¹⁹ in space group setting P2₁/n transforms to the current cell in P2₁/c by the matrix [001, 010, 1̄01̄].

§ There are few exceptions, such as the monoclinic polymorph of PbCuTeO₅,⁵³ where Cu^II and Te^VI are occupationally disordered at the same site.

---