Open Access Article
Open Access ArticleOptical chirality of vortex beams at the nanoscale
Dale
Green
 and
Kayn A.
Forbes
and
Kayn A.
Forbes
 *
*
School of Chemistry, University of East Anglia, Norwich, Norfolk, NR4 7TJ, UK. E-mail: k.forbes@uea.ac.uk
First published on 13th December 2022
Abstract
In this work we undertake a systematic study of the optical chirality density of Laguerre-Gaussian and Bessel laser beams tightly focused into nanoscale volumes. In particular we highlight the unique contributions to optical chirality from longitudinal electromagnetic fields, i.e. light that is polarised in the direction of propagation. The influence that polarisation, spin and orbital angular momentum, radial index, degree of focusing, and diffraction has on the optical chirality is studied. The results show that the optical chirality of structured light beams at the nanoscale is significantly richer than that of the well-known circularly polarised propagating plane wave. The work lays the foundation for chiral nanophotonics, and chiral quantum optics based on structured light illumination.
1. Introduction
An object possesses chirality if it cannot be superimposed onto its mirror image. Such chiral objects come in two distinct forms, or enantiomers, where one is known as left-handed and the other right-handed. Material chirality is inherent to life itself:1 essentially all biomolecules and drugs are chiral, their biological functions acutely linked to their handedness. Light may also be chiral. Optical chirality is most well understood for circularly polarised plane waves: electric and magnetic field vectors trace out chiral helical structures on propagation, twisting to the left, or the right, giving light its helicity σ = ±1 per photon. Plane waves which are linearly polarised or unpolarised possess zero optical chirality. Beyond the obvious importance of studying natural chiral materials, technologies are rapidly developing based on chiral photonics and nanoscience.2–8Beyond the chirality associated with the local state of polarisation in circularly polarised plane waves, light can have geometrical chiral structures associated with global properties, recently termed Kelvin's chirality.9 One extremely important type of such structured light10,11 is the optical vortex beam. Optical vortices possess many novel properties, not least the fact they convey an optical orbital angular momentum (OAM).12 The applications of optical vortices and structured light are both extremely diverse and numerous.11,13–16
A property of optical vortices attracting significant interest in the last five years has been the chiral structure associated with their helical wavefront.17 Due to their azimuthal phase exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ϕ), where
ϕ), where 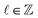 , optical vortices propagate with a wavefront which traces out a helix, the sign of
, optical vortices propagate with a wavefront which traces out a helix, the sign of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) determining the chirality (handedness). The handedness of the vortex, determined by the sign of
determining the chirality (handedness). The handedness of the vortex, determined by the sign of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , is independent of the handedness of the polarisation determined by the sign of σ. Cutting-edge experiments exploiting this vortex chirality include X-ray vortex dichroism in chiral organometallic complexes,18 vortex Raman optical activity of chiral molecular fluids;19,20 vortex differential scattering in plasmonic-molecular hybrid systems;21 and nonlinear vortex dichroism in chiral molecules as small as limonene and fenchone.22
, is independent of the handedness of the polarisation determined by the sign of σ. Cutting-edge experiments exploiting this vortex chirality include X-ray vortex dichroism in chiral organometallic complexes,18 vortex Raman optical activity of chiral molecular fluids;19,20 vortex differential scattering in plasmonic-molecular hybrid systems;21 and nonlinear vortex dichroism in chiral molecules as small as limonene and fenchone.22
Chirality is a scale-dependent phenomena: for the chirality associated with the helical wavefront (a global property) of an optical vortex to interact with small chiral materials, such as molecules, the electromagnetic fields must be shrunk down to the relevant size-scale to match the material dimensions. In this work we undertake a systematic study of the optical chirality density of Laguerre-Gaussian and Bessel optical vortices tightly focused into nanoscale volumes. In section 2 we briefly discuss the analytical theory used to describe electromagnetic fields at the nanoscale; this is followed by section 3 which contains the main results of the work: we demonstrate the various spatial distributions of the optical chirality density for tightly focused Gaussian, Laguerre-Gaussian, and Bessel beams with varying input polarisation states; section 4 concludes the article and discusses the implications of the results and future avenues of exploration.
2. Light at the nanoscale
It is key to begin by pointing out an important characteristic of spatially confined electromagnetic fields: namely, longitudinal fields. The electromagnetic plane wave is a ubiquitous theoretical construction implemented throughout optics and light–matter interactions.23,24 The electric and magnetic fields are polarised transverse to the direction of propagation z and oscillate entirely in the x–y plane. However, Heisenberg's uncertainty principle readily verifies that unless a photon travelling along z has an infinite transverse spatial extent, then components to its wave vector kx,y ≠ 0 and consequently Ez and Bz are finite. As such, longitudinal electromagnetic fields are in fact ubiquitous25,26! However, the magnitudes of these longitudinal field components are generally only significant when the light is confined into volumes on the scale of the wavelength.27 The longitudinal component of the electric Ez and magnetic Bz fields are related to the usually dominant transverse components E⊥, B⊥via| ∇·E⊥ = −ikEz, and ∇·B⊥ = −ikBz. | (1.1) |
It is important to note that this result is based on 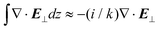 to first order in a smallness parameter.28–31 For Gaussian-like beams the smallness parameter is 1/kw0 where w0 is the beam waist and k = 2π/λ. The usually dominant transverse fields are zeroth order in this smallness parameter, the longitudinal fields are first order. More explicitly, we can calculate the longitudinal components of an electromagnetic field via Maxwell's equations:
to first order in a smallness parameter.28–31 For Gaussian-like beams the smallness parameter is 1/kw0 where w0 is the beam waist and k = 2π/λ. The usually dominant transverse fields are zeroth order in this smallness parameter, the longitudinal fields are first order. More explicitly, we can calculate the longitudinal components of an electromagnetic field via Maxwell's equations:
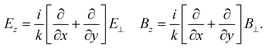 | (1.2) |
In general, cEz ≠ Bz and underpins the necessity of dual electromagnetism.32,33 The basic theory above, first discussed by Lax et al.,28 allows for simple analytical descriptions of electromagnetic phenomena. To first order in the smallness parameter, the explanation of light at the nanoscale requires the inclusion of longitudinal fields. Higher-order fields, both transverse and longitudinal, can be calculated by continued application of Maxwell's equations in an iterative manner. As with all nano-optics and photonics, quantitatively accurate theories require the use of numerical methods. To elucidate the physics behind optical chirality at the nanoscale in a transparent manner we make full use of analytical theory of the electromagnetic fields up to first order, that is they include the (zeroth order) transverse and first-order longitudinal fields; we neglect the second-order transverse fields and above.
3. Optical chirality density of optical vortices at the nanoscale
The optical chirality density is a quantitative measure of how chiral a given electromagnetic field is and plays a crucial role in light–matter interactions. Chiroptical spectroscopy is widely used in a plethora of applications such as determining the absolute configurations of chiral molecules, conformations and functionalities of biomolecules, and molecular structure of viruses.34–36 When combined with plasmonic enhancement, hypersensitive characterisation of material chirality is possible.37 All these methods rely on the chirality-dependent signal generated through the discriminatory interplay between the optical chirality density of the light source and the geometric chirality of the material being studied.It is worth mentioning that the optical chirality density for monochromatic fields is proportional to the more fundamental quantity known as the optical helicity density,38 the proportionality constant being ωk. For a detailed study on the similarities and differences between optical helicity and chirality the reader is referred to ref. 39–42. In this work we are concentrating on the optical chirality density. The cycle-averaged optical chirality density ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) for monochromatic fields is given by the formula39,43
for monochromatic fields is given by the formula39,43
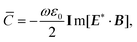 | (1.3) |
3.1. Gaussian beams
The transverse electromagnetic fields of the familiar Gaussian beam propagating along z are given byE(r,t) = E0[α![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) + βŷ]fG, and B(r,t) = B0[αŷ − β + βŷ]fG, and B(r,t) = B0[αŷ − β![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ]fG, ]fG, | (1.4) |
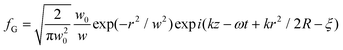 ; R = z + zR2/z; zR = ½kw02;
; R = z + zR2/z; zR = ½kw02; 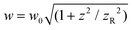 ; w0 is the beam waist; k is the wave number; ω is the angular frequency; r is the radial coordinate; ξ is the Gouy phase; α is the x-component and β the y-component of the corresponding Jones vector for a given polarisation state. Inserting (1.4) into (1.2) yields (we drop most dependencies from here on for notational clarity)
; w0 is the beam waist; k is the wave number; ω is the angular frequency; r is the radial coordinate; ξ is the Gouy phase; α is the x-component and β the y-component of the corresponding Jones vector for a given polarisation state. Inserting (1.4) into (1.2) yields (we drop most dependencies from here on for notational clarity)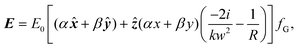 | (1.5) |
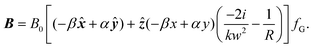 | (1.6) |
Clearly (1.5) and (1.6) both contain ẑ-polarised longitudinal fields, and so to a first approximation in the smallness parameter 1/kw0 we are able to correctly describe a Gaussian beam at the nanoscale. Inserting (1.5) and (1.6) into (1.3) produces the following optical chirality density
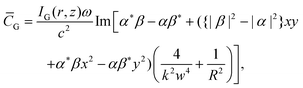 | (1.7) |
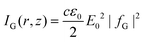 . For linearly polarised light
. For linearly polarised light ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) G = 0 because all quantities αβ, |α|2, or |β|2 will always be real. For circularly polarised light β = σiα, where σ = ± 1 for left/right handed circular polarisation, and therefore:
G = 0 because all quantities αβ, |α|2, or |β|2 will always be real. For circularly polarised light β = σiα, where σ = ± 1 for left/right handed circular polarisation, and therefore: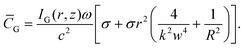 | (1.8) |
The first term in square brackets of (1.8) stems purely from the transverse electromagnetic fields ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ⊥G, whilst the other terms come solely from the longitudinal fields
⊥G, whilst the other terms come solely from the longitudinal fields ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ∥G. As such
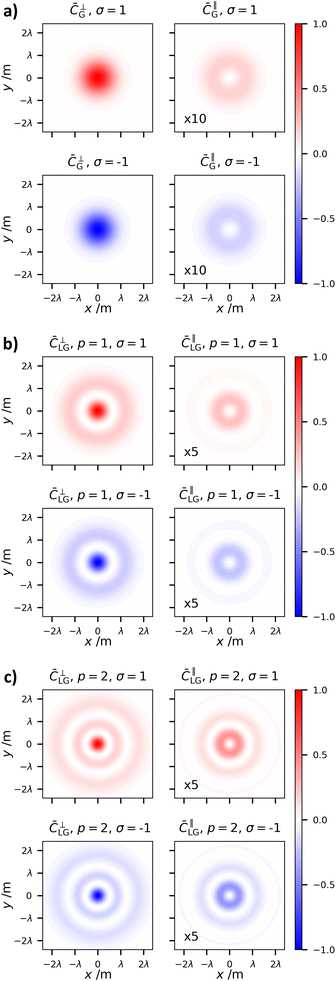
∥G. As such ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ⊥G is what would be measured in a typical experiment carried out through weak focusing in a classical optics experiment (this applies to all of the transverse contributions to the various optical chirality densities studied in this paper). The optical chirality density (1.8) is plotted in Fig. 1.
⊥G is what would be measured in a typical experiment carried out through weak focusing in a classical optics experiment (this applies to all of the transverse contributions to the various optical chirality densities studied in this paper). The optical chirality density (1.8) is plotted in Fig. 1.
It is clear to see that the handedness of the input circular polarization dictates the sign of the optical chirality. Furthermore, the contribution to the optical chirality from longitudinal fields is relatively much smaller than that of the transverse fields. However, the spatial distribution of the optical chirality stemming from longitudinal fields is distinctly different, being a doughnut shape and not a typical Gaussian spot. A proposal to directly measure the optical chirality of tightly-focused Gaussian beams has recently been put forward.44 It is worth noting that this method would be readily applied to all the structured light chirality in this work.45
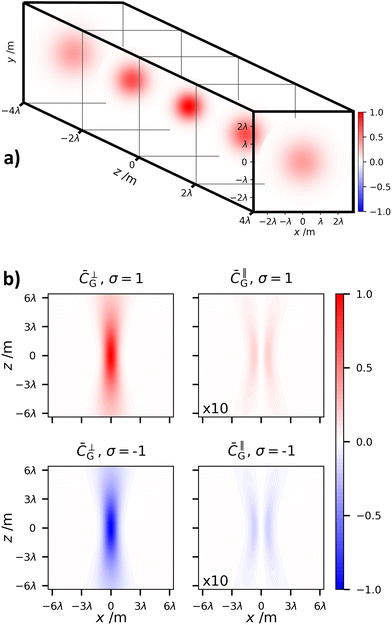
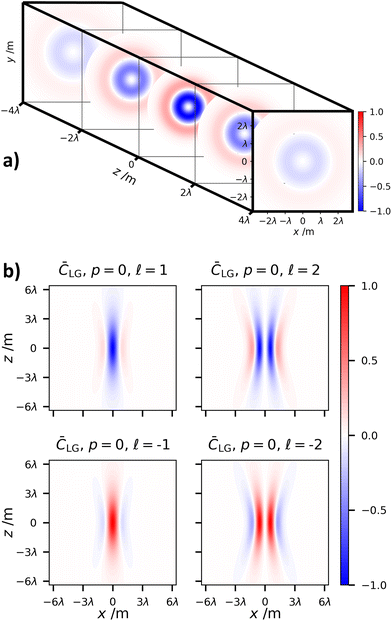
The behaviour of the optical chirality density ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) G as a function of propagation distance z is given in Fig. 2. The transverse component diffracts as would be expected, while the longitudinal contribution soon tends to zero. This behaviour of the longitudinal field is expected as they are essentially near-field electromagnetic phenomena.
G as a function of propagation distance z is given in Fig. 2. The transverse component diffracts as would be expected, while the longitudinal contribution soon tends to zero. This behaviour of the longitudinal field is expected as they are essentially near-field electromagnetic phenomena.
3.2. Laguerre-Gaussian beams
The first optical vortex mode we will study is the Laguerre-Gaussian (LG) beam, a solution to the paraxial wave equation. The LG modes are characterised by two integers, the topological charge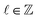 , and the radial index
, and the radial index 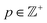 . LG beams carry
. LG beams carry ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ℏ OAM per photon in the direction of propagation, and p + 1 concentric rings in their intensity profile. The transverse electric and magnetic fields for a LG mode are given as:
ℏ OAM per photon in the direction of propagation, and p + 1 concentric rings in their intensity profile. The transverse electric and magnetic fields for a LG mode are given as:E(r,t) = E0[α![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) + βŷ]fLG, and B(r,t) = B0[αŷ − β + βŷ]fLG, and B(r,t) = B0[αŷ − β![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ]fLG ]fLG | (1.9) |
where fLG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 in cylindrical coordinates (r,ϕ,z) is given by
46 in cylindrical coordinates (r,ϕ,z) is given by
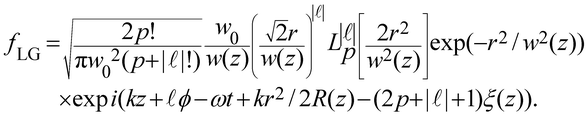 | (1.10) |
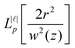 is the Laguerre polynomial with the argument in square brackets. Inserting (1.9) into (1.2) yields the electromagnetic fields for LG modes at the nanoscale:
is the Laguerre polynomial with the argument in square brackets. Inserting (1.9) into (1.2) yields the electromagnetic fields for LG modes at the nanoscale: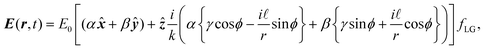 | (1.11) |
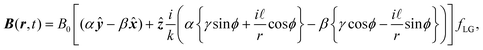 | (1.12) |
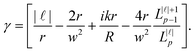 | (1.13) |
Inserting (1.11) and (1.12) into (1.3) gives for the optical chirality density of an LG beam as:
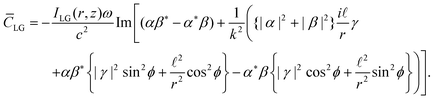 | (1.14) |
In the case of an input circularly polarised LG mode, β = iσα, and (1.14) takes the following form
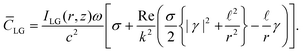 | (1.15) |
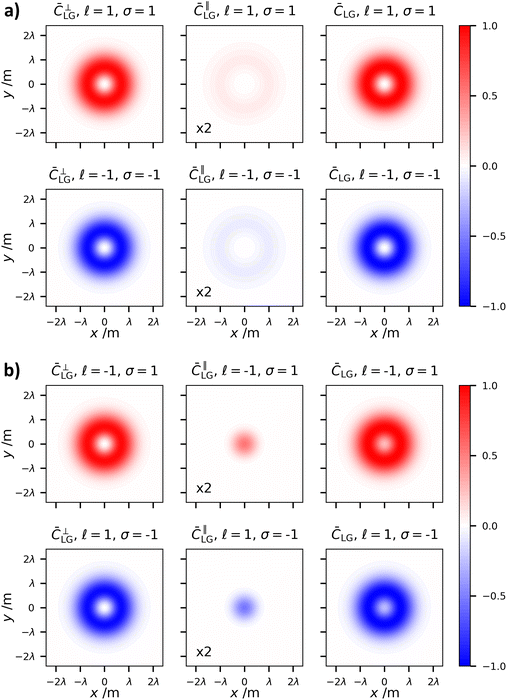
The first term in square brackets in (1.15) directly proportional to σ is the dominant contribution to the optical chirality density; it stems purely from (zeroth-order) transverse electromagnetic fields (i.e. those responsible for the optical chirality of a circularly polarised plane wave). The additional terms in square brackets all stem from longitudinal fields, are second-order in the paraxial parameter 1/(kw)2, and are thus only appreciable under significant spatial confinement at the nanoscale. They do however involve a linear dependence on ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and thus the chirality (handedness) of the optical vortex wavefront.
, and thus the chirality (handedness) of the optical vortex wavefront.
Both σ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are pseudoscalars which determine two distinct types of optical handedness but also the optical SAM and OAM, respectively. Importantly, they are experimentally controllable parameters. For any input optical vortex mode, we have the distinct interplay of either: sgn
are pseudoscalars which determine two distinct types of optical handedness but also the optical SAM and OAM, respectively. Importantly, they are experimentally controllable parameters. For any input optical vortex mode, we have the distinct interplay of either: sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = sgn
= sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ or sgn
σ or sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = −sgn
= −sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ. In the former case we may say that the SAM and OAM are aligned in a parallel fashion; whereas in the latter case we say they are anti-parallel. This interplay of the sign (and magnitude) of SAM and OAM is a critical component in the field of spin–orbit interactions (SOI) of light.47 It is known that in the case of anti-parallel SAM and OAM, for |
σ. In the former case we may say that the SAM and OAM are aligned in a parallel fashion; whereas in the latter case we say they are anti-parallel. This interplay of the sign (and magnitude) of SAM and OAM is a critical component in the field of spin–orbit interactions (SOI) of light.47 It is known that in the case of anti-parallel SAM and OAM, for |![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) | = 1 there exists an on-axis intensity (both electric and magnetic energy densities) distribution; whilst for parallel combinations the on-axis intensity is zero.48Fig. 3 plots (1.15) and highlights how the optical chirality density mirrors this pattern.
| = 1 there exists an on-axis intensity (both electric and magnetic energy densities) distribution; whilst for parallel combinations the on-axis intensity is zero.48Fig. 3 plots (1.15) and highlights how the optical chirality density mirrors this pattern.
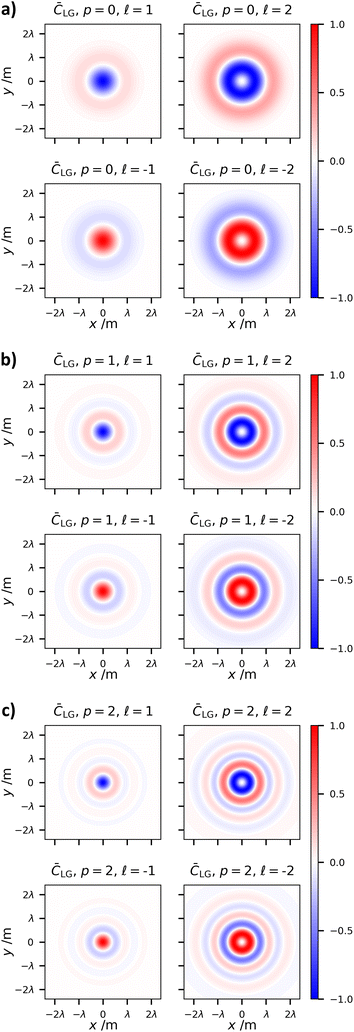
Of the two indices which characterise LG modes, the topological charge ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) has seen an extraordinary amount of research effort. This is mainly due to the fact its value determines the optical OAM, alongside its unbounded nature and ease of experimental manipulation. The radial index on the other hand has seen less interest.49 As far as we are aware it has not been studied with respect to optical chirality. The optical chirality distributions of circularly polarised vortex beams with p = 1 and p = 2 are given in Fig. 4 and 5, respectively.
has seen an extraordinary amount of research effort. This is mainly due to the fact its value determines the optical OAM, alongside its unbounded nature and ease of experimental manipulation. The radial index on the other hand has seen less interest.49 As far as we are aware it has not been studied with respect to optical chirality. The optical chirality distributions of circularly polarised vortex beams with p = 1 and p = 2 are given in Fig. 4 and 5, respectively.
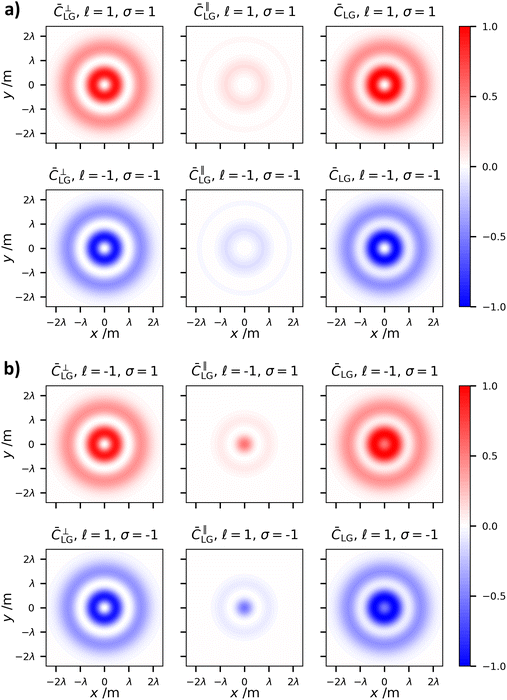 | ||
| Fig. 4 Same as Fig. 3 except p = 1. | ||
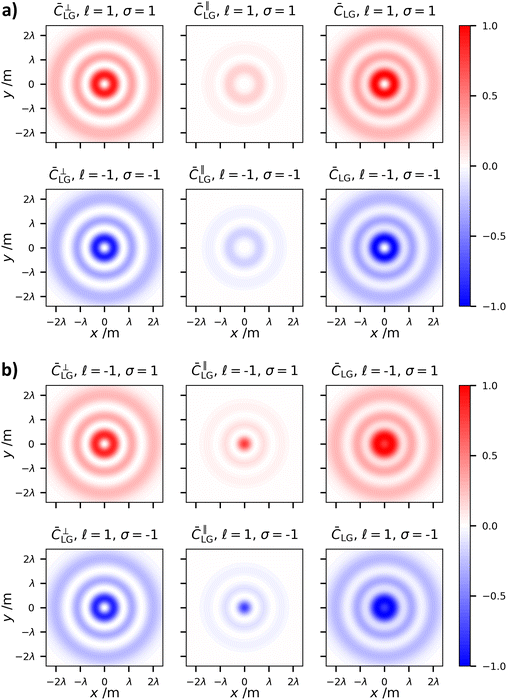 | ||
| Fig. 5 Same as Fig. 3 except p = 2. | ||
There are three distinct changes in the optical chirality density upon changing the radial index:
(1) The overall optical chirality density displays p + 1 rings
(2) On increasing p, the relative magnitude of the on-axis optical chirality in the case of |![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) | = 1 modes increases for the anti-parallel cases.
| = 1 modes increases for the anti-parallel cases.
(3) Increasing p decreases the central intensity ring width regardless of AM configuration.
The explanation behind (2) and (3) is that increasing p increases the relative magnitude of the longitudinal fields (which are responsible for the on-axis chirality and tighter focal spots). Longitudinal fields depend on the gradients of the transverse fields (see (1.2)). Electromagnetic fields consisting of p radial nulls and p + 1 concentric fields clearly have increasing field gradients as p grows, thus increasing the magnitudes of longitudinal fields.
The diffractive behaviour for the optical chirality density of circularly polarised LG modes (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = ±1, p = 0) is given in Fig. 6. Like the Gaussian case, the transverse field contributions to the optical chirality density diffract in the usual manner, and the longitudinal contributions quickly drop off to zero as the radiation moves in to the far-field.
= ±1, p = 0) is given in Fig. 6. Like the Gaussian case, the transverse field contributions to the optical chirality density diffract in the usual manner, and the longitudinal contributions quickly drop off to zero as the radiation moves in to the far-field.
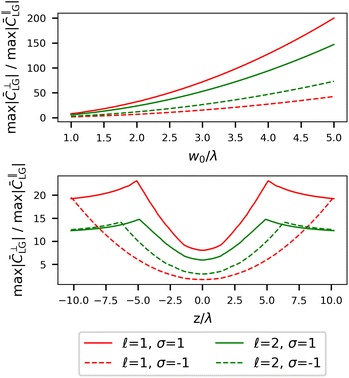
Much has been said so far about the fact longitudinal fields are only significant under significant spatial confinement via tight focusing. The widths of LG (and Gaussian) beams (transverse dimensions) are characterised by the beam waist w0. The magnitude of the longitudinal fields become important when the beam waist is within a few wavelengths of the input light.50Fig. 7 which takes the ratio of max|![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ⊥LG|/max|
⊥LG|/max|![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ∥LG| for p = 1 has been produced to give an indication of how rapidly longitudinal fields tend to zero relative to transverse fields as both (1) w0 increases and (2) z moves from z = 0 (i.e. around the focal plane).
∥LG| for p = 1 has been produced to give an indication of how rapidly longitudinal fields tend to zero relative to transverse fields as both (1) w0 increases and (2) z moves from z = 0 (i.e. around the focal plane).
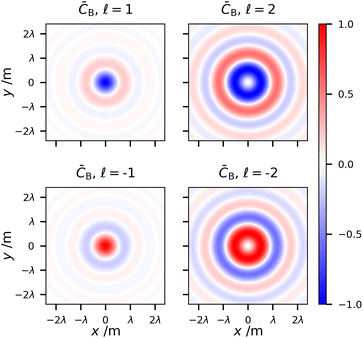
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and p). However, optical vortex beams at the nanoscale are extremely unique because they possess optical chirality densities in the focal plane even for linear polarised fields51–54 (which possess zero optical chirality in the plane wave case). In fact, it was recently highlighted that this optical chirality of vortex beams is unique and fully independent of polarisation, even manifesting for unpolarised sources.55 This is readily verified by choosing α = 1, β = 0, α = 0, β = 1, or any other linearly polarised beam parameter in (1.14) (the optical chirality of unpolarised vortices can be verified by simply averaging over two orthogonal polarisations):
and p). However, optical vortex beams at the nanoscale are extremely unique because they possess optical chirality densities in the focal plane even for linear polarised fields51–54 (which possess zero optical chirality in the plane wave case). In fact, it was recently highlighted that this optical chirality of vortex beams is unique and fully independent of polarisation, even manifesting for unpolarised sources.55 This is readily verified by choosing α = 1, β = 0, α = 0, β = 1, or any other linearly polarised beam parameter in (1.14) (the optical chirality of unpolarised vortices can be verified by simply averaging over two orthogonal polarisations):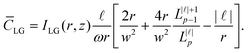 | (1.16) |
The transverse spatial distribution of (1.16) at the focal plane is given in Fig. 8. What we see are two concentric rings of opposite signed optical chirality density in the case of p = 0. The sign of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) takes on the same sign of the outer ring of optical chirality density. The chirality of linearly polarised LG beams was comprehensively studied in ref. 53 for the p = 0 modes and was experimentally verified in ref. 52. Fig. 8 also highlights p > 0 cases and confirms that we get 2p + 2 concentric rings of alternating optical chirality in the case of the polarisation-independent optical chirality density of LG modes. The inner ring has the largest magnitude of optical chirality density, then each ring decreases to the outer ring which has the weakest magnitude.
takes on the same sign of the outer ring of optical chirality density. The chirality of linearly polarised LG beams was comprehensively studied in ref. 53 for the p = 0 modes and was experimentally verified in ref. 52. Fig. 8 also highlights p > 0 cases and confirms that we get 2p + 2 concentric rings of alternating optical chirality in the case of the polarisation-independent optical chirality density of LG modes. The inner ring has the largest magnitude of optical chirality density, then each ring decreases to the outer ring which has the weakest magnitude.
This polarisation-independent optical chirality density stems purely from the longitudinal electromagnetic fields in (1.11) and (1.12). It is therefore unique to light at the nanoscale. However, we have seen that a Gaussian beam does not possess it even if tightly focused. For both Gaussian and LG modes, the components of their transverse electric field and transverse magnetic fields are ±π/2 out of phase with their respective longitudinal components. This ±π/2 phase shift is of course indicative of circular polarisation and underlies the transverse spin momentum of light.56 Optical chirality density however is the inner product of the electric and magnetic field (1.3). The inner product of the transverse component of either the electric field or magnetic field with the longitudinal components will always be zero. Now, comparing the longitudinal components of the electric and magnetic fields of a Gaussian mode (1.5) and (1.6) we see that they oscillate in phase with one another. Comparing the longitudinal components of the LG mode on the other hand, (1.11) and (1.12), we see that the terms ∝![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) oscillate ±π/2 out of phase with those ∝γ, and it is these terms which produce the novel source polarisation independent optical chirality density for optical vortex modes.
oscillate ±π/2 out of phase with those ∝γ, and it is these terms which produce the novel source polarisation independent optical chirality density for optical vortex modes.
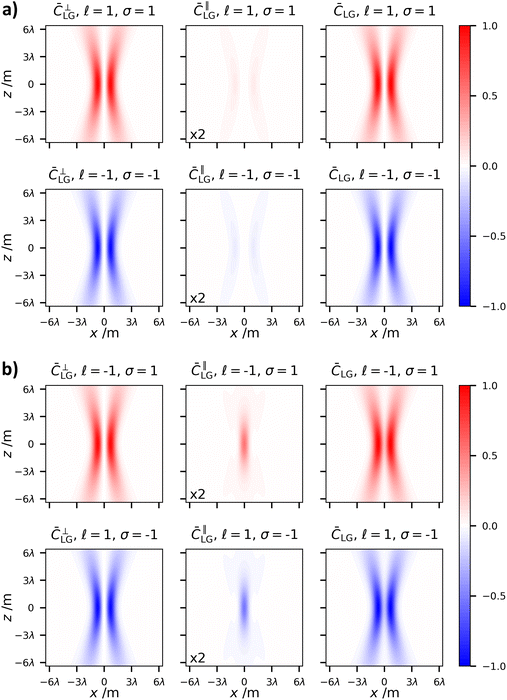
The diffractive behaviour of the polarisation independent optical chirality density of LG modes is shown in Fig. 9. What we see is that due to the fact ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) LG =
LG = ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ∥LG in this case, the optical chirality soon becomes negligible as the field moves away from the focal plane z = 0 for the reasons highlighted previously in the article.
∥LG in this case, the optical chirality soon becomes negligible as the field moves away from the focal plane z = 0 for the reasons highlighted previously in the article.
3.3 Bessel beams
Laguerre-Gaussian modes are solutions to the paraxial wave equation; another optical vortex mode, Bessel beams, are exact solutions to the Helmholtz wave equation. Bessel beams have been subject to a lot of interest57,58 due to their non-diffractive behaviour, i.e., their transverse profile is invariant on propagation. In truth the realisation of such beams is limited by the requirement of a finite aperture, nonetheless they still possess useful properties.46 The transverse fields for a Bessel beam are: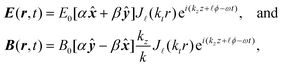 | (1.17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, kt = k
θ, kt = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Moreover
θ. Moreover 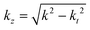 ,
, 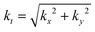 , and J
, and J![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (ktr) are Bessel functions of the first kind. Inserting (1.17) into (1.2) gives the Bessel beam fields at the nanoscale which include their longitudinal fields:
(ktr) are Bessel functions of the first kind. Inserting (1.17) into (1.2) gives the Bessel beam fields at the nanoscale which include their longitudinal fields: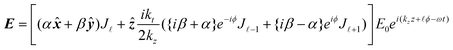 | (1.18) |
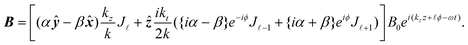 | (1.19) |
Unlike the Gaussian and LG beams which are characterised by a beam waist w0, in the case of Bessel beams, the smallness parameter is kt/kz. Inserting these into (1.3):
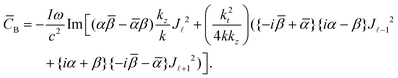 | (1.20) |
In the case of a source Bessel beam that is circularly polarised (1.20) becomes:
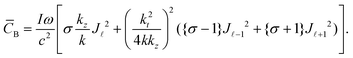 | (1.21) |
Plots of (1.21) for the differing combinations of σ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are presented in Fig. 10. The optical chirality density now takes on the spatial distribution of concentric rings, where the central ring has the largest magnitude. It is obvious to see that the distribution
are presented in Fig. 10. The optical chirality density now takes on the spatial distribution of concentric rings, where the central ring has the largest magnitude. It is obvious to see that the distribution ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) B is very similar to
B is very similar to ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) LG when p is large. Just as in the case of
LG when p is large. Just as in the case of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) LG, the transverse contribution
LG, the transverse contribution ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ⊥B dominates but whether the SAM and OAM are parallel or anti-parallel has significant consequences on the spatial distribution of the optical chirality density
⊥B dominates but whether the SAM and OAM are parallel or anti-parallel has significant consequences on the spatial distribution of the optical chirality density ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) B.
B.
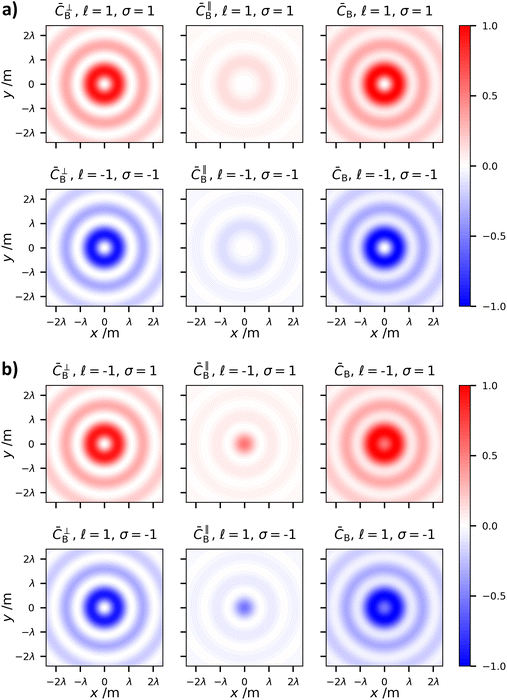 | ||
Fig. 10 (left)Transverse, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ⊥B, (centre) longitudinal, ⊥B, (centre) longitudinal, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ∥B, and (right) combined, ∥B, and (right) combined, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) B, field contributions to the optical chirality densities of circularly polarised σ = ±1 Bessel beams of B, field contributions to the optical chirality densities of circularly polarised σ = ±1 Bessel beams of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = ±1, normalised to the total = ±1, normalised to the total ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) B. (a) Parallel SAM and OAM sgn B. (a) Parallel SAM and OAM sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = sgn = sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ. (b) Anti-parallel SAM and OAM sgn σ. (b) Anti-parallel SAM and OAM sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≠ sgn ≠ sgn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ. The chirality density of the vortex is not zero along the beam axis in the anti-parallel case. In all plots kt/kz = 0.63 which makes the plots comparable to the LG beams in Fig. 4 in terms of spatial confinement of the field. σ. The chirality density of the vortex is not zero along the beam axis in the anti-parallel case. In all plots kt/kz = 0.63 which makes the plots comparable to the LG beams in Fig. 4 in terms of spatial confinement of the field. | ||
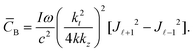 | (1.22) |
The spatial distributions of (1.22) are plotted in Fig. 11. These plots are also similar to the cases of a high p linearly polarised or unpolarised LG beam (Fig. 8).
As previously mentioned, Bessel beams are free from diffraction. Therefore, unlike the Gaussian and LG modes studied above, the optical chirality density is invariant upon propagation. However, we know that such a non-diffractive optical chirality is not a viable experimental observable. Nonetheless, Bessel-like modes still possess unique and useful diffractive properties. In future work we aim to study the experimentally realisable Bessel-Gauss beam to compare the diffractive behaviour of optical chirality versus a standard diffractive mode, such as LG.
4. Discussion and conclusion
The optical chirality density is a property of an optical field. It is the coupling of this optical chirality density (light) to chiral polarisability tensors (matter) which produce chiral light–matter interactions that are the foundation of individual chiroptical spectroscopy techniques. It is for this reason that the optical chirality has seen such a surge in research interest.36,40,41,43,59 Nonetheless, it is extremely important to note that the optical chirality density couples to the interferences between electric and magnetic dipoles (E1M1).60,61 However, chiral light–matter interactions originate from a sum of multipolar interferences of which E1M1 is only one (though usually dominant it must be said).60,61 Another extremely important contribution to the same order in the multipolar expansion comes from the interferences between electric dipole and electric quadrupole coupling (E1E2). As such, the complete description of many chiral light–matter phenomena requires a full analysis involving the interaction Hamiltonian, most frequently the minimal coupling or multipolar coupling form.62,63 It is particularly relevant to point out this important but often neglected issue here because optical vortex beams couple to electric-quadrupole (E2) transitions in unique and enhanced ways.64–69In this work we have studied the optical chirality densities of Gaussian, Laguerre-Gaussian, and Bessel modes at the nanoscale. All of the unique features of optical chirality at the nanoscale compared to that of plane waves comes from longitudinal electromagnetic fields. Unlike the non-vortex Gaussian mode, optical vortex beams are decidedly unique in that they possess optical chirality densities even if the source beam is linearly polarised or even unpolarised. There are similarities between the optical chirality density of LG modes with high p and Bessel modes, and this should not be surprising as Bessel beams may be regarded as a limiting case of LG modes. Nonetheless, future studies aim to determine what advantages the quasi-diffraction free nature of Bessel–Gauss beams have over diffracting Laguerre-Gaussian beams in relation to optical chirality. Further avenues of exploration should look at more exotic optical vortex beams or electromagnetic fields, such as helical Mathieu beams, and vector vortex beams, all which carry the azimuthal phase dependence required to display similar properties to those outlined for LG and Bessel modes in this work.
To date, the use of the optical chirality of light in applications such as chiroptical spectroscopy has predominantly been in the domain of weakly-focused light in classical optics experiments.60,70,71 Here we have highlighted the significantly rich behaviour of optical chirality at the nanoscale, and in particular the unique properties of tightly focused optical vortices. We therefore anticipate this systematic study of the nano-optics of optical chirality will lay the foundation for future work and applications in chiral nanophotonics2,6–8 and chiral quantum optics3 based on structured light illumination.
Author contributions
D. G. methodology; software; formal analysis; visualization; writing – review & editing. K. A. F. conceptualization; methodology; formal analysis; writing – original draft; writing – review & editing; funding acquisition; project administration.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
KAF is grateful to the Leverhulme Trust for funding him through a Leverhulme Trust Early Career Fellowship (Grant No. ECF-2019-398).References
- L. D. Barron, in Strategies of Life Detection, ed. O. Botta, J. L. Bada, J. Gomez-Elvira, E. Javaux, F. Selsis and R. Summons, Springer US, Boston, MA, 2008, pp. 187–201 Search PubMed.
- J. T. Collins, C. Kuppe, D. C. Hooper, C. Sibilia, M. Centini and V. K. Valev, Adv. Opt. Mater., 2017, 5, 1700182 CrossRef.
- P. Lodahl, S. Mahmoodian, S. Stobbe, A. Rauschenbeutel, P. Schneeweiss, J. Volz, H. Pichler and P. Zoller, Nature, 2017, 541, 473 CrossRef CAS PubMed.
- T. Ozawa, Rev. Mod. Phys., 2019, 91, 76 CrossRef.
- G. Long, R. Sabatini, M. I. Saidaminov, G. Lakhwani, A. Rasmita, X. Liu, E. H. Sargent and W. Gao, Nat. Rev. Mater., 2020, 5, 423–439 CrossRef.
- L. A. Warning, A. R. Miandashti, L. A. McCarthy, Q. Zhang, C. F. Landes and S. Link, ACS Nano, 2021, 15, 15538–15566 CrossRef CAS PubMed.
- M. L. Solomon, A. A. E. Saleh, L. V. Poulikakos, J. M. Abendroth, L. F. Tadesse and J. A. Dionne, Acc. Chem. Res., 2020, 53, 588–598 CrossRef CAS PubMed.
- S. Yoo and Q.-H. Park, Nanophotonics, 2019, 8, 249–261 Search PubMed.
- S. Nechayev, J. S. Eismann, R. Alaee, E. Karimi, R. W. Boyd and P. Banzer, Phys. Rev. A, 2021, 103, L031501 CrossRef CAS.
- Structured light and its applications: An introduction to phase-structured beams and nanoscale optical forces, ed. D. L. Andrews, Academic press, Burlington, 2011 Search PubMed.
- A. Forbes, M. de Oliveira and M. R. Dennis, Nat. Photonics, 2021, 15, 253–262 CrossRef CAS.
- L. Allen, M. W. Beijersbergen, R. J. C. Spreeuw and J. P. Woerdman, Phys. Rev. A, 1992, 45, 8185–8189 CrossRef.
- Y. Shen, X. Wang, Z. Xie, C. Min, X. Fu, Q. Liu, M. Gong and X. Yuan, Light: Sci. Appl., 2019, 8, 1–29 CrossRef CAS.
- H. Rubinsztein-Dunlop, et al. , J. Opt., 2016, 19, 013001 CrossRef.
- A. Forbes, Laser Photonics Rev., 2019, 13, 1900140 CrossRef.
- C. Rosales-Guzmán, B. Ndagano and A. Forbes, J. Opt., 2018, 20, 123001 CrossRef.
- K. A. Forbes and D. L. Andrews, JPhys Photonics, 2021, 3, 022007 CrossRef CAS.
- J. R. Rouxel, B. Rösner, D. Karpov, C. Bacellar, G. F. Mancini, F. Zinna, D. Kinschel, O. Cannelli, M. Oppermann and C. Svetina, Nat. Photonics, 2022, 16, 570–574 CrossRef CAS.
- F. Büscher, S. Müllner, D. Wulferding, Y. G. Pashkevich, V. Gnezdilov, A. A. Peshkov, A. Surzhykov and P. Lemmens, Low Temp. Phys., 2021, 47, 959–965 CrossRef.
- S. Müllner, F. Büscher, A. Möller and P. Lemmens, Phys. Rev. Lett., 2022, 12920, 207801 Search PubMed.
- J. Ni, S. Liu, D. Wu, Z. Lao, Z. Wang, K. Huang, S. Ji, J. Li, Z. Huang, Q. Xiong, Y. Hu, J. Chu and C.-W. Qiu, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020055118 CrossRef CAS PubMed.
- J.-L. Bégin, A. Jain, A. Parks, F. Hufnagel, P. Corkum, E. Karimi, T. Brabec and R. Bhardwaj, Nat. Photonics, 2022, 1–7 Search PubMed.
- M. Born and E. Wolf, Principles of optics: electromagnetic theory of propagation, interference and diffraction of light, Elsevier, 2013 Search PubMed.
- G. Grynberg, A. Aspect and C. Fabre, Introduction to Quantum Optics: From the Semi-classical Approach to Quantized Light, Cambridge University Press, Cambridge, U.K., 2010 Search PubMed.
- A. Aiello and P. Banzer, J. Opt., 2016, 18, 085605 CrossRef.
- M. Chekhova and P. Banzer, Polarization of Light: In Classical, Quantum, and Nonlinear Optics, Walter de Gruyter GmbH & Co KG, 2021 Search PubMed.
- L. Novotny and B. Hecht, Principles of Nano-Optics, Cambridge University Press, Cambridge, 2012 Search PubMed.
- M. Lax, W. H. Louisell and W. B. McKnight, Phys. Rev. A, 1975, 11, 1365 CrossRef.
- A. Zangwill, Modern electrodynamics, Cambridge University Press, Cambridge, 2013 Search PubMed.
- C. S. Adams and I. G. Hughes, Optics f2f: from Fourier to Fresnel, Oxford University Press, 2018 Search PubMed.
- G. F. Quinteiro, C. T. Schmiegelow, D. E. Reiter and T. Kuhn, Phys. Rev. A, 2019, 99, 023845 CrossRef CAS.
- M. V. Berry, J. Opt. A: Pure Appl. Opt., 2009, 11, 094001 CrossRef.
- K. Y. Bliokh, A. Y. Bekshaev and F. Nori, New J. Phys., 2013, 15, 033026 CrossRef.
- L. D. Barron, Biomed. Spectrosc. Imaging, 2015, 4, 223–253 CAS.
- T. Kakkar, C. Keijzer, M. Rodier, T. Bukharova, M. Taliansky, A. J. Love, J. J. Milner, A. S. Karimullah, L. D. Barron, N. Gadegaard, A. J. Lapthorn and M. Kadodwala, Light: Sci. Appl., 2020, 9, 195 CrossRef CAS.
- E. Hendry, T. Carpy, J. Johnston, M. Popland, R. V. Mikhaylovskiy, A. J. Lapthorn, S. M. Kelly, L. D. Barron, N. Gadegaard and M. Kadodwala, Nat. Nanotechnol., 2010, 5, 783–787 CrossRef CAS PubMed.
- X.-T. Kong, L. V. Besteiro, Z. Wang and A. O. Govorov, Adv. Mater., 2020, 32, 1801790 CrossRef CAS PubMed.
- N. Mackinnon, J. Opt., 2019, 21, 125402 CrossRef CAS.
- R. P. Cameron, S. M. Barnett and A. M. Yao, New J. Phys., 2012, 14, 053050 CrossRef.
- F. Crimin, N. Mackinnon, J. B. Götte and S. M. Barnett, Appl. Sci., 2019, 9, 828 CrossRef CAS.
- L. V. Poulikakos, J. A. Dionne and A. García-Etxarri, Symmetry, 2019, 11, 1113 CrossRef CAS.
- A. Aiello, J. Phys. A: Math. Theor., 2022, 55, 244004 CrossRef.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef.
- A. A. Sifat, F. Capolino and E. O. Potma, ACS Photonics, 2022, 9, 2660–2667 CrossRef CAS.
- K. A. Forbes and D. Green, Opt. Commun., 2022, 515, 128197 CrossRef CAS.
- G. J. Gbur, Singular optics, CRC Press, Florida, 2016 Search PubMed.
- K. Y. Bliokh, F. J. Rodríguez-Fortuño, F. Nori and A. V. Zayats, Nat. Photonics, 2015, 9, 796–808 CrossRef CAS.
- Y. Iketaki, T. Watanabe, N. Bokor and M. Fujii, Opt. Lett., 2007, 32, 2357–2359 CrossRef.
- W. N. Plick and M. Krenn, Phys. Rev. A, 2015, 92, 063841 CrossRef.
- K. A. Forbes, D. Green and G. A. Jones, J. Opt., 2021, 23, 075401 CrossRef CAS.
- C. Rosales-Guzmán, K. Volke-Sepulveda and J. P. Torres, Opt. Lett., 2012, 37, 3486–3488 CrossRef PubMed.
- P. Woźniak, I. D. Leon, K. Höflich, G. Leuchs and P. Banzer, Optica, 2019, 6, 961–965 CrossRef.
- K. A. Forbes and G. A. Jones, J. Opt., 2021, 23, 115401 CrossRef CAS.
- M. Babiker, J. Yuan, V. E. Lembessis and K. Koksal, Opt. Commun., 2022, 525, 128846 CrossRef CAS.
- K. A. Forbes, Phys. Rev. A, 2022, 105, 023524 CrossRef CAS.
- A. Aiello, P. Banzer, M. Neugebauer and G. Leuchs, Nat. Photonics, 2015, 9, 789–795 CrossRef CAS.
- D. McGloin and K. Dholakia, Contemp. Phys., 2005, 46, 15–28 CrossRef.
- K. Volke-Sepulveda, V. Garcés-Chávez, S. Chávez-Cerda, J. Arlt and K. Dholakia, J. Opt. B: Quantum Semiclassical Opt., 2002, 4, S82 CrossRef.
- R. P. Cameron, J. B. Götte, S. M. Barnett and A. M. Yao, Philos. Trans. R. Soc., A, 2017, 375, 20150433 CrossRef.
- L. D. Barron, Molecular light scattering and optical activity, Cambridge University Press, Cambridge, 2009 Search PubMed.
- D. P. Craig and T. Thirunamachandran, Molecular Quantum Electrodynamics: An Introduction to Radiation-Molecule Interactions, Courier Corporation, New York, 1998 Search PubMed.
- D. L. Andrews, G. A. Jones, A. Salam and R. G. Woolley, J. Chem. Phys., 2018, 148, 040901 CrossRef PubMed.
- R. G. Woolley, Foundations of Molecular Quantum Electrodynamics, Cambridge University Press, 2022 Search PubMed.
- K. A. Forbes and D. L. Andrews, Opt. Lett., 2018, 43, 435–438 CrossRef CAS.
- V. E. Lembessis and M. Babiker, Phys. Rev. Lett., 2013, 110, 083002 CrossRef CAS PubMed.
- K. A. Forbes and D. L. Andrews, Phys. Rev. Res., 2019, 1, 033080 CrossRef CAS.
- K. A. Forbes, Phys. Rev. Lett., 2019, 122, 103201 CrossRef CAS.
- C. T. Schmiegelow, J. Schulz, H. Kaufmann, T. Ruster, U. G. Poschinger and F. Schmidt-Kaler, Nat. Commun., 2016, 7, 12998 CrossRef CAS.
- K. A. Forbes and G. A. Jones, Phys. Rev. A, 2021, 103, 053515 CrossRef CAS.
- P. L. Polavarapu, Chiroptical Spectroscopy: Fundamentals and Applications, CRC Press, Boca Raton, 2016 Search PubMed.
- L. D. Barron and A. D. Buckingham, Chem. Phys. Lett., 2010, 492, 199–213 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |