 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new double spike method for the determination of mass-dependent Te isotope compositions of meteorites and terrestrial materials by MC-ICP-MS
Elin M.
Morton
 *a,
Katharina
Kreissig
a,
Barry J.
Coles
a,
Caris S.
Jaffe
*a,
Katharina
Kreissig
a,
Barry J.
Coles
a,
Caris S.
Jaffe
 a,
Rayssa
Martins
a,
Rayssa
Martins
 a,
Graeme M.
Poole
a,
Graeme M.
Poole
 ab and
Mark
Rehkämper
ab and
Mark
Rehkämper
 a
a
aDepartment of Earth Science and Engineering, Imperial College London, London SW7 2AZ, UK. E-mail: e.rydeblad18@imperial.ac.uk
bImaging and Analysis Centre, Natural History Museum, London SW7 5BD, UK
First published on 20th April 2023
Abstract
This study presents a new method for the determination of mass-dependent Te isotope compositions. The process encompasses a new column chromatographic procedure which separates Te from chondritic and iron meteorites and diverse terrestrial rocks with high yield and purity, combined with a robust 125Te–128Te double spike and optimised multi collector ICP-MS protocols. This allows for precise (2SD = 0.07‰) determination of the mass-dependent 130Te/125Te isotope ratio using analyte solutions containing as little as 6 ng of natural Te. The efficacy of the method is demonstrated by repeat analyses of terrestrial rock reference materials and meteorites, which show overall good agreement with previous work. In addition, an inter-laboratory cross-calibration of three different Te standard solutions was performed. This inter-laboratory cross-calibration is highly advantageous, as a well-calibrated isotope reference material is not yet available for Te. Isotope mass balance and mixing equations performed in this study show that hypothetical mass-independent Te isotope effects of reasonable magnitude are unlikely to have a significant impact on the measured mass-dependent Te isotope compositions at the current level of analytical precision. Finally, this study presents the first precise mass-dependent Te isotope composition obtained for an iron meteorite, Canyon Diablo, and komatiite reference material KAL-1 using the double spike technique.
Introduction
Tellurium is a chalcophile and moderately volatile trace element with a 50% condensation temperature of 655 K, which has 8 stable isotopes with atomic mass numbers between 120 and 130.1 Previous investigations have shown that Te is vulnerable to stable isotope fractionation during nebular and parent body processes, such as partial evaporation/condensation, thermal metamorphism, and aqueous alteration, and Te isotopes can, therefore, be used to investigate such processes through analyses of meteorites.2–4 The mass-dependent Te isotope compositions of terrestrial samples have also received attention in recent years as they may be of use as a proxy for ancient marine and terrestrial redox conditions. Additionally, as a chalcophile element, Te is of interest for investigating the genesis of metal-bearing ore systems, and as an ore exploration tool. Mass-dependent Te isotope fractionation is especially interesting in exploration for high-grade Au mineralisation due to the close association of Te with Au in ore bodies.2,3,5–9Fornadel et al. (2014)5 developed methods for analyses of the mass-dependent Te isotope compositions of ores and ore-related minerals by multi collector ICP-MS (MC-ICP-MS) by expanding on the methodologies presented in Fehr et al. (2004).10 In contrast to stable isotope studies of other elements, Fornadel et al. (2014)5 did not use a double spike, but instead utilised Cd as an external dopant to correct for instrumental mass bias.
The first studies that employed the double spike technique to investigate the mass-dependent Te isotope compositions of meteorites and terrestrial samples were by Fehr et al. (2018)2 and Fukami et al. (2018).8
Fukami et al. (2018)8 determined Te and Se concentrations and mass-dependent Te isotope composition of several reference materials using a 125Te–128Te double spike and MC-ICP-MS. They found that Te/Se ratios covaried with the mass-dependent Te isotope data and hence suggested that Te may be useful as a redox proxy. This was expanded on by Wasserman and Johnson (2020)9 who investigated mass-dependent Te isotope compositions for a range of terrestrial samples using hydride generation MC-ICP-MS and a 120Te–124Te double spike. They found significant mass-dependent Te isotope fractionations in low-temperature terrestrial and marine environments, which they tentatively attributed to redox reactions or adsorption.8,9
Fehr et al. (2018)2 developed new 125Te–128Te double spike and MC-ICP-MS protocols to investigate the mass-dependent Te isotope compositions of meteorites and terrestrial samples and found significant isotopic fractionation for both. Notably, this included substantial within-group variations in the mass-dependent Te isotope compositions of carbonaceous chondrites.
Hellmann et al. (2020)3 used similar Te purification and MC-ICP-MS protocols as Fehr et al. (2018)2 but employed a 123Te–125Te double spike. In contrast to Fehr et al. (2018),2 Hellmann et al. (2020)3 found little to no within-group variations in the Te isotope compositions of carbonaceous chondrites. Instead, they identified coupled between-group differences of mass-dependent Te isotope compositions and concentrations, which they ascribed to variable mixing between a matrix rich component and chondrules or chondrule pre-cursors.3
Despite these recent studies that investigate mass-dependent Te isotope compositions, numerous important questions remain unresolved. In particular, only limited results are currently available to constrain the mass-dependent Te isotope composition of the bulk silicate Earth (BSE), whilst the Te isotope compositions of several chondritic meteorite groups have not been fully investigated, and data is completely lacking for achondrites and iron meteorites.2,4 As such, further analyses of both terrestrial samples and meteorites are needed to better constrain the chondrite group(s) that contributed to Earth's late veneer.2,3 Additionally, resolving the impact of different oxidation states on the behaviour of Te during isotope fractionation would enable the application of Te isotopes as an effective tracer of redox and volatile element fractionation processes in terrestrial and extra-terrestrial environments.2,5–9
This study presents improved procedures for the determination of mass-dependent Te isotope compositions by MC-ICP-MS. The procedures employ a 125Te–128Te double spike, which was developed for this study, coupled with optimised chromatographic procedures that enable separation of Te from silicate rocks as well as stony and iron meteorites with near-quantitative yields and a near-complete separation from elements that generate spectral interferences, including Sn and Cd. The methods are validated by analyses of synthetic samples with known isotope compositions as well meteorites and terrestrial samples that were previously analysed in other laboratories and an intercalibration between the different Te isotope reference materials that were employed. In addition, we also report the first mass-dependent Te isotope compositions obtained using the double spike technique for an iron meteorite, Canyon Diablo, and the komatiite reference material KAL-1.
Methods
Reagents and materials
All sample preparation work was carried out in the ISO Class 6 clean rooms of the MAGIC Laboratories at Imperial College London, with blank-sensitive steps performed in ISO Class 4 laminar flow hoods. All mineral acids (HCl, HNO3, and HF) were purified in-house by sub-boiling distillation and all water used was of ≥18.2 MΩ cm grade sourced from a Millipore purification system. Samples and Te standard solutions were stored either in Teflon bottles or Savillex PFA vials before, during, and after processing. The Savillex PFA vials were cleaned by three subsequent complete submersion steps, first in 8 M HNO3, followed by 6 M HCl, and finally in a mixture of ≥18.2 MΩ cm grade H2O, distilled 6 M HCl, and distilled 15 M HNO3. During each submersion step, the vials were allowed to soak in the acid or acid-water mixture for 72 to 96 hours at approximately 100 °C.Te standard solutions and data notation
A London Te solution that was prepared in-house was used as the primary Te isotope reference material in this study. Briefly, the London Te standard solution was prepared by dissolving 32.8 mg of 99.9999% pure Te (Alfa Aesar, lot number T11E031). The Te standard solution was then made up to a Te concentration of about 33 μg g−1 by dilution, using 6.5 M HCl.To facilitate inter-laboratory comparison, three further Te isotope reference materials from two other laboratories were also analysed. In detail, M. Fehr from ETH Zürich provided aliquots of a NIST SRM 3156 Te standard solution (Lot. no. 892901; termed NIST-ETH Te in the following) and a Te standard solution prepared from Alfa Aesar elemental Te (termed AA-ETH Te in the following). In addition, J. Hellmann from the University of Münster provided an aliquot of their NIST SRM 3156 Te standard solution (Lot. no. 140830; named NIST-Münster Te in the following).
This study uses the δ-notation to report the mass-dependent Te isotope compositions of the measured samples. In detail, the notation denotes the relative deviation of the 130Te/125Te isotope ratio determined for a sample from the value measured for a standard reference material (standard) in parts per 1000 (‰):
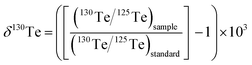 | (1) |
To facilitate direct comparisons between the results of this study and previously published literature that use a δ128/126 notation, the following equation was used for the conversion of delta values:
| δTeA = ([δTeB/1000 + 1]β − 1) × 103 | (2) |
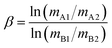 | (3) |
| δ130TeLondon ≈ δ130Te(AA-ETH) + Δ130Te(AA-ETH)-London | (4) |
Te double spike
The choice of isotopes that were used for the double spike and data reduction in this study was guided by the error propagation models of Rudge et al. (2009)13 and made with the aim to (i) minimise the error on the natural mass-fractionation factor (α) and (ii) avoid large isobaric interference corrections.13 Hence, in accord with previous studies, a 125Te–128Te double spike was prepared for, and employed in, this study.2,8 This allows the four most abundant Te isotopes – 125Te, 126Te, 128Te, and 130Te – to be used in the double spike inversion in the form of 126Te/125Te, 128Te/125Te, and 130Te/125Te ratios.
Based on Rudge et al. (2009),13 a 125Te–128Te double spike that is optimised for mass-dependent isotope analyses and is prepared from highly enriched (but slightly impure) 125Te and 128Te single spikes, should have a ratio of 125Te/128Te ≈ 1.08, which is equivalent to 125Te and 128Te proportions of 0.52 and 0.48, respectively, in the double spike (Fig. 1a, y-axis).13 Such a double spike is, furthermore, ideally employed using mixtures that feature ratios of spike-derived Te versus natural Te (S/N) of 1.249, which is equivalent to a proportion of spike-derived Te in the spike-sample mixture of approximately 0.6 (Fig. 1a, x-axis). A double spike of this composition has an estimated error on the natural mass-fractionation factor (α) of approximately 23 ppm per amu (Fig. 1b).13Fig. 1a shows the modelled errors in the natural fractionation factor α for a double spike inversion using the preferred isotope ratios based on the proportion of 125Te in the 125Te–128Te double spike and the proportion of double spike in the double spike – sample mixture. The ideal value is in the center (marked with a red ‘X’). Fig. 1b shows the propagation of the uncertainty of the natural fractionation factor α (in ppm per amu) relative to the proportion of the double spike in the double spike – sample mixture.
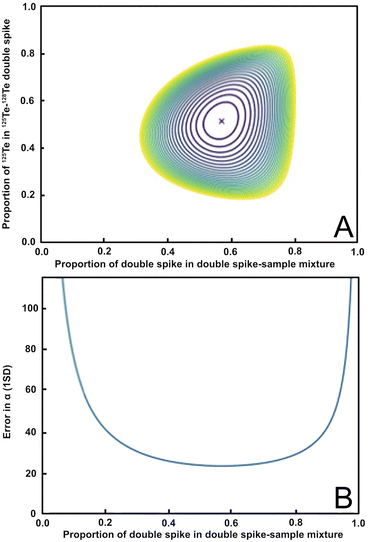 | ||
Fig. 1 Panel (A) shows the error in the natural fractionation factor α for the 125Te–128Te double spike composition and inversion isotopes used in this study. The optimal value ratios of 125Te to 128Te (0.52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.48; y-axis) and the proportion of double spike in the double spike sample mixture (≈0.6; x-axis) are marked by the red ‘X’. (B) Shows the propagation of the uncertainty of the natural fractionation factor α in ppm per amu based on the proportion of the 125Te–128Te double spike in the spike-sample mixture. Both plots were produced using the python double spike package ‘pyspike’ version 1.0.0.13 0.48; y-axis) and the proportion of double spike in the double spike sample mixture (≈0.6; x-axis) are marked by the red ‘X’. (B) Shows the propagation of the uncertainty of the natural fractionation factor α in ppm per amu based on the proportion of the 125Te–128Te double spike in the spike-sample mixture. Both plots were produced using the python double spike package ‘pyspike’ version 1.0.0.13 | ||
Whilst there are other double spike combinations available that would produce smaller uncertainties than the chosen double spike composition, these include minor Te isotopes that suffer from large isobaric interferences from Sn (120Te, 122Te, 124Te), Sb (123Te), and Xe (124Te). Although the more abundant Te isotopes have interferences from Xe (126Te, 128Te, and 130Te) and Ba (130Te), except for 125Te which is interference free, the ratios of the interfering isotopes to the affected Te isotopes are much smaller than for the minor Te isotopes, which minimises the analytical uncertainties introduced from the interference corrections.
Highly enriched samples of 125Te (99.76% purity) and 128Te (99.90% purity) were purchased from IsoFlex USA. The enriched isotopes were digested separately in pre-cleaned Savillex PFA vials using a mixture of 15 M HNO3 and 6.5 M HCl in a ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The solutions were refluxed at 110 °C until the Te was fully dissolved, and subsequently evaporated to incipient dryness. The residues were thereafter dried down three times with 6.5 M HCl to remove any residual HNO3 and dissolved in 6.5 M HCl. The double spike was then prepared as a mixture of the single spike solutions characterised by 125Te/128Te ≈ 1.05. This is equivalent to 125Te and 128Te proportions of about 0.51 and 0.49 in the double spike, respectively, and the use of a 125Te–128Te double spike of this composition allows for accurate determination of mass-dependent Te isotope compositions over a large range of S/N ratios (Fig. 1).
1. The solutions were refluxed at 110 °C until the Te was fully dissolved, and subsequently evaporated to incipient dryness. The residues were thereafter dried down three times with 6.5 M HCl to remove any residual HNO3 and dissolved in 6.5 M HCl. The double spike was then prepared as a mixture of the single spike solutions characterised by 125Te/128Te ≈ 1.05. This is equivalent to 125Te and 128Te proportions of about 0.51 and 0.49 in the double spike, respectively, and the use of a 125Te–128Te double spike of this composition allows for accurate determination of mass-dependent Te isotope compositions over a large range of S/N ratios (Fig. 1).
The accuracy of this initial calibration was verified and optimised based on analyses of London Te – double spike mixtures with variable S/N values relative to bracketing measurements of a London Te – double spike reference mixture with the modelled optimal S/N ratio of 1.249.13 In detail, 14 mixtures with S/N values ranging from 0.09 to 12.6 were analysed during two separate 6 hours measurement sessions. With the optimised double spike calibration, all mixtures except those with S/N ≤ 0.46 yielded δ130Te values that were identical, within error (±0.1‰, 2SD, n = 30), to the value obtained for the reference mixture with S/N = 1.249 (Fig. 2).
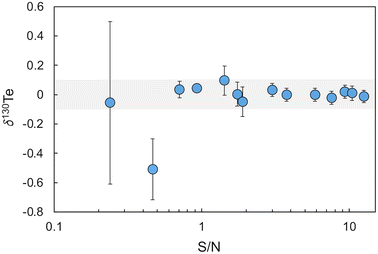 | ||
| Fig. 2 Plot of δ130Te for mixtures of the Te double spike with the London Te standard solution at varying S/N values. The shaded area denotes the within day precision of 0.1‰ (2SD). | ||
A S/N value of 2.5 was subsequently adopted as the standard S/N ratio for all further analyses of samples with Te concentration of 100 ng g−1 or above. For samples with a Te concentration of less than 100 ng g−1, a S/N ratio of about 3.5 was used to ensure that more total Te was available for the measurements. These S/N ratios were chosen as London Te - double spike mixtures with S/N > 1.7 displayed the best between-run reproducibilities, with a mean of 0.05‰ (2SD, n = 9).
Samples and analytical methods
Two meteorites and four terrestrial samples were analysed to characterise the performance of the analytical methods and enable a comparison of results with previously published data. The meteorites analysed in this study are the IAB-complex iron meteorite Canyon Diablo and the CV3 carbonaceous chondrite Allende. The terrestrial samples encompass the Alexo komatiite reference material KAL-1 and three rock reference materials from the USGS, encompassing the ferromanganese (Fe–Mn) nodules, NOD-A-1 and NOD-P-1, and Hawaiian basalt BHVO-2 (Table 6). These samples were chosen as they are either (i) common reference materials (or a widely available meteorite) which were previously characterised in one or more studies (Allende CV3, NOD-A-1, NOD-P-1, BHVO-2) or (ii) previously un-characterised but widely available samples that are therefore valuable novel additions to the data set (Canyon Diablo, KAL-1).The sample powder aliquots ranged in mass from 10 to 12 mg for NOD-A-1, 45 to 46 mg for NOD-P-1, 220 to 260 mg for Canyon Diablo, 290 to 320 mg for Allende, and 3.0 to 3.2 g for BHVO-2. A total of 1.43 g of KAL-1 was digested (Table 6). Digested sample masses were chosen based on Te concentrations reported in previous studies (where available), with the aim to provide enough natural Te for several repeat measurements. In the absence of published Te concentrations, the minimum mass required was estimated based on similar samples. In addition to the established reference materials, a glacial till from Greenland and the NIST high-sulphur steel reference material SRM 129c were used to evaluate the impact of molecular and non-spectral interferences on the measured mass-dependent Te isotope composition, as these samples were taken to be representative for terrestrial rocks and meteorites with a silicate mineralogy and iron meteorites, respectively.
All samples, with the exception of Canyon Diablo, were spiked prior to digestion with appropriate masses of the 125Te–128Te double spike. The glacial till and NIST SRM 129c were additionally doped with 500 ng to 1000 ng of London Te. The digestions were performed in 22 mL or 60 mL Savillex PFA vials. The glacial till, Allende, KAL-1, and BHVO-2 were digested using a three-step digestion protocol adapted from Fehr et al. (2004)10 and Palk et al. (2018).14 In detail, the samples were first treated with a 2.5 + 1 mixture of 28 M HF and 15 M HNO3 in which they were left for 24 to 48 hours at 110 °C. After evaporation to complete dryness, the samples were taken up in a 1 + 1 mixture of 15 M HNO3 and 6 M HCl and subsequently refluxed for up to 48 hours at 110 °C. Following this, the samples were evaporated to incipient dryness and subjected to several dry downs using 6 M HCl to ensure complete removal of any remaining HNO3. Finally, the samples were left to reflux for up to 96 hours in 6 M HCl at 110 °C.
The manganese nodules and NIST SRM 129c were digested using a two-step digestion procedure that encompassed the last two steps of the three-step digestion protocol employed for the glacial till, Allende, KAL-1, and BHVO-2. The Canyon Diablo aliquots analysed in this study were spiked after digestion as they were already digested as part of an earlier study by Poole et al. (2017).15 To ensure full equilibration between sample-derived (natural) Te and spike-derived Te, all samples which were spiked after digestion were evaporated to incipient dryness before being taken up in a 1 + 1 mixture of 15 M HNO3 and 6 M HCl and refluxed on a hotplate at 120 °C to convert Te to the same oxidation state. The samples were subsequently evaporated to incipient dryness and dried down several times using 6 M HCl to ensure complete removal of any remaining HNO3 before being taken up in 6 M HCl and refluxed on a hotplate for up to 96 hours.
Column chromatography
A new purification procedure was developed to separate Te from meteorites and terrestrial samples (Table 1). Special attention was directed towards an efficient separation of Te from Fe, Mo, Sn, Zr, Ag, and Cd without unnecessarily lowering the sample yields.| Eluent | Volume | Purpose/Eluted |
|---|---|---|
| Purification step 1: 10 mL BioRad PolyPrep columns with 2 mL BioRad AG1-X-8 resin (200–400 mesh) | ||
| 1 M HNO3 | 10 mL | Cleaning |
| 2 M HCl | 1 mL | Conditioning |
| 2 M HCl | 10 mL | Conditioning |
| 2 M HCl (sample) | 15 mL | Matrix |
| 2 M HCl | 10 mL | Matrix |
| 12 M HCl | 6 mL | Ag, Cd |
| 5 M HF | 8 mL | Ag, Cd |
| 0.5 M HCl | 10 mL | Te |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Purification step 2: 3.6 mm × 22.5 mm Teflon microcolumns with 200 μL Eichrom TRUSpec™ resin (100–150 mesh) | ||
| 7.5 M HNO3 | 10 mL | Cleaning, conditioning |
| 7.5 M HNO3 (sample) | 0.5 mL | Te |
| 7.5 M HNO3 | 10 mL | Te |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Purification step 3: 10 mL BioRad PolyPrep columns with 2 mL BioRad AG1-X-8 resin (200–400 mesh) | ||
| 0.5 M HCl | 10 mL | Cleaning, conditioning |
| 0.5 M HCl (sample) | 1 mL | Matrix (<1% Te) |
| 0.5 M HCl | 10 mL | Te |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Purification step 4: 10 mL BioRad PolyPrep columns with 0.4 mL BioRad AG1-X-8 resin (200–400 mesh) | ||
| 1 M HNO3 | 6 mL | Cleaning |
| 0.5 M HCl | 6 mL | Cleaning, conditioning |
| 6 M HCl | 4 mL | Conditioning |
| 6 M HCl (sample) | 3 mL | Matrix |
| 6 M HCl | 5 mL | Matrix |
| 2 M HCl | 5 mL | Matrix |
| 0.5 M HCl | 10 mL | Te |
The first step is adapted from the “HCl-protocol” of Fehr et al. (2004)10 and serves to separate Te from the majority of matrix elements, Ag, Sn, and Cd. This purification step uses 10 mL BioRad Poly-Prep chromatography columns with 2 mL AG1-X-8 anion-exchange resin (200–400 mesh). After cleaning and conditioning of the resin using 10 mL 1 M HNO3 followed by 10 mL 2 M HCl, the samples were loaded in 15 mL 2 M HCl. The columns were then rinsed with 10 mL 2 M HCl, followed by 6 mL 12 M HCl and 8 mL 5 M HF. Finally, Te was eluted using 10 mL of 0.5 M HCl (Table 1).
The second step is adapted from Hellmann et al. (2020)3 to further purify Te from Mo and Fe. This step uses Teflon microcolumns with resin bed dimensions of 3.6 mm × 22.5 mm loaded with 230 μL Eichrom TRU-Spec resin (100–150 mesh). The resin was cleaned and conditioned using 10 mL 7.5 M HNO3 before loading the samples in 0.5 mL 7.5 M HNO3. The Te fractions of the samples were collected immediately upon loading. The resin was then rinsed using 2.5 mL 7.5 M HNO3 to elute any remaining Te. The total volume of the Te fraction was 3 mL (Table 1).
The collected Te fractions were cleaned by liquid–liquid extraction with n-heptane immediately after elution to remove any organic compounds derived from the Eichrom TRU-Spec resin.16
The third step further purifies Te from Sn, Ag, and Cd, and was modified from Wang et al. (2017)17 and Wasserman and Johnson (2020).9 Two mL of AG1-X8 anion-exchange resin (200–400 mesh) was loaded into 10 mL BioRad Poly-Prep chromatography columns and subsequently rinsed using 10 mL 0.5 M HCl to clean and condition the resin. Following this, the samples were loaded onto the resin in 1 mL 0.5 M HCl. The Te was subsequently eluted with 10 mL 0.5 M HCl (Table 1).
Samples with Te contents of <50 ng g−1 were processed through an additional purification step to remove residual matrix elements. This fourth step was modified from the protocol of Brennecka et al. (2017)18 and utilises 10 mL BioRad Poly-Prep chromatography columns loaded with 0.4 mL of AG1-X-8 anion-exchange resin (200–400 mesh). The resin was cleaned and conditioned first with 6 mL 1 M HNO3, followed by 6 mL 0.5 M HCl, and finally 4 mL 6 M HCl. Following this, the samples were loaded in 3 mL 6 M HCl. The columns were subsequently rinsed using 5 mL 6 M HCl followed by 5 mL 2 M HCl. Tellurium was finally eluted with 10 mL 0.5 M HCl (Table 1).
Mass spectrometry
| NuPlasma II | |
| Faraday cup resistors | 1011 Ω |
| RF Power | 1300 W |
| Sampler cone | Ni |
| Skimmer cone | Ni |
| Coolant airflow | 13 min−1 |
| Auxiliary airflow | 0.9 min−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Sample introduction system | CETAC Aridus II |
| Nebulizer | PFA MicroMist pneumatic nebulizer |
| Nebulizer uptake rate | 140 μL min−1 |
| Desolvator temperature | 110 °C |
| Membrane oven | 160 °C |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Te isotope measurements | |
| Number of blocks per run | 3 |
| Integration time per cycle | 5 seconds |
| Baseline measurement | 30 seconds |
| Cup | H1 | H2 | H4 | H5 | H6 | H10 |
|---|---|---|---|---|---|---|
| a Monitor isotope used for isobaric interference corrections. b 16O. c 18O. | ||||||
| Tellurium | 125Te | 126Te | 128Te | 130Te | ||
| 7.% | 18.8% | 31.8% | 34.2% | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Isobaric interferences | ||||||
| Xe | 126Xe | 128Xe | 129Xem | 130Xe | 134Xe | |
| 0.09% | 1.9% | 26.4% | 4.1% | 10.4% | ||
| Ba | 130Ba | 134Baa | ||||
| 0.1% | 24.4% | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Polyatomic interferences | ||||||
| Nitrides | 111Cd | 112Cd | 114Cd | 116Cd | ||
| (+14N) | 12.8% | 24.1% | 28.7% | 7.5% | ||
| 112Sn | 114Sn | 116Sn | ||||
| 1% | 0.7% | 14.5% | ||||
| Oxides | 109Agb | 110Cd | 112Cd | 114Cd | ||
| (+16O, 18O) | 48.2% | 12.5% | 24.1% | 28.7% | ||
| 107Agc | 110Pd | 112Sn | 114Sn | |||
| 51.8% | 11.7% | 1% | 0.7% | |||
| Argides | 85Rb | 86Kr | 88Sr | 90Zr | ||
| (+40Ar) | 72.2% | 17.3% | 82.6% | 51.5% | ||
| 86Sr | ||||||
| 9.9% | ||||||
The Faraday cups of the Nu Plasma II were fitted with 1011Ω resistors, and the ion beams of 129Xe, and 134Ba (together with isobaric 134Xe) were collected concomitant with 125Te, 126Te, 128Te, and 130Te by static multi-collection during each measurement sequence to allow for corrections of isobaric interferences (Table 3). The analyte solutions were prepared in a mixture of 0.1 M HNO3 and 0.01 M HF, where the latter was added to avoid Te precipitation during storage and in the sample introduction system. Typical total Te concentrations for the analyte solutions ranged between 20 ng mL−1 and 30 ng mL−1.
The sensitivity for Te was influenced by the instrumental setup and tuning parameters, which were optimised prior to each measurement session. The typical sensitivity was 750 V (μg−1 mL−1) during the course of the study, which is equivalent to a transmission efficiency of 0.50%.
The isotope ratio measurements were carried out in three blocks of 20 cycles, with an integration time of 5 s each. Each block was preceded by a 30 s electronic baseline measurement during which the ion beam was deflected by the electrostatic analyser. The system was flushed between analyses with a mixture of 0.1 M HNO3 and 0.01 M HF. The time required for one measurement, including the wash-out sequence, was about 10 minutes (Table 2). All sample analyses were bracketed by runs of a double-spiked London Te standard solution which was matched to the sample solutions in both concentration and S/N values to within 10%. The Te isotope data reported in this study are expressed relative to the results obtained for multiple runs of the London Te standard during the same measurement session.
The Ba interference on 130Te was monitored using 134Ba, which was corrected for the interference of 134Xe prior to use. The Xe-corrected 134Ba ion beam was then applied to correct the Ba interference on 130Te using a Ba isotope ratio of 130Ba/134Ba = 0.04386.19 However, as the large Xe corrections on 134Ba often resulted in a nominally negative 134Ba ion beam intensity, the Ba interference correction was only applied if the Xe-corrected 134Ba ion beam was ≥0 mV.
All Te concentrations reported in this study were determined by isotope dilution. The technique is employed here using the measured and mass-bias corrected 125Te/130Te and 128Te/130Te ratios of the double spike sample solutions. The data necessary for the calculation of the Te concentration of a sample were obtained during the runs that were carried out to determine the stable isotope compositions. Due to this, the number of measurements (n) given for a sample in Tables 6 and 7 applies both to the Te isotope composition and the Te concentration.
Results and discussion
Yields and blanks
The yields of the column chemistry procedure for the separation of Te were determined by passing known quantities of the London Te standard solution through the columns and subsequent collection of all eluate fractions after the ‘sample’ had been loaded. The total beam intensity – calculated from monitoring 125Te, 126Te, 128Te, and 130Te ion beam intensities – were then measured for the ‘sample’ relative to a London Te standard solution of known concentration, to determine the Te mass recovered for the former.The full procedural yields ranged from 85% to 95%. Stage 1 of the column chemistry achieved yields of 90% to 95%, whilst near-quantitative yields of 97% to 100% were obtained for stages 2, 3, and 4 of the Te separation.
Excluding one outlier, the total Te blank of the analytical procedure ranged from 34 pg to 77 pg, with a mean of 54 ± 15 pg (1SD, n = 7). The single high-Te outlier blank was measured at 390 pg. The measured Te concentrations were corrected for the contribution of the blank. No blank corrections were applied to the Te isotope compositions of samples as the typical blank contributed ≤0.01‰ to the total natural Te analysed and the Te isotope composition of the blank is not well defined.
Evaluation of spectral and non-spectral interferences
Measurements of Te isotopes by MC-ICP-MS can be affected by spectral interferences from isobars and polyatomic ions as well as the presence of elements that can generate non-spectral interferences (i.e., matrix effects).The Xe-corrected ion beam intensity of 134Ba was <0 mV for most samples, and hence Ba-corrections were not commonly applied. When the amount of Ba present was large enough for a Ba correction to be applied, the Ba/Te ratios ranged from 1.6 × 10−5 to 1.7 × 10−4, with a mean of 9.6 × 10−5. At this level, the Ba/Te ratios had no significant effect on the within-day precision nor the measured δ130Te values.
The impact of Rb, Sr, Zr, Ag, Cd, and Sn on the Te isotope analyses was evaluated through repeat analyses of the glacial till and NIST SRM 129c. In addition, appropriate aliquots of the final Te fractions from the column chemistry were analysed using mass scans for the presence of Fe, Rb, Sr, Zr, Ag, Cd and Sn. The ion beam intensities measured for these elements were then compared to the Te ion currents obtained for the same solutions in order to quantify acceptable Element/Te levels, which are not associated with any impacts on the measured Te isotope compositions.
The Sn/Te ratios of the samples ranged from 1.5 × 10−4 to 8.9 × 10−4, with a mean of 2.3 × 10−4. This is nearly identical to the Sn/Te ratios of the London Te standard solution-double spike mixtures which ranged from 1.5 × 10−4 to 5.7 × 10−4. Occasionally, higher Sn/Te ratios of up to 2.9 × 10−3 were measured for some samples. Regardless, even at this higher level, Sn had no influence on measured δ130Te values and the reproducibility of the data.
Strontium was found to have similarly negligible effect on the Te isotope data, even at Sr/Te ratios of up to 0.87, which is significantly higher than the Sr/Te levels of <0.13 specified by Fehr et al. (2004).10
The Zr/Te ratio of the samples ranged from 1.2 × 10−3 to 1.5 × 10−3, whilst the Element/Te levels of Rb, Ag, and Cd did not exceed 0.05 for any of the samples. At these levels, neither Zr, Rb, Ag, or Cd had a noticeable effect on the measured δ130Te values or the reproducibility of the data.
Finally, the Fe/Te ratios of the samples ranged from 0.11 to 0.20, with a mean of about 0.16. At this level the Fe present in the samples had no effect on the measured δ130Te values nor the reproducibility of the data, indicating that the Te isotope compositions presented here are unlikely to have been affected by matrix effects from Fe.
While the production rates of hydrides of Te, I, and Xe in the plasma are expected to be limited due to the use of a desolvating nebuliser system for sample introduction, their presence may still affect the Te isotope compositions. As such, the production rates of these hydrides were evaluated to determine their potential impact (if any) on measured δ130Te values. Given that I and Xe are trace constituents of the plasma gas, hydrides of these elements are expected to generate constant interference levels, and their presence should hence be detectable from variations in Te isotope ratios when Te is present at different concentrations. To investigate this, pure Te standard solutions with concentrations ranging from 50 ng mL−1 to 200 ng mL−1 were analysed against a primary standard with a Te concentration of 100 ng mL−1 in five separate 6- to 8-hours measurement sessions over a period of ten months. No significant deviations in isotopic composition between Te solutions of different concentrations were found in any of the sessions. This demonstrates that problematic levels of IH+ and XeH+ were not present during the analyses due to limited hydride formation. The production of TeH+ was monitored based on variations in ion beam intensities as mass number 129 (129Xe), and the upper limit of 128TeH+/128Te was found to be <5 ppm. This suggest that TeH+ formation in the plasma is essentially negligible and does not compromise the δ130Te values reported here.
Potential impact of mass-independent Te isotope effects
The double spike data reduction assumes that any isotopic variations identified for samples are due to mass-dependent isotope fractionation. However, if the isotope composition of a sample is also altered by radiogenic decay, material of distinct nucleosynthetic origin, or mass-independent isotope fractionation, the data reduction will yield biased mass-dependent isotopic compositions and hence incorrect δ-values. For samples that harbour such isotope anomalies, the issue can be addressed by carrying out additional analyses of the unspiked sample and application of this isotope data in the double spike data reduction.13,20In order to investigate the impact of potential mass-independent isotope effects on mass-dependent Te isotope compositions, the current study calculated the maximum mass-independent isotope anomalies that can be tolerated for a sample before this has a deleterious impact on the measured δ130Te values.20
Nucleosynthetic and radiogenic Te isotope anomalies and mass-independent Te isotope fractionations have yet to be unambiguously identified in natural samples.2,3,18,21–23 The following calculations therefore employed a theoretical sample, which was assigned nucleosynthetic anomalies on the 126Te/125Te, 128Te/125Te and 130Te/125Te ratios and that correspond to anomalies that would be expected for a small deficit of isotopes produced by s-process nucleosynthesis.
The isotopic anomalies are quantified with the ε-notation, which denotes the relative deviation of an isotope ratio determined for a sample from the value measured for a standard reference material in parts per 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. For the modelling, the Te isotope anomalies were scaled to be just larger than the analytical errors that were reported in previous studies for measurements of ε126Te, as scaling the anomalies relative to the analytical errors reported for ε130Te would result in ε126Te anomalies of ≥1.4, which are significantly larger than those reported in any previous studies.3,21,22 The calculations summarized above yield maximum mass-independent Te isotope anomalies of ε126Te = −0.43 and ε130Te = −0.17. If such anomalies were present in a sample, they would generate a shift in δ130Te of only ±0.025‰. Importantly, such a small shift cannot be resolved analytically as it much smaller than the typical within-session reproducibility of ±0.07‰ (2SD) that was obtained in this study for δ130Te measurements.
000. For the modelling, the Te isotope anomalies were scaled to be just larger than the analytical errors that were reported in previous studies for measurements of ε126Te, as scaling the anomalies relative to the analytical errors reported for ε130Te would result in ε126Te anomalies of ≥1.4, which are significantly larger than those reported in any previous studies.3,21,22 The calculations summarized above yield maximum mass-independent Te isotope anomalies of ε126Te = −0.43 and ε130Te = −0.17. If such anomalies were present in a sample, they would generate a shift in δ130Te of only ±0.025‰. Importantly, such a small shift cannot be resolved analytically as it much smaller than the typical within-session reproducibility of ±0.07‰ (2SD) that was obtained in this study for δ130Te measurements.
An additional isotope effect of ε126Te = +0.1 was also incorporated to account for possible additional radiogenic ingrowth of 126Te from decay of extinct 126Sn in meteorites. This addition resulted in a revised mass-independent Te isotope anomaly of ε126Te = −0.33. Applying the updated mass-independent Te isotope anomalies of ε126Te = −0.33 and ε130Te = −0.17 reduced the shift in δ130Te to ±0.022‰. As such, possible radiogenic and nucleosynthetic Te isotope effects in meteorites and terrestrial samples are unlikely to have a significant impact on δ130Te values.
In addition to nucleosynthetic and radiogenic anomalies, anomalous Te isotope effects can be introduced to a sample due the nuclear field shift effect (NFSE).24–26 Isotope fractionations consistent with NFSEs have been reported for Te during solvent extraction experiments.24 The NFSE is generally accepted to occur concurrently with mass-dependent isotope fractionation and is thought to be a significant source of isotope fractionation for the heaviest elements, including Hg, Tl and U.24–27 Consequently, while the behaviour in lighter elements is poorly constrained, NFSEs could be a significant contributor to Te isotope fractionation.
As direct investigations are hampered by the lack of NFSE data for Te, this study calculated an upper constraint on the impact of the NFSE. This was done by numerically adding mass-independent anomalies to the isotopic composition of the London Te standard solution, processing these results through the double spike data reduction, and subsequently calculating the difference in mass-dependent isotope composition between the hypothetical dataset and the standard.26 The mass-independent anomalies were calculated in ε-units using eqn (1) from Fujii et al. (2006):26
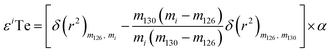 | (5) |
The equation is presented here using the example of εiTe normalised to 130Te/126Te = 1.81684.25 Here mi is the atomic weight of the nuclide ‘i’ in εiTe, m130, m126, are the atomic weights of the nuclides in the normalisation ratio (130Te, 126Te), and δ(r2) is the squared change in the nuclear charge radii of the nuclei. The variable α is an adjustable parameter which is determined through regression.27–29
The above calculations, when scaled according to the maximum analytical errors that were reported in previous studies and which did not observe NFSE, yielded a maximum mass-independent anomaly of ε128Te = −0.91.21–23 Anomalies of this magnitude would contribute a maximum of ±0.037‰ to the mass-dependent δ130Te values, which is significantly less than the typical within-session reproducibility of ±0.07‰ (2SD) that was obtained in this study for δ130Te measurements. If the calculations are instead performed using data normalised to 125Te/128Te = 0.22204, this results in mass-independent Te isotope anomalies of ε126Te = −0.30 and ε130Te = +0.30.30 Anomalies of this magnitude would generate a shift in δ130Te of ±0.080‰ and could hence result in an analytically just resolvable shift for δ130Te.
In summary, the calculations indicate that mass-independent Te isotope anomalies from radiogenic decay, distinct nucleosynthetic matter, and NFSE are expected to have either no or only a barely resolvable impact on the measured δ130Te of samples. This reflects that such anomalies are expected to be small because they were previously not clearly resolved in mass-independent Te isotope analyses of terrestrial and meteorite samples.
Analyses of London Te solutions
The precision obtained in repeated analyses of London Te standard solutions was evaluated over a 19 months period, from July 2020 to January 2022. During this time, 18 measurement sessions of about 8 to 16 hours each, were carried out. Each session encompassed about 50 to 100 Te isotope runs and of these about 25 to 60 were analyses of London Te – double spike mixtures. These London Te – double spike mixtures were characterised by S/N ≈ 2.45 and total Te concentration of 25 to 30 ng mL−1, with each run consuming about 30 to 40 ng of Te, equivalent to 8.5 to 11.5 ng of natural Te. For single measurement sessions, these analyses typically yielded a within-session reproducibility (2SD) of ±0.04‰ to ±0.08‰ with a mean of ±0.07‰ (2SD). For individual runs, the typical within-run reproducibility (2SE) ranged from ±0.03‰ to ±0.05‰, with a mean of ±0.04‰. Three additional measurement sessions of about 4 to 6 hours each were performed using London Te – double spike mixtures with total Te concentrations of 15 to 20 ng mL−1 and S/N ≈ 2.45. These sessions encompassed 25 to 40 isotope runs of London Te – double spike mixtures. Each run consumed about 18 to 24 ng of total Te, equivalent to 6 to 7.5 ng of natural Te. These analyses typically yielded a within-day reproducibility (2SD) of 0.05‰ to 0.09‰ with a mean of 0.07‰. For individual runs, the typical within-run reproducibility (2SE) ranged from 0.05‰ to 0.06‰, with a mean of 0.05‰.| Te standard solution | n | δ 130Te (±2SD) |
|---|---|---|
| AA-ETH Te | 73 | 0.93 ± 0.06‰ |
| NIST-ETH Te | 93 | 0.81 ± 0.05‰ |
| NIST-Münster Te | 17 | 0.44 ± 0.05‰ |
All secondary Te standard solutions used here were thoroughly characterised in previous studies and they can, therefore, be used to verify that the new protocols developed here provide unbiased δ130Te data.2–4 In detail, the results of this study yield a δ130Te of −0.12 ± 0.06‰ for NIST-ETH Te relative to the AA-ETH Te, which is identical to the offset of −0.12 ± 0.03‰ reported by Fehr et al. (2018)2 (Table 5).
| a Recalculated from δ128/126Te using eqn (2) | |||
|---|---|---|---|
| This study | |||
| NIST-ETH Te relative to | NIST-ETH Te | AA-ETH Te | NIST-Münster Te |
| — | −0.12 ± 0.06‰ | 0.37 ± 0.05‰ | |
| AA-ETH Te relative to | NIST-ETH Te | AA-ETH Te | NIST-Münster Te |
| 0.12 ± 0.06‰ | — | 0.49 ± 0.04‰ | |
| NIST-Münster Te relative to | NIST-ETH Te | AA-ETH Te | NIST-Münster Te |
| −0.37 ± 0.05‰ | −0.49 ± 0.04‰ | — | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Previous studies | |||
| Fehr et al. (2018)2 | |||
| NIST-ETH Te relative to | AA-ETH Te | ||
| −0.12 ± 0.03‰ | |||
| Hellmann et al. (2021)4 | |||
| NIST-ETH Te relative to | NIST-Münster Te | ||
| 0.37 ± 0.07‰ | |||
| AA-ETH Te relative to | NIST-Münster Te | ||
| 0.50 ± 0.05‰ | |||
Furthermore, NIST-ETH Te and AA-ETH Te have positive δ130Te values, of 0.37 ± 0.04‰ and 0.49 ± 0.05‰, respectively, relative to NIST-Münster Te (Table 5). To enable a direct comparison of these data with the previous results of Hellmann et al. (2021),4 the latter data were recalculated from δ128/126Te to δ130Te notation using eqn (2) (Table 5).
Based on these calculations, the data of Hellmann et al. (2021)4 yield δ130Te values for NIST-Münster Te relative to NIST-ETH Te and AA-ETH Te of −0.37 ± 0.07‰ and −0.50 ± 0.05‰, respectively, and these are both identical to the results of this study (Table 5).
Tellurium concentrations of meteorites and terrestrial samples
Repeat analyses of a single digestion of komatiite KAL-1 yielded a mean Te concentration of 35.6 ± 0.1 ng g−1 (1SD, n = 4). As KAL-1 has not previously been analysed for its Te concentration, a direct comparison to published results is not possible. However, the Te concentration determined for KAL-1 is in line with Te concentrations of 24 ng g−1 to 53 ng g−1 obtained in three previous studies for the IAG komatiite reference material OKUM.31–33The Hawaiian basalt BHVO-2 displays the lowest Te concentration of the samples analysed in this study, with a combined mean of 14.5 ± 0.4 ng g−1 for three different digestions (1SD, n = 3). This is broadly consistent with the Te concentrations of 11.9 ± 1.4 ng g−1 to 14.6 ± 2.7 ng g−1 reported in seven previous studies (Table 6).3,34–39
| Mass (mg) | δ 130Te (±2SD) | n | Te (±1SD) | |
|---|---|---|---|---|
| a Sample mass in processed sample solution aliquot. b Recalculated using offsets detailed in Table 4. Errors were propagated using: 2SDfinal = √((A2SD2) + (B2SD2)). | ||||
| KAL-1 (Alexo komatiite) | ng g− 1 | |||
| Digestion 1 | 1430 | 0.64 ± 0.06 | 4 | 35.60 ± 0.01 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| BHVO-2 (Basalt) | ng g− 1 | |||
| Digestion 1 | 3035 | 1.13 ± 0.07 | 4 | 14.00 ± 0.01 |
| Digestion 2 | 3175 | 1.15 ± 0.06 | 4 | 15.00 ± 0.01 |
| Digestion 3 | 2950 | 1.15 ± 0.09 | 4 | 14.50 ± 0.01 |
| Mean BHVO-2 | 1.14 ± 0.01 | 3 | 14.50 ± 0.41 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Previous studies | ||||
| Hellmann et al. (2020)3 | 1.06 ± 0.08 | 5 | 14.5 ± 0.6 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NOD-A-1 (Fe–Mn nodule) | μg g− 1 | |||
| Digestion 1 | 12 | 1.59 ± 0.05 | 7 | 34.51 ± 0.02 |
| Digestion 2 | 10 | 1.64 ± 0.06 | 9 | 34.75 ± 0.16 |
| Digestion 3 | 10 | 1.67 ± 0.07 | 7 | 34.79 ± 0.03 |
| Mean NOD-A-1 | 1.63 ± 0.07 | 3 | 34.74 ± 0.38 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Previous studies | ||||
| Fehr et al. (2018)2 | 1.67 ± 0.08 | 3 | n.d. | |
| Fukami et al. (2018)8 | 1.56 ± 0.10 | 5 | 32.4 ± 6.5 | |
| Hellmann et al. (2020)3 | 1.53 ± 0.10 | 5 | 29.6 ± 0.7 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| NOD-P-1 (Fe–Mn nodule) | μg g− 1 | |||
| Digestion 1 | 45 | 1.43 ± 0.05 | 5 | 5.06 ± 0.01 |
| Digestion 2 | 46 | 1.34 ± 0.08 | 5 | 5.08 ± 0.01 |
| Digestion 3 | 45 | 1.40 ± 0.07 | 4 | 5.10 ± 0.01 |
| Mean NOD-P-1 | 1.39 ± 0.07 | 3 | 5.08 ± 0.03 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Previous studies | ||||
| Fehr et al. (2018)2 | 1.35 ± 0.14 | 6 | n.d. | |
| Fukami et al. (2018)8 | 1.12 ± 0.07 | 5 | 5.32 ± 0.26 | |
| Hellmann et al. (2020)3 | 1.22 ± 0.07 | 5 | 4.95 ± 0.05 | |
| Wassermann and Johnson (2020)9 | 1.08 ± 0.17 | 5 | 4.88 ± 0.75 | |
The Fe–Mn nodule NOD-A-1 has the highest Te concentration of the samples analysed in this study, with a mean of 34.7 ± 0.4 μg g−1 (1SD, n = 3). This result is higher than the concentrations of 30.9 ± 0.1 μg g−1 and 29.6 ± 0.7 μg g−1 that were published by Axelsson et al. (2002)40 and Hellmann et al. (2020),3 respectively. This discrepancy most likely reflects minor sample heterogeneity as Te concentrations ranging from 28.8 μg g−1 to 36.0 μg g−1 were reported for different sample powder aliquots analysed in the same laboratory.8 Notably, the imprecise mean value of 32.4 ± 6.5 μg g−1 determined by Fukami et al. (2018)8 is consistent with the result of the current study.
The second analysed Fe–Mn nodule, NOD-P-1, has a Te concentration of 5.1 ± 0.0 μg g−1 (1SD, n = 3), in line with the results of five previous studies which range from 4.8 ± 0.4 μg g−1 to 5.1 ± 0.3 μg g−1 (Table 6).3,8,9,39,41
Considering the meteorites, replicate analyses of four separate digestions of the CV3 chondrite Allende yielded a mean Te concentration of 970 ± 60 ng g−1 (1SD, n = 4), consistent with literature data of 850 ± 140 ng g−1 and 940 ± 30 ng g−1 (Table 6).2,3 The mean Te concentration of 122 ± 2 ng g−1 (1SD, n = 4) obtained in this study for Canyon Diablo is intermediate to two previous results of 176 ± 20 ng g−1 and 90 ± 16 ng g−1 (Table 6).21,41 The observed variability is most likely due to heterogenous distribution of troilite nodules within the Canyon Diablo meteorite as the sulphides are presumably the main carrier phase of Te in iron meteorites.
Tellurium isotope compositions of terrestrial samples
Tellurium isotope data were acquired for four terrestrial samples, Alexo komatiite KAL-1, Hawaiian basalt BHVO-2, and the Fe–Mn nodules NOD-A-1 and NOD-P-1.Komatiite KAL-1 displays the lightest isotope composition of the terrestrial samples analysed in this study with a mean δ130Te value of 0.64 ± 0.06‰ (2SD, n = 4) obtained from repeat analyses of one digested powder aliquot (Fig. 3 and Table 6).
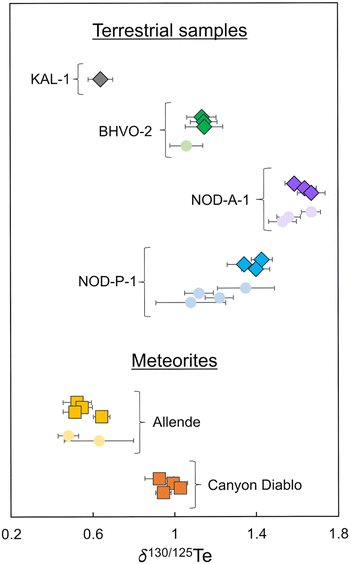 | ||
| Fig. 3 Plot showing the δ130Te values obtained in this and previous studies. Data obtained in this study are shown as diamonds and squares. Literature data is shown as circles.2,3,8,9,21 All data are compiled in Tables 6 and 7. | ||
While no other komatiites have been analysed for the Te isotope compositions to date, the result resembles mass-dependent Te isotope data reported for lherzolites, harzburgites, and dunites in a previous study, which ranged from 0.44 ± 0.05‰ to 0.71 ± 0.054.4
Repeat analyses of three separate digestions of BHVO-2 produced a combined mean δ130Te value of 1.14 ± 0.01‰ (2SD, n = 3; Table 6). This is consistent with the previously reported δ130Te value of 1.06 ± 0.08‰ (Fig. 3 and Table 6).3
Three separate digestions of nodule NOD-A-1 produced a mean δ130Te value of 1.63 ± 0.07‰ (2SD, n = 3; Table 6). This is in accord with previously reported δ130Te values, which range from 1.53 ± 0.10‰ to 1.67 ± 0.08‰ (Fig. 3 and Table 6).2,3,8
The isotope composition of NOD-P-1 is slightly lighter than NOD-A-1, with a mean δ130Te value of 1.39 ± 0.07‰ (2SD, n = 3) from three separate digestions (Table 6). This result is consistent with the δ130Te of 1.35 ± 0.14‰ obtained by Fehr et al. (2018),2 but heavier than the Te isotope compositions of three other studies which reported δ130Te values which ranged from 1.08 ± 0.17‰ to 1.22 ± 0.07‰ (Fig. 3 and Table 6).3,8,9 This variability is further confirmed by reports of variable δ130Te values for different powder aliquots of this sample that were analysed in the same laboratory.2,9 Together, this indicates that the NOD-P-1 reference material exhibits significant heterogeneity, as previously suggested by Fukami et al. (2018)8 and Wasserman and Johnson (2020).9
Tellurium isotope compositions of meteorites
Repeat analyses of four separate digestions of the CV3 chondrite Allende during the course of this study yielded a mean δ130Te value of 0.56 ± 0.10‰ (2SD, n = 4; Table 7). This result is consistent with δ130Te values of 0.63 ± 0.18‰ and 0.48 ± 0.05‰ from two previous studies (Fig. 3 and Table 7).2,3 Of interest is the observation that whilst Allende digestions 1, 2, and 3 yielded very consistent δ130Te values of 0.52 ± 0.07‰ (2SD, n = 4), 0.55 ± 0.05‰ (2SD, n = 8), and 0.51 ± 0.06‰ (2SD, n = 12), respectively, digestion 4 provided a higher δ130Te of 0.64 ± 0.04‰ (2SD, n = 10; Table 7). This occurred even though all digestions were sourced from a single larger homogenised powdered sample of Allende. Furthermore, digestion 4 was processed and analysed alongside digestions 2 and 3, such that the distinctly heavier Te isotope composition is unlikely to be an analytical artefact from sample preparation or the mass spectrometric analyses. Similar variations in the mass-dependent Te isotope composition of Allende were previously described by Fehr et al. (2018),2 who reported a mean δ130Te of 0.63 ± 0.18‰ for three digestions of the meteorite (Table 7). No such variations were found by Hellmann et al. (2020),3 who obtained a mean δ130Te of 0.48 ± 0.05‰ from two Allende digestions (Fig. 3 and Table 7).| Mass (mg) | δ 130Tea (±2SD) | n | Teb (±1SD) | |
|---|---|---|---|---|
| a In case of single analyses, the within-session precision is used as sample 2SD. b Errors for single analyses are less than 0.001 ng g−1 and are not shown. c Recalculated using offsets detailed in Table 4. Errors were propagated using: 2SDfinal = √((A2SD2) + (B2SD2)). d Average of two reported values. e The study did not determine the Te isotope composition. f Sample mass in processed sample solution aliquot. | ||||
| Allende (CV3 chondrite) | ng g− 1 | |||
| Digestion 1 | 285 | 0.52 ± 0.07 | 4 | 1070 ± 0.7 |
| Digestion 2 | 320 | 0.55 ± 0.05 | 8 | 935 ± 1.6 |
| Digestion 3 | 310 | 0.51 ± 0.06 | 12 | 940 ± 1.3 |
| Digestion 4 | 310 | 0.64 ± 0.04 | 10 | 940 ± 1.7 |
| Mean Allende | 0.56 ± 0.10 | 4 | 970 ± 60 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Previous studies | ||||
| Fehr et al. (2018)2 | 0.63 ± 0.17 | 3 | 850 ± 140 | |
| Hellmann et al. (2020)3 | 0.48 ± 0.05 | 2 | 940 ± 30 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Canyon Diablo (IAB-complex iron meteorite) | ng g− 1 | |||
| Aliquot 1 | 220f | 0.92 ± 0.07 | 1 | 120 |
| Aliquot 2 | 220f | 0.99 ± 0.07 | 1 | 121 |
| Aliquot 3 | 260f | 1.03 ± 0.02 | 2 | 124 ± 0.01 |
| Aliquot 4 | 250f | 0.95 ± 0.04 | 3 | 124 ± 0.02 |
| Mean Canyon Diablo | 0.97 ± 0.08 | 4 | 122 ± 3 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Previous studies | ||||
| Goles and Anders, (1962)42 | N/A | 1 | 90 ± 16 | |
| Fehr et al. (2005)21 | −1.31 ± 2.25 | 4 | 176 ± 20 | |
Fehr et al. (2018)2 suggested that the variable δ130Te values they determined for Allende may result from re-distribution of Te during thermal metamorphism. It's unclear, however, whether the weak thermal processing that overprinted Allende was sufficient to mobilise Te and affect its isotope composition on a bulk sample scale.3,43 Conversely, Hellmann et al. (2020)3 suggested that the bulk compositions of carbonaceous chondrites most likely reflect mixing of a volatile depleted chondrule component with isotopically light Te and a volatile-rich matrix component with isotopically heavy Te. The δ130Te variations found in this study and by Fehr et al. (2018)2 for Allende may, therefore, reflect variable amounts of matrix and chondrule components in the separate digestions. Notably, this interpretation predicts correlated variations of Te isotope compositions and concentrations, but no such correlation is evident for the Allende data of this study and Fehr et al. (2018).2 Alternatively, it is possible that the variable δ130Te data for Allende may result from the heterogenous distribution of one or several phases or components with distinct Te isotope composition, such as sulphides or CAIs, as was previously suggested by Fehr et al. (2018).2 The latter explanation, possibly in combination with variable amounts of matrix and chondrule components, can account for the observed decoupled variations of δ130Te values and Te concentrations in different power aliquots of the Allende meteorite.
The four solution aliquots of the IAB complex iron meteorite Canyon Diablo that were analysed in this study yielded a combined mean δ130Te of 0.97 ± 0.08‰ (2SD, n = 4; Table 7 and Fig. 3). Notably, this is the first precise mass-dependent Te isotope composition determined with the double spike technique for any iron meteorite. The only previously available mass-dependent Te isotope data for iron meteorites had much larger errors, of up to ±0.9‰ for δ126/128Te, as they were obtained without use of a double spike or dopant element for correction of the instrumental mass bias. Furthermore, the δTe = 0 reference material that was employed by Fehr et al. (2005)21 has not been analysed relative to the primary Te isotope reference materials that were used in this and other recent studies. However, assuming no isotopic offset between the δTe = 0 reference material of Fehr et al. (2005)21 and the London Te of this study, the combined mean δ126/128Te value of 0.53 ± 0.90‰ reported for Canyon Diablo by Fehr et al. (2005)21 is equivalent to a δ130Te value of −1.3 ± 2.25‰. Within error, this overlaps with the δ130Te value of 0.97 ± 0.08‰ obtained in this study, such that the results can tentatively be assumed as consistent (Table 7).
Conclusions
This study presents new methods for the precise determination of mass-dependent Te isotope compositions. In particular, the technique encompasses a new protocol for the separation of Te from silicate rock and meteorite samples as well as iron meteorites prior to the isotopic analyses. The separation method efficiently isolates Te from elements that produce spectral and non-spectral interferences during the measurements whilst providing yields of >85%. The method employs a 125Te–128Te double spike, which provides a robust correction for any mass-bias effects that are incurred during sample preparation and the MC-ICP-MS analyses.In an 8-to-12-hours measurement session the typical between-run reproducibility (2SD) of the δ130Te data is ±0.07‰, for analyte solutions with Te concentrations of 20 ng mL−1 to 30 ng mL−1 and runs that each consume 30 to 40 ng Te. This is on par with, or better than, the precisions achieved in other recent Te isotope studies.
The methods were validated based on an inter-laboratory cross-calibration of three different Te standard solutions and analyses of three rock reference material and two meteorites for which Te concentrations and isotope compositions were available in the literature. In detail, the δ130Te values determined in this study for AA-ETH Te relative to NIST-ETH Te (−0.12 ± 0.06‰) and for NIST-Münster Te relative to NIST-ETH Te and AA-ETH Te (−0.37 ± 0.04‰ and −0.49 ± 0.05‰, respectively) are identical to the results of previous investigations. Combined, this shows that the δ130Te values obtained in this study are unbiassed.
This study reports δ130Te values for four previously investigated samples; three terrestrial reference samples and the CV3 carbonaceous chondrite Allende. The terrestrial samples include Hawaiian basalt BHVO-2 and Fe–Mn nodules NOD-A-1 and NOD-P-1, which display δ130Te values of 1.14 ± 0.01‰, 1.63 ± 0.07‰, and 1.39 ± 0.07‰, respectively. Type 3 CV chondrite Allende has a δ130Te value of 0.56 ± 0.10‰. Tellurium concentrations were obtained for all four samples via isotope dilution, where BHVO-2, NOD-A-1, NOD-P-1, and Allende display mean Te concentrations of 14.5 ± 0.1 ng g−1, 34.7 ± 0.4 μg g−1, 5.1 ± 0.0 μg g−1, and 970 ± 60 ng g−1, respectively.
The data obtained for BHVO-2, NOD-A-1, and Allende are all in good agreement with the results reported in previous studies. The δ130Te value obtained for NOD-P-1 in this study is consistent with some results obtained for this sample in previous studies, but higher than other published data. However, the large range of δ130Te values reported in the literature for this sample, combined with intra-laboratory variability of δ130Te seen in some previous studies, indicate that NOD-P-1 is somewhat heterogenous in relation to its Te isotope composition.
In addition to the previously categorised samples, this study reports the first precise analysis of the IAB-complex iron meteorite Canyon Diablo obtained using the double spike technique. This study also presents the first mass-dependent Te isotope composition and Te concentration data for the Alexo komatiite KAL-1, which were obtained using the double spike technique and isotope dilution.
The methods developed here hence allow accurate measurements of mass-dependent Te isotope composition in both high- and low-concentration terrestrial and extra-terrestrial samples using MC-ICP-MS. In addition, isotope mass balance and mixing equations were employed to show that possible mass-independent Te isotope effects in meteorites and terrestrial samples are unlikely to have a significant impact on measured δ130Te values at the current level of analytical precision.
Author contributions
MR conceived the study and obtained funding. EMM developed and validated the method. EMM, KK, BJC, and GMP undertook the laboratory and mass spectrometry work. CJ and RM performed the nucleosynthetic Te modelling. EMM performed the NFSE Te modelling and calculated the impact of mass-independent Te isotope anomalies. EMM and MR developed the data reductions, performed the data interpretations, and wrote the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research was supported by UKRI STFC grant ST/W001179/1 to MR and a Hans Rausing PhD studentship to EMM. The authors would like to acknowledge Kirsty Crocket for providing the glacial till, Manuela Fehr for providing NIST SRM 3156 (lot no 892901) and ETH Te, and Jan Hellmann for providing NIST SRM 3156 (lot no 140830). The authors are grateful to the Natural History Museum London for providing the meteorite samples.Notes and references
- B. J. Wood, D. J. Smythe and T. Harrison, Am. Mineral., 2019, 104, 844–856 CrossRef.
- M. A. Fehr, S. J. Hammond and I. J. Parkinson, Geochim. Cosmochim. Acta, 2018, 222, 17–33 CrossRef CAS.
- J. L. Hellmann, T. Hopp, C. Burkhardt and T. Kleine, Earth Planet. Sci. Lett., 2020, 549, 116508 CrossRef CAS.
- J. L. Hellmann, T. Hopp, C. Burkhardt, H. Becker, M. Fischer-Gödde and T. Kleine, Geochim. Cosmochim. Acta, 2021, 309, 313–328 CrossRef CAS.
- A. P. Fornadel, P. G. Spry, S. E. Jackson, R. D. Mathur, J. B. Chapman and I. Girard, J. Anal. At. Spectrom., 2014, 29, 623–637 RSC.
- A. P. Fornadel, P. G. Spry, M. A. Haghnegahdar, E. A. Schauble, S. E. Jackson and S. J. Mills, Geochim. Cosmochim. Acta, 2017, 202, 215–230 CrossRef CAS.
- A. P. Fornadel, P. G. Spry and S. E. Jackson, Ore Geol. Rev., 2019, 113, 103076 CrossRef.
- Y. Fukami, J.-I. Kimura and K. Suzuki, J. Anal. At. Spectrom., 2018, 33, 1233–1242 RSC.
- N. L. Wasserman and T. M. Johnson, J. Anal. At. Spectrom., 2020, 35, 307–319 RSC.
- M. A. Fehr, M. Rehkämper and A. N. Halliday, Int. J. Mass Spectrom., 2004, 232, 83–94 CrossRef CAS.
- F. Wombacher and M. Rehkämper, Geostand. Geoanal. Res., 2004, 28, 173–178 CrossRef CAS.
- M. Rehkämper, F. Wombacher, T. J. Horner and Z. Xue, in Handbook of Environmental Isotope Geochemistry, ed. M. Baskaran, Springer, Berlin, Heidelberg, 2011, pp. 125–154 Search PubMed.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef CAS.
- E. Palk, R. Andreasen, M. Rehkämper, A. Stunt, K. Kreissig, B. Coles, M. Schönbächler and C. Smith, Meteorit. Planet. Sci., 2018, 53, 167–186 CrossRef.
- G. M. Poole, M. Rehkämper, B. J. Coles, T. Goldberg and C. L. Smith, Earth Planet. Sci. Lett., 2017, 473, 215–226 CrossRef CAS.
- K. Murphy, M. Rehkämper, K. Kreissig, B. Coles and T. van de Flierdt, J. Anal. At. Spectrom., 2016, 31, 319–327 RSC.
- X. Wang, C. Fitoussi, B. Bourdon and Q. Amet, J. Anal. At. Spectrom., 2017, 32, 1009–1019 RSC.
- G. A. Brennecka, L. E. Borg, S. J. Romaniello, A. K. Souders, Q. R. Shollenberger, N. E. Marks and M. Wadhwa, Geochim. Cosmochim. Acta, 2017, 201, 331–344 CrossRef CAS.
- M. Berglund and M. E. Wieser, Pure Appl. Chem., 2011, 83, 397–410 CrossRef CAS.
- G. M. Poole, R. Stumpf and M. Rehkämper, J. Anal. At. Spectrom., 2022, 37, 783–794 RSC.
- M. A. Fehr, M. Rehkämper, A. N. Halliday, U. Wiechert, B. Hattendorf, D. Günther, S. Ono, J. L. Eigenbrode and D. Rumble, Geochim. Cosmochim. Acta, 2005, 69, 5099–5112 CrossRef CAS.
- M. A. Fehr, M. Rehkämper, A. N. Halliday, M. Schönbächler, B. Hattendorf and D. Günther, Geochim. Cosmochim. Acta, 2006, 70, 3436–3448 CrossRef CAS.
- M. A. Fehr, M. Rehkämper, A. N. Halliday, B. Hattendorf and D. Günther, Meteorit. Planet. Sci., 2009, 44, 971–984 CrossRef CAS.
- T. Fujii, F. Moynier and F. Albarède, Chem. Geol., 2009, 267, 139–156 CrossRef CAS.
- F. Moynier, T. Fujii and F. Albarède, Meteorit. Planet. Sci., 2009, 44, 1735–1742 CrossRef CAS.
- T. Fujii, F. Moynier and F. Albarede, Earth Planet. Sci. Lett., 2006, 247, 1–9 CrossRef CAS.
- S. Yang and Y. Liu, Acta Geochim., 2016, 35, 227–239 CrossRef CAS.
- M. Méheut, M. Ibañez-Mejia and F. L. H. Tissot, Geochim. Cosmochim. Acta, 2021, 292, 217–234 CrossRef.
- I. Angeli and K. P. Marinova, At. Data Nucl. Data Tables, 2013, 99, 69–95 CrossRef CAS.
- D.-C. Lee and A. N. Halliday, Int. J. Mass Spectrom. Ion Processes, 1995, 146–147, 35–46 CrossRef.
- E. T. Mansur, S. Barnes, D. Savard and P. C. Webb, Geostand. Geoanal. Res., 2020, 44, 147–167 CrossRef CAS.
- Z. Wang and H. Becker, Geostand. Geoanal. Res., 2014, 38, 189–209 CAS.
- Z. Zou, Z. Wang, H. Cheng, T. He, Y. Liu, K. Chen, Z. Hu and Y. Liu, Geostand. Geoanal. Res., 2020, 44, 501–521 CrossRef CAS.
- A. Forrest, R. Kingsley and J.-G. Schilling, Geostand. Geoanal. Res., 2009, 33, 261–269 CrossRef CAS.
- S. König, A. Luguet, J.-P. Lorand, F. Wombacher and M. Lissner, Geochim. Cosmochim. Acta, 2012, 86, 354–366 CrossRef.
- Z. Wang, H. Becker and F. Wombacher, Geostand. Geoanal. Res., 2015, 39, 185–208 CrossRef CAS.
- A. Yierpan, S. König, J. Labidi, T. Kurzawa, M. G. Babechuk and R. Schoenberg, Geochem., Geophys., Geosyst., 2018, 19, 516–533 CrossRef CAS.
- A. Yierpan, S. König, J. Labidi and R. Schoenberg, Geochim. Cosmochim. Acta, 2019, 249, 199–224 CrossRef CAS.
- A. Yierpan, J. Redlinger and S. König, Geochim. Cosmochim. Acta, 2021, 313, 155–172 CrossRef CAS.
- M. D. Axelsson, I. Rodushkin, J. Ingri and B. Öhlander, Analyst, 2002, 127, 76–82 RSC.
- T. Schirmer, A. Koschinsky and M. Bau, Chem. Geol., 2014, 376, 44–51 CrossRef CAS.
- G. G. Goles and E. Anders, Geochim. Cosmochim. Acta, 1962, 26, 723–737 CrossRef.
- L. Bonal, E. Quirico, M. Bourot-Denise and G. Montagnac, Geochim. Cosmochim. Acta, 2006, 70, 1849–1863 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |
