Open Access Article
Open Access ArticleControlling the dynamics of elastomer networks with multivalent brush architectures†
Michika
Onoda
 ab,
Fei
Jia
a,
Yukikazu
Takeoka
b and
Robert J.
Macfarlane
ab,
Fei
Jia
a,
Yukikazu
Takeoka
b and
Robert J.
Macfarlane
 *a
*a
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. E-mail: rmacfarl@mit.edu
bDepartment of Molecular Design and Engineering, Graduate School of Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8603, Japan
First published on 27th April 2022
Abstract
Herein, we report a design strategy for developing mechanically enhanced and dynamic polymer networks by incorporating a polymer with multivalent brush architecture. Different ratios of two types of imidazole functionalized polymers, specifically poly(n-butyl acrylate) (PnBA) and poly(poly(n-butyl acrylate)) (PPnBA) were blended with Zn(II) ions, thereby forming a series of elastomers with consistent composition but varying network topologies. As the weight fraction of PPnBA increased, the melting temperature, plateau modulus, and relaxation time of the melt increased because of the increase in the crosslinking density and coordination efficiency. Remarkably, however, the activation energy of the flow, Ea, decreased with increasing amounts of PPnBA despite the observed increases in mechanical properties. This unique behavior is attributed to the multivalent nature of the brush polymer, which allows the PPnBA to generate a higher crosslinking density than networks of linear PnBA, even though the brush polymers contain a lower weight fraction of the imidazole crosslinks. This method of lowering Ea, while improving the mechanical properties of the elastomers has great potential in the development of various soft materials such as self-healing or 3D-printable elastomeric structures.
Introduction
Bottlebrush polymers (BBPs) with densely grafted side chains have unique properties that are different from those of conventional linear polymers and loosely grafted polymers because of the combination of their large diameters and unentangled backbones that arise from dense grafting of side chains.1,2 The physical properties of BBP elastomers can also be easily tuned due to the large number of design variables available, such as side chain density, side chain length, and backbone length.3 BBPs are thus potentially beneficial for a variety of different functional materials.4–12 For example, by utilizing their non-entangling characteristics and extremely low overlapping concentration, the crosslinking density of BBP networks can be minimized to produce supersoft elastomers.6,7 When hard polymer core domains are introduced to both backbone ends of BBPs, elastomers with mechanical properties comparable to those of various biological materials can be synthesized, enabling their application in biological or biomedical studies.3,9 Furthermore, BBPs have recently been used in the development of self-healing materials,12 soft sensors,10 actuators,8 and 3D-printable materials.13Our group has recently reported the formation of BBP hydrogels by using BBPs as multivalent building blocks; the synthesis of these gels indicated that the BBP architecture potentially leads to unique kinetic behaviors unlike that of similar linear or star polymers.14,15 For example, poly(ethylene glycol) (PEG)-based BBPs with crosslinkable functional groups at the side chain termini formed gels at a rate 100 times faster than four-arm PEG systems at an equivalent concentration.14 This increased rate of gel formation was attributed to the BBPs’ extremely low overlapping concentration, elongated functionalized side chains, and high multivalency. This result suggests that BBP based self-healing materials with excellent processability can be realized if the exchange reactions between the crosslinks are efficient. However, significant questions remain about how the enhanced formation kinetics in these gels affect the dynamicity of the BBP networks, as well as the relationship between the kinetics of network formation and the mechanical behaviors of these materials. Particularly, the difference in thermodynamic physical properties of polymer networks that contain BBPs as a topologically unique building block compared to linear polymer networks have not been explored.
In this study, we investigate the dynamic physical properties of BBP elastomers crosslinked by noncovalent interactions using rheological techniques to explore the thermodynamics and kinetics of supramolecular-bonded BBPs. Furthermore, by mixing these BBPs with different amounts of linear polymers that have the same number of repeat units as the BBP side chains, we are able to tune the network topology and examine its effects on elastomer mechanical response (Fig. 1). We demonstrate that introducing a BBP structure can cause the seemingly contradictory effects of simultaneously decreasing the activation energy of flow (Ea) of an elastomer, while also improving its overall mechanical performance. This study provides insight into new synthesis methods to generate rapidly self-healing or readily processable materials using multivalency to alter the dynamics of network formation.
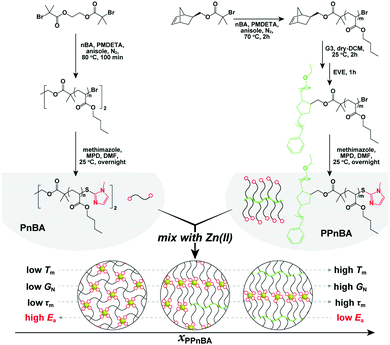 | ||
| Fig. 1 Conceptual illustration of this study and synthesis of the target polymers. Detailed synthetic procedures are provided in the ESI.† | ||
Results and discussion
The target polymers used in this study, poly(n-butyl acrylate) (PnBA) and poly(PnBA) (PPnBA), were synthesized using a combination of atom transfer radical polymerization (ATRP) and ring opening metathesis polymerization (ROMP) followed by end-group functionalization through thioesterification (see Fig. 1, Table 1 and Fig. S1–S3, ESI†). The chain length of the linear polymers and the side-arms of the brush polymers were each synthesized to be ∼5.5 kDa, as this allowed for the chain length of the network strands to be maintained for different mixtures of polymer types. Detailed synthetic procedures of these polymers are provided in the ESI.† To enable dynamic binding, imidazole-Zn(II) coordination bonds were incorporated into the network as noncovalent bonds. Zn(II) was selected for these investigations as it has the weakest and most dynamic interactions (compared with other investigated metal ions such as Ni(II) and Cu(II)).16 The target elastomers were prepared by mixing the two imidazole-functionalized polymers, PnBA and PPnBA, in an acetonitrile/dichloromethane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v)) solution containing zinc di[bis(trifluoromethylsulfonyl)imide] (0.25 eq. with respect to imidazole groups), followed by vacuum-drying at 80 °C for 48 h. The mixtures were prepared such that the relative ratio of imidazole and Zn(II) ions was held constant at 4
1 (v/v)) solution containing zinc di[bis(trifluoromethylsulfonyl)imide] (0.25 eq. with respect to imidazole groups), followed by vacuum-drying at 80 °C for 48 h. The mixtures were prepared such that the relative ratio of imidazole and Zn(II) ions was held constant at 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, regardless of the relative amounts of the brush or linear polymers. This ratio was chosen because it has been previously demonstrated that 4 equivalents of imidazole groups can react with a single Zn(II) ion to produce one crosslinking point.17 Upon incorporating Zn(II) into the polymer blends, a significant increase in their complex viscosity (Fig. S4, ESI†), absorption peak shift (Fig. S5, ESI†), and Fourier-transform infrared (FT-IR) spectral changes (Fig. S6, ESI†) were observed, indicating successful Zn(II)-imidazole coordination.
1, regardless of the relative amounts of the brush or linear polymers. This ratio was chosen because it has been previously demonstrated that 4 equivalents of imidazole groups can react with a single Zn(II) ion to produce one crosslinking point.17 Upon incorporating Zn(II) into the polymer blends, a significant increase in their complex viscosity (Fig. S4, ESI†), absorption peak shift (Fig. S5, ESI†), and Fourier-transform infrared (FT-IR) spectral changes (Fig. S6, ESI†) were observed, indicating successful Zn(II)-imidazole coordination.
| Sample | Polymer formulaa | M n/kDab | Đ |
|---|---|---|---|
| a Abbreviations: imi, 1-methylimidazole; nBA, n-butyl acrylate. Numbers following the abbreviations of monomers indicate the average number of repeating units. b Number-averaged molecular weight of the polymer. The conversion of the monomer to polymer was calculated based on the decrease in the integrated intensity of the 1H-NMR signal of the double bonds of the unreacted monomer before and after polymerization. c Dispersity of polymers, calculated from SEC using tetrahydrofuran as the carrier solvent and calibrated using polystyrene standards. | |||
| PnBA | imi-PnBA45-imi | 5.8 | 1.10 |
| PPnBA | P(PnBA41-imi)50 | 263 | 1.09 |
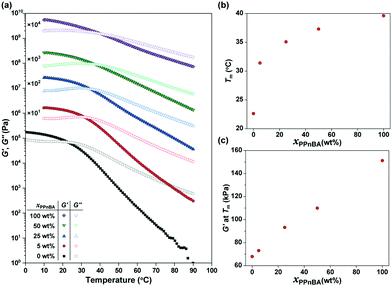
The temperature-dependence of the storage modulus (G′) and loss modulus (G′′) of the PnBA/PPnBA blends was investigated as a function of polymer design (Fig. 2(a)). The melting temperature (Tm) at which G′ and G′′ cross over was observed to shift to a higher temperature as the PPnBA fraction (xPPnBA, wt%) increased (Fig. 2(b)). For example, the Tm at xPPnBA = 0 was 22.6 °C, while the Tm at xPPnBA = 100 wt% was 39.6 °C. Furthermore, the modulus of the elastomer increased with increasing xPPnBA (Fig. 2(c)). In addition, the temperature-dependence of the moduli above Tm decreased as xPPnBA increased, resulting in highly viscous polymer melts (Fig. S7, ESI†). These changes are hypothesized to result from an increase in the overlapping concentration and crosslinking density with the introduction of densely grafted PPnBA with brush architecture, consistent with prior observations.18
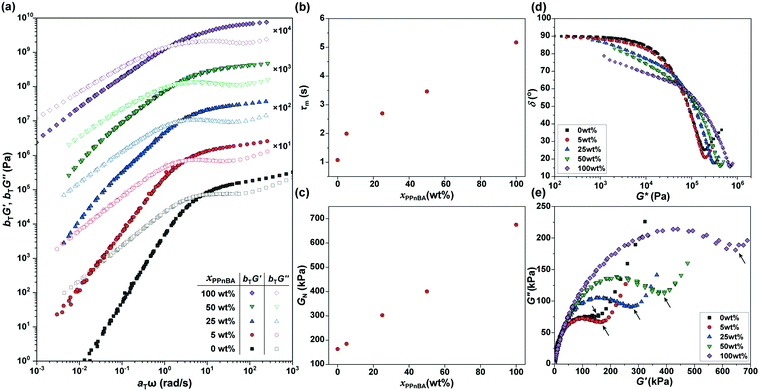
The frequency-dependence of the rheological properties of the elastomers were subsequently probed in order to draw a master curve with a reference temperature of 20 °C (Fig. 3(a)), thereby enabling better examination of how additional BBP quantities affected material mechanical response. In the lower frequency regime, G′ was smaller than G′′, and the slopes of the G′ and G′′ curves for the xPnBA = 100 wt% material in this regime were 2 and 1, respectively, representing the typical rheological behavior of a viscoelastic fluid. However, the slope of the curves decreased as xPPnBA increased, indicating a transformation to highly viscous polymer melts; the slopes of the G′ and G′′ curves at xPPnBA = 100 wt% were 0.89 and 0.73, respectively (Fig. S8, ESI†). These different slopes of G′ and G′′ are common to non-Newtonian fluids of high-molecular-weight polymer melts.19 This behaviour can be explained by the fact that PPnBA has fifty times higher molecular weight and lower overlapping concentration14 compared to PnBA. Furthermore, the PPnBA, which possesses a greater surface area and larger number of imidazole groups per polymer, would be expected to diffuse more slowly as a result of this larger number of potential points of attachment between adjacent bottlebrush polymers.20
For elastomeric samples, the relaxation time of melts (τm) can be calculated from their angular frequency at the cross-over point (ωm):
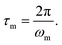 | (1) |
Using these data, the plateau moduli (GN) of the networks were estimated to gain insights into the effect of blending of linear and brush polymers on crosslinking density and coordination efficiency (p). Due to the non-uniform distribution of building blocks in blended systems, we applied a ‘minimum’ method21 to estimate GN, as follows:
| GN = G′(ω)G′→minimum | (2) |
GN = G*(δ)tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ→minimum δ→minimum | (3) |
In addition, considering that the elastomers are composed of two polymer components with large differences in their molecular weights and local imidazole group densities, the distribution of the relaxation time is influenced by xPPnBA. To assess the effect of xPPnBA on the relaxation time, we employed Cole–Cole plots, which are a plots of G′ against G′′.24 In general, a polymer blend shows two arcs in the Cole–Cole plots owing to the existence of two relaxation modes.25 As shown in Fig. 3(e), all the PnBA/PPnBA elastomer samples exhibit two arcs, even at xPPnBA = 0 wt% (i.e., for pure PnBA elastomer). This result suggests that the PnBA elastomer involves the relaxation of the imidazole-Zn(II) dynamic bonds in addition to the relaxation of polymer motion. Furthermore, as xPPnBA increased, the local minimum in the Cole–Cole plot (see the arrows) shifted to the high-viscosity region. This shift suggests that the elastomer has an additional relaxation mode related to the motion of PPnBA.25 Because the percolation of the PPnBA network proceeds with increasing xPPnBA, the upturn was found to significantly shift to the high-viscosity region at xPPnBA = 100 wt%. The existence of multiple relaxation processes was also indicated in the vGP-plot (Fig. 3(d)) as a gradual increase in δ as G* decreases with increasing xPPnBA.26,27 The fact that PnBA and PPnBA elastomers have different relaxation modes motivated us to gain further insights into the thermodynamics of these dynamic polymer interactions, which are predicted to be key to the use of BBPs for self-healing and processable materials.
We therefore estimated the activation energy of flow associated with the glass transition process, Ea, via Arrhenius analysis28 of the viscoelastic response:
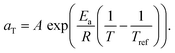 | (4) |
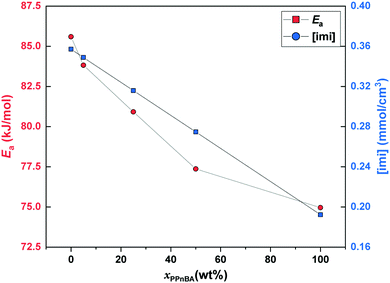 | ||
| Fig. 4 Activation energy of flow (Ea) and mole density of imidazole groups ([imi]) as a function of PPnBA fraction, xPPnBA. | ||
While GN is positively related to the number density of elastically effective network strands, Ea is positively related to the number density of imidazole-Zn(II) coordination bonds that should be broken to acquire fluidity. Here, both chain ends of the linear PnBA are functionalized with imidazole groups. On the other hand, only one end of each side chain of PPnBA is functionalized with an imidazole group, while the other end is covalently bound to the backbone. Therefore, although the number of network strands of both the PnBA and PPnBA networks are equivalent in molecular weight, the concentration of the imidazole groups ([imi]) in each network is different. Indeed, as xPPnBA increased, [imi] decreased monotonically (Fig. 4). Further, the increase of xPPnBA led to the increase of coordination bonds between adjacent side chains, considering the densely grafted polymer architecture of PPnBA. We would note that intramolecular coordination of linear PnBA is negligible because the molecular weight of PnBA is five times smaller than the entanglement molecular weight of PnBA.29 Therefore, while imidazole-Zn coordination between adjacent side chains of PPnBA can decrease Ea, this coordination events can still contribute as mechanically effective crosslinking points because each Zn(II) ion can potentially interact with four imidazole groups.
While the introduction of the brush structure leads to an increase in crosslinking density and thus increased GN, it also leads to a decrease in the number of imidazole-Zn(II) bonds per mass of polymer that need to be broken to enable the material to flow, resulting in the decrease of Ea. Additionally, it should be noted that while [imi] has a linear relationship with xPPnBA, Ea showed an initially rapid decrease followed by a slower decrease as the PPnBA wt% increased. The rapid decrease of Ea can be considered the effect of intramolecular coordination. On the other hand, the increase of xPPnBA leads to increased crosslinking density and coordination efficiency of the building blocks, increasing mechanical stiffness. A slower decrease of Ea would therefore be observed because the network stiffening inhibits the pulling-out of the network strands from imidazole-Zn(II) coordination points.
In general, the activation energy of flow can be referred to as an indicator of processability and self-healing property of the materials. Thus, we conclude that the design strategy of multivalent binding between brush polymers can enhance the bulk material modulus while decreasing Ea could in principle be used to simultaneously improve the processability and mechanical properties of polymeric materials.
Conclusions
In this study, we investigated the physical properties of PnBA/PPnBA mixed elastomers using rheological techniques. As xPPnBA increased, Tm, GN, and τm increased as a result of the multifunctionality of the PPnBA unit, which increased the crosslinking density, but surprisingly decrease Ea. This seemingly contradictory behavior can be attributed to the use of brush polymers causing a decrease in the number density of imidazole groups, but also an increasing in the density of crosslinks. Decreasing Ea is essential for increasing processability of self-healing materials and to ultimately achieve self-healing under ambient conditions. Current self-healing elastomers that include dynamic molecular interactions often sacrifice mechanical robustness in order to achieve processability. Our methodology represents a potential method to achieve processability without compromising mechanical strength and is amenable for methods to further control mechanical properties by controlling the type of binding group, degree of polymerization, or polymer functionality. This design principle should prove useful in developing elastomers with self-healing properties, as such materials often require dynamic molecular interactions that make it difficult to balance mechanical robustness and processability.17,30Author contributions
M. O. performed all experiments and authored the manuscript. F. J., Y. T., and R. J. M. conceived the study, as well as authored the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a NSF CAREER grant, Award Number CHE-1653289. This work is supported by the MRSEC Program of the National Science Foundation under award DMR 1419807 and made use of the MRSEC Shared Experimental Facilities at MIT, and the JSPS KAKENHI Grant Numbers 16J09350 and 20K15341.References
- R. Verduzco, X. Li, S. L. Pesek and G. E. Stein, Chem. Soc. Rev., 2015, 44, 2405–2420 RSC.
- S. L. Pesek, X. Li, B. Hammouda, K. Hong and R. Verduzco, Macromolecules, 2013, 46, 6998–7005 CrossRef CAS.
- M. Vatankhah-Varnosfaderani, W. F. M. Daniel, M. H. Everhart, A. A. Pandya, H. Liang, K. Matyjaszewski, A. V. Dobrynin and S. S. Sheiko, Nature, 2017, 549, 497–501 CrossRef PubMed.
- D. Neugebauer, Y. Zhang, T. Pakula, S. S. Sheiko and K. Matyjaszewski, Macromolecules, 2003, 36, 6746–6755 CrossRef CAS.
- T. Pakula, Y. Zhang, K. Matyjaszewski, H. Lee, H. Boerner, S. Qin and G. C. Berry, Polymer, 2006, 47, 7198–7206 CrossRef CAS.
- L. Cai, T. E. Kodger, R. E. Guerra, A. F. Pegoraro, M. Rubinstein and D. A. Weitz, Adv. Mater., 2015, 27, 5132–5140 CrossRef CAS PubMed.
- W. F. M. Daniel, J. Burdyńska, M. Vatankhah-Varnoosfaderani, K. Matyjaszewski, J. Paturej, M. Rubinstein, A. V. Dobrynin and S. S. Sheiko, Nat. Mater., 2016, 15, 183 CrossRef CAS PubMed.
- M. Vatankhah-Varnoosfaderani, W. F. M. Daniel, A. P. Zhushma, Q. Li, B. J. Morgan, K. Matyjaszewski, D. P. Armstrong, R. J. Spontak, A. V. Dobrynin and S. S. Sheiko, Adv. Mater., 2017, 29, 1604209 CrossRef PubMed.
- M. Vatankhah-Varnosfaderani, A. N. Keith, Y. Cong, H. Liang, M. Rosenthal, M. Sztucki, C. Clair, S. Magonov, D. A. Ivanov, A. V. Dobrynin and S. S. Sheiko, Science, 2018, 359, 1509–1513 CrossRef CAS PubMed.
- V. G. Reynolds, S. Mukherjee, R. Xie, A. E. Levi, A. Atassi, T. Uchiyama, H. Wang, M. L. Chabinyc and C. M. Bates, Mater. Horizons, 2019, 7, 181–187 RSC.
- M. Abbasi, L. Faust and M. Wilhelm, Adv. Mater., 2019, 31, 1806484 CrossRef PubMed.
- J. L. Self, C. S. Sample, A. E. Levi, K. Li, R. Xie, J. R. de Alaniz and C. M. Bates, J. Am. Chem. Soc., 2020, 142, 7567–7573 CrossRef CAS PubMed.
- R. Xie, S. Mukherjee, A. E. Levi, V. G. Reynolds, H. Wang, M. L. Chabinyc and C. M. Bates, Sci. Adv., 2020, 6, eabc6900 CrossRef CAS PubMed.
- F. Jia, J. M. Kubiak, M. Onoda, Y. Wang and R. J. Macfarlane, Adv. Sci., 2021, 8, e2100968 CrossRef PubMed.
- F. Jia, J. Song, J. M. Kubiak, M. Onoda, P. J. Santos, K. Sano, N. Holten-Andersen, K. Zhang and R. J. Macfarlane, Chem. Mater., 2021, 33, 5748–5756 CrossRef CAS.
- J. E. Bauman and J. C. Wang, Inorg. Chem., 1964, 3, 368–373 CrossRef CAS.
- D. Mozhdehi, S. Ayala, O. R. Cromwell and Z. Guan, J. Am. Chem. Soc., 2014, 136, 16128–16131 CrossRef CAS PubMed.
- J. Paturej and T. Kreer, Soft Matter, 2017, 13, 8534–8541 RSC.
- O. O. Mykhaylyk, C. M. Fernyhough, M. Okura, J. P. A. Fairclough, A. J. Ryan and R. Graham, Eur. Polym. J., 2011, 47, 447–464 CrossRef CAS.
- A. Shabbir, H. Goldansaz, O. Hassager, E. van Ruymbeke and N. J. Alvarez, Macromolecules, 2015, 48, 5988–5996 CrossRef CAS.
- C. Liu, J. He, E. van Ruymbeke, R. Keunings and C. Bailly, Polymer, 2006, 47, 4461–4479 CrossRef CAS.
- M. van Gurp and J. Palmen, Rheol. Bull., 1998, 67, 5–8 Search PubMed.
- Z. Qian and G. B. McKenna, Polymer, 2018, 155, 208–217 CrossRef CAS.
- T. Mezger, The Rheology Handbook, Vincentz Network, Hanover, Germany, 2020 Search PubMed.
- D. Wu, L. Wu, Y. Sun and M. Zhang, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 3137–3147 CrossRef CAS.
- S. Trinkle and C. Friedrich, Rheol. Acta, 2001, 40, 322–328 CrossRef CAS.
- M. A. Kanso and A. J. Giacomin, Phys. Fluids, 2020, 32, 033101 CrossRef CAS.
- F. Tanaka and S. F. Edwards, J. Non-Newton Fluid, 1992, 43, 247–271 CrossRef CAS.
- J. D. Tong and R. Jerôme, Polymer, 2000, 41, 2499–2510 CrossRef CAS.
- Y. Chen, A. M. Kushner, G. A. Williams and Z. Guan, Nat. Chem., 2012, 4, 467–472 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00328g |
| This journal is © The Royal Society of Chemistry 2022 |