Open Access Article
Open Access ArticleHygroscopicity of polycatechol and polyguaiacol secondary organic aerosol in sub- and supersaturated water vapor environments†
Kotiba A.
Malek
 a,
Kanishk
Gohil
a,
Kanishk
Gohil
 a,
Hind A.
Al-Abadleh
a,
Hind A.
Al-Abadleh
 *b and
Akua A.
Asa-Awuku
*b and
Akua A.
Asa-Awuku
 *ac
*ac
aDepartment of Chemical and Biomolecular Engineering, University of Maryland, College Park, MD 20742, USA
bDepartment of Chemistry and Biochemistry, Wilfrid Laurier University, Waterloo, ON N2L 3C5, Canada. E-mail: halabadleh@wlu.ca
cDepartment of Chemistry and Biochemistry, University of Maryland, College Park, MD 20742, USA. E-mail: asaawuku@umd.edu
First published on 23rd November 2021
Abstract
Polycatechol and polyguaiacol are light-absorbing and water-insoluble particles that efficiently form from iron-catalyzed reactions with aromatic compounds from biomass burning emissions. Little quantitative information is known about their water uptake and cloud or haze droplet formation ability. In this study, polycatechol and polyguaiacol particles were synthesized in the laboratory, and their cloud condensation nucleation efficiencies were investigated under sub- and supersaturated relative humidity (RH) conditions using a hygroscopicity tandem differential mobility analyzer (H-TDMA) and a cloud condensation nuclei counter (CCNC), respectively. Experimental results show that both polymeric materials are slightly hygroscopic and that their single hygroscopicity parameter (κ) ranges from 0.03 to 0.25, which is within the κ range for secondary organic aerosols (SOA). Polycatechol is more hygroscopic than polyguaiacol, which is explained by differences in their structure. Polyguaiacol has similar water uptake as other insoluble organic compounds, and droplet formation is modelled well with Brunauer–Emmett–Teller (BET) or Frankel Hill Hershey-Adsorption Isotherm theory (FHH-AT). Both polymeric materials are not strongly surface active in range of 0.5 to 30 g L−1, and thus differences in subsaturated and supersaturated hygroscopicity measurement are not attributed to the presence of surface-active materials. Instead, it is due to the solubility limits of both chemicals and H-TDMA being driven by water adsorption. The implications of these results are discussed in the context of aerosol–cloud interactions from the hygroscopicity of aerosols from primary and secondary sources.
Environmental significanceBiomass burning is a major source of aerosols in the atmosphere but their contribution to the radiative budget of the Earth is poorly understood. This is partly due to our poor understanding of the secondary aerosol composition of biomass burning particles. To enhance our knowledge on biomass-emitted aerosols, two prominent water-insoluble organic aerosols, polycatechol and polyguaiacol SOA, were investigated. Their hygroscopic properties were evaluated under subsaturated and supersaturated environments, and their single hygroscopicity parameter was reported. Our results show that both SOA are slightly hygroscopic with polycatechol SOA having a higher hygroscopicity than polyguaiacol SOA. The difference in hygroscopicity is attributed to the presence of hydroxyl functional groups in polycatechol SOA. Thus a seemingly small difference in aerosol functional groups can change the mechanism for water uptake (adsorption vs. dissolution) and must be measured to predict climate and understand environmental impacts. |
1. Introduction
Atmospheric aerosol particles are composed of mixtures of organic and inorganic species.1 Aerosol can affect the Earth's radiative budget through their direct and indirect interactions with solar radiation. The direct effect involves the scattering or absorption of light by aerosol particles; while the indirect effect describes the interactions of aerosols with clouds and their ability to absorb water, act as cloud condensation nuclei (CCN), and form droplets.2–4 The degree to which aerosol uptake water (hygroscopicity) and form cloud droplets has significant impact on air quality and climate.2 While the hygroscopic properties of inorganic aerosol are well studied and characterized, the hygroscopic properties of atmospherically ubiquitous organic species are poorly understood.5,6Biomass burning is a major source of atmospheric organic aerosols,7–9 which emits a wide variety of gases, namely semi-volatile organic compounds (SVOCs), that have major implications on atmospheric chemistry.9 Catechol and guaiacol are two phenolic SVOCs readily released from the combustion of biogenic sources.10–12 The fate of these organic compounds includes several reactions and processes that may change the chemical composition, hygroscopicity, and optical properties of atmospheric aerosols. Examples of these oxidation pathways include those driven by oxidants such as OH, O3, NO3, and those catalyzed by transition metals like Iron (Fe).11,13,14 Fe is an abundant component of mineral dust.15,16 Combustion sources are increasingly being recognized as major contributors to labile iron deposited on the oceans.17 Processing of these Fe-containing particles takes place in the atmosphere through reactions with acidic gases, organics, in the dark or under irradiation, changing the hygroscopicity of these particles and increasing the amount of dissolved iron.14 The processed iron-containing particles can act as a sink for SVOCs and undergo mixing with biomass burning organic aerosol (BBOA) containing derivatives of catechol and guaiacol. The role of Fe in condensed phase transformation of phenolic organic compounds in aerosol particles has recently been reviewed18 where it was shown that Fe can convert catechol and guaiacol into light-absorbing and water-insoluble particles, namely polycatechol and polyguaiacol, respectively.11,14,19–21 Thus, polycatechol and polyguaiacol could be considered secondary organic aerosol (SOA) that form due to aerosol aging of Fe-containing particles under conditions relevant to cloud droplets and aerosol particles.
Previous work has explored the physical aerosol properties of polycatechol and polyguaiacol SOA, the light-absorbing and ice nucleation characteristics.11,20,21 To our knowledge, only one previous study has explored the surface water properties of polycatechol and polyguaiacol SOA with diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) and quartz crystal microbalance (QCM).19 The structure of surface water, investigated by DRIFTS showed evidence of water bonding with organic functional groups in these polymeric materials from the analysis of water and organic vibrational modes. In addition, spectroscopic data showed a network of weak and strong hydrogen bonding, which suggested the formation of water–water and water–organic interactions.19 The QCM studies conducted as a function of relative humidity (RH) showed that gas phase water is best described using a modified Type II multilayer BET adsorption model, and that polycatechol exhibits stronger water–surface interactions that polyguaiacol. These QCM studies were conducted on thin films of these materials. There is still the need to obtain quantitative data on the CCN and droplet formation efficiencies of polycatechol and polyguaiacol under atmospherically relevant conditions for comparison with other SOA formed from metal-free reactions.
The objective of this study is to measure the hygroscopic properties of polycatechol and polyguaiacol SOA under subsaturated and supersaturated conditions, and to quantify their surface activity using surface tension measurements. Specifically, we measured the droplet growth of laboratory synthesized polycatechol and polyguaiacol SOA in a supersaturated environment using a cloud condensation nuclei counter (CCNC), and in a subsaturated environment with a hygroscopicity tandem differential mobility analyzer (H-TDMA). The measurement data were then used to derive critical parameters for aerosol water uptake. Assuming classic Köhler theory, the single hygroscopicity parameter (κ) was calculated from the two measurement techniques and compared. Additionally, the aerosol was assumed to be water insoluble, and two water-adsorption theories are applied to infer water surface coverage and adsorption isotherm parameters to predict droplet growth. Surface tension was also measured and provided additional information regarding SOA surface activity at the droplet air–water interface. Overall, the results of this study highlight the importance of structural characterization of SOA from different sources to improve our understanding of their hygroscopic properties and surface reactivity, and hence better predictions of aerosol–cloud interactions.
2. Experimental and data analysis methodology
2.1 Chemicals
All the chemicals were used as received without further purification: catechol (1,2-benzendiol, >99%, CAS 120-80-9, Sigma-Aldrich), guaiacol (2-methoxyphenol, ≥98%, CAS 90-05-1, Sigma-Aldrich), iron(III) chloride hexahydrate (FeCl3·6H2O, 97%, CAS: 10025-77-1, Sigma-Aldrich), and diamond powder (5 ± 2 μm, Lands Superabrasives LST600T). The chemicals were dissolved in Milli-Q water (18.5 MΩ cm) with the solutions' ionic strength adjusted to 0.01 M by adding potassium chloride (KCl powder, 99.5%, EM Science) to stabilize the pH reading. The pH was adjusted using stock solutions of hydrochloric acid (HCl 6 N, Ricca Chemical Company) and sodium hydroxide (NaOH pellets, 99–100%, EMD) when needed.2.2 Particle synthesis
The synthesis procedure of polycatechol and polyguaiacol was based on the procedure in an earlier report with slight modifications.19 Briefly, aqueous phase standard solutions of iron chloride, catechol and guaiacol were prepared by dissolving the chemicals in Milli-Q water. To prepare polycatechol, the concentration of the catechol was 0.078 M in 40 mL, to which 1 mL of the iron chloride solution (6.4 M) was added to start the reaction in the dark for 1 h. To prepare polyguaiacol, the concentration of the guaiacol was 0.068 M in 40 mL, to which 1 mL of the iron chloride solution (5.6 M) was added to start the reaction in the dark for 1 h. In both cases, the final iron to organic molar ratio was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and pH was 3. At the end of the reaction, reaction solutions containing the particles were centrifuged, supernatant discarded, and the particles were resuspended in Millipore water. Then, the centrifugation and resuspension step were repeated one more time, with supernatant discarded, to remove soluble reactants and to redisperse the particles in water only.
1 and pH was 3. At the end of the reaction, reaction solutions containing the particles were centrifuged, supernatant discarded, and the particles were resuspended in Millipore water. Then, the centrifugation and resuspension step were repeated one more time, with supernatant discarded, to remove soluble reactants and to redisperse the particles in water only.
2.3 Aerosol synthesis and generation
After synthesis, a 1 mL solution (approx. 0.03 g) was diluted in 300 mL of ultra-purified water (18 MΩ cm, Millipore). A 0.1 g L−1 solution was sonicated and heated in a water bath (30 °C) during aerosol generation with a Collison Nebulizer (Atomizer; TSI 3076). Wet aerosols were then passed through a silica gel dryer to remove particle moisture (<5% RH). The subsequent aerosol distribution is then measured with the following H-TDMA or CCNC setup (Fig. 1).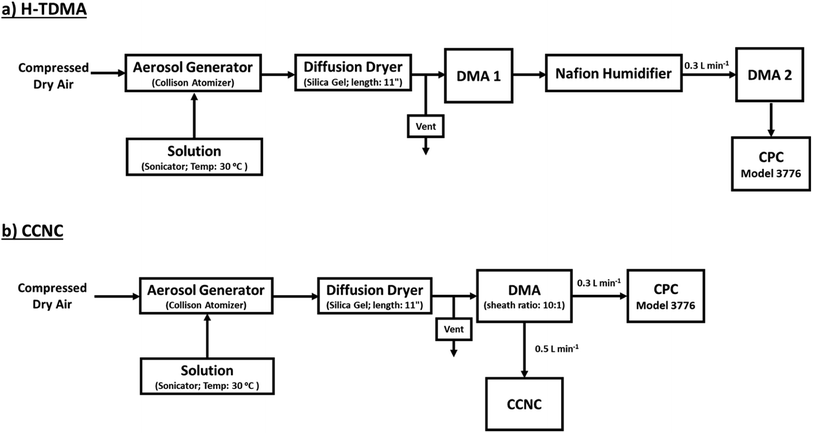 | ||
| Fig. 1 A detailed experimental setup for (a) H-TDMA subsaturated κ measurements and (b) CCNC supersaturated κ measurements. | ||
2.4 H-TDMA – subsaturated measurements
A hygroscopicity tandem differential mobility analyzer (H-TDMA) measured the subsaturated growth factor of polycatechol and polyguaiacol SOA. The H-TDMA is widely used and measures aerosol hygroscopicity under subsaturated conditions. The experimental setup has been described in previous literature.22–24 A description of our H-TDMA setup is shown in Fig. 1. After particle generation, the polydisperse dried particles were charged in a Kr-85 bipolar aerosol neutralizer (TSI 3081) resulting in an equilibrium distribution of charges.25 Charged particles are then passed through a differential mobility analyzer (DMA 1) where aerosols were size selected (25–120 nm) with an electrostatic classifier (TSI 3081). The flow rate and the sheath flow were maintained at 0.3 L min−1 and 3.0 L min−1, respectively. The size-selected particles were then exposed to up to 85% RH with a Nafion humidification line (PermaPure M.H series). After humidification, aerosol particles were passed through an RH equilibrated second DMA (TSI 3081). This second DMA is followed by a condensation particle counter (CPC, TSI 3776) and the wet aerosol size distribution and concentration were measured. The RH of H-TDMA setup was determined by ammonium sulfate calibration (see Fig. S1;† Taylor et al.26). Growth factors (Gf) were obtained by dividing the median wet particle diameter (DMA 2) by the size selected dry particle diameter (DMA 1).16,27,28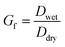 | (1) |
2.5 CCNC – supersaturated measurements
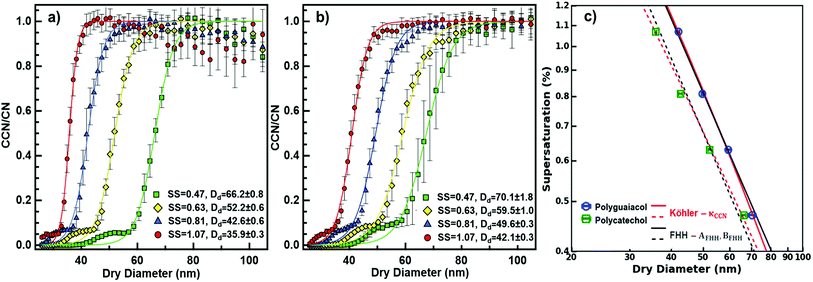
A cloud condensation nuclei counter (CCNC, Droplet Measurement Technologies29,30) measured the droplet activation of polycatechol and polyguaiacol aerosol. A detailed setup is provided in Fig. 1. The Scanning Mobility CCN Analysis (SMCA) method was used and has been extensively applied to CCN analysis in the literature (e.g., but not limited to Engelhart at al;31 Asa-Awuku et al.32 Moore et al.33 Tang et al.34 Tang et al.35 Barati et al.36 Vu et al.37). Briefly described here, the DMA was operated in scanning mode and a size distribution from 8.06 to 352.3 nm was measured every 2.25 minutes. The aerosol stream exiting the DMA was then simultaneously split into two streams: a 0.3 L min−1 stream to the CPC (TSI 3776) where concentration of particles (CN) was measured, and a 0.5 L min−1 stream to the CCNC where number concentration of activated particles was measured (CCN). Using the SMCA, the doubly-charge and triply-charged particles were removed using a charge correction expression from Wiedensohler (1988).25 Additional data regarding SMCA charge corrections are provided in the ESI.† After the data has been charged corrected, the CCN to CN activation ratio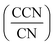 was calculated at every supersaturation.33 A sigmoidal fit was then applied through the activation ratio to obtain the critical diameter, Dd; the size at which 50% of all the particles were activated. Each activation ratio is repeated ten times and the average and standard deviation were reported. Furthermore, the Dd of polycatechol and polyguaiacol SOA were measured at four different supersaturations (0.47, 0.63, 0.81, and 1.07%). The CCNC's supersaturation was calibrated with ammonium sulfate (see Table S1 and Fig. S2†).
was calculated at every supersaturation.33 A sigmoidal fit was then applied through the activation ratio to obtain the critical diameter, Dd; the size at which 50% of all the particles were activated. Each activation ratio is repeated ten times and the average and standard deviation were reported. Furthermore, the Dd of polycatechol and polyguaiacol SOA were measured at four different supersaturations (0.47, 0.63, 0.81, and 1.07%). The CCNC's supersaturation was calibrated with ammonium sulfate (see Table S1 and Fig. S2†).
2.6 Surface tension measurements
Surface tension measurements were obtained with a pendant drop tensiometer (Theta optical tensiometer with One Attention software®). Solutions of different concentrations (in the range of 0.35–50 g L−1) were achieved by diluting stock solution with Millipore ultra-purified water (<18 MΩ cm). Once desired concentrations were prepared, solutions were sonicated at room temperature and drawn using a microneedle syringe. A drop of approximately 10 μL is then suspended, and once equilibrium is reached, the pendant drop tensiometer camera captured more than 100 images at a rate of 33 frames per second. Each image represents one surface tension measurement. For each concentration, an average of surface tensions measurement and standard deviation is reported. Ultra-purified water's surface tension was measured and used as a baseline for calibration.2.7 Water uptake and hygroscopicity analysis
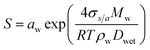 | (2) |
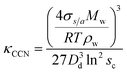 | (3) |
κ-values from subsaturated H-TDMA measurements can also be derived from Gf and RH data. At relative humidity greater than 80%, the vapor pressure of water is assumed to approach that of a flat surface and the droplet water activity to be approximated with RH. It is also noted that this assumption is commonly applied to particle sizes greater than 200 nm;38 however, the linearity of wet diameters to dry diameters within our data suggests that this assumption can also be applied to lower sizes and RH >80% for the specific materials studied here. κ can be obtained using the following simplified equation:16,27
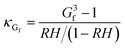 | (4) |
For H-TDMA data, the best fit and average κ is reported as κGf. The κGf value can then be directly compared to the hygroscopic growth derived from supersaturated measurements κCCN.
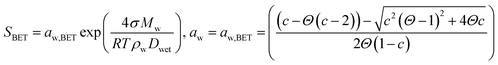 | (5) |
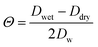 | (6) |
Like BET, in Frenkel-Halsey-Hill Adsorption theory (FHH-AT) aw is directly related to the water surface coverage. The adsorbed multilayer formation on aerosol particles in FHH-AT accounts for a varying potential adsorption gradient along the thickness of the adsorbed water layer on the particle surface. In FHH-AT framework, water activity is defined as,16,41,42
| aw = aw,FHH = exp(−AFHHθ−BFHH) | (7) |
From our data sets, the FHH parameters can be computed in the supersaturated environment. Specifically, it is a common practice to relate the measured sc and Dd data using a power law which is represented as sc = CDdry,50x, where C and x are fit parameters that depend on the measured activation data.42,43 It should also be noted that in Köhler theory x is fixed to −1.5 for soluble particles and FHH allows the slope to vary. The empirical fits of AFHH and BFHH are then fit to the experimental data. This method has been applied in previous studies of mineral dust and black carbon and has yet to be applied to insoluble SOA.
3. Results and discussion
The critical diameters (Dd) were measured for polycatechol and polyguaiacol SOA at varying supersaturations (0.47, 0.63, 0.81, and 1.07%). The CCN activation data obtained from SMCA analysis are shown in Fig. 2. A charge correction is applied to the data; however, it has been noted that this does not lead to a complete removal of the visible influence of the multiply charged particles on the activation curves. Our analysis accounts for this affect and the activation diameters, determined by a sigmoidal fit, reflect activation of the singly charged particles. For both SOAs, the Dd is shown to decrease with increasing supersaturations (Fig. 2a and b). In addition, the FHH adsorption theory was applied to polycatechol and polyguaiacol CCN activity (Fig. 2c). The FHH parameters (AFHH and BFHH) were determined by fitting eqn (S9) (see ESI†) to the CCN experimental data via least squares minimization. The parameters AFHH and BFHH were found to be 0.70 and 0.81 for polycatechol and 0.31 and 0.56 for polyguaiacol. The sc and Dd polycatechol and polyguaiacol data were also fit to Köhler theory (Fig. 2c). The Köhler fit adheres to the Köhler slope of ∼ −3/2,38 while the exponent in the FHH model is not fixed.41 Both the Köhler and FHH model appear to fit with experimental data (Fig. 2c).To understand the hygroscopicity of polycatechol and polyguaiacol SOA under subsaturated conditions, the aerosol growth factor was measured at constant RH (Fig. 3). The average Gf value for polycatechol at 85% RH was 1.15 ± 0.07, while that for polyguaiacol was 1.04 ± 0.03 at 80% RH. This result indicates polycatechol and polyguaiacol are slightly hygroscopic with little water uptake. The result is consistent with Varutbangkul et al.44 where hygroscopic growth factors of various simple and substituted phenolic compounds were investigated.44 Their study reported Gf between 1.09–1.16 for pure organics C5–C8 cycloalkenes, Gf between 1.06–1.10 for monoterpenes and oxygenated terpenes SOAs, and Gf between 1.01–1.04 for the sesquiterpenes SOAs, at 85% RH.44 The polycatechol and polyguaiacol Gf values obtained in this study were then converted to κ using eqn (4). The κGf for polycatechol and polyguaiacol is 0.12 ± 0.05 and 0.03 ± 0.02, respectively.
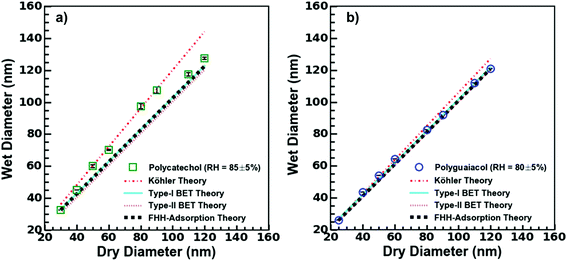 | ||
| Fig. 3 H-TDMA measurements and analysis. Type-I, type-II BET, Köhler model, and FHH model fits to (a) polycatechol and (b) polyguaiacol from experimental hygroscopicity measurements. | ||
The wet diameter for polycatechol and polyguaiacol was predicted with four different models: the Köhler theory, Type-I BET, Type-II BET, and FHH models. For each model, the χ2 was computed to assess goodness of fit (Table 1). Considering that both polycatechol and polyguaiacol are sparingly-soluble, our results show an association to both the Köhler model—that assumes full dissolution, and the FHH model—that assumes no dissolution. Either model can be applied with some degree of deviation from the experimental data sets. Furthermore, there is an observation of model agreement with aerosol size dependence that remains to be resolved. For instance, the Köhler model, which was generated using average experimental κGf, align to the polycatechol and polyguaiacol subsaturated date set with a χ2 value of 4.1 and 4.6, respectively (Fig. 3 and Table 1).
| Model | χ 2 | |
|---|---|---|
| Polycatechol | Polyguaiacol | |
| Köhler theory | 4.1 | 4.6 |
| Type-I BET | 7.3 | 0.3 |
| Type-II BET | 9.2 | 1.0 |
| FHH | 7.7 | 0.6 |
The Type-I BET line was derived using eqn (5) above, while the Type-II BET theory line was developed from parameters published in Rahman and Al-Abadleh19 for which 3 parameters were derived from QCM measurements.19 The Type-I and Type-II BET theory derived from different measurement platforms agree with each other (Fig. 3). The χ2 metric gave slightly different, but low values for polyguaiacol (Fig. 3b and Table 1) with respect to Type-I (0.3) and Type-II (1.0) variants of the BET adsorption model. The relatively low values of χ2 metrics suggested that either of Type-I or Type-II models can be more reliably used compared to Köhler model to describe the hygroscopicity of polyguaiacol. The χ2 metric for polycatechol (Fig. 3a and Table 1) were found to be much larger in both Type-I (7.3) and Type-II (9.2) models than the values obtained for polyguaiacol. On comparing these χ2 values against those for Köhler model fit, it can be concluded that the Köhler model is better representative of polycatechol hygroscopicity. In addition, FHH parameters derived from supersaturated CCN fits (Fig. 2c) can be compared to subsaturated data (Fig. 3). The FHH predictions of wet particle diameter agree with Type-I and Type-II BET models for both polycatechol and polyguaiacol. For the FHH model, the χ2 for polycatechol and polyguaiacol were 7.7 and 0.6, respectively (Table 1). As with the BET models, the FHH prediction agrees well with the H-TDMA polyguaiacol data set more than the polycatechol data set. A noteworthy observation is that despite using the FHH parameters (AFHH and BFHH) derived from CCN activity, FHH model agrees well with H-TDMA measurements (Fig. 3). Pajunoja et al.45 highlighted that H-TDMA water uptake activity of semisolid SOAs is driven by water adsorption rather than dissolution. This supports the results of Fig. 3; the FHH model agrees with polycatechol and polyguaiacol H-TDMA measurements and can be attributed to the sparingly soluble properties of the SOA and the FHH model assuming no dissolution. This apparent association between FHH model and H-TDMA data indicates that the FHH parameters do not need to be exclusively derived from CCN measurements.
Fig. 4 shows the average κ-values under sub- and supersaturated conditions for polycatechol and polyguaiacol calculated from eqn (3) and (4). Both compounds are slightly hygroscopic with κ-values between 0.03-0.25. The average κCCN across all supersaturations for polycatechol and polyguaiacol were calculated to be 0.25 ± 0.03 and 0.16 ± 0.01, respectively. As stated above, the average κGf was 0.13 ± 0.05 (85% RH) for polycatechol and 0.03 ± 0.02 (80% RH) for polyguaiacol.
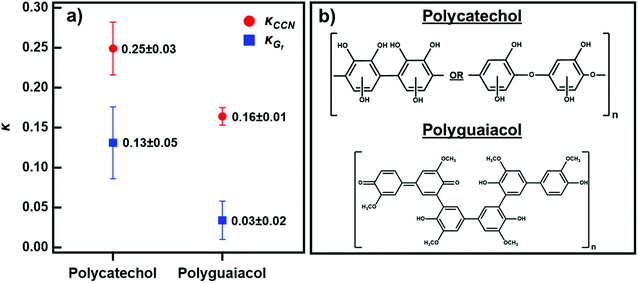 | ||
| Fig. 4 (a) The average κCCN (red circles) and κGf (blue circles) of polycatechol and polyguaiacol. Error bars represent standard deviation. (b) The chemical structures of polycatechol and polyguaiacol adapted from Al-Abadleh.14 | ||
To our knowledge, no previous studies have reported hygroscopicity values for these two aerosol species. The κCCN and κGf reported here are within the range of other SOA hygroscopicity values. This is consistent with organic aerosols having a known kappa value less than 0.3.46 Polycatechol is more hygroscopic than polyguaiacol under sub-and supersaturated environments. The higher κCCN and κGf for polycatechol relative to polyguaiacol can be attributed to the molecular difference between these two chemicals. Polycatechol has a higher density of hydroxyl groups that have strong water affinity compared to the methyl groups present in polyguaiacol.14 This is supported by the work of Rahman and Al-Abadleh19 which offered evidence, through DRIFTS, of strong water bonding with organic functional groups. Polycatechol was shown to have a higher affinity for water than polyguaiacol.19 In agreement with the chemical speciation and the previously published work, a small change from O–H to O–CH3 groups attached to the benzene ring has noticeable effects in the water uptake and droplet formation ability (Fig. 4).
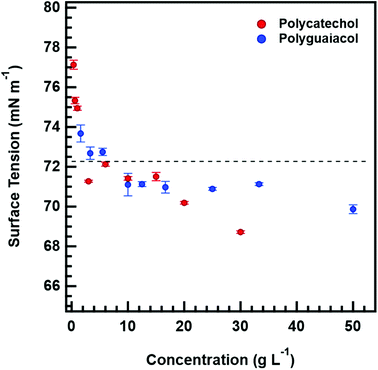
Fig. 4 also shows that κCCN are higher than κGf for both polycatechol and polyguaiacol. While other studies have also observed higher CCN-derived kappa values, they have generally attributed this to surface tension depression by surface active organic molecules.27,47–49 Polycatechol κCCN and polyguaiacol κCCN were computed with the assumption that the surface tension is equal to that of pure water. Typically, differences in measured sub- and supersaturated hygroscopicity κ-values are attributed to surface tension activity that can lower droplet vapor pressure in the supersaturated regime.50 However, the surfactant effect is negligible (less than a 3% depression) for both compounds in water as shown below in the discussion of Fig. 5. The surface tension values measured for both polycatechol and polyguaiacol indicate both species are not strongly surface active within the concentration range of 0.35–50 g L−1. If higher concentrations can be obtained, surface tension at the droplet may be depressed further. Yet both polycatechol and polyguaiacol are sparingly soluble to insoluble organic materials in water and the measured concentrations in Fig. 5 are likely near their respective solubility limits in water.
An alternative justification, apart from the effect of surfactants,47–49 to the difference observed in κCCN and κGf in Fig. 4 is due to the limited solubility of the aerosol solute. A study by Pajunoja et al.45 suggested that the difference between κCCN and κGf is due to SOAs exhibiting adsorption-dominated water uptake under subsaturated conditions. Another finding was that the difference between the κCCN and κGf diminishes with the increase of oxygen particles, a trend observed in our results. The difference in polycatechol's κCCN and κGf is smaller than the difference between polyguaiacol's κCCN and κGf. Polycatechol has higher density of hydroxyl groups than polyguaiacol as evidenced in their molecular structures (Fig. 4).
Fig. 6 considers the non-surface-active droplet formation of a 60 nm polycatechol or polyguaiacol particle exposed to an increasing RH. For both SOAs, the differences in activation assuming κCCN and κGf are very different. More specifically, for polyguaiacol SOA, a supersaturation above 1% is required to activate assuming κGf, but only a 0.5% supersaturation is required to activate assuming κCCN. Furthermore, at subsaturated conditions, the wet diameter is substantially larger assuming κCCN. When the FHH fit is applied to the droplet growth for polyguaiacol, the subsaturated growth behaves like the H-TDMA growth (< than sc; the black and blue lines agree); the sc for FHH is the same as that from Köhler curve (red line) and thus the approximation for droplet growth then agrees with Köhler theory. Polycatechol does not follow the same trend. Polycatechol has a greater hygroscopicity than polyguaiacol likely due to the density of surface hydroxyl groups. Hence, the application of FHH theory does not describe the water uptake on polycatechol well; both the droplet growth curves from κGf and κCCN predict greater wet diameters than that of FHH. Polycatechol SOA is more likely to provide hydrogen bonding acceptor and donor sites and contribute to droplet growth and FHH assumes an insoluble particle where adsorption is the main driver for droplet formation.45 In brief, Köhler theory can be used to predict polycatechol SOA droplet formation and FHH should be applied to polyguaiacol SOA. Such a conclusion highlights the importance of identifying the contribution of polycatechol versus polyguaiacol fractions to ambient SOA in understanding the overall droplet growth mechanisms and predictions of droplet growth.
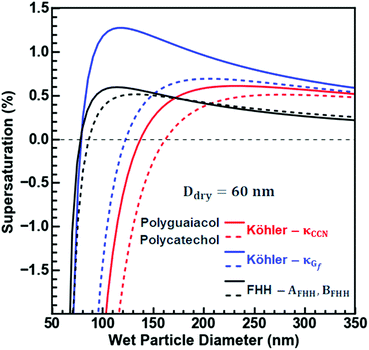 | ||
| Fig. 6 FHH-Adsorption Theory (FHH-AT) and Köhler theory (KT) equilibrium curves are plotted for polycatechol and polyguaiacol for 60 nm dry particles. The FHH-AT curves (solid lines) were plotted using the FHH parameters determined from the CCN measurements (Fig. 2c). κTCCN curves (dashed lines) were plotted using their hygroscopicity parameters (κ) determined from the CCN measurements. κTGf curves (dashed-dot lines) were plotted using their hygroscopicity parameters (κ) determined from the H-TDMA measurements. | ||
4. Summary and implications
The sub- and supersaturated hygroscopic properties of biomass derived SOA namely, polycatechol and polyguaiacol were investigated. For subsaturated conditions, the H-TDMA system measured the growth factor at relative humidity greater than 80%. For supersaturated conditions, the hygroscopicity of polycatechol and polyguaiacol was investigated using the CCNC under 4 different supersaturations. The single hygroscopicity parameter (κ) was then derived using Köhler theory and reported for these two materials – to our knowledge have not been previously reported in literature. Both SOA materials were found to be slightly hygroscopic with κ-values between 0.03–0.25. Under both sub- and supersaturated conditions, polycatechol was found to be more hygroscopic than polyguaiacol due to polycatechol having a higher density of hydroxyl groups. Values of κCCN for both polycatechol and polyguaiacol were found to be greater than κGf, a disparity that is attributed to their insolubility and due to them exhibiting adsorption-dominated water uptake under subsaturated conditions. Both the FHH adsorption theory and the Köhler theory were applied to polycatechol and polyguaiacol CCN activity showing a relatively good fit with experimental data. Similarly, under subsaturated conditions, the FHH model, Type-I and Type-II BET models, and Köhler model were generated to predict the wet diameter for polycatechol and polyguaiacol. FHH, Type-I and Type-II BET models were found to be reliable when describing the subsaturated hygroscopicity of polyguaiacol but not for polycatechol. In short, the Köhler models appeared to agree better with the polycatechol data set, and adsorption models agreed better with the polyguaiacol data set.Overall, our results are significant because quantifying gas phase water uptake and hygroscopic properties of atmospheric particles is important for accurately parametrizing their climate and environmental impacts. The SOA materials studied here were produced efficiently from iron catalyzed reactions under acidic conditions that mimic chemistry in aged mineral dust. The hygroscopicity behavior of these insoluble to sparingly soluble organic polymers in sub-and supersaturated conditions may be representative of the complex organic aerosol condensation nuclei formed in biomass burning events. Our results show that a change in organic solute hydroxyl group density will modify droplet growth mechanisms. Even small changes in hydroxyl group molecular density of polymeric SOA will change the perceived water uptake and the robustness of droplet growth models applied for SOA CCN. Future work should further consider the chemical factors that contribute to adsorption and dissolution of atmospherically relevant compounds. Particularly, new work should explore different aging pathways for insoluble species formed with mineral dust that account for the transformation of organics from condensed phase chemistry and their impact on the hygroscopic properties.
Author contributions
KAM designed, collected, and analyzed H-TDMA, surface tension and CCN experimental data. KG analyzed and produced BET and FHH analysis. HAA conceived the idea for the study and synthesized SOA materials. HAA and AAA designed and developed the experimental and analytical work. All authors contributed to the writing and preparation of the manuscript.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
KAM, KG, and AAA acknowledge support from the NSF: AGS-1723290 and NSF: CHEM-1708337. HAA acknowledges funding from NSERC Discovery Program. HAA would like to thank Wisam Mohammed and Fatemeh Motaghedi for assistance with samples preparation.References
- C. L. Blanchard, Spatial and Temporal Characterization of Particulate Matter in, Particulate Matter Science for Policy Makers: A NARSTO Assessment, ed. P. McMurry, M. Shepherd and J. Vickery, Cambridge University Press, United Kingdom, 2004, ch. 6, ISBN 0521842875 Search PubMed.
- J. Haywood and O. Boucher, Estimates of the direct and indirect radiative forcing due to tropospheric aerosols: A review, Rev. Geophys., 2000, 38, 513–543 CrossRef CAS.
- D. J. Jacob, J. M. Waldman, J. W. Munger and M. R. Hoffmann, J. Geophys. Res., 1986, 91, 1089–1096 CrossRef CAS.
- H. Yu, Y. J. Kaufman, M. Chin, G. Feingold, L. A. Remer, T. L. Anderson, Y. Balkanski, N. Bellouin, O. Boucher, S. Christopher, P. DeCola, R. Kahn, D. Koch, N. Loeb, M. S. Reddy, M. Schulz, T. Takemura and M. Zhou, A review of measurement-based assessments of the aerosol direct radiative effect and forcing, Atmos. Chem. Phys., 2006, 6, 613–666 CrossRef CAS.
- M. Kanakidou, J. H. Seinfeld, S. N. Pandis, I. Barnes, F. J. Dentener, M. C. Facchini, R. Van Dingenen, B. Ervens, A. Nenes, C. J. Nielsen, E. Swietlicki, J. P. Putaud, Y. Balkanski, S. Fuzzi, J. Horth, G. K. Moortgat, R. Winterhalter, C. E. L. Myhre, K. Tsigaridis, E. Vignati, E. G. Stephanou and J. Wilson, Organic aerosol and global climate modelling: A review, Atmos. Chem. Phys., 2005, 5, 1053–1123 CrossRef CAS.
- D. A. Knopf, P. A. Alpert and B. Wang, The Role of Organic Aerosol in Atmospheric Ice Nucleation: A Review, ACS Earth Space Chem., 2018, 2, 168–202 CrossRef CAS.
- J. T. Abatzoglou and A. P. Williams, Impact of anthropogenic climate change on wildfire across western US forests, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11770–11775 CrossRef CAS PubMed.
- J. Chen, C. Li, Z. Ristovski, A. Milic, Y. Gu, M. S. Islam, S. Wang, J. Hao, H. Zhang, C. He, H. Guo, H. Fu, B. Miljevic, L. Morawska, P. Thai, Y. F. LAM, G. Pereira, A. Ding, X. Huang and U. C. Dumka, A review of biomass burning: Emissions and impacts on air quality, health and climate in China, Sci. Total Environ., 2017, 579, 1000–1034 CrossRef CAS PubMed.
- L. G. Jahl, T. A. Brubaker, M. J. Polen, L. G. Jahn, K. P. Cain, B. B. Bowers, W. D. Fahy, S. Graves and R. C. Sullivan, Atmospheric aging enhances the ice nucleation ability of biomass-burning aerosol, Sci. Adv., 2021, 7, eabd3440 CrossRef CAS PubMed.
- P. Veres, J. M. Roberts, I. R. Burling, C. Warneke, J. De Gouw and R. J. Yokelson, Measurements of gas-phase inorganic and organic acids from biomass fires by negative-ion proton-transfer chemical-ionization mass spectrometry, J. Geophys. Res.: Atmos., 2021, 112, D23302 Search PubMed.
- S. Slikboer, L. Grandy, S. L. Blair, S. A. Nizkorodov, R. W. Smith and H. A. Al-Abadleh, Formation of Light Absorbing Soluble Secondary Organics and Insoluble Polymeric Particles from the Dark Reaction of Catechol and Guaiacol with Fe(III), Environ. Sci. Technol., 2015, 49, 7793–7801 CrossRef CAS PubMed.
- L. E. Hatch, A. Rivas-Ubach, C. N. Jen, M. Lipton, A. H. Goldstein and K. C. Barsanti, Measurements of I/SVOCs in biomass-burning smoke using solid-phase extraction disks and two-dimensional gas chromatography, Atmos. Chem. Phys., 2018, 18, 17801–17817 CrossRef CAS.
- J. Ofner, H. U. Krüger, H. Grothe, P. Schmitt-Kopplin, K. Whitmore and C. Zetzsch, Physico-chemical characterization of SOA derived from catechol and guaiacol – A model substance for the aromatic fraction of atmospheric HULIS, Atmos. Chem. Phys., 2011, 11, 1–15 CrossRef CAS.
- H. A. Al-Abadleh, Aging of atmospheric aerosols and the role of iron in catalyzing brown carbon formation, Environ. Sci.: Atmos., 2021, 1, 297–345 CAS.
- O. A. Choobari, P. Zawar-Reza and A. Sturman, The global distribution of mineral dust and its impacts on the climate system: A review, Atmos. Res., 2014, 138, 152–165 CrossRef CAS.
- M. Tang, D. J. Cziczo and V. H. Grassian, Interactions of Water with Mineral Dust Aerosol: Water Adsorption, Hygroscopicity, Cloud Condensation, and Ice Nucleation, Chem. Rev., 2016, 116, 4205–4259 CrossRef CAS PubMed.
- A. Ito, S. Myriokefalitakis, M. Kanakidou, N. M. Mahowald, R. A. Scanza, D. S. Hamilton, A. R. Baker, T. Jickells, M. Sarin and S. Bikkina, Pyrogenic iron: The missing link to high iron solubility in aerosols, Sci. Adv., 2019, 5, eaau7671 CrossRef CAS PubMed.
- H. A. Al-Abadleh, M. S. Rana, W. Mohammed and M. I. Guzman, Dark Iron-Catalyzed Reactions in Acidic and Viscous Aerosol Systems Efficiently Form Secondary Brown Carbon, Environ. Sci. Technol., 2021, 55, 209–219 CrossRef CAS PubMed.
- M. A. Rahman and H. A. Al-Abadleh, Surface Water Structure and Hygroscopic Properties of Light Absorbing Secondary Organic Polymers of Atmospheric Relevance, ACS Omega, 2018, 3, 15519–15529 CrossRef CAS PubMed.
- A. Lavi, P. Lin, B. Bhaduri, R. Carmieli, A. Laskin and Y. Rudich, Characterization of Light-Absorbing Oligomers from Reactions of Phenolic Compounds and Fe(III), ACS Earth Space Chem., 2017, 1, 637–646 CrossRef CAS.
- N. Link, N. Removski, J. Yun, L. T. Fleming, S. A. Nizkorodov, A. K. Bertram and H. A. Al-Abadleh, Dust-Catalyzed Oxidative Polymerization of Catechol and Its Impacts on Ice Nucleation Efficiency and Optical Properties, ACS Earth Space Chem., 2020, 4, 1127–1139 CrossRef CAS.
- D. J. Rader and P. H. McMurry, Application of the tandem differential mobility analyzer to studies of droplet growth or evaporation, J. Aerosol Sci., 1986, 17, 771–787 CrossRef CAS.
- C. N. Cruz and S. N. Pandis, Deliquescence and hygroscopic growth of mixed inorganic–Organic atmospheric aerosol, Environ. Sci. Technol., 2000, 34, 4313–4319 CrossRef CAS.
- E. Swietlicki, H. C. Hansson, K. Hämeri, B. Svenningsson, A. Massling, G. Mcfiggans, P. H. Mcmurry, T. Petäjä, P. Tunved, M. Gysel, D. Topping, E. Weingartner, U. Baltensperger, J. Rissler, A. Wiedensohler and M. Kulmala, Hygroscopic properties of submicrometer atmospheric aerosol particles measured with H-TDMA instruments in various environments – A review, Tellus, Ser. B: Chem. Phys. Meteorol., 2008, 60, 432–469 CrossRef.
- A. Wiedensohler, An approximation of the bipolar charge distribution for particles in the submicron size range, J. Aerosol Sci., 1988, 19, 387–389 CrossRef CAS.
- N. F. Taylor, D. R. Collins, C. W. Spencer, D. H. Lowenthal, B. Zielinska, V. Samburova and N. Kumar, Measurement of ambient aerosol hydration state at Great Smoky Mountains National Park in the southeastern United States, Atmos. Chem. Phys., 2011, 11, 12085–12107 CrossRef CAS.
- M. D. Petters and S. M. Kreidenweis, A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 2007, 7, 1961–1971 CrossRef CAS.
- S. M. Kreidenweis and A. Asa-Awuku, in Treatise on Geochemistry, second edn, 2013, vol. 5, pp. 331–361 Search PubMed.
- S. Lance, J. Medina, J. Smith and A. Nenes, Mapping the operation of the DMT continuous flow CCN counter, Aerosol Sci. Technol., 2006, 40, 242–254 CrossRef CAS.
- G. C. Roberts and A. Nenes, A continuous-flow streamwise thermal-gradient CCN chamber for atmospheric measurements, Aerosol Sci. Technol., 2005, 39, 206–221 CrossRef CAS.
- G. J. Engelhart, A. Asa-Awuku, A. Nenes and S. N. Pandis, CCN activity and droplet growth kinetics of fresh and aged monoterpene secondary organic aerosol, Atmos. Chem. Phys., 2008, 8, 3937–3949 CrossRef CAS.
- A. Asa-Awuku, G. J. Engelhart, B. H. Lee, S. N. Pandis and A. Nenes, Relating CCN activity, volatility, and droplet growth kinetics of β-caryophyllene secondary organic aerosol, Atmos. Chem. Phys., 2009, 9, 795–812 CrossRef CAS.
- R. H. Moore, A. Nenes and J. Medina, Scanning mobility CCN analysis-A method for fast measurements of size-resolved CCN distributions and activation kinetics, Aerosol Sci. Technol., 2010, 44, 861–871 CrossRef CAS.
- X. Tang, D. R. Cocker and A. Asa-Awuku, Are sesquiterpenes a good source of secondary organic cloud condensation nuclei (CCN)? Revisiting β-caryophyllene CCN, Atmos. Chem. Phys., 2012, 12, 8377–8388 CrossRef CAS.
- X. Tang, D. Price, E. Praske, D. N. Vu, K. Purvis-Roberts, P. J. Silva, D. R. Cocker and A. Asa-Awuku, Cloud condensation nuclei (CCN) activity of aliphatic amine secondary aerosol, Atmos. Chem. Phys., 2014, 14, 5959–5967 CrossRef.
- F. Barati, Q. Yao and A. A. Asa-Awuku, Insight into the Role of Water-Soluble Organic Solvents for the Cloud Condensation Nuclei Activation of Cholesterol, ACS Earth Space Chem., 2019, 3, 1697–1705 CrossRef CAS.
- D. Vu, S. Gao, T. Berte, M. Kacarab, Q. Yao, K. Vafai and A. Asa-Awuku, External and internal cloud condensation nuclei (CCN) mixtures: Controlled laboratory studies of varying mixing states, Atmos. Meas. Tech., 2019, 12, 4277–4289 CrossRef CAS.
- J. H. Seinfeld and S. N. Pandis, Atmos. Chem. Phys., 2006, 5, 139–152 Search PubMed.
- B. F. Henson, An adsorption model of insoluble particle activation: Application to black carbon, J. Geophys. Res.: Atmos., 2007, 112, D24S16 CrossRef.
- A. L. Goodman, E. T. Bernard and V. H. Grassian, Spectroscopic study of nitric acid and water adsorption on oxide particles: Enhanced nitric acid uptake kinetics in the presence of adsorbed water, J. Phys. Chem. A, 2001, 105, 6443–6457 CrossRef CAS.
- R. Sorjamaa and A. Laaksonen, The effect of H2O adsorption on cloud drop activation of insoluble particles: A theoretical framework, Atmos. Chem. Phys., 2007, 7, 6175–6180 CrossRef CAS.
- P. Kumar, A. Nenes and I. N. Sokolik, Importance of adsorption for CCN activity and hygroscopic properties of mineral dust aerosol, Geophys. Res. Lett., 2009, 36, L24804 CrossRef.
- P. Kumar, I. N. Sokolik and A. Nenes, Parameterization of cloud droplet formation for global and regional models: Including adsorption activation from insoluble CCN, Atmos. Chem. Phys., 2009, 9, 2517–2532 CrossRef CAS.
- V. Varutbangkul, F. J. Brechtel, R. Bahreini, N. L. Ng, M. D. Keywood, J. H. Kroll, R. C. Flagan, J. H. Seinfeld, A. Lee and A. H. Goldstein, Hygroscopicity of secondary organic aerosols formed by oxidation of cycloalkenes, monoterpenes, sesquiterpenes, and related compounds, Atmos. Chem. Phys., 2006, 6, 2367–2388 CrossRef CAS.
- A. Pajunoja, A. T. Lambe, J. Hakala, N. Rastak, M. J. Cummings, J. F. Brogan, L. Hao, M. Paramonov, J. Hong, N. L. Prisle, J. Malila, S. Romakkaniemi, K. E. J. Lehtinen, A. Laaksonen, M. Kulmala, P. Massoli, T. B. Onasch, N. M. Donahue, I. Riipinen, P. Davidovits, D. R. Worsnop, T. Petäjä and A. Virtanen, Adsorptive uptake of water by semisolid secondary organic aerosols, Geophys. Res. Lett., 2015, 42, 3063–3068 CrossRef CAS.
- J. Wang, J. E. Shilling, J. Liu, A. Zelenyuk, D. M. Bell, M. D. Petters, R. Thalman, F. Mei, R. A. Zaveri and G. Zheng, Cloud droplet activation of secondary organic aerosol is mainly controlled by molecular weight, not water solubility, Atmos. Chem. Phys., 2019, 19, 941–954 CrossRef CAS.
- A. J. Prenni, M. D. Petters, S. M. Kreidenweis, P. J. DeMott and P. J. Ziemann, Cloud droplet activation of secondary organic aerosol, J. Geophys. Res.: Atmos., 2007, 112, D10223 Search PubMed.
- H. Wex, M. D. Petters, C. M. Carrico, E. Hallbauer, A. Massling, G. R. McMeeking, L. Poulain, Z. Wu, S. M. Kreidenweis and F. Stratmann, Towards closing the gap between hygroscopic growth and activation for secondary organic aerosol: Part 1-Evidence from measurements, Atmos. Chem. Phys., 2009, 9, 3987–3997 CrossRef CAS.
- J. N. Dawson, K. A. Malek, P. N. Razafindrambinina, T. M. Raymond, D. D. Dutcher, A. A. Asa-Awuku and M. A. Freedman, Direct Comparison of the Submicron Aerosol Hygroscopicity of Water-Soluble Sugars, ACS Earth Space Chem., 2020, 4, 2215–2226 CrossRef CAS.
- N. Good, D. O. Topping, J. Duplissy, M. Gysel, N. K. Meyer, A. Metzger, S. F. Turner, U. Baltensperger, Z. Ristovski, E. Weingartner, H. Coe and G. McFiggans, Widening the gap between measurement and modelling of secondary organic aerosol properties?, Atmos. Chem. Phys., 2010, 10, 2577–2593 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental procedures, and figures and tables showing data analysis. See DOI: 10.1039/d1ea00063b |
| This journal is © The Royal Society of Chemistry 2022 |