Open Access Article
Open Access ArticleDissociative ionisation of adamantane: a combined theoretical and experimental study†
Alessandra
Candian
 *a,
Jordy
Bouwman‡
*a,
Jordy
Bouwman‡
 *b,
Patrick
Hemberger
*b,
Patrick
Hemberger
 c,
Andras
Bodi
c,
Andras
Bodi
 c and
Alexander G. G. M.
Tielens
a
c and
Alexander G. G. M.
Tielens
a
aLeiden Observatory, Leiden University, P.O. Box 9513, 2300-RA Leiden, The Netherlands. E-mail: candian@strw.leidenuniv.nl
bRadboud University Nijmegen, Institute for Molecules and Materials, FELIX Laboratory, Toernooiveld 7c, NL-6525 ED Nijmegen, The Netherlands. E-mail: bouwman@strw.leidenuniv.nl
cLaboratory for Synchrotron Radiation and Femtochemistry, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland
First published on 17th November 2017
Abstract
Diamond nanoparticles, or nanodiamonds, are intriguing carbon-based materials which, maybe surprisingly, are the most abundant constituent of presolar grains. While the spectroscopic properties of even quite large diamondoids have already been explored, little is known about their unimolecular fragmentation processes. In this paper we characterise the dissociative ionisation of adamantane (C10H16) – the smallest member of the diamondoid family – utilising imaging Photoelectron Photoion Coincidence (iPEPICO) spectroscopy and Density Functional Theory (DFT) calculations. We have found adamantane to dissociatively photoionise via several parallel channels of which H, C3H7 and C4H8 losses are the most important ones. Calculations confirm the existence of a rate-limiting transition state for the multiple C-loss channels, which is located at 10.55 eV with respect to neutral adamantane. In addition, we found dissociation channels leading to small cationic hydrocarbons, which may be relevant in the interstellar medium.
1 Introduction
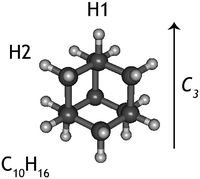
Diamondoids are a class of nanometer-sized hydrocarbons that have a diamond-like fused ring structure, with adamantane (C10H16) being the smallest unit cage. The diamond-like structure results in a remarkable rigidity, strength, and thermodynamic stability; properties that make them intriguing subjects of study for chemists and physicists alike.1,2 On Earth, small diamondoids are found in natural gas reservoirs and are abundant in gas pipeline deposits.3 Recently, larger diamondoids have been isolated from petroleum,4 triggering experimental studies to elucidate the properties of these molecules that bridge the gap between hydrocarbons and nano-sized diamond crystals.The discovery of small (2–3 nm) nanodiamonds in meteorites5 drew the attention of astronomers and geologists to this material. It is now established that nanodiamonds are the most abundant component of presolar grains.6,7 Due to their high stability, diamond-like material is also expected to be present and abundant in the interstellar medium.8,9 Guillois et al.10 attributed two broad emission bands at 3.45 and 3.53 μm, observed in the spectrum of circumstellar disks around the stars Elias 1 and HD 97048 to large (50 nm) gas-phase diamond-like molecules. Later, small nano-diamondoid molecules with sizes up to 130 C were shown to reproduce the above features very well.11,12 The size of astronomical nanodiamonds is still a matter of debate and so is the reason why only a handful of astronomical sources have been found to exhibit diamondoid spectral features. Nevertheless, based on the strength of the emission bands, it was proposed that the amount of cosmic carbon locked in nanodiamonds is of the order of 1–2%.13
A considerable number of investigations have been devoted to diamondoids in the laboratory, too. The IR spectra of large neutral diamondoids (up to hexamantane, 30 C) have been recorded experimentally.14 Vibrational and electronic spectra for a sample of both neutral and cationic species were calculated13 and ionisation potentials were determined experimentally.15 More recently, a comprehensive study of the electronic spectroscopy of adamantane, diamantane and triamantane was performed by Steglich et al.16 As expected for aliphatic compounds, the photoionisation of the diamondoids may result in the loss of atomic hydrogen, especially at low energies. The gas-phase infrared spectrum of the adamantyl cation (C10H15+) – the fragment resulting from the H-loss of adamantane – was recorded and, based on a comparison with quantum chemical calculations, it was found to be consistent with the lowest energy isomer, 1-adamantyl.17 Lu et al.18 computed the ionisation potential of diamondoids and proposed dissociation paths for neutrals and cations, and suggested that the products predominantly consist of small hydrocarbons. The dissociation of adamantane and diamantane was also studied experimentally in an electron impact mass spectrometer.19 It was suggested that, analogous to pyrolysis reactions, i.e. dissociation on the neutral surface, the dissociative ionisation of diamondoids yields mostly benzene derivatives.
While experiments have been conduced to explain the very specific local conditions that may lead to the paucity of nanodiamonds in space,20 little is known about the photodissociation behaviour of nanodiamonds. If these species were easily destroyed by photons, this would be an additional explanation for the lack of detection of their emission spectra. Thus, here we aim to characterise the dissociative photoionisation of the smallest diamondoid, adamantane (C10H16, Fig. 1), by studying the branching ratios and fragmentation rate constants of internal energy selected parent ions experimentally and exploring the potential energy surface (PES) computationally. The results from quantum chemical calculations are used as input for a supporting statistical dissociation model. The products formed from the photodissociation as well as the underlying formation mechanisms are rationalised and 0 K appearance energies are extracted. The findings are discussed in light of their astrophysical relevance.
2 Methods
2.1 Experimental method
Imaging photoelectron photoion coincidence (iPEPICO) experiments have been performed at the Vacuum Ultraviolet (VUV) beamline of the Swiss Light Source. The beamline and the iPEPICO instrument have been discussed in detail elsewhere21,22 and will only be described briefly here.Adamantane (99%, Fig. 1) was purchased from Sigma-Aldrich and was used without further purification. The adamantane sample was kept at room temperature and its vapour was introduced into the detection chamber through a Teflon tube. The effusive adamantane beam intersects with the VUV light from the beamline in the detection chamber, which is kept at a pressure of 5 × 10−7 mbar. The VUV radiation is generated in a bending magnet, is dispersed on a 600 groove mm−1 grating and is focused on the exit slit where the experimental chamber is situated. The light is passed through a noble gas filter before entering the experimental chamber to remove high order radiation.
Photoelectrons and photoions that result from the VUV induced (dissociative) ionisation are extracted in a 120 V cm−1 electric field. Electrons are velocity map imaged onto a RoentDek delay line imaging detector and their arrival time serves as time zero for measuring the time of flight of the coincident ions. The photoions are space focused in a Wiley–McLaren time-of-flight (TOF) tube onto a chevron microchannel plate detector. The flight time yields the mass of the coincident ion. The long first acceleration region at a relatively low field results in ion residence times on the order of several microseconds. If the dissociation is not prompt, the fragment ions will only have a time-dependent fraction of the nominal kinetic energy, which leads to a longer time of flight and shows up as an asymmetric daughter ion peak, broadened towards higher TOF. The peak shape yields information on the total depletion rate of the parent ion. The mass spectrometer is designed such that a compromise is found between the mass resolution (m/Δm ≈ 150) and the low fields needed to resolve the dissociation of metastable ions. Dissociation rates in the 103 < k(E)/s−1 < 107 can be measured in this configuration, and can then be extracted taking into account the ion optics parameters.23
Threshold photoelectrons, i.e. electrons with close to zero kinetic energy, in our case E ≤ 0.01 eV, are imaged onto the center of the detector with a kinetic energy resolution better than 1 meV. Contributions by electrons with non-zero kinetic energy but no lateral momentum, which are also imaged onto the center, have been subtracted as proposed in the literature.24 The threshold photoelectron spectrum is thus obtained by recording this signal as a function of photon energy. Selecting only threshold electrons for coincidences enables internal energy selection of the parent ion. By scanning the monochromatic VUV radiation the dissociation process can now be accurately explored.
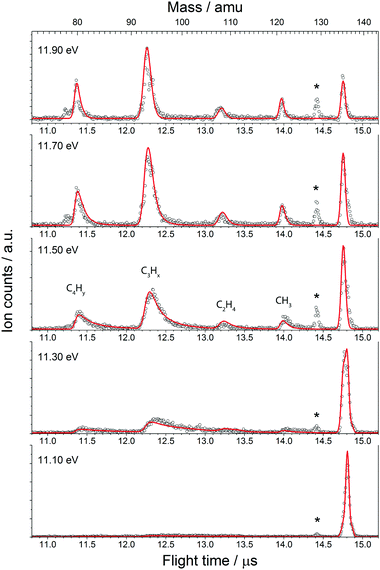
The fractional parent and daughter ion abundances in threshold photoionisation are plotted in the breakdown diagram (BD). In parallel processes, the BD is indicative of the branching ratio of the different channels, whereas the asymmetrically broadened daughter ion peaks in mass spectrum reflect the total dissociation rate of the parent ion.
2.2 Computational methods
Theoretical calculations were performed using Density Functional Theory (DFT) methods with B3LYP/6-311++G(2d,p) and ωB97X-D/6-311++G(2d,p) using Gaussian 09.25 The reactant, product and intermediate structures were optimised and vibrational analysis was performed to confirm that they are local minima on the potential energy surface (absence of imaginary frequencies). Transition states were evaluated using the Synchronous Transit-Guided Quasi-Newton (STQN) method,26,27 which requires the geometry of reactants, products and, optionally, an initial guess for the transition state geometry. The transition state nature of the structure was then confirmed through vibrational analysis by the presence of one imaginary frequency. To analyse the results of the calculations, the visualisation program GABEDIT28 was used.The optimised geometry and normal modes of the neutral and ionic ground state of adamantane computed at the ωB97X-D/6-311++G(2d,p) level of theory are used as input for a Franck–Condon simulation of the adamantane photoelectron spectrum. The eZspectrum software package29 was used to generate a stick diagram of the spectrum, which was subsequently convoluted with a 20 meV Full-Width-at-Half-Maximum (FWHM) Gaussian peak profile to account for the experimental resolution and the rotational envelope at room temperature.
A statistical model was constructed to account for the fractional ion abundances in the BD and the unimolecular dissociation rates measured in the form of TOF peak shapes, as descibed by Sztaray et al.23 The internal energy distribution of the neutral and the density of states of the dissociating species were computed based on B3LYP/6-311G++(2d,p) vibrational frequencies and rotational constants. The same level of theory was used to calculate the number of states of the rate limiting transition states and the barrier heights thereto, also required in the Rice–Ramsperg–Kassel–Marcus (RRKM) rate equation.30 These are the fit parameters that were allowed to relax so that the model reproduces the experimental results faithfully: the three lowest frequencies of the transition state were scaled by a variable factor and the barrier heights were varied to minimise the fit error. Accurate 0 K appearance energies are thus retrieved based on the best fit to the breakdown diagram and time-of-flight distributions.
3 Results
The experimental results are described first. Next, the quantum chemical computations are discussed to rationalise the formation of the detected products. These computational results are subsequently used to model the experimental data and to derive appearance energies.3.1 Experimental results
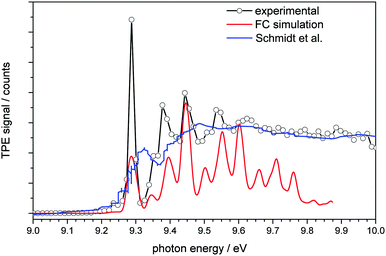 | ||
| Fig. 2 Threshold photoelectron spectrum of adamantane plotted together with a simulated spectrum (red line) and the conventional photoelectron spectrum of Schmidt et al.32 (blue line). | ||
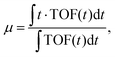 | (1) |
| μ = at1 + (1 − a)t2, | (2) |
The BD, constructed by plotting the integrated ion signal contributions of each dissociation product normalised to the total ion signal as a function of internal energy of the parent ion, is shown in Fig. 4. It can be seen that many of the product channels open up at approximately the same photon energy, hν ≈ 10.9 eV. This hints to a common rate limiting transition state for at least some of the channels, as was observed in the past for other systems as well.38,39 A summary of the parallel dissociation channels and the accompanying co-fragments is shown in Table 1.
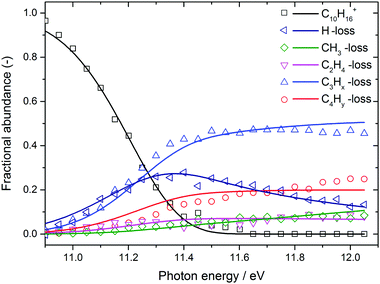 | ||
| Fig. 4 Adamantane breakdown diagram (open symbols) plotted together with the RRKM model fit (solid lines). Appearance energies derived from the fits are summarised in Table 1. | ||
| m/z | Product | Co-fragment | A.E. (eV) | ΔS‡ (K (J mol)−1) |
|---|---|---|---|---|
| 136 | C10H16˙+ | — | — | — |
| 135 | C10H15+ | ˙H-Loss | 10.50 | −32.30 |
| 121 | C9H13+ | ˙CH3-Loss | 10.83 | 11.26 |
| 108 | C8H12˙+ | C2H4-Loss | 10.69 | −22.14 |
| 95 | C7H11+ | ˙C3H5-Loss | ||
| 94 | C7H10˙+ | C3H6-Loss | ||
| 93 | C7H9˙+ | ˙C3H7-Loss* | 10.69 | 1.82 |
| 81 | C6H9˙+ | ˙C4H7-Loss | ||
| 80 | C6H8˙+ | C4H8-Loss* | 10.69 | −8.61 |
| 79 | C6H7+ | ˙C4H9-loss | ||
| 78 | C6H6˙+ | C4H10-loss |
In the breakdown diagram, there is a lingering parent ion signal at <4% abundance in the 11.4–11.6 eV photon energy range. This cannot be reconciled with the internal energy distribution of the neutral sample, and is most likely an artifact of the center-of-gravity analysis. While we cannot rule out competing alternative internal energy loss processes in the parent ion, such as fluorescence, it appears to be extremely unlikely that they should result in such an artifact. In the modelling, we do not consider this remaining fraction of the parent ion in the BD and the parent ion channel is set to zero above 11.65 eV.
3.2 Computational results
The adamantane molecule has a highly symmetric structure, belonging to the Td point group. Upon ionisation, the molecule is affected by Jahn–Teller distortion33,34 along the C3 axis, leading to a structure of C3v symmetry (Fig. 1). The adiabatic ionisation energy is calculated to be 8.84 eV (B3LYP/6-311++G(2d,p) including zero point energy corrections), in agreement with previous theoretical results,16 but slightly lower than the experimentally determined ionisation threshold (see Section 3.1).Numerous pathways were investigated and only those relevant to the experimental findings, i.e., pathways with a rate limiting barrier that compares reasonably with the observed mechanism, are reported here. A summary of the adamantane cation PES containing only the rate limiting transition states leading to the observed carbon dissociation channels is presented in Fig. 5. The full PES landscape, the geometries of all transition and intermediate states and a detailed description of the different routes are available as ESI† to the interested reader. During the exploration of the PES, four intermediate states (int2, int8, int9 and int20) were found to be more stable than the adamantane cation by 0.07, 0.07, 0.49 and 0.61 eV respectively. Since their structures do not suggest high level of aromaticity, we performed calculations on the neutral counterparts of these intermediate states and found that they are all less stable than adamantane by 0.40, 0.95, 0.95 and 0.88 eV, thus pointing to slightly lower ionisation energies.
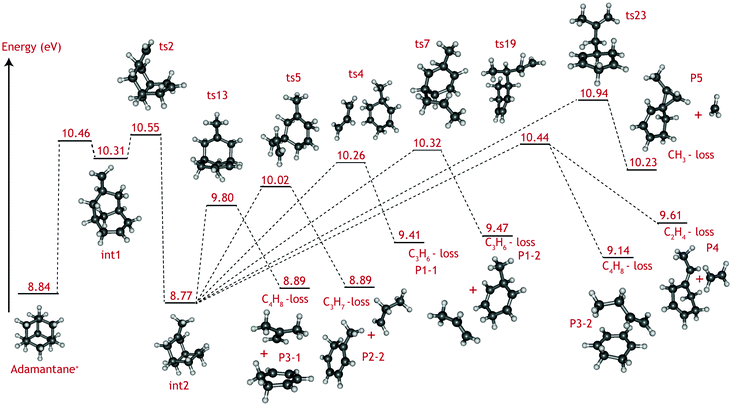 | ||
| Fig. 5 Summary of the adamantane cation potential energy surface showing the rate limiting transition states leading to major dissociation channels. Energies are given in eV. The full PES, together with description of the steps and structures of transition and intermediate steps can be found in the ESI.† | ||
Fragmentation channels involving carbon loss share the same initial two steps. First, the adamantane cation opens up to form int1. Next, a hydrogen atom shifts towards the CH2 dangling group (ts2), resulting in a boat-like C10H16+ intermediate with a methyl group on top (int2) which is slightly more stable than the parent cation by 0.07 eV.
For the loss of a C3H6 unit, two energetically favourable pathways could be identified. Both paths involve a series of hydrogen shifts, eventually leading to formation of propene C3H6 and 3-methyl-1,4-cyclohexadiene cation (C7H10+) (P1-1 and P1-2) through transition states ts4 and ts7 (Fig. 5). The small energy difference between P1-1 and P1-2 is due to the slight change in orientation of C3H6 fragment with respect to C7H10+.
The C3H7-loss channel has a rate-limiting transition state ts5 at 10.02 eV with respect to adamantane and the C3H7 fragment is lost as isopropyl radical (Fig. 5). A second path was found with a much higher (10.90 eV) rate-limiting transition state (see Fig. S1, ESI†). The former path likely dominates and it is the one represent in the overview figure (Fig. 5).
Three routes describing the C4H8-loss channel were found, all leading to the formation of 1,3-cyclohexadiene cation (Fig. S2 ESI†); in two of these, the fragment is released as an isobutene unit (P3-1, Fig. 5) with rate-limiting transition states ts13 and ts23 at 9.80 and 10.62 eV with respect to adamantane. The former route thus appears more favorable and has been included in Fig. 5. In the third route, the fragment is lost as 1-butene unit P3-2, with rate-limiting transition state ts19 at 10.44 eV. The energy difference between P3-1 and P3-2 is due to higher stability of the tertiary carbocation in isobutene.
As for the minor CH3 and C2H4 loss channels, rate limiting transition states at 10.94 eV (ts23) and at 10.44 eV (ts19) were found (Fig. 5).
Contrary to the carbon-loss channels, the loss of hydrogen proceeds via direct abstraction. Two non-equivalent H atoms, H1 and H2 (see Fig. 1), connected to tertiary and secondary C atoms, respectively, can be removed from adamantane+. The cleavage of H1 is calculated to require 1.58 eV (10.42 eV above adamantane), while 2.05 eV is needed for removing H2 (10.89 eV). These values are in good agreement with previous calculations.16,17 The removal of H1 is predicted to be an abstraction without reverse barrier.
4 Statistical modelling
The BD as well as the TOF distributions are modelled using the miniPEPICO program.23 This program uses the measured ionisation energy, transition state barriers as well as normal mode frequencies of the ground state of neutral adamantane, ground state ionic adamantane and rate limiting transition states as input for a RRKM model to simulate the experimental data. The program fits both the relative contributions of the different products (i.e. the breakdown diagram) and the peak shapes in the TPEPICO mass spectra (dissociation rates).Computationally, the formation of 1-adamantyl is found to be lower in energy than the formation of 2-adamantyl. H-loss comprises an abstraction reaction without a reverse barrier and so no true transition state is located for this product. Hence, the transition state was estimated by optimizing the structure with a C–H distance of 4 Å and was used for modelling the dissociative ionisation.
The C2H4, C3Hx, and C4Hy-loss channels were found to share a common rate limiting transition state ts2 (Fig. 5), which is associated with the creation of a boat-like C10H16+ intermediate from the initial opening of the adamantane structure. Ts2 is located at 10.55 eV with respect to the neutral adamantane. The CH3-loss channel is a minor, yet clearly observable product. Computationally it is not found to share the same rate limiting step as the other carbon loss pathways. Instead, its rate limiting transition state (ts23) is located at considerably higher energy (10.94 eV) than those leading to the other observed products.
The fact that the loss of C3H7, C4H8 and C2H4 share the same rate limiting transition is implicitly taken into account in the RRKM model. The barriers for CH3 and H-loss are used as fit parameters, while the common barrier is varied such that the error in the fit is minimised. The normal mode frequencies of the common transition state leading to C3H7, C4H8 and C2H4 are treated independently and are used as fit parameters that statistically determine the branching amongst these channels. In other words, in our model, the branching is determined at the initial transition state by the different phase space volumes belonging to the parallel dissociation pathways. In reality, it is likely that a sizeable fraction of the trajectories explores different dissociation pathways before product formation, giving rise to at least a partial equilibrium past the rate determining transition state. However, our model reproduces the experimental branching ratios quite well, meaning that our assumption is at least phenomenologically correct.
The results of the model fit are plotted as solid lines on top of the experimental points in Fig. 3 and 4. The model considers only the formation of the main product peaks and their 13C isotopes. A reasonable agreement is found between the TOF and BD model and the experimental data. The resulting 0 K appearance energies and entropies of activations are summarised in Table 1.
5 Discussion
The VUV dissociative ionisation of adamantane is studied using a combination of experiments and quantum chemical computations. It is found that adamantane cations dissociate via a number of parallel channels, resulting in cations of C10H15+, C9H13+, C8H12+, C7Hm+ (m = 9, 10, 11) and C6Hn+ (n = 6, 7, 8, 9) composition. The CH3 and C2H4-loss channels comprise the weakest and the formation of C7Hm+ (C3Hx-loss) comprises the strongest channel.DFT computations confirm the experimental suggestion that C2H4, C3Hx and C4Hy-loss channels share the same rate limiting transition state (ts2), which is characterised as H-migration to create a methyl group, following by an opening of the adamantane cage and is located at 10.55 eV (1.71 eV) with respect to adamantane (cation). The formed intermediate (int2) subsequently isomerises via submerged barriers to the detected products.
The lowest submerged barrier is ts13 at 9.80 eV and leads to isobutene + 1,3-cyclohexadiene+. The second lowest pathway has a submerged barrier at 10.02 eV (ts5) and results in C3H7-loss. The computed barrier heights appear to be at odds with the experimental work, which indicates that the C3H7 loss is the most abundant product channel. However, the finding could point to ts13 being a tighter transition state than ts5, causing the rate of the C3H7-loss channel to be significantly faster. Based on DFT harmonic frequencies, the calculated entropies of activation at 1000 K (ΔS‡) for reactions int2 → ts5 and int2 → ts13 are ΔS‡ = 45.97 J (mol K)−1 and 8.55 J (mol K)−1, respectively, confirming the tighter nature of ts13. The RRKM-derived activation entropies for the overall dissociation reaction agree with this picture, i.e. the transition state leading to C3H7-loss is looser and the rate constant is a steeper rising function of energy above the threshold (see Table 1).
Methyl and ethyl loss also proceed by opening the adamantane ring structure (ts2 at 10.55 eV). The rate limiting submerged barrier yielding C2H4 is located at 10.44 eV, which is significantly higher than those leading to the loss of C3H7 or C4H8. Looking at Fig. S2 in the ESI† it is seen that, according to theory, the C2H4-loss channel (ts22) competes with a low-barrier isomerisation channel (ts20). The entropies of activation, calculated from the theoretical DFT frequencies, of the two reactions (−48.80 and −28.87 J (mol K)−1, respectively), combined with the energy barriers (0.63 and 0.04 eV, respectively) suggest that isomerisation is the dominant reaction and only a small amount of int19 will lead to C2H4-loss. This finding is in excellent agreement with the smaller branching ratio to the C2H4-loss observed experimentally.
Demethylation is limited by a larger barrier (ts23) located at 10.94 eV. The relative abundance of the methyl and ethyl loss (Fig. 3) can be explained by the difference in entropy of activation derived from the RRKM modelling for the two reactions; ts23 is a looser transition state than ts19 with ΔS‡ = 11.25 J (mol K)−1 compared to ΔS‡ = −22.14 J (mol K)−1, causing it to compete favorably.
The loss of an H-atom is found, in agreement with prior studies, to yield 1-adamantyl via a reaction without a reverse barrier at an energy of 1.58 eV with respect to the adamantane cation.
6 Astrophysical implications
Diamondoids are elusive components of the interstellar dust family; while abundant in presolar grains, only a handful of sources, mostly young stars with dusty disks, have robust detections of nanodiamonds spectral features, whose strength span 1–2 order of magnitudes.40 In these sources, diamondoids emission is present very close to the central star, where the radiation field is stronger; on the other side emission from 2-D hydrocarbons like Polycyclic Aromatic Hydrocarbons (PAHs) are more intense and widespread in the disk, even at larger distances.11,20 So far, the reason for this paucity has been identified in the very special physical conditions leading to the in situ formation of diamondoids.20 In these astrophysical environments, PAHs and diamondoids are subject to radiation fields that may ionise and/or photodissociate them.Our findings show that adamantane dissociates mostly through the loss of H and CxHy units, yielding small hydrocarbons. The dissociation channels can be compared to those of PAHs, often detected in conjunction with diamondoids in young stars, but much more ubiquitous in the ISM. The binding energy for carbon-loss channel in adamantane cation is found to be 1.85 eV while for a PAH molecule with the same number of atoms, pyrene C16H10+, this number is 6.00 eV.41 For the H-loss channel the experimental binding energies are 1.66 eV and 4.6 eV42 for adamantane and pyrene, respectively. Thus adamantane appears to be less photostable than pyrene, as can be expected for a saturated hydrocarbon when compared to an aromatic one. Naturally the efficiency of dissociation will depend on the strength of the radiation source, e.g. the central star, and on the photo-absorption cross-section of the diamondoids. We speculate that the lower photostability together with the proposed very specific physical conditions needed for diamondoid formation may help explaining the very few detections of this material in astrophysical environments. The result of this work can be used as a key ingredient in photochemical modelling of nanodiamonds in typical sources like HD 97048 to test this hypothesis. Some questions still remain: do larger nanodiamonds share the same fragmentation behaviour with comparable binding energies? If so, what size of diamondoids would then be stable enough to survive close to the central radiation source? This clearly calls for further experimental studies on larger systems of astrophysical interest Finally, the effect of diamondoid dissociation may be evident in astronomical spectra; it is expected that upon dissociation, the strength of the typical C–H stretch bands of nanodiamonds at 3.43 and 3.53 μm will decrease, possibly favouring the appearance of aromatic C–H stretches at 3.30 μm as seen in observations.20
Conflicts of interest
There are no conflicts to declare.Acknowledgements
AC and JB acknowledge the Netherlands Organisation for Scientific Research (Nederlandse Organisatie voor Wetenschappelijk Onderzoek, NWO) for VENI grants (grant number 639.041.543 and 722.013.014, respectively). AB and PH acknowledge funding by the Swiss Federal Office of Energy (BFE Contract Number SI/501269-01). Studies of interstellar molecules at the Leiden Observatory are supported through an advanced European Research Council grant 246976 and a Spinoza award. Calculations were carried out on the Dutch national e-infrastructure (Cartesius) with the support of SURF Cooperative, under project NWO EW project SH-362-15.References
- H. Schwertfeger, A. Fokin and P. Schreiner, Angew. Chem., 2008, 47, 1022–1036 CrossRef CAS PubMed.
- W. A. Clay, J. E. P. Dahl, R. M. K. Carlson, N. A. Melosh and Z. X. Shen, Rep. Prog. Phys., 2015, 78, 21 CrossRef PubMed.
- J. Reiser, E. McGregor, J. Jones, R. Enick and G. Holder, Fluid Phase Equilib., 1996, 117, 160–167 CrossRef CAS.
- J. E. Dahl, S. G. Liu and R. M. K. Carlson, Science, 2003, 299, 96–99 CrossRef CAS PubMed.
- R. S. Lewis, T. Ming, J. F. Wacker, E. Anders and E. Steel, Nature, 1987, 326, 160–162 CrossRef CAS.
- E. Anders and E. Zinner, Meteoritics, 1993, 28, 490–514 CrossRef CAS.
- A. P. Jones, L. B. d'Hendecourt, S.-Y. Sheu, H.-C. Chang, C.-L. Cheng and H. G. M. Hill, Astron. Astrophys., 2004, 416, 235–241 CrossRef CAS.
- W. C. Saslaw and J. E. Gaustad, Nature, 1969, 221, 160–162 CrossRef.
- T. Henning and F. Salama, Science, 1998, 282, 2204 CrossRef CAS PubMed.
- O. Guillois, G. Ledoux and C. Reynaud, Astrophys. J., 1999, 521, L133–L36 CrossRef CAS.
- C. Van Kerckhoven, A. G. G. M. Tielens and C. Waelkens, Astron. Astrophys., 2002, 384, 568–584 CrossRef CAS.
- O. Pirali, M. Vervloet, J. E. Dahl, R. M. K. Carlson, A. G. G. M. Tielens and J. Oomens, Astrophys. J., 2007, 661, 919–925 CrossRef CAS.
- C. J. Bauschlicher, Y. Liu, A. Ricca, A. L. Mattioda and L. J. Allamandola, Astrophys. J., 2007, 671, 458 CrossRef CAS.
- J. Oomens, N. Polfer, O. Pirali, Y. Ueno, R. Maboudian, P. W. May, J. Filik, J. E. Dahl, S. Liu and R. M. Carlson, J. Mol. Spectrosc., 2006, 238, 158–167 CrossRef CAS.
- K. Lenzke, L. Landt, M. Hoener, H. Thomas, J. E. Dahl, S. G. Liu, R. M. K. Carlson, T. Moller and C. Bostedt, J. Chem. Phys., 2007, 127, 084320 CrossRef CAS PubMed.
- M. Steglich, F. Huisken, J. E. Dahl, R. M. K. Carlson and T. Henning, Astrophys. J., 2011, 729, 91 CrossRef.
- N. Polfer, B. G. Sartakov and J. Oomens, Chem. Phys. Lett., 2004, 400, 201–205 CrossRef CAS.
- A. J. Lu, B. C. Pan and J. G. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 9 Search PubMed.
- R. J. Waltman and A. C. Ling, Can. J. Chem., 1980, 58, 2189–2195 CrossRef CAS.
- M. Goto, T. Henning, A. Kouchi, H. Takami, Y. Hayano, T. Usuda, N. Takato, H. Terada, S. Oya, C. Jäger and A. C. Andersen, Astrophys. J., 2009, 693, 610–616 CrossRef CAS.
- M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., 2009, 610, 597–603 CrossRef CAS.
- A. Bodi, M. Johnson, T. Gerber, Z. Gengeliczki, B. Sztaray and T. Baer, Rev. Sci. Instrum., 2009, 80, 034101 CrossRef PubMed.
- B. Sztaray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233–1245 CrossRef CAS PubMed.
- B. Sztaray and T. Baer, Rev. Sci. Instrum., 2003, 74, 3763–3768 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49–56 CrossRef CAS.
- A. Allouche, J. Comput. Chem., 2011, 32, 174–182 CrossRef CAS PubMed.
- A. Mozhayskiy and A. I. Krylov, ezSpectrum, 2009, Version 3.0, http://iopenshell.usc.edu/downloads Search PubMed.
- T. Baer and W. Hase, Unimolecular Reaction Dynamics: Theory and Experiments: Theory and Experiments, Oxford University Press, USA, 1996 Search PubMed.
- NIST, NIST Chemistry WebBook, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2009, NIST Standard Reference Database Number 69 Search PubMed.
- W. Schmidt, Tetrahedron, 1973, 29, 2129–2213 CrossRef CAS.
- A. Patzer, M. Schütz, T. Möller and O. Dopfer, Angew. Chem., 2012, 51, 4925–4929 CrossRef CAS PubMed.
- M. E. Crestoni and S. Fornarini, Angew. Chem., 2012, 51, 7373–7375 CrossRef CAS PubMed.
- S. D. Worley, G. D. Mateescu, C. W. McFarland, R. C. Fort and C. F. Sheley, J. Am. Chem. Soc., 1973, 95, 7580–7586 CrossRef CAS.
- J. Bouwman, B. Sztaray, J. Oomens, P. Hemberger and A. Bodi, J. Phys. Chem. A, 2015, 119, 1127–1136 CrossRef CAS PubMed.
- B. West, C. Joblin, V. Blanchet, A. Bodi, B. Sztaray and P. M. Mayer, J. Phys. Chem. A, 2012, 116, 10999–11007 CrossRef CAS PubMed.
- P. Hemberger, A. Bodi, T. Gerber, M. Wuertemberger and U. Radius, Chem. – Eur. J., 2013, 19, 7090–7099 CrossRef CAS PubMed.
- P. Hemberger, A. Bodi, J. H. J. Berthel and U. Radius, Chem. – Eur. J., 2015, 21, 1434–1438 CrossRef CAS PubMed.
- B. Acke and M. E. van den Ancker, Astron. Astrophys., 2006, 457, 171–181 CrossRef CAS.
- B. West, F. Useli-Bacchitta, H. Sabbah, V. Blanchet, A. Bodi, P. M. Mayer and C. Joblin, J. Phys. Chem. A, 2014, 118, 7824–7831 CrossRef CAS PubMed.
- Y. Ling, Y. Gotkis and C. Lifshitz, Eur. J. Mass Spectrom., 1995, 1, 41–49 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Full PES of observed dissociation channels, structures of intermediate and transition states, cartesian coordinates of the rate limiting transition states. See DOI: 10.1039/c7cp05957d |
| ‡ Present address: Sackler Laboratory for Astrophysics, Leiden Observatory, Leiden University, P.O. Box 9513, 2300-RA Leiden, The Netherlands. |
| This journal is © the Owner Societies 2018 |