Thermoresponsive microgels at the air–water interface: the impact of the swelling state on interfacial conformation
J.
Maldonado-Valderrama
a,
T.
del Castillo-Santaella
a,
I.
Adroher-Benítez
a,
A.
Moncho-Jordá
*b and
A.
Martín-Molina
a
aDepartamento de Física Aplicada, Facultad de Ciencias, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
bDepartamento de Física Aplicada and Instituto Carlos I de Física Teórica y Computacional, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain. E-mail: moncho@ugr.es
First published on 11th July 2016
Abstract
Poly(N-vinylcaprolactam) (PVCL) is a new temperature-responsive type of polymer microgel with improved biocompatibility as compared to more commonly used poly(N-isopropylacrylamide) (PNIPAM). Both polymers swell at low temperatures and collapse at high ones, showing a volume phase transition temperature (VPTT) around the physiological temperature. Exploring the interfacial characteristics of thermoresponsive microgels is important due to their potential application in emulsion based systems with tailored stabilities and controlled degradation profiles. In this work, we study the properties of charged PVCL particles at the air–water interface by a combination of adsorption, dilatational rheology and Langmuir monolayers. Although PVCL particles adsorb spontaneously at the air–water interface in both, swollen and collapsed conformations, the interfacial properties show significant differences depending on the swelling state. In particular, the total amount of adsorbed microgels and the rigidity of the monolayer increase as the temperature increases above the VPTT, which is connected to the more compact morphology of the microgels in this regime. Dilatational rheology data show the formation of a very loose adsorbed layer with low cohesivity. In addition, collapsed microgels yield a continuous increase of the surface pressure, whereas swollen microgels show a phase transition at intermediate compressions caused by the deformation of the loose external polymer shell of the particles. We also provide a qualitative interpretation for the surface pressure behavior in terms of microgel–microgel effective pair potentials, and correlate our experimental findings to recent rescaling models that take into account the importance of the internal polymer degrees of freedom in the rearrangement of the conformation of the microgel particles at the interface.
1 Introduction
Polymer gels are among the most attractive and versatile soft materials. They are present in many everyday products including food and pharmaceutics. Polymer gels typically contain large amounts of liquid confined within a flexible network of polymer chains or colloidal particles.1 Among the different types of gels, all with different properties and applications, microgels are sub-micrometer sized cross-linked polymer particles that can carry or incorporate macromolecules in their network structure. This property, coupled with their “soft” character and the ability to introduce stimuli-responsive characteristics, means that they have many attractive applications, including drug delivery.2,3 The choice of stimuli depends on the application; thermoresponsive microgels are most frequently investigated since their small size enables them to develop a rapid kinetic response to temperature changes.4 In particular, thermoresponsive microgels showing a volume phase transition temperature (VPTT) near physiological temperature have been investigated lately. Microgels based on biocompatible and temperature-sensitive polymers having a lower critical solution temperature (LCST) around 32 °C in aqueous solutions swell at low temperatures and collapse at high temperatures.Since 1986 there have been many publications describing the preparation, characterization and application of temperature sensitive microgels from an experimental point of view3,5–10 as well as their physical properties by theories and simulations.8,9,11–21 Amongst all the temperature-sensitive polymer microgel systems the ones based on poly-N-isopropylacrylamide (PNIPAM) are the most widely studied. PNIPAM microgels are considered to be “smart” or “switchable” materials having the VPTT close to physiological temperature. This means that they have the potential as an intelligent drug delivery vehicle where the release of an active agent or drug can be triggered by changes in temperature. This can be used by simple contact, for example, in transdermal delivery systems via our skin.22 In addition to their ability to change conformation with temperature, PNIPAM microgels adsorb onto fluid/fluid interfaces due to their surface activity (i.e. lower the surface tension of water).22–36 In general, the adsorption and self-assembly of microgel particles at fluid interfaces has been a topic of study for many researchers for the past few years providing many interesting challenges (see ref. 37–39 and references cited therein). The behaviour of polymeric particles lies in between that of colloidal particles and soft polymers while the adsorbed state provides an anisotropic medium which affects their morphology and interactions. These facts, in addition to their temperature responsive nature, make these soft particles potential candidates as Pickering stabilizers for emulsions with tunable stability.30 Therefore, understanding the adsorption behavior of soft PNIPAM microgels onto fluid interfaces has become increasingly important both in terms of fundamental science and applications of microgels as multi-stimuli responsive emulsion stabilizers.23 However, despite the increasing number of studies on adsorbed layers of PNIPAM-based microgels reported in the literature, the properties of the adsorbed state and its link with emulsion stability are not well understood yet.35
Recently, Geisel and coworkers have found differences between Gibbs monolayers, where particles spontaneously adsorb in the presence of excess concentration in the bulk, and Langmuir monolayers, where a fixed amount of particles is spread at the surface. Although both routes offer in principle the possibility of tuning the microstructure of the interface, they demonstrate that the use of Langmuir monolayers is a much more effective technique for the fabrication of 2D ordered microgel arrays, where the interparticle separation can be easily tuned by changing the surface pressure.32,33 Pinaud and coworkers have related the interfacial properties of PNIPAM microgels to their conformation and packing at a model oil–water interface.35 Therein, the authors propose a model for the microgel deformation and packing at the interface during compression comprised various packing states in the Langmuir film for PNIPAM microgels. For their part, Zielińska and coworkers have recently provided valuable information concerning the structure of the adsorbed microgel layer by neutron reflectivity. They prove that PNIPAM microgels form more complex structures at the interface, which have to date not been resolved.22 The specific impact of temperature (swelling state) on the surface conformation has also been addressed in some detail by various authors.23,27,40,41 However, a systematic interfacial study including kinetics, adsorption isotherms, dilatational rheology and Langmuir films has not been actually performed so far.
Another issue is that the use of PNIPAM as a biomaterial may be limited because of its high cytotoxicity and its low cell viability. In this sense, a temperature-sensitive polymer microgel based on poly(N-vinylcaprolactam) (PVCL) appears as an alternative to PNIPAM-based microgels.6 PVCL polymers are especially interesting due their stability against hydrolysis and biocompatibility. In fact, it has been recently shown that PVCL-based microgels are more biocompatible than traditional microgels based on PNIPAM and therefore, more suitable for bio-applications.6 The development of PVLC requires a better understanding of the complex dynamic structure of such micromaterials and currently there is a lack of experimental data about how these materials actually behave at interfaces. With the exception of Wu and coworkers who focus on the properties of mixed PVCL and PNIPAM at the interface.40
In this work we have used PVCL based charged microgels and carried out a complete surface characterisation including kinetics, adsorption isotherms, dilatational rheology and Langmuir monolayers. Such a complete interfacial study has not been attempted before on PVCL and we hence show for the first time the conformational changes undergone at the air–water interface. We evaluate the synergism with the temperature deformation and provide important new aspects on the interfacial properties of PVCL. Understanding the behaviour of microgels at interfaces will enable the rational design of emulsion based systems for the targeted delivery of administered drugs.
2 Experimental
2.1 Materials
Poly(N-vinylcaprolactam)-based microgels (PVCL) were synthesized by emulsion polymerization in a batch reactor. The original protocol was developed by Imaz and Forcada.42 The monomer, N-vinylcaprolactam (VCL, Sigma-Aldrich); the crosslinker, poly(ethylene glycol) diacrylate (PEGDA 200, Polysciences); the anionic initiator, potassium persulfate (KPS, Sigma-Aldrich); the buffer, sodium bicarbonate (NaHCO3, Sigma-Aldrich); and the emulsifier, sodium dodecyl sulfate (SDS, Sigma-Aldrich) were used as supplied with concentrations given in Table 1. And the ionic comonomer, acrylic acid (AA, Sigma-Aldrich), was used to confer charge to the resulting microgel particles. The reaction mixture was heated at 70 °C, stirred at 300 rpm agitation rate, and purged with nitrogen for 1 h before starting the polymerization. After adding the initiator, the reaction was allowed to continue under a nitrogen atmosphere while stirring and a shot of AA was added to the reaction medium after 30 min of reaction. Once the reaction was complete (5 h) the reaction mixture was subsequently cooled to 25 °C, whilst maintaining the stirring and nitrogen flow to prevent possible aggregation. The final dispersion was filtered through glass wool, and cleaned by dialysis (Spectra/Por Dialysis Membrane. Molecular weight cut off: 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–14
000–14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da) at room temperature. The water was exchanged every 12 h and dialysis was allowed to run until the dialysate reached the conductivity and surface tension values close to those of pure water (2 μS cm−1 and 70 mN m−1) The concentration of the final PVLC microgel suspension was 0.662% (w/w).
000 Da) at room temperature. The water was exchanged every 12 h and dialysis was allowed to run until the dialysate reached the conductivity and surface tension values close to those of pure water (2 μS cm−1 and 70 mN m−1) The concentration of the final PVLC microgel suspension was 0.662% (w/w).
| Function | Compound | % w/w |
|---|---|---|
| Monomer | VCL | 1.0126 |
| Ionic comonomer | AA | 0.0798 |
| Crosslinker | PEGDA | 0.0400 |
| Initiator | KPS | 0.0100 |
| Buffer | NaHCO3 | 0.0103 |
| Emulsifier | SDS | 0.0400 |
Dispersions of microgels were prepared by dilution in ultrapure water followed by mixing of the solution by vortexing for 1 min. All measurements were made in ultrapure water at different temperatures. For the preparation of buffer solutions, the cleaning is carried out by dialysis against deionized water (Milli-Q Academic, Millipore, France). All glassware was washed with 10% Micro-90 cleaning solution and exhaustively rinsed with tap water, isopropanol, deionized water, and ultrapure water in sequence. All other chemicals used were of analytical grade and used as received.
2.2 Methods
The hydrodynamic diameter (Dh) of the microgel in solution was measured by means of the Dynamic Light Scattering (DLS) technique using a Zetasizer Nano ZS system from Malvern Instruments. The hydrodynamic diameters were calculated from the diffusion coefficient using the Stokes–Einstein equation. The self-optimization routine and correlogram analysis provided by software was used for all measurements. Samples were diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 with ultrapure water. Measurements were taken every 2 °C, ranging from 20 °C to 54 °C, in order to consider the whole range of sizes of the microgels. At each temperature, we waited two minutes to equilibrate each sample and then we took three measurements. The deviation was found to be less than 2% and final values are plotted as mean values of replicates, with standard deviations obtained according to statistical analysis tools.
20 with ultrapure water. Measurements were taken every 2 °C, ranging from 20 °C to 54 °C, in order to consider the whole range of sizes of the microgels. At each temperature, we waited two minutes to equilibrate each sample and then we took three measurements. The deviation was found to be less than 2% and final values are plotted as mean values of replicates, with standard deviations obtained according to statistical analysis tools.
Adsorption/desorption and dilatational rheology measurements were made using an OCTOPUS (WO2012080536-A1). This is a Pendant Drop Surface Film balance equipped with a subphase multi exchange device.43 The OCTOPUS is fully automated by computer software DINATEN® and CONTACTO®. The detection and calculation of surface area and surface tension are based on axisymmetric drop shape analysis (ADSA). The pendant drop is placed on a three-axis micropositioner and is immersed in a glass cuvette (Hellma®) which is kept in an externally thermostated cell, which was varied from 20 to 55 °C during the experiments. The adsorption/desorption curves comprised three steps: adsorption, dilatational rheology and desorption. A microgel solution droplet is formed at the tip of the double capillary and the surface tension is recorded at constant surface area. Then, we measure the dilatational rheology of the surface by applying an oscillatory perturbation to the surface, by injecting and extracting volume into the pendant drop. The system records the response of the surface tension to this area deformation, and the dilatational modulus (E) of the interfacial layer is calculated from this response. In a general case, the dilatational modulus is a complex quantity that contains a real and an imaginary part
| E = E′ + iE′′ = ε + iνη | (1) |
Langmuir monolayers were measured using a Langmuir film balance equipped with a paper Wilhelmy plate pressure measuring system (KSV) with a sensitivity of 0.1 mN m−1 and a total area of 244.5 cm2. The whole setup is located in a transparent Plexiglas case to avoid air streams and dust deposition connected to a thermostat. The system records the evolution of the surface pressure (Π) as the available surface is compressed. The surface pressure is defined as Π = γ0 − γ, γ0 being the surface tension of the pure water surface. The absence of surface active contaminants was verified by compressing the bare water subphase, obtaining values of Π < 0.2 mN m−1 within the whole compression cycle. The Π–A isotherms were recorded at two temperatures well below and above the transition temperature of the microgels, namely 20 °C and 45 °C respectively. The samples were incubated at the required temperature for 15 min before spreading. Then, the microgel solution (0.5 g l−1 in pure water) was carefully spread on the subphase by means of a microsyringe (Hamilton®). After an equilibration time of 15 min, we record the surface pressure–area (Π–A) isotherm upon symmetric uniaxial compression at a constant rate of 5 mm min−1. Various amounts of solution (50–200 μl) were spread in different experiments to cover the whole compression isotherm at 20 °C while 300 μl were spread to obtain the isotherm at 45 °C. The number of measurements needed was determined depending on the variability of the results and standard deviations obtained. In particular, 3 replicates were needed for the measurements at 45 °C, where deviation was found to be less than 2%, whereas 6 repetitions were needed at 20 °C, where deviations ranged from 2 to 8%.
3 Results and discussion
3.1 Swelling behavior
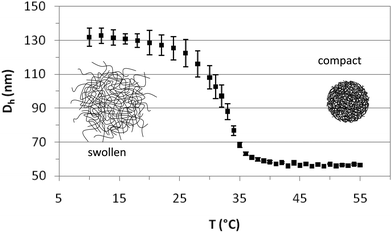
The PVCL charged microgels were first characterized by dynamic light scattering (DLS) to determine their average size, the temperature dependence of the hydrodynamic diameter (Dh), the temperature range of the volume phase transition (VPTT) and the swelling ratio. Fig. 1 depicts the average hydrodynamic diameter of the microgels as a function of temperature. The polydispersity has been calculated by light scattering and the results shown as error bars. As observed, Dh remains constant at temperatures below 20 °C and above 40 °C. The VPTT lies around 32 °C in close agreement with literature values.42 The hydrodynamic diameter of the microgels decreases from 131 ± 3 nm to 56.5 ± 0.5 nm, when the temperature increases from 20 °C to 40 °C, indicating that the internal volume fraction of the microgels increases with increasing temperature. The values are in agreement with those reported in the literature,40,42 and fall within the nanometric scale. The swelling ratio depends fundamentally on the amount of crosslinker used in the synthesis and despite the differences in size the swelling ratio obtained for PVLC based microgels is similar to that reported for PNIPAM based microgels with the same amount of crosslinker.6,40 The variation of temperature induces a change in the hydrophilic/hydrophobic balance of microgels, which leads to a variation in size. The collapse of microgel particles is due to the destruction of hydrogen bonds in the structure of the microgel as the temperature increases above the VPTT. This induces the increase of hydrophobic attractions between polymer chains, leading to the exclusion of water and consequently, to the shrinking of the microgels.13 The PVCL microgel synthesized and used in this work also contains a significant amount of AA (Table 1) which provides the microgel with surface charge.42 Most of the studies in the literature deal with neutral PNIPAM microgels, and this also will possibly make a difference in the characterization.6Fig. 2 illustrates the SEM images of the PVLC microgels. As observed, particles are approximately circular in appearance. The SEM images illustrate the diameter of the dehydrated particle. The values obtained for the diameter in the SEM images practically coincide with those obtained for the compact microgel in Fig. 1, corresponding to the dehydrated particle.
3.2 Gibbs monolayer: dynamics, adsorption and surface rheology
Fig. 3 shows the dynamic adsorption curves of the microgel solution at a fixed concentration of 0.02% w/w recorded at different temperatures below and above the VPTT. In all cases the surface tension decreases with time and eventually attains a plateau. The adsorption of microgels at the air–water interface involves two processes: diffusion of particles towards the interface followed by a much slower reconfiguration of the microgels at the surface.24,34,40 In Fig. 3 we observe clearly these two distinct adsorption regimes, similar to the adsorption of concentrated solutions of surfactants and proteins.44 The dynamic curves comprise a first stage with a sharp decline of the surface tension followed by a second stage in which the variation is much less pronounced. The first adsorption stage is in general size dependent and the decreasing slope illustrates the diffusion of particles onto the air–water interface.24 The second stage is the result of balancing the hydrophobic and hydrophilic moieties to minimize the free energy at the surface (unfolding of polymer chains to optimal conformation). These general trends agree with the dynamic adsorption curves of PNIPAM based microgel solutions published elsewhere.24,34,40 There are, however, no reported results of dynamic adsorption of PVCL microgel solutions in the literature.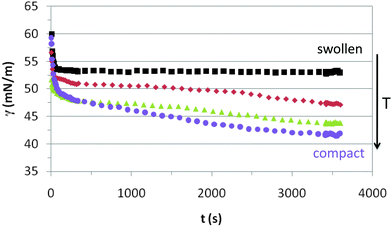 | ||
| Fig. 3 Dynamic surface tension of 0.02% w/w PVLC microgel adsorption onto the air–water interface. Squares: 20 °C, rhomboids: 30 °C, triangles: 45 °C, circles: 55 °C. | ||
The adsorption kinetics of PVLC based microgels in Fig. 3 show similar slopes in the first regime, indicating similar diffusion rates below and above the VPTT. Instead, the impact of temperature appears more evident in the final surface tension attained after the sharp decline, which is higher above the VPTT. Accordingly, this is an indication of a higher number of particles reaching the surface at a rather similar rate as the temperature increases in the system, namely as the microgel particles are more compact. This correlates with the data of Zielińska and coworkers, who reported that the amount of particles adsorbed at the air–water interface increases for more crosslinked microgels.22 Hence, the more compact structure of the microgels above the VPTT allows the accommodation of a higher number of particles and a more efficient packing at the interface. The quasi-equilibrium regime shows that the surface tension reduces slightly over time accounting for surface deformation of the microgels upon adsorption. However, it is difficult to assess the differences between swollen and collapsed states as the high concentration of the surface layer counteracts the different deformability of the nanoparticles below and above the VPTT. This will be analyzed in more detail later on in this paper. Also, the structural changes induced in the particles by surface conformational changes will be addressed specifically in the monolayer study.
After adsorption at the constant surface area for 1 h and once a stationary state is clearly reached (Fig. 3), we replaced the bulk subphase with pure water by using the subphase exchange accessory. We observed no change in surface tension during, or after, the subphase exchange (results not shown). Thus, we can conclude that microgels do not spontaneously desorb from the air–water interface after adsorption. Similar results were obtained by Pinaud and coworkers for PNIPAM microgels at the dodecane–water interface.35 These are important findings supporting the conformational change undergone by microgels upon adsorption and the stability of the adsorbed layers. Moreover, the formation of stable layers at the air–water interface also allows the use of a Langmuir film balance to study the monolayers of PVLC microgels.
Fig. 4 shows the quasi-equilibrium surface tension values obtained for PVLC microgels as a function of temperature. As predicted from the dynamic curves in Fig. 3, the final surface tension, after 1 hour adsorption at constant surface area, decreases with temperature. Specifically, below the VPTT, the values decrease significantly while they reach a quasi-plateau after the VPTT. Wu and coworkers found a similar plateau for PVLC particles at the toluene–water interface.40 At T < VPTT, the swollen microgel particles are very deformable and reorient the hydrophobic moieties towards the air phase so as to cover the interface as much as possible. Recent neutron reflectivity experiments clearly show that swollen microgels confined at the air–water interface adopt a core–shell structure, with a highly crosslinked central region surrounded by a more diluted shell of polymer chains that spread out at the interface and towards the bulk solution.22 These morphological changes of the particles at the surface then lead to connections between adjacent particles forming a loose surface layer.26 Conversely, at T > VPTT, the collapsed microgel particles are less deformable and more rigid. Accordingly, the maximum coverage of the surface is achieved at a higher number of particles and a closer packing density, resulting in a more compact surface layer. This agrees with findings from ellipsometry41 and neutron reflectivity22 for PNIPAM based microgels, showing the increase in adsorption density as the microgel collapses. Moreover, this explains the lower surface tension reached above the VPTT in Fig. 4. The morphology of the adsorbed layers is illustrated schematically in Fig. 4. Namely, a loosely packed layer composed of swollen microgel particles is formed bellow the VPTT and a more condensed layer with higher density is formed above the VPTT.
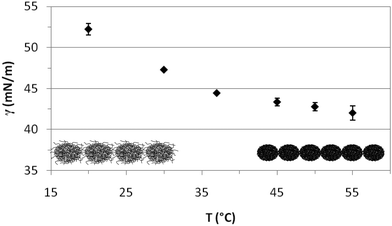 | ||
| Fig. 4 Variation of the quasi-equilibrium surface tension with temperature (1 h adsorption) for PVLC microgel adsorbed layers at the air–water interface (0.02% w/w). | ||
The interfacial behavior of PVLC microgel particles differs from that of PNIPAM microgel particles reported in the literature. PNIPAM particles present a minimum value of interfacial tension around the VPTT rather than the plateau shown for PVLC particles.27,40 The increase in interfacial tension for temperatures above the VPTT is attributed in the literature to the formation of loose aggregates,27 the possible existence of a surface gel41 or the formation of a loosely packed microgel.35 Anyhow, this increase at high temperatures accounts for the lower stability of PNIPAM emulsions above the VPTT. These differences between PNIPAM and PVCL adsorbed layers have also been reported by Wu and coworkers at the toluene/water interface,40 but these authors do not provide an explanation for this different behavior. Nonetheless, the constant value of surface tension above the VPTT for PVLC microparticles suggests the formation of a more stable surface layer on emulsified systems than PNIPAM. On the one hand, this stability could be attributed to the enhanced electrostatic repulsion between the immersed parts of the microgels, which arises when the microgel shrinks. Indeed, charged microgels show a larger effective charge in the shrunken state due to the steric exclusion of the excess counterions from the internal region exerted by the crosslinked polymer network.45,46 On the other hand, the higher condensing ratio of PVLC microgels6 could result in a better packing at the surface resulting in a more stable conformation, resistant to aggregation above the VPTT. Brugger et al. concluded that the presence of charges strongly influences the behavior of charged PNIPAM-co-MAA microgels at oil–water interfaces.26 In particular, the authors showed how the deprotonation of the MAA moieties leads to local amphiphilicity that affects the chain conformation. Moreover, the comparison between the compression isotherms of charged and uncharged microgels indicates that increasing the number of charges in the microgel does not lead to emphasized electrostatic repulsion. Instead, it causes a significant reduction of the surface pressure, which has been attributed to the highest softness of the charged microgels.32 In this sense, some authors point out that the unexpected influence of charges on the compression behaviour of microgel-covered oil–water interfaces has not been explained in detail yet.35 Accordingly, this is an important issue that can have implications for emulsion development and will be explored in a future work.
In order to further explore the characteristics of adsorbed layers of microgels we measured the dilatational rheology after adsorption for 1 h at constant surface area.47,48 There is little work published on the dilatational rheology of microgels at fluid interfaces, and among them, there is a large variability in the published results of dilatational rheology of adsorbed layers of microgels at fluid interfaces.34,35 This is possibly because this magnitude is strongly influenced by the molecular structure and hence small variations in the composition (crosslinker, charge,…) of the microgel can affect severely the obtained parameters.47 In particular, we have found no studies of the dilatational rheology of PVLC based microgels at the fluid interface to date.
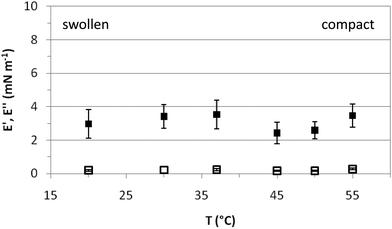
Fig. 5 shows the response of the surface layers, characterized in Fig. 3 and 4, to an imposed deformation. This response is characterized by the elastic (E′) and loss (E′′) moduli of the microgel covered interface at various temperatures. In the entire temperature range, E′ is larger than E′′, indicative of solid-like behavior.34 The elastic moduli obtained for PVLC adsorbed layers range between 2 and 4 mN m−1 for all temperatures, which is just significantly higher than the residual elasticity of the pure air–water interface. However, these results are of the same order as other reported works on PNIPAM based particles adsorbed at fluid interfaces26,29,34 and one order of magnitude lower than those reported by Pinaud and coworkers.35E′ is a measure of the response of the surface layers to surface tension gradients and is sensitive to the diffusion of molecules between the bulk solution and the interface.49 For interfaces covered with irreversibly adsorbed species such as polymers, the dilatational modulus is a complex balance between inter and intramolecular interactions within the adsorbed layers, including the intrinsic mechanical properties of the adsorbed material. Data in Fig. 5 show that E′ is very low in the whole range of surface coverage, below and above VPTT. This indicates the formation of a very loose adsorbed layer with low cohesivity between polymer chains.
3.3 Langmuir monolayer
The properties of surface layers of the microgels build up upon adsorption onto a fluid interface are weakly influenced by the temperature as demonstrated in Fig. 3–5 and in agreement with literature works.26,27,29,35 An additional complication in adsorption experiments is that the surface coverage is not constant. Further adsorption from bulk solution can take place as the size of particles decreases with temperature. Hence, this can counteract the surface deformation caused by the microgel particles.35 To gain a more comprehensive understanding of the temperature effect on the surface conformation of microgels we have used Langmuir monolayers. In these experiments, the number of particles at the interface is constant over the whole range of surface coverage, i.e. the compression range. Hence, the picture provided by these experiments can importantly complement the findings obtained from adsorption layers.Fig. 6 shows the compression isotherms of PVLC microgels below and above the VPTT. The isotherms are normalized to the number of particles at the surface and then represented versus the inter-particle distance, r. This distance is obtained assuming that the particles homogeneously distribute as flat disks at the air–water interface. The number of particles has been calculated considering that, in the collapsed state, the internal polymer volume fraction of the microgels is composed of 70 wt% polymer and 30 wt% water. From the hydrodynamic diameter measured in the collapsed state and the density of the polymer 1.029 g ml−1 we obtain the volume per particle and hence the mass of the polymer particle. This representation allows for an interpretation of the microgel deformation and the packing at the surface upon compression. It can be seen that the shape of the compression isotherm is strongly influenced by the temperature obtaining a clear difference between the swollen and the collapsed states (Fig. 6). The shape of the swollen microgels is similar to results published for PNIPAM microgels below the VPTT.32,33,35 We have found much less literature concerning monolayers in the collapsed state. Hence, to our knowledge, this study is the first to provide comparative compression isotherms of microgels in the collapsed and swollen states.
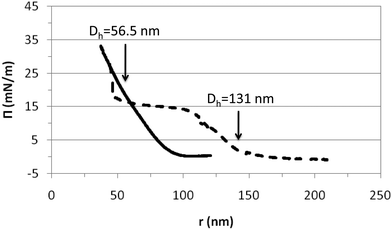 | ||
| Fig. 6 Compression isotherms of PVLC microgels obtained above and below the VPTT. The surface pressure is plotted versus the inter-particle distance (r) assuming a disc-shape. Solid line: 45 °C (collapsed state); dashed line: 20 °C (swollen state). The arrows indicate the hydrodynamic diameters obtained for the collapsed and swollen microgel conformations in Fig. 1. | ||
From Fig. 6 we may distinguish various compression regimes for the microgel in the swollen state. In the first regime, microgels behave as a gas of non-interacting particles leading to the absence of surface pressure. This corresponds to an inter-particle distance larger than the diameter of the swollen particle in bulk according to Fig. 1 (r > 150 nm). The second regime shows a continuous increase of the surface pressure. In this regime, the inter-particle distance is of the order of the diameter of the swollen particles, namely 100 nm < r < 150 nm (Fig. 1). Experimental results obtained by Rey and coworkers clearly show that within this compression regime, microgels are already structured into a 2D hexagonal lattice, with their external shells partially overlapped. Hence, this increase corresponds to the repulsion exerted by the microgel shells when they are mutually interpenetrated.50 The high deformability of the particle in the swollen state means that the structure can deform and reorient the hydrophobic residues onto the air–water interface. Upon further compression, in fact, the surface pressure rises steeply and the work done onto the system goes into compressing the particle coronas, resulting in a continuous change in the lattice constant of the 2D hexagonal packing.
In a third regime, the surface pressure becomes constant as the inter-particle distance is decreased. Classically for lipids, this plateau is described as the coexistence between expanded and condensed phases.51 In the case of microgel particles, this plateau indicates that two packing states coexist at the surface while the density of the polymeric chain at the surface is constant. The two coexisting states would correspond to highly compressed microgels with an inter-particle distance equal to the Dh at 45 °C (compact) and less compressed microgels with an inter-particle distance equal to the Dh at 20 °C (swollen). Another possibility is that within this regime, all particles remain in a swollen conformation and, as the compression proceeds, some segments are forced into the subphase to maintain the surface density. Both hypotheses imply that microgels are soft and deformable particles in this plateau as also suggested by Pinaud and coworkers.35 This plateau maintains until reaching inter-particle distances equal to the diameter of the compact particles: 55 nm (Fig. 1). Then, a second increase of surface pressure arises. This increase appears to be very sharp and maintains at an inter-particle distance of approximately 50 nm. At this stage it becomes difficult to compress the microgels further. The fourth regime corresponds to the condensed phase and we assume that the particles are in a contracted state similar to the collapsed state after the VPTT.
The compression isotherm recorded for the microgels in the collapsed state, above VPTT (45 °C) shows a different distribution of compression regimes (Fig. 6). The first regime, comprised of non-interacting particles leading to the absence of surface pressure, maintains now until much lower inter-particle distance and already within the volume phase transition in Fig. 1 (r < 100 nm). The monolayer then enters into a second regime in which the surface pressure increases continuously until collapse. For inter-particle distances larger than the microgel diameter, the electrostatic repulsion plays the dominant role. However, for r < Dh ≈ 55 nm, the free energy arising from the deformation of the polymer network is expected to be more relevant. The fact that collapsed microgels do not show any transition region suggests that the interaction is now occurring directly between the core of the particles through an elastic repulsive pair potential. Hence, this regime would directly correspond to a condensed state in which microgels are compressed in a collapsed state at the surface. Furthermore, compression isotherms recorded in the swollen and collapsed state overlap at an inter-particle distance of the order of magnitude of dehydrated (or collapsed) microgels (Fig. 6). This suggests that the compression of swollen PVLC microgels at the surface leads to dehydration of the structure and promotes a transition between swollen and collapsed states. Also, it proves that soft PVLC particles present some common features with proteins, which are able to adapt their conformation to the interfacial environment by surface denaturation.35
From the compression isotherms we can also have a guess of how the microgel–microgel effective pair potential, u(r), looks like, at least qualitatively. For the particular case of swollen microgels (20 °C), as the particles get closer during the compression of the monolayer and the external shells overlap, the increase of the surface pressure implies the existence of a repulsive interaction. In principle, this interaction should have two contributions: an electrostatic term and a soft elastic repulsion caused by the loss of entropy of the polymer chains when overlap. However, the fact that upon further compression the surface pressure becomes roughly constant for a range of inter-particle distances means that an additional overlap does not involve a significant free energy cost. In other words, once the particles are forced to reach some degree of overlap, the microgel pair potential can be modelled by a penetrable potential with a constant repulsion, u(r) ≈ ε > 0 for 0.4Dh < r < 0.8Dh. This implies that the microgel shell deforms without compressing the polymer network, as already suggested by Peláez and coworkers in dense microgel bulk suspensions.52 This penetrable potential leads, in bulk solutions, to broad phase coexistence regions where the particles join together to form clusters.53 Therefore, although bulk and the interface are indeed very different geometries, the fact that the equation of state shows a phase transition at large packing fractions means that the deformation of the shell without compression is a common feature in both situations. Our experimental observations and direct visualizations performed by Rey and coworkers show that these clusters are formed by microgels with their mutual cores touching each other, where the number of particles per cluster increases with the monolayer compression.50 As already discussed, additional monolayer compression leads to the overlap of the microgel cores, which brings another increase of the surface pressure. In this case, the crosslinked polymer network of the particles is compressed, and the effective repulsion becomes dominated by the elastic free energy, which is strongly dependent on the inter-particle separation. In this case, an Hertzian model would be able to capture the physics for these inter-particle distances, u(r) = u0(r0 − r)5/2 for r < r0, where u0 > 0 and r0 is of the order of the core diameter.52
It should be emphasized that this picture based on effective potentials is not enough to correctly estimate the surface pressure obtained experimentally. Indeed, the surface pressure calculated from this approximation scales as Π ∼ kBT/Dh2, which leads to values of the order of μN m−1, whereas experimental results provide values about 10 mN m−1, i.e. 4 orders of magnitude larger. This huge difference between theoretical and experimental data has been attributed to the internal degrees of freedom of the polymer network inside the microgel particle, which also contributes to the pressure.54 For this kind of soft nanoparticle, the pressure scales as Π ∼ kBT/dcross2, where dcross is the size of the correlated domains inside the particle, typically given by the separation between two neighbouring crosslinkers.31 In our particular case, for collapsed microgels we estimated a value of dcross ≈ 3–4 nm, so the surface pressure deduced theoretically from the effective interactions must be rescaled by a factor of (Dh/dcross)2 ∼ 104, which leads to values of the order of the experimental results. Nevertheless, future research should focus on supporting this rescaling argument with more accurate theoretical models. This will provide a deeper understanding of the role that the polymer chain fluctuations play in the surface pressure of adsorbed microgels.
4 Conclusions
We have carried out a complete surface characterization of a new type of ionic microgel, based on PVCL, considered to have better biocompatibility than the more commonly used PNIPAM. The Dh of the PVCL microgel decreases from 131 nm to 56.5 nm, when the temperature increases from 20 °C to 40 °C. The dynamic surface tension plot shows two adsorption regimes, similar to the classic kinetics of protein adsorption. The results clearly indicate that a higher number of particles reach the surface above the VPTT while the diffusion coefficient remains unchanged. We evaluate also the influence of the swelling state in the quasi-equilibrium surface tension values, obtaining that the surface tension decreases below the VPTT while it maintains above the VPTT. This behavior indicates that the surface accommodates a higher number of particles and a closer packing density as the microgel collapses, resulting in a more compact surface layer. The plateau above the VPTT contrasts with a well reported minimum for PNIPAM around the VPTT and suggests a more efficient packing at the surface resulting in a more stable conformation, resistant to aggregation above the VPTT. Dilatational rheology data show the formation of a very loose adsorbed layer with low cohesivity within the whole range of surface coverage.The PVCL microgels confined to a 2D monolayer under forced compression show two different behaviors depending on whether the system is above or below the VPTT. On the one hand, the elastic and electrostatic repulsion between collapsed microgels leads to a continuous increase of the surface pressure. On the other hand, swollen microgels display a phase transition at intermediate surface pressures similar to soft polymers, which is attributed to the displacement of the polymer chains in the external shell of the particles, induced by the shell overlapping. In other words, the loose external polymer chains are forced into the subphase by keeping the free energy of the system constant. Therefore, the evolution of the surface pressure allows identifying the interaction of the shells and cores as the inter-particle distance decreases in the monolayer by comparison with the Dh of the microgels. New insights arise from calculations of the surface pressure of the particles alone, obtaining values four orders of magnitude larger than the theoretical predictions obtained using effective pair potentials. This effect points out the importance of the internal degrees of freedom within the particles. All these results represent important findings for the rational use of microgels in emulsified systems.
Acknowledgements
The authors thank the Spanish “Ministerio de Economa y Competitividad (MINECO), Plan Nacional de Investigación, Desarrollo e Innovación Tecnológica (I + D + i)” (Projects FIS2016-80087-C2-1-P, MAT2013-43922-R and MAT2015-63644-C2-1-R), the European Regional Development Fund (ERDF), the “Ramón y Cajal” program (RYC-2012-10556), and the COST action COST-MPN-1106-Green Interfaces. Drs Jacqueline Forcada, Josetxo Ramos and Miguel A. Fernández-Rodríguez are gratefully acknowledged for helpful discussions and assistance during the microgel synthesis.References
- A. Noro, M. Hayashi and Y. Matsushita, Soft Matter, 2012, 8, 6416 RSC.
- R. Pelton and T. Hoare, Microgel Suspensions, Wiley-VCH Verlag GmbH & Co. KGaA, 2011, pp. 1–32 Search PubMed.
- J. Ramos, A. Imaz, J. Callejas-Fernández, L. Barbosa-Barros, J. Estelrich, M. Quesada-Pérez and J. Forcada, Soft Matter, 2011, 7, 5067–5082 RSC.
- C. Alexander, Nat. Mater., 2008, 7, 767–768 CrossRef CAS PubMed.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS PubMed.
- J. Ramos, A. Imaz and J. Forcada, Polym. Chem., 2012, 3, 852 RSC.
- M. Ledesma-Motolinía, M. Braibanti, L. F. Rojas-Ochoa and C. Haro-Pérez, Colloids Surf., A, 2015, 482, 724–727 CrossRef.
- M. Quesada-Pérez, J. Ramos, J. Forcada and A. Martn-Molina, J. Chem. Phys., 2012, 136, 244903 CrossRef PubMed.
- C. H. Lee and Y. C. Bae, Macromolecules, 2015, 48, 4063–4072 CrossRef CAS.
- S. C. Jung, S. Y. Oh and Y. Chan Bae, Polymer, 2009, 50, 3370–3377 CrossRef CAS.
- M. Quesada-Pérez, J. A. Maroto-Centeno, J. Forcada and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 10536 RSC.
- Y. Hertle, M. Zeiser, C. Hasenöhrl, P. Busch and T. Hellweg, Colloid Polym. Sci., 2010, 288, 1047–1059 CAS.
- B. Sierra-Martin, J. J. Lietor-Santos, A. Fernandez-Barbero, T. T. Nguyen and A. Fernandez-Nieves, Microgel Suspensions, Wiley-VCH Verlag GmbH & Co. KGaA, 2011, pp. 73–116 Search PubMed.
- M. Quesada-Pérez, J. G. Ibarra-Armenta and A. Martn-Molina, J. Chem. Phys., 2011, 135, 094109 CrossRef PubMed.
- M. Quesada-Pérez, J. A. Maroto-Centeno and A. Martn-Molina, Macromolecules, 2012, 45, 8872–8879 CrossRef.
- M. Quesada-Pérez and A. Martn-Molina, Soft Matter, 2013, 9, 7086–7094 RSC.
- S. M. Lee and Y. C. Bae, Macromolecules, 2014, 47, 8394–8403 CrossRef CAS.
- M. Quesada-Pérez, S. Ahualli and A. Martn-Molina, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 1403–1411 CrossRef.
- M. Quesada-Pérez, S. Ahualli and A. Martn-Molina, J. Chem. Phys., 2014, 141, 124903 CrossRef PubMed.
- I. Adroher-Benítez, S. Ahualli, A. Martín-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Macromolecules, 2015, 48, 4645–4656 CrossRef.
- P. González-Mozuelos, J. Chem. Phys., 2016, 144, 54902 CrossRef PubMed.
- K. Zielińska, H. Sun, R. A. Campbell, A. Zarbakhsh and M. Resmini, Nanoscale, 2016, 8, 4951–4960 RSC.
- Z. Li, K. Geisel, W. Richtering and T. Ngai, Soft Matter, 2013, 9, 9939 RSC.
- J. Zhang and R. Pelton, Langmuir, 1999, 15, 8032–8036 CrossRef CAS.
- V. Nerapusri, J. L. Keddie, B. Vincent and I. A. Bushnak, Langmuir, 2006, 22, 5036–5041 CrossRef CAS PubMed.
- B. Brugger, S. Rütten, K. H. Phan, M. Moller and W. Richtering, Angew. Chem., 2009, 48, 3978–3981 CrossRef CAS PubMed.
- C. Monteux, C. Marliere, P. Paris, N. Pantoustier, N. Sanson and P. Perrin, Langmuir, 2010, 26, 13839–13846 CrossRef CAS PubMed.
- K. Geisel, L. Isa and W. Richtering, Langmuir, 2012, 28, 15770–15776 CrossRef CAS PubMed.
- Y. Cohin, M. Fisson, K. Jourde, G. G. Fuller, N. Sanson, L. Talini and C. Monteux, Rheol. Acta, 2013, 52, 445–454 CrossRef CAS.
- O. S. Deshmukh, D. van den Ende, M. C. Stuart, F. Mugele and M. H. G. Duits, Adv. Colloid Interface Sci., 2014, 222, 215–227 CrossRef PubMed.
- O. S. Deshmukh, A. Maestro, M. H. Duits, D. van den Ende, M. a. Cohen-Stuart and F. Mugele, Soft Matter, 2014, 9, 2731–2738 Search PubMed.
- K. Geisel, L. Isa and W. Richtering, Angew. Chem., 2014, 53, 4905–4909 CrossRef CAS PubMed.
- K. Geisel, W. Richtering and L. Isa, Soft Matter, 2014, 10, 7968 RSC.
- Z. Li, W. Richtering and T. Ngai, Soft Matter, 2014, 10, 6182–6191 RSC.
- F. Pinaud, K. Geisel, P. Massé, B. Catargi, L. Isa, W. Richtering, V. Ravaine and V. Schmitt, Soft Matter, 2014, 10, 6963–6974 RSC.
- K. Geisel, A. A. Rudov, I. I. Potemkin and W. Richtering, Langmuir, 2015, 31, 13145–13154 CrossRef CAS PubMed.
- Z. Li and T. Ngai, Nanoscale, 2013, 5, 1399–1410 RSC.
- H. Mehrabian, J. Harting and J. H. Snoeijer, Soft Matter, 2015, 12, 1–17 Search PubMed.
- R. W. Style and E. R. Dufresne, Soft Matter, 2015, 11, 1–8 Search PubMed.
- Y. Wu, S. Wiese, A. Balaceanu, W. Richtering and A. Pich, Langmuir, 2014, 30, 7660–7669 CrossRef CAS PubMed.
- L. T. Lee, B. Jean and a. Menelle, Langmuir, 1999, 15, 3267–3272 CrossRef CAS.
- A. Imaz and J. Forcada, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 3218–3227 CrossRef CAS.
- J. Maldonado-Valderrama, A. Torcello-Gómez, T. del Castillo-Santaella, J. A. Holgado-Terriza and M. A. Cabrerizo-Vlchez, Adv. Colloid Interface Sci., 2015, 222, 488–501 CrossRef CAS PubMed.
- J. Maldonado-Valderrama, V. B. Fainerman, E. Aksenenko, M. Jose Gálvez-Ruiz, M. A. Cabrerizo-Vlchez and R. Miller, Colloids Surf., A, 2005, 261, 85–92 CrossRef CAS.
- A. Moncho Jordá and J. Dzubiella, Phys. Chem. Chem. Phys., 2016, 18, 5372–5385 RSC.
- A. Moncho-Jordá, J. Chem. Phys., 2013, 139, 064906 CrossRef PubMed.
- J. Maldonado-Valderrama and J. M. R. Patino, Curr. Opin. Colloid Interface Sci., 2010, 15, 271–282 CrossRef CAS.
- J. Maldonado-Valderrama, A. Martn-Rodriguez, M. J. Gálvez-Ruiz, R. Miller, D. Langevin and M. a. Cabrerizo-Vlchez, Colloids Surf., A, 2008, 323, 116–122 CrossRef CAS.
- D. Langevin, Adv. Colloid Interface Sci., 2000, 88, 209–222 CrossRef CAS PubMed.
- M. Rey, M. A. Fernández-Rodríguez, M. Steinacher, L. Scheidegger, K. Geisel, W. Richtering, T. Squires and L. Isa, Soft Matter, 2016, 12, 3545–3557 RSC.
- G. Luque-Caballero, A. Martn-Molina, A. Y. Sánchez-Treviño, M. A. Rodríguez-Valverde, M. A. Cabrerizo-Vílchez and J. Maldonado-Valderrama, Soft Matter, 2014, 10, 2805–2815 RSC.
- M. Peláez-Fernández, A. Souslov, L. A. Lyon, P. M. Goldbart and A. Fernández-Nieves, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- C. N. Likos, M. Watzlawek and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 58, 16 CrossRef.
- R. D. Groot and S. D. Stoyanov, Soft Matter, 2010, 6, 1682 RSC.
| This journal is © The Royal Society of Chemistry 2017 |