Chain conformations and phase behavior of conjugated polymers
Brooke
Kuei
a and
Enrique D.
Gomez
*bc
aDepartment of Materials Science and Engineering, The Pennsylvania State University, University Park, PA 16802, USA
bDepartment of Chemical Engineering, The Pennsylvania State University, University Park, PA 16802, USA. E-mail: edg12@psu.edu
cMaterials Research Institute, The Pennsylvania State University, University Park, PA 16802, USA
First published on 1st August 2016
Abstract
Conjugated polymers may play an important role in various emerging optoelectronic applications because they combine the chemical versatility of organic molecules and the flexibility, stretchability and toughness of polymers with semiconducting properties. Nevertheless, in order to achieve the full potential of conjugated polymers, a clear description of how their structure, morphology, and macroscopic properties are interrelated is needed. We propose that the starting point for understanding conjugated polymers includes understanding chain conformations and phase behavior. Efforts to predict and measure the persistence length have significantly refined our intuition of the chain stiffness, and have led to predictions of nematic-to-isotropic transitions. Exploring mixing between conjugated polymers and small molecules or other polymers has demonstrated tremendous advancements in attaining the needed properties for various optoelectronic devices. Current efforts continue to refine our knowledge of chain conformations and phase behavior and the factors that influence these properties, thereby providing opportunities for the development of novel optoelectronic materials based on conjugated polymers.
1. Introduction
The combination of semiconducting properties, chemical versatility and polymeric mechanical properties within conjugated polymers is unique. Often, conjugated polymers are functionalized with solubilizing side chains,1,2 thereby enabling solution processing and additive manufacturing.3–5 Thus, this set of materials will likely make an impact in optoelectronic devices with flexible form factors,6–11 portable biomedical devices that can integrate with the body,12–16 and devices capable of distributed power generation.17–19 But, to access the full potential of conjugated polymers, a concrete connection must be made between chemical structure, morphology and macroscopic properties.The electronic properties of conjugated polymers and hence their performance in electronic applications are intimately tied to the conformations of polymer chains and how chains are ordered within films.20–23 Theoretical descriptions of polymers in general begin with the chain conformation, or assumptions of the stiffness of the chain. For example, in solution, chain conformations likely impact assembly in the film and chain conformations in the melt (films) affect the formation of liquid crystalline phases, crystallization, and packing of chains. Conjugated polymers are stiffer than common flexible polymers such as polyethylene, but there are only a few measurements of the persistence length in the literature. We dedicate the first section of this article to chain conformations of conjugated polymers.
In the second half of this review, we discuss the phase behavior of conjugated polymers; specifically, we highlight the crystalline and liquid crystalline phases found in homopolymers, and discuss mixing with solvents, fullerene and other polymers. Solvent choice is a common way to tune the properties of polymeric active layers and therefore the performance of organic electronic devices, and mixing with small molecules such as fullerene lead to significantly enhanced optoelectronic properties, yet open questions remain on determining the solubilities of these materials.24–26 For example, the phase behavior in polymer–fullerene active layers strongly affects charge photogeneration efficacy in photovoltaic devices,27,28 and it is hypothesized that an optimum miscibility exists between the components of the active layer to maximize photovoltaic device performance.29,30 Blending of polymers with conjugated and non-conjugated polymers also has the potential to enhance optoelectronic properties;31,32 for example, blending of different kinds of polymers in the active layer has improved the photoluminescence and electroluminescence efficiencies in LED devices.33 Mixtures containing conjugated polymers, however, are complex because they potentially contain semicrystalline and liquid crystalline components, making the description of the phase behavior challenging.
In this review article, we summarize current knowledge of chain conformations and phase behavior of conjugated polymers. In the first section, we focus on how to measure and predict persistence lengths and what factors influence chain conformations. In the second section, we discuss the phase behavior of conjugated polymers, particularly for homopolymers and mixtures of polymers with small molecules and other polymers. We highlight both emerging concepts to describe such systems, as well as experimentally observed phase behavior.
2. Are conjugated polymers rigid rods, Gaussian coils, or worm-like chains?
Polymer chains without specific intrachain interactions are either random coils (flexible), worm-like (semiflexible), or rigid rods (stiff). The stiffness of chains depends on the length scale; macromolecules that are very stiff locally, such as DNA, behave as random coils when the degree of polymerization is very large and we consider macroscopic properties, such as the viscosity.34,35 The backbone stiffness is described by the persistence length lp, which is the characteristic length scale for the exponential decay of the correlations of backbone tangents and is half the Kuhn length.36 In other words, the persistence length describes how long it takes for the backbone to bend, on average, by 90 degrees. When lp is small, much smaller than the contour length of the chain, the polymer will behave like a flexible coil. When lp approaches the contour length, the polymer is stiff, or semiflexible. Experimentally, lp can be measured via techniques such as light scattering, small-angle neutron scattering (SANS), and viscosity measurements and can be predicted from computational studies using density functional theory (DFT), molecular dynamics (MD) simulations, or Monte Carlo (MC) simulations.The size of polymer chains is described by the average end-to-end distance 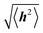 , where h is the sum of the vectors representing monomers in a polymer chain. We can model monomer units making up a polymer backbone by vectors ri with fixed lengths and fixed deflection angles θi between them, as shown in Fig. 1a. The vectors rotate by a dihedral angle ϕi as allowed by the dihedral potential. Thus, if the dihedral potential is known, the persistence length can be extracted by integrating over the distribution of dihedral angles;36 this is known as the hindered rotation model.37 A simplified version is the freely rotating chain model, in which the dihedral potential is simply a constant. The Kratky–Porod chain model based on freely rotating chains gives the relationship for worm-like polymers between 〈h2〉, lp, and the contour length L, which is the length of the polymer chain:
, where h is the sum of the vectors representing monomers in a polymer chain. We can model monomer units making up a polymer backbone by vectors ri with fixed lengths and fixed deflection angles θi between them, as shown in Fig. 1a. The vectors rotate by a dihedral angle ϕi as allowed by the dihedral potential. Thus, if the dihedral potential is known, the persistence length can be extracted by integrating over the distribution of dihedral angles;36 this is known as the hindered rotation model.37 A simplified version is the freely rotating chain model, in which the dihedral potential is simply a constant. The Kratky–Porod chain model based on freely rotating chains gives the relationship for worm-like polymers between 〈h2〉, lp, and the contour length L, which is the length of the polymer chain:
| 〈h2〉 = 2lpL − 2lp2(1 − exp[−L/lp]) | (1) |
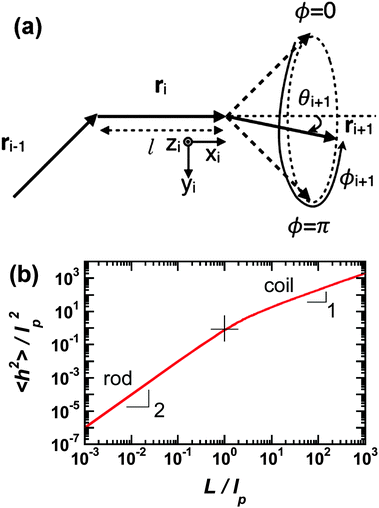 | ||
| Fig. 1 (a) Depiction of the monomer vectors and angles used to construct the freely-rotating and hindered rotation chain models. Monomer units are represented by vectors ri and have fixed lengths and fixed deflection angles θi. They can rotate in a cone with dihedral angle ϕi. Reprinted with permission ref. 36. (b) Average of the end-to-end distance squared (normalized by the persistence length squared) as a function of number of persistence lengths per chain using the freely-rotating worm-like chain model. The rod limit has a slope of 2 and the coil limit a slope of 1. The cross indicates where the chain length is one persistence length. | ||
The persistence lengths of conjugated polymers are governed by the backbone deflection angles and torsional potentials.36 For example, alternating double and single bonds lead to small backbone deflection angles, potentially leading to stiff chain conformations. Also, five-member rings (such as thiophene and selenophene) and other moieties (i.e. pyrrolopyrrole) lead to small deflection angles, circa 15 degrees, and smaller lp. Polymers with six-member rings that have straight backbones such as polyphenylene vinylene (PPV) have zero deflection angles, such that persistence lengths are due to bond-bending along the backbone and are on the order of tens of nanometers.38 As an example, Fig. 2 shows a chain conformation of poly(3-hexylthiophene-2,5-diyl) (P3HT), with a persistence length of 2.8 nm (7 repeat units) and molecular weight of 16.6 kg mol−1 (100 repeat units). The chain is not rod-like, but cannot adopt a random coil conformation either; instead, P3HT behaves as a worm-like chain. The chain can loop and make significant backbone deflections, but over distances larger than seven repeat units.
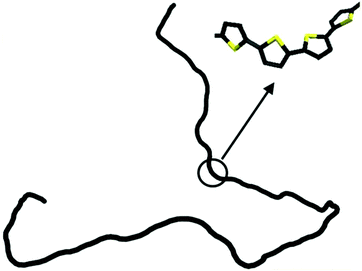 | ||
| Fig. 2 Depiction of a P3HT chain obtained from a dihedral distribution derived using density functional theory. The chain is worm-like, where it can bend significantly over large distances. Reprinted (adapted) with permission from ref. 36. | ||
The next sub-sections highlight the significant progress made on understanding the chain conformations of conjugated polymers. In addition to providing a table of the available persistence lengths, we discuss methods for prediction of the persistence length and present an overview of the different factors that influence chain conformations.
2.1 Measurements of persistence length
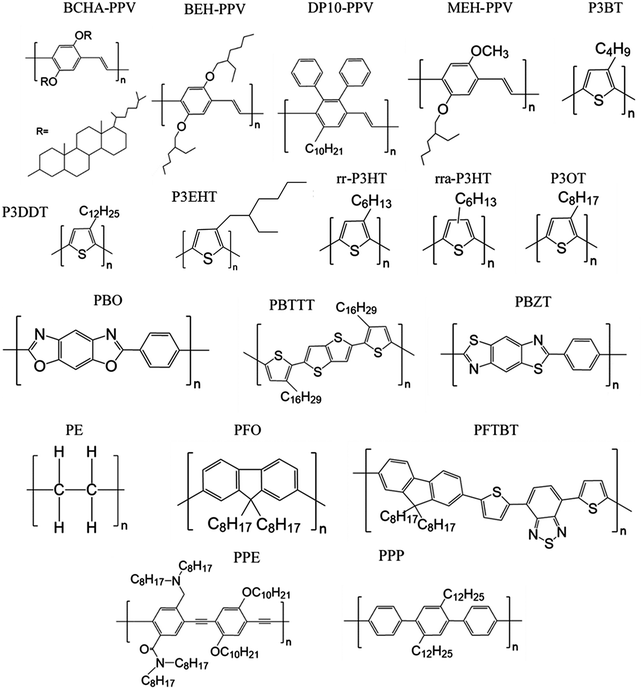
Here we review methods for measuring persistence lengths and tabulate values for common conjugated polymers in Table 1, with the chemical structures shown in Fig. 3. Values from experiment and simulations are included, and are compared to analytical predictions from the freely rotating chain model. A more detailed description of how to predict persistence lengths is discussed in the next subsection.| Polymer | Solvent | Method | Persistence length lp (nm) | Freely rotating chain model |
|---|---|---|---|---|
| a Freely rotating chain model returns lp > 1 μm due to rod-like backbones. Actual lp should be governed by bond bending. | ||||
| P3BT | Nitrobenzene | SANS | 2.7541 | 2.8 |
| rra-P3HT | DCB | SANS | 0.9 ± 0.139 | 2.8 |
| Toluene | SANS | 1.1 ± 0.439 | ||
| rr-P3HT | DCB | SANS | 2.9 ± 0.139 | 2.8 |
| Toluene | SANS | 2.7545 | ||
| Toluene | Viscosity | 2.5 ± 0.245 | ||
| Tetrahydrofuran | Viscosity | 2.2 ± 0.246 | ||
| Tetrahydrofuran | Light scattering | 2.6 ± 0.246 | ||
| DFT dihedral potential | 4.036 | |||
| MD dihedral potential | 3.236 | |||
| MD tangent–tangent correlations | 2.847 | |||
| P3OT | Tetrahydrofuran | Viscosity | 2.2 ± 0.248 | 2.8 |
| Tetrahydrofuran | Light scattering | 2.6 ± 0.548 | ||
| P3BT | Nitrobenzene | SANS | 2.7541 | 2.8 |
| P3EHT | Toluene | SANS | 2.7545 | 2.8 |
| Toluene | Viscosity | 2.5 ± 0.245 | ||
| P3DDT | DCB | SANS | 1.6 ± 0.139 | 2.8 |
| Toluene | SANS | 1.5 ± 0.139 | ||
| PBTTT | Chlorobenzene | Viscosity | 9.049 | 4.1 |
| PFTBT (APFO-3) | MD dihedral potential | 5.936 | 6.6 | |
| PFO | Toluene | Light scattering | 7.052 | 10.9 nm |
| Tetrahydrofuran | Light scattering | 8.653 | ||
| cis-PBO | MSA | Light scattering | 20–3050 | >1 μma |
| MSA | Viscosity | 20–2550 | ||
| MD | 32.551 | |||
| PPP | Chloroform | Light scattering | 2854 | >1 μma |
| Toluene | Viscosity | 15.655 | ||
| MD | 2251 | |||
| trans-PBZT | MD | 21.551 | >1 μma | |
| MEH-PPV | Tetrahydrofuran | Viscosity | 2.2 ± 0.246 | >1 μma |
| Tetrahydrofuran | Light scattering | 2.6 ± 0.22 | ||
| DFT dihedral potential | 4.036 | |||
| BEH-PPV | p-Xylene | Light scattering | 11.02 | >1 μma |
| DP10-PPV | MD tangent–tangent correlations | 2.847 | >1 μma | |
| Chloroform | Light scattering | 6.556 | ||
| Chloroform | MD (coarse-grained) | 25 ± 0.557 | ||
| BCHA-PPV | p-Xylene | Light scattering | 402 | >1 μma |
| PPE | Tetrahydrofuran | Light scattering | 15.058 | >1 μma |
Experimental techniques that can measure the persistence length include small angle neutron scattering (SANS), light scattering, and viscometry. For persistence length measurements of conjugated polymers using SANS, scattering contrast is obtained from either deuterated chains within a nondeuterated melt or between solvent and polymer chains where one component is deuterated.39 The resultant scattering curves can be fitted to several models of scattering from polymer chains,39–41 such as the Debye model,42 the Des Cloizeaux model,43 and the Sharp and Bloomfield model, to determine the radius of gyration.44 The persistence length can then be extracted if the molecular weight of the polymer is known.
Light scattering experiments can also measure the size of polymer chains. Because the wavelength is much larger than that of neutrons and X-rays used in scattering experiments, the accessible range is limited to small scattering vectors. Furthermore, light scattering experiments to determine the size of the chain require polymer chains dispersed in a solvent or other media to generate the needed contrast. Using the Zimm equation, the radius of gyration Rg can be extracted from light scattering data and the persistence length can be inferred.2 Similarly, viscometry of polymer solutions can be used to determine the viscosity-averaged radius of gyration from the Flory–Fox equation.46,59 In both viscometry and light scattering experiments, it is crucial that chains are fully dispersed in the solvent. An assumption is that chains are not aggregated or have crystallized, as that can lead to overestimation of the stiffness.51 A common artifact is then the appearance of different persistence lengths at different polymer concentrations in solution.56
In principle, SANS is the only technique that allows for measurements of chain dimensions in the melt, by deuterating only a small portion of the sample, but no reports of such measurements exist for conjugated polymers. In all of the above techniques, the molecular weight must be known accurately to extract the persistence length. Even though both light scattering and viscometry yield estimates of the molecular weight, these techniques are most useful in combination with gel permeation chromatography to extract a robust measurement of the molecular weight with a combination of refractive index, viscometry and light scattering detectors.37 Alternatively, the molecular weight can be determined using 1H NMR by counting chain ends or using matrix-assisted laser desorption/ionization with a time of flight mass spectrometer (MALDI-TOF) to measure the molecular weights of the individual chains, but these techniques are only accurate at low molecular weights, typically less than 10 kg mol−1.
Table 1 shows the persistence length for various conjugated polymers, in order of the persistence lengths predicted from the freely rotating chain model. Despite the limited set of values currently available, it is apparent that most conjugated polymers are semiflexible. If the smallest persistence length is about that of P3HT (3 nm), that is significantly larger than most repeat units even for push–pull copolymers, and is larger than the persistence length for polyethyelene (lp of 0.7 nm).60 Thus, conjugated polymers span a range in chain stiffness from nearly that of polyethylene to the persistence lengths of liquid-crystalline polyesters (10–20 nm)61 and DNA (approximately 50 nm).62,63
Table 1 also highlights some limitations in our knowledge of the persistence lengths of conjugated polymers. Although all of the persistence lengths of poly(3-alkylthiophene)s should be about 3 nm, experimental measurements vary from about 1 nm for regiorandom P3HT (rra-P3HT) to 3 nm for regioregular P3HT (rr-P3HT). Similarly, for poly(phenylene vinylene)s (PPVs) with various side chains, the persistence length should be on the order of tens of nanometers, yet experimental values can be as low as 2 nm. One possibility is that chemical defects cause significant deflections of the chain and therefore reduce the persistence length; for example, for PPV such defects are likely present and consequently kink the chain.20,64–67
2.2 Predicting persistence lengths
A direct way of obtaining persistence lengths is through molecular dynamics (MD) simulations. With the appropriate force fields, chain conformations in the melt can be simulated and the persistence length extracted from either the average end-to-end distance of the chains or the decay of the correlation function of the backbone tangents. As shown in Table 1, the persistence lengths of P3HT, PBO, PBZT, and PPP were determined using this method.47,51 Nevertheless, MD simulations can be very computationally expensive and rely on developing appropriate force fields. Experimental data on crystal structures or amorphous scattering, density as a function of temperature, and heat of melting of a perfect crystal is thus crucial to validate force fields. Unfortunately, these data do not currently exist except for a few systems such as P3HT.68–71If the dihedral potentials are flat enough, the freely rotating chain model can be used to predict the persistence length from the backbone deflection angles. The barriers for torsion of thiophene backbones are within a few kT,36,72 not too dissimilar than for polyethylene. Recipes for applying the freely-rotating worm-like chain model analytically for alternating copolymers with different monomers and multiple types of dihedral angles analytically are available.36 Unfortunately, comparing the values for the persistence length obtained from experiment and simulations to the values predicted from the freely rotating chain model shown in Table 1 is challenging, because variability among the experimental values suggests further measurements are warranted. Nevertheless, it is not unusual for the freely rotating chain model to provide a good estimate of the chain stiffness, as it appears for P3HT and PFTBT, for example.
Refinements beyond the freely-rotating chain model are needed if the dihedral potentials include two (or more) torsional angles that are important. For example, the rotational isomeric state model can be used to predict the persistence length from the Boltzmann-averaged populations of distinct dihedral angles.73 More generally, the hindered rotation model can take the entire dihedral potential to generate a distribution of dihedral angles and therefore chain conformations. This approach can be done numerically, where an average is taken over many backbone conformations, with each conformation corresponding to a set of dihedral angles that are randomly selected from a dihedral distribution.36 For each set of dihedral angles, a backbone conformation is generated by rotating it from a trans conformation to the selected dihedral angle. For each backbone conformation, the tangent–tangent correlation function can be calculated, from which the persistence length is extracted. This approach relies on dihedral potentials as an input, which can be derived from DFT or MD simulations, and can be generalized for polymers that contain multiple types of monomers and different dihedral potentials.
2.3 Factors influencing chain conformations
The persistence lengths of conjugated polymers are mostly governed by the stiffness and linearity of the backbone. As mentioned earlier, polymers such as PPV that have zero deflection angles due to the chemical structure are not rigid rods for large molecular weights, because the backbone bonds can bend slightly. For polymers with five member rings or other groups that lead to backbone deflections, the deflection angles can govern the persistence length. As a consequence, when the dihedral potential is relative flat with respect to kT, the persistence length can be computed analytically from the freely-rotating chain model.Crystallization can lead to significantly more planar backbone conformations. When conjugated polymers crystallize, clear signatures of strong coupling between chains is apparent in the absorption spectra.74 Furthermore, detailed analysis of the vibronic peaks in polymers such as P3HT suggest an enhancement in chain planarity;75–78 thiophene rings in the unit cell of P3HT are tilted by about 5 degrees,68 and the dihedral distribution is likely within 10% of this angle. Thus, chain conformations are likely extended when compared to the amorphous phase, even though chain folding, or the formation of loops, can occur.79–81 Nevertheless, the planar conformation can have a larger backbone deflection than freely rotating chains, potentially leading to a drop in the persistence length with aggregation or crystallization. In contrast, the radius of gyration of non-conjugated polymers such as polyethylene remain invariant during crystallization as apparent from neutron scattering studies.82–84 Such experiments have not been explored for conjugated polymers.
Chemical defects can kink the chain, decrease the persistence length and disrupt chain packing; an example is the aforementioned PPV derivatives with relatively short persistence lengths (Table 1). The role of various types of defects on chain conformations have been systematically explored using single molecule spectroscopy and MD simulations of MEH-PPV chains (Fig. 4).85 Linear para-terphenyl defects maintain the linearity of the PPV backbone, while ortho-terphenyl defects, even at low concentration, kink the chain and decrease the persistence length. The effect of saturated defects, such as biphenylethane, is concentration dependent; low inclusions do not affect conformations much other than by providing a “hinge” to allow the polymer to fold unto itself. High amounts of inclusions result in a wide distribution of conformations, where both rod-like but folded structures and more random worm-like conformations with shorter persistence lengths are apparent. Similarly, systematically introducing flexible linkers in the PPV backbone makes the chain more flexible.86 These results demonstrate the potential for synthetic strategies based on incorporating defects to tune the chain stiffness and conformations.
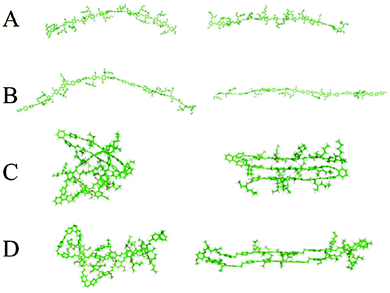 | ||
| Fig. 4 Two representative chain conformations (right and left) for 15 repeat unit oligomers of (A) MEH-PPV, (B) ∼33% para-terphenyl MEH-PPV, (C) ∼33% ortho-terphenyl MEH-PPV, and (D) ∼33% saturated MEH-PPV. Different types of chemical defects perturb chain conformations to different degrees. Results from replica exchange molecular dynamics in the gas phase. Reprinted with permission from ref. 85. | ||
Side chains or groups can also affect the chain stiffness by affecting dihedral potentials or introducing steric constraints.23,39,87–89 For example, bulky side groups can prevent planar conformations due to sterics and therefore kink the chains. An example is regiorandom P3HT (rra-P3HT), where the head-to-head addition of the side chains could prevent planar conformations and therefore reduce lp. Indeed, SANS measurements place the persistence length of rra-P3HT at about 1 nm,39 and more compact conformations are observed in MD simulations,88 but spacing the side chains to every other ring (such as in regiorandom poly(3-hexyl-2,5-thienylene vinylene)) recovers the stiffer chain conformations.23 The fact that the freely rotating chain model works well for rr-P3HT (see Table 1) suggests that the dihedral potentials must be severely disrupted for rra-P3HT to have a significantly lower persistence length.
Overall, the role of side chains on the persistence length of conjugated polymers remains unclear. SANS experiments on saturated polymers poly-1-octene and poly-1-decene with different numbers of CH2 units in their side groups show that the largest side group leads to the largest persistence length,89 and the authors have argued that a similar dependence might be found in conjugated polymers.90 Nevertheless, atomistic simulations suggest that the longer side chains of poly(2,3-diphenylphenylene vinylene) with decyl side chains (DP10-PPV) do not affect chain packing and persistence lengths in a melt of oligomers as compared to PPV with hexyl side chains (DP6-PPV),57 even though the persistence lengths of PPVs appear to vary with side chains (Table 1). The discrepancy is perhaps due to chemical defects in the PPV chain, as discussed earlier. P3DDT also has a significantly lower persistence length than P3HT in solution, at 1 nm versus 3 nm.39 Perhaps the longer side chains can contribute significant steric effects on the dihedral potentials, although it is challenging to imagine such large contributions.36,72,91
Non-bonding interactions can also be exploited to control chain conformations.92–101 In principle, organic heterocylic groups may be able to use attractive interactions to “lock-in” specific chain conformations, such as highly planar backbones. Detailed calculations have assessed the strength of various non-bonding interactions, and have suggested promising targets for stabilization of chain conformations. For example, as shown in Table 2, CH⋯N and CH⋯O interactions are about three to four times that of kT at room temperature (0.593 kcal mol−1). Other interactions are weaker, such as CH⋯F, while O⋯S, N⋯S, and F⋯S have interaction energies of about kT at room temperature or less, and are not expected to perturb molecular conformations.100
| Interaction energies (kcal mol−1) | |
|---|---|
| CH–N | 2.20 |
| CH–O | 1.86 |
| CH–F | 0.94 |
| CH–S | 0.74 |
| S–S | 0.72 |
| O–S | 0.51 |
| N–S | 0.46 |
| F–S | 0.44 |
| N–F | Nonbinding |
| O–F | Nonbinding |
| O–N | Nonbinding |
2.4 Does the persistence length matter?
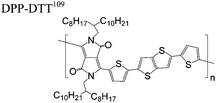
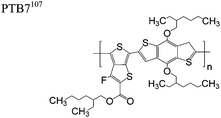
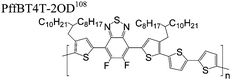
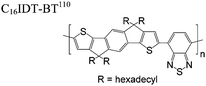
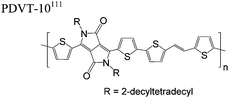
The extent that the persistence length will affect optoelectronic properties is not known. As we discuss in Section 3.1, the predominance of liquid crystalline phases depends on the chain stiffness and can be important for charge transport, because accessing liquid crystalline phases prior to crystallization can enhance long range order102 and chains in liquid crystalline phases can align under applied fields.103,104 Furthermore, recent work has pointed out that deflections in the backbone can lead to tortuous paths for transport in collections of amorphous chains.105 Thus, if tie chains are important for bridging adjacent crystallites, stiffer chains may be more likely to provide straight pathways for transport between crystals. Detailed analyses of crystallite size and number suggest that percolation of charge transport pathways in poly(3-ethylhexylthiophene) (P3EHT) occurs when the length of tie chains bridging crystallites is on the order of the persistence length.106Interestingly, many polymers in the active layer of high performance thin-film transistors or photovoltaics are very stiff. Table 3 shows a few examples of high-performance conjugated polymers and their corresponding persistence lengths, as calculated from the freely rotating chain model.36 PTB7 and PffBT4T-20D are used as donors in organic photovoltaic devices with power conversion efficiencies beyond 10%,107,108 and DPP-DTT, C16IDT-BT, and PDVT-10 are used as the active layer in thin-film transistors with charge mobilities greater than 1 cm2 V−1 s−1.109–111 Even though it is unclear how the persistence length matters, the large persistence lengths of these materials, at 8 nm or greater, or more than twice that of P3HT, suggests it may be important for optoelectronic properties.
3. To mix or not to mix – phase behavior of conjugated polymers
Conjugated polymers and mixtures based on conjugated polymers exhibit a rich phase behavior. Stiff backbones can promote crystalline and liquid crystalline phases, and these ordered phases can be critical for efficient charge transport. Mixing with small molecules or other polymers is crucial for applications in light emitting diodes112 and photovoltaic cells,113 and significantly complicates phase behavior. The presence of crystalline and liquid crystalline phases as well as phase separation has confounded the field for many years. Here we begin with a discussion of phases observed in conjugated homopolymers, and then cover mixtures, highlighting recent progress and pointing out shortcomings of our current understanding.3.1 Phase behavior of homopolymers
Because of their stiff chain conformations and planar ring-like structures, conjugated polymers can have both crystalline and liquid crystalline phases, making their phase behavior complex.114 For example, both crystalline68 and nematic47,115–118 phases have been observed or predicted for P3HT. Nevertheless, predicting and mapping the phase behavior of conjugated polymers is important, because long-range order can affect both optoelectronic and mechanical properties.102,104,119–126Inducing a liquid-crystalline phase prior to crystallization has been shown to improve order and enhance charge mobilities. For example, a semiconducting polythiophene was designed to assemble into large crystalline domains on crystallization from a liquid-crystal phase, resulting in a system with close intermolecular π–π distances that led to 0.2–0.6 cm2 V−1 s−1 field-effect mobilities.102 It is hypothesized that the liquid-crystalline phase facilitates the alignment of chains and that this order is maintained during crystallization. As a consequence, regions between crystalline domains after this method of processing are likely more organized than amorphous regions of a material crystallized from an isotropic melt.
As alluded to in Section 2.4, the alignment of rigid-rod chains in liquid crystals can improve charge transport. For instance, polyfluorene copolymers in a nematic glassy state with chains aligned in the direction parallel to the transport direction in thin-film transistors (TFTs) through the use of an alignment layer showed enhanced charge carrier mobilities and good operating stability.104 Similarly, improved mobility was observed in chains that were aligned using three molecular design components: concentration-induced chain planarization, a tetrahedral carbon linker with out-of-plane bonding, and bulk side chains that prevent side-chain interaction.127 Thus, predicting the propensity for liquid crystalline phases in conjugated polymers is important.
As a starting point, we can consider the formation of liquid crystalline phases by rigid rods. Onsager128 showed that the isotropic to nematic transition in rigid rods occurs when the volume fraction of rods is high enough that a random placement and orientation of rods would lead to approximately one collision per rod. As the isotropic phase becomes less entropically favorable at high concentrations, the rods will align with each other and form a nematic phase. In semiflexible chains, the critical volume fraction at which the isotropic to nematic transition is predicted to occur is influenced largely by d/lp, where d is the diameter of a rod-like chain and lp is the persistence length.129,130 Although this scaling has been verified for polymers with modest persistence length, recent computer simulations suggest a different scaling of (d/lp)2/3 when lp is large; the origin of such scaling is currently unknown.131
As temperature increases, entropy dominates and order gives way to amorphous phases. The nematic-to-isotropic transition temperature is often described in terms of Maier–Saupe theory, where the Maier–Saupe interaction, or nematic coupling parameter, describes the propensity for rods or stiff polymers to form nematic phases.132–137 A combination of self-consistent field theory (SCFT) and MD simulations was used to calculate the nematic coupling constant of P3HT and the isotropic-to-nematic transition temperature TIN as a function of chain length n.47 The combination of these predictions and experimentally determined crystal melting temperatures69,138 give a comprehensive picture of the phase behavior for P3HT.139
An example of a framework to generalize the behavior of semiconducting polymers that have both liquid crystalline and crystalline phases can be found in Fig. 5.114 The isotropic–nematic phase boundary comes from the computational work of Zhang et al. mentioned above, and the equilibrium melting temperature line is confirmed with values reported in the literature.69,116 The nematic phase is most prevalent at low N, where Tm is about 20–60 degrees below TIN. Fig. 5 also shows that regiodefects decrease Tm and potentially increases the window for the nematic phase.114 Altogether, considering the effects of regioregularity and N help explain seemingly contradictory results in the literature, where nematic phases are visible only at low molecular weights and for regiodefective materials.
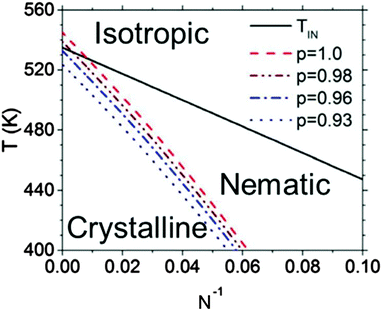 | ||
| Fig. 5 Phase diagram for P3HT. TIN denotes the isotropic–nematic phase boundary, and the dashed curves denote the melting temperatures as a function of N and the regioregularity p. Reproduced with permission from ref. 114. | ||
Despite tremendous efforts and progress, the crystallization of conjugated polymers is not yet fully understood. So far, the structures of only a few conjugated polymers have been determined, such as for P3HT,140 (poly(3-2,5-dioctylphenyl)thiophene) (PDOPT),141 and poly(2,5-bis(3-tetradecylthiophene-2-yl)thieno[3,2-b]thiophene) (PBTTT-C14).142 Early X-ray diffraction (XRD) studies showed that, in general, poly(3-alkylthiophene)s (P3ATs) exhibit a well-organized lamellar structure consisting of stacks of planar thiophene main chains that are uniformly spaced by alkyl side chains. Structural analysis revealed that this organization occurs even in the presence of local side-chain disorder, an observation that suggests that a secondary structural ordering occurs at the alkyl-chain interface between alkyl-thiophene layers; this process could be related to the liquid crystalline behavior of P3ATs.68,140 More recently, the crystal structure of P3HT has been refined through a combination of X-ray diffraction, solid state NMR spectroscopy, and density functional theory calculations.143 The unit cell of P3HT is monoclinic with a space group P21/c and two chains per cell (a = 1.62 nm, b = 0.76 nm, c = 0.77 nm, γ = 87 degrees). This approach is promising for the determination of the crystal structure of conjugated polymers.
In principle, the degree of crystallinity should affect charge mobilities within conjugated polymers. Strong coupling within crystalline regions enhances delocalization of charge carriers, such that transport is enhanced when compared to amorphous regions. As crystallization progresses, mobilities in thin-film transistors can increase by a factor of about 50; this is likely a result of the formation of a crystalline network within an amorphous phase in the active layer.144 Furthermore, accessing different polymorphs with tighter π–π stacking in the active layer can lead to enhancements of the field-effect mobility in thin-film transistors.145 But, introducing unsubstituted thiophene rings to P3HT can enhance coupling between chains and change mobilities by an order of magnitude, despite a drop in the crystallinity.146 Charge mobilities in thin-film transistors are not always correlated with the crystallinity of the active layer.147,148
The crystallization of P3HT is often limited by the diffusion of the chains, such that low molecular weight chains crystallize more readily than high molecular weight P3HT. Nevertheless, charge mobilities increase with molecular weight.78,147,148 The leading hypothesis to explain this dependence is that charge transport is limited by interconnectivity between crystalline domains, such as through tie chains. Thus, varying the crystallization kinetics can lead to differences in tie chain densities, such that faster crystallization leads to more tie chains in the active layer and higher charge mobilities in thin-film transistors.149 Overall, the lack of correlation between the crystallinity and crystal texture (crystal orientation) in the active layer with charge mobilities in thin-film transistors suggests a one-dimensional character to transport,110 where occasional strong coupling between chains is sufficient to achieve high charge mobilities, to date up to 10 cm2 V−1 s−1 in transistors with polymer semiconductors as the active layer.150
3.2 Mixtures of conjugated polymers and fullerene
A description of the mixing between conjugated polymers and small molecules is useful to understand the solution casting process and the microstructure in multi-component active layers of organic electronic devices. The miscibility between conjugated polymers and small molecules is often described using Flory–Huggins Theory and the Flory–Huggins interaction parameter χ. Flory–Huggins is widely useful for describing liquid polymeric mixtures, and has been extended for systems where the components can crystallize.151 In this subsection, we describe efforts to understand mixing in polymer/fullerene mixtures, and defer discussion of the solubility of polymers in solvents to Section 3.4.State-of-the-art solution processed organic solar cells rely on mixtures of conjugated polymers and fullerene as the active layer.113,152–154 If the polymer and fullerene are strongly immiscible, the two components phase separate, leading to structures with length scales larger than hundreds of nanometers107,155 that are too large for efficient exciton harvesting due to exciton diffusion being limited to about 10 nm.156,157 If phase separation is suppressed through either miscibility or a compatibilizing agent, then the system relies on crystallization of one or both of the components to create morphologies and interfaces amenable for charge photogeneration.
Typically, both the conjugated polymer donor and fullerene can crystallize, such that the equilibrium state is likely separate fully crystalline phases. Polymers, however, seldom fully crystallize, making amorphous phases ubiquitous. Furthermore, the crystallization of fullerene is also retarded in mixtures with conjugated polymers.162,163 As a consequence, if the crystallization of the polymer component occurs first, then the microstructure is set by the crystallization motif, as shown in Fig. 6. Polymers that crystallize into fibril-like structures with nanometer dimensions create nanoscale morphologies amenable for exciton dissociation and charge extraction,29,158,160,161,164–168 and polymers that crystallize into plate-like structures can allow the domain sizes to grow with processing.29
 | ||
Fig. 6 Sulfur elemental maps generated from core-loss energy-filtered transmission electron microscopy demonstrating that polymer crystallization dominates the morphology in donor–acceptor mixtures used as the active layer of solar cells. (a) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rr-P3HT/PCBM films as a function of annealing temperature. Reproduced with permission from ref. 158. Copyright 2011 American Chemical Society. (b) 1 1 rr-P3HT/PCBM films as a function of annealing temperature. Reproduced with permission from ref. 158. Copyright 2011 American Chemical Society. (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 poly[2,5-bis(3-hexadecylthiophen-2-yl)thieno[3,2-b]thiophene]/phenyl-C71-butyric acid methyl ester (PC71BM) films, as a function of annealing time and temperature. Adapted from ref. 159 with permission from The Royal Society of Chemistry. (c) 1 4 poly[2,5-bis(3-hexadecylthiophen-2-yl)thieno[3,2-b]thiophene]/phenyl-C71-butyric acid methyl ester (PC71BM) films, as a function of annealing time and temperature. Adapted from ref. 159 with permission from The Royal Society of Chemistry. (c) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 poly[(4,4′-bis(2-ethylhexyl)dithieno[3,2-b:2′,3′-d]germole)-2,6-diyl-alt-(2,1,3-benzothiadiazole)-4,7-diyl]/PC71BM films as-cast and annealed. Reproduced with permission from ref. 160. (d) 1 1 poly[(4,4′-bis(2-ethylhexyl)dithieno[3,2-b:2′,3′-d]germole)-2,6-diyl-alt-(2,1,3-benzothiadiazole)-4,7-diyl]/PC71BM films as-cast and annealed. Reproduced with permission from ref. 160. (d) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 rr-P3HT 2.5 rr-P3HT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N,N′-di((thiophen-2-yl)methyl)-2,6-di(N-cyclohexylamino)-1,4,5,8-naphthalenetetracarboxydiimide films with and without diiodooctane (DIO). Reprinted from ref. 161 with permission from Elsevier. N,N′-di((thiophen-2-yl)methyl)-2,6-di(N-cyclohexylamino)-1,4,5,8-naphthalenetetracarboxydiimide films with and without diiodooctane (DIO). Reprinted from ref. 161 with permission from Elsevier. | ||
Crystallization leads to pure polymer phases, unless the polymer co-crystallizes with fullerene.169–171 The remaining amorphous phase is then enriched in fullerene, such that phase separation driven by limited solubility can then occur. In this context, describing liquid–liquid phase separation becomes relevant, to predict what will occur in the mixed phases between polymer and fullerene. How to treat the miscibility within the non-crystalline domains remains an open challenge.
Perhaps the first question is how to treat fullerene in polymer/fullerene mixtures. Commonly used fullerene derivatives such as [6,6]-phenyl-C61-butyric acid methyl ester (PCBM) have been assumed to behave as nanoparticles, given that they have a diameter of approximately 1 nm.172–174 Others have assumed PCBM is small enough to be treated as a solvent molecule.158,175,176 If particles (or molecules) are large enough, phase separation in mixtures can be driven purely entropically, because the nanoparticle surfaces limit chain conformations and therefore promote separation of the components.
McGarrity and coworkers177 have examined the critical size needed for nanoparticle effects to be important using simulations. In a polymer–nanoparticle mixture with only neutral interactions, they examined the presence of surface segregation as a function of the size of the nanoparticle. They found that when the diameter of the nanoparticle is 1.6 times larger than the statistical segment length of the polymer, the loss of configurational entropy in the polymer becomes important and nanoparticles segregate to the surface entropically (Fig. 7). P3HT has one of the smallest monomer lengths of all conjugated polymers and PC71BM is one of the largest fullerene molecules commonly employed. The ratio of the cube root of the monomer volumes of P3HT and PC71BM (239 and 1080 Å3, respectively178) is about 1.7, right at the onset of entropically-driven phase separation. Thus, although fullerene likely behaves as a small molecule in most mixtures with conjugated polymers, more work is needed to determine the importance of nanoparticle effects in selected systems, such as in P3HT/PC71BM mixtures.
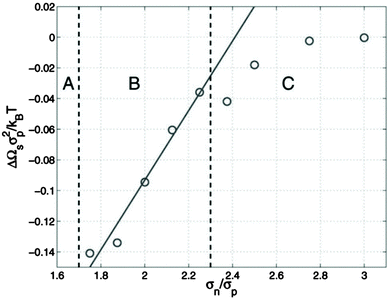 | ||
| Fig. 7 Excess surface energy for a polymer/nanoparticle composite as a function of the ratio of nanoparticle size to the statistical segment length of the polymer (σn/σp). If nanoparticles are larger than σn/σp of 1.6, surface segregation occurs (regions B and C), suggesting entropic effects can drive phase separation. Reprinted with permission from ref. 177. | ||
The miscibility of liquid mixtures of small molecules and polymers can be described using Flory–Huggins theory,37,60,179,180 which describes the phase behavior in terms of the Flory–Huggins interactions parameter χ. Essentially, each lattice site is taken to be the volume of one solvent molecule and we assume that each polymer occupies N lattice sites (number of statistical segment lengths). As a consequence, the statistical segment size is calculated at a reference volume of the solvent. For volume fractions φ1 and φ2, we obtain an expression for the free energy of mixing per site of a polymer solution:
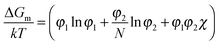 | (2) |
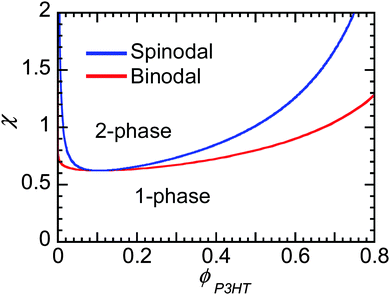
Flory–Huggins can be useful to predict the behavior of mixtures of conjugated polymers and fullerene. If crystallization of fullerene is suppressed, as is often in PCBM and PCBM derivatives, and the polymer crystallizes, leaving behind some amorphous chains enriched in fullerene content, then one can predict whether phase separation will occur if χ is known. Fig. 8 shows the phase behavior predicted from Flory–Huggins for a polymer mixture of P3HT of 50 kg mol−1 and PC61BM. The phase diagram is clearly asymmetric with composition, where the critical volume fraction is fullerene-rich. The asymmetry is a direct result of the large differences in molecular sizes between polymers and small molecules, leading to a smaller contribution to the entropy of mixing by the polymer, as seen in eqn (2). It may be challenging to dissolve even a small amount of polymer in some solvent (or fullerene), while a small amount of small molecules can always infiltrate into amorphous polymer phases. Thus, when phase separation in polymer/fullerene mixtures occurs, fullerene phases will be nearly pure while amorphous polymer phases will contain a significant amount of fullerene unless χ is very high.
χ at the critical point goes to 0.5 as N gets large, such that for systems where χ is below 0.5 the components are miscible at all compositions. As we discuss in Section 3.4, Kozub et al. measured the Flory–Huggins χ parameter to be 0.86, and demonstrated that phase separation in mixtures of amorphous regiorandom P3HT and PC61BM roughly follow the predictions by Flory–Huggins.158,181
Because miscibility governs phase separation, it also affects charge transport.182 Electron charge mobilities through fullerene domains are suppressed in miscible systems, because the fullerenes are dispersed. Transport through these systems is governed by percolation, such that the mobility decreases with decreasing concentration of fullerene as a power law with an exponent of two.181 If the polymer and fullerene phase separate, then charge mobilities decrease more slowly with dilution, linearly with concentration or volume fraction. As a consequence, an optimum miscibility exists for the active layer in organic solar cells. Strongly immiscible systems lead to large scale phase separation and prevent the polymer donor from establishing a nanoscale morphology. Highly miscible systems suffer from poor electron mobilities in the mixed phase between amorphous polymer and fullerene.181 Treat and coworkers demonstrated this concept experimentally, where they optimized the performance of devices with poly(3-hexylselenophene-2,5-diyl) (P3HS)/fullerene mixtures in the active layer by tuning the miscibility with P3HS using various fullerene derivatives, and they found that indeed an optimum polymer–fullerene miscibility exists for application in the active layer of solar cell devices.30 As a consequence, polymer–fullerene phase behavior in the active layer can have a significant impact on device performance.183–187
Despite its utility, there are limitations to Flory–Huggins.37,188 When crystals are present, the chemical potential of the liquid solution has to be compared to that of the crystalline phases.151 Furthermore, the mean-field assumption within Flory–Huggins fails for dilute polymer solutions, because chain connectivity inevitably causes the concentration of solute to be non-uniform throughout the solution. Also, Flory–Huggins assumes no volume change occurs upon mixing. Other problems lie in lumping all interactions into a single χ parameter, which often requires a temperature-independent contribution to χ; χ often has limited applicability to systems with highly polar groups or specific interactions.37 The role of backbone stiffness on polymer miscibility has also been explored.136,189–191
In mixtures where the microstructure can evolve with time, time temperature transformation (TTT) diagrams are useful for describing the microstructure and microstructural evolution.192–196 Although such diagrams do not currently exist for conjugated polymers or mixtures containing conjugated polymers, we propose a rough sketch of what a time temperature transformation diagram might look like for P3HT/PCBM in Fig. 9. Crystallization is delayed as either the glass transition or melting temperature for each component is approached. Furthermore, if the two materials are immiscible, phase separation is expected to occur faster at higher temperatures due to enhanced diffusivities. Clearly, the interplay between phase separation and crystallization can significantly complicate TTT diagrams, but such effects are not included in our schematic shown in Fig. 9. Nevertheless, we propose that generating TTT diagrams would be useful for understanding the morphological evolution in polymer/fullerene mixtures.
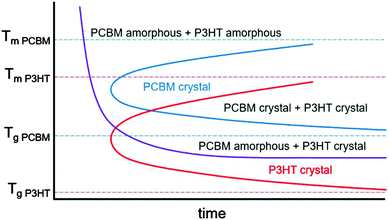 | ||
| Fig. 9 Rough sketch of a proposed time temperature transformation diagram for P3HT and PCBM. The melting and glass transition temperatures are taken from various studies.154,178,197–201 The red and blue curves outline the boundary of P3HT and PCBM crystallization, while the purple curve denotes the onset of liquid–liquid phase separation. | ||
3.3 Phase behavior of polymer–polymer blends
Mixing of polymers is useful to obtain new materials with composite properties of the various components. As a consequence, polymer blends are useful for a variety of applications of conjugated polymers, such light emitting diodes,202,203 flexible conductors and semiconductors,204–207 and solar cells.208–211 Miscible blends composed of two or more polymers are analogous to metal alloys, but more often polymers phase separate with each other.212 Liquid phase behavior can again be described with Flory–Huggins theory, where systems with χN less than 2 are always miscible. Thus, if N is large, almost all polymers are immiscible with each other, unless χ is very small or negative (interactions between polymers are net attractive).Blends of conjugated polymers have demonstrated unique properties. A few decades ago, blends of poly(phenylene-vinylene) (PPV) with an insulating polymer, poly(ethylene oxide) were explored.213 The conductive properties of the blend depend on the compositions and processing conditions, but a composition of greater than 60 wt% PPV gives flexibility, toughness, and the highest conductivity. Others214 made blends of polythiophene (PTh) and polypyrrole (PPy) with insulators polystyrene (PS) and polycarbonate (PC). Interestingly, PTh/PS and PPy/PS blends have high conductivities, but PPy/PC conductivities are lower, likely due to hydrogen bonding between polypyrrole and polycarbonate. Blends of donor and acceptor conjugated polymers are used as the active layer of organic solar cells achieving nearly 8% power conversion efficiencies.215–222 As expected, most of these polymer blends phase separate, as exemplified by the scanning transmission X-ray microscopy (STXM) images shown in Fig. 10 for mixtures of poly(9,9′-dioctylfluorene-cobis(N,N′-(4,butylphenyl))bis(N,N′-phenyl-1,4-phenylene)-diamine) (PFB) and poly(9,9′-dioctylfluorene-co-benzothiadiazole) (F8BT).223
 | ||
| Fig. 10 Composition maps of PFB/F8BT blends generated from STXM experiments. Coarse phase separation is apparent. From ref. 223. | ||
Various approaches have been demonstrated to enhance mixing of semiflexible polymers. Hydrogen bonding has been employed as specific interactions to promote miscibility between mixtures of semi-flexible and flexible polymers.224,225 The addition of flexible side chains to stiff polymers has also been shown to help form a miscible polymer–polymer blend of two stiff polymers, polyester and polyimide.226,227 In some cases, the flexible side chains can induce cocrystallization of the polymers at a molecular level.203,204 A common way to compatibilize immiscible polymer blends is to include a surfactant.227–233 This approach has only been demonstrated for a few conjugated polymer blends. For example, by adding 3-hexylthiophene to mixtures of P3HT and poly[2,7-(9,9-didodecylfluorene)-alt-5,5-(4′,7′-bis(2-thienyl)-2′,1′,3-benzothiadiazole)] (PF12TBT), phase separation can be suppressed such that a decrease in the domain size is apparent.
Another approach to mix conjugated polymers is to rely on alkyl side chains to promote miscibility without decreasing conductivity. For example, a miscibility window was identified for a blend of poly(3-octylthiophene) (P3OT) with poly(ethylene-co-vinylacetate) (EVA).234 The interaction between P3OT and EVA that resulted in miscibility also induced a conformational change in the P3OT. The role of the side chains on mixing has been systematically examined by mapping out the phase diagrams of P3ATs with four different n-alkyl side chains lengths (n = 4, 6, 8, 12) blended with PS. A non-monotonic relationship between the alkyl side chain length and miscibility was found, such that from n = 4 (P3BT) to n = 6 (P3HT), the miscibility in the blends decreases, but from n = 8 to n = 12 the miscibility increases. The phase diagrams of these blends are shown in Fig. 11.31
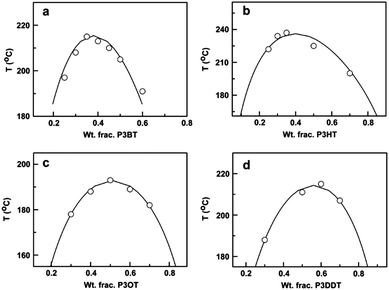 | ||
| Fig. 11 Predicted (solid lines) and experimentally determined (data points) binodal curves for (a) P3BT/PS, (b) P3HT/PS, (c) P3OT/PS, and (d) P3DDT/PS. Reprinted from ref. 31. | ||
Beyond polymer blends, conjugated block copolymers provide a strategy to control the microstructure using the chemical architecture.235–237 The mesostructures in which block copolymers self-assemble are on the length scale of tens of nanometers, providing an opportunity to tune the microstructure in the active layer of organic electronic devices. Furthermore, covalently bonded donor and acceptor blocks may offer a means to manipulate the molecular structure such that donor–acceptor interfaces can be tuned and used to study charge and energy transfer processes.238–243 Incorporating the wormlike chain model into self-consistent field theory calculation of block copolymers have demonstrated that the chain stiffness affects the stability of various diblock copolymer mesostructures, such that the phase space for lamellae grows with stiffness over other typical morphologies such as cylinders and spheres.191 We refer readers to recent reviews on conjugated block copolymers for more in-depth discussions.6,244–246
3.4 Determining the Flory–Huggins interaction parameter for conjugated polymer mixtures
Measurements of the Flory–Huggins interaction parameter χ in flexible polymer blends rely on fitting X-ray or neutron scattering data of miscible systems to predictions by the Random Phase Approximation (RPA).235,247–249 Thus, χ can be extracted for various temperatures. Unfortunately, the application of RPA has not been demonstrated for conjugated polymers. Alternatively, the composition and temperature for phase separation to occur can be measured. For polymer solutions, χ is measured by tracking the degree of swelling of a polymer by a solvent. In either case, crystal or liquid crystalline phases in conjugated polymer confound measurements of χ.Another approach to estimate χ is through Hildebrand solubility parameters (δi) introduced by Hildebrand and Scott250,251 that are defined as the square root of the cohesive energy density. The Flory–Huggins interaction parameter χ can then be estimated from the Hildebrand solubility parameters of the two components:
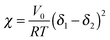 | (3) |
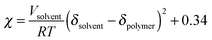 | (4) |
A perturbation by Hansen to the Hildebrand solubility parameters is to split the cohesion energy in terms of three components: dispersion forces (atomic), permanent dipole–permanent dipole forces (molecular), and hydrogen bonding. This adds more terms to the previously stated definition of the solubility parameter such that the square of the total (Hildebrand) solubility parameter is the sum of the squares of the Hansen dispersive, polar, and hydrogen bonding solubility parameters.254,255 Using this approach, the solubility parameters of P3HT, poly[2,6-(4,4-bis-(2-ethylhexyl)-4H-cyclopenta[2,1-b;3,4-b′]dithiophene)-alt-4,7(2,1,3-benzothiadiazole)] (PCPDTBT), and PCBM in various solvents have been estimated.25,256 Furthermore, χ for P3HT/PCBM was extracted using mixtures of solvents and non-solvents to track the transition from solubility to non-solubility.26
Monte Carlo and MD simulations have also been used to estimate χ between P3ATs.31 These estimates do not include entropic contributions to χ, as only the pair-wise interaction energies and coordination numbers between 3-alkylthiophene monomers and styrene dimers are considered. Nevertheless, the values of χ are reasonable when applied in Flory–Huggins and compared to experimental phase diagrams.
Table 4 compares estimates from various techniques of the Flory–Huggins interaction parameter χ for mixtures containing conjugated polymers. Discrepancies exist between values reported for the same mixtures, even by a factor of two or more. The majority of χ values for polymer/small molecule mixtures are high, many above the critical value for phase separation in polymer solutions (χ = 0.5). All of the values reported for polymer/polymer blends are high as well, between 0.2 and 2; for comparison, χ between polystyrene and polyisoprene is about 0.05 at 140 °C. Thus, because phase separation occurs for χN > 2, blends should phase separate even at small N.
| Polymer–solvent (and polymer–fullene) interaction parameters χi-solvent | |||||||
|---|---|---|---|---|---|---|---|
| i | χ i-chloroform | χ i-THF | χ i-cyclohexane | χ i-water | χ i-chlorobenzene | χ i-PC61BM | Temperature (°C) |
| rr-P3HT | ∼0.2–0.4257 | 150 | |||||
| rr-P3HT | 0.92 ± 0.1258 | 150 | |||||
| rr-P3HT | 0.86 ± 0.09158 | ∼210 | |||||
| rr-P3HT | 0.99 ± 0.0124 | 1.04 ± 0.0424 | 0.078256 | 21 | |||
| rr-P3HT | 0.27253 | 0.51253 | 1.02253 | 3.86253 | 30 | ||
| rr-P3DDT | 0.54253 | 0.75253 | 1.02253 | 3.86253 | 30 | ||
| rra-P3BT | −0.37253 | −0.17253 | −0.17253 | 3.21253 | 30 | ||
| rra-P3DDT | −0.69253 | −0.48253 | −0.32253 | 2.09253 | 30 | ||
| rra-P3HT | 0.37253 | 0.41253 | 30 | ||||
| PF12TBT | 0.063256 | 21 | |||||
| Polymer–polymer interaction parameters (reference volume of 0.1 nm3) | ||
|---|---|---|
| Blend | χ | Temperature (K) |
| P3BT/PS (without annealing) | 0.4831 | 423 |
| P3BT/PS (with annealing) | 0.3231 | 423 |
| P3BT/PS | −0.0181 + (32.8 − 13.7 ϕP3BT)/T31 | — |
| P3HT/PS | 0.48 ± 0.0624 | 296 |
| P3HT/PS (without annealing) | 0.631 | 423 |
| P3HT/PS (with annealing) | 0.3731 | 423 |
| P3HT/PS | −0.0433 + (49.3 − 11.8 ϕP3HT)/T31 | — |
| P3OT/PS (without annealing) | 0.7431 | 423 |
| P3OT/PS (with annealing) | 0.3531 | 423 |
| P3OT/PS | −0.0464 + (44.0 − 2.86 ϕP3OT)/T31 | — |
| P3DDT/PS (without annealing) | 1.4931 | 423 |
| P3DDT/PS (with annealing) | 0.231 | 423 |
| P3DDT/PS | −0.0276 + (31.7 − 0.489 ϕP3DDT)/T31 | — |
4. Conclusions
Conjugated polymers are an important class of materials due to their chemical versatility and electronic and mechanical properties. Conjugated polymers are also paradoxical materials – many of their key advantages are also critical limitations. Solution processing is afforded by weak van der Waals interactions, but weak interactions also lead to challenges in controlling the microstructure. The versatility of organic chemistry provides nearly infinite possibilities for functional conjugated polymers, but navigating this space is daunting. We propose that to fully exploit the potential of conjugated polymers we must be able to describe how the chemical structure leads to microstructure, and how the microstructure governs macroscopic optoelectronic and mechanical properties. To effectively develop improved materials or new classes of materials based on the advantages of conjugated polymers, we must be able to predict properties from the chemical structure. The first few steps in this endeavor require a description of chain conformations and nematic interaction parameters of conjugated polymers. Mixing of materials to obtain composite properties has enabled various organic optoelectronic devices, and a description of the phase behavior of conjugated polymer mixtures is needed to predict composite properties. Much progress has been made in understanding chain conformations and phase behavior of conjugated polymers, but much work remains in predicting from the chemical structure.We put a particular emphasis on how chain conformations are governed by the persistence length and described how this parameter can be both experimentally determined and computationally predicted. Besides the stiffness of the polymer backbone, other factors such as side chains, non-bonding interactions, and defects have also been shown to influence chain conformations. In discussing the phase behavior of conjugated polymers, we reviewed Flory–Huggins theory and described the phase behavior of homopolymers, polymer–polymer blends, and polymer–fullerene blends. In both cases, the field has seen significant progress in the last few years, although experiments, simulations and theory are warranted to resolve discrepancies between reported values for fundamental parameters such as the persistence length and the Flory–Huggins interaction parameter χ.
While conjugated polymers have many attractive qualities, their underlying physics is complex, with some areas still under debate. For example, despite recent progress, a direct connection between the chain conformation, microstructure and charge transport efficacy remains elusive. The phase behavior of conjugated polymers is not fully mapped out, yet it is important as creating mixtures is a route for achieving unique functionalities. As methods for probing the fundamentals of these interesting materials continue to improve, their structure–property relationships can be better understood, and such knowledge will inevitably lead to novel materials.
Acknowledgements
Helpful discussions with Wenlin Zhang on semiflexible chain conformations and persistence lengths of conjugated polymers are gratefully acknowledged. Financial support from the National Science Foundation under Award DMR-1056199 is acknowledged.References
- T.-A. Chen and R. D. Rieke, J. Am. Chem. Soc., 1992, 114, 10087–10088 CrossRef CAS.
- C. L. Gettinger, A. J. Heeger, J. M. Drake and D. J. Pine, J. Chem. Phys., 1994, 101, 1673–1678 CrossRef CAS.
- S. N. Patel, G. M. Su, C. Luo, M. Wang, L. A. Perez, D. A. Fischer, D. Prendergast, G. C. Bazan, A. J. Heeger, M. L. Chabinyc and E. J. Kramer, Macromolecules, 2015, 48, 6606–6616 CrossRef CAS.
- H. Youn, H. J. Park and L. J. Guo, Energy Technol., 2015, 3, 340–350 CrossRef CAS.
- B. Doerling, V. Vohra, T. T. Dao, M. Garriga, H. Murata and M. Campoy-Quiles, J. Mater. Chem. C, 2014, 2, 3303–3310 RSC.
- Y. Lee and E. D. Gomez, Macromolecules, 2015, 48, 7385–7395 CrossRef CAS.
- A. Facchetti, Chem. Mater., 2011, 23, 733–758 CrossRef CAS.
- M. S. AlSalhi, J. Alam, L. A. Dass and M. Raja, Int. J. Mol. Sci., 2011, 12, 2036–2054 CrossRef CAS PubMed.
- S. H. Park, A. Roy, S. Beaupré, S. Cho, N. Coates, J. S. Moon, D. Moses, M. Leclerc, K. Lee and A. J. Heeger, Nat. Photonics, 2009, 3, 297–302 CrossRef CAS.
- H. Spanggaard and F. C. Krebs, Sol. Energy Mater. Sol. Cells, 2004, 83, 125–146 CrossRef CAS.
- P. Peumans, A. Yakimov and S. R. Forrest, J. Appl. Phys., 2003, 93, 3693–3723 CrossRef CAS.
- C. M. Frost, P. S. Cederna, D. C. Martin, B. S. Shim and M. G. Urbanchek, 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, 2014, pp. 422–425 Search PubMed.
- A. Peramo, M. G. Urbanchek, S. A. Spanninga, L. K. Povlich, P. Cederna and D. C. Martin, Tissue Eng., Part A, 2008, 14, 423–432 CrossRef CAS PubMed.
- S. M. Richardson-Burns, J. L. Hendricks, B. Foster, L. K. Povlich, D. H. Kim and D. C. Martin, Biomaterials, 2007, 28, 1539–1552 CrossRef CAS PubMed.
- J. T. Mabeck and G. G. Malliaras, Anal. Bioanal. Chem., 2006, 384, 343–353 CrossRef CAS PubMed.
- D. H. Kim, M. Abidian and D. C. Martin, J. Biomed. Mater. Res., Part A, 2004, 71, 577–585 CrossRef PubMed.
- M. Chabinyc, Nat. Mater., 2014, 13, 119–121 CrossRef CAS PubMed.
- W. B. Chang, C.-K. Mai, M. Kotiuga, J. B. Neaton, G. C. Bazan and R. A. Segalman, Chem. Mater., 2014, 26, 7229–7235 CrossRef CAS.
- C.-K. Mai, B. Russ, S. L. Fronk, N. Hu, M. B. Chan-Park, J. J. Urban, R. A. Segalman, M. L. Chabinyc and G. C. Bazan, Energy Environ. Sci., 2015, 8, 2341–2346 CAS.
- T. Adachi, J. Brazard, P. Chokshi, J. C. Bolinger, V. Ganesan and P. Barbara, J. Phys. Chem. C, 2010, 114, 20896–20902 CAS.
- E. Collini and G. D. Scholes, Science, 2009, 323, 369–373 CrossRef CAS PubMed.
- B. J. Schwartz, Annu. Rev. Phys. Chem., 2003, 54, 141–172 CrossRef CAS PubMed.
- Z. Hu, T. Adachi, Y. G. Lee, R. T. Haws, B. Hanson, R. J. Ono, C. W. Bielawski, V. Ganesan, P. J. Rossky and D. A. Vanden Bout, ChemPhysChem, 2013, 14, 4143–4148 CrossRef CAS PubMed.
- J. A. Emerson, D. T. W. Toolan, J. R. Howse, E. M. Furst and T. H. Epps, Macromolecules, 2013, 46, 6533–6540 CrossRef CAS.
- F. Machui, S. Abbott, D. Waller, M. Koppe and C. J. Brabec, Macromol. Chem. Phys., 2011, 212, 2159–2165 CrossRef CAS.
- F. Machui, S. Langner, X. Zhu, S. Abbott and C. J. Brabec, Sol. Energy Mater. Sol. Cells, 2012, 100, 138–146 CrossRef CAS.
- N. C. Miller, R. Gysel, C. E. Miller, E. Verploegen, Z. Beiley, M. Heeney, I. McCulloch, Z. Bao, M. F. Toney and M. D. McGehee, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 499–503 CrossRef CAS.
- B. Schmidt-Hansberg, M. Sanyal, M. F. G. Klein, M. Pfaff, N. Schnabel, S. Jaiser, A. Vorobiev, E. Muller, A. Colsmann, P. Scharfer, D. Gerthsen, U. Lemmer, E. Barrena and W. Schabel, ACS Nano, 2011, 5, 8579–8590 CrossRef PubMed.
- D. R. Kozub, K. Vakhshouri, S. V. Kesava, C. Wang, A. Hexemer and E. D. Gomez, Chem. Commun., 2012, 48, 5859–5861 RSC.
- N. D. Treat, A. Varotto, C. J. Takacs, N. Batara, M. Al-Hashimi, M. J. Heeney, A. J. Heeger, F. Wudl, C. J. Hawker and M. L. Chabinyc, J. Am. Chem. Soc., 2012, 134, 15869–15879 CrossRef CAS PubMed.
- Y. Lee, J. K. Kim, C.-H. Chiu, Y.-K. Lan and C.-I. Huang, Polymer, 2009, 50, 4944–4949 CrossRef CAS.
- R. Meier, M. A. Ruderer, A. Diethert, G. Kaune, V. Korstgens, S. V. Roth and P. Muller-Buschbaum, J. Phys. Chem. B, 2011, 115, 2899–2909 CrossRef CAS PubMed.
- L. Yan and F. Yang, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 1382–1391 CrossRef CAS.
- D. M. Crothers and B. H. Zimm, J. Mol. Biol., 1965, 12, 525–536 CrossRef CAS PubMed.
- G. Cohen and H. Eisenberg, Biopolymers, 1969, 8, 45–55 CrossRef CAS.
- W. Zhang, E. D. Gomez and S. T. Milner, Macromolecules, 2014, 47, 6453–6461 CrossRef CAS.
- P. C. Hiemenz and T. Lodge, Polymer Chemistry, CRC Press, New York, 2007 Search PubMed.
- C. L. Gettinger, A. J. Heeger, J. M. Drake and D. J. Pine, J. Chem. Phys., 1994, 101, 1673–1678 CrossRef CAS.
- B. McCulloch, V. Ho, M. Hoarfrost, C. Stanley, C. Do, W. T. Heller and R. A. Segalman, Macromolecules, 2013, 46, 1899–1907 CrossRef CAS.
- S. Lecommandoux, F. Checot, R. Borsali, M. Schappacher and A. Deffieux, Macromolecules, 2002, 35, 8878–8881 CrossRef CAS.
- J. P. Aime, F. Bargain, M. Schott, H. Eckhardt, G. G. Miller and R. L. Elsenbaumer, Phys. Rev. Lett., 1989, 62, 55–58 CrossRef CAS PubMed.
- P. Debye, J. Phys. Colloid Chem., 1947, 51, 18–32 CrossRef CAS PubMed.
- J. Des Cloizeaux, Macromolecules, 1973, 6, 403 CrossRef.
- P. Sharp and V. A. Bloomfield, Biopolymers, 1968, 6, 1201–1211 CrossRef CAS PubMed.
- X. Bi, Q. Ying and R. Qian, Makromol. Chem., 1992, 193, 2905–2914 CrossRef CAS.
- G. Heffner and D. Pearson, Macromolecules, 1991, 24, 6295–6299 CrossRef CAS.
- W. Zhang, E. D. Gomez and S. T. Milner, Macromolecules, 2015, 48, 1454–1462 CrossRef CAS.
- G. Heffner, D. Pearson and C. L. Gettinger, Polym. Eng. Sci., 1995, 35, 860–867 CAS.
- L.-H. Zhao, R.-Q. Png, J.-M. Zhuo, L.-Y. Wong, J.-C. Tang, Y.-S. Su and L.-L. Chua, Macromolecules, 2011, 44, 9692–9702 CrossRef CAS.
- D. B. Roitman, R. A. Wessling and J. McAlister, Macromolecules, 1993, 26, 5174–5184 CrossRef CAS.
- B. L. Farmer, B. R. Chapman, D. S. Dudis and W. W. Adams, Polymer, 1993, 34, 1589–1601 CrossRef.
- G. Fytas, H. G. Nothofer, U. Scherf, D. Vlassopoulos and G. Meier, Macromolecules, 2002, 35, 481–488 CrossRef CAS.
- M. Grell, D. D. C. Bradlely, X. Long, T. Chamberlain, M. Inbasekaran, E. P. Woo and M. Soliman, Acta Polym., 1998, 49, 439–444 CrossRef CAS.
- G. Petekidis and D. Vlassopoulos, Macromolecules, 1996, 29, 8948–8953 CrossRef CAS.
- K. Harre and G. Wegner, Polymer, 2006, 47, 7312–7317 CrossRef CAS.
- Y. C. Li, C. Y. Chen, Y. X. Chang, P. Y. Chuang, J. H. Chen, H. L. Chen, C. S. Hsu, V. A. Ivanov, P. G. Khalatur and S. A. Chen, Langmuir, 2009, 25, 4668–4677 CrossRef CAS PubMed.
- A. Lukyanov, A. Malafeev, V. Ivanov, H.-L. Chen, K. Kremer and D. Andrienko, J. Mater. Chem., 2010, 20, 10475–10485 RSC.
- P. Cotts, T. M. Swager and Q. Zhou, Macromolecules, 1996, 29, 7323–7328 CrossRef CAS.
- M. Bohdanecky, Macromolecules, 1983, 16, 1483–1492 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford UP, Oxford, 2003 Search PubMed.
- J. Bicerano, Comput. Theor. Polym. Sci., 1998, 8, 9–13 CrossRef CAS.
- G. Manning, Biophys. J., 2006, 91, 3607–3616 CrossRef CAS PubMed.
- S. B. Smith, L. Finzi and C. Bustamante, Science, 1992, 258, 1122–1126 CAS.
- K. F. Wong, M. S. Skaf, C.-Y. Yang, P. J. Rossky, B. Bagchi, D. Hu, J. Yu and P. F. Barbara, J. Phys. Chem. B, 2001, 105, 6103–6107 CrossRef CAS.
- G. D. Hale, S. J. Oldenburg and N. J. Halas, Appl. Phys. Lett., 1997, 71, 1483–1485 CrossRef CAS.
- T. Zyung and J. J. Kim, Appl. Phys. Lett., 1995, 67, 3420–3422 CrossRef CAS.
- D. Hu, J. Yu, K. Wong, B. Bagchi, P. J. Rossky and P. F. Barbara, Nature, 2000, 405, 1030–1033 CrossRef CAS PubMed.
- T. J. Prosa, M. J. Winokur, J. Moulton, P. Smith and A. J. Heeger, Macromolecules, 1992, 25, 4364–4372 CrossRef CAS.
- C. R. Snyder, R. C. Nieuwendaal, D. M. DeLongchamp, C. K. Luscombe, P. Sista and S. D. Boyd, Macromolecules, 2014, 47, 3942–3950 CrossRef CAS.
- N. Van Thuan, T. Vinh Son, T. Quang Trung, T. Thi Thao and N. Nang Dinh, VNU J. Sci.: Mat. – Phys., 2015, 31, 21–27 Search PubMed.
- H. M. Hlaing, PhD thesis, Stony Brook University, 2012.
- S. B. Darling and M. Sternberg, J. Phys. Chem. B, 2009, 113, 6215–6218 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, N.Y., 1953 Search PubMed.
- P. J. Brown, D. S. Thomas, A. Köhler, J. S. Wilson, J.-S. Kim, C. M. Ramsdale, H. Sirringhaus and R. H. Friend, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 0642031 Search PubMed.
- F. C. Spano, J. Chem. Phys., 2005, 122, 234701 CrossRef PubMed.
- E. S. Manas and F. C. Spano, J. Chem. Phys., 1998, 109, 8087–8101 CrossRef CAS.
- D. T. Duong, V. Ho, Z. Shang, S. Mollinger, S. C. B. Mannsfeld, J. Dacuña, M. F. Toney, R. Segalman and A. Salleo, Adv. Funct. Mater., 2014, 24, 4515–4521 CrossRef CAS.
- R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, Nat. Mater., 2013, 12, 1037–1043 CrossRef PubMed.
- Z. Hu, J. Liu, L. Simon-Bower, L. Zhai and A. J. Gesquiere, J. Phys. Chem. B, 2013, 117, 4461–4467 CrossRef CAS PubMed.
- N. E. Jackson, K. L. Kohlstedt, B. M. Savoie, M. Olvera de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2015, 137, 6254–6262 CrossRef CAS PubMed.
- M. Baghgar, J. A. Labastide, F. Bokel, R. C. Hayward and M. D. Barnes, J. Phys. Chem. C, 2014, 118, 2229–2235 CAS.
- J. Schelten, D. G. H. Ballard, G. D. Wignall, G. Longman and W. Schmatz, Polymer, 1976, 17, 751–757 CrossRef CAS.
- D. M. Sadler and A. Keller, Macromolecules, 1977, 10, 1128–1140 CrossRef CAS.
- D. M. Sadler and A. Keller, Science, 1979, 203, 263–265 CAS.
- G. Bounos, S. Ghosh, A. K. Lee, K. N. Plunkett, K. H. DuBay, J. C. Bolinger, R. Zhang, R. A. Friesner, C. Nuckolls, D. R. Reichman and P. F. Barbara, J. Am. Chem. Soc., 2011, 133, 10155–10160 CrossRef CAS PubMed.
- M. C. Traub, K. H. DuBay, S. E. Ingle, X. Zhu, K. N. Plunkett, D. R. Reichman and D. A. Vanden Bout, J. Phys. Chem. Lett., 2013, 4, 2520–2524 CrossRef CAS.
- Y. H. Wijsboom, A. Patra, S. S. Zade, Y. Sheynin, M. Li, L. J. W. Shimon and M. Bendikov, Angew. Chem., Int. Ed., 2009, 48, 5443–5447 CrossRef CAS PubMed.
- T. Adachi, J. Brazard, R. J. Ono, B. Hanson, M. C. Traub, Z.-Q. Wu, Z. Li, J. C. Bolinger, V. Ganesan, C. W. Bielawski, D. A. Vanden Bout and P. F. Barbara, J. Phys. Chem. Lett., 2011, 2, 1400–1404 CrossRef CAS.
- J. P. Aime and P. Garrin, Synth. Met., 1991, 41–43, 859–867 CrossRef.
- J. P. Aime and F. Bargain, Europhys. Lett., 1989, 9, 35–40 CrossRef CAS.
- B. Thémans, W. R. Salaneck and J. L. Brédas, Synth. Met., 1989, 28, 359–364 CrossRef.
- A. S. Özen, C. Atilgan and G. Sonmez, J. Phys. Chem. C, 2007, 111, 16362–16371 Search PubMed.
- Y.-H. Tian and M. Kertesz, Macromolecules, 2009, 42, 2309–2312 CrossRef CAS.
- G. C. Welch, L. A. Perez, C. V. Hoven, Y. Zhang, X.-D. Dang, A. Sharenko, M. F. Toney, E. J. Kramer, T.-Q. Nguyen and G. C. Bazan, J. Mater. Chem., 2011, 21, 12700–12709 RSC.
- G. C. Welch, R. C. Bakus, S. J. Teat and G. C. Bazan, J. Am. Chem. Soc., 2013, 135, 2298–2305 CrossRef CAS PubMed.
- X. Guo, J. Quinn, Z. Chen, H. Usta, Y. Zheng, Y. Xia, J. W. Hennek, R. P. Ortiz, T. J. Marks and A. Facchetti, J. Am. Chem. Soc., 2013, 135, 1986–1996 CrossRef CAS PubMed.
- X. Guo, N. Zhou, S. J. Lou, J. W. Hennek, R. Ponce Ortiz, M. R. Butler, P.-L. T. Boudreault, J. Strzalka, P.-O. Morin, M. Leclerc, J. T. López Navarrete, M. A. Ratner, L. X. Chen, R. P. H. Chang, A. Facchetti and T. J. Marks, J. Am. Chem. Soc., 2012, 134, 18427–18439 CrossRef CAS PubMed.
- N. Hergué, C. Mallet, G. Savitha, M. Allain, P. Frère and J. Roncali, Org. Lett., 2011, 13, 1762–1765 CrossRef PubMed.
- S. Yum, T. K. An, X. Wang, W. Lee, M. A. Uddin, Y. J. Kim, T. L. Nguyen, S. Xu, S. Hwang, C. E. Park and H. Y. Woo, Chem. Mater., 2014, 26, 2147–2154 CrossRef CAS.
- N. E. Jackson, B. M. Savoie, K. L. Kohlstedt, M. Olvera de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2013, 135, 10475–10483 CrossRef CAS PubMed.
- H. Huang, Z. Chen, R. P. Ortiz, C. Newman, H. Usta, S. Lou, J. Youn, Y.-Y. Noh, K.-J. Baeg, L. X. Chen, A. Facchetti and T. Marks, J. Am. Chem. Soc., 2012, 134, 10966–10973 CrossRef CAS PubMed.
- I. McCulloch, M. Heeney, C. Bailey, K. Genevicius, I. Macdonald, M. Shkunov, D. Sparrowe, S. Tierney, R. Wagner, W. M. Zhang, M. L. Chabinyc, R. J. Kline, M. D. McGehee and M. F. Toney, Nat. Mater., 2006, 5, 328–333 CrossRef CAS PubMed.
- M. J. Lee, D. Gupta, N. Zhao, M. Heeney, I. McCulloch and H. Sirringhaus, Adv. Funct. Mater., 2011, 21, 932–940 CrossRef CAS.
- H. Sirringhaus, R. J. Wilson, R. H. Friend, M. Inbasekaran, W. Wu, E. P. Woo, M. Grell and D. D. C. Bradley, Appl. Phys. Lett., 2000, 77, 406–408 CrossRef CAS.
- R. Noriega, A. Salleo and A. J. Spakowitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16315–16320 CrossRef CAS PubMed.
- D. T. Duong, V. Ho, Z. Shang, S. Mollinger, S. C. B. Mannsfeld, J. Dacuña, M. F. Toney, R. Segalman and A. Salleo, Adv. Funct. Mater., 2014, 24, 4515–4521 CrossRef CAS.
- Y. Liang, Z. Xu, J. Xia, S.-T. Tsai, Y. Wu, G. Li, C. Ray and L. Yu, Adv. Mater., 2010, 22, E135–E138 CrossRef CAS PubMed.
- Y. H. Liu, J. B. Zhao, Z. K. Li, C. Mu, W. Ma, H. W. Hu, K. Jiang, H. R. Lin, H. Ade and H. Yan, Nat. Commun., 2014, 5, 5293 CrossRef CAS PubMed.
- J. Li, Y. Zhao, H. S. Tan, Y. Guo, C. A. Di, G. Yu, Y. Liu, M. Lin, S. H. Lim, Y. Zhou, H. Su and B. S. Ong, Sci. Rep., 2012, 2, 754 Search PubMed.
- X. R. Zhang, H. Bronstein, A. J. Kronemeijer, J. Smith, Y. Kim, R. J. Kline, L. J. Richter, T. D. Anthopoulos, H. Sirringhaus, K. Song, M. Heeney, W. M. Zhang, I. McCulloch and D. M. DeLongchamp, Nat. Commun., 2013, 4, 2238 Search PubMed.
- H. Chen, Y. Guo, G. Yu, Y. Zhao, J. Zhang, D. Gao, H. Liu and Y. Liu, Adv. Mater., 2012, 24, 4618–4622 CrossRef CAS PubMed.
- A. P. Kulkarni, C. J. Tonzola, A. Babel and S. A. Jenekhe, Chem. Mater., 2004, 16, 4556–4573 CrossRef CAS.
- S. H. Park, A. Roy, S. Beaupré, S. Cho, N. Coates, J. S. Moon, D. Moses, M. Leclerc, K. Lee and A. J. Heeger, Nat. Photonics, 2009, 3, 297–302 CrossRef CAS.
- C. R. Snyder and E. D. Gomez, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1202–1206 CrossRef CAS.
- P. Gemünden, C. Poelking, K. Kremer, D. Andrienko and K. C. Daoulas, Macromolecules, 2013, 46, 5762–5774 CrossRef.
- V. Ho, B. W. Boudouris and R. A. Segalman, Macromolecules, 2010, 43, 7895–7899 CrossRef CAS.
- M. S. Park, A. Aiyar, J. O. Park, E. Reichmanis and M. Srinivasarao, J. Am. Chem. Soc., 2011, 133, 7244–7247 CrossRef CAS PubMed.
- W. Zhang, E. D. Gomez and S. T. Milner, Macromolecules, 2016, 49, 963–971 CrossRef CAS.
- M. Grell, D. D. C. Bradley, M. Inbasekaran and E. P. Woo, Adv. Mater., 1997, 9, 798–802 CrossRef CAS.
- X. F. Wang, J. Engel and C. Liu, J. Micromech. Microeng., 2003, 13, 628–633 CrossRef CAS.
- S. J. Woltman, G. D. Jay and G. P. Crawford, Nat. Mater., 2007, 6, 929–938 CrossRef CAS PubMed.
- M. Redecker, D. D. C. Bradley, M. Inbasekaran and E. P. Woo, Appl. Phys. Lett., 1999, 74, 1400–1402 CrossRef CAS.
- M. O'Neill and S. M. Kelly, Adv. Mater., 2011, 23, 566–584 CrossRef PubMed.
- L. Kinder, J. Kanicki and P. Petroff, Synth. Met., 2004, 146, 181–185 CrossRef CAS.
- J. F. Chang, B. Q. Sun, D. W. Breiby, M. M. Nielsen, T. I. Solling, M. Giles, I. McCulloch and H. Sirringhaus, Chem. Mater., 2004, 16, 4772–4776 CrossRef CAS.
- H. C. Yang, T. J. Shin, L. Yang, K. Cho, C. Y. Ryu and Z. N. Bao, Adv. Funct. Mater., 2005, 15, 671–676 CrossRef CAS.
- B. G. Kim, E. J. Jeong, J. W. Chung, S. Seo, B. Koo and J. Kim, Nat. Mater., 2013, 12, 659–664 CrossRef CAS PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- A. R. Khokhlov and A. N. Semenov, Physica A, 1981, 108, 546–556 CrossRef.
- A. R. Khokhlov, Phys. Lett. A, 1978, 68, 135–136 CrossRef.
- W. Zhang, E. D. Gomez and S. T. Milner, Soft Matter, 2016, 12, 6141–6147 RSC.
- B. D. Olsen, M. Shah, V. Ganesan and R. A. Segalman, Macromolecules, 2008, 41, 6809–6817 CrossRef CAS.
- B. D. Olsen and R. A. Segalman, Mater. Sci. Eng., R, 2008, 62, 37–66 CrossRef.
- B. D. Olsen and R. A. Segalman, Macromolecules, 2005, 38, 10127–10137 CrossRef CAS.
- G. R. Luckhurst and C. Zannoni, Nature, 1977, 267, 412–414 CrossRef CAS.
- A. J. Liu and G. H. Fredrickson, Macromolecules, 1993, 26, 2817–2824 CrossRef CAS.
- H. W. Chiu and T. Kyu, J. Chem. Phys., 1995, 103, 7471–7481 CrossRef CAS.
- S. Malik and A. K. Nandi, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 2073–2085 CrossRef CAS.
- C. R. Snyder, J. S. Henry and D. M. DeLongchamp, Macromolecules, 2011, 44, 7088–7091 CrossRef CAS.
- N. Kayunkid, S. Uttiya and M. Brinkmann, Macromolecules, 2010, 43, 4961–4967 CrossRef CAS.
- A. Hamidi-Sakr, D. Schiefer, S. Covindarassou, L. Biniek, M. Sommer and M. Brinkmann, Macromolecules, 2016, 49, 3452–3462 CrossRef CAS.
- E. Cho, C. Risko, D. Kim, R. Gysel, N. C. Miller, D. W. Breiby, M. D. McGehee, M. F. Toney, R. J. Kline and J.-L. Bredas, J. Am. Chem. Soc., 2012, 134, 6177–6190 CrossRef CAS PubMed.
- D. Dudenko, A. Kiersnowski, J. Shu, W. Pisula, D. Sebastiani, H. W. Spiess and M. R. Hansen, Angew. Chem., 2012, 51, 11068–11072 CrossRef CAS PubMed.
- B. W. Boudouris, V. Ho, L. H. Jimison, M. F. Toney, A. Salleo and R. A. Segalman, Macromolecules, 2011, 44, 6653–6658 CrossRef CAS.
- B. H. Smith, M. B. Clark, H. Kuang, C. Grieco, A. V. Larsen, C. Zhu, C. Wang, A. Hexemer, J. B. Asbury, M. J. Janik and E. D. Gomez, Adv. Funct. Mater., 2015, 25, 542–551 CrossRef CAS.
- S. Y. Son, Y. Kim, J. Lee, G. Y. Lee, W. T. Park, Y. Y. Noh, C. E. Park and T. Park, J. Am. Chem. Soc., 2016, 138, 8096–8103 CrossRef CAS PubMed.
- R. J. Kline, M. D. McGehee, E. N. Kadnikova, J. S. Liu, J. M. J. Frechet and M. F. Toney, Macromolecules, 2005, 38, 3312–3319 CrossRef CAS.
- J.-F. Chang, J. Clark, N. Zhao, H. Sirringhaus, D. W. Breiby, J. W. Andreasen, M. M. Nielsen, M. Giles, M. Heeney and I. McCulloch, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115318 CrossRef.
- K. Vakhshouri and E. D. Gomez, Macromol. Rapid Commun., 2012, 33, 2133–2137 CrossRef CAS PubMed.
- Y. Yamashita, F. Hinkel, T. Marszalek, W. Zajaczkowski, W. Pisula, M. Baumgarten, H. Matsui, K. Müllen and J. Takeya, Chem. Mater., 2016, 28, 420–424 CrossRef CAS.
- R. A. Matkar and T. Kyu, J. Phys. Chem. B, 2006, 110, 16059–16065 CrossRef CAS PubMed.
- G. Yu, J. Hummelen, F. Wudl and A. Heeger, Science, 1995, 270, 1789–1791 CAS.
- S. C. Price, A. C. Stuart, L. Yang, H. Zhou and W. You, J. Am. Chem. Soc., 2011, 133, 4625–4631 CrossRef CAS PubMed.
- M. Reyes-Reyes, K. Kim and D. L. Carroll, Appl. Phys. Lett., 2005, 87, 83506 CrossRef.
- J. K. J. van Duren, X. N. Yang, J. Loos, C. W. T. Bulle-Lieuwma, A. B. Sieval, J. C. Hummelen and R. A. J. Janssen, Adv. Funct. Mater., 2004, 14, 425–434 CrossRef CAS.
- P. E. Shaw, A. Ruseckas and I. D. W. Samuel, Adv. Mater., 2008, 20, 3516–3520 CrossRef CAS.
- A. Haugeneder, M. Neges, C. Kallinger, W. Spirkl, U. Lemmer, J. Feldmann, U. Scherf, E. Harth, A. Gugel and K. Mullen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15346–15351 CrossRef CAS.
- D. R. Kozub, K. Vakhshouri, L. M. Orme, C. Wang, A. Hexemer and E. D. Gomez, Macromolecules, 2011, 44, 5722–5726 CrossRef CAS.
- D. R. Kozub, K. Vakhshouri, S. V. Kesava, C. Wang, A. Hezemer and E. D. Gomez, Chem. Commun., 2012, 48, 5859–5861 RSC.
- S. V. Kesava, Z. Fei, A. D. Rimshaw, C. Wang, A. Hexemer, J. B. Asbury, M. Heeney and E. D. Gomez, Adv. Energy Mater., 2014, 4, 1400116 CrossRef.
- Z. Mao, T. P. Le, K. Vakhshouri, R. Fernando, F. Ruan, E. Muller, E. D. Gomez and G. Sauvé, Org. Electron., 2014, 15, 3384–3391 CrossRef CAS.
- H.-Y. Chen, H. Yang, G. Yang, S. Sista, R. Zadoyan, G. Li and Y. Yang, J. Phys. Chem. C, 2009, 113, 7946–7953 CAS.
- E. D. Gomez, K. P. Barteau, H. Wang, M. F. Toney and Y.-L. Loo, Chem. Commun., 2011, 47, 436–438 RSC.
- J. D. Roehling, K. J. Batenburg, F. B. Swain, A. J. Moule and I. Arslan, Adv. Funct. Mater., 2013, 23, 2115–2122 CrossRef CAS.
- S. S. van Bavel, E. Sourty, G. de With and J. Loos, Nano Lett., 2009, 9, 507–513 CrossRef CAS PubMed.
- Z. Mao, K. Vakhshouri, C. Jaye, D. A. Fischer, R. Fernando, D. M. DeLongchamp, E. D. Gomez and G. Sauvé, Macromolecules, 2013, 46, 103–112 CrossRef CAS.
- Z. Mao, W. Senevirathna, J.-Y. Liao, J. Gu, S. V. Kesava, C. Guo, E. D. Gomez and G. Sauvé, Adv. Mater., 2014, 26, 6290–6294 CrossRef CAS PubMed.
- S. Vajjala Kesava, R. Dhanker, D. R. Kozub, K. Vakhshouri, U. H. Choi, R. H. Colby, C. Wang, A. Hexemer, N. C. Giebink and E. D. Gomez, Chem. Mater., 2013, 25, 2812–2818 CrossRef CAS.
- A. C. Mayer, M. F. Toney, S. R. Scully, J. Rivnay, C. J. Brabec, M. Scharber, M. Koppe, M. Heeney, I. McCulloch and M. D. McGehee, Adv. Funct. Mater., 2009, 19, 1173–1179 CrossRef CAS.
- N. C. Cates, R. Gysel, Z. Beiley, C. E. Miller, M. F. Toney, M. Heeney, I. McCulloch and M. D. McGehee, Nano Lett., 2009, 9, 4153–4157 CrossRef CAS PubMed.
- J. E. Parmer, A. C. Mayer, B. E. Hardin, S. R. Scully, M. D. McGehee, M. Heeney and I. McCulloch, Appl. Phys. Lett., 2008, 92, 113309 CrossRef.
- J. W. Kiel, B. J. Kirby, C. F. Majkrzak, B. B. Maranville and M. E. Mackay, Soft Matter, 2010, 6, 641–646 RSC.
- J. W. Kiel, A. P. R. Eberle and M. E. Mackay, Phys. Rev. Lett., 2010, 105, 168701 CrossRef PubMed.
- B. R. Saunders and M. L. Turner, Adv. Colloid Interface Sci., 2008, 138, 1–23 CrossRef CAS PubMed.
- B. A. Collins, E. Gann, L. Guignard, X. He, C. R. McNeill and H. Ade, J. Phys. Chem. Lett., 2010, 1, 3160–3166 CrossRef CAS.
- D. A. Chen, A. Nakahara, D. G. Wei, D. Nordlund and T. P. Russell, Nano Lett., 2011, 11, 561–567 CrossRef CAS PubMed.
- E. S. McGarrity, P. M. Duxbury, M. E. Mackay and A. L. Frischknecht, Macromolecules, 2008, 41, 5952–5954 CrossRef CAS.
- D. Leman, M. A. Kelly, S. Ness, S. Engmann, A. Herzing, C. Snyder, H. W. Ro, R. J. Kline, D. M. DeLongchamp and L. J. Richter, Macromolecules, 2015, 48, 383–392 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51 CrossRef CAS.
- M. L. Huggins, J. Am. Chem. Soc., 1942, 64, 1712 CrossRef CAS.
- K. Vakhshouri, D. R. Kozub, C. Wang, A. Salleo and E. D. Gomez, Phys. Rev. Lett., 2012, 108, 026601 CrossRef PubMed.
- J. Y. Kim and C. D. Frisbie, J. Phys. Chem. C, 2008, 112, 17726–17736 CAS.
- C. Müller, T. A. M. Ferenczi, M. Campoy-Quiles, J. M. Frost, D. D. C. Bradley, P. Smith, N. Stingelin-Stutzmann and J. Nelson, Adv. Mater., 2008, 20, 3510–3515 CrossRef.
- B. A. Collins, J. R. Tumbleston and H. Ade, J. Phys. Chem. Lett., 2011, 2, 3135–3145 CrossRef CAS.
- S. Nilsson, A. Bernasik, A. Budkowski and E. Moons, Macromolecules, 2007, 40, 8291–8301 CrossRef CAS.
- W. C. Tsoi, D. T. James, E. B. Domingo, J. S. Kim, M. Al-Hashimi, C. E. Murphy, N. Stingelin, M. Heeney and J. Kim, ACS Nano, 2012, 6, 9646–9656 CrossRef CAS PubMed.
- C. H. Woo, B. C. Thompson, B. J. Kim, M. F. Toney and J. Frechet, J. Am. Chem. Soc., 2008, 130, 16324–16329 CrossRef CAS PubMed.
- J. M. G. Cowie and V. Arrighi, Polymers: Chemistry and Physics of Modern Materials, CRC Press, Boca Raton, FL, 3rd edn, 2007 Search PubMed.
- F. S. Bates, M. F. Schulz and J. H. Rosedale, Macromolecules, 1992, 25, 5547–5550 CrossRef CAS.
- A. J. Liu and G. H. Fredrickson, Macromolecules, 1992, 25, 5551–5553 CrossRef CAS.
- Y. Jiang and J. Z. Chen, Phys. Rev. Lett., 2013, 110, 138305 CrossRef PubMed.
- J. Lange, N. Altmann, C. T. Kelly and P. J. Halley, Polymer, 2000, 41, 5949–5955 CrossRef CAS.
- S. L. Simon and J. K. Gillham, J. Appl. Polym. Sci., 1992, 46, 1245–1270 CrossRef CAS.
- C. J. T. Landry, B. K. Coltrain and B. K. Brady, Polymer, 1992, 33, 1486–1495 CrossRef CAS.
- M. T. Aronhime and J. K. Gillham, in Epoxy Resins and Composites III, ed. K. Dušek, Springer Berlin Heidelberg, Berlin, Heidelberg, 1986, pp. 83–113 DOI:10.1007/BFb0035358.
- J. K. Gillham, Makromol. Chem., Macromol. Symp., 1987, 7, 67–74 CrossRef CAS.
- E. Verploegen, R. Mondal, C. J. Bettinger, S. Sok, M. F. Toney and Z. Bao, Adv. Funct. Mater., 2010, 20, 3519–3529 CrossRef CAS.
- F. Frigerio, M. Casalegno, C. Carbonera, T. Nicolini, S. V. Meille and G. Raos, J. Mater. Chem., 2012, 22, 5434–5443 RSC.
- N. Cheval, V. Kampars, C. Fowkes, N. Shirtcliffe and A. Fahmi, Nanomaterials, 2013, 3, 107–116 CrossRef CAS.
- T. Winands, M. Bockmann, T. Schemme, P.-M. T. Ly, D. H. de Jong, Z. Wang, C. Denz, A. Heuer and N. L. Doltsinis, Phys. Chem. Chem. Phys., 2016, 18, 6217–6227 RSC.
- Y. Zhao, G. Yuan and P. Roche, Polymer, 1995, 36, 2211–2214 CrossRef CAS.
- J. Liu, Y. J. Shi and Y. Yang, Appl. Phys. Lett., 2001, 79, 578–580 CrossRef CAS.
- A. P. Kulkarni and S. A. Jenekhe, Macromolecules, 2003, 36, 5285–5296 CrossRef CAS.
- G. Greczynski, T. Kugler and W. R. Salaneck, Thin Solid Films, 1999, 354, 129–135 CrossRef CAS.
- M. Vosgueritchian, D. J. Lipomi and Z. A. Bao, Adv. Funct. Mater., 2012, 22, 421–428 CrossRef CAS.
- J. E. Yoo, K. S. Lee, A. Garcia, J. Tarver, E. D. Gomez, K. Baldwin, Y. M. Sun, H. Meng, T. Q. Nguyen and Y. L. Loo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5712–5717 CrossRef CAS PubMed.
- S. K. Choi, Y. H. Zhou, W. Haske, J. W. Shim, C. Fuentes-Hernandez and B. Kippelen, Org. Electron., 2015, 17, 349–354 CrossRef CAS.
- C. R. McNeill, J. J. M. Halls, R. Wilson, G. L. Whiting, S. Berkebile, M. G. Ramsey, R. H. Friend and N. C. Greenham, Adv. Funct. Mater., 2008, 18, 2309–2321 CrossRef CAS.
- H. Y. Li, Y. J. Hwang, T. Earmme, R. C. Huber, B. A. E. Courtright, C. O'Brien, S. H. Tolbert and S. A. Jenekhe, Macromolecules, 2015, 48, 1759–1766 CrossRef CAS.
- A. Facchetti, Mater. Today, 2013, 16, 123–132 CrossRef CAS.
- H. Kang, M. A. Uddin, C. Lee, K.-H. Kim, T. L. Nguyen, W. Lee, Y. Li, C. Wang, H. Y. Woo and B. J. Kim, J. Am. Chem. Soc., 2015, 137, 2359–2365 CrossRef CAS PubMed.
- G. R. Strobl, The Physics of Polymers Concepts for Understanding Their Structures and Behavior, Springer-Verlag, 1996 Search PubMed.
- J. M. Machado, J. B. Schlenoff and F. E. Karasz, Macromolecules, 1989, 22, 1964–1973 CrossRef CAS.
- H. L. Wang, L. Toppare and J. E. Fernandez, Macromolecules, 1990, 23, 1053–1059 CrossRef CAS.
- Y.-J. Hwang, B. A. E. Courtright, A. S. Ferreira, S. H. Tolbert and S. A. Jenekhe, Adv. Mater., 2015, 27, 4578–4584 CrossRef CAS PubMed.
- Y. J. Hwang, T. Earmme, B. A. E. Courtright, F. N. Eberle and S. A. Jenekhe, J. Am. Chem. Soc., 2015, 137, 4424–4434 CrossRef CAS PubMed.
- K. D. Deshmukh, T. S. Qin, J. K. Gallaher, A. C. Y. Liu, E. Gann, K. O'Donnell, L. Thomsen, J. M. Hodgkiss, S. E. Watkins and C. R. McNeill, Energy Environ. Sci., 2015, 8, 332–342 CAS.
- Y. Zhou, T. Kurosawa, W. Ma, Y. K. Guo, L. Fang, K. Vandewal, Y. Diao, C. G. Wang, Q. F. Yan, J. Reinspach, J. G. Mei, A. L. Appleton, G. I. Koleilat, Y. L. Gao, S. C. B. Mannsfeld, A. Salleo, H. Ade, D. H. Zhao and Z. N. Bao, Adv. Mater., 2014, 26, 3767–3772 CrossRef CAS PubMed.
- E. Pavlopoulou, C. S. Kim, S. S. Lee, Z. Chen, A. Facchetti, M. F. Toney and Y.-L. Loo, Chem. Mater., 2014, 26, 5020–5027 CrossRef CAS.
- J. Wang and T. Higashihara, Polym. Chem., 2013, 4, 5518–5526 RSC.
- H. Kang, M. A. Uddin, C. Lee, K. H. Kim, T. L. Nguyen, W. Lee, Y. Li, C. Wang, H. Y. Woo and B. J. Kim, J. Am. Chem. Soc., 2015, 137, 2359–2365 CrossRef CAS PubMed.
- H. Kang, K.-H. Kim, J. Choi, C. Lee and B. J. Kim, ACS Macro Lett., 2014, 3, 1009–1014 CrossRef CAS.
- B. Watts and C. R. McNeill, Macromol. Rapid Commun., 2010, 31, 1706–1712 CrossRef CAS PubMed.
- P. C. Painter, W.-L. Tang, J. F. Graf, B. Thomson and M. M. Coleman, Macromolecules, 1991, 24, 3929–3936 CrossRef CAS.
- L. F. Wang, E. M. Pearce and T. K. Kwei, Polymer, 1991, 32, 249–259 CrossRef CAS.
- R. Duran, M. Ballauff, M. Wenzel and G. Wegner, Macromolecules, 1988, 21, 2897–2899 CrossRef CAS.
- J. H. Chen, X. Yu, K. L. Hong, J. M. Messman, D. L. Pickel, K. Xiao, M. D. Dadmun, J. W. Mays, A. J. Rondinone, B. G. Sumpter and S. M. Kilbey, J. Mater. Chem., 2012, 22, 13013–13022 RSC.
- J. Zhao, B. Majumdar, M. F. Schulz, F. S. Bates, K. Almdal, K. Mortensen, D. A. Hajduk and S. M. Gruner, Macromolecules, 1996, 29, 1204–1215 CrossRef CAS.
- F. S. Bates, Science, 1991, 251, 898–905 CrossRef CAS PubMed.
- F. S. Bates, W. W. Maurer, P. M. Lipic, M. A. Hillmyer, K. Almdal, K. Mortensen, G. H. Fredrickson and T. P. Lodge, Phys. Rev. Lett., 1997, 79, 849–852 CrossRef CAS.
- J. H. Lee, N. P. Balsara, R. Krishnamoorti, H. S. Jeon and B. Hammouda, Macromolecules, 2001, 34, 6557–6560 CrossRef CAS.
- W. W. Graessley, R. Krishnamoorti, G. C. Reichart, N. P. Balsara, L. J. Fetters and D. J. Lohse, Macromolecules, 1995, 28, 1260–1270 CrossRef CAS.
- W. W. Graessley, R. Krishnamoorti, N. P. Balsara, R. J. Butera, L. J. Fetters, D. J. Lohse, D. N. Schulz and J. A. Sissano, Macromolecules, 1994, 27, 3896–3901 CrossRef CAS.
- K. Levon, E. Chu, K. S. Ho, T. K. Kwei, J. Mao, W. Y. Zheng and J. Laakso, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 537–645 CrossRef CAS.
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969 RSC.
- R. Verduzco, I. Botiz, D. L. Pickel, S. M. Kilbey, K. L. Hong, E. Dimasi and S. B. Darling, Macromolecules, 2011, 44, 530–539 CrossRef CAS.
- K. A. Smith, Y.-H. Lin, J. W. Mok, K. G. Yager, J. Strzalka, W. Nie, A. D. Mohite and R. Verduzco, Macromolecules, 2015, 48, 8346–8353 CrossRef CAS.
- J. W. Mok, Y.-H. Lin, K. G. Yager, A. D. Mohite, W. Nie, S. B. Darling, Y. Lee, E. Gomez, D. Gosztola, R. D. Schaller and R. Verduzco, Adv. Funct. Mater., 2015, 25, 5578–5585 CrossRef CAS.
- C. Guo, Y.-H. Lin, M. D. Witman, K. A. Smith, C. Wang, A. Hexemer, J. Strzalka, E. D. Gomez and R. Verduzco, Nano Lett., 2013, 13, 2957–2963 CrossRef CAS PubMed.
- Y. H. Lin, S. B. Darling, M. O. Nikiforov, J. Strzalka and R. Verduzco, Macromolecules, 2012, 45, 6571–6579 CrossRef CAS.
- I. Botiz, R. D. Schaller, R. Verduzco and S. B. Darling, J. Phys. Chem. C, 2011, 115, 9260–9266 CAS.
- K. Nakabayashi and H. Mori, Materials, 2014, 7, 3274–3290 CrossRef CAS.
- J. Wang and T. Higashihara, Polym. Chem., 2013, 4, 5518–5526 RSC.
- U. Scherf, A. Gutacker and N. Koenen, Acc. Chem. Res., 2008, 41, 1086–1097 CrossRef CAS PubMed.
- J. H. Lee, N. P. Balsara, A. K. Chakraborty, R. Krishnamoorti and B. Hammouda, Macromolecules, 2002, 35, 7748–7757 CrossRef CAS.
- H. B. Eitouni and N. P. Balsara, in Physical Properties of Polymer Handbook, ed. J. E. Mark, Springer, New York, 2nd edn, 2006 Search PubMed.
- P. G. d. Gennes, Scaling Concepts in Polymer Physics, Oxford University Press, Ithaca and London, 1979 Search PubMed.
- J. Hildebrand and R. L. Scott, The Solubility of Nonelectrolytes, Reinhold, New York, 3rd edn, 1950 Search PubMed.
- J. Hildebrand and R. L. Scott, Regular Solutions, Prentice-Hall Inc., Englewood Cliffs, NJ, 1962 Search PubMed.
- J. Brandrup, E. H. Immergut, E. A. Grulke, A. Abe and D. R. Bloch, Polymer Handbook, John Wiley & Sons, New York, 2003 Search PubMed.
- J. Jaczewska, I. Raptis, A. Budkowski, D. Goustouridis, J. Raczkowska, M. Sanopoulou, E. Pamuła, A. Bernasik and J. Rysz, Synth. Met., 2007, 157, 726–732 CrossRef CAS.
- C.-D. Park, T. A. Fleetham, J. Li and B. D. Vogt, Org. Electron., 2011, 12, 1465–1470 CrossRef CAS.
- C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, CRC Press, New York, NY, 1999 Search PubMed.
- K. Zhou, J. Liu, M. Li, X. Yu, R. Xing and Y. Han, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 288–296 CrossRef CAS.
- F. Liu, D. Chen, C. Wang, K. Luo, W. Gu, A. L. Briseno, J. W. Hsu and T. P. Russell, ACS Appl. Mater. Interfaces, 2014, 6, 19876–19887 CAS.
- J. M. Carrillo, R. Kumar, M. Goswami, B. G. Sumpter and W. M. Brown, Phys. Chem. Chem. Phys., 2013, 15, 17873–17882 RSC.
| This journal is © The Royal Society of Chemistry 2017 |