Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the twist-bend nematic phase: the characterisation of 1-(4-cyanobiphenyl-4′-yloxy)-6-(4-cyanobiphenyl-4′-yl)hexane (CB6OCB) and comparison with CB7CB†
Daniel A.
Paterson
a,
Min
Gao
b,
Young-Ki
Kim
b,
Afsoon
Jamali
b,
Kirsten L.
Finley
c,
Beatriz
Robles-Hernández
c,
Sergio
Diez-Berart
c,
Josep
Salud
c,
M. Rosario
de la Fuente
d,
Bakir A.
Timimi
e,
Herbert
Zimmermann
f,
Cristina
Greco
g,
Alberta
Ferrarini
g,
John M. D.
Storey
a,
David O.
López
c,
Oleg D.
Lavrentovich
b,
Geoffrey R.
Luckhurst
e and
Corrie T.
Imrie
*a
aDepartment of Chemistry, School of Natural and Computing Sciences, University of Aberdeen, Meston Building, Aberdeen, AB24 3UE, UK. E-mail: c.t.imrie@abdn.ac.uk
bLiquid Crystal Institute and Chemical Physics Interdisciplinary Program, Kent State University, Kent, OH 44242, USA
cDepartment of Physics, Polytechnic University of Catalonia, Barcelona, Spain
dDepartment of Applied Physics II, University of the Basque Country, E-48080 Bilbao, Spain
eChemistry, University of Southampton, Highfield, Southampton, SO17 1BJ, UK
fMax-Planck-Institut für Medizinische Förschung, D-69120 Heidelberg, Germany
gDipartimento di Scienze Chimiche, Università di Padova, via Marzolo 1, 35121 Padova, Italy
First published on 11th July 2016
Abstract
The synthesis and characterisation of the nonsymmetric liquid crystal dimer, 1-(4-cyanobiphenyl-4′-yloxy)-6-(4-cyanobiphenyl-4′-yl)hexane (CB6OCB) is reported. An enantiotropic nematic (N)–twist-bend nematic (NTB) phase transition is observed at 109 °C and a nematic–isotropic phase transition at 153 °C. The NTB phase assignment has been confirmed using polarised light microscopy, freeze fracture transmission electron microscopy (FFTEM), 2H-NMR spectroscopy, and X-ray diffraction. The effective molecular length in both the NTB and N phases indicates a locally intercalated arrangement of the molecules, and the helicoidal pitch length in the NTB phase is estimated to be 8.9 nm. The surface anchoring properties of CB6OCB on a number of aligning layers is reported. A Landau model is applied to describe high-resolution heat capacity measurements in the vicinity of the NTB–N phase transition. Both the theory and heat capacity measurements agree with a very weak first-order phase transition. A complementary extended molecular field theory was found to be in suggestive accord with the 2H-NMR studies of CB6OCB-d2, and those already known for CB7CB-d4. These include the reduced transition temperature, TNTBN/TNI, the order parameter of the mesogenic arms in the N phase close to the NTB–N transition, and the order parameter with respect to the helix axis which is related to the conical angle for the NTB phase.
1. Introduction
The nematic phase, N, is the simplest but technologically most important liquid crystal phase. The rod-like molecules in the N phase are anisotropically distributed but on average tend to point in the same direction known as the director. If the constituent molecules are chiral then the chiral nematic phase, N*, is observed. At the molecular level, the N and N* phases are indistinguishable but in the N* phase, the director traces out a helix with an axis perpendicular to the director. A third nematic is represented by so-called blue phases, in which the twist propagates along two axes. A fourth nematic phase, the biaxial nematic phase, NB, has been discovered in lyotropic systems but has yet to be observed unequivocally in a low molar mass thermotropic liquid crystal.1The recent discovery of a fifth nematic phase, the twist-bend nematic phase, NTB, has understandably caused considerable excitement. This was predicted by Meyer,2 and by Dozov3 who proposed that certain mesogenic molecules might have a tendency to pack into bent structures. Pure uniform bend in space is impossible, thus the spontaneous bend must be accompanied by other deformations of the local director, either twist or splay, giving rise to the so-called twist-bend nematic, or splay-bend nematic, respectively. In the NTB phase the director exhibits periodic twist and bend deformations forming a conical helix with doubly degenerate domains having opposite handedness. The director is tilted with respect to the helical axis, and hence, it may be considered as the generalised case of the conventional N* phase in which the director is orthogonal with respect to the helical axis, see Fig. 1. The NTB phase is a particularly fascinating and unique phase for a number of reasons, not least because it is spontaneously chiral although composed of effectively achiral molecules. This qualification requires some explanation since a constituent molecule being flexible exists in a range of conformers. These occur in pairs which are related by a mirror plane and have equal probabilities; consequently the conformationally averaged structure is achiral.4
 | ||
| Fig. 1 Schematic representations of (a) the nematic (N) phase, (b) the chiral nematic (N*) phase, and (c) the twist-bend nematic (NTB) phase. | ||
The NTB phase was first identified for 1,7-bis-4-(4′-cyanobiphenyl) heptane, CB7CB,5 and the assignment confirmed using freeze fracture transmission electron microscopy (FFTEM).6,7 CB7CB is an example of a liquid crystal dimer comprising molecules containing two mesogenic units linked by a flexible spacer.8,9 The para axes of the two cyanobiphenyl mesogenic units in an odd-membered dimer are inclined with respect to each other when the spacer is in the all-trans conformation, and this bent molecular shape which exists for most other conformers is thought to be a prerequisite for the formation of the NTB phase.
Only a limited number of other liquid crystal dimers have been reported to show the NTB phase.10–19 Additional examples of twist-bend nematogens include two liquid crystal trimers,20,21 and a rigid bent-core liquid crystal.22 Given this small set of known twist-bend nematogens, we have yet to develop and understand the empirical relationships linking molecular structure to the formation of the NTB phase. Even at this early stage, however, it does appear clear that a bent molecular shape, most often achieved by using methylene linkages between the spacer and mesogenic units, is a prerequisite for the observation of the NTB phase,23 and this view is supported by predictions made using a generalised Maier–Saupe theory modified to take into account the bent molecular architecture by assuming a V-shaped particle, and the twist-bend modulation of the director.24 This predicts that the NTB–N transition temperature is particularly sensitive to the molecular bend angle, defined as the angle between the mesogenic arms, and that the NTB phase is only seen for a limited range of bend angles. The bent molecular shape yields not only the thermodynamically stable NTB phase but also a standard nematic with anomalously small bend elastic constants.6,19,24 The latter feature leads to interesting electro-optical effects in a nematic doped with chiral dopants, such as electrically controlled selective reflection of light.25 The NTB phase is not necessarily preceded by a nematic phase, and an example of a NTB–I transition has recently been reported for a pure dimer where the transition results from reducing the spacer length to just three methylene groups.26 It has also been found to be possible to induce a NTB–I transition for a dimer having nine methylene groups by the addition of a chiral dopant.27
In an attempt to clarify the relationships between the formation of the NTB phase and molecular structure, and in particular to the molecular curvature, here we describe the transitional properties of a nonsymmetric liquid crystal dimer, 1-(4-cyanobiphenyl-4′-yloxy)-6-(4-cyanobiphenyl-4′-yl)hexane, and refer to this using the acronym CB6OCB. The nonsymmetry in this molecule arises from the differing nature of the links between the mesogenic units and flexible spacer. At one end of the spacer the link is an ether group while at the other it is a methylene unit. As we will see, CB6OCB exhibits the twist-bend nematic phase and this is characterised in detail using a range of techniques. In Section 3.1 we investigate the phase behaviour of CB6OCB using modulated DSC, polarised light microscopy and X-ray diffraction and this reveals an enantiotropic NTB–N phase transition. The chirality of the NTB phase is confirmed using NMR spectroscopy in Section 3.5. In Section 3.2, we study the surface anchoring properties of CB6OCB on a number of alignment layers. The NTB phase assignment is confirmed in Section 3.3 using FFTEM. In Section 3.4, we describe the NTB–N phase transition of CB6OCB using a Landau approach and extract the thermodynamic properties. In Section 3.5 we measure the chirality, a defining quantity of the NTB phase, and the orientational order of the N and NTB phases for CB6OCB-d2. The orientational order of CB6OCB is compared with that of CB7CB which are surprisingly different given the small difference in chemical structure of the dimers. Finally, in Section 3.6 a molecular field theory is described to better understand the phase behaviour of CB6OCB and how it relates to that of the structurally similar CB7CB.
2. Experimental
2.1. Synthesis
The syntheses of CB6OCB and CB6OCB-d2 are described in detail in the ESI.†2.2. Modulated differential scanning calorimetry (MDSC)
Modulated differential scanning calorimetry (MDSC) measurements were performed according to two main procedures in order to obtain heat capacity data. To study the overall thermal behaviour of CB6OCB measurements were performed at heating and cooling rates of 1 K min−1, a temperature amplitude of 0.5 K and a period of 60 s. To study the critical behaviour of the NTB–N and N–I phase transitions, measurements were carried out very slowly using heating and cooling rates of 0.01 K min−1, a temperature amplitude of 0.07 K and a period of 23 s.2.3. X-ray diffraction
X-ray diffraction patterns were obtained at several temperatures using a Panalytical X'Pert Pro diffractometer (λCuKα = 1.54 Å) in a step scanning mode (2θ range from 0.5° to 30°). An Oxford Cryosystem was used as a temperature controller for the sample which consisted of a glass capillary tube (0.5 mm diameter) filled with liquid crystal, spinning around the θ-axis during the experiment.2.4. Optical studies
Flat glass cells were used to explore the optical textures and establish the transitional behaviour of CB6OCB. The cell thickness, d, was set by glass spacers attached with UV-glue NOA 65 (Norland Products, Inc.). All of the experiments were performed above the crystallization temperature to avoid a possible memory effect.28 The temperature was controlled by a LTS350 hot stage with a TMS94 controller (both Linkam Instruments) with 0.01 K accuracy. The typical rate of temperature change was between ±0.10 K min−1 and ±1.00 K min−1 to minimize the effects of thermal expansion on textures.29–312.5. Freeze fracture transmission electron microscopy (FFTEM)
To prepare the replica for FFTEM studies, CB6OCB was heated to the isotropic phase and cooled slowly to 368 K to obtain the NTB phase. The sample was then rapidly frozen in liquid nitrogen and fractured at 123 K in a BalTec BAF060 freeze fracture apparatus. The fractured surface was replicated by the deposition of Pt/C (4 nm in thickness) at 45°, followed by the deposition of a 20 nm carbon film. The replica was collected on carbon coated TEM grids and observed using a FEI Tecnai F20 TEM. Detailed experimental procedures can be found elsewhere.322.6. Deuterium NMR spectroscopy
The deuterium (2H) NMR spectra of CB6OCB-d2 were measured using a Varian Chemagnetics 400 MHz spectrometer operating at 61.54 MHz with a magnetic field strength of 9.40 T. The sample of the dimer was placed in a short NMR tube which was placed orthogonal to the field. A single pulse of 6 μs duration was used with a 0.08 s delay between pulses. 4000 FIDs were accumulated into 4096 words of computer memory with a spectral window of 149.9 kHz. The temperature of the sample was controlled via a Chemagnetics Temperature Controller to ±0.2 K.2.7. Molecular structure calculations
The geometric parameters and torsional potentials of CB6OCB and CB7CB were determined by quantum mechanical (QM) DFT calculations.33 This information was then used to generate molecular conformations by Monte Carlo sampling. Fig. 2 shows the molecular structure of the two compounds, as obtained from geometry optimizations at the DFT/B3LYP/6-31G** level of theory. These calculations provided values for bond lengths and bond angles. The bond angle CarÔC in the ether linkage is equal to 119°, whereas the bond angle CarĈC in the methylene linkage is equal to 113° (Car is the aromatic carbon).The bonds that were allowed to rotate are shown by arrows in Fig. 2; the corresponding dihedral angles are denoted by χi. The torsional potential for the biphenyl twist angle (χ0 and χ9) was deduced from the literature.34 It is characterized by four equivalent minima located at ∼±35° and ∼±145°, and energy barriers of about 8 kJ mol−1 for planar and perpendicular arrangement of the rings. For all other dihedrals, torsional potentials were obtained by DFT calculations on representative molecular fragments. Calculations were performed at the DFT/B3LYP/6-31G** level of theory, with the exception of the χ6 dihedral of CB6OCB, for which the MP2/6-31G** level was used. The torsional potential for the Car–Car–C–C dihedrals (χ1 and χ8 in CB7CB, χ1 in CB6OCB) exhibits two equivalent minima at ±90°, corresponding to perpendicular arrangement of the phenyl ring with respect to the Car–C–C plane; barriers of about 4 kJ mol−1 are found for nearly planar configurations. Two equivalent minima were also found for the Car–Car–O–C dihedral (χ8 in CB6OCB), but these are located at 0° and 180°, corresponding to a coplanar arrangement of the phenyl ring and the Car–O–C plane; the minima are separated by energy barriers of ∼14 kJ mol−1 located at ±90°. These results are in agreement with those reported in the literature for ethyl- and ethoxybenzene at the DFT/B3LYP/6-311G(2d,p) level of theory.35 The C–C–C–C dihedrals χi (i = 3–6 for CB7CB, i = 3–5 for CB6OCB) and the Car–C–C–C dihedrals (χ2 and χ7 in CB7CB, χ2 in CB6OCB) exhibit minima for the trans (180°), gauche + (∼+65°) and gauche− (∼−65°) states with the trans state more stable than the gauche states respectively by ΔVC–C–C–Cgt ∼ 3.5 kJ mol−1 and ΔVCar–C–C–Cgt ∼ 2 kJ mol−1. The Car–O–C–C dihedral (χ7 in CB6OCB) exhibits an absolute minimum for the trans state; relative minima are found at ±80°, which are higher in energy than the trans one by about 6 kJ mol−1. Well-defined trans and gauche minima were found also for the O–C–C–C dihedral (χ6 in CB6OCB), with the gauche states (χ6 ∼ ±62°) more stable than the trans state by ΔVO–C–C–Cgt ∼−3 kJ mol−1. This reversal of the gauche–trans stability order is in keeping with that reported in the literature for 1,3-dimethoxypropane, where it was suggested that this so-called gauche effect may result from favourable electrostatic interactions between the oxygen atom and the CH2 group.36
In Monte Carlo (MC) conformational sampling, at each move a certain (random) number of dihedral angles was changed by a random rotation: the resulting conformation was accepted or rejected on the basis of its torsional energy, according to the Metropolis criterion.37 MC sampling of the full torsional potential was performed for all angles, with the exception of the biphenyl twist angle, for which the RIS approximation was adopted.38 Structures having pairs of atoms closer than a cut-off distance of 0.82σ, where σ is the sum of their van der Waals radii, were discarded. In this way sterically hindered conformations were rejected. van der Waals radii equal to 0.185 nm (C), 0.15 nm (N and O), and 0.1 nm (H) were assumed.39
For each molecular conformation, calculation of the mean field potential requires the definition of the molecular surface. This was generated using the library MSMS,40 with a probe sphere radius of 0.3 nm and a density of vertices of 5 Å−2. The same van der Waals radii used for the cutoff distance were assumed.
3. Results and discussion
3.1. Phase behaviour of CB6OCB
Fig. 3 shows the dependence of the heat capacity on temperature for a sample of CB6OCB which had previously been cooled from the isotropic phase measured with an underlying heating/cooling rate of 1 K min−1. On heating, three transitions are evident, a strong first order transition at 373 K, a weak first-order transition at 382 K and a first-order transition at 426 K. The enthalpy changes associated with these transitions will be discussed in detail later. On cooling from the isotropic phase, a characteristic nematic Schlieren texture develops containing both two and four brush point singularities when viewed through the polarizing microscope, and which flashed when subjected to mechanical stress. A representative Schlieren texture observed for CB6OCB is shown in Fig. 4(a). On further cooling, coexisting regions of elliptical polygonal domain texture and a rope-like texture developed, see Fig. 4(b), characteristic of the twist-bend nematic phase.5,6 At the NTB–N phase transition, the director fluctuations ceased, strongly suggesting a significant increase in viscosity. On further cooling, the sample crystallized.
Fig. 5 shows isothermal X-ray diffraction patterns for CB6OCB as a function of the scattering vector q, defined as (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, collected on cooling from the isotropic phase. The diffraction pattern obtained in the nematic mesophase contains two diffuse and wide scattering peaks at about 0.54 and 1.41 Å−1. The twist-bend nematic phase shows qualitatively the same pattern as for the nematic phase. The absence of layer reflection peaks in the lower temperature phase supports the assignment of a twist-bend nematic phase. The effective molecular length in both the nematic and twist-bend nematic phases of about 12 Å corresponds to approximately half the estimated molecular length of CB6OCB in the all-trans conformation of 26.3 Å. This suggests a locally intercalated arrangement of the molecules consistent with that found for other dimers found to exhibit the twist-bend nematic phase.
θ, collected on cooling from the isotropic phase. The diffraction pattern obtained in the nematic mesophase contains two diffuse and wide scattering peaks at about 0.54 and 1.41 Å−1. The twist-bend nematic phase shows qualitatively the same pattern as for the nematic phase. The absence of layer reflection peaks in the lower temperature phase supports the assignment of a twist-bend nematic phase. The effective molecular length in both the nematic and twist-bend nematic phases of about 12 Å corresponds to approximately half the estimated molecular length of CB6OCB in the all-trans conformation of 26.3 Å. This suggests a locally intercalated arrangement of the molecules consistent with that found for other dimers found to exhibit the twist-bend nematic phase.
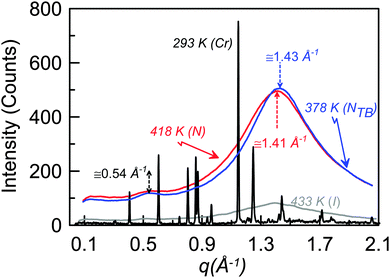 | ||
| Fig. 5 X-ray diffraction patterns of CB6OCB measured in the crystal, twist-bend nematic, nematic and isotropic phases. | ||
3.2. Optical properties of CB6OCB
To explore surface anchoring properties of the compound, we used three polyimides (PIs) and an obliquely deposited SiOx layer as the aligning layers. To achieve a perpendicular (homeotropic) alignment of the director, n, in the N phase and the helix axis in the NTB phase, two PI layers, SE7511 and SE1211 (both Nissan Chemical Industries), have been tested; these PIs provide a homeotropic anchoring for classic uniaxial nematogens such as E7 and 5CB. However, the uniaxial nematic phase of CB6OCB exhibits only Schlieren textures between the plates coated with SE7511 and SE1211, see Fig. 6(a). The Schlieren textures exhibit only point defects-boojums located at the bounding plates, associated with four extinction brushes each, see Fig. 6(a). Defects with two extinction brushes representing disclinations with director reorienting by ±π when one circumnavigates the defect core, are not observed. This feature suggests that SE7511 and SE1211 yield tilted surface alignment of the director; such a boundary condition is incompatible with the director reorientation by ±π in the plane of the cell.41 As the temperature is lowered towards the NTB–N transition, the Schlieren textures become decorated with stripe patterns, see Fig. 6(b), usually associated with the temperature dependence of the pitch in the NTB phase and undulation instability of the pseudo-layered NTB structure.42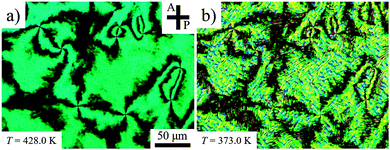 | ||
| Fig. 6 POM textures in the SE7511 cell of d = 3.9 μm (a) at T = 428 K (N phase) and (b) 373 K (NTB phase). | ||
Thin cells treated with PI2555 (HD Microsystems) provide a good tangential anchoring for CB6OCB over the entire temperature ranges of the N and NTB phases. If the cells are thin (d = 3.6 μm), the rubbed PI2555 provides a uniform alignment of the director in the N phase, Fig. 7(a); upon the transition into the NTB phase, the texture develops stripes parallel to the rubbing direction, Fig. 7(b). This orientation correlates with the idea that the stripes represent periodic undulations of the NTB pseudolayers. Since the axis of the twist-bend structure is aligned along the rubbing direction, periodic bend of undulating pseudolayers develops in the orthogonal direction; hence the stripes are parallel to the rubbing direction, as observed, Fig. 7(b). As the cell thickness d increases, PI2555 planar alignment quality deteriorates, see Fig. 7(c and d). However, even in this case, one can observe N textures exhibiting centres with two dark brushes that correspond to ±1/2 disclination lines joining the two opposite glass plates of the cell, see Fig. 7(c). Their existence suggests that the director orientation is close to being tangential to the bounding plates. The quality of planar alignment is best when the material is confined between the plates with SiOx layers. These cells feature monodomain textures in the N phase and well-aligned stripes in the NTB phase even when their thickness is relatively large, d = 6.1 μm, see Fig. 8.
 | ||
| Fig. 7 POM textures in PI2555 cells of (a and b) d = 3.6 μm and (c and d) d = 4.5 μm at (a and c) T = 422.5 K (N phase) and (b and d) 377.1 K (NTB phase). | ||
 | ||
| Fig. 8 POM textures in SiOx cell of d = 6.1 μm at (a) T = 403.0 K (N phase) and (b) 373.0 K (NTB phase). | ||
3.3. FFTEM of CB6OCB
The FFTEM of CB6OCB rapidly frozen at the NTB phase transition temperature (T = 368 K) reveals a domain structure with different orientations, similar to earlier observations of other materials with NTB phases.6,7,32Fig. 9(a) is a representative FFTEM image showing a well-defined 1D periodic structure with a period of 8.9 nm. The lack of surface steps indicates that the fracture surface is parallel to the helical axis.6 Besides the straight layers, slightly bent layers can also be observed. For example, Fig. 9(b) shows an area close to the domain boundary (the right-hand side of the image). The fast Fourier transform (FFT) patterns indicate a decreasing curvature with increasing distance from the domain boundary.The FFTEM textures are very similar to the earlier FFTEM results on CB7CB.6,7 For CB7CB, a comprehensive study showed that the pseudo-layered structure of the NTB phase can only be observed using the surface-sensitive replica FFTEM, while the direct cryo-TEM observation of thin films prepared by cryo-ultramicrotomy produces no clear contrast.32 The absence of the layered structure in cryo-TEM images of the material strongly supports the idea that the NTB structure has no spatial modulations of mass/electron density, and that the periodic pattern seen in FFTEM is caused by the director modulations revealed through the surface shadowing effect during the replica preparation.
Observation of bend deformations of the periodic patterns in FFTEM textures (see Fig. 9(b)), reported also for other NTB materials,6,7,32 is an important feature that further supports the one-dimensional character of structural modulation as opposed to the three-dimensional modulation characteristic of solid crystals. Similar bend deformations are often met in smectics and short-pitch cholesterics in which there is no positional order within the ‘layers’. Note also that, as in our previous observations of the NTB textures,6,32 the period of patterns can vary from region to region. In the case of CB6OCB, the period of the straight layers seen in the parallel fractures, vary between 8.9 nm and 9.1 nm; while an even larger variation can be found for bent layers. For example, in the domain with the bent layers shown in Fig. 9(b), the period changes from 8.6 nm (near the boundary) to 9.3 nm (further away from the boundary).
3.4. The NTB–N phase transition
The NTB–N phase transition of CB7CB was the first to be identified.5 Heat capacity data indicated that a non-zero latent heat (ΔHNTBN) is associated with the transition,5 and birefringence measurements43 show an apparent discontinuity in the conical angle at the phase transition which, as in both the Dozov Landau-like model3 and a more recent molecular field theory,24 is one of the possible order parameters characteristic of the NTB phase.One feature of the existing theoretical models for the NTB–N phase transition is based on the Landau theory3,44,45 with the Oseen–Frank free energy as the starting point for the modeling of a twist-bend nematic phase. Dozov proposed a purely elastic approach taking the conical angle and the pitch as characteristic order parameters.44 Shamid et al. proposed a detailed approach based on the existence of polar order and bend coupling, i.e., a coupling which favours polar order along the bend.45 However, these theoretical approaches predict a second-order NTB–N phase transition that, to date, has not been found experimentally. More recently, a microscopic approach of the generalised Maier–Saupe theory24 giving remarkable advances in the field, also predicts a second-order NTB–N phase transition.
A very recent theoretical study based on the Landau theory by Kats and Lebedev46 argues that because of the short pitch of the heliconical structure, the NTB–N phase transition takes place at a finite pitch in a similar way to the SmA–N phase transition. Likewise, the polar order should not be included in the Landau expansion. The order parameter chosen by Kats and Lebedev is a short-range vector field, φα, containing the conical angle and the pitch of the heliconical structure where α denotes a laboratory frame. On this basis, López et al.47 have developed a Landau model with just two key order parameters for the NTB phase: a symmetric and traceless tensor Qαβ for the orientational order parameter and the vector field φα. The Landau functional, in its simplified form, can be written as a function of φ, the absolute value of the vector field φα, which is related to the tilt angle, θ0, as sin θ0, in such a way that the free energy density for the twist-bend nematic phase is expressed as:
 | (1) |
Eqn (1) depends upon two effective elastic constants Keff3 and Keff2 related to the bend and twist elastic constants K3 and K2, respectively. The key result of eqn (1) is linked with the value of Keff2 that must be negative to be consistent with a finite helix pitch. This fact implies that the NTB–N phase transition is predicted to be always first order, its strength being related to the value of Keff2 which becomes less negative as the nematic range increases. The first-order NTB–N phase transition takes place at T1 defined as
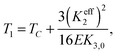 | (2) |
The excess heat capacity (ΔCp= Cp,NTB–Cp,N) is easily obtained from the excess free energy density (Δf = fTB–fN) given by eqn (1) as
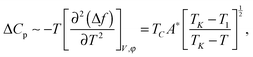 | (3) |
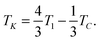 | (4) |
| Cp,N = B* + C*[T − T0], | (5) |
 | (6) |
Fig. 10 shows the heat capacity data for a slow heating run (0.01 K min−1) around the NTB–N phase transition. We also show heat capacity data for a slow cooling run but only in the nematic phase and when the NTB–N phase transition begins. The coexistence region, a signature of the first-order character of the NTB–N phase transition, is delimited by the vertical dashed lines and is determined using ϕ-phase shift data which, for simplicity, are not shown in the figure. Eqn (6) is used to fit only heat capacity data on heating in the NTB phase up to the lower limit of the coexistence region and the result is shown in Fig. 10 as the blue curve. Eqn (5) is used to fit the heat capacity data recorded on cooling the N phase to the upper limit of the coexistence region, shown in Fig. 10 as the red curve. A preliminary, quantitative result from our fittings is given by the temperature-discontinuity metric (T1–TC) which is 0.025 K, a value which is certainly small showing that the NTB–N phase transition is very weakly first-order in nature. The other fitting parameters will be used later to estimate the entropy change at the NTB–N phase transition according to the proposed Landau model.
 | ||
| Fig. 10 Heat capacity data for a slow heating run (0.01 K min−1-black symbols) around the NTB–N phase transition. Also shown are heat capacity data for a slow cooling run (red symbols) in the nematic phase and for the onset of the NTB–N phase transition. The coexistence region, is indicated by the vertical dashed lines. The blue curve shows the fitting of the data using eqn (6) to the lower limit of the coexistence region, and the red curve shows the fitting of the cooling data using eqn (5). The top-left inset shows heat capacity data for a slow heating run for the same conditions around the N–I phase transition. | ||
The latent heat associated with the NTB–N phase transition (ΔHNTBN) has been calculated using
 | (7) |
| ΔSNTBN = 6A*[TK − T1]. | (8) |
| T NTBN (K) | ΔHNTBN (kJ mol−1) | ΔSNTBN/R | T NI (K) | ΔHNI (kJ mol−1) | ΔSNI/R | T NI–TNTBN (K) |
|---|---|---|---|---|---|---|
| 382.3 ± 1.0 | 0.018 ± 0.009 | 0.006 | 426.6 ± 0.3 | 0.38 ± 0.01 | 0.11 | 44.3 ± 1.0 |
Our fittings using eqn (5) and (6) lead to a value for (TK − T1) of 0.009 K with a coefficient A* of 3 × 10−3 J g−1 K−2. Thus, according to eqn (8), the entropy change at the NTB–N phase transition (ΔSNTBN) would be 1.6 × 10−4 J g−1 K−1 or 0.009 expressed as ΔSNTBN/R, a value very close to that listed in Table 1. Here, the nematic range is also listed, being the widest for the twist-bend compounds investigated up to now for which the entropy data are available with the required accuracy.5,12 It should be stressed that the Landau model embodied by eqn (1) establishes that, the wider the nematic range, the weaker the first-order NTB–N phase transition is. Another interesting fact provided by the Landau model represented by eqn (1) is that the height of the heat capacity peak at the N–NTB phase transition must decrease as the first-order transition becomes weaker, a fact that is clearly verified if we observe Fig. 10 and compare this with other high resolution heat capacity measurements for other twist-bend nematogenic compounds.5,12,47
The inset in Fig. 10 shows the heat capacity data around the N–I phase transition measured at the same experimental conditions as the NTB–N phase transition. It is useful to note some of the differences in the critical behaviour of both phase transitions (NTB–N and N–I). Heat capacity data are fitted to the following standard expressions48,49
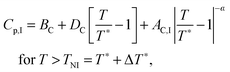 | (9) |
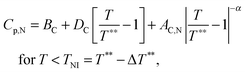 | (10) |
3.5. Chirality and orientational order of the NTB phase
The NTB and N phases of the dimer CB6OCB were studied, using 2H NMR spectroscopy, as a function of temperature for the nematogen deuteriated in the first methylene group of the spacer attached directly to a cyanobiphenyl group. The selection of 2H NMR spectra, given in Fig. 11, shows the single quadrupolar doublet expected in the nematic phase for the equivalent prochiral deuterons on the first methylene group in the spacer. In the NTB phase two quadrupolar doublets are now observed because the two prochiral deuterons have lost their equivalence as a result of the chirality of the NTB phase. This provides clear evidence for the chirality expected of the NTB phase even though the molecules are, in effect, achiral. On passing from the N to the NTB phase the loss of equivalence of the prochiral deuterons is almost continuous in keeping with the very weak nature of the first-order NTB–N transition. The final spectrum shown in Fig. 11 was recorded at a temperature deeper in the NTB phase and shows a significant difference of the quadrupolar splittings for the two prochiral deuterons. This behaviour in the difference of the two quadrupolar splittings, shown in Fig. 11, indicates the chirality of the phase but at a quantitative level it is related to an off-diagonal element of a Saupe ordering matrix for the rigid segment of the molecule containing the deuterons and averaged over all the conformations.51 To connect this to the growth in the helical pitch with increasing temperature requires a molecular model such as that developed by Greco et al.52 | ||
| Fig. 11 The 2H NMR spectra of CB6OCB-d2 measured as a function of temperature in the nematic and twist-bend nematic phases. | ||
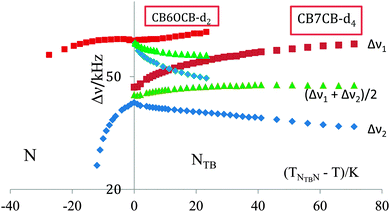
The quadrupolar splittings, Δν, are shown as a function of the shifted temperature, (TNI–T), in Fig. 12. Since the nematic–isotropic transition temperature is high, at 426 K, it was not possible, unfortunately, to make deuterium NMR measurements at or near the transition to the isotropic phase. In the vicinity of the transition to the NTB phase it appears that the quadrupolar splitting in the N phase exhibits a plateau or even passes through a weak maximum. This is not as pronounced, however, as that shown by the KA(0.2) mixture of ether and methylene-linked odd dimers which might be thought of as analogous to a methylene-ether linked odd dimer.10 Here the nematic range is about 39 K slightly less than for CB6OCB which is about 45 K. The temperature dependence of the two prochiral quadrupolar splittings, Δν±, for CB6OCB-d2 is also shown in Fig. 12, one of these, Δν+, increases slightly with decreasing temperature while the other, Δν−, decreases more rapidly.
The quadrupolar splitting in the nematic phase is properly compared with the mean, (Δν+ + Δν−)/2, of the two prochiral splittings determined in the twist-bend nematic phase,51 see Fig. 12. This mean splitting, shown in the figure, is clearly consistent with the notion of the occurrence of a very small maximum in the quadrupolar splitting with decreasing temperature. The mean quadrupolar splitting in the twist-bend nematic phase of CB6OCB-d2 is seen to decrease with decreasing temperature which is in accord with an increase in the conical or tilt angle, θ0; this is another characteristic order parameter for the twist-bend nematic phase. The influence of this on the mean quadrupolar splitting clearly outweighs the increase caused by the growth in the orientational order of the cyanobiphenyl group attached to the methylene group.53 As we have seen the difference in the quadrupolar splittings in the twist-bend nematic phase demonstrates the chirality of the phase. This, so-called, chiral splitting, (Δν+ − Δν−), increases continuously from about zero at the NTB–N transition with decreasing temperature. The influence of the orientational order as well as the director tilt with respect to the helix axis on this behaviour might also be explored as could the fit to theory.52,53
In view of the subtle difference in the structure of the two odd liquid crystal dimers CB7CB and CB6OCB, having the same spacer lengths, where one methylene linking group is replaced with an ether group it is of special interest to compare the quadrupolar splittings found for CB6OCB-d2 with those already measured for CB7CB-d4.5 As has been shown this apparently subtle chemical and hence geometric change has a significant influence on the N–I transitional properties of odd liquid crystal dimers differing in the linkages, either methylene or ether.54 It is also expected to influence the orientational order, as reflected by the quadrupolar splittings in both the nematic and twist-bend nematic phases. This comparison is made in Fig. 13 where the splittings are shown as a function of the shifted temperature, (TNTBN–T); this choice of scale facilitates the comparison of the behaviour in the NTB phase of the two dimers at comparable temperatures.
We start, however, with the results in the nematic phase. It is apparent that for CB7CB-d4 the quadrupolar splitting increases strongly with decreasing temperature as the transition to the NTB phase approaches and the shifted temperature increases. In marked contrast the quadrupolar splitting for CB6OCB-d2 is essentially constant in the vicinity of this transition and even decreases, though slightly, at more negative shifted temperatures. In addition to the slopes of the plots the absolute values of the quadrupolar splittings are significantly larger for CB6OCB-d2 than for CB7CB-d4 at the phase transition. These differences in behaviour appear to be consistent with the smaller curvature of the molecule expected for the conformationally averaged structure of the dimer CB6OCB than for CB7CB. The difference between the absolute splitting in the N phase and the mean quadrupolar splitting in the NTB phase at the transition for CB6OCB-d2 is small, this is consistent with the weak first-order phase transition. In contrast, for CB7CB-d4 the same difference is large and clearly observable in accord with the stronger first-order NTB–N transition. Again the different behaviour found for the two dimers is consistent with the difference in their mean curvatures. In addition, the Landau model developed for the NTB–N phase transition,47 which is similar in some respects with other models devoted to the SmA–N phase transition,48–50 suggests that the closer the reduced temperature, TNTBN/TNI, is to unity the stronger the NTB–N transition should be. This transitional behaviour is also exhibited by the entropy change ΔSNTBN/R which is 0.07 for CB7CB and significantly smaller at 0.006 for CB6OCB. This difference is in keeping with the difference in the nematic range for the two dimers.55
The other significant difference between the two dimers is in the behaviour of the mean quadrupolar splittings in the twist-bend nematic phase. Thus for CB6OCB-d2 the mean splitting decreases with increasing shifted temperature indicating that the influence of the growth in the tilt angle outweighs that in the orientational order. However, for CB7CB-d4 the reverse appears to be the case, thus the mean quadrupolar splitting grows slightly after the phase transition and then reaches an essential plateau.
The chiral splittings for the two dimers are seen to exhibit quite different behaviour at the NTB–N transition. For CB6OCB-d2 the chiral splitting seems to be small in keeping with the weak first-order phase transition. However, for CB7CB-d4 the transition is much stronger and the chiral splitting now differs significantly from zero. It appears that the off-diagonal element in the conformationally averaged Saupe ordering matrix which results from the phase chirality is somewhat larger for CB7CB than for CB6OCB although a theory has yet to be developed that accounts for this difference in behaviour. In spite of this significant difference at the phase transition the chiral splittings at the same shifted temperatures some way from the transition are really quite similar. This result which is not unique56 is again puzzling and poses an interesting challenge to theory.
3.6. Molecular field theory
The experimental NMR and transitional results given in the previous section for the non-symmetric dimer CB6OCB and their comparability to those for the symmetric dimer CB7CB, about which so much is known, provides a valuable opportunity to test the validity of theoretical predictions.3,24,47 This is particularly appropriate given the clear similarity of the structures of the two dimers differing, as they do, simply by the replacement of the ether by a methylene group. Indeed it is possible to explore the effect of this change in the molecular structure and especially the curvature of the conformationally averaged form of this.57 It is expected that the mean curvature for CB7CB will be larger than for CB6OCB. The results of particular importance are the transition temperatures, TNI and TNTBN, as well as the orientational order parameters for both the N and the NTB phases. Using NMR spectroscopy the quadrupolar splittings are measured with respect to the magnetic field of the spectrometer; in the N phase this corresponds to the director, denoted by n, but in the NTB phase it is associated with the helix axis, denoted by h.51We start with a brief description of the molecular-based theory proposed by Greco et al.24 Here the constituent odd-dimer molecules, with the intrinsic flexibility of the central spacer, are represented by a rigid V-shaped particle; this leads to a dramatic but valuable simplification of the model. We need to define the angle between the two mesogenic arms of the V namely, χ, together with their lengths which were taken to be equal at L and the equivalent anisotropy of the arms, ε. The three order parameters employed in the theory to define the twist-bend nematic phase are the pitch, p, of the helix, the conical angle, θ0, made by the director with the helix axis and the second-rank orientational order parameter made by the arm of the molecular V with the director, 〈P2〉. Of these order parameters all but 〈P2〉 vanish in the nematic phase. We should note that the order parameter with respect to the helix axis, 〈Ph2〉, is related to the conical angle which also vanishes in the N phase, and becomes 〈P2〉. If we wished we could take the arms of the V to be unequal and in addition use a truncated V which is a more realistic description of the conformationally averaged shape of an odd dimer.57 However, this is something for the future.
Calculations have been performed with χ equal to 130°, 135° and 140°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 and of these 135° is found appropriate to represent the behaviour of CB7CB. For our other dimer CB6OCB the value of χ needs to be just 3° larger at 138°. Although there are no real mesogens with which these calculations can be compared it is of interest to make contact with the results of a Monte Carlo simulation for an ensemble of rigid V-shaped molecules formed by two Gay–Berne particles with their elliptical shape. This was studied by Memmer58 who set the interarm angle at 140° and found that this model system formed a twist-bend nematic phase. Unfortunately, the system was not investigated in great detail but it may be significant that the angle between the Gay–Berne groups is equal to one of those used with the molecular field model.24
24 and of these 135° is found appropriate to represent the behaviour of CB7CB. For our other dimer CB6OCB the value of χ needs to be just 3° larger at 138°. Although there are no real mesogens with which these calculations can be compared it is of interest to make contact with the results of a Monte Carlo simulation for an ensemble of rigid V-shaped molecules formed by two Gay–Berne particles with their elliptical shape. This was studied by Memmer58 who set the interarm angle at 140° and found that this model system formed a twist-bend nematic phase. Unfortunately, the system was not investigated in great detail but it may be significant that the angle between the Gay–Berne groups is equal to one of those used with the molecular field model.24
It is convenient to start with the orientational order parameters 〈P2〉 and 〈Ph2〉 and these are shown as a function of the scaled temperature, T* = kBT/ε, in Fig. 14; the temperatures scaled in this way are directly comparable to the experimental temperatures. Also included are results for the polar order parameter and although of interest we shall not refer to this further. From the two plots in Fig. 14 we can clearly see the N–I transition and that the NTB–N transition occurs when the order parameter, 〈Ph2〉, shown as a dashed line, branches away from 〈P2〉 When the inter-arm angle, χ, is 138° the scaled transition temperature, TNI*, is about 0.292. What is striking is that a decrease in χ by just 3° to 135° reduces the scaled transition temperature, TNI*, to about 0.272. The ratio of the two scaled nematic–isotropic transition temperatures is 1.074; this is directly comparable to that for the two dimers which for CB6OCB to CB7CB is 1.099. We now turn to the NTB–N transition temperatures. For the interarm angle of 138° the scaled value for TNTBN* is 0.254. On reducing the angle χ to 135° the transition temperature TNTBN* increases slightly to 0.259. The ratio of these two scaled temperatures which is comparable with experiment is 0.982. The experimental value for the ratio of CB6OCB to CB7CB is also close to unity at 1.016 but is slightly larger than predicted although we stress again that the parameters were not adjusted to fit experiment. Of course, at a qualitative level theory predicts that TNTBN* for CB6OCB should be lower than that for CB7CB but the reverse is the case although slightly so. We should also note that the extreme sensitivity of the predictions of the model to the interarm angle is strangely mimicked by a similar sensitivity for the prediction, also based on a V-shaped model, of the transition temperatures of the biaxial nematic phase.59 We should also note that the theory of Greco et al.24 predicts the NTB–N phase transition to be second order whereas experimentally the NTB–N transition for CB7CB is clearly first order;5 that for CB6OCB is also first order but very weak. However, both experimental cases agree with the most recent Landau theory in which the effective curvature of the molecule is also accounted for.47 The details as to how the molecular curvature enters the theory are not given here but may be found in the original paper.
The molecular field theory also predicts the orientational order parameters of the mesogenic arms with respect to the director which are shown as 〈P2〉; these are related to the quadrupolar splittings.5,51 In the nematic phase we see that the order parameters are similar for the two V-shaped molecules at the nematic–isotropic transition. However, as the transition to the twist-bend nematic is approached the order parameter in the N phase is significantly larger for the molecule with the inter-arm angle of 138° than that with the smaller value of 135°. For the model system this difference can be attributed to the longer nematic range for the larger value of χ. Such results are in accord with experimental quadrupolar splittings for the dimers CB6OCB-d2 and CB7CB-d4 (see Fig. 13). Within the twist-bend nematic phase the experimental mean quadrupolar splitting is related to the order parameter defined with respect to the helix axis; this is denoted by 〈Ph2〉 and shown as the red dot-dashed lines in Fig. 14. We can see that for the slightly smaller value of χ there is a steep decrease in the order parameter followed by a gentler but significant increase with further decrease in the temperature. This is consistent with the growth in the order being greater than that resulting from further increase in the conical angle. In contrast for the slightly larger inter-arm angle the order parameter decreases less rapidly and then grows very slowly with decrease in temperature. This behaviour for the two model dimers is in reasonable, qualitative agreement with that shown in Fig. 13 for CB7CB-d4 and CB6OCB-d2. For the latter dimer the mean quadrupolar splitting decreases on entering the NTB phase and then continues to decrease but slightly less slowly. For the former, the results in Fig. 13 show a discontinuous increase in the mean quadrupolar splitting followed by a small growth and a more or less constant value. This low temperature variation is in accord with theory but not the increase in the mean splitting at the NTB–N transition which predicts a decrease.
The results from the molecular field theory suggest that some qualitative understanding of the behaviour of liquid crystal dimers in forming both nematic and twist-bend nematic phases might be obtained from their bent nature via the angle between their mesogenic arms. This might in some way avoid the effect of the molecular complexity especially that originating from the spacer. However the extreme sensitivity of the predictions to the interarm angle shows that the estimation of the angle between the two mesogenic arms will need to be with great care. We now take an initial step in considering how this might be achieved. Frequently the structure of liquid crystal dimers is shown for simplicity, as that when the spacer is in its all-trans conformation which appears to be a convenient starting point. Such structures, obtained from quantum chemical calculations, are shown for CB7CB and CB6OCB in Fig. 15. These clearly resemble a V or perhaps a truncated V-shape which is especially appropriate for our task. The orientations of the mesogenic groups are indicated by the arrows which pass through the carbons at the ends of the cyanobiphenyl groups for CB6OCB. These clearly show that the inter-arm angle for CB7CB is smaller than for CB6OCB as expected following the introduction of the ether link in the spacer. Based on this simple picture alone it might be thought that this difference in the interarm angle and hence the molecular curvature would result in a lower twist-bend nematic transition temperature, TNTBN, for CB7CB than for CB6OCB; this would be in keeping with the predictions of the molecular field theory for V-shaped molecules. However at a quantitative level the angles employed in the theory are significantly larger than those of the dimers in their all-trans forms although the difference in these are far larger than those used in the molecular field theory. We should, however, recall that although the all-trans conformation is the ground state for CB7CB it is not for CB6OCB. Here both experiment and quantum chemical calculations reveal that with an ether group the ground state has a gauche link in the spacer. This conformation is also shown for CB6OCB in Fig. 15 and it is apparent that its shape has a greater curvature or bend than for the all-trans form. In fact the angle between the cyanobiphenyl groups, calculated from the vector product of the vectors associated with the two cyanobiphenyl groups, has decreased and is now 103° in comparison to 127° for the all-trans form. This illustrates quite clearly how misleading the use of single conformers to gauge the curvature of such flexible molecules can be.
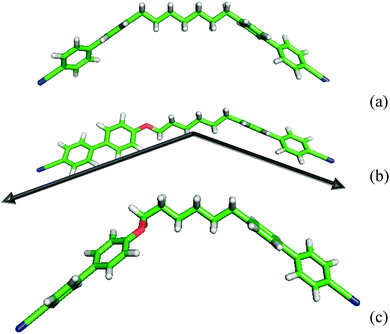 | ||
| Fig. 15 The shapes of the dimers (a) CB7CB and (b) CB6OCB in their all-trans form and (c) CB6OCB in its ground state with a gauche link. | ||
To overcome this particular challenge we need to be able to use all of the conformers in assessing the molecular curvature or those structural factors and properties responsible for the formation of the twist-bend nematic. In addition rather than using discrete conformers as in the RIS model it is desirable and more realistic to use continuous potentials which link the rigid groups forming the molecule such as the important methylene groups.51 The probability of a conformer in the isotropic phase can be determined from the torsional energies which are available from quantum chemical calculations. For each conformer the angle, θ, between the para axes of the cyanobiphenyl groups may be determined irrespective of the conformation of the spacer linking them. This calculation is then repeated for many conformations which would be obtained by Monte Carlo sampling of the coordinates defining the conformers. We sample these simply by using the angle θ given its relevance to the problem and have sorted a significant number of the conformers simply according to the angle between the mesogenic groups and assigned a probability p(θ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ for each. The results of such calculations for the dimers CB7CB and CB6OCB in their isotropic phase are shown in Fig. 16(a) as a function of θ. For CB7CB there is a major peak essentially symmetric about its maximum. This peak corresponds to bent conformers with the most probable angle between the cyanobiphenyl arms of about 120° but with the θ distribution extending widely from about 90° to 140°. In addition, there is a much smaller, less well-defined maximum at about 30° which corresponds to the so-called hairpins where the cyanobiphenyl groups tend to be parallel. What is remarkable is that the distribution function for CB6OCB has essentially the same form as for CB7CB. The essential differences are that the major peak is wider and the fraction of the hairpin conformers is somewhat smaller. It is not clear why these differences could be responsible for the tendency of CB7CB to have a higher TNTBN than CB6OCB.
θ for each. The results of such calculations for the dimers CB7CB and CB6OCB in their isotropic phase are shown in Fig. 16(a) as a function of θ. For CB7CB there is a major peak essentially symmetric about its maximum. This peak corresponds to bent conformers with the most probable angle between the cyanobiphenyl arms of about 120° but with the θ distribution extending widely from about 90° to 140°. In addition, there is a much smaller, less well-defined maximum at about 30° which corresponds to the so-called hairpins where the cyanobiphenyl groups tend to be parallel. What is remarkable is that the distribution function for CB6OCB has essentially the same form as for CB7CB. The essential differences are that the major peak is wider and the fraction of the hairpin conformers is somewhat smaller. It is not clear why these differences could be responsible for the tendency of CB7CB to have a higher TNTBN than CB6OCB.
Given this we have sought an answer from the conformational distribution function p(θ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ for both dimers evaluated in their nematic phases. These calculations differ significantly from those in the isotropic phase because the orientational order influences the conformational probability since the interaction with the director favours the more elongated conformers. In fact the probability now depends on the orientational partition functions of the conformers.60 Again the torsional variables are continuous and the conformations are generated using umbrella sampling.61 The predicted distribution functions in the nematic phases are shown in Fig. 16(b); in these the orientational order parameter for the mesogens was set at 0.35. What the distribution functions show is that there is now a more noticeable difference between these for CB7CB and CB6OCB. Thus the probabilities for CB6OCB have shifted to higher values of the angle θ corresponding to more elongated conformers which would decrease the twist-bend nematic–nematic transition temperature. The shift for the CB7CB dimer is not so pronounced which ensures that TNTBN for this dimer should be greater than that of CB6OCB. The fact that the difference in the conformational distribution functions is relatively small whereas the difference in TNTBN is significant, may well be consistent with the small difference in the inter-arm angle used in the molecular field calculations. However we should not ignore the fact that the changes in the probabilities are not restricted to a single value of the inter-arm angle. Indeed it seems likely that the value of the twist-bend nematic–nematic transition temperature does not rest on a single structural characterisation of the liquid crystal dimer related to just one part of the conformational distribution; more studies, both experimental and theoretical, are clearly required to confirm this. In addition the use of the distribution function for the inter-arm angle may well need other single properties to evaluate the transition temperatures and so obtain a guide to the design of twist-bend nematogens.
θ for both dimers evaluated in their nematic phases. These calculations differ significantly from those in the isotropic phase because the orientational order influences the conformational probability since the interaction with the director favours the more elongated conformers. In fact the probability now depends on the orientational partition functions of the conformers.60 Again the torsional variables are continuous and the conformations are generated using umbrella sampling.61 The predicted distribution functions in the nematic phases are shown in Fig. 16(b); in these the orientational order parameter for the mesogens was set at 0.35. What the distribution functions show is that there is now a more noticeable difference between these for CB7CB and CB6OCB. Thus the probabilities for CB6OCB have shifted to higher values of the angle θ corresponding to more elongated conformers which would decrease the twist-bend nematic–nematic transition temperature. The shift for the CB7CB dimer is not so pronounced which ensures that TNTBN for this dimer should be greater than that of CB6OCB. The fact that the difference in the conformational distribution functions is relatively small whereas the difference in TNTBN is significant, may well be consistent with the small difference in the inter-arm angle used in the molecular field calculations. However we should not ignore the fact that the changes in the probabilities are not restricted to a single value of the inter-arm angle. Indeed it seems likely that the value of the twist-bend nematic–nematic transition temperature does not rest on a single structural characterisation of the liquid crystal dimer related to just one part of the conformational distribution; more studies, both experimental and theoretical, are clearly required to confirm this. In addition the use of the distribution function for the inter-arm angle may well need other single properties to evaluate the transition temperatures and so obtain a guide to the design of twist-bend nematogens.
4. Conclusions
CB6OCB shows a NTB–N transition at 382 K and an N–I transition at 426 K. The NTB phase shows characteristic elliptical polygonal domain and rope-like textures when viewed through the polarising-light microscope. At the NTB–N transition there is a cessation of the optical flickering associated with director fluctuations in a conventional nematic phase. X-ray diffraction studies have confirmed the absence of layer reflection peaks in the lower temperature nematic phase supporting the assignment of NTB. The effective molecular length in both the N and NTB phases corresponds to approximately half the estimated all-trans molecular length of CB6OCB indicating a locally intercalated arrangement of the molecules. The NTB phase assignment is confirmed using FFTEM, and the helicoidal pitch is estimated to be 8.9 nm. We explored different alignment layers and identified approaches that provide tilted and planar alignment of the director in the N phase and the heliconical axis in the NTB phase.High-resolution calorimetric measurements allow us to obtain the heat-capacity data in the vicinity of the NTB–N phase transition. From such data, the latent heat and, hence the entropy change at the phase transition is obtained and they have allowed us to characterize the phase transitions as weakly first order but much closer to second order than for CB7CB5 or the longer chain homologue CB9CB.56 The only published theory that predicts a first-order NTB–N phase transition47 is consistent with our heat capacity results for CB6OCB and also for those published for CB7CB and CB9CB. In particular, it is clearly observed how the nematic range or the reduced temperature TNTBN/TNI is a key parameter in the first-order character of the transition in a way that the larger the reduced temperature (or the narrower the nematic range), the stronger the first-order character of the NTB–N phase transition is, in a way analogous to the SmA–N transition. The chirality of the NTB phase, one of its key properties, is clearly demonstrated by our 2H NMR studies of CB6OCB-d2, thus contributing to the unambiguous identification of the phase. Another defining property of the nematic phases is their orientational order which is related to the quadrupolar splittings available from the NMR experiments. For the N phase of CB6OCB-d2 the ordering increases slowly especially as the NTB phase is approached. In contrast, for the related dimer CB7CB-d4 the order increases rapidly but as the NTB phase is reached its orientational order is significantly smaller than that of CB6OCB-d2. More interestingly, in the NTB phase of CB6OCB-d2 the mean quadrupolar splitting decreases with decreasing temperature showing the tilt of the director with respect to the helix axis. Again this contrasts with that for CB7CB-d4 where the mean splitting increases at the transition and then is essentially independent of temperature. Such results provide valuable and challenging opportunities to test theories for the twist-bend nematic phase. This has certainly proved to be the case for the variational molecular field theory of the twist-bend nematogen but both the extreme sensitivity to the interarm angle and the molecular complexity mean that there are still questions to be answered.
Acknowledgements
The FFTEM data were obtained at the (Cryo) TEM facility at the Liquid Crystal Institute, Kent State University, supported by the Ohio Research Scholars Program Research Cluster on Surfaces in Advanced Materials. ODL acknowledges the support of NSF DMR-1410378 grant. The authors are grateful for financial support from MINECO/FEDER MAT2015-66208-C3-2-P and from the Gobierno Vasco (GI/IT-449-10).References
- Biaxial Nematic Liquid Crystals: Theory, Simulation and Experiment, ed. G. R. Luckhurst and T. J. Sluckin, Wiley, Chichester, 2015 Search PubMed.
- R. B. Meyer, in Les Houches Summer School in Theoretical Physics, ed. R. G. Balian and G. Weil, Gordon and Breach, New York, 1976, pp. 273–373 Search PubMed.
- I. Dozov, Europhys. Lett., 2001, 56, 247–253 CrossRef CAS.
- J. W. Emsley, M. Lelli, A. Lesage and G. R. Luckhurst, J. Phys. Chem. B, 2013, 117, 6547–6557 CrossRef CAS PubMed.
- M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. B. Jackson, D. O. López, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704 CrossRef CAS PubMed.
- V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jakli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635 CAS.
- D. Chen, J. H. Porada, J. B. Hooper, A. Klittnick, Y. Shen, M. R. Tuchband, E. Korblova, D. Bedrov, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15931–15936 CrossRef CAS PubMed.
- C. T. Imrie and P. A. Henderson, Chem. Soc. Rev., 2007, 36, 2096–2124 RSC.
- C. T. Imrie, P. A. Henderson and G.-Y. Yeap, Liq. Cryst., 2009, 36, 755–777 CrossRef CAS.
- K. Adlem, M. Čopič, G. R. Luckhurst, A. Mertelj, O. Parri, R. M. Richardson, B. D. Snow, B. A. Timimi, R. P. Tuffin and D. Wilkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022503 CrossRef CAS PubMed.
- V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801 CrossRef CAS PubMed.
- C. S. P. Tripathi, P. Losada-Perez, C. Glorieux, A. Kohlmeier, M.-G. Tamba, G. H. Mehl and J. Leys, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041707 CrossRef PubMed.
- R. J. Mandle, E. J. Davis, S. A. Lobato, C. C. A. Voll, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2014, 16, 6907–6915 RSC.
- R. J. Mandle, E. J. Davis, C. T. Archbold, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2014, 2, 556–566 RSC.
- P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407–1414 CrossRef CAS.
- M. Sepelj, A. Lesac, U. Baumeister, S. Diele, H. L. Nguyen and D. W. Bruce, J. Mater. Chem., 2007, 17, 1154–1165 RSC.
- R. J. Mandle, E. J. Davis, C. T. Archbold, C. C. A. Voll, J. L. Andrews, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2015, 21, 8158–8167 CrossRef CAS PubMed.
- E. Gorecka, N. Vaupotic, A. Zep, D. Pociecha, J. Yoshioka, J. Yamamoto and H. Takezoe, Angew. Chem., Int. Ed., 2015, 54, 10155–10159 CrossRef CAS PubMed.
- N. Sebastian, D. O. Lopez, B. Robles-Hernandez, M. R. de la Fuente, J. Salud, M. A. Perez-Jubindo, D. A. Dunmur, G. R. Luckhurst and D. J. B. Jackson, Phys. Chem. Chem. Phys., 2014, 16, 21391–21406 RSC.
- S. M. Jansze, A. Martinez-Felipe, J. M. D. Storey, A. T. M. Marcelis and C. T. Imrie, Angew. Chem., Int. Ed., 2015, 54, 643–646 CAS.
- Y. Wang, G. Singh, D. M. Agra-Kooijman, M. Gao, H. K. Bisoyi, C. Xue, M. R. Fisch, S. Kumar and Q. Li, CrystEngComm, 2015, 17, 2778–2782 RSC.
- D. Chen, M. Nakata, R. Shao, M. R. Tuchband, M. Shuai, U. Baumeister, W. Weissflog, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022506 CrossRef PubMed.
- Z. Lu, P. A. Henderson, B. J. A. Paterson and C. T. Imrie, Liq. Cryst., 2014, 41, 471–483 CrossRef CAS.
- C. Greco, G. R. Luckhurst and A. Ferrarini, Soft Matter, 2014, 10, 9318–9323 RSC.
- J. Xiang, Y. Li, Q. Li, D. A. Paterson, J. M. D. Storey, C. T. Imrie and O. D. Lavrentovich, Adv. Mater., 2015, 27, 3014–3018 CrossRef CAS PubMed.
- A. A. Dawood, M. C. Grossel, G. R. Luckhurst, R. M. Richardson, B. A. Timimi, N. J. Wells and Y. Z. Yousif, Liq. Cryst., 2016, 43, 2–12 CrossRef CAS.
- C. T. Archbold, E. J. Davis, R. J. Mandle, S. J. Cowling and J. W. Goodby, Soft Matter, 2015, 11, 7547–7557 RSC.
- B. Senyuk, Y. K. Kim, L. Tortora, S. T. Shin, S. V. Shiyanovskii and O. D. Lavrentovich, Mol. Cryst. Liq. Cryst., 2011, 540, 20–41 CrossRef CAS.
- Y. K. Kim, B. Senyuk and O. D. Lavrentovich, Nat. Commun., 2012, 3, 1133 CrossRef PubMed.
- O. D. Lavrentovich, Y.-K. Kim and B. I. Senyuk, Proc. SPIE, OP211, 2012, 8475, 0G1-7 Search PubMed.
- Y.-K. Kim, M. Majumdar, B. I. Senyuk, L. Tortora, J. Seltmann, M. Lehmann, A. Jakli, J. T. Gleeson, O. D. Lavrentovich and S. Sprunt, Soft Matter, 2012, 8, 8880–8890 RSC.
- M. Gao, Y.-K. Kim, C. Zhang, V. Borshch, S. Zhou, H.-S. Park, A. Jakli, O. D. Lavrentovich, M.-G. Tamba, A. Kohlmeier, G. H. Mehl, W. Weissflog, D. Studer, B. Zuber, H. Gnaegi and F. Lin, Microsc. Res. Tech., 2014, 77, 754–772 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09 (Revision B.01), Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- M. P. Johansson and J. Olsen, J. Chem. Theory Comput., 2008, 4, 1460–1471 CrossRef CAS PubMed.
- G. Cinacchi and G. Prampolini, J. Phys. Chem. A, 2003, 107, 5228–5232 CrossRef CAS.
- G. D. Smith, R. L. Jaffe and D. Y. Yoon, J. Phys. Chem., 1996, 100, 13439–13446 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- P. W. Flory, Statistical Mechanics of Chain Molecules, Wiley-Interscience, New York, 1969 Search PubMed.
- Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 1996 Search PubMed.
- M. F. Sanner, A. J. Olson and J. C. Spehner, Biopolymers, 1996, 38, 305–320 CrossRef CAS PubMed.
- M. Kleman and O. D. Lavrentovich, Soft Matter Physics: An Introduction, Springer-Verlag, NY, 2003 Search PubMed.
- P. K. Challa, V. Borshch, O. Parri, C. T. Imrie, S. N. Sprunt, J. T. Gleeson, O. D. Lavrentovich and A. Jakli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 060501 CrossRef CAS PubMed.
- C. Meyer, G. R. Luckhurst and I. Dozov, J. Mater. Chem. C, 2015, 3, 318–328 RSC.
- C. Meyer, G. R. Luckhurst and I. Dozov, Phys. Rev. Lett., 2013, 111, 067801 CrossRef CAS PubMed.
- S. M. Shamid, S. Dhakal and J. V. Selinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052503 CrossRef PubMed.
- E. I. Kats and V. V. Lebedev, JETP Lett., 2014, 100, 110–113 CrossRef CAS.
- D. O. Lopez, B. Robles-Hernandez, J. Salud, M. R. de la Fuente, N. Sebastian, S. Diez-Berart, X. Jaen, D. A. Dunmur and G. R. Luckhurst, Phys. Chem. Chem. Phys., 2016, 18, 4394–4404 RSC.
- N. Sebastian, M. R. de la Fuente, D. O. López, M. A. Perez-Jubindo, J. Salud, S. Diez-Berart and M. B. Ros, J. Phys. Chem. B, 2011, 115, 9766–9775 CrossRef CAS PubMed.
- N. Sebastian, D. O. López, S. Diez-Berart, M. R. de la Fuente, J. Salud, M. A. Perez-Jubindo and M. B. Ros, Materials, 2011, 4, 1632–1647 CrossRef CAS.
- S. J. Rzoska, A. Drozd-Rzoska, P. K. Mukherjee, D. O. Lopez and J. C. Martinez-Garcia, J. Phys.: Condens. Matter, 2013, 25, 245105 CrossRef PubMed.
- L. Beguin, J. W. Emsley, M. Lelli, A. Lesage, G. R. Luckhurst, B. A. Timimi and H. Zimmermann, J. Phys. Chem. B, 2012, 116, 7940–7951 CrossRef CAS PubMed.
- C. Greco, G. R. Luckhurst and A. Ferrarini, Phys. Chem. Chem. Phys., 2013, 15, 14961–14965 RSC.
- J. P. Jokisaari, G. R. Luckhurst, B. A. Timimi, J. Zhu and H. Zimmermann, Liq. Cryst., 2015, 42, 708–721 CAS.
- A. P. J. Emerson and G. R. Luckhurst, Liq. Cryst., 1991, 10, 861–868 CrossRef CAS.
- C. T. Imrie and G. R. Luckhurst, in Handbook of Liquid Crystals, ed. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. F. Gleeson and P. Raynes, Wiley-VCH Verlag GmbH & Co. KGaA, 2014, ch. 5, vol. 7 Search PubMed.
- B. Robles-Hernandez, N. Sebastian, M. R. de la Fuente, D. O. Lopez, S. Diez-Berart, J. Salud, M. B. Ros, D. A. Dunmur, G. R. Luckhurst and B. A. Timimi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 062505 CrossRef PubMed.
- G. R. Luckhurst, Macromol. Symp., 1995, 96, 1–26 CrossRef CAS.
- R. Memmer, Liq. Cryst., 2002, 29, 483–496 CrossRef CAS.
- G. R. Luckhurst, Thin Solid Films, 2001, 393, 40–52 CrossRef CAS.
- J. W. Emsley and G. R. Luckhurst, Mol. Phys., 1980, 41, 19–29 CrossRef CAS.
- A. Ferrarini, G. R. Luckhurst and P. L. Nordio, Mol. Phys., 1995, 85, 131–143 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00537c |
| This journal is © The Royal Society of Chemistry 2016 |