Collapsing nanoparticle-laden nanotubes
Joseph A.
Napoli
,
Anđela
Šarić
and
Angelo
Cacciuto
*
Department of Chemistry, Columbia University, 3000 Broadway, MC 3123, New York, NY 10027, USA. E-mail: ac2822@columbia.edu
First published on 8th August 2013
Abstract
We show how self-assembly of sticky nanoparticles can drive radial collapse of thin-walled nanotubes. Using numerical simulations, we study the transition as a function of the geometric and elastic parameters of the nanotube and the binding strength of the nanoparticles. We find that it is possible to derive a simple scaling law relating all these parameters, and estimate bounds for the onset conditions leading to the collapse of the nanotube. We also study the reverse process – the nanoparticle release from the folded state – and find that the stability of the collapsed state can be greatly improved by increasing the bending rigidity of the nanotubes. Our results suggest ways to strengthen the mechanical properties of nanotubes, but also indicate that the control of nanoparticle self-assembly on these nanotubes can lead to nanoparticle-laden responsive materials.
I Introduction
Nanotube–nanoparticle composites are currently one of the most promising hybrid materials. Combining the unique properties of these two components can result in exceptional mechanical, electronic and optical properties.1 Efficient protocols for decorating carbon, silica or polymeric nanotubes with a variety of inorganic nanoparticles have opened novel avenues for their application in nanotechnology.2–7 Up-to-date nanoparticle–nanotube composites have successfully been used as chemical- and biosensors,8–10 catalysts and catalyst supports in fuel cells,11–13 high-strength engineering fibers,14,15 as well as components in nanoelectronics,16 photovoltaics17 and neural nets.18 Understanding the interactions between nanoparticles and nanotubes, as well as the structural properties of their assemblies, is essential for the successful design and manipulation of these materials. Here, we consider how the self-assembly of adhering nanoparticles drives a peculiar collapse of nanotubes that has the potential to broaden the application of this class of hybrid materials.Because of their thin walls, nanotubes are quite flexible when subjected to radial deformation, even when their stiffness in the axial direction is extremely high. Consequently, nanotubes are prone to radial buckling. Due to the importance of this transition, a significant body of work has been dedicated to understanding the radial buckling and collapse of nanotubes under point-like mechanical loading or isotropic compressive stresses.19–23 Radial buckling of carbon nanotubes within a carbon nanotube fiber has been shown to improve the mechanical strength of the fiber.14,15 Such a collapse also strongly affects the nanotube's electrical properties, inducing for example their semiconductor–metal transition in single and double walled carbon nanotubes.24–26 Furthermore, the catastrophic collapse of cytoskeletal microtubules under large radial loads has been reported,27 though its biological significance is still unclear. In all cases, the process is characterized as a discontinuous transition that depends only on the nanotube radius and that is often directed by attractions between the opposite walls of the nanotube.
We show, using molecular dynamics simulations, how the collective behavior of nanoparticles assembling on a deformable nanotube can promote this transition, even when the walls of the nanotube are fully noninteracting, and can result in an ordered nanoparticle engulfment inside the collapsed structure. In our simulations the nanotube is modeled in a coarse-grained fashion as a generic elastic tubular surface which, depending on the specific choice of mechanical parameters, can represent a hollow nanotube of a broad range of materials. We study the process for different values of bending stiffness of the nanotube and characterize the dependence of the transition on the ratio of nanotube/nanoparticle radii, the number of nanoparticles, and the strength of the nanoparticle adhesion to the nanotube walls. We demonstrate how the collapse and nanoparticle engulfment can be controlled and reversed by tuning the strength of nanoparticle adhesion, which can be achieved for instance by changing the properties of the medium, suggesting a new class of environment-responsive nanocomposites.
II Methods
We model the nanotube as an elastic membrane of cylindrical shape, using a standard triangulated mesh of hexagonal symmetry.28 Small spherical beads are placed at each node of the membrane in order to impose surface self-avoidance, and any two surface beads interact via a repulsive truncated-shifted Lennard-Jones potential | (1) |
Each bead of the surface is linked to its immediate neighbors via the harmonic spring potential
| Ustretching = Ks(r − rB)2 | (2) |
Keeping Ks constant, we modulate the bending rigidity of the surface according to a dihedral potential between adjacent triangles of the mesh:
Ubending = Kb(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (3) |
The ratio between stretching and bending constants is simply related to the thickness of the material t, Ks/Kb ≃ (1/t)2,29 and in this work we focus on the limiting behavior of nearly unstretchable tubes (σ2Ks/Kb ≥ 102), corresponding to nanotubes with very thin walls. An analogous continuous mechanics descriptions of nanotubes has been shown to be applicable even to study the mechanical properties of carbon nanotubes containing as little as about 10 atoms on the perimeter.19
Nanoparticles of diameter σc = 10σ interact with each other via a purely repulsive truncated-shifted Lennard-Jones potential as described above eqn (1) with σ → σc. A short-ranged Morse potential, acting between the center of the nanoparticles and the centers of the beads describing the nanotube accounts for the generic binding potential between nanoparticles and tube;
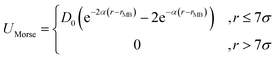 | (4) |
Here, r is the distance between the centers of a nanoparticle and surface bead, rMB = 5.5σ is their contact distance, and D0 is the binding constant. The interaction cutoff is set to 7σ (i.e. 70% of the nanoparticle diameter) and the decay factor to α = 1.25/σ. Typical nanoparticle surface coverage is 0.006–0.016. Simulations were carried out using the LAMMPS molecular dynamics package.30 To avoid boundaries effects, and migration of the particles into the tube, we used periodic boundary conditions in all our simulations, and to prevent stresses on the tube that could be exerted by the boundaries, we adopted an adjustable box size along the tube axial direction x. Stretch-free configurations, are obtained by employing an NPxT ensemble with zero external reduced pressure Px. The timestep was set to dt = 0.002τ0 (τ0 is the dimensionless unit of time). Each simulation was carried out for at least 4 × 106 steps, and the time integration was performed using Langevin dynamics.
We varied the bending rigidity, Kb, the radius of the tube, R, as well as the number of nanoparticles, N, and their adhesion to the nanotube, D0, to characterize how the binding of the particles drives the collapse of the nanotube.
III Results
Nanoparticles exhibit three distinct phases upon adhesion to the surface, as depicted in Fig. 1, depending on the binding constant D0. The first is a gas phase that arises when D0 is insufficient to overcome the resistance to deformation imposed by the bending rigidity and the particles randomly diffuse over the surface (Fig. 1(a)). As D0 is increased, the nanoparticles slightly deform the tube and self-assemble into linear string-like aggregates which are aligned with the cylinder's axis and partially wrapped by the surface, albeit never fully (Fig. 1(b)). This phase is a consequence of the inherent tendency of thin sheets to respond to a deformation by bending uniaxially, the only stretch-free way. Since the stretching rigidity of the surface is much higher than its bending rigidity (the nanotube's walls are very thin), the axial direction is the preferred direction of the deformation and promotes nanoparticle self-assembly into long lines.31–33 However, the range of D0 for which this occurs is relatively narrow, and the phase invariably appears in coexistence with the first gaseous phase, with the majority of the nanoparticles arranging in linear formation and a few diffusing to either side of it. | ||
| Fig. 1 Snapshots of three possible phases upon nanoparticle (orange) adsorption on the nanotube (blue). (a) The random gas state. (b) The axial linear aggregate of nanoparticles. Top panel shows the cross-section when looking down the cylinder axis, the bottom panel shows the view from above. (c) The collapsed state in which a self-assembled linear aggregate of nanoparticles is completely wrapped by the surface of the nanotube. The panels are analogous to those in (b). | ||
As soon as the nanoparticle adhesion or concentration is slightly increased, the linear phase becomes unstable and the third phase (hereafter collapsed) occurs, as shown in Fig. 1(c). This illustrates that in the high-stretching and binding limits, incompletely wrapped axial lines are unstable and as the particles become entirely wrapped by the surface in order to maximize the energy gained by nanoparticle–nanotube binding interactions, the surface collapses to generate a uniform buckle along the axis of the tube. In this configuration, nanoparticles are arranged into strings and are firmly contained within the tubular inner fold. By reversing the transition, for instance by decreasing the nanoparticle binding with changing experimental conditions, a mechanism similar to responsive nanocaging could be achieved.
To characterize the transition from the axial structures to the stable collapsed state, it is insightful to relate the onset value of binding D*0 (i.e. the first value of D0 that is sufficiently large to induce collapse) to the mechanical properties of the surface and the number of nanoparticles in the system. To obtain cleaner results, we initially prepare the nanoparticles in linear formation just above the surface of the tube and oriented parallel to the axis of the cylinder. However, it should be emphasized that the linear configuration is also the lowest-energy configuration, as explained above, and reported in ref. 32. We let the simulation equilibrate and measured the average extent of particle wrapping by the surface, ϕ, as a function of increasingly larger values of D0. Particle wrapping is defined as the total surface area of the nanotube in contact with a nanoparticle, S0, divided by the surface area of a nanoparticle, ϕ = S0/(4πσc2). We consider a bead of the nanotube to be in contact with a nanoparticle when their center-to-center distance is within the cut-off of the Morse potential. Clearly, ϕ = 1 would imply complete wrapping of the nanoparticles. However, because of the large energy costs associated with the stretching energy, this scenario never occurs in our system and the maximum particle wrapping is achieved when a linear aggregate is completely enveloped by the nanotube (as depicted in Fig. 1(c)). This configuration yields typical wrapping values per particle of ϕ ≃ 0.4. To understand the nature of the transition, we also examine the reverse process, i.e. we repeated the simulations for the same set of parameters, but choosing a fully wrapped linear aggregate as an initial configuration and by decreasing D0 until the buckle is released and the cylindrical geometry is restored. This analysis has been repeated for different values of Kb, R, and number of particles, N.
The collapse transition for three bending rigidities is illustrated in Fig. 2, and shows that there is a clear discontinuity in the nanoparticle wrapping parameter above an onset value D*0, corresponding to a first-order transition. Not surprisingly, as Kb increases, D*0 shifts to higher values due to the larger energy needed to deform the surface. Simulations of the reversed process, which started from a wrapped state, show that nanoparticle engulfment can indeed be reversed, with D0 for the nanoparticle release being lower than the onset D*0 needed to promote the collapse. We observe hysteresis broadening for higher values of Kb, indicating a higher energy barrier for the collapse of stiffer nanotubes, but also for the reverse process. This result is important because it suggests a simple way of controlling the stability of the collapsed state against restoring forces.
 | ||
| Fig. 2 From top to bottom, hysteresis plots for Kb = 15 kBT, Kb = 35 kBT, and Kb = 55 kBT, respectively. For each plot, triangles (black) represent the forward direction, where the initial configuration is a line of nanoparticles just above the surface of the cylinder and parallel to its axis, and circles (red) represent simulations where the initial configuration is the fully wrapped linear aggregate (see Fig. 1(c)). The onset value of collapse, D*0, increases with increasing Kb, accompanied by the hysteresis broadening. Here, R = 25.4σ and N = 15. | ||
Our data also reveal that D*0 increases when decreasing the radius of the cylinder or the number of nanoparticles (Fig. 3). In the first case, the nanoparticles need to deform against a larger curvature in order to adhere, resulting in higher values of D*0. This is analogous to the well-known fact that carbon nanotubes of smaller radii are more stable against buckling,21 and it is due to the smaller cost associated to bending deformations of wider tubes. Additionally, since the collapse transition is a consequence of a collective behavior of nanoparticles, at lower nanoparticle densities the surface is deformed to a lesser extent resulting in greater D*0.
 | ||
| Fig. 3 (Color online) Top panel: The onset value of collapse, D*0, increases as the nanotube radius R decreases because the nanoparticles need to deform against the larger curvature. Kb = 35 kBT and N = 15 are kept constant. Bottom panel: D*0 increases as the number of nanoparticles N decreases due to lesser collective deformation by the particles. Kb = 35 kBT and R = 25.4σ are kept constant. | ||
Our findings suggest a general scaling law relating D*0 to the mechanical and geometric properties of the surface, and the number of adhering nanoparticles. A good place to start are the scaling laws for the deformation of thin elastic sheets. Following Witten et al.,34 when a thin sheet of a thickness t, width w, and mechanical parameters Kb and Ks, is subject to a deformation of amplitude h, the associated bending and stretching energies scale as Eb ≃ Kb (h/w2)2wlp and Es ≃ Ks(h2/lp2)2wlp, where lp is the extent of the axial deformation. Minimizing the sum of the bending and stretching energies contributions with respect to lp gives lp ≃ wh1/2(Ks/Kb)1/4 = w(h/t)1/2, a well known expression for the persistence length of a point-like deformation. This result can be generalized to a cylindrical surface of radius R when h ≪ R – which is the relevant case to study the onset of the collapsing transition – and one recovers the large deformation limit lp ≃ R(R/t)1/2 by setting w and h equal to R.27,35
A single particle adhering to an elastic surface imprints a deformation whose shape can be approximated by that of a spherical cap of a height h and radius σc. Binding energy is then Ebind ≃ −πD0hσc/σ2, where πhσc/σ2 accounts for the degree of wrapping of the nanoparticle, i.e. the number of membrane beads it is in contact with. As the depth of the deformation, h, is now controlled by the binding constant D0, we can perform the same minimization described above with the additional energy contribution due to the biding energy, and obtain an expression for the equilibrium value of h, namely
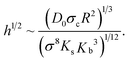 | (5) |
The expression for the extent of the deformation along the axis of the cylinder, lp, upon binding of one nanoparticle, can then be re-written as
 | (6) |
In the case of a single indentation, a necessary condition for the buckling transition to span the entire axis of the cylinder thus leading to the collapse is that lp > L, where L is the length of the cylinder. Whenever lp < L uniform axial buckling does not occur and a local transversal deformation involving the formation of two stress points does instead take place as shown in Fig. 4(a).
 | ||
| Fig. 4 (a) Transversal bucking caused by a large single point deformation. In this case lp < L, and the side rings indicate the location of the transversal stress focus points. (b) Uniform axial buckling and nanotube radial collapse induced by four equidistant localized deformations such that 4lp > L. | ||
These arguments suggest that the collapse of an elastic tube indented by N equidistant and well spaced binding particles can occur whenever L* ≡ Nlp ≥ L, i.e. when the persistence lengths from each independent deformation couple and span the length of the cylinder (see Fig. 4(b) for an illustration). Our system is a bit different from the case discussed above, in fact, in the linear aggregates self-assembled in our study – precursors configuration for tube collapse – particles are in contact with each other, and typically lp ≫ σc, suggesting that a more appropriate measure for the extent of the total longitudinal deformation is L* = Nσc + lp. Imposing that the correlation of the axial deformations between the particles extends beyond the length of the tube, L* ≥ L, leads to a scaling law for D*0
 | (7) |
It should be stressed that in this formula, N is not the total number of particles in the system, but the length of the aggregate driving the collapse transition. To test this scaling ideas, we inserted data from all our simulations for various values of D0, Kb, R and N into a single scatter plot, which has the right-hand side expression of eqn (7) on the y-axis, and the binding constant D0 on the x-axis, as shown in Fig. 5. The points are marked as “collapsed” and “not collapsed”, according to the final state of the simulation. There appears a distinct division between data corresponding to the collapsed state and those that do not, verifying the validity of the scaling law given in eqn (7). We expect deviations to this scaling law when the diameter of the tube becomes comparable to that of the particles, as in this case a more accurate estimate of the elastic energies of the nanotube would be required to better take into account its global deformation.
 | ||
| Fig. 5 Testing the scaling law presented in eqn (7): scatter plot of all simulation data. The right-hand side of eqn (7) is plotted on the y-axis versus D0 from the simulations. Open squares represent simulations which did not induce a collapsed state, while filled squares represent simulations which have ended in a collapsed state. In both cases the initial state was a non-collapsed linear aggregate prepared above the surface of the nanotube containing N particles. The straight line is provided as a guide to the eye to emphasize the clear division between the data. | ||
In conclusion, we have studied a system of nanoparticles adhering to an elastic unstretchable nanotube. We have shown how the nanoparticles self-assemble into a linear aggregate which promotes the collapse transition of the nanotube, resulting in nanoparticle entrapment. The collapse is easier if the nanotube radius or the nanoparticle concentration are increased, and the bending rigidity (the material thickness) is decreased. Using the elasticity theory for thin sheets we establish a scaling law linking the onset of binding energy to the collapsing transition in terms of the elastic and geometric properties of the tube. Finally we show how the process can be reversed and how its hysteretic cycle widens with the bending rigidity of the tube. We suggest that this feature can be exploited to design particle nanotraps, but also as a way to enhance the mechanical strength of nanoparticle–nanotube composites, in addition to altering their electric and optical properties. Clearly the release (un-buckling) transition can be further stabilized by adding a weak attraction between the layers of the nanotube. Unfortunately our scaling theory is not sufficient to fully describe the stability and nature of the collapsing transition as a function of the bending rigidity, in particular the hysteresis broadening observed for higher values of Kb, and a more sophisticated description of the overall shape profile (beyond a simple scaling formulation) of the surface, as already established in studies of fluid surfaces, is required to capture this phenomenology.36
It should be stressed that the results presented in this paper are expected to hold as long as (and only as long as) a description of the nanotube in terms of a continuous elastic medium is reasonable. Under such circumstances, it is possible to just plug the effective bending and stretching rigidities together with the geometric parameters of the tube of the desired material to obtain an estimate of whether a nanotube would collapse in the presence of nanoparticles.
Although elastic representations have been put forward for carbon nanotubes (CNTs), it is fair to say that some problems still exist in consistently defining a relation between a stretching and bending rigidities in terms of the material Young modulus and CNT thickness.37 Furthermore, CNTs also have layer-to-layer attractions, which has been observed to lead to spontaneous (fluctuation-driven) collapse of the nanotubes when the radius is sufficiently large.38 Nevertheless, it is instructive to make some estimates using our scaling hypothesis for this important material. Let us consider a buckyball of diameter σc ≃ 1 nm adsorbing on a CNT of radius R = 10 nm. Experimental estimates for the stretching and bending constants37 are of the order of Ks = Yh ∼ 3 × 105 pN nm−1 and Kb ∼ 200 pN nm. Assuming binding energies between the buckyball and the outer surface of the CNT to be roughly 80 pN nm,39 this would lead to an axial deformation length per buckyball of lp ∼ 70–80 nm, which suggest indeed a rather long-range effect, with ∼10–20 equally-spaced nanoparticles capable of collapsing a 1 μm tube.
Finally, our work focused primarily on the low particle density limit, it would nevertheless, be interesting to generalize our scaling laws for buckling in the presence of multiple linear aggregates (in the large particle coverage limit) and to understand how the presence of one axial collapse may influence the occurrence of further collapse of the nanotube. We expect this effect to be important when σc ∼ 2R. We hope that our research will stimulate experimental investigations of the nanoparticle-induced collapse of nanotubes as well as its application in nanotechnology.
Acknowledgements
This work was supported by the National Science Foundation under Career Grant no. DMR-0846426.References
- X. Peng, J. Chen, J. A. Misewich and S. S. Wong, Carbon nanotube–nanocrystal heterostructures, Chem. Soc. Rev., 2009, 38, 1076–1098 RSC.
- M. Ding, D. C. Sorescu, G. P. Kotchey and A. Star, Welding of gold nanoparticles on graphitic templates for chemical sensing, J. Am. Chem. Soc., 2012, 134(7), 3472–3479 CrossRef CAS.
- R. Y. Zhang, M. Hummelgård and H. Olin, Simple and efficient gold nanoparticles deposition on carbon nanotubes with controllable particle sizes, Mater. Sci. Eng., B, 2009, 158, 4852 CrossRef.
- G. A. Rance, D. H. Marsh, S. J. Bourne, T. J. Reade and A. N. Khlobystov, van der Waals Interactions Between Nanotubes and Nanoparticles for Controlled Assembly of Composite Nanostructures, ACS Nano, 2010, 4(8), 49204928 CrossRef.
- H. Yang, M. Li, L. Fu, A. Tang and S. Mann, Controlled assembly of SbS nanoparticles on silica/polymer nanotubes: insights into the nature of hybrid interfaces, Sci. Rep., 2013, 3, 1336 CAS.
- X. Li, Y. Qin, S. T. Picraux and Z.-X. Guo, Noncovalent assembly of carbon nanotube-inorganic hybrids, J. Mater. Chem., 2011, 21, 7527–7547 RSC.
- A. La Torre, G. A. Rance, J. El Harfi, J. Li, D. J. Irvine, P. D. Brown and A. N. Khlobystov, Transport and encapsulation of gold nanoparticles in carbon nanotubes, Nanoscale, 2010, 2, 1006–1010 RSC.
- Q. Zhao, Z. H. Gan and Q. K. Zhuang, Electrochemical Sensors Based on Carbon Nanotubes, Electroanalysis, 2002, 14, 1609–1613 CrossRef CAS.
- L. C. Jiang and W. D. Zhang, A highly sensitive nonenzymatic glucose sensor based on CuO nanoparticles-modified carbon nanotube electrode, Biosens. Bioelectron., 2010, 25(6), 1402–1407 CrossRef CAS.
- Y. Yu, A. Cimeno, Y. C. Lan, J. Rybczynski, D. Z. Wang, T. Paudel, Z. F. Ren, D. J. Wagner, M. Q. Qiu, T. C. Chiles and D. Cai, Assembly of multi-functional nanocomponents on periodic nanotube array for biosensors, Micro Nano Lett., 2009, 4(1), 27–33 CAS.
- V. Lordi, N. Yao and J. Wei, Method for Supporting Platinum on Single-Walled Carbon Nanotubes for a Selective Hydrogenation Catalyst, Chem. Mater., 2001, 13(3), 733737 CrossRef.
- X. Peng and S. S. Wong, Controlling Nanocrystal Density and Location on Carbon Nanotube Templates, Chem. Mater., 2009, 21(4), 682694 CrossRef.
- C. Wang, M. Waje, X. Wang, J. M. Tang, R. C. Haddon and Y. S. Yan, Proton Exchange Membrane Fuel Cells with Carbon Nanotube Based Electrodes, Nano Lett., 2004, 4(2), 345–348 CrossRef CAS.
- K. Koziol, J. Vilatela, A. Moisala, M. Motta, P. Cunniff, M. Sennett and A. Windle, High-Performance Carbon Nanotube Fiber, Science, 2007, 318, 1892–1895 CrossRef CAS.
- J. N. Zhao, X. H. Zhang, J. T. Di, G. Xu, X. J. Yang, X. Y. Liu, Z. Z. Yong, M. H. Chen and Q. W. Li, Double-peak mechanical properties of carbon-nanotube fibers, Small, 2010, 6(22), 2612–2617 CrossRef CAS.
- Z. Shi, C. Liu, W. Lv, H. Shen, D. Wang, L. Chen, L. S. Li and J. Jin, Free-standing single-walled carbon nanotubeCdSe quantum dots hybrid ultrathin films for flexible optoelectronic conversion devices, Nanoscale, 2012, 4, 4515–4521 RSC.
- P. R. Somani, S. P. Somani and M. Umeno, Application of metal nanoparticles decorated carbon nanotubes in photovoltaics, Appl. Phys. Lett., 2008, 93, 033315 CrossRef.
- D. H. Marsh, G. A. Rance, R. J. Whitby, F. Guistiniano and A. N. Khlobystov, Assembly, structure and electrical conductance of carbon nanotubegold nanoparticle 2D heterostructures, J. Mater. Chem., 2008, 18, 22492256 RSC.
- J. Zang, A. Treibergs, Y. Han and F. Liu, Geometric Constant Defining Shape Transitions of Carbon Nanotubes under Pressure, Phys. Rev. Lett., 2004, 92, 105501 CrossRef.
- S. L. Zhang, R. Khare, T. Belytschko, K. J. Hsia, S. L. Mielke and G. C. Schatz, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 075423 CrossRef.
- J. A. Elliott, J. K. W. Sandler, A. H. Windle, R. J. Young and M. S. P. Shaffer, Collapse of Single-Wall Carbon Nanotubes is Diameter Dependent, Phys. Rev. Lett., 2004, 92, 095501 CrossRef.
- T. Tang, A. Jagota, C.-Y. Hui and N. J. Glassmaker, Collapse of single-walled carbon nanotubes, J. Appl. Phys., 2005, 97, 074310 CrossRef.
- W. Lu and T.-W. Chou, Radial deformation and its related energy variations of single-walled carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134113 CrossRef.
- C. J. Park, Y. H. Kim and K. J. Chang, Band-gap modification by radial deformation in carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 10656 CrossRef CAS.
- A. P. M. Barboza, A. P. Gomes, B. S. Archanjo, P. T. Araujo, A. Jorio, A. S. Ferlauto, M. S. C. Mazzoni, H. Chacham and B. R. A. Neves, Deformation Induced Semiconductor-Metal Transition in Single Wall Carbon Nanotubes Probed by Electric Force Microscopy, Phys. Rev. Lett., 2008, 100, 256804 CrossRef CAS.
- C. E. Giusca, Y. Tison and S. R. Silva, Evidence for metal-semiconductor transitions in twisted and collapsed double-walled carbon nanotubes by scanning tunneling microscopy, Nano Lett., 2008, 8, 3350–3356 CrossRef CAS.
- P. J. de Pablo, I. A. T. Schaap, F. C. MacKintosh and C. F. Schmidt, Deformation and Collapse of Microtubules on the Nanometer Scale, Phys. Rev. Lett., 2003, 91(9), 098101 CrossRef CAS.
- Y. Kantor and D. R. Nelson, Crumpling transition in polymerized membranes, Phys. Rev. Lett., 1987, 58, 2774 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Pergamon, New York, 1970 Search PubMed.
- S. J. Plimpton, Fast Parallel Algorithms for Short Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- A. Šarić and A. Cacciuto, Soft elastic surfaces as a platform for particle self-assembly, Soft Matter, 2011, 7, 8324–8329 RSC.
- A. Šarić, J. C. Pàmies and A. Cacciuto, Effective Elasticity of a Flexible Filament Bound to a Deformable Cylindrical Surface, Phys. Rev. Lett., 2010, 104, 226101 CrossRef.
- J. C. Pàmies and A. Cacciuto, Reshaping Elastic Nanotubes via Self-Assembly of Surface-Adhesive Nanoparticles, Phys. Rev. Lett., 2011, 106, 045702 CrossRef.
- T. A. Witten, Rev. Mod. Phys., 2007, 79, 643–675 CrossRef.
- L. Mahadevan, A. Vaziri and M. Das, Persistence of a pinch in a pipe, Europhys. Lett., 2007, 77, 40003 CrossRef.
- J. Z. Y. Chen and S. Mkrtchyan, Adhesion between a rigid cylindrical particle and a soft fluid membrane tube, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041906 CrossRef.
- Y. Huang, J. Wu and K. C. Hwang, Thickness of graphene and single-wall carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245413 CrossRef.
- N. G. Chopra, L. X. Benedict, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Fully collapsed carbon nanotubes, Nature, 1995, 377, 135 CrossRef CAS.
- L. A. Girifalco, M. Hodak and R. S. Lee, Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 62, 13104 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |
